15 均值的估计
零均值的AR, MA, ARMA模型的参数可以由自协方差函数唯一确定。 有了样本之后,可以先估计均值和自协方差函数, 然后由均值和自协方差函数解出模型参数。 均值和自协方差可以用矩估计法求。 还要考虑相合性、渐近分布、收敛速度等问题。
设\(x_1,x_2,\dots,x_N\)是平稳列\(\{X_t\}\)的观测。 \(\mu=E X_t\)的点估计为 \[\begin{align} \hat \mu = \bar x_N = \frac{1}{N} \sum_{k=1}^N x_k \tag{15.1} \end{align}\] 把观测样本看成随机样本时记做大写的 \(X_1,X_2,\dots,X_N\)。
15.1 相合性
设统计量 \(\hat \theta_N\)
是 \(\theta\) 的估计. 在统计学中有如下的定义
- 如果 \(E\hat\theta_N = \theta\), 则称\(\hat \theta_N\) 是 \(\theta\) 的无偏估计.
- 如果当\(N\to \infty\), \(E\hat \theta_N \to \theta\), 则称\(\hat \theta_N\) 是 \(\theta\) 的渐近无偏估计.
- 如果 \(\hat \theta_N\) 依概率收敛到 \(\theta\), 则称 \(\hat \theta_N\) 是 \(\theta\) 的相合估计.
- 如果 \(\hat \theta_N\) a.s.收敛到 \(\theta\), 则称 \(\hat \theta_N\) 是 \(\theta\) 的强相合估计.
一般情况下, 无偏估计比有偏估计来得好. 对于由 (15.1)定义的\(\bar X_N\), 有 \[ E\bar X_N = \frac1N \sum_{k=1}^N E X_k = \frac1N \sum_{k=1}^N \mu = \mu. \] 所以, \(\bar X_N\) 是均值\(\mu\) 的无偏估计.
好的估计量起码应当是相合的. 否则, 估计量不收敛到要估计的参数, 它无助于实际问题的解决. 对于平稳序列\(\{X_t\}\), 如果它的自协方差函数 \(\{\gamma_k\}\)收敛到零, 则 \[\begin{align} &E(\bar X_N - \mu)^2 = E\Big [\frac1N \sum_{k=1}^N (X_k - \mu)\Big ]^2 \\ =& \frac1{N^2} E[\sum_{j=1}^N \sum_{k=1}^N (X_k-\mu)(X_j -\mu)] = \frac1{N^2} \sum_{j=1}^N\sum_{k=1}^N \gamma_{k-j} \\ =& \frac1{N^2} \sum_{j=1}^N\sum_{m=1-j}^{N-j} \gamma_{m} \quad (\text{令} m=k-j) \\ =& \frac1{N^2} \sum_{m=-N+1}^{N-1} \sum_{j=\max(1-m, 1)}^{\min(N-m, N)} \gamma_m = \frac1{N^2} \sum_{m=-N+1}^{N-1}(N-|m|) \gamma_{m} \\ \leq & \frac1N\sum_{m=-N}^{N} |\gamma_m| \to 0, \quad \text{当} N \to \infty. \tag{15.2} \end{align}\] 即 \(\bar X_N\) 均方收敛到 \(\mu\). 证明用到: 数列趋于零其平均值也趋于零, 见B.1(Stolz定理的推论)。
利用切比雪夫不等式 \[ \Pr(|\bar X_N - \mu |\geq \delta ) \leq \frac{E(\bar X_N-\mu)^2}{\delta^2} \to 0, \quad (\delta >0) \] 得到 \(\bar X_N\) 依概率收敛到 \(\mu\). 于是\(\bar X_N\)是\(\mu\)的相合估计.
定理15.1 设平稳序列\(\{X_t\}\)有均值\(\mu\)和自协方差函数\(\{\gamma_k\}\), 则
- \(\bar X_N\)是 \(\mu\) 的无偏估计.
- 如果 \(\gamma_k \to 0\), 则 \(\bar X_N\) 是 \(\mu\)的相合估计.
- 如果\(\{X_t\}\)还是严平稳遍历序列, 则 \(\bar X_N\)是\(\mu\)的强相合估计.
任何强相合估计一定是相合估计.
由第2章定理2.3可知线性平稳列的自协方差趋于零, 于是由上述定理可知线性平稳列的均值估计是相合估计。
ARMA序列是线性平稳列,所以其均值估计是相合估计。
15.2 中心极限定理
若\(X_1,X_2,\dots,X_N\) iid \(\sim(\mu, \sigma^2)\), 则\(\sqrt{N}(\bar X_N - \mu) \stackrel{\text{d}}{\to} \text{N}(0,\sigma^2)\). 可以据此计算\(\mu\)的\(95\%\)置信区间。 \[\begin{align} [\bar X_N - 1.96 \sigma/\sqrt{N},\ \bar X_N + 1.96 \sigma/\sqrt{N} ]. \tag{15.3} \end{align}\] 其中的1.96也经常用2近似代替。
定理15.2 设\(\{\varepsilon_t\}\)是独立同分布的\(\text{WN}(0,\sigma^2)\). 线性平稳序列\(\{X_t\}\)由 \[\begin{align} X_t = \mu+ \sum_{k=-\infty}^{\infty} \psi_k\varepsilon_{t-k}, \quad t\in \mathbb Z, \tag{15.4} \end{align}\] 定义, 其中\(\{\psi_k\}\)平方可和. 如果\(\{X_t\}\)的谱密度 \[\begin{align} f(\lambda)= \frac{\sigma^2}{2\pi} \left|\sum_{k=-\infty}^{\infty} \psi_k e^{-ik\lambda}\right|^2 \tag{15.5} \end{align}\] 在\(\lambda=0\)连续, 并且\(f(0)\neq 0\), 则当\(N\to \infty\)时, \[\begin{aligned} \sqrt{N}(\bar X_N - \mu) \stackrel{\text{d}}{\to} \text{N}(0,2\pi f(0)) \end{aligned}\]
证明出自Hall, P. and Heyde C.C.(1980), Martingale Limit Theory and Its Applications, Academic Press, 推论5.2。
当\(\{\psi_k\}\)绝对可和时, \(f(\lambda)\)的傅里叶级数表示是绝对一致收敛的, 这时\(f(\lambda)\)连续.
推论15.1 在定理15.2条件下, 如果 \(\sum_{k=-\infty}^{\infty} |\psi_k|<\infty\) 和 \(\sum_{k=-\infty}^{\infty} \psi_k \neq 0\) 成立 , 则当\(N\to \infty\)时 \[\begin{aligned} \sqrt{N}(\bar X_N - \mu) \stackrel{\text{d}}{\to} \text{N}(0,2\pi f(0)) \end{aligned}\] 并且 \[\begin{align} 2\pi f(0) = \gamma_0 + 2\sum_{j=1}^\infty \gamma_j. \tag{15.6} \end{align}\]
中心极限定理成立时可以构造\(\mu\)的渐近置信区间或对\(\mu\)作假设检验。
15.3 收敛速度
相合的估计量的渐近性质除了是否服从中心极限定理外, 还包括这个估计量的收敛速度. 收敛速度的描述方法之一是所谓的重对数律. 重对数律成立时, 得到的收敛速度的阶数一般是 \[ O \left( \sqrt{\frac{2\ln \ln N }{N}}\right). \] 除了个别的情况, 这个阶数一般不能再被改进.
定理15.3 设\(\{\varepsilon_t\}\)是独立同分布的\(\text{WN}(0,\sigma^2)\), 线性平稳序列\(\{X_t\}\)由(15.4)定义, 谱密度 \(f(0)\neq 0\). 当以下的条件之一成立时:
- 当\(k\to \pm \infty\), \(\psi_{|k|}\) 以负指数阶收敛于 0;
- 谱密度\(f(\lambda)\)在\(\lambda=0\)连续, 并且 \(E|\varepsilon_t|^r < \infty\) 对某个 \(r>2\) 成立,
则有重对数律 \[\begin{align} \limsup_{N\to \infty} \sqrt{\frac{N}{2\ln \ln N} } (\bar X_N -\mu) =& \sqrt{2\pi f(0)}, \ \ \text{a.s.} \tag{15.7} \\ \liminf_{N\to \infty} \sqrt{\frac{N}{2\ln \ln N} } (\bar X_N -\mu) =& -\sqrt{2\pi f(0)}, \ \ \text{a.s.} \tag{15.8} \end{align}\]
易见重对数率满足时 \((\bar X_n - \mu) \cdot o(1) = o(\sqrt{\frac{\ln\ln N}{N}})\), \(\sqrt{\frac{N}{2\ln \ln N} } (\bar X_n - \mu) / o(1)\)不收敛。
15.4 \(\bar X_N\)的模拟计算
令 \[\begin{aligned} A(z) = (1 - \rho e^{i\theta} \cdot z)(1 - \rho e^{-i\theta} \cdot z) \end{aligned}\] 考虑AR(2)模型 \[\begin{aligned} A(\mathscr B) X_t =& \varepsilon_t \\ X_t =& 2\rho\cos\theta X_{t-1} - \rho^2 X_{t-2} + \varepsilon_t \end{aligned}\] 为模拟方便设\(\{\varepsilon_t\}\) iid \(\sim\) N(\(0,\sigma^2\))。
\[\begin{aligned} \bar x_N = \frac{1}{N} \sum_{t=1}^N x_t, \quad \bar \varepsilon_N = \frac{1}{N} \sum_{t=1}^N \varepsilon_t \end{aligned}\]
模型方程两边求平均 \[\begin{aligned} \bar x_N =& 2\rho\cos\theta \frac{1}{N} \sum_{k=0}^{N-1} x_k - \rho^2 \frac{1}{N} \sum_{k=-1}^{N-2} x_k + \bar\varepsilon_N \\ =& 2\rho\cos\theta \bar X_N - \rho^2 \bar X_N + \bar\varepsilon_N \\ & + 2\rho\cos\theta\frac{1}{N}(x_0 - x_N) - \rho^2 \frac{1}{N}(x_{-1} + x_0 - x_{N-1} - x_{N-2}) \\ \approx& 2\rho\cos\theta \bar X_N - \rho^2 \bar X_N + \bar\varepsilon_N \\ \bar x_N \approx& \frac{1}{A(1)}\bar\varepsilon_N = \frac{1}{1 - 2\rho\cos\theta + \rho^2} \bar\varepsilon_N \end{aligned}\] \(N\)较大时\(\bar x_N\)和\(\bar\varepsilon_t\)成正比。
为了观察\(N\to\infty\)时\(\bar x_N\)的收敛可以模拟\(L\) 个值然后观察\(\bar x_N, N=n_0, n_0+1, \dots, L\)的变化。
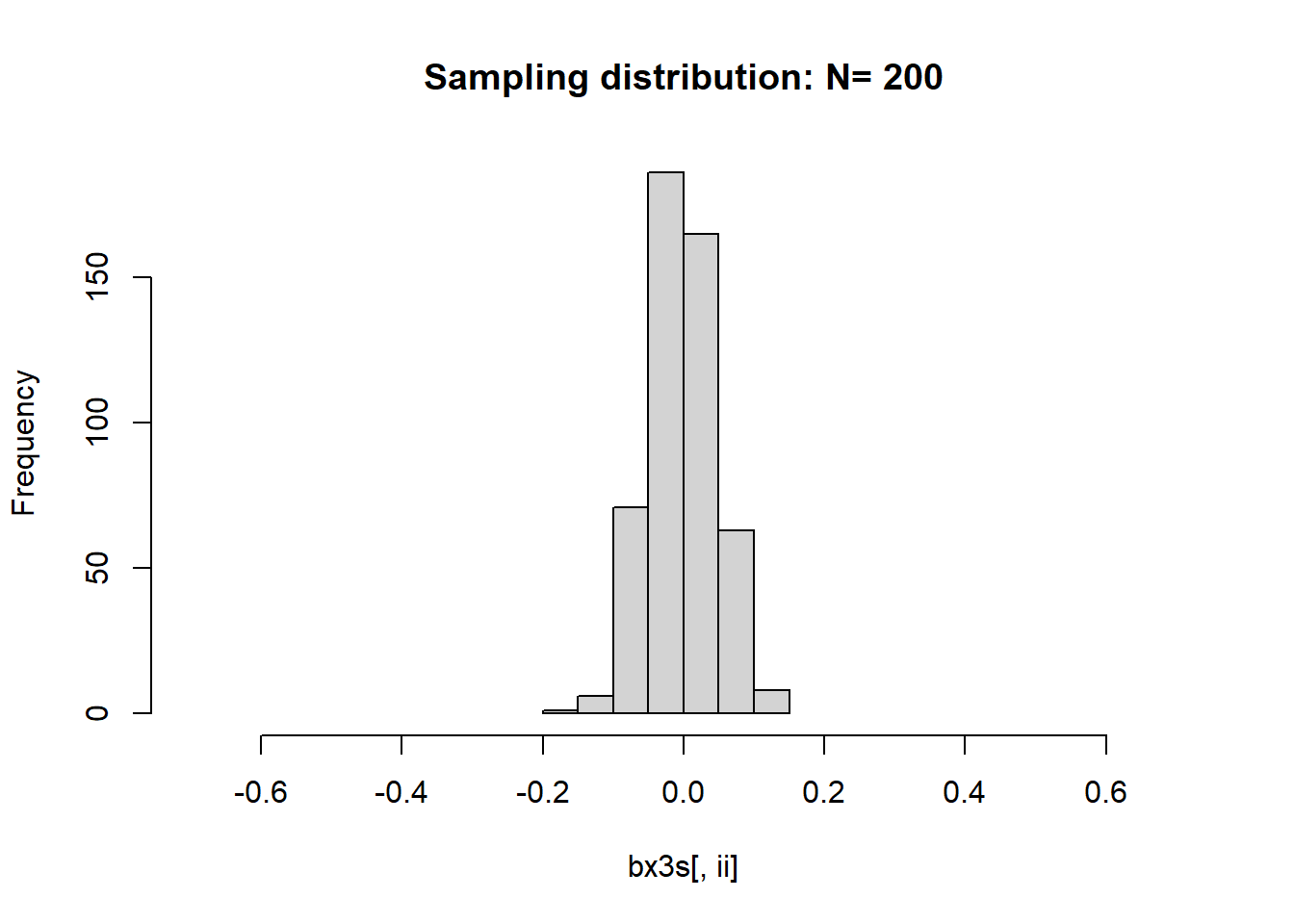
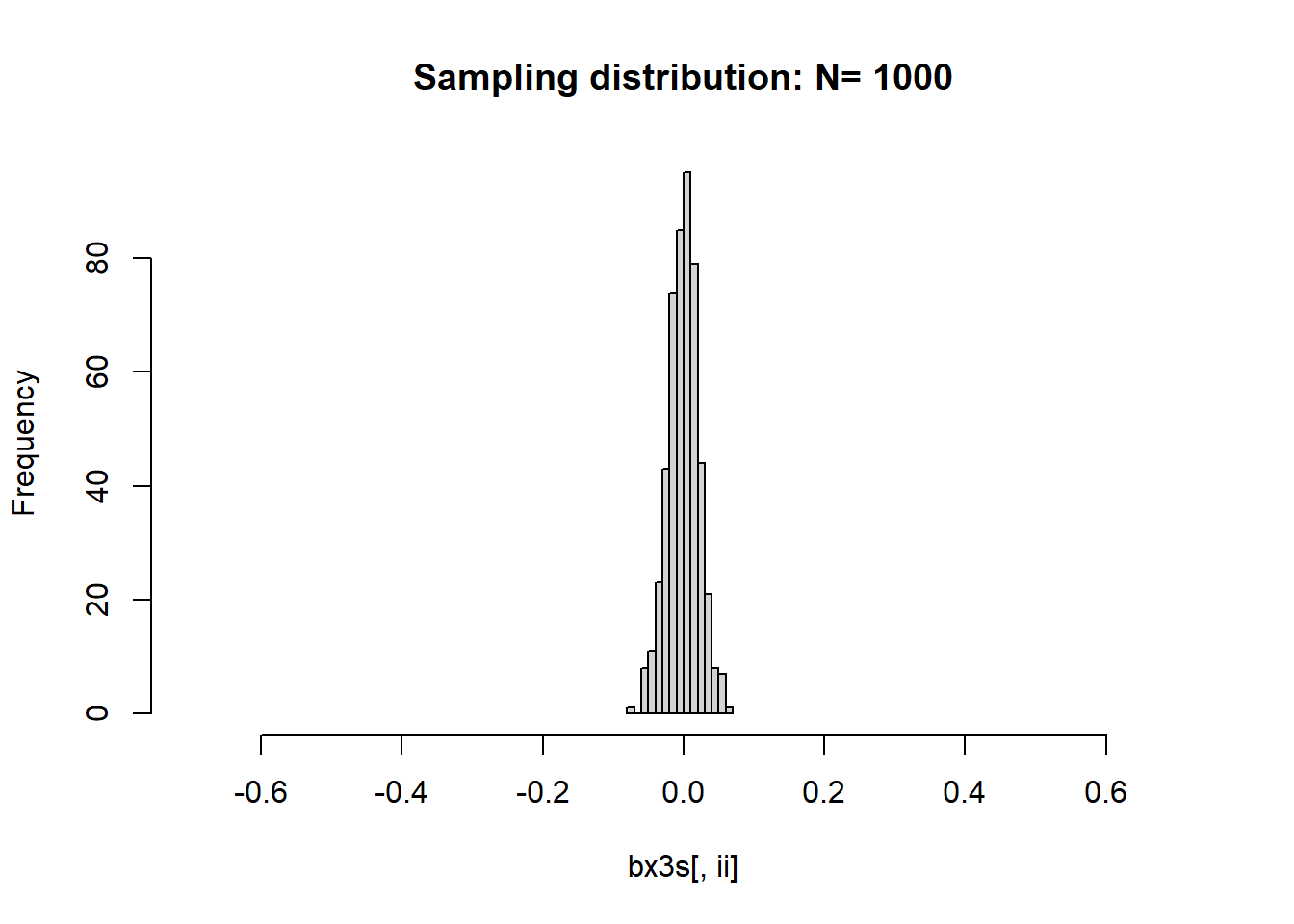
为了研究固定\(N\)情况下\(\bar X_N\)的精度以至于抽样分布, 可以进行\(M\)次独立的随机模拟, 得到\(M\)个\(\bar X_N\)的观测值。 这种方法对于难以得到估计量的理论分布的情况是很有用的。
下面是具体的模拟程序和结果。 模拟生成AR(2)序列。
下面的函数针对变化的样本量\(n\)比较\(\bar X_n\)与\(\bar\varepsilon_n\)的估计, 作\(\bar X_n\)与\(\bar\varepsilon_n\)对\(n\)的曲线图。
estmean.plot <- function(x, eps, subt=""){
barx <- cumsum(x)/seq(L)
bareps <- cumsum(eps)/seq(L)
yr <- range(c(barx, bareps+0.1))
plot(bareps+0.1, type="l",
col="red",
ylim=c(-0.3, 0.3),
main=paste("Effect of sample size N",
subt, sep="\n"),
xlab="N", ylab="Avgs")
lines(barx)
abline(h=c(0, 0.1))
legend(0.7*L, 0.3, lty=c(1,1),
col=c("black","red"),
legend=c("AR(2)", "WN"))
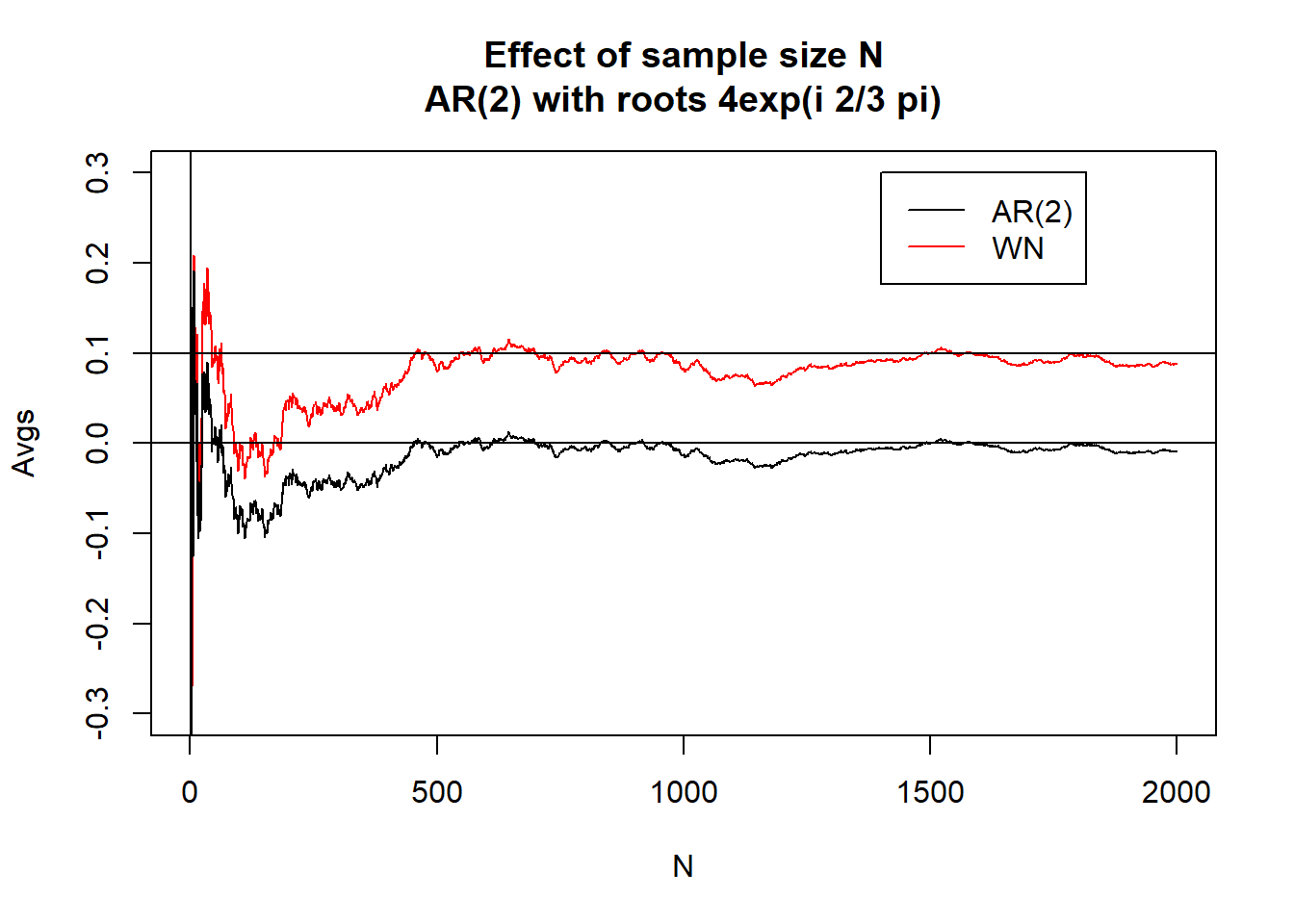
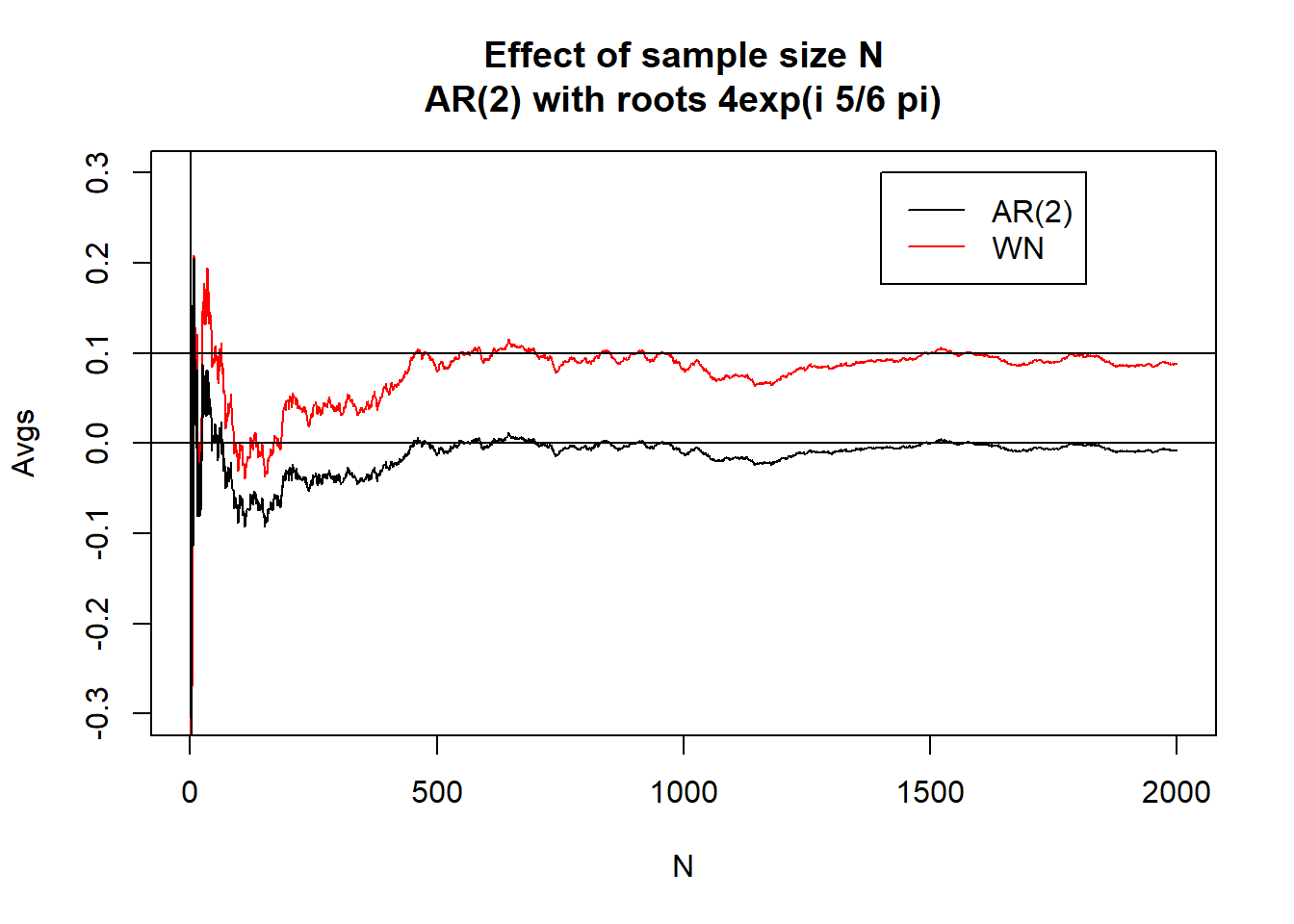
}生成4个不同的AR(2)模型的数据,最大长度\(L=2000\), 比较不同样本量时均值\(\bar X_n\)与\(\bar\varepsilon_n\), 作图时对\(\bar\varepsilon_n\)加了0.1。 四个AR(2)模型的特征根分别为: \[ 1.1 e^{i \frac{2\pi}{3}}, 4.0 e^{i \frac{2\pi}{3}}, 4.0 e^{i \frac{5\pi}{6}}, 1.5 e^{i \frac{\pi}{6}} \]
## 特征根的倒数
roots <- complex(mod=c(1/1.1, 1/4, 1/4, 1/1.5),
arg=c(pi*2/3, pi*2/3, pi*5/6, pi/6))
## 各AR(2)模型的$a_1$和$a_2$系数
coefs <- cbind(2*Re(roots), -Mod(roots)^2)
## $\bar X_n$与$\bar\varepsilon_n$的比值倍数
multi <- apply(coefs, 1, function(a) 1/(1 - a[1] - a[2]))
cat("Magnification of bar X to bar eps:\n", round(multi, 2), "\n")## Magnification of bar X to bar eps:
## 0.37 0.76 0.67 3.45L <- 2000
sigma <- 1
n0 <- 200
n2 <- n0 + L
eps <- rnorm(n2, 0, sigma)
xx <- filter(eps, coefs[1,,drop=T], method="recursive", side=1)
x1 <- xx[(n0+1):n2]
xx <- filter(eps, coefs[2,,drop=T], method="recursive", side=1)
x2 <- xx[(n0+1):n2]
xx <- filter(eps, coefs[3,,drop=T], method="recursive", side=1)
x3 <- xx[(n0+1):n2]
xx <- filter(eps, coefs[4,,drop=T], method="recursive", side=1)
x4 <- xx[(n0+1):n2]
estmean.plot(x1, eps[(n0+1):n2], subt="AR(2) with roots 1.1exp(i 2/3 pi)")

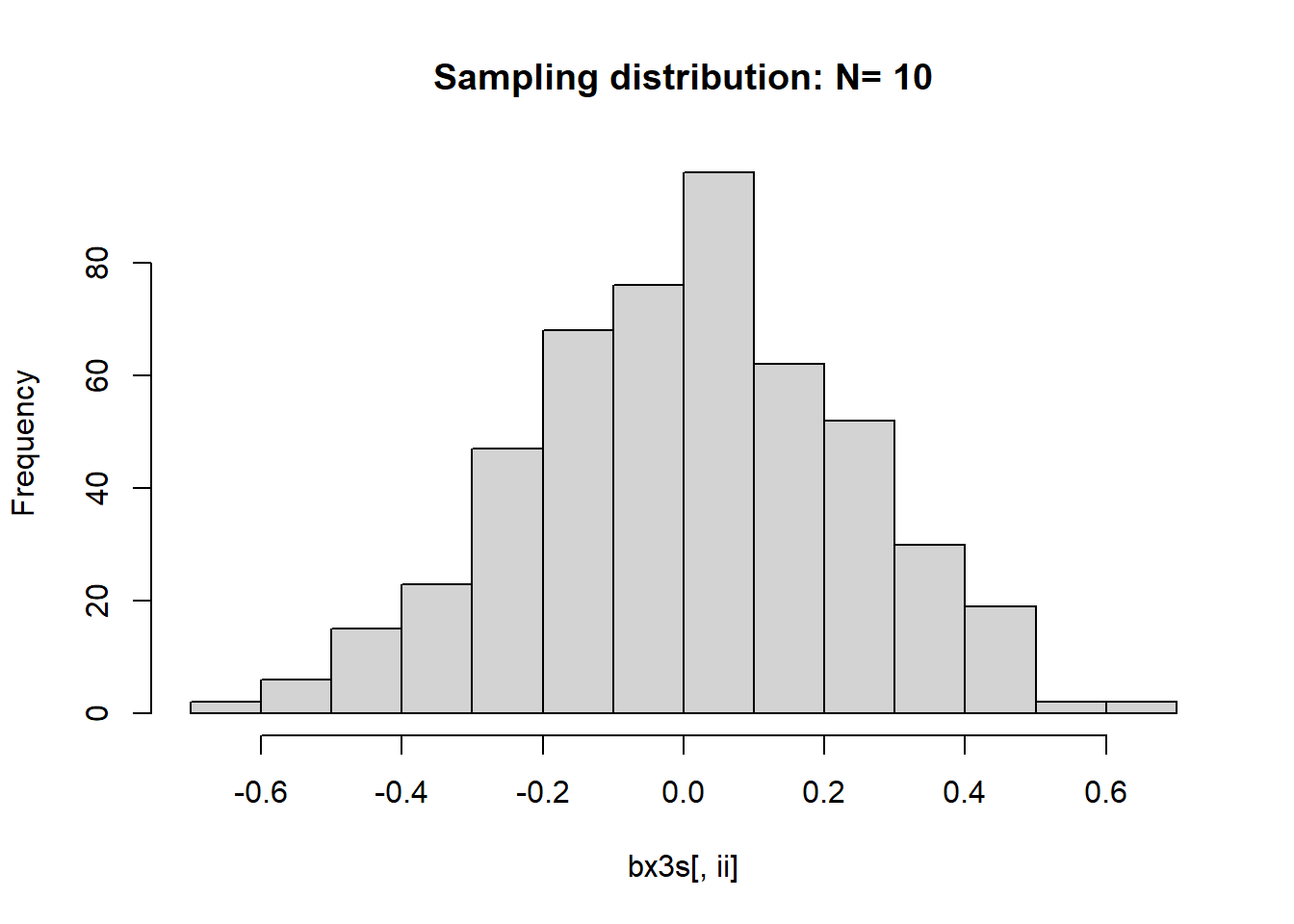
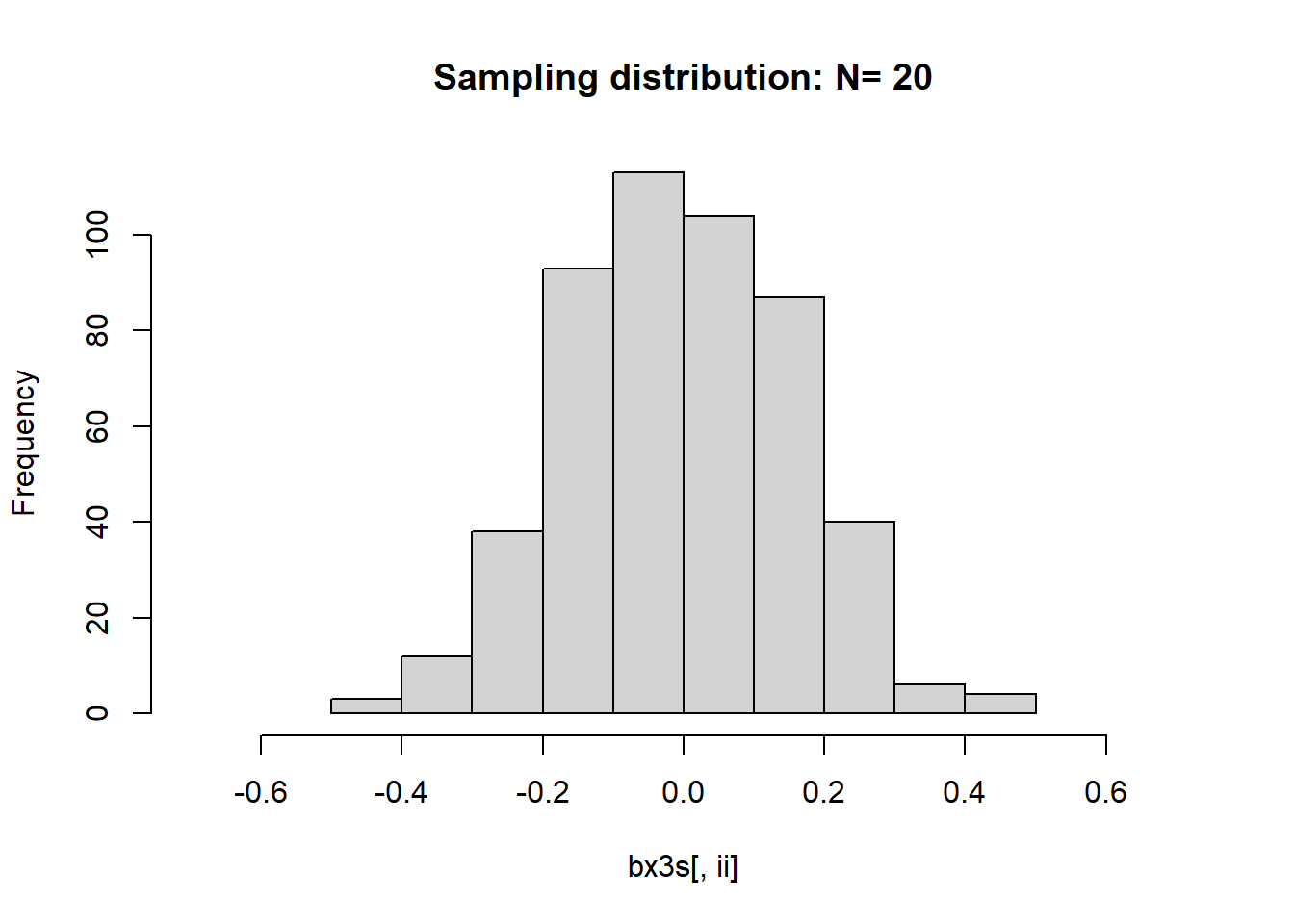
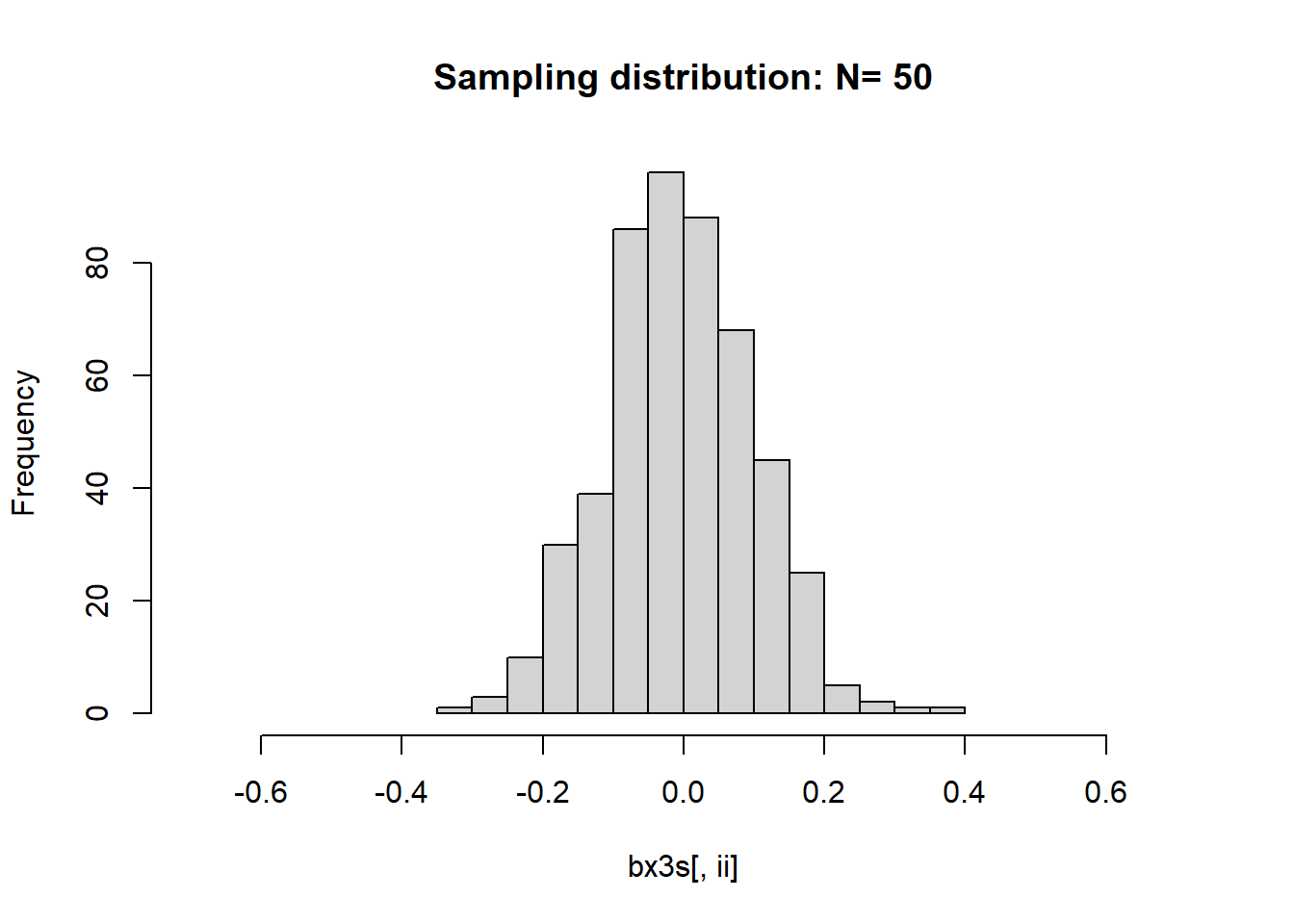
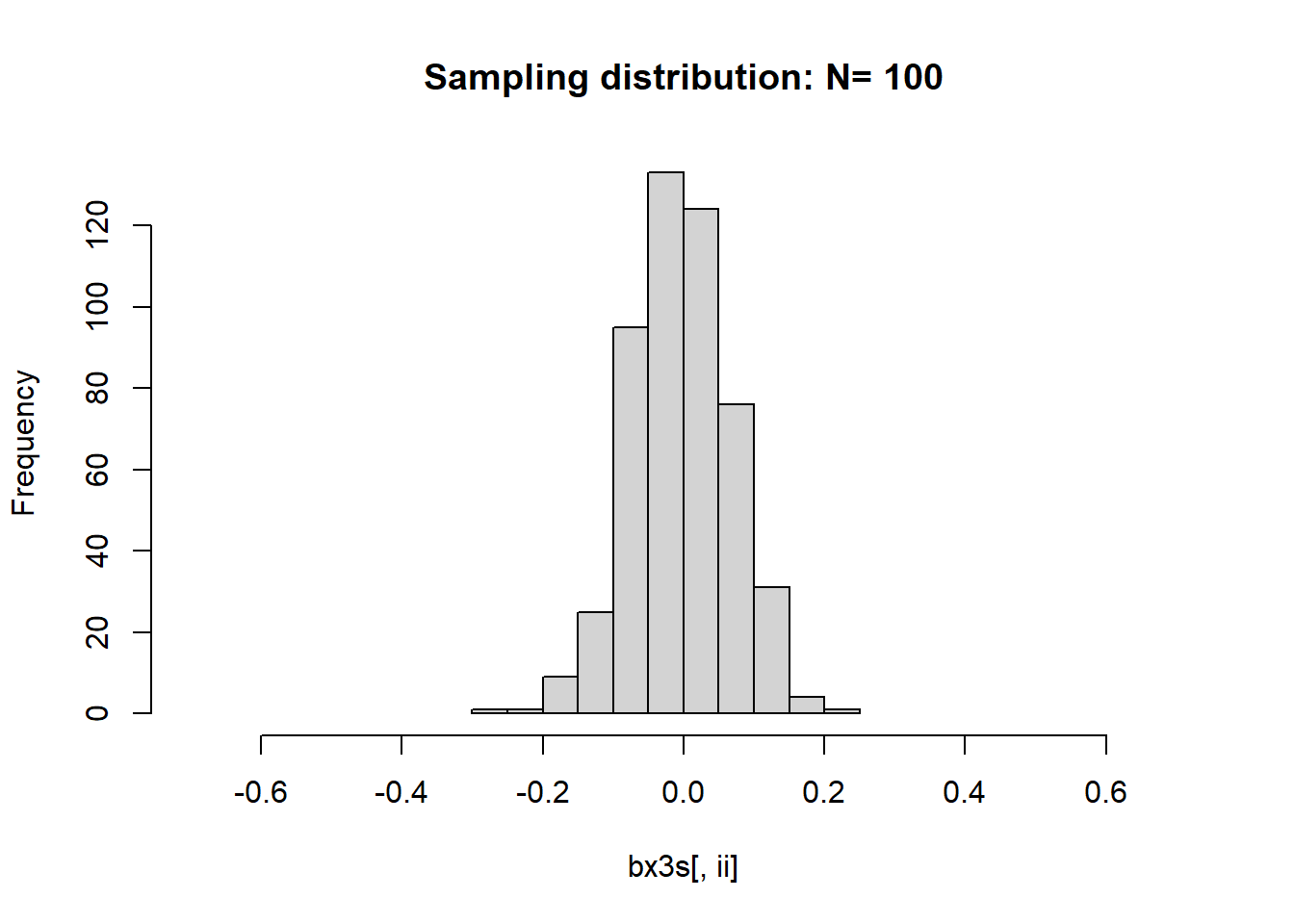
下面比较不同样本量时\(\bar X\)的极限分布。 对每一个样本量\(n\), 重复模拟产生\(M=500\)条轨道的模拟序列。 用了上面的第三个和第四个模型, 作某个样本量下的多条轨道的均值直方图时仅用了第三个模型。
ns <- c(10, 20, 50, 100, 200, 1000)
M <- 500
nn <- length(ns)
bx3s <- matrix(0, nrow=M, ncol=nn)
bx4s <- matrix(0, nrow=M, ncol=nn)
bes <- matrix(0, nrow=M, ncol=nn)
for(mm in seq(M)){
eps <- rnorm(n2, 0, sigma)
xx <- filter(eps, coefs[3,,drop=T], method="recursive", side=1)
x3 <- xx[(n0+1):n2]
xx <- filter(eps, coefs[4,,drop=T], method="recursive", side=1)
x4 <- xx[(n0+1):n2]
barx3 <- cumsum(x3)/seq(L)
barx4 <- cumsum(x4)/seq(L)
bx3s[mm,] <- barx3[ns]
bx4s[mm,] <- barx4[ns]
bare <- cumsum(eps[(n0+1):n2])/seq(L)
bes[mm,] <- bare[ns]
}
avgse <- apply(bes, 2, mean)
stdse <- apply(bes, 2, sd)
avgsx3 <- apply(bx3s, 2, mean)
stdsx3 <- apply(bx3s, 2, sd)
avgsx4 <- apply(bx4s, 2, mean)
stdsx4 <- apply(bx4s, 2, sd)
res <- rbind(avgse, stdse, avgsx3, stdsx3, avgsx4, stdsx4)
rownames(res) <- c("Avg.bareps", "Std.bareps",
"Avg.barx3", "Std.barx3",
"Avg.barx4", "Std.barx4")
colnames(res) <- ns
cat("\nSampling distribution by repeated sampling. ===\n")##
## Sampling distribution by repeated sampling. ===## 10 20 50 100 200 1000
## Avg.bareps 0.0070 -0.0110 -0.0070 -0.0077 -0.0035 -0.0007
## Std.bareps 0.3249 0.2330 0.1512 0.1036 0.0709 0.0324
## Avg.barx3 0.0079 -0.0059 -0.0045 -0.0050 -0.0022 -0.0004
## Std.barx3 0.2296 0.1600 0.1024 0.0697 0.0476 0.0217
## Avg.barx4 0.0071 -0.0360 -0.0249 -0.0293 -0.0136 -0.0024
## Std.barx4 1.0959 0.7938 0.5196 0.3583 0.2442 0.1118for(ii in seq(ns)){
hist(bx3s[,ii], main=paste("Sampling distribution: N=", ns[ii]),
xlim=c(-0.7,0.7))
}