15 统计学习介绍
15.1 介绍
统计学习(statistical learning), 也有数据挖掘(data mining),机器学习(machine learning)等称呼。 主要目的是用一些计算机算法从大量数据中发现知识。 方兴未艾的数据科学就以统计学习为重要支柱。 方法分为有监督(supervised)学习与无监督(unsupervised)学习。
无监督学习方法如聚类问题、购物篮问题、主成分分析等。
有监督学习即统计中回归分析、判别分析、逻辑斯谛回归解决的问题, 现在又有树回归、树判别、最近邻方法、随机森林、lasso、boosting、支持向量机、神经网络、贝叶斯网络、排序算法等许多方法。
统计学习介绍的主要参考书:
- (James et al. 2013): Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani(2013) An Introduction to Statistical Learning: with Applications in R, Springer.
调入需要的扩展包:
## Loading required package: Matrix## Loaded glmnet 4.1-8## randomForest 4.7-1.2## Type rfNews() to see new features/changes/bug fixes.## Loaded gbm 2.2.2## This version of gbm is no longer under development. Consider transitioning to gbm3, https://github.com/gbm-developers/gbm3无监督学习在给了数据之后, 直接从数据中发现规律, 比如聚类分析是发现数据中的聚集和分组现象, 购物篮分析是从数据中找到更多的共同出现的条目 (比如购买啤酒的用户也有较大可能购买火腿肠)。
有监督学习方法众多。 通常,需要把数据分为训练样本和测试样本, 训练样本的因变量(数值型或分类型)是已知的, 根据训练样本中自变量和因变量的关系训练出一个回归函数, 此函数以自变量为输入, 可以输出因变量的预测值。
训练出的函数有可能是有简单表达式的(例如,logistic回归)、 有参数众多的表达式的(如神经网络), 也有可能是依赖于所有训练样本而无法写出表达式的(例如k近邻分类)。
15.1.1 偏差与方差折衷
对回归问题,经常使用均方误差\(E|\hat y - Ey|^2\)来衡量精度。 对分类问题,经常使用分类准确率等来衡量精度。 均方误差可分解: \[ \text{均方误差} = E|\hat y Ey|^2 = \text{Var}(\hat y) + [Ey - E \hat y]^2 = \text{方差} + \text{偏差}^2 . \]
训练的回归函数如果仅考虑对训练样本解释尽可能好, 就会使得估计结果方差很大, 在对测试样本进行计算时因方差大而导致很大的误差, 所以选取的回归函数应该尽可能简单。
如果选取的回归函数过于简单而实际上自变量与因变量关系比较复杂, 就会使得估计的回归函数偏差比较大, 这样在对检验样本进行计算时也会有比较大的误差。
另外,训练样本的样本量也是一个关键因素, 如果因变量和自变量之间的实际关系很复杂但样本量不够大, 这时方差会比较大, 无法使用更复杂的模型。 如果在样本量较小时使用了复杂的模型, 就会造成过度拟合; 如果样本量足够但是模型过于简单, 这时偏差太大, 造成拟合不足。
所以,在有监督学习时, 回归函数的复杂程度是一个很关键的量, 太复杂和太简单都可能导致差的结果, 需要找到一个折衷的值。 这个问题在机器学习中也称为泛化(generalization)问题, 就是从训练样本得到的回归函数能否有效地预测其它没有参与训练的数据。
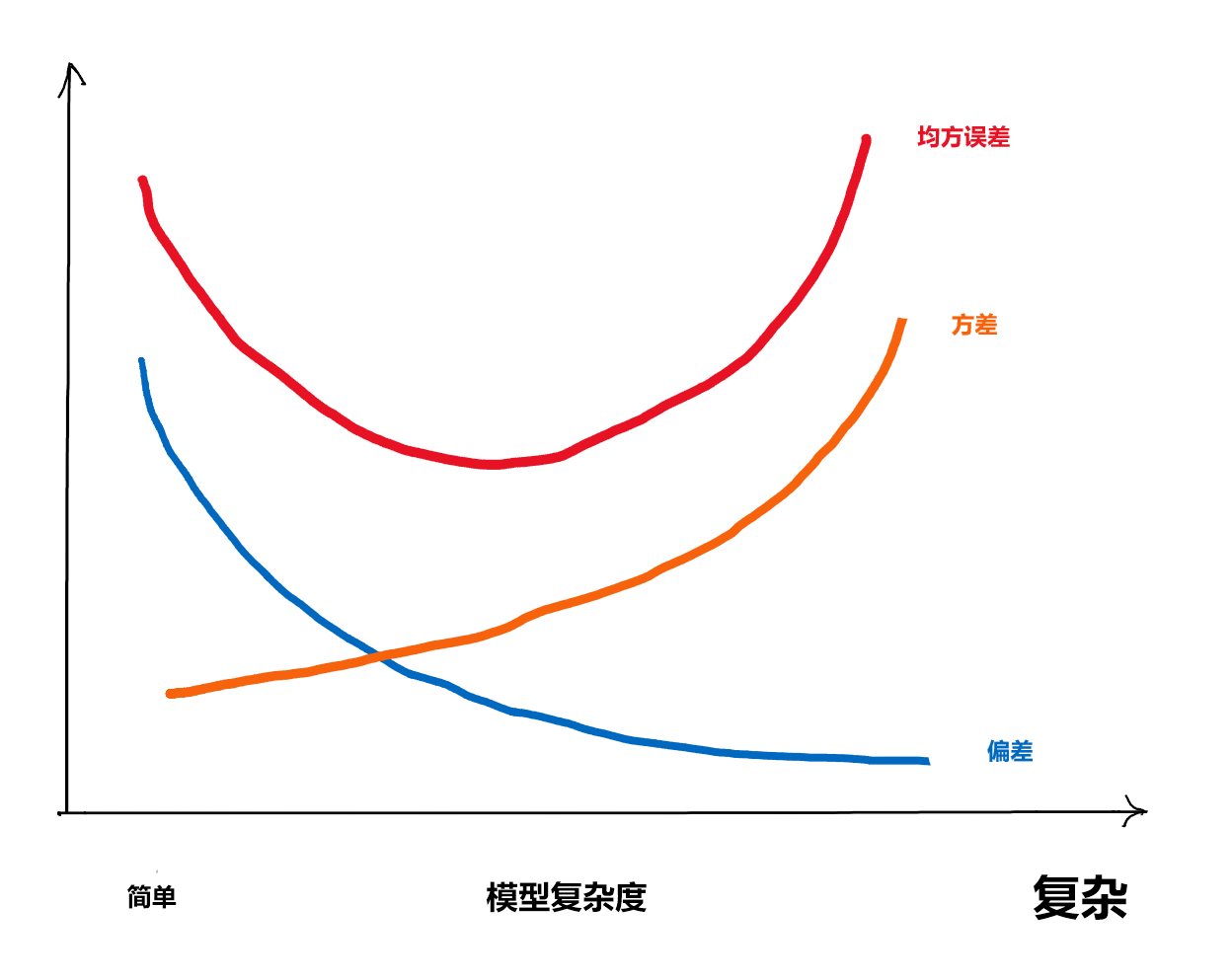
复杂程度在线性回归中就是自变量个数, 在一元曲线拟合中就是曲线的不光滑程度。 在其它指标类似的情况下,简单的模型更稳定、可解释更好, 所以统计学特别重视模型的简化。
15.1.2 训练集、验证集和测试集
设输入的数据的集合为\(D\), 其中每个元素是一个“样例”。 从统计上, \(D\)是来自某个多元分布的独立同分布样本。 有监督学习的目的, 是找到一个最优(或者接近最优)的函数\(f(\cdot)\), 用来描述样本所来自的总体中自变量(也称为特征)和因变量(也称为标记或标签)的关系。 如果我们使用\(D\)中所有样本进行估计, 然后使用对这些样本的模型预测结果评估模型的性能, 就很容易发生过度拟合问题, 不能真实地反映模型的泛化能力。 所以, 可以将\(D\)随机地(或随机分层抽样)划分为\(D_1\)和\(D_2\)两个子集, 在\(D_1\)上估计函数\(f\), 称\(D_1\)为“训练集”; 在\(D_2\)上评估训练得到的函数的性能(误差指标), 成\(D_2\)为“测试集”。
在更实际的应用中, 最后获得的模型是需要应用到类似的未知数据上的, 哪些未知数据若称为“测试集”, 则将\(D_2\)称为“验证集”(validation set)。
因为训练集和测试集的划分是随机的, 所以在测试集上得到的误差指标受到随时划分的影响。 为此, 可以多次进行训练集与测试集的随机划分, 并将得到的多个误差指标进行平均, 以期得到更稳定可靠的泛化误差估计。
15.1.3 交叉验证
即使是在从训练集训练(估计)回归函数时, 也需要适当地选择模型的复杂度。 仅考虑对训练数据的拟合程度是不够的, 这会造成过度拟合问题。
为了相对客观地度量模型的预报误差, 假设训练样本有\(n\)个观测, 可以留出第一个观测不用, 用剩余的\(n-1\)个观测建模,然后预测第一个观测的因变量值, 得到一个误差;对每个观测都这样做, 就可以得到\(n\)个误差。 这样的方法叫做留一法。 利用这样得到的\(n\)个误差评估模型的预测精度, 找到最优的复杂度或在多个候选模型中找到最优的模型。 但是,当样本量\(n\)很大时, 需要估计的模型的个数过多, 计算量太大。
更常用的是十折(\(k\)折)交叉验证。 假设训练集有\(n\)个观测, 将其均分成\(10\)分, 保留第一份不用, 将其余九份合并在一起用来建模,然后预报第一份; 对每一份都这样做, 也可以得到\(n\)个误差, 利用这些误差进行模型比较和选择, 这叫做十折(ten-fold)交叉验证方法。 因为要预报的数据没有用来建模, 交叉验证得到的误差估计更准确。
在划分十折的子集时一般进行随机分组, 这会使得最后的误差估计受到随机分组的影响。 为此, 可以重复地进行多次随机分组, 每一次得到十折交叉验证的误差估计, 然后将误差估计平均, 以期获得较稳定的误差估计。
15.2 回归变量选择
在有监督学习中, 减少自变量个数是常用的降低模型复杂度的方法。 其它的降低模型复杂度方法包括收缩(shrinkage,如lasso、岭回归)、 自变量降维(主成分回归、偏最小二乘)等方法。
有各种筛选自变量的方法, 比如在线性回归分析中,按照BIC准则筛选: \[\begin{aligned} \text{BIC}(p) = \frac{1}{n}( \text{RSS}(p) + p \hat\sigma^2 \log n ), \end{aligned}\] 其中\(p\)为自变量个数,\(n\)为观测个数, \(\text{RSS}(p)\)是子集回归的残差平方和, \(\hat\sigma^2\)是回归误差项方差\(\sigma^2\)的无偏估计, 常用全体自变量模型估计。 取使得BIC(\(p\))最小的自变量子集。
类似地有AIC准则: \[\begin{aligned} \text{AIC}(p) = \frac{1}{n}( \text{RSS}(p) + 2p \hat\sigma^2 ), \end{aligned}\] BIC在大样本情形下能保证得到的子集相合, AIC在中小样本情形下可以使重要变量不被错误删除。
注意,不能用\(R^2\)最小作为模型选择准则, 因为增加更多自变量一定会增大\(R^2\), 但有可能造成过度拟合。
lasso方法可以利用惩罚函数和参数估计收缩达到自变量筛选的目的, 可以控制模型的复杂度。
关于线性回归中过度拟合的示例, 参见统计软件教程中的内容。
15.2.1 维数诅咒
现代的数据中出现了很多高维问题, 可能会有变量个数\(p\)远大于观测个数\(n\)的情况出现, 比如基因表达数据。 高维使得问题变得很难解决甚至无法解决, 其原因是高维空间中的数据点彼此距离都很稀疏, 也就是说, 高维空间的观测点都是很稀疏的。 这个问题叫做维数诅咒。
比如,\(n=100\)的样本量在一维的\([0,1]\)区间中已经比较稠密了。 放到\(p=10\)维空间中,如果每个点占据一个10维超立方体, 每个立方体的边长则有0.63,彼此距离相当远。
回归分析需要比较多的临近数据,否则很难得到有用的回归函数。 即使用了变量选择、收缩、降维等方法, 高维问题还是会造成很大的影响。 并不是自变量越多越好, 增加许多与因变量无关的自变量实际上会使得模型变差。
15.2.2 R中的最优子集回归
在R用leaps包的regsubsets()函数计算最优子集回归,
办法是对某个试验性的子集自变量个数\(\hat p\)值,
都找到\(\hat p\)固定情况下残差平方和最小的变量子集,
这样只要在这些不同\(\hat p\)的最优子集中挑选就可以了。
对拟合结果用coef()加id=指定一种子集。
15.2.3 Hitters数据分析
考虑ISLR包的Hitters数据集。 此数据集有322个运动员的20个变量的数据, 其中的变量Salary(工资)是我们关心的。 变量包括:
## [1] "AtBat" "Hits" "HmRun" "Runs" "RBI" "Walks" "Years" "CAtBat" "CHits" "CHmRun" "CRuns" "CRBI" "CWalks" "League" "Division" "PutOuts" "Assists" "Errors" "Salary" "NewLeague"数据集的详细变量信息如下:
## 'data.frame': 322 obs. of 20 variables:
## $ AtBat : int 293 315 479 496 321 594 185 298 323 401 ...
## $ Hits : int 66 81 130 141 87 169 37 73 81 92 ...
## $ HmRun : int 1 7 18 20 10 4 1 0 6 17 ...
## $ Runs : int 30 24 66 65 39 74 23 24 26 49 ...
## $ RBI : int 29 38 72 78 42 51 8 24 32 66 ...
## $ Walks : int 14 39 76 37 30 35 21 7 8 65 ...
## $ Years : int 1 14 3 11 2 11 2 3 2 13 ...
## $ CAtBat : int 293 3449 1624 5628 396 4408 214 509 341 5206 ...
## $ CHits : int 66 835 457 1575 101 1133 42 108 86 1332 ...
## $ CHmRun : int 1 69 63 225 12 19 1 0 6 253 ...
## $ CRuns : int 30 321 224 828 48 501 30 41 32 784 ...
## $ CRBI : int 29 414 266 838 46 336 9 37 34 890 ...
## $ CWalks : int 14 375 263 354 33 194 24 12 8 866 ...
## $ League : Factor w/ 2 levels "A","N": 1 2 1 2 2 1 2 1 2 1 ...
## $ Division : Factor w/ 2 levels "E","W": 1 2 2 1 1 2 1 2 2 1 ...
## $ PutOuts : int 446 632 880 200 805 282 76 121 143 0 ...
## $ Assists : int 33 43 82 11 40 421 127 283 290 0 ...
## $ Errors : int 20 10 14 3 4 25 7 9 19 0 ...
## $ Salary : num NA 475 480 500 91.5 750 70 100 75 1100 ...
## $ NewLeague: Factor w/ 2 levels "A","N": 1 2 1 2 2 1 1 1 2 1 ...希望以Salary为因变量,查看其缺失值个数:
## [1] 59为简单起见,去掉有缺失值的观测:
## [1] 263 2015.2.4 回归自变量选择
15.2.4.1 最优子集选择
用leaps包的regsubsets()函数计算最优子集回归,
办法是对某个试验性的子集自变量个数\(\hat p\)值,
都找到\(\hat p\)固定情况下残差平方和最小的变量子集,
这样只要在这些不同\(\hat p\)的最优子集中挑选就可以了。
可以先进行一个包含所有自变量的全集回归:
regfit.full <- regsubsets(Salary ~ ., data=d, nvmax=19)
reg.summary <- summary(regfit.full)
reg.summary## Subset selection object
## Call: regsubsets.formula(Salary ~ ., data = d, nvmax = 19)
## 19 Variables (and intercept)
## Forced in Forced out
## AtBat FALSE FALSE
## Hits FALSE FALSE
## HmRun FALSE FALSE
## Runs FALSE FALSE
## RBI FALSE FALSE
## Walks FALSE FALSE
## Years FALSE FALSE
## CAtBat FALSE FALSE
## CHits FALSE FALSE
## CHmRun FALSE FALSE
## CRuns FALSE FALSE
## CRBI FALSE FALSE
## CWalks FALSE FALSE
## LeagueN FALSE FALSE
## DivisionW FALSE FALSE
## PutOuts FALSE FALSE
## Assists FALSE FALSE
## Errors FALSE FALSE
## NewLeagueN FALSE FALSE
## 1 subsets of each size up to 19
## Selection Algorithm: exhaustive
## AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " " " "
## 2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " " " "
## 3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " "*" " " " " " "
## 4 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " " " "
## 5 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " " " "
## 6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " " "*" " " " " "*" "*" " " " " " "
## 7 ( 1 ) " " "*" " " " " " " "*" " " "*" "*" "*" " " " " " " " " "*" "*" " " " " " "
## 8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " "*" "*" " " "*" " " "*" "*" " " " " " "
## 9 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" " " " " " "
## 10 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" "*" " " " "
## 11 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " " " "
## 12 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " " " "
## 13 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*" " "
## 14 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*" " "
## 15 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*" " "
## 16 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*" " "
## 17 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*" "*"
## 18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*" "*"
## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"这里用nvmax=指定了允许所有的自变量都参加,
缺省行为是限制最多个数的。
上述结果表格中每一行给出了固定\(\hat p\)条件下的最优子集。
试比较这些最优模型的BIC值:
## [1] -90.84637 -128.92622 -135.62693 -141.80892 -144.07143 -147.91690 -145.25594 -147.61525 -145.44316 -143.21651 -138.86077 -133.87283 -128.77759 -123.64420 -118.21832 -112.81768 -107.35339 -101.86391 -96.30412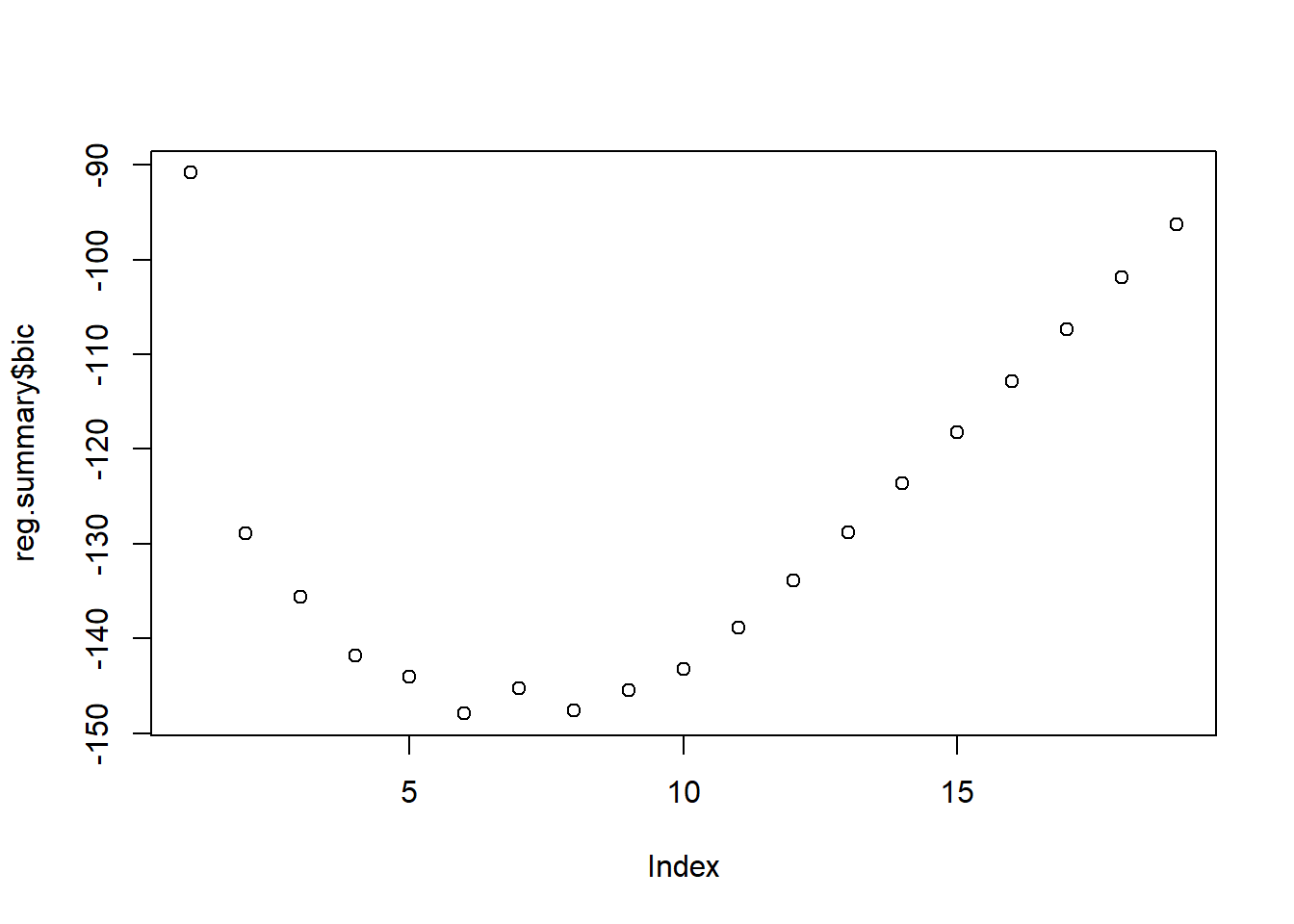
其中\(\hat p=6, 8\)的值相近,都很低,
取\(\hat p=6\)。
用coef()加id=6指定第六种子集:
## (Intercept) AtBat Hits Walks CRBI DivisionW PutOuts
## 91.5117981 -1.8685892 7.6043976 3.6976468 0.6430169 -122.9515338 0.2643076这种方法实现了选取BIC最小的自变量子集。
15.2.4.2 逐步回归方法
在用lm()做了全集回归后,
把全集回归结果输入到step()函数中可以执行逐步回归。
如:
##
## Call:
## lm(formula = Salary ~ ., data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -907.62 -178.35 -31.11 139.09 1877.04
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 163.10359 90.77854 1.797 0.073622 .
## AtBat -1.97987 0.63398 -3.123 0.002008 **
## Hits 7.50077 2.37753 3.155 0.001808 **
## HmRun 4.33088 6.20145 0.698 0.485616
## Runs -2.37621 2.98076 -0.797 0.426122
## RBI -1.04496 2.60088 -0.402 0.688204
## Walks 6.23129 1.82850 3.408 0.000766 ***
## Years -3.48905 12.41219 -0.281 0.778874
## CAtBat -0.17134 0.13524 -1.267 0.206380
## CHits 0.13399 0.67455 0.199 0.842713
## CHmRun -0.17286 1.61724 -0.107 0.914967
## CRuns 1.45430 0.75046 1.938 0.053795 .
## CRBI 0.80771 0.69262 1.166 0.244691
## CWalks -0.81157 0.32808 -2.474 0.014057 *
## LeagueN 62.59942 79.26140 0.790 0.430424
## DivisionW -116.84925 40.36695 -2.895 0.004141 **
## PutOuts 0.28189 0.07744 3.640 0.000333 ***
## Assists 0.37107 0.22120 1.678 0.094723 .
## Errors -3.36076 4.39163 -0.765 0.444857
## NewLeagueN -24.76233 79.00263 -0.313 0.754218
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 315.6 on 243 degrees of freedom
## Multiple R-squared: 0.5461, Adjusted R-squared: 0.5106
## F-statistic: 15.39 on 19 and 243 DF, p-value: < 2.2e-16## Start: AIC=3046.02
## Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + Years +
## CAtBat + CHits + CHmRun + CRuns + CRBI + CWalks + League +
## Division + PutOuts + Assists + Errors + NewLeague
##
## Df Sum of Sq RSS AIC
## - CHmRun 1 1138 24201837 3044.0
## - CHits 1 3930 24204629 3044.1
## - Years 1 7869 24208569 3044.1
## - NewLeague 1 9784 24210484 3044.1
## - RBI 1 16076 24216776 3044.2
## - HmRun 1 48572 24249272 3044.6
## - Errors 1 58324 24259023 3044.7
## - League 1 62121 24262821 3044.7
## - Runs 1 63291 24263990 3044.7
## - CRBI 1 135439 24336138 3045.5
## - CAtBat 1 159864 24360564 3045.8
## <none> 24200700 3046.0
## - Assists 1 280263 24480963 3047.1
## - CRuns 1 374007 24574707 3048.1
## - CWalks 1 609408 24810108 3050.6
## - Division 1 834491 25035190 3052.9
## - AtBat 1 971288 25171987 3054.4
## - Hits 1 991242 25191941 3054.6
## - Walks 1 1156606 25357305 3056.3
## - PutOuts 1 1319628 25520328 3058.0
##
## Step: AIC=3044.03
## Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + Years +
## CAtBat + CHits + CRuns + CRBI + CWalks + League + Division +
## PutOuts + Assists + Errors + NewLeague
##
## Df Sum of Sq RSS AIC
## - Years 1 7609 24209447 3042.1
## - NewLeague 1 10268 24212106 3042.2
## - CHits 1 14003 24215840 3042.2
## - RBI 1 14955 24216793 3042.2
## - HmRun 1 52777 24254614 3042.6
## - Errors 1 59530 24261367 3042.7
## - League 1 63407 24265244 3042.7
## - Runs 1 64860 24266698 3042.7
## - CAtBat 1 174992 24376830 3043.9
## <none> 24201837 3044.0
## - Assists 1 285766 24487603 3045.1
## - CRuns 1 611358 24813196 3048.6
## - CWalks 1 645627 24847464 3049.0
## - Division 1 834637 25036474 3050.9
## - CRBI 1 864220 25066057 3051.3
## - AtBat 1 970861 25172699 3052.4
## - Hits 1 1025981 25227819 3052.9
## - Walks 1 1167378 25369216 3054.4
## - PutOuts 1 1325273 25527110 3056.1
##
## Step: AIC=3042.12
## Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + CAtBat +
## CHits + CRuns + CRBI + CWalks + League + Division + PutOuts +
## Assists + Errors + NewLeague
##
## Df Sum of Sq RSS AIC
## - NewLeague 1 9931 24219377 3040.2
## - RBI 1 15989 24225436 3040.3
## - CHits 1 18291 24227738 3040.3
## - HmRun 1 54144 24263591 3040.7
## - Errors 1 57312 24266759 3040.7
## - Runs 1 63172 24272619 3040.8
## - League 1 65732 24275178 3040.8
## <none> 24209447 3042.1
## - CAtBat 1 266205 24475652 3043.0
## - Assists 1 293479 24502926 3043.3
## - CRuns 1 646350 24855797 3047.1
## - CWalks 1 649269 24858716 3047.1
## - Division 1 827511 25036958 3049.0
## - CRBI 1 872121 25081568 3049.4
## - AtBat 1 968713 25178160 3050.4
## - Hits 1 1018379 25227825 3050.9
## - Walks 1 1164536 25373983 3052.5
## - PutOuts 1 1334525 25543972 3054.2
##
## Step: AIC=3040.22
## Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + CAtBat +
## CHits + CRuns + CRBI + CWalks + League + Division + PutOuts +
## Assists + Errors
##
## Df Sum of Sq RSS AIC
## - RBI 1 15800 24235177 3038.4
## - CHits 1 15859 24235237 3038.4
## - Errors 1 54505 24273883 3038.8
## - HmRun 1 54938 24274316 3038.8
## - Runs 1 62294 24281671 3038.9
## - League 1 107479 24326856 3039.4
## <none> 24219377 3040.2
## - CAtBat 1 261336 24480713 3041.1
## - Assists 1 295536 24514914 3041.4
## - CWalks 1 648860 24868237 3045.2
## - CRuns 1 661449 24880826 3045.3
## - Division 1 824672 25044049 3047.0
## - CRBI 1 880429 25099806 3047.6
## - AtBat 1 999057 25218434 3048.9
## - Hits 1 1034463 25253840 3049.2
## - Walks 1 1157205 25376583 3050.5
## - PutOuts 1 1335173 25554550 3052.3
##
## Step: AIC=3038.4
## Salary ~ AtBat + Hits + HmRun + Runs + Walks + CAtBat + CHits +
## CRuns + CRBI + CWalks + League + Division + PutOuts + Assists +
## Errors
##
## Df Sum of Sq RSS AIC
## - CHits 1 13483 24248660 3036.5
## - HmRun 1 44586 24279763 3036.9
## - Runs 1 54057 24289234 3037.0
## - Errors 1 57656 24292833 3037.0
## - League 1 108644 24343821 3037.6
## <none> 24235177 3038.4
## - CAtBat 1 252756 24487934 3039.1
## - Assists 1 294674 24529851 3039.6
## - CWalks 1 639690 24874868 3043.2
## - CRuns 1 693535 24928712 3043.8
## - Division 1 808984 25044161 3045.0
## - CRBI 1 893830 25129008 3045.9
## - Hits 1 1034884 25270061 3047.4
## - AtBat 1 1042798 25277975 3047.5
## - Walks 1 1145013 25380191 3048.5
## - PutOuts 1 1340713 25575890 3050.6
##
## Step: AIC=3036.54
## Salary ~ AtBat + Hits + HmRun + Runs + Walks + CAtBat + CRuns +
## CRBI + CWalks + League + Division + PutOuts + Assists + Errors
##
## Df Sum of Sq RSS AIC
## - HmRun 1 40487 24289148 3035.0
## - Errors 1 51930 24300590 3035.1
## - Runs 1 79343 24328003 3035.4
## - League 1 114742 24363402 3035.8
## <none> 24248660 3036.5
## - Assists 1 283442 24532103 3037.6
## - CAtBat 1 613356 24862016 3041.1
## - Division 1 801474 25050134 3043.1
## - CRBI 1 903248 25151908 3044.2
## - CWalks 1 1011953 25260613 3045.3
## - Walks 1 1246164 25494824 3047.7
## - AtBat 1 1339620 25588280 3048.7
## - CRuns 1 1390808 25639469 3049.2
## - PutOuts 1 1406023 25654684 3049.4
## - Hits 1 1607990 25856650 3051.4
##
## Step: AIC=3034.98
## Salary ~ AtBat + Hits + Runs + Walks + CAtBat + CRuns + CRBI +
## CWalks + League + Division + PutOuts + Assists + Errors
##
## Df Sum of Sq RSS AIC
## - Errors 1 44085 24333232 3033.5
## - Runs 1 49068 24338215 3033.5
## - League 1 103837 24392985 3034.1
## <none> 24289148 3035.0
## - Assists 1 247002 24536150 3035.6
## - CAtBat 1 652746 24941894 3040.0
## - Division 1 795643 25084791 3041.5
## - CWalks 1 982896 25272044 3043.4
## - Walks 1 1205823 25494971 3045.7
## - AtBat 1 1300972 25590120 3046.7
## - CRuns 1 1351200 25640348 3047.2
## - CRBI 1 1353507 25642655 3047.2
## - PutOuts 1 1429006 25718154 3048.0
## - Hits 1 1574140 25863288 3049.5
##
## Step: AIC=3033.46
## Salary ~ AtBat + Hits + Runs + Walks + CAtBat + CRuns + CRBI +
## CWalks + League + Division + PutOuts + Assists
##
## Df Sum of Sq RSS AIC
## - Runs 1 54113 24387345 3032.0
## - League 1 91269 24424501 3032.4
## <none> 24333232 3033.5
## - Assists 1 220010 24553242 3033.8
## - CAtBat 1 650513 24983746 3038.4
## - Division 1 799455 25132687 3040.0
## - CWalks 1 971260 25304493 3041.8
## - Walks 1 1239533 25572765 3044.5
## - CRBI 1 1331672 25664904 3045.5
## - CRuns 1 1361070 25694302 3045.8
## - AtBat 1 1378592 25711824 3045.9
## - PutOuts 1 1391660 25724892 3046.1
## - Hits 1 1649291 25982523 3048.7
##
## Step: AIC=3032.04
## Salary ~ AtBat + Hits + Walks + CAtBat + CRuns + CRBI + CWalks +
## League + Division + PutOuts + Assists
##
## Df Sum of Sq RSS AIC
## - League 1 113056 24500402 3031.3
## <none> 24387345 3032.0
## - Assists 1 280689 24668034 3033.1
## - CAtBat 1 596622 24983967 3036.4
## - Division 1 780369 25167714 3038.3
## - CWalks 1 946687 25334032 3040.1
## - Walks 1 1212997 25600342 3042.8
## - CRuns 1 1334397 25721742 3044.1
## - CRBI 1 1361339 25748684 3044.3
## - PutOuts 1 1455210 25842555 3045.3
## - AtBat 1 1522760 25910105 3046.0
## - Hits 1 1718870 26106215 3047.9
##
## Step: AIC=3031.26
## Salary ~ AtBat + Hits + Walks + CAtBat + CRuns + CRBI + CWalks +
## Division + PutOuts + Assists
##
## Df Sum of Sq RSS AIC
## <none> 24500402 3031.3
## - Assists 1 313650 24814051 3032.6
## - CAtBat 1 534156 25034558 3034.9
## - Division 1 798473 25298875 3037.7
## - CWalks 1 965875 25466276 3039.4
## - CRuns 1 1265082 25765484 3042.5
## - Walks 1 1290168 25790569 3042.8
## - CRBI 1 1326770 25827172 3043.1
## - PutOuts 1 1551523 26051925 3045.4
## - AtBat 1 1589780 26090181 3045.8
## - Hits 1 1716068 26216469 3047.1##
## Call:
## lm(formula = Salary ~ AtBat + Hits + Walks + CAtBat + CRuns +
## CRBI + CWalks + Division + PutOuts + Assists, data = d)
##
## Coefficients:
## (Intercept) AtBat Hits Walks CAtBat CRuns CRBI CWalks DivisionW PutOuts Assists
## 162.5354 -2.1687 6.9180 5.7732 -0.1301 1.4082 0.7743 -0.8308 -112.3801 0.2974 0.2832最后保留了10个自变量。
15.2.4.3 划分训练集与测试集
在整个数据集中随机选取一部分作为训练集,其余作为测试集。 下面的程序把原始数据大约一分为二:
set.seed(1)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)其中train_id保存了作为训练集的序号,
train则用真值、假值表示每个观测是否入选训练集。
仅用训练集估计模型。 为了在测试集上用模型进行预报并估计预测均方误差, 需要自己写一个预测函数:
predict.regsubsets <- function(object, newdata, id, ...){
form <- as.formula(object$call[[2]])
mat <- model.matrix(form, newdata)
coefi <- coef(object, id=id)
xvars <- names(coefi)
mat[, xvars] %*% coefi
}然后,对每个子集大小,用最优子集在测试集上进行预报, 计算均方误差:
regfit.best <- regsubsets( Salary ~ ., data=d[train,], nvmax=19 )
val.errors <- rep(as.numeric(NA), 19)
for(i in 1:19){
#pred <- predict.regsubsets(regfit.best, newdata=d[test,], id=i)
pred <- predict(regfit.best, newdata=d[test,], id=i)
val.errors[i] <- mean( (d[test, 'Salary'] - pred)^2 )
}
print(val.errors)## [1] 186716.3 162285.2 151838.6 153123.6 149526.5 144196.0 145793.0 151964.3 156090.9 158975.0 161495.8 161019.2 157633.1 157508.2 162951.4 163352.4 166805.0 166986.7 168593.3## [1] 6用测试集得到的最优子集大小为6。 模型子集和回归系数为:
## (Intercept) Walks CAtBat CHits CHmRun DivisionW PutOuts
## 181.7041436 4.2540935 -0.5253895 2.0543314 2.4596055 -131.1657146 0.1751321需要注意的是, 因为划分训练集和测试集是随机划分的, 所以模型选择的结果可能受到随机划分的影响。 为此, 可以进行多次随机划分, 然后取模型最优选择出现最多的一个。
15.2.4.4 用10折交叉验证方法选择最优子集
下列程序对数据中每一行分配一个折号:
下面,对10折中每一折都分别当作测试集一次, 得到不同子集大小的均方误差:
cv.errors <- matrix( as.numeric(NA), k, 19,
dimnames=list(NULL, paste(1:19)) )
for(j in 1:k){
best.fit <- regsubsets(Salary ~ ., data=d[folds != j,], nvmax=19)
for(i in 1:19){
pred <- predict( best.fit, d[folds==j,], id=i)
cv.errors[j, i] <- mean( (d[folds==j, 'Salary'] - pred)^2 )
}
}
head(cv.errors)## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## [1,] 98623.24 115600.61 120884.31 113831.63 120728.51 122922.93 155507.25 137753.36 149198.01 153332.89 155702.91 155842.88 158755.87 156037.17 157739.46 155548.96 156688.01 156860.92 156976.98
## [2,] 155320.11 100425.87 168838.35 159729.47 145895.71 123555.25 119983.35 96609.16 99057.32 80375.78 91290.74 92292.69 100498.84 101562.45 104621.38 100922.27 102198.69 105318.26 106064.89
## [3,] 124151.77 68833.50 69392.29 77221.37 83802.82 70125.41 68997.77 64143.70 65813.14 65120.27 68160.94 70263.77 69765.81 68987.54 69471.32 69294.21 69199.91 68866.84 69195.74
## [4,] 232191.41 279001.29 294568.10 288765.81 276972.83 260121.22 276413.09 259923.88 270151.18 263492.31 259154.53 269017.80 265468.90 269666.65 265518.87 267240.44 267771.74 267670.66 267717.80
## [5,] 115397.35 96807.44 108421.66 104933.55 99561.69 86103.05 89345.61 87693.15 91631.88 88763.37 89801.07 91070.44 92429.43 92821.15 95849.81 96513.70 95209.20 94952.21 94951.70
## [6,] 103839.30 75652.50 69962.31 58291.91 65893.45 64215.56 65800.88 61413.45 60200.70 59599.54 59831.90 60081.48 59662.51 60618.91 62540.03 62776.81 62717.77 62354.97 62268.97cv.errors是一个\(10\times 19\)矩阵,
每行对应一折作为测试集的情形,
每列是一个子集大小,
元素值是测试均方误差。
对每列的10个元素求平均, 可以得到每个子集大小的平均均方误差:
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## 149821.1 130922.0 139127.0 131028.8 131050.2 119538.6 124286.1 113580.0 115556.5 112216.7 113251.2 115755.9 117820.8 119481.2 120121.6 120074.3 120084.8 120085.8 120403.5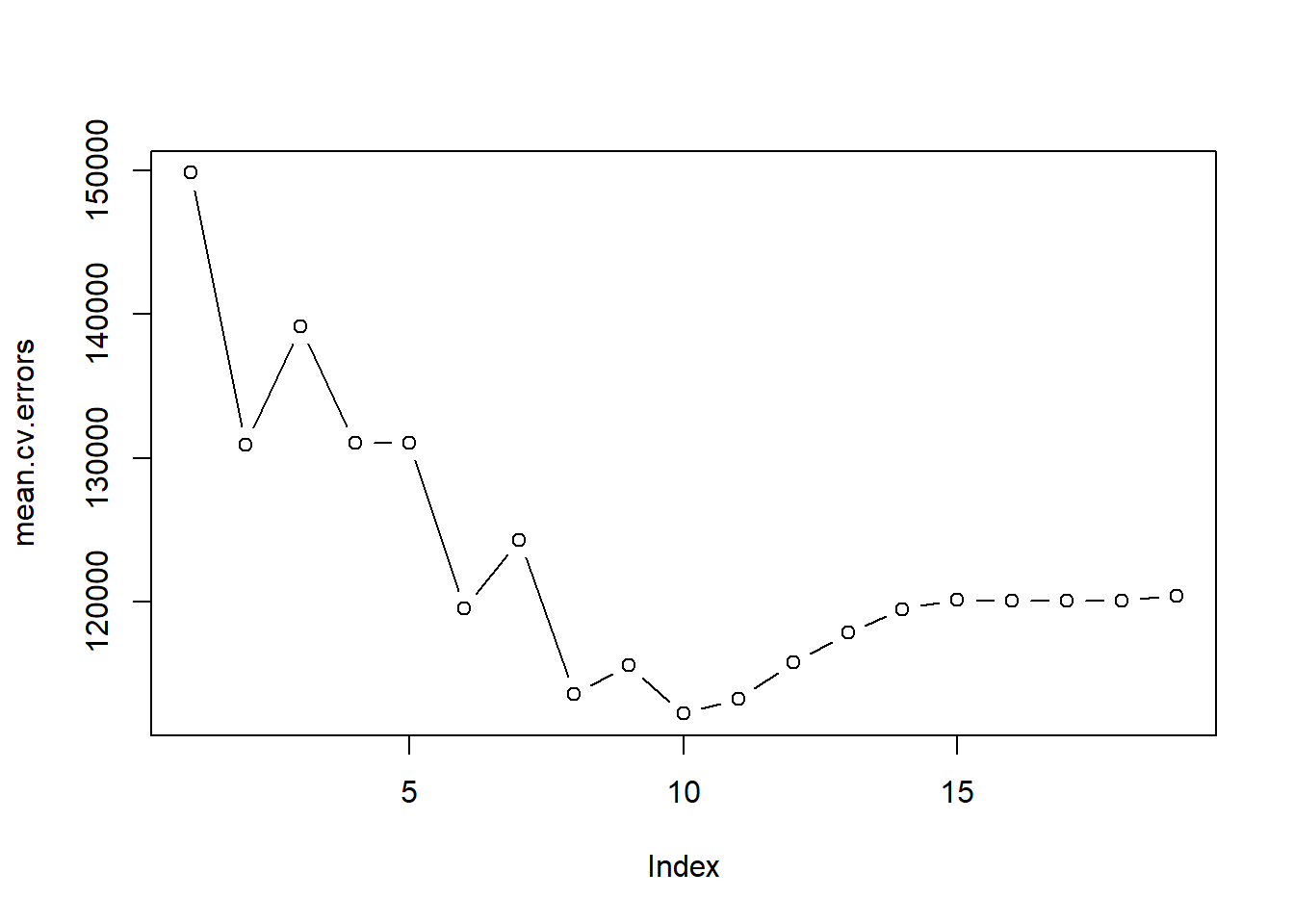 这样找到的最优子集大小是10。
用这种方法找到最优子集大小后,
可以对全数据集重新建模但是选择最优子集大小为10:
这样找到的最优子集大小是10。
用这种方法找到最优子集大小后,
可以对全数据集重新建模但是选择最优子集大小为10:
## (Intercept) AtBat Hits Walks CAtBat CRuns CRBI CWalks DivisionW PutOuts Assists
## 162.5354420 -2.1686501 6.9180175 5.7732246 -0.1300798 1.4082490 0.7743122 -0.8308264 -112.3800575 0.2973726 0.2831680交叉验证的分组是随机划分的, 所以从交叉验证得到的误差估计受到随机划分的影响。 为此, 可以进行多次交叉验证, 每次使用不同的随机分组, 将不同次的误差进行平均。
划分训练集和验证集与交叉验证方法经常联合运用。 取一个固定的较小规模的测试集, 此测试集不用来作子集选择, 对训练集用交叉验证方法选择最优子集, 然后在测试集上验证。
15.3 惩罚最小二乘
15.3.1 岭回归(Ridge regression)介绍
当自变量个数太多时,模型复杂度高, 可能有过度拟合, 模型不稳定。
一种方法是对较大的模型系数施加二次惩罚, 把最小二乘问题变成带有二次惩罚项的惩罚最小二乘问题: \[\begin{aligned} \min\; \sum_{i=1}^n \left( y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_p x_{ip} \right)^2 + \lambda \sum_{j=1}^p \beta_j^2 . \end{aligned}\] 这比通常最小二乘得到的回归系数绝对值变小, 但是求解的稳定性增加了,避免了共线问题。
实际上, 与线性模型\(\boldsymbol Y = \boldsymbol X \boldsymbol\beta + \boldsymbol\varepsilon\) 的普通最小二乘解 \(\hat{\boldsymbol\beta} = (\boldsymbol X^T \boldsymbol X)^{-1} \boldsymbol X^T \boldsymbol Y\) 相比, 岭回归问题的解为 \[ \tilde{\boldsymbol\beta} = (\boldsymbol X^T \boldsymbol X + s \boldsymbol I)^{-1} \boldsymbol X^T \boldsymbol Y \] 其中\(\boldsymbol I\)为单位阵,\(s>0\)与\(\lambda\)有关。
\(\lambda\)称为调节参数,\(\lambda\)越大,相当于模型复杂度越低。 适当选择\(\lambda\)可以在方差与偏差之间找到适当的折衷, 从而减小预测误差。
由于量纲问题,在不同自变量不可比时,数据集应该进行标准化。
用R的glmnet包计算岭回归。
用glmnet()函数,
指定参数alpha=0时执行的是岭回归。
用参数lambda=指定一个调节参数网格,
岭回归将在这些调节参数上计算。
用coef()从回归结果中取得不同调节参数对应的回归系数估计,
结果是一个矩阵,每列对应于一个调节参数。
为了选择调节参数并评估模型预测结果,
通常会:
- 把所有数据划分为训练集与测试集;
- 在训练集上执行五折或十折交叉验证, 从交叉验证的平均均方误差选择最优调节参数;
- 在测试集上计算预测平均误差;
- 最后,在全集是使用最优调节参数建模, 但是预测效果仍使用上面测试集得到的结果。
15.3.2 岭回归Hitters例子
仍采用上面去掉了缺失值的Hitters数据集结果d。 需要使用glmnet包。
如下程序把回归的设计阵与因变量提取出来:
岭回归涉及到调节参数\(\lambda\)的选择, 为了绘图, 先选择\(\lambda\)的一个网格:
用所有数据针对这样的调节参数网格计算岭回归结果,
注意glmnet()函数允许调节参数\(\lambda\)输入多个值:
## [1] 20 100glmnet()函数默认对数据进行标准化。
coef()的结果是一个矩阵,每列对应一个调节参数值。
15.3.2.1 划分训练集与测试集
如下程序把数据分为一半训练、一半测试:
set.seed(1)
train_id <- sample(nrow(x), size=round(0.5*nrow(x)))
train <- rep(FALSE, nrow(x))
train[train_id] <- TRUE
test <- (!train)
y.test <- y[test]仅用训练集建立岭回归:
用建立的模型对测试集进行预测,并计算调节参数等于4时的均方误差:
## [1] 142199.2如果用因变量平均值作预测, 这是最差的预测:
## [1] 224669.9\(\lambda=4\)的结果要好得多。
事实上,取\(\lambda\)接近正无穷时模型就相当于用因变量平均值预测。
取\(\lambda=0\)就相当于普通最小二乘回归(但是glmnet()是对输入数据要做标准化的)。
15.3.2.2 用交叉验证选取调节参数
仍使用训练集,
但训练集再进行交叉验证。
cv.glmnet()函数可以执行交叉验证。
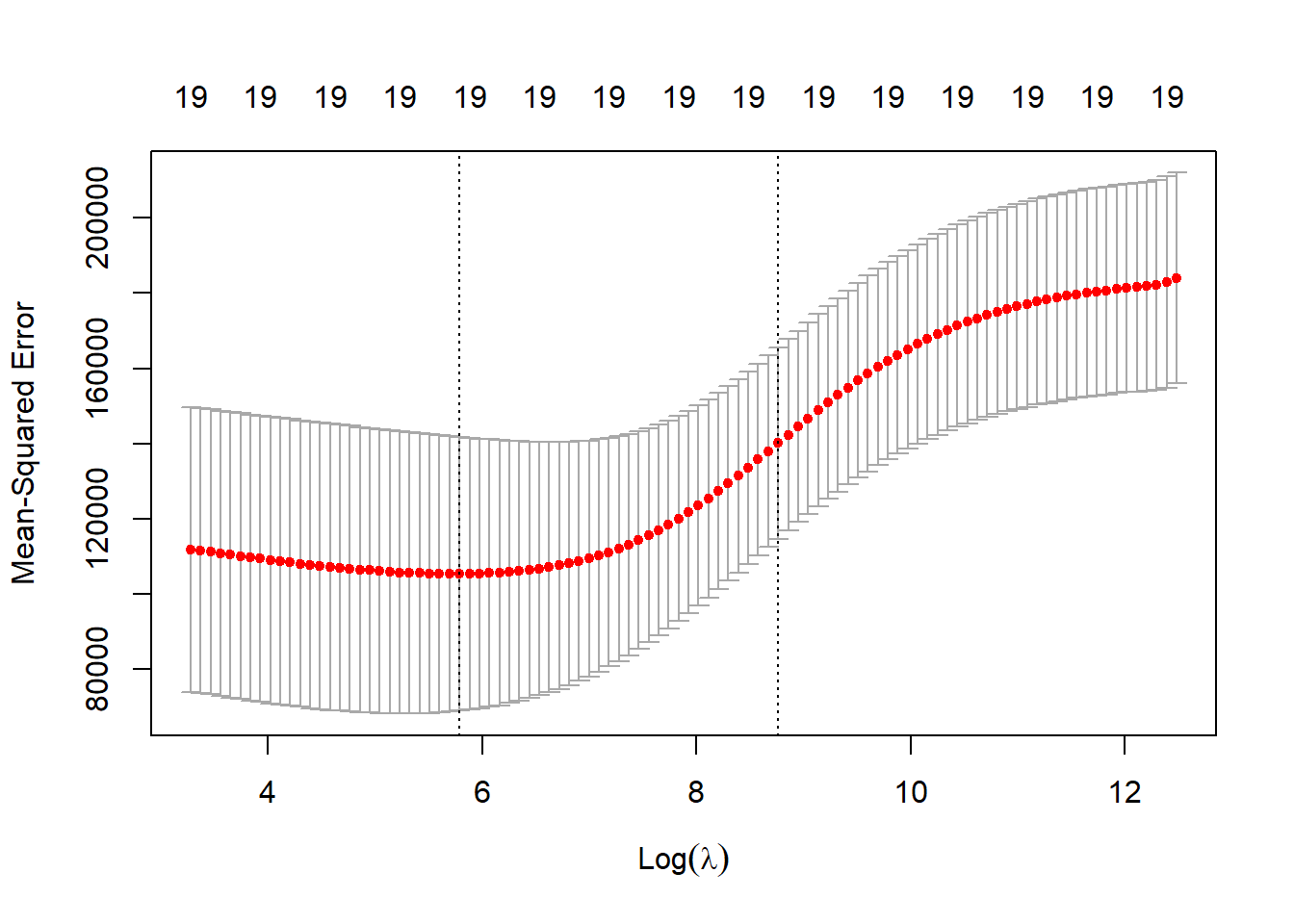
这样获得了最优调节参数\(\lambda=\) 326.0827865。 用最优调节参数对测试集作预测, 得到预测均方误差:
## [1] 139867结果比\(\lambda=4\)略有改进。
要注意的是, 在测试集上得到的误差评估结果, 会受到训练集与测试集随机划分的影响。 为了得到更可靠的泛化误差估计, 可以多次进行训练集与测试集划分, 将所有的误差评估指标进行平均。
在测试集上获得误差评估指标后, 用在训练集选取的最优调节系数对全数据集建模, 得到相应的岭回归系数估计:
## (Intercept) AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 15.44383120 0.07715547 0.85911582 0.60103106 1.06369007 0.87936105 1.62444617 1.35254778 0.01134999 0.05746654 0.40680157 0.11456224 0.12116504 0.05299202 22.09143197 -79.04032656 0.16619903 0.02941950 -1.36092945 9.1248776515.3.3 lasso回归
另一种对回归系数的惩罚是\(L_1\)惩罚: \[\begin{align} \min\; \sum_{i=1}^n \left( y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_p x_{ip} \right)^2 + \lambda \sum_{j=1}^p |\beta_j| . \tag{15.1} \end{align}\] 奇妙地是,适当选择调节参数\(\lambda\),可以使得部分回归系数变成零, 达到了即减小回归系数的绝对值又挑选重要变量子集的效果。
事实上,(15.1)等价于约束最小值问题 \[\begin{aligned} & \min\; \sum_{i=1}^n \left( y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_p x_{ip} \right)^2 \quad \text{s.t.} \\ & \sum_{j=1}^p |\beta_j| \leq s \end{aligned}\] 其中\(s\)与\(\lambda\)一一对应。 这样的约束区域是带有顶点的凸集, 而目标函数是二次函数, 最小值点经常在约束区域顶点达到, 这些顶点是某些坐标等于零的点。 见图15.1。
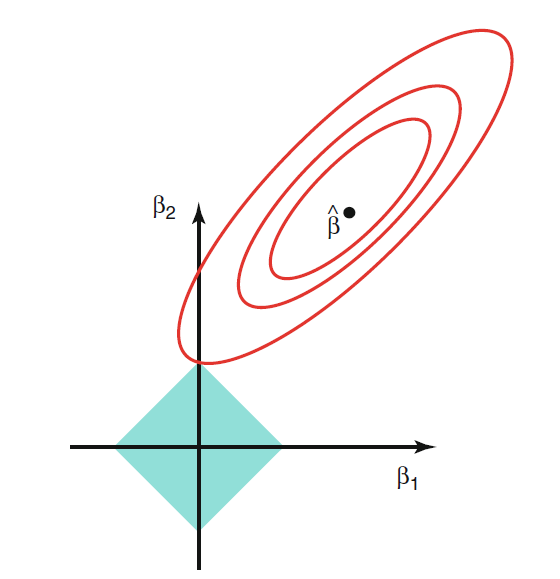
图15.1: Lasso约束优化问题图示
对于每个调节参数\(\lambda\), 都应该解出(15.1)的相应解, 记为\(\hat{\boldsymbol\beta}(\lambda)\)。 幸运的是, 不需要对每个\(\lambda\)去解最小值问题(15.1), 存在巧妙的算法使得问题的计算量与求解一次最小二乘相仿。
通常选取\(\lambda\)的格子点,计算相应的惩罚回归系数。 用交叉验证方法估计预测的均方误差。 选取使得交叉验证均方误差最小的调节参数(一般R函数中已经作为选项)。
用R的glmnet包计算lasso。
用glmnet()函数,
指定参数alpha=1时执行的是lasso。
用参数lambda=指定一个调节参数网格,
lasso将输出这些调节参数对应的结果。
对回归结果使用plot()函数可以画出调节参数变化时系数估计的变化情况。
为了选择调节参数并评估模型预测结果, 通常会:
- 把所有数据划分为训练集与测试集;
- 在训练集上执行五折或十折交叉验证, 从交叉验证的平均均方误差选择最优调节参数;
- 在测试集上计算预测平均误差;
- 最后,在全集是使用最优调节参数建模, 但是预测效果仍使用上面测试集得到的结果。
15.3.4 Lasso回归Hitters例子
仍使用gmlnet包的glmnet()函数计算Lasso回归,
指定一个调节参数网格(沿用前面的网格):
d <- na.omit(Hitters)
set.seed(1)
set.seed(1)
train_id <- sample(nrow(x), size=round(0.5*nrow(x)))
train <- rep(FALSE, nrow(x))
train[train_id] <- TRUE
test <- (!train)
y.test <- y[test]
lasso.mod <- glmnet(x[train,], y[train], alpha=1, lambda=grid)
plot(lasso.mod)## Warning in regularize.values(x, y, ties, missing(ties), na.rm = na.rm): collapsing to unique 'x' values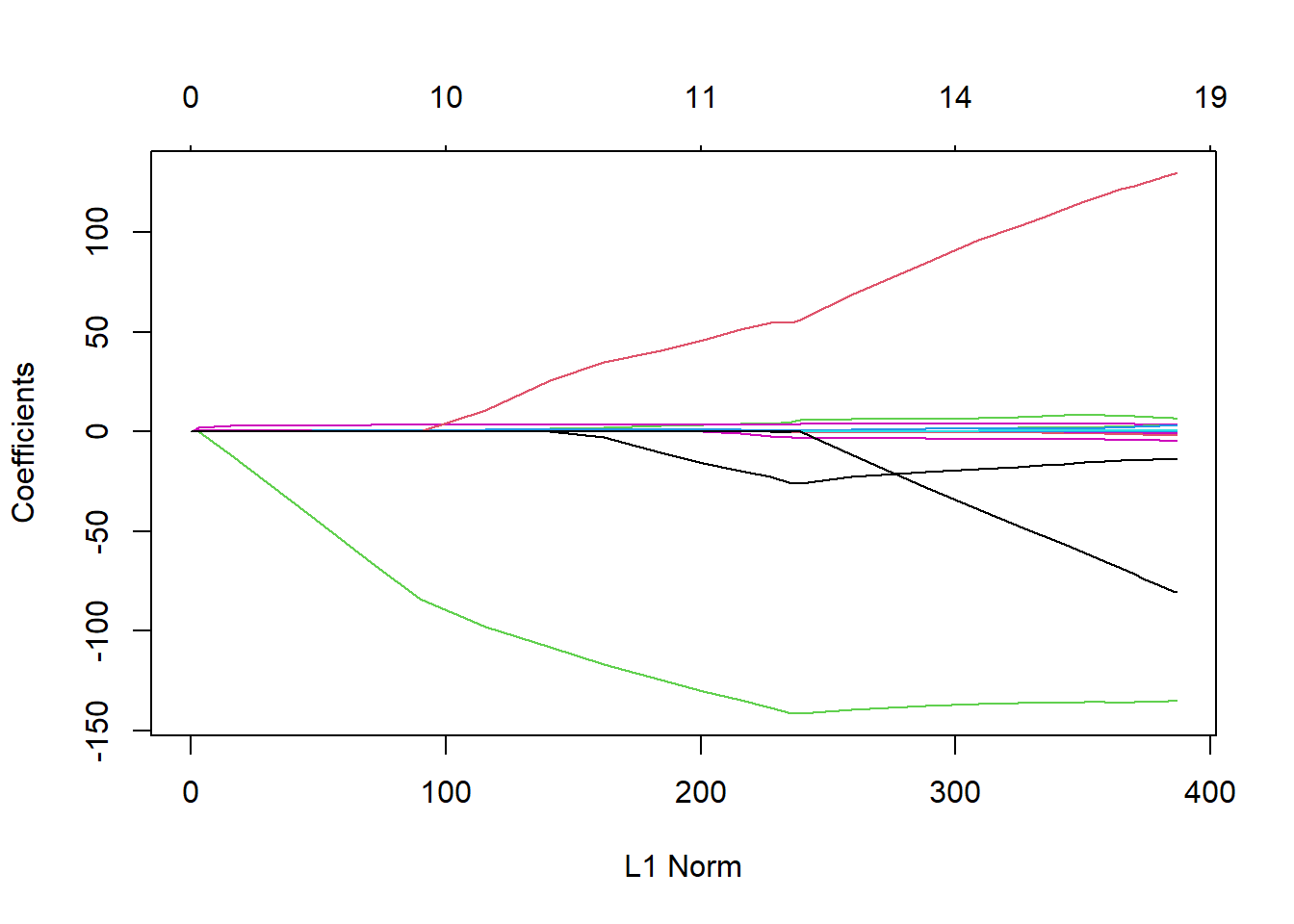
对lasso结果使用plot()函数可以绘制延调节参数网格变化的各回归系数估计,横坐标不是调节参数而是调节参数对应的系数绝对值和,
可以看出随着系数绝对值和增大,实际是调节参数变小,
更多地自变量进入模型。
15.3.4.1 用交叉验证估计调节参数
按照前面划分的训练集与测试集, 仅使用训练集数据做交叉验证估计最优调节参数:
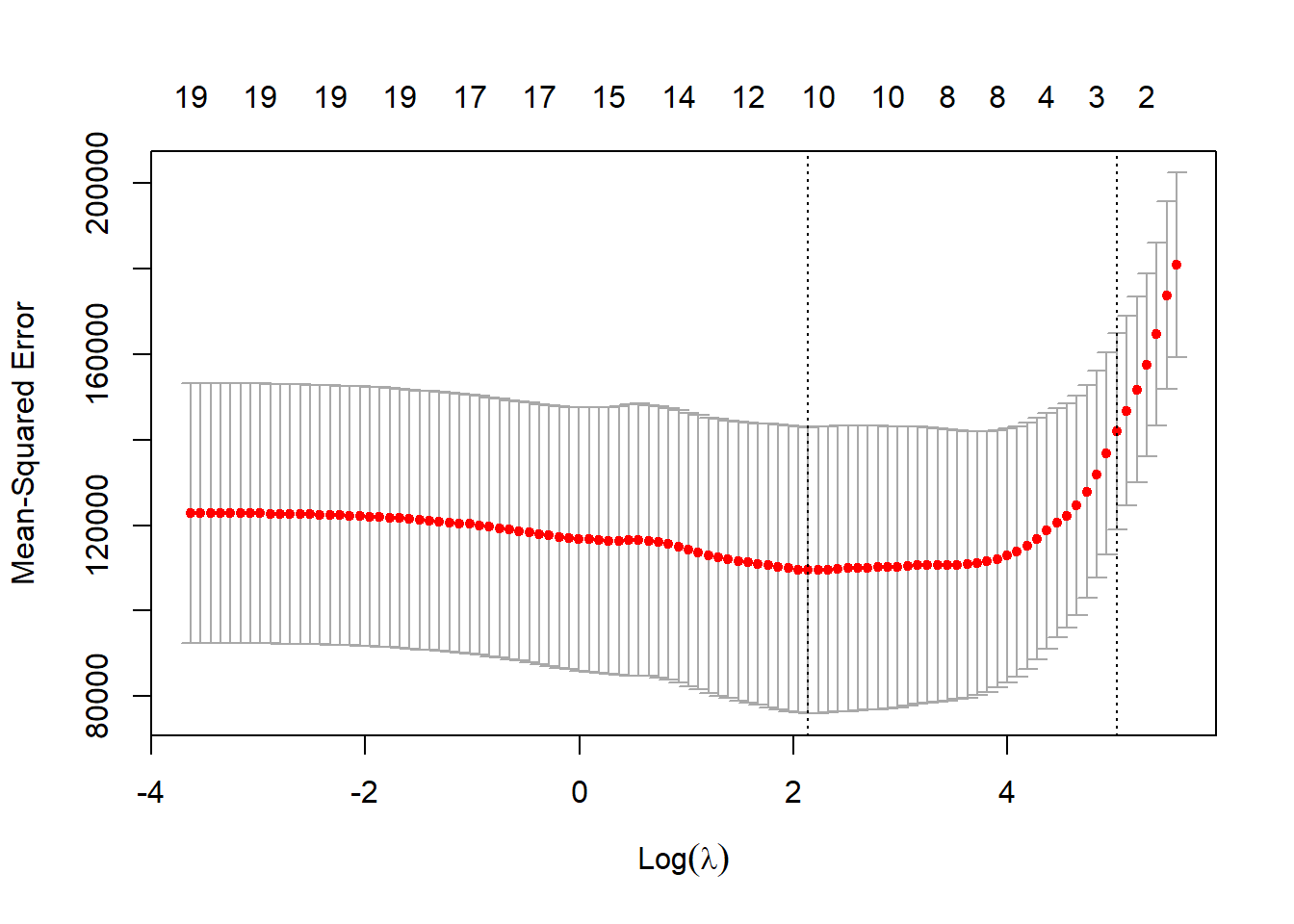
## [1] 8.461927得到调节参数估计后,对测试集计算预测均方误差:
## [1] 143816.9这个效果比岭回归效果略差。
为了充分利用数据, 使用前面获得的最优调节参数, 对全数据集建模:
out <- glmnet(x, y, alpha=1, lambda=grid)
lasso.coef <- predict(out, type='coefficients', s=bestlam)[1:20,]; lasso.coef## (Intercept) AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 1.52097206 -0.08656051 2.29115235 0.00000000 0.00000000 0.00000000 2.30681387 -0.53232640 0.00000000 0.00000000 0.04099882 0.22016773 0.41454813 0.00000000 22.41349696 -117.32653157 0.23956158 0.00000000 -0.98131662 0.00000000## (Intercept) AtBat Hits Walks Years CHmRun CRuns CRBI LeagueN DivisionW PutOuts Errors
## 1.52097206 -0.08656051 2.29115235 2.30681387 -0.53232640 0.04099882 0.22016773 0.41454813 22.41349696 -117.32653157 0.23956158 -0.98131662选择的自变量子集有11个自变量。
15.4 附录
15.4.1 Hitters数据
| AtBat | Hits | HmRun | Runs | RBI | Walks | Years | CAtBat | CHits | CHmRun | CRuns | CRBI | CWalks | League | Division | PutOuts | Assists | Errors | Salary | NewLeague | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -Andy Allanson | 293 | 66 | 1 | 30 | 29 | 14 | 1 | 293 | 66 | 1 | 30 | 29 | 14 | A | E | 446 | 33 | 20 | NA | A |
| -Alan Ashby | 315 | 81 | 7 | 24 | 38 | 39 | 14 | 3449 | 835 | 69 | 321 | 414 | 375 | N | W | 632 | 43 | 10 | 475.000 | N |
| -Alvin Davis | 479 | 130 | 18 | 66 | 72 | 76 | 3 | 1624 | 457 | 63 | 224 | 266 | 263 | A | W | 880 | 82 | 14 | 480.000 | A |
| -Andre Dawson | 496 | 141 | 20 | 65 | 78 | 37 | 11 | 5628 | 1575 | 225 | 828 | 838 | 354 | N | E | 200 | 11 | 3 | 500.000 | N |
| -Andres Galarraga | 321 | 87 | 10 | 39 | 42 | 30 | 2 | 396 | 101 | 12 | 48 | 46 | 33 | N | E | 805 | 40 | 4 | 91.500 | N |
| -Alfredo Griffin | 594 | 169 | 4 | 74 | 51 | 35 | 11 | 4408 | 1133 | 19 | 501 | 336 | 194 | A | W | 282 | 421 | 25 | 750.000 | A |
| -Al Newman | 185 | 37 | 1 | 23 | 8 | 21 | 2 | 214 | 42 | 1 | 30 | 9 | 24 | N | E | 76 | 127 | 7 | 70.000 | A |
| -Argenis Salazar | 298 | 73 | 0 | 24 | 24 | 7 | 3 | 509 | 108 | 0 | 41 | 37 | 12 | A | W | 121 | 283 | 9 | 100.000 | A |
| -Andres Thomas | 323 | 81 | 6 | 26 | 32 | 8 | 2 | 341 | 86 | 6 | 32 | 34 | 8 | N | W | 143 | 290 | 19 | 75.000 | N |
| -Andre Thornton | 401 | 92 | 17 | 49 | 66 | 65 | 13 | 5206 | 1332 | 253 | 784 | 890 | 866 | A | E | 0 | 0 | 0 | 1100.000 | A |
| -Alan Trammell | 574 | 159 | 21 | 107 | 75 | 59 | 10 | 4631 | 1300 | 90 | 702 | 504 | 488 | A | E | 238 | 445 | 22 | 517.143 | A |
| -Alex Trevino | 202 | 53 | 4 | 31 | 26 | 27 | 9 | 1876 | 467 | 15 | 192 | 186 | 161 | N | W | 304 | 45 | 11 | 512.500 | N |
| -Andy VanSlyke | 418 | 113 | 13 | 48 | 61 | 47 | 4 | 1512 | 392 | 41 | 205 | 204 | 203 | N | E | 211 | 11 | 7 | 550.000 | N |
| -Alan Wiggins | 239 | 60 | 0 | 30 | 11 | 22 | 6 | 1941 | 510 | 4 | 309 | 103 | 207 | A | E | 121 | 151 | 6 | 700.000 | A |
| -Bill Almon | 196 | 43 | 7 | 29 | 27 | 30 | 13 | 3231 | 825 | 36 | 376 | 290 | 238 | N | E | 80 | 45 | 8 | 240.000 | N |
| -Billy Beane | 183 | 39 | 3 | 20 | 15 | 11 | 3 | 201 | 42 | 3 | 20 | 16 | 11 | A | W | 118 | 0 | 0 | NA | A |
| -Buddy Bell | 568 | 158 | 20 | 89 | 75 | 73 | 15 | 8068 | 2273 | 177 | 1045 | 993 | 732 | N | W | 105 | 290 | 10 | 775.000 | N |
| -Buddy Biancalana | 190 | 46 | 2 | 24 | 8 | 15 | 5 | 479 | 102 | 5 | 65 | 23 | 39 | A | W | 102 | 177 | 16 | 175.000 | A |
| -Bruce Bochte | 407 | 104 | 6 | 57 | 43 | 65 | 12 | 5233 | 1478 | 100 | 643 | 658 | 653 | A | W | 912 | 88 | 9 | NA | A |
| -Bruce Bochy | 127 | 32 | 8 | 16 | 22 | 14 | 8 | 727 | 180 | 24 | 67 | 82 | 56 | N | W | 202 | 22 | 2 | 135.000 | N |
| -Barry Bonds | 413 | 92 | 16 | 72 | 48 | 65 | 1 | 413 | 92 | 16 | 72 | 48 | 65 | N | E | 280 | 9 | 5 | 100.000 | N |
| -Bobby Bonilla | 426 | 109 | 3 | 55 | 43 | 62 | 1 | 426 | 109 | 3 | 55 | 43 | 62 | A | W | 361 | 22 | 2 | 115.000 | N |
| -Bob Boone | 22 | 10 | 1 | 4 | 2 | 1 | 6 | 84 | 26 | 2 | 9 | 9 | 3 | A | W | 812 | 84 | 11 | NA | A |
| -Bob Brenly | 472 | 116 | 16 | 60 | 62 | 74 | 6 | 1924 | 489 | 67 | 242 | 251 | 240 | N | W | 518 | 55 | 3 | 600.000 | N |
| -Bill Buckner | 629 | 168 | 18 | 73 | 102 | 40 | 18 | 8424 | 2464 | 164 | 1008 | 1072 | 402 | A | E | 1067 | 157 | 14 | 776.667 | A |
| -Brett Butler | 587 | 163 | 4 | 92 | 51 | 70 | 6 | 2695 | 747 | 17 | 442 | 198 | 317 | A | E | 434 | 9 | 3 | 765.000 | A |
| -Bob Dernier | 324 | 73 | 4 | 32 | 18 | 22 | 7 | 1931 | 491 | 13 | 291 | 108 | 180 | N | E | 222 | 3 | 3 | 708.333 | N |
| -Bo Diaz | 474 | 129 | 10 | 50 | 56 | 40 | 10 | 2331 | 604 | 61 | 246 | 327 | 166 | N | W | 732 | 83 | 13 | 750.000 | N |
| -Bill Doran | 550 | 152 | 6 | 92 | 37 | 81 | 5 | 2308 | 633 | 32 | 349 | 182 | 308 | N | W | 262 | 329 | 16 | 625.000 | N |
| -Brian Downing | 513 | 137 | 20 | 90 | 95 | 90 | 14 | 5201 | 1382 | 166 | 763 | 734 | 784 | A | W | 267 | 5 | 3 | 900.000 | A |
| -Bobby Grich | 313 | 84 | 9 | 42 | 30 | 39 | 17 | 6890 | 1833 | 224 | 1033 | 864 | 1087 | A | W | 127 | 221 | 7 | NA | A |
| -Billy Hatcher | 419 | 108 | 6 | 55 | 36 | 22 | 3 | 591 | 149 | 8 | 80 | 46 | 31 | N | W | 226 | 7 | 4 | 110.000 | N |
| -Bob Horner | 517 | 141 | 27 | 70 | 87 | 52 | 9 | 3571 | 994 | 215 | 545 | 652 | 337 | N | W | 1378 | 102 | 8 | NA | N |
| -Brook Jacoby | 583 | 168 | 17 | 83 | 80 | 56 | 5 | 1646 | 452 | 44 | 219 | 208 | 136 | A | E | 109 | 292 | 25 | 612.500 | A |
| -Bob Kearney | 204 | 49 | 6 | 23 | 25 | 12 | 7 | 1309 | 308 | 27 | 126 | 132 | 66 | A | W | 419 | 46 | 5 | 300.000 | A |
| -Bill Madlock | 379 | 106 | 10 | 38 | 60 | 30 | 14 | 6207 | 1906 | 146 | 859 | 803 | 571 | N | W | 72 | 170 | 24 | 850.000 | N |
| -Bobby Meacham | 161 | 36 | 0 | 19 | 10 | 17 | 4 | 1053 | 244 | 3 | 156 | 86 | 107 | A | E | 70 | 149 | 12 | NA | A |
| -Bob Melvin | 268 | 60 | 5 | 24 | 25 | 15 | 2 | 350 | 78 | 5 | 34 | 29 | 18 | N | W | 442 | 59 | 6 | 90.000 | N |
| -Ben Oglivie | 346 | 98 | 5 | 31 | 53 | 30 | 16 | 5913 | 1615 | 235 | 784 | 901 | 560 | A | E | 0 | 0 | 0 | NA | A |
| -Bip Roberts | 241 | 61 | 1 | 34 | 12 | 14 | 1 | 241 | 61 | 1 | 34 | 12 | 14 | N | W | 166 | 172 | 10 | NA | N |
| -BillyJo Robidoux | 181 | 41 | 1 | 15 | 21 | 33 | 2 | 232 | 50 | 4 | 20 | 29 | 45 | A | E | 326 | 29 | 5 | 67.500 | A |
| -Bill Russell | 216 | 54 | 0 | 21 | 18 | 15 | 18 | 7318 | 1926 | 46 | 796 | 627 | 483 | N | W | 103 | 84 | 5 | NA | N |
| -Billy Sample | 200 | 57 | 6 | 23 | 14 | 14 | 9 | 2516 | 684 | 46 | 371 | 230 | 195 | N | W | 69 | 1 | 1 | NA | N |
| -Bill Schroeder | 217 | 46 | 7 | 32 | 19 | 9 | 4 | 694 | 160 | 32 | 86 | 76 | 32 | A | E | 307 | 25 | 1 | 180.000 | A |
| -Butch Wynegar | 194 | 40 | 7 | 19 | 29 | 30 | 11 | 4183 | 1069 | 64 | 486 | 493 | 608 | A | E | 325 | 22 | 2 | NA | A |
| -Chris Bando | 254 | 68 | 2 | 28 | 26 | 22 | 6 | 999 | 236 | 21 | 108 | 117 | 118 | A | E | 359 | 30 | 4 | 305.000 | A |
| -Chris Brown | 416 | 132 | 7 | 57 | 49 | 33 | 3 | 932 | 273 | 24 | 113 | 121 | 80 | N | W | 73 | 177 | 18 | 215.000 | N |
| -Carmen Castillo | 205 | 57 | 8 | 34 | 32 | 9 | 5 | 756 | 192 | 32 | 117 | 107 | 51 | A | E | 58 | 4 | 4 | 247.500 | A |
| -Cecil Cooper | 542 | 140 | 12 | 46 | 75 | 41 | 16 | 7099 | 2130 | 235 | 987 | 1089 | 431 | A | E | 697 | 61 | 9 | NA | A |
| -Chili Davis | 526 | 146 | 13 | 71 | 70 | 84 | 6 | 2648 | 715 | 77 | 352 | 342 | 289 | N | W | 303 | 9 | 9 | 815.000 | N |
| -Carlton Fisk | 457 | 101 | 14 | 42 | 63 | 22 | 17 | 6521 | 1767 | 281 | 1003 | 977 | 619 | A | W | 389 | 39 | 4 | 875.000 | A |
| -Curt Ford | 214 | 53 | 2 | 30 | 29 | 23 | 2 | 226 | 59 | 2 | 32 | 32 | 27 | N | E | 109 | 7 | 3 | 70.000 | N |
| -Cliff Johnson | 19 | 7 | 0 | 1 | 2 | 1 | 4 | 41 | 13 | 1 | 3 | 4 | 4 | A | E | 0 | 0 | 0 | NA | A |
| -Carney Lansford | 591 | 168 | 19 | 80 | 72 | 39 | 9 | 4478 | 1307 | 113 | 634 | 563 | 319 | A | W | 67 | 147 | 4 | 1200.000 | A |
| -Chet Lemon | 403 | 101 | 12 | 45 | 53 | 39 | 12 | 5150 | 1429 | 166 | 747 | 666 | 526 | A | E | 316 | 6 | 5 | 675.000 | A |
| -Candy Maldonado | 405 | 102 | 18 | 49 | 85 | 20 | 6 | 950 | 231 | 29 | 99 | 138 | 64 | N | W | 161 | 10 | 3 | 415.000 | N |
| -Carmelo Martinez | 244 | 58 | 9 | 28 | 25 | 35 | 4 | 1335 | 333 | 49 | 164 | 179 | 194 | N | W | 142 | 14 | 2 | 340.000 | N |
| -Charlie Moore | 235 | 61 | 3 | 24 | 39 | 21 | 14 | 3926 | 1029 | 35 | 441 | 401 | 333 | A | E | 425 | 43 | 4 | NA | A |
| -Craig Reynolds | 313 | 78 | 6 | 32 | 41 | 12 | 12 | 3742 | 968 | 35 | 409 | 321 | 170 | N | W | 106 | 206 | 7 | 416.667 | N |
| -Cal Ripken | 627 | 177 | 25 | 98 | 81 | 70 | 6 | 3210 | 927 | 133 | 529 | 472 | 313 | A | E | 240 | 482 | 13 | 1350.000 | A |
| -Cory Snyder | 416 | 113 | 24 | 58 | 69 | 16 | 1 | 416 | 113 | 24 | 58 | 69 | 16 | A | E | 203 | 70 | 10 | 90.000 | A |
| -Chris Speier | 155 | 44 | 6 | 21 | 23 | 15 | 16 | 6631 | 1634 | 98 | 698 | 661 | 777 | N | E | 53 | 88 | 3 | 275.000 | N |
| -Curt Wilkerson | 236 | 56 | 0 | 27 | 15 | 11 | 4 | 1115 | 270 | 1 | 116 | 64 | 57 | A | W | 125 | 199 | 13 | 230.000 | A |
| -Dave Anderson | 216 | 53 | 1 | 31 | 15 | 22 | 4 | 926 | 210 | 9 | 118 | 69 | 114 | N | W | 73 | 152 | 11 | 225.000 | N |
| -Doug Baker | 24 | 3 | 0 | 1 | 0 | 2 | 3 | 159 | 28 | 0 | 20 | 12 | 9 | A | W | 80 | 4 | 0 | NA | A |
| -Don Baylor | 585 | 139 | 31 | 93 | 94 | 62 | 17 | 7546 | 1982 | 315 | 1141 | 1179 | 727 | A | E | 0 | 0 | 0 | 950.000 | A |
| -Dann Bilardello | 191 | 37 | 4 | 12 | 17 | 14 | 4 | 773 | 163 | 16 | 61 | 74 | 52 | N | E | 391 | 38 | 8 | NA | N |
| -Daryl Boston | 199 | 53 | 5 | 29 | 22 | 21 | 3 | 514 | 120 | 8 | 57 | 40 | 39 | A | W | 152 | 3 | 5 | 75.000 | A |
| -Darnell Coles | 521 | 142 | 20 | 67 | 86 | 45 | 4 | 815 | 205 | 22 | 99 | 103 | 78 | A | E | 107 | 242 | 23 | 105.000 | A |
| -Dave Collins | 419 | 113 | 1 | 44 | 27 | 44 | 12 | 4484 | 1231 | 32 | 612 | 344 | 422 | A | E | 211 | 2 | 1 | NA | A |
| -Dave Concepcion | 311 | 81 | 3 | 42 | 30 | 26 | 17 | 8247 | 2198 | 100 | 950 | 909 | 690 | N | W | 153 | 223 | 10 | 320.000 | N |
| -Darren Daulton | 138 | 31 | 8 | 18 | 21 | 38 | 3 | 244 | 53 | 12 | 33 | 32 | 55 | N | E | 244 | 21 | 4 | NA | N |
| -Doug DeCinces | 512 | 131 | 26 | 69 | 96 | 52 | 14 | 5347 | 1397 | 221 | 712 | 815 | 548 | A | W | 119 | 216 | 12 | 850.000 | A |
| -Darrell Evans | 507 | 122 | 29 | 78 | 85 | 91 | 18 | 7761 | 1947 | 347 | 1175 | 1152 | 1380 | A | E | 808 | 108 | 2 | 535.000 | A |
| -Dwight Evans | 529 | 137 | 26 | 86 | 97 | 97 | 15 | 6661 | 1785 | 291 | 1082 | 949 | 989 | A | E | 280 | 10 | 5 | 933.333 | A |
| -Damaso Garcia | 424 | 119 | 6 | 57 | 46 | 13 | 9 | 3651 | 1046 | 32 | 461 | 301 | 112 | A | E | 224 | 286 | 8 | 850.000 | N |
| -Dan Gladden | 351 | 97 | 4 | 55 | 29 | 39 | 4 | 1258 | 353 | 16 | 196 | 110 | 117 | N | W | 226 | 7 | 3 | 210.000 | A |
| -Danny Heep | 195 | 55 | 5 | 24 | 33 | 30 | 8 | 1313 | 338 | 25 | 144 | 149 | 153 | N | E | 83 | 2 | 1 | NA | N |
| -Dave Henderson | 388 | 103 | 15 | 59 | 47 | 39 | 6 | 2174 | 555 | 80 | 285 | 274 | 186 | A | W | 182 | 9 | 4 | 325.000 | A |
| -Donnie Hill | 339 | 96 | 4 | 37 | 29 | 23 | 4 | 1064 | 290 | 11 | 123 | 108 | 55 | A | W | 104 | 213 | 9 | 275.000 | A |
| -Dave Kingman | 561 | 118 | 35 | 70 | 94 | 33 | 16 | 6677 | 1575 | 442 | 901 | 1210 | 608 | A | W | 463 | 32 | 8 | NA | A |
| -Davey Lopes | 255 | 70 | 7 | 49 | 35 | 43 | 15 | 6311 | 1661 | 154 | 1019 | 608 | 820 | N | E | 51 | 54 | 8 | 450.000 | N |
| -Don Mattingly | 677 | 238 | 31 | 117 | 113 | 53 | 5 | 2223 | 737 | 93 | 349 | 401 | 171 | A | E | 1377 | 100 | 6 | 1975.000 | A |
| -Darryl Motley | 227 | 46 | 7 | 23 | 20 | 12 | 5 | 1325 | 324 | 44 | 156 | 158 | 67 | A | W | 92 | 2 | 2 | NA | A |
| -Dale Murphy | 614 | 163 | 29 | 89 | 83 | 75 | 11 | 5017 | 1388 | 266 | 813 | 822 | 617 | N | W | 303 | 6 | 6 | 1900.000 | N |
| -Dwayne Murphy | 329 | 83 | 9 | 50 | 39 | 56 | 9 | 3828 | 948 | 145 | 575 | 528 | 635 | A | W | 276 | 6 | 2 | 600.000 | A |
| -Dave Parker | 637 | 174 | 31 | 89 | 116 | 56 | 14 | 6727 | 2024 | 247 | 978 | 1093 | 495 | N | W | 278 | 9 | 9 | 1041.667 | N |
| -Dan Pasqua | 280 | 82 | 16 | 44 | 45 | 47 | 2 | 428 | 113 | 25 | 61 | 70 | 63 | A | E | 148 | 4 | 2 | 110.000 | A |
| -Darrell Porter | 155 | 41 | 12 | 21 | 29 | 22 | 16 | 5409 | 1338 | 181 | 746 | 805 | 875 | A | W | 165 | 9 | 1 | 260.000 | A |
| -Dick Schofield | 458 | 114 | 13 | 67 | 57 | 48 | 4 | 1350 | 298 | 28 | 160 | 123 | 122 | A | W | 246 | 389 | 18 | 475.000 | A |
| -Don Slaught | 314 | 83 | 13 | 39 | 46 | 16 | 5 | 1457 | 405 | 28 | 156 | 159 | 76 | A | W | 533 | 40 | 4 | 431.500 | A |
| -Darryl Strawberry | 475 | 123 | 27 | 76 | 93 | 72 | 4 | 1810 | 471 | 108 | 292 | 343 | 267 | N | E | 226 | 10 | 6 | 1220.000 | N |
| -Dale Sveum | 317 | 78 | 7 | 35 | 35 | 32 | 1 | 317 | 78 | 7 | 35 | 35 | 32 | A | E | 45 | 122 | 26 | 70.000 | A |
| -Danny Tartabull | 511 | 138 | 25 | 76 | 96 | 61 | 3 | 592 | 164 | 28 | 87 | 110 | 71 | A | W | 157 | 7 | 8 | 145.000 | A |
| -Dickie Thon | 278 | 69 | 3 | 24 | 21 | 29 | 8 | 2079 | 565 | 32 | 258 | 192 | 162 | N | W | 142 | 210 | 10 | NA | N |
| -Denny Walling | 382 | 119 | 13 | 54 | 58 | 36 | 12 | 2133 | 594 | 41 | 287 | 294 | 227 | N | W | 59 | 156 | 9 | 595.000 | N |
| -Dave Winfield | 565 | 148 | 24 | 90 | 104 | 77 | 14 | 7287 | 2083 | 305 | 1135 | 1234 | 791 | A | E | 292 | 9 | 5 | 1861.460 | A |
| -Enos Cabell | 277 | 71 | 2 | 27 | 29 | 14 | 15 | 5952 | 1647 | 60 | 753 | 596 | 259 | N | W | 360 | 32 | 5 | NA | N |
| -Eric Davis | 415 | 115 | 27 | 97 | 71 | 68 | 3 | 711 | 184 | 45 | 156 | 119 | 99 | N | W | 274 | 2 | 7 | 300.000 | N |
| -Eddie Milner | 424 | 110 | 15 | 70 | 47 | 36 | 7 | 2130 | 544 | 38 | 335 | 174 | 258 | N | W | 292 | 6 | 3 | 490.000 | N |
| -Eddie Murray | 495 | 151 | 17 | 61 | 84 | 78 | 10 | 5624 | 1679 | 275 | 884 | 1015 | 709 | A | E | 1045 | 88 | 13 | 2460.000 | A |
| -Ernest Riles | 524 | 132 | 9 | 69 | 47 | 54 | 2 | 972 | 260 | 14 | 123 | 92 | 90 | A | E | 212 | 327 | 20 | NA | A |
| -Ed Romero | 233 | 49 | 2 | 41 | 23 | 18 | 8 | 1350 | 336 | 7 | 166 | 122 | 106 | A | E | 102 | 132 | 10 | 375.000 | A |
| -Ernie Whitt | 395 | 106 | 16 | 48 | 56 | 35 | 10 | 2303 | 571 | 86 | 266 | 323 | 248 | A | E | 709 | 41 | 7 | NA | A |
| -Fred Lynn | 397 | 114 | 23 | 67 | 67 | 53 | 13 | 5589 | 1632 | 241 | 906 | 926 | 716 | A | E | 244 | 2 | 4 | NA | A |
| -Floyd Rayford | 210 | 37 | 8 | 15 | 19 | 15 | 6 | 994 | 244 | 36 | 107 | 114 | 53 | A | E | 40 | 115 | 15 | NA | A |
| -Franklin Stubbs | 420 | 95 | 23 | 55 | 58 | 37 | 3 | 646 | 139 | 31 | 77 | 77 | 61 | N | W | 206 | 10 | 7 | NA | N |
| -Frank White | 566 | 154 | 22 | 76 | 84 | 43 | 14 | 6100 | 1583 | 131 | 743 | 693 | 300 | A | W | 316 | 439 | 10 | 750.000 | A |
| -George Bell | 641 | 198 | 31 | 101 | 108 | 41 | 5 | 2129 | 610 | 92 | 297 | 319 | 117 | A | E | 269 | 17 | 10 | 1175.000 | A |
| -Glenn Braggs | 215 | 51 | 4 | 19 | 18 | 11 | 1 | 215 | 51 | 4 | 19 | 18 | 11 | A | E | 116 | 5 | 12 | 70.000 | A |
| -George Brett | 441 | 128 | 16 | 70 | 73 | 80 | 14 | 6675 | 2095 | 209 | 1072 | 1050 | 695 | A | W | 97 | 218 | 16 | 1500.000 | A |
| -Greg Brock | 325 | 76 | 16 | 33 | 52 | 37 | 5 | 1506 | 351 | 71 | 195 | 219 | 214 | N | W | 726 | 87 | 3 | 385.000 | A |
| -Gary Carter | 490 | 125 | 24 | 81 | 105 | 62 | 13 | 6063 | 1646 | 271 | 847 | 999 | 680 | N | E | 869 | 62 | 8 | 1925.571 | N |
| -Glenn Davis | 574 | 152 | 31 | 91 | 101 | 64 | 3 | 985 | 260 | 53 | 148 | 173 | 95 | N | W | 1253 | 111 | 11 | 215.000 | N |
| -George Foster | 284 | 64 | 14 | 30 | 42 | 24 | 18 | 7023 | 1925 | 348 | 986 | 1239 | 666 | N | E | 96 | 4 | 4 | NA | N |
| -Gary Gaetti | 596 | 171 | 34 | 91 | 108 | 52 | 6 | 2862 | 728 | 107 | 361 | 401 | 224 | A | W | 118 | 334 | 21 | 900.000 | A |
| -Greg Gagne | 472 | 118 | 12 | 63 | 54 | 30 | 4 | 793 | 187 | 14 | 102 | 80 | 50 | A | W | 228 | 377 | 26 | 155.000 | A |
| -George Hendrick | 283 | 77 | 14 | 45 | 47 | 26 | 16 | 6840 | 1910 | 259 | 915 | 1067 | 546 | A | W | 144 | 6 | 5 | 700.000 | A |
| -Glenn Hubbard | 408 | 94 | 4 | 42 | 36 | 66 | 9 | 3573 | 866 | 59 | 429 | 365 | 410 | N | W | 282 | 487 | 19 | 535.000 | N |
| -Garth Iorg | 327 | 85 | 3 | 30 | 44 | 20 | 8 | 2140 | 568 | 16 | 216 | 208 | 93 | A | E | 91 | 185 | 12 | 362.500 | A |
| -Gary Matthews | 370 | 96 | 21 | 49 | 46 | 60 | 15 | 6986 | 1972 | 231 | 1070 | 955 | 921 | N | E | 137 | 5 | 9 | 733.333 | N |
| -Graig Nettles | 354 | 77 | 16 | 36 | 55 | 41 | 20 | 8716 | 2172 | 384 | 1172 | 1267 | 1057 | N | W | 83 | 174 | 16 | 200.000 | N |
| -Gary Pettis | 539 | 139 | 5 | 93 | 58 | 69 | 5 | 1469 | 369 | 12 | 247 | 126 | 198 | A | W | 462 | 9 | 7 | 400.000 | A |
| -Gary Redus | 340 | 84 | 11 | 62 | 33 | 47 | 5 | 1516 | 376 | 42 | 284 | 141 | 219 | N | E | 185 | 8 | 4 | 400.000 | A |
| -Garry Templeton | 510 | 126 | 2 | 42 | 44 | 35 | 11 | 5562 | 1578 | 44 | 703 | 519 | 256 | N | W | 207 | 358 | 20 | 737.500 | N |
| -Gorman Thomas | 315 | 59 | 16 | 45 | 36 | 58 | 13 | 4677 | 1051 | 268 | 681 | 782 | 697 | A | W | 0 | 0 | 0 | NA | A |
| -Greg Walker | 282 | 78 | 13 | 37 | 51 | 29 | 5 | 1649 | 453 | 73 | 211 | 280 | 138 | A | W | 670 | 57 | 5 | 500.000 | A |
| -Gary Ward | 380 | 120 | 5 | 54 | 51 | 31 | 8 | 3118 | 900 | 92 | 444 | 419 | 240 | A | W | 237 | 8 | 1 | 600.000 | A |
| -Glenn Wilson | 584 | 158 | 15 | 70 | 84 | 42 | 5 | 2358 | 636 | 58 | 265 | 316 | 134 | N | E | 331 | 20 | 4 | 662.500 | N |
| -Harold Baines | 570 | 169 | 21 | 72 | 88 | 38 | 7 | 3754 | 1077 | 140 | 492 | 589 | 263 | A | W | 295 | 15 | 5 | 950.000 | A |
| -Hubie Brooks | 306 | 104 | 14 | 50 | 58 | 25 | 7 | 2954 | 822 | 55 | 313 | 377 | 187 | N | E | 116 | 222 | 15 | 750.000 | N |
| -Howard Johnson | 220 | 54 | 10 | 30 | 39 | 31 | 5 | 1185 | 299 | 40 | 145 | 154 | 128 | N | E | 50 | 136 | 20 | 297.500 | N |
| -Hal McRae | 278 | 70 | 7 | 22 | 37 | 18 | 18 | 7186 | 2081 | 190 | 935 | 1088 | 643 | A | W | 0 | 0 | 0 | 325.000 | A |
| -Harold Reynolds | 445 | 99 | 1 | 46 | 24 | 29 | 4 | 618 | 129 | 1 | 72 | 31 | 48 | A | W | 278 | 415 | 16 | 87.500 | A |
| -Harry Spilman | 143 | 39 | 5 | 18 | 30 | 15 | 9 | 639 | 151 | 16 | 80 | 97 | 61 | N | W | 138 | 15 | 1 | 175.000 | N |
| -Herm Winningham | 185 | 40 | 4 | 23 | 11 | 18 | 3 | 524 | 125 | 7 | 58 | 37 | 47 | N | E | 97 | 2 | 2 | 90.000 | N |
| -Jesse Barfield | 589 | 170 | 40 | 107 | 108 | 69 | 6 | 2325 | 634 | 128 | 371 | 376 | 238 | A | E | 368 | 20 | 3 | 1237.500 | A |
| -Juan Beniquez | 343 | 103 | 6 | 48 | 36 | 40 | 15 | 4338 | 1193 | 70 | 581 | 421 | 325 | A | E | 211 | 56 | 13 | 430.000 | A |
| -Juan Bonilla | 284 | 69 | 1 | 33 | 18 | 25 | 5 | 1407 | 361 | 6 | 139 | 98 | 111 | A | E | 122 | 140 | 5 | NA | N |
| -John Cangelosi | 438 | 103 | 2 | 65 | 32 | 71 | 2 | 440 | 103 | 2 | 67 | 32 | 71 | A | W | 276 | 7 | 9 | 100.000 | N |
| -Jose Canseco | 600 | 144 | 33 | 85 | 117 | 65 | 2 | 696 | 173 | 38 | 101 | 130 | 69 | A | W | 319 | 4 | 14 | 165.000 | A |
| -Joe Carter | 663 | 200 | 29 | 108 | 121 | 32 | 4 | 1447 | 404 | 57 | 210 | 222 | 68 | A | E | 241 | 8 | 6 | 250.000 | A |
| -Jack Clark | 232 | 55 | 9 | 34 | 23 | 45 | 12 | 4405 | 1213 | 194 | 702 | 705 | 625 | N | E | 623 | 35 | 3 | 1300.000 | N |
| -Jose Cruz | 479 | 133 | 10 | 48 | 72 | 55 | 17 | 7472 | 2147 | 153 | 980 | 1032 | 854 | N | W | 237 | 5 | 4 | 773.333 | N |
| -Julio Cruz | 209 | 45 | 0 | 38 | 19 | 42 | 10 | 3859 | 916 | 23 | 557 | 279 | 478 | A | W | 132 | 205 | 5 | NA | A |
| -Jody Davis | 528 | 132 | 21 | 61 | 74 | 41 | 6 | 2641 | 671 | 97 | 273 | 383 | 226 | N | E | 885 | 105 | 8 | 1008.333 | N |
| -Jim Dwyer | 160 | 39 | 8 | 18 | 31 | 22 | 14 | 2128 | 543 | 56 | 304 | 268 | 298 | A | E | 33 | 3 | 0 | 275.000 | A |
| -Julio Franco | 599 | 183 | 10 | 80 | 74 | 32 | 5 | 2482 | 715 | 27 | 330 | 326 | 158 | A | E | 231 | 374 | 18 | 775.000 | A |
| -Jim Gantner | 497 | 136 | 7 | 58 | 38 | 26 | 11 | 3871 | 1066 | 40 | 450 | 367 | 241 | A | E | 304 | 347 | 10 | 850.000 | A |
| -Johnny Grubb | 210 | 70 | 13 | 32 | 51 | 28 | 15 | 4040 | 1130 | 97 | 544 | 462 | 551 | A | E | 0 | 0 | 0 | 365.000 | A |
| -Jerry Hairston | 225 | 61 | 5 | 32 | 26 | 26 | 11 | 1568 | 408 | 25 | 202 | 185 | 257 | A | W | 132 | 9 | 0 | NA | A |
| -Jack Howell | 151 | 41 | 4 | 26 | 21 | 19 | 2 | 288 | 68 | 9 | 45 | 39 | 35 | A | W | 28 | 56 | 2 | 95.000 | A |
| -John Kruk | 278 | 86 | 4 | 33 | 38 | 45 | 1 | 278 | 86 | 4 | 33 | 38 | 45 | N | W | 102 | 4 | 2 | 110.000 | N |
| -Jeffrey Leonard | 341 | 95 | 6 | 48 | 42 | 20 | 10 | 2964 | 808 | 81 | 379 | 428 | 221 | N | W | 158 | 4 | 5 | 100.000 | N |
| -Jim Morrison | 537 | 147 | 23 | 58 | 88 | 47 | 10 | 2744 | 730 | 97 | 302 | 351 | 174 | N | E | 92 | 257 | 20 | 277.500 | N |
| -John Moses | 399 | 102 | 3 | 56 | 34 | 34 | 5 | 670 | 167 | 4 | 89 | 48 | 54 | A | W | 211 | 9 | 3 | 80.000 | A |
| -Jerry Mumphrey | 309 | 94 | 5 | 37 | 32 | 26 | 13 | 4618 | 1330 | 57 | 616 | 522 | 436 | N | E | 161 | 3 | 3 | 600.000 | N |
| -Joe Orsulak | 401 | 100 | 2 | 60 | 19 | 28 | 4 | 876 | 238 | 2 | 126 | 44 | 55 | N | E | 193 | 11 | 4 | NA | N |
| -Jorge Orta | 336 | 93 | 9 | 35 | 46 | 23 | 15 | 5779 | 1610 | 128 | 730 | 741 | 497 | A | W | 0 | 0 | 0 | NA | A |
| -Jim Presley | 616 | 163 | 27 | 83 | 107 | 32 | 3 | 1437 | 377 | 65 | 181 | 227 | 82 | A | W | 110 | 308 | 15 | 200.000 | A |
| -Jamie Quirk | 219 | 47 | 8 | 24 | 26 | 17 | 12 | 1188 | 286 | 23 | 100 | 125 | 63 | A | W | 260 | 58 | 4 | NA | A |
| -Johnny Ray | 579 | 174 | 7 | 67 | 78 | 58 | 6 | 3053 | 880 | 32 | 366 | 337 | 218 | N | E | 280 | 479 | 5 | 657.000 | N |
| -Jeff Reed | 165 | 39 | 2 | 13 | 9 | 16 | 3 | 196 | 44 | 2 | 18 | 10 | 18 | A | W | 332 | 19 | 2 | 75.000 | N |
| -Jim Rice | 618 | 200 | 20 | 98 | 110 | 62 | 13 | 7127 | 2163 | 351 | 1104 | 1289 | 564 | A | E | 330 | 16 | 8 | 2412.500 | A |
| -Jerry Royster | 257 | 66 | 5 | 31 | 26 | 32 | 14 | 3910 | 979 | 33 | 518 | 324 | 382 | N | W | 87 | 166 | 14 | 250.000 | A |
| -John Russell | 315 | 76 | 13 | 35 | 60 | 25 | 3 | 630 | 151 | 24 | 68 | 94 | 55 | N | E | 498 | 39 | 13 | 155.000 | N |
| -Juan Samuel | 591 | 157 | 16 | 90 | 78 | 26 | 4 | 2020 | 541 | 52 | 310 | 226 | 91 | N | E | 290 | 440 | 25 | 640.000 | N |
| -John Shelby | 404 | 92 | 11 | 54 | 49 | 18 | 6 | 1354 | 325 | 30 | 188 | 135 | 63 | A | E | 222 | 5 | 5 | 300.000 | A |
| -Joel Skinner | 315 | 73 | 5 | 23 | 37 | 16 | 4 | 450 | 108 | 6 | 38 | 46 | 28 | A | W | 227 | 15 | 3 | 110.000 | A |
| -Jeff Stone | 249 | 69 | 6 | 32 | 19 | 20 | 4 | 702 | 209 | 10 | 97 | 48 | 44 | N | E | 103 | 8 | 2 | NA | N |
| -Jim Sundberg | 429 | 91 | 12 | 41 | 42 | 57 | 13 | 5590 | 1397 | 83 | 578 | 579 | 644 | A | W | 686 | 46 | 4 | 825.000 | N |
| -Jim Traber | 212 | 54 | 13 | 28 | 44 | 18 | 2 | 233 | 59 | 13 | 31 | 46 | 20 | A | E | 243 | 23 | 5 | NA | A |
| -Jose Uribe | 453 | 101 | 3 | 46 | 43 | 61 | 3 | 948 | 218 | 6 | 96 | 72 | 91 | N | W | 249 | 444 | 16 | 195.000 | N |
| -Jerry Willard | 161 | 43 | 4 | 17 | 26 | 22 | 3 | 707 | 179 | 21 | 77 | 99 | 76 | A | W | 300 | 12 | 2 | NA | A |
| -Joel Youngblood | 184 | 47 | 5 | 20 | 28 | 18 | 11 | 3327 | 890 | 74 | 419 | 382 | 304 | N | W | 49 | 2 | 0 | 450.000 | N |
| -Kevin Bass | 591 | 184 | 20 | 83 | 79 | 38 | 5 | 1689 | 462 | 40 | 219 | 195 | 82 | N | W | 303 | 12 | 5 | 630.000 | N |
| -Kal Daniels | 181 | 58 | 6 | 34 | 23 | 22 | 1 | 181 | 58 | 6 | 34 | 23 | 22 | N | W | 88 | 0 | 3 | 86.500 | N |
| -Kirk Gibson | 441 | 118 | 28 | 84 | 86 | 68 | 8 | 2723 | 750 | 126 | 433 | 420 | 309 | A | E | 190 | 2 | 2 | 1300.000 | A |
| -Ken Griffey | 490 | 150 | 21 | 69 | 58 | 35 | 14 | 6126 | 1839 | 121 | 983 | 707 | 600 | A | E | 96 | 5 | 3 | 1000.000 | N |
| -Keith Hernandez | 551 | 171 | 13 | 94 | 83 | 94 | 13 | 6090 | 1840 | 128 | 969 | 900 | 917 | N | E | 1199 | 149 | 5 | 1800.000 | N |
| -Kent Hrbek | 550 | 147 | 29 | 85 | 91 | 71 | 6 | 2816 | 815 | 117 | 405 | 474 | 319 | A | W | 1218 | 104 | 10 | 1310.000 | A |
| -Ken Landreaux | 283 | 74 | 4 | 34 | 29 | 22 | 10 | 3919 | 1062 | 85 | 505 | 456 | 283 | N | W | 145 | 5 | 7 | 737.500 | N |
| -Kevin McReynolds | 560 | 161 | 26 | 89 | 96 | 66 | 4 | 1789 | 470 | 65 | 233 | 260 | 155 | N | W | 332 | 9 | 8 | 625.000 | N |
| -Kevin Mitchell | 328 | 91 | 12 | 51 | 43 | 33 | 2 | 342 | 94 | 12 | 51 | 44 | 33 | N | E | 145 | 59 | 8 | 125.000 | N |
| -Keith Moreland | 586 | 159 | 12 | 72 | 79 | 53 | 9 | 3082 | 880 | 83 | 363 | 477 | 295 | N | E | 181 | 13 | 4 | 1043.333 | N |
| -Ken Oberkfell | 503 | 136 | 5 | 62 | 48 | 83 | 10 | 3423 | 970 | 20 | 408 | 303 | 414 | N | W | 65 | 258 | 8 | 725.000 | N |
| -Ken Phelps | 344 | 85 | 24 | 69 | 64 | 88 | 7 | 911 | 214 | 64 | 150 | 156 | 187 | A | W | 0 | 0 | 0 | 300.000 | A |
| -Kirby Puckett | 680 | 223 | 31 | 119 | 96 | 34 | 3 | 1928 | 587 | 35 | 262 | 201 | 91 | A | W | 429 | 8 | 6 | 365.000 | A |
| -Kurt Stillwell | 279 | 64 | 0 | 31 | 26 | 30 | 1 | 279 | 64 | 0 | 31 | 26 | 30 | N | W | 107 | 205 | 16 | 75.000 | N |
| -Leon Durham | 484 | 127 | 20 | 66 | 65 | 67 | 7 | 3006 | 844 | 116 | 436 | 458 | 377 | N | E | 1231 | 80 | 7 | 1183.333 | N |
| -Len Dykstra | 431 | 127 | 8 | 77 | 45 | 58 | 2 | 667 | 187 | 9 | 117 | 64 | 88 | N | E | 283 | 8 | 3 | 202.500 | N |
| -Larry Herndon | 283 | 70 | 8 | 33 | 37 | 27 | 12 | 4479 | 1222 | 94 | 557 | 483 | 307 | A | E | 156 | 2 | 2 | 225.000 | A |
| -Lee Lacy | 491 | 141 | 11 | 77 | 47 | 37 | 15 | 4291 | 1240 | 84 | 615 | 430 | 340 | A | E | 239 | 8 | 2 | 525.000 | A |
| -Len Matuszek | 199 | 52 | 9 | 26 | 28 | 21 | 6 | 805 | 191 | 30 | 113 | 119 | 87 | N | W | 235 | 22 | 5 | 265.000 | N |
| -Lloyd Moseby | 589 | 149 | 21 | 89 | 86 | 64 | 7 | 3558 | 928 | 102 | 513 | 471 | 351 | A | E | 371 | 6 | 6 | 787.500 | A |
| -Lance Parrish | 327 | 84 | 22 | 53 | 62 | 38 | 10 | 4273 | 1123 | 212 | 577 | 700 | 334 | A | E | 483 | 48 | 6 | 800.000 | N |
| -Larry Parrish | 464 | 128 | 28 | 67 | 94 | 52 | 13 | 5829 | 1552 | 210 | 740 | 840 | 452 | A | W | 0 | 0 | 0 | 587.500 | A |
| -Luis Rivera | 166 | 34 | 0 | 20 | 13 | 17 | 1 | 166 | 34 | 0 | 20 | 13 | 17 | N | E | 64 | 119 | 9 | NA | N |
| -Larry Sheets | 338 | 92 | 18 | 42 | 60 | 21 | 3 | 682 | 185 | 36 | 88 | 112 | 50 | A | E | 0 | 0 | 0 | 145.000 | A |
| -Lonnie Smith | 508 | 146 | 8 | 80 | 44 | 46 | 9 | 3148 | 915 | 41 | 571 | 289 | 326 | A | W | 245 | 5 | 9 | NA | A |
| -Lou Whitaker | 584 | 157 | 20 | 95 | 73 | 63 | 10 | 4704 | 1320 | 93 | 724 | 522 | 576 | A | E | 276 | 421 | 11 | 420.000 | A |
| -Mike Aldrete | 216 | 54 | 2 | 27 | 25 | 33 | 1 | 216 | 54 | 2 | 27 | 25 | 33 | N | W | 317 | 36 | 1 | 75.000 | N |
| -Marty Barrett | 625 | 179 | 4 | 94 | 60 | 65 | 5 | 1696 | 476 | 12 | 216 | 163 | 166 | A | E | 303 | 450 | 14 | 575.000 | A |
| -Mike Brown | 243 | 53 | 4 | 18 | 26 | 27 | 4 | 853 | 228 | 23 | 101 | 110 | 76 | N | E | 107 | 3 | 3 | NA | N |
| -Mike Davis | 489 | 131 | 19 | 77 | 55 | 34 | 7 | 2051 | 549 | 62 | 300 | 263 | 153 | A | W | 310 | 9 | 9 | 780.000 | A |
| -Mike Diaz | 209 | 56 | 12 | 22 | 36 | 19 | 2 | 216 | 58 | 12 | 24 | 37 | 19 | N | E | 201 | 6 | 3 | 90.000 | N |
| -Mariano Duncan | 407 | 93 | 8 | 47 | 30 | 30 | 2 | 969 | 230 | 14 | 121 | 69 | 68 | N | W | 172 | 317 | 25 | 150.000 | N |
| -Mike Easler | 490 | 148 | 14 | 64 | 78 | 49 | 13 | 3400 | 1000 | 113 | 445 | 491 | 301 | A | E | 0 | 0 | 0 | 700.000 | N |
| -Mike Fitzgerald | 209 | 59 | 6 | 20 | 37 | 27 | 4 | 884 | 209 | 14 | 66 | 106 | 92 | N | E | 415 | 35 | 3 | NA | N |
| -Mel Hall | 442 | 131 | 18 | 68 | 77 | 33 | 6 | 1416 | 398 | 47 | 210 | 203 | 136 | A | E | 233 | 7 | 7 | 550.000 | A |
| -Mickey Hatcher | 317 | 88 | 3 | 40 | 32 | 19 | 8 | 2543 | 715 | 28 | 269 | 270 | 118 | A | W | 220 | 16 | 4 | NA | A |
| -Mike Heath | 288 | 65 | 8 | 30 | 36 | 27 | 9 | 2815 | 698 | 55 | 315 | 325 | 189 | N | E | 259 | 30 | 10 | 650.000 | A |
| -Mike Kingery | 209 | 54 | 3 | 25 | 14 | 12 | 1 | 209 | 54 | 3 | 25 | 14 | 12 | A | W | 102 | 6 | 3 | 68.000 | A |
| -Mike LaValliere | 303 | 71 | 3 | 18 | 30 | 36 | 3 | 344 | 76 | 3 | 20 | 36 | 45 | N | E | 468 | 47 | 6 | 100.000 | N |
| -Mike Marshall | 330 | 77 | 19 | 47 | 53 | 27 | 6 | 1928 | 516 | 90 | 247 | 288 | 161 | N | W | 149 | 8 | 6 | 670.000 | N |
| -Mike Pagliarulo | 504 | 120 | 28 | 71 | 71 | 54 | 3 | 1085 | 259 | 54 | 150 | 167 | 114 | A | E | 103 | 283 | 19 | 175.000 | A |
| -Mark Salas | 258 | 60 | 8 | 28 | 33 | 18 | 3 | 638 | 170 | 17 | 80 | 75 | 36 | A | W | 358 | 32 | 8 | 137.000 | A |
| -Mike Schmidt | 20 | 1 | 0 | 0 | 0 | 0 | 2 | 41 | 9 | 2 | 6 | 7 | 4 | N | E | 78 | 220 | 6 | 2127.333 | N |
| -Mike Scioscia | 374 | 94 | 5 | 36 | 26 | 62 | 7 | 1968 | 519 | 26 | 181 | 199 | 288 | N | W | 756 | 64 | 15 | 875.000 | N |
| -Mickey Tettleton | 211 | 43 | 10 | 26 | 35 | 39 | 3 | 498 | 116 | 14 | 59 | 55 | 78 | A | W | 463 | 32 | 8 | 120.000 | A |
| -Milt Thompson | 299 | 75 | 6 | 38 | 23 | 26 | 3 | 580 | 160 | 8 | 71 | 33 | 44 | N | E | 212 | 1 | 2 | 140.000 | N |
| -Mitch Webster | 576 | 167 | 8 | 89 | 49 | 57 | 4 | 822 | 232 | 19 | 132 | 83 | 79 | N | E | 325 | 12 | 8 | 210.000 | N |
| -Mookie Wilson | 381 | 110 | 9 | 61 | 45 | 32 | 7 | 3015 | 834 | 40 | 451 | 249 | 168 | N | E | 228 | 7 | 5 | 800.000 | N |
| -Marvell Wynne | 288 | 76 | 7 | 34 | 37 | 15 | 4 | 1644 | 408 | 16 | 198 | 120 | 113 | N | W | 203 | 3 | 3 | 240.000 | N |
| -Mike Young | 369 | 93 | 9 | 43 | 42 | 49 | 5 | 1258 | 323 | 54 | 181 | 177 | 157 | A | E | 149 | 1 | 6 | 350.000 | A |
| -Nick Esasky | 330 | 76 | 12 | 35 | 41 | 47 | 4 | 1367 | 326 | 55 | 167 | 198 | 167 | N | W | 512 | 30 | 5 | NA | N |
| -Ozzie Guillen | 547 | 137 | 2 | 58 | 47 | 12 | 2 | 1038 | 271 | 3 | 129 | 80 | 24 | A | W | 261 | 459 | 22 | 175.000 | A |
| -Oddibe McDowell | 572 | 152 | 18 | 105 | 49 | 65 | 2 | 978 | 249 | 36 | 168 | 91 | 101 | A | W | 325 | 13 | 3 | 200.000 | A |
| -Omar Moreno | 359 | 84 | 4 | 46 | 27 | 21 | 12 | 4992 | 1257 | 37 | 699 | 386 | 387 | N | W | 151 | 8 | 5 | NA | N |
| -Ozzie Smith | 514 | 144 | 0 | 67 | 54 | 79 | 9 | 4739 | 1169 | 13 | 583 | 374 | 528 | N | E | 229 | 453 | 15 | 1940.000 | N |
| -Ozzie Virgil | 359 | 80 | 15 | 45 | 48 | 63 | 7 | 1493 | 359 | 61 | 176 | 202 | 175 | N | W | 682 | 93 | 13 | 700.000 | N |
| -Phil Bradley | 526 | 163 | 12 | 88 | 50 | 77 | 4 | 1556 | 470 | 38 | 245 | 167 | 174 | A | W | 250 | 11 | 1 | 750.000 | A |
| -Phil Garner | 313 | 83 | 9 | 43 | 41 | 30 | 14 | 5885 | 1543 | 104 | 751 | 714 | 535 | N | W | 58 | 141 | 23 | 450.000 | N |
| -Pete Incaviglia | 540 | 135 | 30 | 82 | 88 | 55 | 1 | 540 | 135 | 30 | 82 | 88 | 55 | A | W | 157 | 6 | 14 | 172.000 | A |
| -Paul Molitor | 437 | 123 | 9 | 62 | 55 | 40 | 9 | 4139 | 1203 | 79 | 676 | 390 | 364 | A | E | 82 | 170 | 15 | 1260.000 | A |
| -Pete O’Brien | 551 | 160 | 23 | 86 | 90 | 87 | 5 | 2235 | 602 | 75 | 278 | 328 | 273 | A | W | 1224 | 115 | 11 | NA | A |
| -Pete Rose | 237 | 52 | 0 | 15 | 25 | 30 | 24 | 14053 | 4256 | 160 | 2165 | 1314 | 1566 | N | W | 523 | 43 | 6 | 750.000 | N |
| -Pat Sheridan | 236 | 56 | 6 | 41 | 19 | 21 | 5 | 1257 | 329 | 24 | 166 | 125 | 105 | A | E | 172 | 1 | 4 | 190.000 | A |
| -Pat Tabler | 473 | 154 | 6 | 61 | 48 | 29 | 6 | 1966 | 566 | 29 | 250 | 252 | 178 | A | E | 846 | 84 | 9 | 580.000 | A |
| -Rafael Belliard | 309 | 72 | 0 | 33 | 31 | 26 | 5 | 354 | 82 | 0 | 41 | 32 | 26 | N | E | 117 | 269 | 12 | 130.000 | N |
| -Rick Burleson | 271 | 77 | 5 | 35 | 29 | 33 | 12 | 4933 | 1358 | 48 | 630 | 435 | 403 | A | W | 62 | 90 | 3 | 450.000 | A |
| -Randy Bush | 357 | 96 | 7 | 50 | 45 | 39 | 5 | 1394 | 344 | 43 | 178 | 192 | 136 | A | W | 167 | 2 | 4 | 300.000 | A |
| -Rick Cerone | 216 | 56 | 4 | 22 | 18 | 15 | 12 | 2796 | 665 | 43 | 266 | 304 | 198 | A | E | 391 | 44 | 4 | 250.000 | A |
| -Ron Cey | 256 | 70 | 13 | 42 | 36 | 44 | 16 | 7058 | 1845 | 312 | 965 | 1128 | 990 | N | E | 41 | 118 | 8 | 1050.000 | A |
| -Rob Deer | 466 | 108 | 33 | 75 | 86 | 72 | 3 | 652 | 142 | 44 | 102 | 109 | 102 | A | E | 286 | 8 | 8 | 215.000 | A |
| -Rick Dempsey | 327 | 68 | 13 | 42 | 29 | 45 | 18 | 3949 | 939 | 78 | 438 | 380 | 466 | A | E | 659 | 53 | 7 | 400.000 | A |
| -Rich Gedman | 462 | 119 | 16 | 49 | 65 | 37 | 7 | 2131 | 583 | 69 | 244 | 288 | 150 | A | E | 866 | 65 | 6 | NA | A |
| -Ron Hassey | 341 | 110 | 9 | 45 | 49 | 46 | 9 | 2331 | 658 | 50 | 249 | 322 | 274 | A | E | 251 | 9 | 4 | 560.000 | A |
| -Rickey Henderson | 608 | 160 | 28 | 130 | 74 | 89 | 8 | 4071 | 1182 | 103 | 862 | 417 | 708 | A | E | 426 | 4 | 6 | 1670.000 | A |
| -Reggie Jackson | 419 | 101 | 18 | 65 | 58 | 92 | 20 | 9528 | 2510 | 548 | 1509 | 1659 | 1342 | A | W | 0 | 0 | 0 | 487.500 | A |
| -Ricky Jones | 33 | 6 | 0 | 2 | 4 | 7 | 1 | 33 | 6 | 0 | 2 | 4 | 7 | A | W | 205 | 5 | 4 | NA | A |
| -Ron Kittle | 376 | 82 | 21 | 42 | 60 | 35 | 5 | 1770 | 408 | 115 | 238 | 299 | 157 | A | W | 0 | 0 | 0 | 425.000 | A |
| -Ray Knight | 486 | 145 | 11 | 51 | 76 | 40 | 11 | 3967 | 1102 | 67 | 410 | 497 | 284 | N | E | 88 | 204 | 16 | 500.000 | A |
| -Randy Kutcher | 186 | 44 | 7 | 28 | 16 | 11 | 1 | 186 | 44 | 7 | 28 | 16 | 11 | N | W | 99 | 3 | 1 | NA | N |
| -Rudy Law | 307 | 80 | 1 | 42 | 36 | 29 | 7 | 2421 | 656 | 18 | 379 | 198 | 184 | A | W | 145 | 2 | 2 | NA | A |
| -Rick Leach | 246 | 76 | 5 | 35 | 39 | 13 | 6 | 912 | 234 | 12 | 102 | 96 | 80 | A | E | 44 | 0 | 1 | 250.000 | A |
| -Rick Manning | 205 | 52 | 8 | 31 | 27 | 17 | 12 | 5134 | 1323 | 56 | 643 | 445 | 459 | A | E | 155 | 3 | 2 | 400.000 | A |
| -Rance Mulliniks | 348 | 90 | 11 | 50 | 45 | 43 | 10 | 2288 | 614 | 43 | 295 | 273 | 269 | A | E | 60 | 176 | 6 | 450.000 | A |
| -Ron Oester | 523 | 135 | 8 | 52 | 44 | 52 | 9 | 3368 | 895 | 39 | 377 | 284 | 296 | N | W | 367 | 475 | 19 | 750.000 | N |
| -Rey Quinones | 312 | 68 | 2 | 32 | 22 | 24 | 1 | 312 | 68 | 2 | 32 | 22 | 24 | A | E | 86 | 150 | 15 | 70.000 | A |
| -Rafael Ramirez | 496 | 119 | 8 | 57 | 33 | 21 | 7 | 3358 | 882 | 36 | 365 | 280 | 165 | N | W | 155 | 371 | 29 | 875.000 | N |
| -Ronn Reynolds | 126 | 27 | 3 | 8 | 10 | 5 | 4 | 239 | 49 | 3 | 16 | 13 | 14 | N | E | 190 | 2 | 9 | 190.000 | N |
| -Ron Roenicke | 275 | 68 | 5 | 42 | 42 | 61 | 6 | 961 | 238 | 16 | 128 | 104 | 172 | N | E | 181 | 3 | 2 | 191.000 | N |
| -Ryne Sandberg | 627 | 178 | 14 | 68 | 76 | 46 | 6 | 3146 | 902 | 74 | 494 | 345 | 242 | N | E | 309 | 492 | 5 | 740.000 | N |
| -Rafael Santana | 394 | 86 | 1 | 38 | 28 | 36 | 4 | 1089 | 267 | 3 | 94 | 71 | 76 | N | E | 203 | 369 | 16 | 250.000 | N |
| -Rick Schu | 208 | 57 | 8 | 32 | 25 | 18 | 3 | 653 | 170 | 17 | 98 | 54 | 62 | N | E | 42 | 94 | 13 | 140.000 | N |
| -Ruben Sierra | 382 | 101 | 16 | 50 | 55 | 22 | 1 | 382 | 101 | 16 | 50 | 55 | 22 | A | W | 200 | 7 | 6 | 97.500 | A |
| -Roy Smalley | 459 | 113 | 20 | 59 | 57 | 68 | 12 | 5348 | 1369 | 155 | 713 | 660 | 735 | A | W | 0 | 0 | 0 | 740.000 | A |
| -Robby Thompson | 549 | 149 | 7 | 73 | 47 | 42 | 1 | 549 | 149 | 7 | 73 | 47 | 42 | N | W | 255 | 450 | 17 | 140.000 | N |
| -Rob Wilfong | 288 | 63 | 3 | 25 | 33 | 16 | 10 | 2682 | 667 | 38 | 315 | 259 | 204 | A | W | 135 | 257 | 7 | 341.667 | A |
| -Reggie Williams | 303 | 84 | 4 | 35 | 32 | 23 | 2 | 312 | 87 | 4 | 39 | 32 | 23 | N | W | 179 | 5 | 3 | NA | N |
| -Robin Yount | 522 | 163 | 9 | 82 | 46 | 62 | 13 | 7037 | 2019 | 153 | 1043 | 827 | 535 | A | E | 352 | 9 | 1 | 1000.000 | A |
| -Steve Balboni | 512 | 117 | 29 | 54 | 88 | 43 | 6 | 1750 | 412 | 100 | 204 | 276 | 155 | A | W | 1236 | 98 | 18 | 100.000 | A |
| -Scott Bradley | 220 | 66 | 5 | 20 | 28 | 13 | 3 | 290 | 80 | 5 | 27 | 31 | 15 | A | W | 281 | 21 | 3 | 90.000 | A |
| -Sid Bream | 522 | 140 | 16 | 73 | 77 | 60 | 4 | 730 | 185 | 22 | 93 | 106 | 86 | N | E | 1320 | 166 | 17 | 200.000 | N |
| -Steve Buechele | 461 | 112 | 18 | 54 | 54 | 35 | 2 | 680 | 160 | 24 | 76 | 75 | 49 | A | W | 111 | 226 | 11 | 135.000 | A |
| -Shawon Dunston | 581 | 145 | 17 | 66 | 68 | 21 | 2 | 831 | 210 | 21 | 106 | 86 | 40 | N | E | 320 | 465 | 32 | 155.000 | N |
| -Scott Fletcher | 530 | 159 | 3 | 82 | 50 | 47 | 6 | 1619 | 426 | 11 | 218 | 149 | 163 | A | W | 196 | 354 | 15 | 475.000 | A |
| -Steve Garvey | 557 | 142 | 21 | 58 | 81 | 23 | 18 | 8759 | 2583 | 271 | 1138 | 1299 | 478 | N | W | 1160 | 53 | 7 | 1450.000 | N |
| -Steve Jeltz | 439 | 96 | 0 | 44 | 36 | 65 | 4 | 711 | 148 | 1 | 68 | 56 | 99 | N | E | 229 | 406 | 22 | 150.000 | N |
| -Steve Lombardozzi | 453 | 103 | 8 | 53 | 33 | 52 | 2 | 507 | 123 | 8 | 63 | 39 | 58 | A | W | 289 | 407 | 6 | 105.000 | A |
| -Spike Owen | 528 | 122 | 1 | 67 | 45 | 51 | 4 | 1716 | 403 | 12 | 211 | 146 | 155 | A | W | 209 | 372 | 17 | 350.000 | A |
| -Steve Sax | 633 | 210 | 6 | 91 | 56 | 59 | 6 | 3070 | 872 | 19 | 420 | 230 | 274 | N | W | 367 | 432 | 16 | 90.000 | N |
| -Tony Armas | 16 | 2 | 0 | 1 | 0 | 0 | 2 | 28 | 4 | 0 | 1 | 0 | 0 | A | E | 247 | 4 | 8 | NA | A |
| -Tony Bernazard | 562 | 169 | 17 | 88 | 73 | 53 | 8 | 3181 | 841 | 61 | 450 | 342 | 373 | A | E | 351 | 442 | 17 | 530.000 | A |
| -Tom Brookens | 281 | 76 | 3 | 42 | 25 | 20 | 8 | 2658 | 657 | 48 | 324 | 300 | 179 | A | E | 106 | 144 | 7 | 341.667 | A |
| -Tom Brunansky | 593 | 152 | 23 | 69 | 75 | 53 | 6 | 2765 | 686 | 133 | 369 | 384 | 321 | A | W | 315 | 10 | 6 | 940.000 | A |
| -Tony Fernandez | 687 | 213 | 10 | 91 | 65 | 27 | 4 | 1518 | 448 | 15 | 196 | 137 | 89 | A | E | 294 | 445 | 13 | 350.000 | A |
| -Tim Flannery | 368 | 103 | 3 | 48 | 28 | 54 | 8 | 1897 | 493 | 9 | 207 | 162 | 198 | N | W | 209 | 246 | 3 | 326.667 | N |
| -Tom Foley | 263 | 70 | 1 | 26 | 23 | 30 | 4 | 888 | 220 | 9 | 83 | 82 | 86 | N | E | 81 | 147 | 4 | 250.000 | N |
| -Tony Gwynn | 642 | 211 | 14 | 107 | 59 | 52 | 5 | 2364 | 770 | 27 | 352 | 230 | 193 | N | W | 337 | 19 | 4 | 740.000 | N |
| -Terry Harper | 265 | 68 | 8 | 26 | 30 | 29 | 7 | 1337 | 339 | 32 | 135 | 163 | 128 | N | W | 92 | 5 | 3 | 425.000 | A |
| -Toby Harrah | 289 | 63 | 7 | 36 | 41 | 44 | 17 | 7402 | 1954 | 195 | 1115 | 919 | 1153 | A | W | 166 | 211 | 7 | NA | A |
| -Tommy Herr | 559 | 141 | 2 | 48 | 61 | 73 | 8 | 3162 | 874 | 16 | 421 | 349 | 359 | N | E | 352 | 414 | 9 | 925.000 | N |
| -Tim Hulett | 520 | 120 | 17 | 53 | 44 | 21 | 4 | 927 | 227 | 22 | 106 | 80 | 52 | A | W | 70 | 144 | 11 | 185.000 | A |
| -Terry Kennedy | 19 | 4 | 1 | 2 | 3 | 1 | 1 | 19 | 4 | 1 | 2 | 3 | 1 | N | W | 692 | 70 | 8 | 920.000 | A |
| -Tito Landrum | 205 | 43 | 2 | 24 | 17 | 20 | 7 | 854 | 219 | 12 | 105 | 99 | 71 | N | E | 131 | 6 | 1 | 286.667 | N |
| -Tim Laudner | 193 | 47 | 10 | 21 | 29 | 24 | 6 | 1136 | 256 | 42 | 129 | 139 | 106 | A | W | 299 | 13 | 5 | 245.000 | A |
| -Tom O’Malley | 181 | 46 | 1 | 19 | 18 | 17 | 5 | 937 | 238 | 9 | 88 | 95 | 104 | A | E | 37 | 98 | 9 | NA | A |
| -Tom Paciorek | 213 | 61 | 4 | 17 | 22 | 3 | 17 | 4061 | 1145 | 83 | 488 | 491 | 244 | A | W | 178 | 45 | 4 | 235.000 | A |
| -Tony Pena | 510 | 147 | 10 | 56 | 52 | 53 | 7 | 2872 | 821 | 63 | 307 | 340 | 174 | N | E | 810 | 99 | 18 | 1150.000 | N |
| -Terry Pendleton | 578 | 138 | 1 | 56 | 59 | 34 | 3 | 1399 | 357 | 7 | 149 | 161 | 87 | N | E | 133 | 371 | 20 | 160.000 | N |
| -Tony Perez | 200 | 51 | 2 | 14 | 29 | 25 | 23 | 9778 | 2732 | 379 | 1272 | 1652 | 925 | N | W | 398 | 29 | 7 | NA | N |
| -Tony Phillips | 441 | 113 | 5 | 76 | 52 | 76 | 5 | 1546 | 397 | 17 | 226 | 149 | 191 | A | W | 160 | 290 | 11 | 425.000 | A |
| -Terry Puhl | 172 | 42 | 3 | 17 | 14 | 15 | 10 | 4086 | 1150 | 57 | 579 | 363 | 406 | N | W | 65 | 0 | 0 | 900.000 | N |
| -Tim Raines | 580 | 194 | 9 | 91 | 62 | 78 | 8 | 3372 | 1028 | 48 | 604 | 314 | 469 | N | E | 270 | 13 | 6 | NA | N |
| -Ted Simmons | 127 | 32 | 4 | 14 | 25 | 12 | 19 | 8396 | 2402 | 242 | 1048 | 1348 | 819 | N | W | 167 | 18 | 6 | 500.000 | N |
| -Tim Teufel | 279 | 69 | 4 | 35 | 31 | 32 | 4 | 1359 | 355 | 31 | 180 | 148 | 158 | N | E | 133 | 173 | 9 | 277.500 | N |
| -Tim Wallach | 480 | 112 | 18 | 50 | 71 | 44 | 7 | 3031 | 771 | 110 | 338 | 406 | 239 | N | E | 94 | 270 | 16 | 750.000 | N |
| -Vince Coleman | 600 | 139 | 0 | 94 | 29 | 60 | 2 | 1236 | 309 | 1 | 201 | 69 | 110 | N | E | 300 | 12 | 9 | 160.000 | N |
| -Von Hayes | 610 | 186 | 19 | 107 | 98 | 74 | 6 | 2728 | 753 | 69 | 399 | 366 | 286 | N | E | 1182 | 96 | 13 | 1300.000 | N |
| -Vance Law | 360 | 81 | 5 | 37 | 44 | 37 | 7 | 2268 | 566 | 41 | 279 | 257 | 246 | N | E | 170 | 284 | 3 | 525.000 | N |
| -Wally Backman | 387 | 124 | 1 | 67 | 27 | 36 | 7 | 1775 | 506 | 6 | 272 | 125 | 194 | N | E | 186 | 290 | 17 | 550.000 | N |
| -Wade Boggs | 580 | 207 | 8 | 107 | 71 | 105 | 5 | 2778 | 978 | 32 | 474 | 322 | 417 | A | E | 121 | 267 | 19 | 1600.000 | A |
| -Will Clark | 408 | 117 | 11 | 66 | 41 | 34 | 1 | 408 | 117 | 11 | 66 | 41 | 34 | N | W | 942 | 72 | 11 | 120.000 | N |
| -Wally Joyner | 593 | 172 | 22 | 82 | 100 | 57 | 1 | 593 | 172 | 22 | 82 | 100 | 57 | A | W | 1222 | 139 | 15 | 165.000 | A |
| -Wayne Krenchicki | 221 | 53 | 2 | 21 | 23 | 22 | 8 | 1063 | 283 | 15 | 107 | 124 | 106 | N | E | 325 | 58 | 6 | NA | N |
| -Willie McGee | 497 | 127 | 7 | 65 | 48 | 37 | 5 | 2703 | 806 | 32 | 379 | 311 | 138 | N | E | 325 | 9 | 3 | 700.000 | N |
| -Willie Randolph | 492 | 136 | 5 | 76 | 50 | 94 | 12 | 5511 | 1511 | 39 | 897 | 451 | 875 | A | E | 313 | 381 | 20 | 875.000 | A |
| -Wayne Tolleson | 475 | 126 | 3 | 61 | 43 | 52 | 6 | 1700 | 433 | 7 | 217 | 93 | 146 | A | W | 37 | 113 | 7 | 385.000 | A |
| -Willie Upshaw | 573 | 144 | 9 | 85 | 60 | 78 | 8 | 3198 | 857 | 97 | 470 | 420 | 332 | A | E | 1314 | 131 | 12 | 960.000 | A |
| -Willie Wilson | 631 | 170 | 9 | 77 | 44 | 31 | 11 | 4908 | 1457 | 30 | 775 | 357 | 249 | A | W | 408 | 4 | 3 | 1000.000 | A |