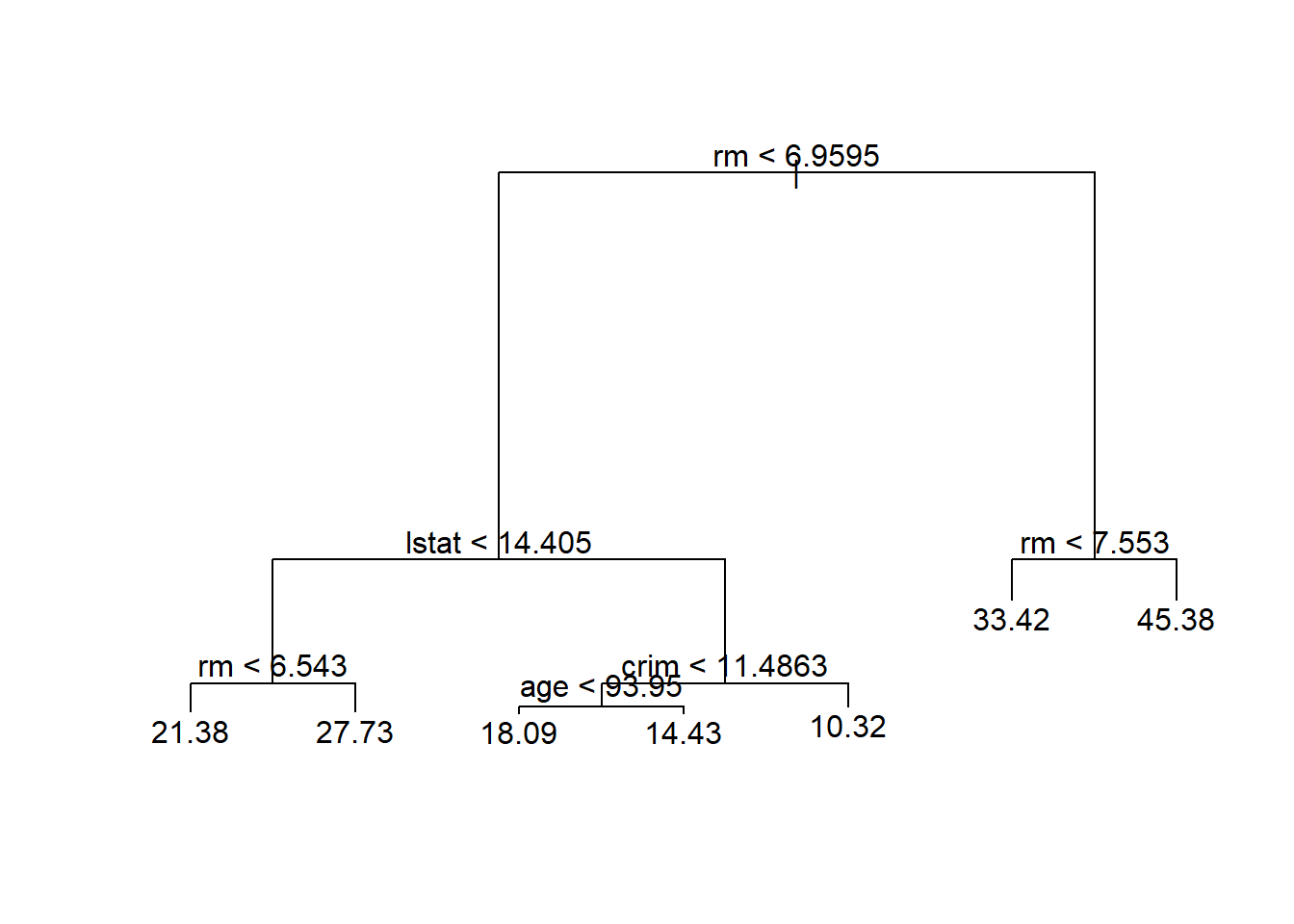16 树方法

调入需要的扩展包:

library(leaps) # 全子集回归
library(ISLR) # 参考书对应的包
library(glmnet) # 岭回归和lasso

## Loading required package: Matrix

## Loaded glmnet 4.1-8

library(tree) # 树回归
library(randomForest) # 随机森林和装袋法

## randomForest 4.7-1.2

## Type rfNews() to see new features/changes/bug fixes.

library(MASS)
library(gbm) # boosting

## Loaded gbm 2.2.2

## This version of gbm is no longer under development. Consider transitioning to gbm3, https://github.com/gbm-developers/gbm3

16.1 决策树

决策树方法按不同自变量的不同值，分层地把训练集分组。每层使用一个变量，所以这样的分组构成一个二叉树表示。为了预测一个观测的类归属，找到它所属的组，用组的类归属或大多数观测的类归属进行预测。这样的方法称为决策树(decision tree)。决策树方法既可以用于判别问题，也可以用于回归问题。

决策树的好处是容易解释，在自变量为分类变量时没有额外困难。但预测准确率可能比其它有监督学习方法差。

改进方法包括装袋法(bagging)、随机森林(random forests)、提升法(boosting)。这些改进方法都是把许多棵树合并在一起，通常能改善准确率但是可解释性变差。

16.1.1 回归树

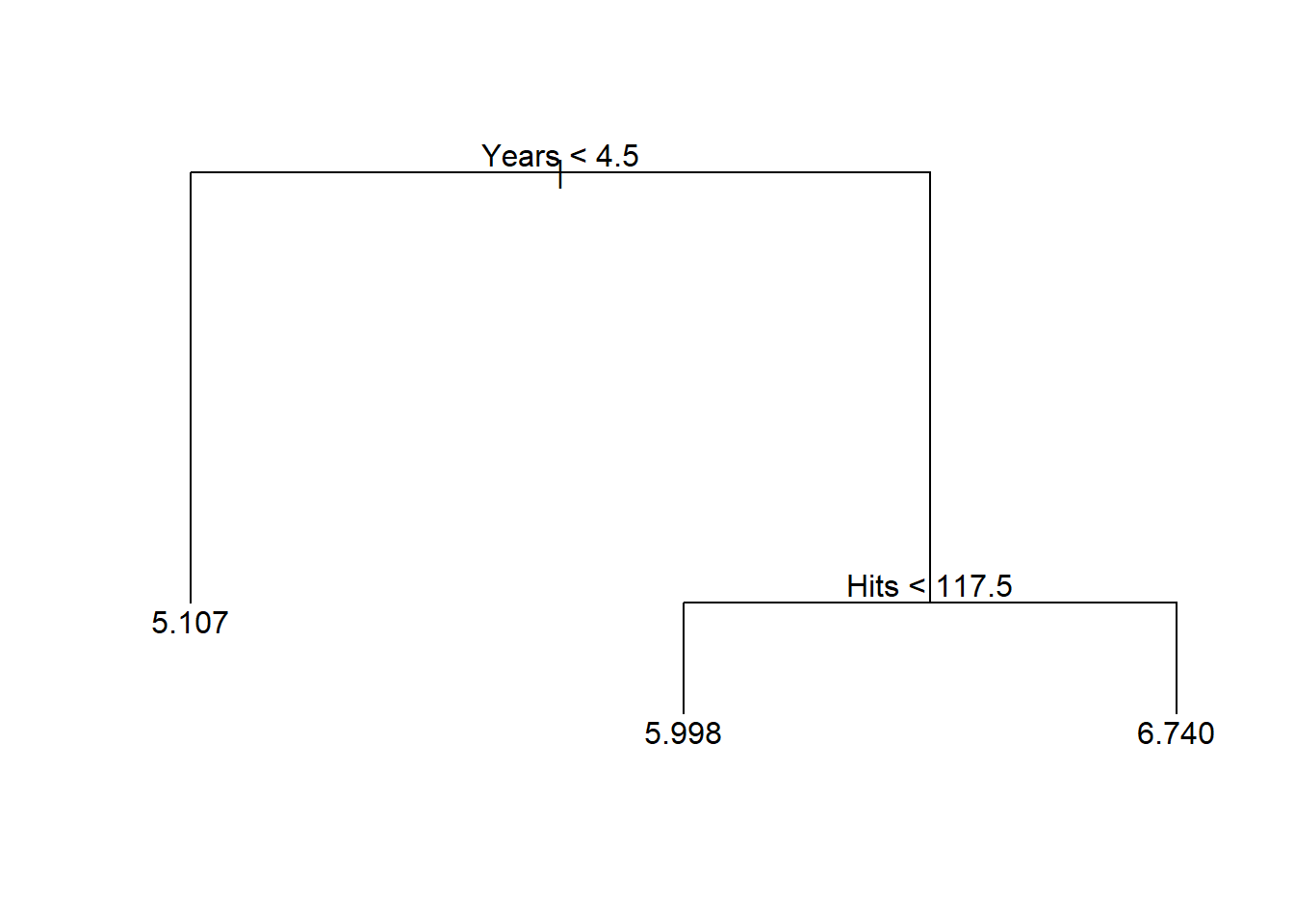
以Hitters数据为例。以Salary为因变量，其它自变量为自变量，预测工资值。为简单起见，仅考虑Years(入行年限)和Hitts(前一年的安打数)两个自变量。数据需要去掉有缺失值的观测; 以Salary的自然对数值为因变量。可以得到如下的树（见图16.1）：

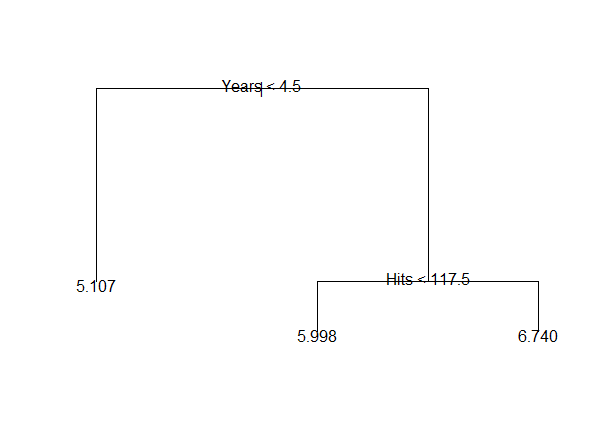
图16.1: Hitters数据的简单树图形

这个树把(Years, Hits)的取值\(\mathbb R^2\)空间分成了三个区域: \[\begin{aligned} R_1 =& \{ (\text{Years}, \text{Hits}):\; \text{Years} < 4.5 \}; \\ R_2 =& \{ (\text{Years}, \text{Hits}):\; \text{Years} \geq 4.5 \text{且} \text{Hits} < 117.5 \}; \\ R_3 =& \{ (\text{Years}, \text{Hits}):\; \text{Years} \geq 4.5 \text{且} \text{Hits} \geq 117.5 \} . \end{aligned}\] 每个区域内用因变量平均值预测因变量值。见图16.2。

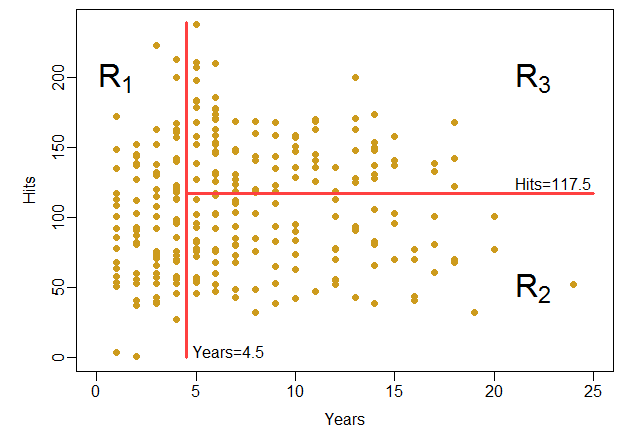
图16.2: Hitters数据的简单树划分的空间

此树对应的文字规则如下：

node), split, n, deviance, yval
      * denotes terminal node

1) root 263 207.20 5.927  
  2) Years < 4.5 90  42.35 5.107 *
  3) Years > 4.5 173  72.71 6.354  
    6) Hits < 117.5 90  28.09 5.998 *
    7) Hits > 117.5 83  20.88 6.740 *

根据某变量的值分为两个分支的节点称为内部节点；不再分割的节点称为叶结点。

\(\text{Year}<4.5\)节点和\(\text{Year} \geq 4.5\) 下面的\(\text{Hits}<117.5\)节点是两个内部节点。 \(R_1, R_2, R_3\)是三个叶结点。叶节点处用训练数据的因变量平均值作预测。

从上述结果看出，为了预测Salary，Years是比Hits更重要的变量。入行年限多的运动员工资高。在入行年限超过4.5年的运动员中， Hits低的运动员工资比入行年限低于4.5年的运动员工资提高有限，而Hits高的运动员工资则提高很多。

树模型可能会过于简单，但是容易解释和绘图。

树回归步骤用变量值作为分界，把自变量取值空间\(\mathbb R^p\)分割为不相交的\(J\)个区域 \(R_1, R_2, \dots, R_J\)。对每个待预测观测，如果自变量值落入\(R_j\)中，则因变量值用\(R_j\)中训练集的因变量平均值来预测。

16.1.1.1 树回归的分叉方法

树回归分割的区域都是高维矩形或盒子。求盒子\(R_1, \dots, R_J\)使得其并集为自变量取值空间，且使得如下的残差平方和最小： \[\begin{align} \text{RSS} = \sum_{j=1}^J \sum_{i \in R_j} (y_i - \hat y_{R_j})^2, \tag{16.1} \end{align}\] 其中\(\hat y_{R_j}\)是\(R_j\)中的训练样本的因变量平均值。

为此，使用由顶向下、贪婪的递归二分叉方法。

由顶向下: 从所有训练样本都在一类中开始，逐步分割，每次按照一个自变量的值把一个类分成两个类。

贪婪是指每次分割时仅考虑当前使得残差平方和减少最多的分割，不考虑会对整棵树的影响。

在所有观测都未分割时，要找到一个变量\(X_j\)和变量值\(s_j\)，使得 \[\begin{aligned} R_1(j, s_j) =\{ \boldsymbol x | x_j < s_j \}, \quad R_2(j, s_j) =\{ \boldsymbol x | x_j \geq s_j \} \end{aligned}\] 对应的RSS总和最小，对每个变量都测试一遍，找到分割后分割的两个区域内的RSS总和最小的变量和分割点。

对变量\(X_j\)，为了求\(s_j\)，只要对\(X_j\)的所有不同样本值穷举即可。

在已经分成两类\(R_1\), \(R_2\)以后，对每一类分别去找到能进行最优分割的变量和截断值\(s\)，然后仅取使得RSS总和更小的那个。这样得到三个类。对每个类都找最优分割，然后仅取使得RSS总和最小的一个，得到四个类。如此重复，直到满足某种停止法则，比如每个类中因变量值都相等，每个类的观测个数至多5个等等。分割结束后，对测试样本可以用自变量所属区域的因变量平均值预测因变量值。

16.1.1.2 剪枝

分类树可能会过于复杂，也会产生过度拟合。剪去一些枝叶，使得模型复杂度降低，可以提高可解释性，降低方差，当然偏差会增大一些，总的来说适当剪枝可以降低测试集上的均方误差。

虽然可以用提前结束分割的方法降低复杂度，但是这样可能会漏掉底层的好分割。所以还是先构造一棵大树再剪枝更好。

剪枝的目标是使得测试均方误差最小。可以用交叉验证或者测试集来估计不同的子树的均方误差。但是对所有可能的子树都估计均方误差带来过多的计算量。应仅考虑部分子树。

剪枝的一种方法是代价复杂度剪枝(cost complexity pruning)，也称为最弱联系剪枝(weakest link pruning)。仅考虑用一个调节参数\(\alpha\)标记的子树的序列。对每个\(\alpha>0\), 存在子树\(T\), 使得如下函数最小化： \[\begin{aligned} \sum_{m=1}^{|T|} \sum_{i:\; x_i \in R_m} (y_i - \hat y_{R_m})^2 + \alpha |T| \end{aligned}\] 其中\(|T|\)是子树\(T\)的叶子节点个数， \(R_m\)是第\(m\)个叶子节点对应的分割区域， \(\hat y_{R_m}\)是用\(R_m\)中样品计算的因变量预测值。

\(\alpha=0\)时对应于不剪枝的树。 \(\alpha\)增大时规则对较大的树有惩罚，所以能选择较小的子树，而且每次子树变化都是从前面较小的\(\alpha\)对应的子树中剪去一个分枝点，是嵌套进行的。

很容易得到所有的\(\alpha\)对应的子树序列。可以用交叉验证或测试集选择合适的\(\alpha\)从而选择合适的子树。得到最优的\(\alpha\)后，可以再利用全部观测以及获得的\(\alpha\)值产生剪枝的树。

16.1.2 Hitters回归树的简单演示

对Hitters数据，用Years和Hits作因变量预测log(Salaray)。

仅取Hitters数据集的Salary, Years, Hits三个变量，并仅保留完全观测：

d <- na.omit(Hitters[,c('Salary', 'Years', 'Hits')])
print(str(d))

## 'data.frame':    263 obs. of  3 variables:
##  $ Salary: num  475 480 500 91.5 750 ...
##  $ Years : int  14 3 11 2 11 2 3 2 13 10 ...
##  $ Hits  : int  81 130 141 87 169 37 73 81 92 159 ...
##  - attr(*, "na.action")= 'omit' Named int [1:59] 1 16 19 23 31 33 37 39 40 42 ...
##   ..- attr(*, "names")= chr [1:59] "-Andy Allanson" "-Billy Beane" "-Bruce Bochte" "-Bob Boone" ...
## NULL

建立完整的树:

tr1 <- tree(log(Salary) ~ Years + Hits, data=d)

剪枝为只有3个叶结点:

tr1b <- prune.tree(tr1, best=3)

显示树:

print(tr1b)

## node), split, n, deviance, yval
##       * denotes terminal node
## 
## 1) root 263 207.20 5.927  
##   2) Years < 4.5 90  42.35 5.107 *
##   3) Years > 4.5 173  72.71 6.354  
##     6) Hits < 117.5 90  28.09 5.998 *
##     7) Hits > 117.5 83  20.88 6.740 *

显示概括:

print(summary(tr1b))

## 
## Regression tree:
## snip.tree(tree = tr1, nodes = c(6L, 2L))
## Number of terminal nodes:  3 
## Residual mean deviance:  0.3513 = 91.33 / 260 
## Distribution of residuals:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -2.24000 -0.39580 -0.03162  0.00000  0.33380  2.55600

做树图:

plot(tr1b); text(tr1b, pretty=0)

16.1.3 Hitters数据回归树的完整演示

把数据随机地分成一半训练集，一半测试集：

d <- na.omit(Hitters[,c('Salary', 'Years', 'Hits')])
set.seed(1)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)

对训练集，建立未剪枝的树：

tr1 <- tree(log(Salary) ~ ., data=d, subset=train)
plot(tr1); text(tr1, pretty=0)

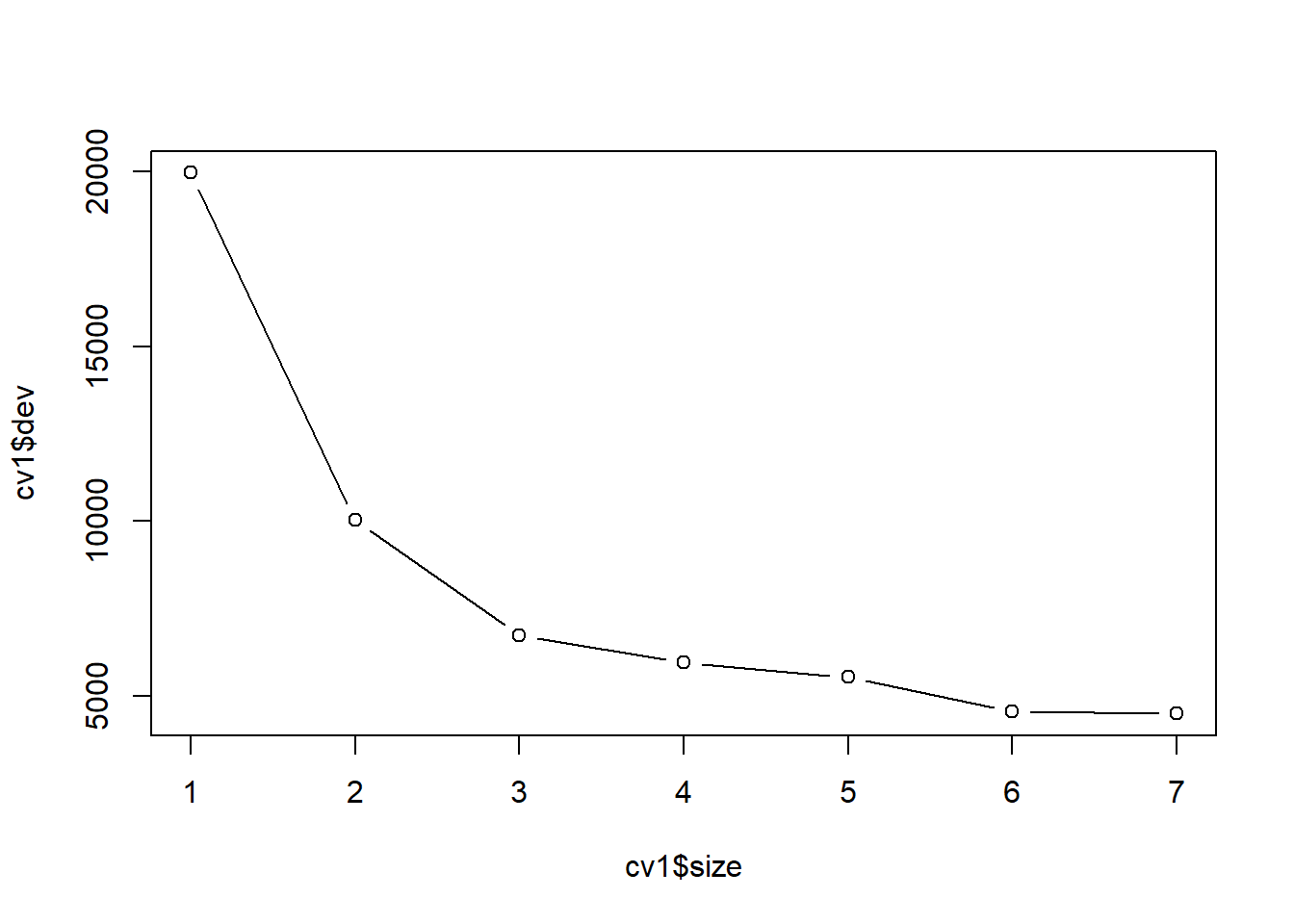
对训练集上的未剪枝树用交叉验证方法寻找最优大小：

cv1 <- cv.tree(tr1)
print(cv1)

## $size
## [1] 7 6 5 4 3 2 1
## 
## $dev
## [1]  49.88386  49.78504  50.36061  50.00678  54.07967  66.20924 104.06611
## 
## $k
## [1]      -Inf  1.558635  1.642895  2.319001  6.275232 11.126931 43.728005
## 
## $method
## [1] "deviance"
## 
## attr(,"class")
## [1] "prune"         "tree.sequence"

plot(cv1$size, cv1$dev, type='b')
best.size <- cv1$size[which.min(cv1$dev)[1]]
abline(v=best.size, col='gray')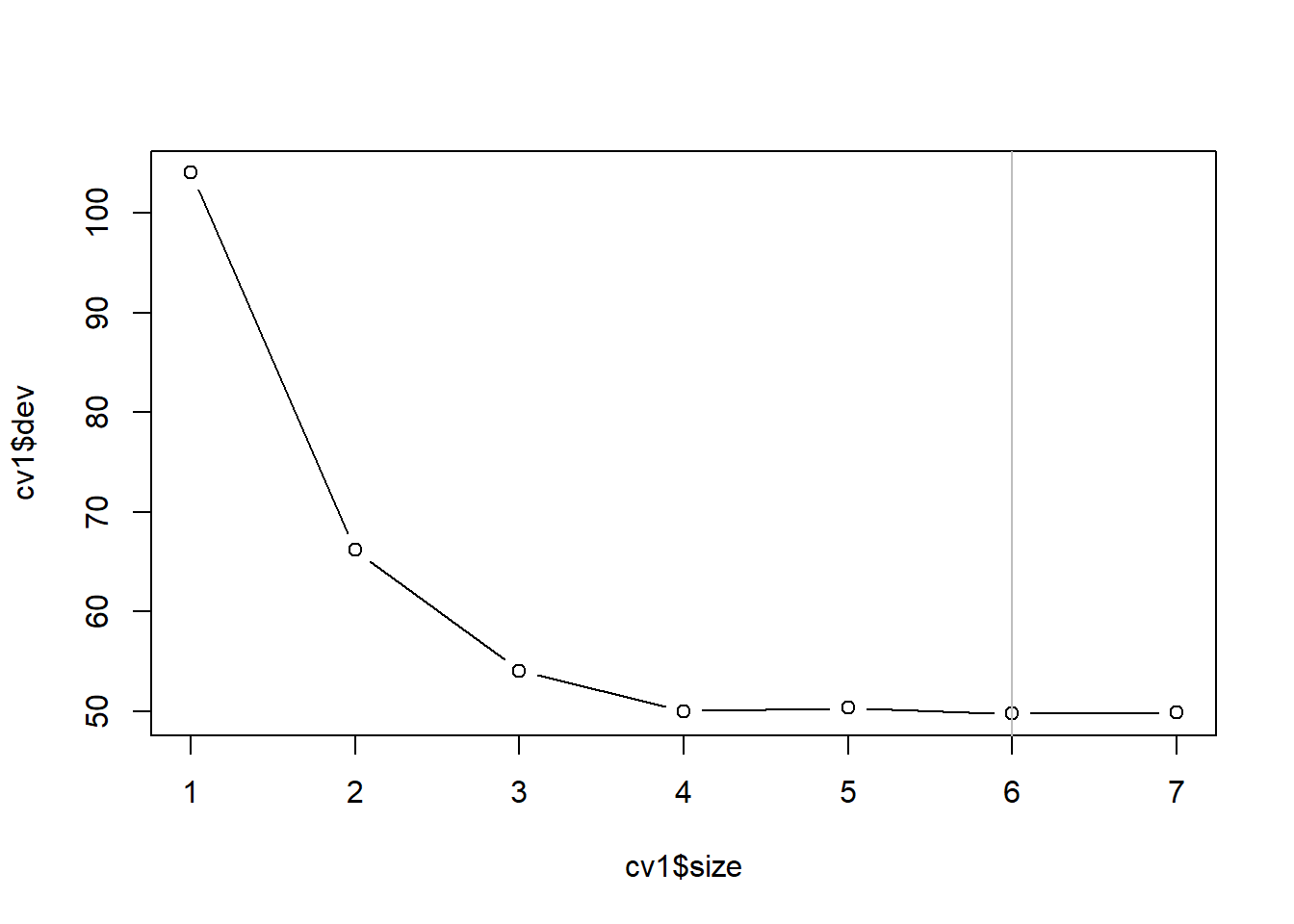

最优大小为6。获得训练集上构造的树剪枝后的结果：

tr1b <- prune.tree(tr1, best=best.size)

在测试集上计算预测均方误差:

pred.test <- predict(tr1b, newdata=d[test,])
test.mse <- mean( (d[test, 'Salary'] - exp(pred.test))^2 )
test.mse

## [1] 135635.4

如果用训练集的因变量平均值估计测试集的因变量值，均方误差为:

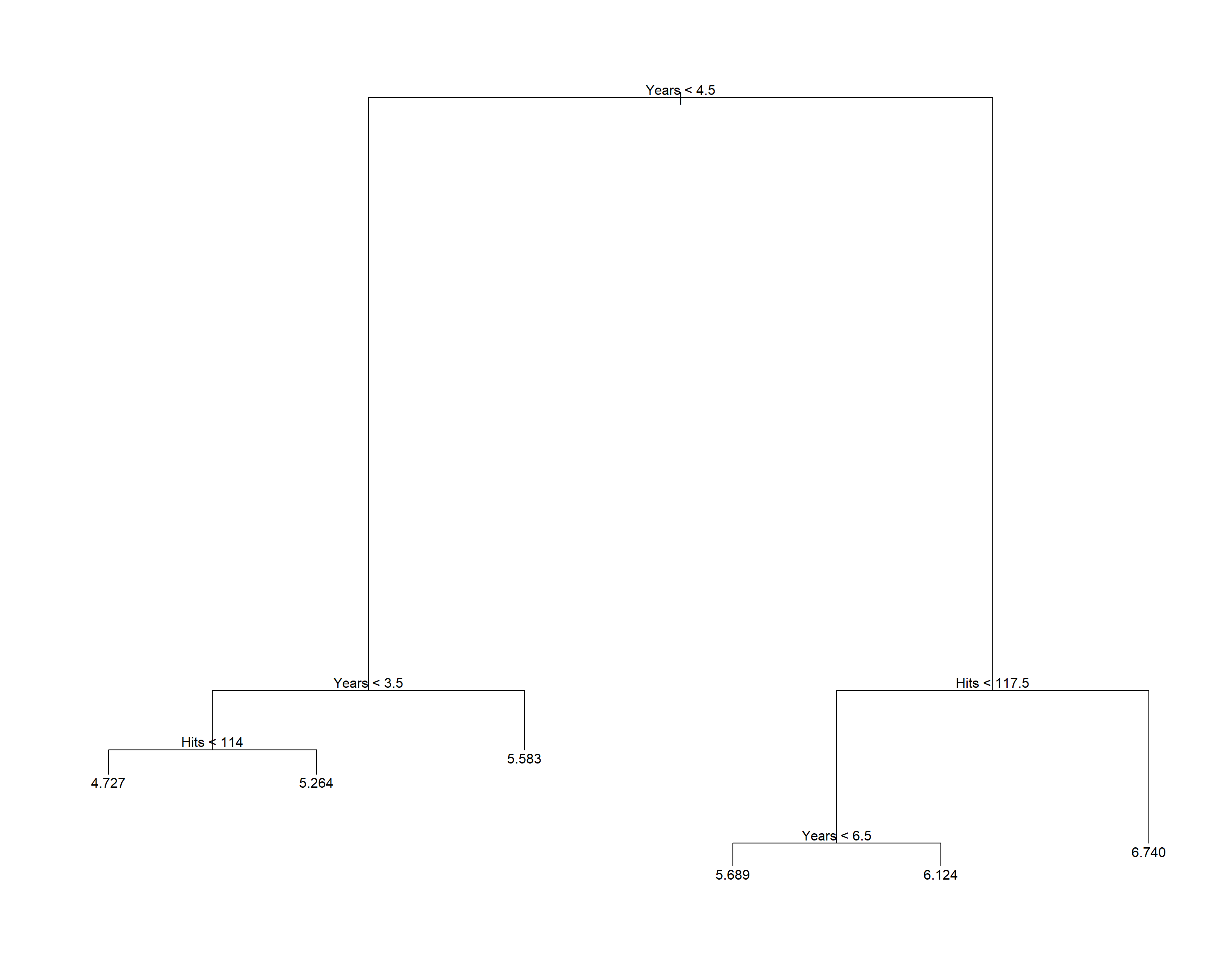
worst.mse <- mean( (d[test, 'Salary'] - mean(d[train, 'Salary']))^2 )
worst.mse

## [1] 224692.1

用所有数据来构造未剪枝树：

tr2 <- tree(log(Salary) ~ ., data=d)

用训练集上得到的子树大小剪枝：

tr2b <- prune.tree(tr2, best=best.size)
plot(tr2b); text(tr2b, pretty=0)

16.1.4 分类树

这里分类树指因变量是分类变量的树模型。回归树对每一分割区域用该区域观测的因变量平均值做预测，而分类树对每一分割区域用该区域因变量的最常见值做预测。训练出来的回归函数不仅包括区域分割信息、每个区域的最常见类别信息，还包括每个分割区域的类别分布信息。

在构造分叉时，不再以拟合均方误差RSS最小为目标，而是以错判率(classification error rate)最小为目标。每个区域的错判率是该区域中最常见类之外的类比例。

设\(\hat p_{mk}\)表示第\(m\)个分割区域的训练样本中，因变量的第\(k\)个类的比例，则 \[\begin{aligned} E = 1 - \max_{k} \hat p_{mk} \end{aligned}\] 是第\(m\)个分割区域的错判率。但是，错判率不容易区分不同树的判别性能。一般改用基尼系数和互熵。

基尼系数(Gini index)定义为 \[\begin{aligned} G = \sum_{k=1}^K \hat p_{mk} (1 - \hat p_{mk}), \end{aligned}\] 易见当比例\(\hat p_{mk}\)中一个接近于1,其余都接近于0时\(G\)很小，这时区域\(m\)基本上都属于因变量的同一类别。所以\(G\)可以看成是某个分割区域的类混杂程度， \(G\)很小时此区域的类是纯一的， \(G\)很大时，此区域的类别比较混杂，应进一步分割。

另一个衡量某分割区域类别分布情况的指标是如下的互熵(cross entropy): \[\begin{aligned} D = - \sum_{k=1}^K \hat p_{mk} \log \hat p_{mk} . \end{aligned}\] 易见\(D \geq 0\), 当比例\(\hat p_{mk}\)中一个接近于1, 其余都接近于0时\(D\)很小，这时区域\(m\)基本上都属于因变量的同一类别。所以\(D\)也可以看成是某个分割区域的类混杂程度， \(D\)很小时此区域的类是纯一的， \(D\)很大时，此区域的类别比较混杂，应进一步分割。事实上，\(G\)与\(D\)的值很接近。

在分叉时，用基尼系数或者互熵可以得到更好的分叉结果。

在剪枝时，仍可以使用基尼系数或互熵，但是如果关心的是剪枝后的树的预测准确率，用错判率剪枝更合适。

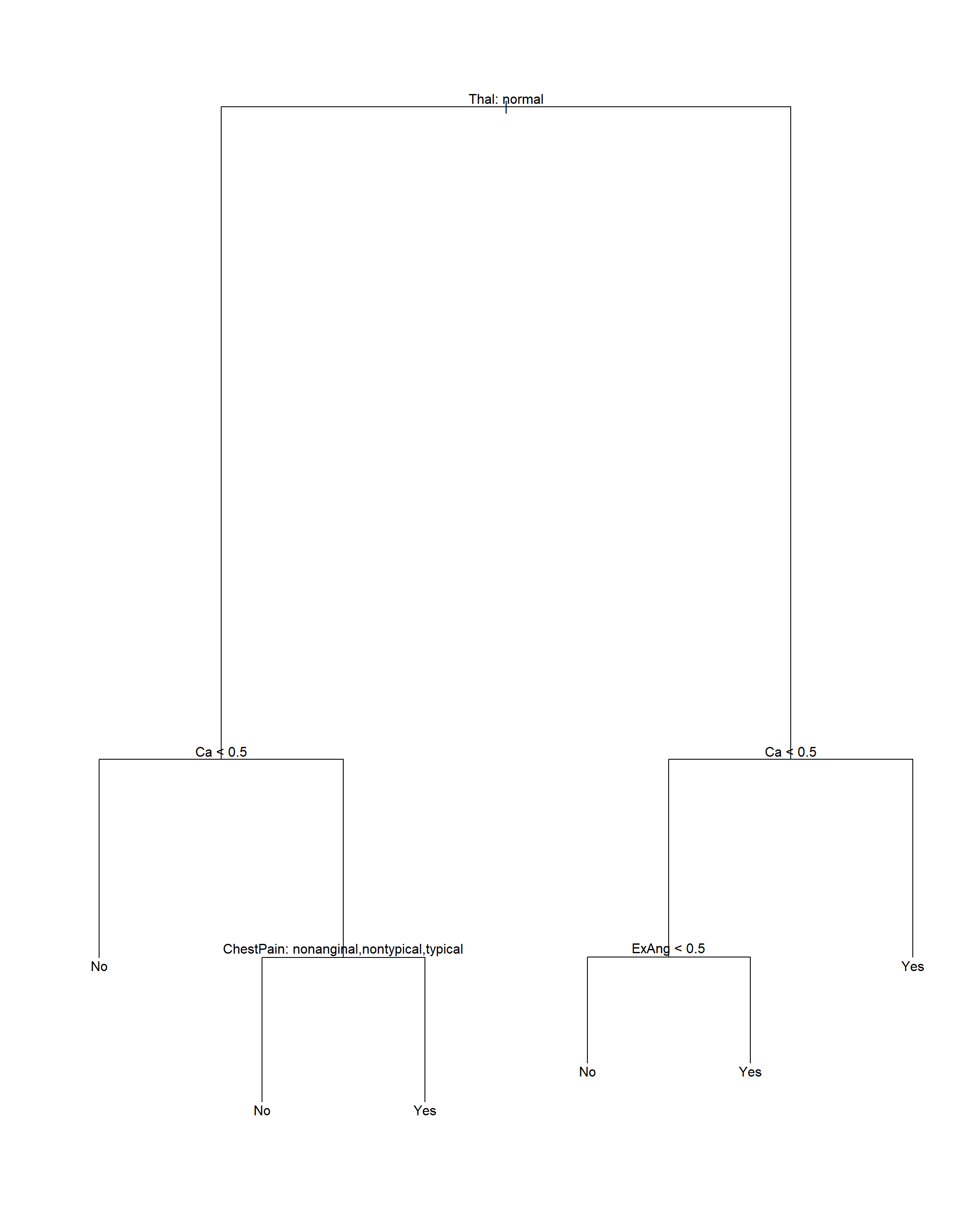
16.1.5 Heart数据判别树演示

数据集Heart中有303个病人的数据，其中变量AHD是二值变量，取Yes表示用血管造影检查确诊心脏病的，No表示没有心脏病的。有13个自变量，包括Age, Sex, Chol(胆固醇化验指标)等。

读入Heart数据集，并去掉有缺失值的观测：

Heart <- read.csv("Heart.csv", header=TRUE,
  row.names=1, 
  stringsAsFactors=TRUE)
Heart <- na.omit(Heart)
str(Heart)

## 'data.frame':    297 obs. of  14 variables:
##  $ Age      : int  63 67 67 37 41 56 62 57 63 53 ...
##  $ Sex      : int  1 1 1 1 0 1 0 0 1 1 ...
##  $ ChestPain: Factor w/ 4 levels "asymptomatic",..: 4 1 1 2 3 3 1 1 1 1 ...
##  $ RestBP   : int  145 160 120 130 130 120 140 120 130 140 ...
##  $ Chol     : int  233 286 229 250 204 236 268 354 254 203 ...
##  $ Fbs      : int  1 0 0 0 0 0 0 0 0 1 ...
##  $ RestECG  : int  2 2 2 0 2 0 2 0 2 2 ...
##  $ MaxHR    : int  150 108 129 187 172 178 160 163 147 155 ...
##  $ ExAng    : int  0 1 1 0 0 0 0 1 0 1 ...
##  $ Oldpeak  : num  2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
##  $ Slope    : int  3 2 2 3 1 1 3 1 2 3 ...
##  $ Ca       : int  0 3 2 0 0 0 2 0 1 0 ...
##  $ Thal     : Factor w/ 3 levels "fixed","normal",..: 1 2 3 2 2 2 2 2 3 3 ...
##  $ AHD      : Factor w/ 2 levels "No","Yes": 1 2 2 1 1 1 2 1 2 2 ...
##  - attr(*, "na.action")= 'omit' Named int [1:6] 88 167 193 267 288 303
##   ..- attr(*, "names")= chr [1:6] "88" "167" "193" "267" ...

knitr::kable(t(summary(Heart)))

Age	Min. :29.00	1st Qu.:48.00	Median :56.00	Mean :54.54	3rd Qu.:61.00	Max. :77.00
Sex	Min. :0.0000	1st Qu.:0.0000	Median :1.0000	Mean :0.6768	3rd Qu.:1.0000	Max. :1.0000
ChestPain	asymptomatic:142	nonanginal : 83	nontypical : 49	typical : 23	NA	NA
RestBP	Min. : 94.0	1st Qu.:120.0	Median :130.0	Mean :131.7	3rd Qu.:140.0	Max. :200.0
Chol	Min. :126.0	1st Qu.:211.0	Median :243.0	Mean :247.4	3rd Qu.:276.0	Max. :564.0
Fbs	Min. :0.0000	1st Qu.:0.0000	Median :0.0000	Mean :0.1448	3rd Qu.:0.0000	Max. :1.0000
RestECG	Min. :0.0000	1st Qu.:0.0000	Median :1.0000	Mean :0.9966	3rd Qu.:2.0000	Max. :2.0000
MaxHR	Min. : 71.0	1st Qu.:133.0	Median :153.0	Mean :149.6	3rd Qu.:166.0	Max. :202.0
ExAng	Min. :0.0000	1st Qu.:0.0000	Median :0.0000	Mean :0.3266	3rd Qu.:1.0000	Max. :1.0000
Oldpeak	Min. :0.000	1st Qu.:0.000	Median :0.800	Mean :1.056	3rd Qu.:1.600	Max. :6.200
Slope	Min. :1.000	1st Qu.:1.000	Median :2.000	Mean :1.603	3rd Qu.:2.000	Max. :3.000
Ca	Min. :0.0000	1st Qu.:0.0000	Median :0.0000	Mean :0.6768	3rd Qu.:1.0000	Max. :3.0000
Thal	fixed : 18	normal :164	reversable:115	NA	NA	NA
AHD	No :160	Yes:137	NA	NA	NA	NA

16.1.5.1 划分训练集与测试集

简单地把观测分为一半训练集、一半测试集：

set.seed(1)
train_id <- sample(nrow(Heart), size=round(0.5*nrow(Heart)))
train <- rep(FALSE, nrow(Heart))
train[train_id] <- TRUE
test <- (!train)
test.y <- Heart[["AHD"]][test]

在训练集上建立未剪枝的判别树:

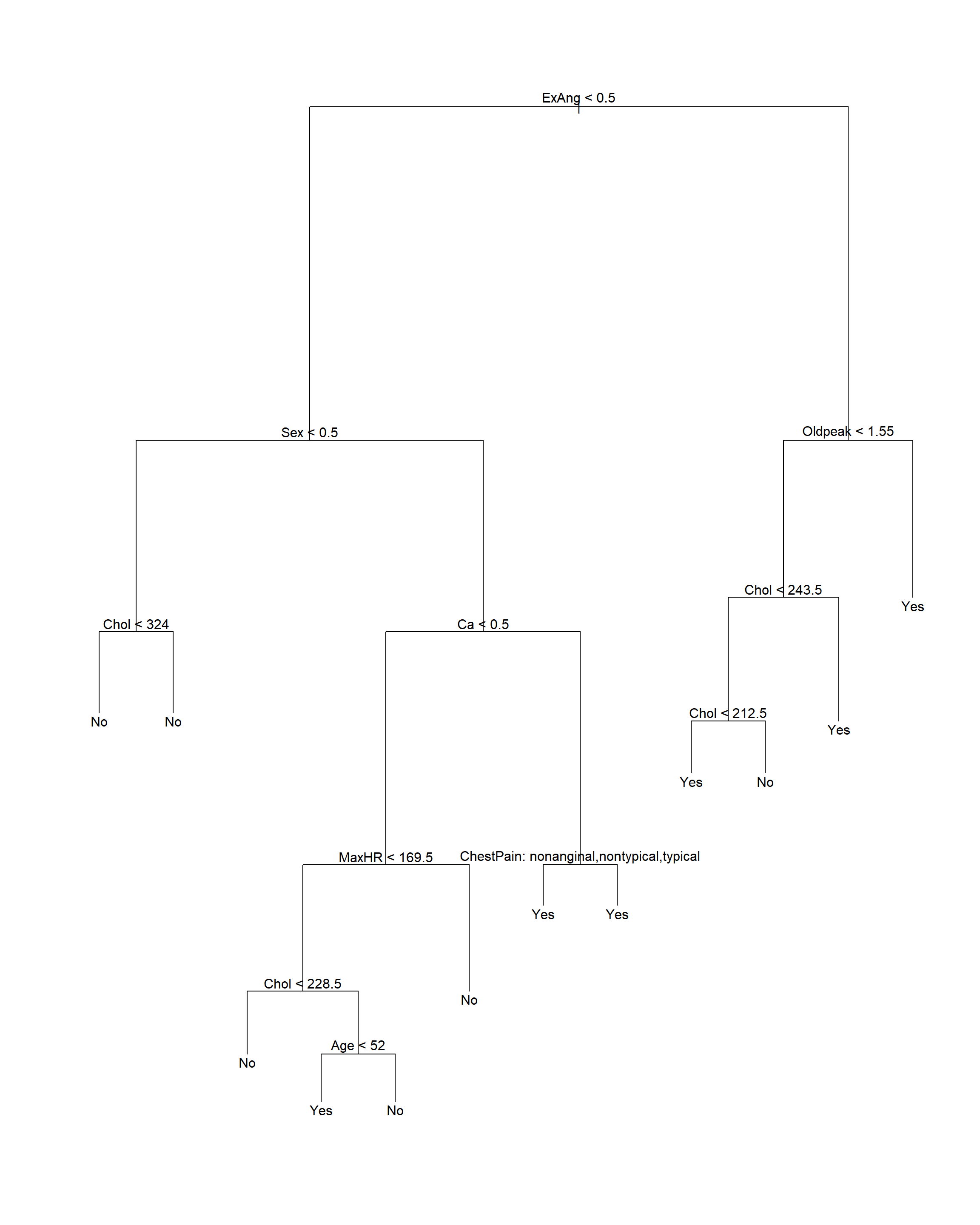
tr1 <- tree(AHD ~ ., data=Heart, subset=train)
plot(tr1); text(tr1, pretty=0)

注意: tree()函数要求输入的分类变量为因子类型，不能直接输入字符型数据作为自变量。

16.1.5.2 适当剪枝

用交叉验证方法确定剪枝保留的叶子个数，剪枝时按照错判率执行：

cv1 <- cv.tree(tr1, FUN=prune.misclass)
cv1

## $size
## [1] 12  9  6  4  2  1
## 
## $dev
## [1] 44 44 40 40 54 66
## 
## $k
## [1]      -Inf  0.000000  1.666667  3.000000  7.000000 26.000000
## 
## $method
## [1] "misclass"
## 
## attr(,"class")
## [1] "prune"         "tree.sequence"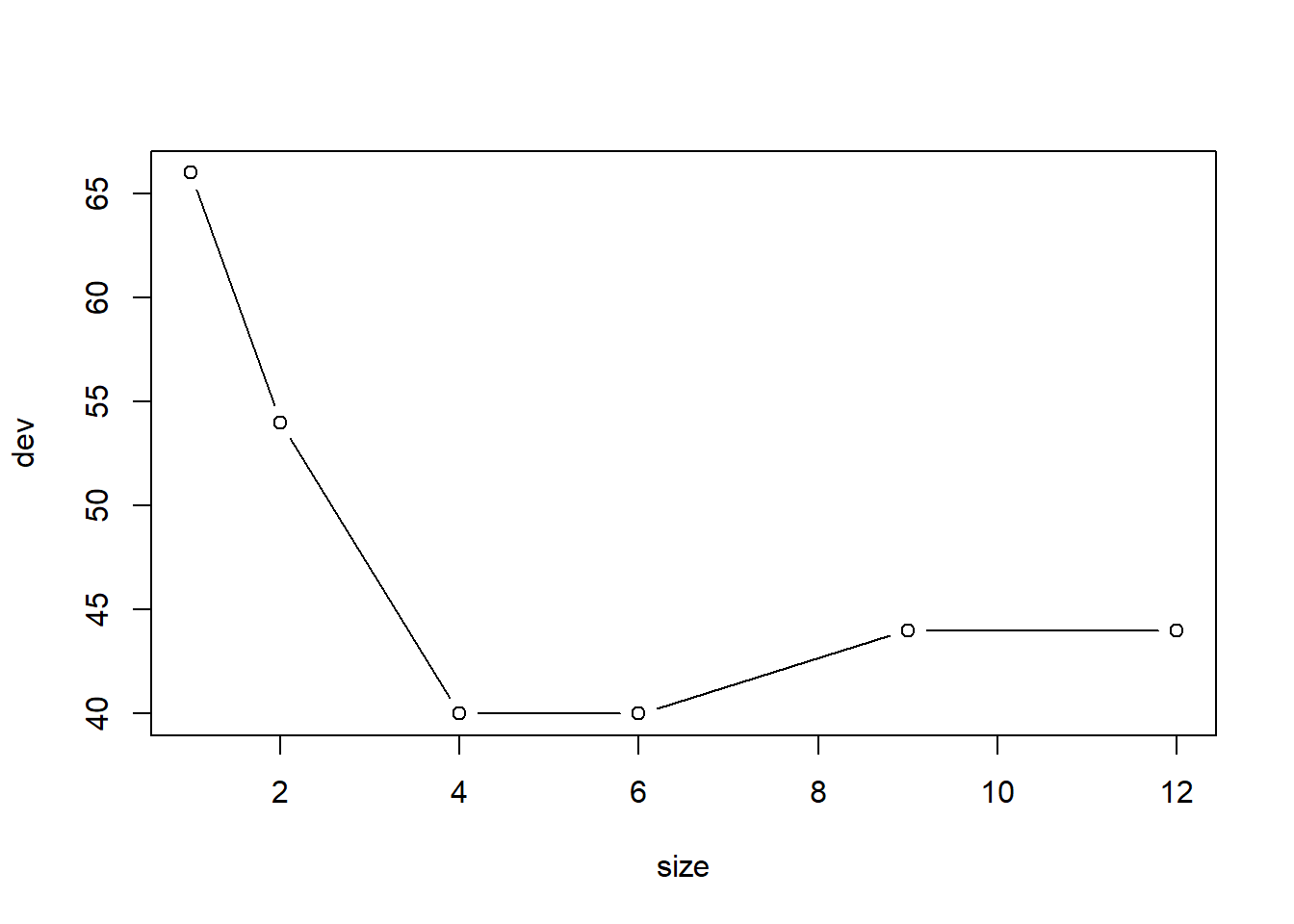

plot(cv1$size, cv1$dev, type='b', xlab='size', ylab='dev')

best.size <- cv1$size[which.min(cv1$dev)]

最优的大小是6。

对训练集生成剪枝结果：

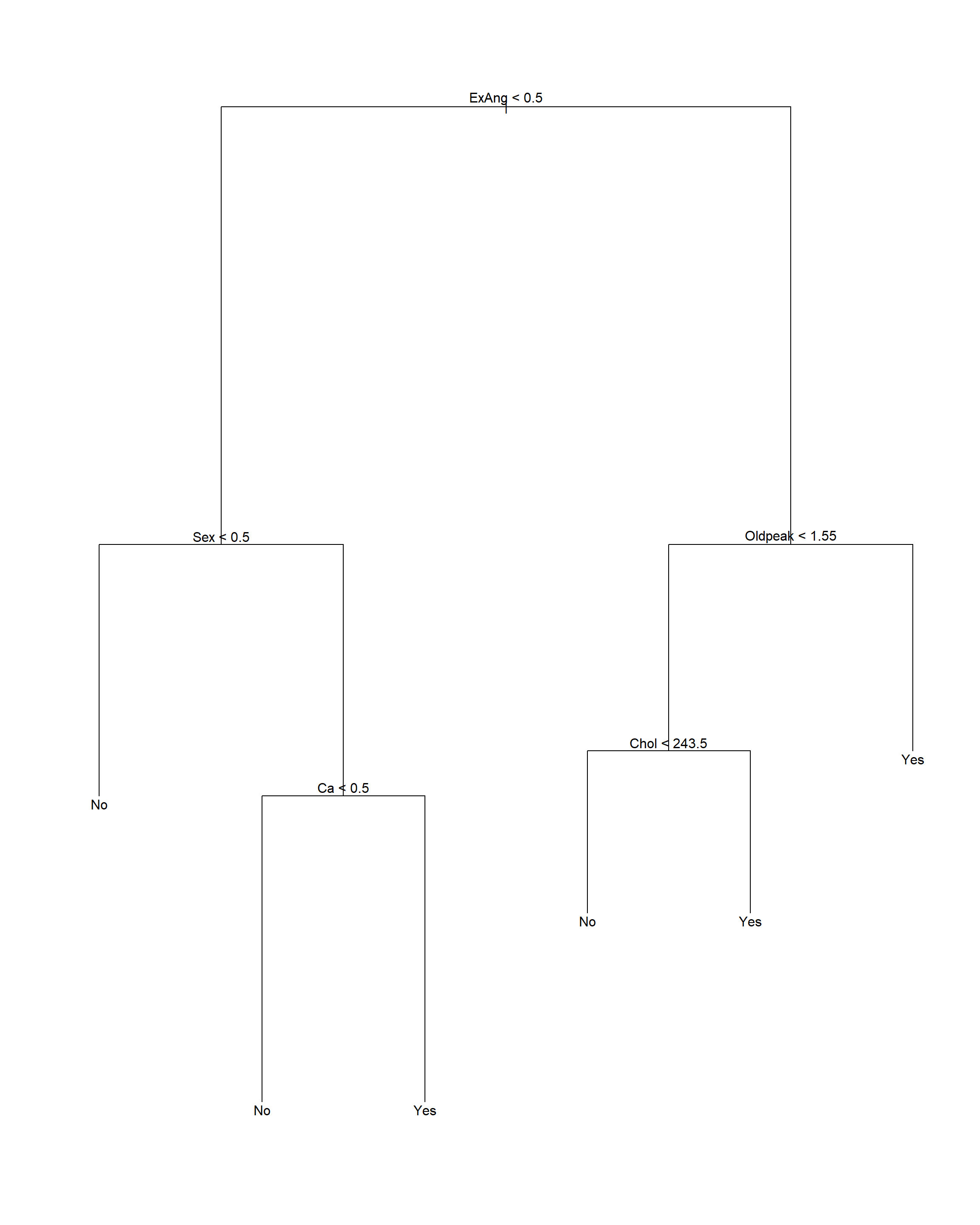
tr1b <- prune.misclass(tr1, best=best.size)
plot(tr1b); text(tr1b, pretty=0)

注意剪枝后树的显示中，内部节点的自变量存在分类变量，这时按照这个自变量分叉时，取指定的某几个分类值时对应分支Yes，取其它的分类值时对应分支No。

16.1.5.3 对测试集计算误判率

pred1 <- predict(tr1b, Heart[test,], type='class')
tab1 <- table(pred1, test.y); tab1

##      test.y
## pred1 No Yes
##   No  61  24
##   Yes 16  48

test.err <- (tab1[1,2]+tab1[2,1])/sum(tab1[]); test.err

## [1] 0.2684564

对测试集的错判率约27%。

利用未剪枝的树对测试集进行预测, 一般比剪枝后的结果差:

pred1a <- predict(tr1, Heart[test,], type='class')
tab1a <- table(pred1a, test.y); tab1a

##       test.y
## pred1a No Yes
##    No  58  21
##    Yes 19  51

test.err1a <- (tab1a[1,2]+tab1a[2,1])/sum(tab1a[]); test.err1a

## [1] 0.2684564

16.1.5.4 利用全集数据建立剪枝判别树

tr2 <- tree(AHD ~ ., data=Heart)
tr2b <- prune.misclass(tr2, best=best.size)
plot(tr2b); text(tr2b, pretty=0)

16.2 装袋法和随机森林

16.2.1 装袋法

判别树在不同的训练集、测试集划分上可以产生很大变化，说明其预测值方差较大。利用bootstrap的思想，可以随机选取许多个训练集，把许多个训练集的模型结果平均，就可以降低预测值的方差。

办法是从一个训练集中用有放回抽样的方法抽取\(B\)个训练集，设第\(b\)个抽取的训练集得到的回归函数为\(\hat f^{*b}(\cdot)\), 则最后的回归函数是这些回归函数的平均值: \[\begin{aligned} \hat f_{\text{bagging}}(x) = \frac{1}{B} \sum_{b=1}^b \hat f^{*b}(x) \end{aligned}\] 这称为装袋法(bagging)。装袋法对改善判别与回归树的精度十分有效。

装袋法的步骤如下：

从训练集中取\(B\)个有放回随机抽样的bootstrap训练集，\(B\)取为几百到几千之间。
对每个bootstrap训练集，估计未剪枝的树。
如果因变量是连续变量，对测试样品，用所有的树的预测值的平均值作预测。
如果因变量是分类变量，对测试样品，可以用所有树预测类的多数投票决定预测值。

装袋法也可以用来改进其他的回归和判别方法。

装袋后不能再用图形表示，模型可解释性较差。但是，可以度量自变量在预测中的重要程度。在回归问题中，可以计算每个自变量在所有\(B\)个树种平均减少的残差平方和的量，以此度量其重要度。在判别问题中，可以计算每个自变量在所有\(B\)个树种平均减少的基尼系数的量，以此度量其重要度。

除了可以用测试集、交叉验证方法以外，还可以使用袋外观测预测误差。用bootstrap再抽样获得多个训练集时每个bootstrap训练集总会遗漏一些观测，平均每个bootstrap训练集会遗漏三分之一的观测。对每个观测，大约有\(B/3\)棵树没有用到此观测，可以用这些树的预测值平均来预测此观测，得到一个误差估计，这样得到的均方误差估计或错判率称为袋外观测估计（OOB估计）。好处是不用很多额外的工作。

16.2.1.1 Hitters数据装袋法演示

对训练集用装袋法：

set.seed(1)
d <- na.omit(Hitters)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)

bag1 <- randomForest(log(Salary) ~ ., data=d, 
  subset=train, mtry=ncol(d)-1, importance=TRUE)
bag1

## 
## Call:
##  randomForest(formula = log(Salary) ~ ., data = d, mtry = ncol(d) -      1, importance = TRUE, subset = train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 19
## 
##           Mean of squared residuals: 0.2488363
##                     % Var explained: 68.1

注意randomForest()函数实际是随机森林法，但是当mtry的值取为所有自变量个数时就是装袋法。

对测试集进行预报:

pred2 <- predict(bag1, newdata=d[test,])
test.mse2 <- mean( (d[test, 'Salary'] - exp(pred2))^2 )
test.mse2

## [1] 90171.44

结果与剪枝过的单课树相近。

在全集上使用装袋法：

bag2 <- randomForest(log(Salary) ~ ., data=d, mtry=ncol(d)-1, importance=TRUE)
bag2

## 
## Call:
##  randomForest(formula = log(Salary) ~ ., data = d, mtry = ncol(d) -      1, importance = TRUE) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 19
## 
##           Mean of squared residuals: 0.1873377
##                     % Var explained: 76.22

变量的重要度数值和图形：各变量的重要度数值及其图形：

importance(bag2)

##               %IncMSE IncNodePurity
## AtBat     12.24054066     8.5996425
## Hits       9.47716109     8.0146504
## HmRun      4.19762724     2.1570060
## Runs       7.68565733     3.9542718
## RBI        7.51172719     5.7689615
## Walks      8.34560927     6.8880129
## Years      9.25986753     2.2505365
## CAtBat    26.74337522    79.8379721
## CHits     13.34178783    27.0067167
## CHmRun     6.93413792     3.9886086
## CRuns     14.33934038    32.9637351
## CRBI      15.42782700    10.2720711
## CWalks     7.02126823     4.6201072
## League    -1.00937275     0.1668663
## Division   0.03884951     0.2590991
## PutOuts    2.96962100     3.7135650
## Assists    1.06380884     1.7233765
## Errors     1.62377900     1.6439786
## NewLeague  1.42880310     0.3362676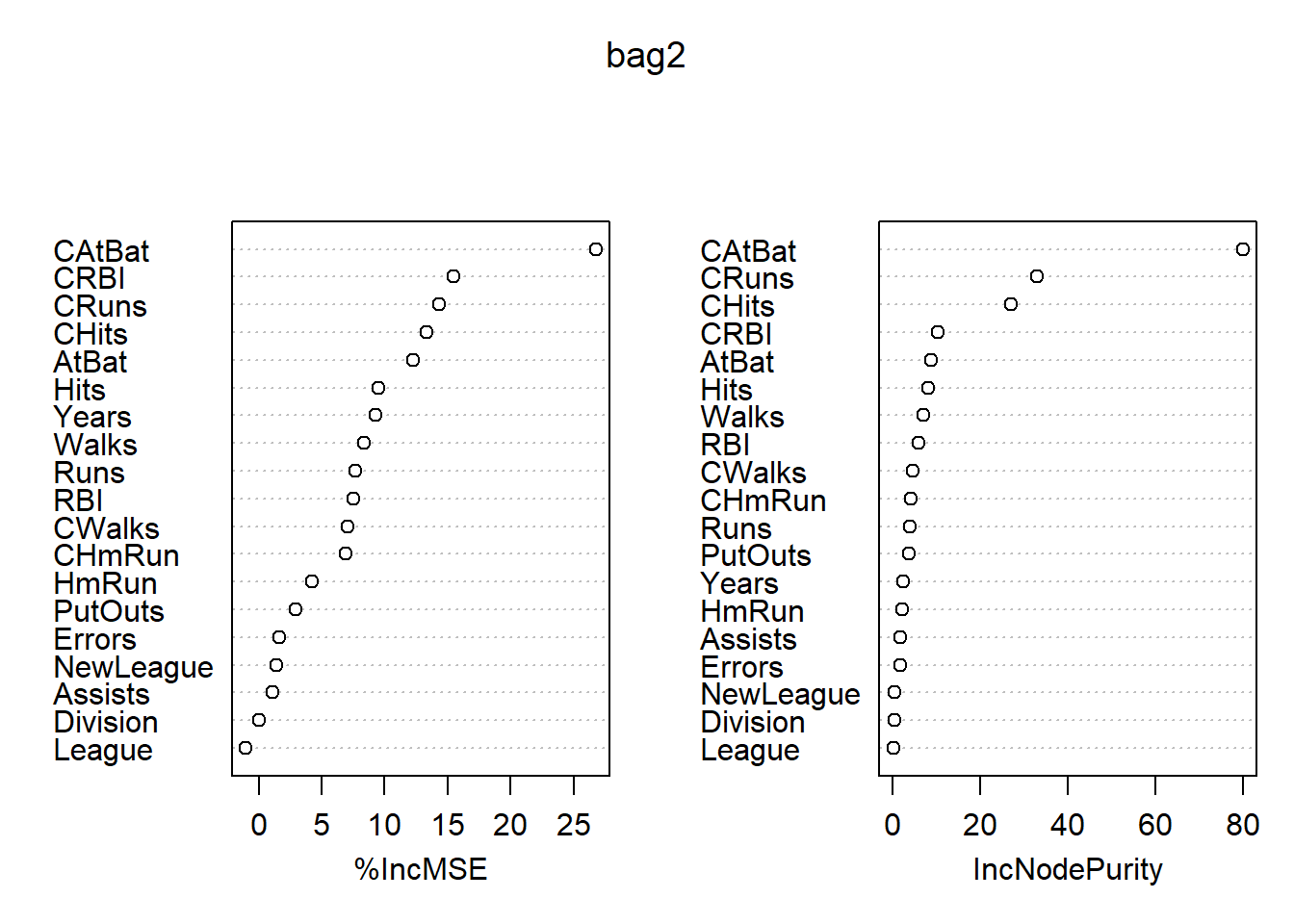

varImpPlot(bag2)

最重要的自变量是CAtBats, 其次有CRuns, CHits, CRBI等。

16.2.1.2 Heart数据用装袋法演示

对训练集用装袋法：

set.seed(1)
train_id <- sample(nrow(Heart), size=round(0.5*nrow(Heart)))
train <- rep(FALSE, nrow(Heart))
train[train_id] <- TRUE
test <- (!train)
test.y <- Heart[["AHD"]][test]

bag1 <- randomForest(AHD ~ ., data=Heart, 
  subset=train, mtry=13, importance=TRUE)
bag1

## 
## Call:
##  randomForest(formula = AHD ~ ., data = Heart, mtry = 13, importance = TRUE,      subset = train) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 13
## 
##         OOB estimate of  error rate: 22.97%
## Confusion matrix:
##     No Yes class.error
## No  70  13   0.1566265
## Yes 21  44   0.3230769

注意randomForest()函数实际是随机森林法，但是当mtry的值取为所有自变量个数时就是装袋法。袋外观测得到的错判率比较差。

对测试集进行预报:

pred2 <- predict(bag1, newdata=Heart[test,])
tab2 <- table(pred2, test.y); tab2

##      test.y
## pred2 No Yes
##   No  66  16
##   Yes 11  56

test.err2 <- (tab2[1,2]+tab2[2,1])/sum(tab2[]); test.err2

## [1] 0.1812081

测试集的错判率约为18%。

对全集用装袋法:

bag1b <- randomForest(AHD ~ ., data=Heart, mtry=13, importance=TRUE)
bag1b

## 
## Call:
##  randomForest(formula = AHD ~ ., data = Heart, mtry = 13, importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 13
## 
##         OOB estimate of  error rate: 19.53%
## Confusion matrix:
##      No Yes class.error
## No  134  26   0.1625000
## Yes  32 105   0.2335766

各变量的重要度数值及其图形：

importance(bag1b)

##                   No        Yes MeanDecreaseAccuracy MeanDecreaseGini
## Age        7.5914270  5.9300895            9.5901487        12.423534
## Sex       11.1035002  4.4224309           12.5552921         3.606976
## ChestPain 11.8110968 17.8134383           20.3909869        23.737158
## RestBP     4.2851096  2.6043117            4.9076443         9.865693
## Chol      -1.9750832 -3.4792229           -3.6808119        10.838036
## Fbs        0.7931423 -2.7452667           -1.2269553         0.874251
## RestECG   -1.7922866  0.8798907           -0.7548197         1.895233
## MaxHR      8.5471129  1.4362163            7.8503704        13.396300
## ExAng      1.8258307  5.7732467            5.2672188         3.941524
## Oldpeak   15.2223889 13.0068694           19.4903808        14.709831
## Slope      2.9181877  5.2329194            5.8296096         4.200541
## Ca        24.3509148 18.4287501           29.6110614        20.004071
## Thal      21.0348018 18.0554814           26.3633854        27.572038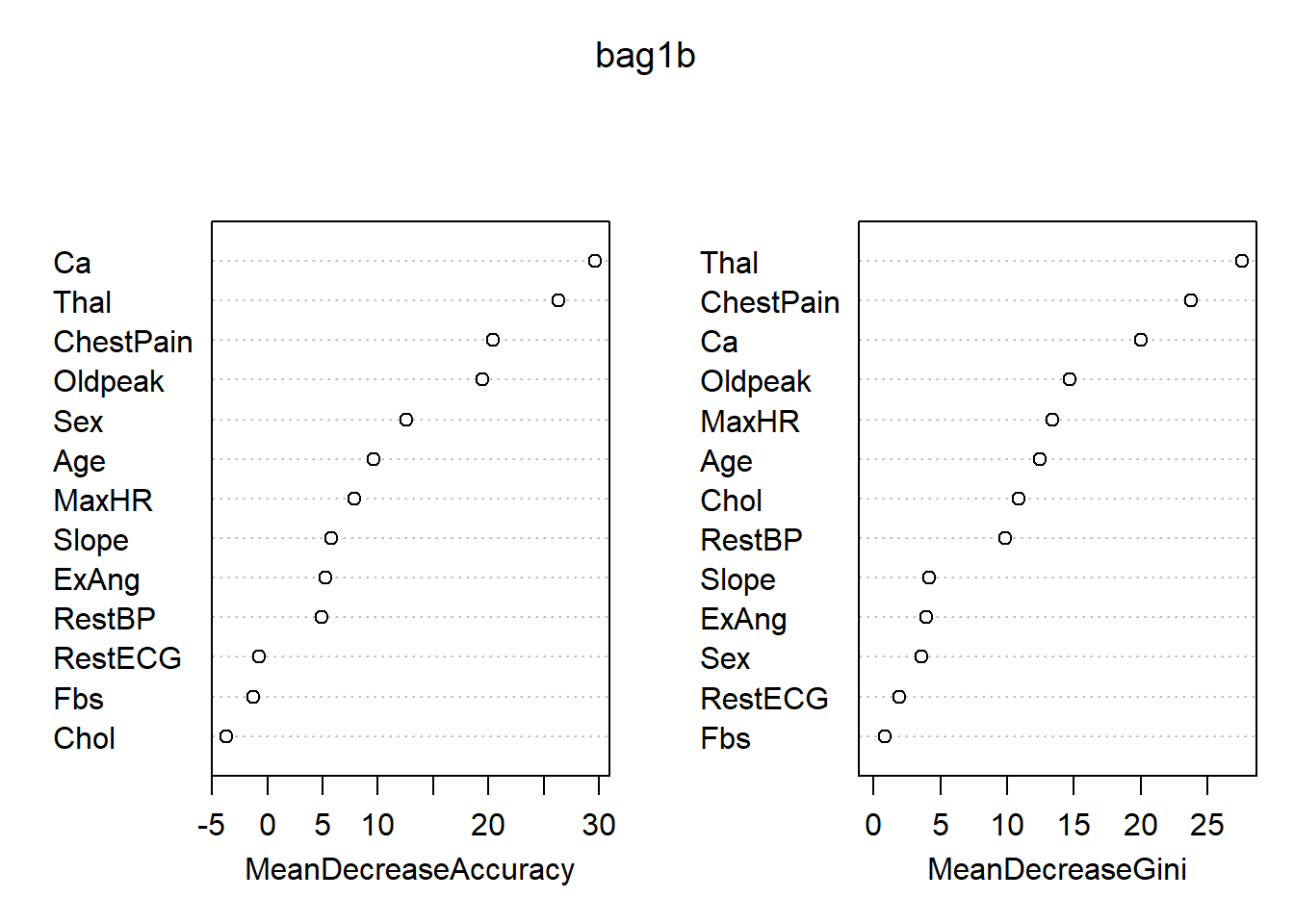

varImpPlot(bag1b)

最重要的变量是Thal, ChestPain, Ca。

16.2.2 随机森林

随机森林的思想与装袋法类似，但是试图使得参加平均的各个树之间变得比较独立。仍采用有放回抽样得到的多个bootstrap训练集，但是对每个bootstrap训练集构造判别树时，每次分叉时不考虑所有自变量，而是仅考虑随机选取的一个自变量子集。

对判别树，每次分叉时选取的自变量个数通常取\(m \approx \sqrt{p}\)个。比如，对Heart数据的13个自变量，每次分叉时仅随机选取4个纳入考察范围。

随机森林的想法是基于正相关的样本在平均时并不能很好地降低方差，独立样本能比较好地降低方差。如果存在一个最重要的变量，如果不加限制这个最重要的变量总会是第一个分叉，使得\(B\)棵树相似程度很高。随机森林解决这个问题的办法是限制分叉时可选的变量子集。

随机森林也可以用来改进其他的回归和判别方法。

装袋法和随机森林都可以用R扩展包randomForest的 randomForest()函数实现。当此函数的mtry参数取为自变量个数时，执行的就是装袋法； mtry取缺省值时，执行随机森林算法。执行随机森林算法时， randomForest()函数在回归问题时分叉时考虑的自变量个数取\(m \approx p/3\)，在判别问题时取\(m \approx \sqrt{p}\)。

16.2.2.1 Hitters数据随机森林演示

对训练集用随机森林法：

set.seed(1)
d <- na.omit(Hitters)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)

rf1 <- randomForest(log(Salary) ~ ., data=d, 
  subset=train, importance=TRUE)
rf1

## 
## Call:
##  randomForest(formula = log(Salary) ~ ., data = d, importance = TRUE,      subset = train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 6
## 
##           Mean of squared residuals: 0.2437535
##                     % Var explained: 68.75

当mtry的值取为缺省值时执行随机森林算法。

对测试集进行预报:

pred3 <- predict(rf1, newdata=d[test,])
test.mse3 <- mean( (d[test, 'Salary'] - exp(pred3))^2 )
test.mse3

## [1] 96229.2

结果与剪枝过的单课树、装袋法相近。

在全集上使用随机森林：

rf2 <- randomForest(log(Salary) ~ ., data=d, importance=TRUE)
rf2

## 
## Call:
##  randomForest(formula = log(Salary) ~ ., data = d, importance = TRUE) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 6
## 
##           Mean of squared residuals: 0.1782609
##                     % Var explained: 77.37

各变量的重要度数值及其图形：

importance(rf2)

##               %IncMSE IncNodePurity
## AtBat     11.81948475     8.2308776
## Hits       8.09787840     7.5075741
## HmRun      5.91570003     2.4320892
## Runs       8.48169025     4.8333805
## RBI        6.29673815     6.3026314
## Walks      9.36982692     6.2217510
## Years     10.61587730     6.5702146
## CAtBat    17.58354435    40.7827117
## CHits     15.64594781    34.4452277
## CHmRun     7.04523612     6.4528435
## CRuns     15.85901741    35.5844665
## CRBI      13.56732483    18.8060878
## CWalks    10.25381701    17.6924487
## League    -0.44093551     0.3050351
## Division   0.32697628     0.2715000
## PutOuts    3.74477178     3.0747050
## Assists   -0.43394356     1.6667284
## Errors     1.58044791     1.7246783
## NewLeague -0.01057482     0.3535943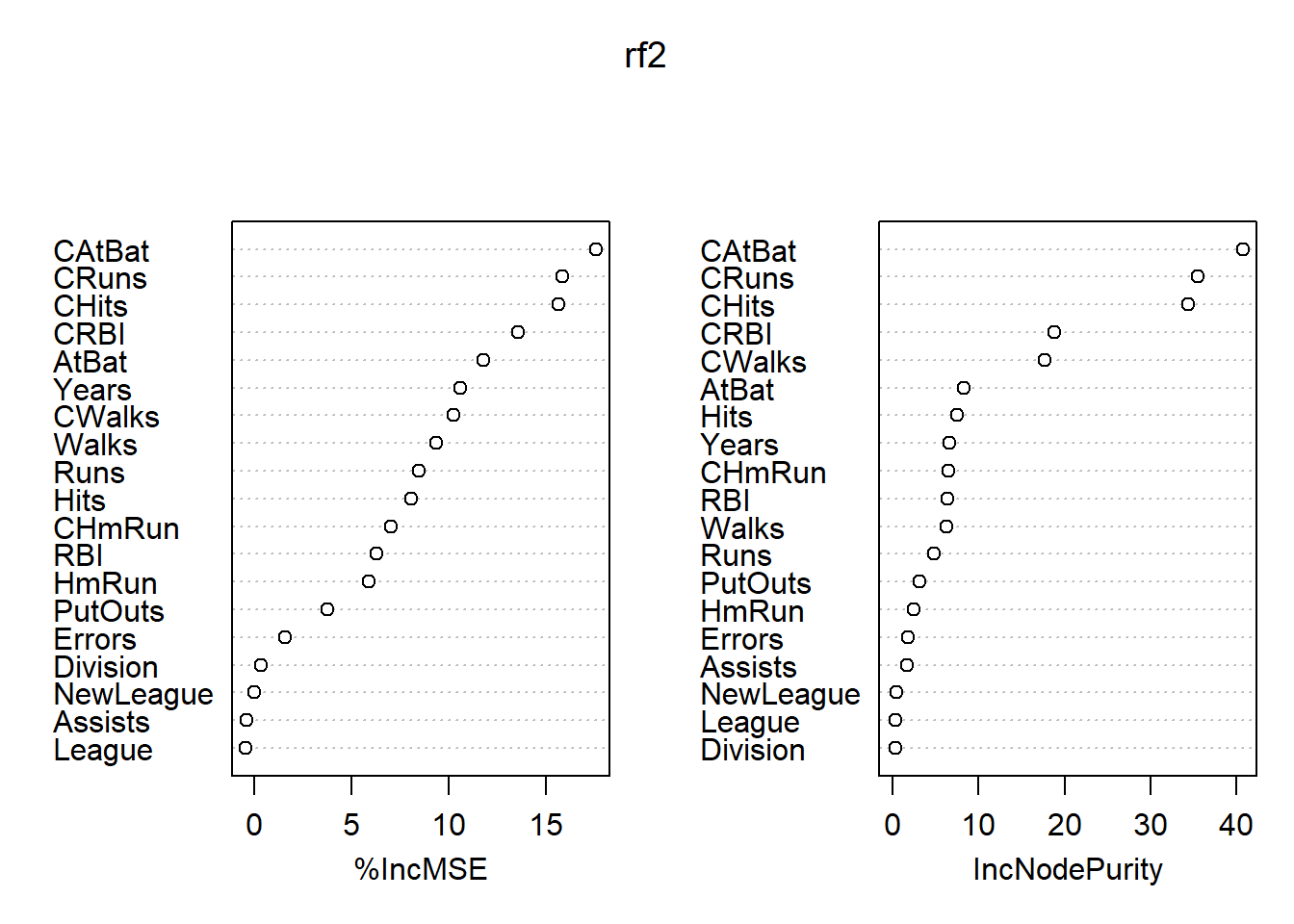

varImpPlot(rf2)

最重要的自变量是CAtBats, CRuns, CHits, CWalks, CRBI等。

16.2.2.2 Heart数据随机森林演示

对训练集用随机森林法：

set.seed(1)
train_id <- sample(nrow(Heart), size=round(0.5*nrow(Heart)))
train <- rep(FALSE, nrow(Heart))
train[train_id] <- TRUE
test <- (!train)
test.y <- Heart[["AHD"]][test]

rf1 <- randomForest(AHD ~ ., data=Heart, subset=train, importance=TRUE)
rf1

## 
## Call:
##  randomForest(formula = AHD ~ ., data = Heart, importance = TRUE,      subset = train) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 22.97%
## Confusion matrix:
##     No Yes class.error
## No  71  12   0.1445783
## Yes 22  43   0.3384615

这里mtry取缺省值，对应于随机森林法。

对测试集进行预报:

pred3 <- predict(rf1, newdata=Heart[test,])
tab3 <- table(pred3, test.y); tab3

##      test.y
## pred3 No Yes
##   No  70  17
##   Yes  7  55

test.err3 <- (tab3[1,2]+tab3[2,1])/sum(tab3[]); test.err3

## [1] 0.1610738

测试集的错判率约为16%。

对全集用随机森林:

rf1b <- randomForest(AHD ~ ., data=Heart,  importance=TRUE)
rf1b

## 
## Call:
##  randomForest(formula = AHD ~ ., data = Heart, importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 17.17%
## Confusion matrix:
##      No Yes class.error
## No  137  23   0.1437500
## Yes  28 109   0.2043796

各变量的重要度数值及其图形：

importance(rf1b)

##                   No        Yes MeanDecreaseAccuracy MeanDecreaseGini
## Age        5.0451528  4.1243916            6.2544913        12.589891
## Sex       11.8830005  5.7666976           13.0527236         4.348853
## ChestPain 12.9853182 15.9344889           20.0063334        18.140518
## RestBP     2.3860139  0.8161766            2.2560609        10.402834
## Chol       0.4441293 -1.7627423           -1.0295881        11.550493
## Fbs        1.3711348 -2.5626917           -0.8151845         1.329501
## RestECG    0.1510264  0.5408153            0.4091251         2.734730
## MaxHR      9.6540260  4.8456013           10.0807989        17.028765
## ExAng      3.8100638  7.2834823            8.0332494         7.365512
## Oldpeak    9.9336236 12.8188739           16.1137642        15.876015
## Slope      1.9767505  8.3713104            7.6713543         6.421739
## Ca        21.6441820 18.4225083           26.1245597        18.106245
## Thal      19.6662985 16.5929688           24.6866916        19.282387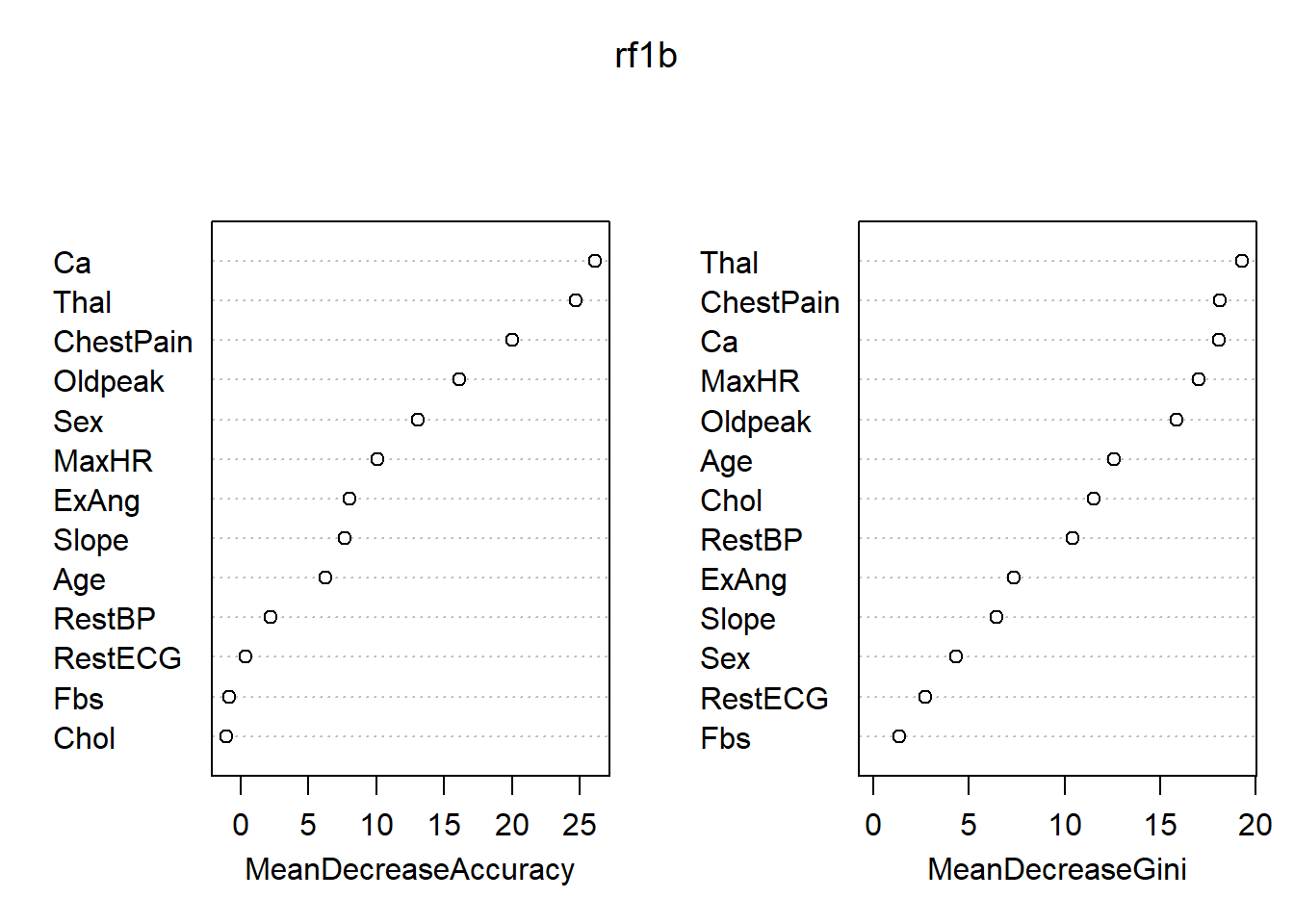

varImpPlot(rf1b)

最重要的变量是ChestPain, Thal, Ca。

16.3 汽车销量数据的演示

Carseats是ISLR包的一个数据集，基本情况如下:

str(Carseats)

## 'data.frame':    400 obs. of  11 variables:
##  $ Sales      : num  9.5 11.22 10.06 7.4 4.15 ...
##  $ CompPrice  : num  138 111 113 117 141 124 115 136 132 132 ...
##  $ Income     : num  73 48 35 100 64 113 105 81 110 113 ...
##  $ Advertising: num  11 16 10 4 3 13 0 15 0 0 ...
##  $ Population : num  276 260 269 466 340 501 45 425 108 131 ...
##  $ Price      : num  120 83 80 97 128 72 108 120 124 124 ...
##  $ ShelveLoc  : Factor w/ 3 levels "Bad","Good","Medium": 1 2 3 3 1 1 3 2 3 3 ...
##  $ Age        : num  42 65 59 55 38 78 71 67 76 76 ...
##  $ Education  : num  17 10 12 14 13 16 15 10 10 17 ...
##  $ Urban      : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 2 2 1 1 ...
##  $ US         : Factor w/ 2 levels "No","Yes": 2 2 2 2 1 2 1 2 1 2 ...

summary(Carseats)

##      Sales          CompPrice       Income        Advertising       Population        Price        ShelveLoc        Age          Education    Urban       US     
##  Min.   : 0.000   Min.   : 77   Min.   : 21.00   Min.   : 0.000   Min.   : 10.0   Min.   : 24.0   Bad   : 96   Min.   :25.00   Min.   :10.0   No :118   No :142  
##  1st Qu.: 5.390   1st Qu.:115   1st Qu.: 42.75   1st Qu.: 0.000   1st Qu.:139.0   1st Qu.:100.0   Good  : 85   1st Qu.:39.75   1st Qu.:12.0   Yes:282   Yes:258  
##  Median : 7.490   Median :125   Median : 69.00   Median : 5.000   Median :272.0   Median :117.0   Medium:219   Median :54.50   Median :14.0                      
##  Mean   : 7.496   Mean   :125   Mean   : 68.66   Mean   : 6.635   Mean   :264.8   Mean   :115.8                Mean   :53.32   Mean   :13.9                      
##  3rd Qu.: 9.320   3rd Qu.:135   3rd Qu.: 91.00   3rd Qu.:12.000   3rd Qu.:398.5   3rd Qu.:131.0                3rd Qu.:66.00   3rd Qu.:16.0                      
##  Max.   :16.270   Max.   :175   Max.   :120.00   Max.   :29.000   Max.   :509.0   Max.   :191.0                Max.   :80.00   Max.   :18.0

把Salses变量按照大于8与否分成两组，结果存入变量High，以High为因变量作判别分析。

d <- na.omit(Carseats)
d$High <- factor(ifelse(d$Sales > 8, 'Yes', 'No'))
dim(d)

## [1] 400  12

16.3.1 判别树

16.3.1.1 全体数据的判别树

对全体数据建立未剪枝的判别树:

tr1 <- tree(High ~ . - Sales, data=d)
summary(tr1)

## 
## Classification tree:
## tree(formula = High ~ . - Sales, data = d)
## Variables actually used in tree construction:
## [1] "ShelveLoc"   "Price"       "Income"      "CompPrice"   "Population"  "Advertising" "Age"         "US"         
## Number of terminal nodes:  27 
## Residual mean deviance:  0.4575 = 170.7 / 373 
## Misclassification error rate: 0.09 = 36 / 400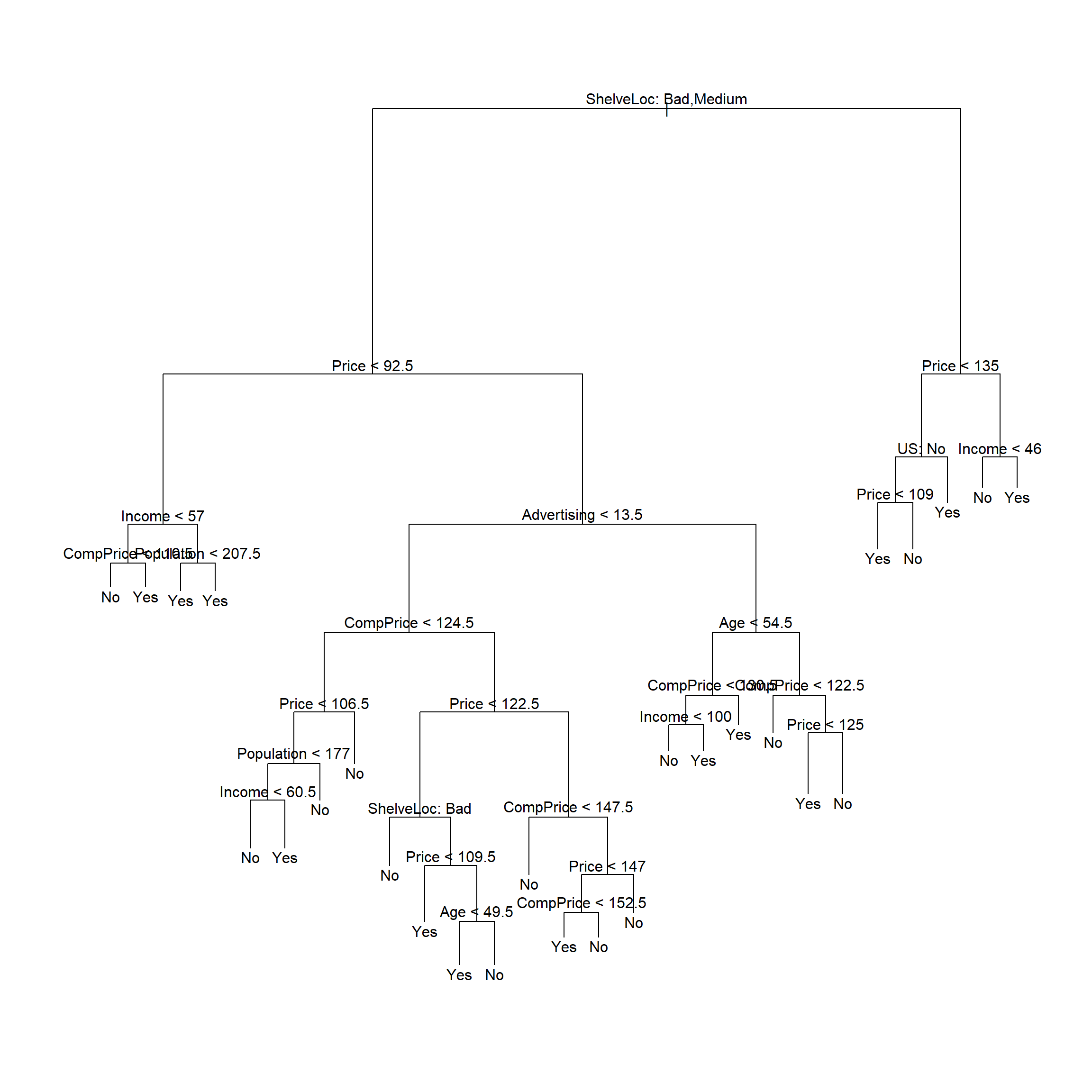

plot(tr1)
text(tr1, pretty=0)

16.3.1.2 划分训练集和测试集

把输入数据集随机地分一半当作训练集，另一半当作测试集：

d <- na.omit(Carseats)
d$High <- factor(ifelse(d$Sales > 8, 'Yes', 'No'))
set.seed(2)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)
test.high <- d[["High"]][test]

用训练数据建立未剪枝的判别树:

tr2 <- tree(High ~ . - Sales, data=d, subset=train)
summary(tr2)

## 
## Classification tree:
## tree(formula = High ~ . - Sales, data = d, subset = train)
## Variables actually used in tree construction:
## [1] "Price"       "Population"  "ShelveLoc"   "Age"         "Education"   "CompPrice"   "Advertising" "Income"      "US"         
## Number of terminal nodes:  21 
## Residual mean deviance:  0.5543 = 99.22 / 179 
## Misclassification error rate: 0.115 = 23 / 200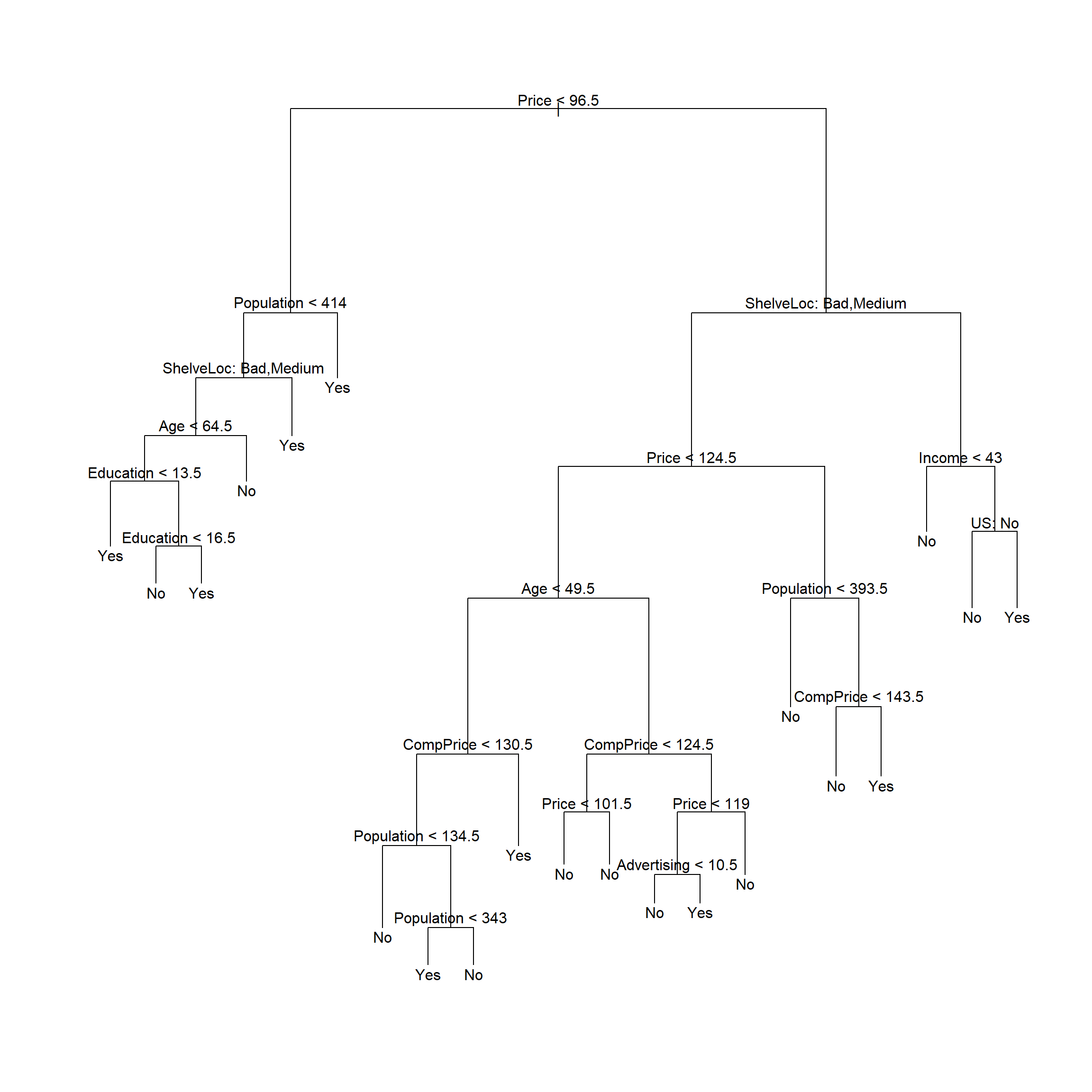

plot(tr2)
text(tr2, pretty=0)

用未剪枝的树对测试集进行预测，并计算误判率：

pred2 <- predict(tr2, d[test,], type='class')
tab <- table(pred2, test.high); tab

##      test.high
## pred2  No Yes
##   No  104  33
##   Yes  13  50

test.err2 <- (tab[1,2] + tab[2,1]) / sum(tab[]); test.err2

## [1] 0.23

16.3.1.3 用交叉验证确定训练集的剪枝

set.seed(3)
cv1 <- cv.tree(tr2, FUN=prune.misclass)
cv1

## $size
## [1] 21 19 14  9  8  5  3  2  1
## 
## $dev
## [1] 74 74 78 77 77 79 75 80 82
## 
## $k
## [1] -Inf  0.0  1.0  1.4  2.0  3.0  4.0  9.0 18.0
## 
## $method
## [1] "misclass"
## 
## attr(,"class")
## [1] "prune"         "tree.sequence"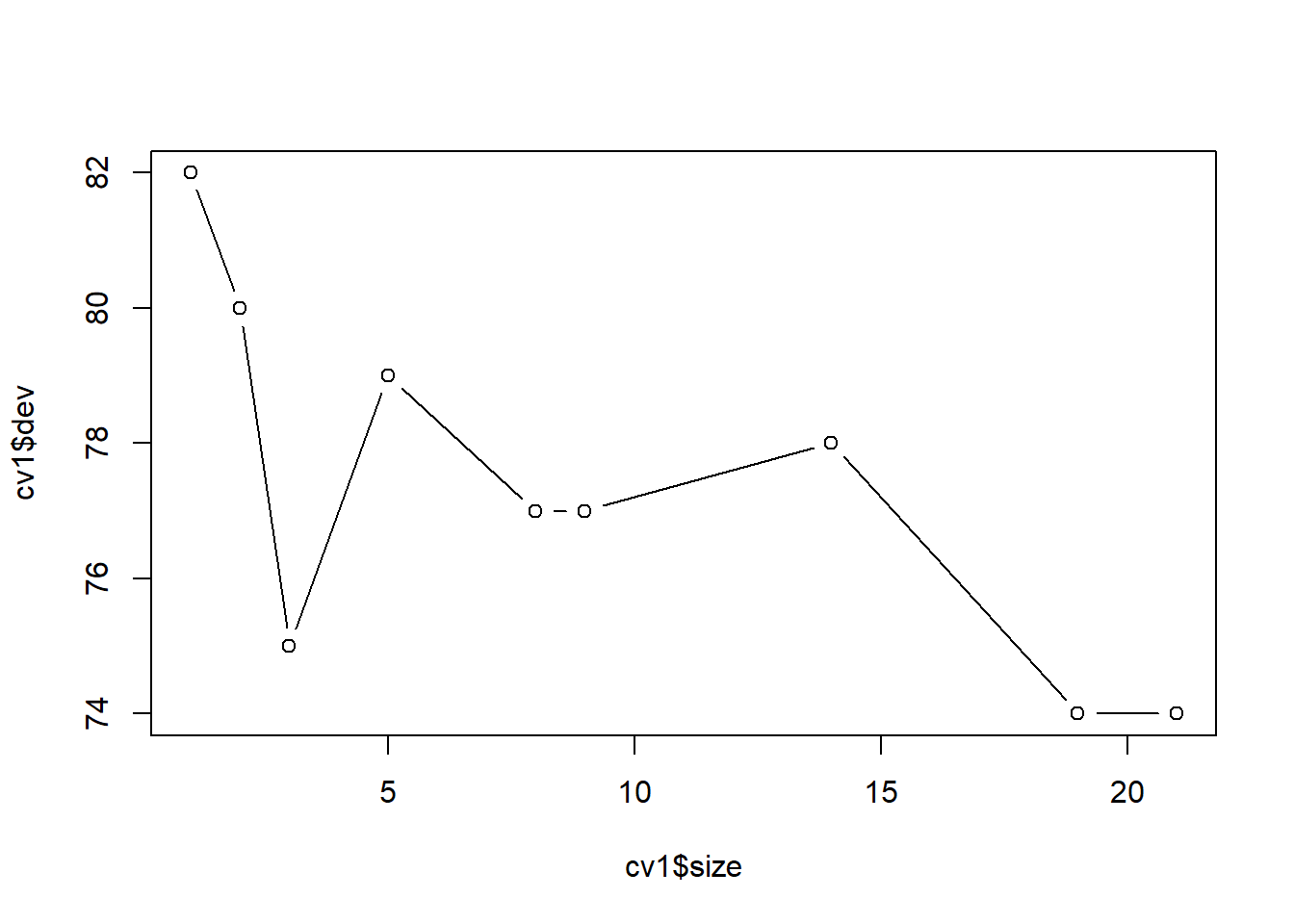

plot(cv1$size, cv1$dev, type='b')

best.size <- cv1$size[which.min(cv1$dev)]

用交叉验证方法自动选择的最佳树大小为21。

剪枝:

tr3 <- prune.misclass(tr2, best=best.size)
summary(tr3)

## 
## Classification tree:
## tree(formula = High ~ . - Sales, data = d, subset = train)
## Variables actually used in tree construction:
## [1] "Price"       "Population"  "ShelveLoc"   "Age"         "Education"   "CompPrice"   "Advertising" "Income"      "US"         
## Number of terminal nodes:  21 
## Residual mean deviance:  0.5543 = 99.22 / 179 
## Misclassification error rate: 0.115 = 23 / 200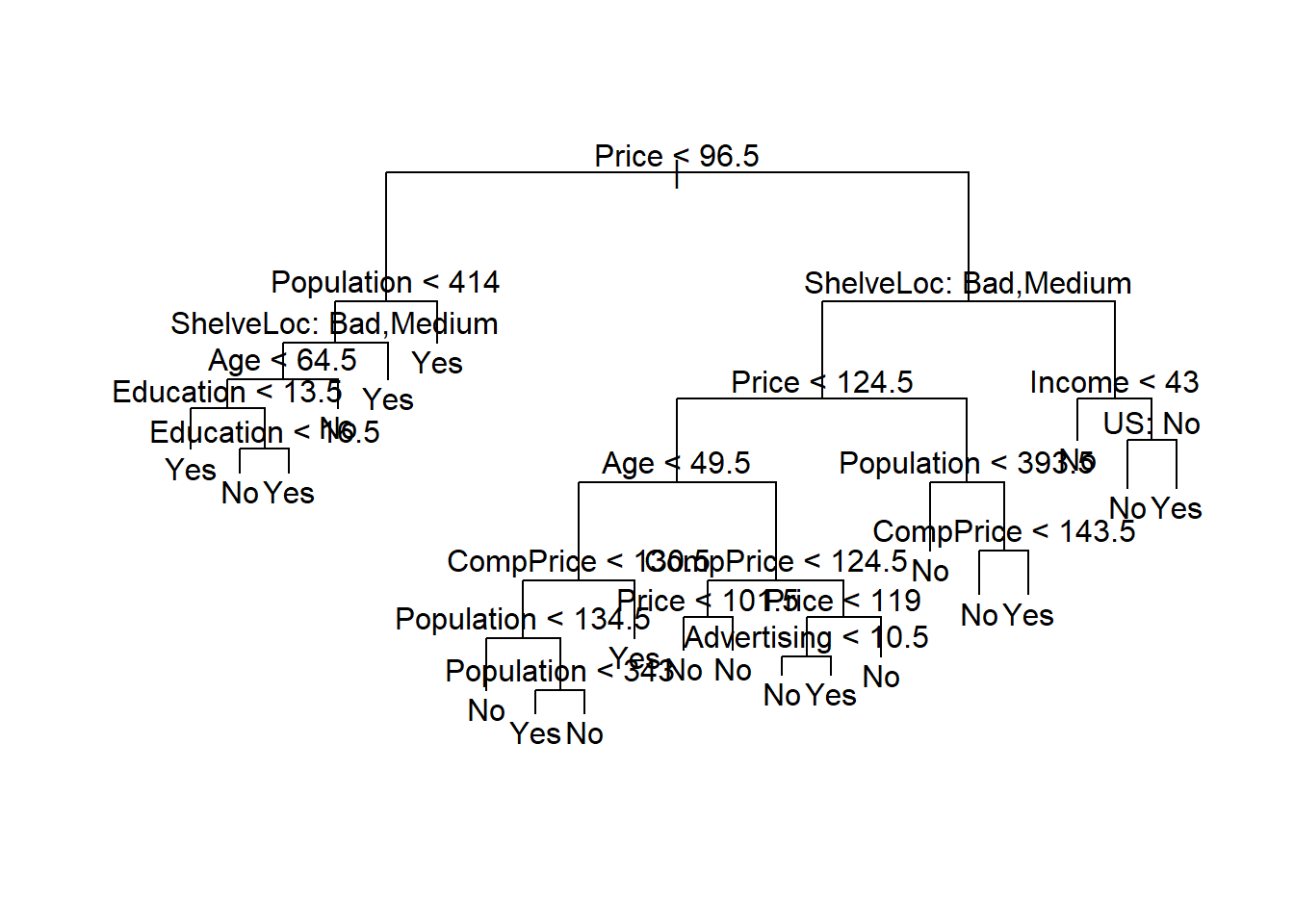

plot(tr3)
text(tr3, pretty=0)

用剪枝后的树对测试集进行预测，计算误判率：

pred3 <- predict(tr3, d[test,], type='class')
tab <- table(pred3, test.high); tab

##      test.high
## pred3  No Yes
##   No  104  32
##   Yes  13  51

test.err3 <- (tab[1,2] + tab[2,1]) / sum(tab[]); test.err3

## [1] 0.225

16.3.2 随机森林

对训练集用随机森林法：

rf4 <- randomForest(High ~ . - Sales, data=d, 
  subset=train, importance=TRUE)
rf4

## 
## Call:
##  randomForest(formula = High ~ . - Sales, data = d, importance = TRUE,      subset = train) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 27%
## Confusion matrix:
##      No Yes class.error
## No  100  19   0.1596639
## Yes  35  46   0.4320988

这里mtry取缺省值，对应于随机森林法。

对测试集进行预报:

pred4 <- predict(rf4, newdata=d[test,])
tab <- table(pred4, test.high); tab

##      test.high
## pred4  No Yes
##   No  108  23
##   Yes   9  60

test.err4 <- (tab[1,2]+tab[2,1])/sum(tab[]); test.err4

## [1] 0.16

注意错判率结果依赖于训练集和测试集的划分，另行选择训练集与测试集可能会得到很不一样的错判率结果。

对全集用随机森林:

rf5 <- randomForest(High ~ . - Sales, data=d,  importance=TRUE)
rf5

## 
## Call:
##  randomForest(formula = High ~ . - Sales, data = d, importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 19%
## Confusion matrix:
##      No Yes class.error
## No  209  27   0.1144068
## Yes  49 115   0.2987805

各变量的重要度数值及其图形：

importance(rf5)

##                       No        Yes MeanDecreaseAccuracy MeanDecreaseGini
## CompPrice   11.033758100  7.7402932          13.33895983        21.229763
## Income       3.866551200  3.5223698           5.31053942        19.861721
## Advertising 10.907742775 16.4431361          18.85477287        24.265021
## Population  -1.036771688 -2.6857178          -2.48427062        15.324194
## Price       33.443509343 27.9971005          40.05127916        43.779513
## ShelveLoc   34.255084236 34.3178518          43.13153318        30.636062
## Age          9.704435069 11.0226748          14.66681661        22.262051
## Education   -0.009866974 -0.1131696          -0.18869317        10.058102
## Urban        0.687787338 -0.9368078          -0.06090853         2.094715
## US           2.929166411  5.1334006           6.60885378         3.436709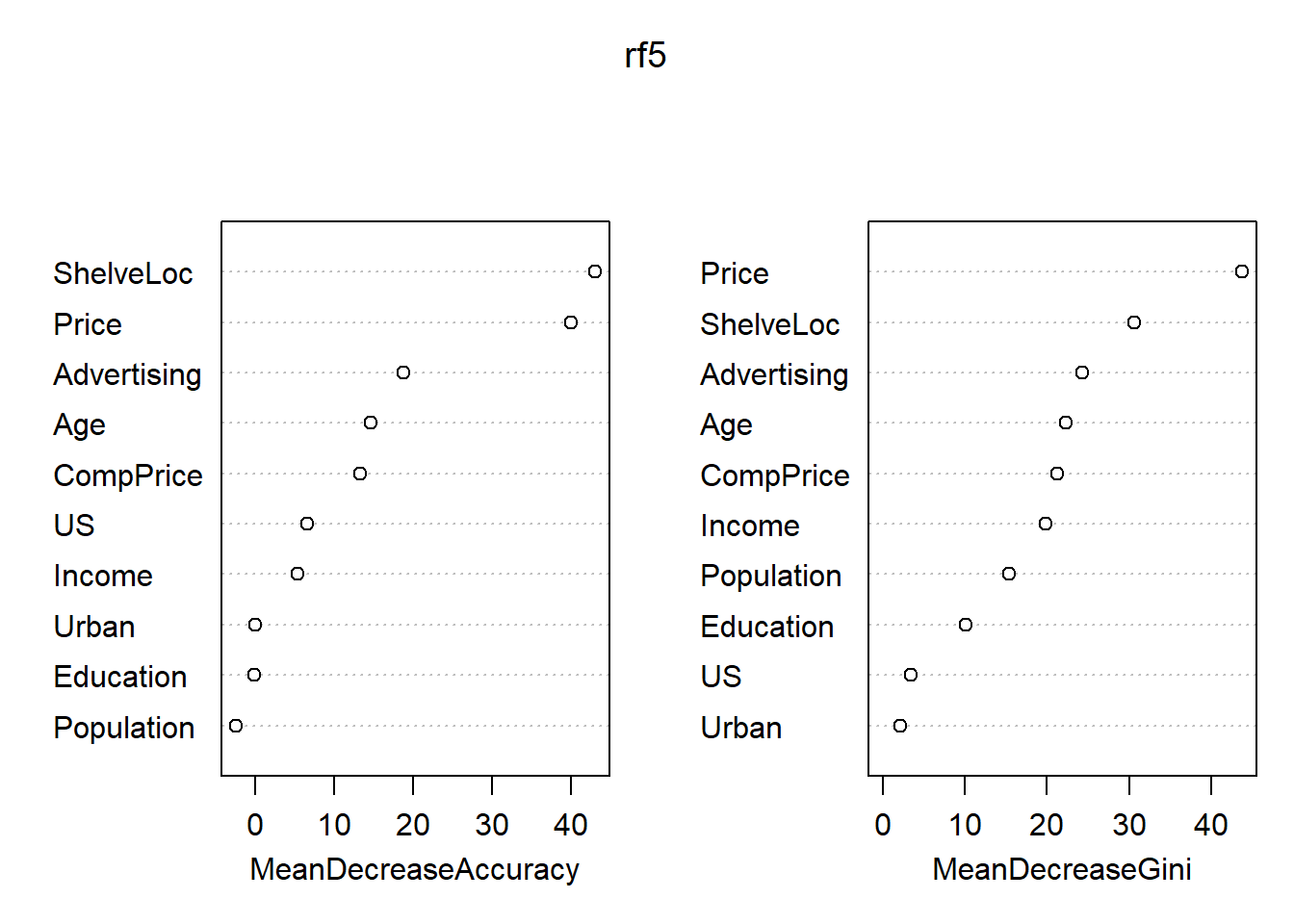

varImpPlot(rf5)

重要的自变量为Price, ShelfLoc, 其次有Age, Advertising, CompPrice, Income等。

16.4 提升法(Boosting)

提升法(Boosting)也是可以用在多种回归和判别问题中的方法。提升法的想法是，用比较简单的模型拟合因变量，计算残差，然后以残差为新的因变量建模，仍使用简单的模型，把两次的回归函数作加权和，得到新的残差后，再以新残差作为因变量建模，如此重复地更新回归函数，得到由多个回归函数加权和组成的最终的回归函数。

加权一般取为比较小的值，其目的是降低逼近速度。统计学习问题中降低逼近速度可以减轻过度拟合问题。

提升法算法:

(1) 对训练集，设置\(r_i = y_i\)，并令初始回归函数为\(\hat f(\cdot)=0\)。
(2) 对\(b=1,2,\dots,B\)重复执行：
- (a) 以训练集的自变量为自变量，以\(r\)为因变量，拟合一个仅有\(d\)个分叉的简单树回归函数，设为\(\hat f_b\)；
- (b) 更新回归函数，添加一个压缩过的树回归函数: \[\begin{aligned} \hat f(x) \leftarrow \hat f(x) + \lambda \hat f_b(x); \end{aligned}\]
- (c) 更新残差: \[\begin{aligned} r_i \leftarrow r_i - \lambda \hat f_b(x_i). \end{aligned}\]
(3) 提升法的回归函数为 \[\begin{aligned} \hat f(x) = \sum_{b=1}^B \lambda \hat f_b(x) . \end{aligned}\]

用多少个回归函数做加权和，即\(B\)的选取问题。取得\(B\)太大也会有过度拟合，但是只要\(B\)不太大这个问题不严重。可以用交叉验证选择\(B\)的值。

收缩系数\(\lambda\)是一个小的正数，控制学习速度，经常用0.01, 0.001这样的值，与要解决的问题有关。取\(\lambda\)很小，就需要取\(B\)很大。

用来控制每个回归函数复杂度的参数，对树回归而言就是树的大小。一个分叉的树往往就很好。取单个分叉时结果模型是可加模型，没有交互项，这是因为每个加权相加得回归函数都只依赖于单一自变量。 \(d>1\)时就加入了交互项。

16.4.1 xgboost

xgboost(eXtreme Gradient Boosting)算法是对boosting算法的一个改进。 R的xgboost可以支持不同的基础模型如线性回归、树方法、逻辑斯谛回归，可以自定义目标函数，支持并行运算，支持多种数据输入方法。

16.4.2 lightgbm

lightGBM是对boosting算法的改进，此算法计算效率高，内存占用少，支持并行计算、GPU，是一个比较先进的算法。 R的lightgbm包提供了R调用lightGBM库的接口。

16.5 统计学习算法调用统一界面

不同的统计学习算法及其实现函数使用了不同的程序语法。但是，这些方法一般也有流程上的共同之处。一般都将数据分为训练集与测试集，在训练集上一般使用交叉验证方法求得调节参数的最优值，然后在测试集上进行预测，得到客观的模型效果评价。

R扩展包caret和mlr可以整合现有的统计学习函数，用一个统一的调用界面访问统一的常用功能，并可以实现交叉验证等功能。

16.6 波士顿郊区房价数据分析演示

MASS包的Boston数据包含了波士顿地区郊区房价的若干数据。以众位房价medv为因变量建立回归模型。首先把缺失值去掉后存入数据集d:

d <- na.omit(Boston)

数据集概况：

str(d)

## 'data.frame':    506 obs. of  14 variables:
##  $ crim   : num  0.00632 0.02731 0.02729 0.03237 0.06905 ...
##  $ zn     : num  18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
##  $ indus  : num  2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
##  $ chas   : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ nox    : num  0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
##  $ rm     : num  6.58 6.42 7.18 7 7.15 ...
##  $ age    : num  65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
##  $ dis    : num  4.09 4.97 4.97 6.06 6.06 ...
##  $ rad    : int  1 2 2 3 3 3 5 5 5 5 ...
##  $ tax    : num  296 242 242 222 222 222 311 311 311 311 ...
##  $ ptratio: num  15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
##  $ black  : num  397 397 393 395 397 ...
##  $ lstat  : num  4.98 9.14 4.03 2.94 5.33 ...
##  $ medv   : num  24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...

summary(d)

##       crim                zn             indus            chas              nox               rm             age              dis              rad              tax           ptratio          black            lstat            medv      
##  Min.   : 0.00632   Min.   :  0.00   Min.   : 0.46   Min.   :0.00000   Min.   :0.3850   Min.   :3.561   Min.   :  2.90   Min.   : 1.130   Min.   : 1.000   Min.   :187.0   Min.   :12.60   Min.   :  0.32   Min.   : 1.73   Min.   : 5.00  
##  1st Qu.: 0.08205   1st Qu.:  0.00   1st Qu.: 5.19   1st Qu.:0.00000   1st Qu.:0.4490   1st Qu.:5.886   1st Qu.: 45.02   1st Qu.: 2.100   1st Qu.: 4.000   1st Qu.:279.0   1st Qu.:17.40   1st Qu.:375.38   1st Qu.: 6.95   1st Qu.:17.02  
##  Median : 0.25651   Median :  0.00   Median : 9.69   Median :0.00000   Median :0.5380   Median :6.208   Median : 77.50   Median : 3.207   Median : 5.000   Median :330.0   Median :19.05   Median :391.44   Median :11.36   Median :21.20  
##  Mean   : 3.61352   Mean   : 11.36   Mean   :11.14   Mean   :0.06917   Mean   :0.5547   Mean   :6.285   Mean   : 68.57   Mean   : 3.795   Mean   : 9.549   Mean   :408.2   Mean   :18.46   Mean   :356.67   Mean   :12.65   Mean   :22.53  
##  3rd Qu.: 3.67708   3rd Qu.: 12.50   3rd Qu.:18.10   3rd Qu.:0.00000   3rd Qu.:0.6240   3rd Qu.:6.623   3rd Qu.: 94.08   3rd Qu.: 5.188   3rd Qu.:24.000   3rd Qu.:666.0   3rd Qu.:20.20   3rd Qu.:396.23   3rd Qu.:16.95   3rd Qu.:25.00  
##  Max.   :88.97620   Max.   :100.00   Max.   :27.74   Max.   :1.00000   Max.   :0.8710   Max.   :8.780   Max.   :100.00   Max.   :12.127   Max.   :24.000   Max.   :711.0   Max.   :22.00   Max.   :396.90   Max.   :37.97   Max.   :50.00

16.6.1 回归树

16.6.1.1 划分训练集和测试集

set.seed(1)
d <- na.omit(Boston)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)

对训练集建立未剪枝的树：

tr1 <- tree(medv ~ ., d, subset=train)
summary(tr1)

## 
## Regression tree:
## tree(formula = medv ~ ., data = d, subset = train)
## Variables actually used in tree construction:
## [1] "rm"    "lstat" "crim"  "age"  
## Number of terminal nodes:  7 
## Residual mean deviance:  10.38 = 2555 / 246 
## Distribution of residuals:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -10.1800  -1.7770  -0.1775   0.0000   1.9230  16.5800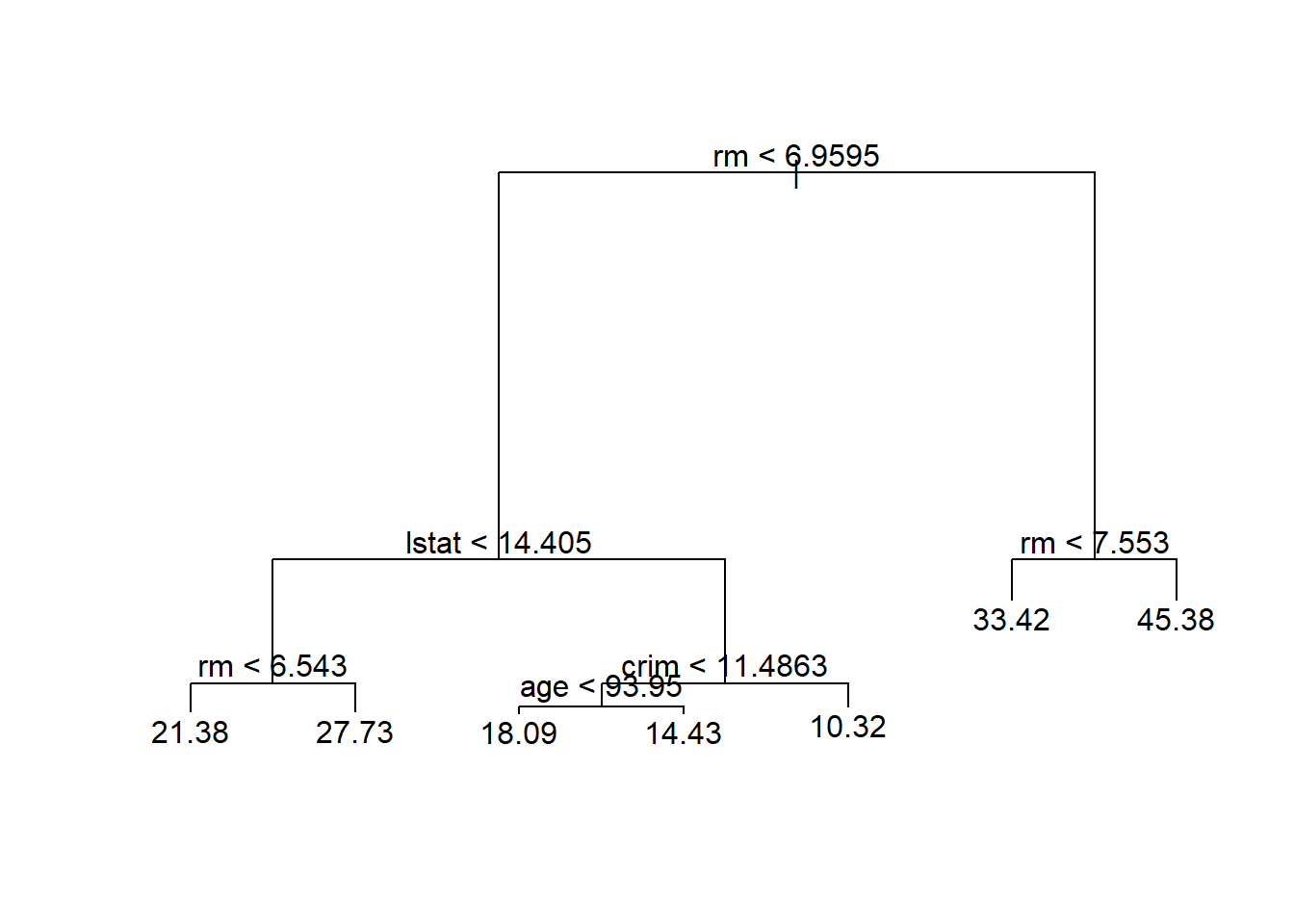

plot(tr1)
text(tr1, pretty=0)

用未剪枝的树对测试集进行预测，计算均方误差：

yhat <-predict(tr1, newdata=d[test,])
mse1 <- mean((yhat - d[test, 'medv'])^2)
mse1

## [1] 35.28688

16.6.1.2 用交叉验证方法确定剪枝复杂度

cv1 <- cv.tree(tr1)
plot(cv1$size, cv1$dev, type='b')

best.size <- cv1$size[which.min(cv1$dev)]; best.size

## [1] 7

剪枝并对测试集进行预测：

tr2 <- prune.tree(tr1, best=best.size)
plot(tr2)
text(tr2, pretty=0)

yhat <-predict(tr2, newdata=d[test,])
mse2 <- mean((yhat - d[test, 'medv'])^2)
mse2

## [1] 35.28688

没有剪枝，效果没有改善。

16.6.2 装袋法

用randomForest包计算。当参数mtry取为自变量个数时按照装袋法计算。对训练集计算。

set.seed(1)
bag1 <- randomForest(medv ~ ., data=d, 
  subset=train, mtry=ncol(d)-1, importance=TRUE)
bag1

## 
## Call:
##  randomForest(formula = medv ~ ., data = d, mtry = ncol(d) - 1,      importance = TRUE, subset = train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 13
## 
##           Mean of squared residuals: 11.24028
##                     % Var explained: 85.38

在测试集上计算装袋法的均方误差：

yhat <- predict(bag1, newdata=d[test,])
mean( (yhat - d[test, 'medv'])^2 )

## [1] 23.2778

比单棵树的结果有明显改善。

16.6.3 随机森林

用randomForest包计算。当参数mtry取为缺省值时按照随机森林方法计算。对训练集计算。

set.seed(1)
rf1 <- randomForest(medv ~ ., data=d, 
  subset=train, importance=TRUE)
rf1

## 
## Call:
##  randomForest(formula = medv ~ ., data = d, importance = TRUE,      subset = train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 4
## 
##           Mean of squared residuals: 10.65524
##                     % Var explained: 86.14

在测试集上计算随机森林法的均方误差：

yhat <- predict(rf1, newdata=d[test,])
mean( (yhat - d[test, 'medv'])^2 )

## [1] 18.73938

比单棵树的结果有明显改善, 比装袋法结果好。但是，如果重新划分训练集合测试集，结果可能就很不一样。

各变量的重要度数值及其图形：

importance(rf1)

##           %IncMSE IncNodePurity
## crim    13.395947    1187.68244
## zn       3.764558     205.19223
## indus    6.634904     941.08254
## chas     2.556251      73.20277
## nox     13.848778    1092.57116
## rm      28.310083    6188.44612
## age     12.175066     659.38628
## dis     10.688898     958.36302
## rad      3.702112     151.38660
## tax     10.732676     516.77833
## ptratio 11.114057    1296.12067
## black    8.047270     336.29628
## lstat   25.983897    5396.58419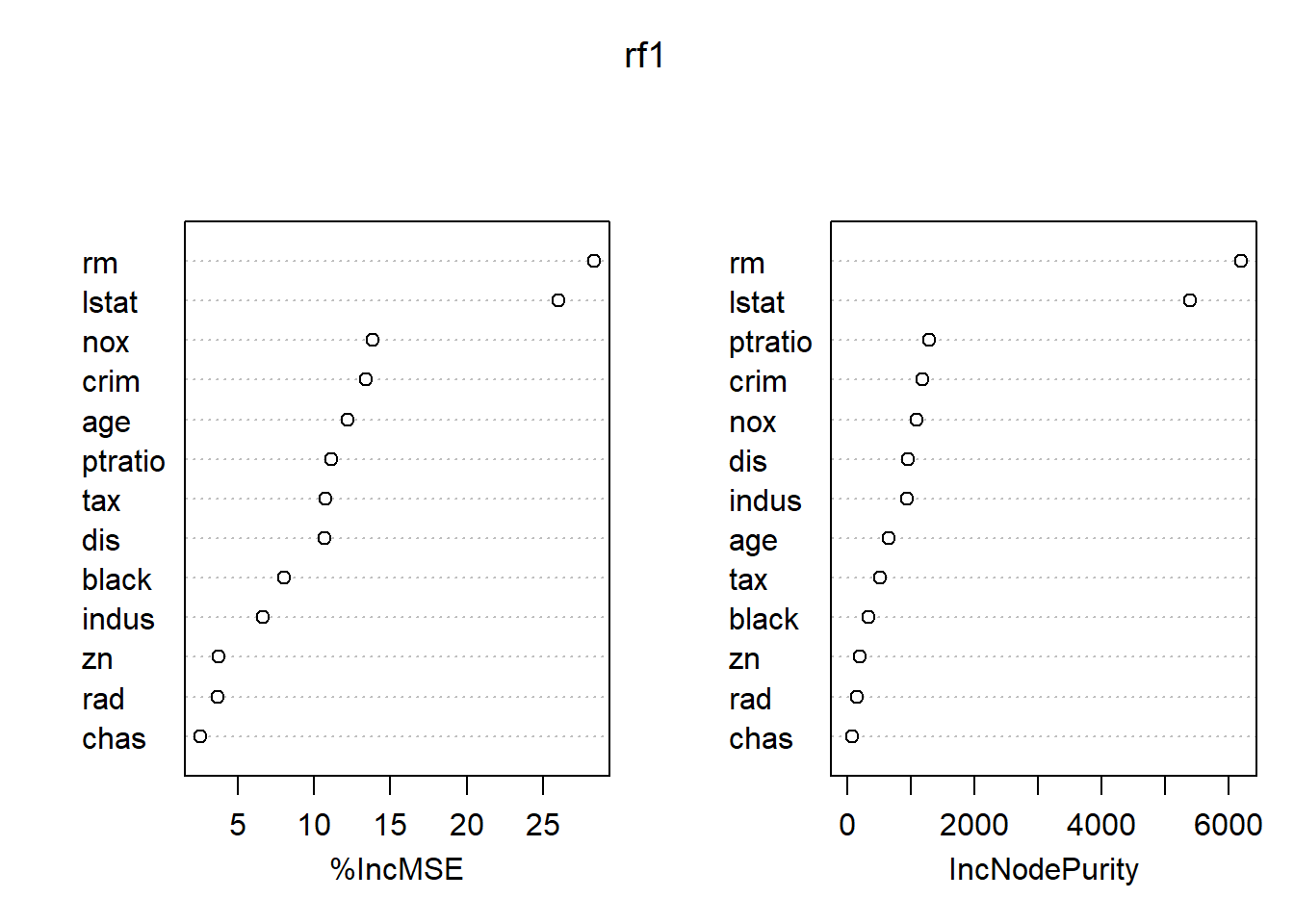

varImpPlot(rf1)

16.6.4 提升法

16.6.4.1 使用gbm包

这里使用gbm包。

在训练集上拟合：

set.seed(1)
bst1 <- gbm(
  medv ~ ., 
  data=d[train,],  
  distribution='gaussian',  
  n.trees=5000,  
  interaction.depth=4)
summary(bst1)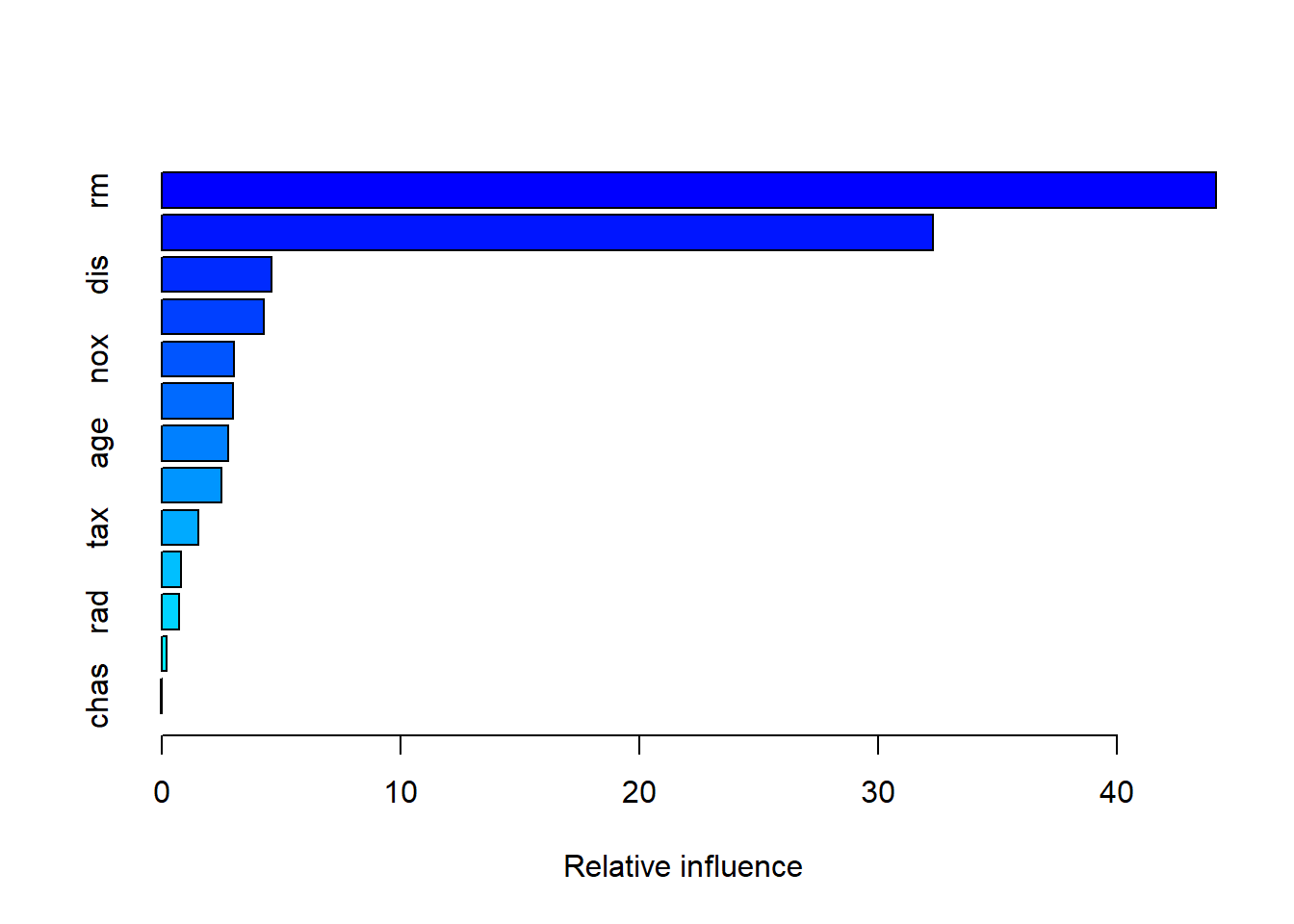

##             var     rel.inf
## rm           rm 44.15951160
## lstat     lstat 32.29267660
## dis         dis  4.61448193
## crim       crim  4.26335913
## nox         nox  3.04501491
## black     black  3.00055105
## age         age  2.78125346
## ptratio ptratio  2.49234381
## tax         tax  1.53209088
## indus     indus  0.83074496
## rad         rad  0.74565664
## zn           zn  0.21988113
## chas       chas  0.02243389

lstat和rm是最重要的变量。

在测试集上预报，并计算均方误差：

yhat <- predict(
  bst1, 
  newdata=d[test,], 
  n.trees=5000)
mean( (yhat - d[test, 'medv'])^2 )

## [1] 18.5659

与随机森林方法结果相近。

如果提高学习速度：

bst2 <- gbm(
  medv ~ ., 
  data=d[train,],  
  distribution='gaussian',  
  n.trees=5000,  
  interaction.depth=4, 
  shrinkage=0.2)
yhat <- predict(
  bst2, 
  newdata=d[test,], 
  n.trees=5000)
mean( (yhat - d[test, 'medv'])^2 )

## [1] 20.45657

效果差不多。但是，如果重新划分训练集和测试集，结果可能很不一样。

16.6.4.2 使用xgboost包

使用xgboost计算。训练：

library(xgboost)
dx.train <- list(
  data=as.matrix(d[train, -ncol(d)]),
  label=d[["medv"]][train])
dx.test <- list(
  data=as.matrix(d[test, -ncol(d)]),
  label=d[["medv"]][test])
xg1 <- xgboost(
  data = dx.train$data,
  label = dx.train$label,
  booster = "gbtree", # 基础模型
  objective ="reg:squarederror", # 目标函数
  max_depth = 2,
  nrounds = 20) # 迭代次数

## [1]  train-rmse:16.550534 
## [2]  train-rmse:12.001012 
## [3]  train-rmse:8.828046 
## [4]  train-rmse:6.666827 
## [5]  train-rmse:5.179067 
## [6]  train-rmse:4.194855 
## [7]  train-rmse:3.574384 
## [8]  train-rmse:3.186898 
## [9]  train-rmse:2.915877 
## [10] train-rmse:2.750005 
## [11] train-rmse:2.631165 
## [12] train-rmse:2.553116 
## [13] train-rmse:2.484000 
## [14] train-rmse:2.441754 
## [15] train-rmse:2.374598 
## [16] train-rmse:2.297728 
## [17] train-rmse:2.239265 
## [18] train-rmse:2.187598 
## [19] train-rmse:2.161275 
## [20] train-rmse:2.134788

预测：

xg1p <- predict(xg1, 
  newdata = dx.test$data)
mean((dx.test$label - xg1p)^2)

## [1] 20.28769

比gbm结果差一些。

注意，xgboost的自变量需要是矩阵类型，不支持数据框。 Boston数据集的自变量都是数值型的。如果有数据中有因子型，应该用Matrix::sparse.model.matrix()函数将数据框转换为数值型矩阵，结果中的因子型变量被转换成哑变量形式。

16.6.4.3 使用lightgbm包

使用lightgbm计算。训练：

library(lightgbm)

## Loading required package: R6

## 
## Attaching package: 'lightgbm'

## The following objects are masked from 'package:xgboost':
## 
##     getinfo, setinfo, slice

dl.train <- list(
  data=as.matrix(d[train, -ncol(d)]),
  label=d[["medv"]][train])
dl.test <- list(
  data=as.matrix(d[test, -ncol(d)]),
  label=d[["medv"]][test])
lgbm1 <- lightgbm(
  data = dl.train$data,
  label = dl.train$label,
  obj ="regression", # 目标函数
  max_depth = 2,  # 树的深度
  nrounds = 50) # 迭代次数

## Warning in (function (params = list(), data, nrounds = 100L, valids = list(), : lgb.train: Found the following passed through '...': max_depth. These will be used, but in future releases of lightgbm, this warning will become an error. Add these to 'params' instead. See ?lgb.train for documentation on how to call this function.

## [LightGBM] [Warning] Auto-choosing col-wise multi-threading, the overhead of testing was 0.000872 seconds.
## You can set `force_col_wise=true` to remove the overhead.
## [LightGBM] [Info] Total Bins 658
## [LightGBM] [Info] Number of data points in the train set: 253, number of used features: 12
## [LightGBM] [Info] Start training from score 21.786561
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[1]:  train's l2:66.2431"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[2]:  train's l2:57.636"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[3]:  train's l2:50.5392"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[4]:  train's l2:44.7832"
## [1] "[5]:  train's l2:39.0265"
## [1] "[6]:  train's l2:34.3006"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[7]:  train's l2:30.6794"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[8]:  train's l2:27.8866"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[9]:  train's l2:25.2917"
## [1] "[10]:  train's l2:22.7395"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[11]:  train's l2:20.8562"
## [1] "[12]:  train's l2:18.9931"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[13]:  train's l2:17.6703"
## [1] "[14]:  train's l2:16.2959"
## [1] "[15]:  train's l2:15.1774"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[16]:  train's l2:14.3231"
## [1] "[17]:  train's l2:13.453"
## [1] "[18]:  train's l2:12.7437"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[19]:  train's l2:12.1731"
## [1] "[20]:  train's l2:11.6418"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[21]:  train's l2:11.2383"
## [1] "[22]:  train's l2:10.7768"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[23]:  train's l2:10.4449"
## [1] "[24]:  train's l2:10.0823"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[25]:  train's l2:9.84566"
## [1] "[26]:  train's l2:9.56599"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[27]:  train's l2:9.38185"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[28]:  train's l2:9.21302"
## [1] "[29]:  train's l2:8.96784"
## [1] "[30]:  train's l2:8.76156"
## [1] "[31]:  train's l2:8.56684"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[32]:  train's l2:8.45506"
## [1] "[33]:  train's l2:8.30198"
## [1] "[34]:  train's l2:8.15626"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[35]:  train's l2:8.0615"
## [1] "[36]:  train's l2:7.91956"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[37]:  train's l2:7.8353"
## [1] "[38]:  train's l2:7.71917"
## [1] "[39]:  train's l2:7.58138"
## [1] "[40]:  train's l2:7.48035"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[41]:  train's l2:7.40417"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[42]:  train's l2:7.35067"
## [1] "[43]:  train's l2:7.25805"
## [1] "[44]:  train's l2:7.14817"
## [1] "[45]:  train's l2:7.07001"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[46]:  train's l2:7.0208"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[47]:  train's l2:6.97039"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[48]:  train's l2:6.90809"
## [1] "[49]:  train's l2:6.84257"
## [LightGBM] [Warning] No further splits with positive gain, best gain: -inf
## [1] "[50]:  train's l2:6.80303"

预测：

lgbm1p <- predict(lgbm1, 
  dl.test$data)
mean((dl.test$label - lgbm1p)^2)

## [1] 24.12621

效果不好，误差比较大。有可能需要调整参数。

lightgbm对输入数据格式也有特殊要求，详见文档。

16.7 附录：数据

16.7.1 Heart数据

knitr::kable(Heart)

	Age	Sex	ChestPain	RestBP	Chol	Fbs	RestECG	MaxHR	ExAng	Oldpeak	Slope	Ca	Thal	AHD
1	63	1	typical	145	233	1	2	150	0	2.3	3	0	fixed	No
2	67	1	asymptomatic	160	286	0	2	108	1	1.5	2	3	normal	Yes
3	67	1	asymptomatic	120	229	0	2	129	1	2.6	2	2	reversable	Yes
4	37	1	nonanginal	130	250	0	0	187	0	3.5	3	0	normal	No
5	41	0	nontypical	130	204	0	2	172	0	1.4	1	0	normal	No
6	56	1	nontypical	120	236	0	0	178	0	0.8	1	0	normal	No
7	62	0	asymptomatic	140	268	0	2	160	0	3.6	3	2	normal	Yes
8	57	0	asymptomatic	120	354	0	0	163	1	0.6	1	0	normal	No
9	63	1	asymptomatic	130	254	0	2	147	0	1.4	2	1	reversable	Yes
10	53	1	asymptomatic	140	203	1	2	155	1	3.1	3	0	reversable	Yes
11	57	1	asymptomatic	140	192	0	0	148	0	0.4	2	0	fixed	No
12	56	0	nontypical	140	294	0	2	153	0	1.3	2	0	normal	No
13	56	1	nonanginal	130	256	1	2	142	1	0.6	2	1	fixed	Yes
14	44	1	nontypical	120	263	0	0	173	0	0.0	1	0	reversable	No
15	52	1	nonanginal	172	199	1	0	162	0	0.5	1	0	reversable	No
16	57	1	nonanginal	150	168	0	0	174	0	1.6	1	0	normal	No
17	48	1	nontypical	110	229	0	0	168	0	1.0	3	0	reversable	Yes
18	54	1	asymptomatic	140	239	0	0	160	0	1.2	1	0	normal	No
19	48	0	nonanginal	130	275	0	0	139	0	0.2	1	0	normal	No
20	49	1	nontypical	130	266	0	0	171	0	0.6	1	0	normal	No
21	64	1	typical	110	211	0	2	144	1	1.8	2	0	normal	No
22	58	0	typical	150	283	1	2	162	0	1.0	1	0	normal	No
23	58	1	nontypical	120	284	0	2	160	0	1.8	2	0	normal	Yes
24	58	1	nonanginal	132	224	0	2	173	0	3.2	1	2	reversable	Yes
25	60	1	asymptomatic	130	206	0	2	132	1	2.4	2	2	reversable	Yes
26	50	0	nonanginal	120	219	0	0	158	0	1.6	2	0	normal	No
27	58	0	nonanginal	120	340	0	0	172	0	0.0	1	0	normal	No
28	66	0	typical	150	226	0	0	114	0	2.6	3	0	normal	No
29	43	1	asymptomatic	150	247	0	0	171	0	1.5	1	0	normal	No
30	40	1	asymptomatic	110	167	0	2	114	1	2.0	2	0	reversable	Yes
31	69	0	typical	140	239	0	0	151	0	1.8	1	2	normal	No
32	60	1	asymptomatic	117	230	1	0	160	1	1.4	1	2	reversable	Yes
33	64	1	nonanginal	140	335	0	0	158	0	0.0	1	0	normal	Yes
34	59	1	asymptomatic	135	234	0	0	161	0	0.5	2	0	reversable	No
35	44	1	nonanginal	130	233	0	0	179	1	0.4	1	0	normal	No
36	42	1	asymptomatic	140	226	0	0	178	0	0.0	1	0	normal	No
37	43	1	asymptomatic	120	177	0	2	120	1	2.5	2	0	reversable	Yes
38	57	1	asymptomatic	150	276	0	2	112	1	0.6	2	1	fixed	Yes
39	55	1	asymptomatic	132	353	0	0	132	1	1.2	2	1	reversable	Yes
40	61	1	nonanginal	150	243	1	0	137	1	1.0	2	0	normal	No
41	65	0	asymptomatic	150	225	0	2	114	0	1.0	2	3	reversable	Yes
42	40	1	typical	140	199	0	0	178	1	1.4	1	0	reversable	No
43	71	0	nontypical	160	302	0	0	162	0	0.4	1	2	normal	No
44	59	1	nonanginal	150	212	1	0	157	0	1.6	1	0	normal	No
45	61	0	asymptomatic	130	330	0	2	169	0	0.0	1	0	normal	Yes
46	58	1	nonanginal	112	230	0	2	165	0	2.5	2	1	reversable	Yes
47	51	1	nonanginal	110	175	0	0	123	0	0.6	1	0	normal	No
48	50	1	asymptomatic	150	243	0	2	128	0	2.6	2	0	reversable	Yes
49	65	0	nonanginal	140	417	1	2	157	0	0.8	1	1	normal	No
50	53	1	nonanginal	130	197	1	2	152	0	1.2	3	0	normal	No
51	41	0	nontypical	105	198	0	0	168	0	0.0	1	1	normal	No
52	65	1	asymptomatic	120	177	0	0	140	0	0.4	1	0	reversable	No
53	44	1	asymptomatic	112	290	0	2	153	0	0.0	1	1	normal	Yes
54	44	1	nontypical	130	219	0	2	188	0	0.0	1	0	normal	No
55	60	1	asymptomatic	130	253	0	0	144	1	1.4	1	1	reversable	Yes
56	54	1	asymptomatic	124	266	0	2	109	1	2.2	2	1	reversable	Yes
57	50	1	nonanginal	140	233	0	0	163	0	0.6	2	1	reversable	Yes
58	41	1	asymptomatic	110	172	0	2	158	0	0.0	1	0	reversable	Yes
59	54	1	nonanginal	125	273	0	2	152	0	0.5	3	1	normal	No
60	51	1	typical	125	213	0	2	125	1	1.4	1	1	normal	No
61	51	0	asymptomatic	130	305	0	0	142	1	1.2	2	0	reversable	Yes
62	46	0	nonanginal	142	177	0	2	160	1	1.4	3	0	normal	No
63	58	1	asymptomatic	128	216	0	2	131	1	2.2	2	3	reversable	Yes
64	54	0	nonanginal	135	304	1	0	170	0	0.0	1	0	normal	No
65	54	1	asymptomatic	120	188	0	0	113	0	1.4	2	1	reversable	Yes
66	60	1	asymptomatic	145	282	0	2	142	1	2.8	2	2	reversable	Yes
67	60	1	nonanginal	140	185	0	2	155	0	3.0	2	0	normal	Yes
68	54	1	nonanginal	150	232	0	2	165	0	1.6	1	0	reversable	No
69	59	1	asymptomatic	170	326	0	2	140	1	3.4	3	0	reversable	Yes
70	46	1	nonanginal	150	231	0	0	147	0	3.6	2	0	normal	Yes
71	65	0	nonanginal	155	269	0	0	148	0	0.8	1	0	normal	No
72	67	1	asymptomatic	125	254	1	0	163	0	0.2	2	2	reversable	Yes
73	62	1	asymptomatic	120	267	0	0	99	1	1.8	2	2	reversable	Yes
74	65	1	asymptomatic	110	248	0	2	158	0	0.6	1	2	fixed	Yes
75	44	1	asymptomatic	110	197	0	2	177	0	0.0	1	1	normal	Yes
76	65	0	nonanginal	160	360	0	2	151	0	0.8	1	0	normal	No
77	60	1	asymptomatic	125	258	0	2	141	1	2.8	2	1	reversable	Yes
78	51	0	nonanginal	140	308	0	2	142	0	1.5	1	1	normal	No
79	48	1	nontypical	130	245	0	2	180	0	0.2	2	0	normal	No
80	58	1	asymptomatic	150	270	0	2	111	1	0.8	1	0	reversable	Yes
81	45	1	asymptomatic	104	208	0	2	148	1	3.0	2	0	normal	No
82	53	0	asymptomatic	130	264	0	2	143	0	0.4	2	0	normal	No
83	39	1	nonanginal	140	321	0	2	182	0	0.0	1	0	normal	No
84	68	1	nonanginal	180	274	1	2	150	1	1.6	2	0	reversable	Yes
85	52	1	nontypical	120	325	0	0	172	0	0.2	1	0	normal	No
86	44	1	nonanginal	140	235	0	2	180	0	0.0	1	0	normal	No
87	47	1	nonanginal	138	257	0	2	156	0	0.0	1	0	normal	No
89	53	0	asymptomatic	138	234	0	2	160	0	0.0	1	0	normal	No
90	51	0	nonanginal	130	256	0	2	149	0	0.5	1	0	normal	No
91	66	1	asymptomatic	120	302	0	2	151	0	0.4	2	0	normal	No
92	62	0	asymptomatic	160	164	0	2	145	0	6.2	3	3	reversable	Yes
93	62	1	nonanginal	130	231	0	0	146	0	1.8	2	3	reversable	No
94	44	0	nonanginal	108	141	0	0	175	0	0.6	2	0	normal	No
95	63	0	nonanginal	135	252	0	2	172	0	0.0	1	0	normal	No
96	52	1	asymptomatic	128	255	0	0	161	1	0.0	1	1	reversable	Yes
97	59	1	asymptomatic	110	239	0	2	142	1	1.2	2	1	reversable	Yes
98	60	0	asymptomatic	150	258	0	2	157	0	2.6	2	2	reversable	Yes
99	52	1	nontypical	134	201	0	0	158	0	0.8	1	1	normal	No
100	48	1	asymptomatic	122	222	0	2	186	0	0.0	1	0	normal	No
101	45	1	asymptomatic	115	260	0	2	185	0	0.0	1	0	normal	No
102	34	1	typical	118	182	0	2	174	0	0.0	1	0	normal	No
103	57	0	asymptomatic	128	303	0	2	159	0	0.0	1	1	normal	No
104	71	0	nonanginal	110	265	1	2	130	0	0.0	1	1	normal	No
105	49	1	nonanginal	120	188	0	0	139	0	2.0	2	3	reversable	Yes
106	54	1	nontypical	108	309	0	0	156	0	0.0	1	0	reversable	No
107	59	1	asymptomatic	140	177	0	0	162	1	0.0	1	1	reversable	Yes
108	57	1	nonanginal	128	229	0	2	150	0	0.4	2	1	reversable	Yes
109	61	1	asymptomatic	120	260	0	0	140	1	3.6	2	1	reversable	Yes
110	39	1	asymptomatic	118	219	0	0	140	0	1.2	2	0	reversable	Yes
111	61	0	asymptomatic	145	307	0	2	146	1	1.0	2	0	reversable	Yes
112	56	1	asymptomatic	125	249	1	2	144	1	1.2	2	1	normal	Yes
113	52	1	typical	118	186	0	2	190	0	0.0	2	0	fixed	No
114	43	0	asymptomatic	132	341	1	2	136	1	3.0	2	0	reversable	Yes
115	62	0	nonanginal	130	263	0	0	97	0	1.2	2	1	reversable	Yes
116	41	1	nontypical	135	203	0	0	132	0	0.0	2	0	fixed	No
117	58	1	nonanginal	140	211	1	2	165	0	0.0	1	0	normal	No
118	35	0	asymptomatic	138	183	0	0	182	0	1.4	1	0	normal	No
119	63	1	asymptomatic	130	330	1	2	132	1	1.8	1	3	reversable	Yes
120	65	1	asymptomatic	135	254	0	2	127	0	2.8	2	1	reversable	Yes
121	48	1	asymptomatic	130	256	1	2	150	1	0.0	1	2	reversable	Yes
122	63	0	asymptomatic	150	407	0	2	154	0	4.0	2	3	reversable	Yes
123	51	1	nonanginal	100	222	0	0	143	1	1.2	2	0	normal	No
124	55	1	asymptomatic	140	217	0	0	111	1	5.6	3	0	reversable	Yes
125	65	1	typical	138	282	1	2	174	0	1.4	2	1	normal	Yes
126	45	0	nontypical	130	234	0	2	175	0	0.6	2	0	normal	No
127	56	0	asymptomatic	200	288	1	2	133	1	4.0	3	2	reversable	Yes
128	54	1	asymptomatic	110	239	0	0	126	1	2.8	2	1	reversable	Yes
129	44	1	nontypical	120	220	0	0	170	0	0.0	1	0	normal	No
130	62	0	asymptomatic	124	209	0	0	163	0	0.0	1	0	normal	No
131	54	1	nonanginal	120	258	0	2	147	0	0.4	2	0	reversable	No
132	51	1	nonanginal	94	227	0	0	154	1	0.0	1	1	reversable	No
133	29	1	nontypical	130	204	0	2	202	0	0.0	1	0	normal	No
134	51	1	asymptomatic	140	261	0	2	186	1	0.0	1	0	normal	No
135	43	0	nonanginal	122	213	0	0	165	0	0.2	2	0	normal	No
136	55	0	nontypical	135	250	0	2	161	0	1.4	2	0	normal	No
137	70	1	asymptomatic	145	174	0	0	125	1	2.6	3	0	reversable	Yes
138	62	1	nontypical	120	281	0	2	103	0	1.4	2	1	reversable	Yes
139	35	1	asymptomatic	120	198	0	0	130	1	1.6	2	0	reversable	Yes
140	51	1	nonanginal	125	245	1	2	166	0	2.4	2	0	normal	No
141	59	1	nontypical	140	221	0	0	164	1	0.0	1	0	normal	No
142	59	1	typical	170	288	0	2	159	0	0.2	2	0	reversable	Yes
143	52	1	nontypical	128	205	1	0	184	0	0.0	1	0	normal	No
144	64	1	nonanginal	125	309	0	0	131	1	1.8	2	0	reversable	Yes
145	58	1	nonanginal	105	240	0	2	154	1	0.6	2	0	reversable	No
146	47	1	nonanginal	108	243	0	0	152	0	0.0	1	0	normal	Yes
147	57	1	asymptomatic	165	289	1	2	124	0	1.0	2	3	reversable	Yes
148	41	1	nonanginal	112	250	0	0	179	0	0.0	1	0	normal	No
149	45	1	nontypical	128	308	0	2	170	0	0.0	1	0	normal	No
150	60	0	nonanginal	102	318	0	0	160	0	0.0	1	1	normal	No
151	52	1	typical	152	298	1	0	178	0	1.2	2	0	reversable	No
152	42	0	asymptomatic	102	265	0	2	122	0	0.6	2	0	normal	No
153	67	0	nonanginal	115	564	0	2	160	0	1.6	2	0	reversable	No
154	55	1	asymptomatic	160	289	0	2	145	1	0.8	2	1	reversable	Yes
155	64	1	asymptomatic	120	246	0	2	96	1	2.2	3	1	normal	Yes
156	70	1	asymptomatic	130	322	0	2	109	0	2.4	2	3	normal	Yes
157	51	1	asymptomatic	140	299	0	0	173	1	1.6	1	0	reversable	Yes
158	58	1	asymptomatic	125	300	0	2	171	0	0.0	1	2	reversable	Yes
159	60	1	asymptomatic	140	293	0	2	170	0	1.2	2	2	reversable	Yes
160	68	1	nonanginal	118	277	0	0	151	0	1.0	1	1	reversable	No
161	46	1	nontypical	101	197	1	0	156	0	0.0	1	0	reversable	No
162	77	1	asymptomatic	125	304	0	2	162	1	0.0	1	3	normal	Yes
163	54	0	nonanginal	110	214	0	0	158	0	1.6	2	0	normal	No
164	58	0	asymptomatic	100	248	0	2	122	0	1.0	2	0	normal	No
165	48	1	nonanginal	124	255	1	0	175	0	0.0	1	2	normal	No
166	57	1	asymptomatic	132	207	0	0	168	1	0.0	1	0	reversable	No
168	54	0	nontypical	132	288	1	2	159	1	0.0	1	1	normal	No
169	35	1	asymptomatic	126	282	0	2	156	1	0.0	1	0	reversable	Yes
170	45	0	nontypical	112	160	0	0	138	0	0.0	2	0	normal	No
171	70	1	nonanginal	160	269	0	0	112	1	2.9	2	1	reversable	Yes
172	53	1	asymptomatic	142	226	0	2	111	1	0.0	1	0	reversable	No
173	59	0	asymptomatic	174	249	0	0	143	1	0.0	2	0	normal	Yes
174	62	0	asymptomatic	140	394	0	2	157	0	1.2	2	0	normal	No
175	64	1	asymptomatic	145	212	0	2	132	0	2.0	2	2	fixed	Yes
176	57	1	asymptomatic	152	274	0	0	88	1	1.2	2	1	reversable	Yes
177	52	1	asymptomatic	108	233	1	0	147	0	0.1	1	3	reversable	No
178	56	1	asymptomatic	132	184	0	2	105	1	2.1	2	1	fixed	Yes
179	43	1	nonanginal	130	315	0	0	162	0	1.9	1	1	normal	No
180	53	1	nonanginal	130	246	1	2	173	0	0.0	1	3	normal	No
181	48	1	asymptomatic	124	274	0	2	166	0	0.5	2	0	reversable	Yes
182	56	0	asymptomatic	134	409	0	2	150	1	1.9	2	2	reversable	Yes
183	42	1	typical	148	244	0	2	178	0	0.8	1	2	normal	No
184	59	1	typical	178	270	0	2	145	0	4.2	3	0	reversable	No
185	60	0	asymptomatic	158	305	0	2	161	0	0.0	1	0	normal	Yes
186	63	0	nontypical	140	195	0	0	179	0	0.0	1	2	normal	No
187	42	1	nonanginal	120	240	1	0	194	0	0.8	3	0	reversable	No
188	66	1	nontypical	160	246	0	0	120	1	0.0	2	3	fixed	Yes
189	54	1	nontypical	192	283	0	2	195	0	0.0	1	1	reversable	Yes
190	69	1	nonanginal	140	254	0	2	146	0	2.0	2	3	reversable	Yes
191	50	1	nonanginal	129	196	0	0	163	0	0.0	1	0	normal	No
192	51	1	asymptomatic	140	298	0	0	122	1	4.2	2	3	reversable	Yes
194	62	0	asymptomatic	138	294	1	0	106	0	1.9	2	3	normal	Yes
195	68	0	nonanginal	120	211	0	2	115	0	1.5	2	0	normal	No
196	67	1	asymptomatic	100	299	0	2	125	1	0.9	2	2	normal	Yes
197	69	1	typical	160	234	1	2	131	0	0.1	2	1	normal	No
198	45	0	asymptomatic	138	236	0	2	152	1	0.2	2	0	normal	No
199	50	0	nontypical	120	244	0	0	162	0	1.1	1	0	normal	No
200	59	1	typical	160	273	0	2	125	0	0.0	1	0	normal	Yes
201	50	0	asymptomatic	110	254	0	2	159	0	0.0	1	0	normal	No
202	64	0	asymptomatic	180	325	0	0	154	1	0.0	1	0	normal	No
203	57	1	nonanginal	150	126	1	0	173	0	0.2	1	1	reversable	No
204	64	0	nonanginal	140	313	0	0	133	0	0.2	1	0	reversable	No
205	43	1	asymptomatic	110	211	0	0	161	0	0.0	1	0	reversable	No
206	45	1	asymptomatic	142	309	0	2	147	1	0.0	2	3	reversable	Yes
207	58	1	asymptomatic	128	259	0	2	130	1	3.0	2	2	reversable	Yes
208	50	1	asymptomatic	144	200	0	2	126	1	0.9	2	0	reversable	Yes
209	55	1	nontypical	130	262	0	0	155	0	0.0	1	0	normal	No
210	62	0	asymptomatic	150	244	0	0	154	1	1.4	2	0	normal	Yes
211	37	0	nonanginal	120	215	0	0	170	0	0.0	1	0	normal	No
212	38	1	typical	120	231	0	0	182	1	3.8	2	0	reversable	Yes
213	41	1	nonanginal	130	214	0	2	168	0	2.0	2	0	normal	No
214	66	0	asymptomatic	178	228	1	0	165	1	1.0	2	2	reversable	Yes
215	52	1	asymptomatic	112	230	0	0	160	0	0.0	1	1	normal	Yes
216	56	1	typical	120	193	0	2	162	0	1.9	2	0	reversable	No
217	46	0	nontypical	105	204	0	0	172	0	0.0	1	0	normal	No
218	46	0	asymptomatic	138	243	0	2	152	1	0.0	2	0	normal	No
219	64	0	asymptomatic	130	303	0	0	122	0	2.0	2	2	normal	No
220	59	1	asymptomatic	138	271	0	2	182	0	0.0	1	0	normal	No
221	41	0	nonanginal	112	268	0	2	172	1	0.0	1	0	normal	No
222	54	0	nonanginal	108	267	0	2	167	0	0.0	1	0	normal	No
223	39	0	nonanginal	94	199	0	0	179	0	0.0	1	0	normal	No
224	53	1	asymptomatic	123	282	0	0	95	1	2.0	2	2	reversable	Yes
225	63	0	asymptomatic	108	269	0	0	169	1	1.8	2	2	normal	Yes
226	34	0	nontypical	118	210	0	0	192	0	0.7	1	0	normal	No
227	47	1	asymptomatic	112	204	0	0	143	0	0.1	1	0	normal	No
228	67	0	nonanginal	152	277	0	0	172	0	0.0	1	1	normal	No
229	54	1	asymptomatic	110	206	0	2	108	1	0.0	2	1	normal	Yes
230	66	1	asymptomatic	112	212	0	2	132	1	0.1	1	1	normal	Yes
231	52	0	nonanginal	136	196	0	2	169	0	0.1	2	0	normal	No
232	55	0	asymptomatic	180	327	0	1	117	1	3.4	2	0	normal	Yes
233	49	1	nonanginal	118	149	0	2	126	0	0.8	1	3	normal	Yes
234	74	0	nontypical	120	269	0	2	121	1	0.2	1	1	normal	No
235	54	0	nonanginal	160	201	0	0	163	0	0.0	1	1	normal	No
236	54	1	asymptomatic	122	286	0	2	116	1	3.2	2	2	normal	Yes
237	56	1	asymptomatic	130	283	1	2	103	1	1.6	3	0	reversable	Yes
238	46	1	asymptomatic	120	249	0	2	144	0	0.8	1	0	reversable	Yes
239	49	0	nontypical	134	271	0	0	162	0	0.0	2	0	normal	No
240	42	1	nontypical	120	295	0	0	162	0	0.0	1	0	normal	No
241	41	1	nontypical	110	235	0	0	153	0	0.0	1	0	normal	No
242	41	0	nontypical	126	306	0	0	163	0	0.0	1	0	normal	No
243	49	0	asymptomatic	130	269	0	0	163	0	0.0	1	0	normal	No
244	61	1	typical	134	234	0	0	145	0	2.6	2	2	normal	Yes
245	60	0	nonanginal	120	178	1	0	96	0	0.0	1	0	normal	No
246	67	1	asymptomatic	120	237	0	0	71	0	1.0	2	0	normal	Yes
247	58	1	asymptomatic	100	234	0	0	156	0	0.1	1	1	reversable	Yes
248	47	1	asymptomatic	110	275	0	2	118	1	1.0	2	1	normal	Yes
249	52	1	asymptomatic	125	212	0	0	168	0	1.0	1	2	reversable	Yes
250	62	1	nontypical	128	208	1	2	140	0	0.0	1	0	normal	No
251	57	1	asymptomatic	110	201	0	0	126	1	1.5	2	0	fixed	No
252	58	1	asymptomatic	146	218	0	0	105	0	2.0	2	1	reversable	Yes
253	64	1	asymptomatic	128	263	0	0	105	1	0.2	2	1	reversable	No
254	51	0	nonanginal	120	295	0	2	157	0	0.6	1	0	normal	No
255	43	1	asymptomatic	115	303	0	0	181	0	1.2	2	0	normal	No
256	42	0	nonanginal	120	209	0	0	173	0	0.0	2	0	normal	No
257	67	0	asymptomatic	106	223	0	0	142	0	0.3	1	2	normal	No
258	76	0	nonanginal	140	197	0	1	116	0	1.1	2	0	normal	No
259	70	1	nontypical	156	245	0	2	143	0	0.0	1	0	normal	No
260	57	1	nontypical	124	261	0	0	141	0	0.3	1	0	reversable	Yes
261	44	0	nonanginal	118	242	0	0	149	0	0.3	2	1	normal	No
262	58	0	nontypical	136	319	1	2	152	0	0.0	1	2	normal	Yes
263	60	0	typical	150	240	0	0	171	0	0.9	1	0	normal	No
264	44	1	nonanginal	120	226	0	0	169	0	0.0	1	0	normal	No
265	61	1	asymptomatic	138	166	0	2	125	1	3.6	2	1	normal	Yes
266	42	1	asymptomatic	136	315	0	0	125	1	1.8	2	0	fixed	Yes
268	59	1	nonanginal	126	218	1	0	134	0	2.2	2	1	fixed	Yes
269	40	1	asymptomatic	152	223	0	0	181	0	0.0	1	0	reversable	Yes
270	42	1	nonanginal	130	180	0	0	150	0	0.0	1	0	normal	No
271	61	1	asymptomatic	140	207	0	2	138	1	1.9	1	1	reversable	Yes
272	66	1	asymptomatic	160	228	0	2	138	0	2.3	1	0	fixed	No
273	46	1	asymptomatic	140	311	0	0	120	1	1.8	2	2	reversable	Yes
274	71	0	asymptomatic	112	149	0	0	125	0	1.6	2	0	normal	No
275	59	1	typical	134	204	0	0	162	0	0.8	1	2	normal	Yes
276	64	1	typical	170	227	0	2	155	0	0.6	2	0	reversable	No
277	66	0	nonanginal	146	278	0	2	152	0	0.0	2	1	normal	No
278	39	0	nonanginal	138	220	0	0	152	0	0.0	2	0	normal	No
279	57	1	nontypical	154	232	0	2	164	0	0.0	1	1	normal	Yes
280	58	0	asymptomatic	130	197	0	0	131	0	0.6	2	0	normal	No
281	57	1	asymptomatic	110	335	0	0	143	1	3.0	2	1	reversable	Yes
282	47	1	nonanginal	130	253	0	0	179	0	0.0	1	0	normal	No
283	55	0	asymptomatic	128	205	0	1	130	1	2.0	2	1	reversable	Yes
284	35	1	nontypical	122	192	0	0	174	0	0.0	1	0	normal	No
285	61	1	asymptomatic	148	203	0	0	161	0	0.0	1	1	reversable	Yes
286	58	1	asymptomatic	114	318	0	1	140	0	4.4	3	3	fixed	Yes
287	58	0	asymptomatic	170	225	1	2	146	1	2.8	2	2	fixed	Yes
289	56	1	nontypical	130	221	0	2	163	0	0.0	1	0	reversable	No
290	56	1	nontypical	120	240	0	0	169	0	0.0	3	0	normal	No
291	67	1	nonanginal	152	212	0	2	150	0	0.8	2	0	reversable	Yes
292	55	0	nontypical	132	342	0	0	166	0	1.2	1	0	normal	No
293	44	1	asymptomatic	120	169	0	0	144	1	2.8	3	0	fixed	Yes
294	63	1	asymptomatic	140	187	0	2	144	1	4.0	1	2	reversable	Yes
295	63	0	asymptomatic	124	197	0	0	136	1	0.0	2	0	normal	Yes
296	41	1	nontypical	120	157	0	0	182	0	0.0	1	0	normal	No
297	59	1	asymptomatic	164	176	1	2	90	0	1.0	2	2	fixed	Yes
298	57	0	asymptomatic	140	241	0	0	123	1	0.2	2	0	reversable	Yes
299	45	1	typical	110	264	0	0	132	0	1.2	2	0	reversable	Yes
300	68	1	asymptomatic	144	193	1	0	141	0	3.4	2	2	reversable	Yes
301	57	1	asymptomatic	130	131	0	0	115	1	1.2	2	1	reversable	Yes
302	57	0	nontypical	130	236	0	2	174	0	0.0	2	1	normal	Yes

16.7.2 CarSeats数据

knitr::kable(Carseats)

Sales	CompPrice	Income	Advertising	Population	Price	ShelveLoc	Age	Education	Urban	US
9.50	138	73	11	276	120	Bad	42	17	Yes	Yes
11.22	111	48	16	260	83	Good	65	10	Yes	Yes
10.06	113	35	10	269	80	Medium	59	12	Yes	Yes
7.40	117	100	4	466	97	Medium	55	14	Yes	Yes
4.15	141	64	3	340	128	Bad	38	13	Yes	No
10.81	124	113	13	501	72	Bad	78	16	No	Yes
6.63	115	105	0	45	108	Medium	71	15	Yes	No
11.85	136	81	15	425	120	Good	67	10	Yes	Yes
6.54	132	110	0	108	124	Medium	76	10	No	No
4.69	132	113	0	131	124	Medium	76	17	No	Yes
9.01	121	78	9	150	100	Bad	26	10	No	Yes
11.96	117	94	4	503	94	Good	50	13	Yes	Yes
3.98	122	35	2	393	136	Medium	62	18	Yes	No
10.96	115	28	11	29	86	Good	53	18	Yes	Yes
11.17	107	117	11	148	118	Good	52	18	Yes	Yes
8.71	149	95	5	400	144	Medium	76	18	No	No
7.58	118	32	0	284	110	Good	63	13	Yes	No
12.29	147	74	13	251	131	Good	52	10	Yes	Yes
13.91	110	110	0	408	68	Good	46	17	No	Yes
8.73	129	76	16	58	121	Medium	69	12	Yes	Yes
6.41	125	90	2	367	131	Medium	35	18	Yes	Yes
12.13	134	29	12	239	109	Good	62	18	No	Yes
5.08	128	46	6	497	138	Medium	42	13	Yes	No
5.87	121	31	0	292	109	Medium	79	10	Yes	No
10.14	145	119	16	294	113	Bad	42	12	Yes	Yes
14.90	139	32	0	176	82	Good	54	11	No	No
8.33	107	115	11	496	131	Good	50	11	No	Yes
5.27	98	118	0	19	107	Medium	64	17	Yes	No
2.99	103	74	0	359	97	Bad	55	11	Yes	Yes
7.81	104	99	15	226	102	Bad	58	17	Yes	Yes
13.55	125	94	0	447	89	Good	30	12	Yes	No
8.25	136	58	16	241	131	Medium	44	18	Yes	Yes
6.20	107	32	12	236	137	Good	64	10	No	Yes
8.77	114	38	13	317	128	Good	50	16	Yes	Yes
2.67	115	54	0	406	128	Medium	42	17	Yes	Yes
11.07	131	84	11	29	96	Medium	44	17	No	Yes
8.89	122	76	0	270	100	Good	60	18	No	No
4.95	121	41	5	412	110	Medium	54	10	Yes	Yes
6.59	109	73	0	454	102	Medium	65	15	Yes	No
3.24	130	60	0	144	138	Bad	38	10	No	No
2.07	119	98	0	18	126	Bad	73	17	No	No
7.96	157	53	0	403	124	Bad	58	16	Yes	No
10.43	77	69	0	25	24	Medium	50	18	Yes	No
4.12	123	42	11	16	134	Medium	59	13	Yes	Yes
4.16	85	79	6	325	95	Medium	69	13	Yes	Yes
4.56	141	63	0	168	135	Bad	44	12	Yes	Yes
12.44	127	90	14	16	70	Medium	48	15	No	Yes
4.38	126	98	0	173	108	Bad	55	16	Yes	No
3.91	116	52	0	349	98	Bad	69	18	Yes	No
10.61	157	93	0	51	149	Good	32	17	Yes	No
1.42	99	32	18	341	108	Bad	80	16	Yes	Yes
4.42	121	90	0	150	108	Bad	75	16	Yes	No
7.91	153	40	3	112	129	Bad	39	18	Yes	Yes
6.92	109	64	13	39	119	Medium	61	17	Yes	Yes
4.90	134	103	13	25	144	Medium	76	17	No	Yes
6.85	143	81	5	60	154	Medium	61	18	Yes	Yes
11.91	133	82	0	54	84	Medium	50	17	Yes	No
0.91	93	91	0	22	117	Bad	75	11	Yes	No
5.42	103	93	15	188	103	Bad	74	16	Yes	Yes
5.21	118	71	4	148	114	Medium	80	13	Yes	No
8.32	122	102	19	469	123	Bad	29	13	Yes	Yes
7.32	105	32	0	358	107	Medium	26	13	No	No
1.82	139	45	0	146	133	Bad	77	17	Yes	Yes
8.47	119	88	10	170	101	Medium	61	13	Yes	Yes
7.80	100	67	12	184	104	Medium	32	16	No	Yes
4.90	122	26	0	197	128	Medium	55	13	No	No
8.85	127	92	0	508	91	Medium	56	18	Yes	No
9.01	126	61	14	152	115	Medium	47	16	Yes	Yes
13.39	149	69	20	366	134	Good	60	13	Yes	Yes
7.99	127	59	0	339	99	Medium	65	12	Yes	No
9.46	89	81	15	237	99	Good	74	12	Yes	Yes
6.50	148	51	16	148	150	Medium	58	17	No	Yes
5.52	115	45	0	432	116	Medium	25	15	Yes	No
12.61	118	90	10	54	104	Good	31	11	No	Yes
6.20	150	68	5	125	136	Medium	64	13	No	Yes
8.55	88	111	23	480	92	Bad	36	16	No	Yes
10.64	102	87	10	346	70	Medium	64	15	Yes	Yes
7.70	118	71	12	44	89	Medium	67	18	No	Yes
4.43	134	48	1	139	145	Medium	65	12	Yes	Yes
9.14	134	67	0	286	90	Bad	41	13	Yes	No
8.01	113	100	16	353	79	Bad	68	11	Yes	Yes
7.52	116	72	0	237	128	Good	70	13	Yes	No
11.62	151	83	4	325	139	Good	28	17	Yes	Yes
4.42	109	36	7	468	94	Bad	56	11	Yes	Yes
2.23	111	25	0	52	121	Bad	43	18	No	No
8.47	125	103	0	304	112	Medium	49	13	No	No
8.70	150	84	9	432	134	Medium	64	15	Yes	No
11.70	131	67	7	272	126	Good	54	16	No	Yes
6.56	117	42	7	144	111	Medium	62	10	Yes	Yes
7.95	128	66	3	493	119	Medium	45	16	No	No
5.33	115	22	0	491	103	Medium	64	11	No	No
4.81	97	46	11	267	107	Medium	80	15	Yes	Yes
4.53	114	113	0	97	125	Medium	29	12	Yes	No
8.86	145	30	0	67	104	Medium	55	17	Yes	No
8.39	115	97	5	134	84	Bad	55	11	Yes	Yes
5.58	134	25	10	237	148	Medium	59	13	Yes	Yes
9.48	147	42	10	407	132	Good	73	16	No	Yes
7.45	161	82	5	287	129	Bad	33	16	Yes	Yes
12.49	122	77	24	382	127	Good	36	16	No	Yes
4.88	121	47	3	220	107	Bad	56	16	No	Yes
4.11	113	69	11	94	106	Medium	76	12	No	Yes
6.20	128	93	0	89	118	Medium	34	18	Yes	No
5.30	113	22	0	57	97	Medium	65	16	No	No
5.07	123	91	0	334	96	Bad	78	17	Yes	Yes
4.62	121	96	0	472	138	Medium	51	12	Yes	No
5.55	104	100	8	398	97	Medium	61	11	Yes	Yes
0.16	102	33	0	217	139	Medium	70	18	No	No
8.55	134	107	0	104	108	Medium	60	12	Yes	No
3.47	107	79	2	488	103	Bad	65	16	Yes	No
8.98	115	65	0	217	90	Medium	60	17	No	No
9.00	128	62	7	125	116	Medium	43	14	Yes	Yes
6.62	132	118	12	272	151	Medium	43	14	Yes	Yes
6.67	116	99	5	298	125	Good	62	12	Yes	Yes
6.01	131	29	11	335	127	Bad	33	12	Yes	Yes
9.31	122	87	9	17	106	Medium	65	13	Yes	Yes
8.54	139	35	0	95	129	Medium	42	13	Yes	No
5.08	135	75	0	202	128	Medium	80	10	No	No
8.80	145	53	0	507	119	Medium	41	12	Yes	No
7.57	112	88	2	243	99	Medium	62	11	Yes	Yes
7.37	130	94	8	137	128	Medium	64	12	Yes	Yes
6.87	128	105	11	249	131	Medium	63	13	Yes	Yes
11.67	125	89	10	380	87	Bad	28	10	Yes	Yes
6.88	119	100	5	45	108	Medium	75	10	Yes	Yes
8.19	127	103	0	125	155	Good	29	15	No	Yes
8.87	131	113	0	181	120	Good	63	14	Yes	No
9.34	89	78	0	181	49	Medium	43	15	No	No
11.27	153	68	2	60	133	Good	59	16	Yes	Yes
6.52	125	48	3	192	116	Medium	51	14	Yes	Yes
4.96	133	100	3	350	126	Bad	55	13	Yes	Yes
4.47	143	120	7	279	147	Bad	40	10	No	Yes
8.41	94	84	13	497	77	Medium	51	12	Yes	Yes
6.50	108	69	3	208	94	Medium	77	16	Yes	No
9.54	125	87	9	232	136	Good	72	10	Yes	Yes
7.62	132	98	2	265	97	Bad	62	12	Yes	Yes
3.67	132	31	0	327	131	Medium	76	16	Yes	No
6.44	96	94	14	384	120	Medium	36	18	No	Yes
5.17	131	75	0	10	120	Bad	31	18	No	No
6.52	128	42	0	436	118	Medium	80	11	Yes	No
10.27	125	103	12	371	109	Medium	44	10	Yes	Yes
12.30	146	62	10	310	94	Medium	30	13	No	Yes
6.03	133	60	10	277	129	Medium	45	18	Yes	Yes
6.53	140	42	0	331	131	Bad	28	15	Yes	No
7.44	124	84	0	300	104	Medium	77	15	Yes	No
0.53	122	88	7	36	159	Bad	28	17	Yes	Yes
9.09	132	68	0	264	123	Good	34	11	No	No
8.77	144	63	11	27	117	Medium	47	17	Yes	Yes
3.90	114	83	0	412	131	Bad	39	14	Yes	No
10.51	140	54	9	402	119	Good	41	16	No	Yes
7.56	110	119	0	384	97	Medium	72	14	No	Yes
11.48	121	120	13	140	87	Medium	56	11	Yes	Yes
10.49	122	84	8	176	114	Good	57	10	No	Yes
10.77	111	58	17	407	103	Good	75	17	No	Yes
7.64	128	78	0	341	128	Good	45	13	No	No
5.93	150	36	7	488	150	Medium	25	17	No	Yes
6.89	129	69	10	289	110	Medium	50	16	No	Yes
7.71	98	72	0	59	69	Medium	65	16	Yes	No
7.49	146	34	0	220	157	Good	51	16	Yes	No
10.21	121	58	8	249	90	Medium	48	13	No	Yes
12.53	142	90	1	189	112	Good	39	10	No	Yes
9.32	119	60	0	372	70	Bad	30	18	No	No
4.67	111	28	0	486	111	Medium	29	12	No	No
2.93	143	21	5	81	160	Medium	67	12	No	Yes
3.63	122	74	0	424	149	Medium	51	13	Yes	No
5.68	130	64	0	40	106	Bad	39	17	No	No
8.22	148	64	0	58	141	Medium	27	13	No	Yes
0.37	147	58	7	100	191	Bad	27	15	Yes	Yes
6.71	119	67	17	151	137	Medium	55	11	Yes	Yes
6.71	106	73	0	216	93	Medium	60	13	Yes	No
7.30	129	89	0	425	117	Medium	45	10	Yes	No
11.48	104	41	15	492	77	Good	73	18	Yes	Yes
8.01	128	39	12	356	118	Medium	71	10	Yes	Yes
12.49	93	106	12	416	55	Medium	75	15	Yes	Yes
9.03	104	102	13	123	110	Good	35	16	Yes	Yes
6.38	135	91	5	207	128	Medium	66	18	Yes	Yes
0.00	139	24	0	358	185	Medium	79	15	No	No
7.54	115	89	0	38	122	Medium	25	12	Yes	No
5.61	138	107	9	480	154	Medium	47	11	No	Yes
10.48	138	72	0	148	94	Medium	27	17	Yes	Yes
10.66	104	71	14	89	81	Medium	25	14	No	Yes
7.78	144	25	3	70	116	Medium	77	18	Yes	Yes
4.94	137	112	15	434	149	Bad	66	13	Yes	Yes
7.43	121	83	0	79	91	Medium	68	11	Yes	No
4.74	137	60	4	230	140	Bad	25	13	Yes	No
5.32	118	74	6	426	102	Medium	80	18	Yes	Yes
9.95	132	33	7	35	97	Medium	60	11	No	Yes
10.07	130	100	11	449	107	Medium	64	10	Yes	Yes
8.68	120	51	0	93	86	Medium	46	17	No	No
6.03	117	32	0	142	96	Bad	62	17	Yes	No
8.07	116	37	0	426	90	Medium	76	15	Yes	No
12.11	118	117	18	509	104	Medium	26	15	No	Yes
8.79	130	37	13	297	101	Medium	37	13	No	Yes
6.67	156	42	13	170	173	Good	74	14	Yes	Yes
7.56	108	26	0	408	93	Medium	56	14	No	No
13.28	139	70	7	71	96	Good	61	10	Yes	Yes
7.23	112	98	18	481	128	Medium	45	11	Yes	Yes
4.19	117	93	4	420	112	Bad	66	11	Yes	Yes
4.10	130	28	6	410	133	Bad	72	16	Yes	Yes
2.52	124	61	0	333	138	Medium	76	16	Yes	No
3.62	112	80	5	500	128	Medium	69	10	Yes	Yes
6.42	122	88	5	335	126	Medium	64	14	Yes	Yes
5.56	144	92	0	349	146	Medium	62	12	No	No
5.94	138	83	0	139	134	Medium	54	18	Yes	No
4.10	121	78	4	413	130	Bad	46	10	No	Yes
2.05	131	82	0	132	157	Bad	25	14	Yes	No
8.74	155	80	0	237	124	Medium	37	14	Yes	No
5.68	113	22	1	317	132	Medium	28	12	Yes	No
4.97	162	67	0	27	160	Medium	77	17	Yes	Yes
8.19	111	105	0	466	97	Bad	61	10	No	No
7.78	86	54	0	497	64	Bad	33	12	Yes	No
3.02	98	21	11	326	90	Bad	76	11	No	Yes
4.36	125	41	2	357	123	Bad	47	14	No	Yes
9.39	117	118	14	445	120	Medium	32	15	Yes	Yes
12.04	145	69	19	501	105	Medium	45	11	Yes	Yes
8.23	149	84	5	220	139	Medium	33	10	Yes	Yes
4.83	115	115	3	48	107	Medium	73	18	Yes	Yes
2.34	116	83	15	170	144	Bad	71	11	Yes	Yes
5.73	141	33	0	243	144	Medium	34	17	Yes	No
4.34	106	44	0	481	111	Medium	70	14	No	No
9.70	138	61	12	156	120	Medium	25	14	Yes	Yes
10.62	116	79	19	359	116	Good	58	17	Yes	Yes
10.59	131	120	15	262	124	Medium	30	10	Yes	Yes
6.43	124	44	0	125	107	Medium	80	11	Yes	No
7.49	136	119	6	178	145	Medium	35	13	Yes	Yes
3.45	110	45	9	276	125	Medium	62	14	Yes	Yes
4.10	134	82	0	464	141	Medium	48	13	No	No
6.68	107	25	0	412	82	Bad	36	14	Yes	No
7.80	119	33	0	245	122	Good	56	14	Yes	No
8.69	113	64	10	68	101	Medium	57	16	Yes	Yes
5.40	149	73	13	381	163	Bad	26	11	No	Yes
11.19	98	104	0	404	72	Medium	27	18	No	No
5.16	115	60	0	119	114	Bad	38	14	No	No
8.09	132	69	0	123	122	Medium	27	11	No	No
13.14	137	80	10	24	105	Good	61	15	Yes	Yes
8.65	123	76	18	218	120	Medium	29	14	No	Yes
9.43	115	62	11	289	129	Good	56	16	No	Yes
5.53	126	32	8	95	132	Medium	50	17	Yes	Yes
9.32	141	34	16	361	108	Medium	69	10	Yes	Yes
9.62	151	28	8	499	135	Medium	48	10	Yes	Yes
7.36	121	24	0	200	133	Good	73	13	Yes	No
3.89	123	105	0	149	118	Bad	62	16	Yes	Yes
10.31	159	80	0	362	121	Medium	26	18	Yes	No
12.01	136	63	0	160	94	Medium	38	12	Yes	No
4.68	124	46	0	199	135	Medium	52	14	No	No
7.82	124	25	13	87	110	Medium	57	10	Yes	Yes
8.78	130	30	0	391	100	Medium	26	18	Yes	No
10.00	114	43	0	199	88	Good	57	10	No	Yes
6.90	120	56	20	266	90	Bad	78	18	Yes	Yes
5.04	123	114	0	298	151	Bad	34	16	Yes	No
5.36	111	52	0	12	101	Medium	61	11	Yes	Yes
5.05	125	67	0	86	117	Bad	65	11	Yes	No
9.16	137	105	10	435	156	Good	72	14	Yes	Yes
3.72	139	111	5	310	132	Bad	62	13	Yes	Yes
8.31	133	97	0	70	117	Medium	32	16	Yes	No
5.64	124	24	5	288	122	Medium	57	12	No	Yes
9.58	108	104	23	353	129	Good	37	17	Yes	Yes
7.71	123	81	8	198	81	Bad	80	15	Yes	Yes
4.20	147	40	0	277	144	Medium	73	10	Yes	No
8.67	125	62	14	477	112	Medium	80	13	Yes	Yes
3.47	108	38	0	251	81	Bad	72	14	No	No
5.12	123	36	10	467	100	Bad	74	11	No	Yes
7.67	129	117	8	400	101	Bad	36	10	Yes	Yes
5.71	121	42	4	188	118	Medium	54	15	Yes	Yes
6.37	120	77	15	86	132	Medium	48	18	Yes	Yes
7.77	116	26	6	434	115	Medium	25	17	Yes	Yes
6.95	128	29	5	324	159	Good	31	15	Yes	Yes
5.31	130	35	10	402	129	Bad	39	17	Yes	Yes
9.10	128	93	12	343	112	Good	73	17	No	Yes
5.83	134	82	7	473	112	Bad	51	12	No	Yes
6.53	123	57	0	66	105	Medium	39	11	Yes	No
5.01	159	69	0	438	166	Medium	46	17	Yes	No
11.99	119	26	0	284	89	Good	26	10	Yes	No
4.55	111	56	0	504	110	Medium	62	16	Yes	No
12.98	113	33	0	14	63	Good	38	12	Yes	No
10.04	116	106	8	244	86	Medium	58	12	Yes	Yes
7.22	135	93	2	67	119	Medium	34	11	Yes	Yes
6.67	107	119	11	210	132	Medium	53	11	Yes	Yes
6.93	135	69	14	296	130	Medium	73	15	Yes	Yes
7.80	136	48	12	326	125	Medium	36	16	Yes	Yes
7.22	114	113	2	129	151	Good	40	15	No	Yes
3.42	141	57	13	376	158	Medium	64	18	Yes	Yes
2.86	121	86	10	496	145	Bad	51	10	Yes	Yes
11.19	122	69	7	303	105	Good	45	16	No	Yes
7.74	150	96	0	80	154	Good	61	11	Yes	No
5.36	135	110	0	112	117	Medium	80	16	No	No
6.97	106	46	11	414	96	Bad	79	17	No	No
7.60	146	26	11	261	131	Medium	39	10	Yes	Yes
7.53	117	118	11	429	113	Medium	67	18	No	Yes
6.88	95	44	4	208	72	Bad	44	17	Yes	Yes
6.98	116	40	0	74	97	Medium	76	15	No	No
8.75	143	77	25	448	156	Medium	43	17	Yes	Yes
9.49	107	111	14	400	103	Medium	41	11	No	Yes
6.64	118	70	0	106	89	Bad	39	17	Yes	No
11.82	113	66	16	322	74	Good	76	15	Yes	Yes
11.28	123	84	0	74	89	Good	59	10	Yes	No
12.66	148	76	3	126	99	Good	60	11	Yes	Yes
4.21	118	35	14	502	137	Medium	79	10	No	Yes
8.21	127	44	13	160	123	Good	63	18	Yes	Yes
3.07	118	83	13	276	104	Bad	75	10	Yes	Yes
10.98	148	63	0	312	130	Good	63	15	Yes	No
9.40	135	40	17	497	96	Medium	54	17	No	Yes
8.57	116	78	1	158	99	Medium	45	11	Yes	Yes
7.41	99	93	0	198	87	Medium	57	16	Yes	Yes
5.28	108	77	13	388	110	Bad	74	14	Yes	Yes
10.01	133	52	16	290	99	Medium	43	11	Yes	Yes
11.93	123	98	12	408	134	Good	29	10	Yes	Yes
8.03	115	29	26	394	132	Medium	33	13	Yes	Yes
4.78	131	32	1	85	133	Medium	48	12	Yes	Yes
5.90	138	92	0	13	120	Bad	61	12	Yes	No
9.24	126	80	19	436	126	Medium	52	10	Yes	Yes
11.18	131	111	13	33	80	Bad	68	18	Yes	Yes
9.53	175	65	29	419	166	Medium	53	12	Yes	Yes
6.15	146	68	12	328	132	Bad	51	14	Yes	Yes
6.80	137	117	5	337	135	Bad	38	10	Yes	Yes
9.33	103	81	3	491	54	Medium	66	13	Yes	No
7.72	133	33	10	333	129	Good	71	14	Yes	Yes
6.39	131	21	8	220	171	Good	29	14	Yes	Yes
15.63	122	36	5	369	72	Good	35	10	Yes	Yes
6.41	142	30	0	472	136	Good	80	15	No	No
10.08	116	72	10	456	130	Good	41	14	No	Yes
6.97	127	45	19	459	129	Medium	57	11	No	Yes
5.86	136	70	12	171	152	Medium	44	18	Yes	Yes
7.52	123	39	5	499	98	Medium	34	15	Yes	No
9.16	140	50	10	300	139	Good	60	15	Yes	Yes
10.36	107	105	18	428	103	Medium	34	12	Yes	Yes
2.66	136	65	4	133	150	Bad	53	13	Yes	Yes
11.70	144	69	11	131	104	Medium	47	11	Yes	Yes
4.69	133	30	0	152	122	Medium	53	17	Yes	No
6.23	112	38	17	316	104	Medium	80	16	Yes	Yes
3.15	117	66	1	65	111	Bad	55	11	Yes	Yes
11.27	100	54	9	433	89	Good	45	12	Yes	Yes
4.99	122	59	0	501	112	Bad	32	14	No	No
10.10	135	63	15	213	134	Medium	32	10	Yes	Yes
5.74	106	33	20	354	104	Medium	61	12	Yes	Yes
5.87	136	60	7	303	147	Medium	41	10	Yes	Yes
7.63	93	117	9	489	83	Bad	42	13	Yes	Yes
6.18	120	70	15	464	110	Medium	72	15	Yes	Yes
5.17	138	35	6	60	143	Bad	28	18	Yes	No
8.61	130	38	0	283	102	Medium	80	15	Yes	No
5.97	112	24	0	164	101	Medium	45	11	Yes	No
11.54	134	44	4	219	126	Good	44	15	Yes	Yes
7.50	140	29	0	105	91	Bad	43	16	Yes	No
7.38	98	120	0	268	93	Medium	72	10	No	No
7.81	137	102	13	422	118	Medium	71	10	No	Yes
5.99	117	42	10	371	121	Bad	26	14	Yes	Yes
8.43	138	80	0	108	126	Good	70	13	No	Yes
4.81	121	68	0	279	149	Good	79	12	Yes	No
8.97	132	107	0	144	125	Medium	33	13	No	No
6.88	96	39	0	161	112	Good	27	14	No	No
12.57	132	102	20	459	107	Good	49	11	Yes	Yes
9.32	134	27	18	467	96	Medium	49	14	No	Yes
8.64	111	101	17	266	91	Medium	63	17	No	Yes
10.44	124	115	16	458	105	Medium	62	16	No	Yes
13.44	133	103	14	288	122	Good	61	17	Yes	Yes
9.45	107	67	12	430	92	Medium	35	12	No	Yes
5.30	133	31	1	80	145	Medium	42	18	Yes	Yes
7.02	130	100	0	306	146	Good	42	11	Yes	No
3.58	142	109	0	111	164	Good	72	12	Yes	No
13.36	103	73	3	276	72	Medium	34	15	Yes	Yes
4.17	123	96	10	71	118	Bad	69	11	Yes	Yes
3.13	130	62	11	396	130	Bad	66	14	Yes	Yes
8.77	118	86	7	265	114	Good	52	15	No	Yes
8.68	131	25	10	183	104	Medium	56	15	No	Yes
5.25	131	55	0	26	110	Bad	79	12	Yes	Yes
10.26	111	75	1	377	108	Good	25	12	Yes	No
10.50	122	21	16	488	131	Good	30	14	Yes	Yes
6.53	154	30	0	122	162	Medium	57	17	No	No
5.98	124	56	11	447	134	Medium	53	12	No	Yes
14.37	95	106	0	256	53	Good	52	17	Yes	No
10.71	109	22	10	348	79	Good	74	14	No	Yes
10.26	135	100	22	463	122	Medium	36	14	Yes	Yes
7.68	126	41	22	403	119	Bad	42	12	Yes	Yes
9.08	152	81	0	191	126	Medium	54	16	Yes	No
7.80	121	50	0	508	98	Medium	65	11	No	No
5.58	137	71	0	402	116	Medium	78	17	Yes	No
9.44	131	47	7	90	118	Medium	47	12	Yes	Yes
7.90	132	46	4	206	124	Medium	73	11	Yes	No
16.27	141	60	19	319	92	Good	44	11	Yes	Yes
6.81	132	61	0	263	125	Medium	41	12	No	No
6.11	133	88	3	105	119	Medium	79	12	Yes	Yes
5.81	125	111	0	404	107	Bad	54	15	Yes	No
9.64	106	64	10	17	89	Medium	68	17	Yes	Yes
3.90	124	65	21	496	151	Bad	77	13	Yes	Yes
4.95	121	28	19	315	121	Medium	66	14	Yes	Yes
9.35	98	117	0	76	68	Medium	63	10	Yes	No
12.85	123	37	15	348	112	Good	28	12	Yes	Yes
5.87	131	73	13	455	132	Medium	62	17	Yes	Yes
5.32	152	116	0	170	160	Medium	39	16	Yes	No
8.67	142	73	14	238	115	Medium	73	14	No	Yes
8.14	135	89	11	245	78	Bad	79	16	Yes	Yes
8.44	128	42	8	328	107	Medium	35	12	Yes	Yes
5.47	108	75	9	61	111	Medium	67	12	Yes	Yes
6.10	153	63	0	49	124	Bad	56	16	Yes	No
4.53	129	42	13	315	130	Bad	34	13	Yes	Yes
5.57	109	51	10	26	120	Medium	30	17	No	Yes
5.35	130	58	19	366	139	Bad	33	16	Yes	Yes
12.57	138	108	17	203	128	Good	33	14	Yes	Yes
6.14	139	23	3	37	120	Medium	55	11	No	Yes
7.41	162	26	12	368	159	Medium	40	18	Yes	Yes
5.94	100	79	7	284	95	Bad	50	12	Yes	Yes
9.71	134	37	0	27	120	Good	49	16	Yes	Yes

16.7.3 Boston数据

knitr::kable(Boston)

crim	zn	indus	chas	nox	rm	age	dis	rad	tax	ptratio	black	lstat	medv
0.00632	18.0	2.31	0	0.5380	6.575	65.2	4.0900	1	296	15.3	396.90	4.98	24.0
0.02731	0.0	7.07	0	0.4690	6.421	78.9	4.9671	2	242	17.8	396.90	9.14	21.6
0.02729	0.0	7.07	0	0.4690	7.185	61.1	4.9671	2	242	17.8	392.83	4.03	34.7
0.03237	0.0	2.18	0	0.4580	6.998	45.8	6.0622	3	222	18.7	394.63	2.94	33.4
0.06905	0.0	2.18	0	0.4580	7.147	54.2	6.0622	3	222	18.7	396.90	5.33	36.2
0.02985	0.0	2.18	0	0.4580	6.430	58.7	6.0622	3	222	18.7	394.12	5.21	28.7
0.08829	12.5	7.87	0	0.5240	6.012	66.6	5.5605	5	311	15.2	395.60	12.43	22.9
0.14455	12.5	7.87	0	0.5240	6.172	96.1	5.9505	5	311	15.2	396.90	19.15	27.1
0.21124	12.5	7.87	0	0.5240	5.631	100.0	6.0821	5	311	15.2	386.63	29.93	16.5
0.17004	12.5	7.87	0	0.5240	6.004	85.9	6.5921	5	311	15.2	386.71	17.10	18.9
0.22489	12.5	7.87	0	0.5240	6.377	94.3	6.3467	5	311	15.2	392.52	20.45	15.0
0.11747	12.5	7.87	0	0.5240	6.009	82.9	6.2267	5	311	15.2	396.90	13.27	18.9
0.09378	12.5	7.87	0	0.5240	5.889	39.0	5.4509	5	311	15.2	390.50	15.71	21.7
0.62976	0.0	8.14	0	0.5380	5.949	61.8	4.7075	4	307	21.0	396.90	8.26	20.4
0.63796	0.0	8.14	0	0.5380	6.096	84.5	4.4619	4	307	21.0	380.02	10.26	18.2
0.62739	0.0	8.14	0	0.5380	5.834	56.5	4.4986	4	307	21.0	395.62	8.47	19.9
1.05393	0.0	8.14	0	0.5380	5.935	29.3	4.4986	4	307	21.0	386.85	6.58	23.1
0.78420	0.0	8.14	0	0.5380	5.990	81.7	4.2579	4	307	21.0	386.75	14.67	17.5
0.80271	0.0	8.14	0	0.5380	5.456	36.6	3.7965	4	307	21.0	288.99	11.69	20.2
0.72580	0.0	8.14	0	0.5380	5.727	69.5	3.7965	4	307	21.0	390.95	11.28	18.2
1.25179	0.0	8.14	0	0.5380	5.570	98.1	3.7979	4	307	21.0	376.57	21.02	13.6
0.85204	0.0	8.14	0	0.5380	5.965	89.2	4.0123	4	307	21.0	392.53	13.83	19.6
1.23247	0.0	8.14	0	0.5380	6.142	91.7	3.9769	4	307	21.0	396.90	18.72	15.2
0.98843	0.0	8.14	0	0.5380	5.813	100.0	4.0952	4	307	21.0	394.54	19.88	14.5
0.75026	0.0	8.14	0	0.5380	5.924	94.1	4.3996	4	307	21.0	394.33	16.30	15.6
0.84054	0.0	8.14	0	0.5380	5.599	85.7	4.4546	4	307	21.0	303.42	16.51	13.9
0.67191	0.0	8.14	0	0.5380	5.813	90.3	4.6820	4	307	21.0	376.88	14.81	16.6
0.95577	0.0	8.14	0	0.5380	6.047	88.8	4.4534	4	307	21.0	306.38	17.28	14.8
0.77299	0.0	8.14	0	0.5380	6.495	94.4	4.4547	4	307	21.0	387.94	12.80	18.4
1.00245	0.0	8.14	0	0.5380	6.674	87.3	4.2390	4	307	21.0	380.23	11.98	21.0
1.13081	0.0	8.14	0	0.5380	5.713	94.1	4.2330	4	307	21.0	360.17	22.60	12.7
1.35472	0.0	8.14	0	0.5380	6.072	100.0	4.1750	4	307	21.0	376.73	13.04	14.5
1.38799	0.0	8.14	0	0.5380	5.950	82.0	3.9900	4	307	21.0	232.60	27.71	13.2
1.15172	0.0	8.14	0	0.5380	5.701	95.0	3.7872	4	307	21.0	358.77	18.35	13.1
1.61282	0.0	8.14	0	0.5380	6.096	96.9	3.7598	4	307	21.0	248.31	20.34	13.5
0.06417	0.0	5.96	0	0.4990	5.933	68.2	3.3603	5	279	19.2	396.90	9.68	18.9
0.09744	0.0	5.96	0	0.4990	5.841	61.4	3.3779	5	279	19.2	377.56	11.41	20.0
0.08014	0.0	5.96	0	0.4990	5.850	41.5	3.9342	5	279	19.2	396.90	8.77	21.0
0.17505	0.0	5.96	0	0.4990	5.966	30.2	3.8473	5	279	19.2	393.43	10.13	24.7
0.02763	75.0	2.95	0	0.4280	6.595	21.8	5.4011	3	252	18.3	395.63	4.32	30.8
0.03359	75.0	2.95	0	0.4280	7.024	15.8	5.4011	3	252	18.3	395.62	1.98	34.9
0.12744	0.0	6.91	0	0.4480	6.770	2.9	5.7209	3	233	17.9	385.41	4.84	26.6
0.14150	0.0	6.91	0	0.4480	6.169	6.6	5.7209	3	233	17.9	383.37	5.81	25.3
0.15936	0.0	6.91	0	0.4480	6.211	6.5	5.7209	3	233	17.9	394.46	7.44	24.7
0.12269	0.0	6.91	0	0.4480	6.069	40.0	5.7209	3	233	17.9	389.39	9.55	21.2
0.17142	0.0	6.91	0	0.4480	5.682	33.8	5.1004	3	233	17.9	396.90	10.21	19.3
0.18836	0.0	6.91	0	0.4480	5.786	33.3	5.1004	3	233	17.9	396.90	14.15	20.0
0.22927	0.0	6.91	0	0.4480	6.030	85.5	5.6894	3	233	17.9	392.74	18.80	16.6
0.25387	0.0	6.91	0	0.4480	5.399	95.3	5.8700	3	233	17.9	396.90	30.81	14.4
0.21977	0.0	6.91	0	0.4480	5.602	62.0	6.0877	3	233	17.9	396.90	16.20	19.4
0.08873	21.0	5.64	0	0.4390	5.963	45.7	6.8147	4	243	16.8	395.56	13.45	19.7
0.04337	21.0	5.64	0	0.4390	6.115	63.0	6.8147	4	243	16.8	393.97	9.43	20.5
0.05360	21.0	5.64	0	0.4390	6.511	21.1	6.8147	4	243	16.8	396.90	5.28	25.0
0.04981	21.0	5.64	0	0.4390	5.998	21.4	6.8147	4	243	16.8	396.90	8.43	23.4
0.01360	75.0	4.00	0	0.4100	5.888	47.6	7.3197	3	469	21.1	396.90	14.80	18.9
0.01311	90.0	1.22	0	0.4030	7.249	21.9	8.6966	5	226	17.9	395.93	4.81	35.4
0.02055	85.0	0.74	0	0.4100	6.383	35.7	9.1876	2	313	17.3	396.90	5.77	24.7
0.01432	100.0	1.32	0	0.4110	6.816	40.5	8.3248	5	256	15.1	392.90	3.95	31.6
0.15445	25.0	5.13	0	0.4530	6.145	29.2	7.8148	8	284	19.7	390.68	6.86	23.3
0.10328	25.0	5.13	0	0.4530	5.927	47.2	6.9320	8	284	19.7	396.90	9.22	19.6
0.14932	25.0	5.13	0	0.4530	5.741	66.2	7.2254	8	284	19.7	395.11	13.15	18.7
0.17171	25.0	5.13	0	0.4530	5.966	93.4	6.8185	8	284	19.7	378.08	14.44	16.0
0.11027	25.0	5.13	0	0.4530	6.456	67.8	7.2255	8	284	19.7	396.90	6.73	22.2
0.12650	25.0	5.13	0	0.4530	6.762	43.4	7.9809	8	284	19.7	395.58	9.50	25.0
0.01951	17.5	1.38	0	0.4161	7.104	59.5	9.2229	3	216	18.6	393.24	8.05	33.0
0.03584	80.0	3.37	0	0.3980	6.290	17.8	6.6115	4	337	16.1	396.90	4.67	23.5
0.04379	80.0	3.37	0	0.3980	5.787	31.1	6.6115	4	337	16.1	396.90	10.24	19.4
0.05789	12.5	6.07	0	0.4090	5.878	21.4	6.4980	4	345	18.9	396.21	8.10	22.0
0.13554	12.5	6.07	0	0.4090	5.594	36.8	6.4980	4	345	18.9	396.90	13.09	17.4
0.12816	12.5	6.07	0	0.4090	5.885	33.0	6.4980	4	345	18.9	396.90	8.79	20.9
0.08826	0.0	10.81	0	0.4130	6.417	6.6	5.2873	4	305	19.2	383.73	6.72	24.2
0.15876	0.0	10.81	0	0.4130	5.961	17.5	5.2873	4	305	19.2	376.94	9.88	21.7
0.09164	0.0	10.81	0	0.4130	6.065	7.8	5.2873	4	305	19.2	390.91	5.52	22.8
0.19539	0.0	10.81	0	0.4130	6.245	6.2	5.2873	4	305	19.2	377.17	7.54	23.4
0.07896	0.0	12.83	0	0.4370	6.273	6.0	4.2515	5	398	18.7	394.92	6.78	24.1
0.09512	0.0	12.83	0	0.4370	6.286	45.0	4.5026	5	398	18.7	383.23	8.94	21.4
0.10153	0.0	12.83	0	0.4370	6.279	74.5	4.0522	5	398	18.7	373.66	11.97	20.0
0.08707	0.0	12.83	0	0.4370	6.140	45.8	4.0905	5	398	18.7	386.96	10.27	20.8
0.05646	0.0	12.83	0	0.4370	6.232	53.7	5.0141	5	398	18.7	386.40	12.34	21.2
0.08387	0.0	12.83	0	0.4370	5.874	36.6	4.5026	5	398	18.7	396.06	9.10	20.3
0.04113	25.0	4.86	0	0.4260	6.727	33.5	5.4007	4	281	19.0	396.90	5.29	28.0
0.04462	25.0	4.86	0	0.4260	6.619	70.4	5.4007	4	281	19.0	395.63	7.22	23.9
0.03659	25.0	4.86	0	0.4260	6.302	32.2	5.4007	4	281	19.0	396.90	6.72	24.8
0.03551	25.0	4.86	0	0.4260	6.167	46.7	5.4007	4	281	19.0	390.64	7.51	22.9
0.05059	0.0	4.49	0	0.4490	6.389	48.0	4.7794	3	247	18.5	396.90	9.62	23.9
0.05735	0.0	4.49	0	0.4490	6.630	56.1	4.4377	3	247	18.5	392.30	6.53	26.6
0.05188	0.0	4.49	0	0.4490	6.015	45.1	4.4272	3	247	18.5	395.99	12.86	22.5
0.07151	0.0	4.49	0	0.4490	6.121	56.8	3.7476	3	247	18.5	395.15	8.44	22.2
0.05660	0.0	3.41	0	0.4890	7.007	86.3	3.4217	2	270	17.8	396.90	5.50	23.6
0.05302	0.0	3.41	0	0.4890	7.079	63.1	3.4145	2	270	17.8	396.06	5.70	28.7
0.04684	0.0	3.41	0	0.4890	6.417	66.1	3.0923	2	270	17.8	392.18	8.81	22.6
0.03932	0.0	3.41	0	0.4890	6.405	73.9	3.0921	2	270	17.8	393.55	8.20	22.0
0.04203	28.0	15.04	0	0.4640	6.442	53.6	3.6659	4	270	18.2	395.01	8.16	22.9
0.02875	28.0	15.04	0	0.4640	6.211	28.9	3.6659	4	270	18.2	396.33	6.21	25.0
0.04294	28.0	15.04	0	0.4640	6.249	77.3	3.6150	4	270	18.2	396.90	10.59	20.6
0.12204	0.0	2.89	0	0.4450	6.625	57.8	3.4952	2	276	18.0	357.98	6.65	28.4
0.11504	0.0	2.89	0	0.4450	6.163	69.6	3.4952	2	276	18.0	391.83	11.34	21.4
0.12083	0.0	2.89	0	0.4450	8.069	76.0	3.4952	2	276	18.0	396.90	4.21	38.7
0.08187	0.0	2.89	0	0.4450	7.820	36.9	3.4952	2	276	18.0	393.53	3.57	43.8
0.06860	0.0	2.89	0	0.4450	7.416	62.5	3.4952	2	276	18.0	396.90	6.19	33.2
0.14866	0.0	8.56	0	0.5200	6.727	79.9	2.7778	5	384	20.9	394.76	9.42	27.5
0.11432	0.0	8.56	0	0.5200	6.781	71.3	2.8561	5	384	20.9	395.58	7.67	26.5
0.22876	0.0	8.56	0	0.5200	6.405	85.4	2.7147	5	384	20.9	70.80	10.63	18.6
0.21161	0.0	8.56	0	0.5200	6.137	87.4	2.7147	5	384	20.9	394.47	13.44	19.3
0.13960	0.0	8.56	0	0.5200	6.167	90.0	2.4210	5	384	20.9	392.69	12.33	20.1
0.13262	0.0	8.56	0	0.5200	5.851	96.7	2.1069	5	384	20.9	394.05	16.47	19.5
0.17120	0.0	8.56	0	0.5200	5.836	91.9	2.2110	5	384	20.9	395.67	18.66	19.5
0.13117	0.0	8.56	0	0.5200	6.127	85.2	2.1224	5	384	20.9	387.69	14.09	20.4
0.12802	0.0	8.56	0	0.5200	6.474	97.1	2.4329	5	384	20.9	395.24	12.27	19.8
0.26363	0.0	8.56	0	0.5200	6.229	91.2	2.5451	5	384	20.9	391.23	15.55	19.4
0.10793	0.0	8.56	0	0.5200	6.195	54.4	2.7778	5	384	20.9	393.49	13.00	21.7
0.10084	0.0	10.01	0	0.5470	6.715	81.6	2.6775	6	432	17.8	395.59	10.16	22.8
0.12329	0.0	10.01	0	0.5470	5.913	92.9	2.3534	6	432	17.8	394.95	16.21	18.8
0.22212	0.0	10.01	0	0.5470	6.092	95.4	2.5480	6	432	17.8	396.90	17.09	18.7
0.14231	0.0	10.01	0	0.5470	6.254	84.2	2.2565	6	432	17.8	388.74	10.45	18.5
0.17134	0.0	10.01	0	0.5470	5.928	88.2	2.4631	6	432	17.8	344.91	15.76	18.3
0.13158	0.0	10.01	0	0.5470	6.176	72.5	2.7301	6	432	17.8	393.30	12.04	21.2
0.15098	0.0	10.01	0	0.5470	6.021	82.6	2.7474	6	432	17.8	394.51	10.30	19.2
0.13058	0.0	10.01	0	0.5470	5.872	73.1	2.4775	6	432	17.8	338.63	15.37	20.4
0.14476	0.0	10.01	0	0.5470	5.731	65.2	2.7592	6	432	17.8	391.50	13.61	19.3
0.06899	0.0	25.65	0	0.5810	5.870	69.7	2.2577	2	188	19.1	389.15	14.37	22.0
0.07165	0.0	25.65	0	0.5810	6.004	84.1	2.1974	2	188	19.1	377.67	14.27	20.3
0.09299	0.0	25.65	0	0.5810	5.961	92.9	2.0869	2	188	19.1	378.09	17.93	20.5
0.15038	0.0	25.65	0	0.5810	5.856	97.0	1.9444	2	188	19.1	370.31	25.41	17.3
0.09849	0.0	25.65	0	0.5810	5.879	95.8	2.0063	2	188	19.1	379.38	17.58	18.8
0.16902	0.0	25.65	0	0.5810	5.986	88.4	1.9929	2	188	19.1	385.02	14.81	21.4
0.38735	0.0	25.65	0	0.5810	5.613	95.6	1.7572	2	188	19.1	359.29	27.26	15.7
0.25915	0.0	21.89	0	0.6240	5.693	96.0	1.7883	4	437	21.2	392.11	17.19	16.2
0.32543	0.0	21.89	0	0.6240	6.431	98.8	1.8125	4	437	21.2	396.90	15.39	18.0
0.88125	0.0	21.89	0	0.6240	5.637	94.7	1.9799	4	437	21.2	396.90	18.34	14.3
0.34006	0.0	21.89	0	0.6240	6.458	98.9	2.1185	4	437	21.2	395.04	12.60	19.2
1.19294	0.0	21.89	0	0.6240	6.326	97.7	2.2710	4	437	21.2	396.90	12.26	19.6
0.59005	0.0	21.89	0	0.6240	6.372	97.9	2.3274	4	437	21.2	385.76	11.12	23.0
0.32982	0.0	21.89	0	0.6240	5.822	95.4	2.4699	4	437	21.2	388.69	15.03	18.4
0.97617	0.0	21.89	0	0.6240	5.757	98.4	2.3460	4	437	21.2	262.76	17.31	15.6
0.55778	0.0	21.89	0	0.6240	6.335	98.2	2.1107	4	437	21.2	394.67	16.96	18.1
0.32264	0.0	21.89	0	0.6240	5.942	93.5	1.9669	4	437	21.2	378.25	16.90	17.4
0.35233	0.0	21.89	0	0.6240	6.454	98.4	1.8498	4	437	21.2	394.08	14.59	17.1
0.24980	0.0	21.89	0	0.6240	5.857	98.2	1.6686	4	437	21.2	392.04	21.32	13.3
0.54452	0.0	21.89	0	0.6240	6.151	97.9	1.6687	4	437	21.2	396.90	18.46	17.8
0.29090	0.0	21.89	0	0.6240	6.174	93.6	1.6119	4	437	21.2	388.08	24.16	14.0
1.62864	0.0	21.89	0	0.6240	5.019	100.0	1.4394	4	437	21.2	396.90	34.41	14.4
3.32105	0.0	19.58	1	0.8710	5.403	100.0	1.3216	5	403	14.7	396.90	26.82	13.4
4.09740	0.0	19.58	0	0.8710	5.468	100.0	1.4118	5	403	14.7	396.90	26.42	15.6
2.77974	0.0	19.58	0	0.8710	4.903	97.8	1.3459	5	403	14.7	396.90	29.29	11.8
2.37934	0.0	19.58	0	0.8710	6.130	100.0	1.4191	5	403	14.7	172.91	27.80	13.8
2.15505	0.0	19.58	0	0.8710	5.628	100.0	1.5166	5	403	14.7	169.27	16.65	15.6
2.36862	0.0	19.58	0	0.8710	4.926	95.7	1.4608	5	403	14.7	391.71	29.53	14.6
2.33099	0.0	19.58	0	0.8710	5.186	93.8	1.5296	5	403	14.7	356.99	28.32	17.8
2.73397	0.0	19.58	0	0.8710	5.597	94.9	1.5257	5	403	14.7	351.85	21.45	15.4
1.65660	0.0	19.58	0	0.8710	6.122	97.3	1.6180	5	403	14.7	372.80	14.10	21.5
1.49632	0.0	19.58	0	0.8710	5.404	100.0	1.5916	5	403	14.7	341.60	13.28	19.6
1.12658	0.0	19.58	1	0.8710	5.012	88.0	1.6102	5	403	14.7	343.28	12.12	15.3
2.14918	0.0	19.58	0	0.8710	5.709	98.5	1.6232	5	403	14.7	261.95	15.79	19.4
1.41385	0.0	19.58	1	0.8710	6.129	96.0	1.7494	5	403	14.7	321.02	15.12	17.0
3.53501	0.0	19.58	1	0.8710	6.152	82.6	1.7455	5	403	14.7	88.01	15.02	15.6
2.44668	0.0	19.58	0	0.8710	5.272	94.0	1.7364	5	403	14.7	88.63	16.14	13.1
1.22358	0.0	19.58	0	0.6050	6.943	97.4	1.8773	5	403	14.7	363.43	4.59	41.3
1.34284	0.0	19.58	0	0.6050	6.066	100.0	1.7573	5	403	14.7	353.89	6.43	24.3
1.42502	0.0	19.58	0	0.8710	6.510	100.0	1.7659	5	403	14.7	364.31	7.39	23.3
1.27346	0.0	19.58	1	0.6050	6.250	92.6	1.7984	5	403	14.7	338.92	5.50	27.0
1.46336	0.0	19.58	0	0.6050	7.489	90.8	1.9709	5	403	14.7	374.43	1.73	50.0
1.83377	0.0	19.58	1	0.6050	7.802	98.2	2.0407	5	403	14.7	389.61	1.92	50.0
1.51902	0.0	19.58	1	0.6050	8.375	93.9	2.1620	5	403	14.7	388.45	3.32	50.0
2.24236	0.0	19.58	0	0.6050	5.854	91.8	2.4220	5	403	14.7	395.11	11.64	22.7
2.92400	0.0	19.58	0	0.6050	6.101	93.0	2.2834	5	403	14.7	240.16	9.81	25.0
2.01019	0.0	19.58	0	0.6050	7.929	96.2	2.0459	5	403	14.7	369.30	3.70	50.0
1.80028	0.0	19.58	0	0.6050	5.877	79.2	2.4259	5	403	14.7	227.61	12.14	23.8
2.30040	0.0	19.58	0	0.6050	6.319	96.1	2.1000	5	403	14.7	297.09	11.10	23.8
2.44953	0.0	19.58	0	0.6050	6.402	95.2	2.2625	5	403	14.7	330.04	11.32	22.3
1.20742	0.0	19.58	0	0.6050	5.875	94.6	2.4259	5	403	14.7	292.29	14.43	17.4
2.31390	0.0	19.58	0	0.6050	5.880	97.3	2.3887	5	403	14.7	348.13	12.03	19.1
0.13914	0.0	4.05	0	0.5100	5.572	88.5	2.5961	5	296	16.6	396.90	14.69	23.1
0.09178	0.0	4.05	0	0.5100	6.416	84.1	2.6463	5	296	16.6	395.50	9.04	23.6
0.08447	0.0	4.05	0	0.5100	5.859	68.7	2.7019	5	296	16.6	393.23	9.64	22.6
0.06664	0.0	4.05	0	0.5100	6.546	33.1	3.1323	5	296	16.6	390.96	5.33	29.4
0.07022	0.0	4.05	0	0.5100	6.020	47.2	3.5549	5	296	16.6	393.23	10.11	23.2
0.05425	0.0	4.05	0	0.5100	6.315	73.4	3.3175	5	296	16.6	395.60	6.29	24.6
0.06642	0.0	4.05	0	0.5100	6.860	74.4	2.9153	5	296	16.6	391.27	6.92	29.9
0.05780	0.0	2.46	0	0.4880	6.980	58.4	2.8290	3	193	17.8	396.90	5.04	37.2
0.06588	0.0	2.46	0	0.4880	7.765	83.3	2.7410	3	193	17.8	395.56	7.56	39.8
0.06888	0.0	2.46	0	0.4880	6.144	62.2	2.5979	3	193	17.8	396.90	9.45	36.2
0.09103	0.0	2.46	0	0.4880	7.155	92.2	2.7006	3	193	17.8	394.12	4.82	37.9
0.10008	0.0	2.46	0	0.4880	6.563	95.6	2.8470	3	193	17.8	396.90	5.68	32.5
0.08308	0.0	2.46	0	0.4880	5.604	89.8	2.9879	3	193	17.8	391.00	13.98	26.4
0.06047	0.0	2.46	0	0.4880	6.153	68.8	3.2797	3	193	17.8	387.11	13.15	29.6
0.05602	0.0	2.46	0	0.4880	7.831	53.6	3.1992	3	193	17.8	392.63	4.45	50.0
0.07875	45.0	3.44	0	0.4370	6.782	41.1	3.7886	5	398	15.2	393.87	6.68	32.0
0.12579	45.0	3.44	0	0.4370	6.556	29.1	4.5667	5	398	15.2	382.84	4.56	29.8
0.08370	45.0	3.44	0	0.4370	7.185	38.9	4.5667	5	398	15.2	396.90	5.39	34.9
0.09068	45.0	3.44	0	0.4370	6.951	21.5	6.4798	5	398	15.2	377.68	5.10	37.0
0.06911	45.0	3.44	0	0.4370	6.739	30.8	6.4798	5	398	15.2	389.71	4.69	30.5
0.08664	45.0	3.44	0	0.4370	7.178	26.3	6.4798	5	398	15.2	390.49	2.87	36.4
0.02187	60.0	2.93	0	0.4010	6.800	9.9	6.2196	1	265	15.6	393.37	5.03	31.1
0.01439	60.0	2.93	0	0.4010	6.604	18.8	6.2196	1	265	15.6	376.70	4.38	29.1
0.01381	80.0	0.46	0	0.4220	7.875	32.0	5.6484	4	255	14.4	394.23	2.97	50.0
0.04011	80.0	1.52	0	0.4040	7.287	34.1	7.3090	2	329	12.6	396.90	4.08	33.3
0.04666	80.0	1.52	0	0.4040	7.107	36.6	7.3090	2	329	12.6	354.31	8.61	30.3
0.03768	80.0	1.52	0	0.4040	7.274	38.3	7.3090	2	329	12.6	392.20	6.62	34.6
0.03150	95.0	1.47	0	0.4030	6.975	15.3	7.6534	3	402	17.0	396.90	4.56	34.9
0.01778	95.0	1.47	0	0.4030	7.135	13.9	7.6534	3	402	17.0	384.30	4.45	32.9
0.03445	82.5	2.03	0	0.4150	6.162	38.4	6.2700	2	348	14.7	393.77	7.43	24.1
0.02177	82.5	2.03	0	0.4150	7.610	15.7	6.2700	2	348	14.7	395.38	3.11	42.3
0.03510	95.0	2.68	0	0.4161	7.853	33.2	5.1180	4	224	14.7	392.78	3.81	48.5
0.02009	95.0	2.68	0	0.4161	8.034	31.9	5.1180	4	224	14.7	390.55	2.88	50.0
0.13642	0.0	10.59	0	0.4890	5.891	22.3	3.9454	4	277	18.6	396.90	10.87	22.6
0.22969	0.0	10.59	0	0.4890	6.326	52.5	4.3549	4	277	18.6	394.87	10.97	24.4
0.25199	0.0	10.59	0	0.4890	5.783	72.7	4.3549	4	277	18.6	389.43	18.06	22.5
0.13587	0.0	10.59	1	0.4890	6.064	59.1	4.2392	4	277	18.6	381.32	14.66	24.4
0.43571	0.0	10.59	1	0.4890	5.344	100.0	3.8750	4	277	18.6	396.90	23.09	20.0
0.17446	0.0	10.59	1	0.4890	5.960	92.1	3.8771	4	277	18.6	393.25	17.27	21.7
0.37578	0.0	10.59	1	0.4890	5.404	88.6	3.6650	4	277	18.6	395.24	23.98	19.3
0.21719	0.0	10.59	1	0.4890	5.807	53.8	3.6526	4	277	18.6	390.94	16.03	22.4
0.14052	0.0	10.59	0	0.4890	6.375	32.3	3.9454	4	277	18.6	385.81	9.38	28.1
0.28955	0.0	10.59	0	0.4890	5.412	9.8	3.5875	4	277	18.6	348.93	29.55	23.7
0.19802	0.0	10.59	0	0.4890	6.182	42.4	3.9454	4	277	18.6	393.63	9.47	25.0
0.04560	0.0	13.89	1	0.5500	5.888	56.0	3.1121	5	276	16.4	392.80	13.51	23.3
0.07013	0.0	13.89	0	0.5500	6.642	85.1	3.4211	5	276	16.4	392.78	9.69	28.7
0.11069	0.0	13.89	1	0.5500	5.951	93.8	2.8893	5	276	16.4	396.90	17.92	21.5
0.11425	0.0	13.89	1	0.5500	6.373	92.4	3.3633	5	276	16.4	393.74	10.50	23.0
0.35809	0.0	6.20	1	0.5070	6.951	88.5	2.8617	8	307	17.4	391.70	9.71	26.7
0.40771	0.0	6.20	1	0.5070	6.164	91.3	3.0480	8	307	17.4	395.24	21.46	21.7
0.62356	0.0	6.20	1	0.5070	6.879	77.7	3.2721	8	307	17.4	390.39	9.93	27.5
0.61470	0.0	6.20	0	0.5070	6.618	80.8	3.2721	8	307	17.4	396.90	7.60	30.1
0.31533	0.0	6.20	0	0.5040	8.266	78.3	2.8944	8	307	17.4	385.05	4.14	44.8
0.52693	0.0	6.20	0	0.5040	8.725	83.0	2.8944	8	307	17.4	382.00	4.63	50.0
0.38214	0.0	6.20	0	0.5040	8.040	86.5	3.2157	8	307	17.4	387.38	3.13	37.6
0.41238	0.0	6.20	0	0.5040	7.163	79.9	3.2157	8	307	17.4	372.08	6.36	31.6
0.29819	0.0	6.20	0	0.5040	7.686	17.0	3.3751	8	307	17.4	377.51	3.92	46.7
0.44178	0.0	6.20	0	0.5040	6.552	21.4	3.3751	8	307	17.4	380.34	3.76	31.5
0.53700	0.0	6.20	0	0.5040	5.981	68.1	3.6715	8	307	17.4	378.35	11.65	24.3
0.46296	0.0	6.20	0	0.5040	7.412	76.9	3.6715	8	307	17.4	376.14	5.25	31.7
0.57529	0.0	6.20	0	0.5070	8.337	73.3	3.8384	8	307	17.4	385.91	2.47	41.7
0.33147	0.0	6.20	0	0.5070	8.247	70.4	3.6519	8	307	17.4	378.95	3.95	48.3
0.44791	0.0	6.20	1	0.5070	6.726	66.5	3.6519	8	307	17.4	360.20	8.05	29.0
0.33045	0.0	6.20	0	0.5070	6.086	61.5	3.6519	8	307	17.4	376.75	10.88	24.0
0.52058	0.0	6.20	1	0.5070	6.631	76.5	4.1480	8	307	17.4	388.45	9.54	25.1
0.51183	0.0	6.20	0	0.5070	7.358	71.6	4.1480	8	307	17.4	390.07	4.73	31.5
0.08244	30.0	4.93	0	0.4280	6.481	18.5	6.1899	6	300	16.6	379.41	6.36	23.7
0.09252	30.0	4.93	0	0.4280	6.606	42.2	6.1899	6	300	16.6	383.78	7.37	23.3
0.11329	30.0	4.93	0	0.4280	6.897	54.3	6.3361	6	300	16.6	391.25	11.38	22.0
0.10612	30.0	4.93	0	0.4280	6.095	65.1	6.3361	6	300	16.6	394.62	12.40	20.1
0.10290	30.0	4.93	0	0.4280	6.358	52.9	7.0355	6	300	16.6	372.75	11.22	22.2
0.12757	30.0	4.93	0	0.4280	6.393	7.8	7.0355	6	300	16.6	374.71	5.19	23.7
0.20608	22.0	5.86	0	0.4310	5.593	76.5	7.9549	7	330	19.1	372.49	12.50	17.6
0.19133	22.0	5.86	0	0.4310	5.605	70.2	7.9549	7	330	19.1	389.13	18.46	18.5
0.33983	22.0	5.86	0	0.4310	6.108	34.9	8.0555	7	330	19.1	390.18	9.16	24.3
0.19657	22.0	5.86	0	0.4310	6.226	79.2	8.0555	7	330	19.1	376.14	10.15	20.5
0.16439	22.0	5.86	0	0.4310	6.433	49.1	7.8265	7	330	19.1	374.71	9.52	24.5
0.19073	22.0	5.86	0	0.4310	6.718	17.5	7.8265	7	330	19.1	393.74	6.56	26.2
0.14030	22.0	5.86	0	0.4310	6.487	13.0	7.3967	7	330	19.1	396.28	5.90	24.4
0.21409	22.0	5.86	0	0.4310	6.438	8.9	7.3967	7	330	19.1	377.07	3.59	24.8
0.08221	22.0	5.86	0	0.4310	6.957	6.8	8.9067	7	330	19.1	386.09	3.53	29.6
0.36894	22.0	5.86	0	0.4310	8.259	8.4	8.9067	7	330	19.1	396.90	3.54	42.8
0.04819	80.0	3.64	0	0.3920	6.108	32.0	9.2203	1	315	16.4	392.89	6.57	21.9
0.03548	80.0	3.64	0	0.3920	5.876	19.1	9.2203	1	315	16.4	395.18	9.25	20.9
0.01538	90.0	3.75	0	0.3940	7.454	34.2	6.3361	3	244	15.9	386.34	3.11	44.0
0.61154	20.0	3.97	0	0.6470	8.704	86.9	1.8010	5	264	13.0	389.70	5.12	50.0
0.66351	20.0	3.97	0	0.6470	7.333	100.0	1.8946	5	264	13.0	383.29	7.79	36.0
0.65665	20.0	3.97	0	0.6470	6.842	100.0	2.0107	5	264	13.0	391.93	6.90	30.1
0.54011	20.0	3.97	0	0.6470	7.203	81.8	2.1121	5	264	13.0	392.80	9.59	33.8
0.53412	20.0	3.97	0	0.6470	7.520	89.4	2.1398	5	264	13.0	388.37	7.26	43.1
0.52014	20.0	3.97	0	0.6470	8.398	91.5	2.2885	5	264	13.0	386.86	5.91	48.8
0.82526	20.0	3.97	0	0.6470	7.327	94.5	2.0788	5	264	13.0	393.42	11.25	31.0
0.55007	20.0	3.97	0	0.6470	7.206	91.6	1.9301	5	264	13.0	387.89	8.10	36.5
0.76162	20.0	3.97	0	0.6470	5.560	62.8	1.9865	5	264	13.0	392.40	10.45	22.8
0.78570	20.0	3.97	0	0.6470	7.014	84.6	2.1329	5	264	13.0	384.07	14.79	30.7
0.57834	20.0	3.97	0	0.5750	8.297	67.0	2.4216	5	264	13.0	384.54	7.44	50.0
0.54050	20.0	3.97	0	0.5750	7.470	52.6	2.8720	5	264	13.0	390.30	3.16	43.5
0.09065	20.0	6.96	1	0.4640	5.920	61.5	3.9175	3	223	18.6	391.34	13.65	20.7
0.29916	20.0	6.96	0	0.4640	5.856	42.1	4.4290	3	223	18.6	388.65	13.00	21.1
0.16211	20.0	6.96	0	0.4640	6.240	16.3	4.4290	3	223	18.6	396.90	6.59	25.2
0.11460	20.0	6.96	0	0.4640	6.538	58.7	3.9175	3	223	18.6	394.96	7.73	24.4
0.22188	20.0	6.96	1	0.4640	7.691	51.8	4.3665	3	223	18.6	390.77	6.58	35.2
0.05644	40.0	6.41	1	0.4470	6.758	32.9	4.0776	4	254	17.6	396.90	3.53	32.4
0.09604	40.0	6.41	0	0.4470	6.854	42.8	4.2673	4	254	17.6	396.90	2.98	32.0
0.10469	40.0	6.41	1	0.4470	7.267	49.0	4.7872	4	254	17.6	389.25	6.05	33.2
0.06127	40.0	6.41	1	0.4470	6.826	27.6	4.8628	4	254	17.6	393.45	4.16	33.1
0.07978	40.0	6.41	0	0.4470	6.482	32.1	4.1403	4	254	17.6	396.90	7.19	29.1
0.21038	20.0	3.33	0	0.4429	6.812	32.2	4.1007	5	216	14.9	396.90	4.85	35.1
0.03578	20.0	3.33	0	0.4429	7.820	64.5	4.6947	5	216	14.9	387.31	3.76	45.4
0.03705	20.0	3.33	0	0.4429	6.968	37.2	5.2447	5	216	14.9	392.23	4.59	35.4
0.06129	20.0	3.33	1	0.4429	7.645	49.7	5.2119	5	216	14.9	377.07	3.01	46.0
0.01501	90.0	1.21	1	0.4010	7.923	24.8	5.8850	1	198	13.6	395.52	3.16	50.0
0.00906	90.0	2.97	0	0.4000	7.088	20.8	7.3073	1	285	15.3	394.72	7.85	32.2
0.01096	55.0	2.25	0	0.3890	6.453	31.9	7.3073	1	300	15.3	394.72	8.23	22.0
0.01965	80.0	1.76	0	0.3850	6.230	31.5	9.0892	1	241	18.2	341.60	12.93	20.1
0.03871	52.5	5.32	0	0.4050	6.209	31.3	7.3172	6	293	16.6	396.90	7.14	23.2
0.04590	52.5	5.32	0	0.4050	6.315	45.6	7.3172	6	293	16.6	396.90	7.60	22.3
0.04297	52.5	5.32	0	0.4050	6.565	22.9	7.3172	6	293	16.6	371.72	9.51	24.8
0.03502	80.0	4.95	0	0.4110	6.861	27.9	5.1167	4	245	19.2	396.90	3.33	28.5
0.07886	80.0	4.95	0	0.4110	7.148	27.7	5.1167	4	245	19.2	396.90	3.56	37.3
0.03615	80.0	4.95	0	0.4110	6.630	23.4	5.1167	4	245	19.2	396.90	4.70	27.9
0.08265	0.0	13.92	0	0.4370	6.127	18.4	5.5027	4	289	16.0	396.90	8.58	23.9
0.08199	0.0	13.92	0	0.4370	6.009	42.3	5.5027	4	289	16.0	396.90	10.40	21.7
0.12932	0.0	13.92	0	0.4370	6.678	31.1	5.9604	4	289	16.0	396.90	6.27	28.6
0.05372	0.0	13.92	0	0.4370	6.549	51.0	5.9604	4	289	16.0	392.85	7.39	27.1
0.14103	0.0	13.92	0	0.4370	5.790	58.0	6.3200	4	289	16.0	396.90	15.84	20.3
0.06466	70.0	2.24	0	0.4000	6.345	20.1	7.8278	5	358	14.8	368.24	4.97	22.5
0.05561	70.0	2.24	0	0.4000	7.041	10.0	7.8278	5	358	14.8	371.58	4.74	29.0
0.04417	70.0	2.24	0	0.4000	6.871	47.4	7.8278	5	358	14.8	390.86	6.07	24.8
0.03537	34.0	6.09	0	0.4330	6.590	40.4	5.4917	7	329	16.1	395.75	9.50	22.0
0.09266	34.0	6.09	0	0.4330	6.495	18.4	5.4917	7	329	16.1	383.61	8.67	26.4
0.10000	34.0	6.09	0	0.4330	6.982	17.7	5.4917	7	329	16.1	390.43	4.86	33.1
0.05515	33.0	2.18	0	0.4720	7.236	41.1	4.0220	7	222	18.4	393.68	6.93	36.1
0.05479	33.0	2.18	0	0.4720	6.616	58.1	3.3700	7	222	18.4	393.36	8.93	28.4
0.07503	33.0	2.18	0	0.4720	7.420	71.9	3.0992	7	222	18.4	396.90	6.47	33.4
0.04932	33.0	2.18	0	0.4720	6.849	70.3	3.1827	7	222	18.4	396.90	7.53	28.2
0.49298	0.0	9.90	0	0.5440	6.635	82.5	3.3175	4	304	18.4	396.90	4.54	22.8
0.34940	0.0	9.90	0	0.5440	5.972	76.7	3.1025	4	304	18.4	396.24	9.97	20.3
2.63548	0.0	9.90	0	0.5440	4.973	37.8	2.5194	4	304	18.4	350.45	12.64	16.1
0.79041	0.0	9.90	0	0.5440	6.122	52.8	2.6403	4	304	18.4	396.90	5.98	22.1
0.26169	0.0	9.90	0	0.5440	6.023	90.4	2.8340	4	304	18.4	396.30	11.72	19.4
0.26938	0.0	9.90	0	0.5440	6.266	82.8	3.2628	4	304	18.4	393.39	7.90	21.6
0.36920	0.0	9.90	0	0.5440	6.567	87.3	3.6023	4	304	18.4	395.69	9.28	23.8
0.25356	0.0	9.90	0	0.5440	5.705	77.7	3.9450	4	304	18.4	396.42	11.50	16.2
0.31827	0.0	9.90	0	0.5440	5.914	83.2	3.9986	4	304	18.4	390.70	18.33	17.8
0.24522	0.0	9.90	0	0.5440	5.782	71.7	4.0317	4	304	18.4	396.90	15.94	19.8
0.40202	0.0	9.90	0	0.5440	6.382	67.2	3.5325	4	304	18.4	395.21	10.36	23.1
0.47547	0.0	9.90	0	0.5440	6.113	58.8	4.0019	4	304	18.4	396.23	12.73	21.0
0.16760	0.0	7.38	0	0.4930	6.426	52.3	4.5404	5	287	19.6	396.90	7.20	23.8
0.18159	0.0	7.38	0	0.4930	6.376	54.3	4.5404	5	287	19.6	396.90	6.87	23.1
0.35114	0.0	7.38	0	0.4930	6.041	49.9	4.7211	5	287	19.6	396.90	7.70	20.4
0.28392	0.0	7.38	0	0.4930	5.708	74.3	4.7211	5	287	19.6	391.13	11.74	18.5
0.34109	0.0	7.38	0	0.4930	6.415	40.1	4.7211	5	287	19.6	396.90	6.12	25.0
0.19186	0.0	7.38	0	0.4930	6.431	14.7	5.4159	5	287	19.6	393.68	5.08	24.6
0.30347	0.0	7.38	0	0.4930	6.312	28.9	5.4159	5	287	19.6	396.90	6.15	23.0
0.24103	0.0	7.38	0	0.4930	6.083	43.7	5.4159	5	287	19.6	396.90	12.79	22.2
0.06617	0.0	3.24	0	0.4600	5.868	25.8	5.2146	4	430	16.9	382.44	9.97	19.3
0.06724	0.0	3.24	0	0.4600	6.333	17.2	5.2146	4	430	16.9	375.21	7.34	22.6
0.04544	0.0	3.24	0	0.4600	6.144	32.2	5.8736	4	430	16.9	368.57	9.09	19.8
0.05023	35.0	6.06	0	0.4379	5.706	28.4	6.6407	1	304	16.9	394.02	12.43	17.1
0.03466	35.0	6.06	0	0.4379	6.031	23.3	6.6407	1	304	16.9	362.25	7.83	19.4
0.05083	0.0	5.19	0	0.5150	6.316	38.1	6.4584	5	224	20.2	389.71	5.68	22.2
0.03738	0.0	5.19	0	0.5150	6.310	38.5	6.4584	5	224	20.2	389.40	6.75	20.7
0.03961	0.0	5.19	0	0.5150	6.037	34.5	5.9853	5	224	20.2	396.90	8.01	21.1
0.03427	0.0	5.19	0	0.5150	5.869	46.3	5.2311	5	224	20.2	396.90	9.80	19.5
0.03041	0.0	5.19	0	0.5150	5.895	59.6	5.6150	5	224	20.2	394.81	10.56	18.5
0.03306	0.0	5.19	0	0.5150	6.059	37.3	4.8122	5	224	20.2	396.14	8.51	20.6
0.05497	0.0	5.19	0	0.5150	5.985	45.4	4.8122	5	224	20.2	396.90	9.74	19.0
0.06151	0.0	5.19	0	0.5150	5.968	58.5	4.8122	5	224	20.2	396.90	9.29	18.7
0.01301	35.0	1.52	0	0.4420	7.241	49.3	7.0379	1	284	15.5	394.74	5.49	32.7
0.02498	0.0	1.89	0	0.5180	6.540	59.7	6.2669	1	422	15.9	389.96	8.65	16.5
0.02543	55.0	3.78	0	0.4840	6.696	56.4	5.7321	5	370	17.6	396.90	7.18	23.9
0.03049	55.0	3.78	0	0.4840	6.874	28.1	6.4654	5	370	17.6	387.97	4.61	31.2
0.03113	0.0	4.39	0	0.4420	6.014	48.5	8.0136	3	352	18.8	385.64	10.53	17.5
0.06162	0.0	4.39	0	0.4420	5.898	52.3	8.0136	3	352	18.8	364.61	12.67	17.2
0.01870	85.0	4.15	0	0.4290	6.516	27.7	8.5353	4	351	17.9	392.43	6.36	23.1
0.01501	80.0	2.01	0	0.4350	6.635	29.7	8.3440	4	280	17.0	390.94	5.99	24.5
0.02899	40.0	1.25	0	0.4290	6.939	34.5	8.7921	1	335	19.7	389.85	5.89	26.6
0.06211	40.0	1.25	0	0.4290	6.490	44.4	8.7921	1	335	19.7	396.90	5.98	22.9
0.07950	60.0	1.69	0	0.4110	6.579	35.9	10.7103	4	411	18.3	370.78	5.49	24.1
0.07244	60.0	1.69	0	0.4110	5.884	18.5	10.7103	4	411	18.3	392.33	7.79	18.6
0.01709	90.0	2.02	0	0.4100	6.728	36.1	12.1265	5	187	17.0	384.46	4.50	30.1
0.04301	80.0	1.91	0	0.4130	5.663	21.9	10.5857	4	334	22.0	382.80	8.05	18.2
0.10659	80.0	1.91	0	0.4130	5.936	19.5	10.5857	4	334	22.0	376.04	5.57	20.6
8.98296	0.0	18.10	1	0.7700	6.212	97.4	2.1222	24	666	20.2	377.73	17.60	17.8
3.84970	0.0	18.10	1	0.7700	6.395	91.0	2.5052	24	666	20.2	391.34	13.27	21.7
5.20177	0.0	18.10	1	0.7700	6.127	83.4	2.7227	24	666	20.2	395.43	11.48	22.7
4.26131	0.0	18.10	0	0.7700	6.112	81.3	2.5091	24	666	20.2	390.74	12.67	22.6
4.54192	0.0	18.10	0	0.7700	6.398	88.0	2.5182	24	666	20.2	374.56	7.79	25.0
3.83684	0.0	18.10	0	0.7700	6.251	91.1	2.2955	24	666	20.2	350.65	14.19	19.9
3.67822	0.0	18.10	0	0.7700	5.362	96.2	2.1036	24	666	20.2	380.79	10.19	20.8
4.22239	0.0	18.10	1	0.7700	5.803	89.0	1.9047	24	666	20.2	353.04	14.64	16.8
3.47428	0.0	18.10	1	0.7180	8.780	82.9	1.9047	24	666	20.2	354.55	5.29	21.9
4.55587	0.0	18.10	0	0.7180	3.561	87.9	1.6132	24	666	20.2	354.70	7.12	27.5
3.69695	0.0	18.10	0	0.7180	4.963	91.4	1.7523	24	666	20.2	316.03	14.00	21.9
13.52220	0.0	18.10	0	0.6310	3.863	100.0	1.5106	24	666	20.2	131.42	13.33	23.1
4.89822	0.0	18.10	0	0.6310	4.970	100.0	1.3325	24	666	20.2	375.52	3.26	50.0
5.66998	0.0	18.10	1	0.6310	6.683	96.8	1.3567	24	666	20.2	375.33	3.73	50.0
6.53876	0.0	18.10	1	0.6310	7.016	97.5	1.2024	24	666	20.2	392.05	2.96	50.0
9.23230	0.0	18.10	0	0.6310	6.216	100.0	1.1691	24	666	20.2	366.15	9.53	50.0
8.26725	0.0	18.10	1	0.6680	5.875	89.6	1.1296	24	666	20.2	347.88	8.88	50.0
11.10810	0.0	18.10	0	0.6680	4.906	100.0	1.1742	24	666	20.2	396.90	34.77	13.8
18.49820	0.0	18.10	0	0.6680	4.138	100.0	1.1370	24	666	20.2	396.90	37.97	13.8
19.60910	0.0	18.10	0	0.6710	7.313	97.9	1.3163	24	666	20.2	396.90	13.44	15.0
15.28800	0.0	18.10	0	0.6710	6.649	93.3	1.3449	24	666	20.2	363.02	23.24	13.9
9.82349	0.0	18.10	0	0.6710	6.794	98.8	1.3580	24	666	20.2	396.90	21.24	13.3
23.64820	0.0	18.10	0	0.6710	6.380	96.2	1.3861	24	666	20.2	396.90	23.69	13.1
17.86670	0.0	18.10	0	0.6710	6.223	100.0	1.3861	24	666	20.2	393.74	21.78	10.2
88.97620	0.0	18.10	0	0.6710	6.968	91.9	1.4165	24	666	20.2	396.90	17.21	10.4
15.87440	0.0	18.10	0	0.6710	6.545	99.1	1.5192	24	666	20.2	396.90	21.08	10.9
9.18702	0.0	18.10	0	0.7000	5.536	100.0	1.5804	24	666	20.2	396.90	23.60	11.3
7.99248	0.0	18.10	0	0.7000	5.520	100.0	1.5331	24	666	20.2	396.90	24.56	12.3
20.08490	0.0	18.10	0	0.7000	4.368	91.2	1.4395	24	666	20.2	285.83	30.63	8.8
16.81180	0.0	18.10	0	0.7000	5.277	98.1	1.4261	24	666	20.2	396.90	30.81	7.2
24.39380	0.0	18.10	0	0.7000	4.652	100.0	1.4672	24	666	20.2	396.90	28.28	10.5
22.59710	0.0	18.10	0	0.7000	5.000	89.5	1.5184	24	666	20.2	396.90	31.99	7.4
14.33370	0.0	18.10	0	0.7000	4.880	100.0	1.5895	24	666	20.2	372.92	30.62	10.2
8.15174	0.0	18.10	0	0.7000	5.390	98.9	1.7281	24	666	20.2	396.90	20.85	11.5
6.96215	0.0	18.10	0	0.7000	5.713	97.0	1.9265	24	666	20.2	394.43	17.11	15.1
5.29305	0.0	18.10	0	0.7000	6.051	82.5	2.1678	24	666	20.2	378.38	18.76	23.2
11.57790	0.0	18.10	0	0.7000	5.036	97.0	1.7700	24	666	20.2	396.90	25.68	9.7
8.64476	0.0	18.10	0	0.6930	6.193	92.6	1.7912	24	666	20.2	396.90	15.17	13.8
13.35980	0.0	18.10	0	0.6930	5.887	94.7	1.7821	24	666	20.2	396.90	16.35	12.7
8.71675	0.0	18.10	0	0.6930	6.471	98.8	1.7257	24	666	20.2	391.98	17.12	13.1
5.87205	0.0	18.10	0	0.6930	6.405	96.0	1.6768	24	666	20.2	396.90	19.37	12.5
7.67202	0.0	18.10	0	0.6930	5.747	98.9	1.6334	24	666	20.2	393.10	19.92	8.5
38.35180	0.0	18.10	0	0.6930	5.453	100.0	1.4896	24	666	20.2	396.90	30.59	5.0
9.91655	0.0	18.10	0	0.6930	5.852	77.8	1.5004	24	666	20.2	338.16	29.97	6.3
25.04610	0.0	18.10	0	0.6930	5.987	100.0	1.5888	24	666	20.2	396.90	26.77	5.6
14.23620	0.0	18.10	0	0.6930	6.343	100.0	1.5741	24	666	20.2	396.90	20.32	7.2
9.59571	0.0	18.10	0	0.6930	6.404	100.0	1.6390	24	666	20.2	376.11	20.31	12.1
24.80170	0.0	18.10	0	0.6930	5.349	96.0	1.7028	24	666	20.2	396.90	19.77	8.3
41.52920	0.0	18.10	0	0.6930	5.531	85.4	1.6074	24	666	20.2	329.46	27.38	8.5
67.92080	0.0	18.10	0	0.6930	5.683	100.0	1.4254	24	666	20.2	384.97	22.98	5.0
20.71620	0.0	18.10	0	0.6590	4.138	100.0	1.1781	24	666	20.2	370.22	23.34	11.9
11.95110	0.0	18.10	0	0.6590	5.608	100.0	1.2852	24	666	20.2	332.09	12.13	27.9
7.40389	0.0	18.10	0	0.5970	5.617	97.9	1.4547	24	666	20.2	314.64	26.40	17.2
14.43830	0.0	18.10	0	0.5970	6.852	100.0	1.4655	24	666	20.2	179.36	19.78	27.5
51.13580	0.0	18.10	0	0.5970	5.757	100.0	1.4130	24	666	20.2	2.60	10.11	15.0
14.05070	0.0	18.10	0	0.5970	6.657	100.0	1.5275	24	666	20.2	35.05	21.22	17.2
18.81100	0.0	18.10	0	0.5970	4.628	100.0	1.5539	24	666	20.2	28.79	34.37	17.9
28.65580	0.0	18.10	0	0.5970	5.155	100.0	1.5894	24	666	20.2	210.97	20.08	16.3
45.74610	0.0	18.10	0	0.6930	4.519	100.0	1.6582	24	666	20.2	88.27	36.98	7.0
18.08460	0.0	18.10	0	0.6790	6.434	100.0	1.8347	24	666	20.2	27.25	29.05	7.2
10.83420	0.0	18.10	0	0.6790	6.782	90.8	1.8195	24	666	20.2	21.57	25.79	7.5
25.94060	0.0	18.10	0	0.6790	5.304	89.1	1.6475	24	666	20.2	127.36	26.64	10.4
73.53410	0.0	18.10	0	0.6790	5.957	100.0	1.8026	24	666	20.2	16.45	20.62	8.8
11.81230	0.0	18.10	0	0.7180	6.824	76.5	1.7940	24	666	20.2	48.45	22.74	8.4
11.08740	0.0	18.10	0	0.7180	6.411	100.0	1.8589	24	666	20.2	318.75	15.02	16.7
7.02259	0.0	18.10	0	0.7180	6.006	95.3	1.8746	24	666	20.2	319.98	15.70	14.2
12.04820	0.0	18.10	0	0.6140	5.648	87.6	1.9512	24	666	20.2	291.55	14.10	20.8
7.05042	0.0	18.10	0	0.6140	6.103	85.1	2.0218	24	666	20.2	2.52	23.29	13.4
8.79212	0.0	18.10	0	0.5840	5.565	70.6	2.0635	24	666	20.2	3.65	17.16	11.7
15.86030	0.0	18.10	0	0.6790	5.896	95.4	1.9096	24	666	20.2	7.68	24.39	8.3
12.24720	0.0	18.10	0	0.5840	5.837	59.7	1.9976	24	666	20.2	24.65	15.69	10.2
37.66190	0.0	18.10	0	0.6790	6.202	78.7	1.8629	24	666	20.2	18.82	14.52	10.9
7.36711	0.0	18.10	0	0.6790	6.193	78.1	1.9356	24	666	20.2	96.73	21.52	11.0
9.33889	0.0	18.10	0	0.6790	6.380	95.6	1.9682	24	666	20.2	60.72	24.08	9.5
8.49213	0.0	18.10	0	0.5840	6.348	86.1	2.0527	24	666	20.2	83.45	17.64	14.5
10.06230	0.0	18.10	0	0.5840	6.833	94.3	2.0882	24	666	20.2	81.33	19.69	14.1
6.44405	0.0	18.10	0	0.5840	6.425	74.8	2.2004	24	666	20.2	97.95	12.03	16.1
5.58107	0.0	18.10	0	0.7130	6.436	87.9	2.3158	24	666	20.2	100.19	16.22	14.3
13.91340	0.0	18.10	0	0.7130	6.208	95.0	2.2222	24	666	20.2	100.63	15.17	11.7
11.16040	0.0	18.10	0	0.7400	6.629	94.6	2.1247	24	666	20.2	109.85	23.27	13.4
14.42080	0.0	18.10	0	0.7400	6.461	93.3	2.0026	24	666	20.2	27.49	18.05	9.6
15.17720	0.0	18.10	0	0.7400	6.152	100.0	1.9142	24	666	20.2	9.32	26.45	8.7
13.67810	0.0	18.10	0	0.7400	5.935	87.9	1.8206	24	666	20.2	68.95	34.02	8.4
9.39063	0.0	18.10	0	0.7400	5.627	93.9	1.8172	24	666	20.2	396.90	22.88	12.8
22.05110	0.0	18.10	0	0.7400	5.818	92.4	1.8662	24	666	20.2	391.45	22.11	10.5
9.72418	0.0	18.10	0	0.7400	6.406	97.2	2.0651	24	666	20.2	385.96	19.52	17.1
5.66637	0.0	18.10	0	0.7400	6.219	100.0	2.0048	24	666	20.2	395.69	16.59	18.4
9.96654	0.0	18.10	0	0.7400	6.485	100.0	1.9784	24	666	20.2	386.73	18.85	15.4
12.80230	0.0	18.10	0	0.7400	5.854	96.6	1.8956	24	666	20.2	240.52	23.79	10.8
10.67180	0.0	18.10	0	0.7400	6.459	94.8	1.9879	24	666	20.2	43.06	23.98	11.8
6.28807	0.0	18.10	0	0.7400	6.341	96.4	2.0720	24	666	20.2	318.01	17.79	14.9
9.92485	0.0	18.10	0	0.7400	6.251	96.6	2.1980	24	666	20.2	388.52	16.44	12.6
9.32909	0.0	18.10	0	0.7130	6.185	98.7	2.2616	24	666	20.2	396.90	18.13	14.1
7.52601	0.0	18.10	0	0.7130	6.417	98.3	2.1850	24	666	20.2	304.21	19.31	13.0
6.71772	0.0	18.10	0	0.7130	6.749	92.6	2.3236	24	666	20.2	0.32	17.44	13.4
5.44114	0.0	18.10	0	0.7130	6.655	98.2	2.3552	24	666	20.2	355.29	17.73	15.2
5.09017	0.0	18.10	0	0.7130	6.297	91.8	2.3682	24	666	20.2	385.09	17.27	16.1
8.24809	0.0	18.10	0	0.7130	7.393	99.3	2.4527	24	666	20.2	375.87	16.74	17.8
9.51363	0.0	18.10	0	0.7130	6.728	94.1	2.4961	24	666	20.2	6.68	18.71	14.9
4.75237	0.0	18.10	0	0.7130	6.525	86.5	2.4358	24	666	20.2	50.92	18.13	14.1
4.66883	0.0	18.10	0	0.7130	5.976	87.9	2.5806	24	666	20.2	10.48	19.01	12.7
8.20058	0.0	18.10	0	0.7130	5.936	80.3	2.7792	24	666	20.2	3.50	16.94	13.5
7.75223	0.0	18.10	0	0.7130	6.301	83.7	2.7831	24	666	20.2	272.21	16.23	14.9
6.80117	0.0	18.10	0	0.7130	6.081	84.4	2.7175	24	666	20.2	396.90	14.70	20.0
4.81213	0.0	18.10	0	0.7130	6.701	90.0	2.5975	24	666	20.2	255.23	16.42	16.4
3.69311	0.0	18.10	0	0.7130	6.376	88.4	2.5671	24	666	20.2	391.43	14.65	17.7
6.65492	0.0	18.10	0	0.7130	6.317	83.0	2.7344	24	666	20.2	396.90	13.99	19.5
5.82115	0.0	18.10	0	0.7130	6.513	89.9	2.8016	24	666	20.2	393.82	10.29	20.2
7.83932	0.0	18.10	0	0.6550	6.209	65.4	2.9634	24	666	20.2	396.90	13.22	21.4
3.16360	0.0	18.10	0	0.6550	5.759	48.2	3.0665	24	666	20.2	334.40	14.13	19.9
3.77498	0.0	18.10	0	0.6550	5.952	84.7	2.8715	24	666	20.2	22.01	17.15	19.0
4.42228	0.0	18.10	0	0.5840	6.003	94.5	2.5403	24	666	20.2	331.29	21.32	19.1
15.57570	0.0	18.10	0	0.5800	5.926	71.0	2.9084	24	666	20.2	368.74	18.13	19.1
13.07510	0.0	18.10	0	0.5800	5.713	56.7	2.8237	24	666	20.2	396.90	14.76	20.1
4.34879	0.0	18.10	0	0.5800	6.167	84.0	3.0334	24	666	20.2	396.90	16.29	19.9
4.03841	0.0	18.10	0	0.5320	6.229	90.7	3.0993	24	666	20.2	395.33	12.87	19.6
3.56868	0.0	18.10	0	0.5800	6.437	75.0	2.8965	24	666	20.2	393.37	14.36	23.2
4.64689	0.0	18.10	0	0.6140	6.980	67.6	2.5329	24	666	20.2	374.68	11.66	29.8
8.05579	0.0	18.10	0	0.5840	5.427	95.4	2.4298	24	666	20.2	352.58	18.14	13.8
6.39312	0.0	18.10	0	0.5840	6.162	97.4	2.2060	24	666	20.2	302.76	24.10	13.3
4.87141	0.0	18.10	0	0.6140	6.484	93.6	2.3053	24	666	20.2	396.21	18.68	16.7
15.02340	0.0	18.10	0	0.6140	5.304	97.3	2.1007	24	666	20.2	349.48	24.91	12.0
10.23300	0.0	18.10	0	0.6140	6.185	96.7	2.1705	24	666	20.2	379.70	18.03	14.6
14.33370	0.0	18.10	0	0.6140	6.229	88.0	1.9512	24	666	20.2	383.32	13.11	21.4
5.82401	0.0	18.10	0	0.5320	6.242	64.7	3.4242	24	666	20.2	396.90	10.74	23.0
5.70818	0.0	18.10	0	0.5320	6.750	74.9	3.3317	24	666	20.2	393.07	7.74	23.7
5.73116	0.0	18.10	0	0.5320	7.061	77.0	3.4106	24	666	20.2	395.28	7.01	25.0
2.81838	0.0	18.10	0	0.5320	5.762	40.3	4.0983	24	666	20.2	392.92	10.42	21.8
2.37857	0.0	18.10	0	0.5830	5.871	41.9	3.7240	24	666	20.2	370.73	13.34	20.6
3.67367	0.0	18.10	0	0.5830	6.312	51.9	3.9917	24	666	20.2	388.62	10.58	21.2
5.69175	0.0	18.10	0	0.5830	6.114	79.8	3.5459	24	666	20.2	392.68	14.98	19.1
4.83567	0.0	18.10	0	0.5830	5.905	53.2	3.1523	24	666	20.2	388.22	11.45	20.6
0.15086	0.0	27.74	0	0.6090	5.454	92.7	1.8209	4	711	20.1	395.09	18.06	15.2
0.18337	0.0	27.74	0	0.6090	5.414	98.3	1.7554	4	711	20.1	344.05	23.97	7.0
0.20746	0.0	27.74	0	0.6090	5.093	98.0	1.8226	4	711	20.1	318.43	29.68	8.1
0.10574	0.0	27.74	0	0.6090	5.983	98.8	1.8681	4	711	20.1	390.11	18.07	13.6
0.11132	0.0	27.74	0	0.6090	5.983	83.5	2.1099	4	711	20.1	396.90	13.35	20.1
0.17331	0.0	9.69	0	0.5850	5.707	54.0	2.3817	6	391	19.2	396.90	12.01	21.8
0.27957	0.0	9.69	0	0.5850	5.926	42.6	2.3817	6	391	19.2	396.90	13.59	24.5
0.17899	0.0	9.69	0	0.5850	5.670	28.8	2.7986	6	391	19.2	393.29	17.60	23.1
0.28960	0.0	9.69	0	0.5850	5.390	72.9	2.7986	6	391	19.2	396.90	21.14	19.7
0.26838	0.0	9.69	0	0.5850	5.794	70.6	2.8927	6	391	19.2	396.90	14.10	18.3
0.23912	0.0	9.69	0	0.5850	6.019	65.3	2.4091	6	391	19.2	396.90	12.92	21.2
0.17783	0.0	9.69	0	0.5850	5.569	73.5	2.3999	6	391	19.2	395.77	15.10	17.5
0.22438	0.0	9.69	0	0.5850	6.027	79.7	2.4982	6	391	19.2	396.90	14.33	16.8
0.06263	0.0	11.93	0	0.5730	6.593	69.1	2.4786	1	273	21.0	391.99	9.67	22.4
0.04527	0.0	11.93	0	0.5730	6.120	76.7	2.2875	1	273	21.0	396.90	9.08	20.6
0.06076	0.0	11.93	0	0.5730	6.976	91.0	2.1675	1	273	21.0	396.90	5.64	23.9
0.10959	0.0	11.93	0	0.5730	6.794	89.3	2.3889	1	273	21.0	393.45	6.48	22.0
0.04741	0.0	11.93	0	0.5730	6.030	80.8	2.5050	1	273	21.0	396.90	7.88	11.9