17 支持向量机

17.1 介绍

支持向量机是1990年代有计算机科学家发明的一种有监督学习方法，使用范围较广，预测精度较高。

本章内容主要来自: (James et al. 2013): Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani(2013) An Introduction to Statistical Learning: with Applications in R, Springer.

17.2 最大分隔边界判别法

17.2.1 分隔超平面

对因变量为两分类的情形，设自变量$\boldsymbol x_i, i=1,2,\dots,n$在$\mathbb R^p$空间中，如果存在曲面将$\mathbb R^p$分隔成两部分，使得两类的样本可以分开，就有了一种简单的判别准则。超平面是最简单的分隔曲面。

在平面空间$\mathbb R^2 = \{(x_1, x_2): x_1, x_2 \in \mathbb R \}$中，超平面就是直线，其方程为 \[ \beta_0 + \beta_1 x_1 + \beta_2 x_2 = 0 \] 其中$(\beta_1, \beta_2)^T \neq \boldsymbol 0$。在平面空间$\mathbb R^2$中，直线将空间分为两个部分，分别满足$\beta_0 + \beta_1 x_1 + \beta_2 x_2 > 0$和$\beta_0 + \beta_1 x_1 + \beta_2 x_2 < 0$。

可以用其方程的法向$\boldsymbol\beta=(\beta_1, \beta_2)^T$的指向区分两个部分，设$\tilde{\boldsymbol x} = (\tilde x_1, \tilde x_2)^T$在直线上，而点$\boldsymbol x = (x_1, x_2)^T$满足$\beta_0 + \beta_1 x_1 + \beta_2 x_2 > 0$，则利用 \[\begin{aligned} \beta_0 + \beta_1 \tilde x_1 + \beta_2 \tilde x_2 =& 0 \\ \beta_0 + \beta_1 x_1 + \beta_2 x_2 >& 0 \end{aligned}\] 两式相减得 \[ (\beta_1, \beta_2) \; \left(\begin{matrix} x_1 - \tilde x_1 \\ x_2 - \tilde x_2 \end{matrix}\right) > 0 \] 用$\langle \cdot, \cdot \rangle$表示$\mathbb R^2$中的内积，则$\boldsymbol x = (x_1, x_2)^T$在满足$\beta_0 + \beta_1 x_1 + \beta_2 x_2 > 0$的半空间的充分必要条件是 \[ \langle \boldsymbol\beta, \boldsymbol x - \tilde{\boldsymbol x} \rangle > 0 \] 即从平面上的点$\tilde{\boldsymbol x}$出发到$\boldsymbol x$的向量$\boldsymbol x - \tilde{\boldsymbol x}$与分隔线的法线方向$\boldsymbol\beta=(\beta_1, \beta_2)^T$成锐角； $\tilde{\boldsymbol x} = (\tilde x_1, \tilde x_2)^T$在满足$\beta_0 + \beta_1 x_1 + \beta_2 x_2 < 0$的半空间的充分必要条件是 \[ \langle \boldsymbol\beta, \boldsymbol x - \tilde{\boldsymbol x} \rangle < 0 \] 即即从平面上的点$\tilde{\boldsymbol x}$出发到$\boldsymbol x$的向量$\boldsymbol x - \tilde{\boldsymbol x}$与分隔线的法线方向$\boldsymbol\beta=(\beta_1, \beta_2)^T$成钝角。

例如，考虑分隔线 \[ 1 + 2 x_1 + 3 x_2 = 0 \] 法线方向为$\boldsymbol\beta = (2,3)^T$, 上面的一个点$\tilde{\boldsymbol x} = (1, -1)$。参见图17.1。

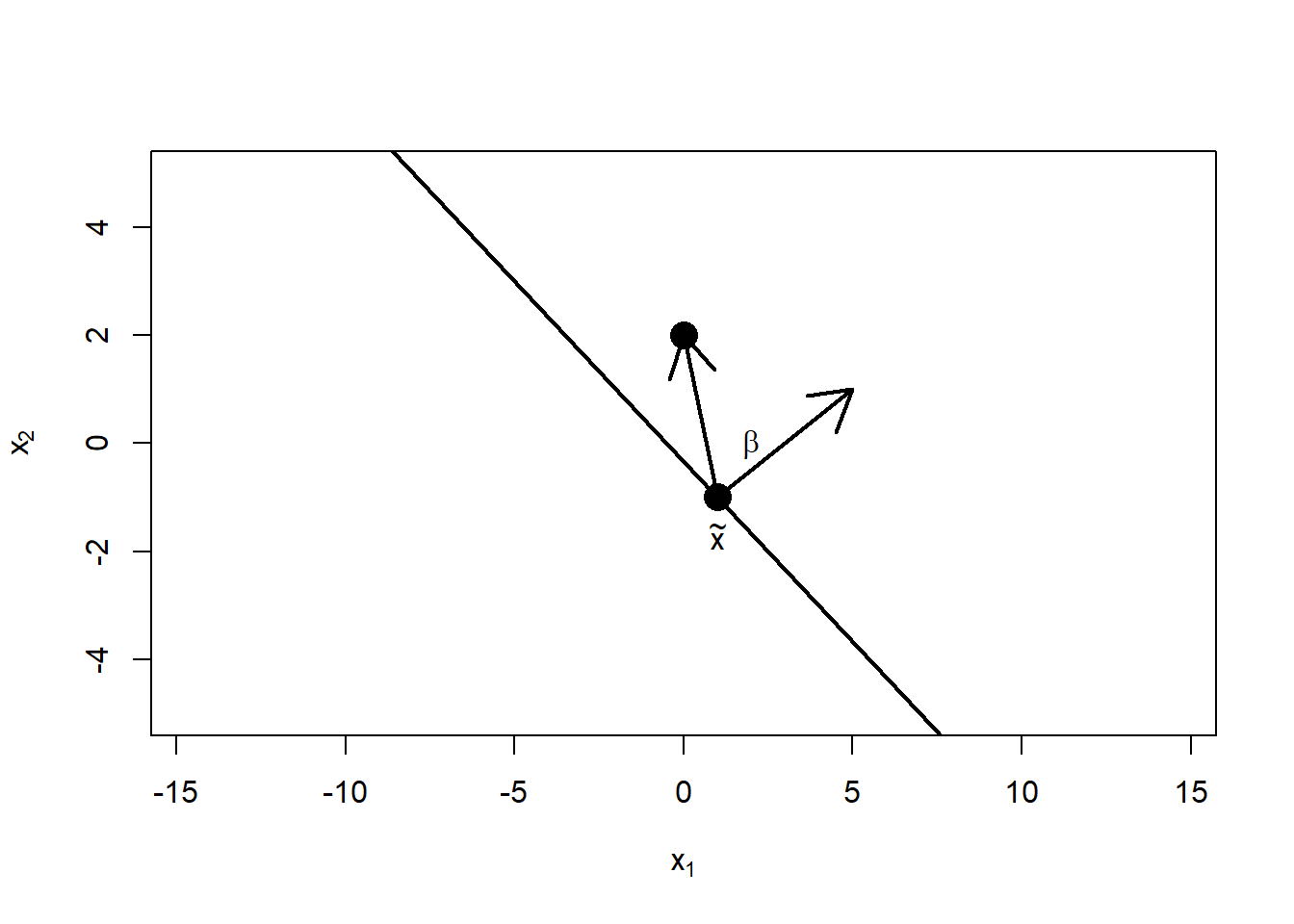
图17.1: 直线将平面分为两部分

对于自变量$\boldsymbol x \in \mathbb R^p$的情形，可以定义分隔超平面： \[ \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p = 0 \] 将$\mathbb R^p$分隔为满足 $\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p > 0$的半空间与满足 $\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p < 0$的半空间，两个空间的点可以用分隔超平面上的一个点$\tilde{\boldsymbol x}$到$\boldsymbol x$的矢量 $\boldsymbol x - \tilde{\boldsymbol x}$与超平面的法向量 $\boldsymbol\beta = (\beta_1, \dots, \beta_p)^T$的夹角是锐角还是钝角来区分，即内积$\langle \boldsymbol\beta, \boldsymbol x - \tilde{\boldsymbol x} \rangle$的正负号来区分。

设两类判别问题的自变量数据保存为矩阵$\boldsymbol X = (x_{ij})_{n \times p}$，其中的每一行为$\boldsymbol R^n$的一个点；对应于每个点有一个$y_i \in \{ -1, 1 \}$作为类别标签， $\boldsymbol y = (y_1, \dots, y_n)^T$。设法找到一个超平面将两类的点分开在两边。

例如，在图17.2中，要区分蓝色和粉红色的点。在左图中有三条直线都可以分开两种点。

knitr::include_graphics("svm-demo-seplines01.png")

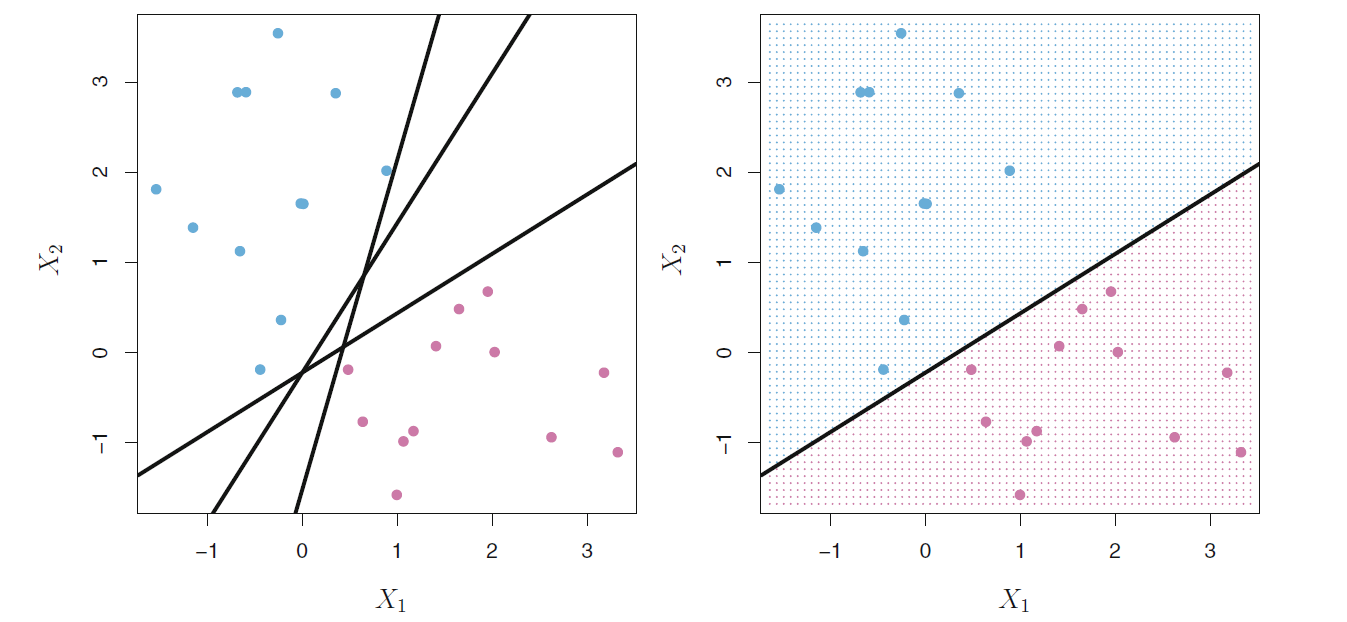
图17.2: 分隔线选择

找到的分隔线必须满足 \[\begin{aligned} & \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} > 0 \Longleftrightarrow y_i > 0 \\ & \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} < 0 \Longleftrightarrow y_i < 0 \end{aligned}\] 可以统一地写成 \[\begin{aligned} y_i (\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2}) > 0, \ i=1,2,\dots,n . \end{aligned}\]

这种要求可以推广到$\boldsymbol x_i \in \mathbb R^p$的情形。即找到超平面使得 \[ y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) > 0, \ i=1,2,\dots,n . \]

当分隔超平面存在时，就可以用$\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}$的正负号来选择$y=1$还是$-1$。对一个待判别的观测$\boldsymbol x^*$，计算 \[ f(\boldsymbol x^*) = \beta_0 + \beta_1 x_{i1}^* + \dots + \beta_p x_{ip}^* \] 就可以判别$y$的类别， $f(\boldsymbol x^*) > 0$时判为1， $f(\boldsymbol x^*) < 0$时判为-1。 $f(\boldsymbol x^*)$的绝对值大小也有意义，绝对值越大时， $\boldsymbol x^*$距离分隔边界越远，判决越可靠。如果$f(\boldsymbol x^*)$的绝对值接近于零，则点$\boldsymbol x^*$靠近分隔边界，对其判决不够可信。

17.2.2 最大分隔边界超平面

如图17.2的左图所示，只要分隔超平面能分隔开训练集的样本点，就不止有一个分隔超平面。需要找到最优的分隔超平面。想法是让两类的点都尽可能远离分隔面。对某个候选的分隔超平面，计算各个观测样本点到超平面的距离并求出最近距离，称为margin（分隔边界）。从所有的分隔超平面中求margin最大的一个（见图17.3），用这个最大边界的超平面作为判决准则，这种方法称为最大分隔边界判别法(maximal margin classifier)。

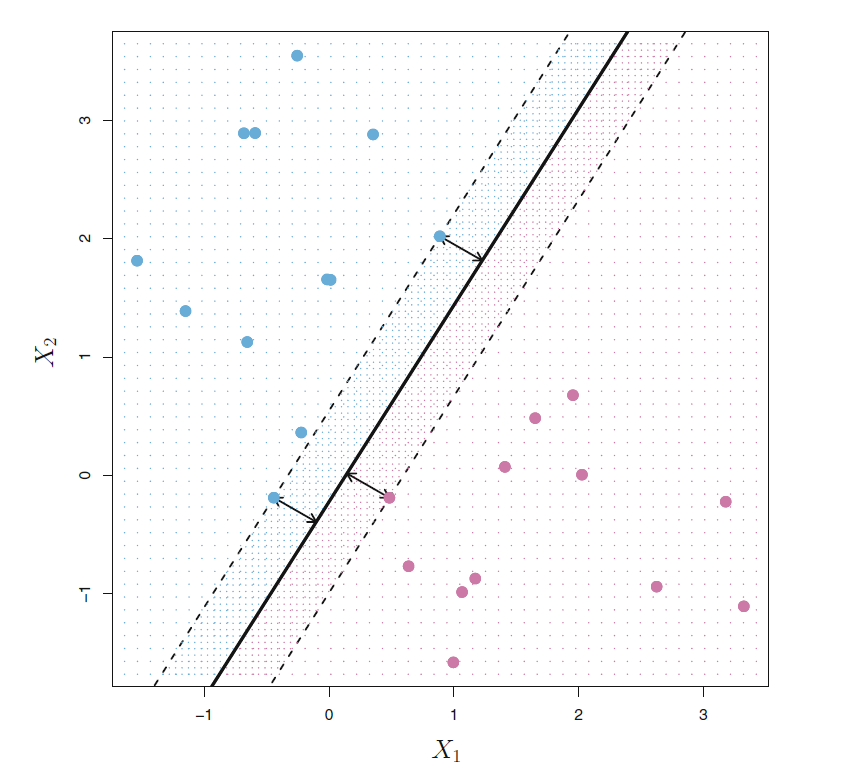
图17.3: 分隔边界

在图17.3中，有三个观测点到最优超平面的距离相等，都等于最大分隔边界（margin），这样的点称为支持向量(support vector)。这些点改变位置会使得分隔线改变位置，而其它点轻微改变位置则不会使得分隔线改变位置，除非其它点到分隔线的距离小于分隔边界了。这是最大分隔边界判别法以及后面讲到的支持向量机方法的重要性质。

17.2.3 最大分隔边界超平面的构造

设法求最大分隔边界超平面。为了标准化，令法向量$\boldsymbol\beta$长度等于1。求$\beta_0, \beta_1, \dots, \beta_p$为如下优化问题的解： \[\begin{aligned} & \max_{\beta_0, \beta_1, \dots, \beta_p} \text{分隔边界} \text{ s.t.} \\ & y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \geq \text{分隔边界}, \ i=1,2,\dots,n . \\ & \beta_1^2 + \dots + \beta_p^2 = 1 \end{aligned}\] 其中的第二个约束条件对可行的分隔超平面是不需要的约束，而$\boldsymbol\beta$长度为1的约束也不是必须的，找到长度不为1的解后除以其长度即可。不过，当$\| \boldsymbol\beta \| = 1$成立时， $y_i (\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2})$正是$\boldsymbol x_i$到分隔超平面的垂直距离。有高效的算法可以快速求解上述优化问题。

17.2.4 不能分隔的情形

如果两类的点混杂在一起，有可能任何的超平面都不能将两个类完全分开。见图17.4。这时，只能退而求其次，试图找到超平面使得两类尽可能被分开。

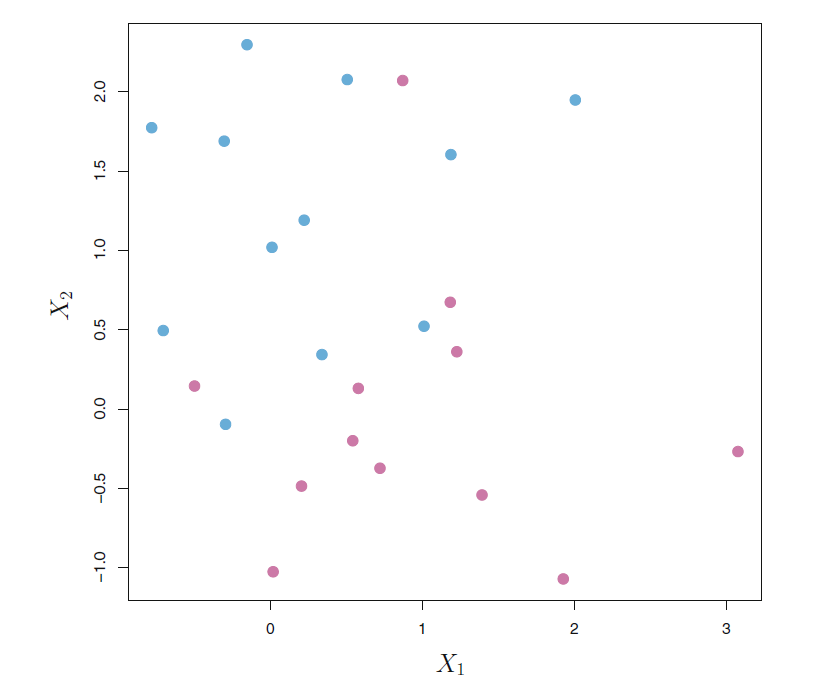
图17.4: 找不到分隔超平面的情形

17.3 支持向量判别法

17.3.1 问题

要求分隔超平面将两类完全分开有时不能做到，即使能做到，因为最大分隔边界超平面的选取过于依赖于边界处的支持向量，几个点对结果的影响过大，结果不够稳健，也容易造成过度拟合。见图17.5，右图中增加一个点后，分隔线偏离了很多，分隔边界变得很窄而且对原有点的判别效果变差了。各个点距离边界越远，判别效果越好。

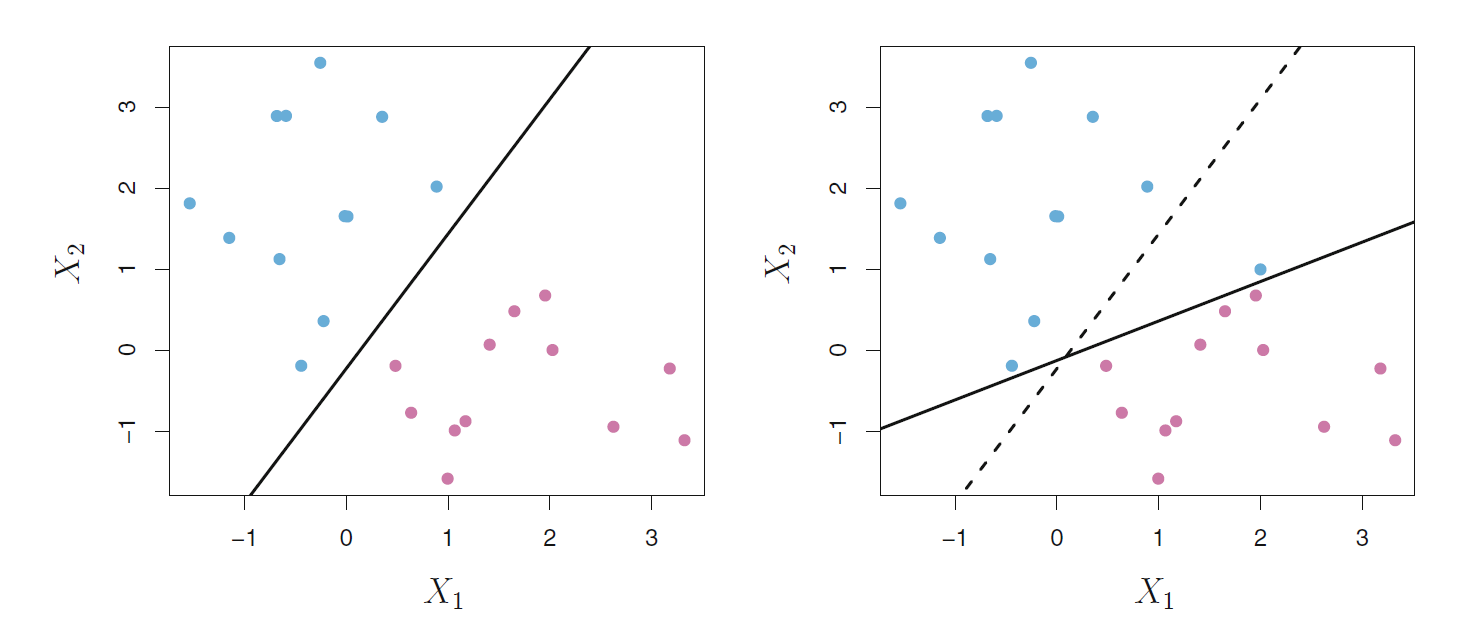
图17.5: 分隔超平面的不稳健性

解决这个问题的办法是，不严格要求能够区分所有点，而是将大多数点区分好，结果更具有稳健性，有少数点可以落在边界区域，甚至于落入分隔超平面的错误一面。这种方法称为支持向量判别法，或者软分隔边界法。见图17.6，左图中的1号和8号点进入了分隔区域，右图中的1号和8号点进入了分隔区域， 11和12号点进入了错误的一面。

knitr::include_graphics("svm-demo-softmargin01.png")

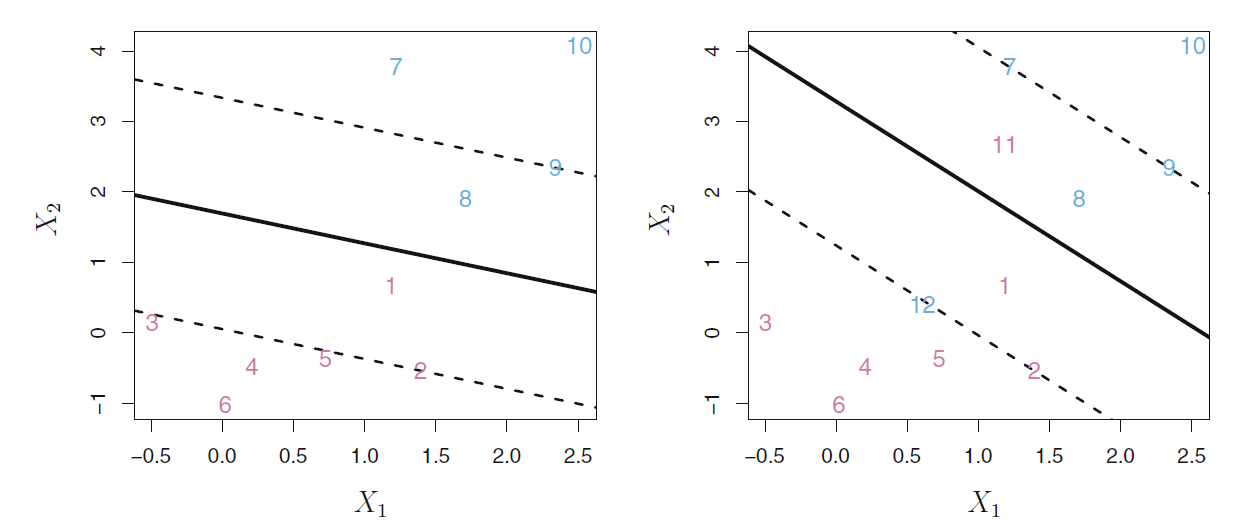
图17.6: 软分隔边界演示

17.3.2 支持向量判别法

支持向量判别法仍然求出一个分隔超平面，对待判的观测点，按其在超平面的那一面判决其类属。超平面的求法使用软分隔边界，表述为如下的优化问题： \[\begin{aligned} & \max_{\beta_0, \beta_1, \dots, \beta_p, \epsilon_1, \dots, \epsilon_n} \text{分隔边界} \text{ s.t.} \\ & y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \geq \text{分隔边界} \times (1 - \epsilon_i), \ i=1,2,\dots,n . \\ & \sum_{i=1}^p \beta_i^2 = 1, \quad\epsilon_i \geq 0, i=1,\dots,n;\ \sum_{i=1}^n \epsilon_i \leq C \end{aligned}\] 其中$C$是一个非负的调节参数， $C$越大，容许进入边界和错判的点的比例越大。 $\epsilon_1, \dots, \epsilon_n$是松弛变量，使得对点在分割边界以外的要求略微放宽。

求得上述优化问题的解以后，对新的观测$\boldsymbol x^* = (x_1^*, \dots, x_p^*)^T$, 只要计算函数 $f(\boldsymbol x^*) = \beta_0 + \beta_1 x_1^* + \dots x_p^*$，以$f(\boldsymbol x^*)$的正负号决定将因变量判入1或者-1。

优化问题中的$\epsilon_i$由第$i$个点与分隔区域的关系决定。如果$\epsilon_i = 0$，则软分隔规则对第$i$个点不起作用，第$i$个点仍然被分隔区域分开，例如图17.6右图的3, 4, 5, 6，10和2, 7, 9号点。当$0 < \epsilon_i < 1$时，第$i$个点可以进入分隔边界规定的分隔区域范围内，如第1，8号点。当$\epsilon_i > 1$时，第$i$个点可以在超平面的错误一侧，如第11, 12号点。

调节参数$C$控制将严格要求所有点在正确一侧且不能进入分隔区域的要求放松到多大程度。当$C=0$时对应于最大分隔边界判别法，不能有任何点在错误一侧，也不能进入分隔边界区域。对$C>0$，至多有$\text{floor}(C)$个点可以位于分隔超平面的错误一侧。增大$C$的值，解出的边界宽度也会增大。见图17.7，各图形对应的调节参数由大到小，过大的$C$使得错判点较多，结果方差较小，偏差较大；过小的$C$使得结果不稳健，预测方差较大，偏差较小。所以，这里的调节参数与其它有监督学习方法中的调节参数类似，应该在偏差与方差之间折衷，可以用交叉验证方法求最优调节参数值。 $C$越小，模型复杂度越高。

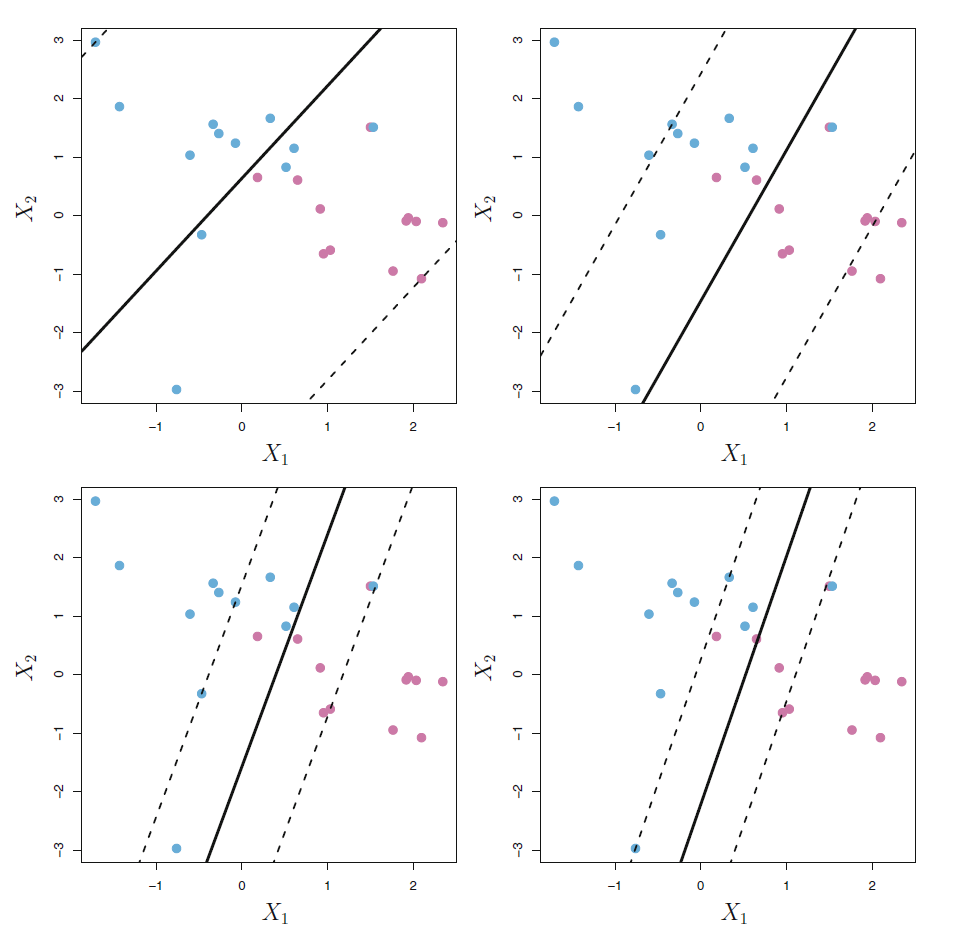
图17.7: 软分隔边界不同调节参数的影响

上面的优化问题的解有一个重要性质：最终的解仅仅依赖边界点（即落在分隔区域的边界上的点）以及进入边界区域或者进入错误一面的点，这些点称为支持向量；那些被分隔区域完全正确地区分在两边的点不起作用。

从这个性质来看条件参数$C$的影响，当$C$大的时候，分隔边界很宽，许多点进入了边界区域或者错误一面，有许多个支持向量，最终解由许多个点决定，这时解的方差较低，但对应于较简单的模型，所以可能会有较大偏差。当$C$小的时候，只有少数几个支持向量，模型稳定性差，有过度拟合危险，方差可能较大。

支持向量判别法只依赖于少数支持向量这个性质与距离判别法很不同，结果仅由靠近边界的点决定，那些离边界很远的点则不起作用；距离判别法则是由所有点决定。逻辑回归判别法与支持向量判别法有类似的性质，也是主要依赖那些边界附近的点。

17.4 支持向量机

支持向量判别法仅仅支持超平面作为分隔，对于分隔区域是曲面的情形则不能处理。支持向量机方法可以解决这个问题。

17.4.1 非线性边界方法

分隔超平面是线性边界，对于图17.8这样的分隔边界非线性的问题无法解决，其它的线性判别法也不能解决这样的非线性边界判别问题。

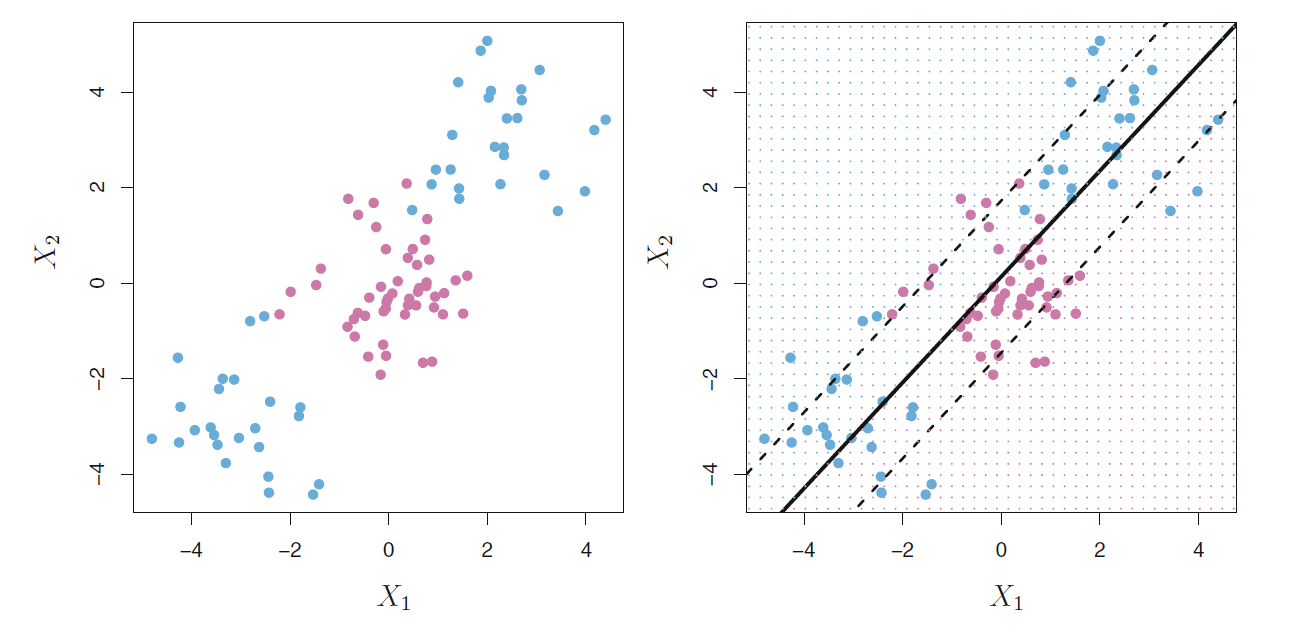
图17.8: 线性边界无法解决的例子

解决非线性问题的常用方法是增加非线性项如二次项、三次项。比如，将自变量由$x_1, \dots, x_p$增加到 \[ x_1, \dots, x_p; x_1^2, \dots, x_p^2 \] 则支持向量判别法的优化问题变成了 \[\begin{aligned} & \max_{\beta_0, \beta_{11}, \dots, \beta_{p1}, \beta_{12}, \dots, \beta_{p2}, \epsilon_1, \dots, \epsilon_n} \text{分隔边界} \text{ s.t.} \\ & y_i (\beta_0 + \sum_{j=1}^p \beta_{j1} x_{ij} + \sum_{j=1}^p \beta_{j2} x_{ij}^2) \geq \text{分隔边界} \times (1 - \epsilon_i), \ i=1,2,\dots,n . \\ & \sum_{k=1}^2 \sum_{j=1}^p \beta_{jk}^2 = 1 \\ & \epsilon_i \geq 0, \sum_{i=1}^n \epsilon_i \leq C \end{aligned}\] 这样得到的边界在$(x_1, \dots, x_p, x_1^2, \dots, x_p^2)$所在的$\mathbb R^{2p}$空间内是线性的超平面，但是在原来$(x_1, \dots, x_p)$所在的$\mathbb R^p$空间内则是由 $q(\boldsymbol x) = 0$决定的曲面， $q(\boldsymbol x)$是二次多项式函数。

还可以增加高次项和交叉项，或者考虑其它的非线性变换。增加非线性项的方法有无数多种，一一测试是不现实的，支持向量机方法则给出了一种增加非线性项的一般方法，对应的边界可以快速求解。

17.4.2 支持向量机

支持向量机利用了Hilbert空间的方法将线性问题扩展为非线性问题。线性的支持向量判别法可以通过$\mathbb R^p$的内积转化为如下的等价方法：

判别函数可以表示成 \[\begin{aligned} f(\boldsymbol x) = \beta_0 + \sum_{i=1}^n \alpha_i \langle \boldsymbol x, \boldsymbol x_i \rangle \end{aligned}\] 其中$\beta_0, \alpha_1, \dots, \alpha_n$是待定参数。为了估计参数，不需要用到各$\boldsymbol x_i$的具体值，而只需要其两两的内积值，而且在判别函数中只有支持向量对应的$\alpha_i$才非零，记$\mathcal S$为支持向量点集，则线性判别函数为 \[\begin{aligned} f(\boldsymbol x) = \beta_0 + \sum_{i \in \mathcal S} \alpha_i \langle \boldsymbol x, \boldsymbol x_i \rangle . \end{aligned}\]

支持向量机方法将$\mathbb R^p$中的内积推广为如下的核函数值： \[\begin{aligned} K(\boldsymbol x, \boldsymbol x') \end{aligned}\] 核函数$K(\boldsymbol x, \boldsymbol x')$, $\boldsymbol x, \boldsymbol x' \in \mathbb R^p$ 是度量两个观测点$\boldsymbol x, \boldsymbol x'$的相似程度的函数。比如，取 \[\begin{aligned} K(\boldsymbol x, \boldsymbol x') = \sum_{j=1}^p x_j x_j' \end{aligned}\] 就又回到了线性的支持向量判别法。

利用核代替内积后，判别法的判别函数变成 \[\begin{aligned} f(\boldsymbol x) = \beta_0 + \sum_{i \in \mathcal S} \alpha_i K(\boldsymbol x, \boldsymbol x_i) . \end{aligned}\]

核有多种取法。例如，取 \[\begin{aligned} K(\boldsymbol x, \boldsymbol x') = \left\{ 1 + \sum_{j=1}^p x_j x_j' \right\}^d \end{aligned}\] 其中$d>1$为正整数，称为多项式核，则结果是多项式边界的判别法，本质上是对线性的支持向量方法添加了高次项和交叉项。前一小节就是$d=2$时的多项式核。可以看出，增加了二次项以后，将$\mathbb R^p$空间的点$\boldsymbol x = (x_1, \dots, x_p)$映射到了$\mathbb R^{2p}$空间$\phi(\boldsymbol x) = (x_1, \dots, x_p, x_1^2, \dots, x_p^2)$，考虑在高维的$\mathbb R^{2p}$空间的分隔超平面，但在$\boldsymbol x$所在的$\mathbb R^p$这是分隔曲面。判决函数可以表示为$\mathbb R^{2p}$中$\phi(\boldsymbol x) = (x_1, \dots, x_p, x_1^2, \dots, x_p^2)$的线性组合，这又可以表示为内积形式： \[ f(\boldsymbol x) = \beta_0 + \sum_{i \in \mathcal S} \alpha_i \langle \phi(\boldsymbol x), \phi(\boldsymbol x_i) \rangle = \beta_0 + \sum_{i \in \mathcal S} \alpha_i K(\boldsymbol x, \boldsymbol x_i) . \]

理论研究表明，给定核函数$K(\cdot, \cdot)$后，必存在一个Hilbert空间$H$使得$\phi(\boldsymbol x) \in H$，且 \[ K(\boldsymbol x, \boldsymbol x') = \langle \phi(\boldsymbol x), \phi(\boldsymbol x') \rangle_H . \] 于是，给了一个核函数，就可以将原来的$\mathbb R^p$空间的判别问题，通过映射$\phi$映射为了$H$空间的线性判别问题，这样得到的判别函数在$H$空间是线性的，但在原始的$\mathbb R^p$中是非线性的。

训练这样的SVM时只要计算观测两两的$\binom{n}{2}$个核函数值。为什么不直接增加非线性项？原因是计算这些核函数值计算量是确定的，而增加许多非线性项，则可能有很大的计算量，映射$\phi(\boldsymbol x)$的值域$H$可能是高维甚至于无穷维空间，计算核函数值而不是计算映射$\phi(\boldsymbol x)$效率更高。

支持向量机的理论基于再生核希尔伯特空间(RKHS)，可参见(Trevor Hastie 2009)节5.8和节12.3.3。

图17.9的左图是用多项式核解决非线性边界判别问题的演示。两条粗实线是分隔曲面，虚线是边界区域的边缘。

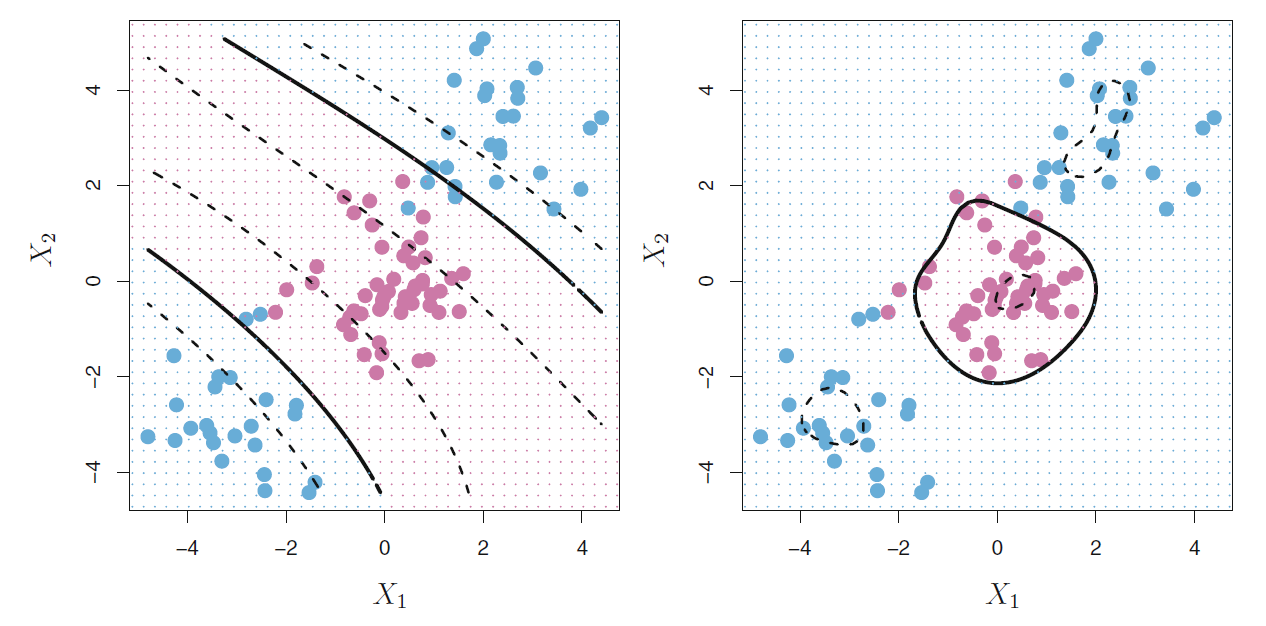
图17.9: 多项式核与径向核判别的例子

另一种常用的核是径向核(radial kernel)，定义为 \[\begin{aligned} K(\boldsymbol x, \boldsymbol x') = \exp\left\{ - \gamma \sum_{j=1}^p (x_j - x_j')^2 \right\} \end{aligned}\] $\gamma$为正常数。当$\boldsymbol x$和$\boldsymbol x'$分别落在以原点为中心的两个超球面上时，其核函数值不变。 17.9的右图是用径向核支持向量机进行判别的演示。

使用径向核时，判别函数为 \[\begin{aligned} f(\boldsymbol x) = \beta_0 + \sum_{i \in \mathcal S} \alpha_i \exp\left\{ - \gamma \sum_{j=1}^p (x_{j} - x_{ij})^2 \right\} \end{aligned}\] 对一个待判别的观测$\boldsymbol x^*$，如果$\boldsymbol x^*$距离训练观测点$\boldsymbol x_i$较远，则$K(\boldsymbol x^*, \boldsymbol x_i)$的值很小， $\boldsymbol x_i$对$\boldsymbol x^*$的判别基本不起作用。这样的性质使得径向核方法具有很强的局部性，只有离$\boldsymbol x^*$很近的点才对其判别起作用。

17.5 支持向量机用于Heart数据

考虑心脏病数据Heart的判别。共297个观测，随机选取其中207个作为训练集， 90个作为测试集。

set.seed(1)
Heart <- read.csv(
  'Heart.csv', header=TRUE, row.names=1, 
  stringsAsFactors=TRUE)
d <- na.omit(Heart)
set.seed(1)
train_id <- sample(nrow(d), size=round(0.5*nrow(d)))
train <- rep(FALSE, nrow(d))
train[train_id] <- TRUE
test <- (!train)
d[["AHD"]] <- factor(d[["AHD"]], levels=c("No", "Yes"))

定义一个错判率函数：

classifier.error <- function(truth, pred){
  tab1 <- table(truth, pred)
  err <- 1 - sum(diag(tab1))/sum(c(tab1))
  err
}

17.5.1 线性判别与线性的支持向量机

使用e1071包的svm()函数进行支持向量判别和SVM判别。为了进行判别而不是回归，需要将因变量值设为因子。

在训练集上同时使用线性判别法(LDA)和支持向量判别法。

先进行线性判别，用线性判别自动确定的判别界：

res.ld <- lda(AHD ~ ., data=d[train,], prior=rep(1/2, 2))
fit.ld <- predict(res.ld)$class
tab1 <- table(truth=d[train,"AHD"], fitted=fit.ld); tab1
##      fitted
## truth No Yes
##   No  75   8
##   Yes 12  53
cat("LDA错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## LDA错判率： 0.14

支持向量判别法就是SVM取多项式核，阶数$d=1$的情形。需要一个调节参数cost， cost越大，分隔边界越窄，过度拟合危险越大。

先随便取调节参数cost=1试验支持向量判别法：

res.svc <- svm(
  AHD ~ ., data=d[train,], 
  kernel="linear", cost=1, scale=TRUE)
fit.svc <- predict(res.svc)
summary(res.svc)
## 
## Call:
## svm(formula = AHD ~ ., data = d[train, ], kernel = "linear", cost = 1, scale = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  1 
## 
## Number of Support Vectors:  63
## 
##  ( 33 30 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  No Yes

计算拟合结果并计算错判率：

tab1 <- table(truth=d[train,"AHD"], fitted=fit.svc); tab1
##      fitted
## truth No Yes
##   No  75   8
##   Yes 13  52
cat("SVC错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## SVC错判率： 0.14

e1071函数提供了tune()函数，可以在训练集上用十折交叉验证选择较好的调节参数。

set.seed(101)
res.tune <- tune(
  svm, AHD ~ ., 
  data=d[train,], kernel="linear", scale=TRUE,
  ranges=list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100, 1000)))
summary(res.tune)
## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost
##   0.1
## 
## - best performance: 0.1957143 
## 
## - Detailed performance results:
##    cost     error dispersion
## 1 1e-03 0.4376190 0.13728920
## 2 1e-02 0.1957143 0.09619755
## 3 1e-01 0.1957143 0.10263473
## 4 1e+00 0.2161905 0.10304510
## 5 5e+00 0.2361905 0.08357712
## 6 1e+01 0.2428571 0.07684901
## 7 1e+02 0.2495238 0.09315716
## 8 1e+03 0.2495238 0.09315716

找到的最优调节参数为0.1，可以用res.tune$best.model获得对应于最优调节参数的模型：

summary(res.tune$best.model)
## 
## Call:
## best.tune(method = svm, train.x = AHD ~ ., data = d[train, ], ranges = list(cost = c(0.001, 0.01, 
##     0.1, 1, 5, 10, 100, 1000)), kernel = "linear", scale = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  0.1 
## 
## Number of Support Vectors:  72
## 
##  ( 37 35 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  No Yes

在测试集上测试两种方法：

pred.ld <- predict(res.ld, d[test,])$class
tab1 <- table(truth=d[test,"AHD"], predict=pred.ld); tab1
##      predict
## truth No Yes
##   No  67  10
##   Yes 13  59
cat("LDA错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## LDA错判率： 0.15

pred.svc <- predict(res.tune$best.model, newdata=d[test,])
tab1 <- table(truth=d[test,"AHD"], predict=pred.svc); tab1
##      predict
## truth No Yes
##   No  71   6
##   Yes 18  54
cat("SVC错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## SVC错判率： 0.16

可见两种方法表现相近，在测试集上错误率都比在训练集上错误率高。

线性判别法和支持向量判别法的判别函数都是 $\hat f(\boldsymbol x) = \hat\beta_0 + \hat\beta_1 x_1 + \dots + \hat\beta_p x_p$这样的线性函数，只不过模型参数不同。

17.5.2 ROC曲线分析

关于敏感度、特异度、真阳性率、假阳性率、ROC、AUC的概念参见7.5。

图17.10做出了Heart数据的训练集上LDA(线性判别)和SVC(线性支持向量机)的ROC曲线。两种方法效果相近。

library (ROCR)
pred.ld <- predict(res.ld, newdata=d[train,], 
                   decision.values = TRUE)
decf.ld <- pred.ld$posterior[,"Yes"]
predobj <- prediction(decf.ld, d[train, "AHD"], 
                      label.ordering=c("No", "Yes"))
perf <- performance(predobj, "tpr", "fpr")
plot(perf, main="训练数据的ROC", col="cyan")

pred.svc <- predict(
  res.tune$best.model, 
  newdata=d[train,], 
  decision.values = TRUE)
decf.svc <- attributes(pred.svc)$decision.values
predobj <- prediction(
  decf.svc, d[train, "AHD"], 
  label.ordering=c("No", "Yes"))
perf <- performance(predobj, "tpr", "fpr")
plot(perf, add=TRUE, col="blue")
legend("bottomright", lty=1, col=c("cyan", "blue"),
       legend=c("LDA", "SVC"))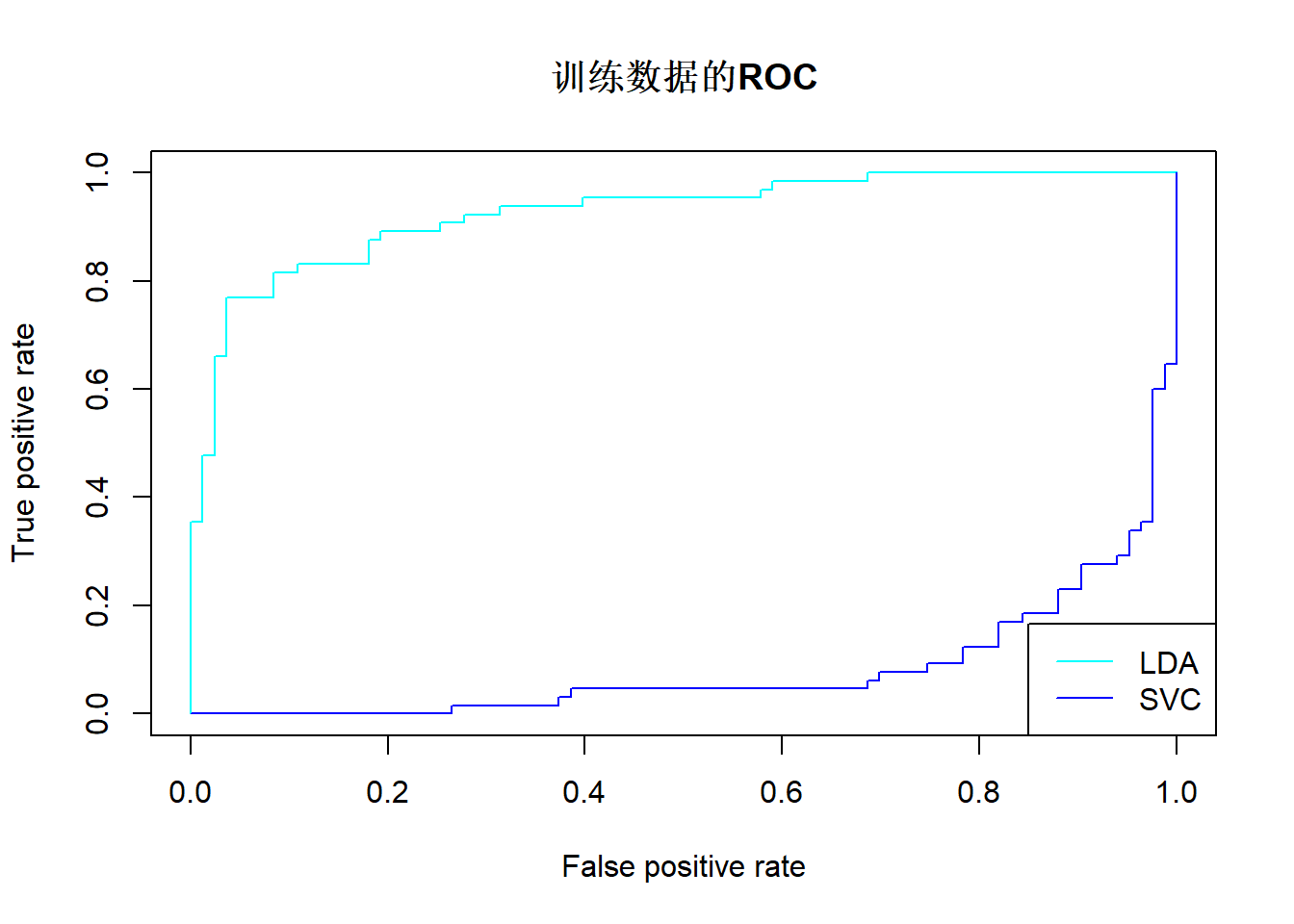

图17.10: Heart训练数据用LDA和SVC判别的ROC曲线

17.5.3 多项式核SVM

用多项式核的SVM建模。用二阶多项式，参数order=2。

res.svm1 <- svm(AHD ~ ., data=d[train,], kernel="polynomial", 
                order=2, cost=0.1, scale=TRUE)
fit.svm1 <- predict(res.svm1)
summary(res.svm1)
## 
## Call:
## svm(formula = AHD ~ ., data = d[train, ], kernel = "polynomial", order = 2, cost = 0.1, scale = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  polynomial 
##        cost:  0.1 
##      degree:  3 
##      coef.0:  0 
## 
## Number of Support Vectors:  138
## 
##  ( 73 65 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  No Yes
tab1 <- table(truth=d[train,"AHD"], fitted=fit.svm1); tab1
##      fitted
## truth No Yes
##   No  83   0
##   Yes 63   2
cat("2阶多项式核SVM错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 2阶多项式核SVM错判率： 0.43

尝试找到调节参数cost的最优值：

set.seed(101)
res.tune2 <- tune(
  svm, AHD ~ ., data=d[train,], kernel="polynomial", 
  order=2, scale=TRUE,
  ranges=list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100, 1000)))
summary(res.tune2)
## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost
##     1
## 
## - best performance: 0.23 
## 
## - Detailed performance results:
##    cost     error dispersion
## 1 1e-03 0.4376190 0.13728920
## 2 1e-02 0.4376190 0.13728920
## 3 1e-01 0.4309524 0.12609310
## 4 1e+00 0.2300000 0.06544805
## 5 5e+00 0.2442857 0.10034082
## 6 1e+01 0.2580952 0.10844418
## 7 1e+02 0.2709524 0.09656353
## 8 1e+03 0.2709524 0.09656353
fit.svm2 <- predict(res.tune2$best.model)
tab1 <- table(truth=d[train,"AHD"], fitted=fit.svm2); tab1
##      fitted
## truth No Yes
##   No  82   1
##   Yes 21  44
cat("2阶多项式核最优参数SVM错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 2阶多项式核最优参数SVM错判率： 0.15

看这个最优调节参数的模型在测试集上的表现：

pred.svm2 <- predict(res.tune2$best.model, d[test,])
tab1 <- table(truth=d[test,"AHD"], predict=pred.svm2); tab1
##      predict
## truth No Yes
##   No  73   4
##   Yes 33  39
cat("2阶多项式核最优参数SVM测试集错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 2阶多项式核最优参数SVM测试集错判率： 0.25

在测试集上的表现与线性方法相近。

17.5.4 径向核SVM

径向核需要的参数为$\gamma$值。取参数gamma=0.1。

res.svm3 <- svm(
  AHD ~ ., data=d[train,], kernel="radial", 
  gamma=0.1, cost=0.1, scale=TRUE)
fit.svm3 <- predict(res.svm3)
summary(res.svm3)
## 
## Call:
## svm(formula = AHD ~ ., data = d[train, ], kernel = "radial", gamma = 0.1, cost = 0.1, scale = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  0.1 
## 
## Number of Support Vectors:  134
## 
##  ( 69 65 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  No Yes
tab1 <- table(truth=d[train,"AHD"], fitted=fit.svm3); tab1
##      fitted
## truth No Yes
##   No  82   1
##   Yes 38  27
cat("径向核（gamma=0.1, cost=0.1）SVM错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 径向核（gamma=0.1, cost=0.1）SVM错判率： 0.26

选取最优cost, gamma调节参数：

set.seed(101)
res.tune4 <- tune(
  svm, AHD ~ ., data=d[train,], kernel="radial", 
  scale=TRUE,
  ranges=list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100, 1000),
              gamma=c(0.1, 0.01, 0.001)))
summary(res.tune4)
## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma
##   100 0.001
## 
## - best performance: 0.1895238 
## 
## - Detailed performance results:
##     cost gamma     error dispersion
## 1  1e-03 0.100 0.4376190 0.13728920
## 2  1e-02 0.100 0.4376190 0.13728920
## 3  1e-01 0.100 0.3095238 0.11133764
## 4  1e+00 0.100 0.2376190 0.08895831
## 5  5e+00 0.100 0.2161905 0.08749474
## 6  1e+01 0.100 0.2300000 0.09074174
## 7  1e+02 0.100 0.2366667 0.08512585
## 8  1e+03 0.100 0.2366667 0.08512585
## 9  1e-03 0.010 0.4376190 0.13728920
## 10 1e-02 0.010 0.4376190 0.13728920
## 11 1e-01 0.010 0.4376190 0.13728920
## 12 1e+00 0.010 0.1957143 0.07931586
## 13 5e+00 0.010 0.2166667 0.08336734
## 14 1e+01 0.010 0.2095238 0.08068740
## 15 1e+02 0.010 0.2504762 0.07879797
## 16 1e+03 0.010 0.2442857 0.11415447
## 17 1e-03 0.001 0.4376190 0.13728920
## 18 1e-02 0.001 0.4376190 0.13728920
## 19 1e-01 0.001 0.4376190 0.13728920
## 20 1e+00 0.001 0.4100000 0.15149295
## 21 5e+00 0.001 0.1957143 0.09619755
## 22 1e+01 0.001 0.2023810 0.08245570
## 23 1e+02 0.001 0.1895238 0.09464897
## 24 1e+03 0.001 0.2157143 0.08670939

fit.svm4 <- predict(res.tune4$best.model)
tab1 <- table(truth=d[train,"AHD"], fitted=fit.svm4); tab1
##      fitted
## truth No Yes
##   No  76   7
##   Yes 13  52
cat("径向核最优参数SVM错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 径向核最优参数SVM错判率： 0.14

看这个最优调节参数的模型在测试集上的表现：

pred.svm4 <- predict(res.tune4$best.model, d[test,])
tab1 <- table(truth=d[test,"AHD"], predict=pred.svm2); tab1
##      predict
## truth No Yes
##   No  73   4
##   Yes 33  39
cat("径向核最优参数SVM测试集错判率：", 
    round((tab1[1,2] + tab1[2,1])/ sum(c(tab1)), 2), "\n")
## 径向核最优参数SVM测试集错判率： 0.25

与线性方法结果相近。

17.6 多分类的支持向量机

当因变量不止两个类的时候，从分隔超平面推广过来的支持向量机分类方法很难直接推广到多个类。所以最常用的方法是按两类处理，或者是两两判别，或者是一个类相对于其余类判别。

17.6.1 两两判别

设因变量有$K$个类，为每两个类都分别用SVM构造判别函数，得到$m= {{K}\choose{2}}=K(K-1)/2$个判别函数。对于待判样品$\boldsymbol x^*$，用这些判别函数每一个都判一遍，得到$m$个判别结果，然后这$m$个结果投票，那个类别的票最高就判入哪一类。

17.6.2 一对多判别

设因变量有K个类，对其中的每一个类，都以此类以及此类之外的其它类作为一个两类判别问题，建立$K$个判别函数。对于待判样品$\boldsymbol x^*$，计算$K$个判别函数值，以判别函数值最大的类作为最后的判别结果。

17.6.3 多分类支持向量机鸢尾花数据计算实例

考虑著名的鸢尾花数据集的判别问题。所有数据用作训练集合。

取径向基，先用指定的调整参数：

res.msvm1 <- svm(Species ~ ., data=iris, kernel="radial", 
                 gamma=0.01, cost=1, scale=TRUE)
summary(res.msvm1)
## 
## Call:
## svm(formula = Species ~ ., data = iris, kernel = "radial", gamma = 0.01, cost = 1, scale = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  1 
## 
## Number of Support Vectors:  109
## 
##  ( 19 49 41 )
## 
## 
## Number of Classes:  3 
## 
## Levels: 
##  setosa versicolor virginica
fit.msvm1 <- predict(res.msvm1)
tab1 <- table(truth=iris[,"Species"], fitted=fit.msvm1); tab1
##             fitted
## truth        setosa versicolor virginica
##   setosa         50          0         0
##   versicolor      0         46         4
##   virginica       0         11        39
cat("径向核（gamma=0.01, cost=1）多类SVM错判率：", 
    round(1 - (sum(diag(tab1)))/ sum(c(tab1)), 2), "\n")
## 径向核（gamma=0.01, cost=1）多类SVM错判率： 0.1

对cost和gamma参数用tune()函数寻找最优值：

res.tune5 <- tune(
  svm, Species ~ ., data=iris, kernel="radial", 
  scale=TRUE,
  ranges=list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100, 1000),
              gamma=c(0.1, 0.01, 0.001)))
summary(res.tune5)
## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma
##    10   0.1
## 
## - best performance: 0.03333333 
## 
## - Detailed performance results:
##     cost gamma      error dispersion
## 1  1e-03 0.100 0.70666667 0.23136738
## 2  1e-02 0.100 0.70666667 0.23136738
## 3  1e-01 0.100 0.10666667 0.04661373
## 4  1e+00 0.100 0.04666667 0.06324555
## 5  5e+00 0.100 0.04000000 0.06440612
## 6  1e+01 0.100 0.03333333 0.04714045
## 7  1e+02 0.100 0.05333333 0.06126244
## 8  1e+03 0.100 0.06666667 0.06285394
## 9  1e-03 0.010 0.71333333 0.21093560
## 10 1e-02 0.010 0.71333333 0.21093560
## 11 1e-01 0.010 0.57333333 0.23768430
## 12 1e+00 0.010 0.08666667 0.06324555
## 13 5e+00 0.010 0.04000000 0.05621827
## 14 1e+01 0.010 0.04000000 0.05621827
## 15 1e+02 0.010 0.04000000 0.04661373
## 16 1e+03 0.010 0.05333333 0.05258738
## 17 1e-03 0.001 0.71333333 0.21093560
## 18 1e-02 0.001 0.71333333 0.21093560
## 19 1e-01 0.001 0.71333333 0.21093560
## 20 1e+00 0.001 0.54666667 0.21727834
## 21 5e+00 0.001 0.10666667 0.07166451
## 22 1e+01 0.001 0.08000000 0.06126244
## 23 1e+02 0.001 0.04000000 0.05621827
## 24 1e+03 0.001 0.03333333 0.04714045

fit.msvm2 <- predict(res.tune5$best.model)
tab1 <- table(truth=iris[,"Species"], fitted=fit.msvm2); tab1
##             fitted
## truth        setosa versicolor virginica
##   setosa         50          0         0
##   versicolor      0         47         3
##   virginica       0          0        50
cat("径向核最优参数多类SVM错判率：", 
    round(1 - (sum(diag(tab1)))/ sum(c(tab1)), 2), "\n")
## 径向核最优参数多类SVM错判率： 0.02

注意这个错判率是拟合结果，拟合结果一般比测试结果要乐观一些。

17.6.4 多分类支持向量机基因数据计算实例

ISLR包中的Khan数据是基因数据，每个观测对应于一个组织标本的数据，这些标本分为4类，对应于4种小圆蓝色细胞瘤。变量xtrain和ytrain是训练样本， xtest和ytest是测试样本。

str(Khan)
## List of 4
##  $ xtrain: num [1:63, 1:2308] 0.7733 -0.0782 -0.0845 0.9656 0.0757 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:63] "V1" "V2" "V3" "V4" ...
##   .. ..$ : NULL
##  $ xtest : num [1:20, 1:2308] 0.14 1.164 0.841 0.685 -1.956 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:20] "V1" "V2" "V4" "V6" ...
##   .. ..$ : NULL
##  $ ytrain: num [1:63] 2 2 2 2 2 2 2 2 2 2 ...
##  $ ytest : num [1:20] 3 2 4 2 1 3 4 2 3 1 ...
table(Khan$ytrain)
## 
##  1  2  3  4 
##  8 23 12 20
table(Khan$ytest)
## 
## 1 2 3 4 
## 3 6 6 5
d2a <- data.frame(x = Khan$xtrain, y=as.factor(Khan$ytrain))
d2b <- data.frame(x = Khan$xtest, y=as.factor(Khan$ytest))

因为自变量个数有两千多个，所以自变量空间已经维数很高，不需要用多项式或者径向基增加维度。直接用线性的SVM。

res.tune6 <- tune(
  svm, y ~ ., data=d2a, kernel="linear", 
  scale=TRUE,
  ranges=list(cost=c(0.0001, 0.001, 0.01, 0.1, 1, 5, 10, 100)))
summary(res.tune6)
## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##   cost
##  0.001
## 
## - best performance: 0.01666667 
## 
## - Detailed performance results:
##    cost      error dispersion
## 1 1e-04 0.40952381 0.22637837
## 2 1e-03 0.01666667 0.05270463
## 3 1e-02 0.01666667 0.05270463
## 4 1e-01 0.01666667 0.05270463
## 5 1e+00 0.01666667 0.05270463
## 6 5e+00 0.01666667 0.05270463
## 7 1e+01 0.01666667 0.05270463
## 8 1e+02 0.01666667 0.05270463

在训练集上的判别效果：

fit.msvm3 <- predict(res.tune6$best.model)
cat("最优参数多类线性SVM训练集错判率：", 
    round(classifier.error(d2a$y, fit.msvm3), 2), "\n")
## 最优参数多类线性SVM训练集错判率： 0

在训练集上没有错误。在测试集上：

pred.msvm3 <- predict(res.tune6$best.model, newdata=d2b)
table(truth=d2b$y, prediction=pred.msvm3)
##      prediction
## truth 1 2 3 4
##     1 3 0 0 0
##     2 0 6 0 0
##     3 0 2 4 0
##     4 0 0 0 5
cat("最优参数多类线性SVM测试集错判率：", 
    round(classifier.error(d2b$y, pred.msvm3), 2), "\n")
## 最优参数多类线性SVM测试集错判率： 0.1

在测试集中，只有第3类有两个样品误判到了第2类。可见即使用了十折交叉验证来选择调节参数，训练集上的错误率估计仍然过于乐观了。

注意这里的基因数据是典型的$n < p$问题（观测数少于自变量数），无法执行全集的线性判别，如果用线性判别只能用某种逐步判别方法。

17.7 附录：特征空间、正定核、再生核希尔伯特空间

参考：

Jean Gallier and Jocelyn Quaintance(2019). Algebra, Topology, Differential Calculus, and Optimization Theory For Computer Science and Machine Learning, Chapter 54. http://www.cis.upenn.edu/~jean/math-basics.pdf
Mohri, Mehryar / Rostamizadeh, Afshin / Talwalkar, Ameet(2018). Foundations of Machine Learning, Chpater 6. 2nd Ed., MIT Press. https://cs.nyu.edu/~mohri/mlbook/

17.7.1 正定核

17.7.1.1 介绍

设$\mathcal X$为非空的观测集合，要考虑$\mathcal X$的许多非线性变换作为新的自变量，希望将$\mathcal X$的非线性函数转换为经过非线性变换后的线性函数。设存在映射$\phi(x): \mathcal X \to \mathcal H$，其中$\mathcal H$为有限维内积空间或无穷维希尔伯特空间，具有内积$\langle \cdot, \cdot \rangle_{\mathcal H}$。称$\mathcal H$为$\mathcal X$的特征空间(feature space)，称$\phi$为特征映射(feature map)。 $\mathcal H$可以是复数域或实数域上的希尔伯特空间。

定义 \[ K(x, y) = \langle \phi(x), \phi(y) \rangle_{\mathcal H}, \ \forall x, y \in \mathcal X, \] 称$K(\cdot, \cdot)$为一个对称正定核函数(positive definite symmetric kernel, PDS核)，简称正定核。

例17.1 设$\mathcal X = \mathbb R^2$， $\phi(x) = (x_1^2, x_2^2, \sqrt{2} x_1 x_2) \in \mathbb R^3$。令 \[ K(x, y) = \langle \phi(x), \phi(y) \rangle . \] 有 \[\begin{aligned} K(x, y) =& x_1^2 y_1^2 + x_2^2 y_2^2 + \sqrt{2} x_1 x_2 \sqrt{2} y_1 y_2 \\ =& (x_1 y_1 + x_2 y_2)^2 \\ =& \langle x, y \rangle^2 . \end{aligned}\] $K(x,y)$是一个正定核，涉及到从原始空间$\mathbb R^2$到特征空间$\mathbb R^3$的映射$\phi(\cdot)$。

对任意$n\geq 1$和任意$x_1, x_2, \dots, x_n \in \mathcal X$，有 \[ \sum_{i=1}^n \sum_{j=1}^n x_i K(x_i, x_j) \bar x_j \geq 0 . \]

这蕴含$K(x, x) \geq 0$, $K(x, y) = \overline{K(y, x)}$，不要求$x \neq 0$时$K(x, x) > 0$，所以严格来说应该称为“对称半正定核”，但是“正定核”的叫法已经广泛采用。

令 \[ K_S = (K(x_j, x_i))_{i=1,\dots, n; j=1, \dots,n}, \] 则$K_S$是厄米特阵： \[ \boldsymbol u^* K_S \boldsymbol u \geq 0, \ \forall \boldsymbol u \in \mathbb C^n . \]

这给出了正定核的等价定义：设$K(x, y)$是$\mathcal X \times \mathcal X \to \mathbb C$的映射，对任意$n$和任意$x_1, x_2, \dots, x_n \in \mathcal X$，都有 \[ \sum_{i=1}^n \sum_{j=1}^n x_i K(x_i, x_j) \bar x_j \geq 0 , \] 则称$K$为一个正定核函数。这时$K(x,x) \geq 0$， $K_S$矩阵为厄米特阵。

若$K$为$\mathcal X \times \mathcal X \to \mathbb R$的映射，则$K$是正定核，当且仅当$K(x, y) = K(y, x)$, $\forall x, y \in X$，且对任意$n$和任意$x_1, x_2, \dots, x_n \in \mathcal X$，有 \[ \sum_{i=1}^n \sum_{j=1}^n x_i K(x_i, x_j) x_j \geq 0 , \] 即$K_S$矩阵对称半正定。称这样的正定核为实对称正定核，仍简称正定核。

因为正定核是$\mathcal H$上的内积，所以满足Cauchy-Schwarz不等式： \[ |K(x, y)|^2 \leq K(x,x) K(y, y), \ \forall x, y \in \mathcal X . \]

17.7.1.2 运算封闭性

正定核的运算封闭性（见(Mohri, Rostamizadeh, and Talwalkar 2018)定理6.10）：

两个正定核的和仍为正定核。
两个正定核的乘积仍为正定核。
正定核的正常数倍仍为正定核。
正定核的张量积仍为正定核。即若$K_1(x, y)$, $K_2(x', y')$为正定核，则$K(u, v) = K_1(x,y) K_2(x', y')$为正定核，其中$u = (x, x')$, $v = (v, v')$。
正定核的点极限仍为正定核。即设$K_n(\cdot, \cdot)$为正定核且$\lim_{n\to\infty} K_n(x, y) = K(x,y)$, $\forall x, y$，则$K(x,y)$为正定核。
设映射$\psi: \mathcal X \to \mathbb R^n$， $K_0$是$\mathbb R^n \times \mathbb R^n \to \mathbb C$的正定核，则$K(x,y) = K_0(\psi(x), \psi(y))$是正定核。
设幂级数$h(x) = \sum_{j=0}^\infty a_j x^j$在$(-\rho, \rho)$收敛($\rho>0$)， $X(x,y)$为正定核，取值在$(-\rho, \rho)$内，则$h(K(x,y))$为正定核。

正定核的标准化（见(Mohri, Rostamizadeh, and Talwalkar 2018)引理6.9）：设$K(x,y)$为正定核，定义 \[ \tilde K(x,y) = \begin{cases} 0, & \text{若} K(x,x)=0 \text{ 或 } K(y,y)=0; \\ \frac{K(x,y)}{\sqrt{K(x,x) K(y, y)}}, & \text{否则}. \end{cases} \] 称$\tilde K$为$K$的标准化， $\tilde K$也是正定核。

17.7.1.3 一些正定核

对$\mathcal X \subset R^n$，设$A$是对称半正定阵，则$K(x, y) = x^T A y$是正定核。事实上， \[ \sum_{i,j} \alpha_i \alpha_j \boldsymbol x_i^T A \boldsymbol x_j = \sum_{i,j} (\alpha_i \boldsymbol x_i)^T A (\alpha_j \boldsymbol x_j) \geq 0 . \]

对$\mathcal X \subset R^n$， $K(\boldsymbol x, \boldsymbol y) = \boldsymbol x^T \boldsymbol y$（欧式空间内积）是正定核。这是上一个正定核当$A=I$时的特例。

对映射$f: \mathcal X \to \mathbb C$， $K(\boldsymbol x, \boldsymbol y) = f(\boldsymbol x) \overline{f(\boldsymbol y)}$是正定核。事实上， \[ \sum_{i,j} \alpha_i \alpha_j f(\boldsymbol x_i) \overline{f(\boldsymbol x_j)} = (\sum_i \alpha_i f(\boldsymbol x_i)) \overline{(\sum_j \alpha_j f(\boldsymbol x_j))} \geq 0. \]

对$\ell > 0$， $\mathcal X \subset R^n$，令 \[ K(\boldsymbol x, \boldsymbol y) = \exp(- \| \boldsymbol x - \boldsymbol y \|^2 / (2 \ell^2)), \] 这是一个正定核，称为高斯核或者径向基函数。

证明：取$K_1(\boldsymbol x, \boldsymbol y) = \exp(- \boldsymbol x^T \boldsymbol y / \ell^2)$，易见$K$是$K_1$的标准化。只要证明$K_1$是正定核。而$K_2(\boldsymbol x, \boldsymbol y) = \boldsymbol x^T \boldsymbol y / (2 \ell^2)$是正定核，幂级数$exp(x) = \sum_{j=0}^\infty \frac{x^j}{j!}$收敛且系数为正，所以$exp(K_2(\boldsymbol x, \boldsymbol y))$是正定核。

17.7.2 再生核希尔伯特空间

设$K$是$\mathcal X \times \mathcal X \to \mathbb C$的正定核（包括实正定核）。是否存在希尔伯特空间$\mathcal H$和映射$\phi: \mathcal X \to \mathcal H$使得 \[ K(x, y) = \langle \phi(x), \phi(y) \rangle ? \]

这个空间是存在的，称为$K$决定的再生核希尔伯特空间(RKHS, reproducing kernel Hilbert space)。一般地，可以构造$\mathcal X$到$\mathbb C$的函数组成的空间作为$\mathcal H$。某些具体的$\mathcal H$可以通过同构映射转换成其它类型的H空间。

设$K$是$\mathcal X \times \mathcal X \to \mathbb C$的正定核， $\forall x \in \mathcal X$，定义$\mathcal X \to \mathbb C$的函数$k_x$为 \[ k_x(y) = K(x, y), \ \forall y \in \mathcal X . \] 记$\mathbb C^{\mathcal X}$为$\mathcal X \to \mathbb C$的函数组成的线性空间，则$\{k_x: x \in \mathcal X \}$是$\mathbb C^{\mathcal X}$的子集。令$\mathcal H_0$为$\{k_x: x \in \mathcal X \}$的所有有限线性组合在$\mathbb C^{\mathcal X}$中构成的子线性空间，可以定义$\mathcal X \to \mathcal H_0$的映射$\phi$使得 \[ \phi(x) = k_x \in \mathcal H_0, \ \forall x \in \mathcal X . \] 在$\mathcal H_0$上可以定义内积，使得 \[ \langle \phi(x), \phi(y) \rangle_{\mathcal H_0} = K(x, y), \ \forall x, y \in \mathcal X . \] 设$\mathcal H$为$\mathcal H_0$的闭包，则$\mathcal H$为希尔伯特空间，可以定义映射$\eta: \mathcal H \to \mathbb C^{\mathcal X}$，使得 \[ \eta(f)(x) = \langle f, k_x \rangle, \ \forall x \in \mathcal X, \ \forall f \in \mathcal H , \] 则$\eta$是$\mathcal H$到$\mathbb C^{\mathcal X}$的单射和线性映射，于是$\eta$构成从$H$到$\mathbb C^{\mathcal X}$的一个子希尔伯特空间的同构映射，可以将$\mathcal H$看作$\mathbb C^{\mathcal X}$的一个子希尔伯特空间。对于$\mathcal H$上的内积仍有 \[ \langle \phi(x), \phi(y) \rangle_{\mathcal H} = K(x, y), \ \forall x, y \in \mathcal X . \] 对任意$f \in \mathcal H_0$，有 \[ \langle f, k_x \rangle = f(x), \ \forall x \in \mathcal X, \] 上式称为再生性，即通过特征空间$\mathcal H$的内积，也即核函数$K$，可以恢复（再生）$\mathcal H$中的元素。

当$K$是实对称正定核时， $\mathcal H_0$为实数域上的线性空间， $\mathcal H$为实数域上的希尔伯特空间。

References

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning with Applications in r. Springer.

Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. 2018. Foundations of Machine Learning. 2nd Edition. MIT Press.

Trevor Hastie, Jerome Friedman, Robert Tibshirani. 2009. The Elements of Statistical Learning. 2nd Ed. Springer.