10 对应分析

《多元统计分析—基于R》课程的R示例, 主要参考书: 费宇《多元统计分析-基于R》，人民大学出版社，2012。

10.1 对应分析介绍

对应分析是列联表分析方法，考察把行类别和列类别分组降维后，行、列之间的关系。

列联表是有两个分类变量交叉分组后形成的频数（个数）表，比如：

性别	吸烟	不吸烟
男	105	225
女	19	300

这是一个\(2 \times 2\)列联表，内容简单，不需要降维，对应分析不适用。更大的列联表则可以用对应分析发现行类与列类之间的关系。

对应分析把行变量的各个不同值进行降维，把列变量的各个不同值进行降维，与主成分分析和因子分析的思想类似。降维后，行、列两个方向的降维结果具有内在联系，可以用关联的投影方向同时表示行和列的降维结果。

在行、列都降维到二维时，可以把降维结果同时画到坐标平面上，每个行画一个点，每个列也画一个点，从中查看每行行与每列接近与否。这样，可以发现行的类与列的类之间的对应关系。

记号:

设列联表保存为矩阵\(M = (x_{ij})_{n \times p}\), \(x_{ij}\)一般是非负整数，表示行变量取第\(i\)种值并且列变量取第\(j\)种值的观测个数（频数）。列联表的每一行对应于行变量的某个类，每一列对应于列变量的某个类。行、列变量可以是分类变量(如性别、行业、所在地区等)，也可以是数值型变量（如家中孩子个数，一般应存在很多重复值）, 或者数值型变量的分段值（比如年龄1—18, 19—60, 60以上）。

令 \[\begin{align*} N =& \sum_{i=1}^n \sum_{j=1}^p x_{ij} \quad\text{(总频数)}, \quad P = (p_{ij})_{n \times p} = \frac{1}{N} M \quad\text{(百分比)}, \\ x_{i\bullet} =& \sum_{j=1}^p x_{ij}, \ i=1,2,\dots,n \ \text{(行和)}, \\ x_{\bullet j} =& \sum_{i=1}^n x_{ij}, \ j=1,2,\dots,p \ \text{(列和)} \\ p_{i\bullet} =& \frac{x_{i\bullet}}{N} \ \text{(行变量边缘百分比),} \quad p_{\bullet j} = \frac{x_{\bullet j}}{N} \ \text{(列变量边缘百分比)} , \\ \boldsymbol a =& (p_{1 \bullet}, p_{2 \bullet}, \dots, p_{n \bullet})^T = P \boldsymbol 1_p, \\ \boldsymbol b =& (p_{\bullet 1}, p_{\bullet 2}, \dots, p_{\bullet p})^T = P^T \boldsymbol 1_n . \end{align*}\]

对应分析与主成分分析的区别:

主成分分析在计算时，把数据矩阵进行某种标准化后，取出能够最好地保留原来的方差的少数指标。对应分析要保留的是行与列的关联指标，通常是列联表独立性卡方统计量值。

10.2 对应分析的原理

10.2.1 线性代数依据

设\(C\)是\(n \times p\)矩阵，则\(C^T C\)是\(p \times p\)矩阵； \(C C^T\)是\(n \times n\)矩阵。 \(C^T C\)和\(C C^T\)都是对称半正定矩阵，所有特征值都非负。 \(C^T C\)和\(C C^T\)的正特征值都是相同的。

如果\(\boldsymbol\delta\)是\(C^T C\)的正特征值\(\lambda\)的特征向量，则\(C \boldsymbol\delta\)是\(C C^T\)的特征值\(\lambda\)的特征向量。如果\(\boldsymbol\gamma\)是\(C C^T\)的正特征值\(\lambda\)的特征向量，则\(C^T \boldsymbol\gamma\)是\(C^T C\)的特征向量。

证明:

设\(n \geq p\), \(C^T C\)的正特征值为 \(\lambda_1 \geq \lambda_2 \geq \dots \lambda_r > 0\), \(r \leq p \leq n\)。设\(\boldsymbol\delta_k\)是\(C^T C\)的对应于\(\lambda_k\)的特征向量，即 \[\begin{align*} & C^T C \boldsymbol\delta_k = \lambda_k \boldsymbol\delta_k, \\ & \text{则} \\ & C C^T C \boldsymbol\delta_k = \lambda_k C \boldsymbol\delta_k, \\ & \text{即} \\ & (C C^T) (C \boldsymbol\delta_k) = \lambda_k (C \boldsymbol\delta_k) \end{align*}\] 所以\(\lambda_k\)是\(C C^T\)的特征值，\(C \boldsymbol\delta_k\)是对应的特征向量。

反之类似。若\(\lambda_k>0\)和\(\boldsymbol\gamma_k\)是\(C C^T\)的正特征值和对应的特征向量，则 \[\begin{align*} C C^T \boldsymbol\gamma_k =& \lambda_k \boldsymbol\gamma_k \\ \text{于是} & \\ C^T C C^T \boldsymbol\gamma_k =& \lambda_k C^T \boldsymbol\gamma_k \\ \text{即} & \\ (C^T C) (C^T \boldsymbol\gamma_k) =& \lambda_k (C^T \boldsymbol\gamma_k) \end{align*}\] 所以\(\lambda_k\)也是\(C^T C\)的特征值，\(C^T \boldsymbol\gamma_k\)是对应的特征向量。

所以，\(C^T C\)与\(C C^T\)的正特征值完全相同，对应的特征向量可以互相决定。

10.2.1.1 奇异值分解

对\(n \times p\)矩阵\(C\)，设\(C^T C\)和\(C C^T\)共同的正特征值为\(\lambda_1, \dots, \lambda_r\), \(1 \leq r \leq \min(n,p)\)， \(C^T C\)对应于\(\lambda_k\)的特征向量为\(\boldsymbol\delta_k\), \(C C^T\)对应于\(\lambda_k\)的特征向量为\(\boldsymbol\gamma_k\), 令\(\Delta = (\boldsymbol\delta_1, \dots, \boldsymbol\delta_r)_{p \times r}\), \(\Gamma = (\boldsymbol\gamma_1, \dots, \boldsymbol\gamma_r)_{n \times r}\)。则\(C\)有如下的奇异值分解： \[\begin{align} C = \Gamma \Lambda \Delta^T = \sum_{k=1}^r \lambda_k^{1/2} \boldsymbol\gamma_k \boldsymbol\delta_k^T, \end{align}\] 其中\(\Lambda = \text{diag}(\lambda_1^{1/2}, \dots, \lambda_r^{1/2})\)。

注意在主成分分析中，特征向量用来作为各个行向量的线性组合系数（R型主成分），或各个列向量的线性组合系数（Q型主成分）。这样，如果同时得到了每行的前两个因子得分(R型主成分)，以及每列的前两个因子得分(R型主成分), 可以将两种第一主成分放在同一个横轴，将两种第二主成分放在同一个纵轴，同时把代表各行的散点与代表各列的散点画在同一坐标系中。

10.2.2 卡方分解

设\(M=(x_{ij})_{n \times p}\)是列联表，通常用如下的卡方统计量进行列联表独立性检验： \[\begin{align} V = \sum_{i=1}^n \sum_{j=1}^p \frac{(x_{ij} - N p_{i\bullet} p_{\bullet j} )^2}{N p_{i\bullet} p_{\bullet j}} = N \sum_{i=1}^n \sum_{j=1}^p \frac{(p_{ij} - p_{i\bullet} p_{\bullet j})^2}{p_{i\bullet} p_{\bullet j}} . \tag{10.1} \end{align}\]

记\(E_{ij}= p_{i\bullet} p_{\bullet j}\), 这是是在行、列变量独立情况下的联合概率， \(E = (E_{ij})_{n\times p} = \boldsymbol a \boldsymbol b^T\)。当行、列变量独立时，\(V\)近似服从\(\chi^2((n-1)(p-1))\)分布。

行、列独立时，对应分析没有意义。当行、列不独立时，对应分析可以发现哪些行与哪些列有正向或负向的关联，即代表行的变量与代表列的变量在哪些组合中比独立情形出现更多或更少。

令矩阵\(C = (c_{ij})_{n \times p}\), 其中 \[\begin{aligned} c_{ij} = \frac{1}{\sqrt{N}} \frac{x_{ij} - N p_{i\bullet} p_{\bullet j}}{(N p_{i\bullet} p_{\bullet j})^{1/2}} = \frac{p_{ij} - p_{i\bullet} p_{\bullet j}}{(p_{i\bullet} p_{\bullet j})^{1/2}}, \ i=1,2,\dots,n, \, j=1,2,\dots, p . \end{aligned}\] 这是(10.1)中\(V/N\)通项的平方根，易见 \[\begin{align} V/N = \sum_{i=1}^n \sum_{j=1}^p c_{ij}^2 = \text{trace}(C^T C) . \end{align}\] 令\(A = \text{diag}(\boldsymbol a)\), \(B = \text{diag}(\boldsymbol b)\), 则\(A \boldsymbol 1_n = \boldsymbol a\), \(B \boldsymbol 1_p = \boldsymbol b\)。易见 \[\begin{align} C = A^{-1/2} (P - \boldsymbol a \boldsymbol b^T) B^{-1/2} . \tag{10.2} \end{align}\]

记 \[\begin{aligned} \boldsymbol a^{1/2} =& (p_{1 \bullet}^{1/2}, p_{2 \bullet}^{1/2}, \dots, p_{n \bullet}^{1/2})^T, \\ \boldsymbol b^{1/2} =& (p_{\bullet 1}^{1/2}, p_{\bullet 2}^{1/2}, \dots, p_{\bullet p}^{1/2})^T, \\ \end{aligned}\] 容易验证 \[\begin{align} C \boldsymbol b^{1/2} = \boldsymbol 0, \quad C^T \boldsymbol a^{1/2} = \boldsymbol 0 . \tag{10.3} \end{align}\]

事实上， \[\begin{aligned} C \boldsymbol b^{1/2} =& A^{-1/2} (P - \boldsymbol a \boldsymbol b^T) B^{-1/2} B^{1/2} \boldsymbol 1_p \\ =& A^{-1/2} (P \boldsymbol 1_p - \boldsymbol a \boldsymbol b^T \boldsymbol 1_p) \\ =& A^{-1/2} ( \boldsymbol a - \boldsymbol a ) = \boldsymbol 0, \\ C^T \boldsymbol a^{1/2} =& B^{-1/2} (P^T - \boldsymbol b \boldsymbol a^T) A^{-1/2} A^{1/2} \boldsymbol 1_n \\ =& B^{-1/2} (P^T \boldsymbol 1_n - \boldsymbol b \boldsymbol a^T \boldsymbol 1_n) \\ =& B^{-1/2} ( \boldsymbol b - \boldsymbol b ) = \boldsymbol 0 . \end{aligned}\]

设\(r = \text{rank}(C) \leq \min(n-1, p-1)\), 矩阵\(C\)有奇异值分解 \[\begin{align} C = \Gamma \Lambda \Delta^T = \sum_{k=1}^r \lambda_k \boldsymbol\gamma_k \boldsymbol\delta_k^T, \tag{10.4} \end{align}\] 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_r)\), \(\lambda_1, \lambda_2, \dots, \lambda_r\)是\(C\)的奇异值， \(\Gamma^T \Gamma = I_r\), \(\Delta^T \Delta = I_r\), \(\Gamma_{n \times r}\)的第\(k\)列\(\boldsymbol\gamma_k\)是\(C C^T\)对应于\(\lambda_k^2\)的特征向量， \(\Delta_{p \times r}\)的第\(k\)列\(\boldsymbol\delta_k\)是\(C^T C\)对应于\(\lambda_k^2\)的特征向量。奇异值分解(10.4)说明 \[\begin{align} c_{ij} = \sum_{k=1}^r \lambda_k \gamma_{ik} \delta_{jk}, \ i=1,2,\dots, n, \, j=1,2,\dots, p . \tag{10.5} \end{align}\]

这里有 \[\begin{align} V/N =& \text{trace}(C^T C) = \text{trace}(\Delta \Lambda \Gamma^T \Gamma \Lambda \Delta^T) = \text{trace}(\Delta \Lambda^2\Delta^T) \nonumber\\ =& \text{trace}(\Lambda^2 \Delta^T \Delta) = \text{trace}(\Lambda^2) \nonumber\\ =& \sum_{k=1}^r \lambda_k^2 . \end{align}\] 可见列联表独立性卡方统计量\(V/N\)可以分解为\(C^T C\)的特征值之和，可以类似主成分分析解释方差那样解释列联表统计量的分解。称\(V = \sum_{k=1}^r \lambda_k^2\)为数据的总惯量（total inertia）。

当\(\sum_{k=1}^K \lambda_k^2 / \sum_{k=1}^r \lambda_k^2\)较大时，在(10.4)中可以用前\(K\)项逼近\(C\)。由于\(\lambda_1 \geq \lambda_2 \geq \dots\), 对应于\(\lambda_1\)和\(\lambda_2\)的左奇异向量\(\boldsymbol\gamma_1, \boldsymbol\gamma_2\) 和右奇异向量\(\boldsymbol\delta_1, \boldsymbol\delta_2\)是更重要的降维向量, 常取\(K=2\)。

在奇异值分解式(10.4)中， \(\boldsymbol\gamma_k\)和\(\boldsymbol\delta_k\)是互相决定的： \[\begin{align} \boldsymbol\delta_k =& \pm \lambda_k^{-1} C^T \boldsymbol\gamma_k, \quad \boldsymbol\gamma_k = \pm \lambda_k^{-1} C \boldsymbol\delta_k , k=1,2,\dots, r . \tag{10.6} \end{align}\]

由(10.3)可知 \[\begin{align} \boldsymbol\delta_k^T \boldsymbol b^{1/2} = 0, \quad \boldsymbol\gamma_k^T \boldsymbol a^{1/2} = 0, \ k=1,2,\dots,r . \tag{10.7} \end{align}\] 这一点是因为\(\boldsymbol\delta_k\)是\(C^T C\)的正特征值\(\lambda_k\)的特征向量，而(10.3)说明\(\boldsymbol b^{1/2}\)是\(C^T C\)的零特征值的特征向量，两者必须正交。

类似于主成分分析中把\(\boldsymbol\delta_k\)作为计算主成分得分的线性组合系数，把\(C\)的每个行向量分别用\(\boldsymbol\delta_1, \boldsymbol\delta_2, \dots\)作线性组合，得到降维表示 \[\begin{align*} C \boldsymbol\delta_j = \lambda_j \boldsymbol\gamma_j, \ j=1,2,\dots \end{align*}\] 其中的前面几个可以作为\(C\)的各行的低维表示，把原来\(C\)中每行的\(p\)个元素压缩到较低维数。所以，将\(C\)矩阵保持行数不变，将列数进行压缩，公式为 \[\begin{align} \Gamma \Lambda . \tag{10.8} \end{align}\] 当\(\lambda_1, \lambda_2\)较大而其它奇异值较小时，可以取\(\Gamma \Lambda\)的前两列，这可以较好地保留\(C\)矩阵每一行的信息。

类似地，把\(C\)的每个列向量用\(\boldsymbol\gamma_1, \boldsymbol\gamma_2, \dots\)作线性组合，得到降维表示 \[\begin{align*} C^T \boldsymbol\gamma_i = \lambda_i \boldsymbol\delta_i, \ i=1,2,\dots \end{align*}\] 写成矩阵形式即 \[\begin{align} \Delta \Lambda . \tag{10.9} \end{align}\] 当\(\lambda_1, \lambda_2\)较大而其它奇异值较小时，可以取\(\Delta \Lambda\)的前两列，这个矩阵转置后变成\(2 \times p\)矩阵，可以较好地保留\(C\)的各列的信息。

当\(\lambda_1\)远大于其它奇异值时， \(n\)维列向量\(\lambda_1 \boldsymbol\gamma_1\)可以作为\(C\)的\(n\)行的降维表示，可以用\(\boldsymbol\gamma_1\)的\(n\)个元素作为\(C\)的行变量的\(n\)个类的代表； \(p\)维行向量\(\lambda_1 \boldsymbol\delta_1^T\)可以作为\(C\)的各列的降维表示，可以用\(\lambda_1 \boldsymbol\delta_1\)的\(p\)个元素作为\(C\)的列变量的\(p\)个类的代表。这时 \[\begin{align*} c_{ij} \approx \lambda_1 \gamma_{i1} \delta_{j1} . \end{align*}\]

当\(\gamma_{i1}\)和\(\delta_{j1}\)同号且都比较大时， \(c_{ij}\)也比较大，这时行变量的第\(i\)类与列变量的第\(j\)类存在正向的关联；当\(\gamma_{i1}\)和\(\delta_{j1}\)异号且绝对值都比较大时， \(c_{ij}\)为负且绝对值较大，这时行变量的第\(i\)类与列变量的第\(j\)类存在负向的关联。这里正向的关联是指这两个类同时出现概率比独立情形明显地大。当\(\gamma_{i1}\)和\(\delta_{j1}\)绝对值较小时，行变量的第\(i\)类与列变量的第\(j\)类没有什么关联。这种思想是对应分析能够反映列联表中第\(i\)个行类和第\(j\)个列类的正向或者负向关联的理论基础。

在更一般的情形中，\(\lambda_1^2\)和\(\lambda_2^2\) 在卡方统计量值\(V/N=\sum_{k=1}^r \lambda_k^2\)中占据较大比重。这时，用 \[\begin{align*} (\lambda_1\boldsymbol\gamma_1, \lambda_2\boldsymbol\gamma_2)_{n\times 2} =& \left(\begin{array}{cc} \lambda_1\gamma_{11} & \lambda_2\gamma_{12} \\ \lambda_1\gamma_{21} & \lambda_2\gamma_{22} \\ \vdots & \vdots \\ \lambda_1\gamma_{n1} & \lambda_2\gamma_{n2} \end{array}\right) \end{align*}\] 作为\(C\)的每个行向量的降维表示，用这\(n\)个二维行向量近似表示\(C\)的\(n\)行（原来每行是\(p\)维，现在每行用二维近似表示）。

用 \[\begin{align*} \left(\begin{array}{c} \lambda_1\boldsymbol\delta_1^T \\ \lambda_2\boldsymbol\delta_2^T \end{array}\right)_{2 \times p} =& \left(\begin{array}{ccccc} \lambda_1\delta_{11} & \lambda_1\delta_{21} & \cdots & \lambda_1\delta_{p1} \\ \lambda_2\delta_{12} & \lambda_2\delta_{22} & \cdots & \lambda_2\delta_{p2} \end{array}\right) \end{align*}\] 作为\(C\)的每个列向量的降维表示，用这\(p\)个二维列向量近似表示\(C\)的\(p\)个列（原来每列是\(n\)维，现在每列用二维近似表示）。

把\((\lambda_1\boldsymbol\gamma_1, \lambda_2\boldsymbol\gamma_2)_{n\times 2}\)和 \((\lambda_1\boldsymbol\delta_1, \lambda_2\boldsymbol\delta_2)_{p\times 2}\)适当标准化后，可以分别作散点图并画在同一坐标平面中。这样标准化的散点图可以用来考察行变量类\(i\)与列变量\(j\)的关联性，以及两行之间按比例的相似性，两列之间按比例的相似性。

10.2.3 按行轮廓和列轮廓降维

为了将\(C\)的每个行向量降维，计算\(C \boldsymbol\delta_1, C \boldsymbol\delta_2\), 即用\(\boldsymbol\delta_1\)和\(\boldsymbol\delta_2\)对\(C\)的每行作线性组合。因为\(\| \boldsymbol\delta_k \|=1\)，所以这样降维得到的第\(i\)行两个新坐标受到\(P\)的第\(i\)行的行边缘百分比\(p_{i \bullet}\)影响。

例如，考虑如下的一个假想的东部、中部、西部家庭收入分配的表格：

	食品	耐用消费品	投资
东部	1000	1500	500
中部	500	750	250
西部	300	200	50

在上表中，东部和中部的绝对数值相差一倍，所以降维后的表示也会相差一倍，但是，这两个地区在三类分配中的比例都是\(2:3:1\)，我们认为这两个地区从分配比例上是相近的。需要将降维的结果排除行百分比\(p_{i \bullet}\)影响。

类似地，用\(C^T \boldsymbol\gamma_1, C^T \boldsymbol\gamma_2\)对\(C\)的每个列向量降维，得到的第\(j\)列的两个新坐标受到\(P\)的第\(j\)列的列边缘百分比\(p_{\bullet j}\)影响。需要将降维的结果排除列百分比\(p_{\bullet j}\)影响。

实际上，我们无法同时排除行百分比和列百分比的影响，只能分别进行。

我们希望降维后的行坐标仅代表该行的“行轮廓”(row profile)即行百分比 \(\left( \frac{p_{i1}}{p_{i\bullet}}, \frac{p_{i2}}{p_{i\bullet}}, \dots, \frac{p_{ip}}{p_{i\bullet}} \right)\)，希望降维后的列坐标仅代表该列的“列轮廓”(column profile)即列百分比 \(\left( \frac{p_{1j}}{p_{\bullet j}}, \frac{p_{2j}}{p_{\bullet j}}, \dots, \frac{p_{nj}}{p_{\bullet j}} \right)\)。

为了把\(C\)的各个行向量进行按行轮廓降维，需要改造\(C\)为代表行轮廓的矩阵，然后再保持行数不变，对每行用较低维数表示。

原来 \[\begin{aligned} c_{ij} = \frac{p_{ij} - p_{i\bullet} p_{\bullet j}} { p_{i\bullet}^{1/2} p_{\bullet j}^{1/2}}, \end{aligned}\] 令\(\tilde C = A^{-1/2} C\), 则 \[\begin{align} \tilde c_{ij} = \frac{1}{p_{i\bullet}^{1/2}} c_{ij} = \frac{ \frac{p_{ij}}{p_{i\bullet}} - p_{\bullet j}}{p_{\bullet j}^{1/2}} . \tag{10.10} \end{align}\] 这里\((\frac{p_{ij}}{p_{i\bullet}}, j=1,2,\dots,p)\)是第\(i\)行的行百分比，代表了第\(i\)行的特殊分布，而\((p_{\bullet j}, j=1,2,\dots,p)\)代表列变量的边缘分布。 \((\tilde c_{ij}, j=1,2,\dots, p)\) 代表了第\(i\)行的\(p\)个比例与列变量的边缘分布的差异。只要保持\(\tilde C\)的行数不变，用较低维数表示每一行，就可以降维表示每一行的行轮廓。

于是，为了把\(C\)的各个行轮廓进行降维，由\(C\)的奇异值分解可知 \[\begin{aligned} \tilde C =& A^{-1/2} C = A^{-1/2} \Gamma \Lambda \Delta^T \\ =& \sum_{k=1}^r \lambda_k A^{-1/2} \boldsymbol\gamma_k \boldsymbol\delta_k^T . \end{aligned}\] 于是可以降维为 \[\begin{align} \boldsymbol r_k = \tilde C \boldsymbol\delta_k = A^{-1/2} C \boldsymbol\delta_k = \lambda_k A^{-1/2} \boldsymbol\gamma_k, \ k=1,2,\dots, r. \tag{10.11} \end{align}\] 写成矩阵形式即行轮廓的降维表示为如下矩阵： \[\begin{align} A^{-1/2} \Gamma \Lambda . \tag{10.12} \end{align}\]

这样，仅取前两个奇异值， \[\begin{aligned} (\boldsymbol r_1, \boldsymbol r_2)_{n\times 2} =& \left(\begin{array}{cc} r_{11} & r_{12} \\ r_{21} & r_{22} \\ \vdots & \vdots \\ r_{n1} & r_{n2} \\ \end{array}\right) . \end{aligned}\] 可以用来代表原来的\(n\)行，把每行从\(p\)维降低到二维，矩阵的每一行代表一个行轮廓，如果以第一列作为横坐标，以第二列作为纵坐标作\(n\)点的散点图，则如果代表某两行的两个点接近，就代表这两行的行轮廓接近，即这两行代表的分配比例接近。这样的坐标称为“各行的主坐标”(principle coordinates of rows)。

类似地，为了把\(C\)的各个列轮廓进行降维，令 \[\begin{align} \boldsymbol s_k =& B^{-1/2} C^T \boldsymbol\gamma_k = \lambda_k B^{-1/2} \boldsymbol\delta_k . \tag{10.13} \end{align}\] 写成矩阵形式即 \[\begin{align} B^{-1/2} \Delta \Lambda. \tag{10.14} \end{align}\]

这样，仅取前两个特征值， \[\begin{aligned} \left(\begin{array}{c} \boldsymbol s_1^T \\ \boldsymbol s_2^T \end{array}\right)_{2 \times p} =& \left(\begin{array}{ccccc} s_{11} & s_{21} & \cdots & s_{p1} \\ s_{12} & s_{22} & \cdots & s_{p2} \end{array}\right) \end{aligned}\] 可以用来代表原来的\(p\)个列轮廓，每列从\(n\)维降低到二维。

以\((s_{j1}, s_{j2})\), \(j=1,2,\dots,p\)作为\(p\)个列轮廓的降维坐标画散点图，则表示某两列的散点接近时，可以表示这两列对应的列轮廓接近，即这两列代表的分配比例接近。这样的坐标称为“各列的主坐标”(principle coordinates of columns)。

可以将\((r_{i1}, r_{i2}), i=1,2,\dots,n\)对应的\(n\)个行轮廓点，与\((s_{j1}, s_{j2}), j=1,2,\dots,p\)对应的\(p\)个列轮廓点，画在同一坐标系中。这时，某个行轮廓点与某个列轮廓点接近，通常也可以认为这个行类与这个列类有正向关联，但不如在转化为行、列轮廓前的降维那样容易解释。

由(10.7)可知 \[\begin{align} \boldsymbol r_k^T \boldsymbol a = 0, \quad \boldsymbol s_k^T \boldsymbol b = 0, k=1,2,\dots,r . \tag{10.15} \end{align}\] 所以，上述散点图中的四种横、纵坐标都是满足加权平均为零的，其取值都在原点左右（或上下）相对平衡地分布，加权系数为\(\boldsymbol a\)或\(\boldsymbol b\)。

由(10.6)易见 \[\begin{aligned} \begin{cases} \boldsymbol r_k = \pm \lambda_k^{-1} A^{-1/2} C B^{1/2} \boldsymbol s_k, \\ \boldsymbol s_k = \pm \lambda_k^{-1} B^{-1/2} C^T A^{1/2} \boldsymbol r_k . \\ \end{cases} \end{aligned}\] 这又可以化简为 \[\begin{align} \begin{cases} \boldsymbol r_k = \pm \lambda_k^{-1} A^{-1} P \boldsymbol s_k, \\ \boldsymbol s_k = \pm \lambda_k^{-1} B^{-1} P^T \boldsymbol r_k . \end{cases} \tag{10.16} \end{align}\] 这说明压缩后的\(n\)行的\(n\)个第\(1\)坐标\(\boldsymbol r_1\) 与压缩后的\(p\)列的\(p\)个第\(1\)坐标\(\boldsymbol s_1\)存在一一对应关系, 其它坐标类似。

证明:

来证明(10.16)。事实上， \[\begin{aligned} \boldsymbol r_k =& \pm \lambda_k^{-1} A^{-1/2} C B^{1/2} \boldsymbol s_k \\ =& \pm \lambda_k^{-1} A^{-1/2} \; A^{-1/2} (P - \boldsymbol a \boldsymbol b^T) B^{-1/2} \; B^{1/2} \boldsymbol s_k \\ =& \pm \lambda_k^{-1} A^{-1} (P - \boldsymbol a \boldsymbol b^T) \boldsymbol s_k \\ =& \pm \lambda_k^{-1} A^{-1} \left( P \boldsymbol s_k - \boldsymbol a \boldsymbol b^T \, \boldsymbol s_k \right) \\ =& \pm \lambda_k^{-1} A^{-1} P \boldsymbol s_k \end{aligned}\] (注意\(\boldsymbol b^T \boldsymbol s_k = 0\))。而 \[\begin{aligned} \boldsymbol s_k =& \pm \lambda_k^{-1} B^{-1/2} C^T A^{1/2} \boldsymbol r_k \\ =& \pm \lambda_k^{-1} B^{-1/2} \, B^{-1/2} (P^T - \boldsymbol b \boldsymbol a^T) A^{-1/2} \, A^{1/2} \boldsymbol r_k \\ =& \pm \lambda_k^{-1} B^{-1} ( P^T \boldsymbol r_k - \boldsymbol b \boldsymbol a^T \boldsymbol r_k) \\ =& \pm \lambda_k^{-1} B^{-1} P^T \boldsymbol r_k \end{aligned}\] (注意\(\boldsymbol a^T \boldsymbol r_k = 0\))。

10.3 对应分析做法

从\(M=(x_{ij})_{n\times p}\)得\(P = \frac{1}{N} M\), 计算得到\(C=(c_{ij})_{n \times p}\)。
求\(C^T C\)的前两个特征值\(\lambda_1, \lambda_2\)(比例不足时可以取更多个), 得到\(C^T C\)的前两个特征向量\(\boldsymbol\delta_1, \boldsymbol\delta_2\), 然后利用(10.6)计算\(C C^T\)的前两个特征向量 \(\boldsymbol\gamma_1, \boldsymbol\gamma_2\)。
用(10.11)和(10.13)得到标准化的行得分 \(\boldsymbol r_1, \boldsymbol r_2\)和列得分\(\boldsymbol s_1, \boldsymbol s_2\)。
以\((r_{i1}, r_{i2})\), \(i=1,2,\dots, n\)为坐标画行类的散点图，以\((s_{j1}, s_{j2})\), \(j=1,2,\dots,p\)为坐标画列类的散点图。

10.3.1 对应分析结果图形的解释—两个行类之间或两个列类之间

对于图上的两个行类，其散点相近，表示这两行的行轮廓很相近。
对于图上两个列类，其散点相近，表示这两列的列轮廓很相近。
两个行类的散点距离远则代表这两行的行轮廓取值差别大。两个列类的散点距离远则代表这两列的列轮廓取值差别大。
以上解释是来自于行轮廓与列轮廓的降维方法。
因为横坐标\(\boldsymbol r_1, \boldsymbol s_1\)的加权平均为零，纵坐标\(\boldsymbol r_2, \boldsymbol s_2\)的加权平均为零，所以落在原点附近的行类的行百分比取值与列变量的边缘百分比 \(\boldsymbol b^T\)相近，落在原点附近的列类的列百分比取值与行变量的边缘百分比\(\boldsymbol a\)相近。

10.3.2 对应分析结果图形的解释—一个行类与一个列类之间

当行类\(i\)与列类\(j\)的散点距离近而且都远离原点时，这个行类与这个列类有较强的正向关联；
当行类\(i\)与列类\(j\)的散点到原点的距离较远且位于相反方向时，这个行类与这个列类有较强的负向关联；
当行类\(i\)与列类\(j\)至少有一个靠近原点时，这两个类的关联不大。
当\(\lambda_1^2 + \lambda_2^2\)占据\(V/N = \sum_{k=1}^r \lambda_k^2\)的很大比例时，对应分析的散点图是有意义的，否则仅能解释两个行轮廓之间，两个列轮廓之间是否相近。
事实上，\(c_{ij}\)绝对值大小代表了第\(i\)行类与第\(j\)行类的关联性强弱，当\(\lambda_1^2 + \lambda_2^2\)占据\(V/N = \sum_{k=1}^r \lambda_k^2\)的很大比例时， \[\begin{align} c_{ij} =& \sum_{k=1}^r \lambda_k \gamma_{ik} \delta_{jk} \approx \sum_{k=1}^2 \lambda_k \gamma_{ik} \delta_{jk} \tag{10.17} \\ =& \sum_{k=1}^2 \lambda_k \cdot \lambda_k^{-1} p_{i\bullet}^{1/2} r_{ik} \cdot \lambda_k^{-1} p_{\bullet j}^{1/2} s_{jk} \nonumber\\ =& (p_{i \bullet} p_{\bullet j})^{1/2} \sum_{k=1}^2 \lambda_k^{-1} r_{ik} s_{jk} . \tag{10.18} \end{align}\]
\(\sum_{k=1}^2 \lambda_k^{-1} r_{ik} s_{jk}\)是向量\((r_{i1}, r_{i2})\) 和向量\((s_{ji}, s_{j2})\)的一种内积。注意(10.17)中的\(\gamma_{ik}\)和\(\delta_{jk}\) 都来自单位特征向量，所以(10.17)中的加权 \(\lambda_1\)和\(\lambda_2\)使得内积更侧重于第一特征向量； (10.18)中的\(r_{ik}\)和\(s_{ik}\)并不是来自单位向量。
当\((r_{i1}, r_{i2})\)与\((s_{j1}, s_{j2})\)两个散点接近而且离原点较远时，这两个向量同方向，内积较大，使得\(c_{ij}\)较大，这时第\(i\)行类与第\(j\)列类有较强的正向关联。

10.3.3 推广用法

因为对应分析计算中只要求列联表\(M = (x_{ij})_{n \times p}\)所有元素非负，所以对应分析也可以对一般的数据集\(M\)计算，但是要求元素都为正而且各变量之间是可比的。
这样的推广用法可以作为主成分分析的补充。主成分分析关心的是解释更多的方差，而对应分析则考虑更一般的关联性。

可以看出，即使在各行主坐标表示和各列主坐标表示中，第一坐标的作用也是高于第二坐标的， \(\lambda_1/\lambda_2\)的值越大，这个差距越大。所以，另一种关于行轮廓和列轮廓的降维坐标是不对各个坐标乘以相应的奇异值，用 \[ X = A^{-1/2} \Gamma \] 表示行轮廓的降维，称为各行的标准坐标(standard coordinates of rows)。 \(X\)满足 \[ X^T A X = I . \] 类似地，用 \[ Y = B^{-1/2} \Delta \] 表示列轮廓的降维，称为各列的标准坐标，满足 \[ Y^T B Y = I . \]

10.3.4 软件支持

基本R的MASS包提供了corresp()函数，可以计算经典的对应分析结果，并画双重散点图，但图形不够美观。

ca扩展包提供了基本的对应分析能力和利用ggplot2的高质量图形，也能进行多重和联合的对应分析(multiple and joint correspondence analysis)。

factoMineR包与factoextra包配合，能进行多种对应分析计算，并可以作多种对应分析图形。

10.4 案例8.1：现金支出定位问题

P. 112案例8.1。2012年我国城镇居民按收入等级分组，每种收入等级内人均年消费的不同种类分配情况表。行变量为收入分组，共7个级别: ‘最低’, ‘较低’, ‘中下’, ‘中等’, ‘中上’, ‘较高’, ‘最高’ 列变量为不同的消费项目（肉、蛋、鱼、奶、衣、耐用、文娱）。

library(MASS)
incomeUse <- readr::read_csv(
  "data/不同收入组支出分配.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
d0 <- as.data.frame(incomeUse)
rownames(d0) <- c('最低', '较低', '中下', '中等', '中上', '较高', '最高')
d.inc <- d0[,-1]
colnames(d.inc) <- c('肉', '蛋', '鱼', '奶', '衣', '耐', '文')

knitr::kable(d.inc)

	肉	蛋	鱼	奶	衣	耐	文
最低	767.51	84.30	173.39	125.75	494.80	119.37	144.68
较低	946.71	96.64	235.60	169.02	746.36	185.89	209.60
中下	1088.30	112.02	308.75	208.34	1018.94	272.85	284.93
中等	1249.37	125.68	412.72	260.07	1288.06	395.16	404.79
中上	1341.13	133.33	522.70	308.80	1637.68	532.17	565.38
较高	1480.40	142.42	630.61	365.39	2067.91	738.16	793.42
最高	1555.67	147.05	768.17	423.34	3019.31	1195.76	1187.24

作列联表独立性卡方检验。虽然这里不是列联表但还是可以用的。

chisq.test(d.inc)

## 
##  Pearson's Chi-squared test
## 
## data:  d.inc
## X-squared = 1030.1, df = 36, p-value < 2.2e-16

用corresp()作对应分析, 用nf指定因子个数。为作散点图一般取2:

co <- corresp(d.inc, nf=2)

## Warning in corresp.matrix(as.matrix(x), ...): negative or non-integer entries
## in table

co

## First canonical correlation(s): 0.17933228 0.01896212 
## 
##  Row scores:
##             [,1]       [,2]
## 最低 -1.96830644 -1.3285223
## 较低 -1.44856190 -0.9070070
## 中下 -0.97068022 -0.4603836
## 中等 -0.54845375  0.5670742
## 中上 -0.03232808  1.3639620
## 较高  0.43507458  0.9414503
## 最高  1.25763257 -1.0453509
## 
##  Column scores:
##           [,1]       [,2]
## 肉 -1.36707828 -0.4637594
## 蛋 -1.59707661 -1.1112356
## 鱼  0.02725855  2.6175325
## 奶 -0.46697640  1.5261695
## 衣  0.48491880 -0.2497690
## 耐  1.33266208 -0.8879205
## 文  1.13861727 -0.1015123

输出中典型相关系数的解释：把行变量的每个类当作两点分布结果，共有\(n\)个二值行变量；把列变量的每个类当作两点分布结果，共有\(p\)个二值列变量； \(c_{ij}\)近似等于第\(i\)个二值行变量和第\(j\)个二值列表量的相关系数，把所有\(n\)个二值行变量当成一组，所有\(p\)个二值列变量当成一组，可以计算两组的典型相关系数。

作对应分析的biplot():

biplot(co)
abline(h=0, v=0, lty=3, col='gray')

结果分析：

纵坐标都很小，说明第二因子基本不起作用。
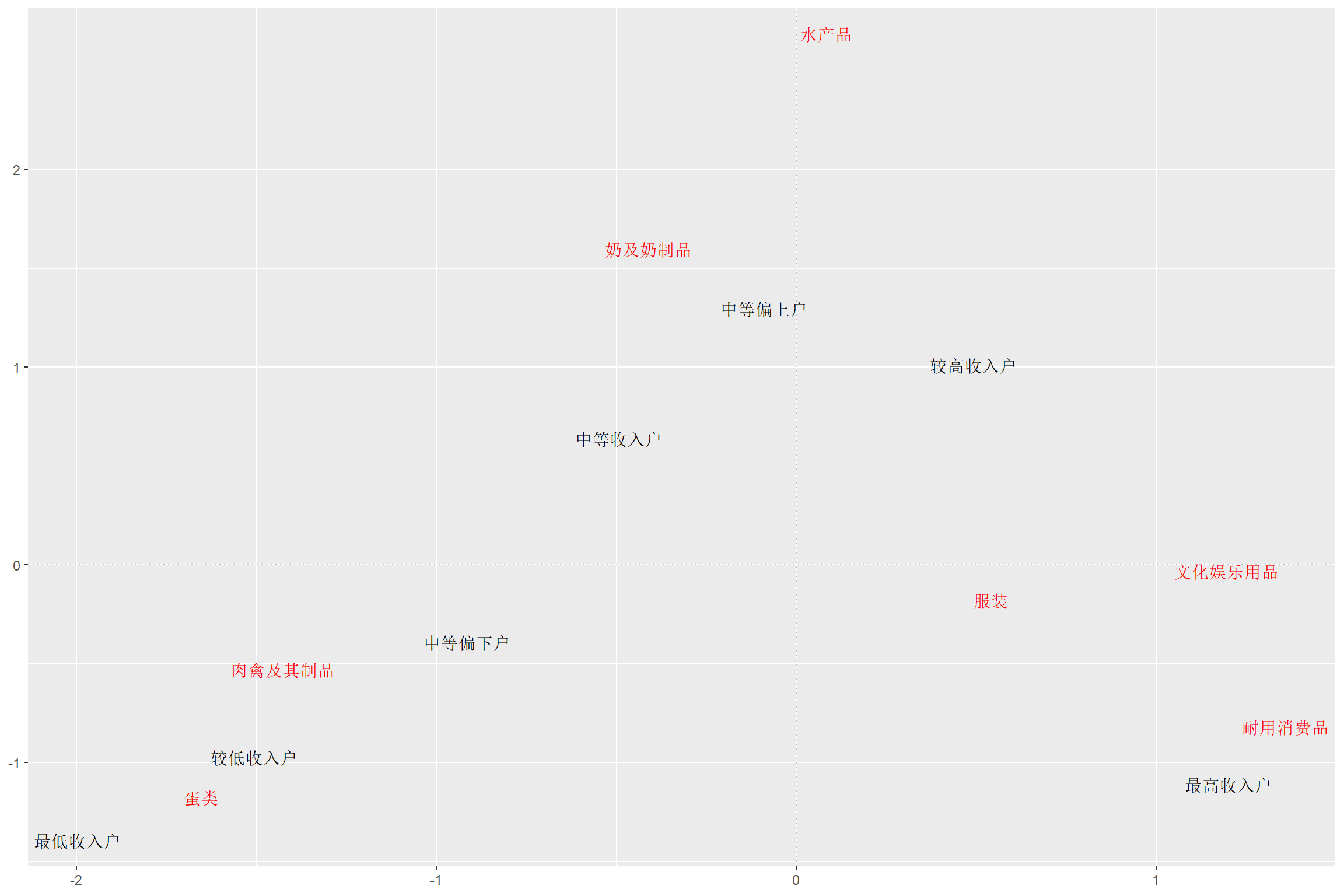
在第一坐标上，比较均匀地分布了从最低到最高的七个收入组，次序完全正确，反映了七个行类在对应分析图中的接近关系是完全正确的。
关于行类（收入组）与列类（消费类型）之间的关系：
最高收入组，其支出结构更偏向耐用消费品和文娱。
较高收入组，其支出结构更偏向服装。
较低收入组，其支出结构在肉类、蛋类占得较多。注意，并不是说这个收入组花费在肉类、蛋类的钱比高收入组还多，这里比的是相对比例。
中等收入组，其支出结构在奶和奶制品占得相对较多。
中上收入组靠近原点，其支出结构和平均的结构相近。

注意MASS.plot.corresp()有四个坐标轴，下、左轴为行类压缩的两个坐标，上、右为列类压缩的两个坐标。这样，两个行类相近，代表了其轮廓（消费分布）相近；两个列类相近，代表其轮廓（层级分布）相近；但某个行类与某个列类相近，则没有好的理论支持，但在图中往往也代表这两个类别倾向于更多同时出现。

见10.10中的做法，可以在fviz_ca_biplot()函数中加map ="rowprincipal"选项表示都映射到行类压缩的降维坐标，或仅画行类，或仅画列类。

10.4.1 多元图形辅助分析

收入组与支出分配的对应分析的多元图形:

library(graphics)
library(aplpack)

用星图验证分类:

stars(log(d.inc), scale=TRUE,
      len=0.6, cex=1, key.loc=c(5, 2),
      draw.segments=TRUE)

因为归一化，所以不如对应分析结果可解释。

脸谱图：

faces(d.inc)

## effect of variables:
##  modified item       Var 
##  "height of face   " "肉"
##  "width of face    " "蛋"
##  "structure of face" "鱼"
##  "height of mouth  " "奶"
##  "width of mouth   " "衣"
##  "smiling          " "耐"
##  "height of eyes   " "文"
##  "width of eyes    " "肉"
##  "height of hair   " "蛋"
##  "width of hair   "  "鱼"
##  "style of hair   "  "奶"
##  "height of nose  "  "衣"
##  "width of nose   "  "耐"
##  "width of ear    "  "文"
##  "height of ear   "  "肉"

这些图没有给出很好的解释。

10.5 苏格兰Caithness地区的人的眼睛颜色和头发颜色组合情况

眼睛颜色和头发颜色列联表:

data(caith)
d.caith <- caith

knitr::kable(d.caith)

	fair	red	medium	dark	black
blue	326	38	241	110	3
light	688	116	584	188	4
medium	343	84	909	412	26
dark	98	48	403	681	85

作列联表独立性卡方检验:

chisq.test(d.caith)

## 
##  Pearson's Chi-squared test
## 
## data:  d.caith
## X-squared = 1240, df = 12, p-value < 2.2e-16

10.5.1 作对应分析，取两个特征值

co <- corresp(d.caith, nf=2)
co

## First canonical correlation(s): 0.4463684 0.1734554 
## 
##  Row scores:
##               [,1]       [,2]
## blue    0.89679252  0.9536227
## light   0.98731818  0.5100045
## medium -0.07530627 -1.4124778
## dark   -1.57434710  0.7720361
## 
##  Column scores:
##               [,1]       [,2]
## fair    1.21871379  1.0022432
## red     0.52257500  0.2783364
## medium  0.09414671 -1.2009094
## dark   -1.31888486  0.5992920
## black  -2.45176017  1.6513565

10.5.2 作对应分析的biplot

biplot(co)
abline(h=0, v=0, lty=3, col='gray')

从眼睛颜色与头发颜色关系看：

发色fair则眼睛颜色多blue, light;
发色medium, 眼睛颜色多medium;
发色black, 眼睛颜色多dark。

10.6 奶牛场规模与患病

奶牛场规模小、中、大与某种牛传染病发病无、轻、重的列联表。

d.cow <- data.frame(
    herdsize=factor(
      rep(c('小', '中', '大'), each=3),
      levels=c('小', '中', '大')),
    disease=factor(
      rep(c('无', '轻', '重'), 3),
      levels=c('无', '轻', '重')),
    count=c(9, 5, 9,  18, 4, 19,  11, 88, 136))
## 下面把d1转置成列联表格式, 用xtabs()函数
d.cow.cf <- xtabs(count ~ herdsize + disease, data=d.cow)

knitr::kable(d.cow.cf)

	无	轻	重
小	9	5	9
中	18	4	19
大	11	88	136

作对应分析，取两个特征值:

co <- corresp(d.cow.cf, nf=2)
co

## First canonical correlation(s): 0.47152500 0.04338242 
## 
##  herdsize scores:
##          [,1]        [,2]
## 小 -1.6594198  3.04077718
## 中 -2.0490587 -1.44708027
## 大  0.5199067 -0.04513866
## 
##  disease scores:
##          [,1]       [,2]
## 无 -2.5727754  0.4992470
## 轻  0.6396978  1.2935459
## 重  0.2177730 -0.8807642

作对应分析的biplot:

biplot(co)
abline(h=0, v=0, lty=3, col='gray')

图形解释:

第二因子作用很小。
病情轻、重很接近，与无方向相隔很远，是合理的。
大的牛场倾向于有病；中、小牛场倾向于无病。

10.7 美国50个州数据

state.x77数据，美国50个州在1970年代的基本情况数据。变量:

Population: 人口
Illiteracy: 文盲比例
Life Exp: 期望寿命
Murder: 每十万人杀人犯罪数
HS Grad: 高中毕业生比例
Frost: 日最低温度在结霜点以下平均天数
Area: 面积，平方英里

data(state.x77)

## Warning in data(state.x77): data set 'state.x77' not found

d.st <- state.x77
rownames(d.st) <- state.abb
colnames(d.st) <- c('人口', '收入', '文盲',
                 '寿命', '谋杀', '高中生',
                 '无霜期', '面积')

knitr::kable(d.st)

	人口	收入	文盲	寿命	谋杀	高中生	无霜期	面积
AL	3615	3624	2.1	69.05	15.1	41.3	20	50708
AK	365	6315	1.5	69.31	11.3	66.7	152	566432
AZ	2212	4530	1.8	70.55	7.8	58.1	15	113417
AR	2110	3378	1.9	70.66	10.1	39.9	65	51945
CA	21198	5114	1.1	71.71	10.3	62.6	20	156361
CO	2541	4884	0.7	72.06	6.8	63.9	166	103766
CT	3100	5348	1.1	72.48	3.1	56.0	139	4862
DE	579	4809	0.9	70.06	6.2	54.6	103	1982
FL	8277	4815	1.3	70.66	10.7	52.6	11	54090
GA	4931	4091	2.0	68.54	13.9	40.6	60	58073
HI	868	4963	1.9	73.60	6.2	61.9	0	6425
ID	813	4119	0.6	71.87	5.3	59.5	126	82677
IL	11197	5107	0.9	70.14	10.3	52.6	127	55748
IN	5313	4458	0.7	70.88	7.1	52.9	122	36097
IA	2861	4628	0.5	72.56	2.3	59.0	140	55941
KS	2280	4669	0.6	72.58	4.5	59.9	114	81787
KY	3387	3712	1.6	70.10	10.6	38.5	95	39650
LA	3806	3545	2.8	68.76	13.2	42.2	12	44930
ME	1058	3694	0.7	70.39	2.7	54.7	161	30920
MD	4122	5299	0.9	70.22	8.5	52.3	101	9891
MA	5814	4755	1.1	71.83	3.3	58.5	103	7826
MI	9111	4751	0.9	70.63	11.1	52.8	125	56817
MN	3921	4675	0.6	72.96	2.3	57.6	160	79289
MS	2341	3098	2.4	68.09	12.5	41.0	50	47296
MO	4767	4254	0.8	70.69	9.3	48.8	108	68995
MT	746	4347	0.6	70.56	5.0	59.2	155	145587
NE	1544	4508	0.6	72.60	2.9	59.3	139	76483
NV	590	5149	0.5	69.03	11.5	65.2	188	109889
NH	812	4281	0.7	71.23	3.3	57.6	174	9027
NJ	7333	5237	1.1	70.93	5.2	52.5	115	7521
NM	1144	3601	2.2	70.32	9.7	55.2	120	121412
NY	18076	4903	1.4	70.55	10.9	52.7	82	47831
NC	5441	3875	1.8	69.21	11.1	38.5	80	48798
ND	637	5087	0.8	72.78	1.4	50.3	186	69273
OH	10735	4561	0.8	70.82	7.4	53.2	124	40975
OK	2715	3983	1.1	71.42	6.4	51.6	82	68782
OR	2284	4660	0.6	72.13	4.2	60.0	44	96184
PA	11860	4449	1.0	70.43	6.1	50.2	126	44966
RI	931	4558	1.3	71.90	2.4	46.4	127	1049
SC	2816	3635	2.3	67.96	11.6	37.8	65	30225
SD	681	4167	0.5	72.08	1.7	53.3	172	75955
TN	4173	3821	1.7	70.11	11.0	41.8	70	41328
TX	12237	4188	2.2	70.90	12.2	47.4	35	262134
UT	1203	4022	0.6	72.90	4.5	67.3	137	82096
VT	472	3907	0.6	71.64	5.5	57.1	168	9267
VA	4981	4701	1.4	70.08	9.5	47.8	85	39780
WA	3559	4864	0.6	71.72	4.3	63.5	32	66570
WV	1799	3617	1.4	69.48	6.7	41.6	100	24070
WI	4589	4468	0.7	72.48	3.0	54.5	149	54464
WY	376	4566	0.6	70.29	6.9	62.9	173	97203

把各列都归一化到[1,100]内:

cmin <- apply(d.st, 2, min)
cmax <- apply(d.st, 2, max)
cra <- cmax - cmin
d.st <- 1 + scale(d.st, center=cmin, scale=cra)*99

作对应分析，取两个特征值:

co <- corresp(d.st, nf=2)

## Warning in corresp.matrix(d.st, nf = 2): negative or non-integer entries in
## table

co

## First canonical correlation(s): 0.4409611 0.2444077 
## 
##  Row scores:
##           [,1]         [,2]
## AL -2.20149269 -0.542965161
## AK -0.01576789 -0.789803960
## AZ -0.55117605 -0.326692416
## AR -1.37991754 -1.145878975
## CA -0.34790488  2.917753726
## CO  0.73194052 -0.287074654
## CT  0.69466978 -0.118727593
## DE  0.41142720 -0.564367149
## FL -0.65670163  1.351785206
## GA -1.82576130 -0.263388506
## HI -0.07737277 -0.374989147
## ID  0.88627116 -0.586078435
## IL -0.14211633  1.380675923
## IN  0.35846989  0.466472638
## IA  1.21710818  0.008725745
## KS  0.92379266 -0.062928170
## KY -1.15502945 -0.683091362
## LA -2.55092046 -0.901072520
## ME  1.03160918 -1.013970323
## MD  0.10018053  0.359506400
## MA  0.51371677  0.530696459
## MI -0.13877369  0.961650956
## MN  1.08950670  0.047468793
## MS -2.55064321 -1.553753389
## MO -0.02780331  0.273019338
## MT  0.85220769 -0.747805794
## NE  1.12446618 -0.370803801
## NV  0.48584817 -0.639999952
## NH  1.06242729 -0.847482114
## NJ  0.21419679  0.833466286
## NM -0.71656957 -1.431216293
## NY -0.62005972  2.332760102
## NC -1.52184972 -0.151884256
## ND  1.11033958 -0.805523565
## OH  0.12284257  1.444811688
## OK  0.08235278 -0.273159323
## OR  0.84322394  0.362572895
## PA -0.03360095  1.605533210
## RI  0.46497447 -0.942590729
## SC -2.37399259 -1.281210099
## SD  1.35270900 -0.841481787
## TN -1.21730665 -0.335524928
## TX -1.21222663  0.966800790
## UT  1.06582655 -0.496582396
## VT  0.94318448 -0.930617172
## VA -0.53953828  0.182976274
## WA  0.80914377  0.800396474
## WV -0.72738284 -1.152727330
## WI  0.88958550  0.164651407
## WY  0.78056003 -0.798408387
## 
##  Column scores:
##              [,1]        [,2]
## 人口   -0.7387762  3.42345189
## 收入    0.4110482  0.47045368
## 文盲   -2.0307400 -1.05538283
## 寿命    0.7094660 -0.02244498
## 谋杀   -1.3476948 -0.12249617
## 高中生  0.8287947  0.02609934
## 无霜期  0.6810850 -0.81204484
## 面积   -0.1071694 -0.31923610

作对应分析的biplot:

biplot(co)
abline(h=0, v=0, lty=3, col='gray')

print(cbind(state.abb, state.name))

##       state.abb state.name      
##  [1,] "AL"      "Alabama"       
##  [2,] "AK"      "Alaska"        
##  [3,] "AZ"      "Arizona"       
##  [4,] "AR"      "Arkansas"      
##  [5,] "CA"      "California"    
##  [6,] "CO"      "Colorado"      
##  [7,] "CT"      "Connecticut"   
##  [8,] "DE"      "Delaware"      
##  [9,] "FL"      "Florida"       
## [10,] "GA"      "Georgia"       
## [11,] "HI"      "Hawaii"        
## [12,] "ID"      "Idaho"         
## [13,] "IL"      "Illinois"      
## [14,] "IN"      "Indiana"       
## [15,] "IA"      "Iowa"          
## [16,] "KS"      "Kansas"        
## [17,] "KY"      "Kentucky"      
## [18,] "LA"      "Louisiana"     
## [19,] "ME"      "Maine"         
## [20,] "MD"      "Maryland"      
## [21,] "MA"      "Massachusetts" 
## [22,] "MI"      "Michigan"      
## [23,] "MN"      "Minnesota"     
## [24,] "MS"      "Mississippi"   
## [25,] "MO"      "Missouri"      
## [26,] "MT"      "Montana"       
## [27,] "NE"      "Nebraska"      
## [28,] "NV"      "Nevada"        
## [29,] "NH"      "New Hampshire" 
## [30,] "NJ"      "New Jersey"    
## [31,] "NM"      "New Mexico"    
## [32,] "NY"      "New York"      
## [33,] "NC"      "North Carolina"
## [34,] "ND"      "North Dakota"  
## [35,] "OH"      "Ohio"          
## [36,] "OK"      "Oklahoma"      
## [37,] "OR"      "Oregon"        
## [38,] "PA"      "Pennsylvania"  
## [39,] "RI"      "Rhode Island"  
## [40,] "SC"      "South Carolina"
## [41,] "SD"      "South Dakota"  
## [42,] "TN"      "Tennessee"     
## [43,] "TX"      "Texas"         
## [44,] "UT"      "Utah"          
## [45,] "VT"      "Vermont"       
## [46,] "VA"      "Virginia"      
## [47,] "WA"      "Washington"    
## [48,] "WV"      "West Virginia" 
## [49,] "WI"      "Wisconsin"     
## [50,] "WY"      "Wyoming"

人口变量：CA和NY都是人口多的。

寿命变量与高中毕业生比例相近，说明这两个变量相关性强。

图中离谋杀变量近的并不是谋杀犯罪率最高的。

10.8 使用ca包

ca扩展包提供了对应分析更多功能（比如多重和联合对应分析），以及利用ggplot2进行可视化。

以我国城镇居民收入等级和消费组成为例进行分析。

library(ca)
ca.inc <- ca(d.inc)
summary(ca.inc)

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.032160  98.3  98.3  *************************
##  2      0.000360   1.1  99.4                           
##  3      0.000175   0.5  99.9                           
##  4      1.7e-050   0.1 100.0                           
##  5      6e-06000   0.0 100.0                           
##  6      00000000   0.0 100.0                           
##         -------- -----                                 
##  Total: 0.032717 100.0                                 
## 
## 
## Rows:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 | 最低 |   61  991  234 | -353 986 235 |  -25   5 107 |
## 2 | 较低 |   82  999  171 | -260 994 173 |  -17   4  68 |
## 3 | 中下 |  105  981   99 | -174 979  99 |   -9   2  22 |
## 4 | 中等 |  131  987   40 |  -98 975  40 |   11  12  42 |
## 5 | 中上 |  160  972    4 |   -6  46   0 |   26 925 298 |
## 6 | 较高 |  197  971   40 |   78 923  37 |   18  48 175 |
## 7 | 最高 |  264 1000  413 |  226 992 417 |  -20   8 288 |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |   肉 |  268 1000  493 | -245 998 500 |   -9   1  58 |
## 2 |   蛋 |   27  995   68 | -286 990  68 |  -21   5  33 |
## 3 |   鱼 |   97  990    7 |    5  10   0 |   50 981 664 |
## 4 |   奶 |   59  997   14 |  -84 891  13 |   29 106 138 |
## 5 |   衣 |  326  968   78 |   87 966  77 |   -5   3  20 |
## 6 |   耐 |  109  998  192 |  239 993 194 |  -17   5  86 |
## 7 |   文 |  114  982  148 |  204 982 148 |   -2   0   1 |

结果中的主惯量(Principal inertias)即对独立性卡方统计量\(V/N\)的贡献，即各个\(\lambda_k^2\)的值。在行和列的信息显示中，数值都用乘以1000显示。 mass是\(1000 \boldsymbol a\)或\(1000 \boldsymbol b\)，即边缘比例。 k = 1和k = 2分别表示两个主坐标，即行轮廓或列轮廓降维的二维的表示，单位是千分之一。

plot(ca.inc)

10.9 使用FactoMineR包

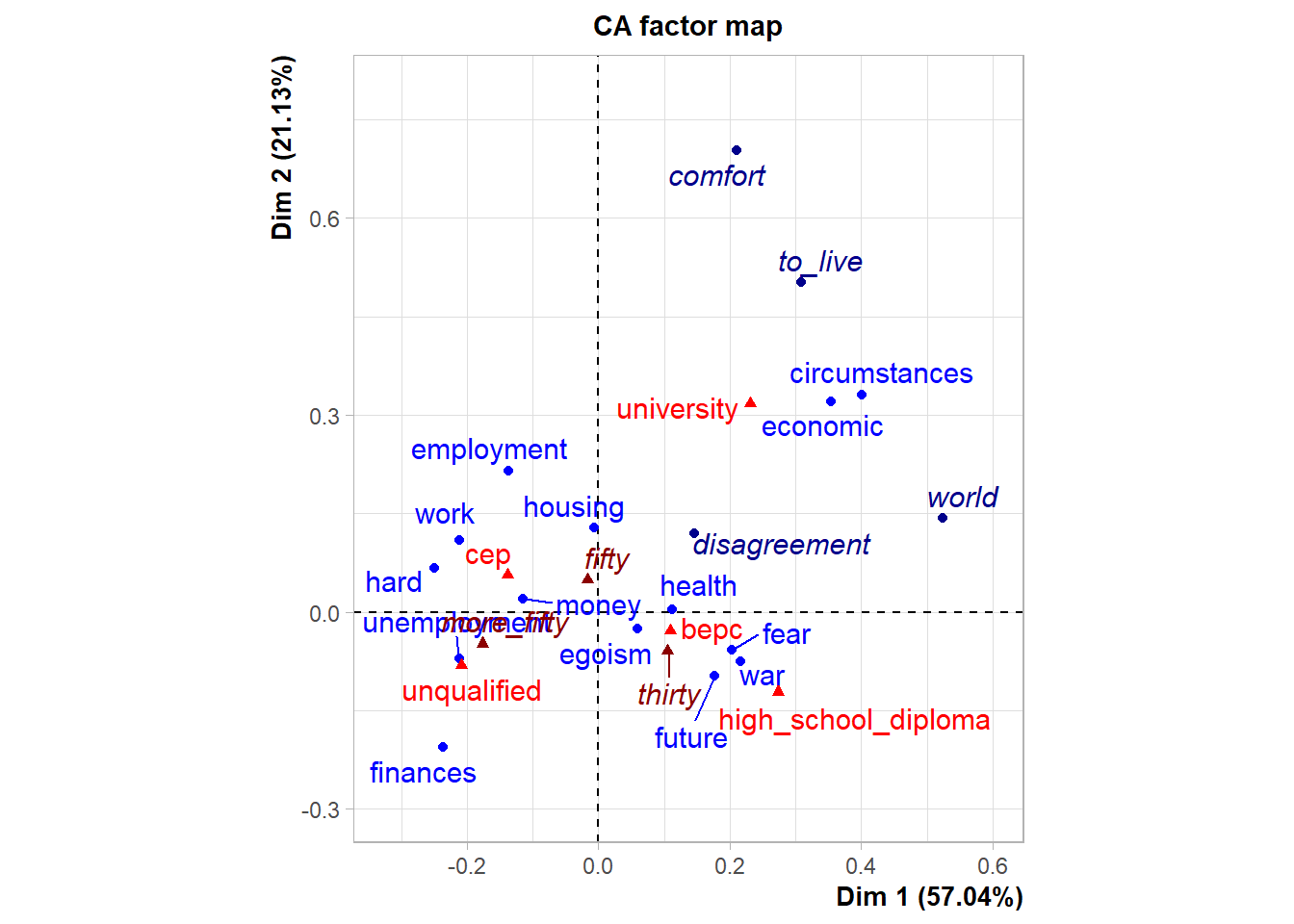
例子来自FactoMineR包文档。数据children来自一项妇女生育意愿的调查， 10行代表妇女对生育有疑虑的原因， 8列代表受访人口的教育水平、年龄组等人口学特征。

library(FactoMineR)
data(children)
res.ca <- CA (children, row.sup = 15:18, col.sup = 6:8)

summary(res.ca)

## 
## Call:
## CA(X = children, row.sup = 15:18, col.sup = 6:8) 
## 
## The chi square of independence between the two variables is equal to 98.80159 (p-value =  9.748064e-05 ).
## 
## Eigenvalues
##                        Dim.1   Dim.2   Dim.3   Dim.4
## Variance               0.035   0.013   0.007   0.006
## % of var.             57.043  21.132  11.764  10.061
## Cumulative % of var.  57.043  78.175  89.939 100.000
## 
## Rows (the 10 first)
##                       Iner*1000    Dim.1    ctr   cos2    Dim.2    ctr   cos2  
## money               |     3.759 | -0.115  4.550  0.428 |  0.020  0.371  0.013 |
## future              |     8.690 |  0.176 17.567  0.716 | -0.098 14.587  0.220 |
## unemployment        |     9.151 | -0.212 22.616  0.875 | -0.071  6.779  0.097 |
## circumstances       |     3.804 |  0.401  6.274  0.584 |  0.331 11.544  0.398 |
## hard                |     1.199 | -0.250  2.994  0.884 |  0.068  0.592  0.065 |
## economic            |     8.787 |  0.354 12.005  0.484 |  0.321 26.604  0.397 |
## egoism              |     3.287 |  0.060  0.681  0.073 | -0.026  0.338  0.013 |
## employment          |     5.648 | -0.137  2.621  0.164 |  0.215 17.555  0.408 |
## finances            |     3.576 | -0.237  2.790  0.276 | -0.206  5.690  0.209 |
## war                 |     1.025 |  0.217  2.169  0.749 | -0.075  0.694  0.089 |
##                      Dim.3    ctr   cos2  
## money                0.101 16.884  0.328 |
## future              -0.053  7.568  0.064 |
## unemployment        -0.004  0.046  0.000 |
## circumstances       -0.016  0.046  0.001 |
## hard                 0.060  0.845  0.051 |
## economic             0.084  3.280  0.027 |
## egoism               0.179 29.496  0.655 |
## employment          -0.213 30.815  0.398 |
## finances            -0.044  0.469  0.010 |
## war                 -0.098  2.139  0.152 |
## 
## Columns
##                       Iner*1000    Dim.1    ctr   cos2    Dim.2    ctr   cos2  
## unqualified         |    13.146 | -0.209 25.110  0.676 | -0.081 10.082  0.101 |
## cep                 |    10.044 | -0.139 18.297  0.645 |  0.056  8.079  0.105 |
## bepc                |     7.670 |  0.109  6.758  0.312 | -0.028  1.251  0.021 |
## high_school_diploma |    17.732 |  0.274 37.976  0.758 | -0.121 20.099  0.149 |
## university          |    13.468 |  0.231 11.859  0.312 |  0.318 60.488  0.589 |
##                      Dim.3    ctr   cos2  
## unqualified          0.073 14.659  0.081 |
## cep                 -0.018  1.520  0.011 |
## bepc                -0.147 59.874  0.570 |
## high_school_diploma  0.077 14.407  0.059 |
## university           0.094  9.540  0.052 |
## 
## Supplementary rows
##                       Dim.1  cos2   Dim.2  cos2   Dim.3  cos2  
## comfort             | 0.210 0.069 | 0.703 0.775 | 0.071 0.008 |
## disagreement        | 0.146 0.131 | 0.119 0.087 | 0.171 0.180 |
## world               | 0.523 0.876 | 0.143 0.065 | 0.084 0.023 |
## to_live             | 0.308 0.139 | 0.502 0.369 | 0.521 0.397 |
## 
## Supplementary columns
##                        Dim.1   cos2    Dim.2   cos2    Dim.3   cos2  
## thirty              |  0.105  0.138 | -0.060  0.044 | -0.103  0.132 |
## fifty               | -0.017  0.011 |  0.049  0.090 | -0.016  0.009 |
## more_fifty          | -0.177  0.286 | -0.048  0.021 |  0.101  0.093 |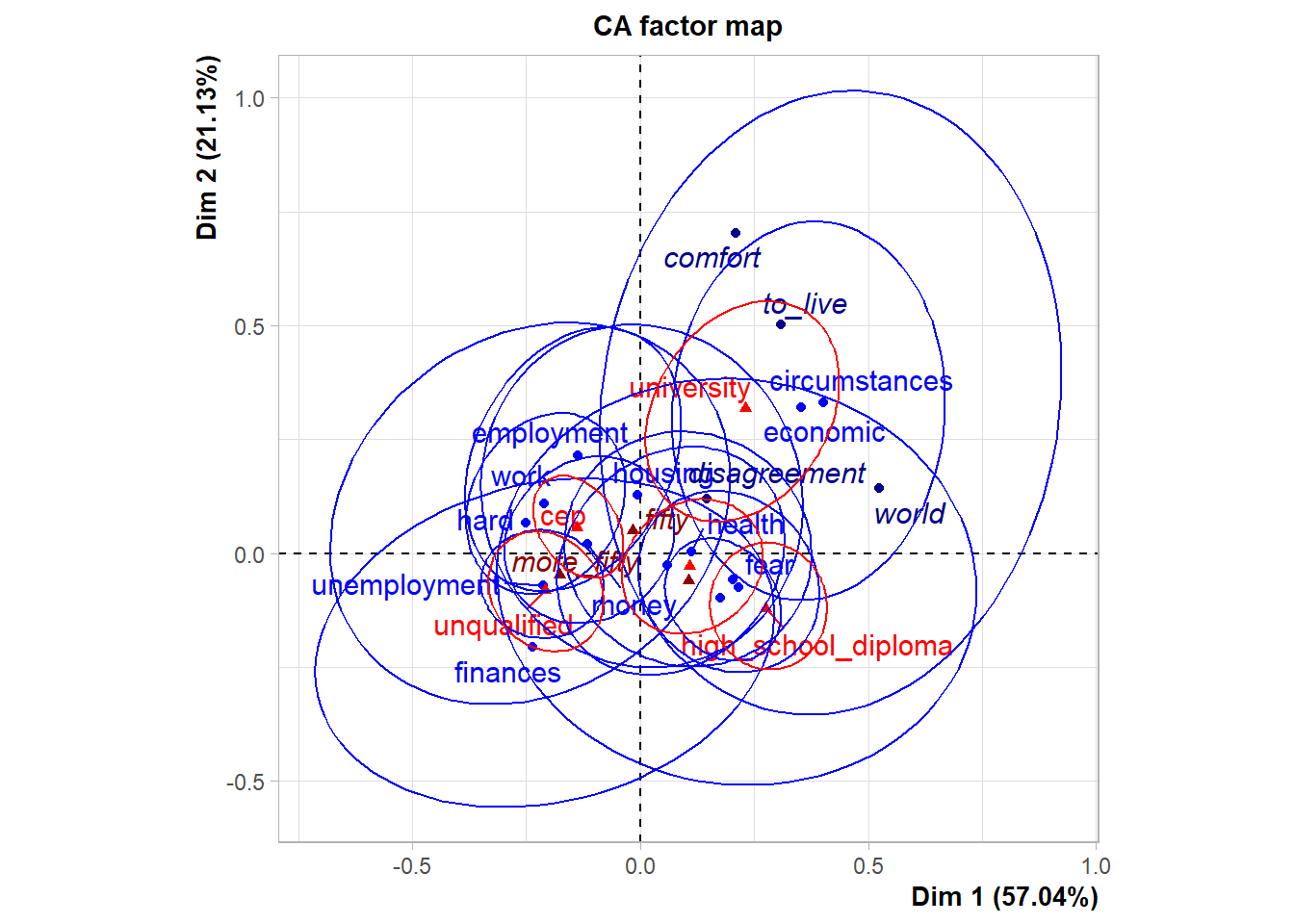

## Ellipses for all the active elements
ellipseCA(res.ca)

## Ellipses around some columns only
ellipseCA(res.ca,ellipse="col",col.col.ell=c(rep("blue",2),rep("transparent",3)),
     invisible=c("row.sup","col.sup"))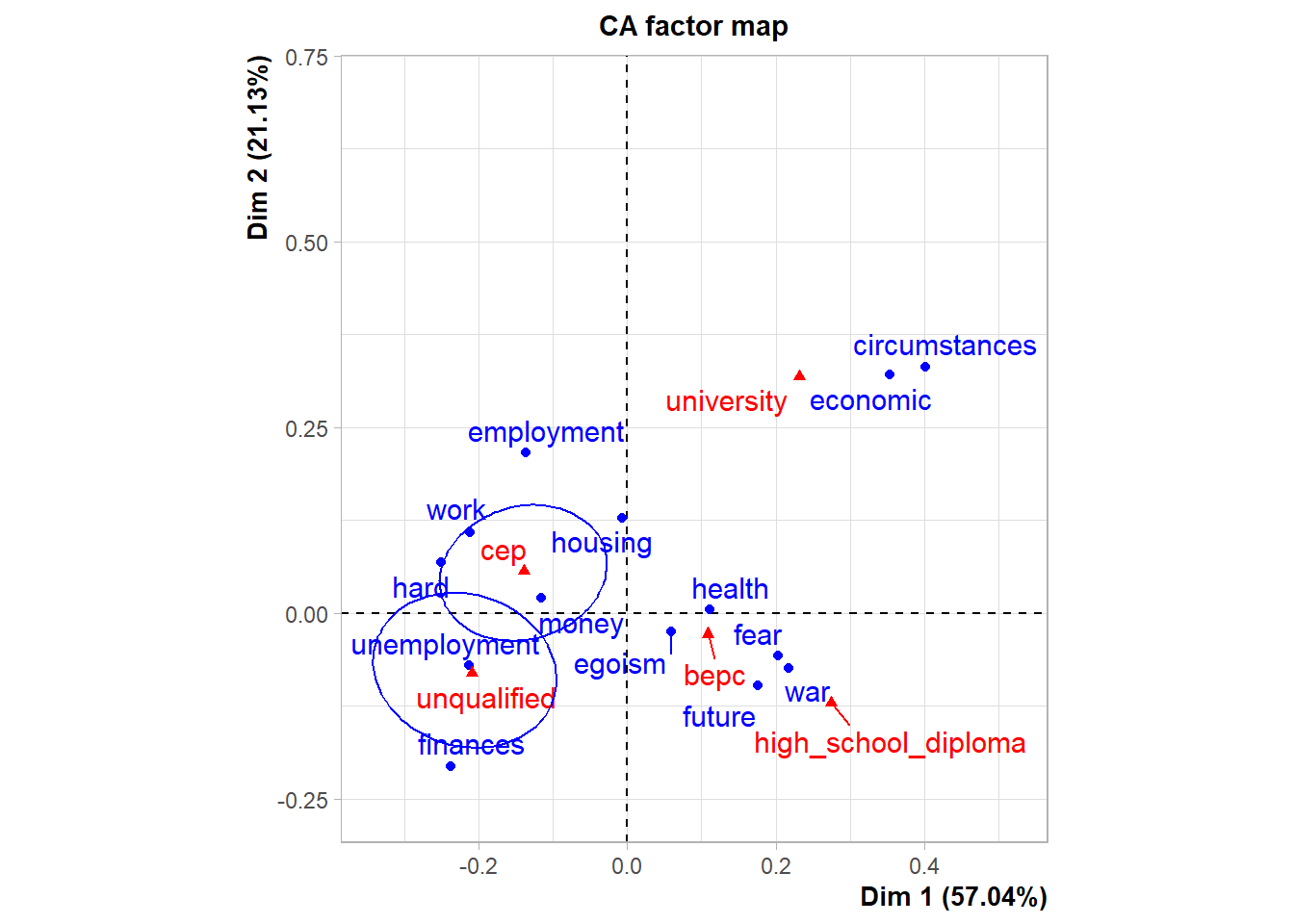

结果中的方差百分比应该是按照卡方统计量贡献占比计算的。行、列结果中Dim.1是降维后第一维坐标， Dim.2是第二维， ctr表示该行或列对该维形成时的贡献大小， cos2表征前两维在恢复该行或列时的质量指标，取值于\([0,1]\)内，取值越大表示恢复越好。程序中的row.sup和col.sup用于添加辅助变量。

第一个图是降维到二维的对应分析双重散点图，蓝色代表行，红色代表列。第二个图用椭圆代表每一行、列类别，分离的椭圆代表差异显著，较小的椭圆代表较高置信度。

10.10 使用FactoMineR包和factoextra包

例子来自factoextra包的使用文档。数据集housetasks是一对夫妻关于家务活分配的列联表，各行列出了若干中家务活，各列则为分配给妻子、轮流、分配给丈夫、合作四种分配方式。

library(factoextra)
library("FactoMineR")
data(housetasks)
head(housetasks)

##            Wife Alternating Husband Jointly
## Laundry     156          14       2       4
## Main_meal   124          20       5       4
## Dinner       77          11       7      13
## Breakfeast   82          36      15       7
## Tidying      53          11       1      57
## Dishes       32          24       4      53

res.ca <- CA(housetasks, graph=FALSE)
summary(res.ca)

## 
## Call:
## CA(X = housetasks, graph = FALSE) 
## 
## The chi square of independence between the two variables is equal to 1944.456 (p-value =  0 ).
## 
## Eigenvalues
##                        Dim.1   Dim.2   Dim.3
## Variance               0.543   0.445   0.127
## % of var.             48.692  39.913  11.395
## Cumulative % of var.  48.692  88.605 100.000
## 
## Rows (the 10 first)
##               Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
## Laundry     |   134.160 |  -0.992  18.287   0.740 |   0.495   5.564   0.185 |
## Main_meal   |    90.692 |  -0.876  12.389   0.742 |   0.490   4.736   0.232 |
## Dinner      |    38.246 |  -0.693   5.471   0.777 |   0.308   1.321   0.154 |
## Breakfeast  |    41.124 |  -0.509   3.825   0.505 |   0.453   3.699   0.400 |
## Tidying     |    24.667 |  -0.394   1.998   0.440 |  -0.434   2.966   0.535 |
## Dishes      |    19.587 |  -0.189   0.426   0.118 |  -0.442   2.844   0.646 |
## Shopping    |    14.970 |  -0.118   0.176   0.064 |  -0.403   2.515   0.748 |
## Official    |    53.300 |   0.227   0.521   0.053 |   0.254   0.796   0.066 |
## Driving     |   101.509 |   0.742   8.078   0.432 |   0.653   7.647   0.335 |
## Finances    |    29.564 |   0.271   0.875   0.161 |  -0.618   5.559   0.837 |
##               Dim.3     ctr    cos2  
## Laundry      -0.317   7.968   0.075 |
## Main_meal    -0.164   1.859   0.026 |
## Dinner       -0.207   2.097   0.070 |
## Breakfeast    0.220   3.069   0.095 |
## Tidying      -0.094   0.489   0.025 |
## Dishes        0.267   3.634   0.236 |
## Shopping      0.203   2.223   0.189 |
## Official      0.923  36.940   0.881 |
## Driving       0.544  18.596   0.233 |
## Finances      0.035   0.062   0.003 |
## 
## Columns
##               Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
## Wife        |   301.019 |  -0.838  44.462   0.802 |   0.365  10.312   0.152 |
## Alternating |   117.824 |  -0.062   0.104   0.005 |   0.292   2.783   0.105 |
## Husband     |   381.373 |   1.161  54.234   0.772 |   0.602  17.787   0.208 |
## Jointly     |   314.725 |   0.149   1.200   0.021 |  -1.027  69.118   0.977 |
##               Dim.3     ctr    cos2  
## Wife         -0.200  10.822   0.046 |
## Alternating   0.849  82.549   0.890 |
## Husband      -0.189   6.133   0.020 |
## Jointly      -0.046   0.495   0.002 |

fviz_ca_biplot()作双重散点图，既有行类别又有列类别。

# Biplot of rows and columns
# ++++++++++++++++++++++++++
# Symetric Biplot of rows and columns
fviz_ca_biplot(res.ca, repel=TRUE)

上图用了经典的双重散点图做法，蓝色圆点代表行类别，红色三角代表列类别。

# Asymetric biplot, use arrows for columns
fviz_ca_biplot(res.ca, map ="rowprincipal",
 arrow = c(FALSE, TRUE), repel=TRUE)

上图图的选项arrow = c(FALSE, TRUE)将列用箭头表示，而map ="rowprincipal"则仅行类是行轮廓，列轮廓则映射到行表示的压缩空间中。这时，两行接近表示这两个类别在各列中分布接近。

加选项label ="row"则仅有行有标签，加选项label ="col"则仅列有标签：

# Keep only the labels for row points
fviz_ca_biplot(res.ca, label ="row")

# Keep only labels for column points
fviz_ca_biplot(res.ca, label ="col")

用select.row和select.col选择仅在构成降维向量时贡献较大的那些类别:

# Select the top 7 contributing rows
# And the top 3 columns
fviz_ca_biplot(res.ca,  
               select.row = list(contrib = 7),
               select.col = list(contrib = 3))

函数fviz_ca_row()仅画行的降维图， fviz_ca_col()仅画列的降维图，仍可用select.row和select.col选项仅选择贡献较大的类别：

# Graph of row variables
# +++++++++++++++++++++
   
# Control automatically the color of row points
   # using the "cos2" or the contributions "contrib"
   # cos2 = the quality of the rows on the factor map
   # Change gradient color
   # Use repel = TRUE to avoid overplotting (slow if many points)
fviz_ca_row(res.ca, col.row = "cos2",
   gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
   repel = TRUE)

# You can also control the transparency 
# of the color by the "cos2" or "contrib"
fviz_ca_row(res.ca, alpha.row="contrib")

# Select and visualize some rows with select.row argument.
 # - Rows with cos2 >= 0.5: select.row = list(cos2 = 0.5)
 # - Top 7 rows according to the cos2: select.row = list(cos2 = 7)
 # - Top 7 contributing rows: select.row = list(contrib = 7)
 # - Select rows by names: select.row = list(name = c("Breakfeast", "Repairs", "Holidays"))
 
 # Example: Select the top 7 contributing rows
fviz_ca_row(res.ca, select.row = list(contrib = 7))

# Graph of column points
# ++++++++++++++++++++++++++++

 
# Control colors using their contributions
fviz_ca_col(res.ca, col.col = "contrib",
   gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"))

# Select columns with select.col argument
   # You can select by contrib, cos2 and name 
   # as previously described for ind
# Select the top 3 contributing columns
fviz_ca_col(res.ca, select.col = list(contrib = 3))

10.11 附录：用ggplot2改写biplot

require(ggplot2)
require(ggrepel)
require(tibble)
ggbiplot.corresp <- function(obj) {
  rscore <- tibble(
    label = rownames(obj$rscore),
    x = obj$rscore[,1],
    y = obj$rscore[,2]
  )
  cscore <- tibble(
    label = rownames(obj$cscore),
    x = obj$cscore[,1],
    y = obj$cscore[,2]
  )
  p <- ggplot(mapping = aes(x = x, y = y, label=label)) +
    geom_text_repel(data = rscore, color="black") +
    geom_text_repel(data = cscore, color="red") +
    geom_hline(yintercept=0, linetype=3, col="gray") +
    geom_vline(xintercept=0, linetype=3, col="gray") +
    labs(x=NULL, y=NULL)
  p
}

现金支出问题的测试：

library(MASS)
d0 <- as.data.frame(incomeUse)
rownames(d0) <- d0[[1]]
d <- d0[,-1]
co <- corresp(d, nf=2)

## Warning in corresp.matrix(as.matrix(x), ...): negative or non-integer entries in
## table

ggbiplot.corresp(co)