5 多重比较
5.1 错误率定义
5.1.1 多重比较问题
假设检验是应用统计中被使用最多的方法之一, 在现在这样的大数据年代,越来越多的数据被收集, 可以支持更多的假设检验。 对高维数据的分析也经常要同时做多次假设检验。 在生物、医学、药学的基因数据研究中经常遇到这种问题, 同时检验的次数达到成百上千甚至于百万级别。
多次进行检验, 如果每次检验的第一类错误概率是\(\alpha\), 各次检验独立, 则检验\(m\)次, 在所有零假设都成立的情况下至少犯一次第一类错误的概率为 \[ 1 - (1 - \alpha)^m \] 比如, \(m=100\),\(\alpha=0.05\)时, 至少犯一次第一类错误概率为0.994。
这就使得我们怀疑, \(m\)次比较中找到的若干个显著差异, 其中有很大比例是虚假的。 这类问题称为多重比较(Multiple Comparison)或者多重检验(Multiple Testing), 统计文献中有许多对这种问题进行处理的方法, 比如, 控制总的第一类错误概率, 控制错误发现率, 用重抽样方法控制总错误率(Dudoit and Laan 2008), 等等。
如果不对多重检验进行调整, 可能导致如下问题:
- 可能报告实际没有效应的水平为显著。
- 从多个检验结论中挑选最优时, 报告的最优效应一定会偏高, 不论这些效应实际有还是没有, 挑选最大的一组一定使得结果比实际效应高。
- 某些显著结论的方向是反的。 如果用了双侧检验但对显著结果做出单向的结论, 在多个检验的情况下可能有错误的显著性而且方向错误。
- 研究结果不可重复展现。 比如,为了分析临床试验数据, 有四种模型可以利用, 有一个模型的结果是有效的, 就采用该模型而发表的论文中不提其它模型, 其实就已经有多重检验问题, 别的研究人员就不容易得到相同结论。 药监部门的统计分析规定中一般都对多重比较调整做了要求。
5.1.2 各种第一类错误
设有\(m\)个检验(比较) \(H_i, i=1,2,\dots, m\), 每一个称为一个基础检验。
对一个检验, 可以发生如下三种错误:
- 第一类错误,\(H_0\)成立但被拒绝,假阳性;
- 第二类错误,\(H_0\)不成立但接受\(H_0\),假阴性;
- \(H_0\)不成立也正确拒绝\(H_0\),但判决的方向反了。
将\(m\)次检验的结果情况用下表表示:
| 实际 \ 判决 | 接受\(H_0\) | 拒绝\(H_0\) | 总计 |
|---|---|---|---|
| \(H_0\)真 | \(U\)(TN) | \(V\)(FP) | \(m_0\) |
| \(H_0\)假 | \(T\)(FN) | \(S\)(TP) | \(m-m_0\) |
| 总计 | \(W\) | \(R\) | \(m\) |
在表5.1中\(m\)是给定的检验个数, \(m_0\)是未知的零假设成立个数, \(R\)是可观测的在\(m\)个检验中总的拒绝个数, 是随机的; \(U, V, T, S\)都是不可观测的随机变量。 \(V\)是犯第一类错误的个数, 或假阳性的个数; \(T\)是犯第二类错误的个数, 或假阴性的个数。
假设检验一般都是控制第一类错误, 所以在多重比较问题中主要关心的也是错误拒绝零假设的错误。 对表5.1的\(m\)个检验, 可以定义平均单次比较错误率(PCER) \[ \text{PCER} = \frac{E V}{m} \] 注意这个定义是所有\(m\)中的平均假阳性比例, 如果每个检验用水平\(\alpha\)进行检验, 则\(\text{PCER} = \alpha m_0 / m \leq \alpha\)。 所以, 控制每次比较的检验水平就可以控制平均单次比较错误率。
在表5.1的划分下, 定义总错误率(FWER)为 \[ \text{FWER} = P(V > 0), \] 即所有检验中至少有一个假阳性结论的概率。 这是多重比较常用的错误率控制方法, 在比较数量中小规模以及需要强证据做出显著结论时常用。 当\(m=1\)时, 这就是一次检验的第一类错误概率。
当比较个数很多时, 单个比较的检验\(\alpha\)给定情况下\(m \to \infty\)总错误率可能会趋于1, 比如,所有零假设都成立而且检验统计量相互独立时有 \[ \text{FWER} = 1 - P(V=0) = 1 - (1-\alpha)^m \to 1, \ m \to \infty. \]
当比较个数很多或者需要尽可能多地检出显著结果时, 控制总错误率就过于保守而不适用, 可以将总错误率从至少一个假阳性的概率推广为超过\(k\)个假阳性的概率, 而少于\(k\)个假阳性被容忍。 定义广义总错误率(gFWER)为 \[ \text{gFWER} = P(V > k) . \] 控制gFWER的方法允许以比较大的概率有不多于\(k\)个假阳性。
错误发现率(False Discovery Rate, FDR)是判断为阳性(显著,拒绝零假设)的结果中假阳性的比例的期望值。 令 \[ Q = \begin{cases} \frac{V}{R} = \frac{FP}{FP + TP} & R=FP+TP > 0, \\ 0 & R = 0. \end{cases} \] \[ \text{FDR} = E Q = E \left( \left. \frac{V}{R} \right| R > 0 \right) P(R > 0) \]
控制错误发现率比控制总错误率更适用于探索性研究, 它控制在找到的显著结果中错误的显著结果的比例, 而总错误率控制的是至少有一个第一类错误的概率, 过于严格, 仅适用于比较个数很少的情形。 控制FDR的方法适用于有成千上万甚至于百万级别的比较的错误率控制, 在这样的大规模的研究中, 目的是尽可能发现较多的显著(阳性)结果, 而又不能有太多的假阳性结果。
从错误发现率又推广出其它一些错误率。 正错误发现率(positive FDR, pFDR)定义为 \[ \text{pFDR} = E \left( \left. \frac{V}{R} \right| R > 0 \right), \] 边缘错误发现率(marginal FDR, mFDR)定义为 \[ \text{mFDR} = \frac{E V}{E R} . \]
控制错误发现率可以放松到控制错误发现比例的概率, 即控制 \[ \text{PFP} = P(\frac{V}{R} > g), \] 其中\(0 < g < 1\)给定。
注意当\(m_0 = m\), 即所有零假设都为真时, \(R = V\), \(\text{pFDR} = \text{mFDR} = 1\), 而FDR因为有额外的\(P(R>0)\)项, 所以总是小于1的。 在有大量比较时, FDR, pFDR, mFDR给出的结果比较接近。
对于PCER, FDR, FWER,一般有 \[ \text{PCER} \leq \text{FDR} \leq \text{FWER} , \] 这是因为 \[ \frac{V}{m} \leq Q \leq \boldsymbol{1}_{\{V > 0\}}, \] 故其期望也有同样大小次序。 于是,控制总错误率就能控制错误发现率, 控制错误发现率可以控制平均单次错误率。 控制总错误率一般比控制错误发现率保守, 即发现的显著结果个数更少。 科研项目应预先选定要控制哪一种错误率而不是在看到所有结果后选择对自己有利的结果。
只有当所有的检验的真实情况都是零假设为真(\(m_0=m\)), 才必有\(V=R\), 这时才有\(\text{FDR} = \text{FWER}\), 因为这时 \[ \text{FDR} = E(1 | R>0) P(R>0) = P(V>0) = \text{FWER} . \] 除此以外,FDR总是小于FWER。
5.1.3 弱控制与强控制
控制这些错误率时, 因为\(m\)个检验中哪些假设为真是未知的, 个数\(m_0\)也是未知的, 所以一种简单的办法是控制在所有假设同时为真的假设下的错误率, 比如控制总错误率FWER为\(\alpha\),可以要求 \[ P(V > 0 | H_1, \dots, H_m \text{都成立}) \leq \alpha . \] 这样的方法称为弱控制。
在弱控制下, 控制FDR和控制FWER是等价的。 这是因为弱控制假定\(m_0 = m\), 这样表5.1中\(T = S = 0\), \(V = R\), 于是 \[\begin{aligned} \text{FDR} =& E(\frac{V}{R} | R > 0) P(R>0) = E(1 | R>0) P(R > 0) \\ =& P(R>0) = P(V > 0) = \text{FWER}. \end{aligned}\]
因为实际情况下\(m\)个比较中真实情况可能是部分假设成立, 部分假设不成立, 应控制这些实际成立的比较的第一类错误概率。 (王静龙 2008)节5.6中定义了如下的错误率: 设\(m\)个检验编号为\(\Omega=\{ 1, 2, \dots, m \}\), 设\(H_0\)实际成立的集合为\(I\),不成立的集合为\(\Omega \backslash I\), \(I\)和\(I\)的元素个数\(m_0\)都未知。 设\(\Theta_I\)为集合\(I\)对应的参数\(\boldsymbol\theta\)的集合, 定义给定\(I\)的错误率为 \[\begin{aligned} \sup_{\boldsymbol\theta \in \Theta_I} P \left( \bigcup_{j \in I} \{ \text{拒绝第} j \text{个零假设} \} \right) \end{aligned}\] 因为集合\(I\)未知, 所以总错误率应为 \[\begin{aligned} \sup_{I \subset \Omega} \sup_{\boldsymbol\theta \in \Theta_I} P \left( \bigcup_{j \in I} \{ \text{拒绝第} j \text{个零假设} \} \right) \end{aligned}\] 控制此总错误率称为强控制。
例如, 要对总错误率进行强控制, 就是控制 \[ \sup_{I \subset \{1,2,\dots,m \}}\; P \left(V > 0 | \bigcap_{j \in I} H_i \right) \leq \alpha . \] 这里\(\bigcap_{j \in I} H_i\)表示集合\(I\)对应的零假设都成立的条件。
强控制的直观解释是, 不管\(\{ 1, 2, \dots, m \}\)这些编号的零假设中到底哪些是真的, 用满足强控制的检验法进行检验, 对真的零假设中一个或多个发生错误拒绝的概率小于等于\(\alpha\)。
显然, 强控制也满足弱控制的要求。
5.1.4 功效和第二类错误
对于多个比较, 也需要检验有最优的功效, 即最小的第二类错误。 类似于第一类错误, 多重比较中第二类错误也有不同的一些定义。
仍设有\(m\)个比较, 其中\(m_0\)个零假设为真, \(m_1 = m-m_0\)个零假设为假, \(m_0\)未知。 记\(\Omega\)为所有检验的集合, \(I\)为\(H_0\)成立的的检验的集合, \(S\)为不成立的零假设中被正确拒绝的个数, 是不可观测的随机变量。
对\(i \in \Omega\backslash I\), 即\(H_i\)不成立时, 定义单个检验的功效为 \[ \pi_i^{\text{ind}} = P(\text{拒绝} H_i), \ i \in \Omega\backslash I . \]
定义平均功效为\(m_1\)个不成立的零假设中平均被拒绝的比例, 即 \[ \pi^{\text{ave}} = \frac{E S}{m_1} = \frac{1}{m_1} \sum_{i \in \Omega\backslash I} \pi_i^{\text{ind}} . \]
Disjunctive(反意的,隔离的)功效是\(m\)个比较中至少正确拒绝一个的概率: \[ \pi^{\text{dis}} = P(S \geq 1) . \]
Conjunctive(合取得)功效是所有应该拒绝的假设(即\(H_i, i \in \Omega\backslash I\))全部被拒绝的概率, 即: \[ \pi^{\text{con}} = P(S = m_1) \]
如果\(m\)个检验问题是两两比较问题, 则\(\pi^{\text{ave}}\), \(\pi^{\text{dis}}\), \(\pi^{\text{con}}\)又称为每对功效、至少一对功效、所有对功效。 对\(\Omega\backslash I\)的子集\(S\)也可以类似地定义各种功效。
5.1.5 第三类错误
第三类错误是零假设为等于假设, 对立假设是不等于, 对不成立的零假设, 正确地拒绝但是结论的方向与实际参数符号相反的错误。
对\(m\)个比较, 设\(A_1\)表示至少有一个第一类错误的事件, \(A_2\)表示至少有一个第三类错误的事件, 希望控制这两种错误的概率: \[ P(A_1 \cup A_2) . \]
一般控制总错误率的方法不能同时控制这两种错误概率, 有一些特殊设计的方法可以控制这两种错误概率, 但会损失一些功效。 详见(Bretz, Hothorn, and Westfall 2011)节2.1.1。
5.2 多重比较方法的一些基本概念
定义了各种错误率后, 在\(m\)个检验(比较)中控制某种错误率的方法称为多重比较方法。 (Bretz, Hothorn, and Westfall 2011)是一本比较详细介绍了多重比较问题、理论框架和具体R软件使用的专著, 该书主要考虑中小规模的比较量、需要强证据的情形, 主要考虑对总错误率FWER进行强控制。
5.2.1 单步和逐步方法
多重比较方法可以按各个检验之间的关系分为:
- 单步方法,各个检验分别进行, 每个检验是否拒绝零假设与其他检验的结果无关, 以Bonferroni方法为代表;
- 逐步方法,每个检验是否拒绝依赖于其它检验的结果, 以Holm方法为代表。
逐步方法又分为逐步向下(step down)和逐步向上(step up)方法。 将\(m\)个检验按照计算结果按显著性程度从高到低排序(如未调整的单个检验p值 从小到大排列)为\(H_{(1)}, H_{(2)}, \dots, H_{(m)}\), 逐步向下方法从\(H_{(1)}\)开始检验, 如果能拒绝, 就继续检验\(H_{(2)}\), 如此重复直到第一个不能拒绝的假设\(H_{(i)}\)为止, 这时\(H_{(1)}\)到\(H_{(i-1)}\)被拒绝, \(H_{(i)}\)到\(H_{(m)}\)被接受。 Holm方法就是逐步向下进行的。
逐步向上方法从最不显著的\(H_{(m)}\)开始判决, 如果不能拒绝, 就继续考虑\(H_{(m-1)}\), 如此重复一直到第一个能被拒绝的\(H_{(j)}\)为止, 这时\(H_{(1)}\)到\(H_{(j)}\)被拒绝, \(H_{(j+1)}\)到\(H_{(m)}\)被接受。
逐步方法一般从单步方法改进而来, 比单步方法功效更高。 但逐步方法要构造参数的联立置信域就比较困难或者不能得到比单步方法更优的联立置信域。
5.2.2 修正p值
实际进行多重比较, 主要的表现方式是计算修正p值(adjusted p-values)。 对每个检验\(H_i\)计算一个修正p值\(q_i\), 设要控制的指定类型的多重比较错误率为\(\alpha\), \(q_i\)就是在这种多重比较错误率下\(H_i\)能被拒绝的最小\(\alpha\)值, 即 \[ q_i = \inf\{ \alpha:\; 0<\alpha<1 \text{是要控制的多重比较错误率,在}\alpha\text{下可以拒绝}H_i \} \] 其中\(\inf \emptyset = 1\)。 给定一种多重比较错误率控制方法和错误率控制界限\(\alpha\), 只要计算\(q_i, i=1,2,\dots,m\), 对每个\(H_i\), 当且仅当\(q_i \leq \alpha\)时拒绝\(H_i\), 就可以实现控制多重比较错误率小于等于\(\alpha\)的效果。
5.2.3 置信域方法
单参数的假设检验问题与置信区间密切相关。 对参数\(\theta\),考虑\(H_0: \theta = \theta_0\), 对给定样本\(X_1, \dots, X_n\),给定检验水平\(\alpha\), 选取不同的\(\theta_0\)使得\(H_0\)在水平\(\alpha\)下能被接受, 这些\(\theta_0\)的集合就构成\(\theta\)的\(1-\alpha\)置信区间。 反之, 已知置信区间可以作为接受域的构造。
这样从假设检验构造置信区间的方法实际是将参数空间划分为子空间, 每个子空间仅包含一个参数值。 在对多个参数的多个检验中, 也可以利用联立置信域构造检验。 单步方法常常可以找到对应的联立置信域, 但逐步方法则很难找到对应的联立置信域。
5.2.4 自由组合与受限组合
对由假设\(H_i, i=1,2,\dots,m\)组成的多重比较问题, 如果对\(\Omega = \{1,2,\dots,m\}\)的任意子集\(I\), 都可以保证\(H_i, i \in I\)成立而\(H_j, j \notin I\)不成立不构成矛盾, 则称此多重比较为自由组合的; 否则称其为受限组合的。
比如, 两个处理组与对照组的2个检验是自由组合的。 三个均值之间两两比较的3个检验是受限组合的, 因为如果\(H_1: \mu_1 = \mu_2\)和\(H_2: \mu_2 = \mu_3\)都成立时, \(H_3: \mu_1 = \mu_3\)必成立, \(H_1, H_2\)成立与\(H_3\)不成立矛盾。
5.2.5 连贯与共鸣
一种多重比较方法,如果对\(H_i \subseteq H_j\), 拒绝\(H_j\)必然拒绝\(H_i\), 则称为是连贯的(coherent)。 这是多重比较方法应有的性质, 如果不满足, 多重比较的结果就可以给出矛盾的解释。 不连贯的多重比较方法一定可以进行改造得到连贯的方法, 而且功效一致不降。
共鸣(consonance)也是多重比较方法最好能够满足的要求, 只不过不像连贯的要求那样重要。 对\(I \subseteq \Omega\), 记\(H_I = \bigcap_{i \in I} H_i\), 称\(H_I\)非最大, 如果存在\(J \subseteq \Omega\)使得\(H_I\)是\(H_J\)的真子集, 否则称\(H_I\)最大。 一种多重比较方法, 如果在拒绝了非最大的\(H_I\)时, 至少能找到一个\(H_J \supset H_I\), \(H_J\)为最大且拒绝\(H_J\), 则称此方法为共鸣的。 在满足共鸣性时可以保证, 假设的交集\(H_I\)被拒绝时, 至少一个基础假设\(H_i\)也能被拒绝。
5.3 多重比较方法的构造
这部分内容来自(Bretz, Hothorn, and Westfall 2011) 节2.2。
5.3.1 并交法
并交法和交并法主要看多重检验的对立假设。
设有\(m\)个处理组,每一个与对照组比较, 产生\(H_i, i=1,2,\dots,m\)假设。 希望将\(\{ H_i \}\)中所有不成立的假设都拒绝, 但至少应该拒绝其中一个不成立的假设。 设\(H_i\)的对立假设为\(K_i\), 希望检验假设\(H = \bigcap_{i \in \Omega} H_i\), 检验的零假设和对立假设为 \[ H = \bigcap_{i \in \Omega} H_i \longleftrightarrow K = \bigcup_{i \in \Omega} K_i \]
在多个处理组与一个对照组比较时, 拒绝假设交集\(H\)相当于至少有一个处理组是显著的。
检验\(H\)的一种方法是对每个\(H_i\)分别计算统计量\(t_i\), 取适当的临界值\(c_i\)使得某个\(t_i\)超出临界值时就拒绝\(H\)。 所以零假设交集\(H\)的拒绝域是并集 \[ \bigcup_{i \in \Omega} \{ t_i > c_i \} \] 这种多重检验方法就称为并交法。
这种方法对每个\(H_i\)是等价对待的, 拒绝\(H\)以后并不知道具体是哪一个\(H_i\)显著, 这一点可以用许多技术手段改进, 并交法是许多多重比较方法的基础。
最大t值检验是并交法中比较重要的一种方法。 设\(H_i\)的检验统计量为\(t_i\), 且拒绝域是\(t_i > c_i\), \(c_i\)待定。 这时, 为了进行并交法多重检验, 可以取 \[ t_{\mbox{max}} = \max_{i \in \Omega} t_i \] 当且仅当\(t_{\mbox{max}} \geq c\)时拒绝零假设交集\(H\)。 取\(c\)使得 \[ P(t_{\mbox{max}} \geq c | H) = \alpha \] \(t_{\mbox{max}}\)的分布取决于\((t_1, \dots, t_m)\)的联合分布, 此联合分布常常难以获得, 数值方法也不一定能求临界值, 这时只好采用更保守的临界值。
最大t检验常常能满足连贯性和共鸣性, 许多常用多重比较方法本质上是最大t检验法, 如Bonferroni检验, Dunnett检验, Tukey检验。 以这些检验为基础, 使用闭包(closure)方法还可以构造逐步检验法, 从而获得对每个\(H_i\)的检验结果。
如果单个检验的拒绝域是\(\{ t_i < c_i \}\), 只要取最小的统计量值; 如果单个检验的拒绝域是\(\{ |t_i| > c_i \}\), 只要取统计量绝对值的最大值。
5.3.2 交并法
有些多重比较问题要求所有比较同时显著才判定显著。 例如, 在多药物联合治疗研究中, 要求联合治疗方法比每个单个药物治疗都有显著的改进。
对比较\(H_i, i=1,2,\dots,m\), \(K_i\)为\(H_i\)的对立假设, 考虑假设检验问题 \[ H' = \bigcup_{i \in \Omega} H_i \longleftrightarrow K' = \bigcap_{i \in \Omega} K_i \] 只有所有比较都显著时才拒绝\(H'\)。 称这样的多重比较方法为交并法。
如果每个单独检验\(H_i\)的统计量为\(t_i\), 且各\(t_i\)边缘分布相同, 则\(H'\)的\(\alpha\)水平拒绝域为 \[ \{ \min_{i \in \Omega} t_i \geq c \} \] \(c\)是单个\(t_i\)的上侧\(\alpha\)分位数。
如果\(m\)个检验中有不显著的结果, 则整个检验都不显著, 每个\(H_i\)都不能判定是显著的。 这并不会造成控制总错误率的保守检验法。
5.3.3 闭包法则
在并交法中, 如果拒绝了交集假设\(H = \bigcap_{i \in \Omega} H_i\), 只能推断各个单独的假设中至少一个被拒绝, 但不能给出哪一个显著的结论。 闭包法则是一种一般性的多重比较构造方法, 可以构造逐步检验方法, 能够在控制多重比较错误率的同时对每个单独的假设给出显著与否的结论。
以\(m=2\)的对照试验来说明闭包法则。 考虑两个处理组与对照组的比较, 对照组与两个处理组的指标均值分别为\(\mu_0, \mu_1, \mu_2\), 令\(\theta_i = \mu_i - \mu_0, i=1,2\)为两个处理的平均效应。 考虑两个零假设\(H_i: \theta_i \leq 0\), 对立假设为\(K_i: \theta_i > 0\),\(i=1,2\)。 设\(W_i\)表示拒绝\(H_i\), 因为 \[ P(W_1 \cup W_2 | H_1 \cap H_2) \leq P(W_1 | H_1 \cap H_2) + P(W_2 | H_1 \cap H_2) \] 设两种处理独立,\(\theta_1\)与\(\theta_2\)无关, 则只要控制每个\(H_i\)的水平为\(\alpha/2\), 则总错误率小于等于\(\alpha\)。 这称为Bonferroni方法。
这样得到的检验法比较保守, 这是单步检验法, 可以用闭包法则将其改为多步检验法, 获得功效的提升。 注意到\(H_{12} = H_1 \cap H_2\)对应于参数空间\(\{(\theta_1, \theta_2): \theta_1 \leq 0, \theta_2 \leq 0\}\), 所以检验\(H_{12}\)需要控制总错误率, 可以用Bonferroni方法进行调整; 但是, 对\(H_1 - H_{12}\), 即\(H_1\)成立但\(H_2\)不成立的情况, 因为仅需要控制\(H_1\)的第一类错误而不需要控制\(H_2\)的第一类错误, 所以对参数空间 \(\{(\theta_1, \theta_2): \theta_1 \leq 0, \theta_2 > 0\}\) 的情形只需要对\(H_1\)进行水平\(\alpha\)的单独的检验。 \(H_2 - H_{12}\)情况类似。
所以, 作为改进, 可以先用Bonferroni方法对\(H_{12}\)进行检验, 控制总错误率; 如果拒绝, 就继续检验。 对\(H_1 - H_{12}\)进行仅考虑\(H_1\)的检验, 如果也拒绝, 就保证控制总错误率拒绝\(H_1\), 对\(H_2 - H_{12}\)进行仅考虑\(H_2\)的检验, 如果也拒绝, 就保证控制总错误率拒绝\(H_2\)。 如果\(H_{12}\)被接受, 就不再继续检验, 因为如果\(H_{12}\)接受而\(H_1 - H_{12}\)拒绝, 会得出不相容的结论(违反连贯性)。
将闭包法则推广到\(m\)个检验的情形, 典型情况如\(m\)个处理组与一个共同的对照组之间的比较。 考虑这\(m\)个检验的所有可能的零假设交集, 对每个交集在水平\(\alpha\)在水平\(\alpha\)下作并交法检验, 可以选用任何的并交法检验, 不同的交集假设也可以使用不同的检验方法。 在控制总错误率下为了拒绝某个零假设\(H_i\), 当且仅当\(H_i\)单独的水平\(\alpha\)检验被拒绝, 而且包含\(H_i\)的任何交集零假设的水平\(\alpha\)检验都被各自拒绝。 这种方法可以在强控制意义下控制总错误率FWE。 参见(Marcus, Peritz, and Gabriel 1976)。
基于闭包法则的多重比较方法称为闭合检验法(closed tests)。 具体步骤如下:
- (1) 确定要检验的多个零假设的集合\(\mathcal H = \{ H_1, H_2, \dots, H_m \}\)。
- (2) 构造闭包集合系: \[\overline{\mathcal H} = \left\{ H_I = \bigcap_{i \in I} H_i:\ I \subseteq \{1,2,\dots,m\}, I \neq \emptyset \right\} \]
- (3) 对每个\(H_I \in \overline{\mathcal H}\)都单独构造一个水平\(\alpha\)的检验法。
- (4) 对每个\(H_i\),当且仅当所有\(H_I \in \overline{\mathcal H}\)且\(i \in I\)的检验(包括\(H_i\)本身) 都分别在水平\(\alpha\)下被拒绝,就拒绝\(H_i\),否则不拒绝\(H_i\)。
对于闭合检验法, 可以用如下的方法计算调整的p值。 因为第\(i\)个检验\(H_i\)需要对所有包含\(i\)的集合\(I\)的交集假设\(H_I\)都显著, 这就需要这些检验的p值都小于等于\(\alpha\), 所以,定义第\(i\)个检验\(H_i\)的调整p值为\(H_i\)的单独检验的p值以及所有包含\(i\)的集合\(I\)的交集假设\(H_I\)的p值的最大值: \[ q_i = \max_{i \in I} p_I \] 其中\(p_I\)是对交集假设\(H_I\)的并交法检验的p值。
闭包法则理论上需要检验\(2^m\)个检验, 但是, 有许多算法可以简化检验, 理想情形下可以得到\(O(m)\)的方法。 R的multtest包提供了这样的简化方法。
5.3.4 分割法则
闭包法则适用于许多情况, 但是不利于产生多维参数的联立置信区间。 分割方法将多维参数的取值空间分割为不交的子集, 在每个子集上设计水平为\(\alpha\)的检验, 因为真实参数属于且仅属于其中一个子集, 所以这种方法能实现对总错误率的强控制。
以两个处理组与一个共同的对照组的比较为例, \(\theta_1, \theta_2\)分别是两组的均值与对照组均值的差, 零假设\(H_1, H_2\)分别表示\(\theta_1 \leq 0\), \(\theta_2 \leq 0\), 对立假设\(K_1, K_2\)分别表示\(\theta_1 > 0\), \(\theta_2 > 0\), 将\((\theta_1, \theta_2)\)取值的\(\mathbb R^2\)空间分割为4块: \[ H_1 H_2, \ H_1 K_2, \ H_2 K_1, \ K_1 K_2 \] 然后将\(H_1 H_2\)和\(H_1 K_2\)合并为\(H_1\), 将\(\mathbb R^2\)空间分割为3块: \[ H_1, \ H_2 K_1, \ K_1 K_2 \] 真实参数\(\boldsymbol\theta = (\theta_1, \theta_2)\)属于且仅属于其中的某一块。 这里,\(K_1 K_2\)这一块不会发生第一类错误, 在对于多重假设检验不起作用, 但是构造联立置信区间时有用。
将参数的这三块分别作为零假设构造水平为\(\alpha\)的假设检验。 因为各个块之间不相交且组成参数空间的分割, 每组参数只能属于其中的一个, 从而造成第一类错误, 控制了每个检验的第一类错误就控制了总错误率。
这样的证明不够严谨,严格证明待整理补充。
一般地, 设有\(m\)个检验\(H_1, \dots, H_m\), 可以用如下的分割方法进行多重检验并构造联立置信区间:
- 选择参数空间\(\Theta\)的适当分割\(\{ \Theta_{\ell}, \ell \in L \}\);
- 在\(\alpha\)水平下检验参数属于\(\Theta_{\ell}\)的零假设;
- 对每一零假设\(H_i\),当且仅当每一个使得\(\Theta_{\ell} \cap H_i \neq \emptyset\)的\(\Theta_{\ell}\)都被拒绝时才拒绝\(H_i\);
- 所有没有被拒绝的\(\Theta_{\ell}\)的并集构成参数的置信水平为\(1 - \alpha\)的置信域。
5.4 基于Bonferroni方法的检验
5.4.1 Bonferroni方法
设\(A_1, A_2, \dots, A_m\)是\(m\)个事件,则有如下的Bonferroni不等式 \[ P(\bigcup_{j=1}^m A_j) \leq \sum_{j=1}^m P(A_j) \] 所以, 如果有\(m\)个假设检验同时进行, 这些检验可以独立也可以不独立, 用\(A_j\)表示第\(j\)个检验犯第一类错误的事件, 则至少犯一次第一类错误的概率为 \[ P(\bigcup_{j=1}^m A_j) \leq \sum_{j=1}^m P(A_j) \] 只要取\(0 < \alpha < 1\), 令每一次检验的检验水平为\(\alpha/m\), 则总错误率小于等于\(\alpha\)。
这样的控制总错误率的方法简单可行, 适用于任何假设检验问题, 但是控制过于严格, 使得检验结果过于保守。 比如, \(\alpha=0.05\), \(m=1000\)时, 每次的检验水平要控制在\(0.00005\), 很难有显著结果出现。
R的stats::p.adjust()函数可以计算用Bonferroni方法调整的p值,如:
实际就是将p值乘以比较个数\(m\)。
5.4.2 Holm方法
Holm方法是Bonferroni方法的逐步检验改进版本, 使用逐步向下的做法。 按照强控制意义控制总错误率(FWE)。 各个检验之间可以是独立, 可以是相关的, 检验之间有固定的逻辑关系(比如第1,2个零假设成立则第3个零假设必成立)要具体问题具体分析。 参见(Holm 1979)。
设有\(m\)个检验,要控制的FWE为\(\alpha\), \(m\)个检验的p值由小到大排列为 \[ p_{(1)} \leq p_{(2)} \leq \dots \leq p_{(m)} , \] Holm方法的算法步骤如下:
- 如果\(p_{(1)} > \frac{\alpha}{m}\), 就不拒绝所有的\(m\)个检验, 给出结论,算法结束; 如果\(p_{(1)} \leq \frac{\alpha}{m}\), 就拒绝\(p_{(1)}\)所对应的零假设, 进入下一步。
- 设已经拒绝了\(p_{(1)}, p_{(2)}, \dots, p_{(i-1)}\)对应的零假设。 如果\(p_{(i)} > \frac{\alpha}{m - i + 1}\), 就不拒绝\(p_{(i)}\)所对应的零假设, 从而做出拒绝\(p_{(1)}, p_{(2)}, \dots, p_{(i-1)}\)对应的零假设, 不拒绝其余零假设的结论,算法结束; 如果\(p_{(i)} \leq \frac{\alpha}{m - i + 1}\), 就拒绝\(p_{(i)}\)所对应的零假设, 继续考虑\(p_{(i+1)}\), 直到\(i > m\)为止。
在实际应用时, 因为拒绝\(H_{(i)}\)当且仅当\(H_{(1)}, \dots, H_{(i-1)}\)被拒绝, 且\(p_{(i)} \leq \frac{\alpha}{m - i + 1}\),所以定义 所以定义 \[\begin{aligned} q_{(1)} =& \min\{ m p_{(1)}, 1 \}, \\ q_{(i)} =& \min\{ \max((m - i + 1) p_{(i)},\; q_{(i-1)}), \; 1 \} \end{aligned}\] 检验步骤可以改为对每个检验计算\(q_i\), 当且仅当\(q_i \leq \alpha\)时拒绝\(H_i\)。
定理5.1 上述的Holm-Bonferroni多重检验法在强控制意义下的总第一类错误率小于等于\(\alpha\)。
证明: 设\(I\)为零假设为真的下标的集合, \(I\)中的检验个数为\(k\), 先考虑\(I\)中检验都在\(\frac{\alpha}{k}\)水平下不显著的概率: \[\begin{aligned} & P \left( \bigcap_{i \in I} \left\{ p_i > \frac{\alpha}{k} \right\} \right) \\ =& 1 - P \left( \bigcup_{i \in I} \left\{ p_i \leq \frac{\alpha}{k} \right\} \right) \\ \geq& 1 - \sum_{i \in I} P \left( p_i \leq \frac{\alpha}{k} \right) \\ \end{aligned}\] 对零假设成立的第\(i\)个检验, 由p值检验方法的定义, 必有 \[ P( p\text{值} \leq \alpha' \;|\; \text{零假设成立}) \leq \alpha', \ 0 < \alpha' < 1, \] 所以 \[\begin{aligned} & P \left( \bigcap_{i \in I} \left\{ p_i > \frac{\alpha}{k} \right\} \right) \\ \geq& 1- \sum_{i \in I} \frac{\alpha}{k} \\ \geq& 1 - k \cdot \frac{\alpha}{k} \\ =& 1 - \alpha \end{aligned}\]
如果I中的所有检验的p值都大于\(\frac{\alpha}{k}\), \(k\)为\(I\)中的检验的个数, 那么所有的\(m\)个检验的\(p\)值中就至少有\(k\)个大于\(\frac{\alpha}{k}\), 至多有\(m-k\)个小于等于\(\frac{\alpha}{k}\), 所以\(p_{(m-k+1)} > \frac{\alpha}{k}\), 记\(i = m-k+1\), 则有\(p_{(i)} > \frac{\alpha}{m-i+1}\), 检验会在第\(i = m-k+1\)或之前停止, \(p_1, p_2, \dots, p_m\)对应的零假设中所有p值大于\(\frac{\alpha}{k}\)的都被接受, 这也包括I中的所有检验。 所以, 按照Holm的步骤, I中的所有检验都被接受的概率至少为\(1 - \alpha\), 从而强控制意义下的FWE小于\(\alpha\)。
○○○○○○
与单步的Bonferroni方法相比较, Bonferroni的每个p值都与相同的阈值\(\frac{\alpha}{m}\)相比较, 而Holm方法的p值则可以与较大的阈值\(\frac{\alpha}{m-i+1}\)相比较, 所以Holm方法能够发现更多的显著差异, 可以完全涵盖Bonferroni方法的应用, 实际应用中应该用Holm方法代替Bonferroni方法。
当检验之间可以自由组合而没有限制时(有限制的典型情形是两两多重比较), Holm步骤是闭包法则以Bonferroni方法检验每个交集的简化算法。 要检验每个交集需要\(2^m\)个检验, 但是Holm步骤只需要做\(m\)个检验。
Holm方法使用的Bonferroni检验因为不需要假定检验之间的独立或者相关性, 所以比较保守; 在已知检验之间的关系的情况下可以构造更有效的检验。
当各个检验之间有限制时, Holm方法仍然成立, 不过比较保守。 比如三个组均值的两两比较的三个检验, \(\mu_1 = \mu_2\), \(\mu_1 = \mu_3\)情况下必须\(\mu_2 = \mu_3\), 否则就有矛盾。 这时Holm方法成立, 但较保守。 Shaffer(1986)对这类情形用闭包法则进行了改进, 闭包法则的各个交集在检验时也将p值从小到大排列并在某个位置截止。
在有些有限制的情形中Holm可能不满足连贯性(coherent)。
R的p.adjust()函数支持用Holm方法进行p值调整,
调整后的p值只要与同一的\(\alpha\)相比就可以控制FWE。
例如:
p.adjust(c(0.01, 0.015, 0.005), method="bonferroni")
## [1] 0.030 0.045 0.015
p.adjust(c(0.01, 0.015, 0.005), method="holm")
## [1] 0.020 0.020 0.015可以看出,Holm调整的p值比Bonferroni调整的p值可以有所降低。
5.4.3 Šidák方法
Šidák方法(Šidák(1967))比Bonferroni方法的保守性有略微的改善, 但需要假定检验之间独立或有非负相关。 调整p值的公式为 \[ q_j = 1 - (1 - p_j)^k, \ j=1,2,\dots,k \] 如果所有p值独立同标准均匀分布, 则用Šidák修正p值小于等于\(\alpha\)得到的总第一类错误概率恰好等于\(\alpha\)。 如果检验满足positive orthant dependence condition, 此检验法是保守的(Holland and Copenhaver(1987))。
如果各个零假设相互独立,检验统计量概率分布相同, 则令
\[\begin{aligned} \alpha =& P\left( \bigcup_{j=1}^k {\text{拒绝} H_{0j}} | 所有零假设都成立 \right) \\ =& 1 - P\left( \bigcap_{j=1}^k {\text{接受} H_{0j}} | 所有零假设都成立 \right) \\ =& 1 - \prod_{j=1}^k P(\text{接受} H_{0j} | 所有零假设都成立) \\ =& 1 - (1 - \alpha_1)^k \end{aligned}\] 在上式中\(\alpha_1\)代表一次检验会犯的第一类错误概率, \(\alpha\)代表\(k\)次检验中至少犯一次第一类错误的概率, \[ p_j \leq \alpha_1, \ j=1,2,\dots,k \Longleftrightarrow \tilde p_j \leq \alpha, \ j=1,2,\dots,k \] 所以这种情况下控制\(\tilde p_j \leq \alpha\), 总错误率恰好等于\(\alpha\)。
5.5 基于Simes不等式的检验方法
Simes(1986)提出了一种检验法, 对所有\(m\)个检验都不显著的零假设\(H = \bigcap_{i=1}^m H_i\), 得到了当各个检验独立情况下对FWER实现弱控制的检验法。 此方法对每个\(j=1,2,\dots,m\), 只要有一个\(j\)满足 \[ p_{(j)} \leq \frac{j}{m} \alpha \] 就拒绝\(H\)。 此检验比Holm方法功效略高, 但不能对每个\(H_i\)给出假设检验判决。
Hochberg(1988)将Simes检验改造成了递增逐步检验方法, 这实际是用与Holm方法相同的p值阈值但是从最不显著到最显著这个方向逐步检验: 对\(j=m, m-1, \dots, 2, 1\), 判断是否\((m-j+1) p_{(j)} \leq \alpha\), 找到第一个满足条件的\(j\), 然后拒绝\(H_{(1)}, \dots, H_{(j)}\), 接受\(H_{(j+1)}, \dots, H_{(m)}\)。 调整p值为 \[\begin{aligned} q_{(m)} =& p_{(m)} \\ q_{(i)} =& \min \left\{ 1, \ \min[ (m-i+1) p_{(i)}, \; q_{(i+1)}] \right\} \end{aligned}\]
这个方法要求各个检验独立, 比Holm方法功效更高。 实际上, 在检查\((m-j+1) p_{(j)} \leq \alpha\)时, 并不是总存在一个\(j_0\), 使得\(1,\dots,j_0\)满足不等式而\(j_0 + 1, \dots, m\)不满足, 满足不等式的与不满足不等式的\(j\)并不一定总是分成前后两组, 而是有可能间隔出现, 所以Hochberg方法往往能产生更多的显著结果。
例如:
| pvalues | threshold | Holm | Hochberg |
|---|---|---|---|
| 0.010 | 0.0125 | 显著 | 显著 |
| 0.020 | 0.0167 | 不显著 | 显著 |
| 0.022 | 0.0250 | 不显著 | 显著 |
| 0.090 | 0.0500 | 不显著 | 不显著 |
Hommel(1988)对Hochberg方法进行了改进,
使用闭包准则,
对每个检验交集用Simes方法进行检验,
此方法比Hochberg方法功效更高。
用p.adjust()计算调整p值如下:
pvalues <- c(0.01, 0.02, 0.022, 0.09)
knitr::kable(data.frame(
pvalues = pvalues,
padj.holm = p.adjust(pvalues, method="holm"),
padj.hochberg = p.adjust(pvalues, method="hochberg"),
padj.hommel = p.adjust(pvalues, method="hommel")),
digits=4)| pvalues | padj.holm | padj.hochberg | padj.hommel |
|---|---|---|---|
| 0.010 | 0.04 | 0.040 | 0.030 |
| 0.020 | 0.06 | 0.044 | 0.040 |
| 0.022 | 0.06 | 0.044 | 0.044 |
| 0.090 | 0.09 | 0.090 | 0.090 |
5.6 联立置信区间方法
一些假设检验与置信区间是等价的。比如,对于假设检验问题: \[\begin{aligned} H_0: \mu = \mu_0 \longleftrightarrow H_a: \mu \neq \mu_0 \end{aligned}\] 对给定样本,如果有置信区间\((\hat a, \hat b)\)使得 \[ P(\hat a < \mu < \hat b | \text{真实参数为} \mu) = 1 - \alpha \] 则 \[\begin{aligned} P(\hat a < \mu_0 < \hat b | \text{真实参数为} \mu_0) =& 1 - \alpha \\ P(\mu_0 \notin (\hat a, \hat b) | \text{真实参数为} \mu_0) =& \alpha \end{aligned}\] 所以用\(\mu_0 \notin (\hat a, \hat b)\)作为拒绝域可以得到检验水平为\(\alpha\)的假设检验。
如果有\(k\)个检验, 第\(j\)个为 \[ H_{0j}: \mu_j = \mu_{0j} \longleftrightarrow H_a: \mu_j \neq \mu_{0j} \] 对给定样本, 如果可以计算联立置信区间, 使得 \[\begin{aligned} P(\hat a_j < \mu_j < \hat b_j, \ j=1,2,\dots,k | \text{真实参数为} (\mu_{1}, \dots, \mu_{k})) \geq 1 - \alpha \end{aligned}\] 则 \[\begin{aligned} P\left( \bigcap_{j=1}^k \{ \hat a_j < \mu_{0j} < \hat b_j \} | \text{真实参数为} (\mu_{01}, \dots, \mu_{0k}) \right) \geq& 1 - \alpha \\ P\left( \bigcup_{j=1}^k \{ \mu_{0j} \notin (\hat a_j, \hat b_j) \} | \text{真实参数为} (\mu_{01}, \dots, \mu_{0k}) \right) \leq& \alpha \end{aligned}\] 即至少犯一次第一类错误的概率不超过\(\alpha\)。 于是, 可以用\(\mu_{0j} \notin (\hat a_j, \hat b_j)\)作为\(H_{0j}\)的拒绝域, 使得\(k\)个检验的总错误率小于等于\(\alpha\)。
5.6.1 Scheffe方法
在节4.8.2中, 给出了多元正态分布样本单样本均值联立置信域。 设总体\(\boldsymbol X\)服从多元正态分布\(\text{N}(\boldsymbol\mu, \Sigma)\), 其\(n\)组独立观测组成一个观测数据集\(M\), \(M\)的每一行为一个观测, \(M_C\)是将\(M\)的每一列都中心化后得到的矩阵, \(\bar{\boldsymbol x}\)为样本均值, \(S = \frac{1}{n-1} M_C^T M_C\)是协方差阵估计。
考虑多重比较问题 \[\begin{align} H_{0j}: \mu_j = \mu_{0j} \longleftrightarrow H_{aj}: \mu_j \neq \mu_{0j}, \quad j=1,2,\dots,p \tag{5.1} \end{align}\]
对所有\(\boldsymbol \beta \in \mathbb R^p\), \(\boldsymbol \beta^T \boldsymbol\mu\)有置信度为\(1-\alpha\)的联立置信域 \[\begin{aligned} \boldsymbol \beta^T \bar{\boldsymbol x} \pm \sqrt{\frac{p(n-1)}{n-p} F_{1-\alpha}(p,n-p)} \sqrt{\boldsymbol \beta^T \left(\frac{1}{n-1} \frac{1}{n} M_C^T M_C \right) \boldsymbol \beta} \end{aligned}\] 记这个区间为\(\text{CI}_{\boldsymbol\beta}\), 则 \[\begin{aligned} P \left( \bigcap_{\boldsymbol\beta \in \mathbb R^p} \left\{ \boldsymbol\beta^T \boldsymbol\mu \in \text{CI}_{\boldsymbol\beta} \right\} \right) = 1 - \alpha \end{aligned}\] 分别取\(\boldsymbol\beta\)为各个单位向量(\(p\)阶单位阵的各个列向量), 记为\(\boldsymbol e_1, \boldsymbol e_2, \dots, \boldsymbol e_p\),则 \[\begin{aligned} P \left( \bigcap_{j=1}^p \left\{ \mu_j \in \text{CI}_{\boldsymbol e_j} \right\} \right) \geq 1 - \alpha \\ P \left( \bigcup_{j=1}^p \left\{ \mu_j \notin \text{CI}_{\boldsymbol e_j} \right\} \right) \leq \alpha \end{aligned}\] 这样就可以找到\(\mu_1, \mu_2, \dots, \mu_p\)的联立置信区间。 据此可以得到控制总错误率为\(\alpha\)的多重比较假设检验。
令 \[\begin{aligned} t_j = \frac{\bar x_j - \mu_{0j}}{\sqrt{s_{jj} / n}} \end{aligned}\] 其中\(\bar x_j\)和\(s_{jj}\)是第\(j\)个分量的样本均值和样本方差, \(t_j\)就是一元的\(t\)检验统计量。 但是,给定总第一类错误概率\(\alpha\)后, 采用上述联立置信区间的规则, 取临界值为 \[\begin{align} \lambda_p = \sqrt{\frac{p(n-1)}{n-p} F_{1-\alpha}(p, n-p)} \tag{5.2} \end{align}\] 当\(|t_j| > \lambda_p\)时拒绝\(H_{0j}\)。 由于上面推导中的\(\geq\)部分, 这种方法也是保守的, 在很多情况下比Bonferroni方法还要保守。
如果采用Bonferroni方法, 则取\(\lambda_p = \text{tinv}(1 - \frac{\alpha}{p}, n-1)\)。 一般Bonferroni方法的临界值更小, 所以在相同的总错误率控制下Bonferroni方法较优, 这两种方法都很保守。
5.6.2 Shaffer-Holm逐步检验方法
仍考虑多重比较问题(5.1)。 Shaffer-Holm逐步检验方法是对Sheffe方法或者Bonferonni方法的一个改进, 减少了第二类错误的概率。
计算出\(p\)个检验统计量\(t_j, j=1,2,\dots,p\)以后, 将其按绝对值大小由小到大排序, 为简单起见仍记为\(t_j\), 相应的分量的假设仍记为\(H_{0j}\)和\(H_{aj}\)。 用如下步骤进行多重比较:
- 如果\(t_p\)(绝对值最大的一个检验统计量)满足\(|t_{p}| < \lambda_p\), 则所有的零假设都不拒绝, \(p\)个比较没有任何显著差异; 否则拒绝\(H_{0p}\),进入下一步。
- 如果\(|t_{p-1}| < \lambda_{p-1}\), 则除了第\(p\)个以外其它的\(p-1\)个比较都没有显著差异; 否则,拒绝\(H_{0,p-1}\), 得到两个显著差异结果, 其它\(p-2\)个比较无显著差异,进入下一步。
- …………
- 如果\(|t_1| < \lambda_1\), 则第1个比较没有显著差异, 其余\(p-1\)个有显著差异; 否则, 所有的\(p\)个都有显著差异。
\(\lambda_j\)定义见(5.2), 它是\(j\)的增函数, 所以以上的逐步检验的临界值是递减的, 可以减少原来的Sheffe或者Bonferroni检验的保守性, 减少第二类错误概率。
这种逐步检验方法的总错误率不超过\(\alpha\), 见(王静龙 2008)节5.6.6。
5.7 计算软件
SAS的GLM、ANOVA、MULTTEST过程可以执行多重比较检验。
R中的p.adjust、pairwise.t.test等函数提供了简单的进行多重比较的功能。
(Bretz, Hothorn, and Westfall 2011)叙述了多重比较的一般理论, 讲解比较深入浅出, 并给出了在线性模型、广义线性模型、混合线性模型等情形的功效较好的多重比较方法, R扩展包multcomp实现了其中的方法。
(Dudoit and Laan 2008)论述了多重比较的一系列理论, 并用bootstrap方法进行检验, R扩展包multtest实现了其中的方法。 此扩展包需要从Bioconductor网站安装。
qvalue是Bioconductor的一个R扩展包, 可以控制FDR。
5.7.1 p.adjust函数
R函数stats::p.adjust()输入一系列检验p值,
用method指定一种p值调整方法,
输出调整后的p值。
调整方法包括:
"bonferroni",给每个p值乘以检验的个数\(m\), 结果大于1时取1。 这种方法对各个检验独立或不独立都使用, 但过于保守。 关于总第一类错误率为强控制。"holm",Holm方法是对Bonferroni检验的一种逐步向下的改进, 也适用于各个检验独立或不独立的情况, 改进了Bonferroni方法, 关于总第一类错误率为强控制。"hochberg"或者"hommel", 需要各个检验独立,或者检验之间的相关性为非负, Hochberg方法功效略强一点, 关于总第一类错误率为强控制。"BH"与"fdr"为相同方法, 是控制FDR(错误发现率)的方法。"none"不做调整。
5.8 qvalue包
qvalue是Bioconductor的一个R扩展包, 可以控制FDR。 主要参考论文为http://genomine.org/papers/Storey_FDR_2011.pdf。
qvalue包安装方法如下:
if (!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
BiocManager::install(c("qvalue"))FDR控制方法一般要求各个检验之间独立, 或者相关性很弱。
5.8.1 FDR的两种用法
多重比较中使用FDR有两种主要的方法。 第一种方法称为FDR控制, 做法是预先确定一个可接收的错误发现率水平, 然后找到一个与数据值有关的阈值规则, 使得最终实现的FDR的期望值小于等于预定的水平。 第二种方法称为基于点估计的方法,对一个p值的阈值, 估计一个FDR点估计, 使得这个点估计的期望值大于等于实际的FDR。
Benjamini & Hochberg (1995)给出的FDR控制算法如下:
- 将\(m\)个比较的\(p\)值由小到大排序为\(p_{(1)} \leq \dots \leq p_{(m)}\);
- 求\(\hat k = \max\{ 1 \leq k \leq m:\ p_{(k)} \leq \alpha k / m \}\), \(\alpha\)为要控制的FDR;
- 若\(\hat k\)存在,就拒绝\(p_{(1)}, \dots, p_{(\hat k)}\)对应的零假设, 否则就一个也不拒绝。
对于基于点估计的方法, 记FDR(\(t\))是以\(p_i \leq t\)作为拒绝规则时的FDR值, 这是未知的, 一个估计为 \[ \widehat{\text{FDR}}(t) = \frac{\hat m_0(\lambda)\, t}{\max(R(t), 1)}, \] 其中\(R(t)\)表示选择\(p_i \leq t\)规则中的\(t\)产生的显著结果个数, \(\hat m_0(\lambda)\)是\(m\)个检验中零假设为真的检验个数的一种估计, \(\lambda\)是调节参数, 用来在偏差和方差之间进行折衷。 \[ \hat m_0(\lambda) = \frac{m - R(\lambda)}{1 - \lambda} . \] 当\(p_1, \dots, p_m\)独立同U(0,1)分布时, \(E \hat m_0(\lambda) \geq m_0\)。
5.8.2 qvalue定义
对于单个的检验, p值可以定义为适当的检验水平\(\alpha\), 使得在\(\alpha\)水平下可以拒绝零假设, 但任何更小的检验水平就不能拒绝零假设。
对于多重比较问题, FDR并不是显著性水平的单调函数, 所以定义了q值, 第\(i\)个检验的p值\(p_i\)对应的q值为恰好能够使得第\(i\)个检验被拒绝的检验阈值对应的FDR值, 即 \[ q\text{值}(p_i) = \min\{ \text{FDR}(t): p_i \leq t, \ 0 < t < 1 \} \] 其中的FDR(\(t\))是未知的,需要估计,所以 \[ \hat q\text{值}(p_i) = \min\{ \widehat{\text{FDR}}(t): p_i \leq t, \ 0 < t < 1 \} \]
这样, 我们可以用q值小于等于\(\alpha\)来决定拒绝那些零假设, 结果控制了FDR。
使用q值, 要要假定各个检验独立, 或者只有很弱的相关性。
5.8.3 使用qvalue包
qvalue包可以从输入的各个检验的p值计算相应的q值, 可以估计\(m\)个检验中为真的零假设的比例\(\pi_0 = m_0/m\), 可以估计局部错误发现率。
某个检验的局部错误发现率是以给定的p值为条件, 零假设为真的贝叶斯后验概率估计。
先用qvalue包的例子简单说明。 hedenfalk数据中, 有3170个基因的两种变异型的两样本t检验的p值, 检验统计量值, 其中两组的观测个数分别为7个和8个; 数据中还包含了用100次独立的随机置换两样本标签产生的3170个基因的检验t统计量绝对值的\(3170\times 100\)矩阵。 如下程序得到q值分析结果:
qvobj是一个列表, 其中包含了估计的q值等结果。 因为检验个数太多(\(m=3170\))所以不显示得到的q值。 提取其中的结果如:
pi0是估计的真实成立的零假设在所有检验中的比例\(\pi_0 = m_0 / m\)。
根据qvalues与pvalues的一一对应关系,
还可以找到按某个p值的阈值\(t\)进行检验判决对应的FDR估计值,如:
即取\(t=0.01\)为检验的p值阈值时, 对应的FDR估计为0.079。
显示概括:
summary(qvobj)
##
## Call:
## qvalue(p = pvalues)
##
## pi0: 0.669926
##
## Cumulative number of significant calls:
##
## <1e-04 <0.001 <0.01 <0.025 <0.05 <0.1 <1
## p-value 15 76 265 424 605 868 3170
## q-value 0 0 1 73 162 319 3170
## local FDR 0 0 3 30 85 167 2241可见在控制FDR小于等于0.05的水平上有162个显著结果。 作得到的p值的直方图并叠加对应的q值曲线:
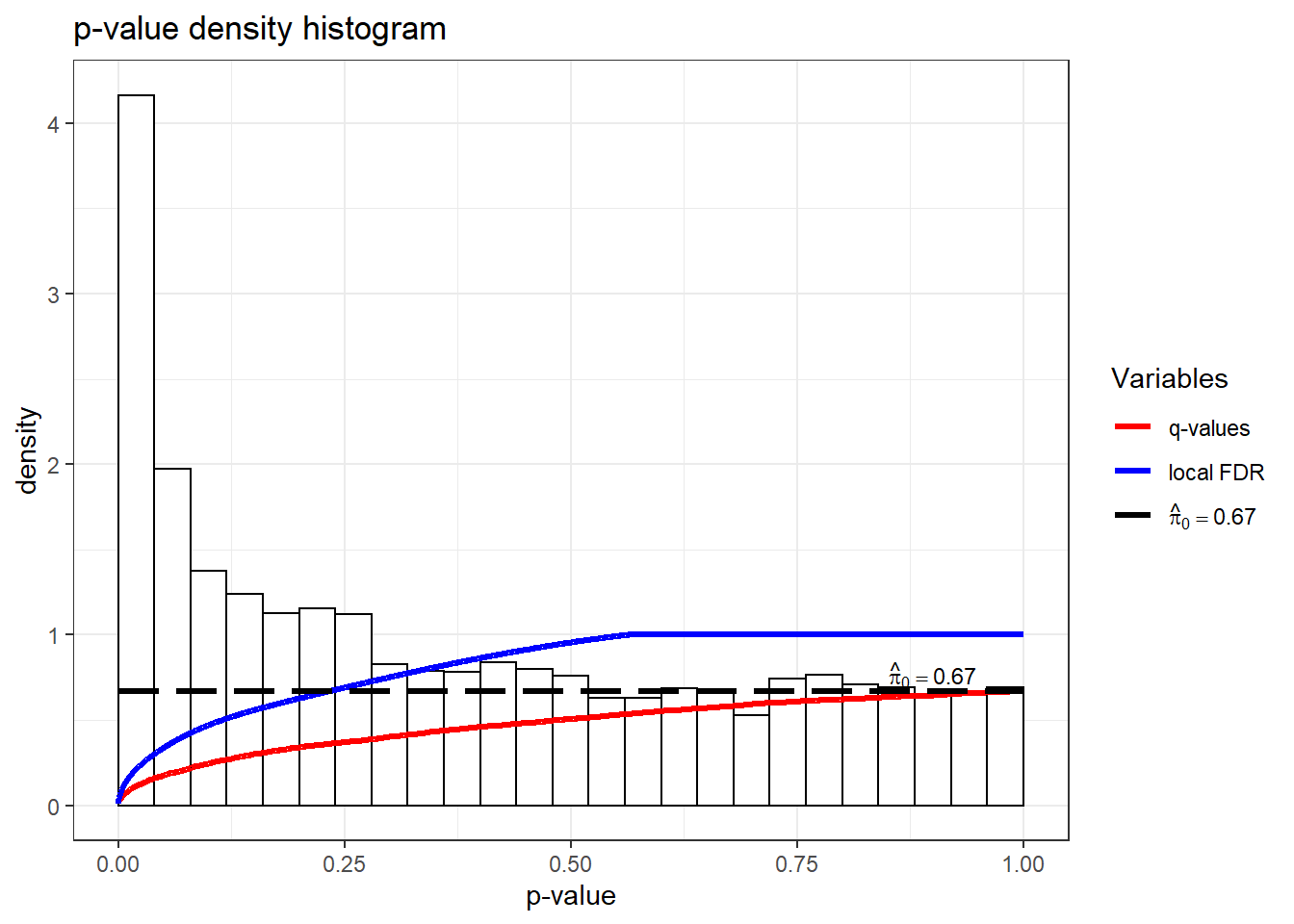
p值的直方图右侧应该是比较平坦的, 如果右侧隆起, 使得整个p值分布呈现U形, 提示使用q值分析的前提假定可能不成立。
作概括结果的图形:
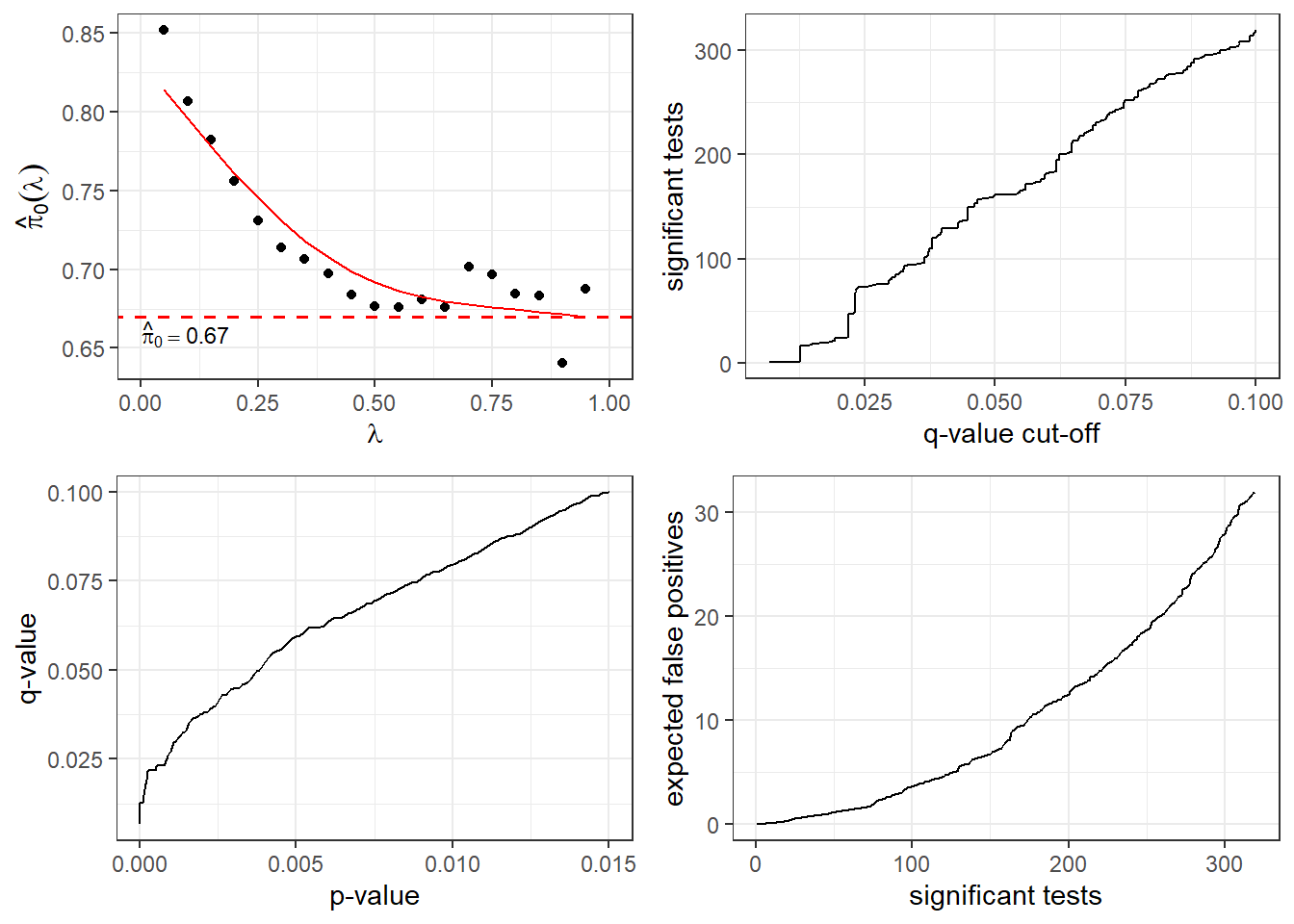
上面的四幅图中, 左上图是用不同的调节参数估计的\(\pi_0\); 右上图是不同q值阈值会产生多少个显著结果; 左下图表现了p值和q值的一一对应关系; 右下图是显著结果个数与其中的假阳性个数的关系。
还可以从置换检验的结果用empPvals()函数计算p值,
然后进行q值分析,如:
这里,
hedenfalk$stat0包含了对3170个基因的零假设下的检验统计量绝对值的多次独立抽样,
生成的方法是对某个基因的两组要比较的样本,
进行随机重新分组,
然后再计算两样本t检验的绝对值,
重复100次。
因为随机分组了,
所以用来计算t统计量的两组不再有显著差异,
可以看作是零假设成立情况下的统计量的独立抽样值。
实际上,只要有数据中计算出的各个检验统计量,
以及一批零假设下用再抽样方法得到的统计量,
而且检验是统计量值越大越倾向于拒绝零假设的,
就可以用empPvals()函数生成检验p值。
5.9 统计模型参数的多重比较
(Bretz, Hothorn, and Westfall 2011)叙述了多重比较的一般理论, 讲解比较深入浅出, 并给出了在线性模型、广义线性模型、混合线性模型等情形的功效较好的多重比较方法, R扩展包multcomp实现了其中的方法。
5.9.1 线性模型中的多重比较
多重比较问题如果各个检验相互独立, 则Hochberg等方法已经可以比较有效。 如果各个检验问题相关, 为了降低多重检验方法的保守性, 需要利用检验问题之间的关系提出功效更高的方法。 本节讨论线性模型的方差分析、协方差分析、回归分析中的多重检验问题, 利用关于分布的信息,尤其是检验统计量之间相关性,来改善检验功效。
对于线性模型 \[\begin{align} \boldsymbol y = X \boldsymbol\beta + \boldsymbol\varepsilon, \tag{5.3} \end{align}\] 如果要检验如下的线性约束: \[\begin{aligned} \boldsymbol c^T \boldsymbol\beta = a \end{aligned}\] 其中\(\boldsymbol c\)满足线性可估条件, 即\(\boldsymbol c\)是\(X\)的行向量的某个线性组合。 如果\(\boldsymbol c^T \boldsymbol 1 = 0\), 称\(\boldsymbol c\)为一个对照(contrast), 比如在单因素方差分析问题中检验各个主效应相等的零假设就对应这样的\(\boldsymbol c^T \boldsymbol\beta = 0\)的问题。
设有\(m\)个线性可估函数\(\boldsymbol c_j^T \boldsymbol\beta\), 有\(m\)个检验 \[\begin{aligned} H_j:\ \boldsymbol c_j^T \boldsymbol\beta = a_j, \ j=1,2,\dots,m, \end{aligned}\] 对于这样的联立检验, 线性模型理论已经有成熟的F检验法, 但仅检验\(\bigcap_{j=1}^m H_j\)而不给出每个\(H_j\)的控制总错误率的结果。
例5.1 考虑一元线性回归模型。 \[\begin{aligned} y_i =& \beta_1 + \beta_2 x_i + \varepsilon_i, \ i=1,2,\dots,n , \\ \varepsilon_i \sim& \text{ iid N}(0, \sigma^2) . \end{aligned}\]
\(X\)是一列1与\(x_1, \dots, x_n\)组成的两列的矩阵, \(\boldsymbol\beta = (\beta_1, \beta_2)^T\), \(\boldsymbol y = (y_1, \dots, y_n)^T\), \(\boldsymbol\varepsilon = (\varepsilon_1, \dots, \varepsilon_n)^T\)。 考虑如下的零假设组: \[\begin{aligned} & H_1: \beta_1 = 0 \\ & H_2: \beta_2 = 0, \end{aligned}\] 这时 \[\begin{aligned} & \boldsymbol c_1 = (1, 0)^T, \\ & \boldsymbol c_2 = (0, 1)^T, \\ & C = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} . \end{aligned}\]
○○○○○○
对线性模型(5.3), 系数的最小二乘估计总存在, 可以用广义逆表示为 \[\begin{aligned} \hat{\boldsymbol\beta} = (X^T X)^{+} X^T \boldsymbol y, \end{aligned}\] \(\sigma^2\)的估计为 \[\begin{aligned} \hat\sigma^2 =& \frac{1}{n-r} (\boldsymbol y - X \hat{\boldsymbol\beta})^T (\boldsymbol y - X \hat{\boldsymbol\beta}) \\ =& \frac{1}{n-r} \sum_{i=1}^n (y_i - \hat\beta_1 - \hat\beta_2 x_i)^2 . \end{aligned}\] 其中\(r = \text{rank}(X)\)。 \(\hat\sigma^2\)是\(\sigma^2\)的无偏估计。
对于例5.1, 当\(x_1, \dots, x_n\)不全相同时\(\text{rank}(X)=2\), \(X\)列满秩。 一般地,如果\(X\)列满秩, \[\begin{aligned} \hat{\boldsymbol\beta} = (X^T X)^{-1} X^T \boldsymbol y \end{aligned}\] 是\(\boldsymbol\beta\)的无偏估计, 任何的\(\boldsymbol c\)都使得\(\boldsymbol c^T \boldsymbol\beta\)线性可估。
对于单独的\(H_j\), 可以使用如下的\(t\)统计量: \[\begin{aligned} t_j = \frac{\boldsymbol c_j^T \hat{\boldsymbol\beta}}{ \hat\sigma \sqrt{\boldsymbol c_j^T (X^T X)^{+} \boldsymbol c_j} } \end{aligned}\] 当\(H_j\)成立时\(t_j\)服从自由度为\(n-r\)的中心t分布; 当\(H_j\)不成立时,\(t_j\)服从自由度为\(n-r\)的非中心t分布。 \((t_1, \dots, t_m)\)服从多元t分布, 自由度为\(n-r\), 相关阵为 \[ R = D C^T (X^T X)^+ C D, \] 其中\(D\)是由\(\left(\boldsymbol c_j^T (X^T X)^+ \boldsymbol c_j \right)^{-1/2}\), \(j=1,2,\dots,m\)组成的对角阵。 如果\(\sigma\)已知, 或者\(\hat\sigma\)相合, 则\(n\to\infty\)时\((t_1, \dots, t_m)\)渐近服从多元正态分布。
从多元t分布或者多元正态分布, 可以得到联立的临界值\(u_{1-\alpha}\), 当\(|t_j| \geq u_{1-\alpha}\)时拒绝\(H_j\)的总错误率控制在\(\alpha\)之下。 也可以计算调整的p值\(q_j\), 当\(q_j \leq \alpha\)时拒绝\(H_j\), 也可以控制总错误率。 实际上,线性模型理论中已有\(F\)检验, 但只能对\(\bigcap_{j=1}^m H_j\)检验, 而不能给出单个的\(H_j\)的控制总错误率的检验结果。
也可以给出单个\(\boldsymbol c_j \boldsymbol\beta - a_j\)的联立置信区间: \[\begin{aligned} \boldsymbol c_j^T \hat{\boldsymbol\beta} - a_j \;\pm\; u_{1-\alpha} \hat\sigma \sqrt{\boldsymbol c_j^T (X^T X)^{+} \boldsymbol c_j}, \ j=1,2,\dots,m . \end{aligned}\]
对于单侧检验问题和单侧置信区间问题, 只要将公式中的\(|t_j|\)替换成\(t_j\), 并计算单侧临界值或者单侧调整p值。
这种方法考虑到了统计量的联合分布, 所以比Bonferroni方法利用了更多信息。 这是单步方法, 可以在考虑联合分布的情况下利用统计量最大值, 以及闭合检验法, 构造出功效更高的逐步检验法。
例5.2 multcomp包有一个thuesen数据集, 作一元线性回归对截距项和斜率项作等于0的检验。
数据为:
| blood.glucose | short.velocity |
|---|---|
| 15.3 | 1.76 |
| 10.8 | 1.34 |
| 8.1 | 1.27 |
| 19.5 | 1.47 |
| 7.2 | 1.27 |
| 5.3 | 1.49 |
| 9.3 | 1.31 |
| 11.1 | 1.09 |
| 7.5 | 1.18 |
| 12.2 | 1.22 |
| 6.7 | 1.25 |
| 5.2 | 1.19 |
| 19.0 | 1.95 |
| 15.1 | 1.28 |
| 6.7 | 1.52 |
| 8.6 | NA |
| 4.2 | 1.12 |
| 10.3 | 1.37 |
| 12.5 | 1.19 |
| 16.1 | 1.05 |
| 13.3 | 1.32 |
| 4.9 | 1.03 |
| 8.8 | 1.12 |
| 9.5 | 1.70 |
这是一型糖尿病人的心室缩短速度和血糖值, 有23个完全观测, 建立一元线性回归模型, 用血糖值预测心室缩短速度:
lm.th <- lm(
short.velocity ~ blood.glucose,
data = thuesen
)
summary(lm.th)
##
## Call:
## lm(formula = short.velocity ~ blood.glucose, data = thuesen)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.40141 -0.14760 -0.02202 0.03001 0.43490
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.09781 0.11748 9.345 6.26e-09 ***
## blood.glucose 0.02196 0.01045 2.101 0.0479 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2167 on 21 degrees of freedom
## (因为不存在,1个观察量被删除了)
## Multiple R-squared: 0.1737, Adjusted R-squared: 0.1343
## F-statistic: 4.414 on 1 and 21 DF, p-value: 0.0479记模型为\(y_i = \beta_1 + \beta_2 x_i + \varepsilon_i\), 考虑检验\(H_1: \beta_1 = 0\)和\(H_2: \beta_2 = 0\)。 以\(\alpha=0.05\)为检验水平, 单独地检验\(H_1\)和\(H_2\), 都是显著的; 如果用Bonferroni方法计算调整p值, 则\(H_2\)的p值加倍, 在0.05水平下不显著。
multcomp实现了上面所述的利用检验统计量的联合分布改进的检验方法,
只要调用glht(),
输入线性模型的结果以及要检验的线性约束矩阵\(C\),
如:
library(multcomp)
mc.th <- glht(
lm.th, linfct = rbind(
c(1, 0),
c(0, 1) ))
summary(mc.th)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = short.velocity ~ blood.glucose, data = thuesen)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 1.09781 0.11748 9.345 1e-08 ***
## 2 == 0 0.02196 0.01045 2.101 0.0645 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)这里给出的第二个检验的p值为0.0645, 小于Bonferroni方法给出的调整p值, 但在0.05水平下仍不显著。 上面使用的仍是单步检验的方法, 控制总错误率。
从联立假设检验的结果计算联立置信区间:
confint(mc.th)
##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = short.velocity ~ blood.glucose, data = thuesen)
##
## Quantile = 2.23
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 1.097815 0.835837 1.359793
## 2 == 0 0.021963 -0.001348 0.045274使用逐步检验:
summary(mc.th, test = adjusted(type = "Westfall"))
##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = short.velocity ~ blood.glucose, data = thuesen)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 1.09781 0.11748 9.345 1e-08 ***
## 2 == 0 0.02196 0.01045 2.101 0.0479 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- Westfall method)现在控制总错误率0.05的情况下两个检验都显著了。
○○○○○○
5.9.2 一般参数模型的多重比较
将前一节的线性模型中的多重比较问题推广, 允许误差项没有正态性和方差齐性, 考虑一般的多个参数估计之间有相关结构的检验问题, 设每个检验用参数的线性组合表示, 共有\(m\)个检验。 这样的方法可以用于更一般的线性模型, 以及广义线性模型、线性混合效应模型等。
5.9.2.1 模型参数估计的渐近分布
考虑一般的模型\(M(\{ \boldsymbol z_1, \dots, \boldsymbol z_n \}, \boldsymbol \theta, \boldsymbol \eta)\), 其中\(\boldsymbol z_1, \dots, \boldsymbol z_n\)是\(n\)组独立观测, \(\boldsymbol\theta\)是代表固定效应的参数向量, \(\boldsymbol\eta\)是其它参数, 如随机效应、方差、讨厌参数等。 主要考虑\(\boldsymbol\vartheta = C^T \boldsymbol\theta\), 其中\(C\)是\(p \times m\)的矩阵, 每一列是代表一个可估线性组合。 设\(\hat{\boldsymbol\theta}_n\)是\(\boldsymbol\theta\)的估计。
例如,在一元线性回归模型5.1中, \(\boldsymbol z_i = (y_i, x_i)\), \(\boldsymbol\theta = (\beta_1, \beta_2)\), \(\boldsymbol\eta = \sigma^2\)。
设\(\hat{\boldsymbol\theta}_n\)是\(\boldsymbol\theta\)的估计, \(p\times p\)矩阵\(S_n\)是\(\text{Var}(\hat{\boldsymbol\theta}_n)\)的估计, 且有 \[\begin{align} a_n S_n \stackrel{\text{Pr}}{\longrightarrow} \Sigma, \tag{5.4} \end{align}\] 其中\(a_n\)是单调增正数序列, 进一步假设中心极限定理成立: \[\begin{align} a_n^{1/2} (\hat{\boldsymbol\theta}_n - \boldsymbol\theta) \stackrel{\text{d}}{\longrightarrow} \text{N}_p(0, \Sigma) . \tag{5.5} \end{align}\]
如果(5.4)和(5.5)都成立, 可以记 \[ \hat{\boldsymbol\theta}_n \stackrel{\cdot}{\sim} \text{N}_p(\boldsymbol\theta, a_n^{-1} \Sigma) . \] 这时对感兴趣的参数\(\boldsymbol\vartheta = C^T \boldsymbol\theta\), 有 \[\begin{aligned} \hat{\boldsymbol\vartheta} = C^T \hat{\boldsymbol\theta} \stackrel{\cdot}{\sim} \text{N}_p(\boldsymbol\vartheta, a_n^{-1} \Sigma^*) , \end{aligned}\] 其中\(\Sigma^* = C^T \Sigma C\)是\(m \times m\)矩阵。 设\(\Sigma^*\)的对角元素都为正数, 令\(D_n\)为\(\Sigma^*\)的对角元素组成的对角阵, \[\begin{aligned} R_n = D_n^{-1/2} S_n^* D_n^{-1/2}, \end{aligned}\] 则统计量 \[\begin{aligned} \boldsymbol t_n = D_n^{-1/2} (\hat{\boldsymbol\vartheta} - \boldsymbol\vartheta) \stackrel{\cdot}{\sim} \text{N}_m(0, R_n) . \end{aligned}\] 这里\(R_n\)依概率收敛到\(R\)。
在这样的假定下, 可以处理许多种模型的参数检验问题。 这些模型的标准的软件包都可以用来估计\(\hat{\boldsymbol\theta}\)和\(S_n\)。
5.9.2.2 模型参数的多重检验
考虑\(H_0: \boldsymbol{\vartheta} = \boldsymbol a\)的联合检验, 其中\(\boldsymbol{\vartheta} = C^T \boldsymbol\theta\), 并需要给出其中各个单个的检验的结果。
在5.9.2.1的参数估计渐近分布假定下, 有 \[\begin{aligned} \boldsymbol t_n = D_n^{-1/2} (\hat{\boldsymbol{\vartheta}} - \boldsymbol a) \stackrel{\cdot}{\sim} \text{N}_m(\boldsymbol 0, R_n) . \end{aligned}\] 如果\(\hat{\boldsymbol{\theta}}\)有精确的正态分布, 此多元检验统计量也可以有精确分布,比如多元t分布。
对\(H_0\)可以用经典的F检验给出判决。 另一种办法是采用多元\(\boldsymbol t_n\)的最大值统计量 \[ t_{\max} = \max(|t_{1n}|, |t_{2n}|, \dots, |t_{mn}|) . \] 当\(H_0\)成立时有渐近分布或者精确分布, 分布函数记为\(g_{\nu}(R, t)\), 其中\(R\)是相关阵,\(t\)是自变量,\(\nu\)是自由度参数。 检验时用估计的相关阵\(R_n\)代替\(R\), 计算p值为\(1 - g_{\nu}(R_n, t_{\max})\)。
使用t最大值统计量比使用比F统计量的一个优势是可以对每个单独的检验给出判决。 注意\(\boldsymbol{\vartheta} = C^T \boldsymbol\theta\), \(C = (\boldsymbol c_1, \dots, \boldsymbol c_m)\), 记\(\vartheta_j = c_j^T \boldsymbol\theta\), \(H_j: \vartheta_j = a_j\), 则\(H_0 = \bigcap_{j=1}^m H_j\), F检验和t最大值检验都可以检验\(H_0\), 但是t最大值统计量还可以用来检验每一个\(H_j\)。 每个\(H_j\)的调整p值为 \[\begin{aligned} q_j = 1 - g_{\nu}(R_n, |t_{jn}|) . \end{aligned}\] 对\(H_j\), 当且仅当\(q_j \leq \alpha\)时拒绝\(H_j\), 这样可以控制总错误率为\(\alpha\)。
可以利用闭包原则将最大t统计量检验法改造为功效更高的逐步检验法。 R的multcomp包提供了能满足参数间约束的功效更高、计算高效的检验程序。
5.9.2.3 应用
5.9.2.1的框架对许多模型都适用。 线性模型, 包括线性回归、方差分析、协方差分析可以使用该框架, 所以5.9.1的方法可以作为本节方法的特例。
广义线性模型的参数估计通常没有精确分布, 一般都用渐近分布进行统计推断, 在对其中的分类自变量进行组间比较时可以用本节方法。
在线性或者非线性的混合效应模型中, 参数估计通常使用限制最大似然估计(REML), 统计推断一般基于参数的渐近正态分布与方差的相合估计进行, 可以适用本节方法, 也可以构造联立置信区间。 Cox比例风险模型的检验也可以适用本节方法。
上述的各种模型还可以使用稳健估计方法, 比如, 当方差齐性假设不满足时, 可以用三明治法估计\(\text{Var}(\hat{\boldsymbol\theta})\)为\(S_n\)。 在线性模型中使用各种文件估计也能得到渐近正态的估计量。
模拟比较结果表明本节的方法一般都在控制总错误率的前提下有更好的功效。
5.9.3 R的multcomp扩展包
R的multcomp扩展包实现了(Bretz, Hothorn, and Westfall 2011)中的对线性模型和各种类似模型的多重比较。
5.9.3.1 glht函数
multcomp的glht()函数用来进行模型参数的多重比较,
是Generilized Linear model Hypothesis Testing的缩写。
考虑一个方差分析问题,
datasets包的warpbreaks数据框包含了纺织中断线次数的数据,
影响因素是两种类型的毛线(A, B),
三种不同水平的张力(L, M, H)。
简单起见仅研究张力的影响。
str(warpbreaks)
## 'data.frame': 54 obs. of 3 variables:
## $ breaks : num 26 30 54 25 70 52 51 26 67 18 ...
## $ wool : Factor w/ 2 levels "A","B": 1 1 1 1 1 1 1 1 1 1 ...
## $ tension: Factor w/ 3 levels "L","M","H": 1 1 1 1 1 1 1 1 1 2 ...library(ggplot2)
ggplot(
data = warpbreaks, mapping = aes(
x = tension, y = breaks ) ) +
geom_boxplot()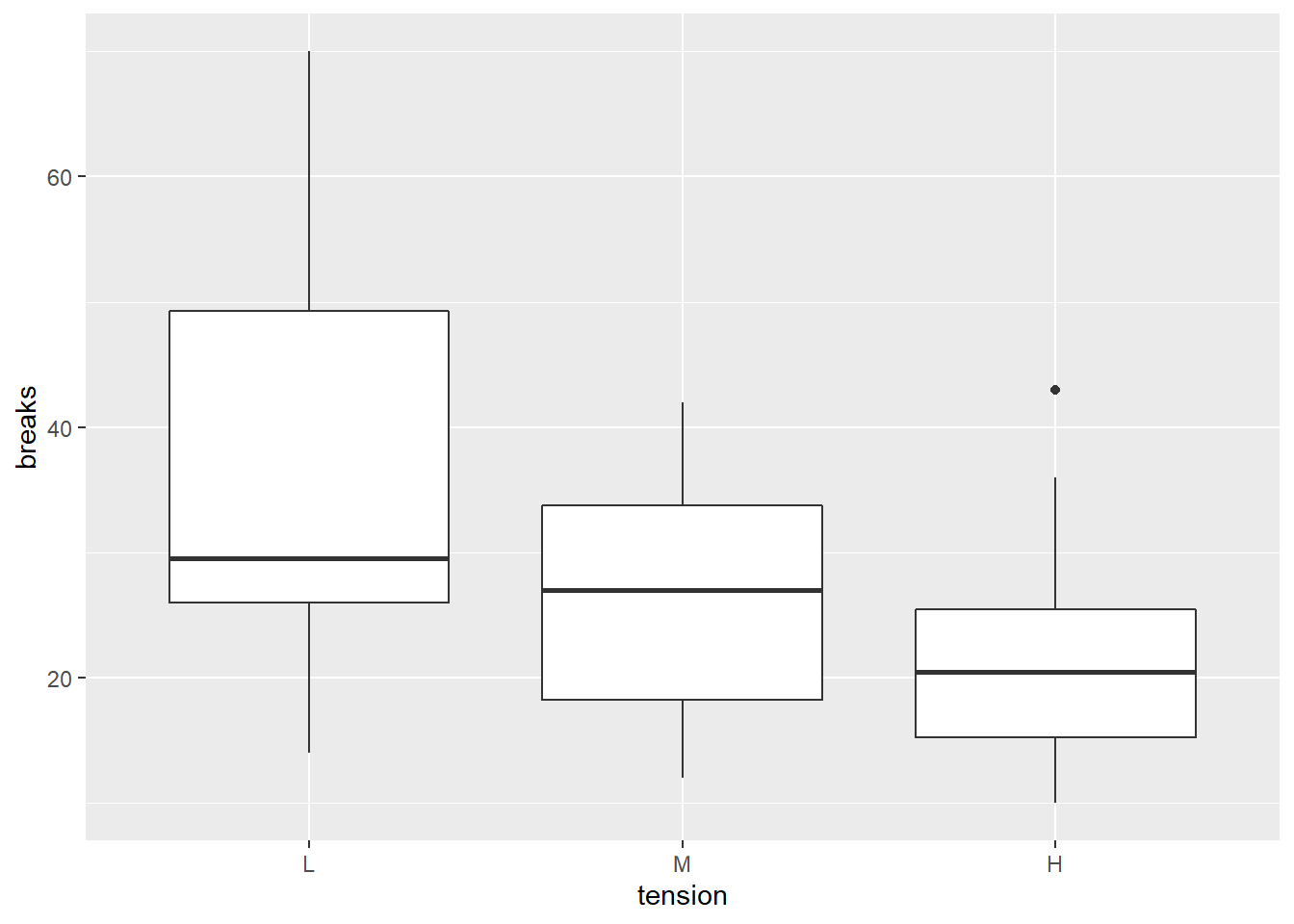
考虑不同组的均值的比较问题, \(H_{ij}: \mu_i - \mu_j = 0\), 对立假设为不等于0。 先用方差分析检验是否所有均值都相等:
aov.wb <- aov(breaks ~ tension, data=warpbreaks)
summary(aov.wb)
## Df Sum Sq Mean Sq F value Pr(>F)
## tension 2 2034 1017.1 7.206 0.00175 **
## Residuals 51 7199 141.1
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1在0.05水平下认为三个组的均值不全相等。
可以用glht()函数在控制总错误率以及考虑到各检验之间的约束关系的前提下给出单独检验的结果:
library(multcomp)
glht(aov.wb, linfct = mcp(tension = "Tukey"))
##
## General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Linear Hypotheses:
## Estimate
## M - L == 0 -10.000
## H - L == 0 -14.722
## H - M == 0 -4.722这显示了两两比较的均值差估计,
后续可以用summary()函数给出多重比较结果。
glht()可以诊断许多模型的拟合结果进行模型参数的联立的线性约束检验。
一般格式为
其中model可以是lm, aov, glm的结果。
需要模型参数估计以及参数估计的协方差阵估计都可以从model中提取出来。
linfct指定需要检验的参数线性约束组成的矩阵\(C^T\),
每一行是一个约束,
还提供了一些常用约束的简写形式。
\(C^T\)矩阵可以是对照矩阵,
也可以是其它矩阵。
最方便的是使用mcp函数指定\(C^T\),
均值的多重比较就可以用mcp函数指定,
这时会调用contrMat函数产生对照矩阵,
对照矩阵的类型有"Tukey",
"Dunnett", "Williams", "Changepoint"等,
参见下一小节。
也可以用字符串形式表示各个线性约束, 例如:
glht(aov.wb, linfct = mcp(tension = c(
"M - L = 0",
"H - L = 0",
"H - M = 0")))
##
## General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Linear Hypotheses:
## Estimate
## M - L == 0 -10.000
## H - L == 0 -14.722
## H - M == 0 -4.722也可以在mcp中直接输入比较用的矩阵,如:
cmat <- rbind(
"M - L" = c(-1, 1, 0),
"H - L" = c(-1, 0, 1),
"H - M" = c(0, -1, 1))
cmat
## [,1] [,2] [,3]
## M - L -1 1 0
## H - L -1 0 1
## H - M 0 -1 1
glht(aov.wb, linfct = mcp(tension = cmat))
##
## General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Linear Hypotheses:
## Estimate
## M - L == 0 -10.000
## H - L == 0 -14.722
## H - M == 0 -4.722也可以直接生成表示比较的矩阵而不通过mcp函数。
例如,
有三个水平的因子,
在线性模型中转换为如下的哑变量编码:
这种因子编码是将第一个水平作为对照组。
可以如下生成linfct要求的矩阵:
glht(aov.wb, linfct = cbind(
0, cmat %*% contr.treatment(3)))
##
## General Linear Hypotheses
##
## Linear Hypotheses:
## Estimate
## M - L == 0 -10.000
## H - L == 0 -14.722
## H - M == 0 -4.722下面查看glht函数输出。
mcr <- glht(aov.wb, linfct = mcp(tension = "Tukey"))
names(mcr)
## [1] "model" "linfct" "rhs" "coef" "vcov" "df" "alternative" "type"
## [9] "focus"coef是参数估计,
在默认的因子哑变量编码方案中,
第一个水平作为对照组,
三个水平的因子用两个哑变量表示,
模型可以写成
\[
y = \beta_0 + \beta_1 \text{tensionM}
+ \beta_2 \text{tensionH}
+ \varepsilon.
\]
这时,
\(\mu_L = \beta_0\),
\(\mu_M = \beta_0 + \beta_1\),
\(\mu_H = \beta_0 + \beta_2\)。
vcov是参数估计的协方差阵估计。
linfct给出要检验的联立线性约束矩阵,
每一行是一个线性约束,
rhs是线性约束等式的右侧值,
缺省为0。
mcr$linfct
## (Intercept) tensionM tensionH
## M - L 0 1 0
## H - L 0 0 1
## H - M 0 -1 1
## attr(,"type")
## [1] "Tukey"第一行检验\(\beta_1 = 0\), 就代表\(\mu_M - \mu_L = 0\); 第三行检验\(\beta_2 - \beta_1 = 0\), 就代表\(\mu_H - \mu_M = 0\)。
结果中的df是检验要用的多元t分布的自由度,
本例中为\(n-3\),
是观测个数减去因素水平数。
5.9.3.2 用summary函数给出多重检验结果
可以用summary()函数将glht()的输出转换多重检验结果。
如:
summary(mcr)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = breaks ~ tension, data = warpbreaks)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## M - L == 0 -10.000 3.960 -2.525 0.03847 *
## H - L == 0 -14.722 3.960 -3.718 0.00143 **
## H - M == 0 -4.722 3.960 -1.192 0.46308
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)结果给出了控制总错误率的每个比较的调整p值, 使用单步方法。 调整p值的计算利用了多元t分布。
取出部分结果如:
smr <- summary(mcr)
names(smr)
## [1] "model" "linfct" "rhs" "coef" "vcov" "df" "alternative" "type"
## [9] "focus" "test"
names(smr$test)
## [1] "pfunction" "qfunction" "coefficients" "sigma" "tstat" "pvalues" "type"
smr$test$pvalues
## [1] 0.038424524 0.001471752 0.463049578
## attr(,"error")
## [1] 0.0002845923summary()函数还可以用test选项选择使用的检验方法,
例如,
作普通的单因素方差分析F检验:
summary(mcr, test = Ftest())
##
## General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Linear Hypotheses:
## Estimate
## M - L == 0 -10.000
## H - L == 0 -14.722
## H - M == 0 -4.722
##
## Global Test:
## F DF1 DF2 Pr(>F)
## 1 7.206 2 51 0.001753指定test = Chisqtest()可以做Wald检验。
如果不需要做多重比较p值调整,
可以指定test = univariate(),如:
summary(mcr, test = univariate())
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = breaks ~ tension, data = warpbreaks)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## M - L == 0 -10.000 3.960 -2.525 0.014717 *
## H - L == 0 -14.722 3.960 -3.718 0.000501 ***
## H - M == 0 -4.722 3.960 -1.192 0.238614
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Univariate p values reported)test的参数可以取为adjusted(type = "..."),
这时使用指定的p值调整方法,
包括p.adjust()支持的p值调整方法。
可用方法包括
"none", 不调整;"BH"或"BY", 控制错误发现率的方法;"bonferroni";"holm", bonferroni的逐步方法,优于bonferroni;"hochberg", 基于Simes检验法,如果前提条件满足比Holm方法功效高;"hommel", 比Hochberg方法功效高;"single-step", 这是默认方法,会利用各统计量的相关性,比Bonferroni功效高;"free", 是"single-step"对应的逐步方法, 假定参数之间没有确定性的约束关系,功效更高;"Shaffer", 是考虑了参数之间约束关系的Bonferroni方法产生的逐步方法;"Westfall",是Shaffer方法的改进,利用了参数估计之间的相关性。
5.9.3.3 用confint函数给出联立置信区间
单步的多重比较方法一般都有对应的联立置信区间,
但是逐步方法则比较难产生联立置信区间。
multcomp包的confint函数从glht的输出结果用单步方法产生联立置信区间。
例如:
cir <- confint(mcr, level = 0.95); cir
##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = breaks ~ tension, data = warpbreaks)
##
## Quantile = 2.4134
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## M - L == 0 -10.0000 -19.5575 -0.4425
## H - L == 0 -14.7222 -24.2797 -5.1648
## H - M == 0 -4.7222 -14.2797 4.8352上面给出了三个均值之间两两的差的联立的95%置信区间, 利用了参数估计之间的相关性和多元t分布。 可以做置信区间的图形:
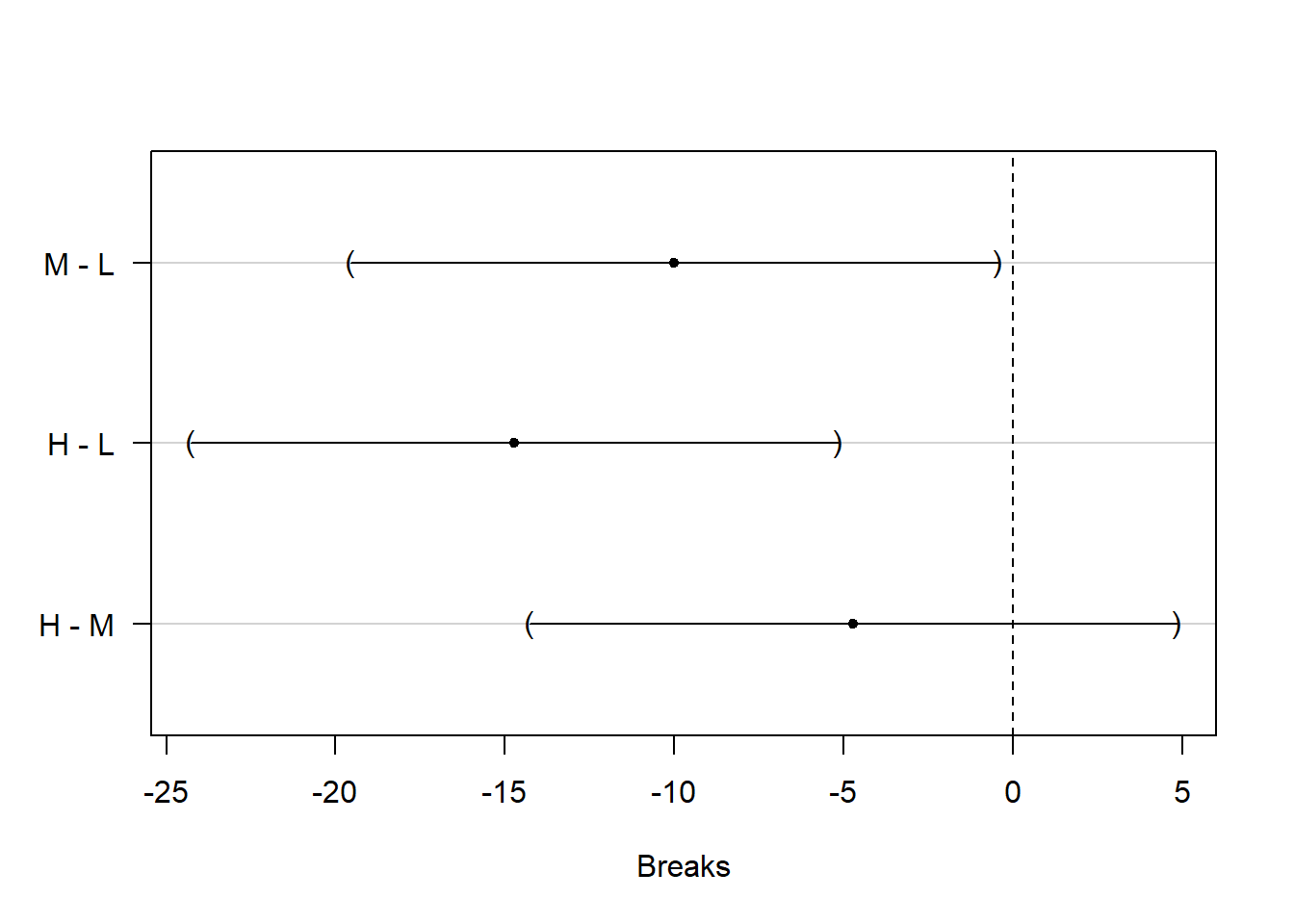
这里\(\mu_M - \mu_L\)与\(\mu_H - \mu_L\)的置信区间都在0的左侧, 所以在控制总错误率0.05的前提下可以认为M和H的断线个数都显著地低于L的断线个数; 而M和H的断线个数没有显著差异。
在confint()中指定calpha = univariate_calpha()可以做单个参数非联立的置信区间。
calpha也可以直接指定t统计量绝对值的临界值,
比如,
对应于联立的Bonferroni方法检验的临界值:
cbon <- qt(1 - 0.05/2/3, 51)
confint(mcr, calpha = cbon)
##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = breaks ~ tension, data = warpbreaks)
##
## Quantile = 2.4755
## 95% confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## M - L == 0 -10.0000 -19.8035 -0.1965
## H - L == 0 -14.7222 -24.5257 -4.9187
## H - M == 0 -4.7222 -14.5257 5.0813在处理组之间两两比较时如果处理组个数很多,
也可以使用简化的可交叉分组字母式显示比较结果,
有同一字母的就没有显著差异。
可以用cld()函数对glht()的结果做预处理,
然后绘图。如:
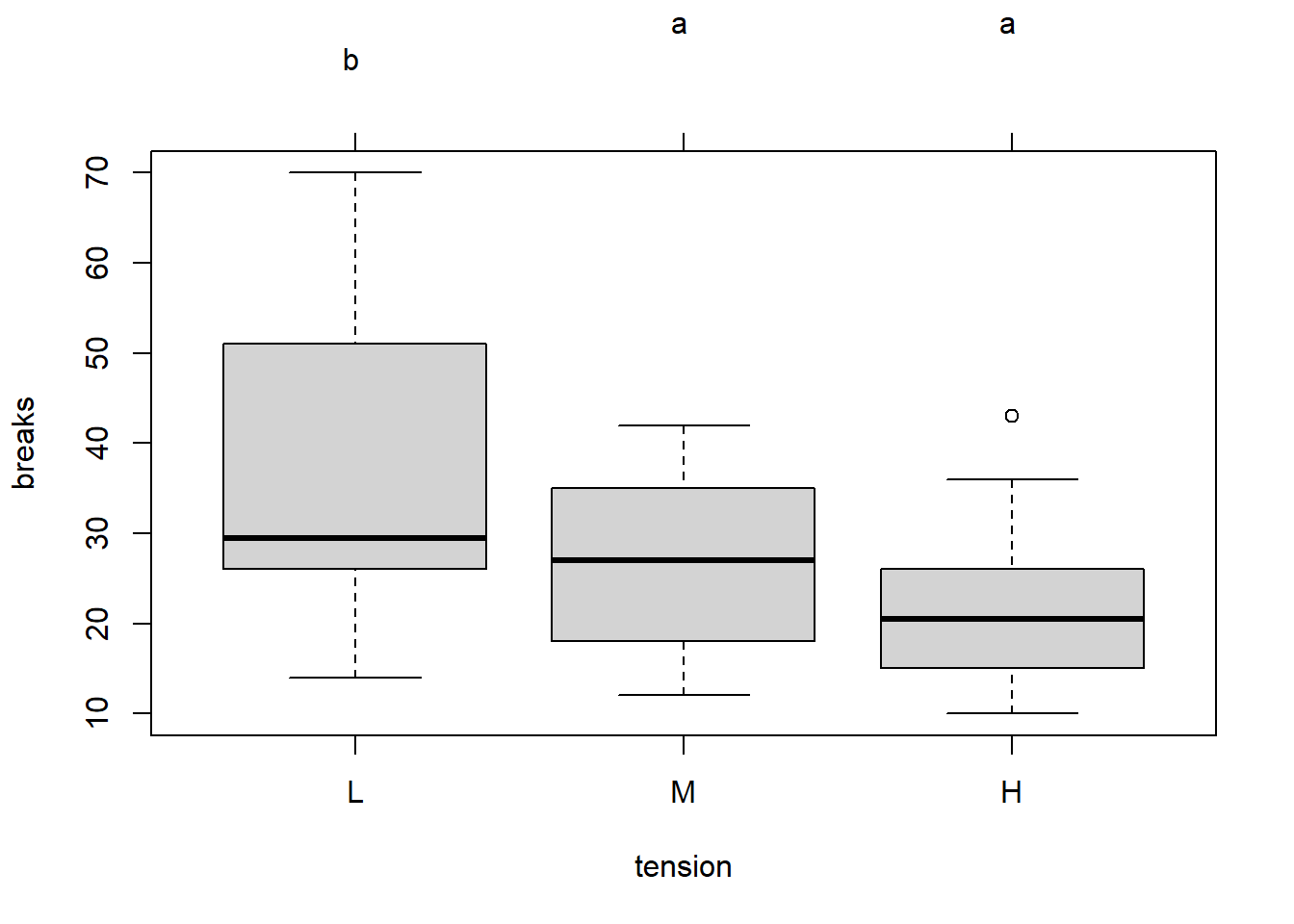
注意图形上方的字母“b, a, a”, 这表明M和H之间没有显著差异, 而其它两两比较有显著差异。 对单因素或者多因素方差分析模型, 每个因素都在水平之间进行两两比较。
5.9.4 与对照组的比较
5.9.4.1 单步方法
一种常见的情形是多个处理组与一个对照组的比较, 这种比较使用Dunnet检验。 设模型为 \[\begin{aligned} y_{ij} = \mu + \alpha_i + e_{ij}, \ j=1,2,\dots,n_i; \ i=0, 1,\dots,m \end{aligned}\] 因素的第一个水平是对照组, 其它水平与对照组相比。 可以两两做两样本t检验 \[\begin{aligned} t_i = \frac{\bar y_{i\cdot} - \bar y_{0\cdot}}{ S \sqrt{\frac{1}{n_i} + \frac{1}{n_0}} } \end{aligned}\] 其中\(S\)是合并的标准差估计: \[\begin{aligned} S^2 = \frac{1}{n - m - 1} \sum_{i=0}^m \sum_{j=1}^{n_i} (y_{ij} - \bar y_{i\cdot})^2 , \end{aligned}\] 其中\(n = \sum_{i=0}^m r_i\)是总试验次数。
为了控制总错误率, 利用\((t_1, \dots, t_m)\)为多元t分布并可求出其相关系数阵, 比如各组重复试验次数相同时相关系数都等于\(0.5\); 利用统计量的联合分布可以给出单步的多重比较方法。
以multcomp中的recovery数据为例, 比较使用3种新保温毯(blanket = b1, b2, b3)与使用原型号保温毯(b0)的手术后病人的恢复时间(minutes)。
data(recovery, package="multcomp")
summary(recovery)
## blanket minutes
## b0:20 Min. : 5.00
## b1: 3 1st Qu.:12.00
## b2: 3 Median :13.00
## b3:15 Mean :13.49
## 3rd Qu.:16.00
## Max. :19.00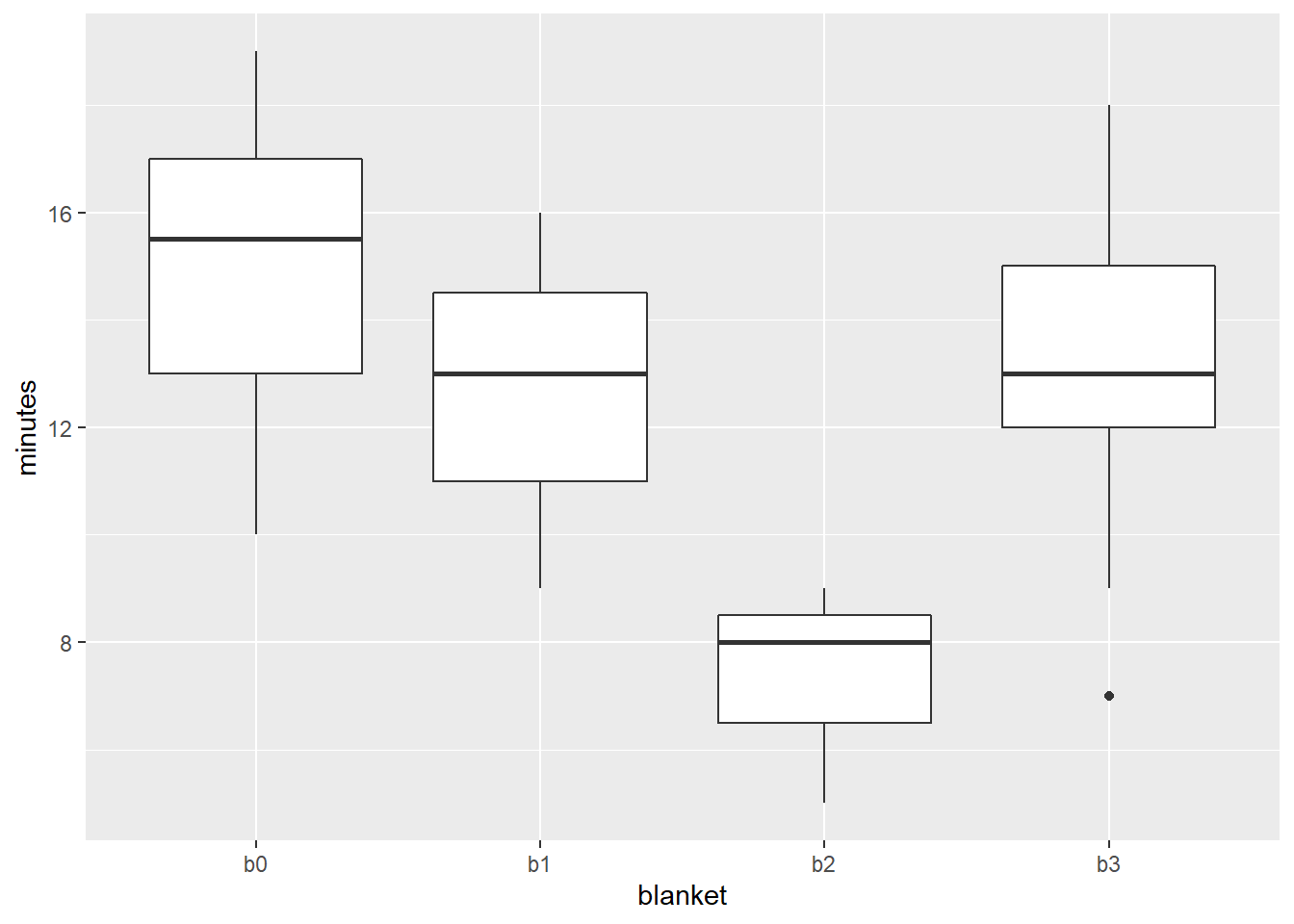
用multcomp包进行Dunnet检验:
aov.blkt <- aov(minutes ~ blanket, data=recovery)
mc.blkt <- glht(
aov.blkt,
linfct = mcp(blanket = "Dunnet"),
alternative = "less")
summary(mc.blkt)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(<t)
## b1 - b0 >= 0 -2.1333 1.6038 -1.330 0.2412
## b2 - b0 >= 0 -7.4667 1.6038 -4.656 <1e-04 ***
## b3 - b0 >= 0 -1.6667 0.8848 -1.884 0.0925 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)这里对立假设是\(\mu_i - \mu_0 < 0\), 即恢复时间缩短。 输出为控制了总错误率的调整p值。 在0.05水平下b2显著优于b0; 其它两个比较不显著。
作为比较, 用Bonferroni方法也进行多重检验:
summary(mc.blkt, test = adjusted(type = "bonferroni"))
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(<t)
## b1 - b0 >= 0 -2.1333 1.6038 -1.330 0.287
## b2 - b0 >= 0 -7.4667 1.6038 -4.656 6.1e-05 ***
## b3 - b0 >= 0 -1.6667 0.8848 -1.884 0.101
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- bonferroni method)报告的调整p值有一些比Dunnet方法的结果变大了。
计算检验对应的联立置信区间, 这时为只有右边界的区间:
ci.blkt <- confint(mc.blkt, level = 0.95)
ci.blkt
##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Quantile = 2.1825
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## b1 - b0 >= 0 -2.1333 -Inf 1.3670
## b2 - b0 >= 0 -7.4667 -Inf -3.9664
## b3 - b0 >= 0 -1.6667 -Inf 0.2644只有b2-b0的区间在0的左侧,
说明b2的恢复时间显著低于b0的恢复时间。
置信区间作图:
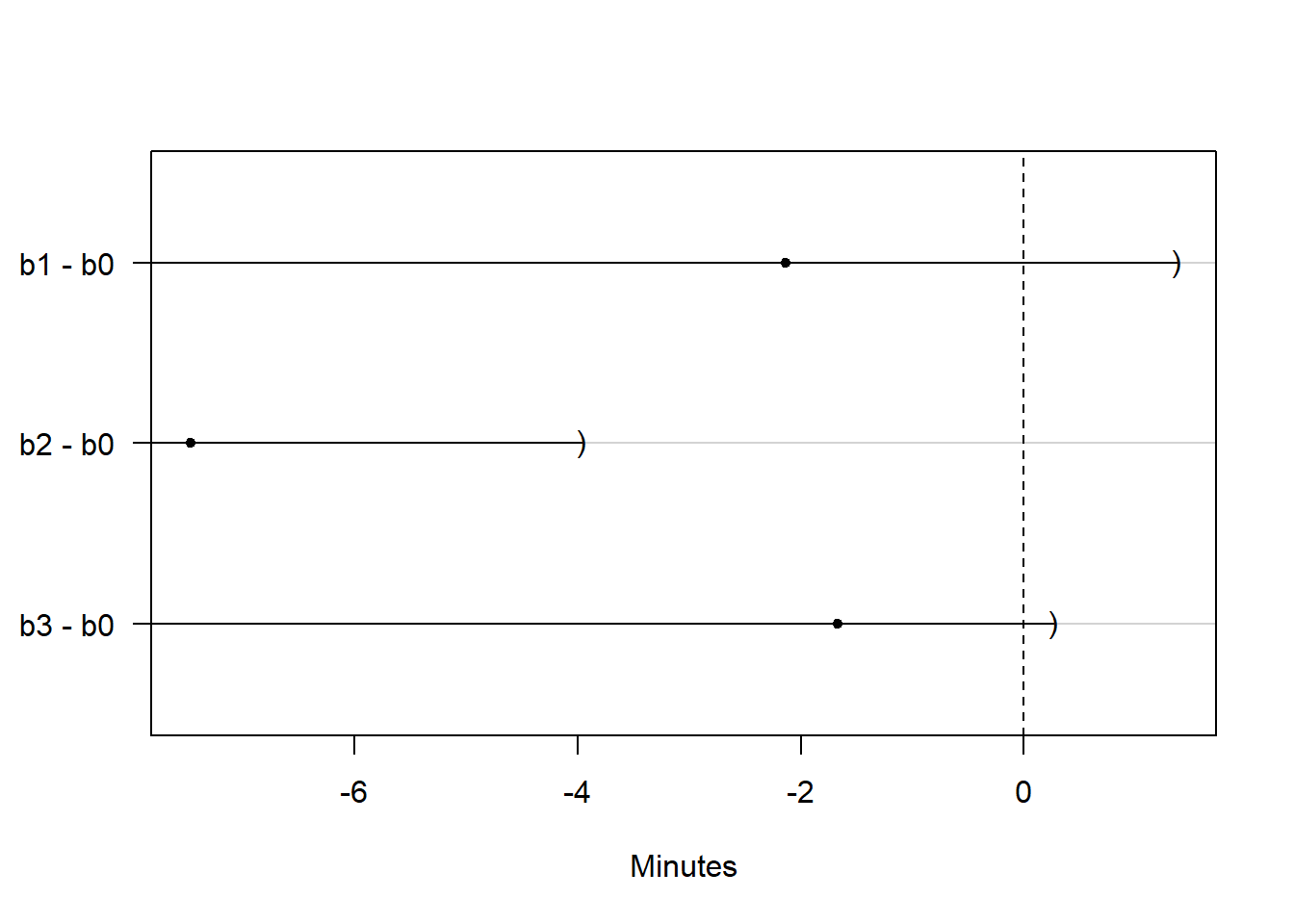
这里的模型可以写成 \[\begin{aligned} y_{ij} =& \beta_0 b_0 + \beta_1 b_1 + \beta_2 b_2 + \beta_3 b_3 + e_{ij},\\ & j=1,2,\dots,n_i; \ i=0,1,2,3, \end{aligned}\] 其中\(b_0, b_1, b_2, b_3\)是四个组的示性变量。 多重检验线性约束矩阵\(C^T\)相当于 \[\begin{aligned} \begin{pmatrix} -1 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \end{pmatrix} \end{aligned}\] 要检验的线性约束为 \[\begin{aligned} C^T \boldsymbol{\beta} = \begin{pmatrix} \beta_1 - \beta_0 \\ \beta_2 - \beta_0 \\ \beta_3 - \beta_0 \end{pmatrix} = \boldsymbol{0} . \end{aligned}\]
Dunnet检验就是将第一个组作为对照组, 其它组作为处理组的多重比较。
因为是单侧检验,所以实际检验的是\(\beta_i - \beta_0 \geq 0\)。
自定义对照矩阵, 可以得到相同结果:
cmat <- rbind(
"b1 - b0" = c(-1, 1, 0, 0),
"b2 - b0" = c(-1, 0, 1, 0),
"b3 - b0" = c(-1, 0, 0, 1))
mc.blkt2 <- glht(
aov.blkt,
linfct = mcp(blanket = cmat),
alternative = "less")
summary(mc.blkt2)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(<t)
## b1 - b0 >= 0 -2.1333 1.6038 -1.330 0.2412
## b2 - b0 >= 0 -7.4667 1.6038 -4.656 <0.001 ***
## b3 - b0 >= 0 -1.6667 0.8848 -1.884 0.0924 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)得到的调整p值与Dunnet方法相同。 能够输入对照矩阵使得我们可以不限于使用multcomp现成的多重比较, 可以进行定制的检验。 例如, 将b2, b3作为处理组,b0, b1作为对照组, 分别两两比较:
cmat3 <- rbind(
"b2 - b0" = c(-1, 0, 1, 0),
"b2 - b1" = c(0, -1, 1, 0),
"b3 - b0" = c(-1, 0, 0, 1),
"b3 - b1" = c(0, -1, 0, 1))
mc.blkt3 <- glht(
aov.blkt,
linfct = mcp(blanket = cmat3),
alternative = "less")
summary(mc.blkt3)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(<t)
## b2 - b0 >= 0 -7.4667 1.6038 -4.656 <0.001 ***
## b2 - b1 >= 0 -5.3333 2.1150 -2.522 0.0274 *
## b3 - b0 >= 0 -1.6667 0.8848 -1.884 0.1051
## b3 - b1 >= 0 0.4667 1.6383 0.285 0.9150
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)5.9.4.2 逐步方法
用闭包原则对单步的Dunnet方法进行改造。 比如, 有三个处理组与一个对照组比较, 记为\(H_1\), \(H_2\), \(H_3\), 则需要考虑各个交集\(H_1\), \(H_2\), \(H_3\), \(H_{12}\), \(H_{13}\), \(H_{23}\), \(H_{123}\)。 要拒绝\(H_1\), 只要拒绝被\(H_1\)包含的任一个交集假设, 所以每个检验是一种并交法检验, 可以使用Dunnet方法, 统计量使用最大t统计量。 比如, 为了检验\(H_{123}\), 如果检验是双侧的, 统计量就采用三个t统计量的绝对值的最大值, 只要最大值超过临界值就拒绝\(H_{123}\)。
最大t统计量检验法在各检验可自由组合时有一个优点, 即不需要检验所有的交集, 而是只要检验其中的一部分。 这是一个逐步向下的检验法(从最显著的开始判决), 算法如下:
\[\begin{aligned} & I = \{1, 2, \dots, m \}, \ q = 0 \\ & \text{计算各个单独的检验的t统计量}t_1, t_2, \dots, t_m \\ & \text{for } j=1, 2, \dots, m \\ & \qquad H_{Ij} = \bigcap_{i \in I} H_i; \\ & \qquad \text{计算最大t统计量tmax}, \text{设达到最大值的是}t_{i_j}; \\ & \qquad \text{计算tmax对应的p值} p \\ & \qquad \text{if } p \leq \alpha \\ & \qquad\qquad \text{拒绝} H_{i_j}, \text{计算其调整p值} q = \max\{ q, p \} \\ & \qquad\qquad I = I - \{ i_j \} \\ & \qquad \text{else } \\ & \qquad\qquad \text{break} \\ & \qquad \text{end if } \\ & \text{end for} \end{aligned}\]
在算法中, tmax对双边检验是各个检验的统计量的绝对值的最大值; 对右侧检验,是各个检验的统计量的最大值; 对左侧检验,是各个检验的统计量的相反数的最大值。
作为例子, 对前面的recovery数据框做最大t统计量逐步下降的Dunnet检验:
summary(mc.blkt, test = adjusted(type = "free"))
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = minutes ~ blanket, data = recovery)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(<t)
## b1 - b0 >= 0 -2.1333 1.6038 -1.330 0.0958 .
## b2 - b0 >= 0 -7.4667 1.6038 -4.656 6.32e-05 ***
## b3 - b0 >= 0 -1.6667 0.8848 -1.884 0.0640 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- free method)调整p值比单步方法的调整p值都减小了许多。
下面用recovery数据解释闭包法则, 以及为什么可以不必检验所有的交集假设。 这里单个的t统计量为 \[\begin{aligned} t_1 =& -1.33 \\ t_2 =& -4.66 \\ t_3 =& -1.89 \end{aligned}\]
先检验\(H_{123} = H_1 \cap H_2 \cap H_3\), 如果不拒绝\(H_{123}\), 就意味着三个检验都成立, 就应该同时接受这三个检验, 而不必再继续检验。 这里\(\text{tmax} = 4.66\), 达到最大值的是\(i_1 = 2\), 可以用Dunnet方法计算其对应的p值 \[\begin{aligned} P(\max(-t_1, -t_2, -t_3) > 4.66) < 0.001 \end{aligned}\] 在0.05水平下可以拒绝\(H_{123}\)。
在拒绝了\(H_{123}\)以后, \(H_{12}\)和\(H_{13}\)也应该拒绝, 事实上,因为 \[\begin{aligned} P(\max(-t_1, -t_2, -t_3) > 4.66) < 0.001 \end{aligned}\] 而 \[\begin{aligned} \max(-t_1, -t_2) > 4.66 \Longrightarrow \max(-t_1, -t_2, -t_3) > 4.66 \end{aligned}\] 所以 \[\begin{aligned} & P(\max(-t_1, -t_2) > 4.66) \\ & \leq P(\max(-t_1, -t_2, -t_3) > 4.66) < 0.001 \end{aligned}\] 于是拒绝\(H_{123}\)就一定拒绝\(H_{12}\), 同理一定拒绝\(H_{23}\)和\(H_2\)。 这样\(H_{12}\), \(H_{23}\),\(H_2\)也被拒绝而不需要再计算相应的p值。
现在\(H = \{1,2,3\} - \{2\} = \{1,3\}\), 继续检验\(H_{13}\)。 \(\text{tmax} = 1.89\), 达到最大值的是\(t_3\),\(i_2 = 3\)。 用最大t统计量法计算\(H_{13}\)的p值为 \[\begin{aligned} P(\max(-t_1, -t_3) > 1.89) = 0.064 \end{aligned}\] 超过0.05, 不拒绝\(H_{13}\), 这也就不能拒绝\(H_1\)和\(H_3\)。 检验结束。
5.9.5 处理组之间两两比较
5.9.5.1 Tukey检验
考虑有\(m\)个处理组之间两两比较的检验问题。 这样的问题检验之间不仅检验统计量有相关性, 检验的命题之间也有逻辑关系。 比如, 同时承认\(\mu_1 = \mu_2\)和\(\mu_1 = \mu_3\), 就不能拒绝\(\mu_2 = \mu_3\)。
均值的两两比较通常使用Tukey检验, 第\(i\)组与第\(j\)组比较的统计量为 \[\begin{aligned} t_{ij} = \frac{\bar y_{i\cdot} - \bar y_{j\cdot}}{ S \sqrt{\frac{1}{n_i} + \frac{1}{n_j}} } \end{aligned}\] 其中 \[\begin{aligned} S^2 = \frac{1}{n-m} \sum_{i=1}^m \sum_{j=1}^{n_i} (y_{ij} - \bar y_{i\cdot})^2 . \end{aligned}\]
为了控制总错误率而计算每个\(t_{ij}\)的调整p值或者临界值比较困难, 仅在单因素均衡设计时有理论结果, 更复杂的情况可以用数值计算方法计算调整p值。
以MASS包的immer数据为例, 有两年的大麦产量试验数据, 影响因素包括5个种粮品种(Var)和6个不同地块(Loc), 使用可加的两因素方差分析, 指标取两年平均值。 方差分析:
data(immer, package="MASS")
aov.im <- aov((Y1+Y2)/2 ~ Var + Loc,
data = immer)
summary(aov.im)
## Df Sum Sq Mean Sq F value Pr(>F)
## Var 4 2655 663.7 5.989 0.00245 **
## Loc 5 10610 2122.1 19.148 5.21e-07 ***
## Residuals 20 2217 110.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1考虑5个种粮品种的两两比较, 如下程序显示各组的均值:
model.tables(aov.im, type="means")$table$Var
## Var
## M P S T V
## 94.39167 102.54167 91.13333 118.20000 99.18333进行\(\binom{5}{2} = 10\)次两两比较, 使用glht进行多重检验:
mc.im <- glht(aov.im,
linfct = mcp(Var = "Tukey"))
mc.im
##
## General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Linear Hypotheses:
## Estimate
## P - M == 0 8.150
## S - M == 0 -3.258
## T - M == 0 23.808
## V - M == 0 4.792
## S - P == 0 -11.408
## T - P == 0 15.658
## V - P == 0 -3.358
## T - S == 0 27.067
## V - S == 0 8.050
## V - T == 0 -19.017用summary()输出用单步方法调整的p值:
summary(mc.im)
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = (Y1 + Y2)/2 ~ Var + Loc, data = immer)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## P - M == 0 8.150 6.078 1.341 0.67006
## S - M == 0 -3.258 6.078 -0.536 0.98242
## T - M == 0 23.808 6.078 3.917 0.00673 **
## V - M == 0 4.792 6.078 0.788 0.93102
## S - P == 0 -11.408 6.078 -1.877 0.36074
## T - P == 0 15.658 6.078 2.576 0.11323
## V - P == 0 -3.358 6.078 -0.553 0.98035
## T - S == 0 27.067 6.078 4.453 0.00208 **
## V - S == 0 8.050 6.078 1.324 0.67984
## V - T == 0 -19.017 6.078 -3.129 0.03776 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)结果包含控制总错误率的调整p值, 计算时利用了t统计量之间的相关性信息, 在10对比较中只有3对显著差异。
实际上,
R中的TukeyHSD()函数也提供了计算Tukey多重比较检验的功能,如:
TukeyHSD(aov.im, which="Var")
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = (Y1 + Y2)/2 ~ Var + Loc, data = immer)
##
## $Var
## diff lwr upr p adj
## P-M 8.150000 -10.037586 26.3375861 0.6700640
## S-M -3.258333 -21.445919 14.9292527 0.9824197
## T-M 23.808333 5.620747 41.9959194 0.0067837
## V-M 4.791667 -13.395919 22.9792527 0.9310208
## S-P -11.408333 -29.595919 6.7792527 0.3606801
## T-P 15.658333 -2.529253 33.8459194 0.1132216
## V-P -3.358333 -21.545919 14.8292527 0.9803501
## T-S 27.066667 8.879081 45.2542527 0.0020271
## V-S 8.050000 -10.137586 26.2375861 0.6798245
## V-T -19.016667 -37.204253 -0.8290806 0.0377100结果与multcomp包结果差别很小。
TukeyHSD()主要适用于单因素方差分析,
而multcomp可以支持多因素方差分析,
以及协方差分析、广义线性模型等。
计算均值差的联立置信区间:
ci.im <- confint(mc.im, level=0.95)
ci.im
##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = (Y1 + Y2)/2 ~ Var + Loc, data = immer)
##
## Quantile = 2.9939
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## P - M == 0 8.1500 -10.0467 26.3467
## S - M == 0 -3.2583 -21.4550 14.9384
## T - M == 0 23.8083 5.6116 42.0050
## V - M == 0 4.7917 -13.4050 22.9884
## S - P == 0 -11.4083 -29.6050 6.7884
## T - P == 0 15.6583 -2.5384 33.8550
## V - P == 0 -3.3583 -21.5550 14.8384
## T - S == 0 27.0667 8.8700 45.2634
## V - S == 0 8.0500 -10.1467 26.2467
## V - T == 0 -19.0167 -37.2134 -0.8200置信区间作图:
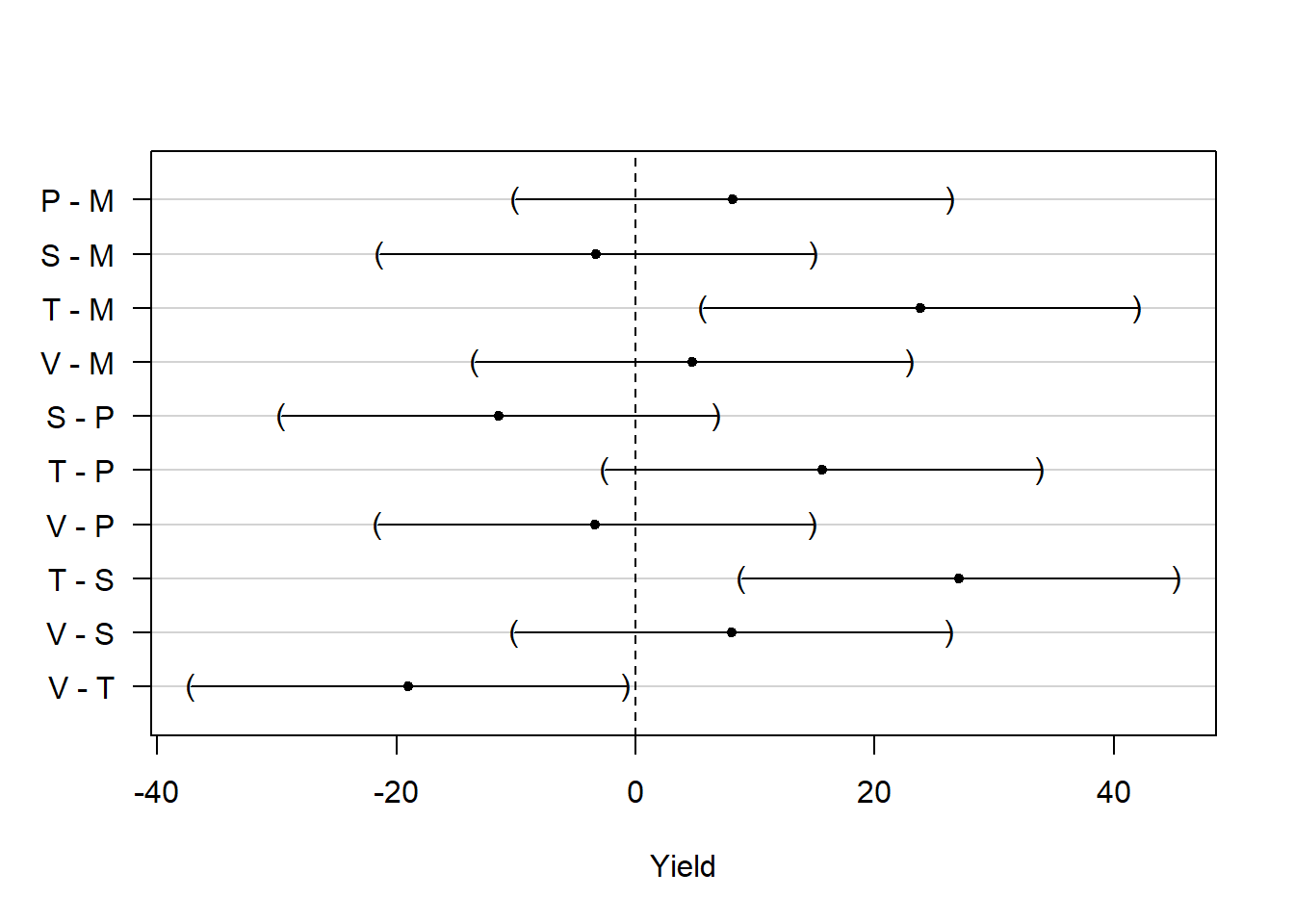
使用可交叉字母分组表示显著差异:
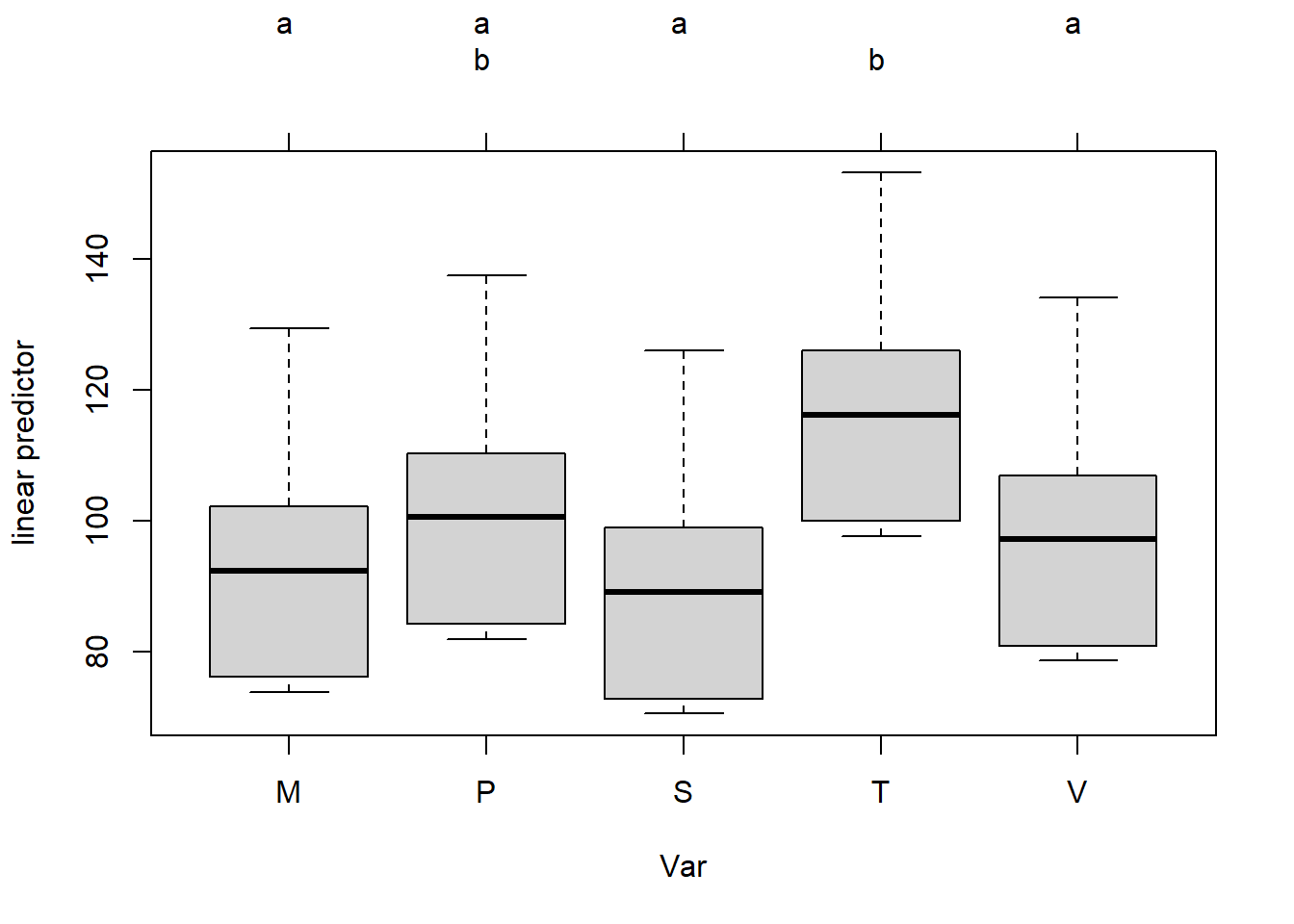
这里M, P, S, V都属于a组, 在0.05水平下相互没有显著差异; P和T属于b组,相互之间没有显著差异。 P既属于a组也属于b组, 但并不能因此将两个组合并。 结果表明T与M, S, V之间有显著差异。
5.9.5.2 用闭包法则生成Tukey逐步检验
两两比较检验的交集有许多是重复的, 比如三个组的两两比较, 接受\(H_{12}\)和\(H_{13}\)就必须接受\(H_{23}\)和\(H_{123}\)。 交集个数减少, 意味着检验功效增大。
如果当子集\(I \neq I'\)时一定有\(H_{I} \neq H_{I'}\), 称检验的集合是自由组合的; 否则称为组合受限的。 多个处理组与一个对照组的比较是自由组合的, 两两比较、响应面比较、一般复杂对照是组合受限的。
对immer数据, 用闭包法则与Tukey检验:
summary(mc.im, test=adjusted(type="Westfall"))
##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = (Y1 + Y2)/2 ~ Var + Loc, data = immer)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## P - M == 0 8.150 6.078 1.341 0.38990
## S - M == 0 -3.258 6.078 -0.536 0.82566
## T - M == 0 23.808 6.078 3.917 0.00439 **
## V - M == 0 4.792 6.078 0.788 0.43973
## S - P == 0 -11.408 6.078 -1.877 0.26916
## T - P == 0 15.658 6.078 2.576 0.06168 .
## V - P == 0 -3.358 6.078 -0.553 0.82566
## T - S == 0 27.067 6.078 4.453 0.00208 **
## V - S == 0 8.050 6.078 1.324 0.39850
## V - T == 0 -19.017 6.078 -3.129 0.01910 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- Westfall method)调整p值比单步方法有所降低。
如果指定type="Shaffer",
则单步检验采用Bonferroni方法,
Westfall采用Tukey检验,
Westfall功效优于Shaffer方法。
(Bretz, Hothorn, and Westfall 2011)中还有更多的内容, 比如, 协方差分析, 回归变量选择, 两个回归模型的比较, 方差非齐性下的比较, 逻辑回归、生存分析、混合效应模型中的多重比较, 基于再抽样的多重比较方法, 分组序贯和适应性设计的方法, 将多重比较与建模有机结合, 等等。
5.10 SAS单因素方差分析中的多重比较
参考:SAS Stat 9.22 User’s Guide, MULTTEST,GLM过程说明。
在单因素方差分析问题中, 将数据按照某个因素(分组变量)分成若干组, 零假设为所有各组的指标均值都相等。 在拒绝零假设后, 还需要比较那些组的指标最好,那些组的指标均值最差, 要避免多次比较的第一类错误概率增加。 这样的方法统称为多重比较步骤(Multiple Testing Procedures)。
同时进行多个检验时, 可以输出修正过的p值, 使得按照p值小于等于\(\alpha\)对每个检验进行判决时, 总错误率(FWER)不超过\(\alpha\)。
Bonferroni方法和Šidák只需要各次检验的p值而不需要了解检验问题, 但是都过于保守。 Step-down方法,Step-up方法(Hochberg(1988)),自适应方法, 可以减少这样的保守性。 bootstrap检验方法、置换(permutation)检验方法用有放回或无放回抽样方法生成许多样本, 得到所有比较p值最小值的分布。 这两种方法需要很大计算量, 但可以容许各次检验之间有各种关联性。 参见(Westfall and Young 1989; Westfall et al. 1999)。
5.10.1 控制FWE的p值调整方法
一步完成的调整方法只需要一次性地计算调整的p值, 不需要考虑其它零假设。 这样的方法有Bonferroni和Šidák调整方法, 只需要原始p值作为输入,结果是p值的简单函数。 bootstrap和置换检验法也可以一步完成, 但是需要原始数据。
另一类方法是逐步检验方法, 或称序贯拒绝检验。 将各个检验按照p值递增(step-up, 从小到大排列)或者递减方法重排, 然后按重排后的次序逐一决定对相应零假设的判决。 逐步检验方法比一步完成的方法功效更高, 即保持控制总错误率的条件下降低第二类错误概率, 而且还可以减少要做的检验次数。 这些方法包括: 递增的Bonferroni(Holm方法), 递减的Šidák, 递减的bootstrap或置换检验, Hochberg(1988)的递增方法, Hommel(1988)方法, Fisher综合方法。 Holm的递增Bonferroni方法、Hochberg的递增Bonferroni方法都可以有适应版本, 会用到真实的零假设个数的估计值。
Liu (1996)的文章证明所有仅利用边缘p值的单步和逐步方法可以用来构造闭合(closed)检验, 闭合检验不仅能控制总错误率, 还能比原始的检验功效更高。 Westfall and Wolfinger (2000)讨论了一些闭合检验, 比如递减方法, Hommel方法, Fisher综合方法。 关于闭合检验参见 Marcus, Peritz, and Gabriel (1976), Dmitrienko et al. (2005)。
boostrap和置换检验这些再抽样方法需要原始数据, 其它p值调整方法都只需要原始p值或者边缘置换分布进行一些简单计算。 再抽样方法会保持问题的相关结构, 所以这些方法相对而言会有较低的保守性。
5.10.1.1 Bonferroni方法
对同时进行\(k\)个比较, 修正p值的公式就是简单地 \[ \tilde p_j = \min(1, k p_j), \ j=1,2,\dots,k \] 这样的方法不管各个检验之间是独立还是存在何种关联都能控制总错误率FWE。
5.10.1.2 Bootstrap方法
Bootstrap方法需要原始数据与检验统计量计算公式。 设原始数据按照某个分类变量分成若干组, 要进行两两比较或者选取所有两两比较中的一部分进行比较, 设共有\(k\)个检验,p值为\(p_j, j=1,\dots,k\)。 用有放回随机抽样方法生成一个与原来数据观测个数相等的新bootstrap数据集, 对此再抽样数据集重新计算\(k\)检验的p值; 设置\(k\)个计数器\(L_j, j=1,\dots,k\), 计算再抽样数据集的所有p值的最小值\(p^*\), 如果\(p^* \leq p_j\), 就令计数器\(L_j\)加一。 再抽样生成新bootsrap数据集重复\(B\)次(如1000次), 每次执行上面的计数器操作。 令 \[ \tilde p_j = \frac{L_j}{B} \] 参见Westfall and Young (1993)。
Bootstrap方法的好处是修正的p值会自动包含数据中原有的相关性, 包括多重对照和多变量相关性。 可以对FWE实现弱控制, 当subset pivotality条件成立时对FWE实现强控制, 此条件的含义是, 对所有零假设的一个任意子集, 在此子集下所有p值的联合分布, 应该与全部零假设下的联合分布相同。
5.10.1.3 置换检验方法
置换检验方法与bootstrap方法基本相同, 但是在生成再抽样的样本数据集时采用无放回抽样, 而不是有放回抽样。 类似地计算调整p值。
Bootsrap方法和置换检验方法实际上是将所有组合并看成一个同分布的总体, 从中随机抽样。 得到的修正p值是在所有各组均值都相等条件下的p值。
5.10.1.4 递减逐步检验方法
对Bonferroni, Šidák, bootstrap和置换检验方法都可以改造为递减的逐步检验方法, 使这些检验功效更高(第二类错误概率更低)。 最初的文献是Holm (1979), 后续有Shaffer (1986), Holland and Copenhaver (1987), Hochberg and Tamhane (1987)。
将\(p_1, p_2, \dots, p_k\)从小到大排序为 \[ p_{(1)} \leq p_{(2)} \leq \dots p_{(k)} \] 并将\(p_{(j)}\)对应的零假设也重新编号为\(H_{0(j)}\)。 Bonferroni递减调整p值(也称为Holm方法)的公式为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} k p_{(1)} & j=1 \\ \max\left(\tilde p_{(j-1)},\; (k-j+1) p_{(j)} \right) & j=2,\dots,k \end{cases} \end{aligned}\] 当调整p值超过1时就设为1。
Šidák调整p值的公式为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} 1 - (1 - p_{(1)})^k & j=1 \\ \max\left(\tilde p_{(j-1)},\; 1 - (1 - p_{(j)})^{k-j+1} \right) & j=2,\dots,k \end{cases} \end{aligned}\]
对bootstrap和置换检验方法进行递减逐步方法改进不会增加计算量, 能近似控制总错误率。 参见 Westfall and Young (1993), Westfall et al. (1999), Westfall and Wolfinger (2000)。
5.10.1.5 Hommel方法
Hommel(1988)是一个闭合检验过程(closed testing procedure), 基于Simes(1986)的检验法。 对有\(m\)个检验且p值为\(p_{(1)} \leq p_{(2)} \leq \dots \leq p_{(m)}\)的问题, Simes调整p值为 \[\begin{aligned} \min\left( \frac{m}{1} p_{(1)}, \frac{m}{2} p_{(2)}, \dots, \frac{m}{m} p_{(m)} \right) \end{aligned}\] Hommel对第\(j\)个检验的调整p值是考虑所有包含第\(j\)个检验的联立检验的Simes p值的最大值。
5.10.1.6 Hochberg方法
设在各个零假设成立的条件下, 各个p值独立同标准均匀分布。 Hochberg(1988)证明Holm的递减方法能控制总错误率, 改为递增方法也能控制总错误率。 Hochberg方法与Holm方法相比总是给出更低的调整p值, 所以功效更高,但是Hochberg方法需要假定各个检验独立。 Hochberg方法可以从Hommel方法导出(见Liu(1996)), 所以也可以从Simes方法导出。
Hochberg调整p值总是大于等于Hommel方法的调整p值。 Sarkar and Chang (1997)证明Simes方法在p值独立或者正相关时成立, 所以Hommel方法与Hochberg方法在这样的情况下也成立。
Hochberg方法是以递减Bonferroni方法的反方向来计算调整p值的: \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} p_{(k)} & j=k \\ \min\left(\tilde p_{(j+1)},\; (k-j+1) p_{(j)} \right) & j=k-1,\dots,2,1 \end{cases} \end{aligned}\]
5.10.1.7 Fisher综合方法
Fisher综合方法基于Fisher的综合检验, 利用闭合检验进行p值调整。 对有\(m\)个检验的联立检验, 利用服从\(\chi^2(2 m)\)的检验统计量 \(\chi^2 = -2 \sum \log(p_i)\), 为了得到第\(j\)个检验的调整p值, 对所有包含第\(j\)个检验的联立检验进行Fisher综合检验, 以所有这些综合检验的p值的最大值作为调整p值。 此方法在各个检验p值独立的条件下成立。
5.10.1.8 适应调整方法
适应调整方法将真实成立的零假设的个数\(k_0\)或者比例\(k_0/k\)纳入考虑, 估计这些值,在调整时利用此信息。 如Hochberg and Benjamini (1990), 提供了适应的递减Bonferroni(称为适应Holm方法)和适应的递增Bonferroni方法(称为适应Hochberg方法), 因为\(k_0\)是估计的, 所以对FWE的控制是近似的。
适应Holm方法的调整p值公式为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} \min(k, \hat k_0)\; p_{(1)} & j=1 \\ \max\left(\tilde p_{(j-1)},\; \min(k-j+1, \hat m_0)\; p_{(j)} \right) & j=2,\dots,k \end{cases} \end{aligned}\]
适应Hochberg方法的调整p值为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} \min(1, \hat k_0)\; p_{(k)} & j=k \\ \min\left(\tilde p_{(j+1)},\; \min(k-j+1, \hat k_0)\; p_{(j)} \right) & j=k-1,\dots,2,1 \end{cases} \end{aligned}\]
5.10.2 控制FDR的p值调整方法
Benjamini and Hochberg(1995)描述了控制FDR的多重比较方法。 这些方法一般不控制FWE, 一般比控制FWE的方法能够发现更多的显著差异。 当零假设个数很多的时候控制FDR的方法比较合适。 Storey(2002) 描述了控制pFDR的方法。
FDR修正p值的计算与Hochberg方法类似采用递增方法, 但是乘的系数比Hochberg方法的系数小: \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} p_{(k)} & j=k \\ \min\left(\tilde p_{(j+1)},\; \frac{k}{j} p_{(j)} \right) & j=k-1,\dots,2,1 \end{cases} \end{aligned}\]
如果各个检验的p值独立且在各自的零假设成立时服从标准均匀分布, FDR方法可保证控制 \[\begin{aligned} \text{FDR} \leq \frac{k_0}{k} \alpha \leq \alpha \end{aligned}\] Benjamini and Yekateuli (2001)证明了在各零假设满足正回归相依(positive regression dependent)条件下仍可控制FDR。
5.10.2.1 相依FDR
Benjamini and Yekateuli(2001)给出了在各零假设任何相关性条件下都可控制FDR的方法。 令 \[ \gamma = \sum_{j=1}^k \frac{1}{j} \] 可以控制FDR小于等于\(\frac{k_0}{k} \alpha \gamma\)。 因为当\(k\)很大时\(\gamma\)可以很大, 这种方法很保守。 修正p值为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} \gamma p_{(k)} & j=k \\ \min\left(\tilde p_{(j+1)},\; \gamma\frac{k}{j} p_{(j)} \right) & j=k-1,\dots,2,1 \end{cases} \end{aligned}\]
5.10.2.2 用再抽样控制FDR
可以借助于boostrap或者置换检验方法进行FDR控制, 当成立的各零假设独立, 或者subset pivotality条件成立时, 可以近似控制FDR。 见Yekateuli and Benjamini (1999)。
5.10.2.3 适应FDR
因为FDR方法可以控制FDR在\(\frac{k_0}{k} \alpha\), 所以知道\(k_0\)可以增强功效, 但是\(k_0\)未知, 可以用其估计值。 可以近似控制FDR。 参见Benjamini and Hochberg (2000)。 修正p值公式为 \[\begin{aligned} \tilde p_{(j)} =& \begin{cases} \frac{\hat k_0}{k} p_{(k)} & j=k \\ \min\left(\tilde p_{(j+1)},\; \frac{\hat k_0}{j} p_{(j)} \right) & j=k-1,\dots,2,1 \end{cases} \end{aligned}\] 这样得到比FDR调整p值更小的结果。
5.10.2.4 pFDR
pFDR方法计算的修正p值称为q值\(\hat q_{\lambda}(p_j)\), 见Storey (2002), Storey, Taylor, and Siegmund (2004)。 当各p值独立且在零假设成立时服从标准均匀分布时, pFDR方法对FDR达到强控制。 记\(N(\lambda)\)为p值中小于等于\(\lambda\)的个数, \(f=0\)或\(1\), 估计零假设成立的比例为 \[\begin{aligned} \hat\pi_0(\lambda) = \frac{k - N(\lambda) + f}{(1-\lambda) k} \end{aligned}\] FDR估计为 \[\begin{aligned} \widehat{\text{FDR}}_\lambda(p) = \frac{\hat\pi_0(\lambda) \, p}{\max(N(\lambda), 1) / k} \end{aligned}\] pFDR估计为 \[\begin{aligned} \widehat{\text{pFDR}}_\lambda(p) = \frac{\widehat{\text{FDR}}_\lambda(p)}{1 - (1-p)^k} \end{aligned}\] 修正的p值公式为 \[\begin{aligned} \tilde p_j = \hat q_{\lambda}(p_j) = \inf_{p \geq p_j} \text{FDR}_\lambda(p) \end{aligned}\]
5.11 参考文献
- Agresti, A. (2002), Categorical Data Analysis, Second Edition, New York: John Wiley & Sons.
- Allison, D. B., Gadbury, G. L., Moonseong, H., Fernández, J. R., Lee, C., Prolla, T. A., and Weindruch, R. (2002), “A Mixture Model Approach for the Analysis of Microarray Gene Expression Data,” Computational Statistics & Data Analysis, 39, 1–20.
- Armitage, P. (1955), “Tests for Linear Trend in Proportions and Frequencies,” Biometrics, 11, 375–386.
- Benjamini, Y. and Hochberg, Y. (1995), “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing,” Journal of the Royal Statistical Society, B, 57, 289–300.
- Benjamini, Y. and Hochberg, Y. (2000), “On the Adaptive Control of the False Discovery Rate in Multiple Testing with Independent Statistics,” Journal of Educational and Behavioral Statistics, 25, 60–83.
- Benjamini, Y., Krieger, A. M., and Yekutieli, D. (2006), “Adaptive Linear Step-up False Discovery Rate Controlling Procedures,” Biometrika, 93, 491–507.
- Benjamini, Y. and Yekateuli, D. (2001), “The Control of the False Discovery Rate in Multiple Testing under Dependency,” Annals of Statistics, 29, 1165–1188.
- Bickis, M. and Krewski, D. (1986), “Statistical Issues in the Analysis of the Long Term Carcinogenicity Bioassay in Small Rodents: An Empirical Evaluation of Statistical Decision Rules,” Environmental Health Directorate.
- Brown, B. W. and Russell, K. (1997), “Methods Correcting for Multiple Testing: Operating Characteristics,” Statistics in Medicine, 16, 2511–2528.
- Brown, C. C. and Fears, T. R. (1981), “Exact Significance Levels for Multiple Binomial Testing with Application to Carcinogenicity Screens,” Biometrics, 37, 763–774.
- Cochran, W. G. (1954), “Some Methods for Strengthening the Common 2x2 Tests,” Biometrics, 10, 417–451.
- Dinse, G. E. (1985), “Testing for Trend in Tumor Prevalence Rates: I. Nonlethal Tumors,” Biometrics, 41, 751–770.
- Dmitrienko, A., Molenberghs, G., Chuang-Stein, C., and Offen, W. (2005), Analysis of Clinical Trials Using SAS: A Practical Guide, Cary, NC: SAS Institute Inc.
- Dudoit, S., Shaffer, J. P., and Boldrick, J. C. (2003), “Multiple Hypothesis Testing in Microarray Experiments,” Statistical Science, 18, 71–103.
- Freedman, D. A. (1981), “Bootstrapping Regression Models,” Annals of Statistics, 9, 1218–1228.
- Freeman, M. F. and Tukey, J. W. (1950), “Transformations Related to the Angular and the Square Root,” Annals of Mathematical Statistics, 21, 607–611.
- Gibson, G. and Wolfinger, R. D. (2004), “Gene Expression Profiling Using Mixed Models,” in A. M. Saxton, ed., Genetic Analysis of Complex Traits Using SAS, 251–278, Cary, NC: SAS Publishing.
- Good, I. J. (1987), “A Survey of the Use of the Fast Fourier Transform for Computing Distributions,” Journal of Statistical Computation and Simulation, 28, 87–93.
- Heyse, J. and Rom, D. (1988), “Adjusting for Multiplicity of Statistical Tests in the Analysis of Carcinogenicity Studies,” Biometrical Journal, 30, 883–896.
- Hochberg, Y. (1988), “A Sharper Bonferroni Procedure for Multiple Significance Testing,” Biometrika, 75, 800–803.
- Hochberg, Y. and Benjamini, Y. (1990), “More Powerful Procedures for Multiple Significance Testing,” Statistics in Medicine, 9, 811–818.
- Hochberg, Y. and Tamhane, A. C. (1987), Multiple Comparison Procedures, New York: John Wiley & Sons.
- Hoel, D. G. and Walburg, H. E. (1972), “Statistical Analysis of Survival Experiments,” Journal of the National Cancer Institute, 49, 361–372. References F 4875
- Holland, B. S. and Copenhaver, M. D. (1987), “An Improved Sequentially Rejective Bonferroni Test Procedure,” Biometrics, 43, 417–424.
- Holm, S. (1979), “A Simple Sequentially Rejective Bonferroni Test Procedure,” Scandinavian Journal of Statistics, 6, 65–70.
- Hommel, G. (1988), “A Comparison of Two Modified Bonferroni Procedures,” Biometrika, 75, 383–386.
- Hsueh, H., Chen, J. J., and Kodell, R. L. (2003), “Comparison of Methods for Estimating the Number of True Null Hypotheses in Multiplicity Testing,” Journal of Biopharmaceutical Statistics, 13, 675–689.
- Lagakos, S. W. and Louis, T. A. (1985), “The Statistical Analysis of Rodent Tumorigenicity Experiments,” in D. B. Clayson, D. Krewski, and I. Munro, eds., Toxicological Risk Assessment, 144–163, Boca Raton, FL: CRC Press.
- Liu, W. (1996), “Multiple Tests of a Non-hierarchical Finite Family of Hypotheses,” Journal of the Royal Statistical Society, Series B, 58, 455–461. Mantel, N. (1980), “Assessing Laboratory Evidence for Neoplastic Activity,” Biometrics, 36, 381–399.
- Mantel, N. and Haenszel, W. (1959), “Statistical Aspects of Analysis of Data from Retrospective Studies of Disease,” Journal of the National Cancer Institute, 22, 719–748.
- Marcus, R., Peritz, E., and Gabriel, K. R. (1976), “On Closed Testing Procedures with Special Reference to Ordered Analysis of Variance,” Biometrika, 63, 655–660.
- Miller, J. J. (1978), “The Inverse of the Freeman-Tukey Double Arcsine Transformation,” The American Statistician, 32, 138.
- Osborne, J. A. (2006), “Estimating the False Discovery Rate Using SAS,” in Proceedings of the Thirty-first Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc. *Pagano, M. and Tritchler, D. (1983), “On Obtaining Permutation Distributions in Polynomial Time,” Journal of the American Statistical Association, 78, 435–440.
- Peto, R., Pike, M. C., and Day, N. E. (1980), “Guidelines for Simple, Sensitive Significance Tests for Carcinogenic Effects in Long-Term Animal Experiments,” Long-Term and Short-Term Screening Assays for Carcinogens: A Critical Appraisal.
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1992), Numerical Recipes in C: The Art of Scientific Computing, Second Edition, Cambridge, UK: Cambridge University Press.
- Sarkar, S. K. and Chang, C.-K. (1997), “The Simes Method for Multiple Hypothesis Testing with Positively Dependent Test Statistics,” Journal of the American Statistical Association, 92, 1601–1608.
- Satterthwaite, F. E. (1946), “An Approximate Distribution of Estimates of Variance Components,” Biometrics Bulletin, 2, 110–114.
- Schweder, T. and Spjøtvoll, E. (1982), “Plots of P-Values to Evaluate Many Tests Simultaneously,” Biometrika, 69, 493–502.
- Shaffer, J. P. (1986), “Modified Sequentially Rejective Multiple Test Procedures,” Journal of the American Statistical Association, 81, 826–831.
- Šidák (1967), “Rectangular Confidence Regions for the Means of Multivariate Normal Distributions,” Journal of the American Statistical Association, 62, 626–633.
- Simes, R. J. (1986), “An Improved Bonferroni Procedure for Multiple Tests of Significance,” Biometrika, 73, 751–754.
- Soper, K. A. and Tonkonoh, N. (1993), “The Discrete Distribution Used for the Log-Rank Test Can Be Inaccurate,” Biometrical Journal, 35, 291–298.
- Storey, J. D. (2002), “A Direct Approach to False Discovery Rates,” JRSS-B, 64, 479–498.
- Storey, J. D., Taylor, J. E., and Siegmund, D. (2004), “Strong Control, Conservative Point Estimation, and Simultaneous Conservative Consistency of False Discovery Rates: A Unified Approach,” JRSS-B, 66, 187–205.
- Storey, J. D. and Tibshirani, R. (2003), “Statistical Significance for Genomewide Studies,” in Proceedings of the National Academy of Sciences of the United States of America, volume 100, 9440–9445.
- Turkheimer, F. E., Smith, C. B., and Schmidt, K. (2001), “Estimation of the Number of ’True’ Null Hypotheses in Multivariate Analysis of Neuroimaging Data,” NeuroImage, 13, 920–930.
- Westfall, P. H. and Lin, Y. (1988), “Estimating Optimal Continuity Corrections in Run Time,” Proceedings of the Statistical Computing Section.
- Westfall, P. H. and Soper, K. A. (1994), “Nonstandard Uses of PROC MULTTEST: Permutational Peto Tests; Permutational and Unconditional t and Binomial Tests,” in Proceedings of the Nineteenth Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.
- Westfall, P. H., Tobias, R. D., Rom, D., Wolfinger, R. D., and Hochberg, Y. (1999), Multiple Comparisons and Multiple Tests Using the SAS System, Cary, NC: SAS Institute Inc.
- Westfall, P. H. and Wolfinger, R. D. (1997), “Multiple Tests with Discrete Distributions,” The American Statistician, 51, 3–8.
- Westfall, P. H. and Wolfinger, R. D. (2000), “Closed Multiple Testing Procedures and PROC MULTTEST,” Observations.
- Westfall, P. H. and Young, S. S. (1989), “P-Value Adjustments for Multiple Tests in Multivariate Binomial Models,” Journal of the American Statistical Association, 84, 780–786.
- Westfall, P. J. and Young, S. S. (1993), Resampling-Based Multiple Testing, New York: John Wiley & Sons.
- Yates, F. (1984), “Tests of Significance for 2x2 Contingency Tables,” Journal of the Royal Statistical Society.
- Yekateuli, D. and Benjamini, Y. (1999), “Resampling-Based False Discovery Rate Controlling Multiple Test Procedures for Correlated Test Statistics,” Journal of Statistical Planning and Inference, 82, 171–196.