6 聚类分析

6.1 介绍

本章内容主要参考费宇等《多元统计分析：基于R》，中国人民大学出版社。

需要额外安装的软件包：

options(repos=c(CRAN="https://mirrors.tuna.tsinghua.edu.cn/CRAN/"))
#install.packages(c())

将一些个体分类是人类具有的必不可少的能力，从婴儿开始，就学着分辨各种事物，奶瓶、铃铛、猫、狗，……。同样一些事物，可以分成不同的类别。比如，图书可以按学科分类，也可以按封面图案分类，显然学科分类更有用。一副扑克牌，可以按花色分类，可以按点数分类，可以按有无人物分类，等等。

多元统计分析学科中的聚类分析一般指把多元观测数据的观测按照某种临近或相似性标准分成若干组，每一组内的观测是比较相近或相似的。这样的聚类又称为Q型聚类，即对样品的聚类。

另一种聚类是把多个变量按照其在所有观测上的取值分成若干个变量组，每一组内的变量比较相近或相似，这样的聚类分析称为变量聚类或R型聚类。

从数学上看两种聚类没有本质差别（只要把观测矩阵转置就得到另一种聚类问题）。

聚类分析在机器学习领域又称为无监督（无指导）学习，这是因为数据中并没有现成的分类可供参考。而回归分析、判别分析方法则称为有监督学习。

常用的聚类方法包括：

系统（谱系）聚类法(hierarchical clustering)，从每类只有单个元素开始，每次合并两类；
k均值聚类法(k-means clustering)，需要设定类的个数，然后迭代地调整元素的类属使同类的元素接近而异类元素分离。
基于统计模型的方法，如混合密度模型。

如果不基于数学方法，对于二维和三维数据，我们也能利用图像很容易地分类。比如，鸢尾花数据：

ggplot(iris, aes(
  x = Sepal.Length, y = Sepal.Width)) +
  geom_point()

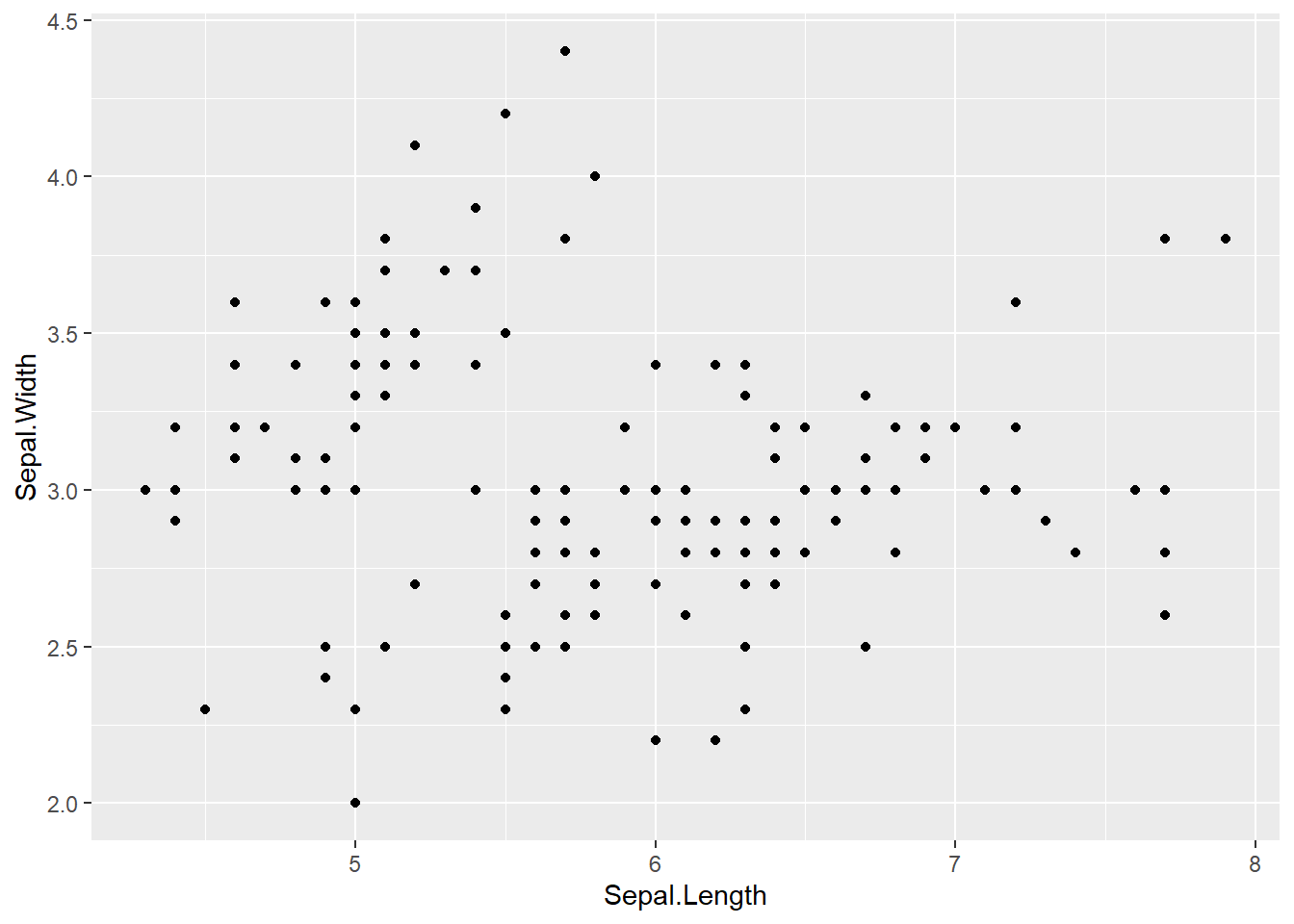
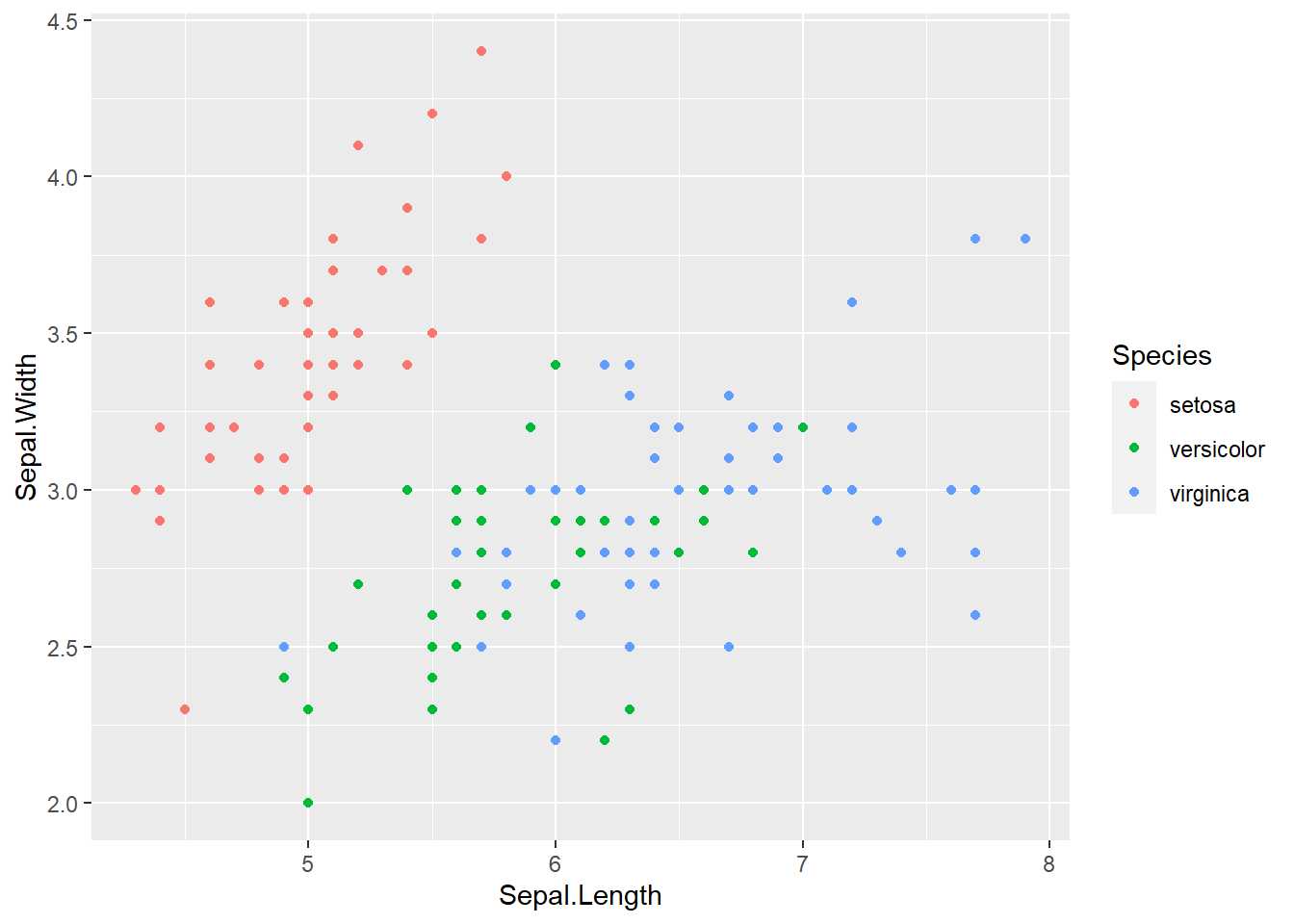
可以看出至少有两个类。实际类别情况：

ggplot(iris, aes(
  x = Sepal.Length, y = Sepal.Width, color=Species)) +
  geom_point()

三维数据演示：

library(rgl)
with(iris, plot3d(
  Sepal.Length, Sepal.Width, Petal.Length, 
  type="s", col=as.numeric(Species)))

这样分类会有主观性，对高维数据也不易使用。为判断一般的高维数据点是否属于同一类，首先应该定义两个点之间相异或者相近（相似）程度的指标。

6.2 相似性的度量

聚类的思想是把相近的元素聚集到一起。不同的元素距离定义会造成不同聚类结果。

设 $X$ 是实数域上的线性空间，在 $X$ 中定义二元函数 $d(x,y)$ ，如果 $d(x,y)$ 满足：

正定性： $d(x,y) \geq 0$ , $\forall x, y \in X$ ; $d(x,y) = 0$ 当且仅当 $x=y$ ;
对称性： $d(x,y) = d(y,x)$ , $\forall x, y \in X$ ;
三角不等式： $d(x,y) \leq d(x,z) + d(z,y)$ , $\forall x, y, z \in X$ ,

则称 $d(x,y)$ 是 $X$ 上的一个距离，称 $(X,d)$ 为距离空间或度量空间。

下面定义了一些距离，其中有一些不满足距离定义，严格来讲只能算是相异度（dissimilarity）：

欧式距离(2范数): $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_2 = \sqrt{\sum_{j=1}^p (x_j - y_j)^2} . \end{aligned}$
曼哈顿距离(1范数): $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_1 = \sum_{j=1}^p | x_j - y_j | . \end{aligned}$
最大值距离(切比雪夫距离，上确界距离，无穷范数)： $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_\infty = \max_{j} | x_j - y_j | . \end{aligned}$
闵可夫斯基（Minkowski）距离( $\alpha$ 范数)： $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_\alpha = \left[ \sum_{j=1}^p |x_j - y_j|^\alpha \right]^{1/\alpha} . \end{aligned}$ 其中 $\alpha>0$ 。
马氏(Mahalanobis)距离: $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \sqrt{ (\boldsymbol x - \boldsymbol y)^T S^{-1} (\boldsymbol x - \boldsymbol y) }, \end{aligned}$

其中 $S$ 是一个正定矩阵，一般取为样本协方差阵，可以消除量纲与相关性的影响（相关性又与多元观测取值的聚集方向有关）。
兰氏(Lance)距离: $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = \sum_{j=1}^p \frac{|x_j - y_j|}{x_j + y_j}, \end{aligned}$ 其中所有 $x_j, y_j$ 均为正数。
二进(Binary)距离：若所有分量都取0或1，则 $\boldsymbol x$ 与 $\boldsymbol y$ 的距离是各对应分量中恰有一个1的对数与至少有一个1的对数的比值。这也称为Jaccard距离，来自生物学中Jaccard指数的定义。设 $\boldsymbol x$ 与 $\boldsymbol y$ 的各对分量中同时为1的有 $f_{11}$ 对，至少有一个1的有 $f_{01} + f_{10} + f_{11}$ 对，则Jaccard指数为 $J(\boldsymbol x,\boldsymbol y) = \frac{f_{11}}{f_{01} + f_{10} + f_{11}},$ 而Jaccard距离为 $\begin{aligned} d(\boldsymbol x, \boldsymbol y) = 1 - J(\boldsymbol x, \boldsymbol y) = \frac{f_{01} + f_{10}}{f_{01} + f_{10} + f_{11}} . \end{aligned}$

距离越小，两个观测点 $\boldsymbol x$ 与 $\boldsymbol y$ 之间越接近。

欧氏距离、曼哈顿距离、最大值距离都是闵可夫斯基距离的特例，如果各个分量的取值差距很大，则距离将主要由绝对值大的那个分量决定。部分问题可以通过标准化每个分量解决，采用马氏距离也是较好的解决方法。

以上的距离中观测的各分量都是数值型的，实际数据中的分量有些是数值型的，有些是分类数据。这时常用Gower距离，设观测数据矩阵为 $M=(x_{ij})_{n\times p}$ ，每行为一个观测，每列为一个变量（feature），第 $s$ 行与第 $t$ 行的Gower距离定义为 $d(s, t) = \frac{1}{p} \sum_{j=1}^p d_j(s, t, M),$ 如果第 $j$ 个分量是分类变量，则 $d_j(s, t, M)$ 仅当观测 $s$ 和观测 $t$ 的第 $j$ 分量属于同一类时等于0，否则等于1。如果第 $j$ 分量是数值型变量，则定义 $d_j(s, t, M) = \frac{|x_{sj} - x_{tj}|}{\text{range}(x_{1j}, x_{2j}, \dots, x_{nj})} .$ 其中 $\text{range}$ 表示极差（最大值减去最小值）。这样，每个 $d_j(s,t,M)$ 都取值于 $[0,1]$ 中，最终的 $d(s,t)$ 也取值于 $[0,1]$ 中。 R的cluster包的daisy()函数可以计算Gower距离。

为了度量两个变量的所有观测值之间的距离，更多地使用相似性的概念。设数据为 $n$ 个观测，每个观测有 $p$ 个变量，第 $i$ 个观测为 $(x_{i1}, x_{i2}, \dots, x_{ip})$ ，则第 $k$ 个变量的 $n$ 个观测值与第 $j$ 个变量的 $n$ 个观测值的相近程度可以用样本相关系数度量: $\begin{aligned} r_{kj} = \frac{\sum_{i=1}^n (x_{ik} - \bar x_{\cdot k}) (x_{ij} - \bar x_{\cdot j}) } {\sqrt{ \sum_{i=1}^n (x_{ik} - \bar x_{\cdot k})^2 \; \sum_{i=1}^n (x_{ij} - \bar x_{\cdot j})^2}}, \ k, j = 1,2,\dots,p . \end{aligned}$ $r_{kj}$ 越大相似度越高。在仅关心两个变量关系的强弱而不关心关系是正向还是反向的时候，也可以用 $|r_{kj}|$ 度量相似度。式中 $\bar x_{\cdot k} = \frac{1}{n} \sum_{i=1}^n x_{ik}$ 是数据矩阵 $(x_{ik})_{n\times p}$ 的第 $k$ 列的样本平均值。

用相关系数转化的距离： $d_{kj} = \sqrt{2[1 - r_{kj}]}$

把第 $k$ 个变量的 $n$ 个观测值与第 $j$ 个变量的 $n$ 个观测值看作 $\mathbb R^n$ 中的两个向量，用这两个向量的夹角余弦度量其相近程度: $\begin{aligned} \cos\theta_{kj} = \frac{\sum_{i=1}^n x_{ik} x_{ij}} {\sqrt{ \sum_{i=1}^n x_{ik}^2 \; \sum_{i=1}^n x_{ij}^2 }} \end{aligned}$ 此余弦取值于 $[-1, 1]$ 之间，值越大表明第 $k$ 和第 $j$ 变量相似性越高。

当观测数据集各列是中心化（每列均值为零）时，两列的相关系数和夹角余弦是相等的。但是，使用夹角余弦时不取绝对值。

对其它更复杂的对象往往也需要计算相异度或者距离。 igraph扩展包的shortest.paths()函数计算图中各节点之间的距离， xkcd扩展包的cophenetic()函数计算一棵树的叶结点之间的距离， distory扩展包的dist.multiPhylo()函数可以用来计算两棵树之间的距离。

两个图之间的Jaccard距离也可以有定义，假设两个图的节点相同，则只要比较共同的边，据此定义Jaccard距离， igraph扩展包的similarity()函数实现了这一个功能。

距离和相异度也可以用于比较图像、音频、地图、文档等复杂对象。细心设计的距离定义可以包含学科知识，并可以将包含许多异质数据的困难问题简化。例如，对新闻文本，经常先切分词语再计算词语频数作为数据。对数据的相似度或相异度的理解可以引发对数据的更好的呈现。

6.3 系统聚类法

设数据为 $n$ 个观测（样品），每个观测有 $p$ 个变量，第 $i$ 个观测为 $(x_{i1}, x_{i2}, \dots, x_{ip})$ ，数据组成数据矩阵 $(x_{ij})_{n \times p}$ 。

Q型系统聚类法的基本步骤是：开始时将 $n$ 个样品看作单独的 $n$ 个类，将最接近得两个样品合并成一类，变成 $n-1$ 个类；继续从 $n-1$ 个类中找到最相近的两个类将其合并，变成 $n-2$ 个类，如此重复直到合并成了一个大类为止。 R型系统聚类法步骤类似，只不过是针对变量组合并。

系统聚类算法需要考虑两个问题：如何衡量两个类的相近程度；如何选择最终分成多少个类。前一个问题比较基本，后一个问题更困难。

6.3.1 Q型系统聚类的距离

设 $G_s$ 和 $G_t$ 为两个类， $d_{ij}$ 表示第 $i$ 样品与第 $j$ 样品的距离（常用欧式距离），度量两个类 $G_s$ 与 $G_t$ 之间的距离 $D_{st}$ 有如下几种常用方法：

最小距离法(single linkage)：

$G_s$ 与 $G_t$ 之间的距离是两类中距离最近的两个样品的距离，即 $\begin{align*} D_{st} = \min_{i \in G_s,\; j \in G_t} d_{ij} . \end{align*}$

最大距离法(complete linkage)： $G_s$ 与 $G_t$ 之间的距离是两类中距离最远的两个样品的距离，即

$\begin{align*} D_{st} = \max_{i \in G_s,\; j \in G_t} d_{ij} . \end{align*}$

中间距离法(median linkage)，这是介于最小距离与最大距离之间的一种类间距离。
重心距离法(centroid linkage)：用 $\bar{\boldsymbol x}_s$ 表示 $G_s$ 中的所有观测的样本平均值，定义 $G_s$ 与 $G_t$ 之间的距离为 $D_{st} = d(\bar{\boldsymbol x}_s, \bar{\boldsymbol x}_t)$ 。
类平均距离法：设 $G_s$ 中有 $n_s$ 个观测， $G_t$ 中有 $n_t$ 个观测，定义 $G_s$ 与 $G_t$ 之间的距离两类的观测之间所有两两组合的距离平均，即

$\begin{align*} D_{st} = \frac{1}{n_s n_t} \sum_{i \in G_s} \sum_{j \in G_t} d_{ij} . \end{align*}$

离差平方和法(Ward法)：基于方差分析思想，如果分类正确，类内的离差平方和应该较小而类间离差平方和应该较大。设 $G_s$ 的 $n_s$ 个样品的样本平均值为 $\bar{\boldsymbol x}_s = (\bar x_{s1}, \dots, \bar x_{sp})^T$ , 则 $G_s$ 的类内离差平方和为 $W_s = \sum_{i \in G_s} \sum_{j=1}^p (x_{ij} - \bar x_{sj})^2$ ，如果把 $G_s$ 和 $G_t$ 合并，记为类 $G_c$ , 定义 $G_s$ 与 $G_t$ 的Ward距离为 $W_r - (W_s + W_t)$ ，即合并造成的类内离差平方和的增量。

6.3.2 R型类间距离

设 $G_s$ 和 $G_t$ 为两个变量类，用 $r_{ij}$ 表示第 $i$ 变量与第 $j$ 变量的相似型度量值，可以定义 $\begin{align*} R_{st} = \max_{i \in G_s, \; j \in G_t} r_{ij} \end{align*}$ 作为两个变量组 $G_s$ 与 $G_t$ 之间的相似度。

注意，如果要用相关系数作为变量间相似度， $r_{ij}$ 应取为相关系数绝对值。夹角余弦可能也需要取绝对值。

6.3.3 身体测量指标聚类

measure数据框包含了10个成年男性、10个成年女性的胸围、腰围、臀围测量值(单位：英寸)。对这三种测量值使用聚类分析，看能否区分男女。

measure <- read_csv("data/measure.csv",
  col_types = cols(
    .default = col_double(),
    gender = col_factor(levels=c("male", "female"))),
  show_col_types = FALSE)
knitr::kable(measure)

chest	waist	hips	gender
34	30	32	male
37	32	37	male
38	30	36	male
36	33	39	male
38	29	33	male
43	32	38	male
40	33	42	male
38	30	40	male
40	30	37	male
41	32	39	male
36	24	35	female
36	25	37	female
34	24	37	female
33	22	34	female
36	26	38	female
37	26	37	female
34	25	38	female
36	26	37	female
38	28	40	female
35	23	35	female

作散点图矩阵：

library(GGally)

## Warning: package 'GGally' was built under R version 4.2.2

## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2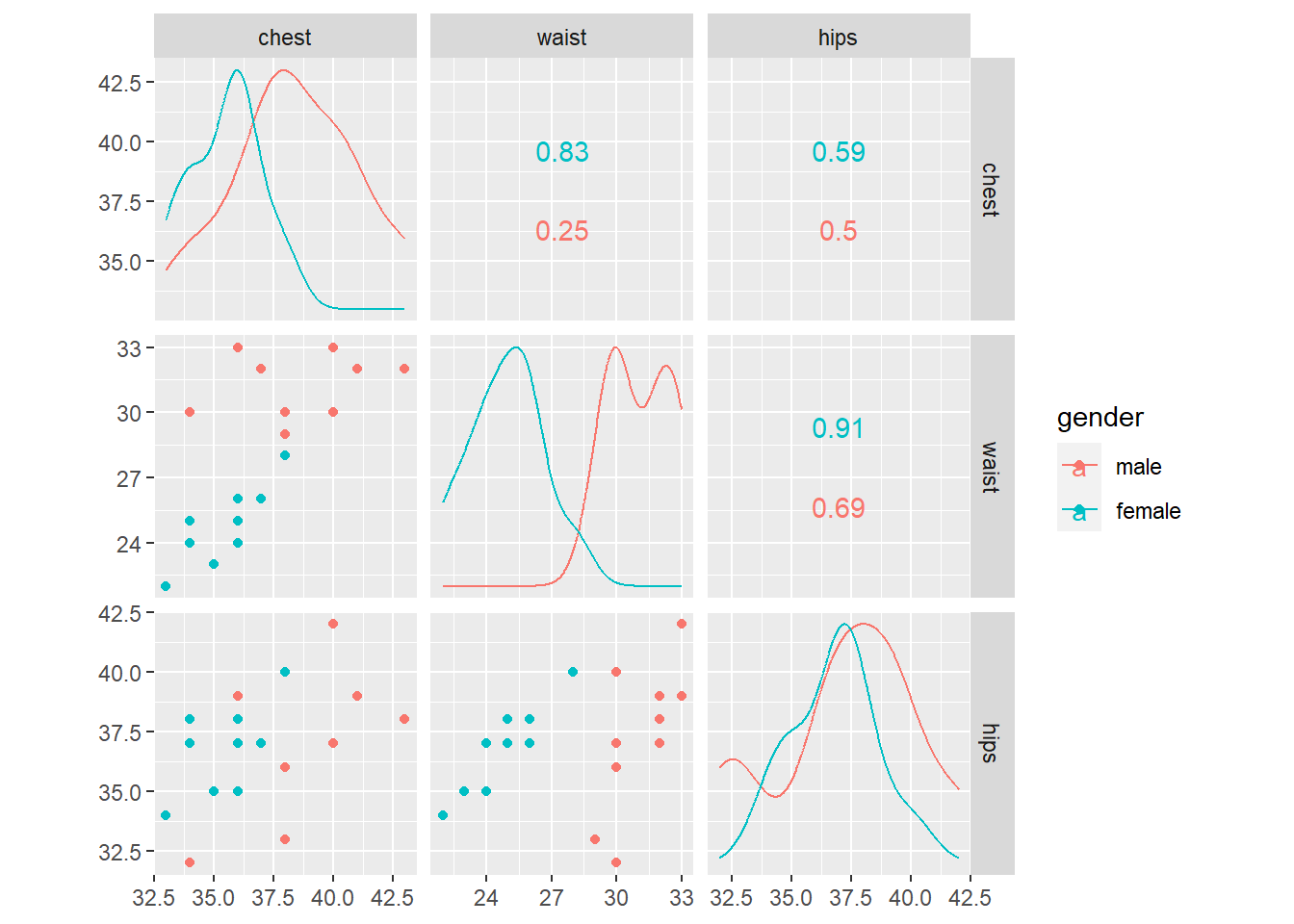

ggscatmat(data = measure, 
  columns = 1:3, color = "gender")

用主成分方法降维，作散点图：

m_pca <- princomp(measure[,1:3])
m_pscore <- cbind(measure, predict(m_pca)[,1:2])
ggplot(m_pscore, aes(
  x = Comp.1, y = Comp.2, color = gender)) +
  geom_point()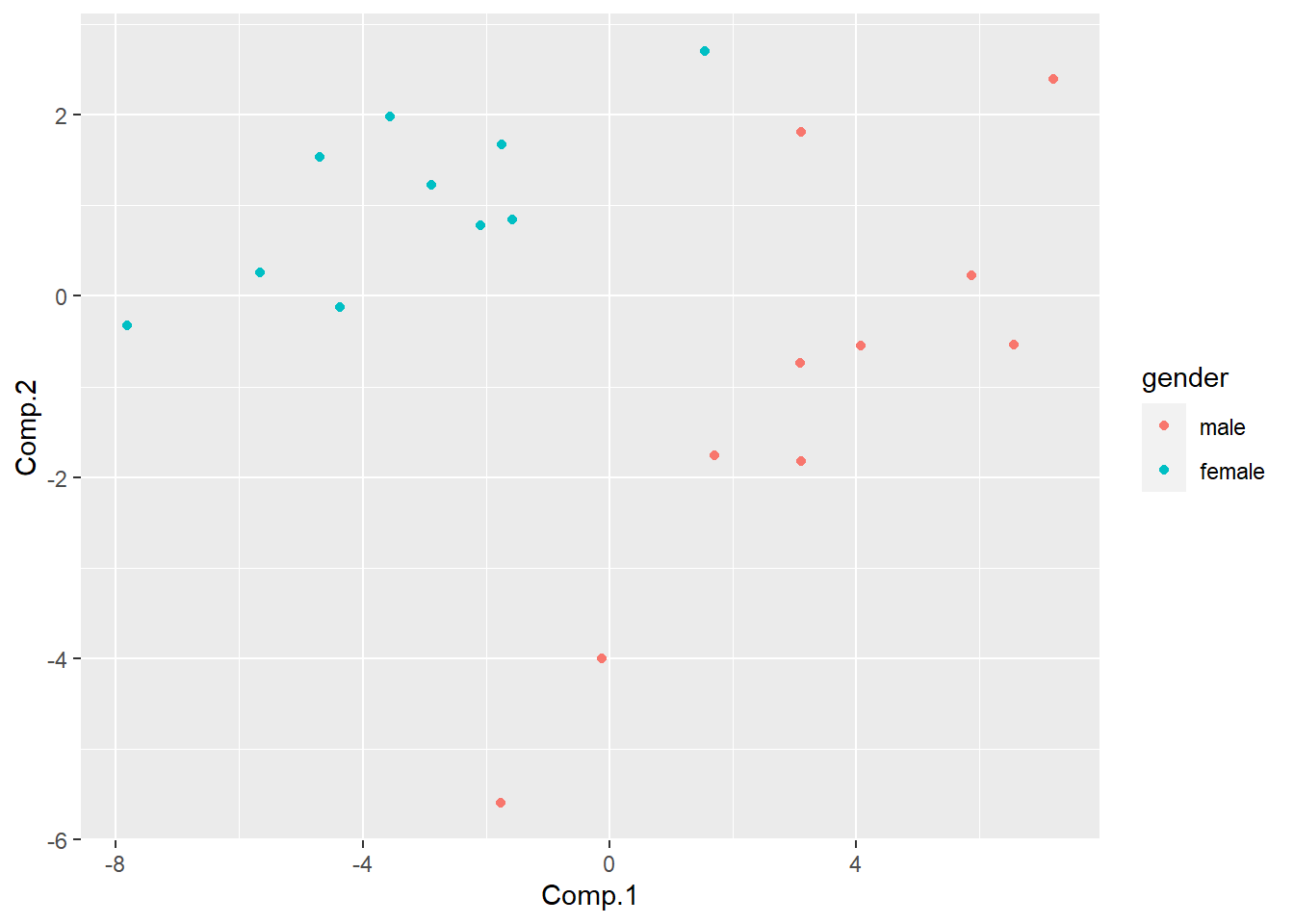

计算样本间欧氏距离（仅显示一部分）：

m_dist <- dist(measure[,1:3], 
  method='euclidean',
  diag=TRUE, upper=FALSE)
knitr::kable(as.data.frame(as.matrix(
  m_dist)[c(1:2, 11:12), c(1:2, 11:12)]), digits=2)

	1	2	11	12
1	0.00	6.16	7.00	7.35
2	6.16	0.00	8.31	7.07
11	7.00	8.31	0.00	2.24
12	7.35	7.07	2.24	0.00

使用最短距离法聚类：

m_clus1 <- hclust(m_dist, method="single")
m_clus1

## 
## Call:
## hclust(d = m_dist, method = "single")
## 
## Cluster method   : single 
## Distance         : euclidean 
## Number of objects: 20

作树图：

plot(m_clus1)

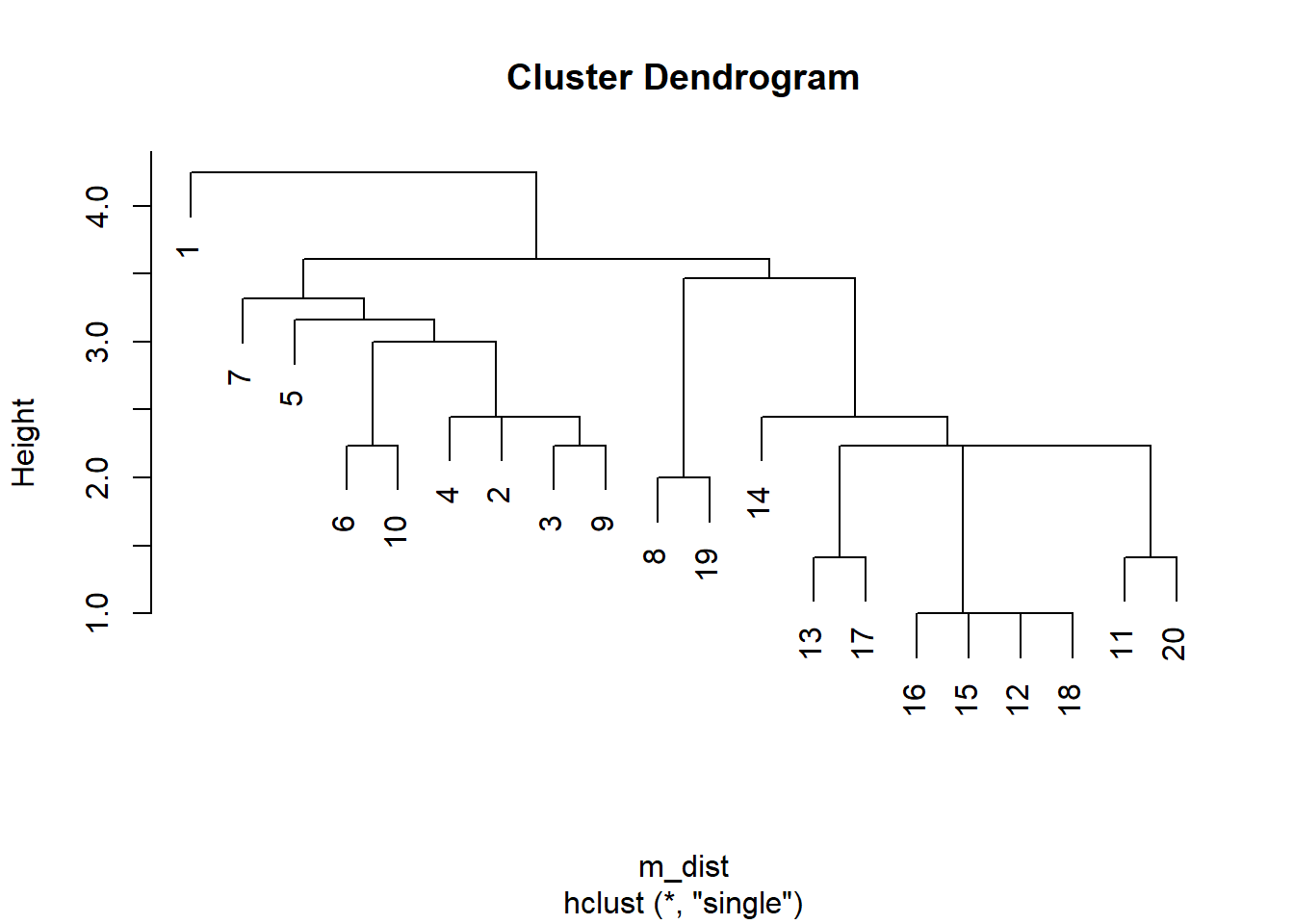
直观地，可以在树图纵向找比较长的连线，在该连线处分组。这里考虑到其中一组仅有一个观测，所以分成三个组，用主成分作图：

m_gr1 <- cutree(m_clus1, k=3)
m_gr1

##  [1] 1 2 2 2 2 2 2 3 2 2 3 3 3 3 3 3 3 3 3 3

dd <- m_pscore |>
  mutate(group = factor(m_gr1))
ggplot(dd, aes(
  x=Comp.1, y = Comp.2, color=group, shape=gender)) + 
  geom_point()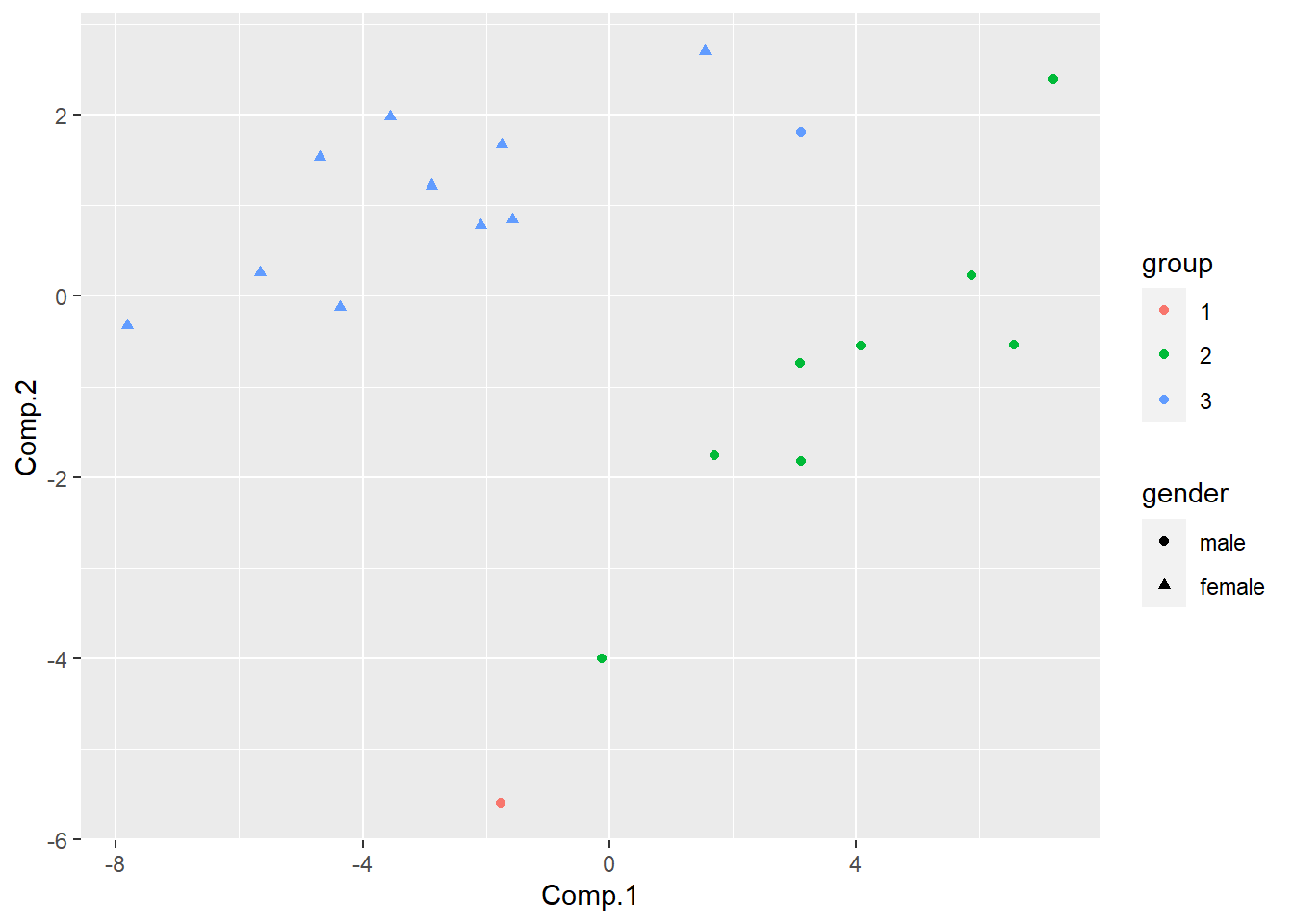

分组与性别的对应基本是合理的，但从两组合并成一组时，其中一个组仅有一个观测。

使用最长距离法聚类：

m_clus2 <- hclust(m_dist, method="complete")
m_clus2

## 
## Call:
## hclust(d = m_dist, method = "complete")
## 
## Cluster method   : complete 
## Distance         : euclidean 
## Number of objects: 20

作树图：

plot(m_clus2)

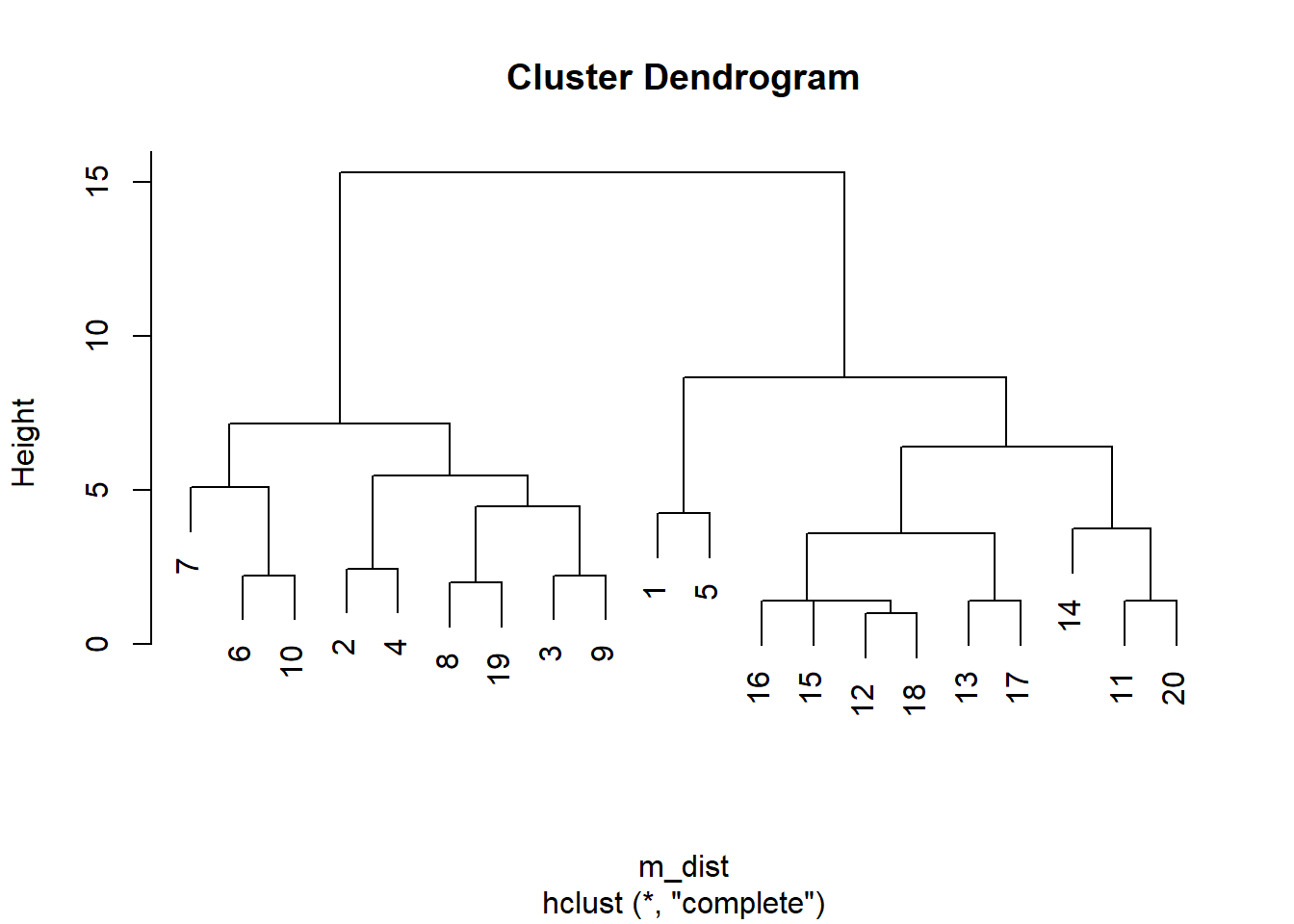
从纵向距离来看明显第应该分成两类，用主成分作图：

m_gr2 <- cutree(m_clus2, k=2)
m_gr2

##  [1] 1 2 2 2 1 2 2 2 2 2 1 1 1 1 1 1 1 1 2 1

dd <- m_pscore |>
  mutate(group = factor(m_gr2))
ggplot(dd, aes(
  x=Comp.1, y = Comp.2, color=group, shape=gender)) + 
  geom_point()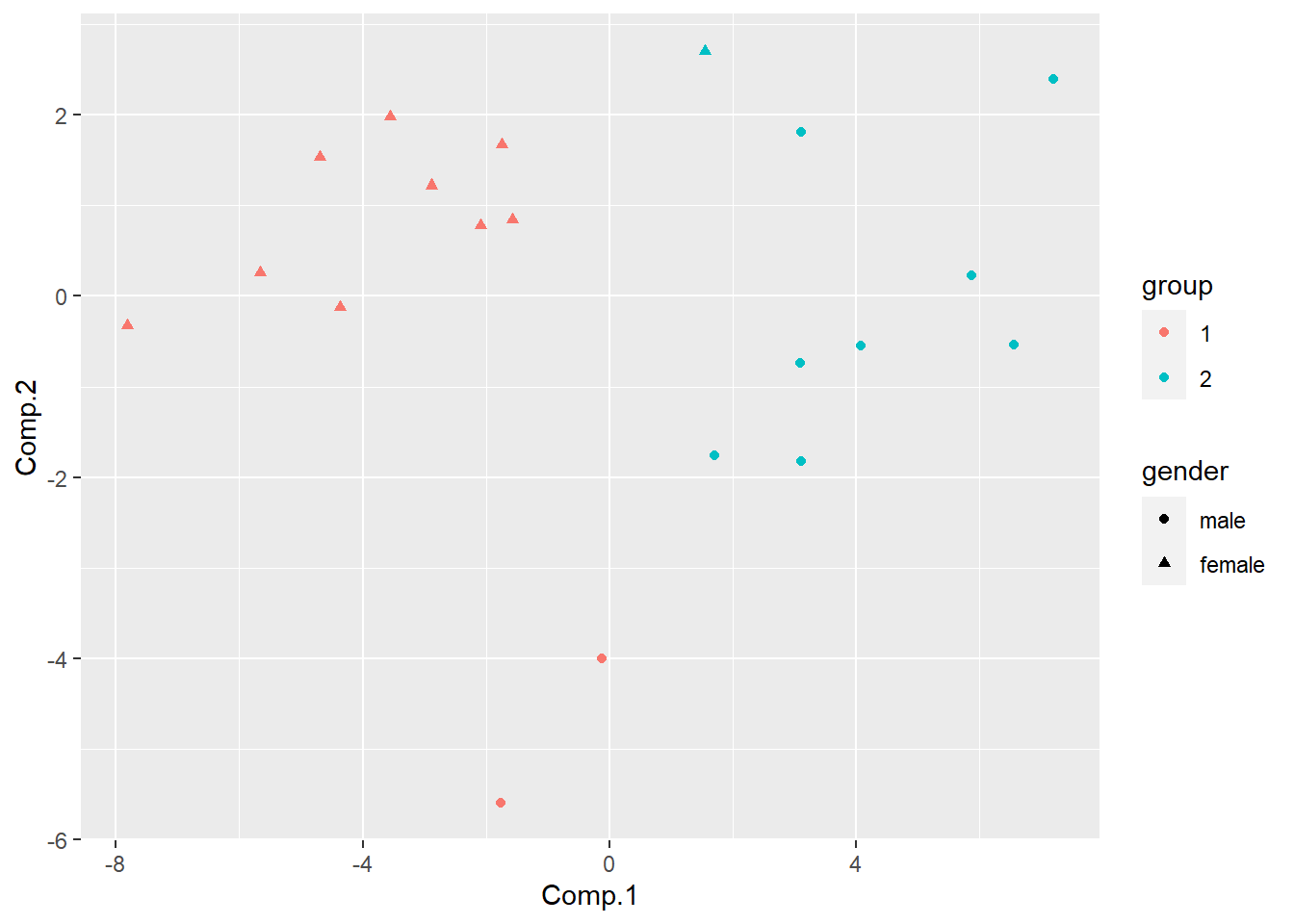

聚类结果与性别没有完全吻合：

table(dd[["gender"]], dd[["group"]])

##         
##          1 2
##   male   2 8
##   female 9 1

有3例不一致。

使用类平均距离法聚类：

m_clus3 <- hclust(m_dist, method="average")
m_clus3

## 
## Call:
## hclust(d = m_dist, method = "average")
## 
## Cluster method   : average 
## Distance         : euclidean 
## Number of objects: 20

作树图：

plot(m_clus3)

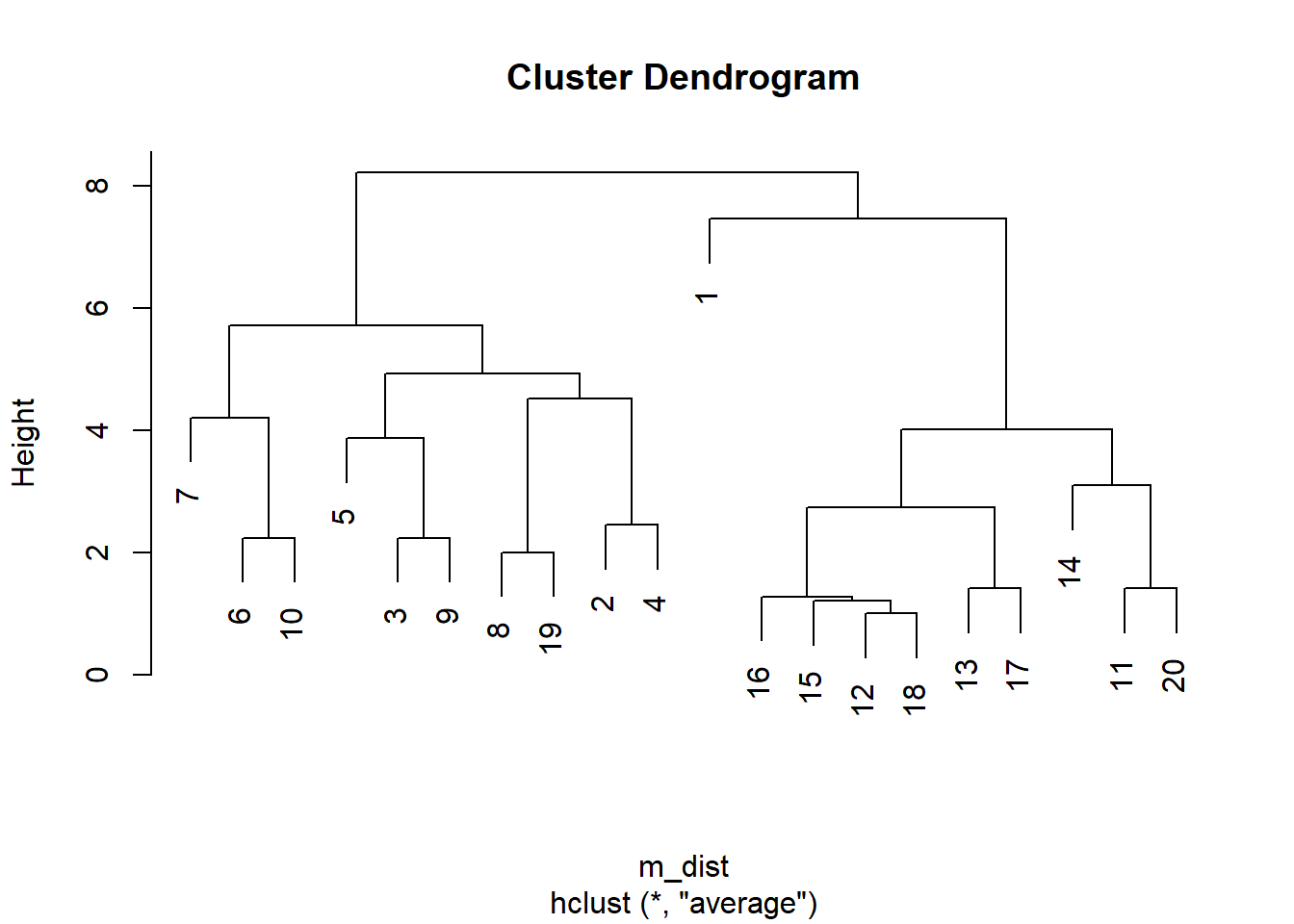
分成两类，用主成分作图：

m_gr3 <- cutree(m_clus3, k=2)
m_gr3

##  [1] 1 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 1

dd <- m_pscore |>
  mutate(group = factor(m_gr3))
ggplot(dd, aes(
  x=Comp.1, y = Comp.2, color=group, shape=gender)) + 
  geom_point()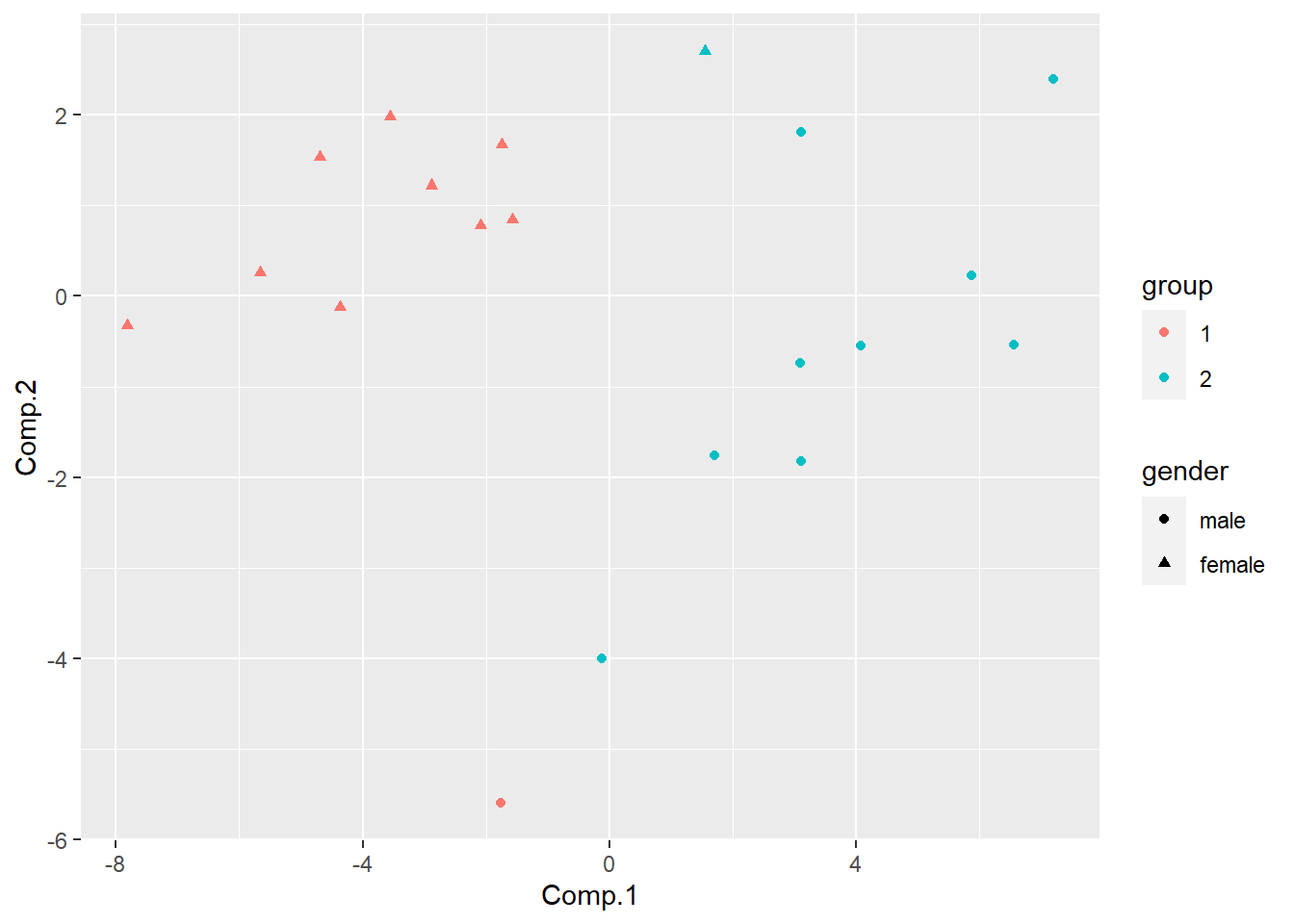

聚类结果与性别没有完全吻合：

table(dd[["gender"]], dd[["group"]])

##         
##          1 2
##   male   1 9
##   female 9 1

有2例不一致。

6.3.4 葡萄酒的聚类实例

6.3.4.1 数据

教材P.41例4.1： 10种葡萄酒有6个评分, 用系统聚类法聚类。

数据：

wineScore <- read_csv("data/葡萄酒评分.csv",
  show_col_types = FALSE)
knitr::kable(wineScore)

x1	x2	x3	x4	x5	x6
4.65	4.22	5.01	4.50	4.15	4.12
6.32	6.11	6.21	6.85	6.52	6.33
4.87	4.60	4.95	4.15	4.02	4.11
4.88	4.68	4.43	4.12	4.03	4.14
6.73	6.65	6.72	6.13	6.51	6.36
7.45	7.56	7.60	7.80	7.20	7.18
8.10	8.23	8.01	7.95	8.31	8.26
8.42	8.54	8.12	7.88	8.26	7.98
6.45	6.81	6.52	6.31	6.27	6.06
7.50	7.32	7.42	7.52	7.10	6.95

数据概括：

summary(wineScore)

##        x1              x2              x3              x4       
##  Min.   :4.650   Min.   :4.220   Min.   :4.430   Min.   :4.120  
##  1st Qu.:5.240   1st Qu.:5.037   1st Qu.:5.310   1st Qu.:4.907  
##  Median :6.590   Median :6.730   Median :6.620   Median :6.580  
##  Mean   :6.537   Mean   :6.472   Mean   :6.499   Mean   :6.321  
##  3rd Qu.:7.487   3rd Qu.:7.500   3rd Qu.:7.555   3rd Qu.:7.730  
##  Max.   :8.420   Max.   :8.540   Max.   :8.120   Max.   :7.950  
##        x5              x6       
##  Min.   :4.020   Min.   :4.110  
##  1st Qu.:4.680   1st Qu.:4.620  
##  Median :6.515   Median :6.345  
##  Mean   :6.237   Mean   :6.149  
##  3rd Qu.:7.175   3rd Qu.:7.122  
##  Max.   :8.310   Max.   :8.260

6.3.4.2 样本点间的距离

首先用欧式距离计算距离矩阵：

d.mat <- dist(wineScore, method='euclidean',
  diag=TRUE, upper=FALSE)
knitr::kable(as.data.frame(as.matrix(d.mat)),
  digits=2)

1	2	3	4	5	6	7	8	9	10
0.00	4.88	0.58	0.87	5.14	7.43	9.13	9.26	4.87	7.03
4.88	0.00	4.94	5.07	1.11	2.72	4.36	4.56	1.01	2.34
0.58	4.94	0.00	0.53	5.10	7.44	9.11	9.22	4.83	7.02
0.87	5.07	0.53	0.00	5.26	7.60	9.26	9.37	4.99	7.19
5.14	1.11	5.10	5.26	0.00	2.46	4.02	4.14	0.57	2.04
7.43	2.72	7.44	7.60	2.46	0.00	1.86	1.99	2.66	0.48
9.13	4.36	9.11	9.26	4.02	1.86	0.00	0.54	4.32	2.21
9.26	4.56	9.22	9.37	4.14	1.99	0.54	0.00	4.42	2.32
4.87	1.01	4.83	4.99	0.57	2.66	4.32	4.42	0.00	2.26
7.03	2.34	7.02	7.19	2.04	0.48	2.21	2.32	2.26	0.00

R中用dist(data, method=)函数计算观测间的距离。在dist()函数中， diag选项决定显示距离阵时是否显示对角线元素， upper决定显示距离阵时是否显示上三角元素， method是距离种类:

euclidean 欧式距离;
manhattan 曼哈顿距离;
maximum 最大（上确界）距离;
minkowski 闵可夫斯基距离;
canberra 兰氏距离。

本例的6个评分取值范围相近，所以不需要标准化。如果变量取值范围差别很大，在计算距离前一般应该把每列标准化(scale()函数)。

6.3.4.3 用最短距离法聚类

res1 <- hclust(d.mat, method='single'); res1

## 
## Call:
## hclust(d = d.mat, method = "single")
## 
## Cluster method   : single 
## Distance         : euclidean 
## Number of objects: 10

hclust()函数中选项method选择系统聚类的类间距离，包括：

single最短距离法，
complete最大距离法
average类平均法
median中间距离法
centrold重心法
ward Ward法

对hclust()的输出结果用plot()画聚类树状图：

plot(res1)

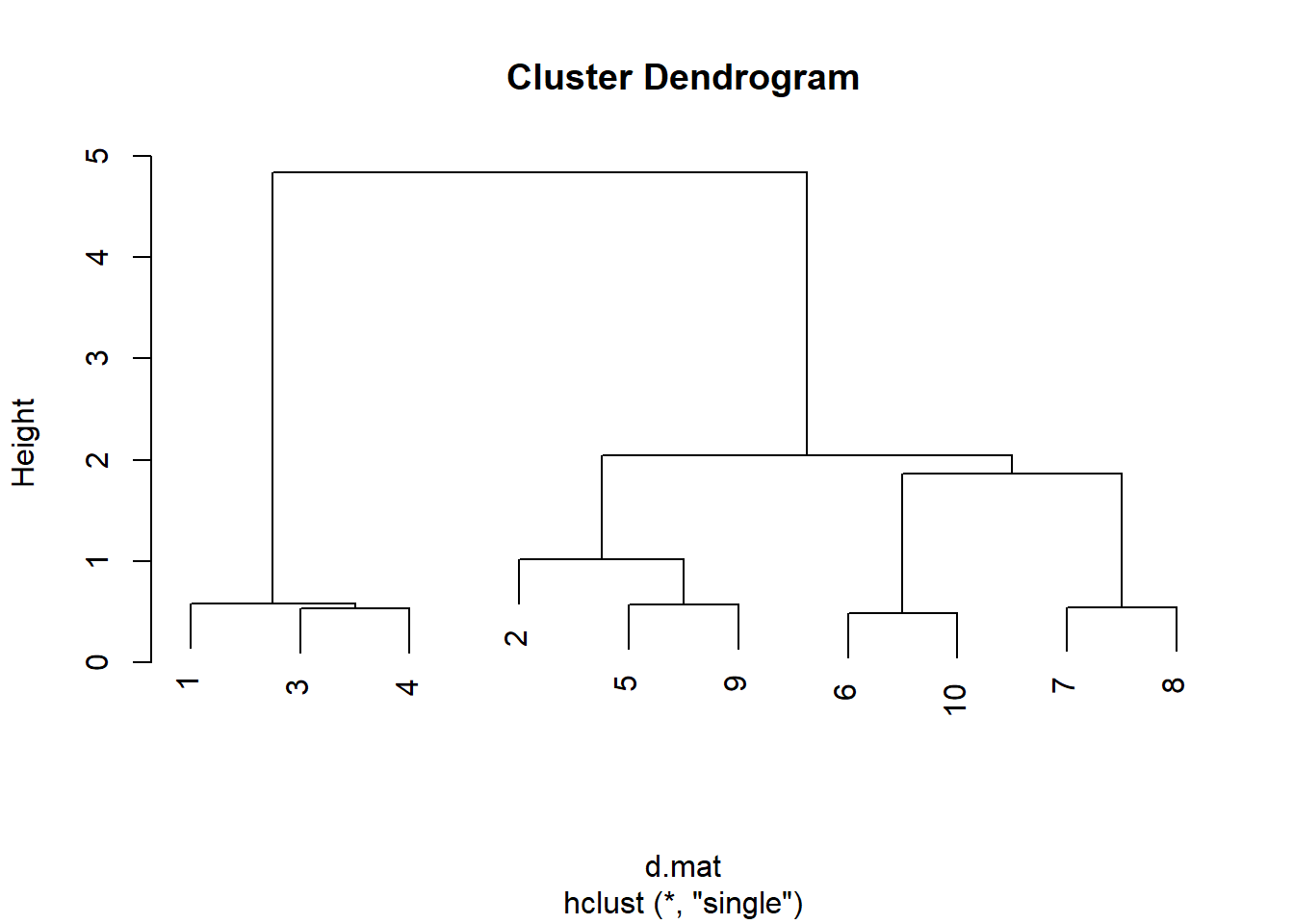
注意：观测的左右关系不代表距离，两类相连时纵轴的高度才代表两类之间的距离，距离越大，越不应该合并到一起。

从图上看分为两类比较合适。

第一类: 1, 3, 4;
第二类: 2, 5, 6, 7, 8, 9, 10。

对hclust()的输出结果用cutree(tree, k=)得到每个观测的分类号，输出类号组成的向量。注意聚类方法的结果是一些分类，具体的类编号并没有意义。

cut1 <- cutree(res1, k=2); cut1

##  [1] 1 2 1 1 2 2 2 2 2 2

结果cut1是分为两类后每个观测的类编号。

用并列盒形图验证分类：

boxplot(t(as.matrix(wineScore)))

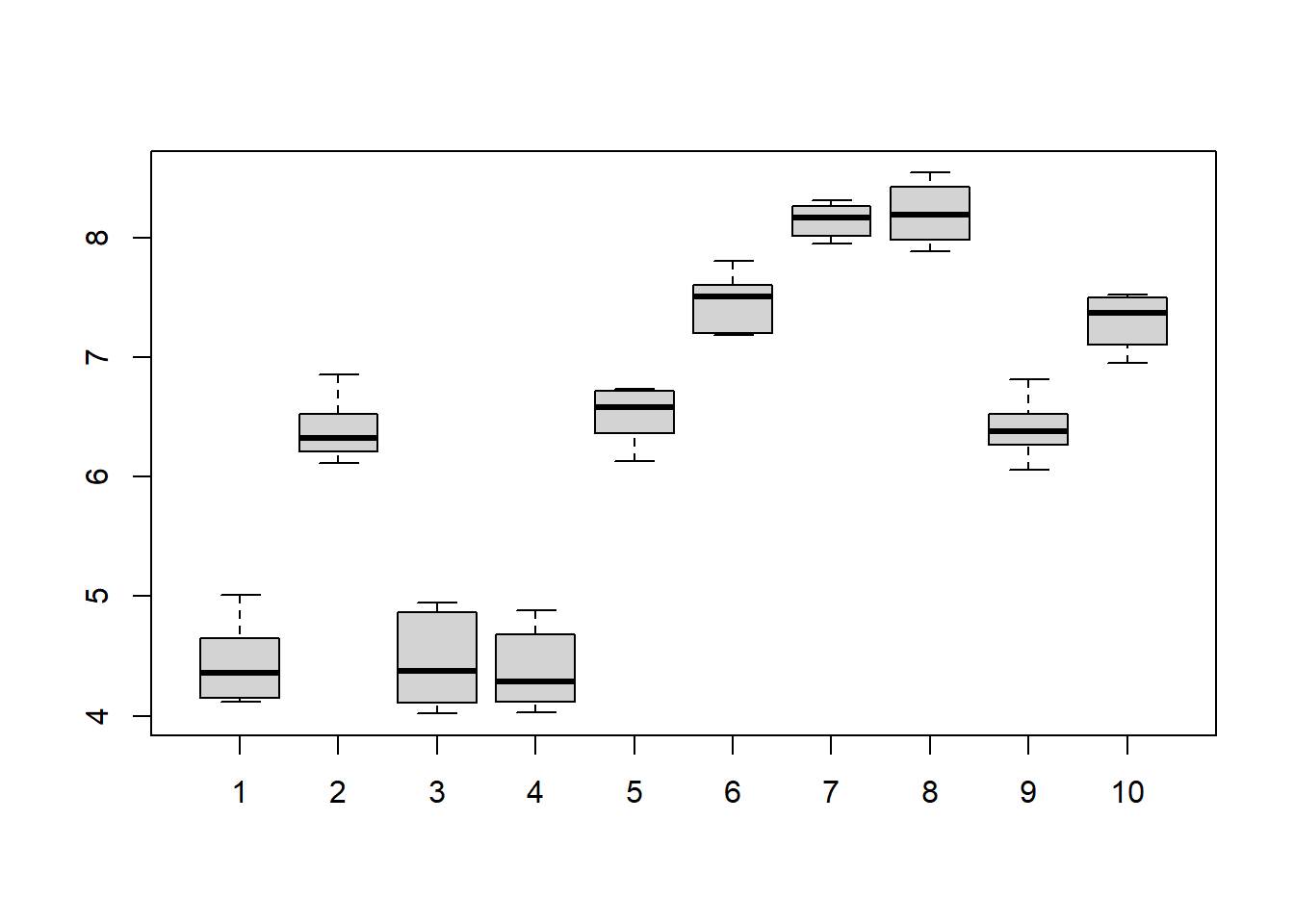
6.3.4.4 用最长距离法聚类

聚类并画聚类树状图：

res2 <- hclust(d.mat, method='complete'); res2

## 
## Call:
## hclust(d = d.mat, method = "complete")
## 
## Cluster method   : complete 
## Distance         : euclidean 
## Number of objects: 10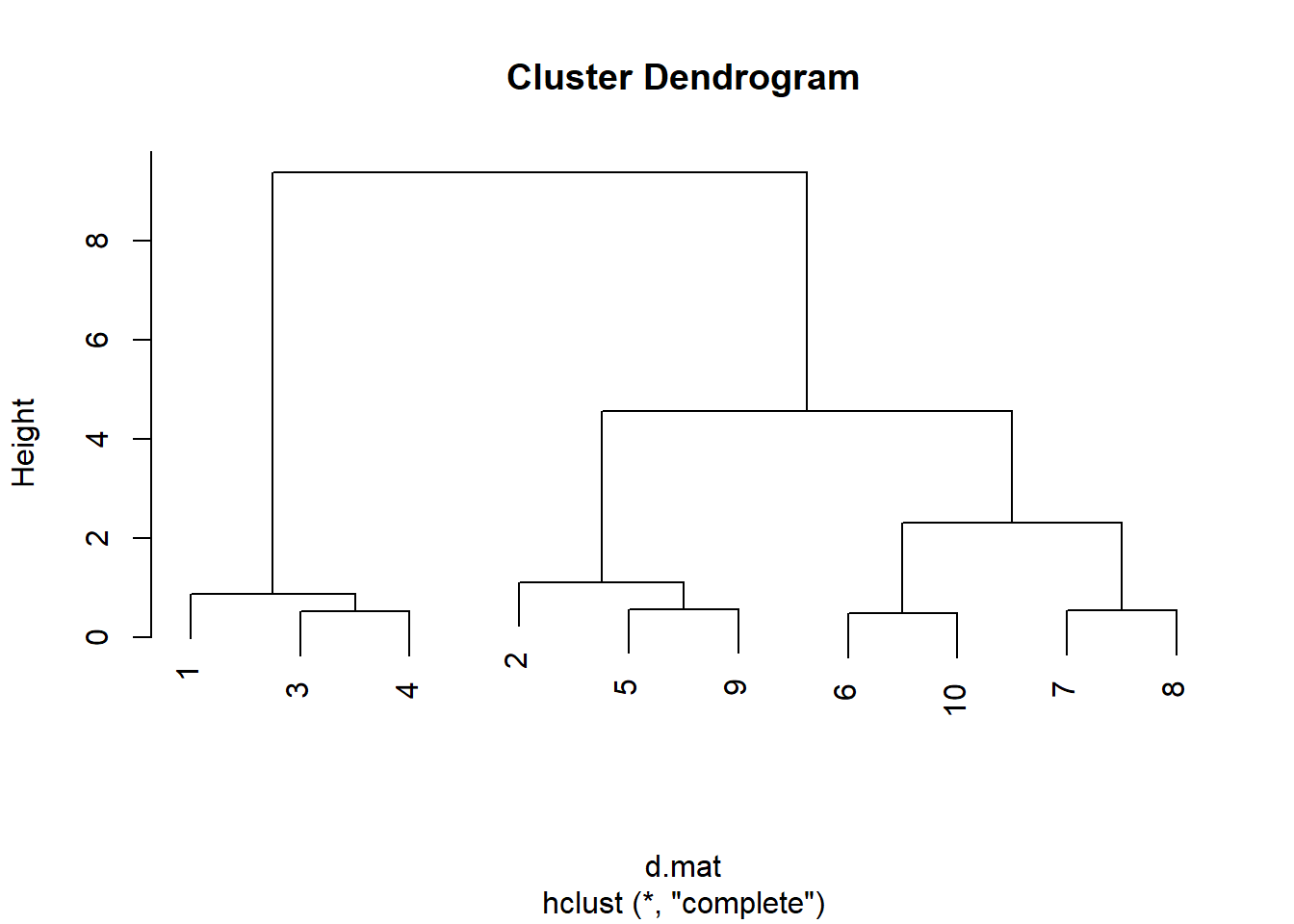

plot(res2)

分为两类或三类合适。

分为两类：

cut2 <- cutree(res2, k=2); cut2

##  [1] 1 2 1 1 2 2 2 2 2 2

两类：

第一类: 1, 3, 4；
第二类: 2, 5, 6, 7, 8, 9, 10。

分为两类时最短距离和最长距离结果相同。

分为三类：

cut2b <- cutree(res2, k=3); cut2b

##  [1] 1 2 1 1 2 3 3 3 2 3

第一类: 1, 3, 4
第二类: 2, 5, 9
第三类: 6, 7, 8, 10

6.3.4.5 用星图验证分类

palette(rainbow(10))
graphics::stars(
  wineScore, len=0.9, cex=1, 
  nrow=3, ncol=4,
  key.loc=c(8, 1),
  ylim=c(0, 8),
  labels=paste(seq(nrow(wineScore))),
  draw.segments=TRUE)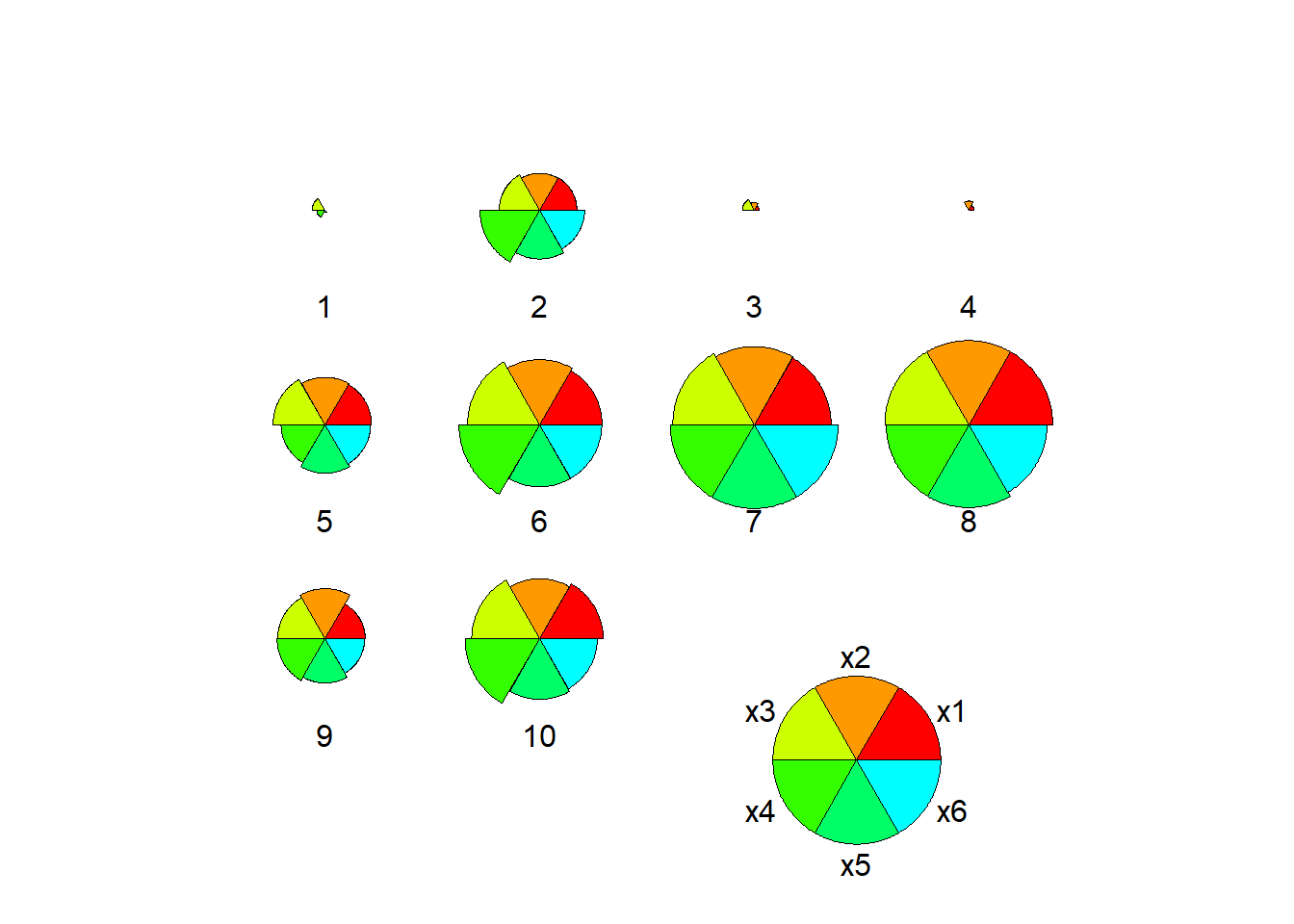

6.3.4.6 用脸谱图验证分类

aplpack::faces(wineScore)

## effect of variables:
##  modified item       Var 
##  "height of face   " "x1"
##  "width of face    " "x2"
##  "structure of face" "x3"
##  "height of mouth  " "x4"
##  "width of mouth   " "x5"
##  "smiling          " "x6"
##  "height of eyes   " "x1"
##  "width of eyes    " "x2"
##  "height of hair   " "x3"
##  "width of hair   "  "x4"
##  "style of hair   "  "x5"
##  "height of nose  "  "x6"
##  "width of nose   "  "x1"
##  "width of ear    "  "x2"
##  "height of ear   "  "x3"

脸谱图与最长距离法分三类的结果比较吻合。

6.3.4.7 用平行坐标图验证分类

opar <- par(mar=c(3,3,1,0.5), mgp=c(2,1, 0))
logd <- log(as.matrix(wineScore))
logd <- cbind(obs=seq(nrow(logd)), logd)
MASS::parcoord(logd)
axis(2, at=seq(0,1, length=10), label=seq(10))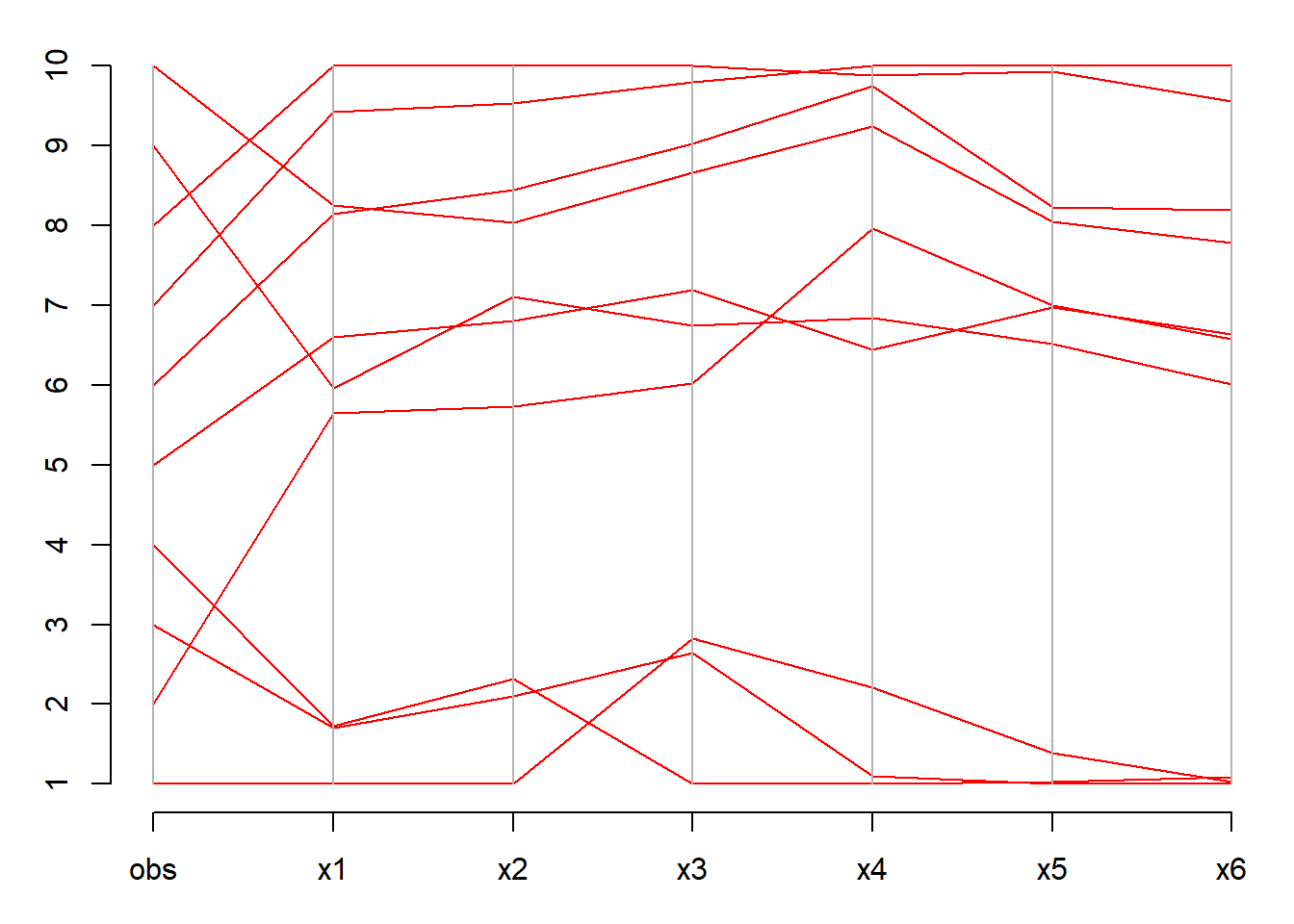

par(opar)

将上图分为三类：

opar <- par(mar=c(3,3,1,0.5), mgp=c(2,1, 0))
logd <- log(as.matrix(wineScore))
logd <- cbind(obs=seq(nrow(logd)), logd)
MASS::parcoord(logd, col=rainbow(9)[5:7][cut2b])
axis(2, at=seq(0,1, length=10), label=seq(10))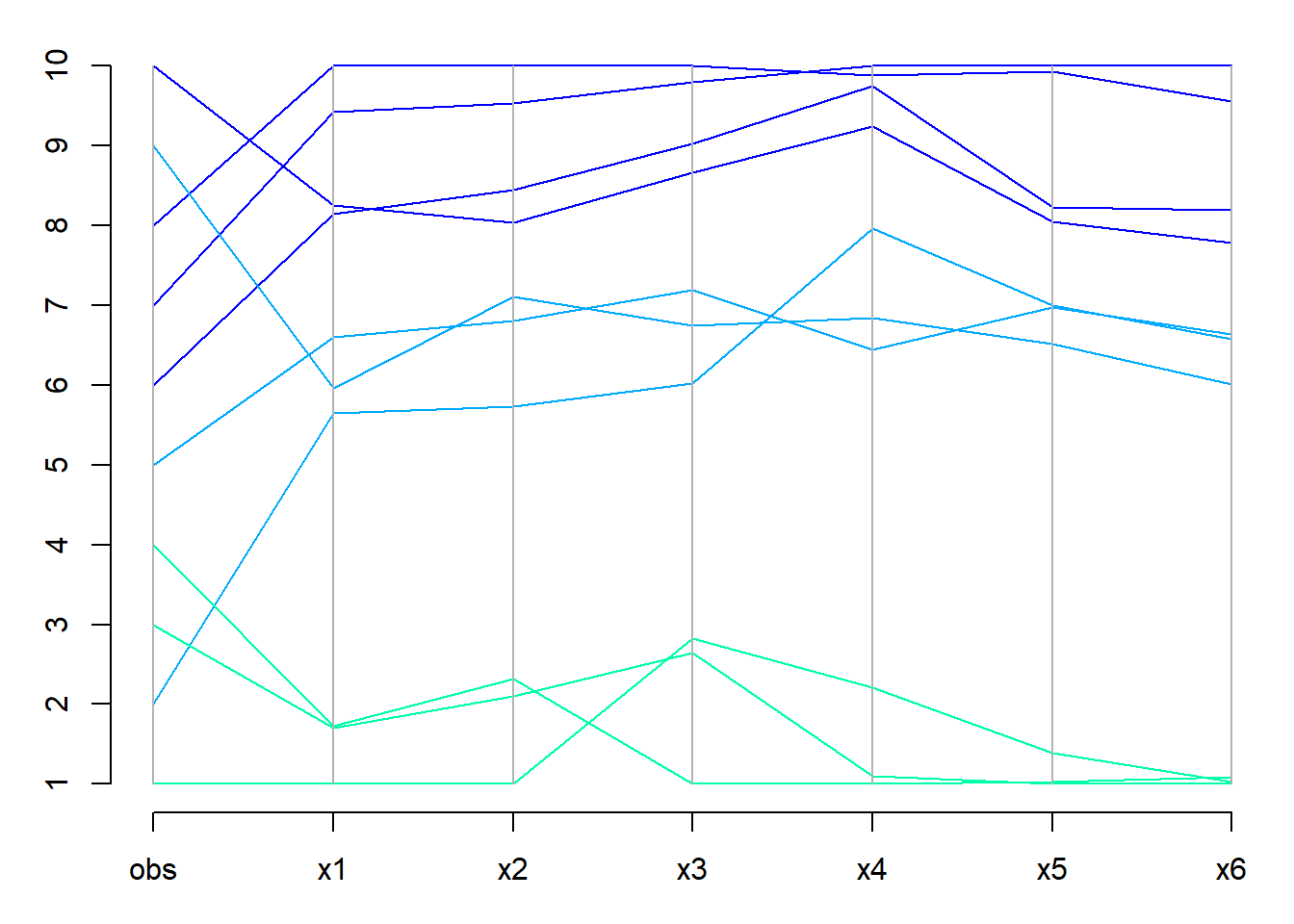

par(opar)

6.4 k均值聚类法

6.4.1 方法

假设观测分为 $k$ 个组， $k$ 已知，并假定每组观测服从多元正态分布。 k均值聚类需要确定 $k$ 个类中心，并把每个观测分配到 $k$ 个类之一当中。

做法类似于系统聚类中离差平方和法(Ward法), 目标是选择类中心和观测类属使得所有类的类内离差平方和的总和最小。具体算法是随机选取类中心（应尽量互相远离），然后迭代地把每个观测分配到最近的类，更新类中心的值，再重新把每个观测分配到最近的类，再更新类中心的值，如此重复直到类属不再改变。这个算法是快速算法，在观测数很多时比系统聚类效率高得多。系统聚类有 $n$ 个观测时要计算 $\frac12 n(n-1)$ 个距离，计算量很大。但是，算法收敛时的结果不一定是目标函数的全局最大值点，可以用不同初值多次计算，保留目标函数最优的一个结果。

k均值是PAM方法的一个变种， PAM(partitioning around medroids)方法步骤如下：

输入 $n\times p$ 的观测数据集。
从 $n$ 个观测中随机选取 $k$ 个，作为临时的类中心。初始类中心应彼此距离较远。
将所有 $n$ 个观测按照距离最近原则分配给各个类。
对每个类，从类成员中选择一个作为新的类中心，使得类成员到类中心的距离和达到最小，这样的类中心称为medroid。
重复步骤3、4直至结果稳定下来（每个观测的类属与类中心不再变化）。

每次运行算法时第2步的初值应重新选取，这样得到的最终结果可能会不同。 cluster扩展包中提供了pam()函数。

k均值法与PAM类似，但是在第4步不是找一个类成员作为类中心，而是用类均值（重心）作为类中心。

k均值法需要预先确定类的个数，但是完全可以选择一个类数的范围，对每一个类个数运行算法，然后基于某种准则选择一个类个数。比如，当增加类个数时类内离差平方和减少幅度明显变小时，就不再增加类个数。

k某某方法是各种软件中常见的聚类方法，最适用于各类的个数相近，空间形状接近凸集的情形。如果真实类别的成员个数有很大差别，用k某某方法可能会将大的类拆分；如果真实类别的空间形状不是球形或者椭球形，用k某某方法的效果可能也不好。

6.4.2 各省消费性支出的聚类

6.4.2.1 数据

P.43例4.2： 2011年全国31个省级行政区的城镇居民家庭人均消费性支出的8个主要指标的数据。根据这些数据，把31个省用k均值聚类法分成4到5类。

数据在provConsume中。

provConsume <- readr::read_csv(
  "data/各省城镇居民人均消费支出.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
attr(provConsume, '变量说明') <- c(
  'x1'='食品',
  'x2'='衣着',
  'x3'='居住',
  'x4'='家庭设备及用品',
  'x5'='交通和通信',
  'x6'='文教娱乐',
  'x7'='医疗保健',
  'x8'='其他'  )
knitr::kable(provConsume, digits=0)

city	x1	x2	x3	x4	x5	x6	x7	x8
北京	6906	2266	1924	1563	3521	3307	1523	975
天津	6663	1755	1763	1175	2700	2116	1415	837
河北	3927	1426	1372	810	1527	1204	956	387
山西	3558	1462	1328	833	1488	1419	851	415
内蒙古	4962	2514	1419	1163	2004	1812	1239	765
辽宁	5255	1855	1386	929	1899	1615	1208	643
吉林	4253	1769	1468	839	1541	1468	1109	562
黑龙江	4348	1682	1186	724	1364	1191	1083	477
上海	8906	2054	2226	1826	3808	3746	1141	1395
江苏	6061	1772	1188	1194	2262	2696	962	647
浙江	7066	2139	1518	1109	3728	2816	1249	812
安徽	5247	1371	1501	691	1365	1631	908	468
福建	6535	1495	1662	1180	2470	1879	773	667
江西	4675	1273	1114	915	1310	1429	641	389
山东	4828	2009	1511	1014	2204	1538	939	518
河南	4213	1707	1087	978	1574	1374	920	485
湖北	5364	1678	1172	815	1382	1490	916	348
湖南	4944	1499	1293	941	1976	1526	791	434
广东	7472	1405	2005	1370	3631	2648	948	773
广西	5074	1019	1238	885	2001	1503	779	349
海南	5674	780	1342	730	1831	1142	783	361
重庆	5848	2057	1206	1079	1719	1475	1051	541
四川	5572	1484	1226	1020	1758	1369	735	533
贵州	4566	1210	1103	858	1395	1331	578	312
云南	4802	1587	828	570	1906	1351	822	381
西藏	5184	1261	781	428	1278	514	424	528
陕西	5040	1673	1194	914	1502	1858	1101	500
甘肃	4182	1470	1140	660	1290	1158	874	413
青海	4260	1394	1055	723	1293	968	854	407
宁夏	4483	1702	1247	885	1638	1441	978	521
新疆	4537	1716	888	791	1378	1122	913	494

str(provConsume)

## spc_tbl_ [31 × 9] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ city: chr [1:31] "北京" "天津" "河北" "山西" ...
##  $ x1  : num [1:31] 6906 6663 3927 3558 4962 ...
##  $ x2  : num [1:31] 2266 1755 1426 1462 2514 ...
##  $ x3  : num [1:31] 1924 1763 1372 1328 1419 ...
##  $ x4  : num [1:31] 1563 1175 810 833 1163 ...
##  $ x5  : num [1:31] 3521 2700 1527 1488 2004 ...
##  $ x6  : num [1:31] 3307 2116 1204 1419 1812 ...
##  $ x7  : num [1:31] 1523 1415 956 851 1239 ...
##  $ x8  : num [1:31] 975 837 387 415 765 ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   city = col_character(),
##   ..   x1 = col_double(),
##   ..   x2 = col_double(),
##   ..   x3 = col_double(),
##   ..   x4 = col_double(),
##   ..   x5 = col_double(),
##   ..   x6 = col_double(),
##   ..   x7 = col_double(),
##   ..   x8 = col_double()
##   .. )
##  - attr(*, "problems")=<externalptr> 
##  - attr(*, "变量说明")= Named chr [1:8] "食品" "衣着" "居住" "家庭设备及用品" ...
##   ..- attr(*, "names")= chr [1:8] "x1" "x2" "x3" "x4" ...

summary(provConsume)

##      city                 x1             x2               x3        
##  Length:31          Min.   :3558   Min.   : 780.1   Min.   : 781.1  
##  Class :character   1st Qu.:4510   1st Qu.:1415.3   1st Qu.:1156.0  
##  Mode  :character   Median :5040   Median :1673.2   Median :1247.1  
##                     Mean   :5303   Mean   :1628.5   Mean   :1334.5  
##                     3rd Qu.:5761   3rd Qu.:1770.8   3rd Qu.:1484.8  
##                     Max.   :8906   Max.   :2514.1   Max.   :2225.7  
##        x4               x5             x6               x7        
##  Min.   : 428.0   Min.   :1278   Min.   : 514.4   Min.   : 424.1  
##  1st Qu.: 800.6   1st Qu.:1389   1st Qu.:1341.0   1st Qu.: 806.6  
##  Median : 914.3   Median :1719   Median :1474.9   Median : 919.8  
##  Mean   : 955.2   Mean   :1959   Mean   :1681.9   Mean   : 950.5  
##  3rd Qu.:1094.3   3rd Qu.:2104   3rd Qu.:1834.8   3rd Qu.:1091.7  
##  Max.   :1826.2   Max.   :3808   Max.   :3746.4   Max.   :1523.3  
##        x8        
##  Min.   : 311.6  
##  1st Qu.: 410.1  
##  Median : 500.4  
##  Mean   : 559.3  
##  3rd Qu.: 645.1  
##  Max.   :1394.9

6.4.2.2 用快速聚类法分成4类

因为各列都是某一类别的消费的平均值，所以是可比的，不需要进行标准化处理。如果各列不可比而且方差相差比较悬殊，则应该进行标准化处理，比如每列除以标准差，每列除以极差，每列改成秩统计量，等等。

R中用kmeans()函数聚类，用centers=指定类个数。为了得到稳定的结果，通常希望从不同的随机选取的中心出发，找到最终类内离差平方和最小的分类结果，所以可以用一个nstart=选项指定重复多少次随机初值比较。

k <- 4
res1 <- kmeans(provConsume[,-1], centers=k, nstart=20)
res1

## K-means clustering with 4 clusters of sizes 13, 4, 3, 11
## 
## Cluster means:
##         x1       x2       x3       x4       x5       x6        x7       x8
## 1 4383.881 1512.278 1122.931  770.340 1460.059 1228.612  846.4638 444.0038
## 2 7587.390 1965.820 1918.150 1467.118 3672.115 3129.315 1215.3050 988.7275
## 3 6419.720 1674.000 1537.673 1182.757 2477.300 2230.183 1050.3667 716.9600
## 4 5255.227 1630.774 1316.993  925.520 1785.396 1541.681  949.9445 496.3827
## 
## Clustering vector:
##  [1] 2 3 1 1 4 4 1 1 2 3 2 4 3 1 4 1 4 4 2 4 4 4 4 1 1 1 4 1 1 1 1
## 
## Within cluster sum of squares by cluster:
## [1] 4922082 4673100 1126730 5409421
##  (between_SS / total_SS =  81.2 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

在聚类结果中，cluster元素是每个观测的类号， centers是各类的中心， totss是总离差平方和， tot.withinss是总类内离差平方和， 1 - tot.withinss/totss可以看成分类解释的百分比。因为类别编号有随机性，所以把类别编号按照类中心的元素平均值降序排序，可以得到一致的结果。

因为有随机中心，所以重复运行会使得类不变但是类号改变。下面按类中心的8个指标平均值降序排序为类号次序。

library(forcats)
cluster_reorder <- function(data, km_res, 
  label=rownames(data)) {
  xrmean <- rowMeans(data)
  clus_old <- km_res$cluster
  names(clus_old) <- label
  clus_new <- clus_old
  clus_new[] <- as.integer(fct_reorder(
    factor(clus_new), xrmean, mean, .desc=TRUE))
  clus_new
}

cl.new <- cluster_reorder(provConsume[,-1], res1, 
  provConsume[["city"]])
tibble("省份" = names(cl.new),
  "类别"=cl.new) |>
  arrange(`类别`) |>
  knitr::kable()

省份	类别
北京	1
上海	1
浙江	1
广东	1
天津	2
江苏	2
福建	2
内蒙古	3
辽宁	3
安徽	3
山东	3
湖北	3
湖南	3
广西	3
海南	3
重庆	3
四川	3
陕西	3
河北	4
山西	4
吉林	4
黑龙江	4
江西	4
河南	4
贵州	4
云南	4
西藏	4
甘肃	4
青海	4
宁夏	4
新疆	4

上面的程序利用了forcats包的fct_reorder()函数。此函数对输入的一个因子进行水平重新排序，排序的准则是伴随输入的第二自变量大小，第三自变量mean指定对每一组的xrmean变量值计算组平均值，按组平均值大小对各组进行重新编号，选项.desc=TRUE使得新的组号是平均值从大到小排列的，返回值是每个观测的新分类编号，输入的label用于区分每个观测，默认使用原始数据集中的行名。

如果不用forcats包，可以编程如：

cluster_reorder2 <- function(clus_res, label){
  xm <- rowMeans(clus_res$centers)
  ind <- order(xm, decreasing = TRUE)   
  ## ind[1]是新的第一类原来类号，ind[2]是新的第二类原来类号，……
  level_map <- order(ind) 
  ## level_map[1]是原来第一类的新类号，
  ## level_map[2]是原来第二类的新类号，……
  cl_new <- level_map[ clus_res$cluster ]
  names(cl_new) <- label
  
  cl_new
}
cl.new <- cluster_reorder2(res1, 
  provConsume[["city"]])
tibble("省份" = names(cl.new),
  "类别"=cl.new) |>
  arrange(`类别`) |>
  knitr::kable()

省份	类别
北京	1
上海	1
浙江	1
广东	1
天津	2
江苏	2
福建	2
内蒙古	3
辽宁	3
安徽	3
山东	3
湖北	3
湖南	3
广西	3
海南	3
重庆	3
四川	3
陕西	3
河北	4
山西	4
吉林	4
黑龙江	4
江西	4
河南	4
贵州	4
云南	4
西藏	4
甘肃	4
青海	4
宁夏	4
新疆	4

6.4.2.3 用散点图矩阵表现分类效果

cmap <- rainbow(9)[4:7]
pairs(provConsume[,-1], 
  labels=attr(provConsume, '变量说明'),
  col=cmap[res1$clust])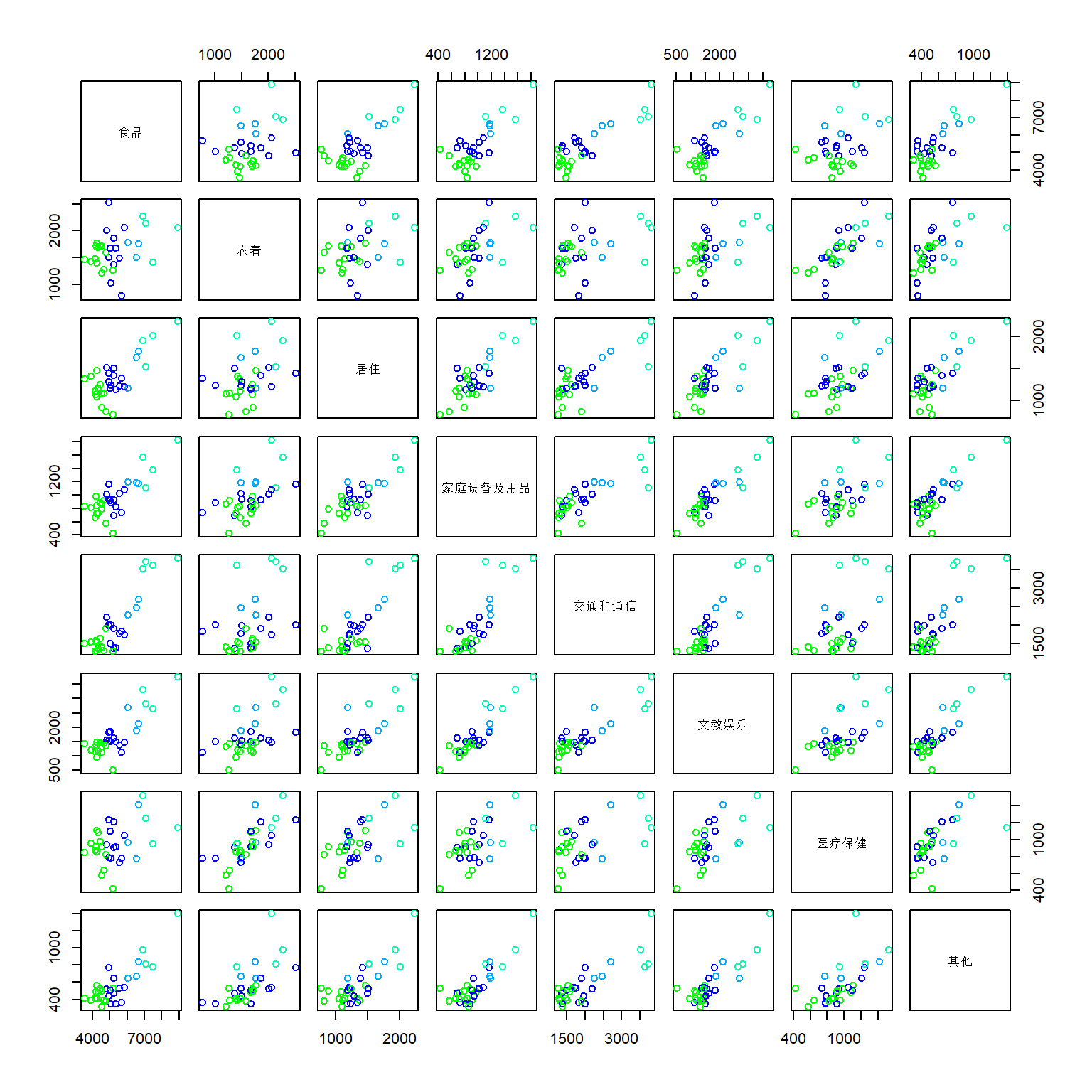

6.4.2.4 用主成分图表现分类

因为聚类的数据是多元的，所以难以用普通散点图表现聚类结果。可以计算数据的主成分分析，用前两个主成分作散点图并用不同颜色表示不同类别。 ggfortify包提供了这样的功能，例如：

library(ggfortify)
autoplot(res1, data=provConsume[,-1], 
  label=TRUE, frame=TRUE)

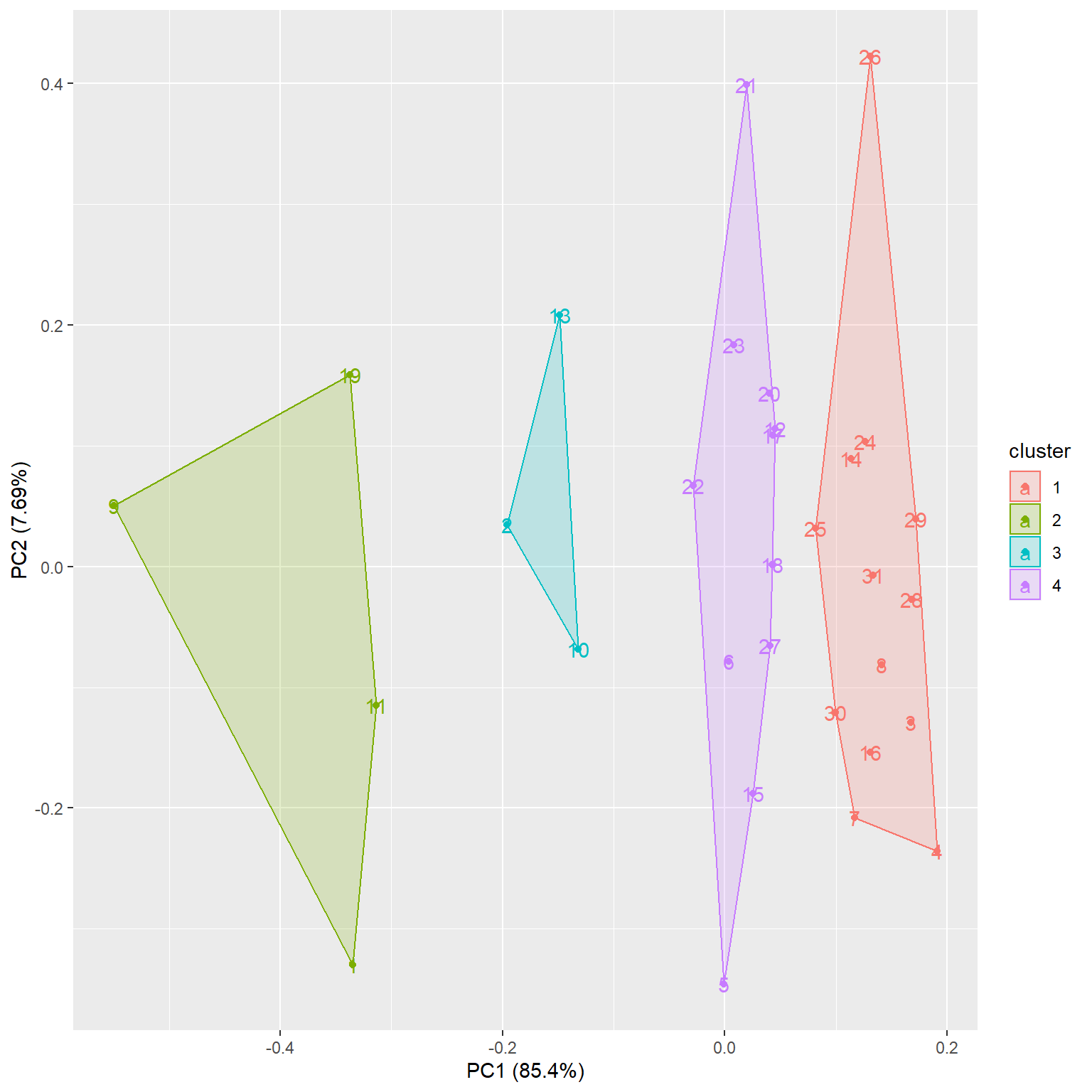
6.4.2.5 用星图验证分类

## 按类排序
ind1 <- order(cl.new)
d1 <- as.data.frame(provConsume[,-1])
rownames(d1) <- provConsume[["city"]]
names(d1) <- attr(provConsume, '变量说明')
d1 <- d1[ind1,]

graphics::stars(
  d1, len=0.9, cex=0.8, 
  nrow=6, ncol=6, key.loc=c(10, 1),
  ylim=c(0, 15),
  label=paste0(row.names(d1), '(', cl.new[ind1], ')'),
  draw.segments=TRUE)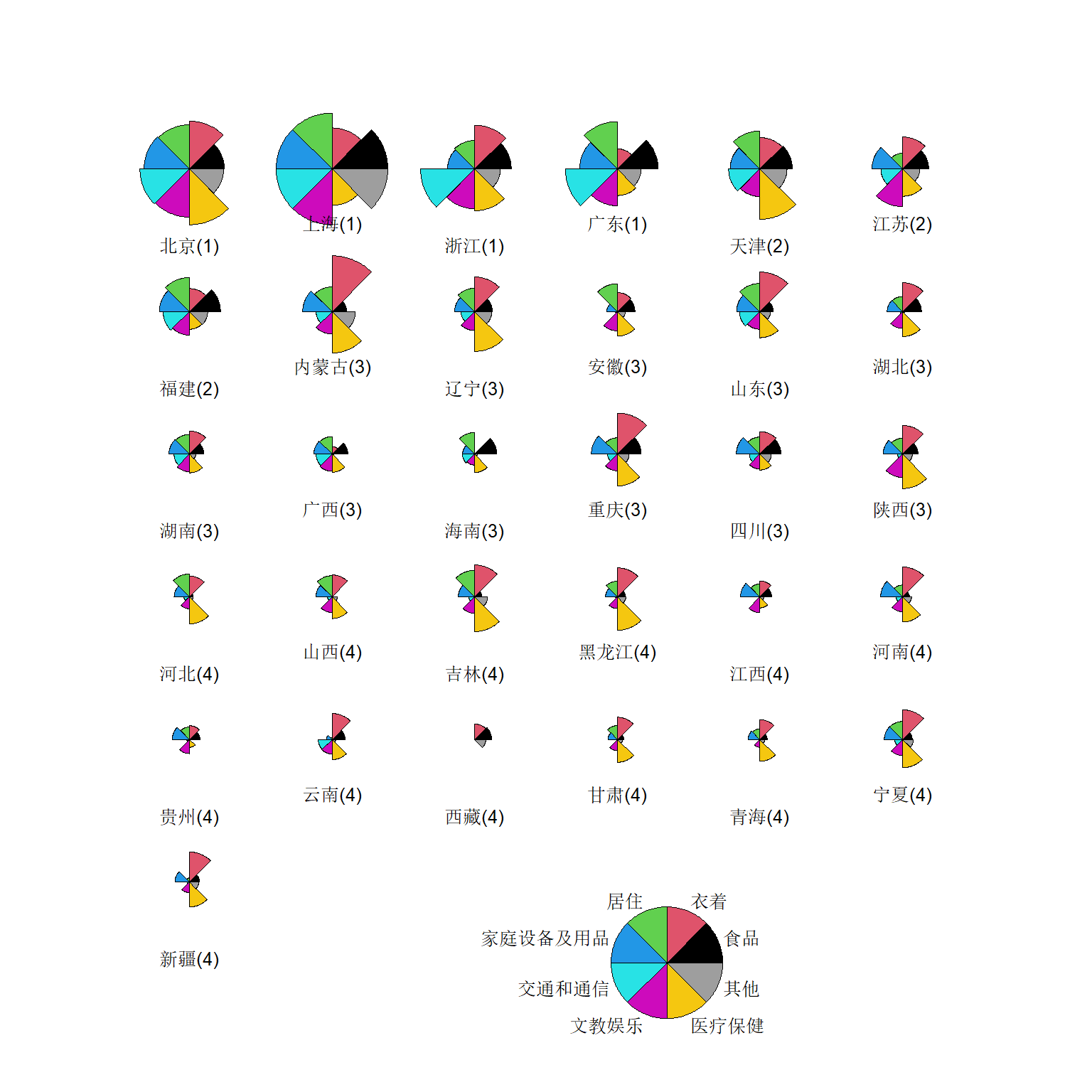

6.4.2.6 用脸谱图验证分类

palette(rainbow(12))
aplpack::faces(
  d1, label=paste0(row.names(d1), '(', cl.new[ind1], ')') )

## effect of variables:
##  modified item       Var             
##  "height of face   " "食品"          
##  "width of face    " "衣着"          
##  "structure of face" "居住"          
##  "height of mouth  " "家庭设备及用品"
##  "width of mouth   " "交通和通信"    
##  "smiling          " "文教娱乐"      
##  "height of eyes   " "医疗保健"      
##  "width of eyes    " "其他"          
##  "height of hair   " "食品"          
##  "width of hair   "  "衣着"          
##  "style of hair   "  "居住"          
##  "height of nose  "  "家庭设备及用品"
##  "width of nose   "  "交通和通信"    
##  "width of ear    "  "文教娱乐"      
##  "height of ear   "  "医疗保健"

6.4.2.7 分类个数的考察

作解释变差比例的图形。

elbow_plot <- function(
    data, 
    max_k=min(ncol(data), 10)) {
  rat <- numeric(max_k)
  rat[1] <- 0
  for(k in 2:max_k){
    rkm <- kmeans(
      data, 
      centers=k,
      nstart=20)
    rat[k] <- (1 - rkm$tot.withinss / rkm$totss)*100
  }
  plot(rat, xlab="类数", ylab="离差平方和解释百分比",
    type="b")
  
}
elbow_plot(provConsume[,-1], max_k=8)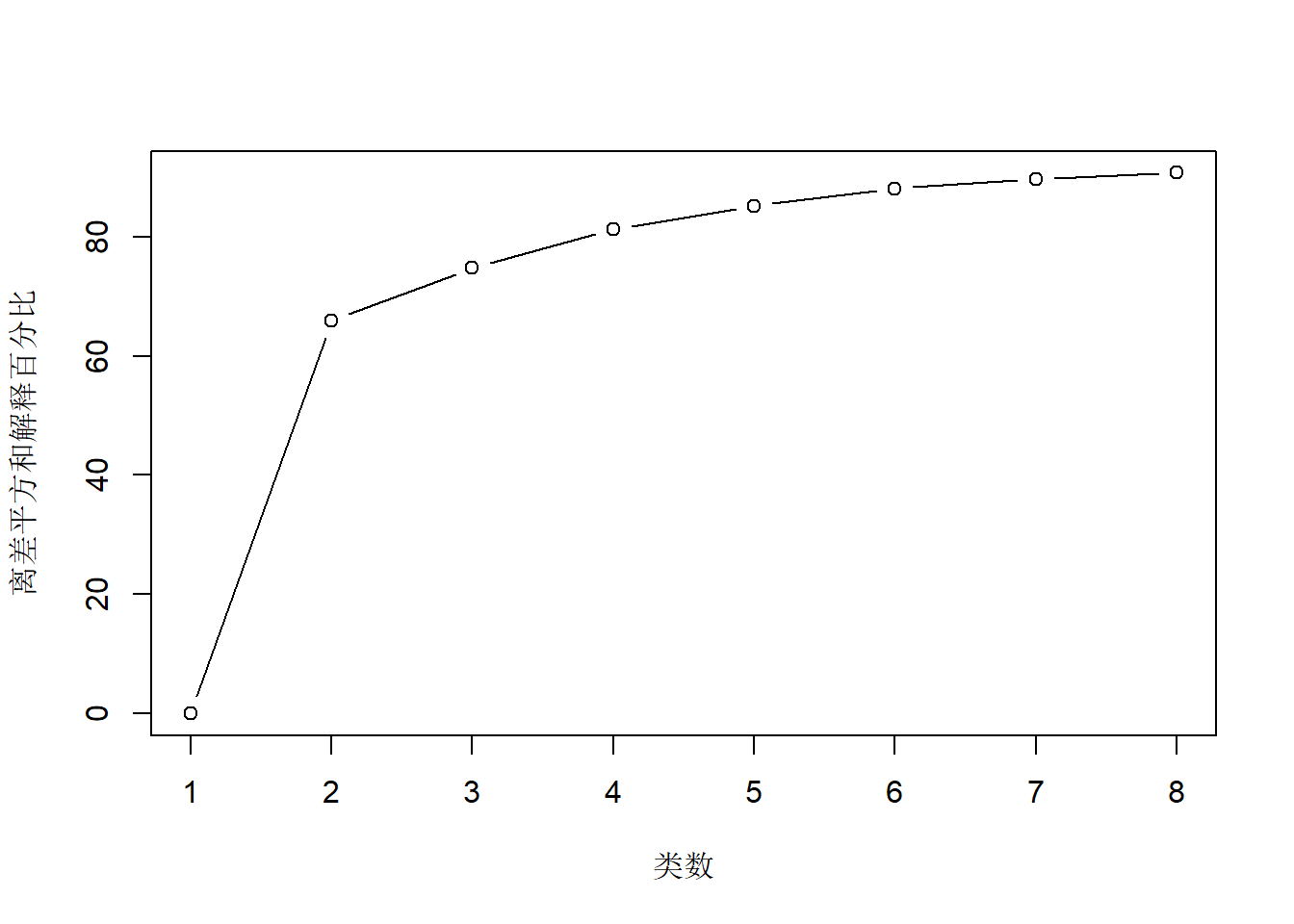

从图形看2大类比较好。

6.4.3 陶器考古聚类

data("pottery", package = "HSAUR2")
knitr::kable(head(pottery, 5))

Al2O3	Fe2O3	MgO	CaO	Na2O	K2O	TiO2	MnO	BaO	kiln
18.8	9.52	2.00	0.79	0.40	3.20	1.01	0.077	0.015	1
16.9	7.33	1.65	0.84	0.40	3.05	0.99	0.067	0.018	1
18.2	7.64	1.82	0.77	0.40	3.07	0.98	0.087	0.014	1
16.9	7.29	1.56	0.76	0.40	3.05	1.00	0.063	0.019	1
17.8	7.24	1.83	0.92	0.43	3.12	0.93	0.061	0.019	1

数据集pottery包含了对罗马统治时期英国的5个窑出土的陶器的化学测量数据。这5个窑分别处于3个不同地区。用k均值法聚类。

散点图矩阵：

library(GGally)
ggscatmat(data = pottery, 
  columns = 1:9, color = "kiln")

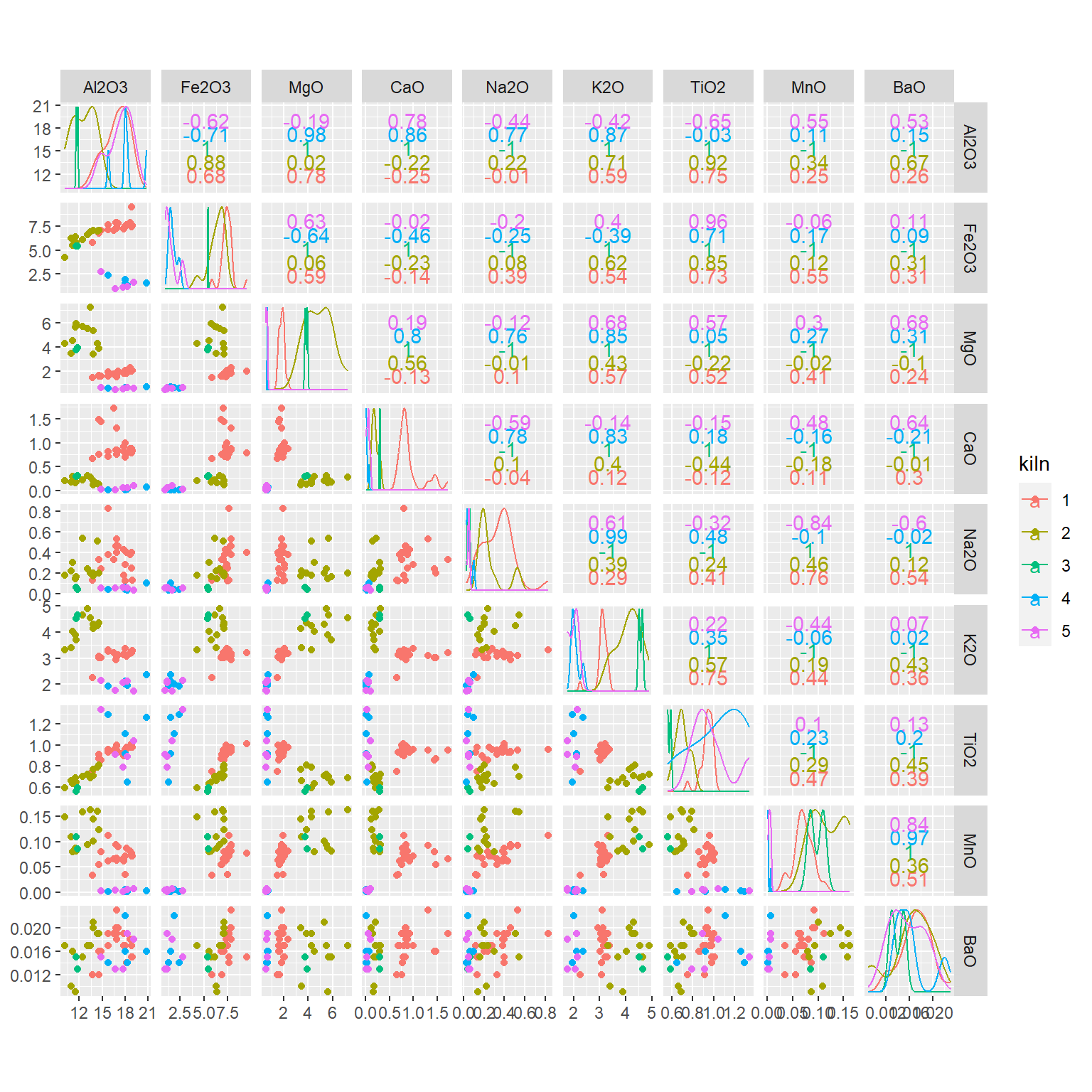
各个变量的方差：

pottery |>
  summarise(across(
    -kiln, var  )) |>
  pivot_longer(everything(),
    names_to = "Chemical",
    values_to = "Var") |>
  knitr::kable()

Chemical	Var
Al2O3	7.3062828
Fe2O3	5.7879286
MgO	3.0349498
CaO	0.2063689
Na2O	0.0317710
K2O	0.7271409
TiO2	0.0323318
MnO	0.0021903
BaO	0.0000089

方差的差别较大，应进行标准化。这里每列除以标准差：

pottery_scale <- pottery |>
  mutate(across(-kiln, \(x) x / sd(x)))

基于相关阵计算主成分，作前两个主成分的散点图：

pot_pca <- princomp(pottery[,1:9], cor=TRUE, scores=TRUE) |>
  predict() 
as_tibble(pot_pca) |>
  mutate(kiln = pottery[["kiln"]]) |>
  ggplot(aes(
    x = Comp.1, y = Comp.2, color = kiln  )) +
  geom_point()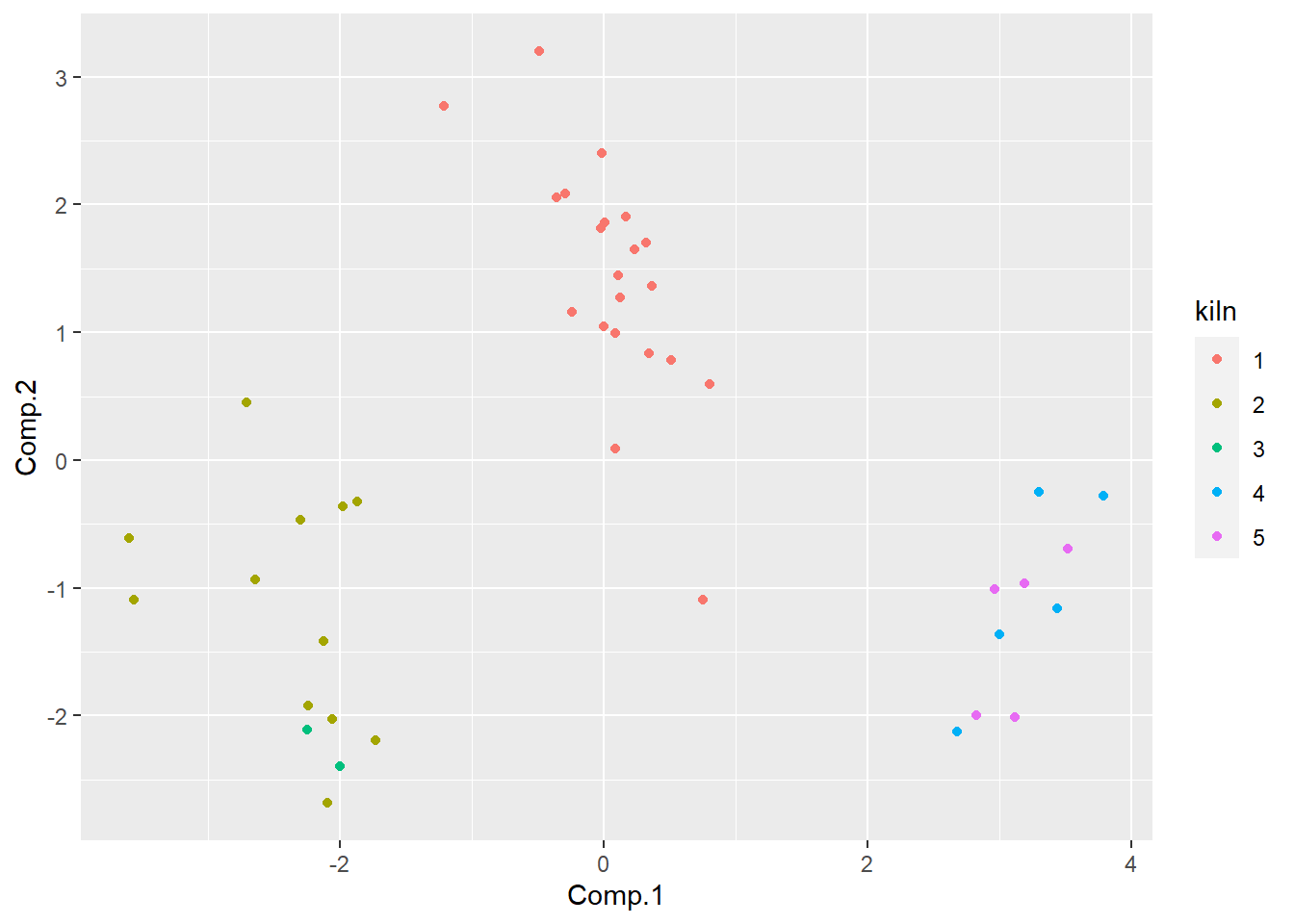

从主成分看明显分成3组，恰好是5个窑所在的三个地区。

用k均值聚类，对不同的类数计算解释百分比，作图显示：

elbow_plot(pottery_scale[,1:9], max_k=6)

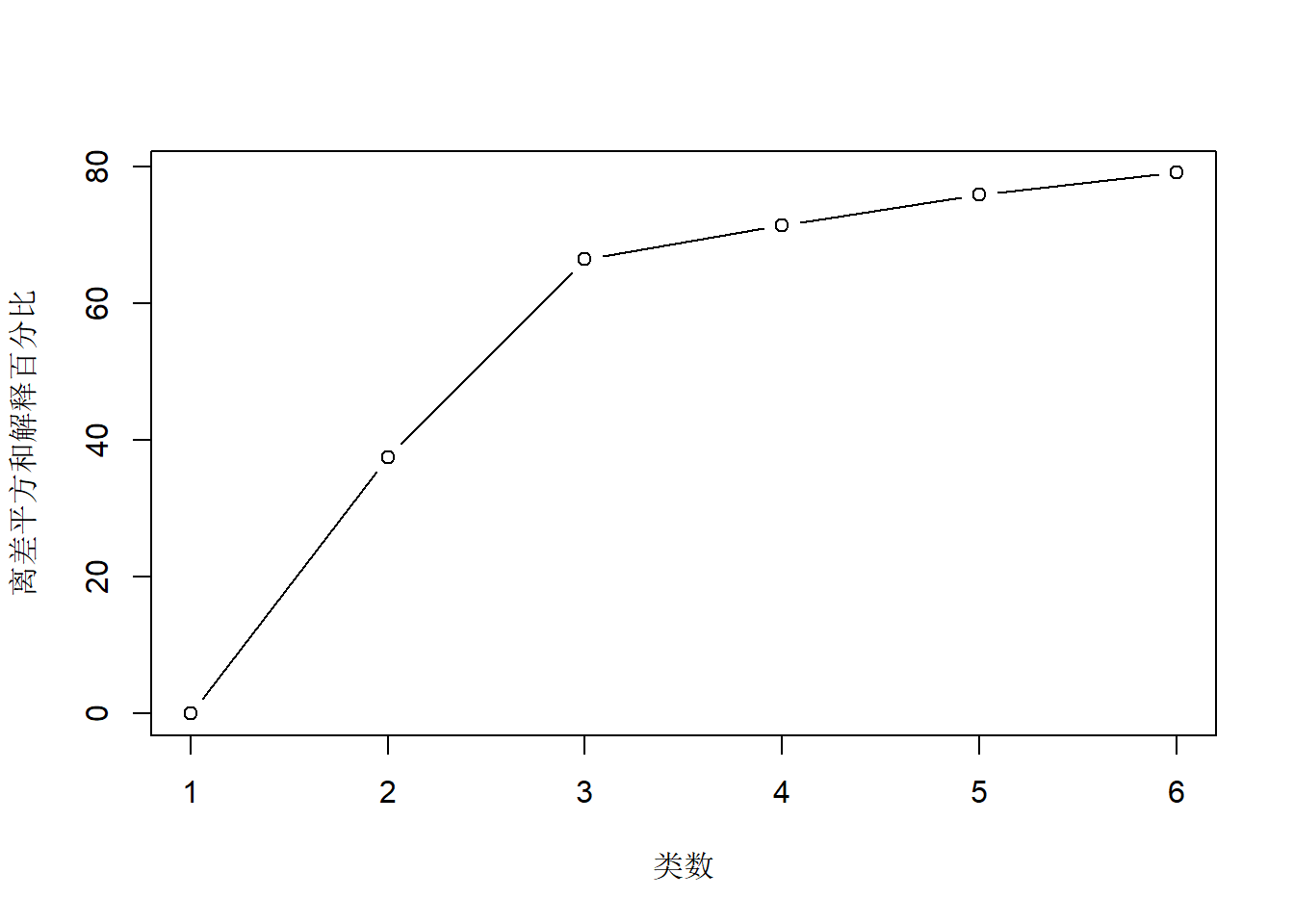
可以看出分成3类以后再增加分类的效益明显降低。

作k均值聚类：

pot_km <- kmeans(pottery_scale[,1:9], 
  centers=3, nstart=20)
pot_km

## K-means clustering with 3 clusters of sizes 21, 14, 10
## 
## Cluster means:
##      Al2O3     Fe2O3       MgO        CaO      Na2O      K2O     TiO2
## 1 6.259327 3.0877613 1.0575567 2.06711911 1.9395537 3.638752 5.214484
## 2 4.600685 2.5803590 2.7425680 0.47170568 1.2663202 4.911143 3.797649
## 3 6.566744 0.6700442 0.3673704 0.08585043 0.2861242 2.370047 5.672638
##          MnO      BaO
## 1 1.52010958 5.748909
## 2 2.51367517 5.341695
## 3 0.06837441 5.365649
## 
## Clustering vector:
##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 
##  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  2  2  2  2  2 
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 
##  2  2  2  2  2  2  2  2  2  3  3  3  3  3  3  3  3  3  3 
## 
## Within cluster sum of squares by cluster:
## [1] 55.91185 49.30545 27.71633
##  (between_SS / total_SS =  66.4 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

按各类中心的变量值对类别重新编号，这样可以使得聚类的编号有稳定结果：

clus_new <- cluster_reorder(
  pottery_scale[,1:9], 
  pot_km, 
  label=pottery_scale[["kiln"]])

对比kiln和clus_new的值：

table(clus_new, pottery_scale[["kiln"]])

##         
## clus_new  1  2  3  4  5
##        1 21  0  0  0  0
##        2  0 12  2  0  0
##        3  0  0  0  5  5

可以看出，分类1由1号窑组成，分类2由2、3号窑组成，分类3由4、5号窑组成，这3个分类恰好对应了5个窑所在的3各地区。

按分类作主成分图：

as_tibble(pot_pca) |>
  mutate(cluster = factor(clus_new)) |>
  ggplot(aes(
    x = Comp.1, y = Comp.2, color = cluster  )) +
  geom_point()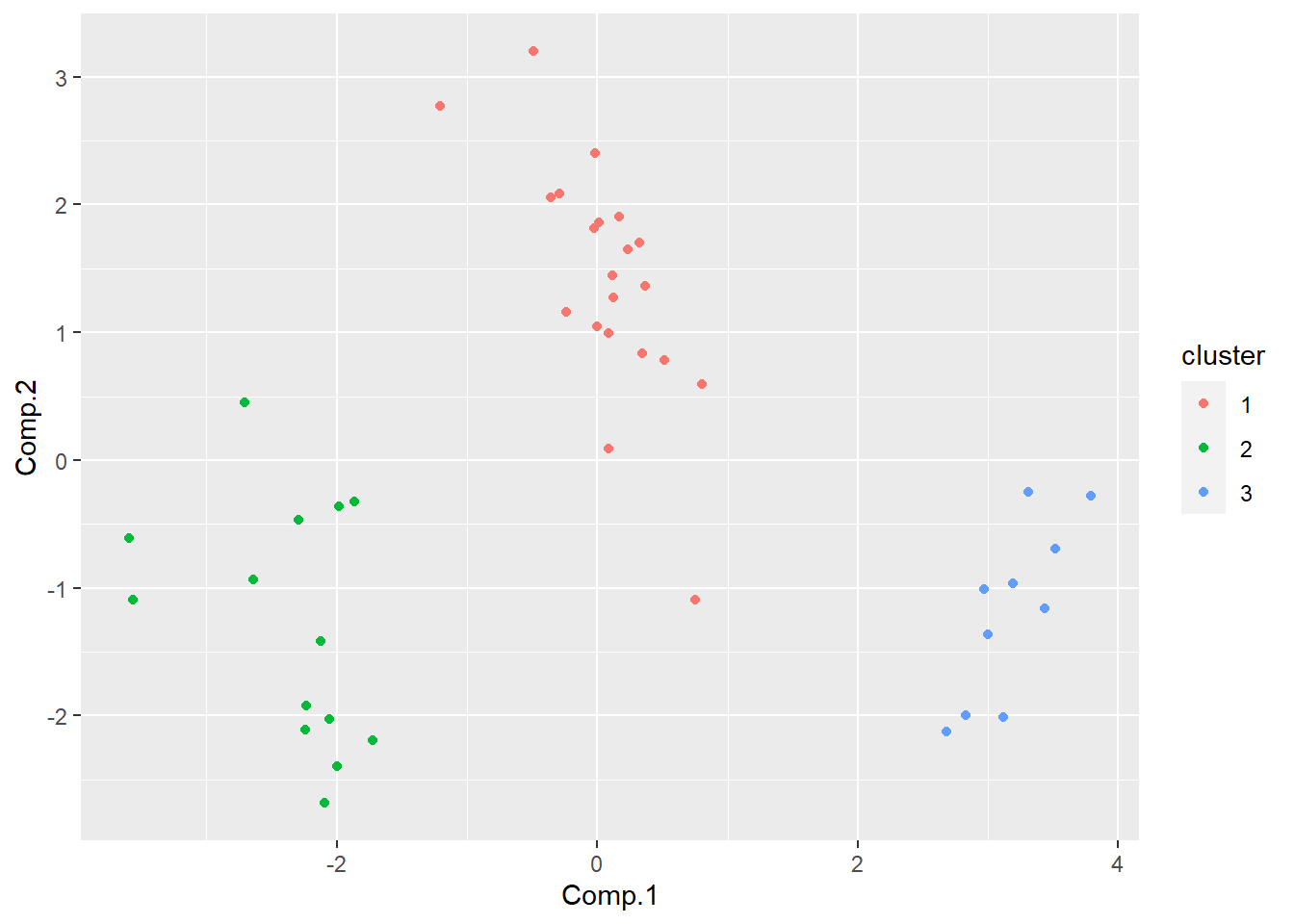

6.5 cluster包

hclust和kmeans都是R的基本stats包的函数。 cluster包提供了一些其它的聚类函数。

pam(x, k, pamonce=6)是一种比K均值方法更稳健的预先指定类数的聚类方法，找到各类的代表点，最小化每个观测与代表点的不相似度的和而不是欧式距离的平方和。 x为数值型数据框或者不相似度矩阵。

clara()函数使用了一种支持大型数据的聚类算法，它将数据分成小的子数据集进行聚类。

6.6 factoextra包

例子来自factoextra包文档。

library(factoextra)

## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa

set.seed(123)

# Data preparation
# +++++++++++++++
data("iris")
head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

# Remove species column (5) and scale the data
iris.scaled <- scale(iris[, -5])

# K-means clustering
# +++++++++++++++++++++
km.res <- kmeans(iris.scaled, 3, nstart = 10)

# Visualize kmeans clustering
# use repel = TRUE to avoid overplotting
fviz_cluster(km.res, iris[, -5], ellipse.type = "norm")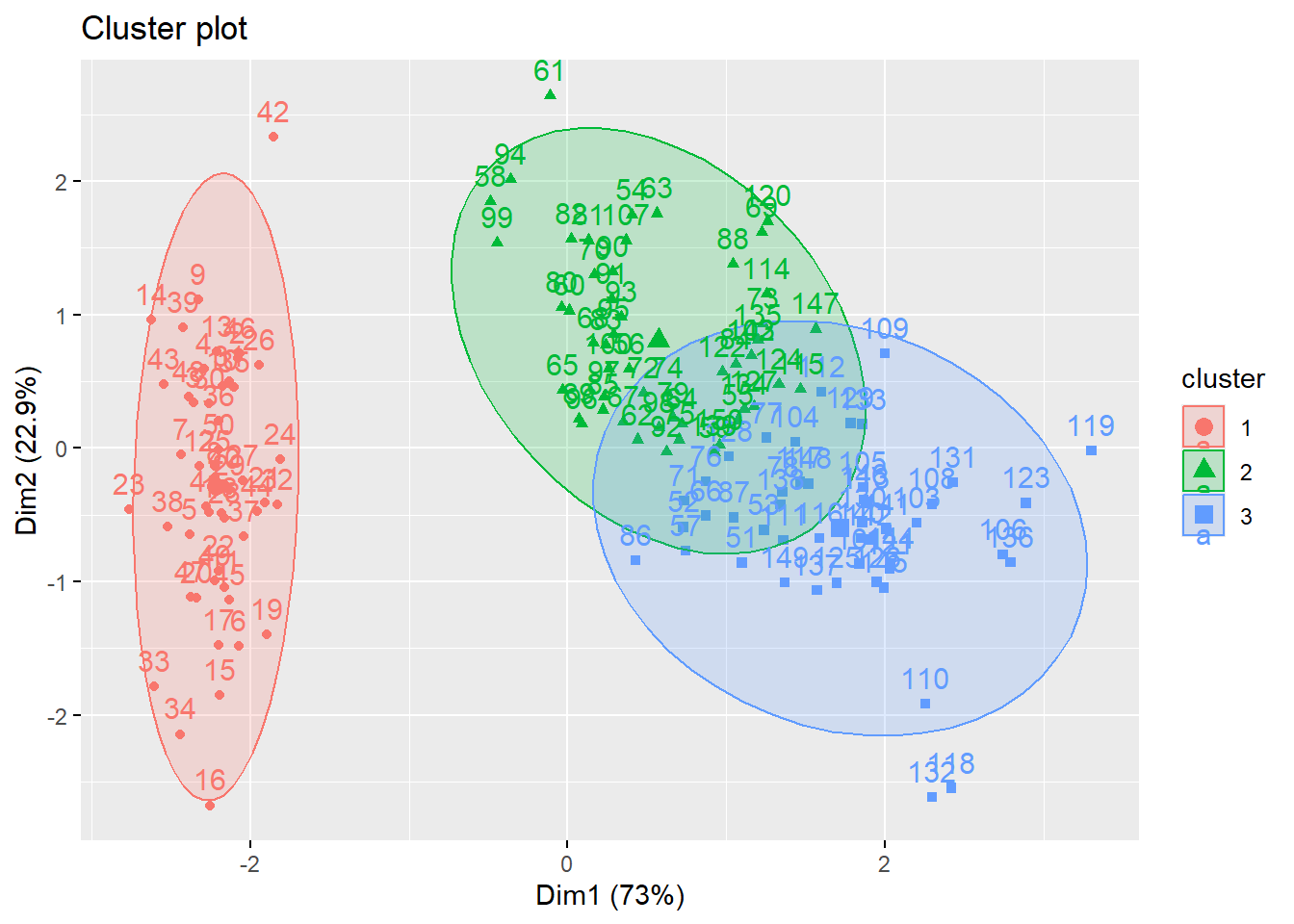

# Change the color palette and theme
fviz_cluster(km.res, iris[, -5],
   palette = "Set2", ggtheme = theme_minimal())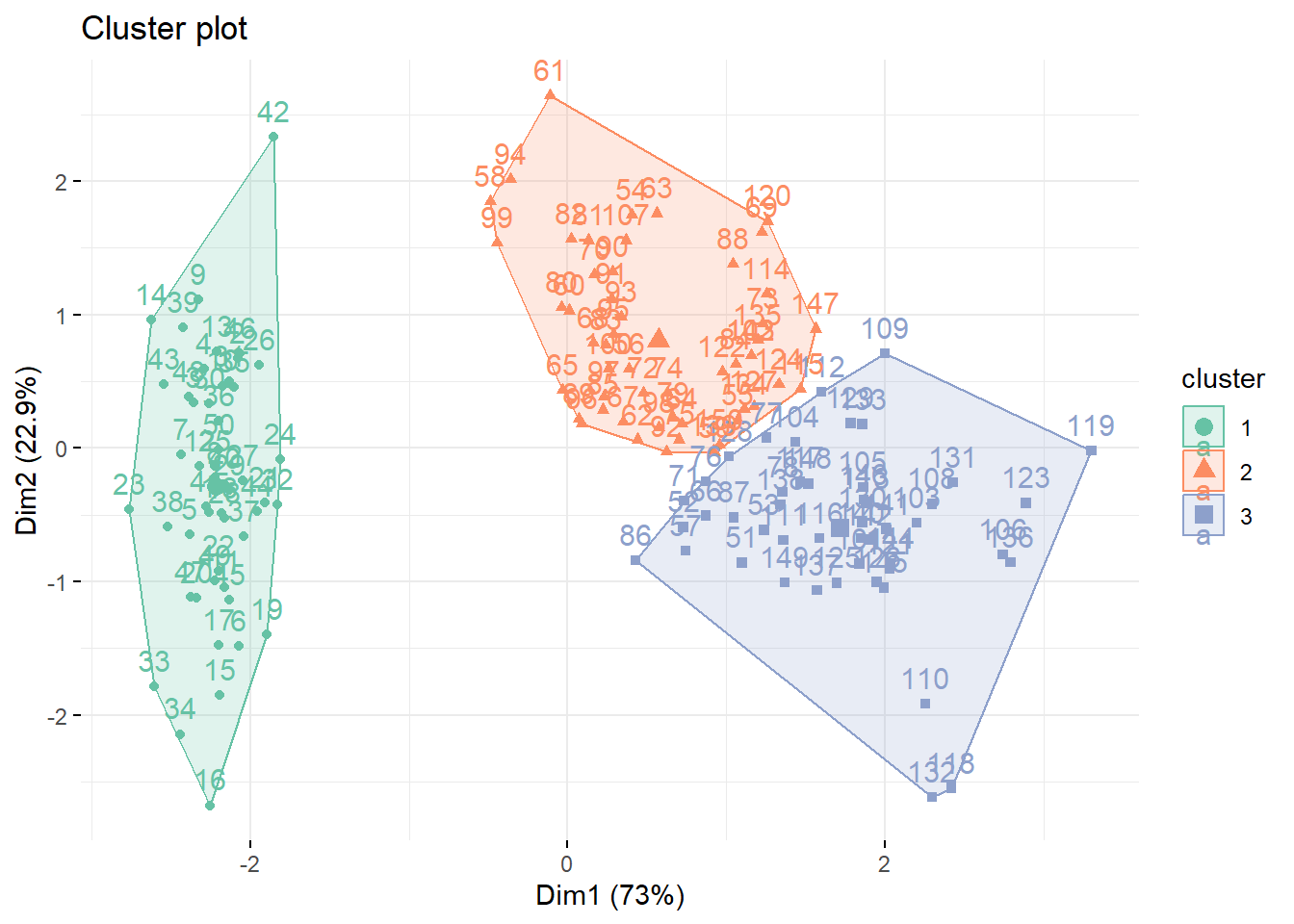

# PAM clustering
# ++++++++++++++++++++
require(cluster)

## Loading required package: cluster

pam.res <- pam(iris.scaled, 3)
 # Visualize pam clustering
fviz_cluster(pam.res, geom = "point", ellipse.type = "norm")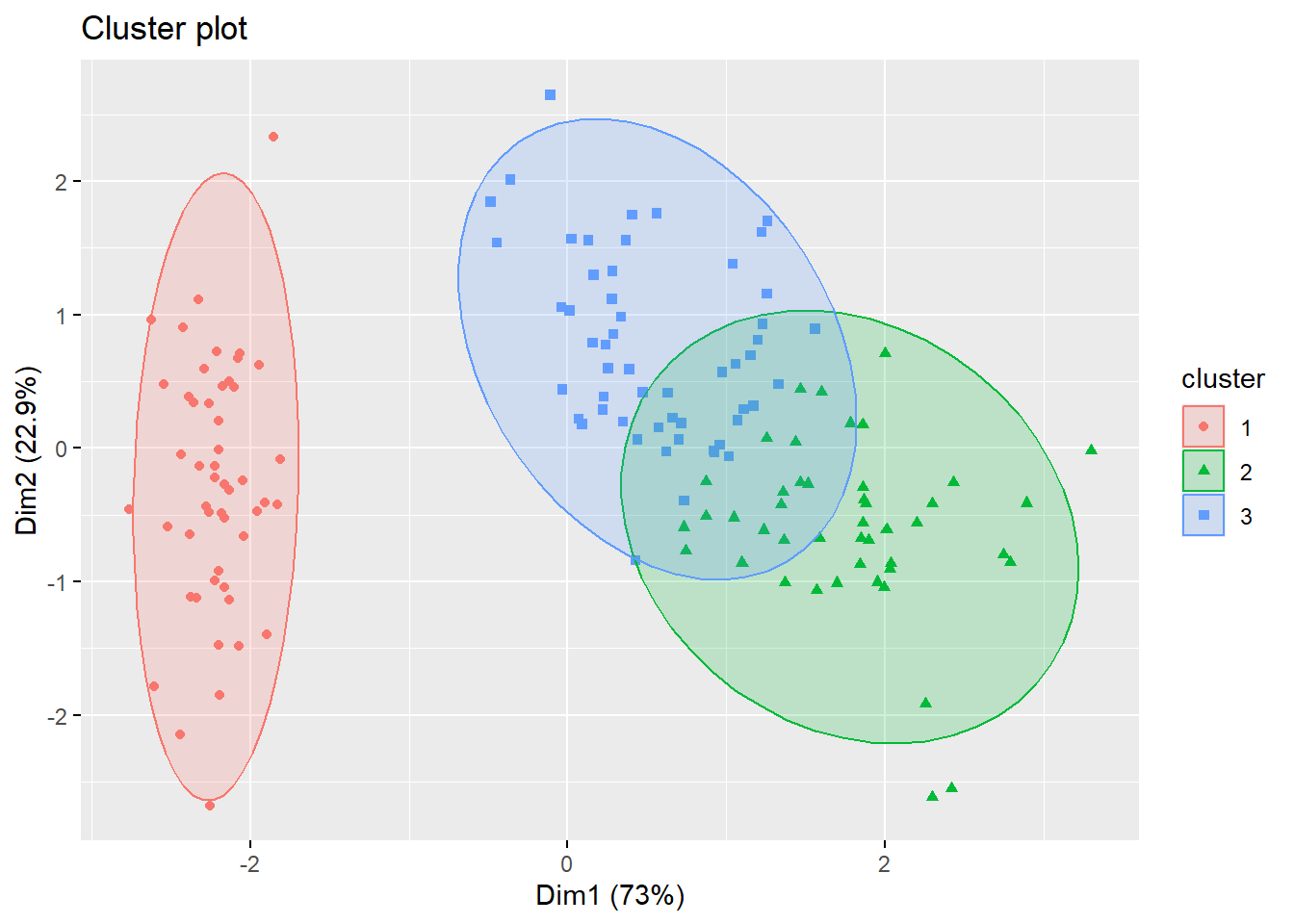

# Hierarchical clustering
# ++++++++++++++++++++++++
# Use hcut() which compute hclust and cut the tree
hc.cut <- hcut(iris.scaled, k = 3, hc_method = "complete")
# Visualize dendrogram
fviz_dend(hc.cut, show_labels = FALSE, rect = TRUE)

## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
## of ggplot2 3.3.4.
## ℹ The deprecated feature was likely used in the factoextra package.
##   Please report the issue at <https://github.com/kassambara/factoextra/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.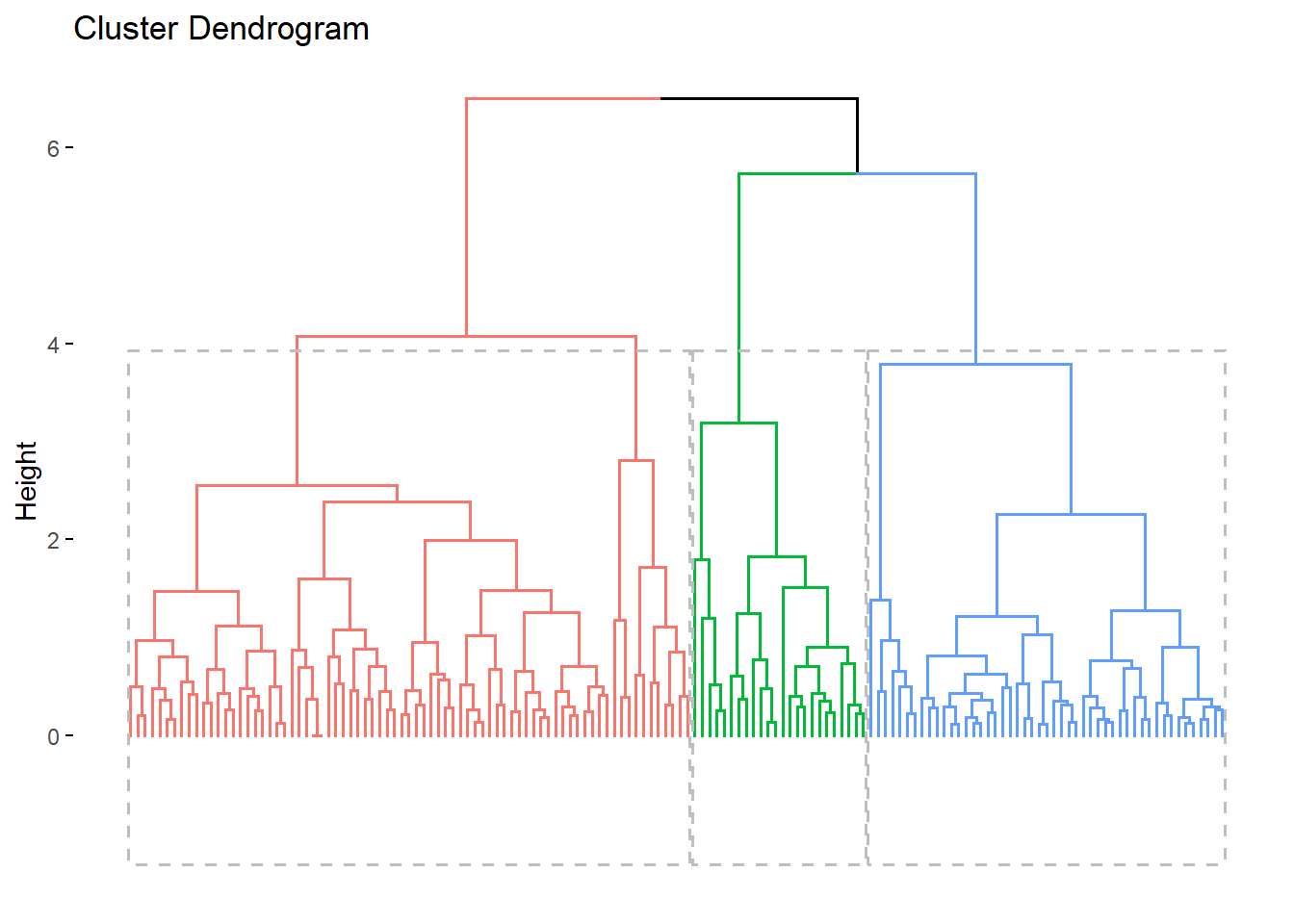

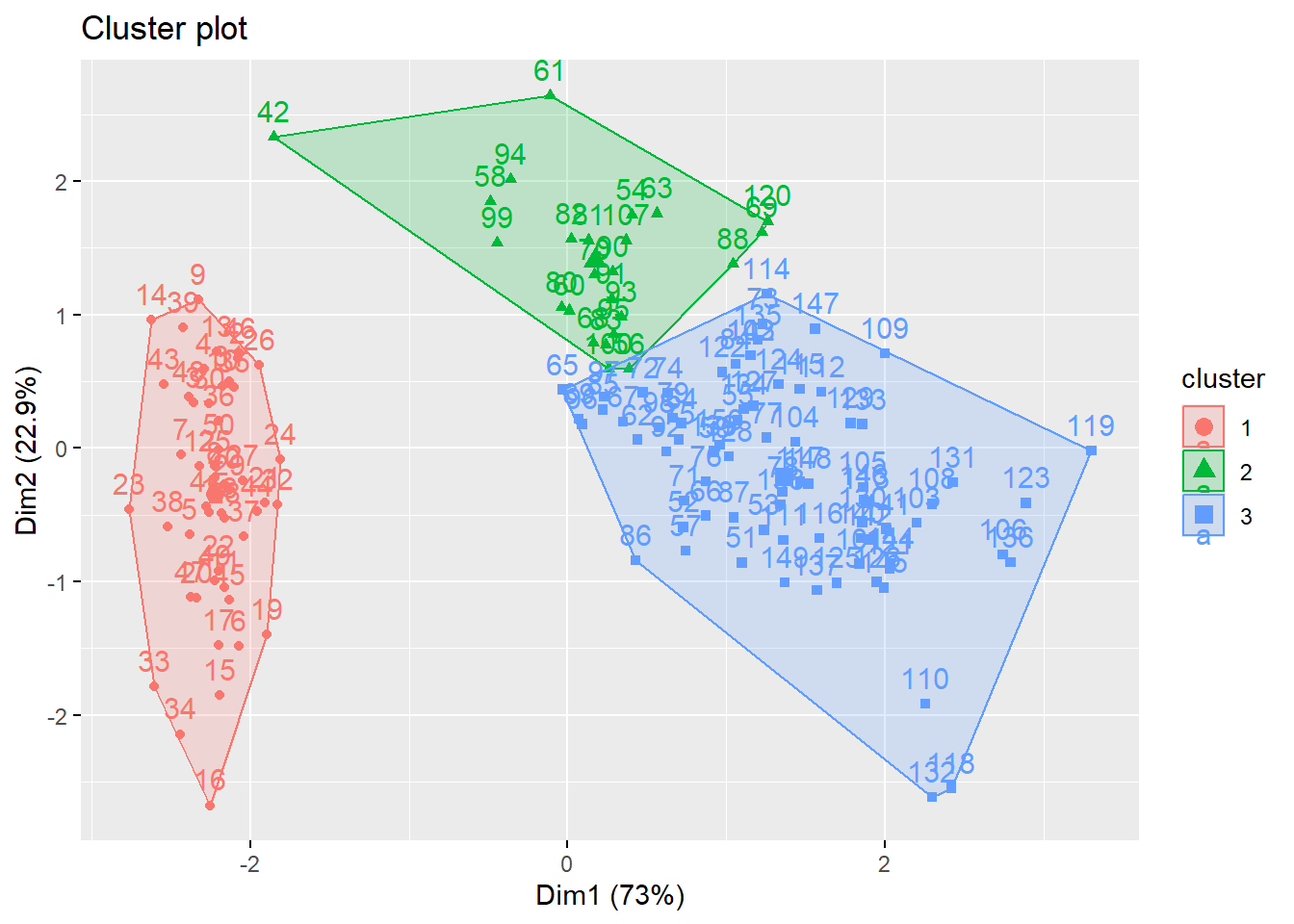
# Visualize cluster
fviz_cluster(hc.cut, ellipse.type = "convex")

6.7 flexclust包

提供了更多的类似k均值的聚类方法并支持可视化。

6.8 案例分析：世界146个国家和地区的人文发展水平聚类

6.8.1 数据

联合国开发计划署《人文发展报告2011》给出了世界146个国家和地区的人文发展水平的8个指标。数据在nationHuman:

nationHuman <- readr::read_csv(
  "data/国家人文聚类.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
knitr::kable(nationHuman)

nation	x1	x2	x3	x4	x5	x6	x7	x8
挪威	0.943	81.1	17.3	12.6	0.985	0.883	0.964	0.075
澳大利亚	0.929	81.9	18.0	12.0	0.981	0.837	0.976	0.136
荷兰	0.910	80.7	16.8	11.6	0.931	0.845	0.958	0.052
美国	0.910	78.5	16.0	12.4	0.939	0.869	0.923	0.299
新西兰	0.908	80.7	18.0	12.5	1.000	0.783	0.957	0.195
加拿大	0.908	81.0	16.0	12.1	0.927	0.840	0.962	0.140
爱尔兰	0.908	80.6	18.0	11.6	0.963	0.814	0.955	0.203
德国	0.905	80.4	15.9	12.2	0.928	0.838	0.953	0.085
瑞典	0.904	81.4	15.7	11.7	0.904	0.842	0.969	0.049
瑞士	0.903	82.3	15.6	11.0	0.872	0.858	0.983	0.067
日本	0.901	83.4	15.1	11.6	0.883	0.827	1.000	0.123
冰岛	0.898	81.8	18.0	10.4	0.912	0.814	0.975	0.099
韩国	0.897	80.6	16.9	11.6	0.934	0.808	0.956	0.111
丹麦	0.895	78.8	16.9	11.4	0.924	0.836	0.928	0.060
以色列	0.888	81.6	15.5	11.9	0.907	0.796	0.972	0.145
比利时	0.886	80.0	16.1	10.9	0.882	0.832	0.947	0.114
奥地利	0.885	80.9	15.3	10.8	0.858	0.842	0.960	0.131
法国	0.884	81.5	16.1	10.6	0.870	0.819	0.971	0.106
斯洛文尼亚	0.884	79.3	16.9	11.6	0.933	0.790	0.936	0.175
芬兰	0.882	80.0	16.8	10.3	0.877	0.828	0.946	0.075
西班牙	0.878	81.4	16.6	10.4	0.874	0.799	0.969	0.117
意大利	0.874	81.9	16.3	10.1	0.856	0.799	0.976	0.124
卢森堡	0.867	80.0	13.3	10.1	0.771	0.892	0.946	0.169
新加坡	0.866	81.1	14.4	8.8	0.751	0.897	0.964	0.086
捷克	0.865	77.7	15.6	12.3	0.924	0.769	0.910	0.136
英国	0.863	80.2	16.1	9.3	0.815	0.832	0.949	0.209
希腊	0.861	79.9	16.5	10.1	0.861	0.783	0.945	0.162
阿联酋	0.846	76.5	13.3	9.3	0.741	0.916	0.892	0.234
塞浦路斯	0.840	79.6	14.7	9.8	0.798	0.790	0.940	0.141
爱沙尼亚	0.835	74.8	15.7	12.0	0.916	0.734	0.865	0.194
斯洛伐克	0.834	75.4	14.9	11.6	0.875	0.759	0.875	0.194
马耳他	0.832	79.6	14.4	9.9	0.797	0.769	0.941	0.272
卡塔尔	0.831	78.4	12.0	7.3	0.623	1.000	0.921	0.549
匈牙利	0.816	74.4	15.3	11.1	0.866	0.732	0.858	0.237
波兰	0.813	76.1	15.3	10.0	0.822	0.739	0.885	0.164
立陶宛	0.810	72.2	16.1	10.9	0.883	0.729	0.824	0.192
葡萄牙	0.809	79.5	15.9	7.7	0.739	0.763	0.938	0.140
巴林	0.806	75.1	13.4	9.4	0.747	0.808	0.868	0.288
拉脱维亚	0.805	73.3	15.0	11.5	0.873	0.711	0.841	0.216
智利	0.805	79.1	14.7	9.7	0.797	0.701	0.932	0.374
阿根廷	0.797	75.9	15.8	9.3	0.806	0.713	0.882	0.372
克罗地亚	0.796	76.6	13.9	9.8	0.778	0.724	0.893	0.170
巴巴多斯	0.793	76.8	13.4	9.3	0.747	0.743	0.896	0.364
乌拉圭	0.783	77.0	15.5	8.5	0.763	0.700	0.899	0.352
罗马尼亚	0.781	74.0	14.9	10.4	0.831	0.674	0.851	0.333
古巴	0.776	79.1	17.5	9.9	0.876	0.572	0.933	0.337
巴哈马	0.771	75.6	12.0	8.5	0.671	0.779	0.877	0.332
保加利亚	0.771	73.4	13.7	10.6	0.802	0.678	0.842	0.245
沙特阿拉伯	0.770	73.9	13.7	7.8	0.689	0.781	0.850	0.646
墨西哥	0.770	77.0	13.9	8.5	0.726	0.700	0.898	0.448
巴拿马	0.768	76.1	13.2	9.4	0.743	0.690	0.885	0.492
马来西亚	0.761	74.2	12.6	9.5	0.730	0.704	0.855	0.286
特立尼达和多巴哥	0.760	70.1	12.3	9.2	0.712	0.782	0.791	0.331
科威特	0.760	74.6	12.3	6.1	0.577	0.884	0.861	0.229
利比亚	0.760	74.8	16.6	7.3	0.731	0.693	0.864	0.314
俄罗斯联邦	0.755	68.8	14.1	9.8	0.784	0.713	0.770	0.338
哈萨克斯坦	0.745	67.0	15.1	10.4	0.834	0.668	0.742	0.334
哥斯达黎加	0.744	79.3	11.7	8.3	0.659	0.667	0.936	0.361
阿尔巴尼亚	0.739	76.9	11.3	10.4	0.721	0.624	0.898	0.271
黎巴嫩	0.739	72.6	13.8	7.9	0.695	0.698	0.830	0.440
委内瑞拉	0.735	74.4	14.2	7.6	0.692	0.669	0.858	0.447
格鲁吉亚	0.733	73.7	13.1	12.1	0.839	0.554	0.848	0.418
乌克兰	0.729	68.5	14.7	11.3	0.858	0.591	0.765	0.335
毛里求斯	0.728	73.4	13.6	7.2	0.659	0.696	0.842	0.353
前南马其顿	0.728	74.8	13.3	8.2	0.696	0.641	0.865	0.151
牙买加	0.727	73.1	13.8	9.6	0.768	0.598	0.838	0.450
秘鲁	0.725	74.0	12.9	8.7	0.704	0.634	0.852	0.415
厄瓜多尔	0.720	75.6	14.0	7.6	0.686	0.620	0.877	0.469
巴西	0.718	73.5	13.8	7.2	0.663	0.662	0.844	0.449
亚美尼亚	0.716	74.2	12.0	10.8	0.760	0.566	0.856	0.343
哥伦比亚	0.710	73.7	13.6	7.3	0.667	0.633	0.847	0.482
伊朗	0.707	73.0	12.7	7.3	0.640	0.662	0.836	0.485
阿曼	0.705	73.0	11.8	5.5	0.539	0.778	0.836	0.309
阿塞拜疆	0.700	70.7	11.8	8.6	0.671	0.639	0.800	0.314
土耳其	0.699	74.0	11.8	6.5	0.583	0.689	0.851	0.443
伯利兹	0.699	76.1	12.4	8.0	0.663	0.582	0.884	0.493
突尼斯	0.698	74.5	14.5	6.5	0.645	0.614	0.860	0.293
约旦	0.698	73.4	13.1	8.6	0.710	0.569	0.842	0.456
阿尔及利亚	0.698	73.1	13.6	7.0	0.652	0.621	0.838	0.412
斯里兰卡	0.691	74.9	12.7	8.2	0.680	0.559	0.867	0.419
多米尼加	0.689	73.4	11.9	7.2	0.616	0.629	0.842	0.480
中国	0.687	73.5	11.6	7.5	0.623	0.618	0.843	0.209
泰国	0.682	74.1	12.3	6.6	0.597	0.622	0.854	0.382
萨尔瓦多	0.674	72.2	12.1	7.5	0.637	0.585	0.823	0.487
加蓬	0.674	62.7	13.1	7.5	0.660	0.689	0.674	0.509
巴拉圭	0.665	72.5	12.1	7.7	0.643	0.552	0.828	0.476
玻利维亚	0.663	66.6	13.7	9.2	0.749	0.530	0.735	0.476
马尔代夫	0.661	76.8	12.4	5.8	0.568	0.568	0.897	0.320
蒙古	0.653	68.5	14.1	8.3	0.722	0.505	0.765	0.410
摩尔多瓦	0.649	69.3	11.9	9.7	0.716	0.490	0.778	0.298
菲律宾	0.644	68.7	11.9	8.9	0.684	0.508	0.769	0.427
圭亚那	0.633	69.9	11.9	8.0	0.650	0.496	0.787	0.511
博茨瓦纳	0.633	53.2	12.2	8.9	0.693	0.698	0.523	0.507
叙利亚	0.632	75.8	11.3	5.7	0.534	0.537	0.881	0.474
纳米比亚	0.625	62.5	11.6	7.4	0.617	0.591	0.670	0.466
洪都拉斯	0.625	73.1	11.4	6.5	0.574	0.507	0.838	0.511
南非	0.619	52.8	13.1	8.5	0.705	0.652	0.517	0.490
印度尼西亚	0.617	69.4	13.2	5.8	0.584	0.518	0.779	0.505
吉尔吉斯斯坦	0.615	67.7	12.5	9.3	0.716	0.432	0.753	0.370
塔吉克斯坦	0.607	67.5	11.4	9.8	0.704	0.425	0.750	0.347
越南	0.593	75.2	10.4	5.5	0.503	0.478	0.870	0.305
尼加拉瓜	0.589	74.0	10.8	5.8	0.525	0.457	0.852	0.506
摩洛哥	0.582	72.2	10.3	4.4	0.447	0.535	0.823	0.510
危地马拉	0.574	71.2	10.6	4.1	0.438	0.534	0.807	0.542
伊拉克	0.573	69.0	9.8	5.6	0.491	0.495	0.774	0.579
印度	0.547	65.4	10.3	4.4	0.450	0.508	0.717	0.617
加纳	0.541	64.2	10.5	7.1	0.574	0.396	0.698	0.598
刚果(布)	0.533	57.4	10.5	5.9	0.523	0.490	0.590	0.628
老挝	0.524	67.5	9.2	4.6	0.432	0.445	0.749	0.513
柬埔寨	0.523	63.1	9.8	5.8	0.502	0.418	0.680	0.500
斯威士兰	0.522	48.7	10.6	7.1	0.578	0.545	0.453	0.546
不丹	0.522	67.2	11.0	2.3	0.336	0.568	0.744	0.495
肯尼亚	0.509	57.1	11.0	7.0	0.582	0.387	0.586	0.627
巴基斯坦	0.504	65.4	6.9	4.9	0.386	0.464	0.717	0.573
孟加拉国	0.500	68.9	8.1	4.8	0.415	0.391	0.772	0.550
缅甸	0.483	65.2	9.2	4.0	0.404	0.391	0.713	0.492
喀麦隆	0.482	51.6	10.3	5.9	0.520	0.431	0.499	0.639
坦桑尼亚	0.466	58.2	9.1	5.1	0.454	0.370	0.603	0.590
巴布亚新几内亚	0.466	62.8	5.8	4.3	0.335	0.447	0.675	0.674
也门	0.462	65.5	8.6	2.5	0.310	0.444	0.718	0.769
塞内加尔	0.459	59.3	7.5	4.5	0.385	0.406	0.620	0.566
尼泊尔	0.458	68.8	8.8	3.2	0.356	0.351	0.770	0.558
海地	0.454	62.1	7.6	4.9	0.406	0.346	0.664	0.599
毛里塔尼亚	0.453	58.6	8.1	3.7	0.366	0.419	0.609	0.605
莱索托	0.450	48.2	9.9	5.9	0.507	0.403	0.445	0.532
乌干达	0.446	54.1	10.8	4.7	0.475	0.347	0.538	0.577
多哥	0.435	57.1	9.6	5.3	0.473	0.297	0.585	0.602
赞比亚	0.430	49.0	7.9	6.5	0.480	0.362	0.458	0.627
卢旺达	0.429	55.4	11.1	3.3	0.407	0.348	0.559	0.453
贝宁	0.427	56.1	9.2	3.3	0.365	0.374	0.569	0.634
冈比亚	0.420	58.5	9.0	2.8	0.334	0.365	0.607	0.610
苏丹	0.408	61.5	4.4	3.1	0.247	0.421	0.654	0.611
科特迪瓦	0.400	55.4	6.3	3.3	0.304	0.377	0.558	0.655
马拉维	0.400	54.2	8.9	4.2	0.410	0.289	0.540	0.594
阿富汗	0.398	48.7	9.1	3.3	0.367	0.380	0.452	0.707
津巴布韦	0.376	51.4	9.9	7.2	0.566	0.190	0.495	0.583
马里	0.359	51.4	8.3	2.0	0.270	0.346	0.496	0.712
中非	0.343	48.4	6.6	3.5	0.321	0.280	0.448	0.669
塞拉利昂	0.336	47.8	7.2	2.9	0.304	0.286	0.438	0.662
布基纳法索	0.331	55.4	6.3	1.3	0.187	0.349	0.559	0.596
利比里亚	0.329	56.8	11.0	3.9	0.439	0.140	0.580	0.671
乍得	0.328	49.6	7.2	1.5	0.219	0.344	0.466	0.735
莫桑比克	0.322	50.2	9.2	1.2	0.222	0.314	0.477	0.602
布隆迪	0.316	50.4	10.5	2.7	0.353	0.186	0.480	0.478
尼日尔	0.295	54.7	4.9	1.4	0.177	0.266	0.547	0.724
刚果(金)	0.286	48.4	8.2	3.5	0.356	0.147	0.448	0.710

简单概括：

str(nationHuman)

## spc_tbl_ [146 × 9] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ nation: chr [1:146] "挪威" "澳大利亚" "荷兰" "美国" ...
##  $ x1    : num [1:146] 0.943 0.929 0.91 0.91 0.908 0.908 0.908 0.905 0.904 0.903 ...
##  $ x2    : num [1:146] 81.1 81.9 80.7 78.5 80.7 81 80.6 80.4 81.4 82.3 ...
##  $ x3    : num [1:146] 17.3 18 16.8 16 18 16 18 15.9 15.7 15.6 ...
##  $ x4    : num [1:146] 12.6 12 11.6 12.4 12.5 12.1 11.6 12.2 11.7 11 ...
##  $ x5    : num [1:146] 0.985 0.981 0.931 0.939 1 0.927 0.963 0.928 0.904 0.872 ...
##  $ x6    : num [1:146] 0.883 0.837 0.845 0.869 0.783 0.84 0.814 0.838 0.842 0.858 ...
##  $ x7    : num [1:146] 0.964 0.976 0.958 0.923 0.957 0.962 0.955 0.953 0.969 0.983 ...
##  $ x8    : num [1:146] 0.075 0.136 0.052 0.299 0.195 0.14 0.203 0.085 0.049 0.067 ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   nation = col_character(),
##   ..   x1 = col_double(),
##   ..   x2 = col_double(),
##   ..   x3 = col_double(),
##   ..   x4 = col_double(),
##   ..   x5 = col_double(),
##   ..   x6 = col_double(),
##   ..   x7 = col_double(),
##   ..   x8 = col_double()
##   .. )
##  - attr(*, "problems")=<externalptr>

summary(nationHuman)

##     nation                x1               x2              x3       
##  Length:146         Min.   :0.2860   Min.   :47.80   Min.   : 4.40  
##  Class :character   1st Qu.:0.5232   1st Qu.:64.45   1st Qu.:10.50  
##  Mode  :character   Median :0.7025   Median :73.40   Median :12.65  
##                     Mean   :0.6707   Mean   :69.93   Mean   :12.51  
##                     3rd Qu.:0.8083   3rd Qu.:76.88   3rd Qu.:14.90  
##                     Max.   :0.9430   Max.   :83.40   Max.   :18.00  
##        x4               x5               x6               x7        
##  Min.   : 1.200   Min.   :0.1770   Min.   :0.1400   Min.   :0.4380  
##  1st Qu.: 5.625   1st Qu.:0.5022   1st Qu.:0.4455   1st Qu.:0.7017  
##  Median : 7.950   Median :0.6820   Median :0.6230   Median :0.8420  
##  Mean   : 7.718   Mean   :0.6499   Mean   :0.6025   Mean   :0.7877  
##  3rd Qu.:10.075   3rd Qu.:0.8050   3rd Qu.:0.7675   3rd Qu.:0.8978  
##  Max.   :12.600   Max.   :1.0000   Max.   :1.0000   Max.   :1.0000  
##        x8        
##  Min.   :0.0490  
##  1st Qu.:0.2303  
##  Median :0.4185  
##  Mean   :0.3942  
##  3rd Qu.:0.5450  
##  Max.   :0.7690

因为各列不可比，所以做每列标准化。

d <- scale(nationHuman[,-1])
rownames(d) <- nationHuman[["nation"]]

6.8.2 聚类

指定4个类，用k均值方法聚类。

k <- 4
res1 <- kmeans(d, centers=k, nstart=20)

因为有随机中心，所以重复运行会使得类不变但是类号改变。按类中心的8个指标平均值降序排序为类号次序。

library(forcats)
xmean <- rowMeans(d)
cl.new <- res1$cluster
cl.new[] <- as.integer(fct_reorder(
  factor(cl.new), xmean, mean, .desc=TRUE))
knitr::kable(as.data.frame(sort(cl.new)))

	sort(cl.new)
挪威	1
澳大利亚	1
荷兰	1
美国	1
新西兰	1
加拿大	1
爱尔兰	1
德国	1
瑞典	1
瑞士	1
日本	1
冰岛	1
韩国	1
丹麦	1
以色列	1
比利时	1
奥地利	1
法国	1
斯洛文尼亚	1
芬兰	1
西班牙	1
意大利	1
卢森堡	1
新加坡	1
捷克	1
英国	1
希腊	1
阿联酋	1
塞浦路斯	1
爱沙尼亚	1
斯洛伐克	1
马耳他	1
匈牙利	1
波兰	1
立陶宛	1
葡萄牙	1
拉脱维亚	1
克罗地亚	1
古巴	1
卡塔尔	2
巴林	2
智利	2
阿根廷	2
巴巴多斯	2
乌拉圭	2
罗马尼亚	2
巴哈马	2
保加利亚	2
沙特阿拉伯	2
墨西哥	2
巴拿马	2
马来西亚	2
特立尼达和多巴哥	2
科威特	2
利比亚	2
俄罗斯联邦	2
哈萨克斯坦	2
哥斯达黎加	2
阿尔巴尼亚	2
黎巴嫩	2
委内瑞拉	2
格鲁吉亚	2
乌克兰	2
毛里求斯	2
前南马其顿	2
牙买加	2
秘鲁	2
厄瓜多尔	2
巴西	2
亚美尼亚	2
哥伦比亚	2
伊朗	2
阿曼	2
阿塞拜疆	2
土耳其	2
伯利兹	2
突尼斯	2
约旦	2
阿尔及利亚	2
斯里兰卡	2
多米尼加	2
中国	2
泰国	2
萨尔瓦多	2
加蓬	2
巴拉圭	2
玻利维亚	2
马尔代夫	2
蒙古	2
摩尔多瓦	2
菲律宾	2
吉尔吉斯斯坦	2
塔吉克斯坦	2
圭亚那	3
博茨瓦纳	3
叙利亚	3
纳米比亚	3
洪都拉斯	3
南非	3
印度尼西亚	3
越南	3
尼加拉瓜	3
摩洛哥	3
危地马拉	3
伊拉克	3
印度	3
加纳	3
刚果(布)	3
老挝	3
柬埔寨	3
不丹	3
肯尼亚	3
巴基斯坦	3
孟加拉国	3
缅甸	3
尼泊尔	3
斯威士兰	4
喀麦隆	4
坦桑尼亚	4
巴布亚新几内亚	4
也门	4
塞内加尔	4
海地	4
毛里塔尼亚	4
莱索托	4
乌干达	4
多哥	4
赞比亚	4
卢旺达	4
贝宁	4
冈比亚	4
苏丹	4
科特迪瓦	4
马拉维	4
阿富汗	4
津巴布韦	4
马里	4
中非	4
塞拉利昂	4
布基纳法索	4
利比里亚	4
乍得	4
莫桑比克	4
布隆迪	4
尼日尔	4
刚果(金)	4

sort(cl.new)

##             挪威         澳大利亚             荷兰             美国 
##                1                1                1                1 
##           新西兰           加拿大           爱尔兰             德国 
##                1                1                1                1 
##             瑞典             瑞士             日本             冰岛 
##                1                1                1                1 
##             韩国             丹麦           以色列           比利时 
##                1                1                1                1 
##           奥地利             法国       斯洛文尼亚             芬兰 
##                1                1                1                1 
##           西班牙           意大利           卢森堡           新加坡 
##                1                1                1                1 
##             捷克             英国             希腊           阿联酋 
##                1                1                1                1 
##         塞浦路斯         爱沙尼亚         斯洛伐克           马耳他 
##                1                1                1                1 
##           匈牙利             波兰           立陶宛           葡萄牙 
##                1                1                1                1 
##         拉脱维亚         克罗地亚             古巴           卡塔尔 
##                1                1                1                2 
##             巴林             智利           阿根廷         巴巴多斯 
##                2                2                2                2 
##           乌拉圭         罗马尼亚           巴哈马         保加利亚 
##                2                2                2                2 
##       沙特阿拉伯           墨西哥           巴拿马         马来西亚 
##                2                2                2                2 
## 特立尼达和多巴哥           科威特           利比亚       俄罗斯联邦 
##                2                2                2                2 
##       哈萨克斯坦       哥斯达黎加       阿尔巴尼亚           黎巴嫩 
##                2                2                2                2 
##         委内瑞拉         格鲁吉亚           乌克兰         毛里求斯 
##                2                2                2                2 
##       前南马其顿           牙买加             秘鲁         厄瓜多尔 
##                2                2                2                2 
##             巴西         亚美尼亚         哥伦比亚             伊朗 
##                2                2                2                2 
##             阿曼         阿塞拜疆           土耳其           伯利兹 
##                2                2                2                2 
##           突尼斯             约旦       阿尔及利亚         斯里兰卡 
##                2                2                2                2 
##         多米尼加             中国             泰国         萨尔瓦多 
##                2                2                2                2 
##             加蓬           巴拉圭         玻利维亚         马尔代夫 
##                2                2                2                2 
##             蒙古         摩尔多瓦           菲律宾     吉尔吉斯斯坦 
##                2                2                2                2 
##       塔吉克斯坦           圭亚那         博茨瓦纳           叙利亚 
##                2                3                3                3 
##         纳米比亚         洪都拉斯             南非       印度尼西亚 
##                3                3                3                3 
##             越南         尼加拉瓜           摩洛哥         危地马拉 
##                3                3                3                3 
##           伊拉克             印度             加纳         刚果(布) 
##                3                3                3                3 
##             老挝           柬埔寨             不丹           肯尼亚 
##                3                3                3                3 
##         巴基斯坦         孟加拉国             缅甸           尼泊尔 
##                3                3                3                3 
##         斯威士兰           喀麦隆         坦桑尼亚   巴布亚新几内亚 
##                4                4                4                4 
##             也门         塞内加尔             海地       毛里塔尼亚 
##                4                4                4                4 
##           莱索托           乌干达             多哥           赞比亚 
##                4                4                4                4 
##           卢旺达             贝宁           冈比亚             苏丹 
##                4                4                4                4 
##         科特迪瓦           马拉维           阿富汗         津巴布韦 
##                4                4                4                4 
##             马里             中非         塞拉利昂       布基纳法索 
##                4                4                4                4 
##         利比里亚             乍得         莫桑比克           布隆迪 
##                4                4                4                4 
##           尼日尔         刚果(金) 
##                4                4

上面显示了重排后的分类号。

6.8.3 用系统聚类

刚才数据已经标准化。

计算欧式距离：

load('nationHuman.RData')
d <- scale(nationHuman[,-1])
rownames(d) <- nationHuman[["nation"]]
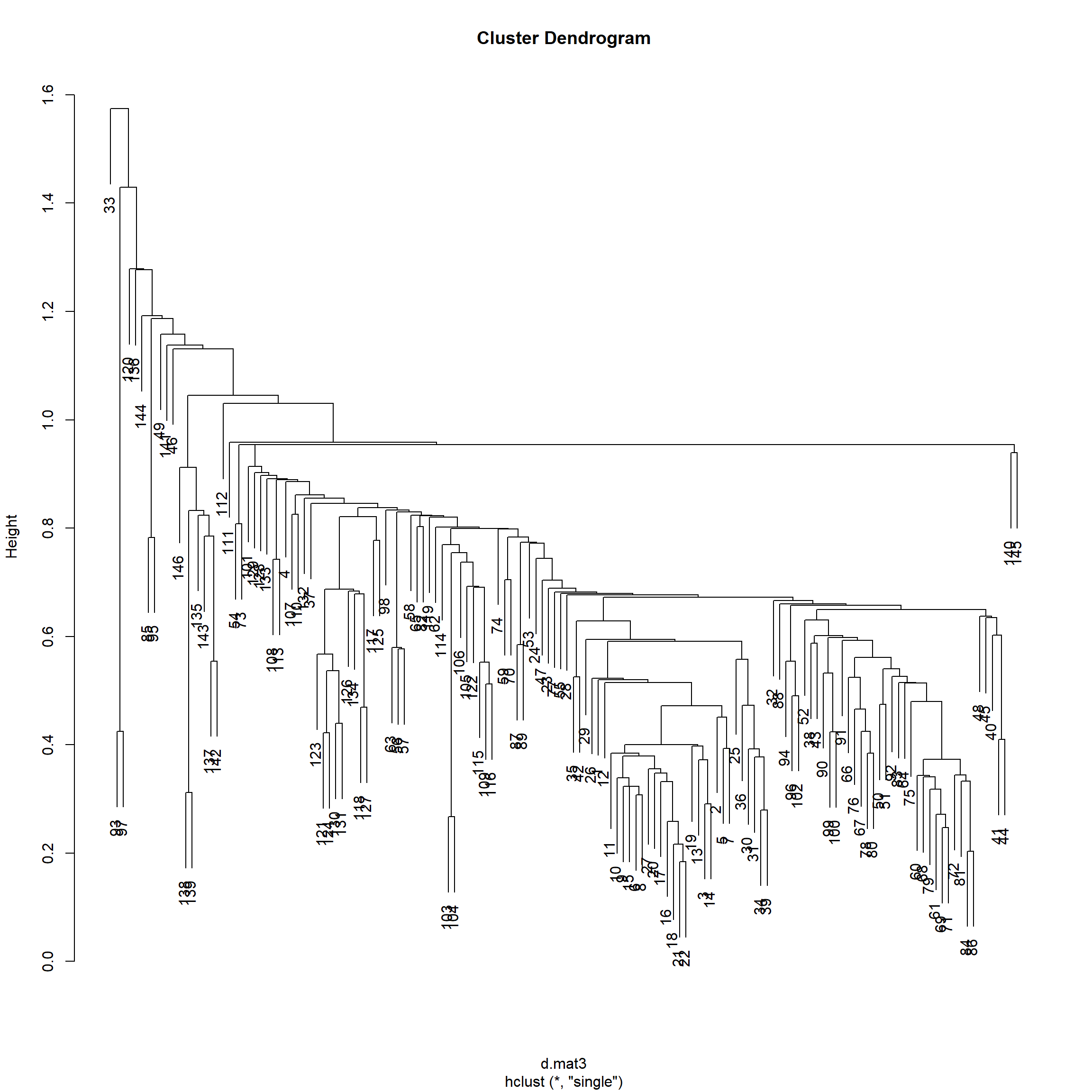
d.mat3 <- dist(d, method='euclidean')

用最短距离法作系统聚类：

res3 <- hclust(d.mat3, method='single'); res3

## 
## Call:
## hclust(d = d.mat3, method = "single")
## 
## Cluster method   : single 
## Distance         : euclidean 
## Number of objects: 146

聚类树状图：

plot(res3)

6.9 聚类个数的选择方法

这部分内容选自

Susan Holmes, Wolfgang Huber(2019) Modern Statistics for Modern Biology： https://www.huber.embl.de/msmb/index.html

聚类算法只是一种算法，即使所有观测属于一类，聚类算法也可以将其分为几个类，只不过类间距离可能比较近。需要设法相对较客观地验证分类是否合理。

6.9.1 用组内平方距离和

一种思路是类似方差分析，要求分类结果使得类间距离大，类内观测之间距离小。比如，定义WSS(组内平方距离之和)： $\text{WSS}_k = \sum_{\ell=1}^k \sum_{x_i \in C_{\ell}} d^2(x_i, \bar x_{\ell})$ 其中 $k$ 是类的个数， $C_{\ell}$ 表示第 $\ell$ 个类的观测集合， $\bar x_{\ell}$ 是第 $\ell$ 个类的重心。

可以在不同的 $k$ 之间比较 $\text{WSS}_k$ 的值，当然，分类越多这个值越小， $\text{WSS}_k$ 是 $k$ 的减函数，在其减小很快的时候应继续多分类，但是减小很慢的时候就不应该继续分类了，找到这样的“拐点”就可以确定类的个数。

$\text{WSS}_k$ 的另一种等价定义是： $\text{WSS}_k = \sum_{\ell=1}^k \frac{1}{2 n_{\ell}} \sum_{x_i \in C_{\ell}} \sum_{x_j \in C_{\ell}} d^2(x_i, x_j)$

6.9.2 组内平方距离和的模拟

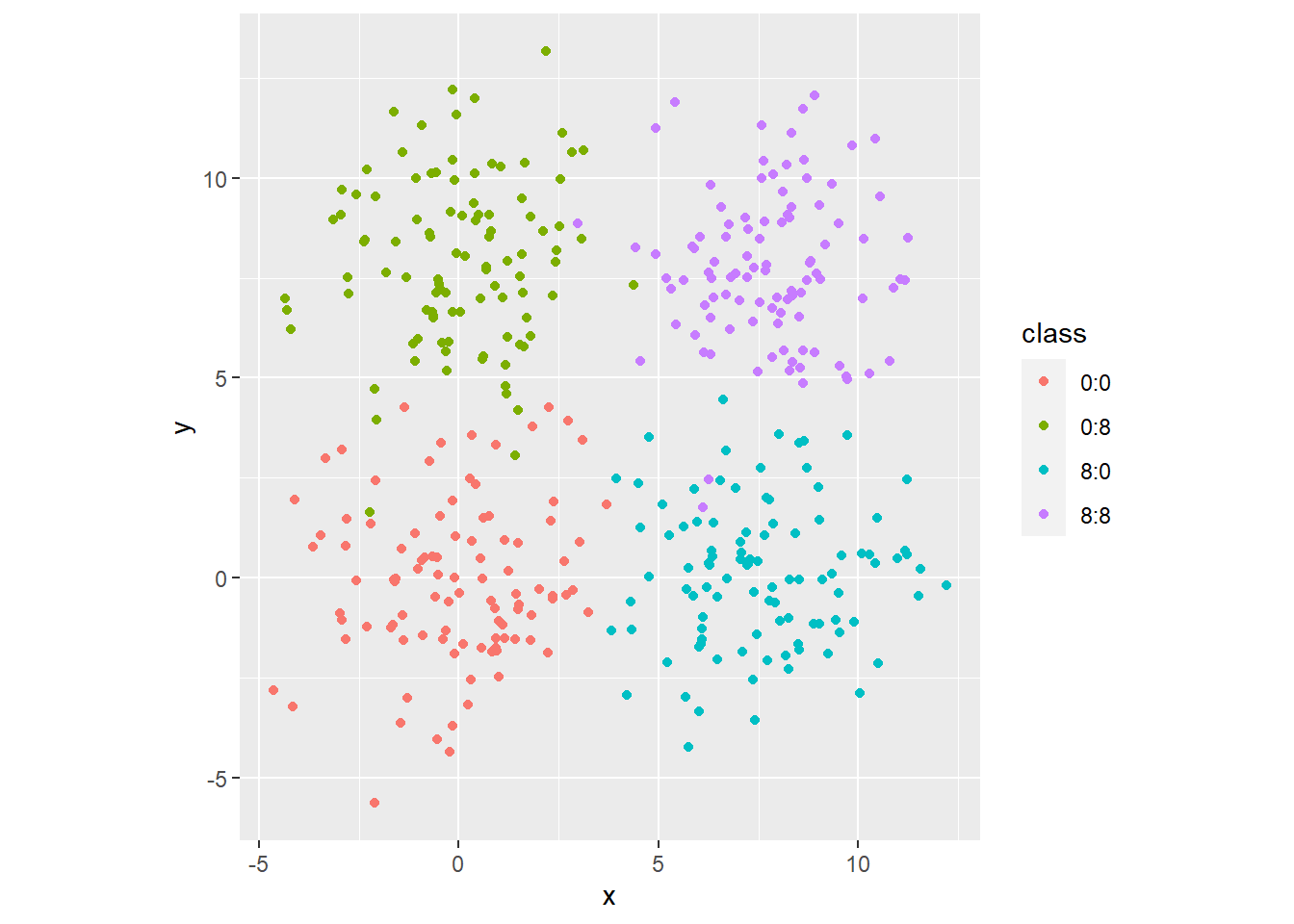
在研究分类问题时，计算一些已知类别的数据的聚类会有一定指导意义。下面是一个模拟已知类别的数据：

set.seed(101)
simdatn <- expand_grid(
  mx=c(0,8), my=c(0,8)) %>%
  mutate(data = pmap(
    ., ~ tibble(
    x = rnorm(100, mean = .x, sd = 2),
    y = rnorm(100, mean = .y, sd = 2),
    class = paste(.x, .y, sep = ":")))) %>%
  unnest(data)
simdatnxy <- simdatn %>%
  dplyr::select(x, y)
simdatn

## # A tibble: 400 × 5
##       mx    my      x      y class
##    <dbl> <dbl>  <dbl>  <dbl> <chr>
##  1     0     0 -0.652  0.536 0:0  
##  2     0     0  1.10  -1.18  0:0  
##  3     0     0 -1.35   4.27  0:0  
##  4     0     0  0.429  2.35  0:0  
##  5     0     0  0.622  1.49  0:0  
##  6     0     0  2.35  -0.461 0:0  
##  7     0     0  1.24   0.176 0:0  
##  8     0     0 -0.225 -4.37  0:0  
##  9     0     0  1.83  -0.933 0:0  
## 10     0     0 -0.447  3.37  0:0  
## # … with 390 more rows

上述程序生成四个二维正态的混合分布数据。用真实类别染色的散点图：

ggplot(data = simdatn, mapping = aes(
  x = x, y = y, col = class)) + 
  geom_point() +
  coord_fixed()

用k均值方法指定不同类别数分别聚类，计算相应的WSS值。 kmeans()函数结果中的withinss就是每个类的类内平方和值：

wss <- tibble(k = 1:8) %>%
  mutate(
    value = map_dbl(k, function(i) {
      if(i==1) {
        sum(scale(simdatnxy, scale = FALSE)^2)
      } else {
        km  = kmeans(simdatnxy, centers = i)
        sum(km$withinss)
      }
    })
  )
ggplot(data = wss, mapping = aes(
  x = k, y = value)) + 
  geom_col()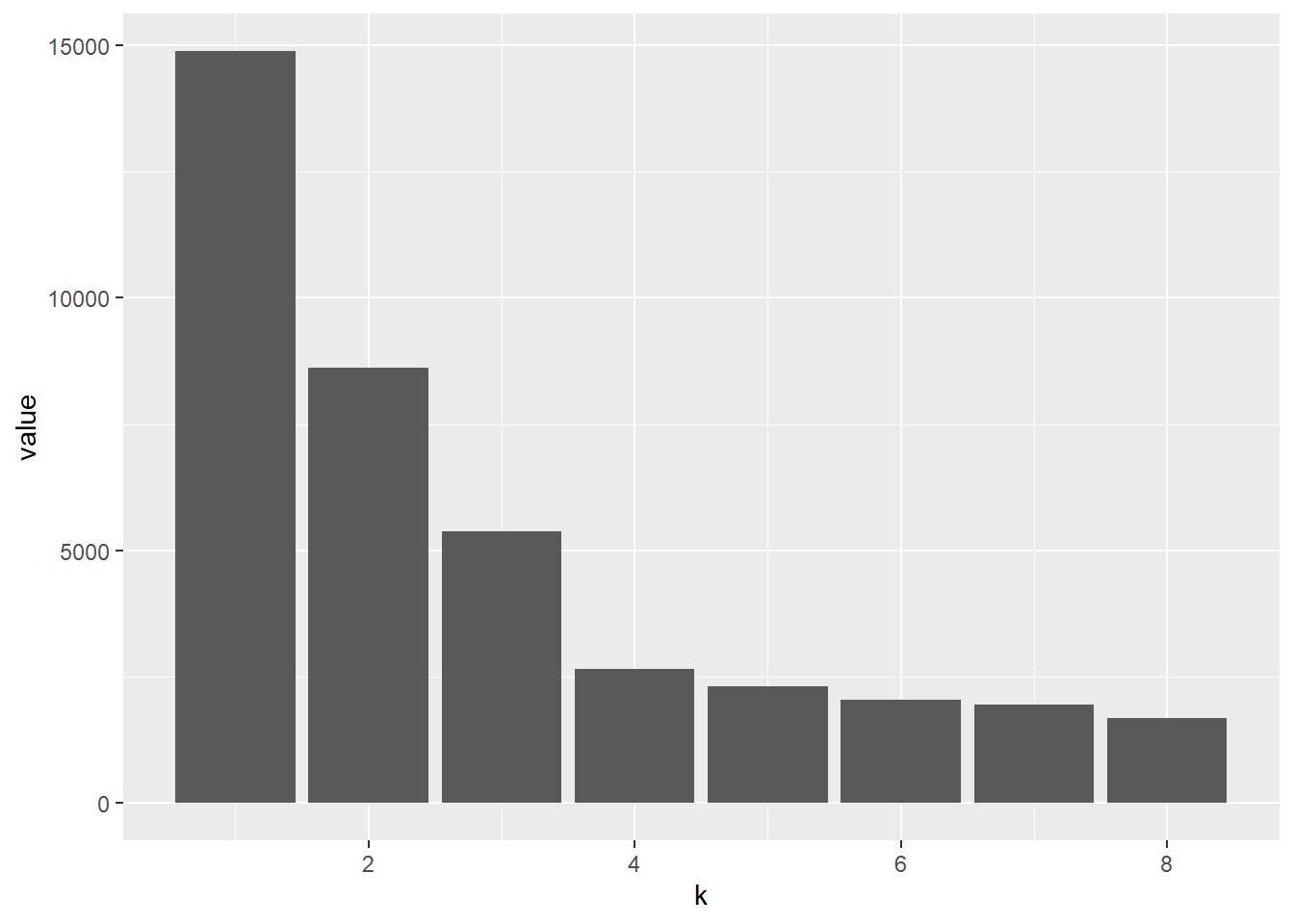

上述程序更容易理解的写法：

wss = tibble(k = 1:8, value = NA_real_)
wss$value[1] = sum(scale(simdatnxy, scale = FALSE)^2)
for (i in 2:nrow(wss)) {
  km  = kmeans(simdatnxy, centers = wss$k[i])
  wss$value[i] = sum(km$withinss)
}
ggplot(data = wss, mapping = aes(
  x = k, y = value)) + 
  geom_col()

可以看出，从1到2，从2到3，从3到4都有较大的WSS下降，但是从4再增加类数就没有多少WSS下降了。

下面将分布改成均匀分布：

set.seed(101)
simdat <- expand_grid(
  mx=c(0,8), my=c(0,8)) %>%
  mutate(data = pmap(
    ., ~ tibble(
    x = runif(100, .x - 4, .x + 4),
    y = runif(100, .y - 4, .y + 4),
    class = paste(.x, .y, sep = ":")))) %>%
  unnest(data)
simdatxy <- simdat %>%
  dplyr::select(x, y)

ggplot(data = simdat, mapping = aes(
  x = x, y = y, col = class)) + 
  geom_point() +
  coord_fixed()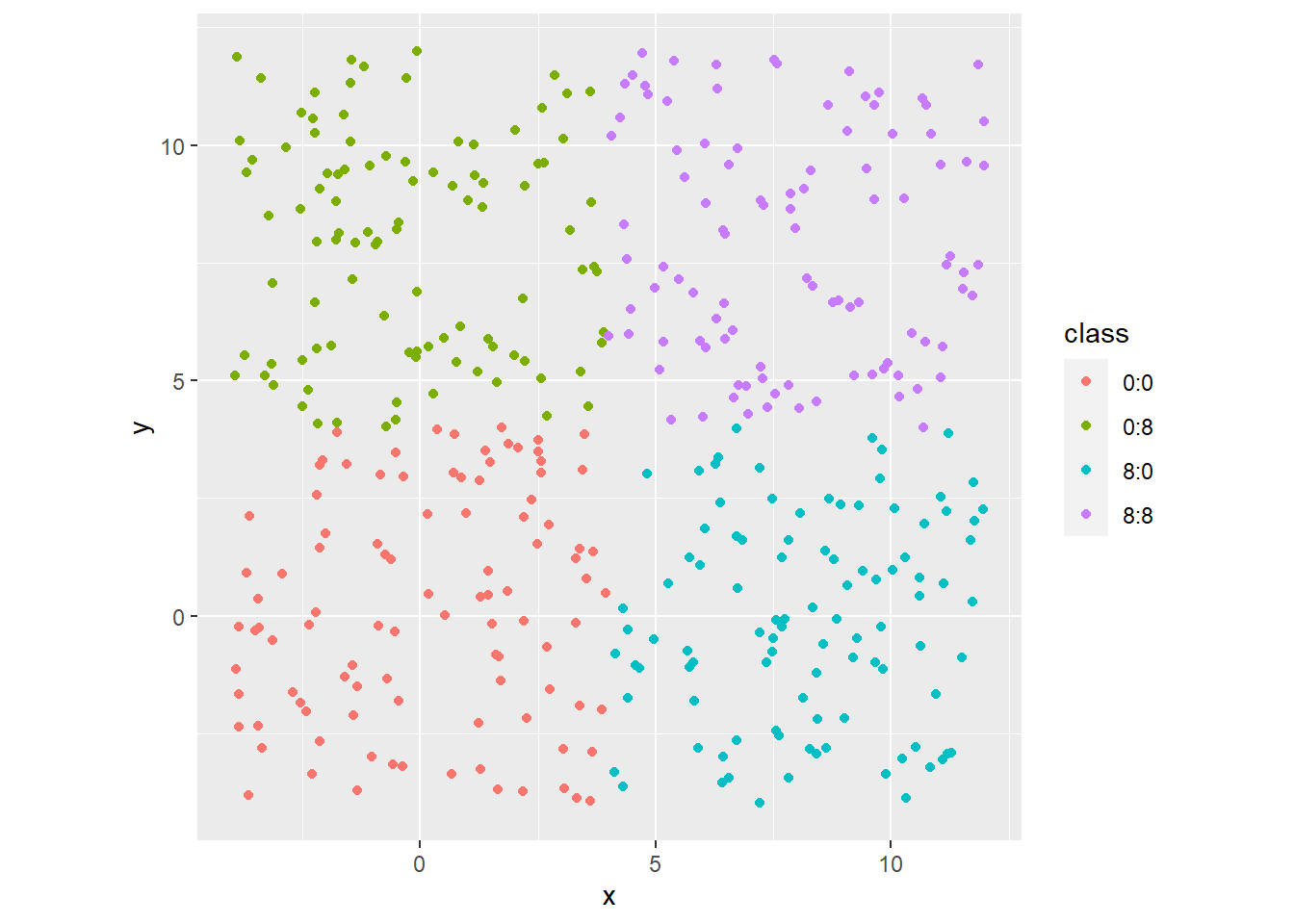

wss <- tibble(k = 1:8) %>%
  mutate(
    value = map_dbl(k, function(i) {
      if(i==1) {
        sum(scale(simdatxy, scale = FALSE)^2)
      } else {
        km  = kmeans(simdatxy, centers = i)
        sum(km$withinss)
      }
    })
  )
ggplot(data = wss, mapping = aes(
  x = k, y = value)) + 
  geom_col()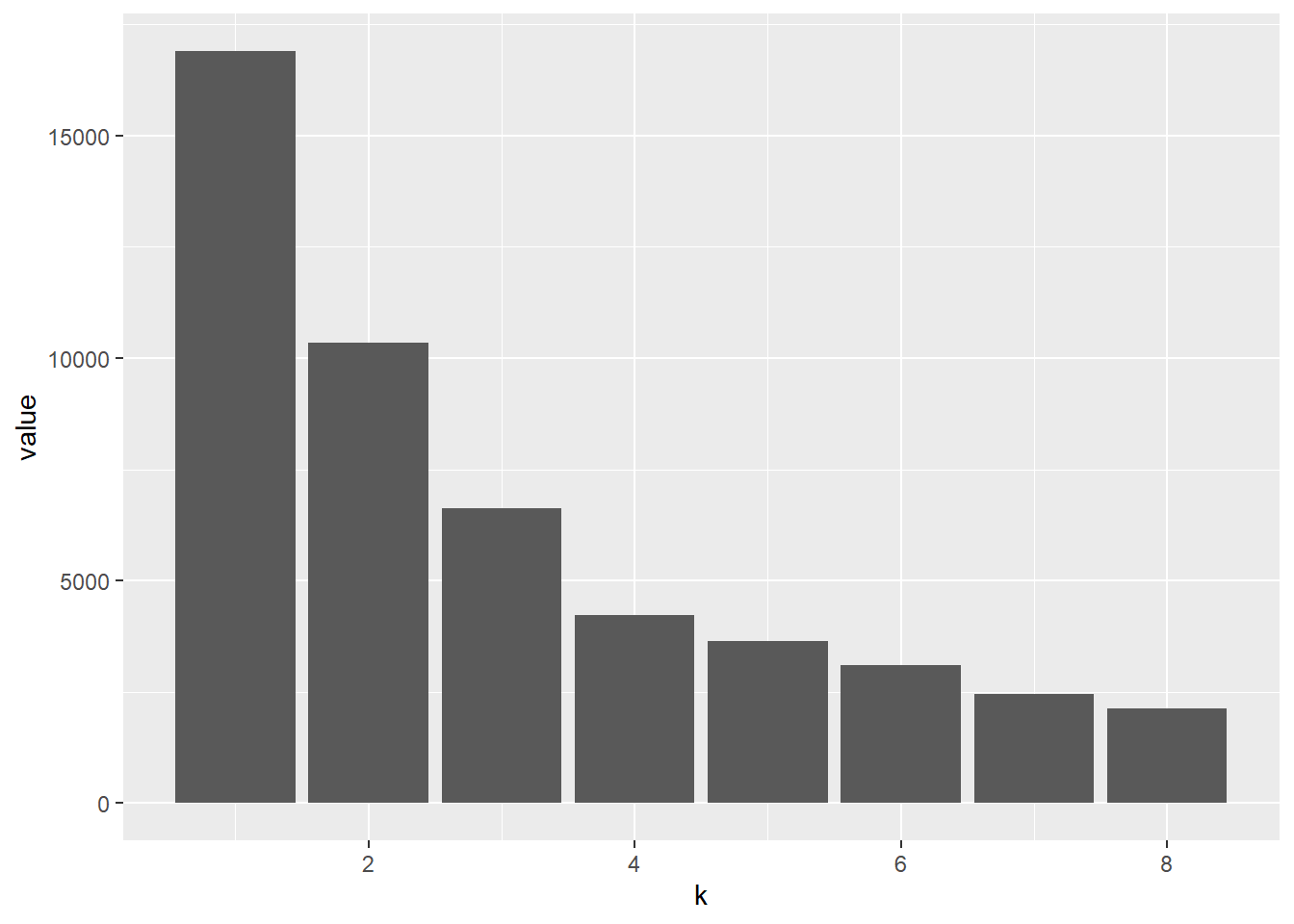

6.9.3 用CH指数

与WSS有关的另一种判断分组效果的指标是Calinski-Harabasz指数，类似方差分析中的F统计量，是组间差距与组内差距的比值。 $\text{CH}_k = \frac{\text{BSS}_k}{\text{WSS}_k} \times \frac{N-k}{N-1}$ 其中 $\text{BSS}_k = \sum_{\ell=1}^k n_{\ell} (\bar x_{\ell} - \bar x)^2$ 而 $n_{\ell}$ 是第 $\ell$ 类的观测点数， $\bar x_{\ell}$ 是第 $\ell$ 类的重心（平均值）， $\bar x$ 是所有观测的平均值。

对上面的均匀分布模拟数据，取不同的类别数用PAM方法聚类，计算相应的CH指标后作图：

#library("fpc")
#library("cluster")
CH = tibble(
  k = 2:8,
  value = map_dbl(k, function(i) {
    p = cluster::pam(simdatxy, i)
    fpc::calinhara(simdatxy, p$cluster)
  })
)
ggplot(data = CH, mapping = aes(
  x = k, y = value)) + 
  geom_line() + 
  geom_point() +
  ylab("CH index")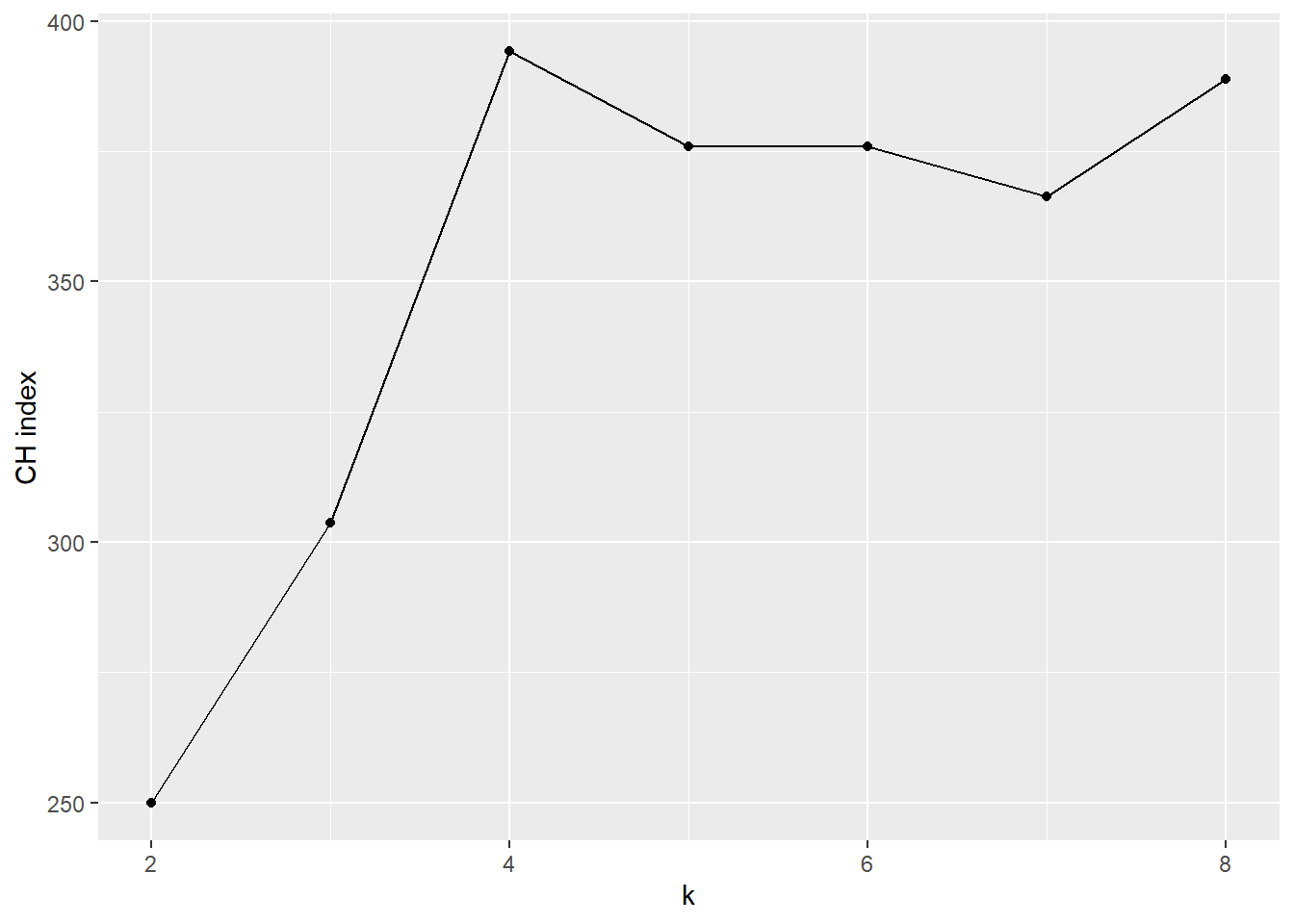

在 $k=4$ 最大，提示分4个类。

cluster包的pam(x, k)对输入数据框x用PAM方法聚成k个类。 fpc包的calinhara(x,clustering)函数在输入了数据框x和类标签向量clustering以后，输出CH指标的值。

6.9.4 用间隙统计量

$\text{WSS}_k$ 指标只能观察其随着 $k$ 的变化的剧烈程度，另一种做法是类似假设检验的思想，与只有一类的类似数据的 $\text{WSS}_k$ 进行比较。间隙统计量就是对 $\log(\text{WSS}_k)$ 进行这种比较。对若干个组数 $k$ 计算 $\log(\text{WSS}_k)$ ，并与变量维数相同、均匀分布或者协方差结构相同的模拟样本的统计量进行比较。

计算间隙(gap)统计量的算法如下：

对若干个 $k$ 值，分别进行聚类，计算相应的 $\log(\text{WSS}_k)$ 值；
模拟产生 $B$ 组参考数据，从一个非混合的分布中抽样，并对模拟的数据分别计算相应的统计量。这会产生 $W_{kb}^*$ , $k$ 为分组个数， $b=1,2,\dots,B$ 。
计算间隙统计量： $\text{gap}_k = \bar l_k - \log \text{WSS}_k, \text{ 其中 } \bar l_k = \frac{1}{B} \sum_{b=1}^B \log W_{kb}^*$ 如果分类正确， $\text{gap}_k$ 应该较大，模拟数据的组合离差应该比有规律分组的实际数据的组内离差和大。
计算方差 $\text{sd}_k^2 = \frac{1}{B-1} \sum_{b=1}^B (\log W_{kb}^* - \bar l_k)^2$ 这是不同模拟样本的组内离差和对数值之间的差异大小的度量。一种选 $k$ 的规则是 $\text{gap}_k \geq \text{gap}_{k+1} - s_{k+1}' \text{ 其中 } s_{k+1}' = \text{sd}_{k+1} \sqrt{1 + \frac{1}{B}}$

扩展包cluster和clusterCrit中实现了间隙法则。 clusGap用指定的聚类函数对多个不同的聚类个数进行聚类并计算间隙统计量。因为要对每个模拟数据聚类，所以计算量较大，运行速度较慢。

#library("cluster")
library("ggplot2")

pamfun = function(x, k)
  list(cluster = cluster::pam(
    x, k, cluster.only = TRUE))

gss = cluster::clusGap(
  simdatnxy, FUN = pamfun, 
  K.max = 8, B = 50, verbose = FALSE)

plot_gap = function(x) {
  gstab <- as_tibble(x$Tab) %>%
    mutate(
      k = seq_len(nrow(x$Tab)))
  ggplot(data = gstab, mapping = aes(
    x = k, y = gap)) + 
    geom_line() +
    geom_errorbar(mapping = aes(
      ymax = gap + SE.sim,
      ymin = gap - SE.sim), 
      width=0.1) +
    geom_point(size = 3, col=  "red")
}
plot_gap(gss)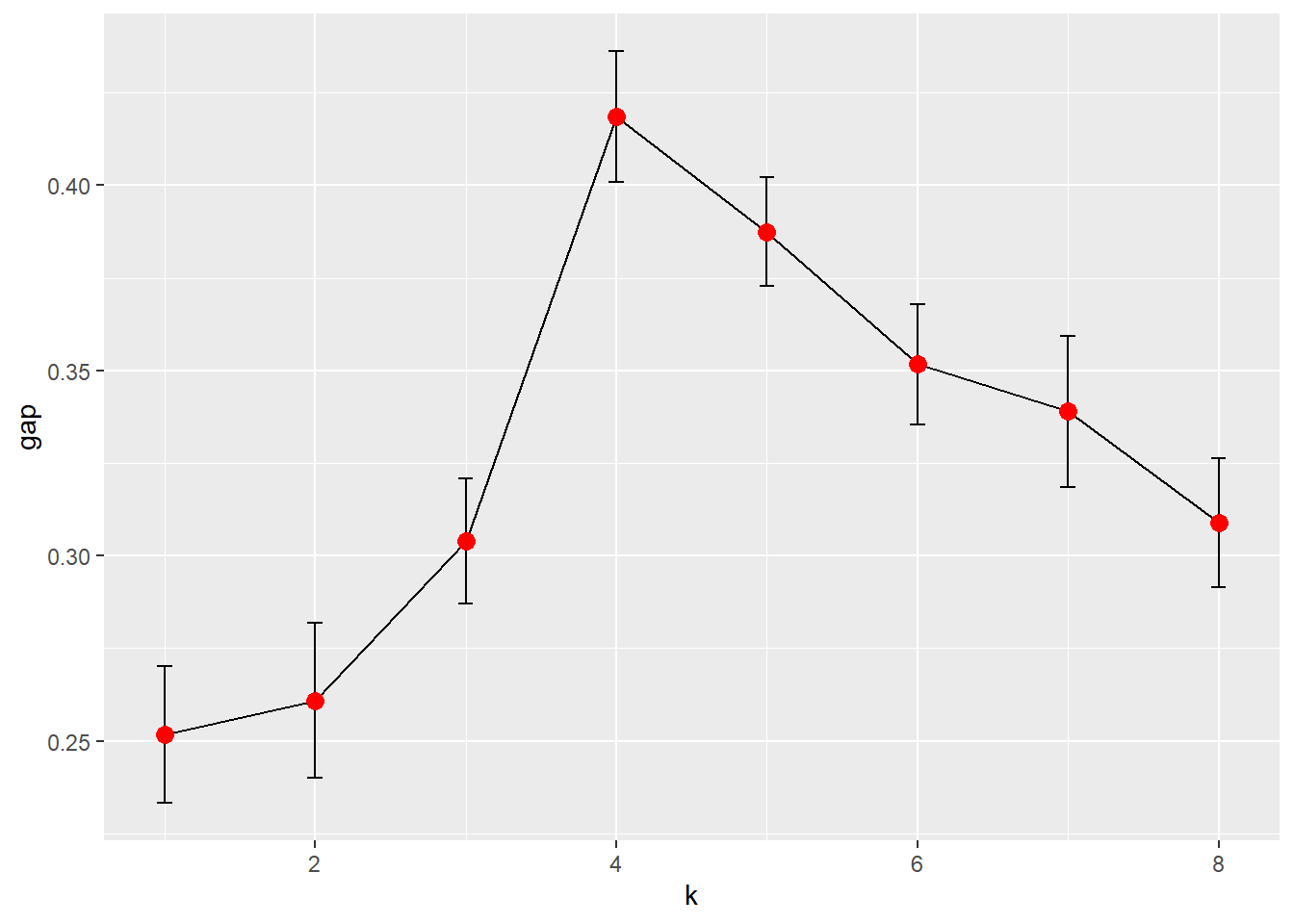

图形明显提示分成4类，是正确的结果。

6.10 混合分布模型聚类方法

参考：

(Everitt and Hothorn 2011)

谱系聚类和k均值聚类主要依赖距离概念和直观想法，没有利用统计推断理论，所以在比较不同方法优劣、确定聚类个数等方面没有说服力强的手段，可以作为探索性分析和实用算法来使用。

如果数据服从一定的统计模型，就可以用统计估计、假设检验方法来聚类并比较不同结果优劣，获得聚类个数的有理论支持的结果。但是，如果数据不符合设定的统计模型，结果也不一定更好。

本节讲述用混合分布模型进行聚类的方法。设要聚类的观测来自是某总体的样本，而此总体实际由若干个子总体构成，抽样时从每个子总体有固定的比例抽取。

6.10.1 混合密度模型

设总体 $\boldsymbol X$ 由 $c$ 个子总体构成，第 $j$ 个子总体的密度为 $g_j(\boldsymbol x, \boldsymbol\theta_j)$ ，其中第 $j$ 个子总体的比例为 $p_j$ ，则总体密度为混合密度 $f(\boldsymbol x, \boldsymbol\theta) = \sum_{j=1}^c p_j g_j(\boldsymbol x, \boldsymbol\theta_j) ,$ 其中 $\boldsymbol\theta = (\boldsymbol\theta_1^T, \dots, \boldsymbol\theta_j^T)^T$ 。 $p_j \geq 0$ , $\sum_{j=1}^c p_j = 1$ 。

这可以看成是聚类分析的模型，在有了这个总体的简单随机样本后，估计 $c$ 的值就是聚类个数值，估计 $g_j(\boldsymbol x, \boldsymbol\theta_j)$ 可以获得对类中心和整个类的分布形状的认识。

比较简单的情况是各个子总体密度类型相同，仅分布参数不同，比如，子总体都服从多元正态分布。

如果各个子总体的密度是参数模型，在估计了各个子总体参数和比例参数 $\hat p_j$ 后，可以用后验概率估计每个观测属于每个子总体的概率： $P(\text{第}i\text{观测属于子总体}j \;|\; \boldsymbol x_i) = \frac{\hat p_j g_j(\boldsymbol x_i ; \hat{\boldsymbol\theta}_j)}{ \sum_{\ell=1}^c \hat p_\ell g_\ell(\boldsymbol x_i ; \hat{\boldsymbol\theta}_\ell) } .$

6.10.2 混合正态模型最大似然估计

混合正态模型的似然函数过于复杂，使用通常的基于导数的优化方法很难收敛。要估计的参数分为子总体分布参数，与混合比例参数两部分，同时估计这两部分很难。所以通常使用EM算法进行估计，迭代方程为 $\begin{aligned} \hat P(j | \boldsymbol x_i) =& P(\text{第}i\text{观测属于子总体}j \;|\; \boldsymbol x_i) = \frac{\hat p_j g_j(\boldsymbol x_i ; \hat{\boldsymbol\theta}_j)}{ \sum_{\ell=1}^c \hat p_\ell g_\ell(\boldsymbol x_i ; \hat{\boldsymbol\theta}_\ell) } \\ \hat p_j =& \frac{1}{n} \sum_{i=1}^n \hat P(j | \boldsymbol x_i) \\ \hat{\boldsymbol\mu}_j =& \frac{1}{n \hat p_j} \sum_{i=1}^n \boldsymbol x_i \hat P(j | \boldsymbol x_i) \\ \hat\Sigma_j =& \frac{1}{n} \sum_{i=1}^n (\boldsymbol x_i - \hat{\boldsymbol\mu}_j ) (\boldsymbol x_i - \hat{\boldsymbol\mu}_j )^T \hat P(j | \boldsymbol x_i) . \end{aligned}$

这样的迭代应对 $\Sigma_j$ 的结构有所约束，比如，要求所有 $\Sigma_j$ 都相同，等等。

除了使用最大似然估计和EM算法，还可以采用贝叶斯模型，并使用MCMC方法进行计算。

为了约束 $\Sigma_j$ 的形式，可以写成特征值分解形式 $\Sigma_j = \Gamma_j \Lambda_j \Gamma_j^T,$ 并将特征值组成的对角阵 $\Lambda_j$ 写成 $\lambda_j A_j$ ，其中 $\lambda_j$ 是 $\Gamma_j$ 的最大特征值， $A_j$ 是对角元素为 $(1,\alpha_2, \dots, \alpha_p)$ 的对角阵，其中 $1 \geq \alpha_2 \geq \dots \geq \alpha_p$ 。 $\lambda_j$ 代表了第 $j$ 子总体的分布范围大小， $\alpha_2, \dots, \alpha_p$ 代表分布形状，而 $\Gamma_j$ 仅代表同样大小、形状的分布的不同方向。

R扩展包mclust的Mclust()函数实现了正态混合密度模型的最大似然估计，并据此进行聚类，支持如下的关于子总体协方差的约束方法：

EII，球形，大小相同；
VII，球形，不同大小；
EEI，对角阵，大小和形状相同；
VEI，对角阵，大小不同，形状相同；
EVI，对角阵，大小相同，形状不同；
VVI，对角阵，大小和形状都不同；
EEE，协方差阵相等；
EEV，各个协方差阵的大小和形状相同（方向不同）；
VEV，各个协方差阵形状相同（大小和方向不同）；
VVV，各个协方差阵没有约束。

上述约束的简写中， E表示参数相等， V表示参数不相等， I表示要求协方差为对角阵。最后一个字母取I、E、V分别表示各协方差阵要求对角、要求相等、不要求对角或相等。第一个字母取E、V分别表示大小相等、大小不相等，第二个字母取I、E、V分别要求对角并形状相同、形状相同、形状不同。

6.10.3 示例：身体测量指标聚类

考虑前面的男女的身体测量指标聚类问题。

library(mclust)

## Package 'mclust' version 5.4.10
## Type 'citation("mclust")' for citing this R package in publications.

## 
## Attaching package: 'mclust'

## The following object is masked from 'package:purrr':
## 
##     map

(mea_md <- Mclust(measure[,1:3]))

## 'Mclust' model object: (EEV,2) 
## 
## Available components: 
##  [1] "call"           "data"           "modelName"      "n"             
##  [5] "d"              "G"              "BIC"            "loglik"        
##  [9] "df"             "bic"            "icl"            "hypvol"        
## [13] "parameters"     "z"              "classification" "uncertainty"

结果估计了2个类，各协方差阵大小、形状相同，方向不同。

分类结果概括：

summary(mea_md)

## ---------------------------------------------------- 
## Gaussian finite mixture model fitted by EM algorithm 
## ---------------------------------------------------- 
## 
## Mclust EEV (ellipsoidal, equal volume and shape) model with 2 components: 
## 
##  log-likelihood  n df       BIC       ICL
##       -116.0007 20 16 -279.9331 -279.9841
## 
## Clustering table:
##  1  2 
##  9 11

每个观测的分类在结果的classification元素中，与性别对比：

table(measure[["gender"]], mea_md$classification)

##         
##           1  2
##   male    9  1
##   female  0 10

可见用三个身体测量指标区分男女效果很好，仅有一例错判，将男性错判为女性。

6.11 聚类效果判断

为了判断聚类结果是否合理，可以对第 $i$ 观测计算如下指标： $s(\boldsymbol x_i) = \frac{2 d(\boldsymbol x_i, c(\boldsymbol x_i))}{ d(\boldsymbol x_i, c(\boldsymbol x_i)) + d(\boldsymbol x_i, \tilde c(\boldsymbol x_i))} ,$ 其中 $d(\cdot,\cdot)$ 表示距离， $c(\boldsymbol x_i))$ 表示第 $i$ 观测所属的类中心， $\tilde c(\boldsymbol x_i)$ 表示与第 $i$ 观测第二近的类中心。 $s(\boldsymbol x_i)$ 取值在0到1之间，如果 $s(\boldsymbol x_i)$ 取值接近0，则第 $i$ 观测明确属于所在类；如果 $s(\boldsymbol x_i)$ 取值接近1，则第 $i$ 观测在最近的两类之间的类属是含糊的。

对于两个类 $i, j$ ，也可以定义两个类的接近程度指标： $s_{ij} = \frac{1}{n_i} \sum_{\boldsymbol x \in A_{ij}} s(\boldsymbol x),$ 其中 $A_{ij}$ 表示以 $i$ 为类属、以 $j$ 为次最近类属的所有观测的集合， $n_i$ 是以 $i$ 为类属的观测个数。如果 $s_{ij}$ 较大，则这两个类很接近。

R扩展包flexclust设计了两种图形，可以表示类之间的模糊程度。一种叠加在二维散点图基础上，另一种用类似条码图的方法表现两类之间的观测次最近距离。

References

Everitt, Brian, and Torsten Hothorn. 2011. An Introduction to Applied Multivariate Analysis with r. Springer New York.