4 多元分布的统计推断

4.1 多元分布样本

设总体为\(p\)元随机向量\(\boldsymbol X\)，此总体的一个简单随机样本为 \(\boldsymbol x^{(i)}, i=1,2,\dots,n\), 其中\(\boldsymbol x^{(i)}\)与\(\boldsymbol X\)同分布。

这些数据一共有\(n \times p\)个值，通常写成一个矩阵\(M = (x_{ij})_{n\times p}\)的形式，矩阵的第\(i\)行是\([\boldsymbol x^{(i)}]^T\)，即第\(i\)个观测（样品）的\(p\)个分量。这样的矩阵称为观测数据集。

设总体\(\boldsymbol X\)的期望为\(\boldsymbol\mu\)，方差阵为\(\Sigma\)，则随机矩阵\(M\)满足 \[ E(M) = \boldsymbol 1_n \boldsymbol\mu^T, \quad \text{Var}(\text{vec}(M^T)) = I_n \otimes \Sigma . \]

4.1.1 样本均值

总体期望值\(\boldsymbol\mu = E\boldsymbol X\)可以用如下样本均值估计： \[\begin{aligned} \bar{\boldsymbol x} = (\bar x_{\cdot 1}, \bar x_{\cdot 2}, \dots, \bar x_{\cdot p})^T = \frac{1}{n} M^T \boldsymbol 1_n, \end{aligned}\] 其中\(\boldsymbol 1_n\)是元素都等于1的\(n\)维列向量。\(\bar{\boldsymbol x}\)的第\(j\)元素为 \[\begin{aligned} \bar x_{\cdot j} = \frac{1}{n} \sum_{i=1}^n x_{ij}, \ j=1,2,\dots, p. \end{aligned}\]

易见 \[ E(\bar{\boldsymbol x}) = \boldsymbol\mu, \ \text{Var}(\bar{\boldsymbol x}) = \frac{1}{n} \Sigma . \] 事实上， \[\begin{aligned} E(\bar{\boldsymbol x}) =& E(\frac{1}{n} M^T \boldsymbol 1_n) = \frac{1}{n} E(M^T) \boldsymbol 1_n \\ =& \frac{1}{n} \boldsymbol\mu \boldsymbol 1_n^T \boldsymbol 1_n = \boldsymbol\mu .\\ \text{Var}(\bar{\boldsymbol x}) =& \text{Var}(\frac{1}{n} \sum_{i=1}^n \boldsymbol x^{(i)}) \\ =& \frac{1}{n^2} \sum_{i=1}^n \text{Var}(\boldsymbol x^{(i)}) = \frac{1}{n} \Sigma. \end{aligned}\]

4.1.2 样本协方差阵

总体协方差阵\(\Sigma=\text{Var}(\boldsymbol X)\)可以用如下样本协方差阵估计 \[\begin{aligned} S = \frac{1}{n} \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T, \end{aligned}\] 其\((k,j)\)元为 \[\begin{aligned} s_{kj} = \frac{1}{n} \sum_{i=1}^n (x_{ik} - \bar x_{\cdot k})(x_{ij} - \bar x_{\cdot j}) . \end{aligned}\] 这里用了\(1/n\)的公式，多元分析中经常用这个公式。如果用\(1/(n-1)\)的公式，得到的\(S\)是\(\Sigma\)的无偏估计。即 \[ E(S) = \frac{n-1}{n} \Sigma . \] 事实上， \[\begin{aligned} s_{kj} =& \frac{1}{n} \sum_{i=1}^n (x_{ik} - \bar x_{\cdot k}) (x_{ij} - \bar x_{\cdot j}) \\ =& \frac{1}{n} \sum_{i=1}^n [(x_{ik} - \mu_k) - (\bar x_{\cdot k} - \mu_k)] [(x_{ij} - \mu_j) - (\bar x_{\cdot j} - \mu_j)] \\ =& \frac{1}{n} \sum_{i=1}^n (x_{ik} - \mu_k) (x_{ij} - \mu_j) - (\bar x_{\cdot k} - \mu_k) (\bar x_{\cdot j} - \mu_j) \\ E(s_{kj}) =& \frac{1}{n} \sum_{i=1}^n \sigma_{kj} - \text{Cov}(\bar x_{\cdot k}, \bar x_{\cdot j}) \\ =& \sigma_{kj} - \frac{1}{n^2} \sum_s \sum_t \text{Cov}(x_{sk}, x_{tj}) \\ =& \sigma_{kj} - \frac{1}{n^2} \sum_s \text{Cov}(x_{sk}, x_{sj}) \\ =& \sigma_{kj} - \frac{1}{n^2} n \sigma_{kj} \\ =& \frac{n-1}{n} \sigma_{kj} . \end{aligned}\] 即\(ES = \frac{n-1}{n} \Sigma\)。

4.1.3 观测数据集的中心化

观测数据集每列减去列平均值，称为中心化。设各列平均值组成样本平均值向量\(\bar{\boldsymbol x}\)，中心化可以表达为如下矩阵乘法 \[\begin{aligned} M_C =& M - \boldsymbol 1_n \; \bar{\boldsymbol x}^T = M - \boldsymbol 1_n \; \frac{1}{n} \boldsymbol 1_n^T M \nonumber\\ =& (I_n - \frac{1}{n} \boldsymbol 1_n \boldsymbol 1_n^T) M \stackrel{\triangle}{=} H M, \end{aligned}\] 其中 \[ H = I_n - \frac{1}{n} \boldsymbol 1_n \boldsymbol 1_n^T \] 称为中心化矩阵。 \(H\)满足\(H^2=H\)，是一个对称幂等矩阵，又称为投影阵。

设\(M_C\)为中心化矩阵，这时有 \[\begin{aligned} S = \frac{1}{n} M_C^T M_C = \frac{1}{n} M^T H^T H M = \frac{1}{n} M^T H M . \end{aligned}\] 由\(S = M_C^T M_C\)可见\(S\)是非负定阵。

还可得 \[ S = \frac{1}{n} M_C^T M = \frac{1}{n} M^T M_M - \bar{\boldsymbol x} \bar{\boldsymbol x}^T . \]

4.1.4 观测数据集标准化与相关阵估计

把观测数据集\(M\)变成矩阵\(M_S\), \(M_S\)的\((i,j)\)号元素为 \[\begin{aligned} x_{ij}^{(s)} = \frac{x_{ij} - \bar x_{\cdot j}}{\sqrt{s_{jj}}}, i=1,2,\dots,n,\ j=1,2,\dots,p \end{aligned}\] \(M_S\)称为\(M\)的标准化，实际是每列减去列平均值，除以标准差估计。

设\(D = \text{diag}(s_{11}, s_{22}, \dots, s_{pp})\), 则 \[\begin{aligned} M_S = H M D^{-1/2} . \end{aligned}\]

利用标准化数据可得样本相关系数阵的估计为 \[\begin{aligned} \hat R =& \frac{1}{n} M_S^T M_S = \frac{1}{n} D^{-1/2} M^T H^T H M D^{-1/2} \nonumber\\ =& \frac{1}{n} D^{-1/2} M^T H M D^{-1/2} = D^{-1/2} S D^{-1/2} . \end{aligned}\]

4.1.5 观测数据的线性变换

设随机向量\(\boldsymbol Y = A \boldsymbol X\), 其中\(A\)是\(q \times p\)矩阵，则\(\boldsymbol Y\)是\(q\)元随机向量。对每个观测\(\boldsymbol x^{(i)}\)作线性变换\(\boldsymbol y^{(i)} = A \boldsymbol x^{(i)}\), 写成\((\boldsymbol y^{(i)})^T = (\boldsymbol x^{(i)})^T A^T\), 则\(\boldsymbol X\)的观测数据集\(M\)变成了\(\boldsymbol Y\)的观测数据集\(Q = M A^T\)，为\(n \times q\)矩阵。 \(\boldsymbol Y\)的样本均值为 \[\begin{aligned} \bar{\boldsymbol y} =& \frac{1}{n} Q^T \boldsymbol 1_n = \frac{1}{n} A M^T \boldsymbol 1_n = A \bar{\boldsymbol x} . \end{aligned}\] 这与\(E(\boldsymbol Y) = E(A \boldsymbol X) = A E(\boldsymbol X)\)相似。

\(\boldsymbol Y\)的观测数据集\(Q = M A^T\)对应的样本协方差阵为 \[\begin{aligned} S_{\boldsymbol Y} =& \frac{1}{n} Q^T H Q = \frac{1}{n} A M^T H M A^T = A S A^T, \end{aligned}\] 这个公式与\(\text{Var}(\boldsymbol Y) = A \text{Var}(X) A^T\)相似。

若变换为\(\boldsymbol Y = A \boldsymbol X + \boldsymbol b\), 则\(\boldsymbol Y\)对应的数据集\(Q\)满足\(\bar{\boldsymbol y} = A \bar{\boldsymbol x} + \boldsymbol b\), \(S_{\boldsymbol Y} = A S A^T\)。

考虑变换\(\boldsymbol y^{(i)} = S^{-1/2} (\boldsymbol x^{(i)} - \bar{\boldsymbol x})\)，数据集\(Q\)的第\(i\)行为\((\boldsymbol y^{(i)})^T\)（\(i=1,2,\dots,n\)）。 \(M_C = HM\)是中心化的数据， \(S = \frac{1}{n} M_C^T M_C = \frac{1}{n} M^T H M\)。 \(Q = M_C S^{-1/2} = H M S^{-1/2}\)。

用\(Q\)估计\(\boldsymbol Y\)的期望为 \[\begin{aligned} \bar{\boldsymbol y} = \frac{1}{n} Q^T \boldsymbol 1_n = \frac{1}{n} S^{-1/2} M^T H \boldsymbol 1_n = \boldsymbol 0 . \end{aligned}\] \(Q\)对应的协方差阵为 \[\begin{aligned} S_{\boldsymbol Y} =& \frac{1}{n} Q^T H Q = \frac{1}{n} S^{-1/2} M^T H H H M S^{-1/2} \\ =& S^{-1/2} \left(\frac{1}{n} M^T H M \right) S^{-1/2} = S^{-1/2} S S^{-1/2} = I_p . \end{aligned}\] 将变换\(\boldsymbol y^{(i)} = S^{-1/2} (\boldsymbol x^{(i)} - \bar{\boldsymbol x})\)称为Mahalanobis变换。

4.2 最大似然估计

参考：(Wolfgang Härdle 2015)节6.2。

对于多元总体的样本\(M\)（其中每一行是一个观测点），仍可以用最大似然估计方法估计参数。设\(\ell(\boldsymbol\theta)\)是对数似然函数，令 \[ S(\boldsymbol\theta) = \frac{\partial}{\partial\boldsymbol\theta} \ell(\boldsymbol\theta) = \frac{\frac{\partial}{ \partial\boldsymbol\theta} L(\boldsymbol\theta)}{L(\boldsymbol\theta)}, \] 称\(S(\boldsymbol\theta)\)为得分函数。适当正则性条件下 \[ E[S(\boldsymbol\theta)] = \boldsymbol 0 , \] 且有 \[ F_n = \text{Var}(S(\boldsymbol\theta)) = - E[\frac{\partial^2}{\partial\boldsymbol\theta \partial\boldsymbol\theta^T} \ell(\boldsymbol\theta)], \] 称\(F_n\)为样本的Fisher信息量矩阵， \(n\)为样本量，有Cramer–Rao不等式： \[ \text{Var}(t(M)) \geq F_n^{-1}, \] 其中\(t(M)\)是\(\boldsymbol\theta\)的任意无偏估计量。这里矩阵\(A \geq B\)表示\(A - B\)是对称半正定矩阵。

对独立同分布样本，有\(F_n = n F_1\)， \(F_1\)是样本量\(n=1\)时的Fisher信息量矩阵。最大似然估计\(\hat{\boldsymbol\theta}\)的渐近方差趋于上述的C-R下界： \[ \sqrt{n}(\hat{\boldsymbol\theta} - \boldsymbol\theta) \stackrel{d}{\to} \text{N}(\boldsymbol 0, F_1^{-1}), \] 这说明最大似然估计是渐近无偏、渐近有效（渐近最小方差）、渐近正态、相合的。

若\(\hat F_1\)是\(F_1\)的相合估计，则还有 \[ n(\hat{\boldsymbol\theta} - \boldsymbol\theta)^T \hat F_1 (\hat{\boldsymbol\theta} - \boldsymbol\theta) \stackrel{d}{\to} \chi^2_m, \] 其中\(m\)是参数\(\boldsymbol\theta\)的维数。

4.3 似然比检验

设参数\(\boldsymbol\theta\)属于\(\mathbb R^q\)的某个子集\(\Omega\)，称为“完全模型”（full model）。要检验的零假设\(H_0\)是参数属于某个受限制的子集\(\Omega_0\)，维数为\(r\)，称为“约束模型”(restricted model)。令\(\ell^*\)为完全模型的最大似然估计对应的对数似然函数值， \(\ell_0^*\)为约束模型的相应值，令 \[ t = 2(\ell^* - \ell_0^*), \] 在相当一般的正则性条件下，当约束模型成立时\(t\)渐近服从\(\chi^2(q-r)\)分布，从而当\(t\)超过右侧临界值时可以拒绝零假设。

当总体是正态总体时，似然比检验统计量在某些情况下有精确分布，比如卡方分布或者Hotelling T方分布。

4.4 多元正态分布统计

设总体\(\boldsymbol X\)服从多元正态分布\(\text{N}_p(\boldsymbol\mu, \Sigma)\)， \(M\)是\(\boldsymbol X\)的样本量为\(n\)的简单随机样本的数据集。记随机矩阵\(M\)的分布为 \[ N(\boldsymbol 1_n \boldsymbol\mu^T, \; I_n \otimes \Sigma), \] 其中\(E(M) = \boldsymbol 1_n \boldsymbol\mu^T\)，而\(I_n \otimes \Sigma\)是\(M\)按行拉直后的方差阵。

4.4.1 最大似然估计

\(M\)对应的对数似然函数为 \[\begin{aligned} \ell(\boldsymbol\mu, \Sigma) =& \sum_{i=1}^n \ln \left\{ (2\pi)^{-p/2} |\Sigma|^{-1/2} \exp \left[ -\frac{1}{2} (\boldsymbol x^{(i)} - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x^{(i)} - \boldsymbol\mu) \right] \right\} \\ =& -\frac{np}{2} \ln(2\pi) -\frac{n}{2} \ln|\Sigma| -\frac{1}{2} \sum_{i=1}^n (\boldsymbol x^{(i)} - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x^{(i)} - \boldsymbol\mu) . \end{aligned}\] 注意到 \[\begin{aligned} & (\boldsymbol x^{(i)} - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x^{(i)} - \boldsymbol\mu) \\ =& [(\boldsymbol x^{(i)} - \bar{\boldsymbol x}) - (\boldsymbol\mu - \bar{\boldsymbol x})]^T \Sigma^{-1} [(\boldsymbol x^{(i)} - \bar{\boldsymbol x}) - (\boldsymbol\mu - \bar{\boldsymbol x})] \\ =& (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) + (\boldsymbol\mu - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol\mu - \bar{\boldsymbol x}) \\ & - 2 (\boldsymbol\mu - \bar{\boldsymbol x}) \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}), \end{aligned}\] 以及 \[ \sum_{i=1}^n (\boldsymbol\mu - \bar{\boldsymbol x}) \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) = 0, \] 变换得 \[\begin{aligned} \ell(\boldsymbol\mu, \Sigma) =& -\frac{np}{2} \ln(2\pi) - \frac{n}{2} \ln|\Sigma| \\ & - \frac{1}{2} \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) \\ & -\frac{n}{2} (\boldsymbol\mu - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol\mu - \bar{\boldsymbol x}) . \end{aligned}\]

继续分解： \[\begin{aligned} & \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) \\ =& \sum_{i=1}^n \text{tr} \left\{ (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) \right\} \\ =& \sum_{i=1}^n \text{tr} \left\{ \Sigma^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) \right\} \\ =& \text{tr} \left\{ \Sigma^{-1} \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) \right\} \\ =& n \text{tr}(\Sigma^{-1} S) . \end{aligned}\]

于是 \[\begin{aligned} \ell(\boldsymbol\mu, \Sigma) =& -\frac{np}{2} \ln(2\pi) -\frac{n}{2} \ln|\Sigma| - \frac{n}{2} \text{tr}(\Sigma^{-1} S) \\ & - \frac{n}{2} (\boldsymbol\mu - \bar{\boldsymbol x})^T \Sigma^{-1} (\boldsymbol\mu - \bar{\boldsymbol x}) . \end{aligned}\]

易见无论\(\Sigma\)如何取值，为了使得\(\ell(\cdot)\)最大都应取\(\hat{\boldsymbol\mu} = \bar{\boldsymbol x}\)。利用一些复杂的矩阵记号进行推导可以得到\(\Sigma\)的最大似然估计为\(S\)(分母为\(n\)的版本)。

4.4.2 均值估计的分布

当总体\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\)时, 由多元正态分布性质可知 \[ \bar{\boldsymbol x} \sim \text{N}(\boldsymbol\mu, \frac{1}{n} \Sigma) . \]

4.4.3 多元均值的中心极限定理

设\(\boldsymbol X_i, i=1,2,\dots,n\)独立同分布，共同期望为\(\boldsymbol\mu\), 共同方差阵为\(\Sigma\)，则\(\hat{\boldsymbol\mu} = \frac{1}{n} \sum_{i=1}^n \boldsymbol X_i\) 满足如下多元中心极限定理 \[\begin{aligned} \sqrt{n} (\hat{\boldsymbol\mu} - \boldsymbol\mu) \stackrel{d}{\rightarrow} N(\boldsymbol 0, \Sigma) \quad\text{当} n \to \infty . \end{aligned}\] 若\(\hat\Sigma\)是\(\Sigma\)的一个相合估计， \(\Sigma\)正定，则有如下的中心极限定理 \[\begin{aligned} \sqrt{n} \hat\Sigma^{-1/2} (\hat{\boldsymbol\mu} - \boldsymbol\mu) \stackrel{d}{\rightarrow} N(\boldsymbol 0, I) \quad\text{当} n \to \infty . \end{aligned}\]

Delta方法: 若随机向量序列\(\boldsymbol X_n\)满足 \[ \sqrt{n}( \boldsymbol X_n - \boldsymbol\mu ) \stackrel{d}{\rightarrow} N(0, \Sigma), \] 当\(n\to\infty\), \(f(\cdot)\)是一个\(\mathbb R^p \to \mathbb R^q\)的多元函数，在\(\boldsymbol\mu\)处可微，令 \[\begin{aligned} G = \left.\left( \frac{\partial f_j(\boldsymbol x)}{\partial x_i} \right)\right|_{\boldsymbol x = \boldsymbol\mu} , \end{aligned}\] 为一阶偏导数组成的\(p \times q\)矩阵，则 \[\begin{aligned} \sqrt{n}[f(\boldsymbol X_n) - f(\boldsymbol\mu)] \stackrel{d}{\rightarrow} \text{N}(\boldsymbol 0, G^T \Sigma G) \quad\text{当}n\to \infty . \end{aligned}\] 这里的极限分布是(广义的)多元正态分布。

例如，考虑\(f(\boldsymbol \mu) = \boldsymbol\mu^T A \boldsymbol\mu\)，其中\(A\)是正定阵，则\(G = 2 A \boldsymbol\mu\)，有 \[ \sqrt{n}(\bar{\boldsymbol x}^T A \bar{\boldsymbol x} - \boldsymbol\mu^T A \boldsymbol\mu) \stackrel{d}{\rightarrow} \text{N}(\boldsymbol 0, 4 \boldsymbol\mu^T A \Sigma A \boldsymbol \mu) . \]

4.5 Wishart分布

在一元正态总体的推断中，卡方，t, F分布起到重要作用。多元正态总体推断中需要推广为Wishart分布和Hotelling T方分布。

设总体\(\boldsymbol X\)为\(N(\boldsymbol 0, \Sigma)\)分布(\(\Sigma>0\)), 矩阵\(M_{n \times p}\)为\(\boldsymbol X\)的观测数据集，每一行是\(\boldsymbol X\)的一个样本点，令随机矩阵\(Z = M^T M\)，称\(Z\)服从Wishart分布\(W_p(\Sigma, n)\)。

记\(M\)的第\(i\)行为\((\boldsymbol X^{(i)})^T\)，则

\[ Z = M^T M = (\boldsymbol X^{(1)}, \boldsymbol X^{(2)}, \dots, \boldsymbol X^{(n)}) \begin{pmatrix} (\boldsymbol X^{(1)})^T \\ (\boldsymbol X^{(2)})^T \\ \vdots \\ (\boldsymbol X^{(n)})^T \end{pmatrix} = \sum_{i=1}^n \boldsymbol X^{(i)} (\boldsymbol X^{(i)})^T . \]

标准Wishart分布为\(W_p(I_p, n)\)。

当\(p=1\)时，总体\(X \sim \text{N}(0, \sigma^2)\), \(W_1(\sigma^2, n)\)即\(\sigma^2 \chi^2(n)\)分布。

Wishart分布的随机矩阵\(W\)包括\(p(p+1)/2\)个分量（矩阵的下三角部分），其分布可以看成是\(\text{Svec}(W)\)的分布。取值需要需要满足正定约束。

4.5.1 Wishart分布性质

当\(n \geq p\)时\(W_p(\Sigma, n)\)随机矩阵以概率1为正定阵。
\(E\left(\frac{1}{n} W_p(\Sigma, n) \right) = \Sigma\)。
如果随机矩阵\(Z \sim W_p(\Sigma, n)\), \(B\)为\(p \times q\)矩阵，\(q \leq p\)且\(B\)列满秩，则\(B^T Z B\)服从\(W_q(B^T \Sigma B, n)\)分布。
如果随机矩阵\(Z \sim W_p(\Sigma, n)\), \(\boldsymbol a\)为向量且\(\boldsymbol a^T \Sigma \boldsymbol a > 0\), 则

\[\begin{aligned} \frac{\boldsymbol a^T Z \boldsymbol a}{\boldsymbol a^T \Sigma \boldsymbol a} \sim \chi^2(n) . \end{aligned}\]
若随机矩阵\(Z_i \sim W_p(\Sigma, n_i)\), \(i=1,\dots, k\)且相互独立，则\(Z = \sum_{i=1}^k Z_i \sim W_p(\Sigma, n)\)，其中\(n=\sum_{i=1}^k n_i\)。

4.5.2 多元正态总体样本与Wishart分布

设\(M_{n \times p}\)是正态总体\(\text{N}(\boldsymbol 0, \Sigma)\)的观测数据集， \(C\)为对称阵，则

(1) \(M^T C M\)服从加权Wishart分布，即 \[\begin{aligned} M^T C M = \sum_{i=1}^n \lambda_i W_p(\Sigma, 1) , \end{aligned}\] 其中\(\lambda_i, i=1,\dots, n\)是\(C\)的各个特征值，右式中各个Wishart分布相互独立。

(2) \(M^T C M\)服从Wishart分布当且仅当\(C^2=C\)，这时 \[\begin{aligned} M^T C M \sim W_p(\Sigma, r) , \end{aligned}\] \(r = \text{rank}(C) = \text{tr}(C)\)。

定理4.1 设\(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)}\) iid \(\sim \text{N}(\boldsymbol\mu, \Sigma)\), \(M^T = (\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)})\), 即\(M_{n \times p}\)是正态总体\(\text{N}(\boldsymbol\mu, \Sigma)\)的观测数据集，样本统计量 \[\begin{aligned} \bar{\boldsymbol x} =& \frac{1}{n} \sum_{i=1}^n \boldsymbol x^{(i)}, \\ S =& \frac{1}{n} M_C^T M_C = \frac{1}{n} M^T H M \\ =& \frac{1}{n} \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T , \end{aligned}\] 则有

(1) \(\bar{\boldsymbol x} \sim \text{N}(\boldsymbol\mu, \frac{1}{n} \Sigma)\)。

(2) \(n S = M_C^T M_C = M^T H M \sim W_p(\Sigma, n-1)\)。

(3) \(\bar{\boldsymbol x}\)与\(S\)相互独立。

证明： (1) 前面已经证明。

(2)和(3)的证明：取\(n \times n\)正交阵\(\Gamma\)，设其各个列向量为\(\boldsymbol\gamma_i\)， \(i=1,2,\dots,n\)，取\(\boldsymbol\gamma_n = \frac{1}{\sqrt{n}} \boldsymbol 1_n\)。令 \[ N = \Gamma^T M = (\boldsymbol z^{(1)}, \boldsymbol z^{(2)}, \dots, \boldsymbol z^{(n)})^T , \ N^T = M^T \Gamma, \] 最后一行 \[ \boldsymbol z^{(n)} = M \boldsymbol\gamma_n = \frac{1}{\sqrt{n}} M^T \boldsymbol 1_n = \sqrt{n} \bar{\boldsymbol x} . \]

由随机矩阵性质和正交阵性质， \[ E(N) = \Gamma^T E(M) = \Gamma^T \boldsymbol 1_n \boldsymbol\mu^T = \begin{pmatrix} \boldsymbol 0_{(n-1) \times n} \\ \sqrt{n} \boldsymbol\mu^T \end{pmatrix} . \] 所以 \[\begin{aligned} E(\boldsymbol z^{(i)}) =& \boldsymbol 0_p, \ i=1,2,\dots, n-1, \\ E(\boldsymbol z^{(n)}) =& \sqrt{n} \boldsymbol\mu . \end{aligned}\]

由随机矩阵性质(3.5)式，可得 \[\begin{aligned} & \text{Var}(\text{vec}(N^T)) \\ =& (\Gamma^T \Gamma) \otimes (I \Sigma I) = I_n \otimes \Sigma , \end{aligned}\] 从而\(\boldsymbol z^{(i)}\)， \(i=1,2,\dots,n\)相互不相关，由多元正态性质可知其相互独立，都服从多元正态分布，且 \[\begin{aligned} \boldsymbol z^{(i)} \sim& \text{N}_p(\boldsymbol 0, \Sigma), \; n=1,2,\dots, n-1, \\ \boldsymbol z^{(n)} \sim& \text{N}_p(\sqrt{n} \boldsymbol\mu, \Sigma) . \end{aligned}\]

注意 \[ N^T N = M^T \Gamma \Gamma^T M = M^T M, \] 而 \[\begin{aligned} M^T M =& (\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)}) \begin{pmatrix} [\boldsymbol x^{(1)}]^T \\ [\boldsymbol x^{(2)}]^T \\ \vdots \\ [\boldsymbol x^{(n)}]^T \end{pmatrix} \\ =& \sum_{i=1}^n \boldsymbol x^{(i)} [\boldsymbol x^{(i)}]^T, \\ N^T N =& \sum_{i=1}^n \boldsymbol z^{(i)} [\boldsymbol z^{(i)}]^T, \end{aligned}\] 注意到\(\boldsymbol z^{(n)} = \sqrt{n} \bar{\boldsymbol x}\)，于是 \[\begin{aligned} & \sum_{i=1}^{n-1} \boldsymbol z^{(i)} [\boldsymbol z^{(i)}]^T \\ =& \sum_{i=1}^n \boldsymbol x^{(i)} [\boldsymbol x^{(i)}]^T - n \bar{\boldsymbol x} \bar{\boldsymbol x}^T \\ =& \sum_{i=1}^n (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T \\ =& n S = n M^T H M . \end{aligned}\] 因为\(\sum_{i=1}^{n-1} \boldsymbol z^{(i)} [\boldsymbol z^{(i)}]^T\)服从\(W_p(\Sigma, n-1)\)，所以\(n S\)服从\(W_p(\Sigma, n-1)\)，由\(\boldsymbol z^{(n)}\)与\(\boldsymbol z^{(1)}, \dots, \boldsymbol z^{(n-1)}\)的独立性可知\(\bar{\boldsymbol x}\)与\(S\)独立。

○○○○○○

4.6 Hotelling T方分布

设\(\boldsymbol Y \sim \text{N}(\boldsymbol 0, I_p)\), 随机矩阵\(Z \sim W_p(I_p, n)\)与\(\boldsymbol Y\)独立，则\(\boldsymbol Y^T \left(\frac{1}{n} Z \right)^{-1} \boldsymbol Y\) 服从Hotelling \(T^2_{p, n}\)分布。

这是\(t\)分布的推广，一元(\(p=1\))的时候相当于\(t(n)\)分布随机变量的平方。

如果\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\), 随机矩阵\(Z \sim W_p(\Sigma, n)\)与\(\boldsymbol X\)独立，则 \[\begin{aligned} (\boldsymbol X - \boldsymbol\mu)^T \left(\frac{1}{n} Z \right)^{-1} (\boldsymbol X - \boldsymbol\mu) \sim T^2_{p,n} . \end{aligned}\]

如果\(\bar{\boldsymbol x}, S\)是从多元正态总体\(N(\boldsymbol\mu, \Sigma)\) 的\(n\)个独立观测得到的样本均值和样本方差阵(\(S\)用了\(1/n\)公式)，则 \[\begin{aligned} & (\bar{\boldsymbol x} - \boldsymbol\mu)^T \left(\frac{1}{n-1} S \right)^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu) \\ =& (\bar{\boldsymbol x} - \boldsymbol\mu)^T \left(\frac{1}{n-1} \frac{1}{n}M_C^T M_C \right)^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu) \\ =& [\sqrt{n} (\bar{\boldsymbol x} - \boldsymbol\mu)]^T \left(\frac{1}{n-1} M^T H M \right)^{-1} [\sqrt{n} (\bar{\boldsymbol x} - \boldsymbol\mu)] \sim T^2_{p, n-1} . \end{aligned}\]

Hotelling \(T^2_{p,n}\)可以转化为\(F\)分布： \[\begin{aligned} T^2_{p,n} = \frac{np}{n-p+1} F_{p, n-p+1} . \end{aligned}\]

当\(p=1\)时， \[\begin{aligned} t =& \frac{\bar x - \mu}{\sqrt{ \frac{1}{n} \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2}} \sim t(n-1) \\ t^2 =& (\bar x - \mu)^T \left( \frac{1}{n} \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2 \right)^{-1} (\bar x - \mu) \sim T^2_{1,n-1} = F_{1,n-1} . \end{aligned}\]

4.7 Wilks分布

设\(\Sigma > 0\), \(W_1 \sim W_p(\Sigma, n_1)\), \(W_2 \sim W_p(\Sigma, n_2)\), \(W_1\)和\(W_2\)相互独立，令 \[ \Lambda = \frac{\text{det}(W_1)}{ \text{det}(W_1) + \text{det}(W_2)}, \] 称\(\Lambda\)服从Wilks分布\(\Lambda(p, n_1, n_2)\)。

当\(p=1\)时， \(\Lambda \sim \text{Beta}(n_1/2, n_2/2)\)。

4.8 多元正态分布单总体均值的推断

4.8.1 多元正态分布均值的联立置信域

由上面的Hotelling \(T^2\)分布，可得\(\boldsymbol\mu\)的置信度为\(1-\alpha\)的置信域为 \[\begin{aligned} (\boldsymbol\mu - \bar{\boldsymbol x})^T \left(\frac{1}{n-1} \frac{1}{n} M_C^T M_C \right)^{-1} (\boldsymbol\mu - \bar{\boldsymbol x}) \leq \frac{p(n-1)}{n-p} F_{1-\alpha}(p, n-p) . \end{aligned}\] 其中\(F_{1-\alpha}(p, n-p)\)是\(F(p, n-p)\)分布的上侧\(\alpha\)分位数。二维时其边界是椭圆，三维时其边界是椭球。若令\(S = \frac{1}{n} M_C^T M_C\)，则置信域可以写成 \[ \frac{n-p}{p} (\bar{\boldsymbol x} - \boldsymbol\mu_0)^T S^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu_0) \leq F_{1-\alpha}(p, n-p) . \]

多元时联立置信域形状难以把握。对所有\(\boldsymbol a \in \mathbb R^p\)，\(\boldsymbol a^T \boldsymbol\mu\)有置信度为\(1-\alpha\)的联立置信域 \[\begin{aligned} \boldsymbol a^T \bar{\boldsymbol x} \pm \sqrt{\frac{p(n-1)}{n-p} F_{1-\alpha}(p,n-p)} \sqrt{\boldsymbol a^T \left(\frac{1}{n-1} \frac{1}{n} M_C^T M_C \right) \boldsymbol a} , \end{aligned}\] 或 \[ \boldsymbol a^T \bar{\boldsymbol x} \pm \sqrt{\frac{p}{n-p} F_{1-\alpha}(p,n-p)} \sqrt{\boldsymbol a^T S \boldsymbol a} . \] 这样可以分别找到\(\mu_1, \mu_2, \dots, \mu_p\)的置信区间并保证置信区间是同时成立的，只要取\(\boldsymbol a\)为\(p\)阶单位阵的第\(j\)列，即可得关于\(\mu_1, \dots, \mu_p\)的联立置信区间: \[ \bar x_j \pm \sqrt{\frac{p}{n-p} F_{1-\alpha}(p,n-p) s_{jj} }, \ j=1,2,\dots, p . \] 其中\(\bar x_j\)是第\(j\)分量的样本均值，而 \[ s_{jj} = \frac{1}{n} \sum_{i=1}^n (x_{ij} - \bar x_j)^2 . \]

4.8.2 多元正态单总体的均值检验

设总体\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\), \(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)}\)为其样本。对给定的\(\boldsymbol\mu_0\)，为检验 \[\begin{aligned} H_0: \boldsymbol\mu = \boldsymbol\mu_0 \longleftrightarrow H_a: \boldsymbol\mu \neq \boldsymbol\mu_0 , \end{aligned}\] 使用检验统计量 \[\begin{aligned} & (\bar{\boldsymbol x} - \boldsymbol\mu_0)^T \left(\frac{1}{n-1} \frac{1}{n} M_C^T M_C \right)^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu_0) \\ \stackrel{H_0}{\sim} & T^2_{p,n-1} , \end{aligned}\] 或 \[\begin{aligned} & \frac{n-p}{p(n-1)} (\bar{\boldsymbol x} - \boldsymbol\mu_0)^T \left(\frac{1}{n-1} \frac{1}{n} M_C^T M_C \right)^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu_0) \\ \stackrel{H_0}{\sim}& F(p,n-p) . \end{aligned}\] 当检验统计量大于右侧的临界值\(F_{1-\alpha}(p,n-p)\)时拒绝\(H_0\)。

这里为了避免样本协方差阵定义中分母取\(n\)还是取\(n-1\)的歧义所以没有用\(S\)。如果用分母取\(n\)的\(S\)定义，则Hotelling T方统计量为 \[\begin{aligned} & (n-1) (\bar{\boldsymbol x} - \boldsymbol\mu_0)^T S^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu_0) \\ \stackrel{H_0}{\sim} & T^2_{p,n-1} , \end{aligned}\] \(F\)统计量为 \[\begin{aligned} & \frac{n-p}{p} (\bar{\boldsymbol x} - \boldsymbol\mu_0)^T S^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu_0) \\ \stackrel{H_0}{\sim}& F(p,n-p) . \end{aligned}\]

R中用ICSNP::HotellingsT2()或检验rrcov::T2.test()。

例： ICSNP::LASERI数据框中包含了223个芬兰健康受试者的32个测量指标。其中，受试者仰卧和坐起两种姿势的几种指标的差别的变量：

HRT1T4 平均心律变化
COT1T4 心脏输出变化
SVRIT1T4 平均系统心血管阻力指数变化
PWVT1T4 平均脉搏波速率变化

用单样本多元正态Hotelling \(T^2\)检验法检验平均变化是否等于零。

data(LASERI, package="ICSNP")
pairs(LASERI[,25:28])

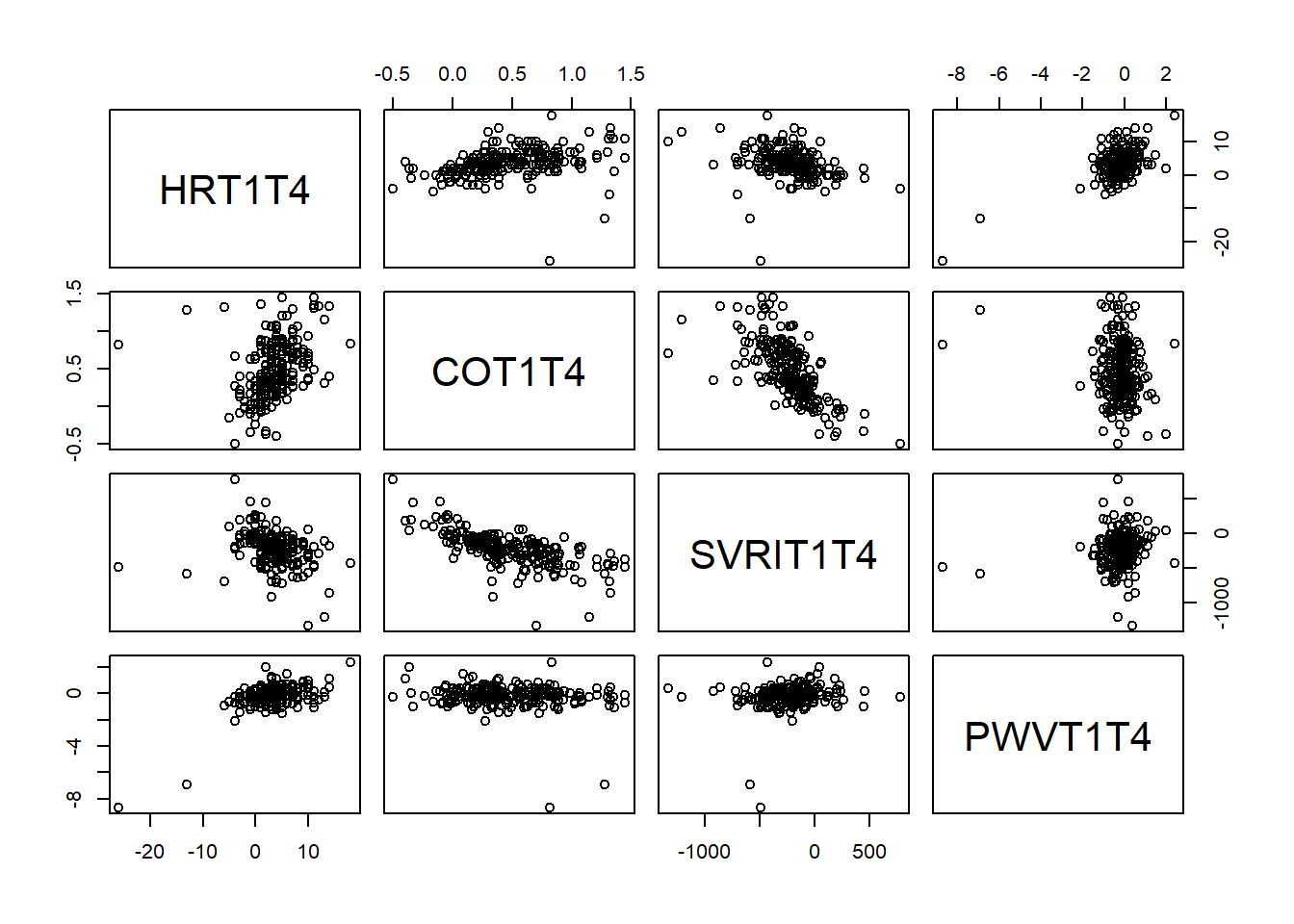
图4.1: 四种指标在仰卧和坐起的变化

ICSNP::HotellingsT2(LASERI[,25:28])

## 
##  Hotelling's one sample T2-test
## 
## data:  LASERI[, 25:28]
## T.2 = 101.67, df1 = 4, df2 = 219, p-value < 2.2e-16
## alternative hypothesis: true location is not equal to c(0,0,0,0)

结果p值小于万分之一，否定前后变化平均值为零。

4.9 独立两样本多元正态分布均值比较

作为两样本一元正态分布均值比较的t检验的推广, 设有两个独立多元正态总体\(\boldsymbol X \sim \text{N}_p(\boldsymbol \mu_X, \Sigma)\)和\(\boldsymbol Y \sim \text{N}_p(\boldsymbol \mu_Y, \Sigma)\)，分别有样本\(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)}\)和 \(\boldsymbol y^{(1)}, \boldsymbol y^{(y)}, \dots, \boldsymbol y^{(m)}\)。考虑如下零假设 \[ H_0:\; \boldsymbol\mu_X = \boldsymbol\mu_Y . \]

设两个样本的样本统计量分别为 \(\bar{\boldsymbol x}, S_X, \bar{\boldsymbol y}, S_Y\)，前面已假定两个总体协方差阵相同，故可以得到合并的协方差阵估计 \[\begin{aligned} S_p = \frac{1}{n+m-2}\left[ (M_C^{(\boldsymbol X)})^T M_C^{(\boldsymbol X)} + (M_C^{(\boldsymbol Y)})^T M_C^{(\boldsymbol Y)} \right], \end{aligned}\] 其中\(M_C^{(\boldsymbol X)}\)和\(M_C^{(\boldsymbol Y)}\)分别是\(\boldsymbol X\)和\(\boldsymbol Y\)的中心化数据矩阵。注意这里\(n+m-2\)是Wishart分布中的自由度， \((n+m-2) S \sim W_p(\Sigma, n+m-2)\)。

检验统计量 \[\begin{aligned} T^2 =& \frac{1}{\frac{1}{n} + \frac{1}{m}} (\bar{\boldsymbol x} - \bar{\boldsymbol y})^T S_p^{-1} (\bar{\boldsymbol x} - \bar{\boldsymbol y}) \\ =& \frac{1}{\frac{1}{n} + \frac{1}{m}} (\bar{\boldsymbol x} - \bar{\boldsymbol y})^T \Big[ \frac{1}{n+m-2} \\ & \left( (M_C^{(\boldsymbol X)})^T M_C^{(\boldsymbol X)} + (M_C^{(\boldsymbol Y)})^T M_C^{(\boldsymbol Y)} \right) \Big]^{-1} (\bar{\boldsymbol x} - \bar{\boldsymbol y}) \\ \stackrel{H_0}{\sim}& T^2(p, n+m-2) , \end{aligned}\] 或 \[\begin{aligned} & \frac{n+m-p-1}{p(n+m-2)} \frac{1}{\frac{1}{n} + \frac{1}{m}} (\bar{\boldsymbol x} - \bar{\boldsymbol y})^T S_p^{-1} (\bar{\boldsymbol x} - \bar{\boldsymbol y}) \\ \stackrel{H_0}{\sim} & F(p, n+m-p-1) . \end{aligned}\]

R中用rrcov::T2.test()检验。

令 \[ \boldsymbol\delta = \boldsymbol\mu_X - \boldsymbol\mu_Y, \] 为了构造\(\boldsymbol\delta\)的置信域，可以用如下的分布： \[\begin{aligned} & \frac{n+m-p-1}{p(n+m-2)} \frac{1}{\frac{1}{n} + \frac{1}{m}} (\bar{\boldsymbol x} - \bar{\boldsymbol y} - \boldsymbol\delta)^T S_p^{-1} (\bar{\boldsymbol x} - \bar{\boldsymbol y} - \boldsymbol\delta) \\ \sim& F(p, n+m-p-1) . \end{aligned}\]

对所有的\(\boldsymbol a \in \mathbb R^p\)， \(\boldsymbol a^T \boldsymbol\delta\)有如下的联立置信区间 \[\begin{aligned} & \boldsymbol a^T (\bar{\boldsymbol x} - \bar{\boldsymbol y}) \\ & \pm \sqrt{\frac{p(n+m-2)}{n+m-p-1} (\frac{1}{n} + \frac{1}{m}) F_{1-\alpha}(p, n+m-p-1) \boldsymbol a^T S_p \boldsymbol a} . \end{aligned}\] 特别地，对每个分量有联立\(1-\alpha\)置信区间 \[ \bar x_j - \bar y_j \pm \sqrt{\frac{p(n+m-2)}{n+m-p-1} (\frac{1}{n} + \frac{1}{m}) F_{1-\alpha}(p, n+m-p-1) S_{p,jj} } . \] 其中\(S_{p,jj}\)是\(S_p\)的\((j,j)\)元素。

如果两个总体的方差阵明显不相同，在大样本情形可以给出关于两总体均值相等的近似的检验。要检验两个总体的方差是否相同，其检验十分依赖于正态性假设，如果总体分布偏离正态则检验结果会很不精确。当关于两个总体均值相等的零假设成立时，大样本情形下 \[ (\bar{\boldsymbol x} - \bar{\boldsymbol y})^T (\frac{S_X}{n} + \frac{S_Y}{m})^{-1} (\bar{\boldsymbol x} - \bar{\boldsymbol y}) \] 近似服从\(\chi^2_p\)分布。统计量超过右侧临界值时拒绝零假设。令\(\boldsymbol\delta = \boldsymbol\mu_X - \boldsymbol\mu_Y\)，则各\(\delta_j\)的联立\(1-\alpha\)置信区间为 \[ \bar x_j - \bar y_j \pm \sqrt{\chi^2_{1-\alpha}(p) \left( \frac{S_{X,jj}}{n} + \frac{S_{Y,jj}}{n} \right)}, \ j=1,2,\dots,p . \]

4.10 独立多样本多元正态分布均值比较

作为一元方差分析和独立两样本多元正态均值比较问题的推广，设有\(k\)个独立多元正态总体\(\boldsymbol X^{(s)}, s=1,2,\dots,k\)，分别有样本\(\boldsymbol x^{(s,i)}, i=1,2,\dots,n_s,\; s=1,2,\dots,k\)。令\(n = n_1 + n_2 + \dots + n_k\)。设\(\boldsymbol X^{(s)} \sim \text{N}_p(\boldsymbol\mu^{(s)}, \Sigma)\), \(s=1,2,\dots,k\)。设\(\boldsymbol X^{(s)}\)的样本均值为\(\bar{\boldsymbol x}^{(s)}\), 令 \[\begin{aligned} \bar{\boldsymbol x} = \frac{1}{n} \sum_{s=1}^k \sum_{i=1}^{n_s} \boldsymbol x^{(s,i)} = \frac{1}{n} \sum_{s=1}^k n_s \bar{\boldsymbol x}^{(s)} . \end{aligned}\] 为所有样本的总平均值。

欲检验 \[\begin{aligned} H_0:\; \boldsymbol\mu^{(1)} = \boldsymbol\mu^{(2)} = \dots = \boldsymbol\mu^{(k)} . \end{aligned}\]

设第\(s\)个总体\(X^{(s)}\)的中心化数据集为\(M_{C}^{(s)}\)，可以得到合并的协方差阵估计 \[\begin{aligned} S = \frac{1}{n-k} \sum_{s=1}^k (M_{C}^{(s)})^T M_{C}^{(s)} . \end{aligned}\] 所有样本的总离差阵有如下分解： \[\begin{aligned} T = & \sum_{s=1}^k \sum_{i=1}^{n_s} (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}) (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x})^T \\ =& \sum_{s=1}^k \sum_{i=1}^{n_s} (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)} + \bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x}) (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)} + \bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x})^T \\ =& \sum_{s=1}^k \sum_{i=1}^{n_s} (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)}) (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)})^T \\ &+ \sum_{s=1}^k \sum_{i=1}^{n_s} (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x}) (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x})^T . \end{aligned}\]

令 \[\begin{aligned} A_s =& \sum_{i=1}^{n_s} (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)}) (\boldsymbol x^{(s,i)} - \bar{\boldsymbol x}^{(s)})^T, \\ =& (M_C^{(s)})^T M_C^{(s)}, \ s=1,2,\dots,k, \\ A =& A_1 + A_2 + \dots + A_k, \end{aligned}\] 称\(A\)为组内离差阵。则\(A_s \sim W_p(\Sigma, n_s - 1)\)且\(A_1, A_2, \dots, A_k\)相互独立，于是\(A \sim W_p(\Sigma, n-k)\)。令 \[\begin{aligned} B =& \sum_{s=1}^k \sum_{i=1}^{n_s} (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x}) (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x})^T \\ =& \sum_{s=1}^k n_s (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x}) (\bar{\boldsymbol x}^{(s)} - \bar{\boldsymbol x})^T , \end{aligned}\] 称为组间离差阵。

方差分解公式： \[\begin{aligned} T = A + B . \end{aligned}\]

当\(H_0\)成立时， \(B \sim W_p(\Sigma, k-1)\)，且与\(A\)独立，这时\(T \sim W_p(\Sigma, n-1)\)。

在\(H_0\)成立时如下统计量 \[\begin{aligned} \Lambda = \frac{\text{det}(A)}{\text{det}(A + B)} = \frac{\text{det}(A)}{\text{det}(T)} \end{aligned}\] 服从Wilks分布\(\Lambda(p, n-k, k-1)\). 当\(\Lambda\)统计量的值低于左侧\(\alpha\)临界值时拒绝\(H_0\)。

在R中，用rrcov::Wilks.test()计算。

4.11 重复测量问题及其检验

在一元的统计中有“成对均值比较”问题，可以采用成对t检验。将这个问题推广到多元。

设有\(n\)个不同的个体，针对某个共同的指标对每个个体在不同时间进行\(p\)次测量，或者在不同条件（处理组）下进行了\(p\)次测量，结果仍可以保存为一个观测数据集\(M\)，第\(i\)行\(\boldsymbol x^{(i)}\)为第\(i\)个体的\(p\)次测量值。设样本均值为\(\bar{\boldsymbol x}\)，样本方差阵为\(S\)。设\(\boldsymbol x^{(i)}\)独立同\(N_p(\boldsymbol\mu, \Sigma)\)分布。这样的模型称为重复测量。

实际应用中经常需要对\(p\)个均值\(\mu_1, \dots, \mu_p\)进行检验，比如， \[\begin{align} H_0: \mu_1 = \dots = \mu_p . \tag{4.1} \end{align}\] 这个零假设就代表了没有处理效应，所有的处理组没有区别。

这是线性假设检验的一个应用。下面先给出一般的线性假设问题及其检验方法。

设\(A\)是已知的\(q \times p\)行满秩矩阵(\(q\leq p\))， \(\boldsymbol a\)是已知向量，要检验 \[\begin{align} H_0: A \boldsymbol\mu = \boldsymbol a . \tag{4.2} \end{align}\] 第\(i\)个观测为\(\boldsymbol x^{(i)}\)，令\(\boldsymbol y^{(i)} = A \boldsymbol x^{(i)}\)，有\(\boldsymbol y^{(i)} \sim \text{N}(A \boldsymbol\mu, A \Sigma A^T)\)，以\(\boldsymbol y^{(i)}\), \(i=1,\dots,n\)为样本时，样本均值为\(A \bar{\boldsymbol x}\)，样本方差阵为\(A S A^T\)。当\(H_0\)成立时， \(E[\boldsymbol y^{(i)}] = \boldsymbol a\)，有 \[ n (A \bar{\boldsymbol x} - \boldsymbol a)^T (A \Sigma A^T)^{-1} (A \bar{\boldsymbol x} - \boldsymbol a) \sim \chi^2_q . \] 若\(\Sigma\)未知，用\(S\)代替\(\Sigma\)，有 \[\begin{align} (n-1) (A \bar{\boldsymbol x} - \boldsymbol a)^T (A S A^T)^{-1} (A \bar{\boldsymbol x} - \boldsymbol a) \sim T^2_{q, n-1} . \tag{4.3} \end{align}\]

检验问题(4.1)是(4.2)的特例，可以写成 \[\begin{align} C \boldsymbol\mu = \boldsymbol 0, \tag{4.4} \end{align}\] 其中 \[ C = \begin{pmatrix} 1 & -1 & 0 & \cdots & 0 \\ 0 & 1 & -1 & \cdots & 0 & \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & 1 & -1 \end{pmatrix} . \] \(C\)的每一行称为参数\(\boldsymbol\mu\)的一个“对照”(contrast)，因为每一行的元素和等于零。这样，当(4.1)的\(H_0\)成立时，统计量 \[\begin{align} (n-1) \bar{\boldsymbol x}^T C^T (C S C^T)^{-1} C \bar{\boldsymbol x} \sim T^2_{p-1,n-1}, \tag{4.5} \end{align}\] \[ \] 而 \[ \frac{n-p+1}{p-1} \bar{\boldsymbol x}^T C^T (C S C^T)^{-1} C \bar{\boldsymbol x} \sim F(p-1, n-p+1) . \] 超过右侧临界值时拒绝零假设。

注意这个检验结果显著时，仅能知道\(p\)个组的均值不是完全相等的，不能推断具体哪些均值之间有显著差异。在试验设计时，常常有一个“对照组”，其余的\(p\)个组都与对照组进行比较。这时，仍可以检验(4.1)中的\(H_0\)，问题化为 \[\begin{align} C \boldsymbol\mu = \boldsymbol 0, \tag{4.6} \end{align}\] 其中 \[ C = \begin{pmatrix} 1 & -1 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & 0 & \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 1 & 0 & \cdots & 0 & -1 \end{pmatrix} . \] (4.6)本质上和(4.4)相同，都是检验(4.1)，但可以用来进行与对照组的单个比较。对于这样取值的\(C\)， (4.5)仍成立。令\(\boldsymbol y^{(i)} = C \boldsymbol x^{(i)}\)，则 \[ \boldsymbol y^{(i)} \sim \text{N}_{p-1}(C \boldsymbol\mu, C \Sigma C^T) . \] 对所有\(\boldsymbol a \in \mathbb R^{p-1}\)， \(\boldsymbol a^T C \boldsymbol\mu\)有如下联立\(1-\alpha\)置信区间： \[\begin{align} \boldsymbol a^T C \bar{\boldsymbol x} \pm \sqrt{ \frac{p-1}{n-p+1} F_{1-\alpha}(p-1, n-p+1) \boldsymbol a^T C S C^T \boldsymbol a } . \tag{4.7} \end{align}\]

注意\(C \boldsymbol 1_{p} = \boldsymbol 0_{p-1}\)，于是\(\boldsymbol a^T C 1_{p} = 0\)，即\(\boldsymbol b = C^T \boldsymbol a \in \mathbb R^p\)是一个对照， \(\boldsymbol b^T \boldsymbol 1_p = 0\)。于是， (4.7)可以写成如下的关于\(\boldsymbol b^T \boldsymbol\mu\)的联立置信区间 \[\begin{align} \boldsymbol b^T \bar{\boldsymbol x} \pm \sqrt{ \frac{p-1}{n-p+1} F_{1-\alpha}(p-1, n-p+1) \boldsymbol b^T S \boldsymbol b } . \tag{4.8} \end{align}\] 不同的\(\boldsymbol b\)的选取可以用于各个处理组与对照组的均值比较。比如，取\(\boldsymbol b = (1,-1,0,0)^T\)比较\(\mu_1\)和\(\mu_2\)，取\(\boldsymbol b = (1,0,0,-1)^T\)比较\(\mu_1\)和\(\mu_4\)，取\(\boldsymbol b = (1,-1/3,-1/3,-1/3)^T\)比较\(\mu_1\)和其余三个组的均值。

\(\boldsymbol b\)也可以取\(\boldsymbol b = C^T \boldsymbol a\)以外的形式。比如，取\(\boldsymbol b = (0, 1, 0, -1)^T\)可以比较\(\mu_2\)与\(\mu_4\)，

4.12 多元正态分布的特殊方差阵

当变量维数\(p\)较高时，正态分布方差阵\(\Sigma\)含有\(p(p+1)/2\)个自由参数，需要估计的参数较多，使得中小样本时的估计自由度不足。为此可以进行一些方差阵结构的简化，如：

\(\Sigma = \sigma^2 I_p\)，所有分量相互独立且有共同方差。
\(\Sigma = \text{diag}(\sigma_1^2, \dots, \sigma_p^2)\)，这时各分量相互独立。
可交换分布(interchangable, 任意边缘分布都相同)：

\[\begin{aligned} \Sigma = \sigma^2 \left(\begin{array}{cccc} 1 & \rho & \cdots & \rho \\ \rho & 1 & \cdots & \rho \\ \vdots & \vdots & \ddots & \vdots \\ \rho & \rho & \cdots & 1 \end{array}\right) . \end{aligned}\]

可推广到方差允许不同的情形。
一阶自相关型：\(\text{corr}(X_i, X_j) = \rho^{|j-i|}\)。

4.13 多元正态性检验

可以查看各个分量的QQ图、作一元正态性检验。可以画散点图矩阵，看每个二元边缘分布散点形状。

4.13.1 推广的QQ图

设观测为\(\boldsymbol x^{(i)}, i=1,\dots,n\)， \(\bar{\boldsymbol x}\), \(S\)为样本均值和样本协方差阵。定义 \[\begin{aligned} D_i^2 = (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T S^{-1} (\boldsymbol x^{(i)} - \bar{\boldsymbol x}), \ i=1,\dots,n \end{aligned}\] 为每个观测点到中心的Mahalanobis距离。当观测个数\(n\)远大于变量个数\(p\)时， \(D_1^2, \dots, D_n^2\)近似独立地服从\(\chi^2(p)\)分布。令\(t_i = \chi^2_{i/(n+1)}(p)\), 作\((t_i, D_{(i)}^2)\)的散点图，应该近似位于一条直线附近。还可以做变换\(z_i = \Phi^{-1}( \text{pchisq}(D_i^2, p) )\)，认为\(z_i\)是正态分布样本，作一元正态性检验。

4.13.2 多元偏度峰度检验

定义 \[\begin{aligned} D_{ij} = (\boldsymbol x^{(i)} - \bar{\boldsymbol x})^T S^{-1} (\boldsymbol x^{(j)} - \bar{\boldsymbol x}), \end{aligned}\] 作为两个观测点之间的距离。

多元偏度定义为 \[\begin{aligned} \hat\gamma_3 = n^{-2} \sum_{i \neq j} D_{ij}^3 , \end{aligned}\] 则在正态总体假设下 \(\frac{n}{6} \hat\gamma_3\)渐近服从\(\chi^2(p(p+1)(p+2)/6)\)分布，取右侧临界值作否定域。

多元峰度定义为 \[\begin{aligned} \hat\gamma_4 = n^{-1} \sum_{i} D_{ii}^2 , \end{aligned}\] 则在正态总体假设下 \(\hat\gamma_4\)渐近服从\(\text{N}(p(p+2),\; 8p(p+2)/n)\)分布。

R中psych::mardia执行多元偏度峰度检验并作广义QQ图。

4.13.3 多元Shaprio-Wilk检验

R中mvnormtest::mshapiro.test()执行多元的Shapiro-Wilk检验。

4.13.4 例子

使用Zelterman(2015) P. 197 Table 7.4 著名品牌糖果营养值数据。

数据的散点图矩阵：

candy <- read_csv("data/candy.csv",
  show_col_types = FALSE)

d <- as.matrix(candy[,2:7])
n <- nrow(d)
p <- ncol(d)

pairs(d)

图4.2: 糖果营养值散点图矩阵

用到中心的距离作广义QQ图：

mah <- mahalanobis(d, colMeans(d), var(d))
## p=6, 应该近似独立chi^2(6)分布
y <- sort(mah)
x <- qchisq((1:n)/(n+1), p)
plot(x, y, main='Mahalanobis distance vs. chi-square quantiles',
     xlab='Chi-square quantile',
     ylab='Obs')
lm.res <- lm(y ~ x); abline(lm.res)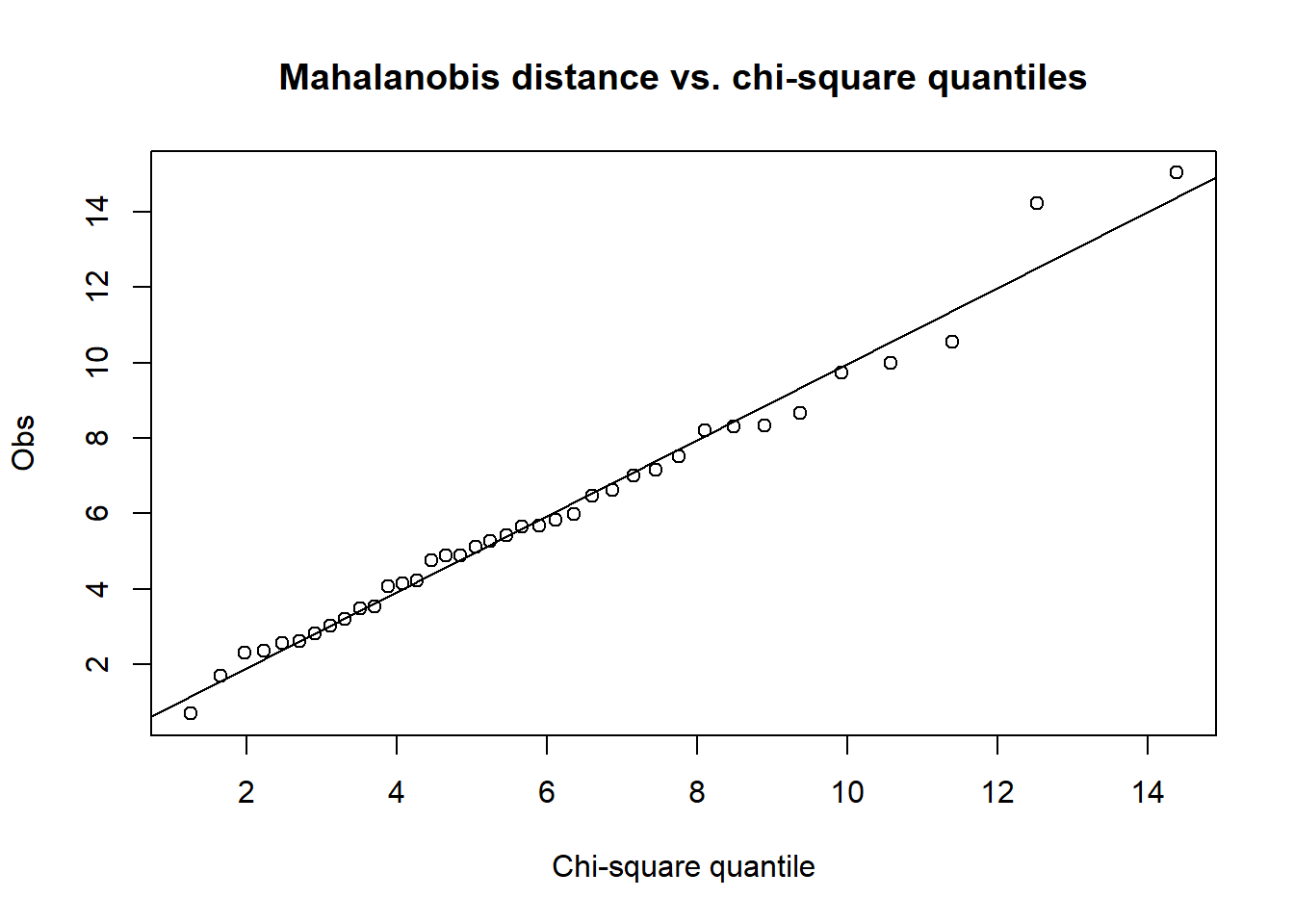

图4.3: 糖果营养值广义QQ图

作正态化变换, 然后用Shapiro-Wilk检验:

z <- qnorm(pchisq(mah, 6))
shapiro.test(z)

## 
##  Shapiro-Wilk normality test
## 
## data:  z
## W = 0.98968, p-value = 0.9752

正态性很好。

用psych::mardia对糖果数据进行多元偏度峰度检验并作广义QQ图:

psych::mardia(d)

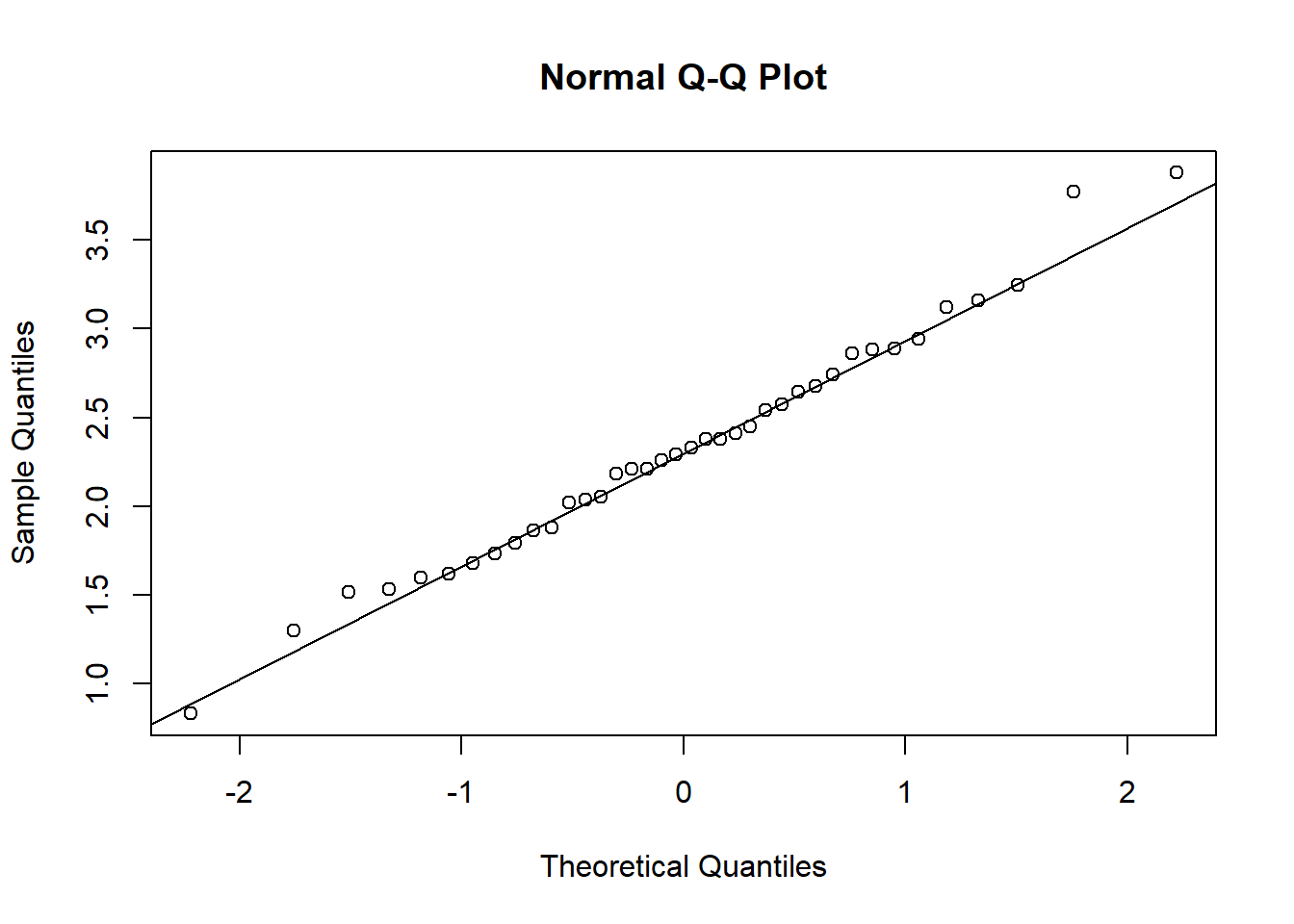
图4.4: 糖果营养值广义QQ图

## Call: psych::mardia(x = d)
## 
## Mardia tests of multivariate skew and kurtosis
## Use describe(x) the to get univariate tests
## n.obs = 38   num.vars =  6 
## b1p =  8.2   skew =  51.96  with probability  <=  0.63
##  small sample skew =  57.32  with probability <=  0.43
## b2p =  44.12   kurtosis =  -1.22  with probability <=  0.22

用mvnormtest::mvshapiro.test()对糖果数据检验多元正态性。要求输入每个观测占一列，每个变量占一行

d <- t(as.matrix(candy[,2:7]))
mvnormtest::mshapiro.test(d)

## 
##  Shapiro-Wilk normality test
## 
## data:  Z
## W = 0.87314, p-value = 0.0004835

p值为0.00048高度显著。这个检验法以及相应的程序的可靠性有待检查。

用mvShapiroTest::mvShapiro.Test()对糖果数据检验多元正态性:

mvShapiroTest::mvShapiro.Test(as.matrix(candy[,2:7]))

## 
##  Generalized Shapiro-Wilk test for Multivariate Normality by
##  Villasenor-Alva and Gonzalez-Estrada
## 
## data:  as.matrix(candy[, 2:7])
## MVW = 0.96002, p-value = 0.05529

结果p值为0.05529

References

Wolfgang Härdle, Léopold Simar. 2015. Applied Multivariate Statistical Analysis. 4th Edition. Springer.