12 多维标度分析

《多元统计分析—基于R》课程的R示例, 主要参考书: 费宇《多元统计分析-基于R》，人民大学出版社，2012。

12.1 介绍

多维数据如果想做二维或三维图， 需要进行降维。 虽然主成分、因子分析、对应分析、典型相关分析也可以降维， 但是关注的保留信息不同。 多维标度分析关注的是保留原来的距离信息或相似度信息。

例如： \(p\)维降维到1,2或3维， 尽可能保持距离； 地图上的城市之间的距离并不是车程或时间距离， 重新绘图使其反映两两之间的车程； 在仅知道一组城市彼此哪是最近， 哪是次近等信息的情况下， 作图表示这些关系。 “城市”可以换成“产品”、“品牌”、“指标”等。

距离可以理解为“不相似度”， 其反面是“相似度”， 可以从近似估计、打分表等来源产生。 也可以用“邻近程度”(proximity)同时表示距离、不相似度、相似度。 需要仅从彼此的不相似度或者相似度， 找到欧式空间的点使得这些点的欧式距离能够表示原来的不相似度或者相似度。

用欧式空间点之间的距离近似表示邻近程度， 称为空间方法。 表示邻近程度的模型还有树方法和混合方法。

多维标度分析于1940年代发明， 广泛应用于心理学、市场营销、经济管理、 交通、生态学、地质学等领域。 内容丰富，方法较多。

常用：

• 度量分析法：从具体的距离、比例等数据出发进行化简。
• 非度量分析法：用顺序、秩等信息推断相互关系。

12.2 古典多维标度法

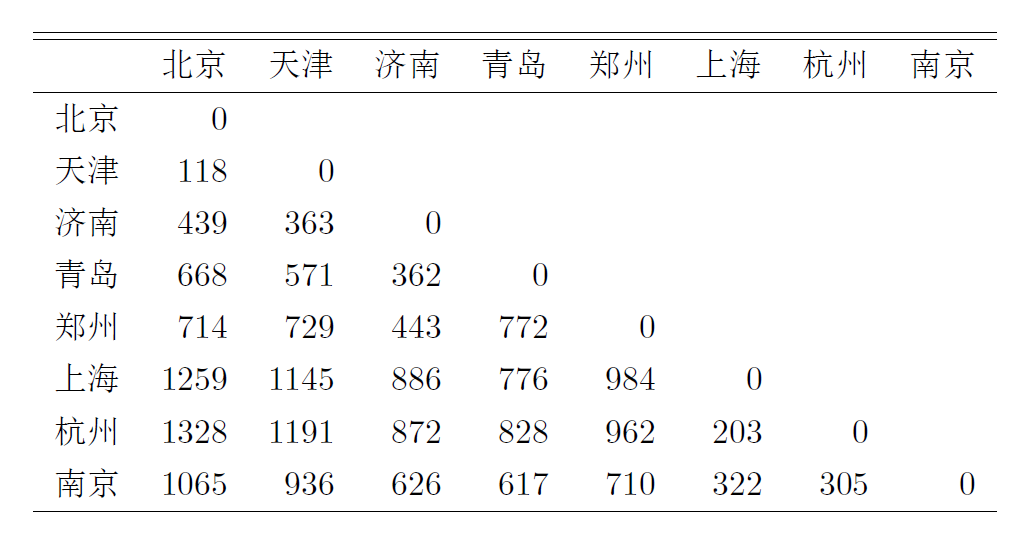
考虑如下问题： 中国八个城市间道路里程（非直线距离）见下表。 要画图表示这样的距离。

12.2.1 概念

\(n\)阶方阵\(D = (d_{ij})_{n \times n}\)如果满足条件 \[\begin{aligned} (1)&\quad D = D^T; \\ (2)&\quad d_{ij} \geq 0, \ d_{ii}=0\ (i, j = 1,2,\dots,n) \end{aligned}\] 则称矩阵\(D\)为广义距离阵， 简称距离阵， \(d_{ij}\)称为第\(i\)点与第\(j\)点间的距离。

广义距离不一定满足三角不等式。

给定广义距离阵\(D\), 对较低的维数\(k\)(一般\(k=1,2,3\))， 如果在\(\mathbb R^k\)中能找到点\(\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n\)， \(\boldsymbol x_i\)与\(\boldsymbol x_j\)的欧式距离为\(\hat d_{ij}\), \(\hat D = (\hat d_{ij})_{n \times n}\)， 使得\(\hat D\)与\(D\)在某种意义上最接近， 则\(n \times k\)矩阵\(M_X = (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)^T\) 称为\(D\)的一个古典多维标度解(CMDS)。

称\(\boldsymbol x_i\)为\(D\)的一个拟合构造点, 称\(M_X\)为\(D\)的拟合构图, 称\(\hat D\)为\(D\)的拟合距离阵。

如果能做到\(\hat D = D\), 则称\(\boldsymbol x_i\)为\(D\)的构造点， 称\(M_X\)为\(D\)的构图。

如果\(M_X\)是\(D\)的\(k\)维构图，矩阵\(P\)为\(k\)阶正交阵， \(\boldsymbol a \in \mathbb R^k\)为常数向量，令 \[\begin{aligned} \boldsymbol y_i = P \boldsymbol x_i + \boldsymbol a, \end{aligned}\] 则\(M_Y = (\boldsymbol y_1, \boldsymbol y_2, \dots, \boldsymbol y_n)^T\)也是\(D\)的构图。 这是因为平移与正交变换都不改变欧式距离。

所以，构图如果存在也不唯一。

对一个\(n\)阶广义距离阵\(D\), 如果存在某个正整数\(k\)和\(\mathbb R^k\)中的\(n\)个点 \(\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n\)使得 \[\begin{aligned} d_{ij} = \| \boldsymbol x_i - \boldsymbol x_j \| = \sqrt{ (\boldsymbol x_i - \boldsymbol x_j)^T (\boldsymbol x_i - \boldsymbol x_j) }, \ i, j = 1,2,\dots,n \end{aligned}\] 则称\(D\)为欧式距离阵。

12.2.2 构图的求解

若已知欧式距离阵\(D\)， 如何反过来求出构图\(M_X\)？

为此， 先假设\(M_X\)为\(n \times k\)已知矩阵， \(D\)是\(M_X\)的\(n\)行之间的欧式距离矩阵。 考虑\(M_X\)各行之间的内积： \[ B = M_X M_X^T, \]

设\(M_X\)的第\(i\)行为\(\boldsymbol x_i^T\)， 第\((i,\ell)\)元素为\(x_{i\ell}\)， 则\(B\)的\((i,j)\)元素为\(\boldsymbol x_i^T \boldsymbol x_j\)， \[\begin{align} b_{ij} =& \boldsymbol x_i^T \boldsymbol x_j \\ =& \sum_{\ell=1}^k x_{i \ell} x_{j \ell} , \ i, j = 1,2,\dots, n . \tag{12.1} \end{align}\]

\(M_X\)中\(i, j\)两行的欧式距离平方为 \[\begin{align} d_{ij}^2 =& \sum_{\ell=1}^k (x_{i\ell} - x_{j\ell})^2 \\ =& \sum_{\ell=1}^k x_{i\ell}^2 + \sum_{\ell=1}^k x_{j\ell}^2 - 2 \sum_{\ell=1}^k x_{i\ell} x_{j\ell} \\ =& b_{ii} + b_{jj} - 2 b_{ij} . \tag{12.2} \end{align}\]

如果能从\(D\)矩阵得到\(B\)矩阵， 就可以从\(B\)矩阵分解\(B = M_X M_X^T\)得到\(M_T\)矩阵。 因为\(M_X\)代表的\(n\)个点在平移、旋转（正交变换）下都构成\(D\)的构图， 所以不妨设\(M_X\)的每一列和为0， 即 \[\begin{align} \sum_{i=1}^n x_{i \ell} = 0, \ \ell = 1,2,\dots, k. \tag{12.3} \end{align}\] 代入到(12.1)中， 可得 \[ \sum_{i=1}^n b_{ij} = 0, \quad \sum_{j=1}^n b_{ij} = 0 . \] 再代入到(12.2)中， 可得 \[\begin{aligned} \sum_{i=1}^n d_{ij}^2 =& T + n b_{jj}, \\ \sum_{j=1}^n d_{ij}^2 =& T + n b_{ii}, \\ \sum_{i=1}^n \sum_{j=1}^n d_{ij}^2 =& 2 n T . \end{aligned}\] 其中\(T = \sum_{i=1}^n b_{ii}\)是矩阵\(B\)的迹。 于是， 先求出\(T\)， 再求出每一个\(b_{ii}\)， 则可以解出 \[ b_{ij} = (b_{ii} + b_{ij} - d_{ij}^2) / 2 , \ i \neq j . \] 简单推导可得\(b_{ij}\)的一般公式为 \[ b_{ij} = -\frac{1}{2} (d_{ij}^2 - d_{i.}^2 - d_{.j}^2 + d_{..}^2) . \] 其中 \[\begin{aligned} d_{i.}^2 =& \frac{1}{n} \sum_{j=1}^n d_{ij}^2, \\ d_{.j}^2 =& \frac{1}{n} \sum_{i=1}^n d_{ij}^2, \\ d_{..}^2 =& \frac{1}{n^2} \sum_{i=1}^n \sum_{i=1}^n d_{ij}^2 . \end{aligned}\]

得到矩阵\(B\)以后， 为了求\(M_X\)使得\(B = M_X M_X^T\)， 只要作特征值分解 \[ B = \Gamma \Lambda \Gamma^T, \] 其中\(\lambda\)是\(B\)的\(k\)个正特征值组成的对角阵， 取\(M_X = \Gamma \Lambda^{1/2}\)即可。

12.2.3 欧式距离阵的判断

上述的从\(D\)到\(B\)， 从\(B\)到\(M_X\)的过程， 也是判断一个广义距离阵\(D\)是否欧式距离阵的方法。 下面用矩阵方法表述。

令\(H = I_n - \frac{1}{n} \boldsymbol 1_n \boldsymbol 1_n^T\)， 这是\(n\)阶中心化矩阵。 设\(D\)为广义距离阵，令\(a_{ij} = -\frac12 d_{ij}^2\), \(A = (a_{ij})_{n \times n}\)， \(B = HAH\)。 这相当于前一小节的\(B\)矩阵。

定理 \(D\)是欧式距离阵的充分必要条件是\(B \geq 0\)(半正定)。

注：即特征值都是正数或者0。

证明: 先证明必要性。 若\(D\)为欧式距离阵， 则存在正整数\(k\)和\(n\)个\(\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n \in \mathbb R^k\)， 使得 \[\begin{aligned} d_{ij}^2 = -2 a_{ij} = (\boldsymbol x_i - \boldsymbol x_j)^T (\boldsymbol x_i - \boldsymbol x_j) . \end{aligned}\] 记\(M_X = (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)^T\), \(J = \boldsymbol 1_n \boldsymbol 1_n^T\)是元素全为1的\(n\)阶方阵， 令\(\bar{\boldsymbol a} = (\bar a_{1\bullet}, \bar a_{2\bullet}, \dots, \bar a_{n\bullet})^T\)， \[\begin{aligned} \bar a_{\ell \bullet} =& \frac{1}{n} \sum_{j=1}^n a_{\ell j} = \frac{1}{n} \sum_{i=1}^n a_{i \ell}, \\ \bar a_{\bullet\bullet} =& \frac{1}{n^2} \sum_{i=1}^n \sum_{j=1}^n a_{ij} = \frac{1}{n} \sum_{\ell=1}^n \bar a_{\ell \bullet}, \end{aligned}\] 则\(\bar{\boldsymbol a} = \frac{1}{n} A \boldsymbol 1 = (\frac{1}{n}\boldsymbol 1^T A)^T\), \(\bar a_{\bullet\bullet} = \frac{1}{n^2} \boldsymbol 1^T A \boldsymbol 1\)。 于是 \[\begin{aligned} B =& HAH = (I - \frac{1}{n} J) A (I - \frac{1}{n} J) \\ =& A - \frac{1}{n} A J - \frac{1}{n} J A + \frac{1}{n^2} J A J \end{aligned}\] 其中 \[\begin{aligned} \frac{1}{n} A J =& (\frac{1}{n} A \boldsymbol 1) \boldsymbol 1^T = \bar{\boldsymbol a} \boldsymbol 1^T, \\ \frac{1}{n} J A =& \left( \frac{1}{n} A J \right)^T = \boldsymbol 1 \bar{\boldsymbol a}^T, \\ \frac{1}{n^2} J A J =& \boldsymbol 1 \left( \frac{1}{n^2} \boldsymbol 1^T A \boldsymbol 1 \right) \boldsymbol 1^T = \bar a_{\bullet\bullet} \boldsymbol 1 \boldsymbol 1^T, \end{aligned}\] 所以 \[\begin{aligned} B =& A - \bar{\boldsymbol a} \boldsymbol 1^T - \boldsymbol 1 \bar{\boldsymbol a}^T + \bar a_{\bullet\bullet} J, \nonumber\\ b_{ij} =& a_{ij} - \bar a_{i\bullet} - \bar a_{j\bullet} + \bar a_{\bullet\bullet} \ . \end{aligned} \tag{*} \]

由于 \[\begin{aligned} a_{ij} = -\frac12(\boldsymbol x_i - \boldsymbol x_j)^T (\boldsymbol x_i - \boldsymbol x_j) = -\frac12 \boldsymbol x_i^T \boldsymbol x_i - \frac12 \boldsymbol x_j^T \boldsymbol x_j + \boldsymbol x_i^T \boldsymbol x_j, \end{aligned}\] 记\(c = \frac{1}{n} \sum_{k=1}^n \boldsymbol x_k^T \boldsymbol x_k\), 则 \[\begin{aligned} \bar a_{i\bullet} =& -\frac12 \boldsymbol x_i^T \boldsymbol x_i - \frac12 c + \boldsymbol x_i^T \bar{\boldsymbol x}, \\ \bar a_{\bullet\bullet} =& \frac{1}{n} \sum_{i=1}^n \bar a_{i\bullet} = -\frac12 c - \frac12 c + \bar{\boldsymbol x}^T \bar{\boldsymbol x} = -c + \bar{\boldsymbol x}^T \bar{\boldsymbol x}, \end{aligned}\] 所以 \[\begin{aligned} b_{ij} =& -\frac12 \boldsymbol x_i^T \boldsymbol x_i - \frac12 \boldsymbol x_j^T \boldsymbol x_j + \boldsymbol x_i^T \boldsymbol x_j \\ & + \frac12 \boldsymbol x_i^T \boldsymbol x_i + \frac12 c - \boldsymbol x_i^T \bar{\boldsymbol x} \\ & + \frac12 \boldsymbol x_j^T \boldsymbol x_j + \frac12 c - \boldsymbol x_j^T \bar{\boldsymbol x} \\ & - c + \bar{\boldsymbol x}^T \bar{\boldsymbol x} \\ =& \boldsymbol x_i^T \boldsymbol x_j - \boldsymbol x_i^T \bar{\boldsymbol x} - \boldsymbol x_j^T \bar{\boldsymbol x} + \bar{\boldsymbol x}^T \bar{\boldsymbol x} \\ =& (\boldsymbol x_i - \bar{\boldsymbol x})^T (\boldsymbol x_j - \bar{\boldsymbol x}) . \end{aligned}\]

考虑中心化构图\(H M_X\), 记\(\bar{\boldsymbol x} = \frac{1}{n} \sum_{i=1}^n \boldsymbol x_i\), 则 \[\begin{aligned} H M_X =& (I - \frac{1}{n} \boldsymbol 1 \boldsymbol 1^T) M_X = M_X - \boldsymbol 1 \left( \frac{1}{n} \boldsymbol 1^T M_X \right) \\ =& M_X - \boldsymbol 1 \left( \frac{1}{n} \sum_{i=1}^n \boldsymbol x_i^T \right) = M_X - \boldsymbol 1 \bar{\boldsymbol x}^T \\ =& (\boldsymbol x_1 - \bar{\boldsymbol x}, \boldsymbol x_2 - \bar{\boldsymbol x}, \dots, \boldsymbol x_n - \bar{\boldsymbol x})^T , \end{aligned}\] 于是 \((H M_X) (H M_X)^T\)的\((i,j)\)元为\((\boldsymbol x_i - \bar{\boldsymbol x})^T (\boldsymbol x_j - \bar{\boldsymbol x}) = b_{ij}\), 所以 \[\begin{aligned} B = HAH = (H M_X) (H M_X)^T \end{aligned}\] 是半正定矩阵。

再来证明充分性。 若\(B = HAH\)是半正定矩阵， 则\(B\)有特征值分解 \[\begin{aligned} B = \Gamma \Lambda \Gamma^T, \end{aligned}\] 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_k)\)， 对角线元素为\(B\)的所有正特征值， \(\Gamma\)是\(n \times k\)矩阵， 满足\(\Gamma^T \Gamma = I_k\)。 令\(\Gamma \Lambda^{1/2} = M_X = (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)^T\), 则\(B = M_X M_X^T = (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)^T (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)\), \(\boldsymbol x_i \in \mathbb R^k\), 有\(b_{ij} = \boldsymbol x_i^T \boldsymbol x_j\)。 于是 \[\begin{aligned} (\boldsymbol x_i - \boldsymbol x_j)^T (\boldsymbol x_i - \boldsymbol x_j) =& \boldsymbol x_i^T \boldsymbol x_i + \boldsymbol x_j^T \boldsymbol x_j - 2 \boldsymbol x_i^T \boldsymbol x_j \\ =& b_{ii} + b_{jj} - 2 b_{ij} \\ =& a_{ii} - 2 \bar a_{i\bullet} + \bar a_{\bullet\bullet} \qquad\text{(用(*))代入)} \\ & + a_{jj} - 2 \bar a_{j\bullet} + \bar a_{\bullet\bullet} \\ & - 2 a_{ij} + 2 \bar a_{i\bullet} + 2 \bar a_{j\bullet} - 2 \bar a_{\bullet\bullet} \\ =& a_{ii} + a_{jj} - 2 a_{ij} \\ =& -2 a_{ij} \qquad\text{(注意$a_{ii}=a_{jj}=0$)} \\ =& d_{ij}^2 \end{aligned}\] 这证明了\(D\)是欧式距离阵。 证毕。

12.2.4 欧式距离阵的构图求解

设\(D\)是欧式距离阵，存在\(k\)维的构图， 求解\(M_X\)的步骤如下：

• \(D \longrightarrow A\);
• \(A \longrightarrow B\);
• 对\(B\)作特征值分解\(B = \Gamma \Lambda \Gamma^T\), \(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_k)\), \(\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_k\)是\(B\)的正特征值， \(\Gamma\)是\(n \times k\)阵满足\(\Gamma^T \Gamma = I_k\);
• 令\(M_X = \Gamma \Lambda^{1/2}\)，则\(n \times k\) 矩阵\(M_X = (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n)^T\)是\(D\)的构图, \(\boldsymbol x_i \in \mathbb R^k\)。

理论上可以证明， 若\(D\)是\(n \times p\)矩阵\(M\)代表的\(n\)个点的欧式距离阵， 则从\(D\)求解的\(n \times k\)构图矩阵\(M_X\)， 等价于\(M\)的主成分分解结果。 若取\(M\)的\(m \leq k\)个样本主成分， 这些样本主成分代表的\(n\)个点的距离为\(D^{(m)}\)， 则在所有的\(n \times m\)矩阵代表的\(n\)个点的欧式距离近似\(D\)当中， 前\(m\)个样本主成分得到的结果是最好的。

12.2.5 广义距离阵求解

若\(D\)是广义距离阵，\(B = HAH\), 如果\(B\)有负特征值， 则\(D\)没有严格的构图。 如果负特征值的绝对值都比较小， 可以用拟合构图近似\(D\)。 即使\(D\)存在\(k\)维构图，如果\(k\)比较大， 这样降维也用处不大， 也用更低维数的拟合构图近似\(D\)。

令 \[\begin{aligned} p_{1k} = \frac{\sum_{i=1}^k \lambda_i}{\sum_{i=1}^n |\lambda_i|}, \quad p_{2k} = \frac{\sum_{i=1}^k \lambda_i^2}{\sum_{i=1}^n \lambda_i^2}, \end{aligned}\] 其中\(\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_k > 0\), \(p_{1k}\)和\(p_{2k}\)相当于降维的累积贡献率， 希望在\(k\)较小（\(k=1,2,3\)）时得到满意的累积贡献率如80%。 实际中还应要求前\(k\)个特征值为正。

设\(k\)较小同时前\(k\)个特征值的累积贡献率较高， 取\(\lambda_i\)对应的单位特征向量\(\boldsymbol\gamma_i \in \mathbb R^n\), 令\(M_X = (\lambda_1^{1/2} \boldsymbol\gamma_1, \lambda_2^{1/2} \boldsymbol\gamma_2, \dots, \lambda_k^{1/2} \boldsymbol\gamma_k)\), 则\(M_X\)是\(n \times k\)矩阵， 每一行\(\boldsymbol x_i^T\)是\(k\)维行向量， \(\boldsymbol x_i\)是\(D\)的第\(i\)个拟合构造点。

如果\(B\)有绝对值比较大的负特征值， 古典多维标度法不适用， 可以考虑其它方法， 如非度量多维标度法。

12.2.6 R中的古典多维标度法

已知广义距离阵\(D\), 可以用R的cmdscale()函数求解。

12.2.6.1 例10-3：城市距离

例如： P.134例10.3，输入我国八个城市的里程距离矩阵，作二维图。

cityDist <- readr::read_csv(
  "data/八城市间里程.csv",
  locale=readr::locale(encoding = "GB18030"),
  show_col_types = FALSE)

## New names:
## • `` -> `...1`

names(cityDist)[1] <- "城市"
d <- as.data.frame(cityDist[,-1])
row.names(d) <- cityDist[["城市"]]

获取矩阵的下三角部分，上三角部分置缺失:

lower.triangle <- function(A){
  n <- nrow(A)
  A[outer(1:n, 1:n, `<`)] <- NA
  A
}

用热力图表现距离矩阵：

library(pheatmap)

## Warning: 程辑包'pheatmap'是用R版本4.1.3 来建造的

pheatmap(d)

pheatmap()会自动对矩阵的各行、各列用谱系聚类法分类并作图表现出来。

八个城市距离的多维标度分析结果:

res <- cmdscale(d, k = 2, eig=TRUE)
print(res)

## $points
##            [,1]        [,2]
## 北京 -658.14610  -52.301759
## 天津 -522.00992 -133.917153
## 济南 -229.30657   32.365307
## 青岛  -80.72182 -277.225217
## 郑州 -171.98297  474.047645
## 上海  610.52727 -102.636996
## 杭州  659.93216    5.717159
## 南京  391.70794   53.951014
## 
## $eig
## [1]  1.756015e+06  3.367695e+05  7.888679e+04  3.770390e+04  1.320482e+04
## [6] -7.275958e-12 -1.434722e+04 -3.259473e+04
## 
## $x
## NULL
## 
## $ac
## [1] 0
## 
## $GOF
## [1] 0.9221257 0.9416014

参数中k是降低到的维数，eig=TRUE要求输出特征值。 结果是列表，其中：

• points是\(n \times k\)矩阵，每行是一个降维坐标
• eig是n个特征值
• GOF是绝对值累积贡献率和平方累积贡献率。
• 降到2维时贡献率很高。

作降维图:

library(ggplot2)
library(ggrepel)
dp <- as.data.frame(res$points)
colnames(dp) <- c("x", "y")
dp[["label"]] <- names(d)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="八个城市多维标度分析结果")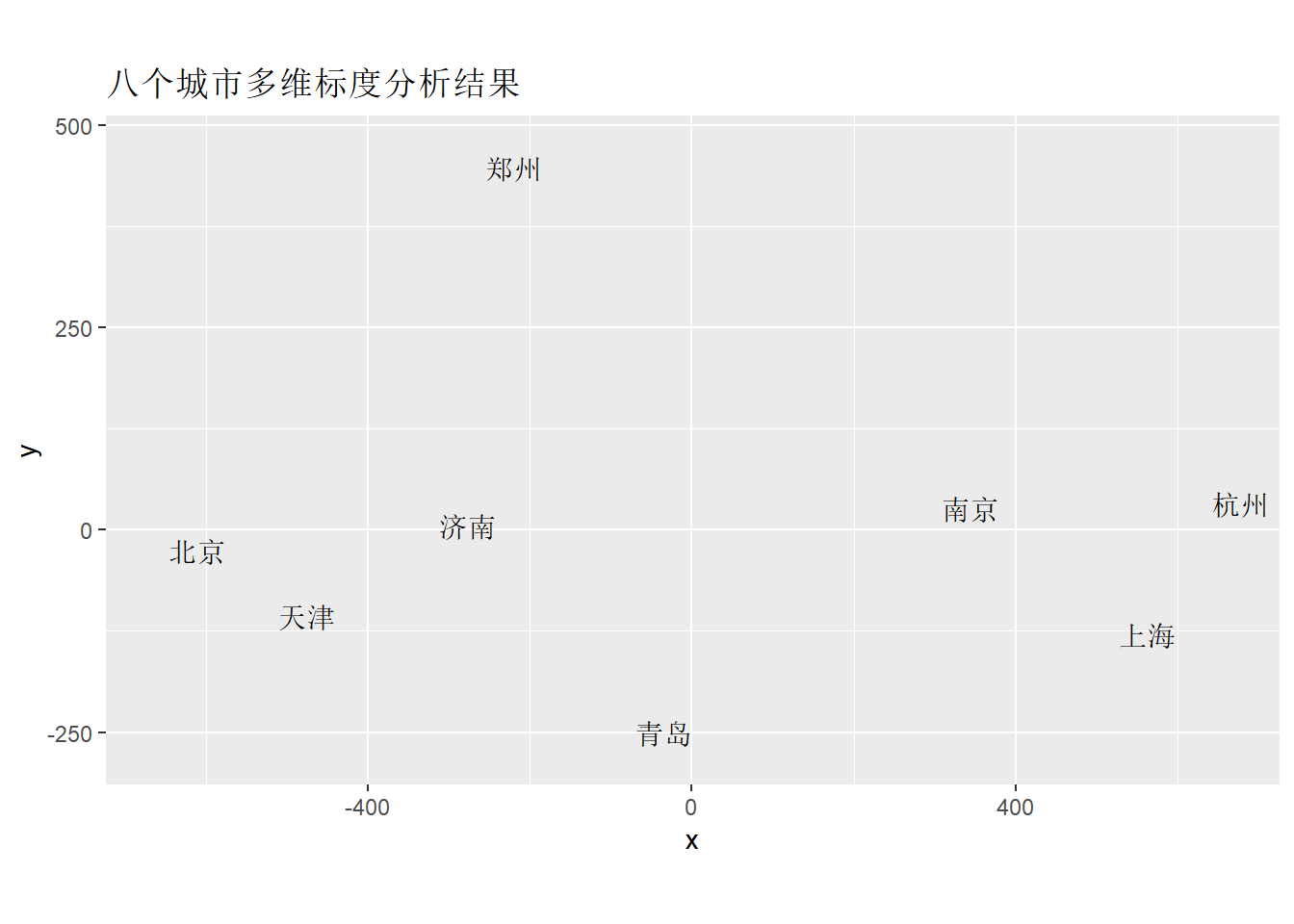

程序中coord_fixed()是为了让x方向和y方向的距离为\(1:1\)。

下面对比原始里程矩阵和降维到2维的近似距离矩阵。 原始：

as.dist(d)

##      北京 天津 济南 青岛 郑州 上海 杭州
## 天津  118                              
## 济南  439  363                         
## 青岛  668  571  362                    
## 郑州  714  729  443  772               
## 上海 1259 1145  886  776  984          
## 杭州 1328 1191  872  828  962  203     
## 南京 1065  936  626  617  710  322  305

降维到2维的近似距离矩阵:

round(dist(res$points))

##      北京 天津 济南 青岛 郑州 上海 杭州
## 天津  159                              
## 济南  437  337                         
## 青岛  620  464  343                    
## 郑州  717  702  445  757               
## 上海 1270 1133  851  713  972          
## 杭州 1319 1190  890  793  955  119     
## 南京 1055  933  621  577  703  269  273

适当的正交变换可以与地理位置方向更为接近。 坐标系顺时针旋转，结果散点逆时针旋转。

## 进行逆时针旋转theta弧度的坐标变换的矩阵
rotate.mat <- function(theta){
  rbind(c(cos(theta), sin(theta)),
        c(-sin(theta), cos(theta)))
}
deg <- 250
theta <- pi/180 * deg
MX <- res$points %*% t(rotate.mat(-theta))

## 横向反射
MX <- MX %*% cbind(c(-1,0), c(0,1))

dp <- as.data.frame(MX)
colnames(dp) <- c("x", "y")
dp[["label"]] <- names(d)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="八个城市多维标度分析结果（适当正交变换）")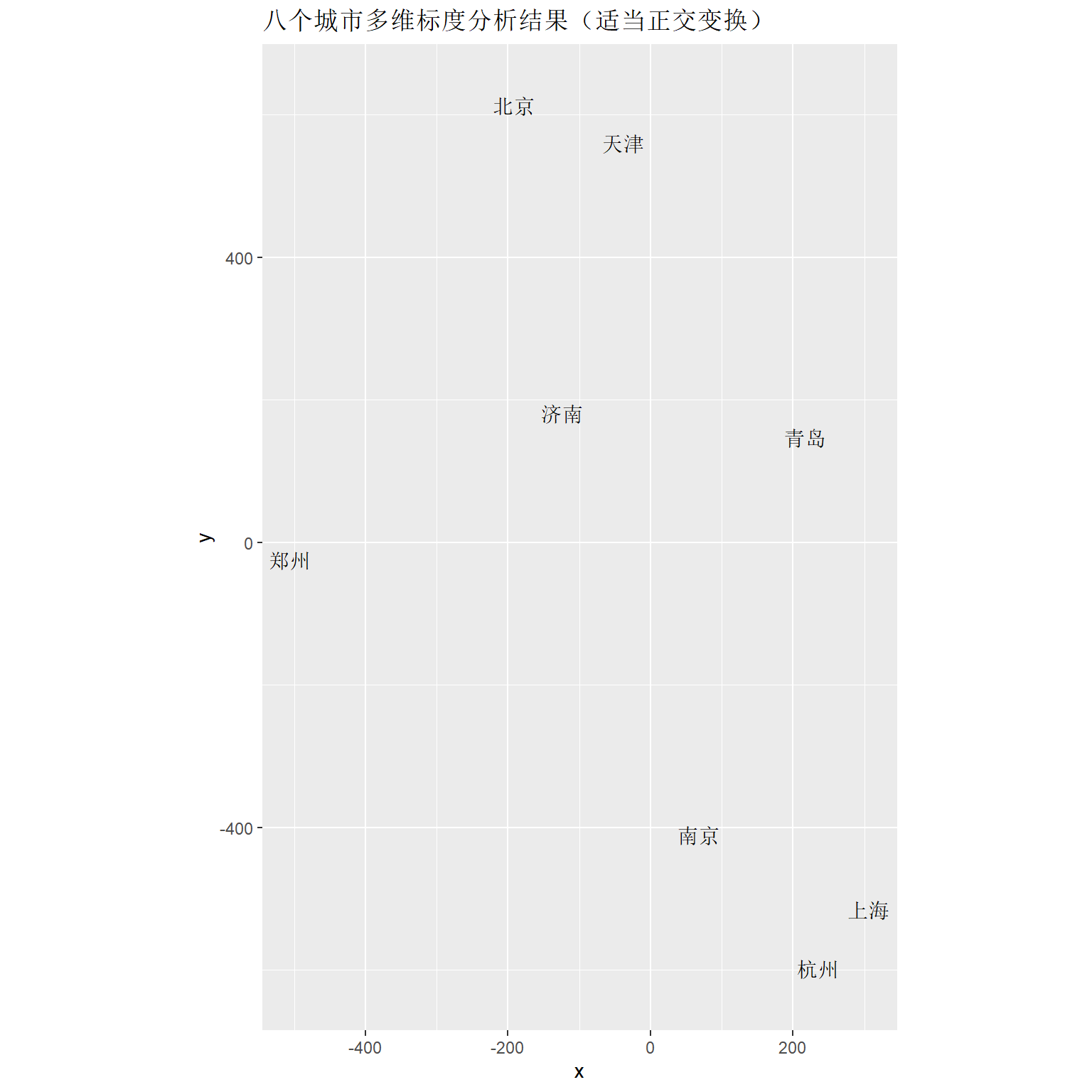

12.2.6.2 考古数据应用

data(skulls, package="HSAUR2")
str(skulls)

## 'data.frame':    150 obs. of  5 variables:
##  $ epoch: Ord.factor w/ 5 levels "c4000BC"<"c3300BC"<..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ mb   : num  131 125 131 119 136 138 139 125 131 134 ...
##  $ bh   : num  138 131 132 132 143 137 130 136 134 134 ...
##  $ bl   : num  89 92 99 96 100 89 108 93 102 99 ...
##  $ nh   : num  49 48 50 44 54 56 48 48 51 51 ...

HSAUR2的skulls数据集包含了古埃及男性头骨化石的4种测量值(mb, bh, bl, nh)， 分为5个不同年代(epoch)， 每个年代有30个样品。 设法将这这5个年代计算距离后进行多维标度分析。

因为4个不同变量的取值范围有差距， 所以在欧式距离中的贡献也不同， 所以改用马氏距离(Mahalonobis)。 设5个年代的方差阵相同，但均值可能有显著差异， 于是估计一个合并的方差阵， 分别估计5个年代的测量值均值， 计算马氏距离。

计算每个年代变量均值的程序：

sk_mean <- skulls |>
  group_by(epoch) |>
  summarize(across(
    mb:nh, 
    \(x) mean(x, na.rm=TRUE)))

计算合并协方差阵的程序：

cpd <- function(x) var(x) * (nrow(x) - 1)
sk_S <- skulls |>
  group_by(epoch) |>
  nest() |>
  mutate(Si = map(data, cpd)) |>
  pull(Si) |>
  reduce(`+`) |>
  (\(x) x / (nrow(skulls) - 1))()

对5个年代已经计算的平均测量值与合并方差阵估计， 计算马氏距离：

sk_dist <- matrix(0, 5, 5)
colnames(sk_dist) <- sk_mean[["epoch"]]
row.names(sk_dist) <- sk_mean[["epoch"]]
sk_mean_m <- as.matrix(sk_mean[,-1])
for(i in 1:5) for(j in 1:5) {
  sk_dist[i,j] = mahalanobis(sk_mean_m[i, ], sk_mean_m[j, ], sk_S)
}
round(sk_dist, 4)

##         c4000BC c3300BC c1850BC c200BC cAD150
## c4000BC  0.0000  0.0935  0.9280 1.9330 2.7712
## c3300BC  0.0935  0.0000  0.7490 1.6380 2.2357
## c1850BC  0.9280  0.7490  0.0000 0.4553 0.9360
## c200BC   1.9330  1.6380  0.4553 0.0000 0.2253
## cAD150   2.7712  2.2357  0.9360 0.2253 0.0000

用热力图表示距离阵：

library(pheatmap)
pheatmap(sk_dist)

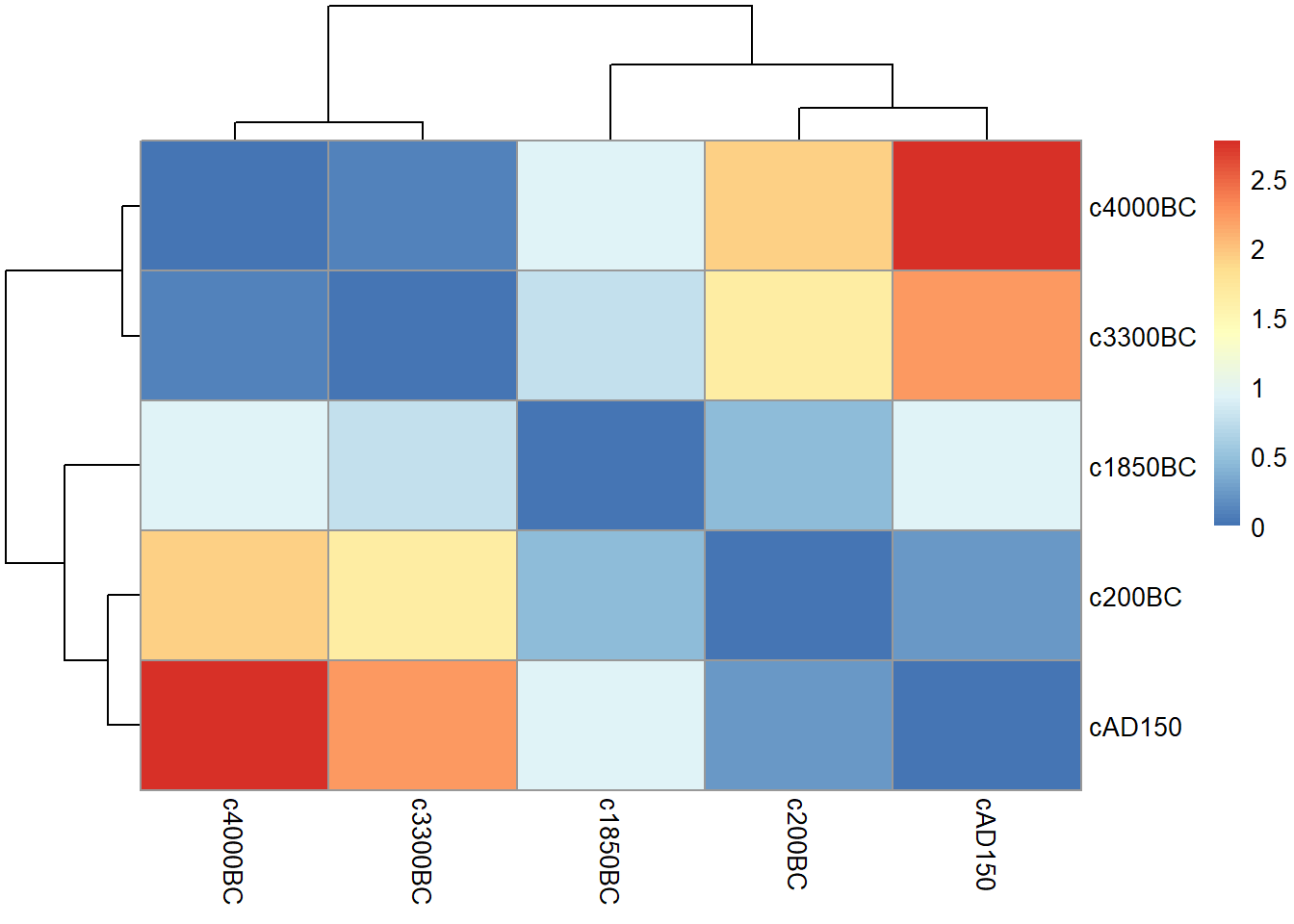
多维标度分析：

sk_mds <- cmdscale(sk_dist, k = 2, eig = TRUE)
sk_mds

## $points
##                [,1]         [,2]
## c4000BC -1.32692955 -0.134145042
## c3300BC -0.87427188  0.215462512
## c1850BC  0.04073376 -0.009300239
## c200BC   0.72499547 -0.160637724
## cAD150   1.43547219  0.088620493
## 
## $eig
## [1]  5.112951e+00  9.816355e-02 -5.551115e-16 -1.008636e-01 -7.777015e-01
## 
## $x
## NULL
## 
## $ac
## [1] 0
## 
## $GOF
## [1] 0.8557288 1.0000000

有负特征值，与最大的正特征值相比影响不大。

利用二维拟合构图作散点图：

library(ggplot2)
library(ggrepel)
dp <- as.data.frame(sk_mds$points)
colnames(dp) <- c("x", "y")
dp[["label"]] <- colnames(sk_dist)
ggplot(dp, aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="五个不同年代的古典多维标度分析")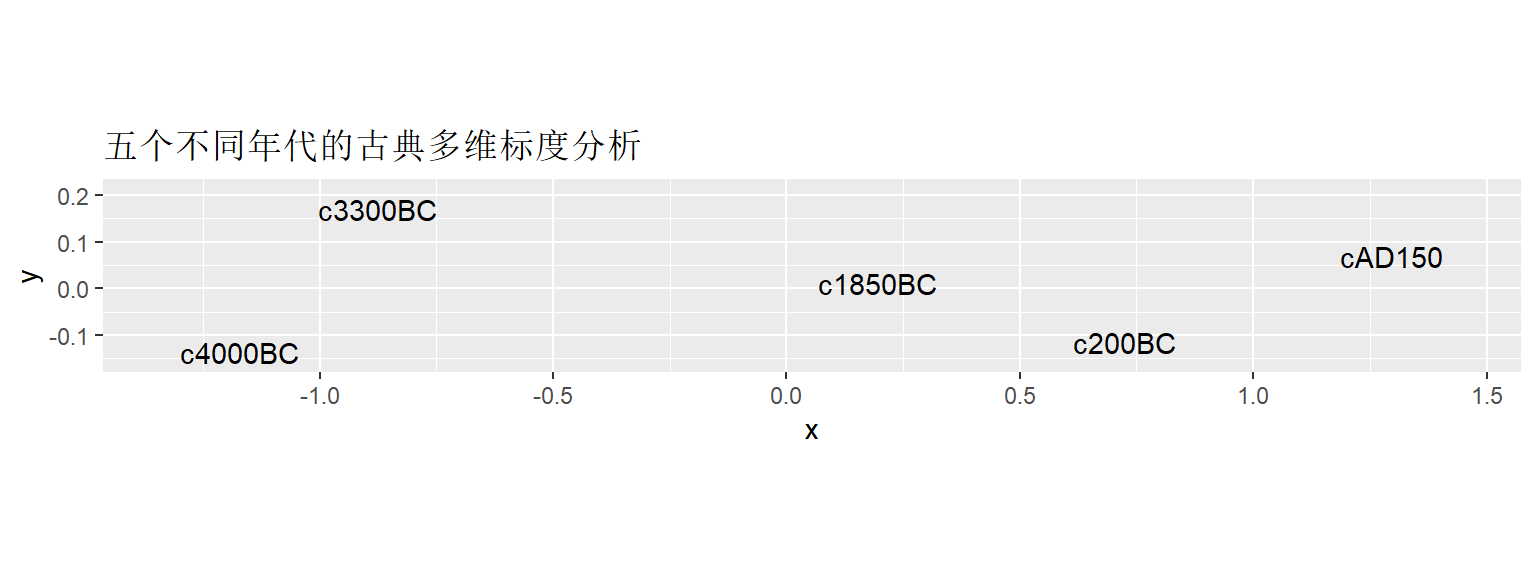

注意这里用了横纵坐标\(1:1\)的作图设置。 可以明显看出不同年代的相邻关系， 以及年代之间的距离大小比较。

12.2.7 相似矩阵的古典多维标度

设\(C=(c_{ij})_{n \times n}\)是\(n\)阶方阵，如果 \[\begin{aligned} (1)&\quad C = C^T; \\ (2)&\quad c_{ij} \leq c_{ii}, \ i, j=1,2,\dots, n, \end{aligned}\] 则称\(C\)为相似系数矩阵, \(c_{ij}\)称为第\(i\)点与第\(j\)点间的相似系数。

令\(D = (d_{ij})_{n \times n}\), \[\begin{aligned} d_{ij} = \left( c_{ii} + c_{jj} - 2 c_{ij} \right)^{1/2}, \end{aligned}\] 则\(D\)是广义距离阵。

可以证明，当\(C\)是半正定阵时， 相应的广义距离阵\(D\)是欧式距离阵。

12.2.7.1 例10-4：六门课相似系数矩阵作古典多维标度分析

P.136例10.4，六门课相似系数矩阵作古典多维标度分析。

courseSimi <- readr::read_csv(
  "data/六门课相似系数矩阵.csv",
  locale=readr::locale(encoding = "GB18030"),
  show_col_types = FALSE)

## New names:
## • `` -> `...1`

names(courseSimi)[1] <- "科目"
d <- as.data.frame(courseSimi[,-1])
row.names(d) <- courseSimi[["科目"]]
d <- as.matrix(d)
n <- 6

六门课的相似系数矩阵:

knitr::kable(d)

	盖尔语	英语	历史	算术	代数	几何
盖尔语	1.000	0.439	0.410	0.288	0.329	0.248
英语	0.439	1.000	0.351	0.354	0.320	0.329
历史	0.410	0.351	1.000	0.164	0.190	0.181
算术	0.288	0.354	0.164	1.000	0.595	0.470
代数	0.329	0.320	0.190	0.595	1.000	0.464
几何	0.248	0.329	0.181	0.470	0.464	1.000

把相似系数矩阵变成广义距离阵的函数:

ones <- function(n) rep(1, n)
sim2dist <- function(cmat){
  cmat <- as.matrix(cmat)
  n <- nrow(cmat)
  sqrt( cbind(ones(n)) %*% diag(cmat) 
      + diag(cmat) %*% rbind(ones(n)) 
      - 2 * cmat )
}

注：R函数diag()输入一个矩阵， 返回一个保存了矩阵主对角线元素的R向量。

d2 <- sim2dist(d)
knitr::kable(d2, digits=2)

	盖尔语	英语	历史	算术	代数	几何
盖尔语	0.00	1.06	1.09	1.19	1.16	1.23
英语	1.06	0.00	1.14	1.14	1.17	1.16
历史	1.09	1.14	0.00	1.29	1.27	1.28
算术	1.19	1.14	1.29	0.00	0.90	1.03
代数	1.16	1.17	1.27	0.90	0.00	1.04
几何	1.23	1.16	1.28	1.03	1.04	0.00

根据距离阵作古典多维标度分析。

res <- cmdscale(d2, k = 2, eig=TRUE)
print(res)

## $points
##              [,1]        [,2]
## 盖尔语  0.4036033  0.26663633
## 英语    0.2414601  0.48205851
## 历史    0.6206160 -0.50829928
## 算术   -0.4576949  0.04001356
## 代数   -0.4213827 -0.03889458
## 几何   -0.3866018 -0.24151454
## 
## $eig
## [1] 1.142872e+00 6.232867e-01 6.021029e-01 5.247970e-01 3.962750e-01
## [6] 2.220446e-15
## 
## $x
## NULL
## 
## $ac
## [1] 0
## 
## $GOF
## [1] 0.5369351 0.5369351

k 是降低到的维数，eig=TRUE要求输出特征值。 注意降到2维累积贡献率只有54%。

作降维图：

dp <- as.data.frame(res$points)
colnames(dp) <- c("x", "y")
dp[["label"]] <- rownames(res$points)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="六门课相似度多维标度分析结果")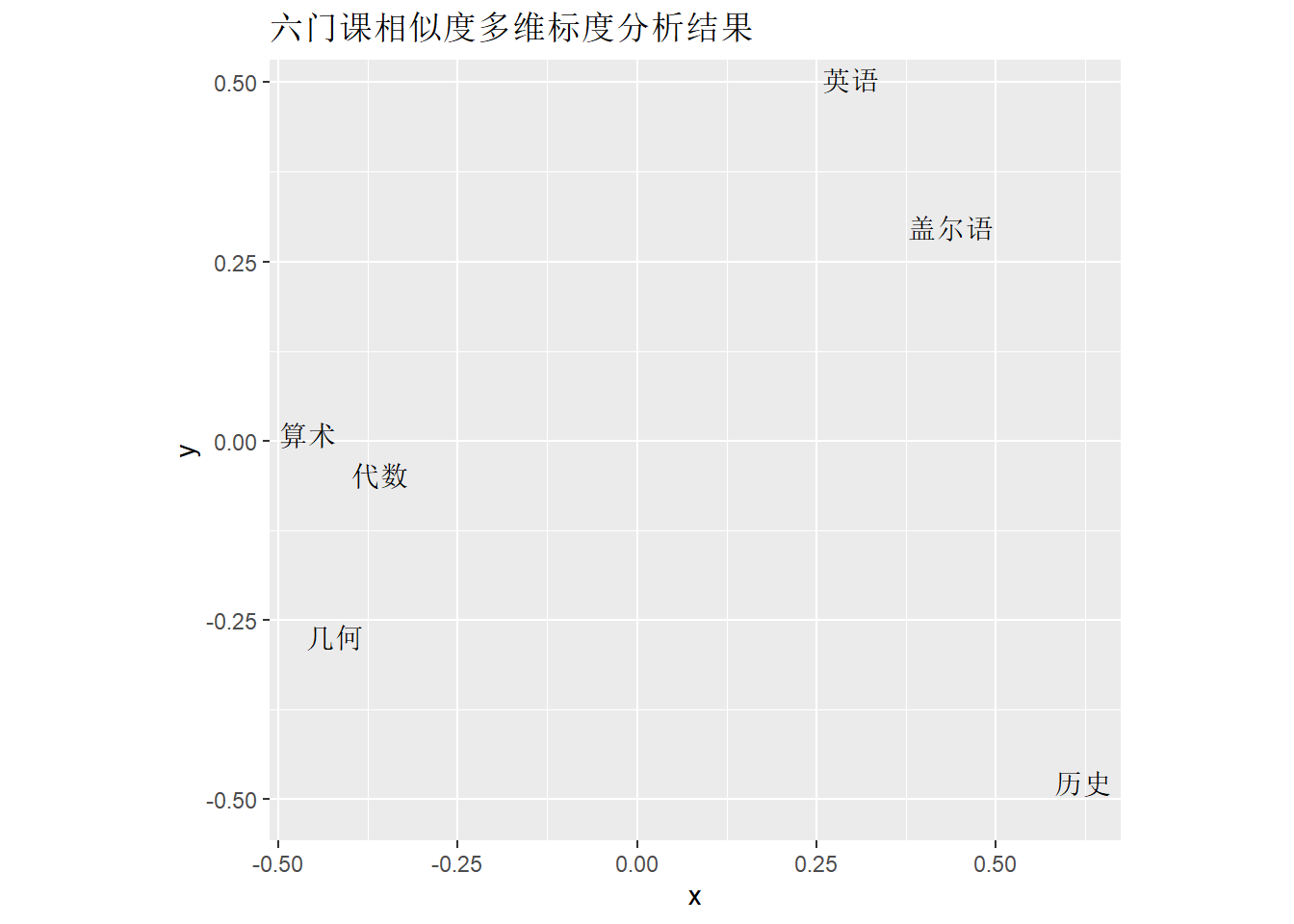

12.3 非度量多维标度法

12.3.1 方法

距离和相似度有时只有比较，没有具体数值。 例如，八个城市中距离最近的是北京与天津， 次近的是上海与杭州，……，最远的是北京与杭州； 六门功课中，最相似的是算数与代数， 次相似的是代数与几何，……， 最不相似的是历史与算数。 在社会科学如心理学研究中， 数据经常是评分， 一般仅有次序比较而没有明确差值意义， 或者只有两两比较的次序结果， 比如， 心理学研究中受试者比较两个颜色哪一个更明亮， 一般可以给出结果， 但是要让受试者说出明亮了多少， 就很困难了。

古典多维标度法的近似可以看成是\(d_{ij} = \hat d_{ij} +\varepsilon_{ij}\), \(d_{ij}\)是广义距离，\(\hat d_{ij}\)是拟合距离，\(\varepsilon_{ij}\)是拟合误差。

非度量多维标度法模型可以看成 \[\begin{aligned} d_{ij} = f(\hat d_{ij} + \varepsilon_{ij}), \end{aligned}\] 其中\(d_{ij}\)是观测到的广义距离或者相似系数， \(f(\cdot)\)是一个未知的单调增函数（不要求严格单调）。 这样，观测数据\(D\)中能够利用的信息只有\(d_{ij}\)的秩。 把\(\{ d_{ij}, i < j \}\)从小到大排列， 共有\(m = n(n-1)/2\)个， 重排后\(d_{ij}\)在上面排列中的序号称为\(d_{ij}\)的秩。 希望找到拟合构图\(M_X\), 使得\(M_X\)对应的拟合距离\(\hat D\)与一个和\(D\)满足单调关系的构图最接近。 广义距离阵（相似系数阵）\(D\)和\(D^*\)满足单调关系， 是指其对应元素的秩相等。

求解常用Shepard-Kruskal算法：

• (1) 已知相似系数矩阵\(D\), 将其不含对角线的右上角元素 (有\(m=n(n-1)/2\)个)计算秩。

• (2) 对某个\(k\)维拟合构图\(M_X\), 设相应的相似系数阵为\(\hat D = (\hat d_{ij})\), 定义 \[\begin{aligned} S^2(M_X) =& \frac{\min \sum_{i<j} (d_{ij}^* - \hat d_{ij})^2} { \sum_{i<j} d_{ij}^2 }, \end{aligned}\] 其中\((d_{ij}^*)\)是与\(D\)满足单调关系的任意相似系数矩阵， 求最小值针对所有的这样的\((d_{ij}^*)\)来求。 这个问题称为\(\{ \hat d_{ij} \}\)对\(\{ d_{ij} \}\) 的最小二乘单调回归。

  注意\((\hat d_{ij})\)不一定与\(D\)满足单调关系， 如果满足，则\(S^2(M_X)=0\)。

• (3) 设\(k\)固定，若存在拟合构图\(\hat M_X\)使得 \[\begin{aligned} S_k \stackrel{\triangle}{=} S(\hat M_X) = \min_{M_X} S(M_X) \end{aligned}\] 则称\(\hat M_X\)为\(D\)的k维最佳拟合构图。

• (4) 由于\(S_k\)(称为压力指数,stress)是\(k\)的单调降序列， 取较小的\(k\)使得\(S_k\)也较小， \(S_k \leq 5\%\)最好， \(S_k \in (5\%, 10\% ]\)次之， \(S_k > 10\%\)较差。

12.3.2 例子：投票和党派

HSAUR2包的voting矩阵是美国新泽西州的15名议员在19次决议投票中的两两差异的矩阵， 这是一个\(15 \times 15\)矩阵， 矩阵元素为两个议员在19次投票中有多少次投票相反。 希望分析民主党议员和共和党议员的投票差异。

data(voting, package="HSAUR2")
m_v <- voting
colnames(m_v) <- paste0("R", 1:15)
d_v <- as.data.frame(m_v)
n_v <- gsub("(.*)\\((R|D)\\)", "\\1", rownames(voting))
p_v <- gsub("(.*)\\((R|D)\\)", "\\2", rownames(voting))
d_v[["Party"]] <- p_v
d_v

##                   R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 Party
## Hunt(R)            0  8 15 15 10  9  7 15 16  14  15  16   7  11  13     R
## Sandman(R)         8  0 17 12 13 13 12 16 17  15  16  17  13  12  16     R
## Howard(D)         15 17  0  9 16 12 15  5  5   6   5   4  11  10   7     D
## Thompson(D)       15 12  9  0 14 12 13 10  8   8   8   6  15  10   7     D
## Freylinghuysen(R) 10 13 16 14  0  8  9 13 14  12  12  12  10  11  11     R
## Forsythe(R)        9 13 12 12  8  0  7 12 11  10   9  10   6   6  10     R
## Widnall(R)         7 12 15 13  9  7  0 17 16  15  14  15  10  11  13     R
## Roe(D)            15 16  5 10 13 12 17  0  4   5   5   3  12   7   6     D
## Heltoski(D)       16 17  5  8 14 11 16  4  0   3   2   1  13   7   5     D
## Rodino(D)         14 15  6  8 12 10 15  5  3   0   1   2  11   4   6     D
## Minish(D)         15 16  5  8 12  9 14  5  2   1   0   1  12   5   5     D
## Rinaldo(R)        16 17  4  6 12 10 15  3  1   2   1   0  12   6   4     R
## Maraziti(R)        7 13 11 15 10  6 10 12 13  11  12  12   0   9  13     R
## Daniels(D)        11 12 10 10 11  6 11  7  7   4   5   6   9   0   9     D
## Patten(D)         13 16  7  7 11 10 13  6  5   6   5   4  13   9   0     D

library(MASS)
mds_v <- isoMDS(m_v)

## initial  value 15.268246 
## iter   5 value 10.264075
## final  value 9.879047 
## converged

mds_v

## $points
##                         [,1]       [,2]
## Hunt(R)           -8.4354008  0.9063380
## Sandman(R)        -7.4050250  7.8770232
## Howard(D)          6.0930164 -1.4971986
## Thompson(D)        3.5187022  5.2486888
## Freylinghuysen(R) -7.2457425 -4.1821704
## Forsythe(R)       -3.2787096 -2.5689673
## Widnall(R)        -9.7110008 -1.1187710
## Roe(D)             6.3429759  1.0388694
## Heltoski(D)        6.2983842  0.2706499
## Rodino(D)          4.2829160 -0.9151604
## Minish(D)          4.2642545 -0.3919690
## Rinaldo(R)         5.0285425  0.2665701
## Maraziti(R)       -4.4577693 -6.2177727
## Daniels(D)         0.8129854 -0.9417672
## Patten(D)          3.8918709  2.2256372
## 
## $stress
## [1] 9.879047

用图形表示拟合构图：

library(ggrepel)
dd <- mds_v$points
colnames(dd) <- c("x", "y")
dd <- as_tibble(dd)
dd[["Name"]] <- n_v
dd[["Party"]] <- p_v
ggplot(dd, aes(x=x, y=y, color=Party, label=Name)) +
  geom_point(alpha=0.2) +
  geom_text_repel() + coord_fixed()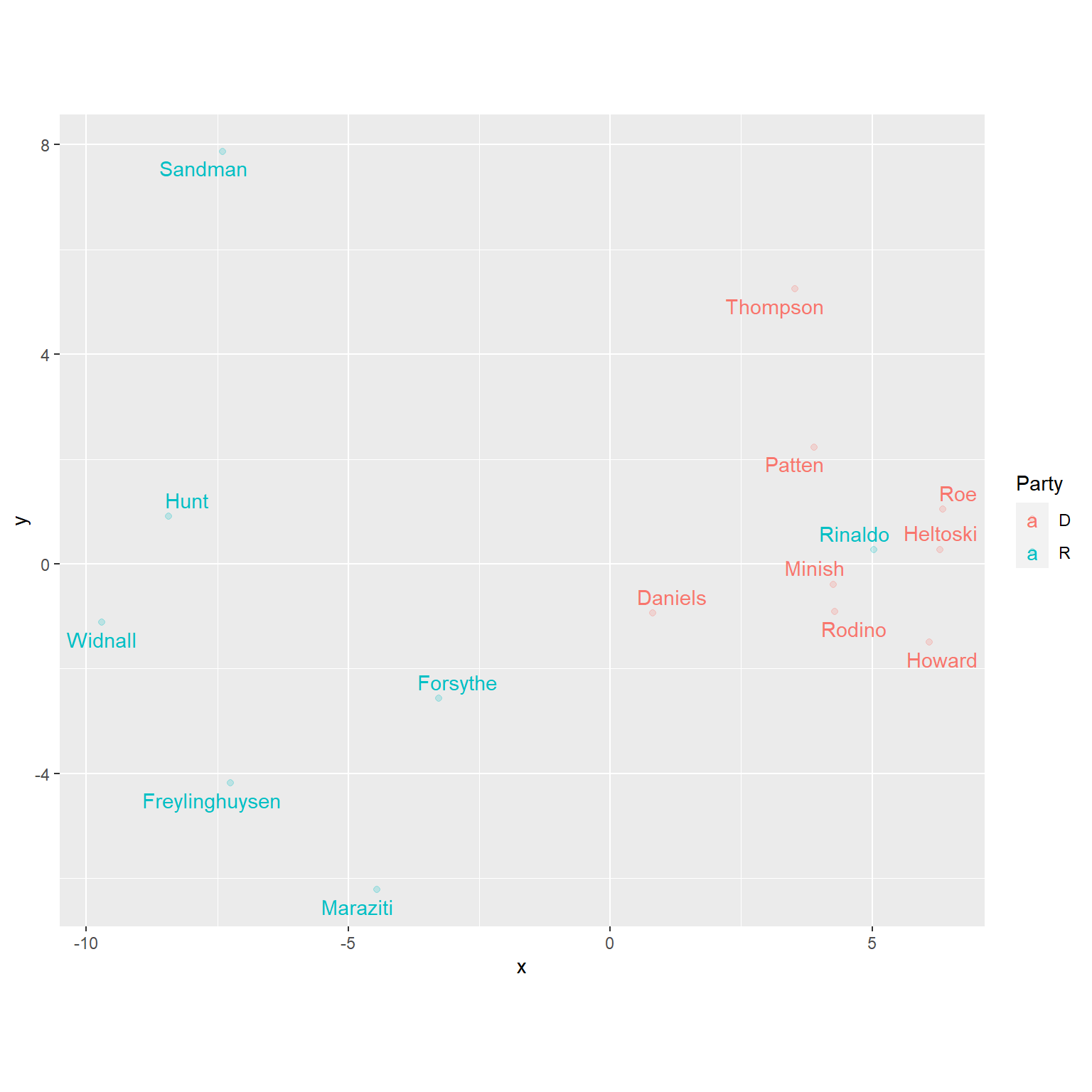

可以看出， 民主党和共和党的议员的投票差异很大， 其中例外的是Rinaldo。 另外， 民主党议员内部的意见差异较小， 而共和党议员内部意见差异较大。

12.4 案例10-1: 各省农村人均消费支出的8个指标

P.140案例10.1，各省农村人均消费支出的8个指标， 分析各省差距。 用多维标度分析，实际上与用主成分分析类似。

agriConsume <- readr::read_csv(
  "data/各省农村人均消费支出.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
names(agriConsume)[[1]] <- "city"
d_a <- as.data.frame(agriConsume[,-1])
rownames(d_a) <- agriConsume[[1]]

n <- nrow(d_a)
p <- ncol(d_a)

12.4.1 各省之间的相近程度分析

各省间距离（部分）:

D1 <- dist(d_a) 
print(round(as.matrix(D1)[1:5, 1:5], 0))

##        北京 天津 河北 山西 内蒙古
## 北京      0 1775 2279 2426   2062
## 天津   1775    0  721  755    457
## 河北   2279  721    0  267    395
## 山西   2426  755  267    0    436
## 内蒙古 2062  457  395  436      0

多维标度分析：

res1 <- cmdscale(D1, k=2, eig=TRUE)
print(res1)

## $points
##               [,1]          [,2]
## 北京   1879.279646 -402.49618382
## 天津    178.157251   85.23730988
## 河北   -381.735504 -316.51835707
## 山西   -523.378386 -162.39364584
## 内蒙古 -143.690835 -117.15678932
## 辽宁   -137.181780  -95.24807410
## 吉林   -314.457145 -196.40456416
## 黑龙江 -260.394252 -303.04139346
## 上海   2569.739911  161.79540083
## 江苏    863.228525   24.90508373
## 浙江   1887.558242 -271.97725230
## 安徽   -245.509613  -55.20968715
## 福建    559.486804  427.22402566
## 江西   -190.812179  151.40399349
## 山东     20.797731  -66.31470827
## 河南   -484.121893 -163.67050988
## 湖北   -189.363345   70.46678517
## 湖南      8.596533  319.03362788
## 广东    642.662984  473.68424513
## 广西   -380.451346  166.60806906
## 海南   -365.973719  229.73195217
## 重庆   -363.960184  227.47202708
## 四川   -209.255748  263.81961068
## 贵州   -712.535069    0.01467818
## 云南   -438.762436  119.48142315
## 西藏   -839.842006  164.59064776
## 陕西   -479.413566 -309.10055554
## 甘肃   -716.091067  -10.57794425
## 青海   -375.377165 -189.29492722
## 宁夏   -324.297566 -122.74029353
## 新疆   -532.902821 -103.32399395
## 
## $eig
##  [1]  1.932747e+07  1.521077e+06  3.589841e+05  1.913554e+05  1.336292e+05
##  [6]  6.342937e+04  4.073997e+04  8.626661e+03  3.371024e-09  1.762099e-09
## [11]  1.972401e-10  1.019303e-10  8.874128e-11  7.492228e-11  5.128601e-11
## [16]  4.669768e-11  2.656533e-11  2.266618e-11 -1.243993e-11 -2.915948e-11
## [21] -3.912074e-11 -4.389427e-11 -6.158854e-11 -8.387777e-11 -1.538815e-10
## [26] -2.530966e-10 -3.704756e-10 -6.524765e-10 -1.085817e-09 -1.214245e-09
## [31] -1.299525e-09
## 
## $x
## NULL
## 
## $ac
## [1] 0
## 
## $GOF
## [1] 0.96319 0.96319

作降维图:

library(ggrepel)
dp <- as.data.frame(res1$points)
colnames(dp) <- c("x", "y")
dp[["label"]] <- rownames(res1$points)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed()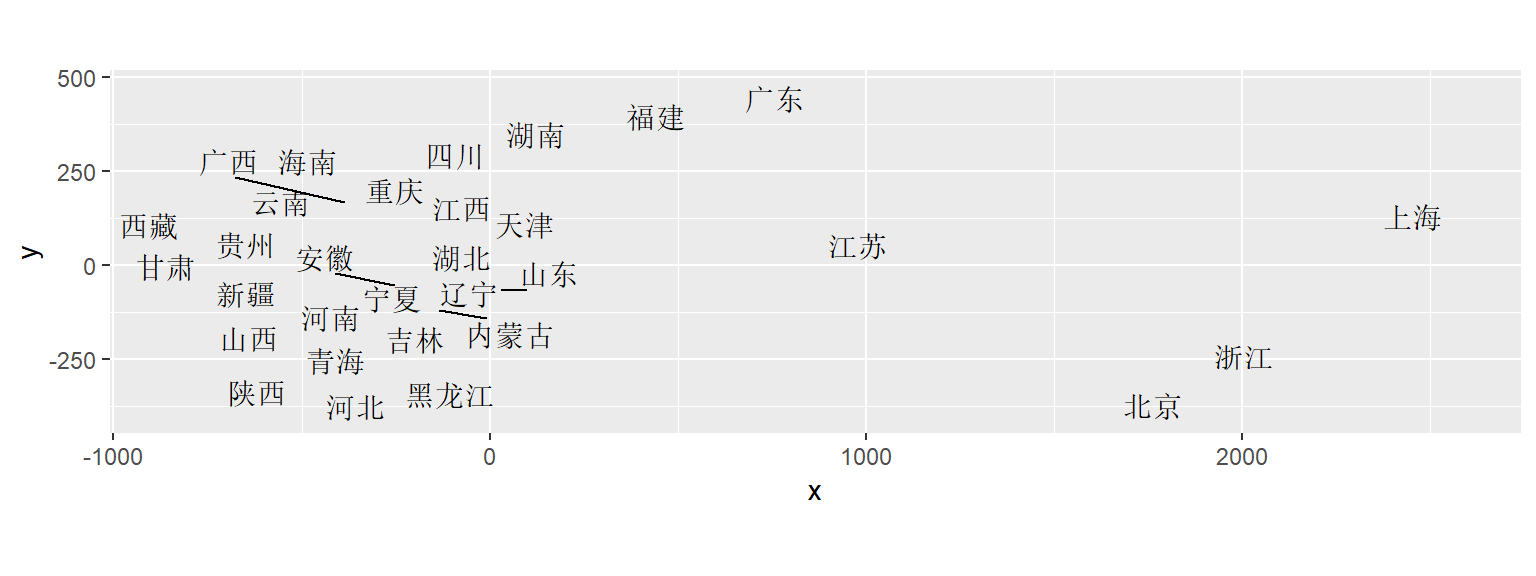

  labs(title="31个省农村人均消费指标多维标度分析结果")

## $title
## [1] "31个省农村人均消费指标多维标度分析结果"
## 
## attr(,"class")
## [1] "labels"

用主成分分析降维:

pca1 <- princomp(d_a, cor=FALSE)
pr1 <- predict(pca1)[,1:2]
dp <- as.data.frame(pr1)
colnames(dp) <- c("x", "y")
dp[["label"]] <- rownames(d_a)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="31个省农村人均消费指标主成分降维")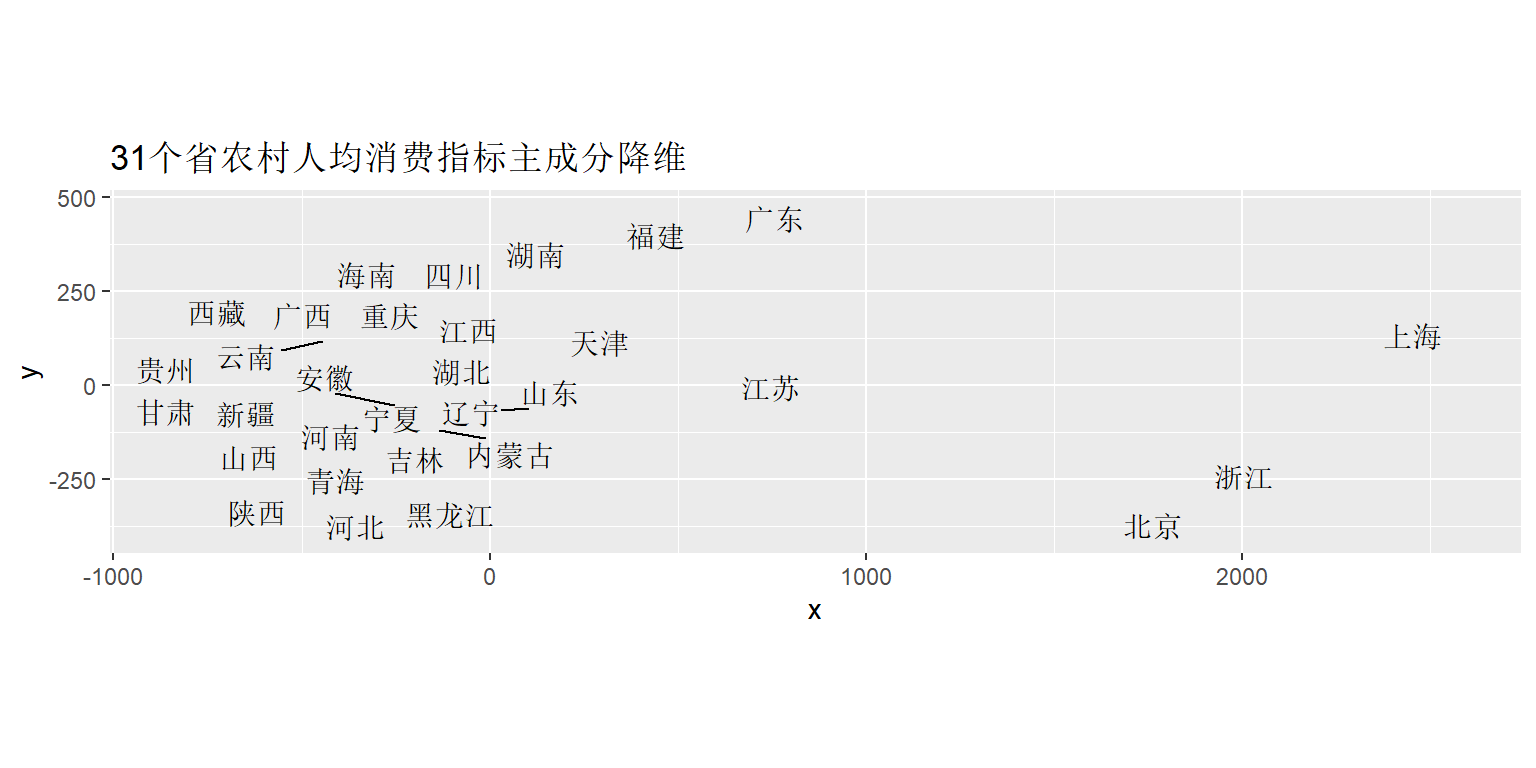

两个图十分接近。

12.4.2 8个消费类型变量的相似性

考虑此数据中8个变量的相关性。 计算八个变量的相关系数阵, 当作相似系数矩阵:

D1 <- cor(d_a)
knitr::kable(D1, digits=2)

	食品	衣着	居住	家用	交信	文娱	医疗	其它
食品	1.00	0.65	0.85	0.87	0.90	0.77	0.60	0.88
衣着	0.65	1.00	0.81	0.74	0.83	0.80	0.87	0.74
居住	0.85	0.81	1.00	0.88	0.93	0.86	0.84	0.83
家用	0.87	0.74	0.88	1.00	0.89	0.79	0.69	0.78
交信	0.90	0.83	0.93	0.89	1.00	0.87	0.79	0.87
文娱	0.77	0.80	0.86	0.79	0.87	1.00	0.80	0.81
医疗	0.60	0.87	0.84	0.69	0.79	0.80	1.00	0.70
其它	0.88	0.74	0.83	0.78	0.87	0.81	0.70	1.00

转换为距离:

D2 <- sim2dist(D1)
knitr::kable(D2, digits=2)

	食品	衣着	居住	家用	交信	文娱	医疗	其它
食品	0.00	0.84	0.55	0.51	0.45	0.67	0.89	0.49
衣着	0.84	0.00	0.62	0.72	0.59	0.63	0.52	0.72
居住	0.55	0.62	0.00	0.49	0.37	0.53	0.56	0.59
家用	0.51	0.72	0.49	0.00	0.47	0.64	0.78	0.66
交信	0.45	0.59	0.37	0.47	0.00	0.50	0.65	0.50
文娱	0.67	0.63	0.53	0.64	0.50	0.00	0.63	0.61
医疗	0.89	0.52	0.56	0.78	0.65	0.63	0.00	0.78
其它	0.49	0.72	0.59	0.66	0.50	0.61	0.78	0.00

多维标度分析：

res1 <- cmdscale(D2, k=2, eig=TRUE)
print(res1)

## $points
##              [,1]        [,2]
## 食品  0.403348780  0.02080423
## 衣着 -0.358651876  0.03724398
## 居住  0.000932444 -0.13824518
## 家用  0.199667891 -0.29563037
## 交信  0.091772668 -0.03795361
## 文娱 -0.083240322  0.11102776
## 医疗 -0.449193653 -0.02746233
## 其它  0.195364067  0.33021552
## 
## $eig
## [1]  5.864828e-01  2.318931e-01  1.741565e-01  1.493715e-01  8.834308e-02
## [6]  5.953026e-02  4.457193e-02 -5.946043e-17
## 
## $x
## NULL
## 
## $ac
## [1] 0
## 
## $GOF
## [1] 0.6133147 0.6133147

作降维图:

dp <- as.data.frame(res1$points)
colnames(dp) <- c("x", "y")
dp[["label"]] <- rownames(res1$points)
ggplot(data = dp, mapping = aes(
  x=x, y=y, label=label)) +
  geom_text_repel() +
  coord_fixed() +
  labs(title="农村人均消费指标八个变量相似度多维标度分析结果")

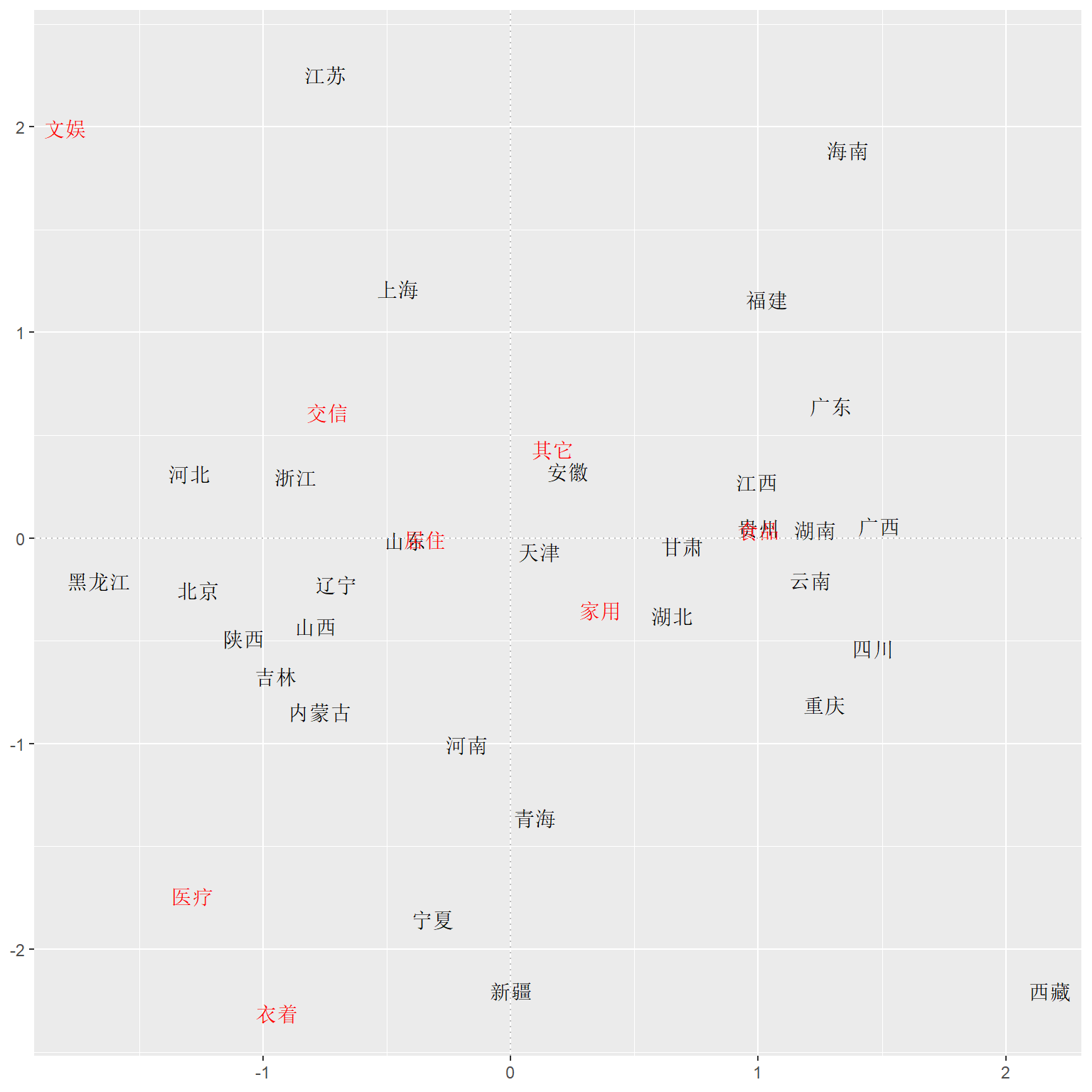
12.4.3 对应分析

由于有各省的各个变量的数据矩阵， 可以做对应分析， 好处是还可以查看各省的消费分配特点。 数据各列可比， 不需要标准化。

library(MASS)

co <- corresp(d_a, nf=2)

## Warning in corresp.matrix(as.matrix(x), ...): negative or non-integer entries in
## table

print(co)

## First canonical correlation(s): 0.12436826 0.07457466 
## 
##  Row scores:
##               [,1]        [,2]
## 北京   -1.32925829 -0.33426473
## 天津    0.04945956 -0.14776851
## 河北   -1.22863213  0.39443037
## 山西   -0.85347954 -0.34934912
## 内蒙古 -0.70231013 -0.76207856
## 辽宁   -0.76957852 -0.30780147
## 吉林   -1.01519418 -0.75297750
## 黑龙江 -1.59540474 -0.29239824
## 上海   -0.38613364  1.29398154
## 江苏   -0.67970281  2.33599344
## 浙江   -0.93551764  0.21391812
## 安徽    0.16371317  0.24168924
## 福建    0.96856467  1.07949379
## 江西    1.06193105  0.35254870
## 山东   -0.35869664  0.06897665
## 河南   -0.10607593 -0.92136121
## 湖北    0.72074655 -0.29721011
## 湖南    1.30042373  0.12426810
## 广东    1.36068239  0.72431118
## 广西    1.55563628  0.13790943
## 海南    1.43167039  1.96884384
## 重庆    1.33560549 -0.72887137
## 四川    1.39436305 -0.61843055
## 贵州    1.07875609 -0.03051918
## 云南    1.14355321 -0.12337980
## 西藏    2.11289483 -2.28624935
## 陕西   -1.00875349 -0.40676584
## 甘肃    0.62700931 -0.12277114
## 青海    0.03186983 -1.44027881
## 宁夏   -0.24502900 -1.77381670
## 新疆    0.07023869 -2.11791842
## 
##  Column scores:
##            [,1]        [,2]
## 食品  1.0714294  0.11647208
## 衣着 -0.8758854 -2.22885684
## 居住 -0.4120152 -0.08570852
## 家用  0.4327640 -0.27012171
## 交信 -0.6721225  0.69228348
## 文娱 -1.7319970  2.07426138
## 医疗 -1.3527017 -1.82151210
## 其它  0.1052890  0.34764977

ggbiplot.corresp <- function(obj) {
  require(ggplot2)
  require(ggrepel)
  require(tibble)
  rscore <- tibble(
    label = rownames(obj$rscore),
    x = obj$rscore[,1],
    y = obj$rscore[,2]
  )
  cscore <- tibble(
    label = rownames(obj$cscore),
    x = obj$cscore[,1],
    y = obj$cscore[,2]
  )
  p <- ggplot(mapping = aes(x = x, y = y, label=label)) +
    geom_text_repel(data = rscore, color="black") +
    geom_text_repel(data = cscore, color="red") +
    geom_hline(yintercept=0, linetype=3, col="gray") +
    geom_vline(xintercept=0, linetype=3, col="gray") +
    labs(x=NULL, y=NULL)
  p
}

ggbiplot.corresp(co)