13 联合测量分析

13.1 介绍

联合测量分析（Conjoint measurement analysis），或称联合分析，是多元分析主要工具之一，在社会学、生物统计学、数量心理学、市场营销、产品管理、运筹学等领域的统计实证分析应用广泛。尤其适用于市场营销研究，用来分析产品的多个特性如何影响消费者购买决策问题。

在设计产品时，希望了解产品的不同方面给消费者带来的不同效用。市场营销和广告策略主要针对产品的总体的效用。例如，设计一款新的汽车，就希望知道提高运动性能、改善安全性、增加一个方便性的部件，哪一种改变可以更好地提高产品的总效用，从而在设计和推广产品时可以侧重那一方面。联合测量分析用于评估不同属性对消费者的相对重要性，以及不同属性水平给消费者带来的效用的统计分析方法。联合测量分析可以从消费者问卷调查中对同类产品的排序求解出每个产品各个方面的效用贡献值，假定总效用等于各个方面效用的总和。

例1.

某汽车厂商计划开发一款新车，需要提供消费者喜欢的特性，从而能够畅销。考虑增加的新特性包括

\(X_1\): 增加舒适性或安全性的设备（如主动方向盘、GPS导航等），记为2，否则为1
\(X_2\): 偏向运动性（如真皮方向盘、增大发动机功率），记为2，否则为1

这样可以考虑四款车：

(1,1)
(1,2)
(2,1)
(2,2)

厂商需要消费者给这四款车打分，从而了解消费者对\(X_1\)和\(X_2\)的偏好情况。某个消费者的打分可能如:

\[ \begin{array}{c|cccc} \text{产品} & 1 & 2 & 3 & 4 \\ \text{排序} & 1 & 2 & 4 & 3 \end{array} \]

在这个问题中，产品的基本效用包括舒适性设备和运动性水平两种，分析的目的是从消费者打分中分解出两种基本效用对分数的贡献。

例2 某食品厂商要开发一款新的人造奶油产品。考虑的设计因素为

口味，低卡路里1还是高卡路里2
包装，用塑料杯1还是纸袋2

这样可以比较四款产品：

(1,1)
(1,2)
(2,1)
(2,2)

设消费者对产品打分如

\[ \begin{array}{c|cccc} \text{产品} & 1 & 2 & 3 & 4 \\ \text{排序} & 3 & 4 & 1 & 2 \end{array} \]

联合分析需要求解产品的两种特性对排序结果的贡献，即两种特性分别的效用。

通过联合分析可以比较不同特性的效用，可以用来改进产品设计，或者提供广告营销的侧重点。

13.2 试验设计

产品被定义为各个特性的组合，一个激励（stimulus，或称轮廓，或剖面, profile）是一种特性组合，比如上面的两个例子中分别有4种激励。

在人造奶油的例子中，考虑两种口味和两种包装，可以将特性表达为变量： \[\begin{aligned} X_1(\text{口味}) =& \begin{cases} 1 & \text{低热量} \\ 2 & \text{高热量} \end{cases} \\ X_2(\text{包装}) =& \begin{cases} 1 & \text{塑料杯} \\ 2 & \text{纸袋} \end{cases} \\ \end{aligned}\]

共有\(2 \times 2=4\)种激励。如果还有第三个特性用途，可以表示为：

\[\begin{aligned} X_3(\text{用途}) =& \begin{cases} 1 & \text{抹面包} \\ 2 & \text{烹调} \\ 3 & \text{通用} \end{cases} \end{aligned}\]

则可以考虑\(2 \times 2 \times 3=12\)种激励。

在汽车设计的例子中，用\(X_1=1,2\)分别表示安全性低配还是高配，用\(X_2=1,2\)表示没有或者有运动特性，增加特性 \[\begin{aligned} X_3(\text{功率}) =& \begin{cases} 1 & 50 \text{kW} \\ 2 & 70 \text{kW} \\ 3 & 90 \text{kW} \end{cases} \\ X_4(\text{车门数}) =& \begin{cases} 1 & 2 \text{门} \\ 2 & 4 \text{门} \\ 3 & 5 \text{门} \end{cases} \end{aligned}\] 则有\(2\times 2 \times 3 \times 3=36\)种激励。设计消费者调查问卷时，每个消费者需要对36种车型排序。

轮廓法(profile method)需要所有激励的效用信息，如果要考虑的因素和水平数较多，消费者需要对许多激励排序，使得此方法变得不可行。比如，有6个特性，每个特性有3种水平，则可以产生\(3^6=729\)种激励，即消费者需要比较729种产品，这既过于劳烦也不能得到可信的结果。

另一种方法是两因子法，每次仅同时考虑两个特性，也可称为权衡(trade-off)分析，想法是每次仅呈现两个激励，最后将多次比较的结果综合分析，权衡分析定义一个权衡矩阵，将两个特性的各个激励进行比较。

人造奶油的三个特性的两两的权衡矩阵如下：

\[\begin{aligned} &\begin{array}{c|cccc} X_3 \backslash X_2 & 1 & 2 \\ \hline 1 & * & * \\ 2 & * & * \\ 3 & * & * \end{array} \\ &\begin{array}{c|cccc} X_3 \backslash X_1 & 1 & 2 \\ \hline 1 & * & * \\ 2 & * & * \\ 3 & * & * \end{array} \\ &\begin{array}{c|cccc} X_2 \backslash X_1 & 1 & 2 \\ \hline 1 & * & * \\ 2 & * & * \\ \end{array} \end{aligned}\]

选择轮廓法还是选择两因子法，基于如下的考虑：

对受访者评估不同产品的能力要求；
消耗的时间；
对产品的认识深度。

第一个方面的考虑会倾向于选用两因子法，两因子法不需要面访，调查问卷就可以。但是，轮廓法因为给受访者看的不是孤立的特性而是整个的产品，所以受访者对产品的认识更容易，但是当要比较的激励个数太多时就需要考虑完成问卷的时间太长的影响。

总的来说消费者对产品的认知更重要，所以轮廓法更多使用，在要比较的激励太多时也可以提供给受访者一个激励子集。

13.3 偏好次序的估计

考虑轮廓法。设一共有\(J\)个特性，第\(j\)特性有\(L_j\)个水平，第\(j\)特性的各个水平用\(X_j = x_{jl}\), \(l=1,2,\dots,L_j\)表示，这时有\(K = \prod_{j=1}^J L_j\)个激励，每个激励的效用表示为各个特性的单独效用之和，用\(Y_k\)表示第\(k\)个激励（产品）的效用，模型为 \[\begin{aligned} Y_k = \sum_{j=1}^J \sum_{l=1}^{L_j} \beta_{jl} I(X_j = x_{jl}) + \mu,\ \ k=1,2,\dots, K \end{aligned}\] 其中\(\beta_{jl}\)表示第\(j\)特性取第\(l\)水平时对总效用的贡献。 \(\mu\)表示平均效用水平。

上述模型不包含误差项，也有参数过多问题。为了将其转换成线性模型形式，先举例说明。考虑\(J=2\)情形，考虑设计新款汽车的两种特性，设\(X_1\)表示三种发动机功率， \(X_2\)表示两种气囊配置，某个调查问卷的打分（排序）结果如 \[\begin{aligned} \begin{array}{r|cccc} \text{发动机} \backslash \text{气囊配置} & 1 & 2 \\ \hline 1(50\text{kW}) & Y_1 & Y_2 \\ 2(70\text{kW}) & Y_3 & Y_4 \\ 3(90\text{kW}) & Y_5 & Y_6 \end{array} \end{aligned}\] 这里\(Y_1\)激励对应于发动机配置1，气囊配置1， \(Y_2\)激励对应于发动机配置1，气囊配置2，等等。初步的模型为 \[\begin{aligned} Y_1 =& \beta_{11} + \beta_{21} + \mu \\ Y_2 =& \beta_{11} + \beta_{22} + \mu \\ Y_3 =& \beta_{12} + \beta_{21} + \mu \\ Y_4 =& \beta_{12} + \beta_{22} + \mu \\ Y_5 =& \beta_{13} + \beta_{21} + \mu \\ Y_6 =& \beta_{13} + \beta_{22} + \mu \end{aligned}\]

如何从多个受访者给出的\(\{Y_1, \dots, Y_6 \}\)排序值估计\(\beta_{ij}\)这些效用？有度量法和非度量法两种方法。

13.3.1 度量法

联合测量分析可以用方差分析技术解决。这种方法的前提假定是偏好排序的差别代表固定的效用差异，比如，第一名和第二名的效用差异，等于第五名和第六名的效用差异。这样，可以将各个激励的排序值看作是数值，而不仅仅是次序。 \(\mu\)总是1到\(K\)的整数的平均值，即\((1+K)/2\)。为了比较每个特性的各个水平，计算某个特性的某个水平的排序值平均值，记特性\(X_j\)的第\(l\)水平的排序值平均值为\(\bar p_{x_{jl}}\)。然后，计算此平均值与总平均值\(\mu\)的差，记特性\(X_j\)的第\(l\)水平的差值为\(\beta_{jl} = \bar p_{x_{jl}} - \mu\)。例如，对汽车的例子，设\(Y_1\)到\(Y_6\)的值如下表： \[\begin{aligned} &\begin{array}{c|cc|cc} X_1(\text{发动机}) \backslash X_2(\text{气囊}) & 1 & 2 & \bar p_{x_{1l}} & \beta_{1l} \\ \hline 1(50\text{kW}) & 1 & 3 & 2 & -1.5 \\ 2(70\text{kW}) & 2 & 6 & 4 & 0.5 \\ 3(90\text{kW}) & 4 & 5 & 4.5 & 1 \\ \hline \bar p_{x_{2l}} & 2.33 & 4.67 & 3.5 & \\ \beta_{2l} & -1.17 & 1.17 \end{array} \end{aligned}\] 其中\(\beta_{jl} = \bar p_{x_{jl}} - \mu\)。

这样，可以对\(k=1,\dots,6\)列出原始分值和用估计的\(\beta_{jl}\)计算的拟合值\(\hat Y_k\)，如：

score1 <- matrix(c(1,3, 2,6, 4,5), nrow=3, ncol=2, byrow=TRUE)
rownames(score1) <- c("50kW", "70kW", "90kW")
colnames(score1) <- c("airbag1", "airbag2")
knitr::kable(score1)

	airbag1	airbag2
50kW	1	3
70kW	2	6
90kW	4	5

计算行平均、列平均、总平均：

barp1 <- rowMeans(score1)
barp2 <- colMeans(score1)
mu1 <- mean(c(score1))
rbind(cbind(score1, barp1), c(barp2, mu1))

##       airbag1  airbag2 barp1
## 50kW 1.000000 3.000000   2.0
## 70kW 2.000000 6.000000   4.0
## 90kW 4.000000 5.000000   4.5
##      2.333333 4.666667   3.5

计算\(\beta_{1l}\), \(\beta_{2l}\):

beta1 <- barp1 - mu1; beta1

## 50kW 70kW 90kW 
## -1.5  0.5  1.0

beta2 <- barp2 - mu1; beta2

##   airbag1   airbag2 
## -1.166667  1.166667

计算拟合值：

hatymat <- outer(beta1, beta2, function(x,y) x + y + mu1)
hatymat

##        airbag1  airbag2
## 50kW 0.8333333 3.166667
## 70kW 2.8333333 5.166667
## 90kW 3.3333333 5.666667

原始分值与拟合值、拟合残差：

errmat <- score1 - hatymat
cbind("原始分值"=c(t(score1)), "拟合值"=c(t(hatymat)), "拟合残差"=c(t(errmat)))

##      原始分值    拟合值   拟合残差
## [1,]        1 0.8333333  0.1666667
## [2,]        3 3.1666667 -0.1666667
## [3,]        2 2.8333333 -0.8333333
## [4,]        6 5.1666667  0.8333333
## [5,]        4 3.3333333  0.6666667
## [6,]        5 5.6666667 -0.6666667

可以通过最小化拟合残差平方和来估计参数\(\beta_{jl}\)。这就是自变量为分类变量的线性模型问题，有\(L_j\)个水平的分类变量\(X_j\)需要用\(L_j-1\)个哑变量表示，约束\(\sum_{j=1}^{L_j} \beta_{jl} = 0\)。这样就对一个受访者的打分矩阵数据\(Y_1, \dots, Y_K\)，可以用最小二乘法估计出所有的\(\beta_{jl}\)值。实际的计算是\(\beta_{jl} = \bar p_{x_{jl}} - \mu\)。

实际中有\(n\)个受访者的\(nK\)个分数时，只要将所有人的\(nK\)个观测的方程写成适当的线性模型矩阵表示，就可以用最小二乘法估计效用系数\(\beta_{jl}\)。

13.3.2 非度量法

如果不能假定排序的差值代表固定的效用差异，比如，第一、二名的差异大于第三、四名的差异，则需要使用非度量法。可以使用Kruskal(1965)年提出的单调方差分析方法。首先用上述度量法得到拟合值\(\hat Y_k\)，这时\(Y_k\)到\(\hat Y_k\)的变换可能不单调，比如上面的汽车问题，从\(Y_k\)到\(\hat Y_k\)的变化图形为：

y1 <- c(score1)
y2 <- c(hatymat)
ord1 <- order(y1)
plot(y1[ord1], y2[ord1], xlab="原始分值", ylab="拟合分值",
     type="b", lwd=2, pch=16, cex=2)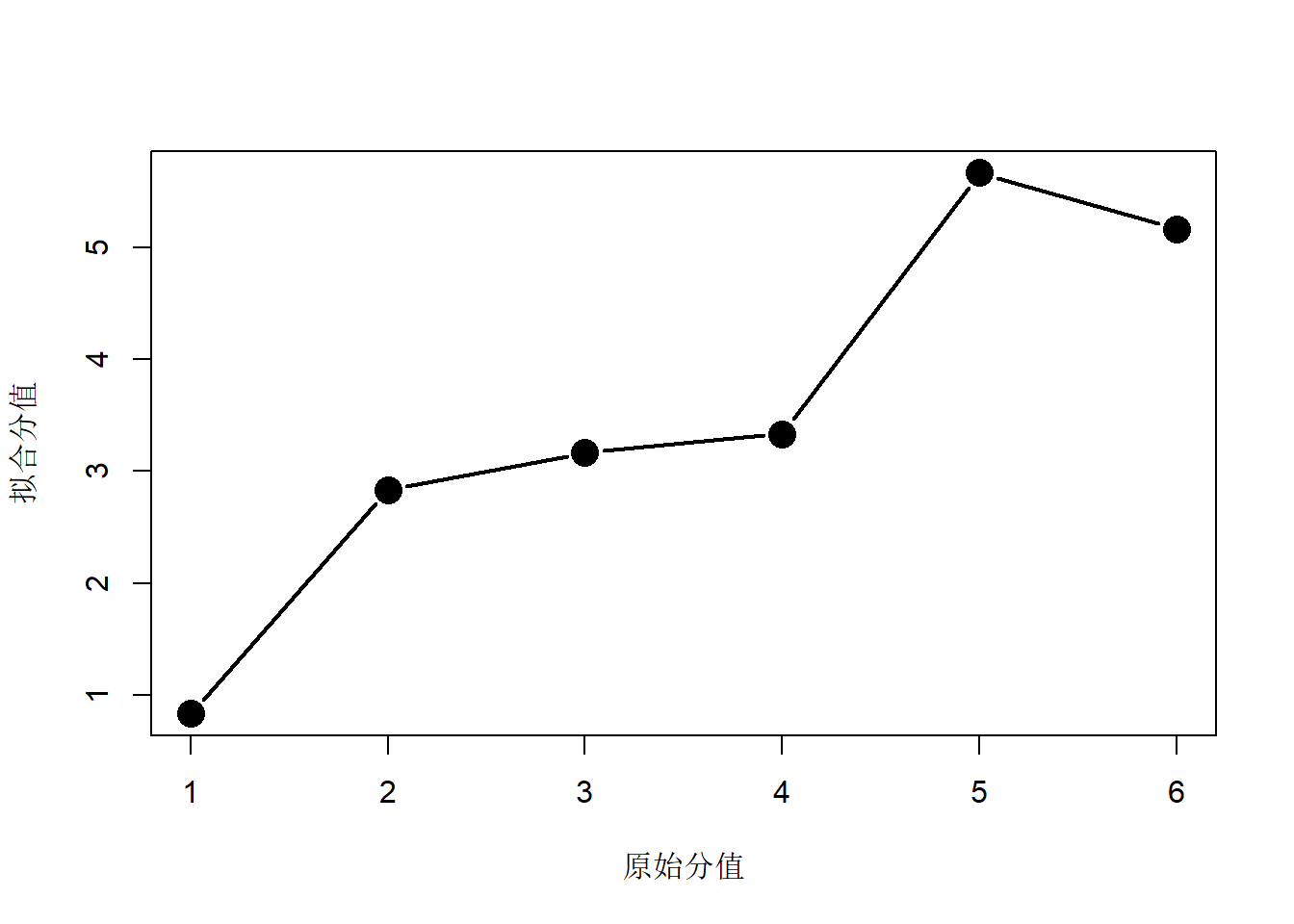

可以看出\(Y_k=5, 6\)时\(\hat Y_k\)的对应值出现了相反次序。

为了使得拟合值保持原来的次序，令新的拟合值为\(\hat Z_k = f(\hat Y_k)\)，其中\(f(\cdot)\)是一个未知的单调非降函数。比如，上面的例子中令\(\hat Y_k=5,6\)时对应的\(\hat Z_k\)为\(\hat Y_k\)的这两个反序值的平均值。

变换以后模型可能不再适合，所以需要迭代第修改\(\beta_{jl}\)估计和函数\(f(\cdot)\)。汇集相邻反序（Pool-adjacent-violators, PAV）算法可以迭代地进行估计，使得如下度量最小： \[\begin{aligned} \text{STRESS} = \frac{\sum_{k=1}^K (\hat Z_k - \hat Y_k)^2}{\sum_{k=1}^K (\hat Y_k - \bar{\hat Y}_k)^2} \end{aligned}\]

13.4 实例分析

R中与联合分析有关的扩展包有conjoint包， MLCM包（用于心理实验，受试者每次观看两个激励，基于两因子法）， cjoint包（实现了比较新的AMCE估计）， MConjoint包（试验设计）等。

library(conjoint)
data(tea)
colnames(tprof) <- c("price", "variety", "kind", "aroma")
tprof2 <- tprof
tprof2[["price"]] <- factor(tprof[["price"]], levels=1:3, labels=c("low", "medium", "high"))
tprof2[["variety"]] <- factor(tprof[["variety"]], levels=1:3, labels=c("black", "green", "red"))
tprof2[["kind"]] <- factor(tprof[["kind"]], levels=1:3, labels=c("bags", "granulated", "leafy"))
tprof2[["aroma"]] <- factor(tprof[["aroma"]], levels=1:2, labels=c("yes", "no"))
str(tprof)

## 'data.frame':    13 obs. of  4 variables:
##  $ price  : int  3 1 2 2 3 2 3 2 3 1 ...
##  $ variety: int  1 2 2 1 3 1 2 3 1 3 ...
##  $ kind   : int  1 1 2 3 3 1 1 1 2 2 ...
##  $ aroma  : int  1 1 1 1 1 2 2 2 2 2 ...

考虑茶产品的四个特性price，variety, kind, aroma，各变量的水平为：

price：low, medium, high；
variety：black, green, red；
kind：bags, granulated, leafy；
aroma：yes, no。

完全试验需要\(3 \times 3 \times 3 \times 2=54\)种组合，为试验简单进行了试验设计，仅选择其中的13种组合（激励, 这里称为profile（轮廓）），组合值在tprof中，下面显示将代码显示成了水平含义：

knitr::kable(tprof2)

price	variety	kind	aroma
high	black	bags	yes
low	green	bags	yes
medium	green	granulated	yes
medium	black	leafy	yes
high	red	leafy	yes
medium	black	bags	no
high	green	bags	no
medium	red	bags	no
high	black	granulated	no
low	red	granulated	no
low	black	leafy	no
medium	green	leafy	no
high	green	leafy	no

对100位受试者进行了调查，得到\(100\times 13\)的分值矩阵：

knitr::kable(head(tprefm, 10))

profil1	profil2	profil3	profil4	profil5	profil6	profil7	profil8	profil9	profil10	profil11	profil12	profil13
8	1	1	3	9	2	7	2	2	2	2	3	4
0	10	3	5	1	4	8	6	2	9	7	5	2
4	10	3	5	4	1	2	0	0	1	8	9	7
6	7	4	9	6	3	7	4	8	5	2	10	9
5	1	7	8	6	10	7	10	6	6	6	10	7
10	1	1	5	1	0	0	0	0	0	0	1	1
8	0	0	0	9	0	0	0	0	0	5	10	8
5	2	1	4	3	8	5	9	6	8	3	1	2
7	3	3	9	0	5	3	0	5	0	5	10	8
8	7	3	10	9	1	2	2	2	2	8	10	8

将这些分值按行拉直后得到向量为tpref。四个特性的\(3+3+3+2=11\)个水平之名称tlevn向量中：

tlevn2 <- paste(
  rep(c("price", "variaty", "kind", "aroma"), c(3,3,3,2)), 
  as.character(tlevn[[1]]), sep=":")
tlevn2

##  [1] "price:low"       "price:medium"    "price:high"      "variaty:black"  
##  [5] "variaty:green"   "variaty:red"     "kind:bags"       "kind:granulated"
##  [9] "kind:leafy"      "aroma:yes"       "aroma:no"

分别表示price的low, medium, high, variaty的black, green, red, kind的bags, granulated, leafy, aroma的yes, no。

计算联合测量分析结果，输入中tpref是将100个人的13个回答按行拉直的向量， tprof是13个激励对应的4个特性值的对应矩阵， tlevn是各个特性的所有水平值的名称：

Conjoint(tpref, tprof, tlevn2)

## 
## Call:
## lm(formula = frml)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5,1888 -2,3761 -0,7512  2,2128  7,5134 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         3,55336    0,09068  39,184  < 2e-16 ***
## factor(x$price)1    0,24023    0,13245   1,814    0,070 .  
## factor(x$price)2   -0,14311    0,11485  -1,246    0,213    
## factor(x$variety)1  0,61489    0,11485   5,354 1,02e-07 ***
## factor(x$variety)2  0,03489    0,11485   0,304    0,761    
## factor(x$kind)1     0,13689    0,11485   1,192    0,234    
## factor(x$kind)2    -0,88977    0,13245  -6,718 2,76e-11 ***
## factor(x$aroma)1    0,41078    0,08492   4,837 1,48e-06 ***
## ---
## Signif. codes:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1
## 
## Residual standard error: 2,967 on 1292 degrees of freedom
## Multiple R-squared:  0,09003,    Adjusted R-squared:  0,0851 
## F-statistic: 18,26 on 7 and 1292 DF,  p-value: < 2,2e-16

## [1] "Part worths (utilities) of levels (model parameters for whole sample):"
##             levnms    utls
## 1        intercept  3,5534
## 2        price:low  0,2402
## 3     price:medium -0,1431
## 4       price:high -0,0971
## 5    variaty:black  0,6149
## 6    variaty:green  0,0349
## 7      variaty:red -0,6498
## 8        kind:bags  0,1369
## 9  kind:granulated -0,8898
## 10      kind:leafy  0,7529
## 11       aroma:yes  0,4108
## 12        aroma:no -0,4108
## [1] "Average importance of factors (attributes):"
## [1] 24,76 32,22 27,15 15,88
## [1] Sum of average importance:  100,01
## [1] "Chart of average factors importance"

结果包括每个特性的每个水平的\(\beta_{11}, \beta_{1,L_j}\)的满足约束 \(\sum_{l=1}^{L_j} \beta_{jl} = 0\)的估计值，即每个特性各个水平的Part worth(部分效用值)。还给出了每个特性（factors）对效用解释贡献百分比的度量（Average importance of factors），比如上例中最重要的variaty，解释比例32.22%，其水平中效用最高的是black tea(红茶)，效用0.6149，最低的是red tea(路易波士茶)，效用-0.6498。最不重要的是aroma，解释比例15.88%， yes效用为0.4108， no效用为-0.4108。

profil1	profil2	profil3	profil4	profil5	profil6	profil7	profil8	profil9	profil10	profil11	profil12	profil13
8	1	1	3	9	2	7	2	2	2	2	3	4
0	10	3	5	1	4	8	6	2	9	7	5	2
4	10	3	5	4	1	2	0	0	1	8	9	7
6	7	4	9	6	3	7	4	8	5	2	10	9
5	1	7	8	6	10	7	10	6	6	6	10	7
10	1	1	5	1	0	0	0	0	0	0	1	1
8	0	0	0	9	0	0	0	0	0	5	10	8
5	2	1	4	3	8	5	9	6	8	3	1	2
7	3	3	9	0	5	3	0	5	0	5	10	8
8	7	3	10	9	1	2	2	2	2	8	10	8

profil1	profil2	profil3	profil4	profil5	profil6	profil7	profil8	profil9	profil10	profil11	profil12	profil13
8	1	1	3	9	2	7	2	2	2	2	3	4
0	10	3	5	1	4	8	6	2	9	7	5	2
4	10	3	5	4	1	2	0	0	1	8	9	7
6	7	4	9	6	3	7	4	8	5	2	10	9
5	1	7	8	6	10	7	10	6	6	6	10	7
10	1	1	5	1	0	0	0	0	0	0	1	1
8	0	0	0	9	0	0	0	0	0	5	10	8
5	2	1	4	3	8	5	9	6	8	3	1	2
7	3	3	9	0	5	3	0	5	0	5	10	8
8	7	3	10	9	1	2	2	2	2	8	10	8

profil1	profil2	profil3	profil4	profil5	profil6	profil7	profil8	profil9	profil10	profil11	profil12	profil13
8	1	1	3	9	2	7	2	2	2	2	3	4
0	10	3	5	1	4	8	6	2	9	7	5	2
4	10	3	5	4	1	2	0	0	1	8	9	7
6	7	4	9	6	3	7	4	8	5	2	10	9
5	1	7	8	6	10	7	10	6	6	6	10	7
10	1	1	5	1	0	0	0	0	0	0	1	1
8	0	0	0	9	0	0	0	0	0	5	10	8
5	2	1	4	3	8	5	9	6	8	3	1	2
7	3	3	9	0	5	3	0	5	0	5	10	8
8	7	3	10	9	1	2	2	2	2	8	10	8