2 多元数据图形

• 希望用图形方法回答如下问题：
• 某些分量是否比其它分量更为分散？有没有显示分组的分量？ 分量中有没有离群值？数据分布“正态”吗？ 有没有线性组合表现非正态？
• 可以查看每个变量的图形，如直方图、核密度图、盒形图、散点图、茎叶图等。
• 可以每两个变量画散点图，组成散点图矩阵。 可以借助一些软件画动态三维散点图。
• 更高维数需要作一些降维处理再作图。

主要参考：

• Zelterman, D.(2015) Applied Multivariate Statistics with R, Springer.

图形需要安装一些R扩展包。 可以用RGUI或者RStudio的菜单安装， 也可以用如下命令安装：

options(repos=c(CRAN="https://mirrors.tuna.tsinghua.edu.cn/CRAN/"))
install.packages(c(
  "mvtnorm", "aplpack", "MVA", "hexbin", "tourr", "rgl"))

2.1 一些辅助程序

2.1.1 开头匹配

top.match(x, table)对字符型向量table的每个元素， 判断其是否等于字符型向量x中的某个元素头部， 对table的每个元素返回其在x中匹配的元素的下标，找不到返回0。

top.match <- function(x, table){
    ind <- integer(length(table))
    for(k in seq(along=table)){
      item <- table[k]
      ii <- which(startsWith(x, item))
      if(length(ii)>0){
        ind[k] <- ii[1]
      }
    }
    ind
}

2.1.2 零一标准化

scale01()将输入的数据框或矩阵x各列标准化到\([0,1]\)范围。

scale01 <- function(x){
  cmin <- apply(x, 2, min)
  cmax <- apply(x, 2, max)
  scale(x, cmin, cmax-cmin)
}

2.1.3 挑选颜色的函数

R扩展包colourpicker提供了一个RStudio软件中用的Addin小程序Colour Picker，可以用鼠标选择颜色并返回颜色名字符串或者颜色值字符串， 可以用于绘图时指定点、线、文字等的颜色。

2.2 一元数据图形

2.2.1 茎叶图

• 以“茎”为坐标轴，每个“叶子”代表一个观测。
• 可以查看数据分布情况；检查数据错误；查看异常值。
• 并排茎叶图（背靠背茎叶图）可以比较两个变量分布。

2.2.1.1 cd4数据

boot包中的cd4数据集是某个临床试验20个病人开始(baseline)以及一年后的cd4测量值， 数据中cd4值单位是100（实际值是保存值乘以100）。cd4值越低说明免疫越差， cd4在200以下是艾滋病诊断依据。

调入cd4数据框：

data(cd4, package="boot")

用str()查看数据的结构， 用head()显示开头：

str(cd4) 

## 'data.frame':    20 obs. of  2 variables:
##  $ baseline: num  2.12 4.35 3.39 2.51 4.04 5.1 3.77 3.35 4.1 3.35 ...
##  $ oneyear : num  2.47 4.61 5.26 3.02 6.36 5.93 3.93 4.09 4.88 3.81 ...

head(cd4)

##   baseline oneyear
## 1     2.12    2.47
## 2     4.35    4.61
## 3     3.39    5.26
## 4     2.51    3.02
## 5     4.04    6.36
## 6     5.10    5.93

开始时的cd4测量值的茎叶图：

stem(cd4[["baseline"]])

## 
##   The decimal point is at the |
## 
##   1 | 9
##   2 | 15567
##   3 | 000444468
##   4 | 0124
##   5 | 1

一年后的cd4测量值的茎叶图：

stem(cd4[["oneyear"]])

## 
##   The decimal point is at the |
## 
##   2 | 4568
##   3 | 02389
##   4 | 1234679
##   5 | 369
##   6 | 4

2.2.1.2 各省可支配收入与消费性输出

cityIncomeConsume <- read_csv(
  "data/居民收入支出.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)

数据框cityIncomeConsume包含31个省的可支配收入、消费性支出。 开头如下：

knitr::kable(head(cityIncomeConsume))

地区	可支配收入	消费性支出
北京	21988.71	15330.44
天津	16357.35	12028.88
河北	11690.47	8234.97
山西	11564.95	8101.84
内蒙古	12377.84	9281.46
辽宁	12300.39	9429.73

可支配收入的茎叶图：

stem(cityIncomeConsume[["可支配收入"]])

## 
##   The decimal point is 3 digit(s) to the right of the |
## 
##   10 | 023378901135555567
##   12 | 23346
##   14 | 35
##   16 | 447
##   18 | 
##   20 | 6
##   22 | 06

消费性支出的茎叶图:

stem(cityIncomeConsume[["消费性支出"]])

## 
##   The decimal point is 3 digit(s) to the right of the |
## 
##    7 | 5558888999
##    8 | 122345677
##    9 | 03479
##   10 | 7
##   11 | 1
##   12 | 0
##   13 | 
##   14 | 13
##   15 | 3
##   16 | 
##   17 | 3

2.2.2 并排茎叶图

并排茎叶图又称背对背茎叶图， 可以比较两个变量的分布。 需要安装aplpack扩展包， 使用其中的stem.leaf.backback()函数。

2.2.2.1 cd4数据的并排茎叶图

aplpack::stem.leaf.backback(
  cd4[["baseline"]], cd4[["oneyear"]])

## ________________________________
##   1 | 2: represents 1.2, leaf unit: 0.1 
## cd4[["baseline"]]
##                    cd4[["oneyear"]]
## ________________________________
##              | 1* |             
##    1        8| 1. |             
##    3       41| 2* |44       2   
##    7     9655| 2. |58       4   
##   (6)  333300| 3* |022      7   
##    7       75| 3. |89       9   
##    5     3110| 4* |0233    (4)  
##              | 4. |678      7   
##    1        1| 5* |2        4   
##              | 5. |59       3   
##              | 6* |3        1   
##              | 6. |             
##              | 7* |             
## ________________________________
## n:         20      20       
## ________________________________

结果是背对背茎叶图， 每侧都有中位数所在茎的频数值用括号包围， 而其它频数则是从外侧向中位数计数的累计频数。

茎叶图不适合数据量比较多的情形。

2.2.2.2 各省城镇居民收入支出并排茎叶图

aplpack::stem.leaf.backback(
  cityIncomeConsume[["可支配收入"]],
  cityIncomeConsume[["消费性支出"]])

## __________________________________________
##   1 | 2: represents 1200, leaf unit: 100 
## cityIncomeConsume[["可支配收入"]]
##                         cityIncomeConsume[["消费性支出"]]
## __________________________________________
##                   |  7 |5557888889   10   
##                   |  8 |1122455679  (10)  
##                   |  9 |2468         11   
##     8     98763220| 10 |7             7   
##   (10)  6544444210| 11 |0             6   
##    13        53322| 12 |0             5   
##                   | 13 |                  
##     8            2| 14 |03            4   
##     7            5| 15 |3             2   
##     6           33| 16 |                  
##     4            6| 17 |2             1   
##                   | 18 |                  
## __________________________________________
## HI: 20573.82                              
## 21988.71 23622.73                         
## n:              31      31            
## __________________________________________

2.2.3 盒形图

表现了中位数、四分之一和四分之三分位数、最小值、最大值和离群值情况。 能够体现数据分布的集中趋势、分散程度、对称与否、离群值情况。 适合数据量大的情形且有利于多个变量或多个组的比较。 盒形图不能表现数据分布的分组情况和多峰分布情况。

基本作图函数boxplot()可以做盒形图，这里用ggplot2扩展包。

2.2.3.1 单个变量的盒形图

cd4中baseline（试验开始时20个病人的CD4测量值）的盒形图：

library(ggplot2)
p <- ggplot(data = cd4, mapping = aes(
  y = baseline))
p + geom_boxplot() + 
  scale_x_continuous(breaks = NULL) +
  labs(x = NULL, y = "Baseline")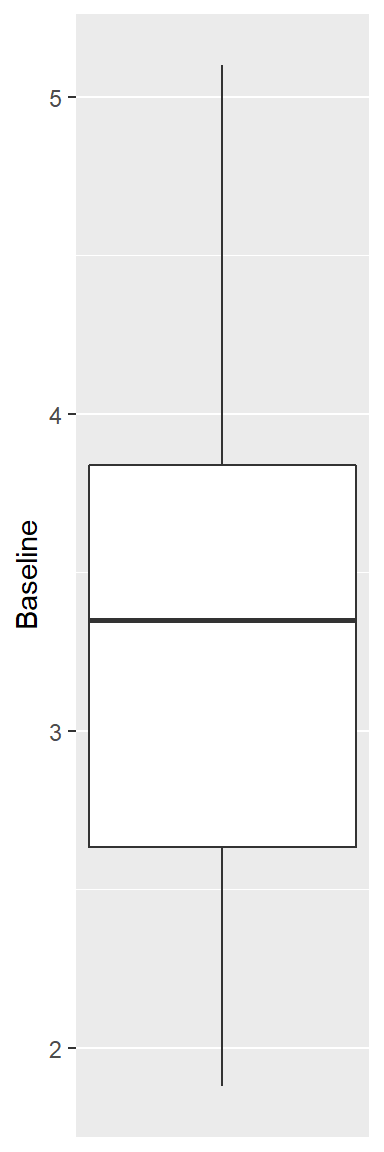

使用基本作图函数的方法：

boxplot(cd4[["baseline"]])

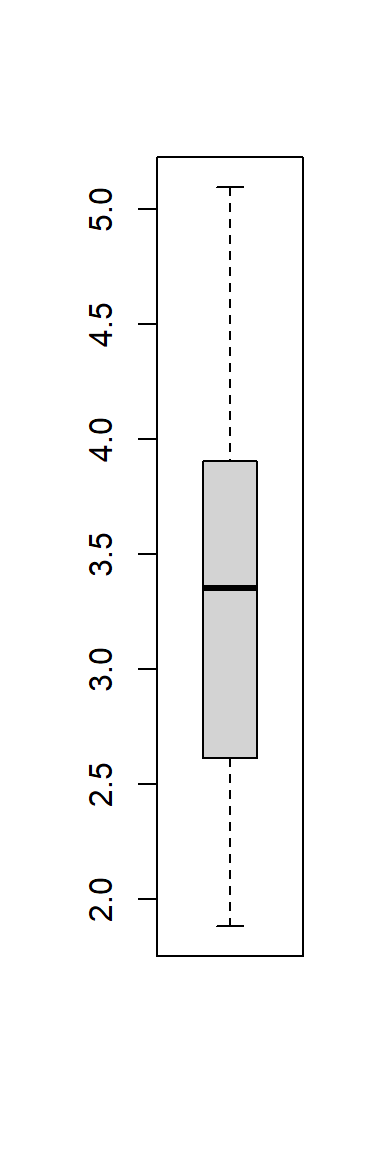
各省城镇居民收入的盒形图：

boxplot(cityIncomeConsume[["可支配收入"]])

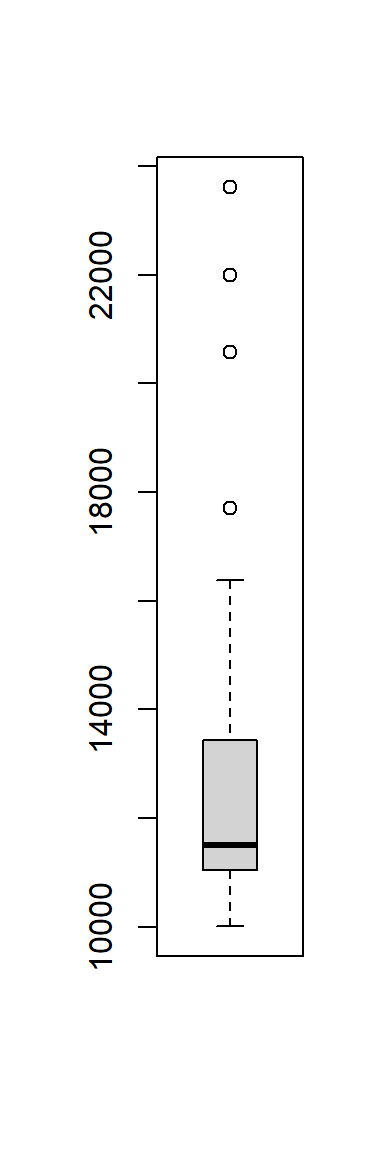
触须线长度不超过盒子长度的1.5倍， 触须线外的点称为离群值， 离群值较多的数据需要特殊方法， 离群值应仔细检查。

2.2.3.2 数据框中多个变量的盒形图

如果boxplot()的自变量是一个各列都是数值型的数据框， 则会对数据框每一列作盒形图并且画到同一坐标系中， 有利于比较各个变量的分布。 如，各省城镇居民收入、支出的并排盒形图：

boxplot(cityIncomeConsume[,2:3])

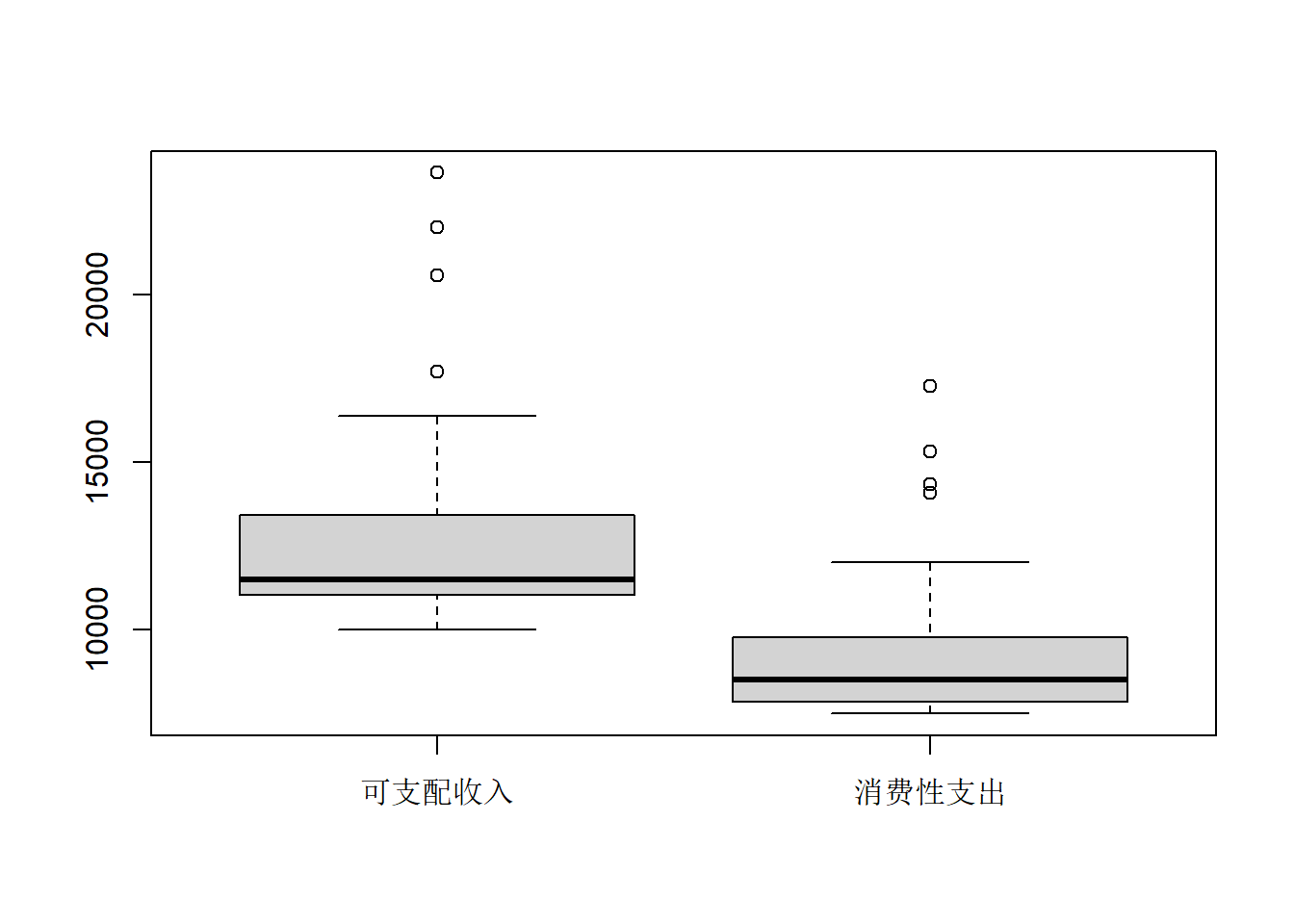
为了用ggplot2扩展包作两个变量的并列盒形图， 需要做数据变换， 使得待比较变量处于同一列， 另外增加一个标志列。 如：

library(tidyverse)
d <- cityIncomeConsume %>%
  pivot_longer(c(`可支配收入`, `消费性支出`), 
    names_to="variable", values_to="value")
p <- ggplot(data = d, mapping = aes(
  x = variable, y = value))
p + geom_boxplot() + 
  labs(x = NULL, y = NULL)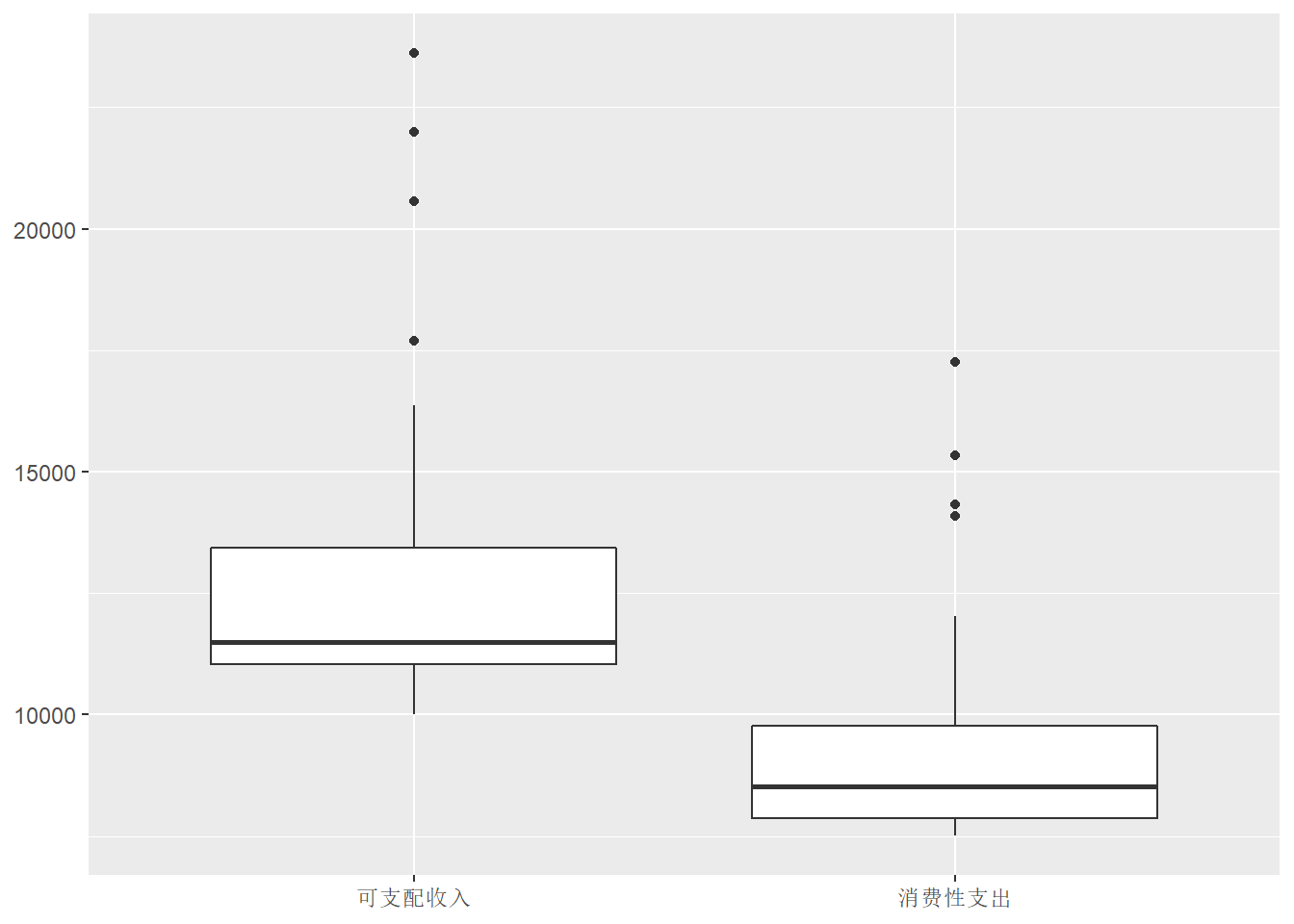

2.2.3.3 数据框中某个变量按分类变量分组的盒形图

bankNotes <- read_csv(
  "data/瑞士银行真假钞.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
bankNotes <- bankNotes |>
  mutate(
    genuine = factor(
      rep(c("genuine", "conterfeit"), each=100)))

bankNotes数据框包含了瑞士银行的某种钞票的200张钞票的测量数据， 前100行为真钞，后100行为假钞。 读入数据并简单显示数据结构如下：

str(bankNotes)

## tibble [200 × 7] (S3: tbl_df/tbl/data.frame)
##  $ length : num [1:200] 215 215 215 215 215 ...
##  $ left   : num [1:200] 131 130 130 130 130 ...
##  $ right  : num [1:200] 131 130 130 130 130 ...
##  $ bottom : num [1:200] 9 8.1 8.7 7.5 10.4 9 7.9 7.2 8.2 9.2 ...
##  $ top    : num [1:200] 9.7 9.5 9.6 10.4 7.7 10.1 9.6 10.7 11 10 ...
##  $ diag   : num [1:200] 141 142 142 142 142 ...
##  $ genuine: Factor w/ 2 levels "conterfeit","genuine": 2 2 2 2 2 2 2 2 2 2 ...

head(bankNotes)

## # A tibble: 6 × 7
##   length  left right bottom   top  diag genuine
##    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <fct>  
## 1   215.  131   131.    9     9.7  141  genuine
## 2   215.  130.  130.    8.1   9.5  142. genuine
## 3   215.  130.  130.    8.7   9.6  142. genuine
## 4   215.  130.  130.    7.5  10.4  142  genuine
## 5   215   130.  130.   10.4   7.7  142. genuine
## 6   216.  131.  130.    9    10.1  141. genuine

将观测按真假钞分成两组并列地作对角线长度的盒形图:

ggplot(bankNotes, aes(
    x = genuine, y = diag)) + 
  geom_boxplot() + 
  labs(x = NULL, y = "对角线长度")

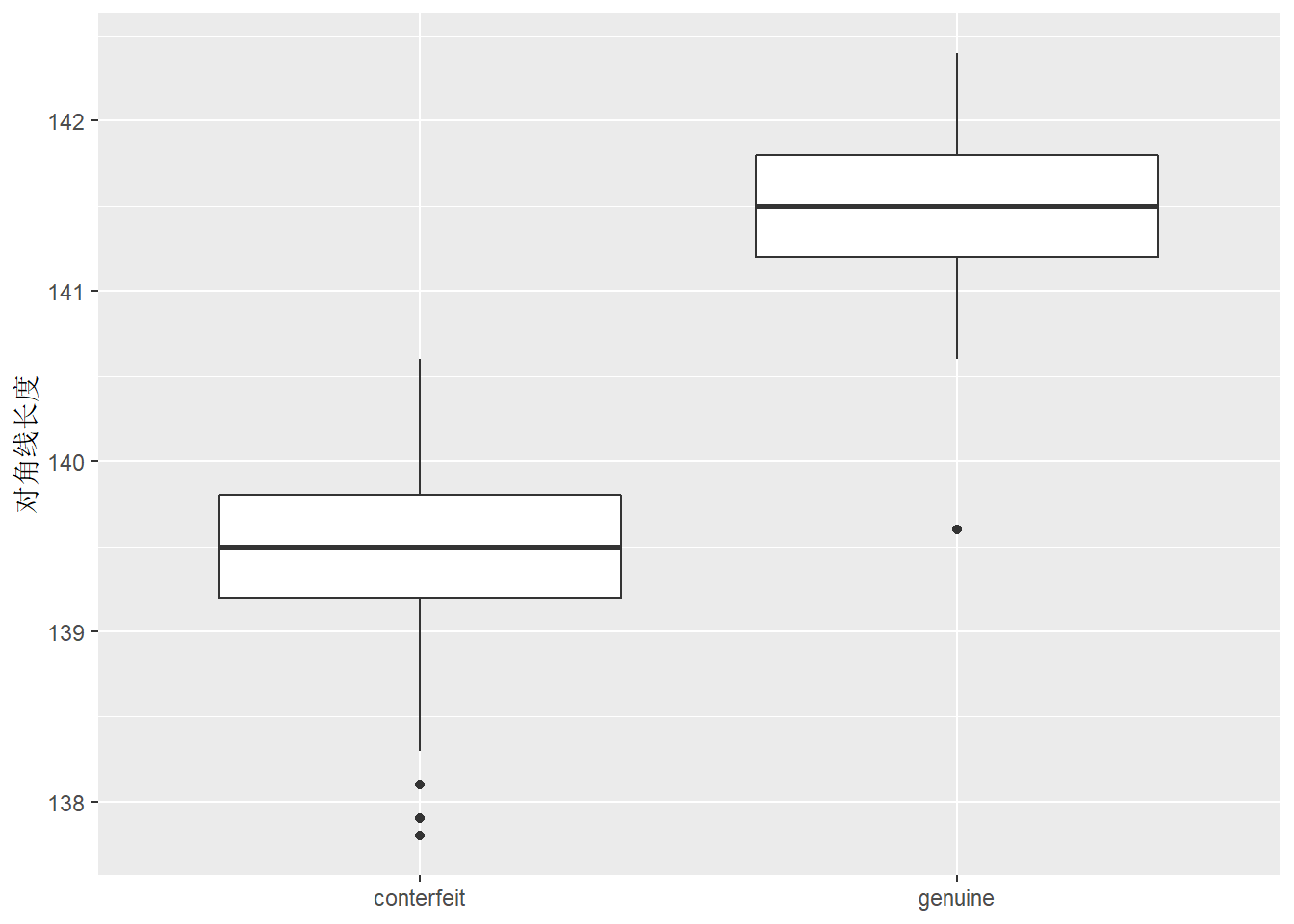
上图比较了真假钞的对角线长度。 除了一个例外， 假钞的对角线长度比真钞都短。

票面长度的盒形图比较：

ggplot(bankNotes, aes(
    x = genuine, y = length)) + 
  geom_boxplot() + 
  labs(x = NULL, y = "票面长度")

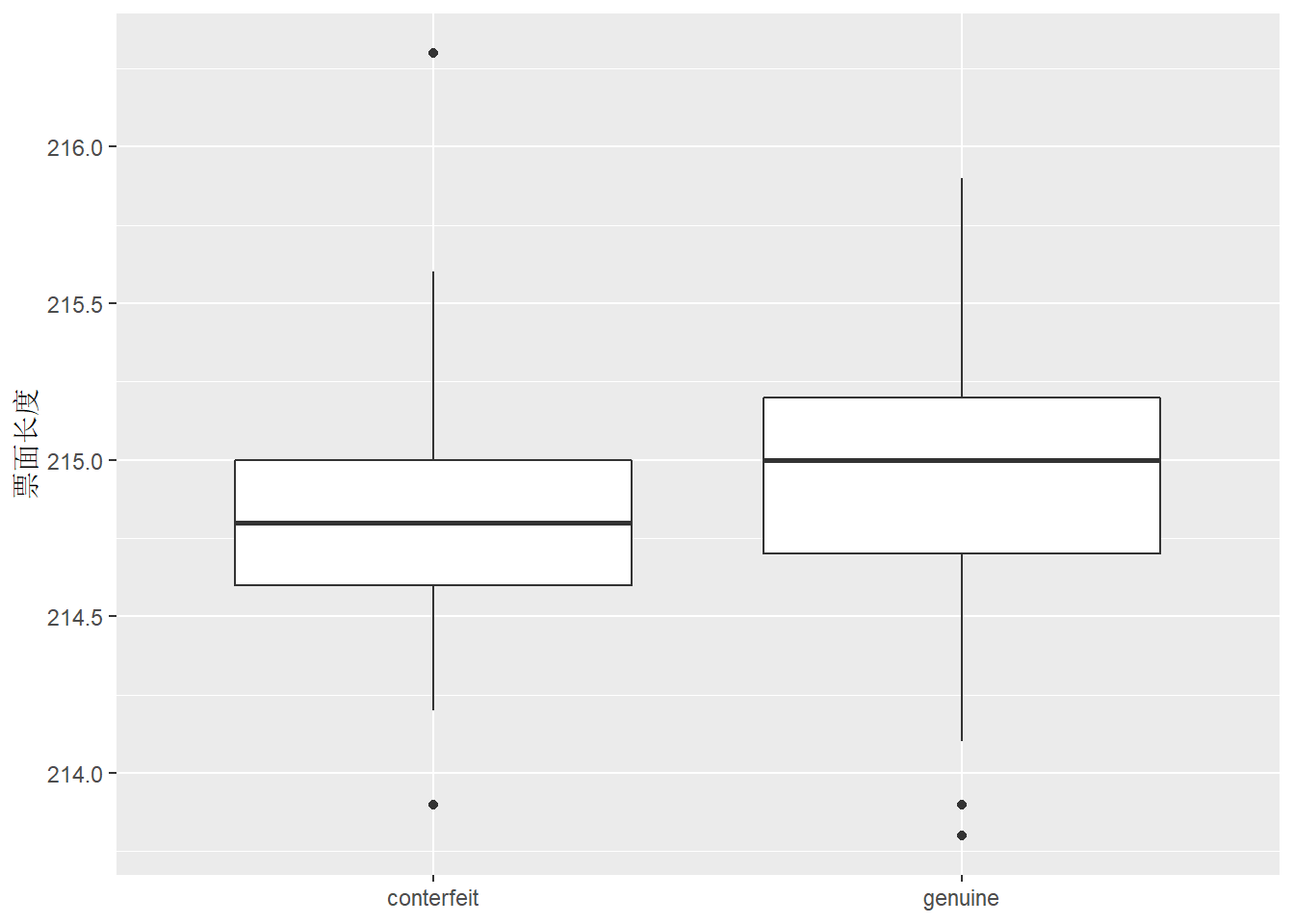
真假钞长度区别不明显。

carOil <- read_csv(
  "data/汽车油耗.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
carOil <- carOil |>
  mutate(
    Company = factor(
      Company, levels=c(1,2,3),
      labels=c("US", "Japan", "EU") ) )

在carOil数据框中保存了三个国家的若干种汽车的一些数据， 其中一个变量Mileage是每加仑汽油平均行驶的英里数。 下面的程序用并排盒形图比较三个国家的汽车的油耗。

ggplot(carOil, aes(
    x = Company, y = Mileage)) +
  geom_boxplot() + 
  labs(x = NULL, y = "Mileage")

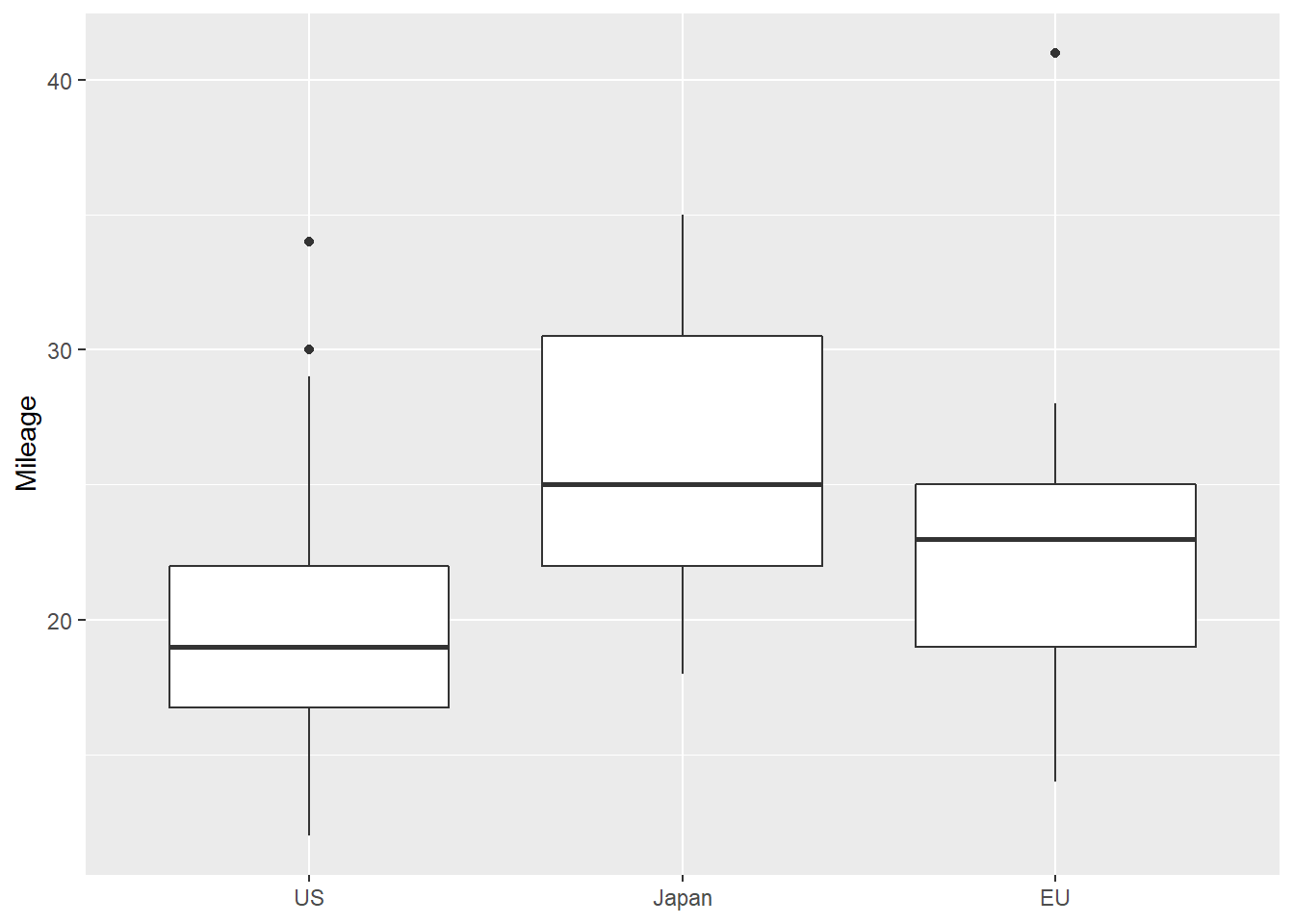
可以看出日本出产的汽车油耗性能最高。

2.2.4 直方图

• 作为分布密度估计。hist()
• 组距不同则图形也不同。
• 开始点不同图形可能不同。
• 分在一组内的观测值的具体值不起作用，损失信息。
• 估计的密度形状是不连续的。

用hist(x)作向量x的直方图。 如

hist(cd4[["baseline"]], 
  main="CD4 at baseline", xlab="")

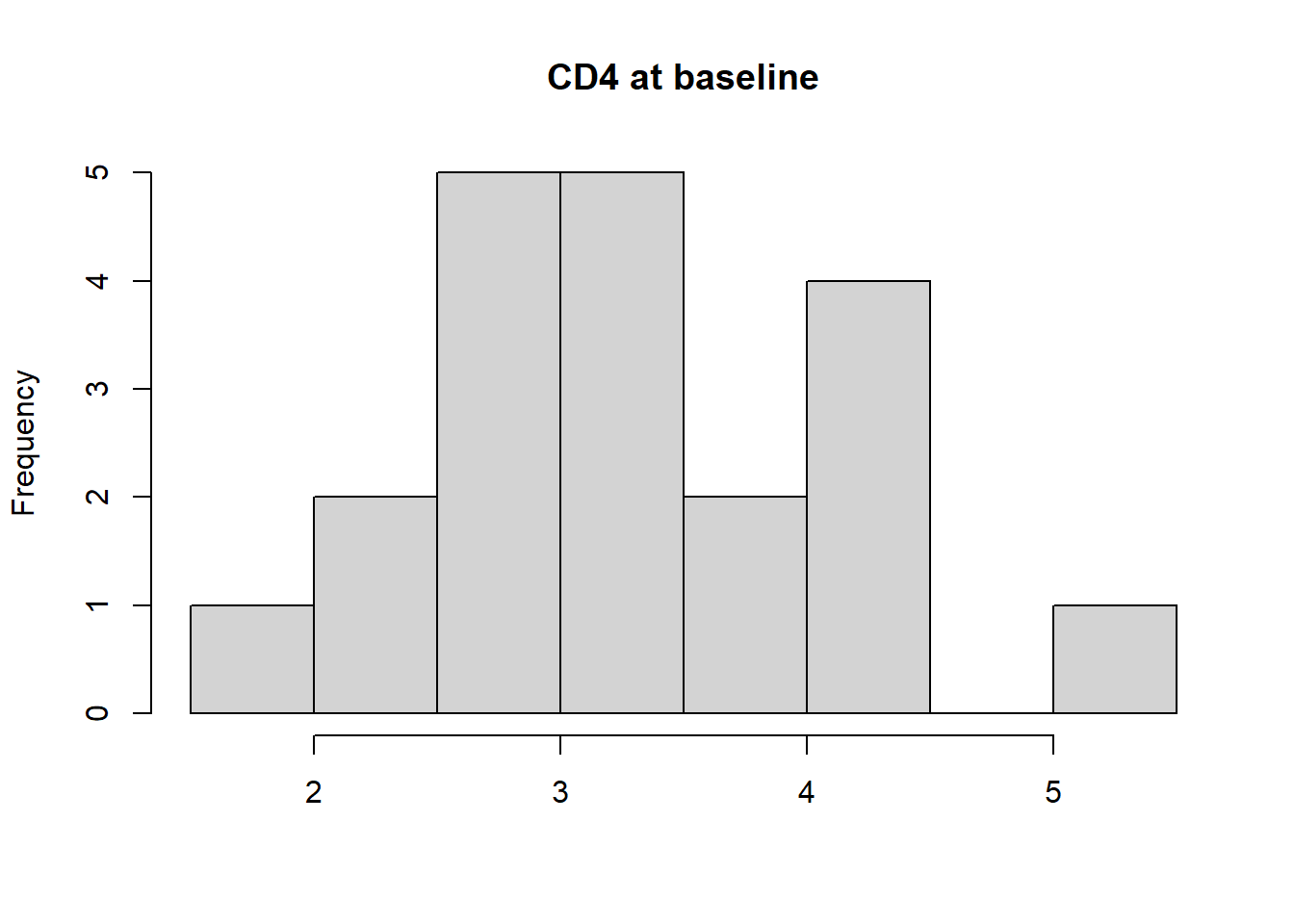
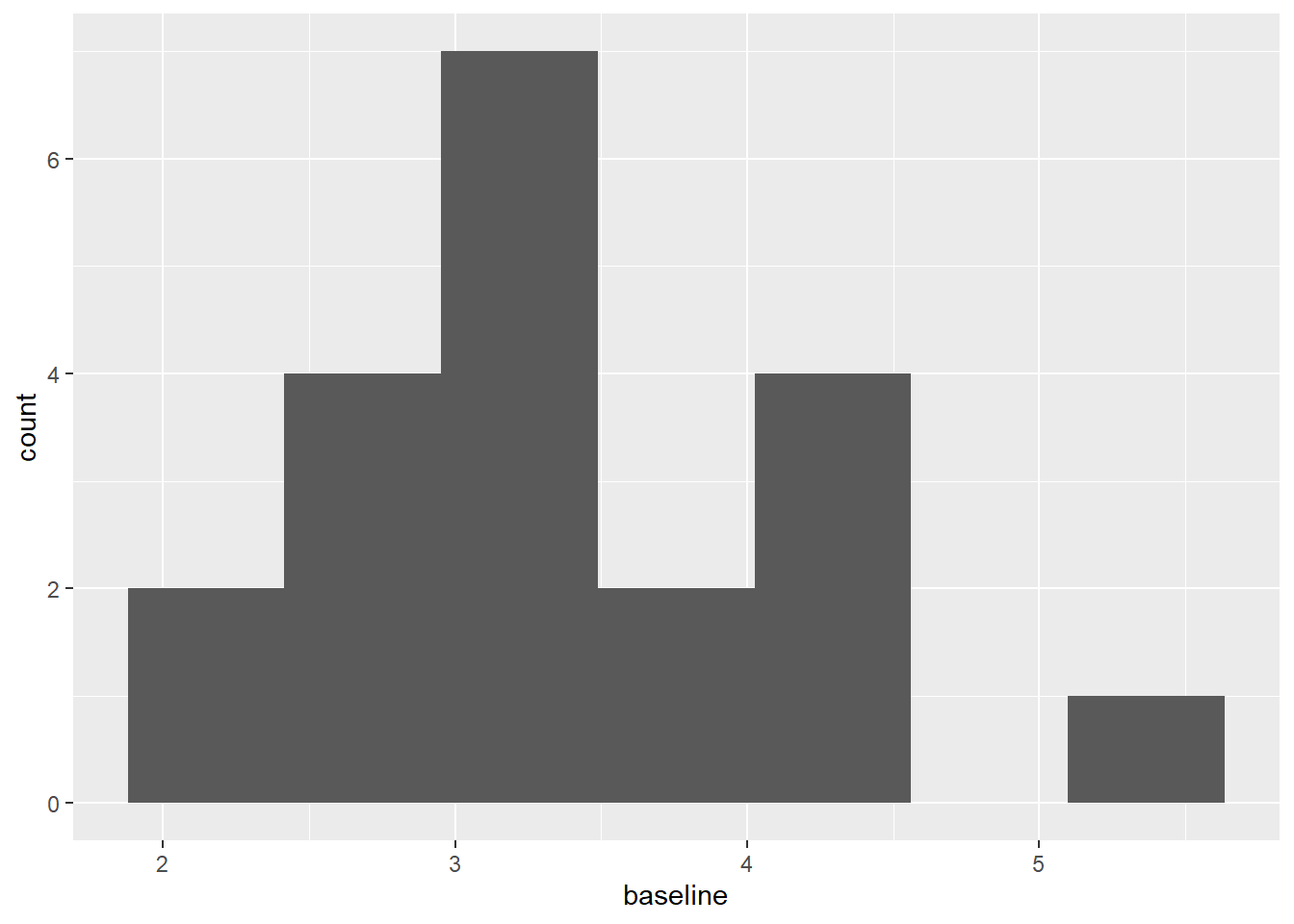
用ggplot2包作直方图，需要人为用bins指定指定分组数。 也可以用width指定分组宽度。

ggplot(cd4, aes(
  x = baseline )) + 
  geom_histogram(bins = 7)

下面用分格的办法并排地作cd4在baseline与oneyear的直方图。 为了比较两个变量， 一定注意坐标轴要标准化成相同的范围。

f <- function(){
    opar <- par(mfrow=c(1,2)); on.exit(par(opar))
    xlim <- range(cd4[,1:2])
    with(cd4, hist(baseline, main="", xlab="At baseline",
                   xlim=xlim))
    with(cd4, hist(oneyear, main="", xlab="At 1 year",
                   xlim=xlim))
}
f()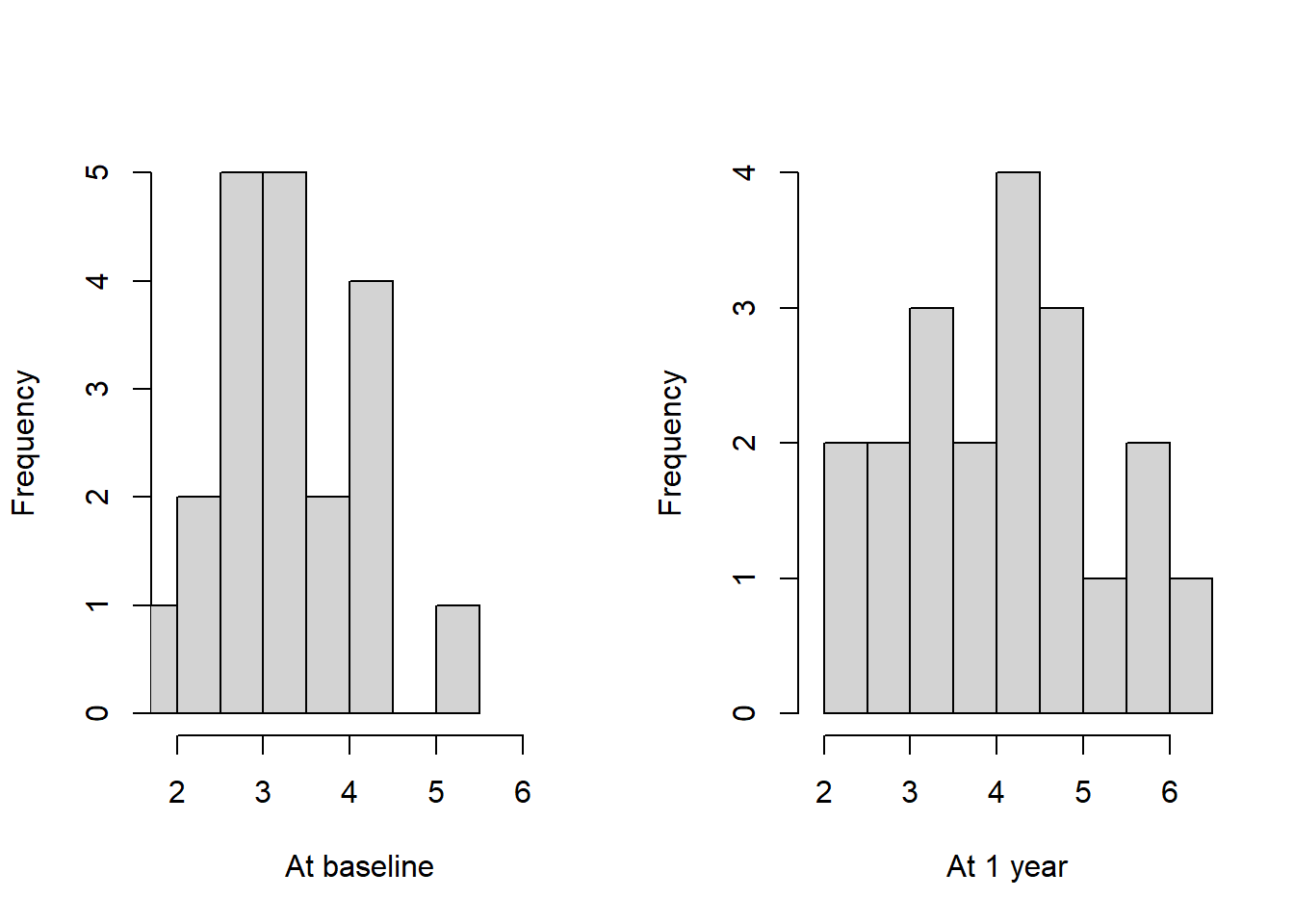

2.2.4.1 直方图的缺点

直方图的缺点是图形对组距（从而决定分组数）和分组起始点的选择特别敏感。 下面的程序选取不同的组距对假钞对角线长度做了四种直方图：

f <- function(){
    opar <- par(mfrow=c(2,2)); on.exit(par(opar))
    x <- bankNotes |>
      slice(101:200) |>
      pull(diag)

    origin = 137.75
    ## 四种不同的组距
    y1 = seq(137.75,141.05,0.1)
    y2 = seq(137.75,141.05,0.2)
    y3 = seq(137.75,141.05,0.3)
    y4 = seq(137.75,141.05,0.4)

    hist(x, breaks=y1,
         ylab="Diagonal",
         xlab="h = 0.1",
         xlim=c(137.5,141),
         ylim=c(0,10.5),
         main="Swiss Bank Notes", axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,10,2),labels=seq(0,10,2))

    hist(x, breaks=y2,
         ylab="Diagonal",
         xlab="h = 0.2",
         xlim=c(137.5,141),
         ylim=c(0,21),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,20,5),labels=seq(0,20,5))

    hist(x, breaks=y3,
         ylab="Diagonal",
         xlab="h = 0.3",
         xlim=c(137.5,141),
         ylim=c(0,31.5),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,30,5),labels=seq(0,30,5))

    hist(x, breaks=y4,
         ylab="Diagonal",
         xlab="h = 0.4",
         xlim=c(137.5,141),
         ylim=c(0,42),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,40,10),labels=seq(0,40,10))    
}
f()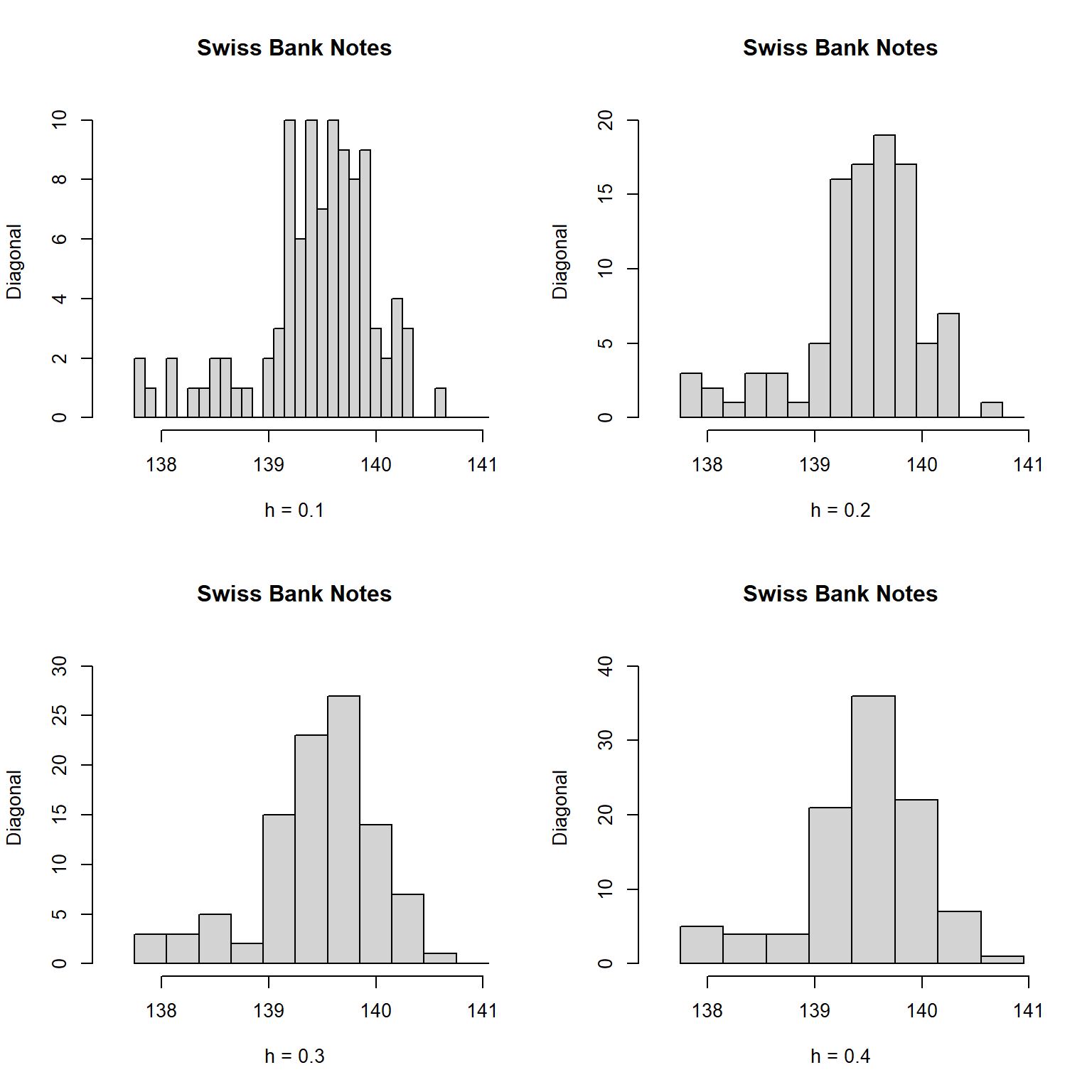

hist()函数用breaks选项可以直接给出分点。 ggplot2的geom_histogram()函数的width可以给出分组宽度， boundary参数可以给出其中一个分点的位置， 从而确定所有分点。 也可以用center参数指定某一个分点的中心。

下面的程序选取不同分组起始位置， 对假钞对角线长度做了四种直方图。

f <- function(){
    opar <- par(mfrow=c(2,2)); on.exit(par(opar))
    x <- bankNotes |>
      slice(101:200) |>
      pull(diag)

    origins <- c(137.65, 137.75, 137.85, 137.95)

    y1 = seq(origins[1], 141.05, 0.4)
    y2 = seq(origins[2], 141.05, 0.4)
    y3 = seq(origins[3]-0.4, 141.05, 0.4) # origin>min(x)
    y4 = seq(origins[4]-0.4, 141.05, 0.4) # origin>min(x)

    hist(x, breaks=y1,
         ylab="Diagonal",
         xlab="x_0 = 137.65",
         xlim=c(137.5,141),
         ylim=c(0,42),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,40,20),labels=seq(0,40,20))

    hist(x, breaks=y2,
         ylab="Diagonal",
         xlab="x_0 = 137.75",
         xlim=c(137.5,141),
         ylim=c(0,42),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,40,20),labels=seq(0,40,20))

    hist(x, breaks=y3,
         ylab="Diagonal",
         xlab="x_0 = 137.85",
         xlim=c(137.5,141),
         ylim=c(0,42),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,40,20),labels=seq(0,40,20))

    hist(x, breaks=y4,
         ylab="Diagonal",
         xlab="x_0 = 137.95",
         xlim=c(137.5,141),
         ylim=c(0,42),
         main="Swiss Bank Notes",
         axes=FALSE)
    axis(side=1, at=seq(138,141), labels=seq(138,141))
    axis(side=2, at=seq(0,40,20),labels=seq(0,40,20))
}
f()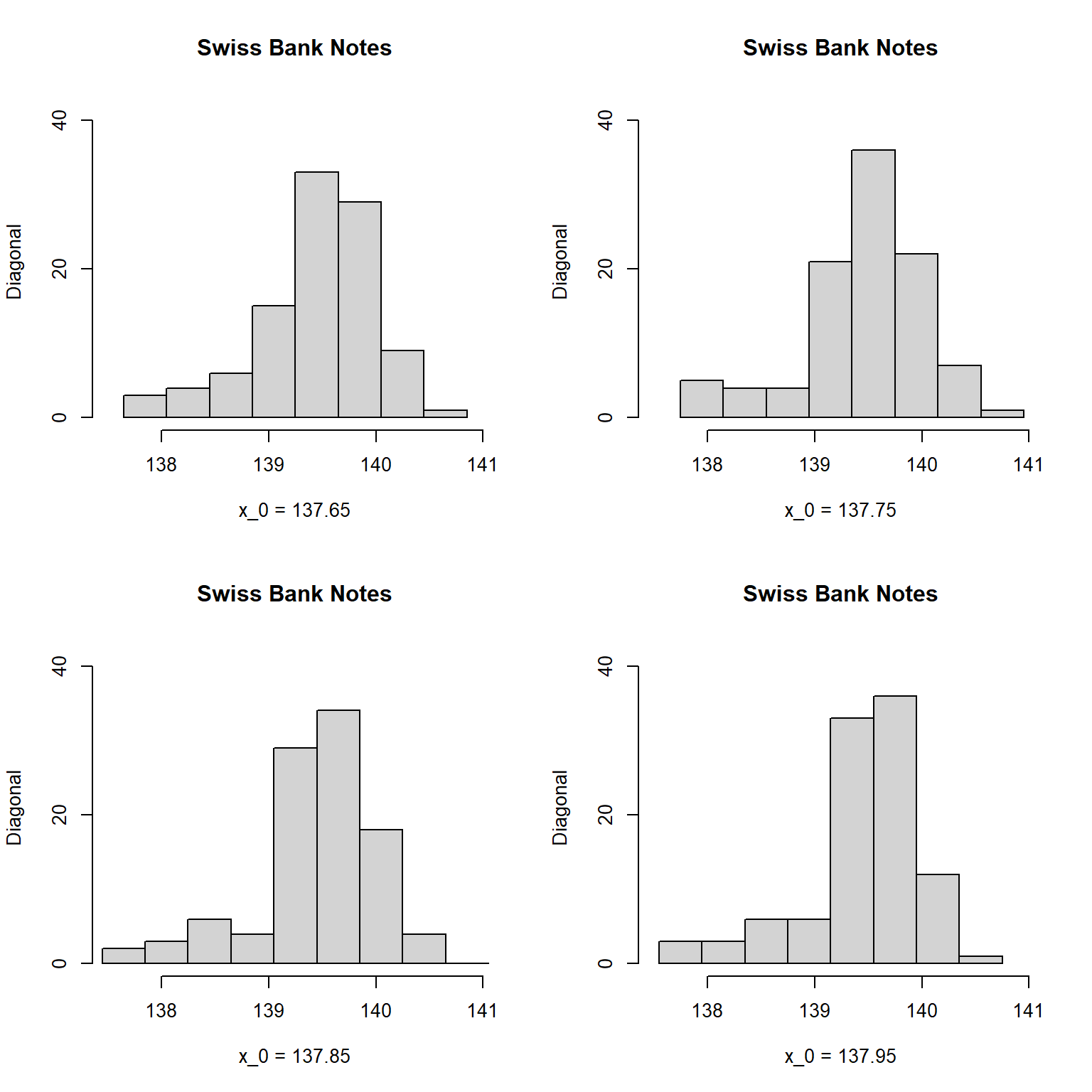

2.2.5 核密度估计图

核密度估计图对每个\(x\)值计算密度估计， 而不是像直方图那样用一个阶梯函数近似。 这种方法避免了选区间开始点问题， 也有一些自动选择窗宽（光滑程度）的方法。 核密度图是连续的、光滑的， 可以查看分布的位置、分散程度、偏斜方向、有无多个峰、分布尾部等情况。 这种方法可以推广到多元， 但是主要是二元和三元。 更多变量时空间变得稀疏，估计很不稳定。

公式: \[\begin{aligned} \hat f_h(x) = \frac{1}{n h} \sum_{i=1}^n K \left( \frac{x - x_i}{h} \right) \end{aligned}\] 其中\(K(\cdot)\)称为核函数， 典型代表是标准正态分布密度， 又比如四次核函数 \[\begin{aligned} K(u) = \frac{15}{16}(1 - u^2)^2 I_{[-1,1]}(u) . \end{aligned}\]

公式中\(h\)是窗宽， 是最重要的影响因素。可用交叉验证(CV)等方法选取。 使用交叉验证方法时， 目标是选取\(h\)使得密度估计误差平方的积分达到最小。

窗宽的一个传统选择是经验规则值 \[\begin{aligned} h_G = 1.06 \hat\sigma n^{-1/5} \end{aligned}\] 这个规则是假定总体来自正态分布， 使用标准正态密度函数作为核函数进行理论推导得到的最优值， 其中\(\hat\sigma\)是样本标准差， \(n\)为样本量。 如果总体分布不变， 但核函数改用四次核函数， 则相应的窗宽应取为\(h_Q = 2.62 h_G\)。

在基本R中用density()函数计算核密度估计， 用plot()将density()的输出画成密度曲线。

在ggplot2包中用geom_density()可以做核密度估计图。

下面的程序对假钞的对角线长度画核密度估计曲线：

ggplot(bankNotes |> slice(101:200), aes(
    x = diag )) +
  geom_density() + 
  labs(x = "假钞对角线长度")

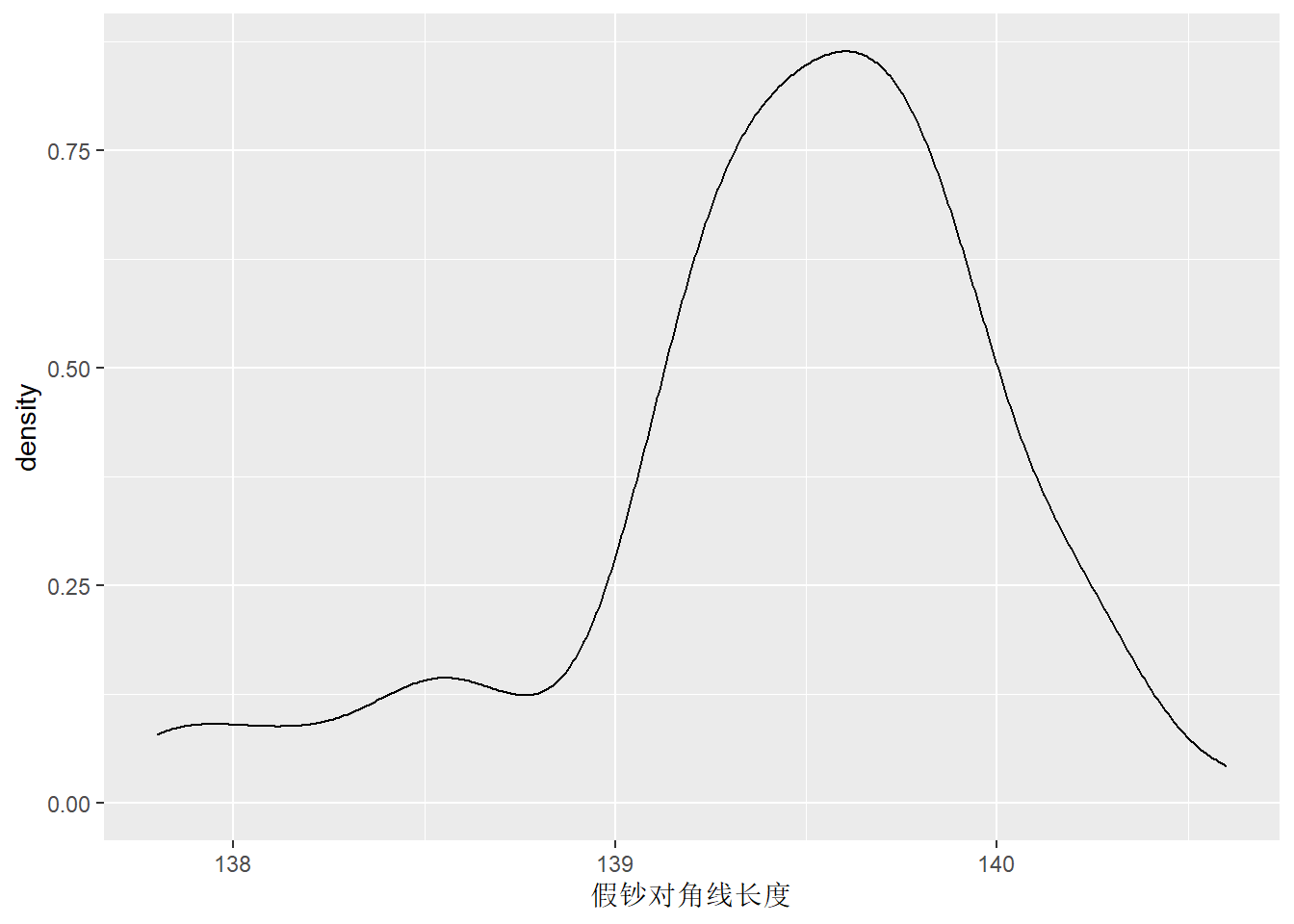
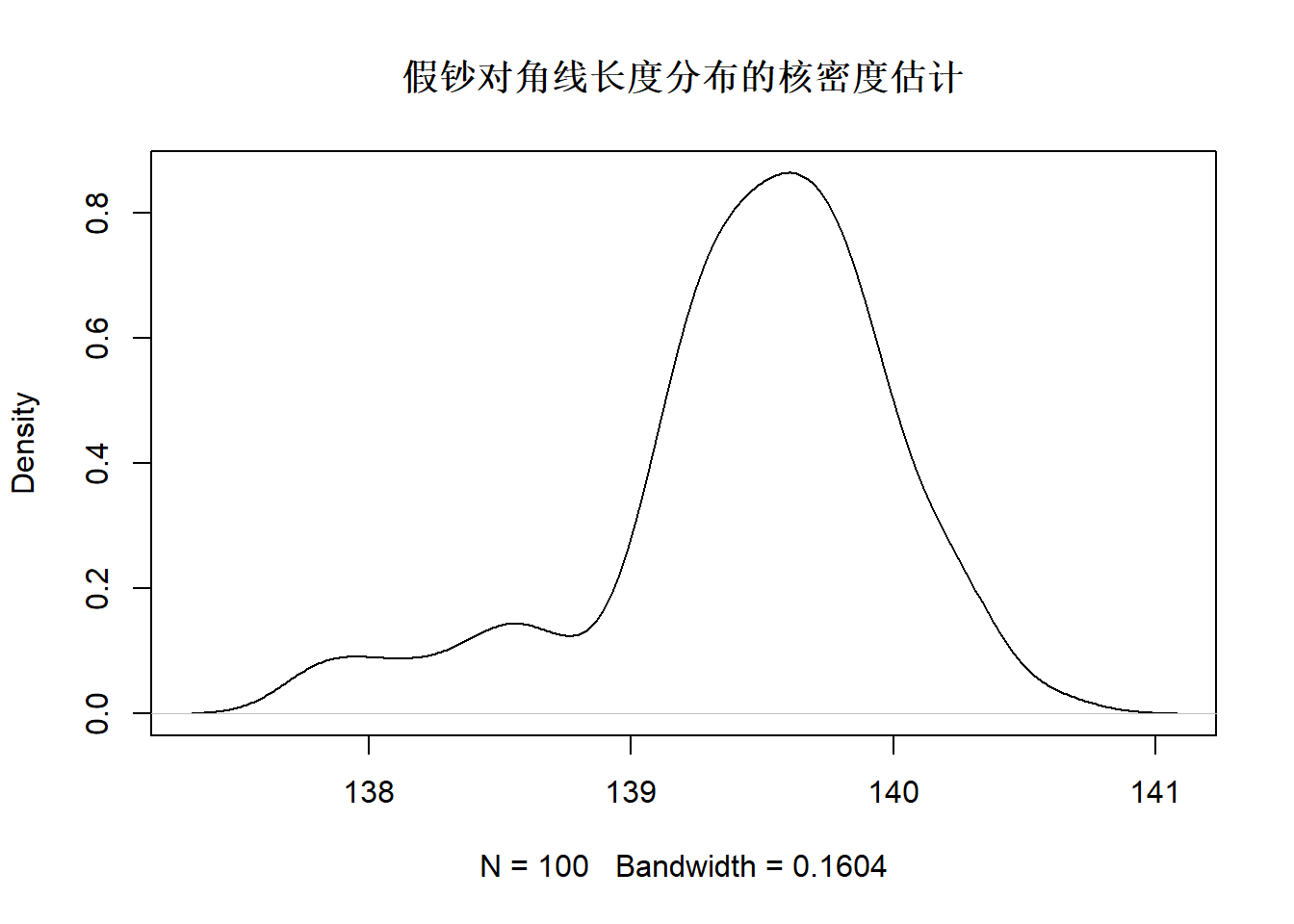
用基本R函数作图：

res <- density(bankNotes[["diag"]][101:200])
plot(res, main="假钞对角线长度分布的核密度估计")

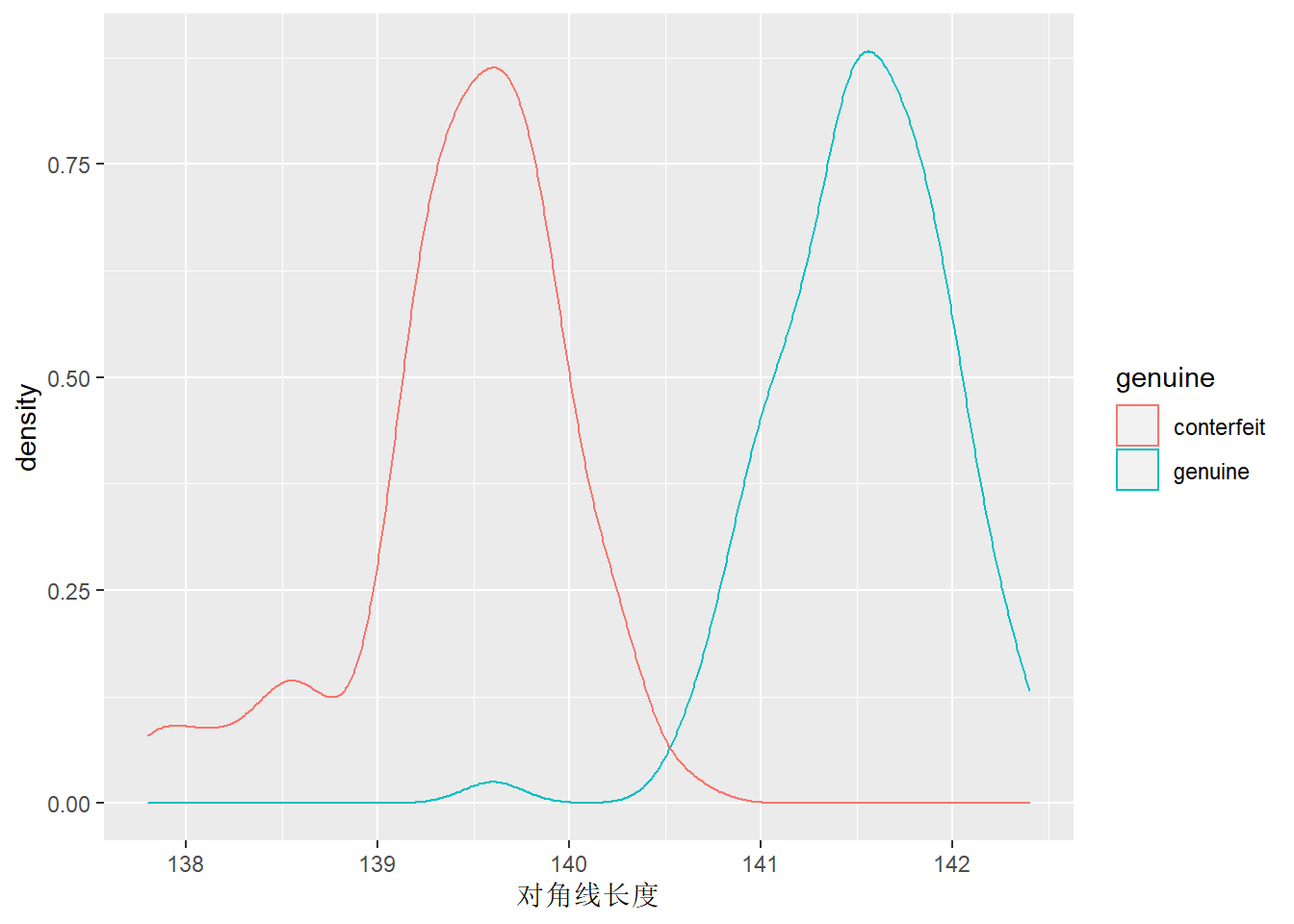
下面的程序在同一坐标系中绘制真钞、假钞对角线长度分别的核密度曲线： 下面的程序在同一坐标系中绘制真钞、假钞对角线长度分别的核密度曲线：

ggplot(bankNotes, aes(
    x = diag, color = genuine )) +
  geom_density() + 
  labs(x = "对角线长度")

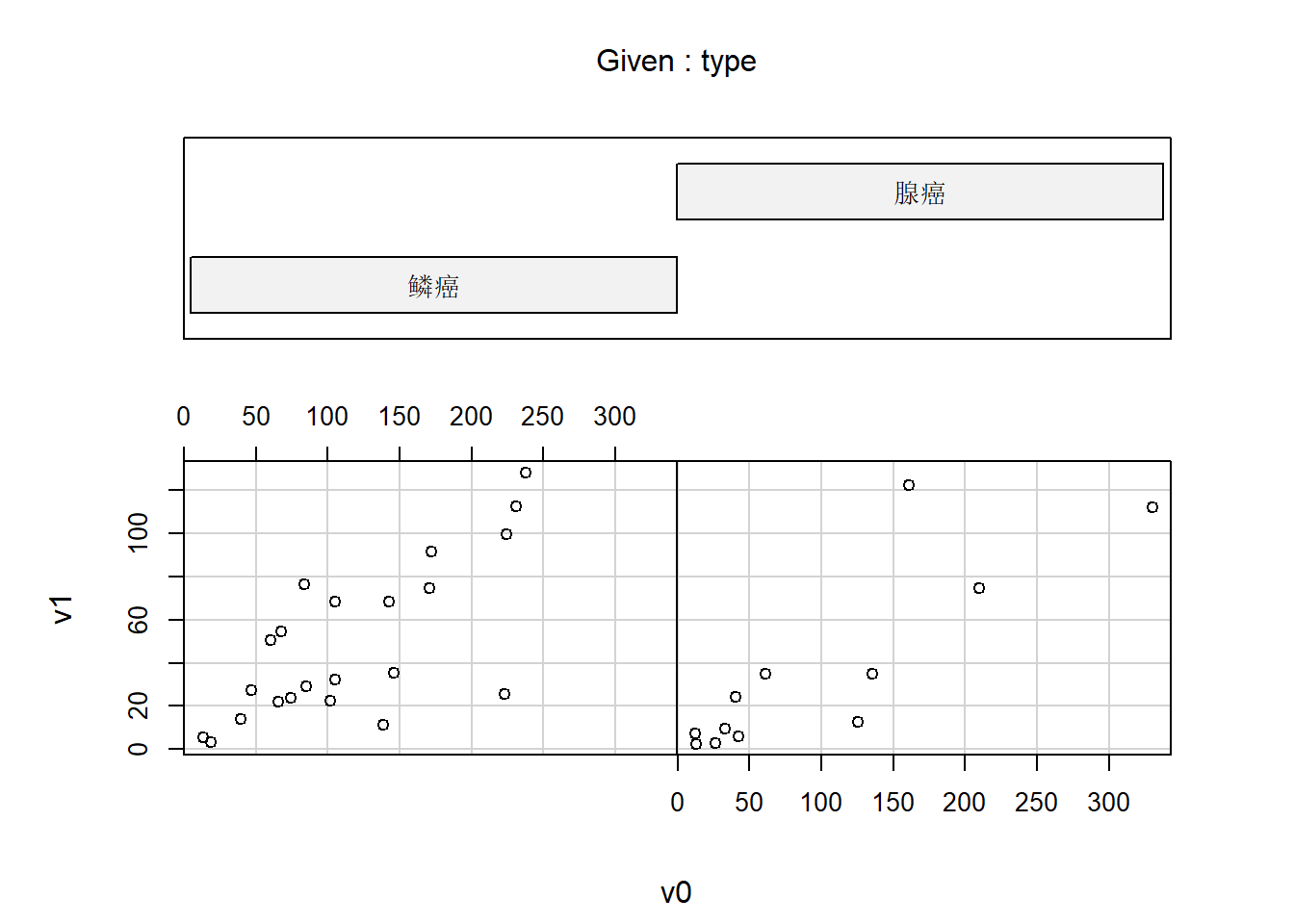
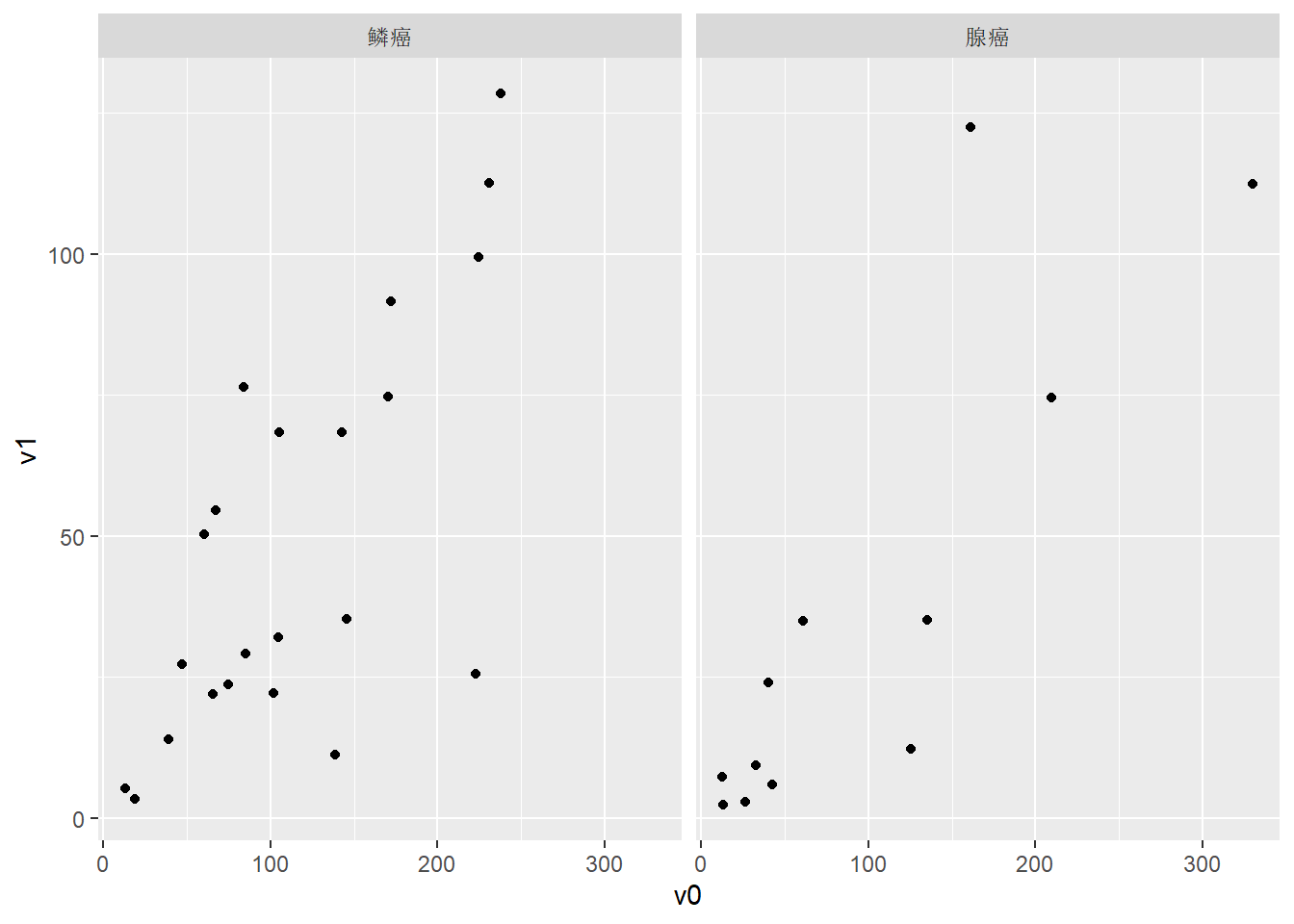
2.3 二元变量图形

2.3.1 散点图

散点图有二维散点图和三维散点图， 三维时需要能提供旋转功能。 散点图可以反映变量之间的关系（线性、曲线、不相关等）， 以及观测的聚类情况。 可以使用不同颜色、不同符号代表分类信息。

可以用基本R函数: plot(), points(), pairs()作散点图。

graphics::rug()函数紧贴坐标轴标出单个横坐标或单个纵坐标的位置。

ggplot2包的geom_point()作散点图， geom_jitter()作每个点轻微偏移的散点图（在点重叠时有用）。

cd4数据中，以开始时的cd4值为横坐标， 用一年后的cd4值为纵坐标作散点图：

ggplot(cd4, aes(
  x = baseline, y = oneyear)) +
  geom_point() +
  labs(x = "起始值", y = "一年后值")

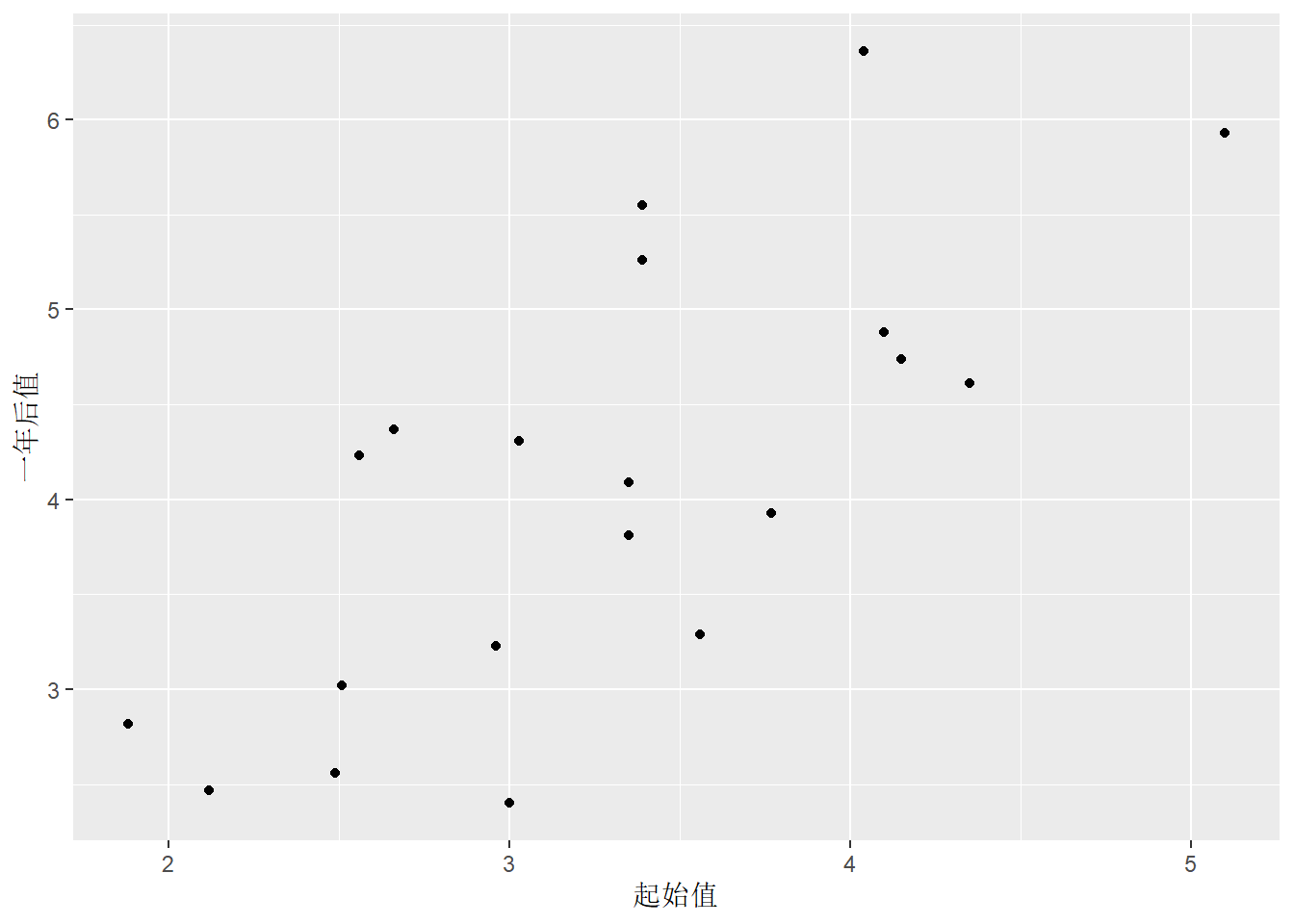
添加轴须线：

ggplot(cd4, aes(
  x = baseline, y = oneyear)) +
  geom_point() +
  geom_rug() + 
  labs(x = "起始值", y = "一年后值")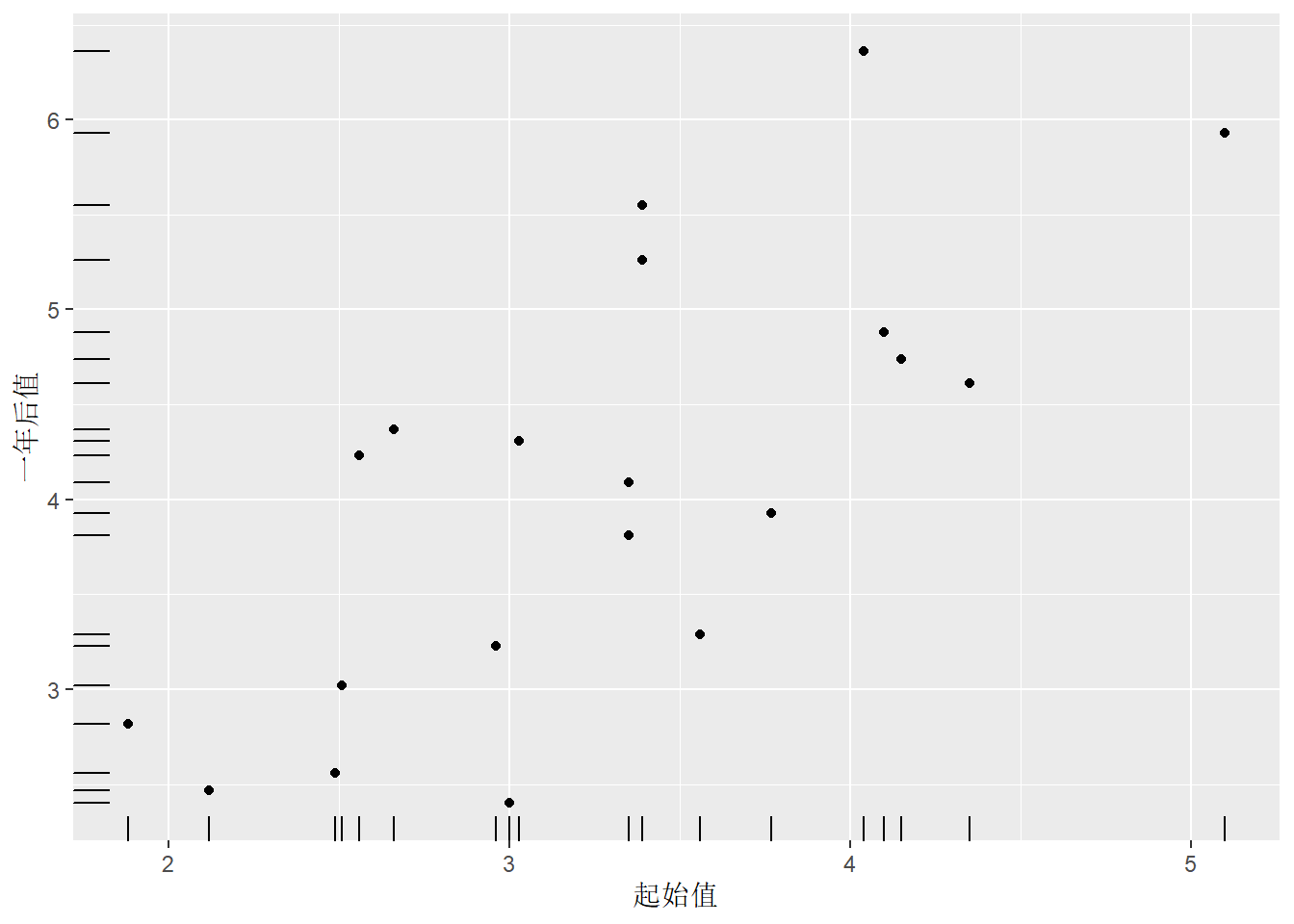

用基本R绘图功能：

plot(cd4[["baseline"]], cd4[["oneyear"]],
  main="cd4变化",
  xlab="起始值", ylab="一年后值")

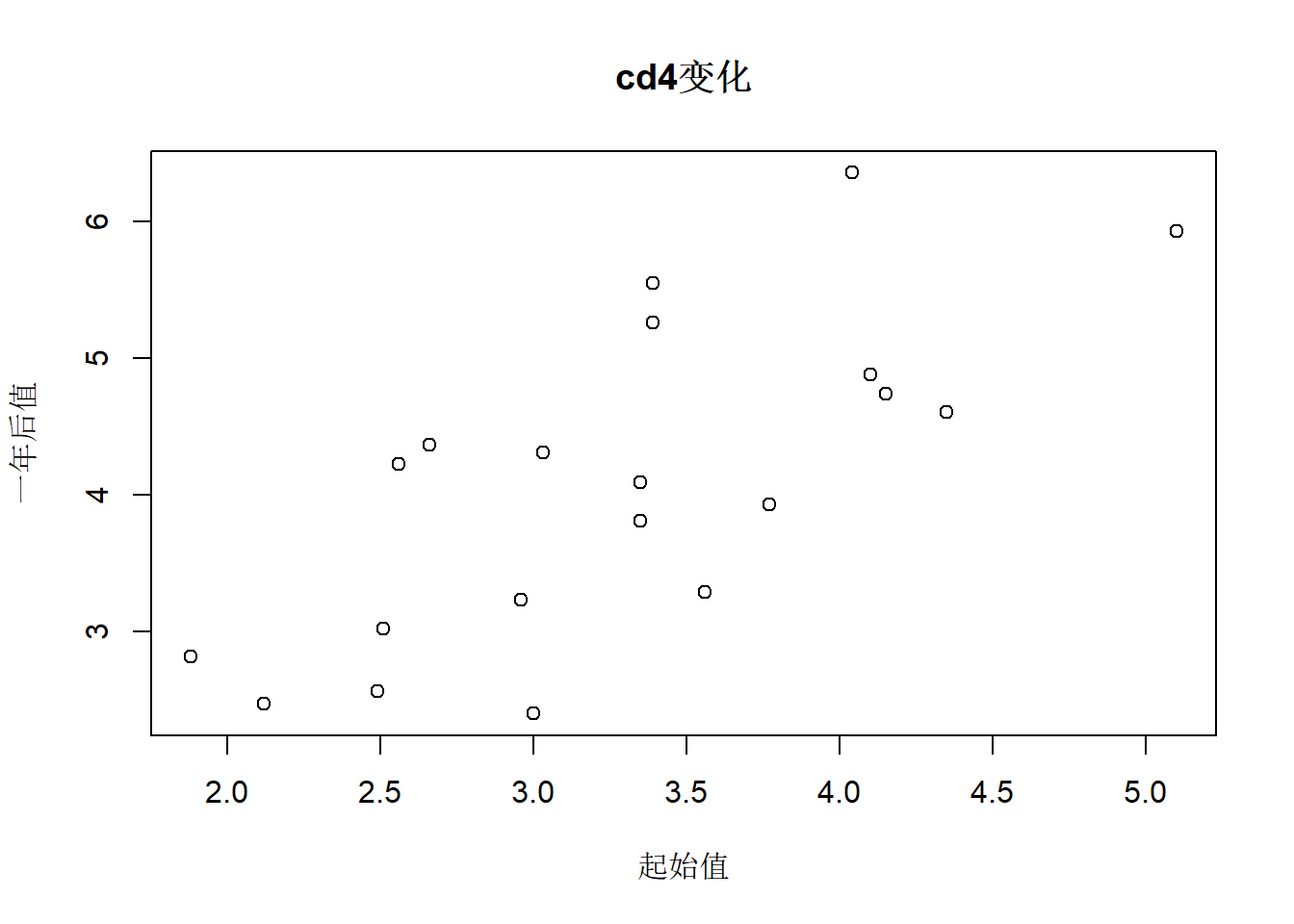
数据呈现明显的线性关系。

作图的一种观点是尽可能突出数据， 减少不必要的图形元素。 下面对cd4两个变量做了简化的散点图， 并在x轴和y轴做了轴须线(rug)。

f <- function(){
  library(graphics) # rug()函数
  
  rg <- range(cd4)
  rg[1] <- rg[1] - (rg[2]-rg[1])*0.05

  with(cd4,
       plot(baseline, oneyear,
            xlim=rg, ylim=rg,
            axes=F,
            cex=1.5, pch=16, col="red"))
  rug(cd4$baseline, side=1)
  rug(cd4$oneyear, side=2)
  box()
}
f()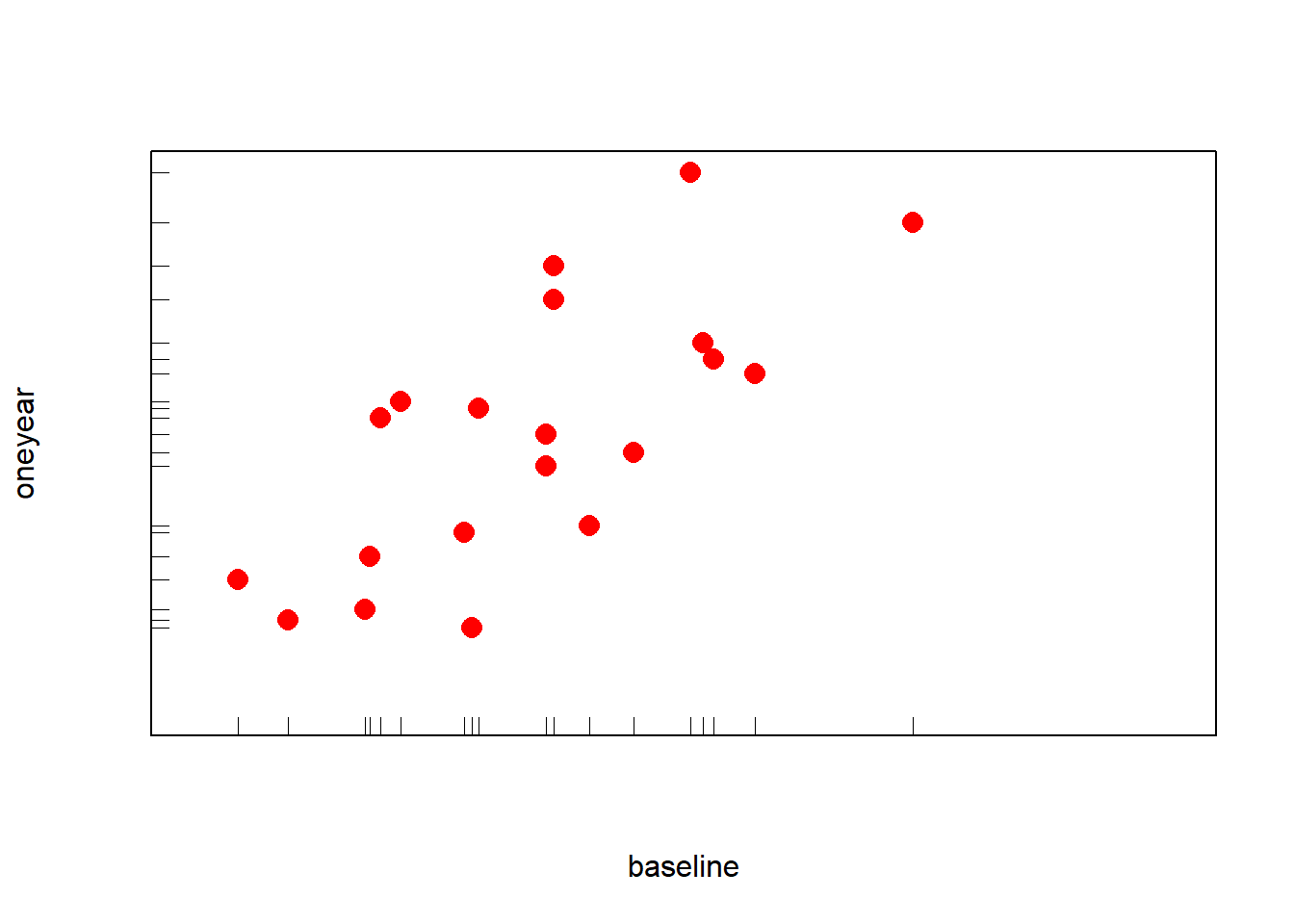

类似地，下面程序做了各省城镇居民收入与消费数据的精简散点图：

f <- function(){
    library(graphics) # rug()函数
    d <- cityIncomeConsume
    rg <- range(d[,2:3])
    rg[1] <- rg[1] - (rg[2]-rg[1])*0.05

    plot(d[["可支配收入"]],
         d[["消费性支出"]],
         xlim=rg, ylim=rg,
         axes=FALSE,
         cex=1.5, pch=16, col="red",
         xlab="可支配收入",
         ylab="消费性支出"
         )
    rug(d[["可支配收入"]], side=1)
    rug(d[["消费性支出"]], side=2)
    abline(lm(`消费性支出` ~ `可支配收入`, data=d),
           col="blue", lwd=2)
    box()
}
f()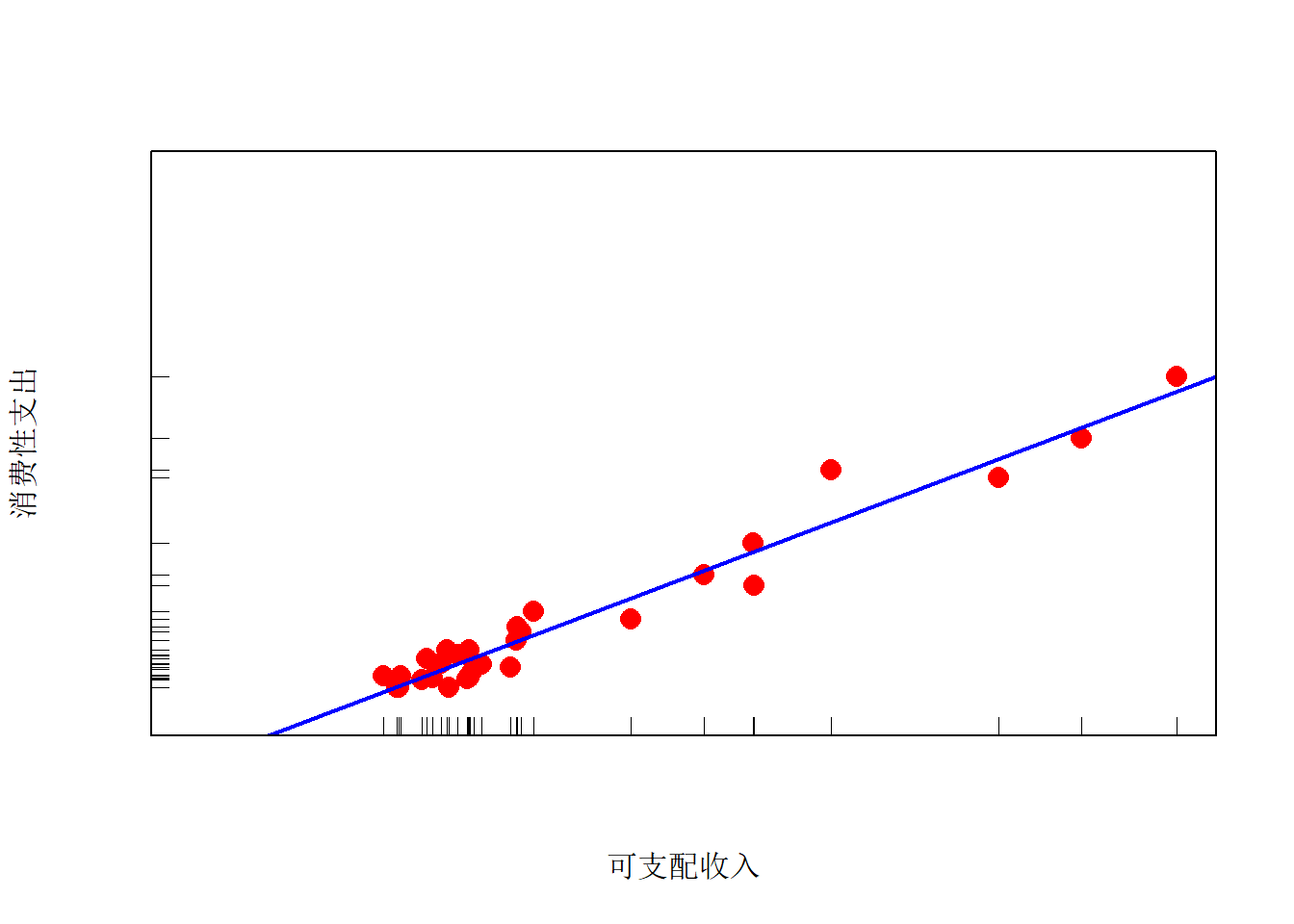

基本R图形函数的散点图可以使用xlim、ylim、cex、axes、pch、col等选项定制修改。

R Studio中有一个Color Picker Addin， 类似于小程序， 安装Shiny包时可以安装， 或者单独安装colourPicker扩展包， 这个小程序可以很方便地挑选颜色并以R字符串形式返回。

rainbow(n)可以生成有𝑛种颜色的颜色值。

下面的程序对cd4数据中值小于等于2的点用特殊的符号和不同的颜色区分：

d <- cd4 |>
  mutate(special = ifelse(
    baseline <= 2 | oneyear <= 2, "red", "green"))
ggplot(d, aes(
  x = baseline, y = oneyear, color = special )) +
  geom_point() + 
  geom_vline(xintercept = c(2.0)) +
  geom_hline(yintercept = c(2.0)) +
  scale_color_identity()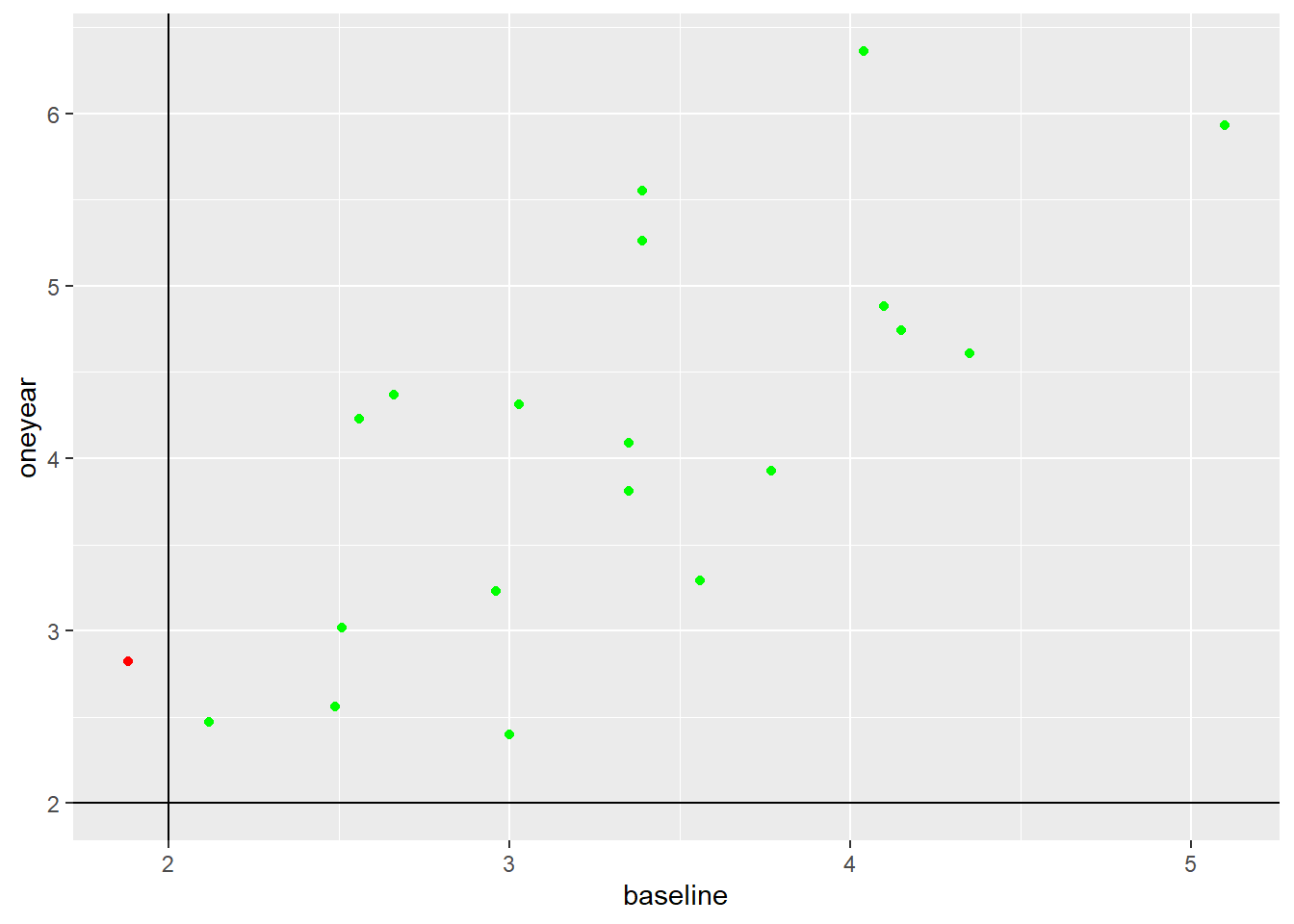

基本R绘图函数函数的做法：

f <- function(){
    rg <- range(cd4)
    sele <- with(cd4, baseline <= 2 | oneyear <= 2)
    with(cd4,
         plot(baseline, oneyear,
              xlim=rg, ylim=rg,
              xlab="Baseline",
              ylab="1 year",
              col=ifelse(sele, "red", "blue"),
              pch=ifelse(sele, 4, 1)
              ))
    abline(h=2, v=2, col="grey")
}
f()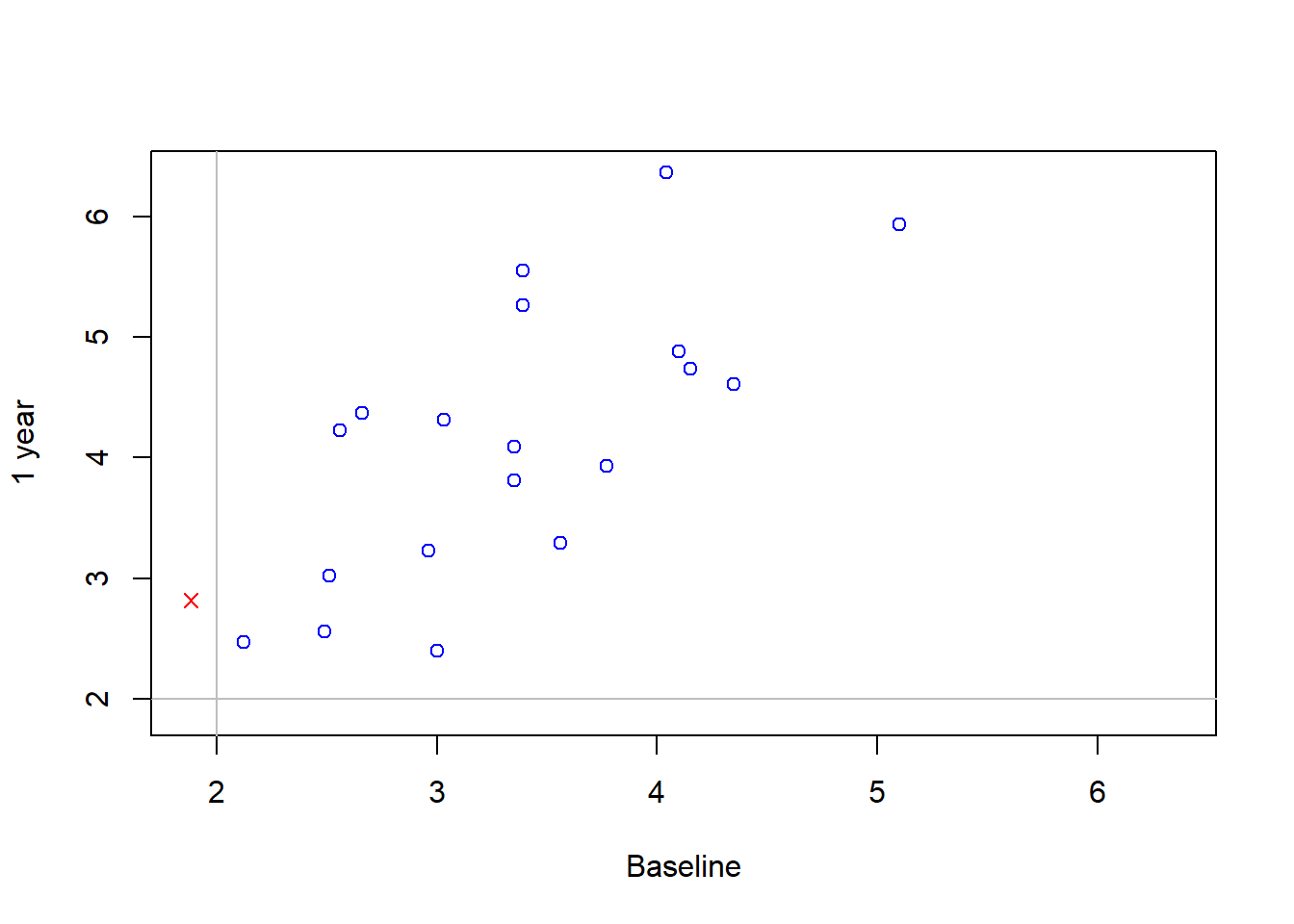

基本R绘图的identify()函数可以在散点图中标出鼠标点击的点的标签。

下面的程序画各省城镇居民收入与消费的散点图， 并调用了identify()函数来交互地显示感兴趣的点的省份。

f <- function(){
    d <- cityIncomeConsume
    xylim <- range(d[,2:3])
    plot(d[["可支配收入"]],
         d[["消费性支出"]],
         xlim=xylim, ylim=xylim,
         xlab="可支配收入",
         ylab="消费性支出")
    identify(d[["可支配收入"]],
             d[["消费性支出"]],
             d[["地区"]])
    invisible()
}
f()

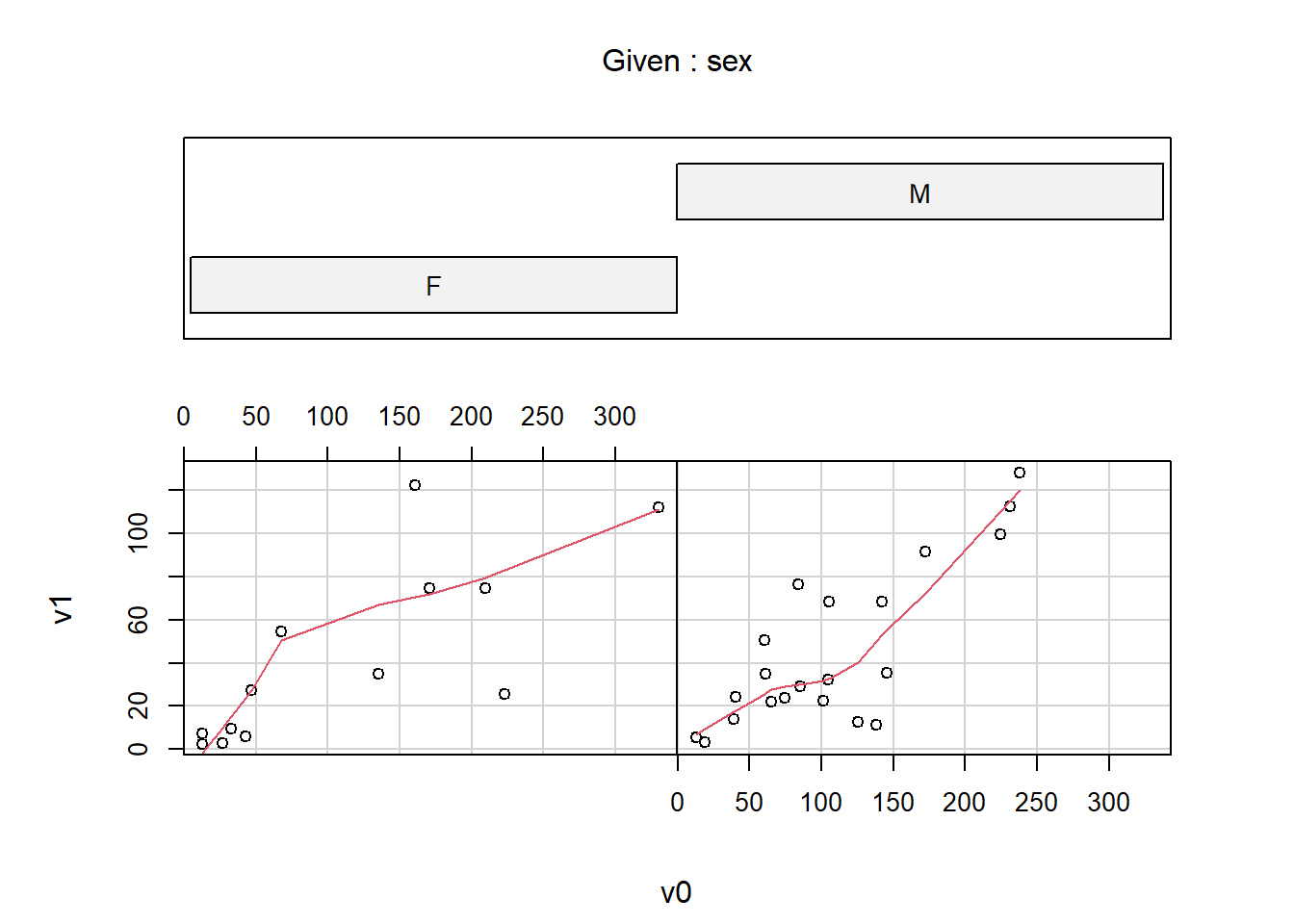
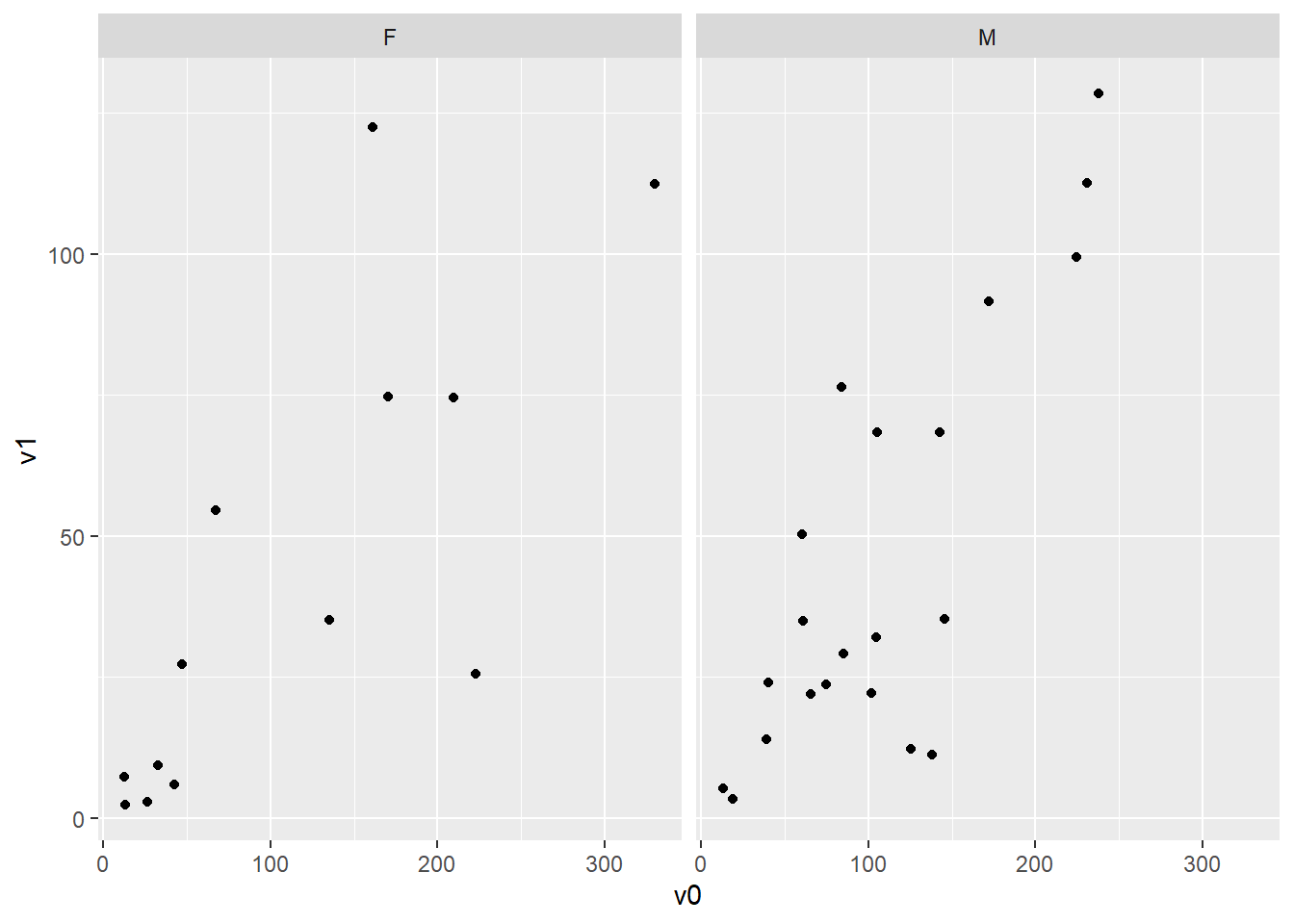
2.3.2 散点图的曲线拟合

ggplot2的geom_smooth()可以对输入数据做曲线拟合。 缺省使用loess方法。可以带有一个置信带。

比如，cd4数据的散点图与曲线拟合：

ggplot(cd4, aes(
  x = baseline, y = oneyear)) +
  geom_point() +
  geom_smooth() + 
  labs(x = "起始值", y = "一年后值")

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'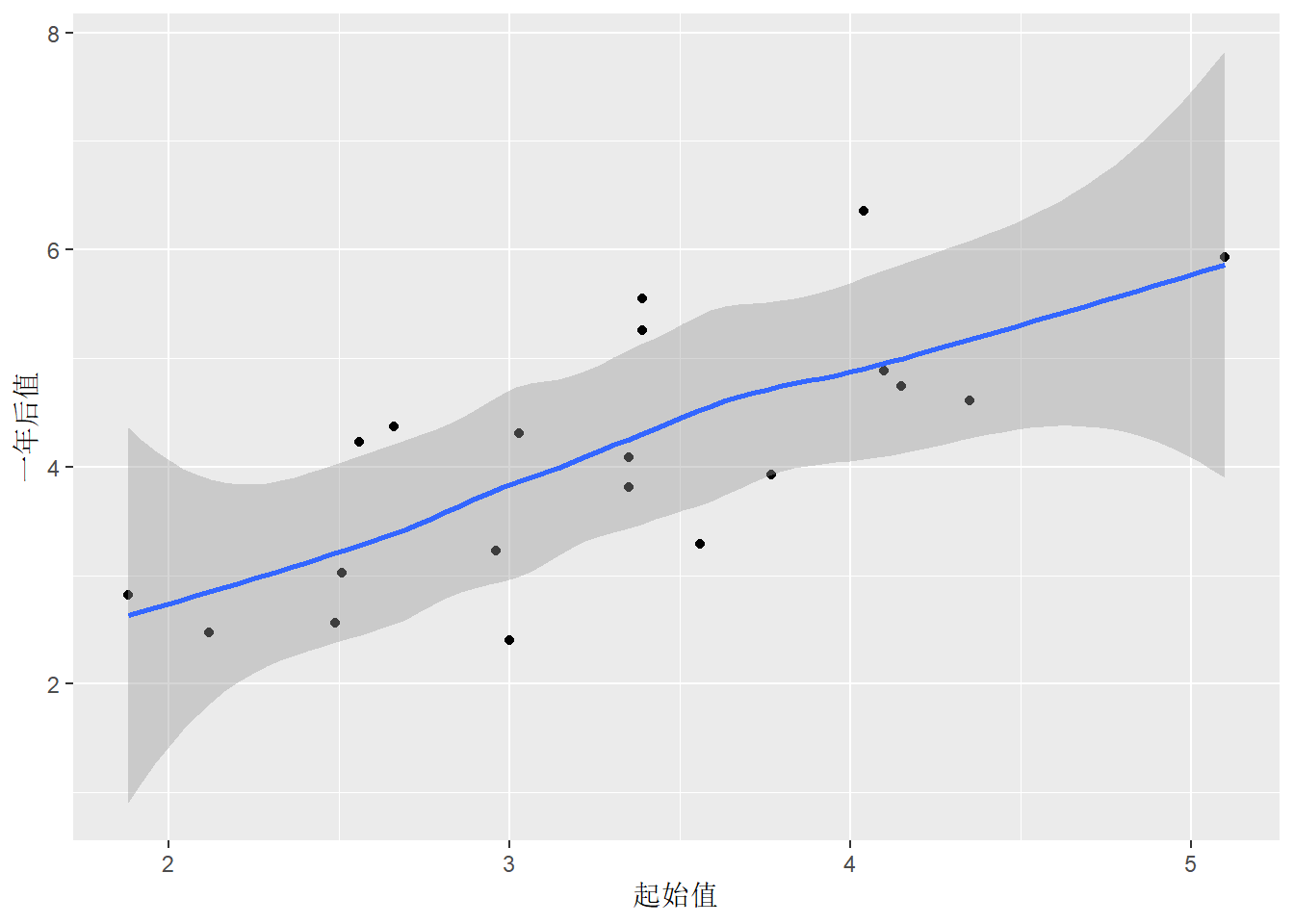

2.3.3 二元盒形图

散点图与凸壳的配合。

2.3.3.1 MVA::bvbox()

MVA扩展包的bvbox()函数提供了一种基于二元正态分布的二元盒形图：

library(MVA)
bvbox(cd4,
  xlab="Baseline",
  ylab="1 year",
  pch=19, cex=1.25, col="red")

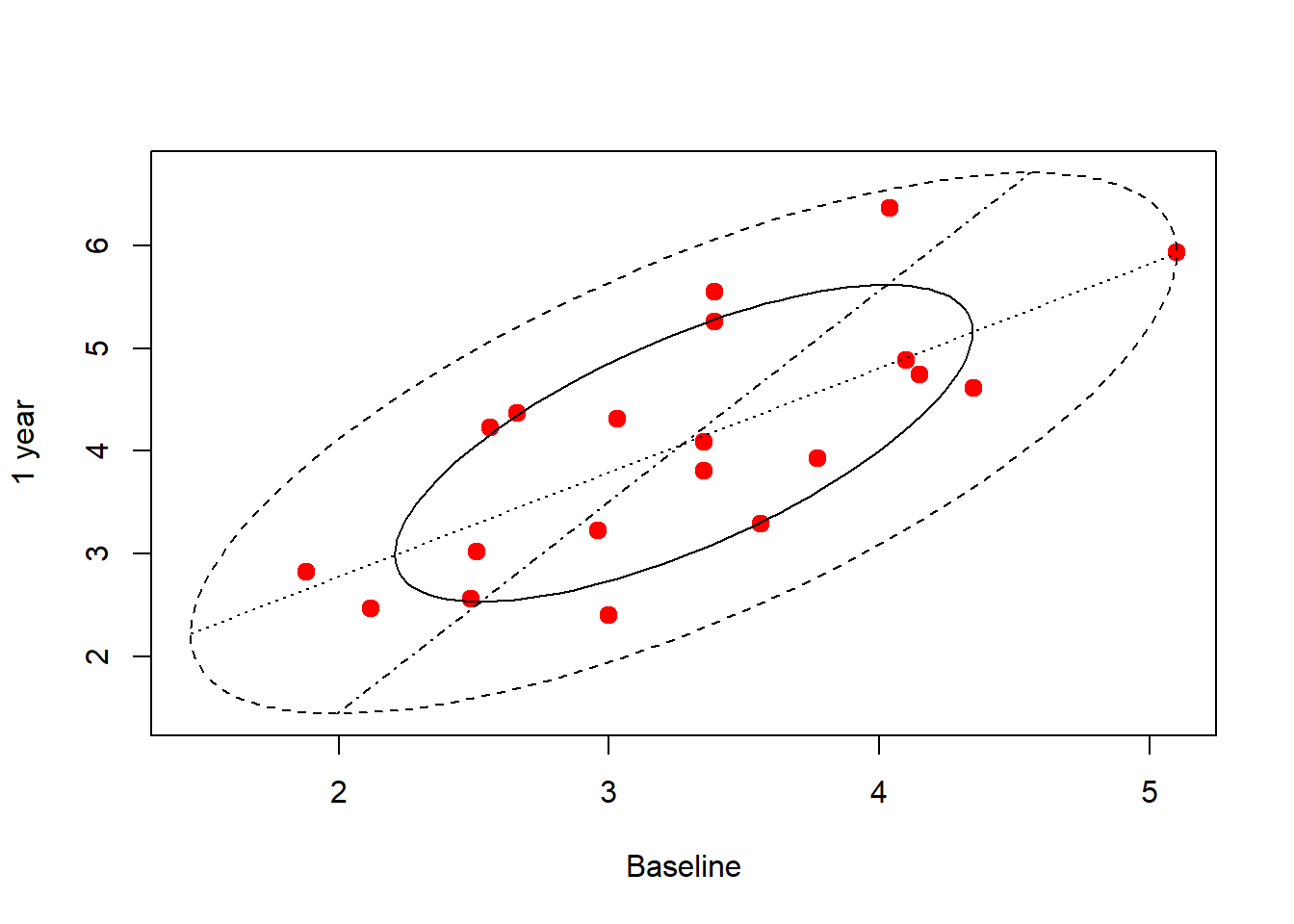
这里的位置参数、刻度参数和相关系数都使用了稳健估计方法， 图中有两个椭圆， 在二元正态情况下， 二元盒形图内椭圆（称为合页，hinge）包含50%的值， 外椭圆（称为栅栏，fence）包含95%的值， 在外椭圆外的点可以认为是离群值。 图中还包含了\(y\)关于\(x\)的回归线， 与\(x\)关于\(y\)的回归线， 两条线的交点是估计的二元分布均值位置。 两条回归线的夹角锐角的角度当相关性强时较小， 当相关性弱时较大。

各省城镇居民收入与消费的二元盒形图:

library(MVA)
bvbox(as.data.frame(cityIncomeConsume[,2:3]),
  xlab="可支配收入",
  ylab="消费性支出",
  pch=19, cex=1.25, col="red")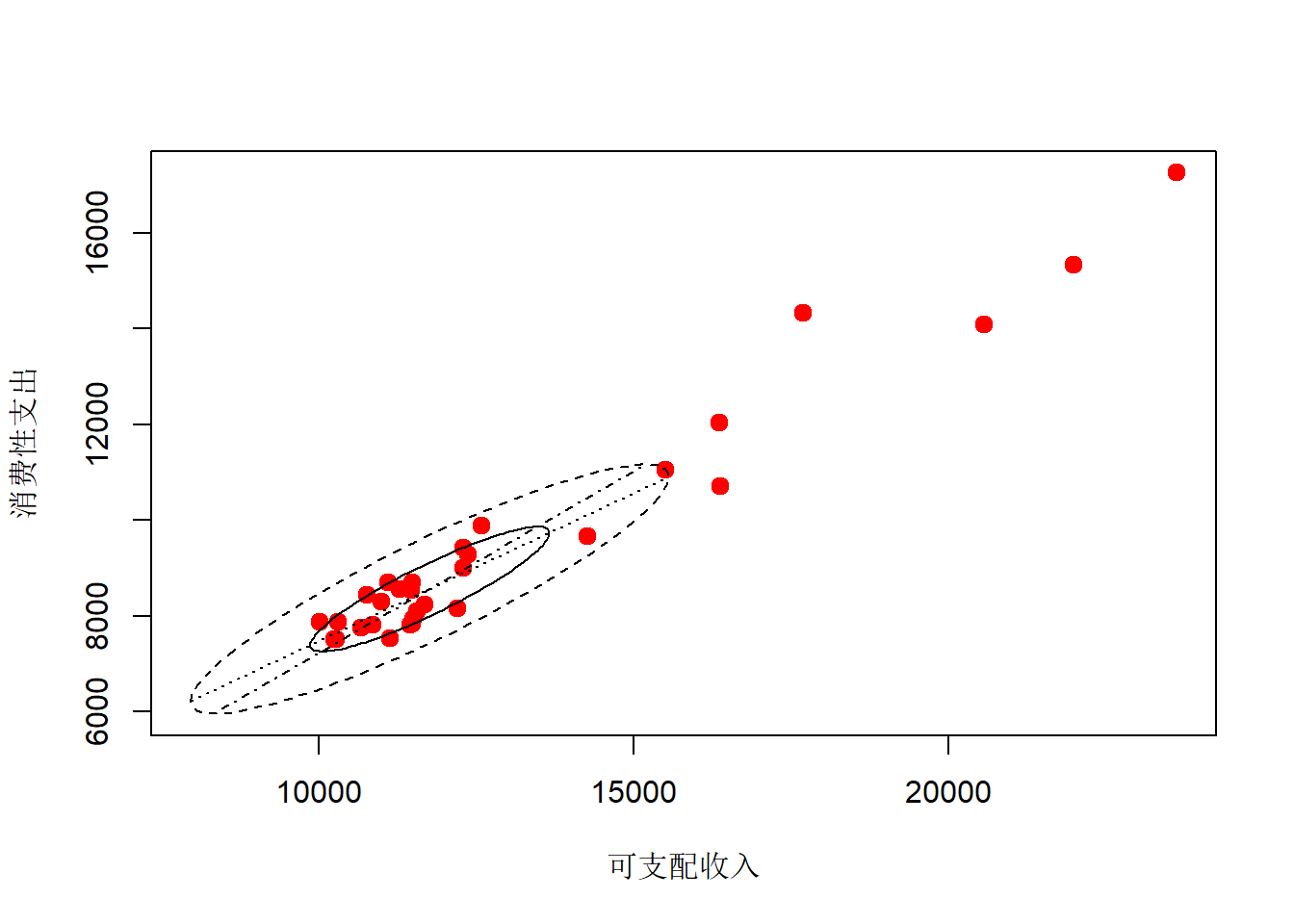

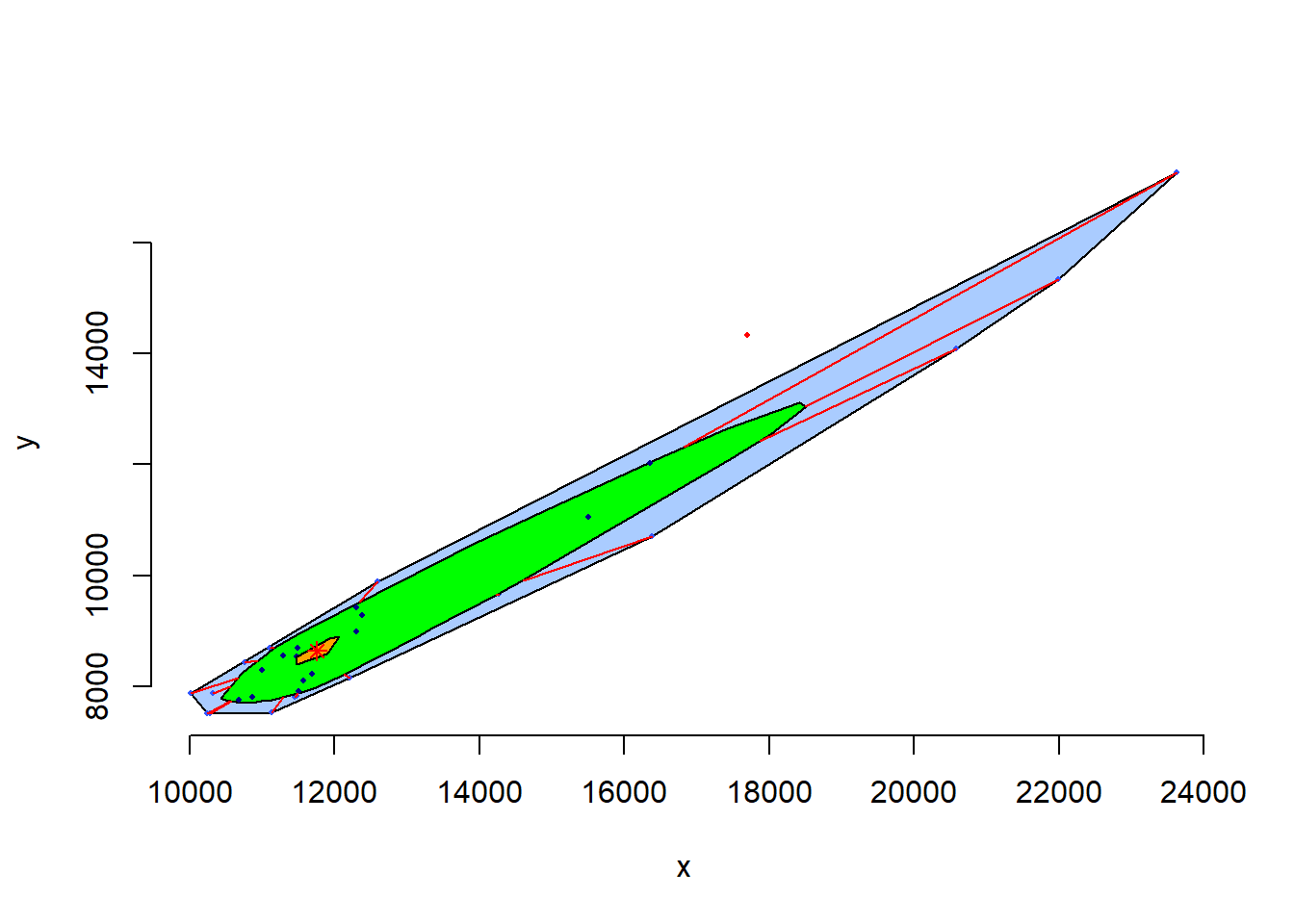
2.3.3.2 凸壳

凸壳是二元数据散点图中， 可以包含所有点在内部和顶点、边上的最小凸多边形， 在有离群值时， 剥去凸壳上的观测点， 不影响对数据的整体分布的粗略刻画， 可以用剩余的观测点给出相关系数的稳健估计。

cd4中两个变量的散点图对应的凸壳(convex hull)：

ch <- with(cd4, chull(baseline, oneyear)) # 凸壳的支撑点下标
ch <- c(ch, ch[1]) # 首尾相连
with(cd4,
  plot(baseline, oneyear,
    pch=19, col=2, cex=1.25))
with(cd4,
  lines(baseline[ch], oneyear[ch],
    col=3, lwd=2))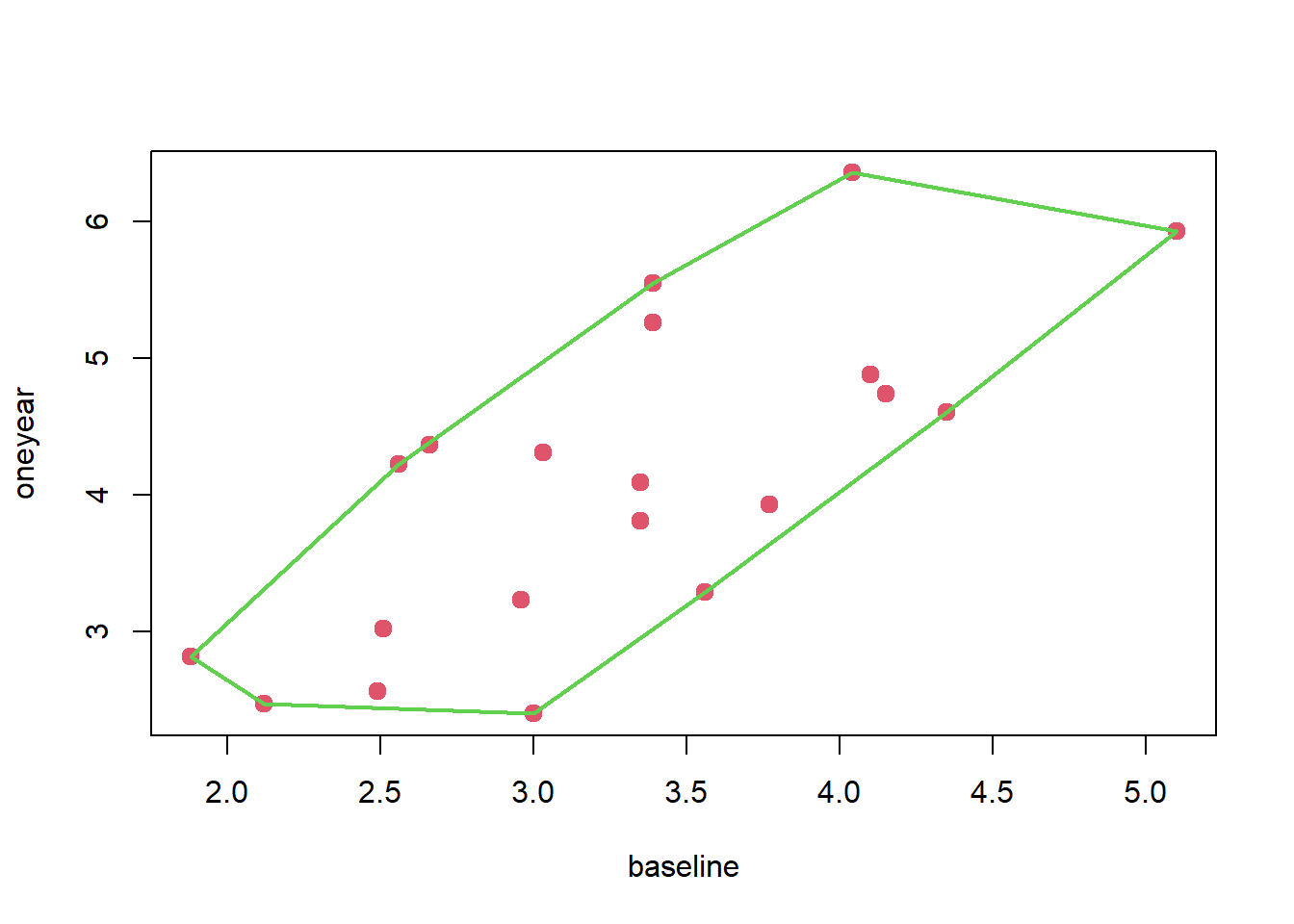

2.3.3.3 洋葱图

洋葱图是逐层剥去凸壳支撑点再画凸壳。 R扩展包aplpack的plothulls()函数作洋葱图。

cd4中两个变量的散点图与洋葱图：

library(aplpack)

nlev <- 3
cols <- heat.colors(9)[3:(nlev+2)]
fig1 <- plothulls(
  cd4,
  n.hull=nlev,
  col.hull=cols,
  xlab="Baseline",
  ylab="1 year",
  lty.hull=1:nlev, density=NA,
  col=0, main="")
with(cd4, points(
  baseline, oneyear,
  pch=16, cex=1, col="blue"))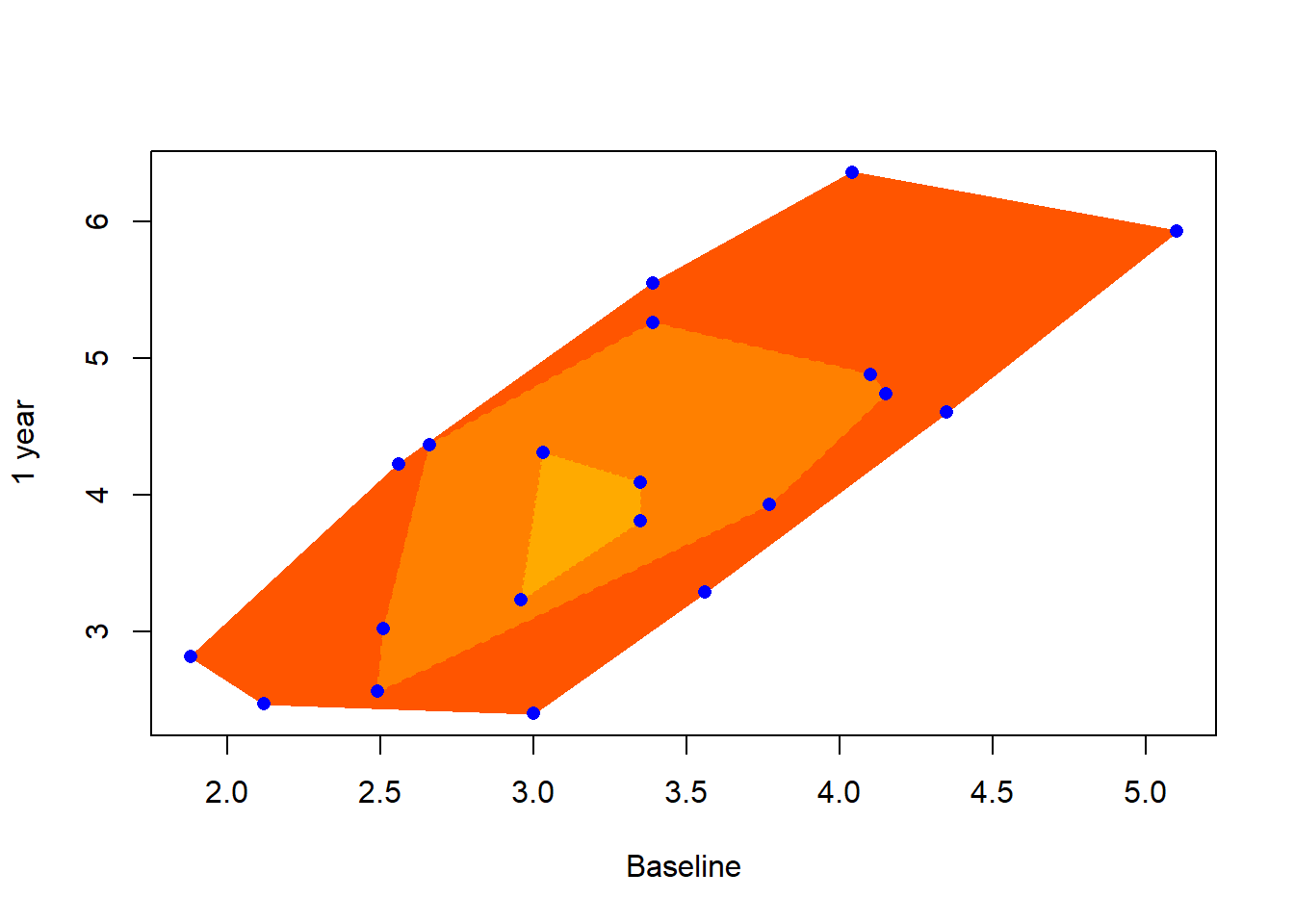

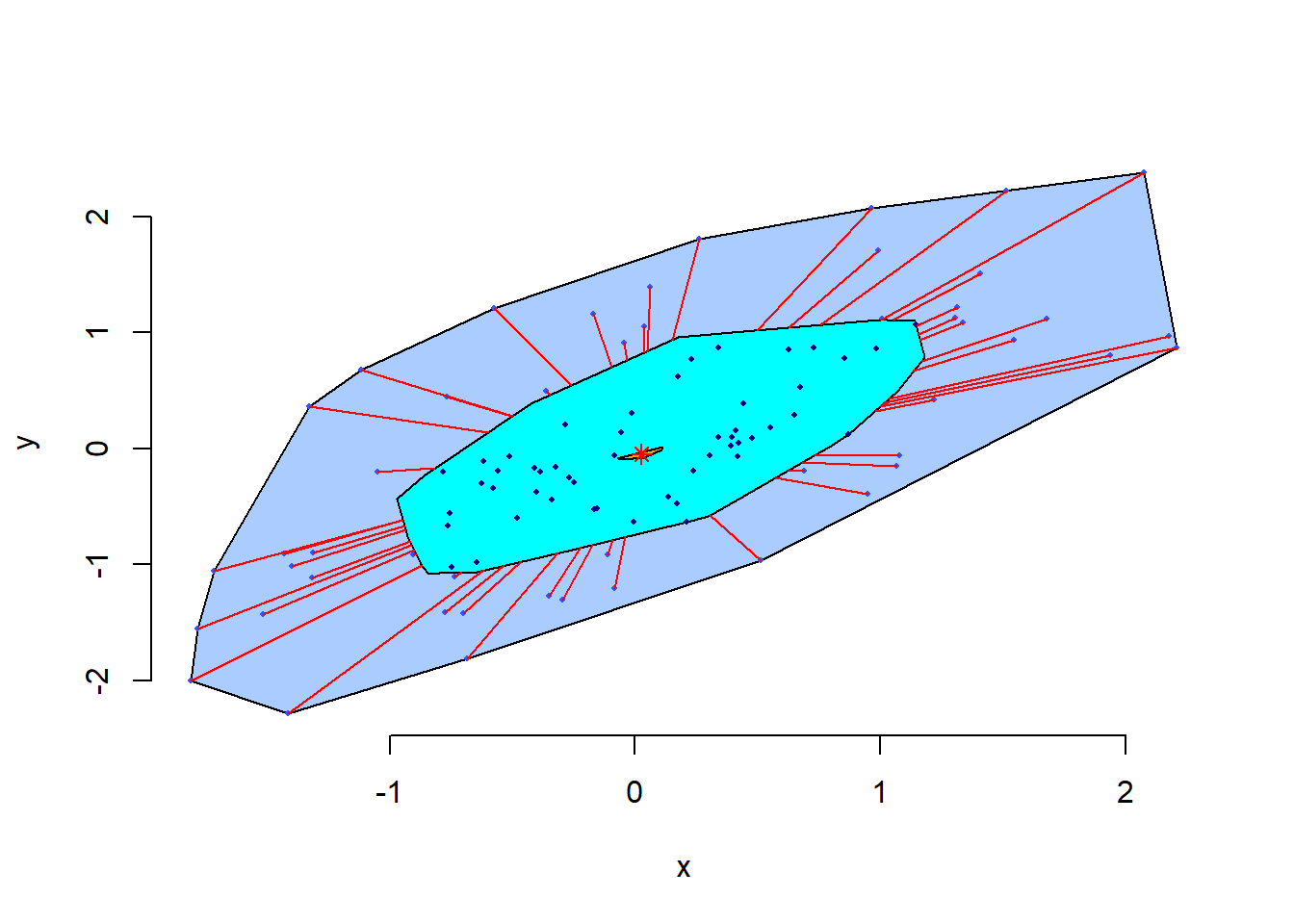
模拟的二元正态分布数据的洋葱图：

library(aplpack)
library(mvtnorm)

set.seed(1)
da <- rmvnorm(
  100, mean=c(0,0),
  sigma=rbind(c(1,0.7), c(0.7,1)))

nlev <- 5
cols <- heat.colors(9)[3:(nlev+2)]
fig1 <- plothulls(
  da,
  n.hull=nlev,
  col.hull=cols,
  xlab="x",
  ylab="y",
  lty.hull=1:nlev, density=NA,
  col=0, main="")
points(da,
  pch=16, cex=1, col="blue")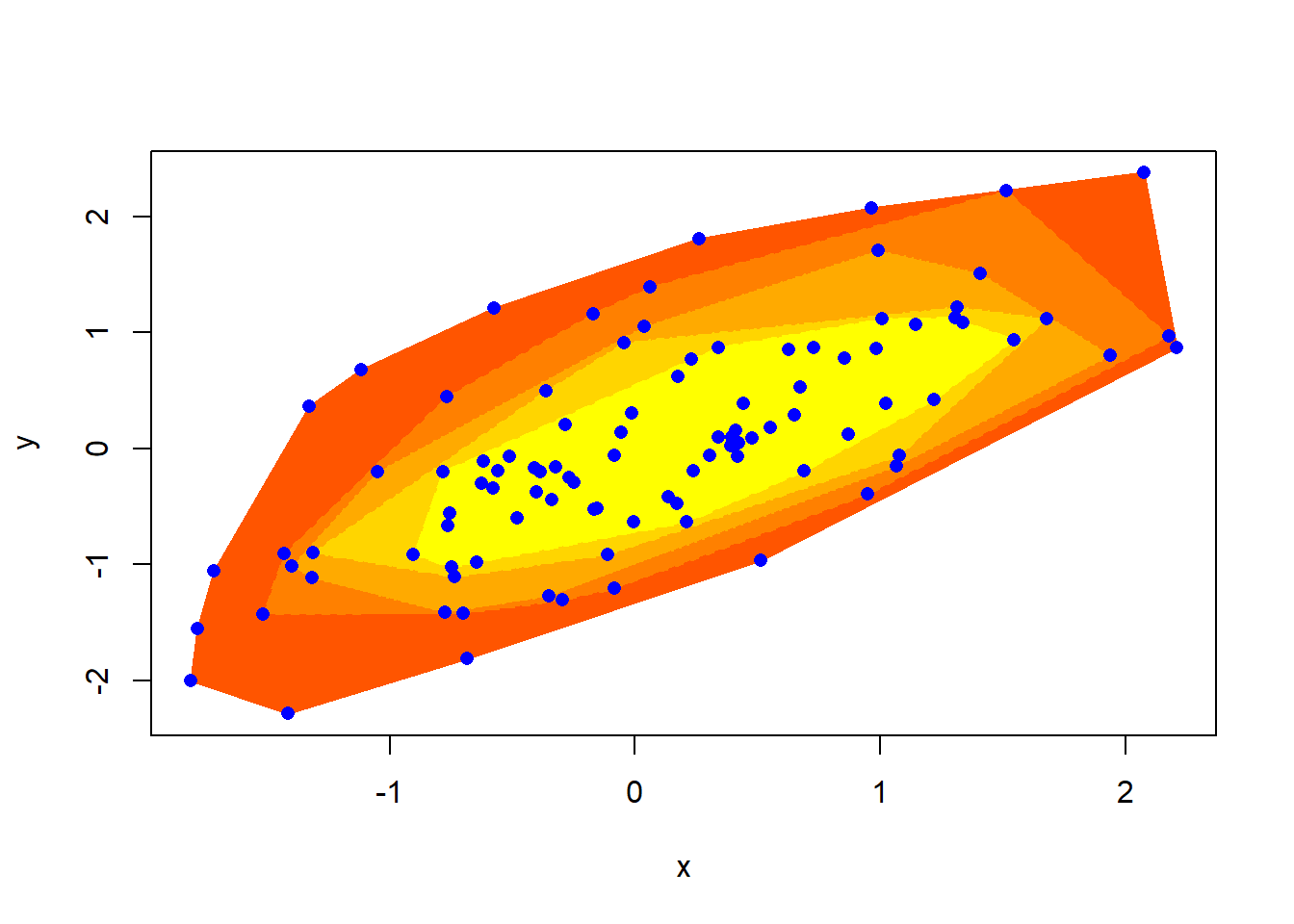

各省城镇居民收入与消费的洋葱图:

library(aplpack)
d <- as.data.frame(cityIncomeConsume)

nlev <- 3
cols <- heat.colors(9, alpha=1)[3:(nlev+2)]
plothulls(d[,2:3],
  n.hull=nlev,
  col.hull=cols,
  xlab="可支配收入",
  ylab="消费性支出",
  lty.hull=1:nlev, density=NA,
  col=0, main="")

## [[1]]
##         x.hull   y.hull
##  [1,] 16378.01 10715.15
##  [2,] 12200.44  8151.26
##  [3,] 11130.93  7532.07
##  [4,] 10276.06  7512.39
##  [5,] 10245.28  7519.28
##  [6,] 10012.34  7875.78
##  [7,] 17699.30 14336.87
##  [8,] 23622.73 17255.38
##  [9,] 21988.71 15330.44
## [10,] 20573.82 14091.19
## 
## [[2]]
##         x.hull   y.hull
##  [1,] 11477.05  7826.72
##  [2,] 11451.69  7810.73
##  [3,] 10678.40  7758.69
##  [4,] 10313.44  7874.27
##  [5,] 10763.34  8427.06
##  [6,] 12590.78  9890.31
##  [7,] 16357.35 12028.88
##  [8,] 15506.05 11055.13
##  [9,] 14264.70  9666.61
## 
## [[3]]
##        x.hull  y.hull
## [1,] 11496.11 7921.83
## [2,] 10859.33 7817.28
## [3,] 11098.28 8691.99
## [4,] 12300.39 9429.73
## [5,] 12377.84 9281.46
## [6,] 12293.54 8990.72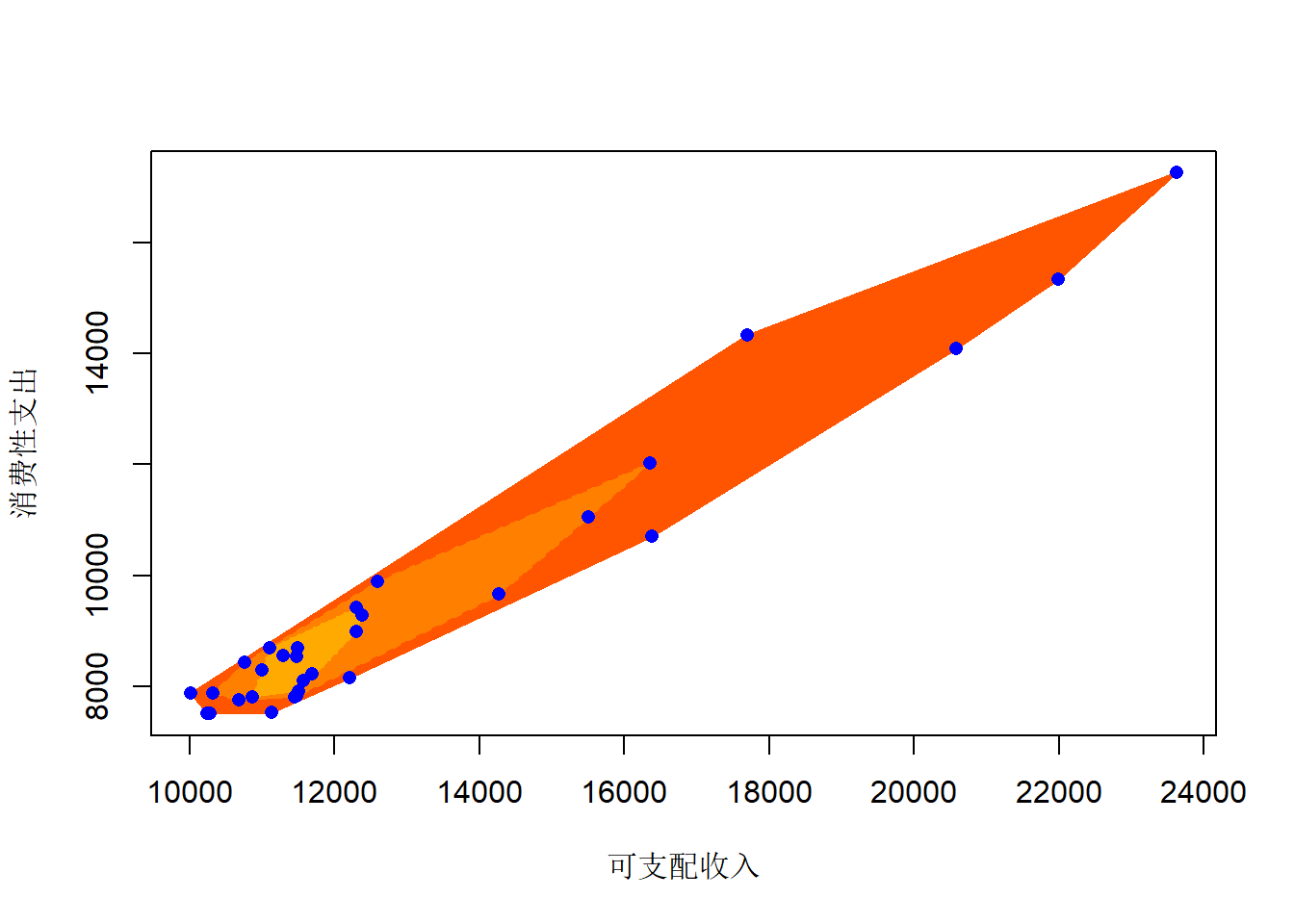

points(d[,2:3],
  pch=16, cex=1, col="blue")

2.3.3.4 口袋图

aplpack扩展包的bagplot()函数作口袋图(bag plot)。 外层包络是排除极端值后的凸壳，内层包络是包含50%点的凸壳, 两层之间的点画线连向二维中位点。

各省城镇居民收入与支出的数据的口袋图：

library(aplpack)
bagplot(cityIncomeConsume[,2:3],
        col.baghull="green")

模拟的多元正态分布的口袋图:

library(aplpack)
library(mvtnorm)

set.seed(1)
da <- rmvnorm(100, mean=c(0,0),
              sigma=rbind(c(1,0.7), c(0.7,1)))
bagplot(da, col.baghull="cyan")

2.3.4 二元联合密度图

二元数据作为二元随机向量的观测值， 其密度估计\(\hat f(x,y)\)是二元函数， 需要用曲面表示。

ggplot2包的stat_density_2d()可以做二元联合密度估计的等值线图。 使用二元核密度估计方法。

瑞士银行真假钞数据的二元核密度估计图的等高线图， 与半透明的散点图叠加：

ggplot(bankNotes, aes(
  x = top, y = diag )) +
  geom_point(alpha = 0.5, color = "green4") + 
  stat_density_2d(color = "black")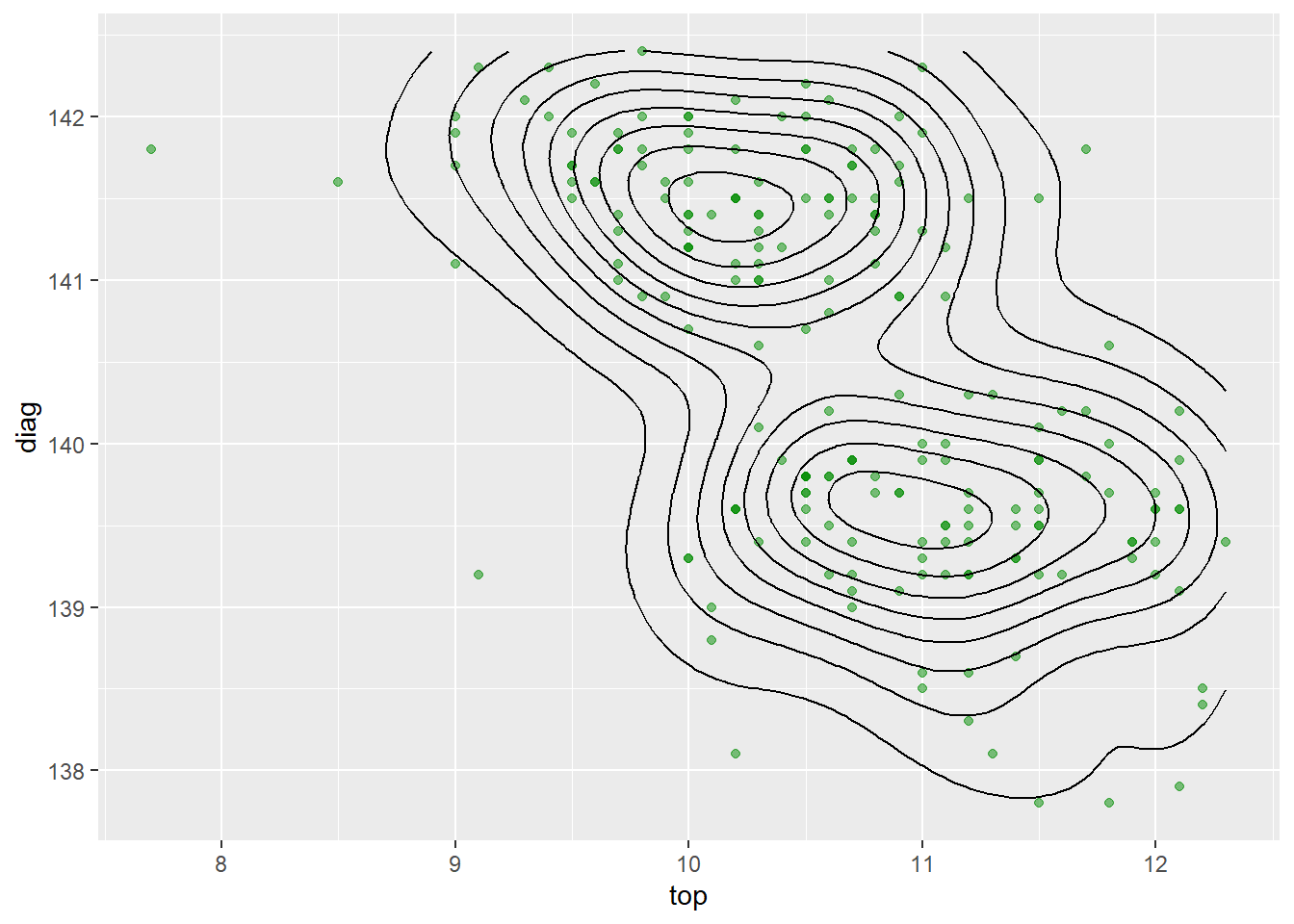

不画散点，用不同颜色深浅代表密度大小：

ggplot(bankNotes, aes(
  x = top, y = diag )) +
  stat_density_2d_filled()

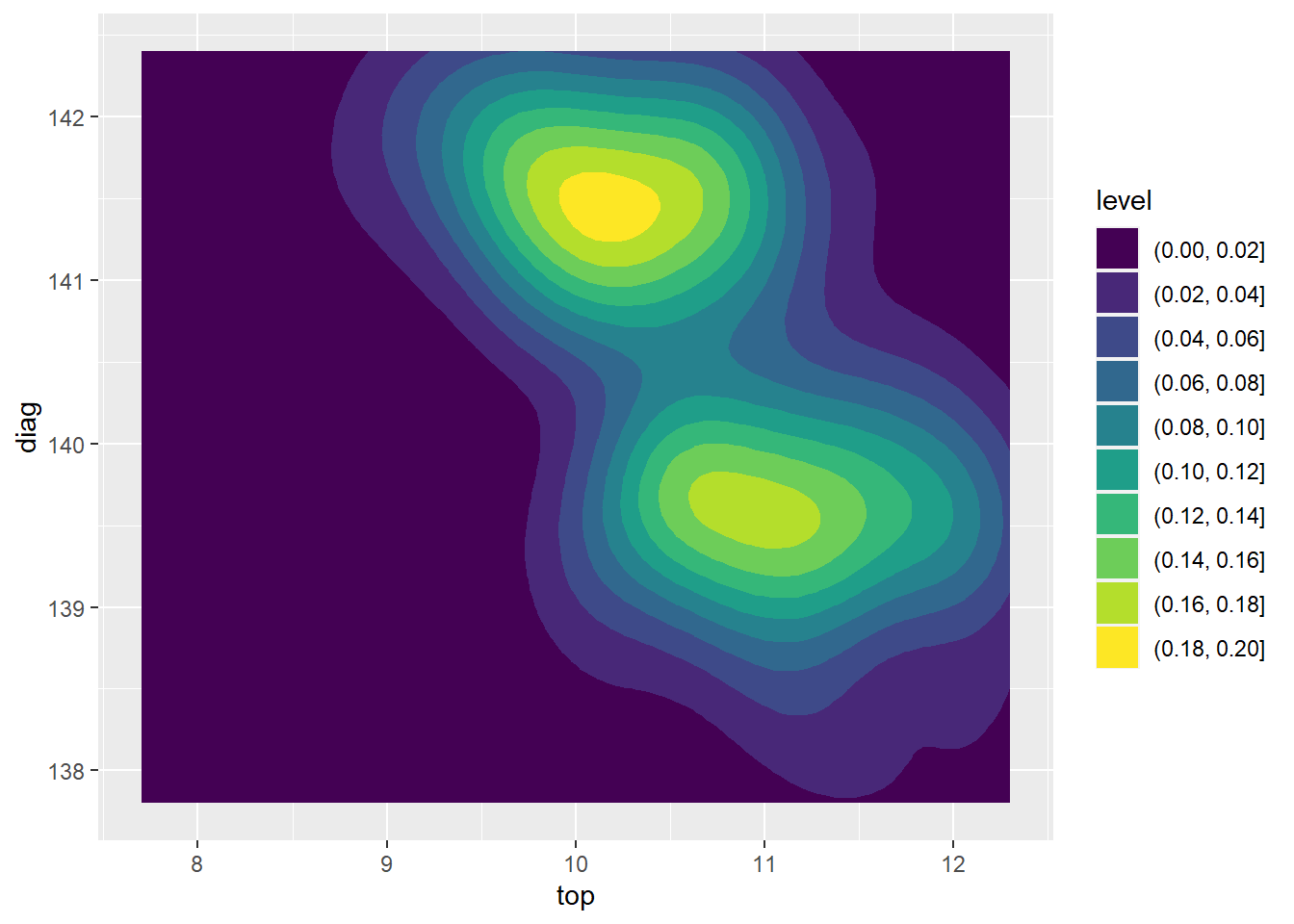
KernSmooth扩展包的bkde2D()函数可以对二元数据估计分布密度曲面。 曲面可以用contour()函数制作等高线图，如：

library(KernSmooth)

d <- as.data.frame(bankNotes[, c("top", "diag")])
n <- nrow(d)
res  = bkde2D(d, bandwidth = 1.06*c(sd(d[[1]]), sd(d[[2]]))* n^(-1/5))
contour(res$x1, res$x2, res$fhat,
  xlim = c(8.5, 12.5),
  ylim = c(137.5, 143),
  ##col = c("blue", "black", "yellow", "cyan",
  ##    "red", "magenta", "green", "blue", "black"),
  col=rainbow(9),
  lwd=1, cex.axis = 1)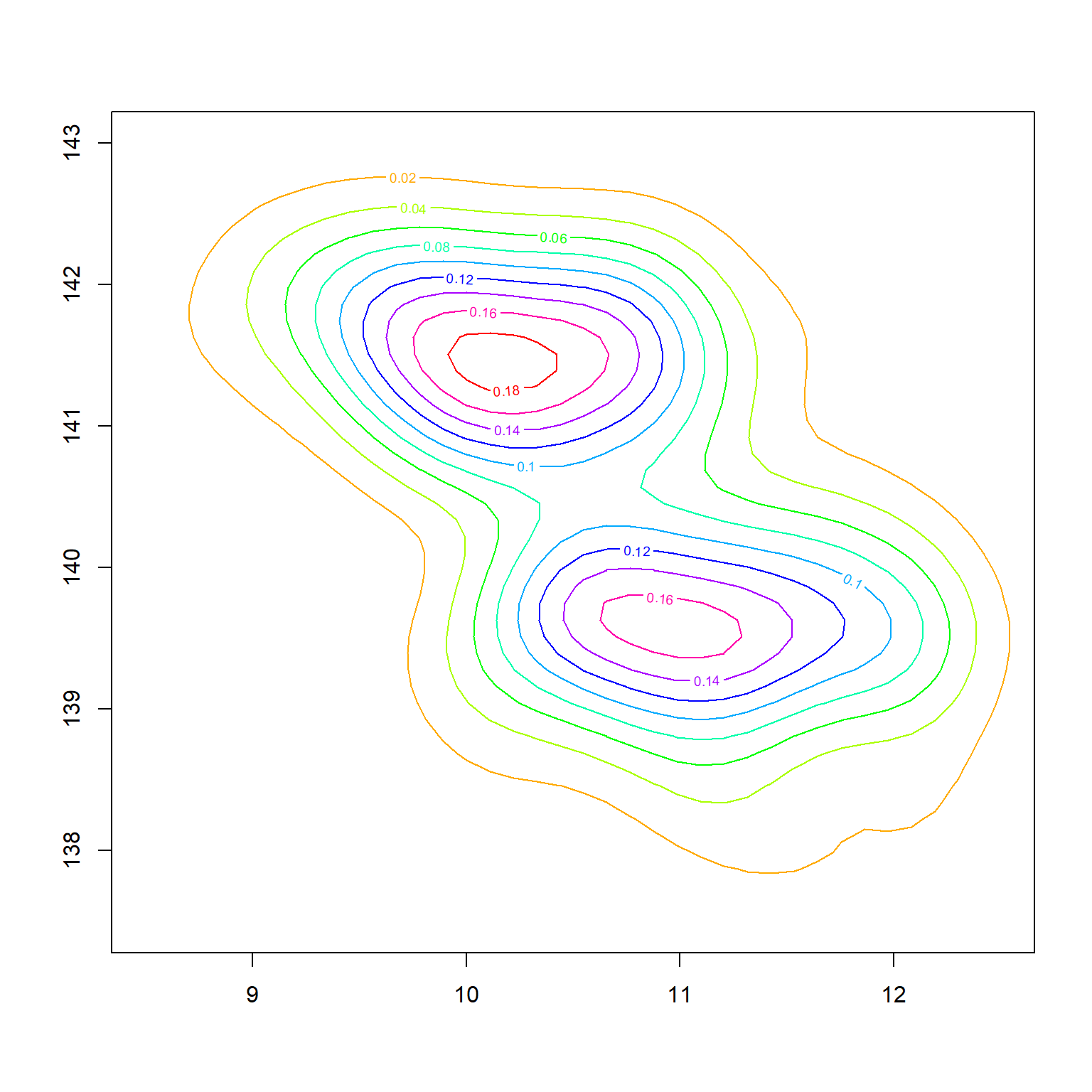

这里选取了上边缘宽度与图案对角线长度两个变量。 等高线图明显有双峰，但是边缘有重叠部分。

2.3.5 蜂窝图

蜂窝图是一种二元直方图。 在有点的地方画六边形， 用不同灰度深浅表示点的密集度。 六边形大小类似于直方图组距的作用。 作为直方图的二维推广， 蜂窝图也存在与直方图类似的缺点， 比如依赖于六边形大小和左右、上下位移。

二元数据的密度如果作直方图， 因为已经占用了x方向和y方向， 所以取值频数大小可以用灰度深浅或者颜色渐变来表示。

ggplot2包的geom_hex()作蜂窝图， 相当于二元的直方图。

hexbin扩展包的hexbinplot()函数作蜂窝图。

考虑ageIncome调查问卷数据：

ageIncome <- read_csv(
  "data/年龄与收入.csv",
  show_col_types = FALSE)
str(ageIncome)

## spc_tbl_ [2,946 × 9] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ Age          : num [1:2946] 30 82 63 74 70 29 78 62 27 20 ...
##  $ Income       : num [1:2946] 300 800 750 1100 1300 360 1400 150 800 350 ...
##  $ TVMinutes    : num [1:2946] 120 240 180 240 300 240 240 240 120 300 ...
##  $ WorkHours    : num [1:2946] 0 0 0 0 0 0 0 0 30 0 ...
##  $ ComputerHours: num [1:2946] 0 0 0 0 0 ...
##  $ IllDays      : num [1:2946] 996 996 996 996 996 996 996 996 5 996 ...
##  $ LiveArea     : num [1:2946] 100 60 95 998 45 68 73 108 100 97 ...
##  $ Size         : num [1:2946] 163 163 165 160 168 160 168 183 174 180 ...
##  $ Weight       : num [1:2946] 88 80 70 999 89 62 999 999 90 60 ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   Age = col_double(),
##   ..   Income = col_double(),
##   ..   TVMinutes = col_double(),
##   ..   WorkHours = col_double(),
##   ..   ComputerHours = col_double(),
##   ..   IllDays = col_double(),
##   ..   LiveArea = col_double(),
##   ..   Size = col_double(),
##   ..   Weight = col_double()
##   .. )
##  - attr(*, "problems")=<externalptr>

library(hexbin)
head(ageIncome, 3)

## # A tibble: 3 × 9
##     Age Income TVMinutes WorkHours ComputerHours IllDays LiveArea  Size Weight
##   <dbl>  <dbl>     <dbl>     <dbl>         <dbl>   <dbl>    <dbl> <dbl>  <dbl>
## 1    30    300       120         0             0     996      100   163     88
## 2    82    800       240         0             0     996       60   163     80
## 3    63    750       180         0             0     996       95   165     70

先对数据进行了合理性筛选， 然后作收入对年龄的散点图：

library(tidyverse)
dai <- ageIncome |>
  filter(
    Age <= 100 & Income < 99997 
    & ComputerHours <= 24*7 & LiveArea < 998)
ggplot(dai, aes(
  x = Age, y = Income)) +
  geom_point(alpha = 0.3)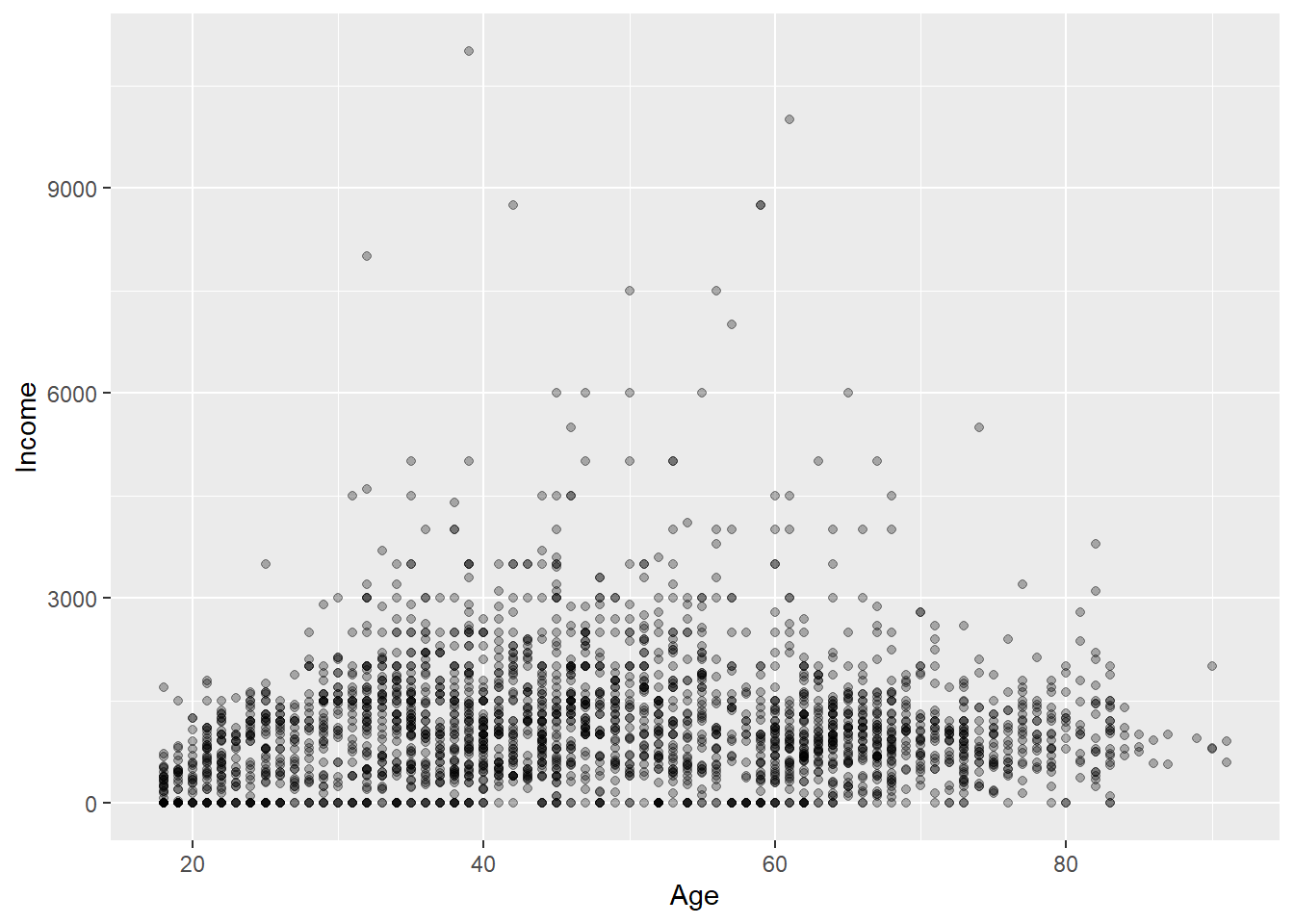

当点很多或者不同可取值个数有限时，散点图可能有重叠问题。 可以用alpha=给点加上透明度， 这样颜色越深代表点越多， 但是重叠的点太多时就无法表现出来。

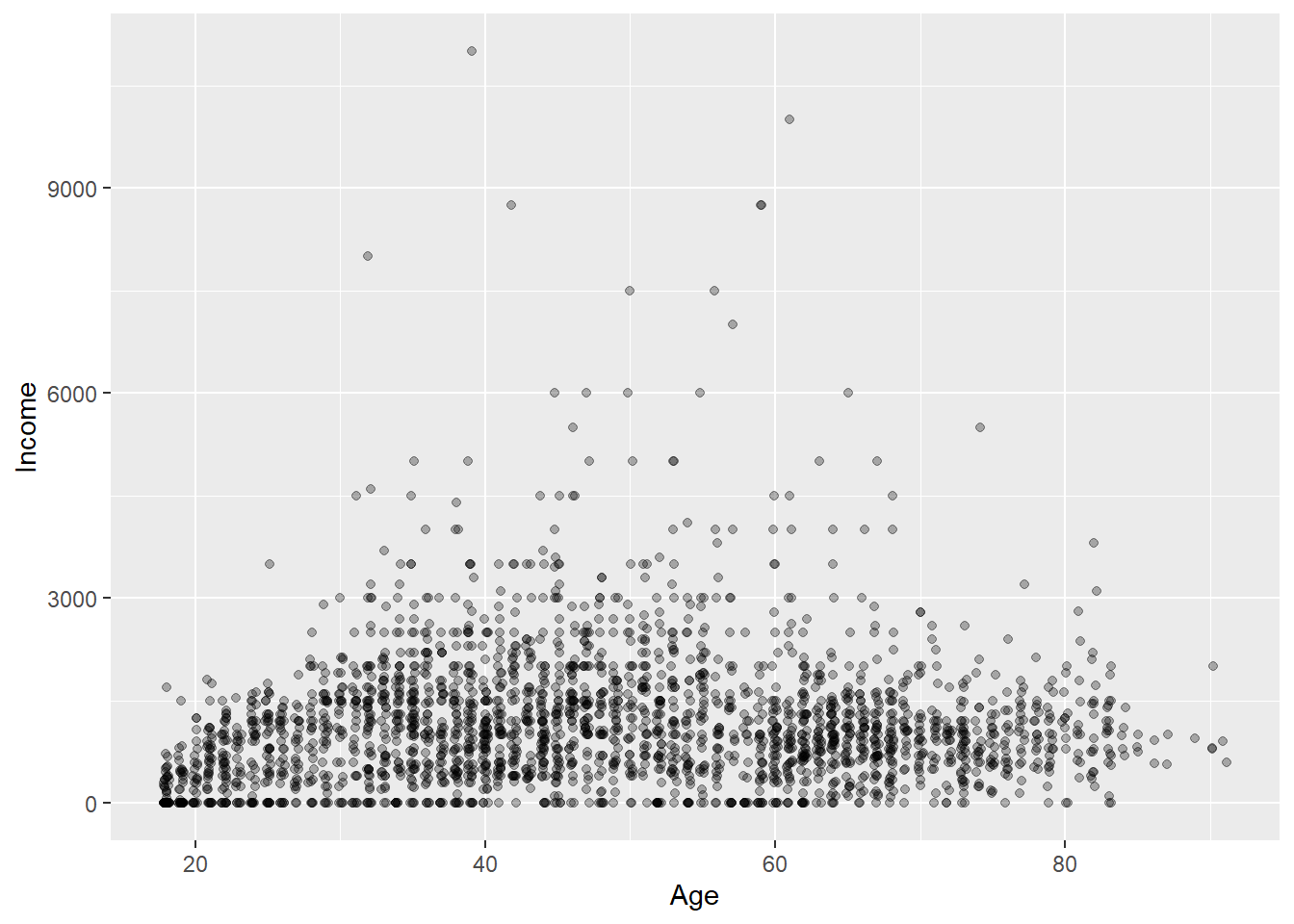
当点较少时如果有重叠， 可以令每个点有小的抖动。 参数width以横坐标之间最小非零差距为单位给出抖动比例。 可以同时使用alpha参数。 加了左右抖动的散点图：

ggplot(dai, aes(
  x = Age, y = Income)) +
  geom_jitter(width = 0.2, alpha = 0.3)

作蜂窝图，用颜色深浅代表不同区域的观测点个数， 颜色越深代表个数越多：

ggplot(dai, aes(
  x = Age, y = Income)) +
  geom_hex(bins = 25) +
  scale_fill_gradient(
    low = "#9696F2", 
    high = "#0A0A3D")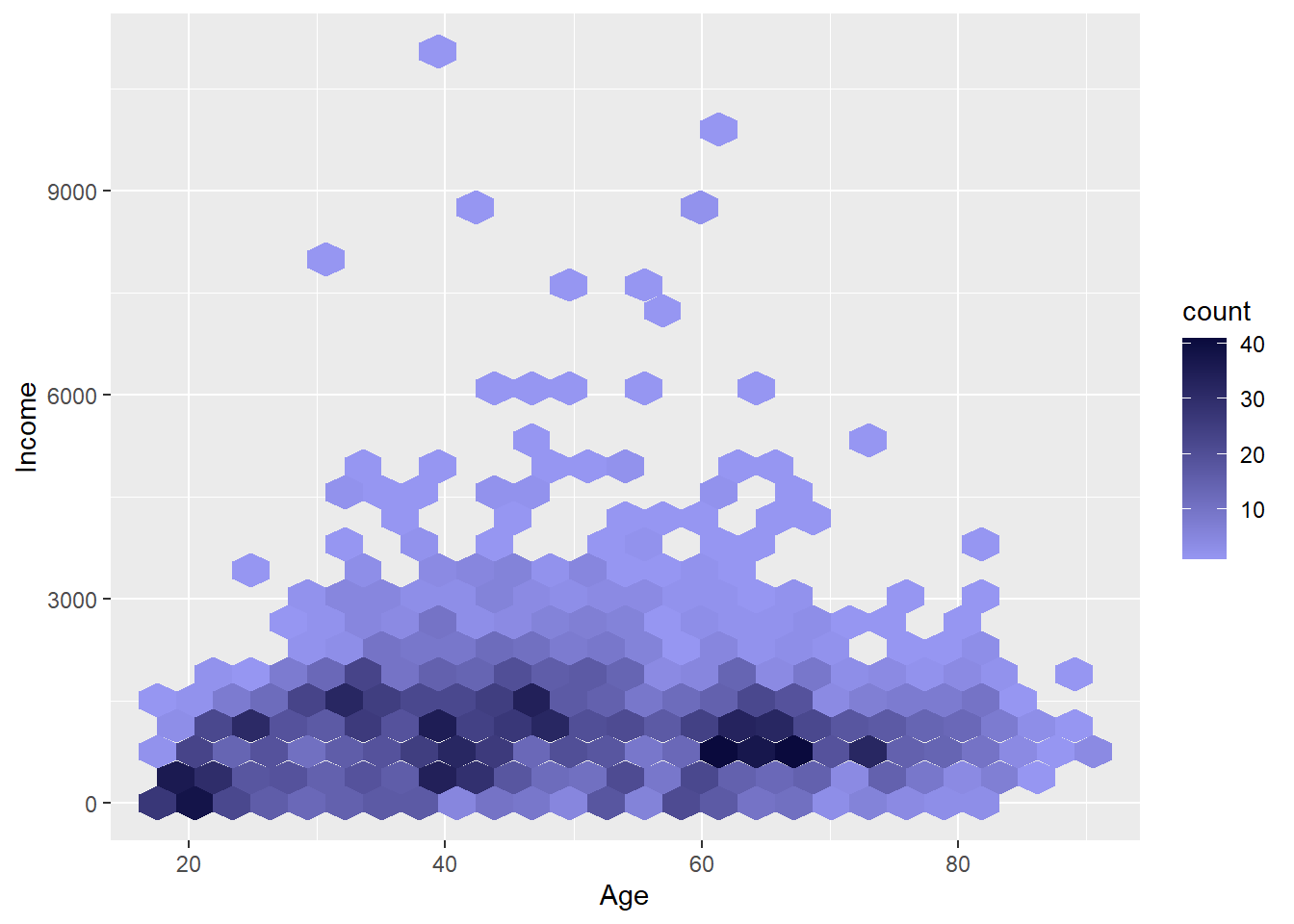

用hexbin包作蜂窝图：

library(hexbin)
allbus1 = as.data.frame(ageIncome[, 1:2])

## exclude invalid observations
allbus1 <- subset(
  allbus1, Age <= 100 & Income < 99997)
ages      = allbus1[[1]]      # Ages
netincome = allbus1[[2]]      # Net income

## Scatter plot
plot(ages, netincome,
     xaxt = "n",
     xlab = "Age", ylab = "Net income", cex = 0.1)
axis(1, at = c(20, 30, 40, 50, 60, 70, 80, 90))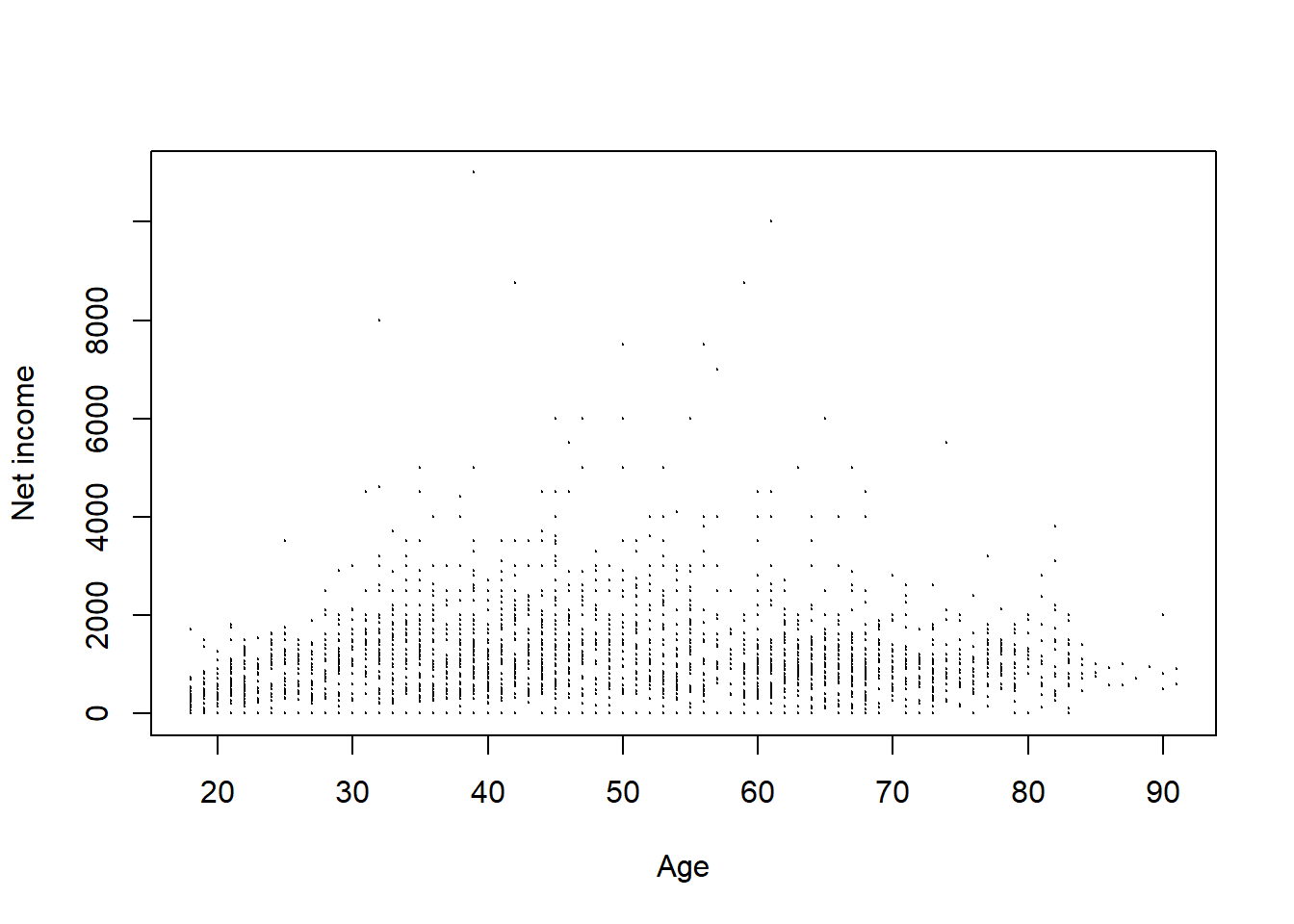

## Hexagon plot
print(hexbinplot(
    netincome ~ ages,
    xlab = "Age", ylab = "Net income",
    style = "colorscale", 
    border = TRUE,
    aspect = 1,
    trans = sqrt,
    inv = function(x) x ^ 2))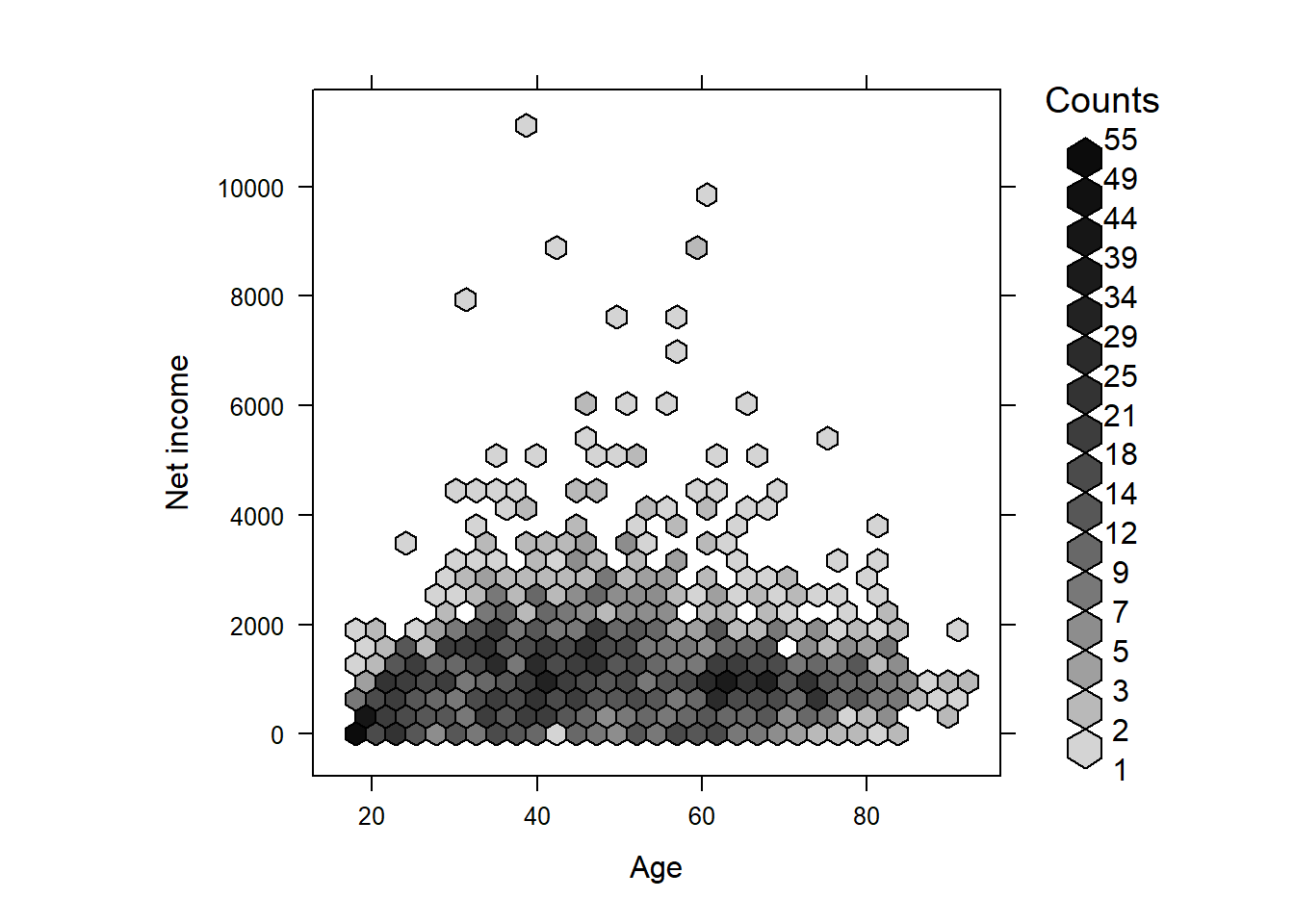

ageIncome调查问卷数据, 收入与居住面积的蜂窝图：

ggplot(data = dai, aes(
  x = Income, y = LiveArea)) +
  geom_hex(bins = 25) +
  scale_fill_gradient(
    low = "#9696F2", 
    high = "#0A0A3D")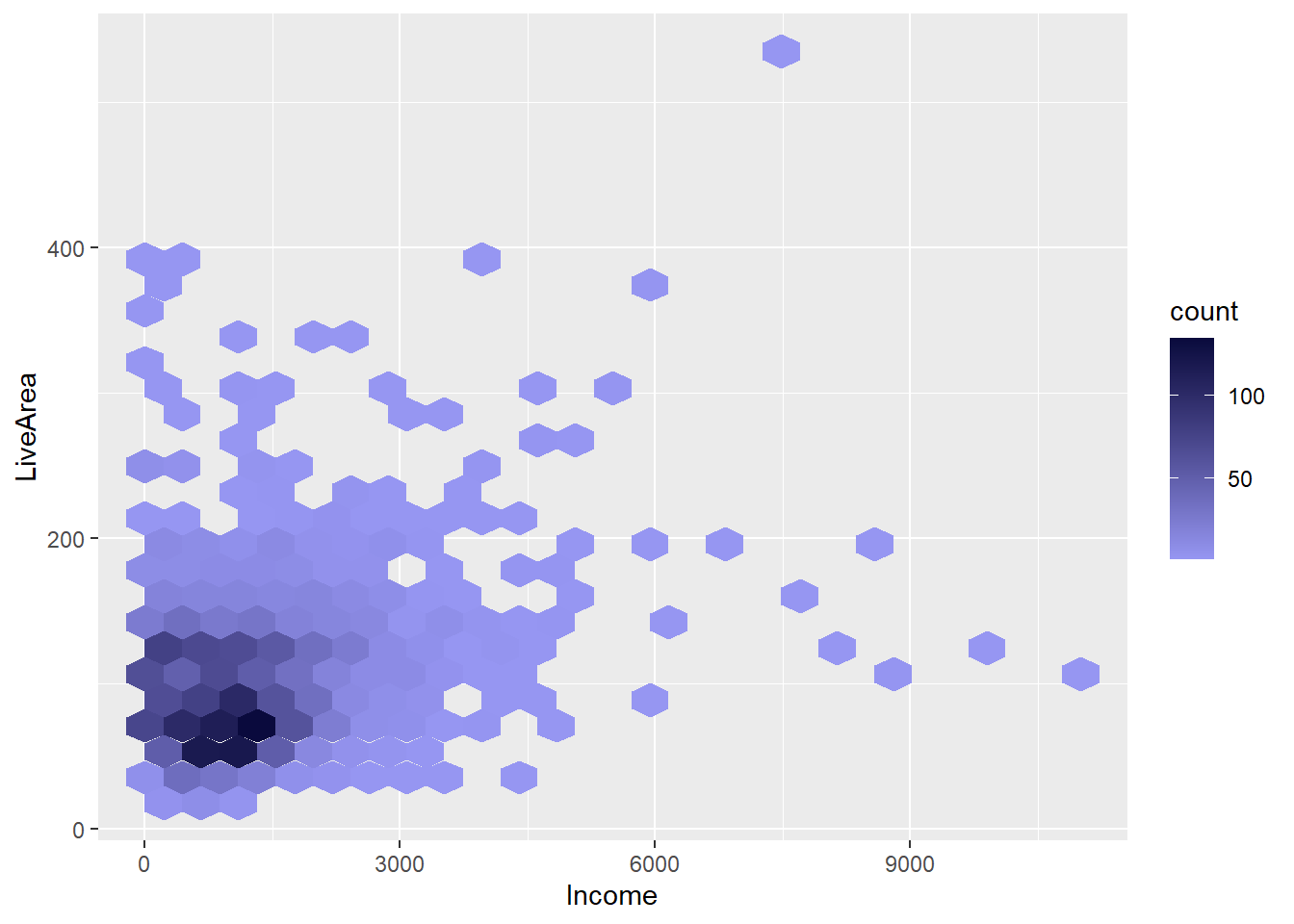

收入低，居住面积小。

2.3.6 \(\chi\)图

\(\chi\)图用来检查两个变量是否相互独立。 当\(X\), \(Y\)相互独立时， 应有 \[ P(X \leq x, Y \leq y) = P(X \leq x) P(Y \leq y) . \]

对每个观测\(i\)， 可以计算\(\chi_i\)和\(\lambda_i\)， 其中\(\chi_i\)是将\(X\)以\(x_{i}\)为界限分为两类， 将\(Y\)按\(y_{i}\)为界限分为两类， 进行\(2 \times 2\)列联表卡方检验的统计量的平方根， 在\(X, Y\)独立时渐近零均值的正态分布。 \(\lambda_i\)独立第\(i\)观测与二元分布均值的偏离程度。 函数chiplot()作\(\chi\)图， 比如cd4数据：

with(cd4, chiplot(
  baseline, oneyear))

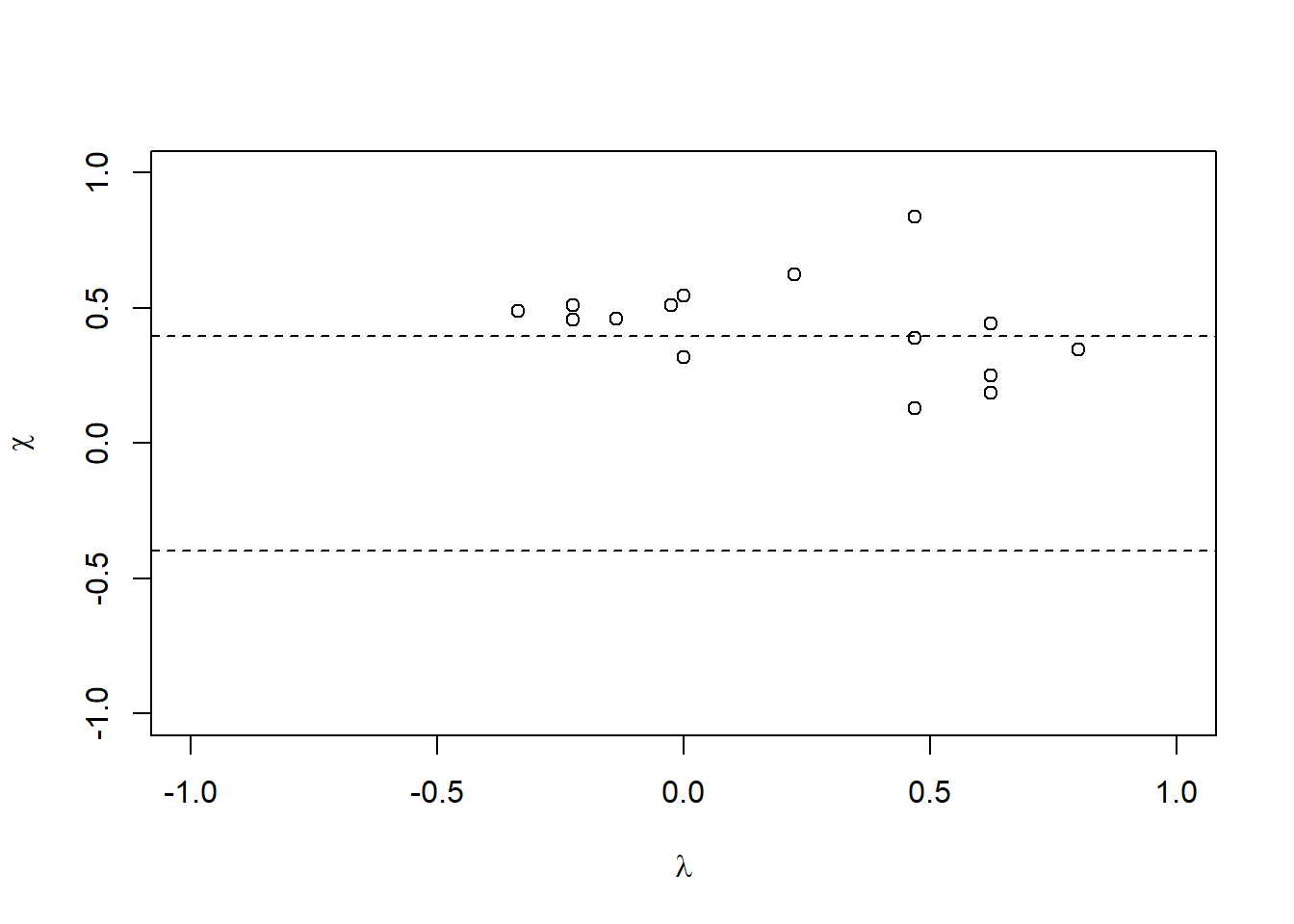
在这个图中， 用虚线分成了三个水平条带， 某一条带中空白就提示非独立。

2.4 三元变量的图形

2.4.1 三维散点图

rgl扩展包支持三维动态图像。 会在独立的窗口中显示可以拖动旋转的三维的散点图。

iris数据中三个变量的三维动态散点图：

library(rgl)
plot3d(iris[,1:3], 
  col=rainbow(9)[4:6][as.numeric(factor(iris[["Species"]]))], 
  size=10)

lattice包的cloud函数可以作三维散点图。

2.4.2 气泡图

散点图仅有二元数据， 可以用每个散点大小代表第三个变量大小。

JanTemp数据框变量： - T: 城市的一月份最高温度(华氏度) - Lat, Long, Alt: 纬度(北纬度)，经度(西经度)，高度(海拔英尺) - Name: 城市名称

JanTemp <- read_csv("data/JanTemp.csv",
  show_col_types = FALSE)

head(JanTemp, 3)

## # A tibble: 3 × 5
##       T   Lat  Long   Alt Name          
##   <dbl> <dbl> <dbl> <dbl> <chr>         
## 1    61    30    88     5 Mobile, AL    
## 2    59    32    86   160 Montgomery, AL
## 3    30    58   134    50 Juneau, AK

画经纬度坐标散点图，点大小表示高度，标记突出的四个州::

library(ggrepel)
landmarks <- c("AK", "HI", "MA", "PR")
## 逆转东西方向。西经度是右方在西的，所以需要逆转。
d <- JanTemp |>
  mutate(Longe = 180 - Long) 
d1 <- d |>
  mutate(state = substr(Name, nchar(Name)-1, nchar(Name))) |>
  filter(state %in% landmarks) 
ggplot(d, aes(
  x = Long, y = Lat, size = Alt)) +
  geom_point(shape = "circle open") + 
  geom_text_repel(data = d1, aes(
    x = Long, y = Lat, label = state), size = 3)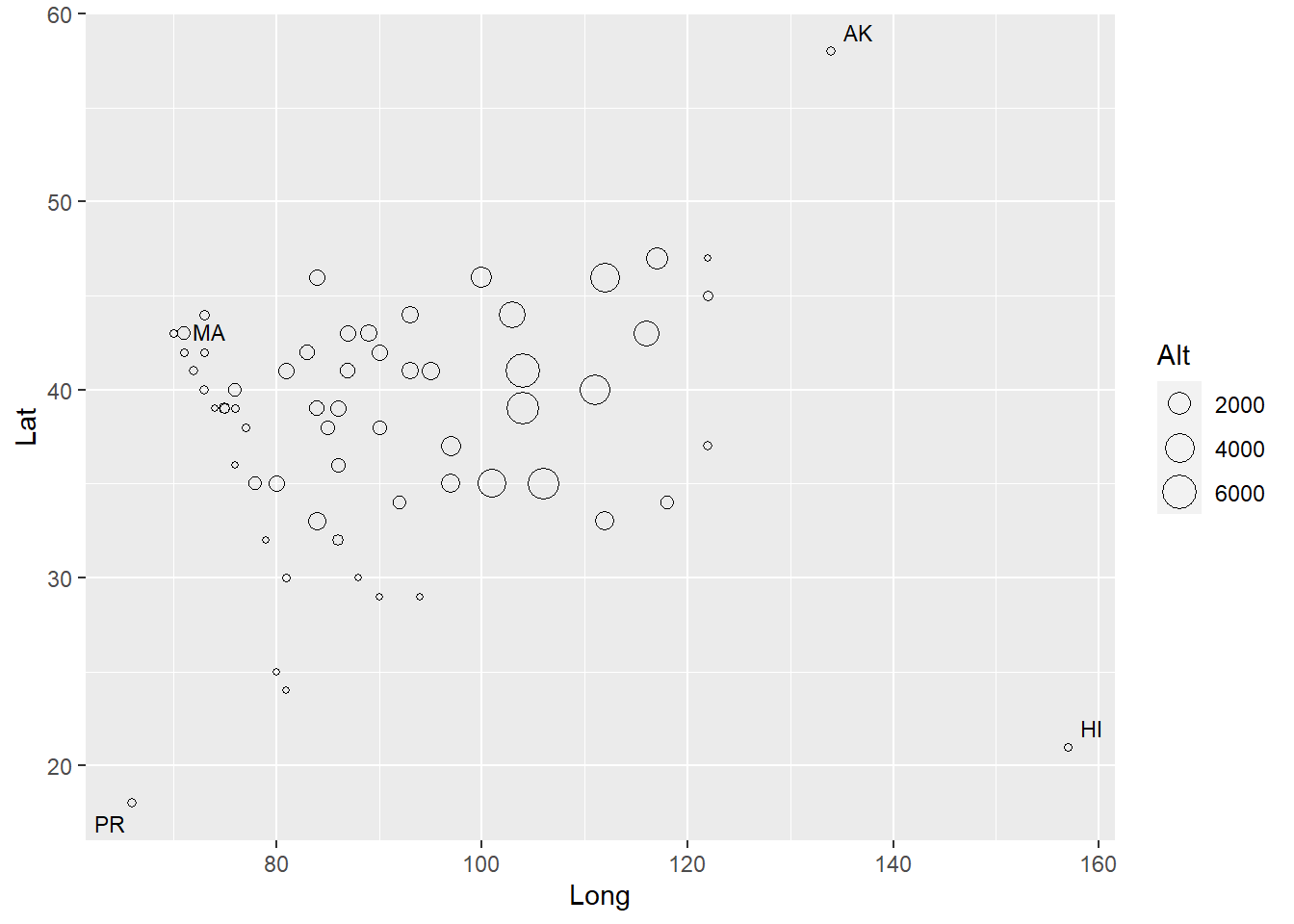

用基本graphics包实现：

library(MASS)

## 逆转东西方向。西经度是右方在西的，所以需要逆转。
d <- JanTemp
d[["Longe"]] <- -d[["Long"]]
plot(d[["Longe"]], d[["Lat"]], 
     pch=16, cex=0.7,
     xlab="Longitude, east",
     ylab="Latitude",
     col="red")
symbols(d[["Longe"]], d[["Lat"]],
        circles=d[["Alt"]],
        inches=0.3, add=TRUE,
        lwd=3, fg="green")
landmarks <- c("AK", "HI", "MA", "PR")
state <- substring(d[["Name"]], nchar(d[["Name"]])-1)
lmi <- match(landmarks, state)
text(d[["Longe"]][lmi], d[["Lat"]][lmi],
     labels=landmarks,
     pos=c(1,1,4,3), col="blue")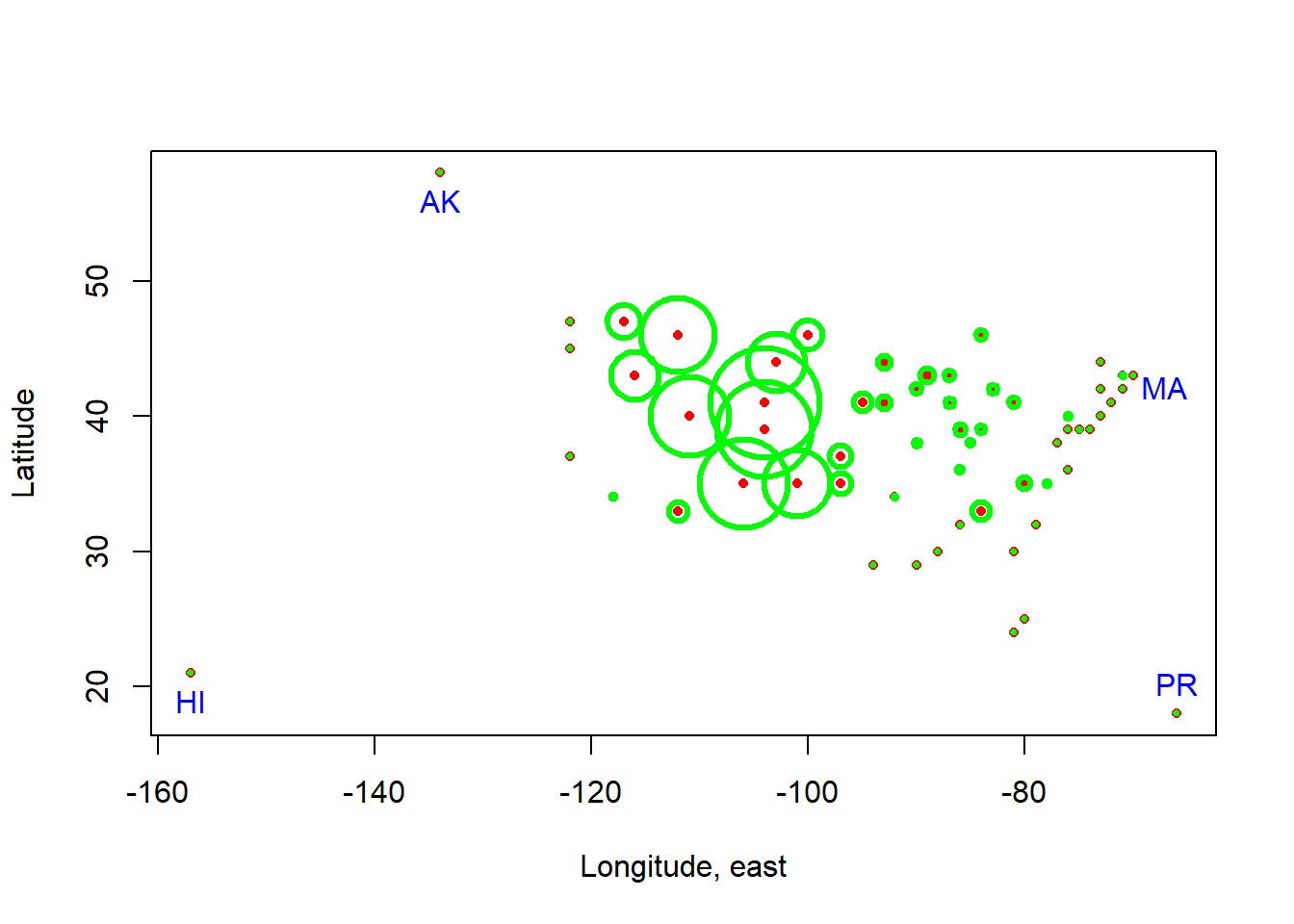

symbol()函数在图上增加圈、方块、矩形、星形、温度计、盒形图等符号， inches参数是最大一个符号的大小，以英寸为单位。 text()的pos: 1,2,3,4分别在下，左，上，右。

2.4.3 kriging 方法拟合曲面

• kriging方法进行曲面拟合。
• 等高线图表现二元函数曲面。
• R中contour()函数。

kriging是一种用多项式拟合二元函数曲面的方法。

JanTemp数据的Kriging等高线图:

library(MASS)
library(spatial)

d <- JanTemp
d[["Longe"]] <- -d[["Long"]]
## 用Kriging方法拟合三维曲面.
## surf.ls()拟合多项式曲面，第一参数是多项式次数
alt.kr <- surf.ls(
  4, d[["Longe"]], d[["Lat"]], d[["Alt"]])
## 用trmat()计算多项式的网格点
altsur <- trmat(alt.kr, -125, -70, 28, 50, 50)
## MASS::eqscplot()产生纵横比为1的散点图, type="n"仅建立坐标系
eqscplot(altsur,
  type="n",
  xlab="Longitude, east",
  cex.lab=1.5,
  ylab="Latitude")
## contour()在散点图上叠加拟合曲面
contour(altsur, levels=c(0, 1000, 2000, 4000),
        add=TRUE, col="blue")
points(d[["Longe"]], d[["Lat"]], 
       pch=16, col="red")
ex <- c("Miami", "Seattle", "San Francisco",
  "Denver", "Cheyenne")
exi <- top.match(d[["Name"]], ex)
print(exi)

## [1] 14 56  7  8 60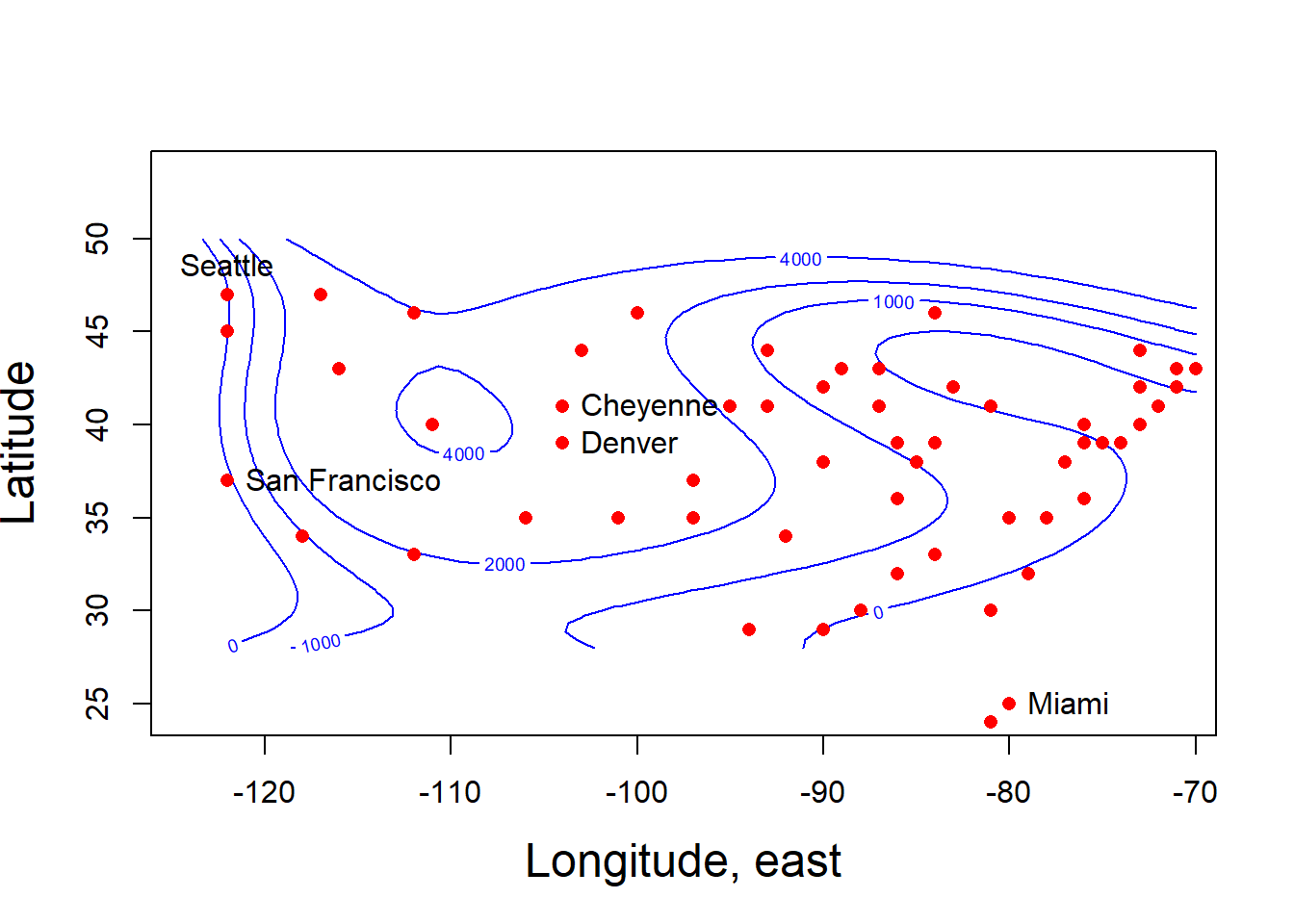

text(d[["Longe"]][exi], d[["Lat"]][exi], 
  labels=ex,
  pos=c(4,3,4,4,4), cex=1)

R的quakes数据是Fiji附近1964年来1000个震级MB>4.0的地震观测数据， 变量为：

• lat, long: 纬度，经度
• depth: 震中深度
• mag: 震级
• stations: 报告此次地震的台站数

先画地震中心经纬度坐标散点图，点大小表示震级：

library(MASS)

plot(quakes[["long"]], quakes[["lat"]], 
  type="n",
  xlab="Longitude",
  ylab="Latitude")
symbols(quakes[["long"]], quakes[["lat"]],
  circles=exp(quakes[["mag"]]),
  inches=0.2, add=TRUE,
  lwd=1, fg="orange")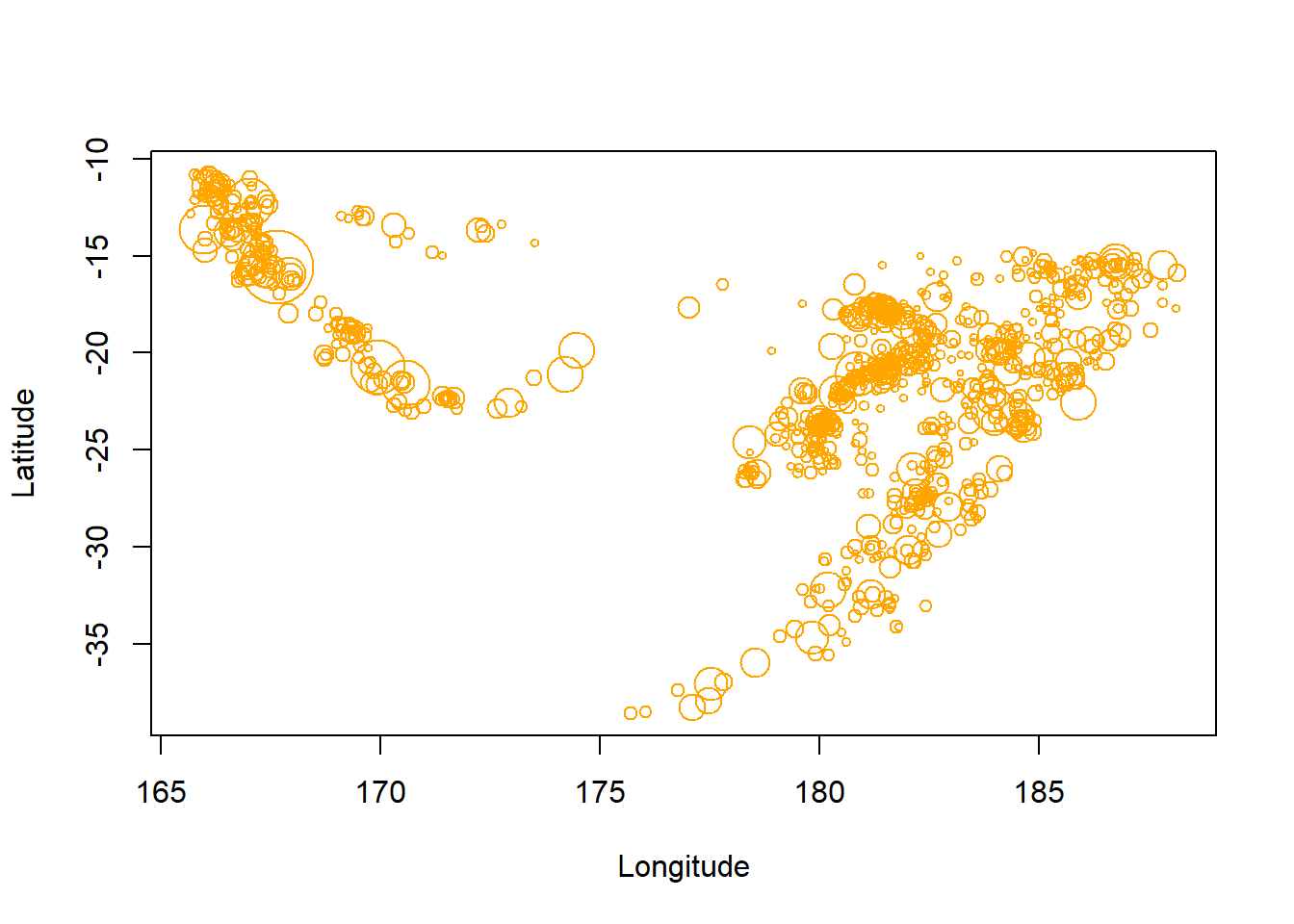

这里震级做了指数变换以更好地区分大小地震。

曲面图选取适当视角可以直观表现二元函数曲面。 R中persp()函数作曲面图。

2.5 多元变量的图形

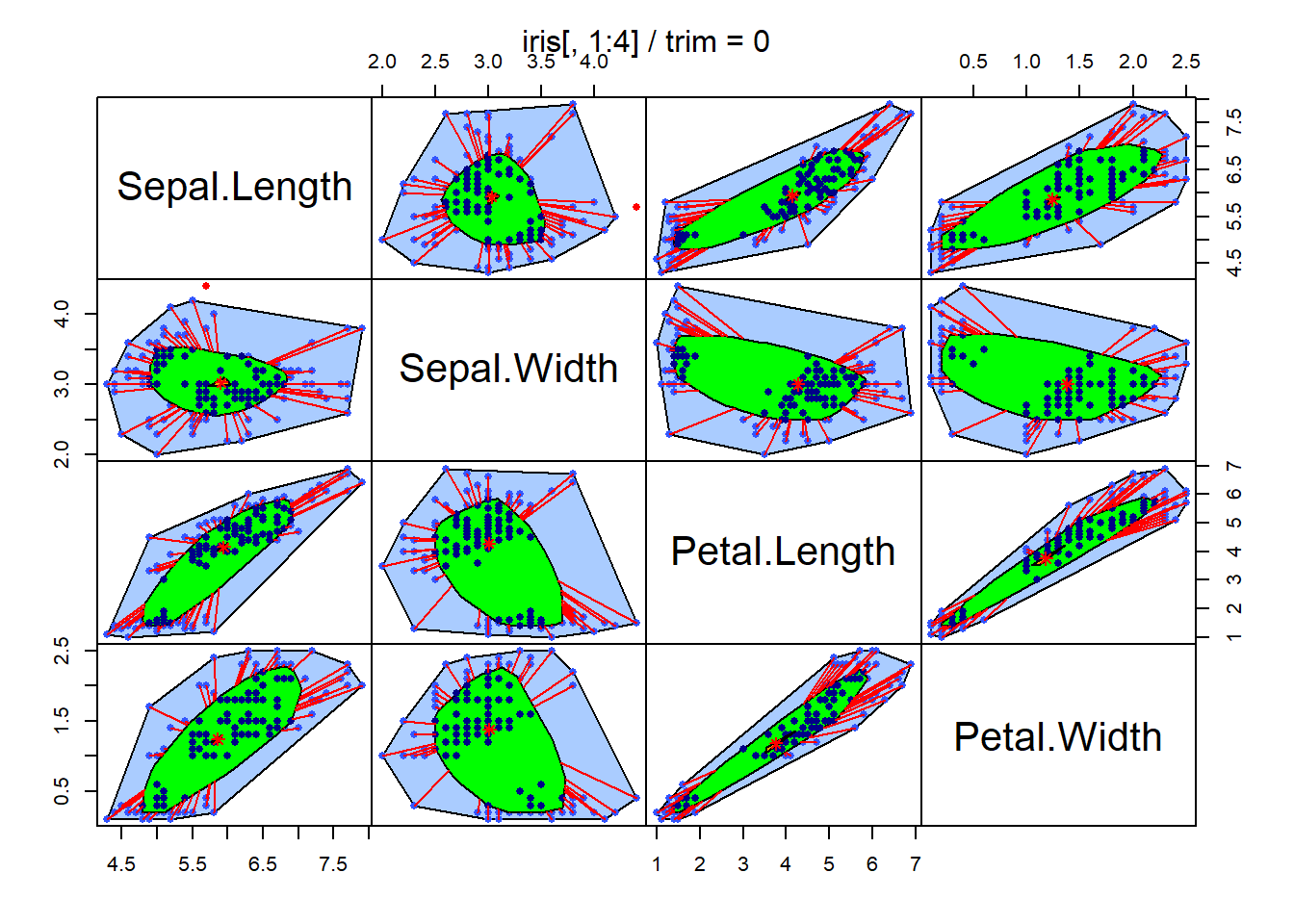
2.5.1 散点图矩阵

散点图矩阵同时做两两的散点图， 同时查看多个关系。

Ggally包提供了ggplot风格的散点图矩阵， 可以显示散点图、单个变量的核密度、相关系数。

鸢尾花数据的散点图矩阵， 用不同颜色区分花的品种：

library(GGally)
ggscatmat(data = iris, columns = 1:4)

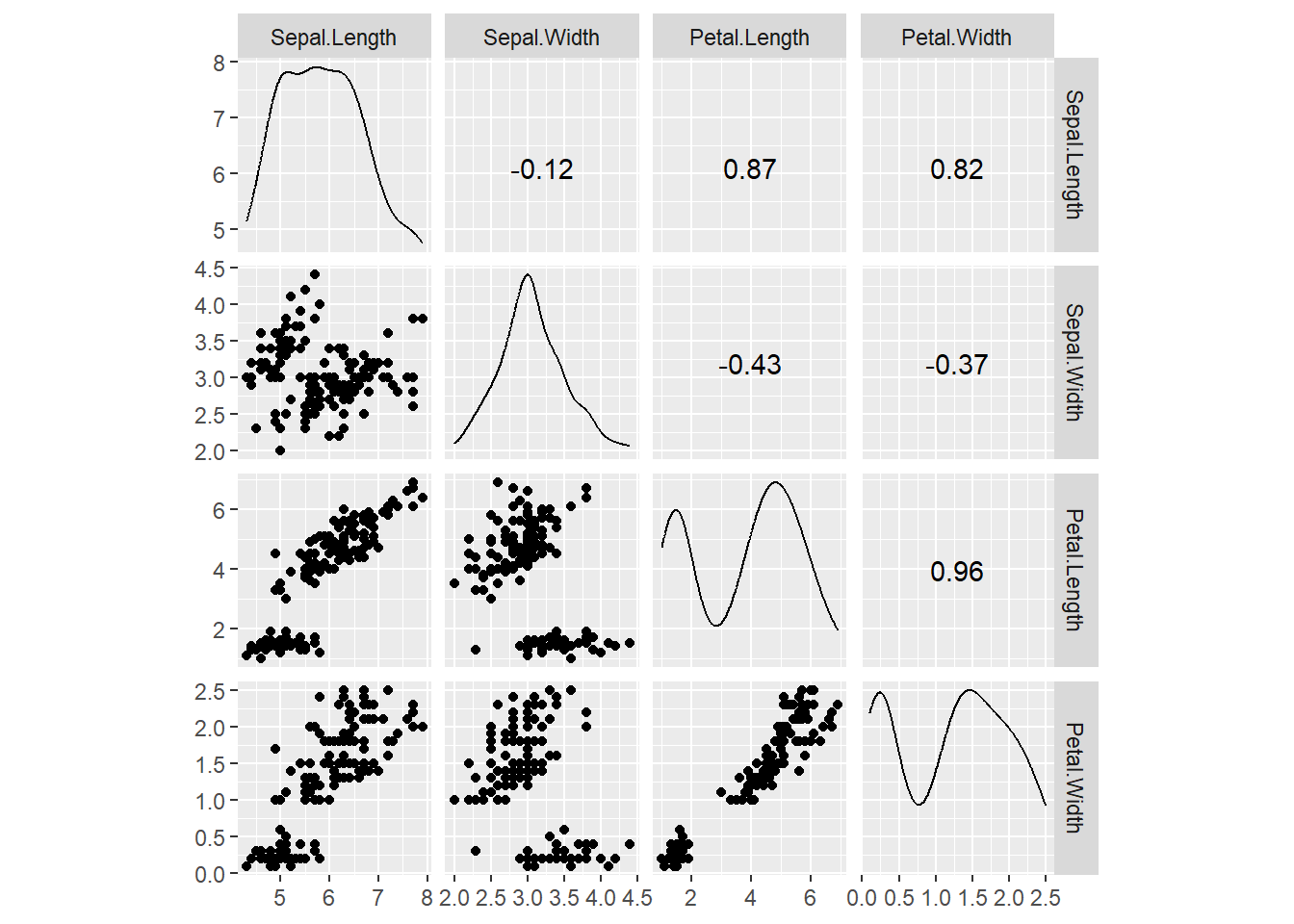
用不同颜色区分三种花的品种：

ggscatmat(
  data = iris, columns = 1:4,
  color = "Species")

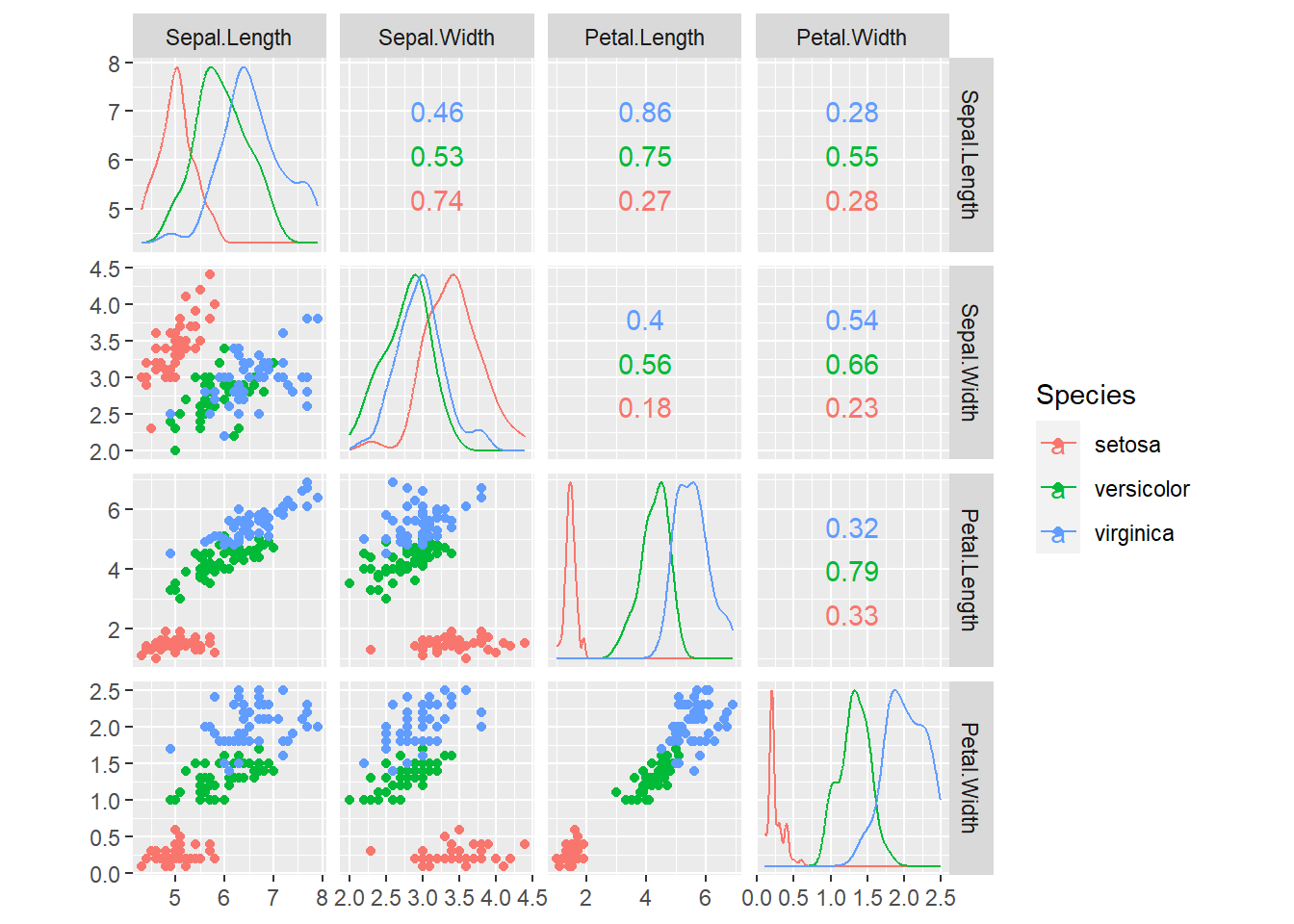
GGally的ggpairs()函数提供了另一种矩阵图， 可以比较变量两两分布或者关系。 例如， 取iris数据集的花瓣长、花萼长与种类：

ggpairs(
  data = iris, 
  columns = c(
    "Petal.Length", "Sepal.Length", "Species"))

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.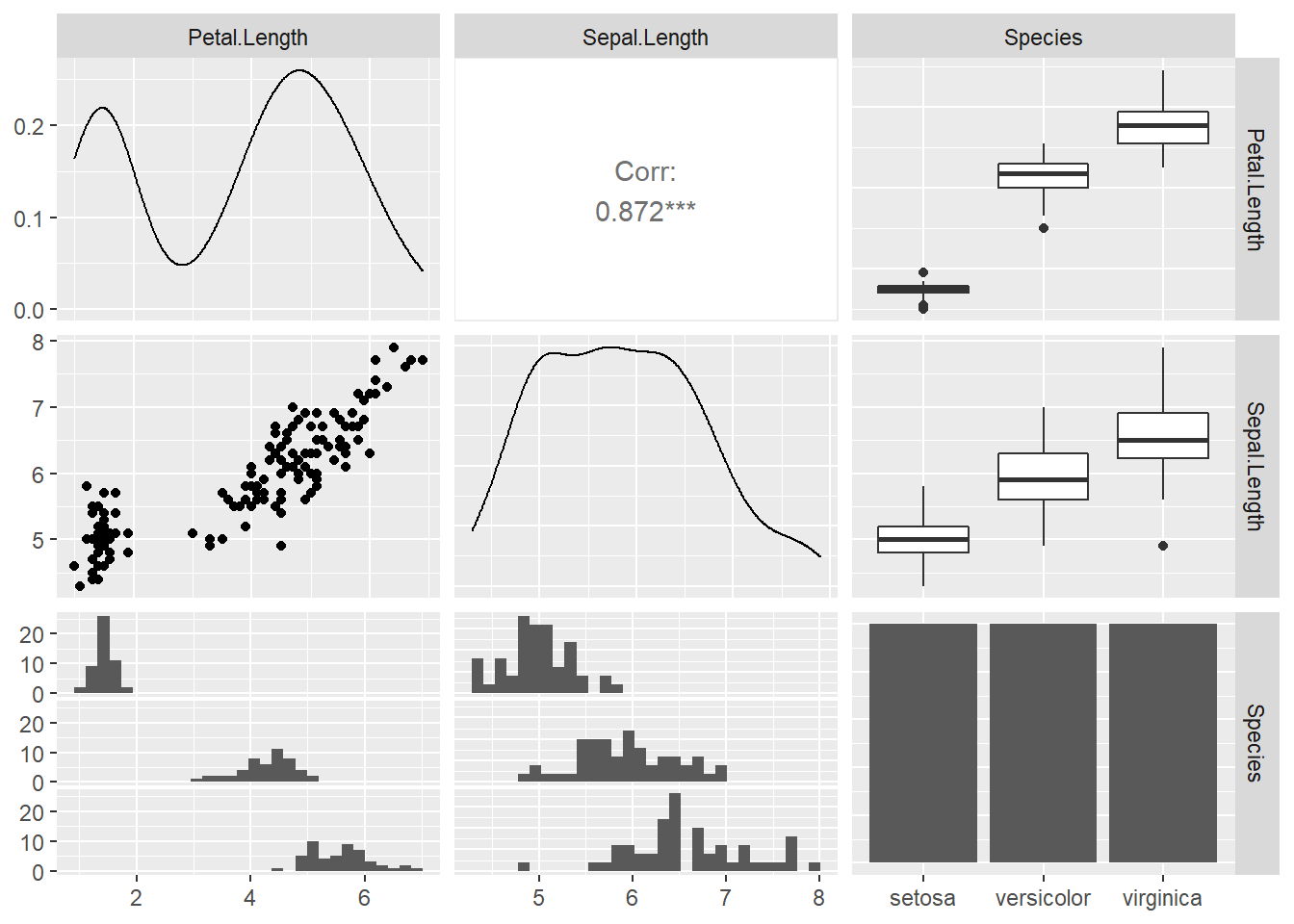

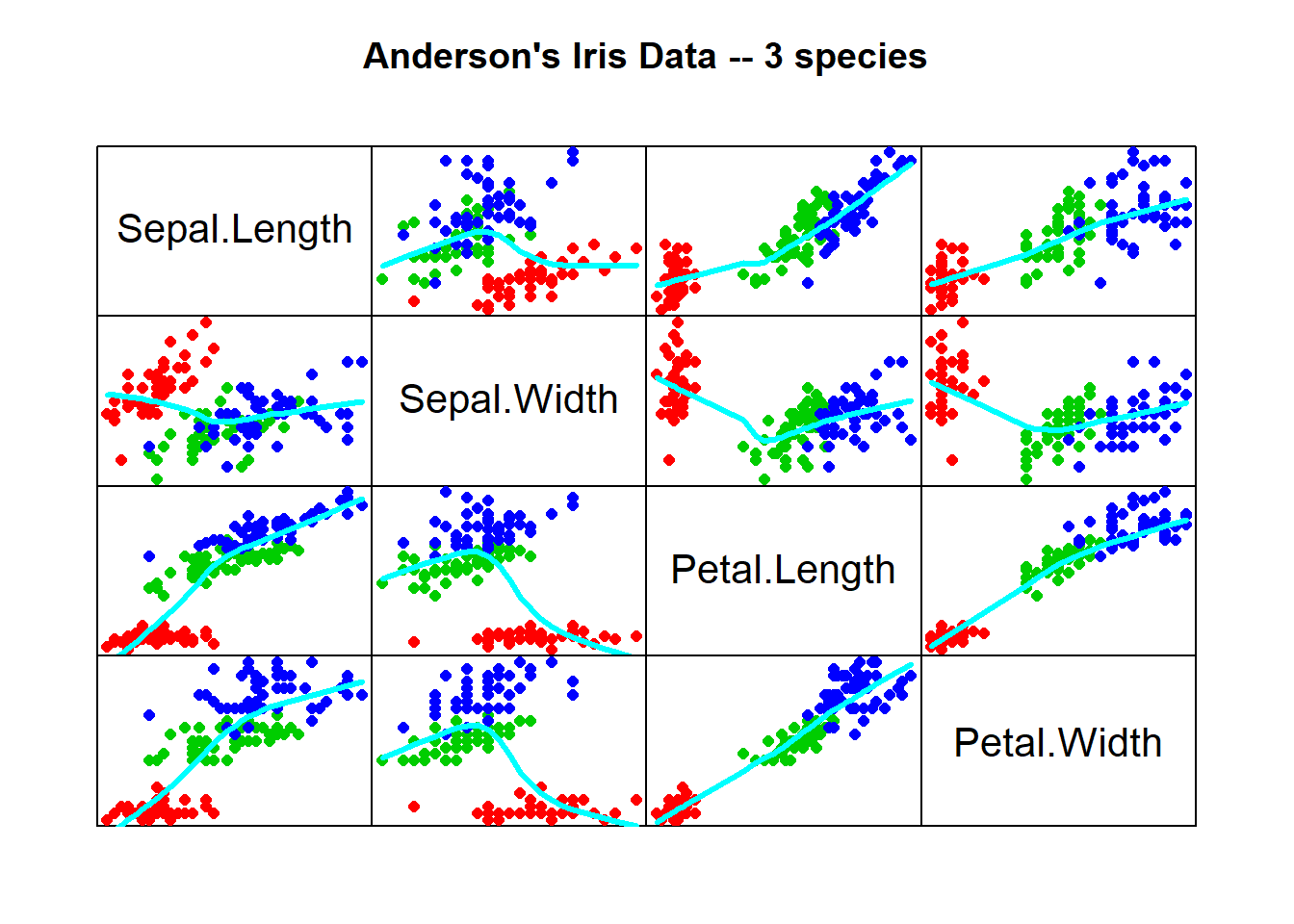
基本R的graphics::pairs()函数作两两的散点图，称为散点图矩阵:

pairs(iris[,1:4],
  main = "Anderson's Iris Data -- 3 species",
  pch = 21,
  bg = c(
    "red", "green3", "blue")[
         as.numeric(factor(iris$Species))])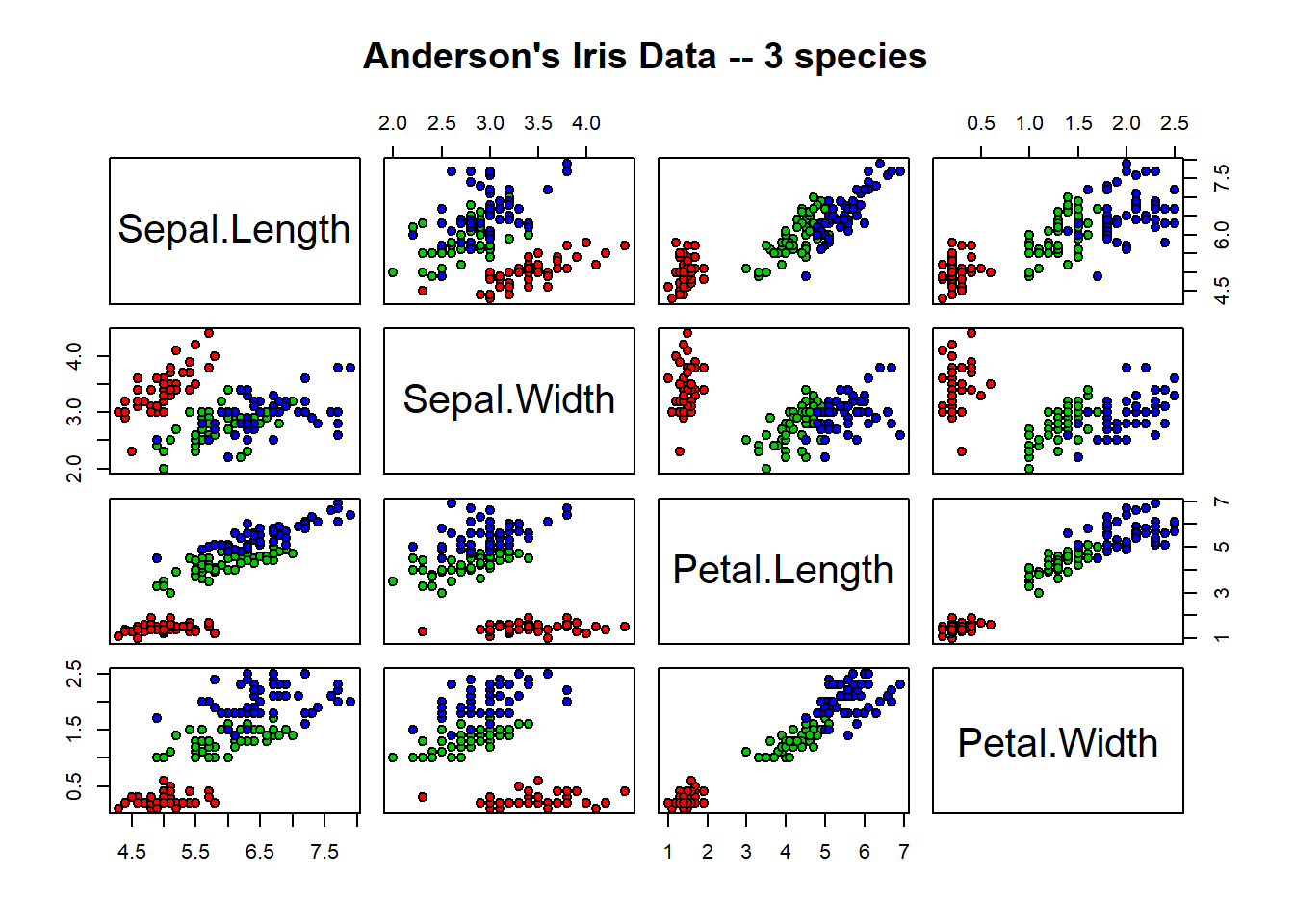

pairs()中用panel=panle.smooth()增加拟合曲线。如

pairs(iris[,1:4],
  main = "Anderson's Iris Data -- 3 species",
  pch = 16,
  cex=1.25,
  col = c("red", "green3", "blue")[
    as.numeric(factor(iris$Species))],
  gap=0, # 各个格子之间不留空隙
  xaxt="n", yaxt="n", # 坐标轴不标数值
  lwd=3,
  panel=function(x,y,...) panel.smooth(x, y, col.smooth="cyan", ...)
  )

2.5.1.1 成对散点图与口袋图

aplpack扩展包的bagplot.pairs()可以做成对散点图与口袋图。

鸢尾花数据的成对散点图与口袋图：

library(aplpack)
invisible(bagplot.pairs(iris[,1:4],
  gap=0, col.baghull="green"))

2.5.1.2 绘图员散点图矩阵

Draftman’s plot是散点图矩阵把右上三角部分改成二元核密度估计等高线图。

刷亮技术：散点图矩阵或绘图员散点图矩阵在一个图中选定部分区域并移动， 其它图的对应观测也被加亮显示。 SAS的Insight模块中有实现。

如瑞士银行真假钞数据：

library(KernSmooth)
f <- function(){
  opar = par(mfrow=c(4, 4), cex=.2)
  on.exit(par(opar))
  x = as.data.frame(bankNotes[,3:6])
  
  for(i in 1:4){
    for(j in 1:4){
      
      if(i==j){
        plot(1:2, type="n", axes=FALSE,
             xlab="", ylab="",
             main="", cex.main=5)
        text(1.5, 1.5,
             substitute(X[k], list(k=i)),
             cex=5)
      }
      
      if(i<j){
        xx = cbind(x[[i]],x[[j]], c(rep(0,100),rep(1,100)))
        zz = bkde2D(xx[,-3], 0.4)
        contour(zz$x1, zz$x2, zz$fhat,
                nlevels=12, col=rainbow(20),
                drawlabels=FALSE, xlab="X", ylab="Y")
      }
      
      if(i>j){
        yy = cbind(x[[i]], x[[j]], c(rep(0,100),rep(1,100)))
        plot(yy[,-3], pch=as.numeric(yy[,3]),
             xlab="X", ylab="Y",
             cex=3,
             col=ifelse(yy[[3]], "red", "blue"))
      } # if
    } # while j
  } # while i

}
f()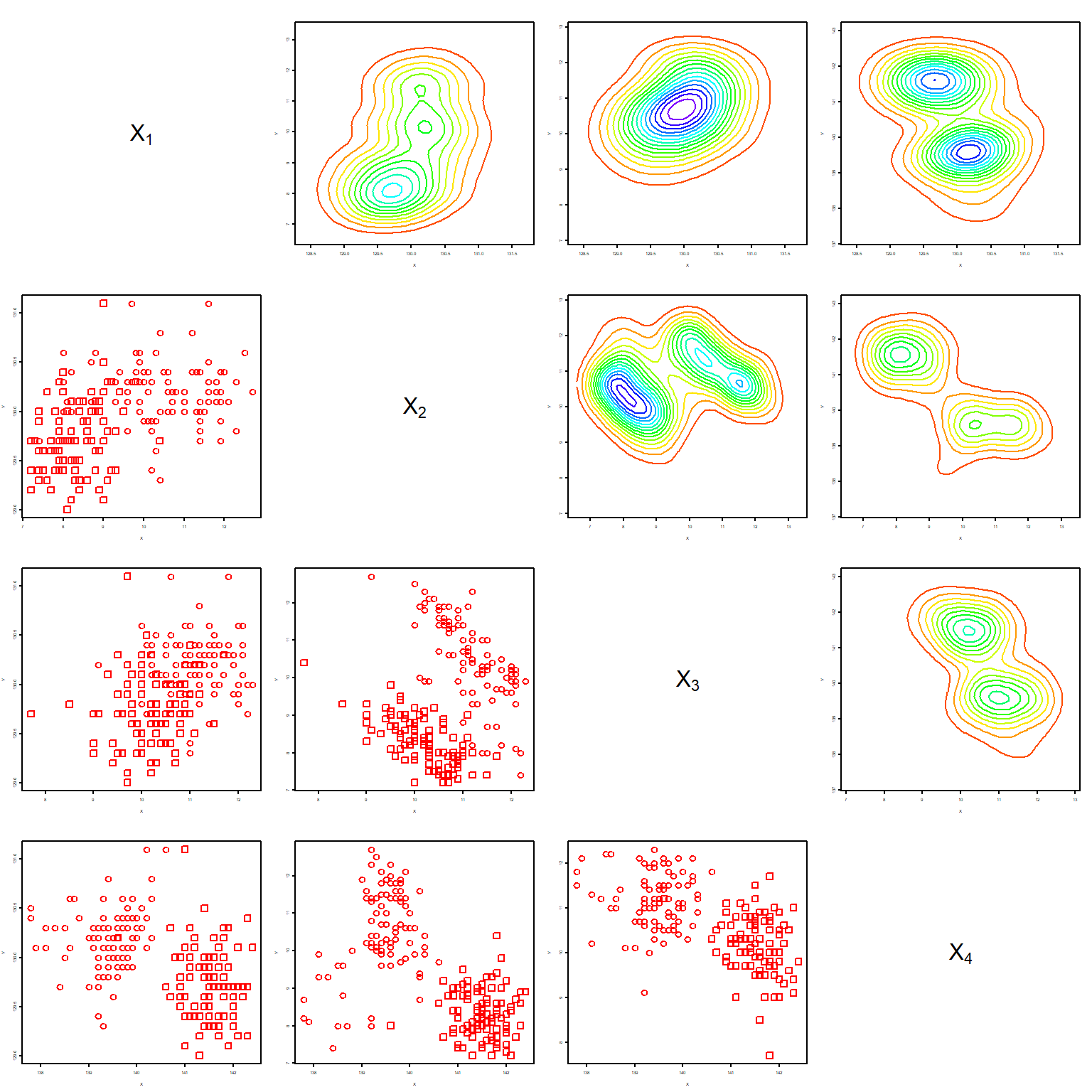

2.5.2 相关系数图

多个变量之间的相关系数矩阵可以用色块图表示， ggcorrplot包提供了这样的功能， 例如， 对datasets包的mtcars数据框作相关系数图：

library(ggcorrplot)

## Warning: package 'ggcorrplot' was built under R version 4.2.2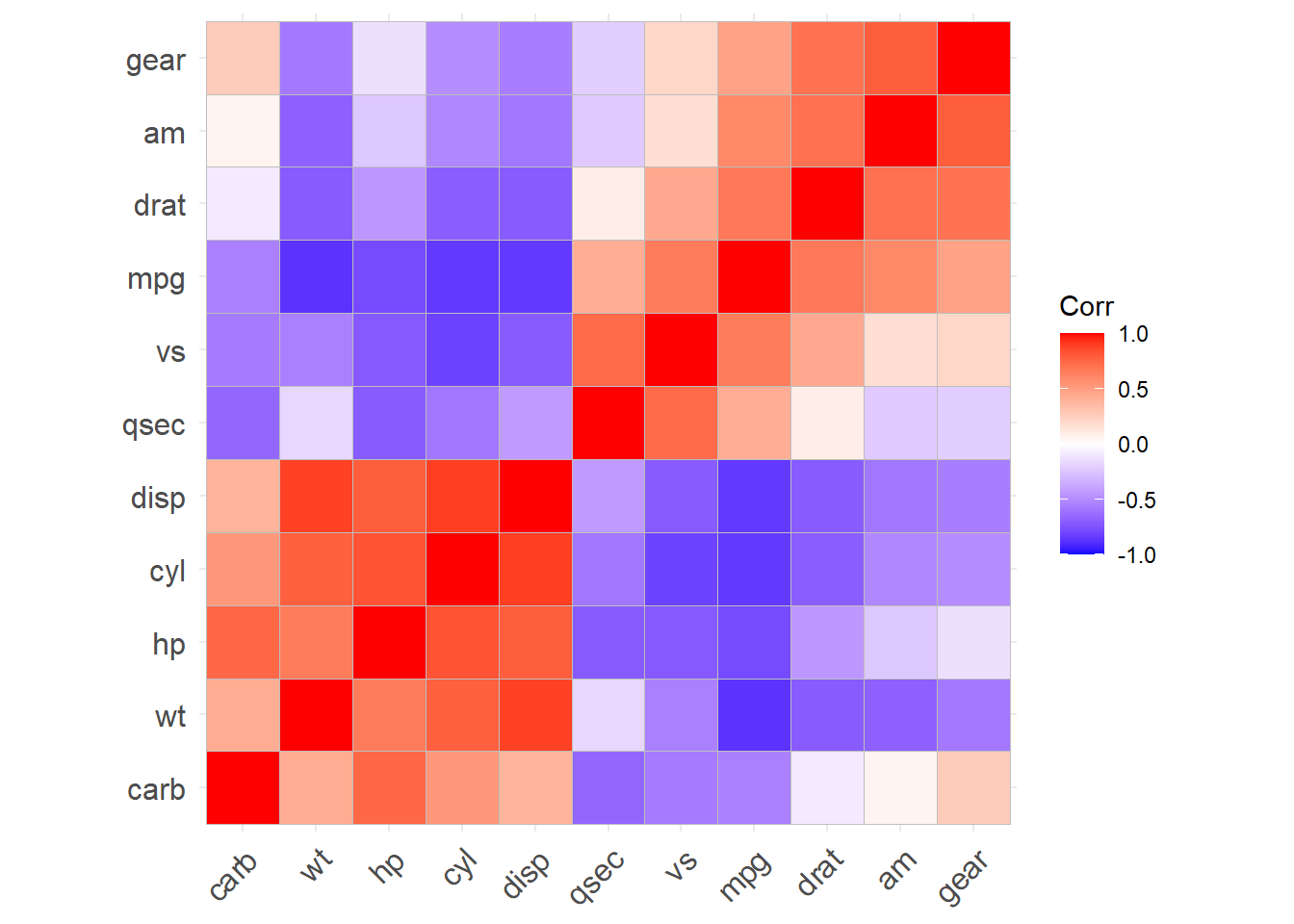

data(mtcars)
ggcorrplot(cor(mtcars),
  hc.order=TRUE)

其中hc.order=TRUE对变量进行聚类， 使得正相关的变量排列在相邻位置。 可以用lab选项标出数值， 用cor_pmat()函数计算每个相关系数p值， 在ggcorrplot()中用选项p.mat输入p值矩阵后可以标出不显著的相关系数。 如：

ggcorrplot(cor(mtcars),
  hc.order=TRUE,
  lab = TRUE)

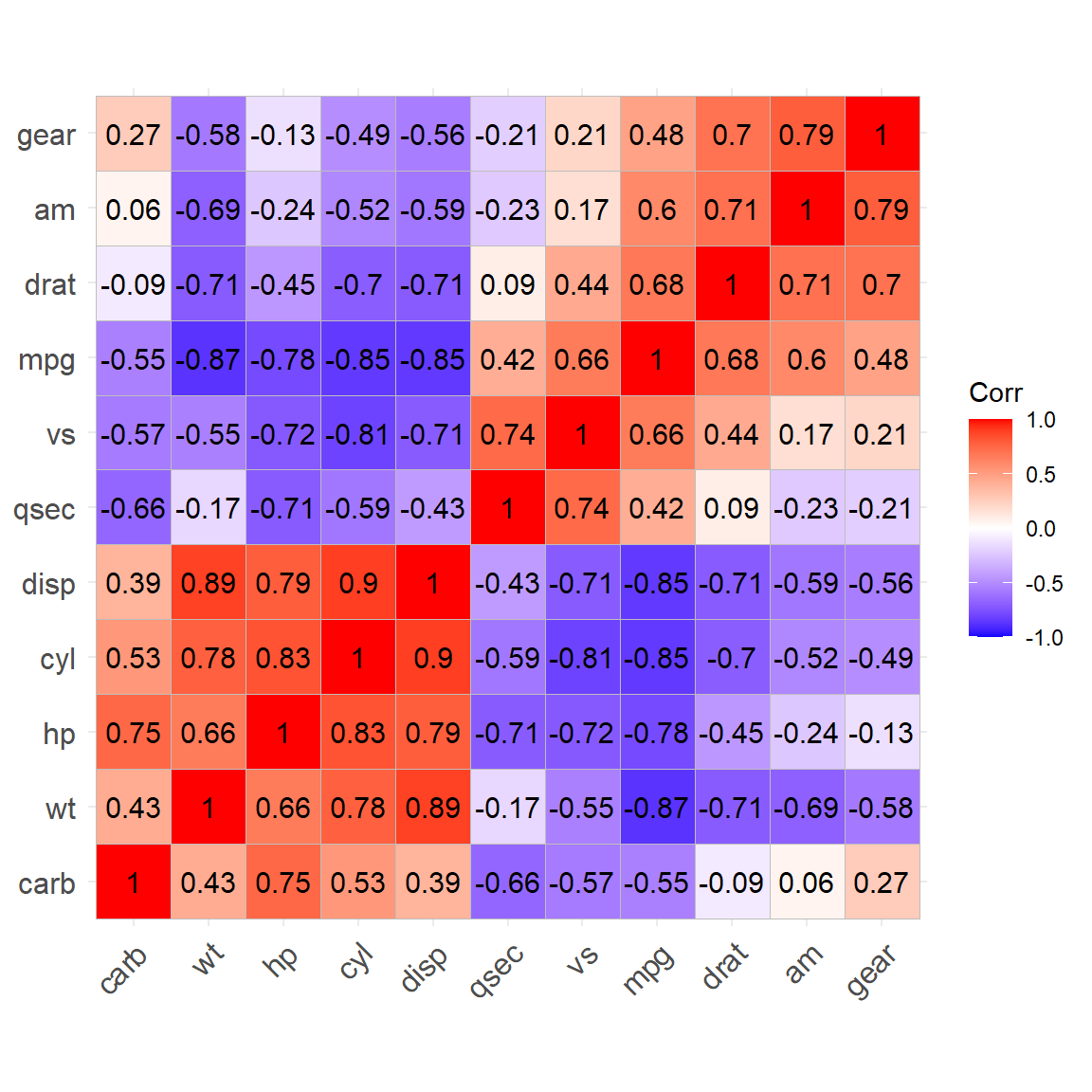
corrgram包的corrgram()函数可以将相关系数阵用图形表示， 系数绝对值大小用色块颜色深浅表示， 正负用两种颜色区分。

例如， 计算iris数据框中四个测量值的相关系数并用矩阵表示：

library(corrgram)
R.iris <- cor(iris[,1:4])
print(round(R.iris, 2))

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length         1.00       -0.12         0.87        0.82
## Sepal.Width         -0.12        1.00        -0.43       -0.37
## Petal.Length         0.87       -0.43         1.00        0.96
## Petal.Width          0.82       -0.37         0.96        1.00

corrgram(
  R.iris, order=TRUE, 
  lower.panel=panel.shade,
  upper.panel = panel.pie,
  text.panel = panel.txt)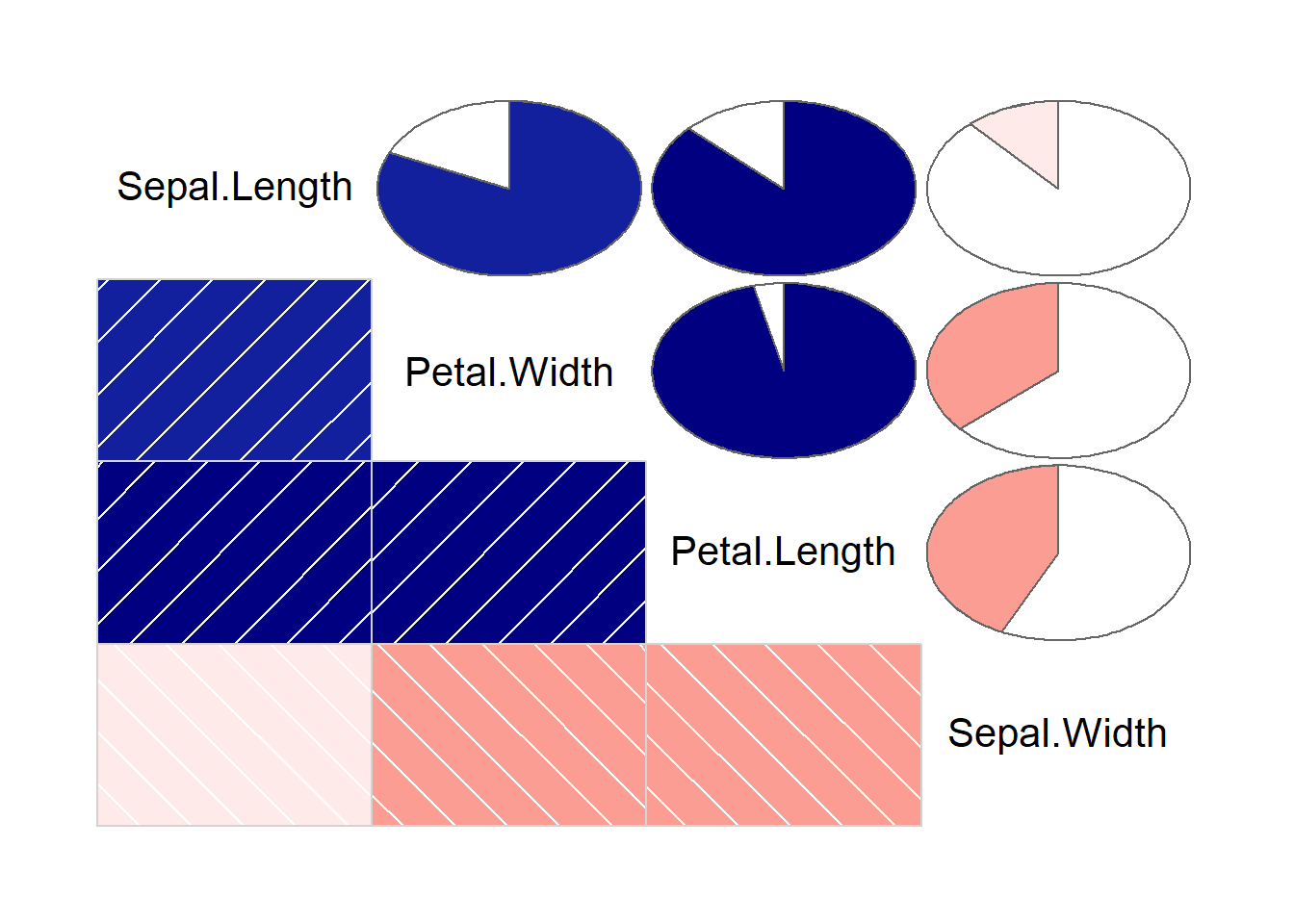

2.5.3 协同图

协同图(coplot)画出在变量\(z\)的值变化时， 另外两个变量\(x\)和\(y\)的变化情况。 更强大的软件提供了brushing技术可以动态地变化一个或两个变量的值， 同时观察另外的变量的变化情况。

2.5.3.1 地震数据的协同图

下图对quakes地震数据，在不同深度查看震中位置分布：

coplot(lat ~ long | depth, data = quakes)

#locator(1)

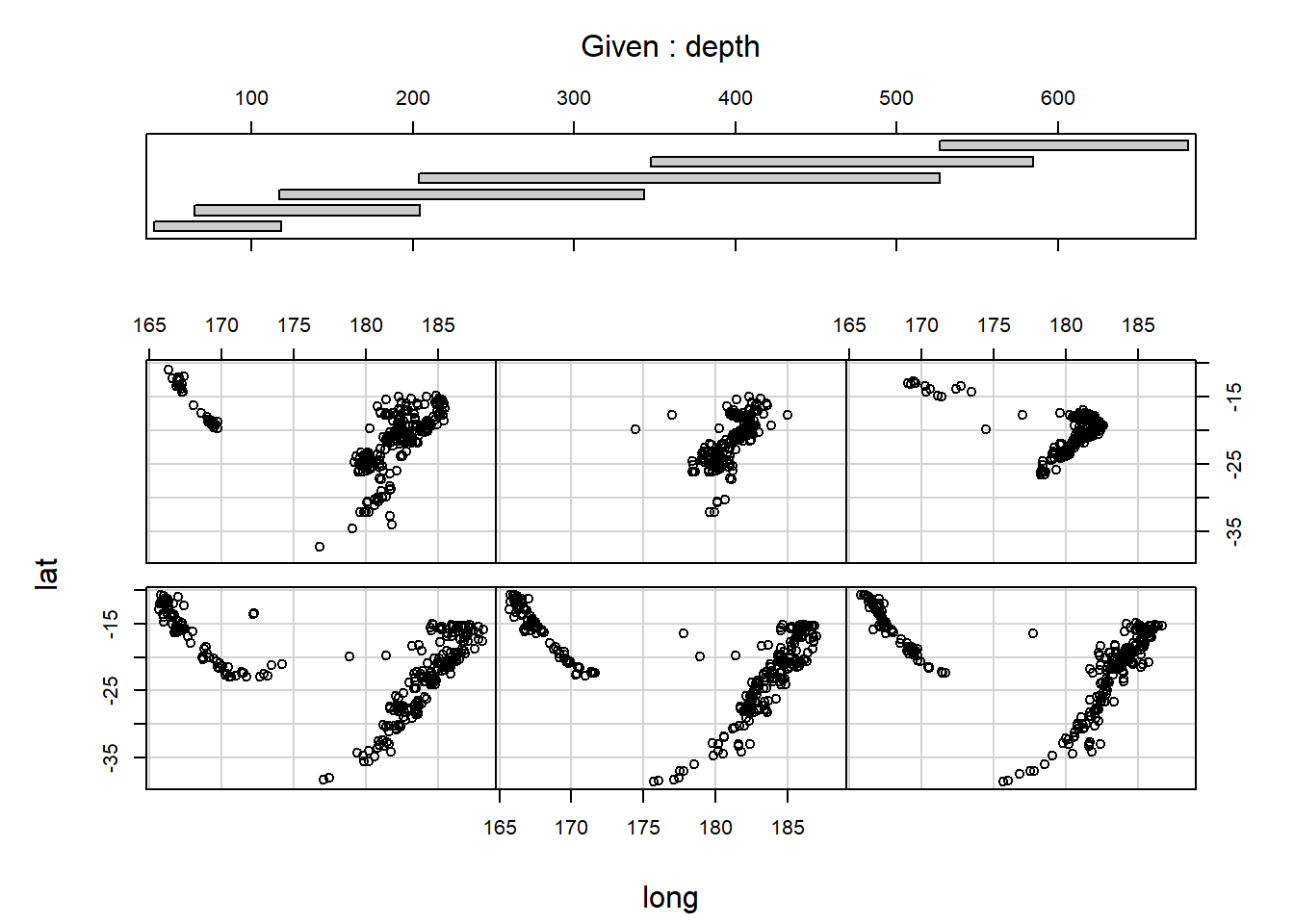
用co.intervals()对\(z\)变量人为地分段。 co.intervals()用来把第一参数取值范围分割为带有重叠的区间， number为区间个数， overlap()为重叠比例， 结果是每行为一段的两个区间端点的矩阵。

given.depth <- co.intervals(
  quakes$depth, number = 4, 
  overlap = .1)
coplot(lat ~ long | depth, data = quakes, 
  given.v = given.depth, rows = 1)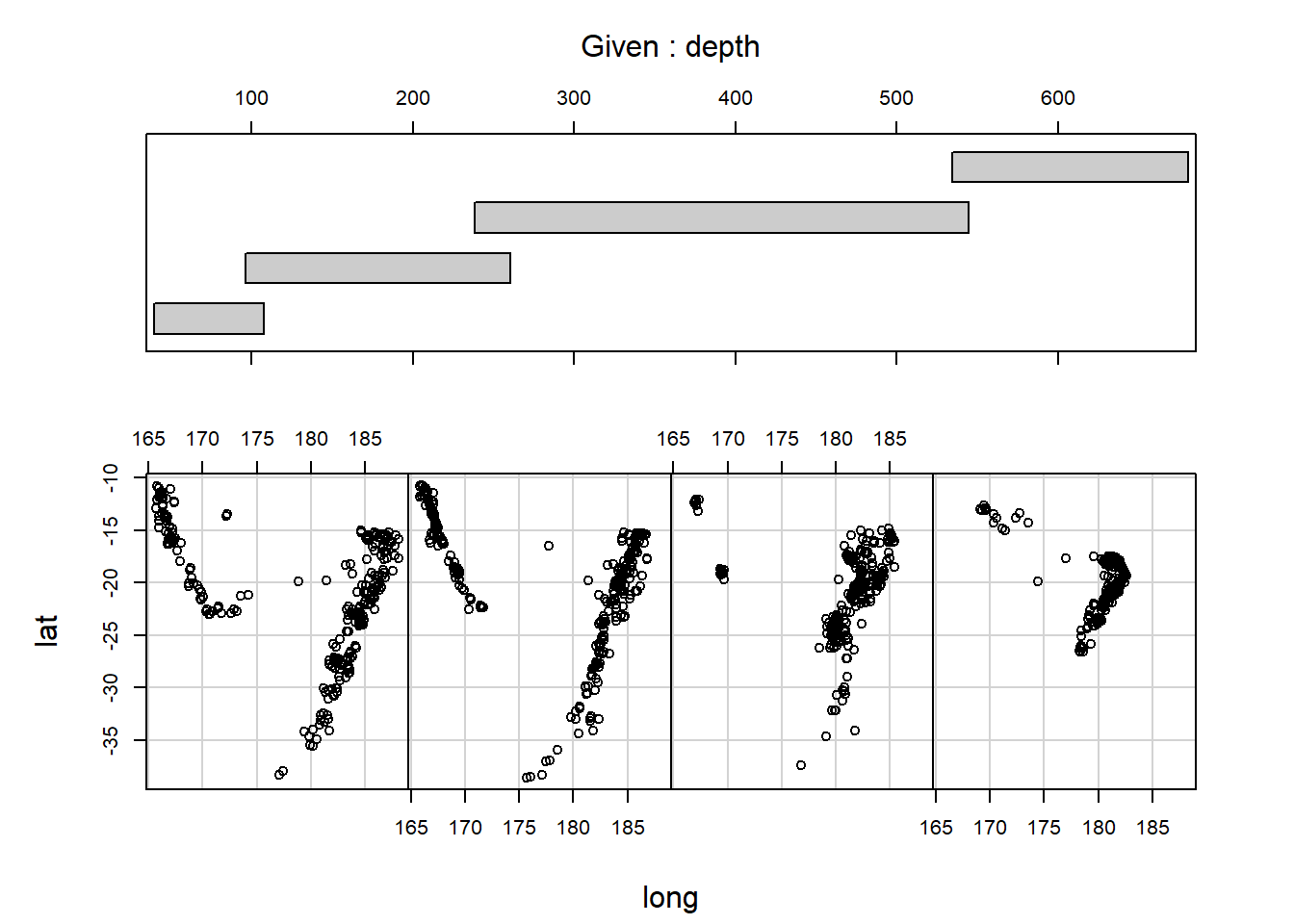

2.5.3.2 肺癌病人数据的协同图

cancer <- read_csv(
  "data/cancer.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)

cancer数据框保存了34个肺癌病人放疗前后的数据。 变量包括：

• id: 编号
• age: 年龄
• sex: F, M性别
• type: 腺癌，鳞癌类型
• v0, v1: 放疗前和放疗后体积（立方厘米）

下面用协同图固定病理类型后考察体积关系：

coplot(v1 ~ v0 | type, data=cancer)

用ggplot2实现， 将某个分类变量的不同值分配到不同的小图(facet)：

ggplot(cancer, aes(
  x = v0, y = v1)) +
  geom_point() +
  facet_wrap(~ type)

固定性别后考察体积关系:

coplot(v1 ~ v0 | sex, data=cancer,
  panel=panel.smooth)

或：

ggplot(cancer, aes(
  x = v0, y = v1)) +
  geom_point() +
  facet_wrap(~ sex)

2.5.4 星图与雷达图

设数据集有\(p\)个数值型变量， 星图把圆面平分为角度相等的\(p\)个扇形， 然后用半径大小表示每个变量的大小。 雷达图把圆面评分为角度相等的\(p\)个扇形， 然后用\(p\)个半径线段的长度表示每个变量的大小， 并将相邻的半径端点相连。 graphics扩展包的stars()函数作星图与雷达图， 对各变量自动标准化到\([0,1]\)范围。

这样的图形在观测较多时需要较大的绘图区域， 最好绘制到图形文件中。

state.x77数据是美国50个州在1970年代的基本情况数据。 变量包括:

• Population: 人口
• Illiteracy: 文盲比例
• Life Exp: 期望寿命
• Murder: 每十万人杀人犯罪数
• HS Grad: 高中毕业生比例
• Frost: 日最低温度在结霜点以下平均天数
• Area: 面积，平方英里

在下面的程序中， 将数据按照人口数由高到低排序， 并将变量次序调整为人口、面积、期望寿命、高中毕业生比例、收入， 然后是文盲比例、杀人犯罪率、结霜天数。 将图形制作为pdf图形而不是在屏幕上绘制， 这样的好处是pdf图形可以任意放大。 graphics::stars()的draw.segments=TRUE选项作星图。 选项len=给出每个星图的大小倍数， 这里略缩小了一些以避免图形与标签重叠。 选项cex=给出标签的大小倍数，这里缩小了一些。 选项nrow=和ncol=指定各个观测对应的星图的排列行、列数。 为了绘制图例，需要用key.loc=指定图例的坐标位置， 这里的坐标按照每个星图宽度约等于2，高度大于2计算， 并使用ylim选项把坐标区域向下延伸了一些以容纳图例。 程序中key.loc=c(12,1)使得图例大约在星图矩阵的右下角位置。 用col.segments选项指定各个变量对应的扇形的颜色。 可以用select.colors()函数选择颜色。

pdf("美国50州星图.pdf", width=5, height=7)
cols <- c("blue1", "chocolate1", "deepskyblue",
          "green", "thistle1", 
          "grey25", "lightsteelblue4", "salmon4")
vars <- c("Population", "Area",
          "Life Exp", "HS Grad", "Income",
          "Illiteracy", "Murder", "Frost")
d <- state.x77[order(-state.x77[["Population"]]), vars]
graphics::stars(d, draw.segments=TRUE,
      nrow=9, ncol=6,
      ylim=c(-1, 21),
      len=0.9,  cex=0.6,
      col.segments = cols,
      key.loc=c(12,1)
      )
dev.off()

图2.1: 美国50个州的星图

在结果图中，浅蓝、绿色、浅粉越大越好，暗色越大越差。 其中表现好的州有Wisconsin, Minnesota, Washington, Connecticut, Iowa, Oregon, Kansas, Nebraska, Uta, 表现差的州有Louisiana, Alabama, South Caralina, Mississipi.

在graphics::stars()函数中指定segments=FALSE则作雷达图。如

pdf("美国50州雷达图.pdf", width=5, height=7)
vars <- c("Population", "Area",
          "Life Exp", "HS Grad", "Income",
          "Illiteracy", "Murder", "Frost")
d <- state.x77[order(-state.x77[["Population"]]), vars]
graphics::stars(d, draw.segments=FALSE,
      nrow=9, ncol=6,
      ylim=c(-1, 21),
      len=0.9,  cex=0.6,
      key.loc=c(12,1)
      )
dev.off()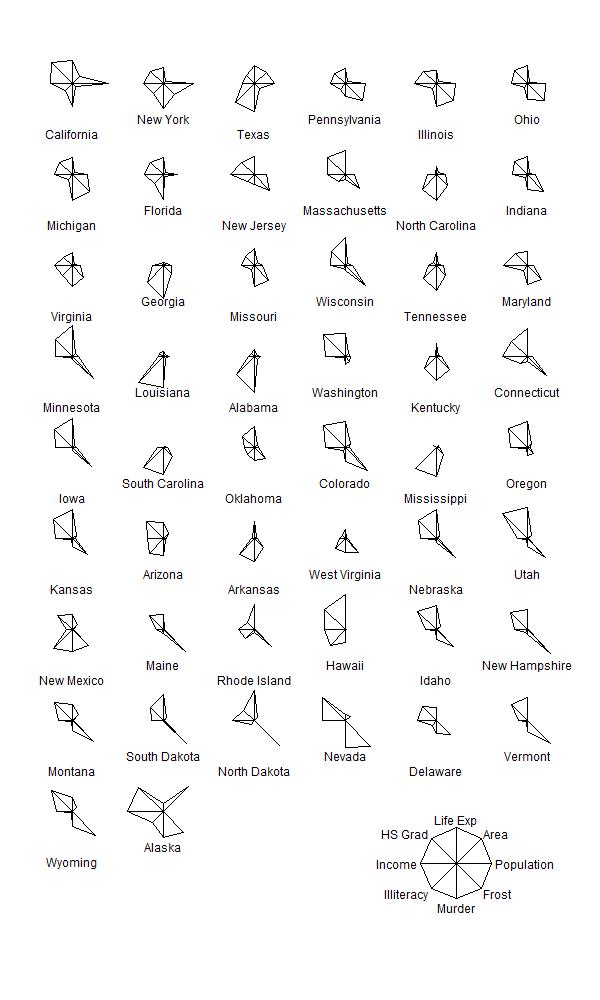

图2.2: 美国50个州的雷达图

2.5.5 脸谱图

脸谱图(Chernoff-Flury faces)每个观测画一张人脸, 用人脸五官、头发、颜色表示不同的数值型变量的值。 观测数不能太多。

R中aplpack::faces()函数作这种图形。 脸谱图结果依赖于输入数据框的各列的次序。

输入数据的各列分别表现在:

1. 脸高度
2. 脸宽度
3. 脸型
4. 嘴高度
5. 嘴宽度
6. 微笑形状
7. 眼睛高度
8. 眼睛宽度
9. 头发高度
10. 头发宽度
11. 头发发型
12. 鼻子高度
13. 鼻子宽度
14. 耳朵宽度
15. 耳朵高度

各部分颜色由部分变量均值决定:

• 7,8变量平均决定瞳仁颜色
• 1,2,3变量平均决定嘴唇颜色
• 14,15变量平均决定耳朵颜色
• 12,13变量平均决定鼻子颜色
• 9,10,11变量平均决定头发颜色
• 1,2变量平均决定脸色。

美国50个州的数据的脸谱图：

library(aplpack)
pdf("美国50州脸谱图.pdf", width=10, height=15)

## 把州按人口数降序排列
d <- state.x77[order(-state.x77[,"Population"]),
               c("Population", "Area",
                 "Life Exp", "HS Grad", "Income",
                 "Illiteracy", "Murder",
                 "Frost"
                 )
               ]
faces(d, nrow.plot=9, ncol.plot=6)
dev.off()

图2.3: 美国50个州的脸谱图

2.5.6 Andrew曲线

对每个多元观测，把观测的各个分量的值当作一个傅立叶级数的系数。 各列一般应归一化到\([0,1]\)之间。 设第\(i\)个观测的各个分量为 \((X_{i,1}, X_{i,2}, \dots, X_{i,p})\)， 定义对应于第\(i\)个观测的傅立叶级数函数为 \[\begin{aligned} f_i(t) =& \begin{cases} X_{i,1} \frac{\sqrt{2}}{2} + X_{i,2} \sin(t) + X_{i,3} \cos(t) \\ \quad + \dots + X_{i,p-1} \sin(\frac{p-1}{2} t) + X_{i,p} \cos(\frac{p-1}{2} t), & \text{当}p\text{为奇数} \\ X_{i,1} \frac{\sqrt{2}}{2} + X_{i,2} \sin(t) + X_{i,3} \cos(t) \\ \quad + \dots + X_{i,p} \sin(\frac{p}{2} t), & \text{当}p\text{为偶数} \end{cases} \end{aligned}\]

R函数tourr::andrews()可以从一行的观测生成对应的傅立叶级数函数。

Andrew曲线的形状与分量的次序有关， 可以将变量用主成分方法降维， 再作Andrew曲线。 另外，观测太多时会比较杂乱， 所以观测数在20个之内为宜。

下面取瑞士银行真钞、假钞数据各5例，作Andrew曲线：

f <- function(){
  x = as.matrix(bankNotes[96:105, 1:6])
  y = scale01(x)
  
  grid = seq(0, 2 * pi, length = 1000)
  
  plot(grid, tourr::andrews(y[1, ])(grid),
    type = "l", lwd = 1.5,
    main = "Andrews curves (Bank data)", 
    ylim = c(-0.3, 0.5), ylab = "", xlab = "")
  for (i in 2:5){
    lines(grid, tourr::andrews(y[i, ])(grid),
      col = "black", lwd = 1.5)
  }
  
  for (i in 6:10){
    lines(grid, tourr::andrews(y[i, ])(grid),
      col = "red3", lwd = 1.5, lty = "dotted")
  }
  legend("topright",
    lty=c(1,3), 
    col=c("black", "red3"),
    legend=c("Genuine", "Counterfeit"))
}
f()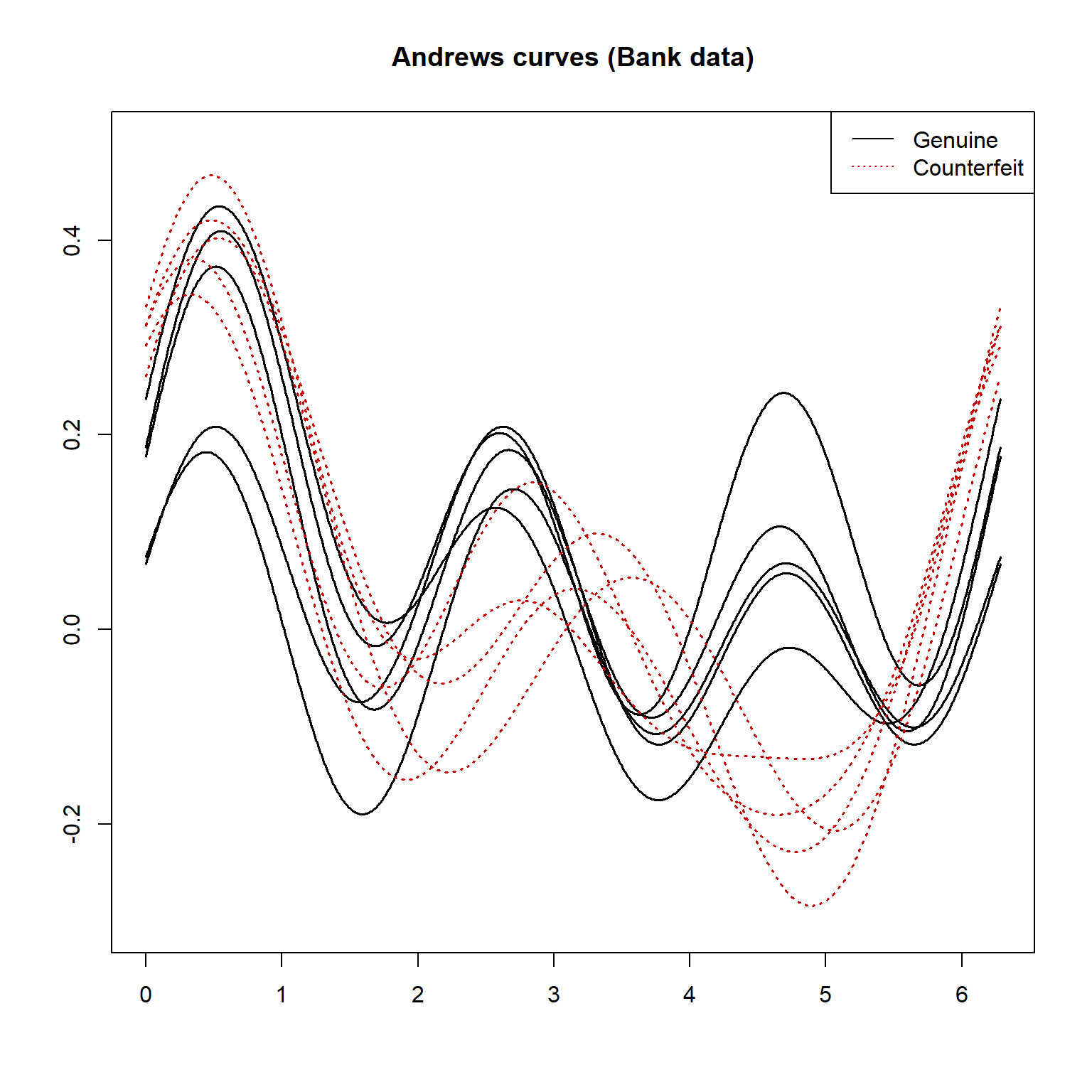

其中自定义函数scale01()将输入的数据框或矩阵的每列标准化到\([0,1]\)范围。

所有的100真钞与100 假钞都画Andrew曲线的效果：

f <- function(){
  x <- as.matrix(bankNotes[, 1:6])
  y <- scale01(x)
  
  grid = seq(0, 2 * pi, length = 1000)
  
  plot(grid, tourr::andrews(y[1, ])(grid),
       type = "l", lwd = 1.5,
       main = "Andrews curves (Bank data)", 
       ylim = c(-0.3, 0.5), ylab = "", xlab = "")
  for (i in 2:100){
      lines(grid, tourr::andrews(y[i, ])(grid),
            col = "black", lwd = 1.5)
  }
  
  for (i in 101:200){
      lines(grid, tourr::andrews(y[i, ])(grid),
            col = "red3", lwd = 1.5, lty = "dotted")
  }
  legend("topright",
         lty=c(1,3), 
         col=c("black", "red3"),
         legend=c("Genuine", "Counterfeit"))
}
f()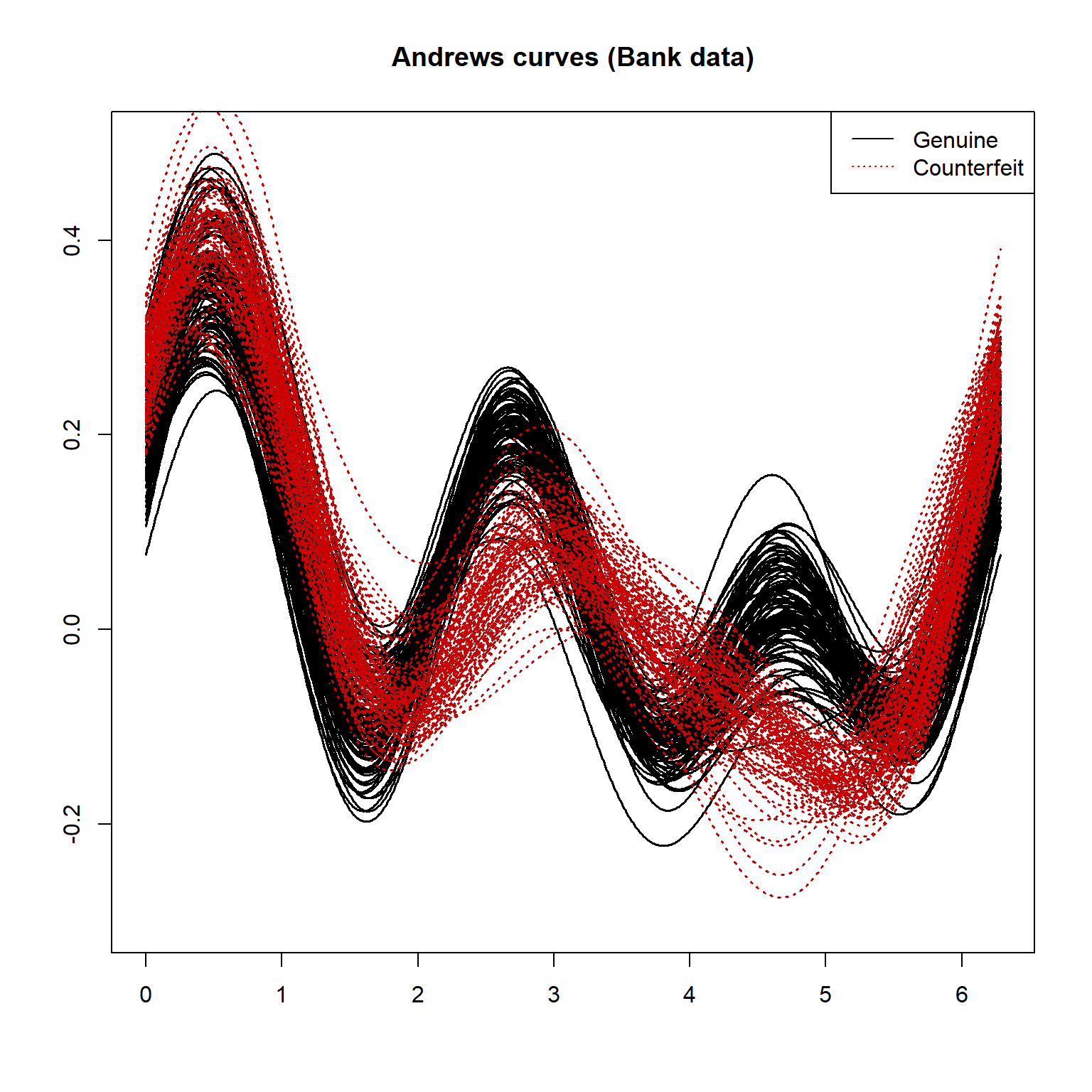

2.5.7 平行坐标(parallel coordinates, parallel axes)图

平行坐标图作多条平行的纵轴， 然后将每个观测的各个变量值在各个纵轴上找到， 将同一观测的两个相邻纵轴的位置用线段相连。

横坐标是不同的变量， 纵坐标是这些变量的值， 每个观测对应的点用折线连接。

不需要标准化变量，但是经常用对数值。

相当于画了多个纵坐标轴，每列对应一个纵坐标轴， 每个观测的各个分量在不同的纵轴上绘点并连接同一观测的相邻点。

使用R函数MASS::parcoord()或GGally包的ggparcoord()。

这种图形的形状与分量的次序有关。

两个变量\(x, y\)之间的连线， 平行的线提示正相关。 这是因为平行则较大的\(x\)对应较大的\(y\)， 较小的\(x\)对应较小的\(y\)。

两个变量\(x, y\)之间的连线， 在中间交叉的线提示负相关。 这是因为交叉则较大的\(x\)对应较小的\(y\)， 较小的\(x\)对应较大的\(y\)。

某个变量也可以是分类的，这时在这个纵轴的几个点上交叉。

用不同颜色来区分观测分组，可以发现不同组的规律。

观测太多时会比较杂乱。

如果在某个中间的纵轴上交叉， 则交叉线的后续走向无法分辨。 可以适当调整输入数据框的变量次序， 或者用三次样条插值而不是折线。

下面用ggparcoord()函数制作鸢尾花数据的平行坐标图：

data(iris)
library(GGally)
ggparcoord(
  data = iris,
  columns=1:4,
  scale = "uniminmax",
  groupColumn="Species")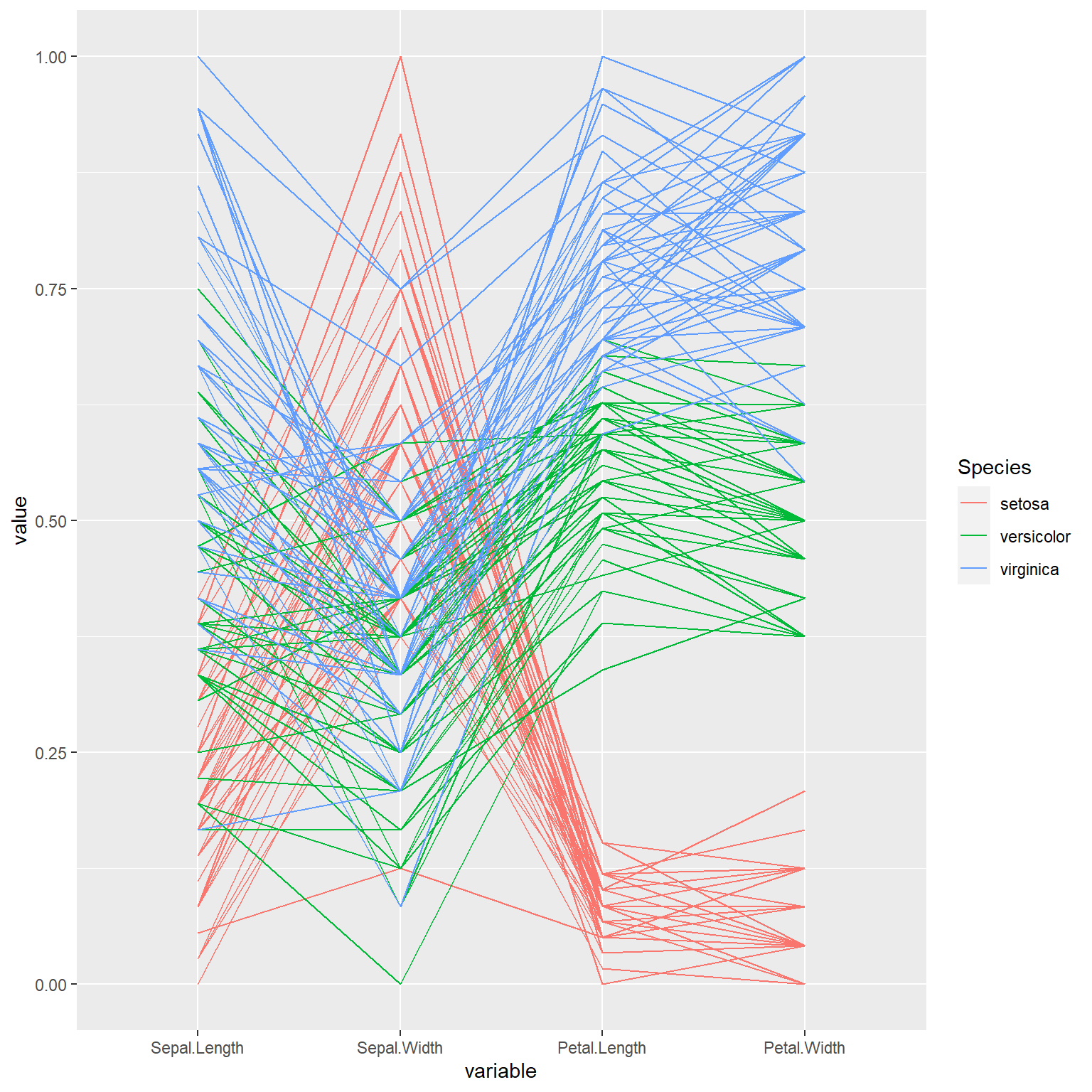

其中对每个变量单独进行了0-1标准化线性变换。 这种图中平行的连线代表了正向的线性相关， 交叉连线代表了反向的线性相关。 如果不区分数据中的三个子类别， 则花萼长度和宽度存在负相关， 花瓣长度和花萼宽度存在负相关。 如果仅看一种颜色， 则线段基本是同向的。

下面适当调整四个数值变量次序， 使得交叉更少而且三个组的区分更清晰：

data(iris)
library(GGally)
ggparcoord(
  data = iris,
  columns=1:4,
  order=c(3,4,1,2),
  scale = "uniminmax",
  groupColumn="Species")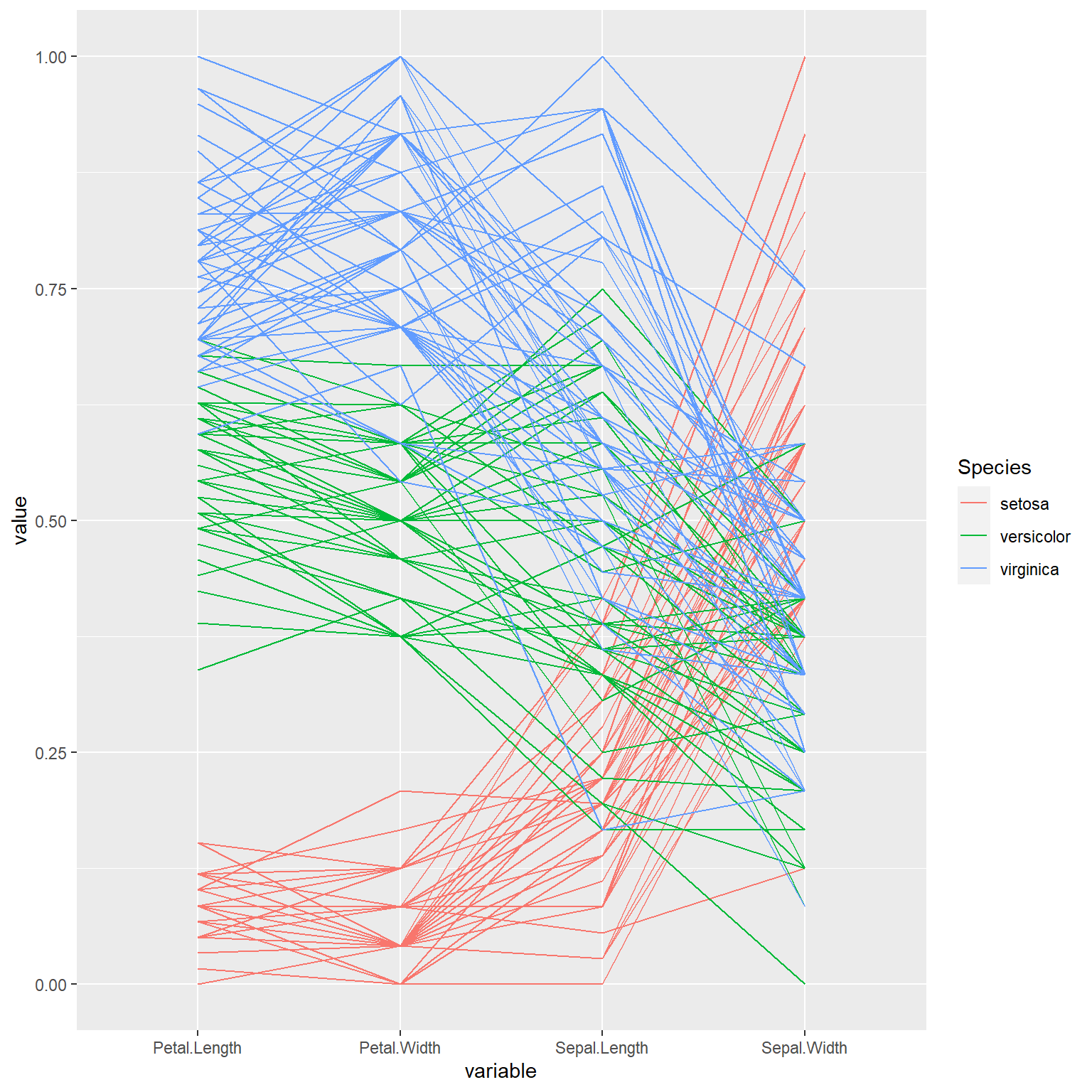

下面的程序用MASS::parcoord()制作平行坐标图， 对数值型数据进行了对数变换， 对数变换起到了一定的标准化作用。 平行线意味着正相关， 相交线意味着负相关。

cmap <- c(
  "setosa"="red", 
  "versicolor"="green", 
  "virginica"="blue")
d <- log(as.matrix(iris[,1:4]))
vars <- c("Petal.Length", "Petal.Width", 
          "Sepal.Length", "Sepal.Width")
MASS::parcoord(d[, vars], col=cmap[iris$Species])
legend(1.05, 0.62, lty=1,
       col=cmap, legend=names(cmap))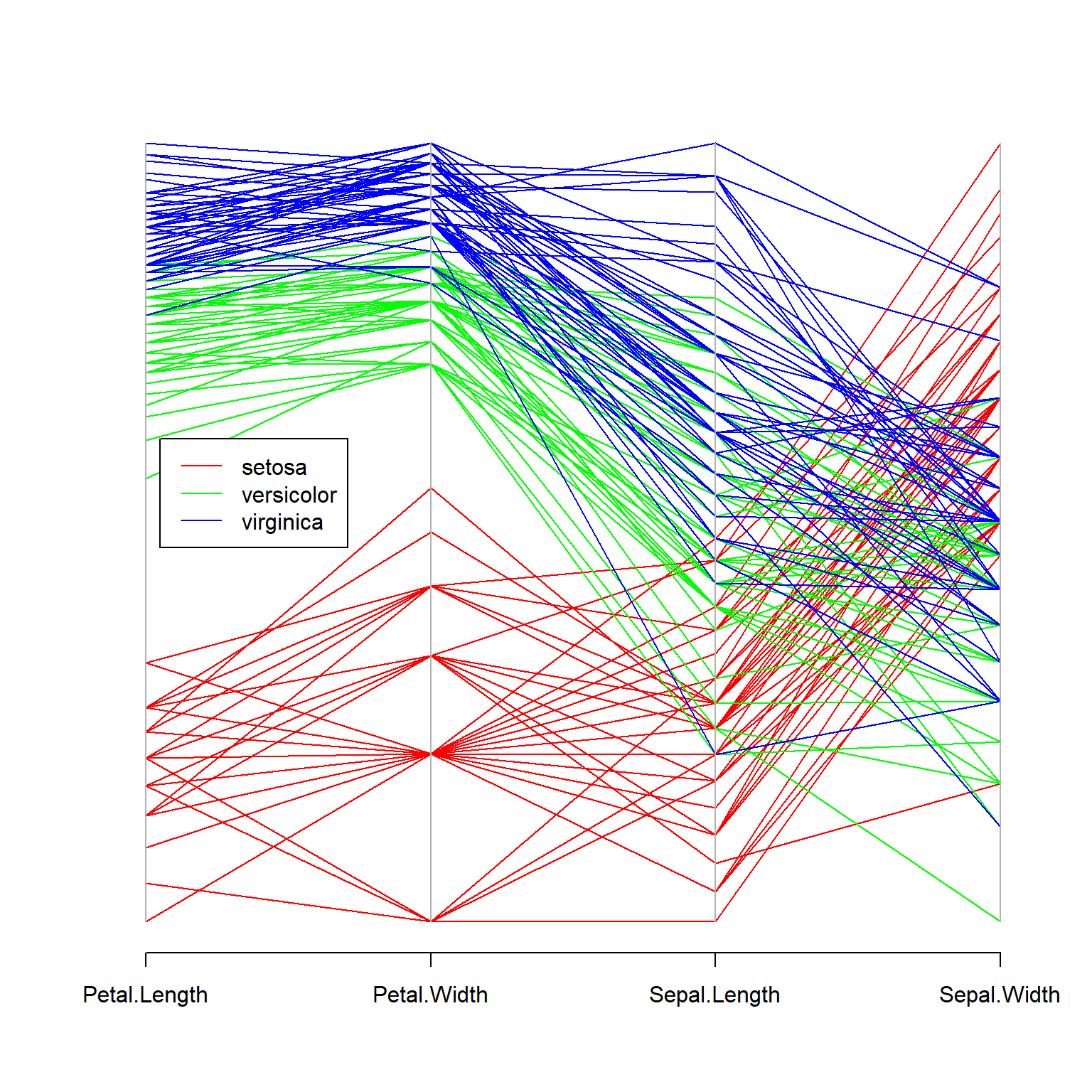

对瑞士银行真钞、假钞各5例的平行坐标图：

d <- bankNotes[96:105, ]
ggparcoord(
  data = d,
  columns = 1:6,
  order = c(6, 1, 2,3,4,5),
  scale = "uniminmax",
  groupColumn="genuine")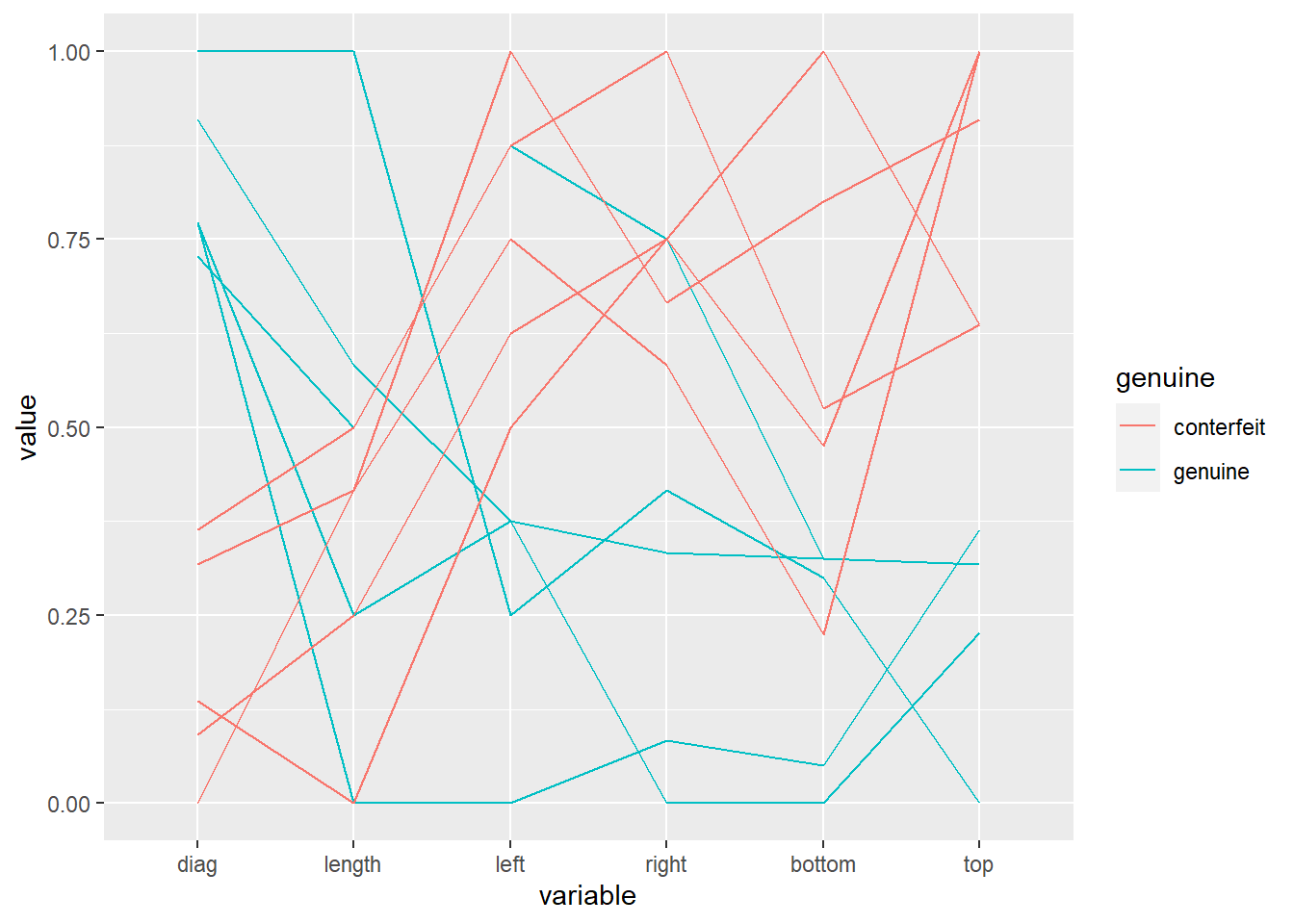

或：

x = as.matrix(bankNotes[96:105,1:6])
MASS::parcoord(log(x), lwd =2, 
  col = c(rep("black", 5), rep("red",5)),
  lty=c(rep(1,5), rep(2,5)), 
  main="Parallel coordinates plot (Bank data)")
axis(side=2, at=seq(0, 1, 0.2),
  labels=seq(0,1,0.2))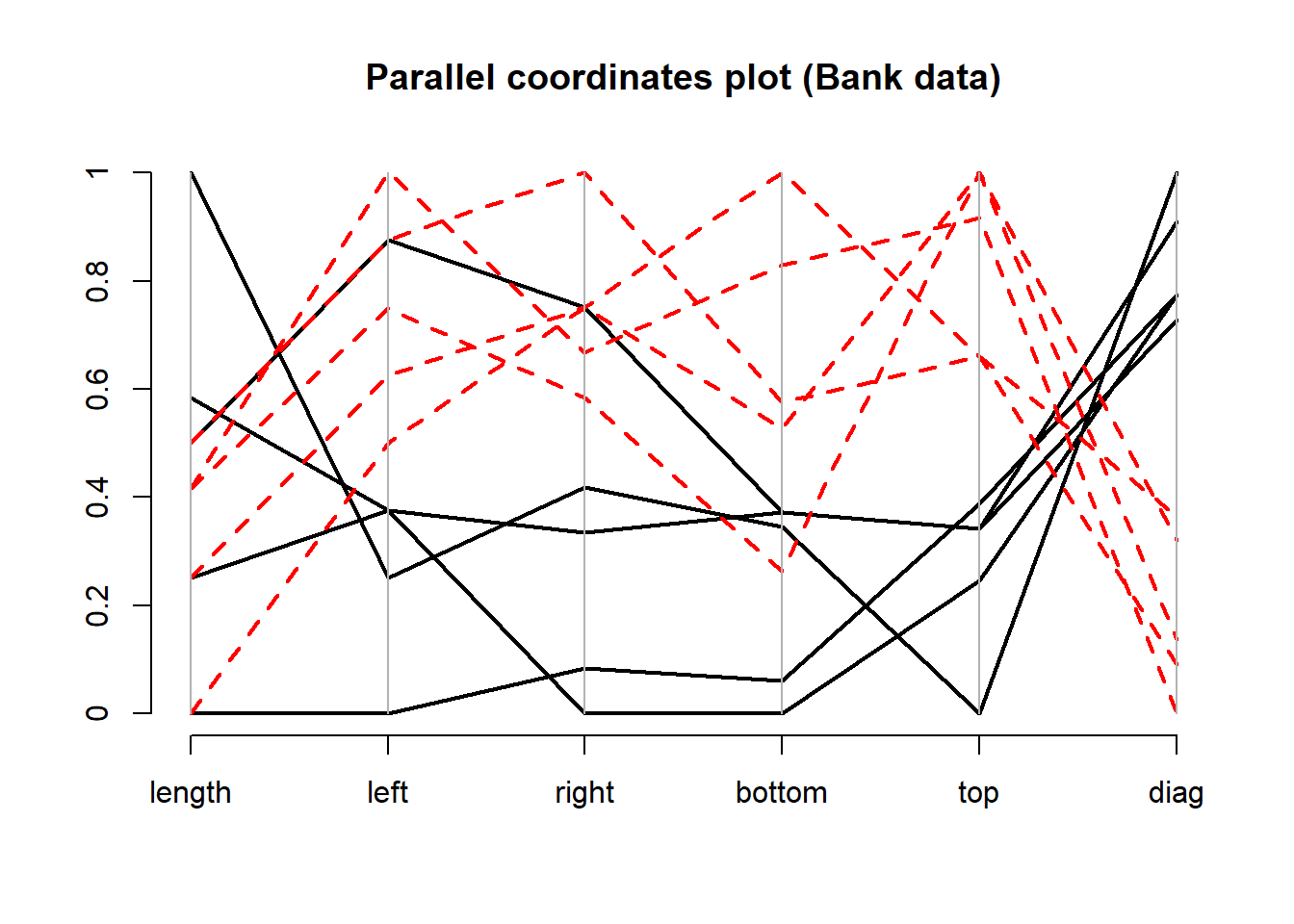

数据框carOil中包含了74辆汽车的数据。 车重与排量的平行坐标图：

x = as.matrix(carOil[,c("Weight", "Displace")])
MASS::parcoord(log(x), lwd = 1, 
  main="Parallel coordinates plot (Car Data)")
axis(side=2, at=seq(0, 1, 0.2),
  labels=seq(0,1,0.2))

基本平行，表现出正相关。

汽车油耗数据中mileage是每加仑汽油形式英里数， 是油耗性能的度量。 油耗性能与车重呈现负相关：

x = as.matrix(carOil[,c("Mileage", "Weight")])
MASS::parcoord(log(x), lwd = 1, 
  main="Parallel coordinates plot (Car Data)")
axis(side=2, at=seq(0, 1, 0.2),
  labels=seq(0,1,0.2))

油耗数据中， 排量(Displace)、高挡位齿轮比(Gear)、厂商总部所在国(Company)的平行坐标图：

d <- carOil
d$Company <- as.numeric(d$Company)
x = as.matrix(d[,c("Displace", "Gear", "Company")])
MASS::parcoord(log(x), lwd = 1, 
  main="Parallel coordinates plot (Car Data)")
axis(side=2, at=seq(0, 1, 0.2),
  labels=seq(0,1,0.2))

排量与齿轮比负相关，Company只有三种值，分别代表美国、日本、欧洲。

汽车油耗数据中头顶空间、后排座椅空间、行李箱大小的平行坐标图：

x = as.matrix(carOil[,c("Headroom", "Rear", "Trunk")])
MASS::parcoord(log(x), lwd = 1, var.label=TRUE,
  main="Parallel coordinates plot (Car Data)")
axis(side=2, at=seq(0, 1, 0.2),
  labels=seq(0,1,0.2))

基本平行，有两个离群值。 定位离群值:

cat("=== 离群值:\n")

## === 离群值:

sele <- log(x[,"Rear"]) < 2.93 | log(x[,"Rear"]) > 3.60
print(carOil[sele,])

##    Price Mileage R78 R77 Headroom Rear Trunk Weight Length Turn Displace Gear
## 3   3799      22 NaN NaN      3.0 18.5    12   2640    168   35      121 3.08
## 73  7140      23   4   3      2.5 37.5    12   2160    172   36       97 3.74
##    Company
## 3        1
## 73       3

对汽车油耗carOil数据所有13个变量作平行坐标图， 用不同颜色表示不同国家生产:

d <- carOil
d$Company <- as.numeric(d$Company)
x <- as.matrix(d)
comp <- x[,"Company"]

ltys <- c(1,3,2)
cols <- c("black", "green", "blue")
MASS::parcoord(log(x), lwd =1, 
  lty=ltys[comp], 
  col = cols[x[,"Company"] ], 
  main="Parallel Coordinates Plot (Car Data)")
axis(side=2, at=seq(0,1,0.2), labels=seq(0,1,0.2))
legend("bottom",
  c("US","Japan","Europe"),
  lty=ltys,
  col=cols,
  horiz = TRUE,
  cex =0.6)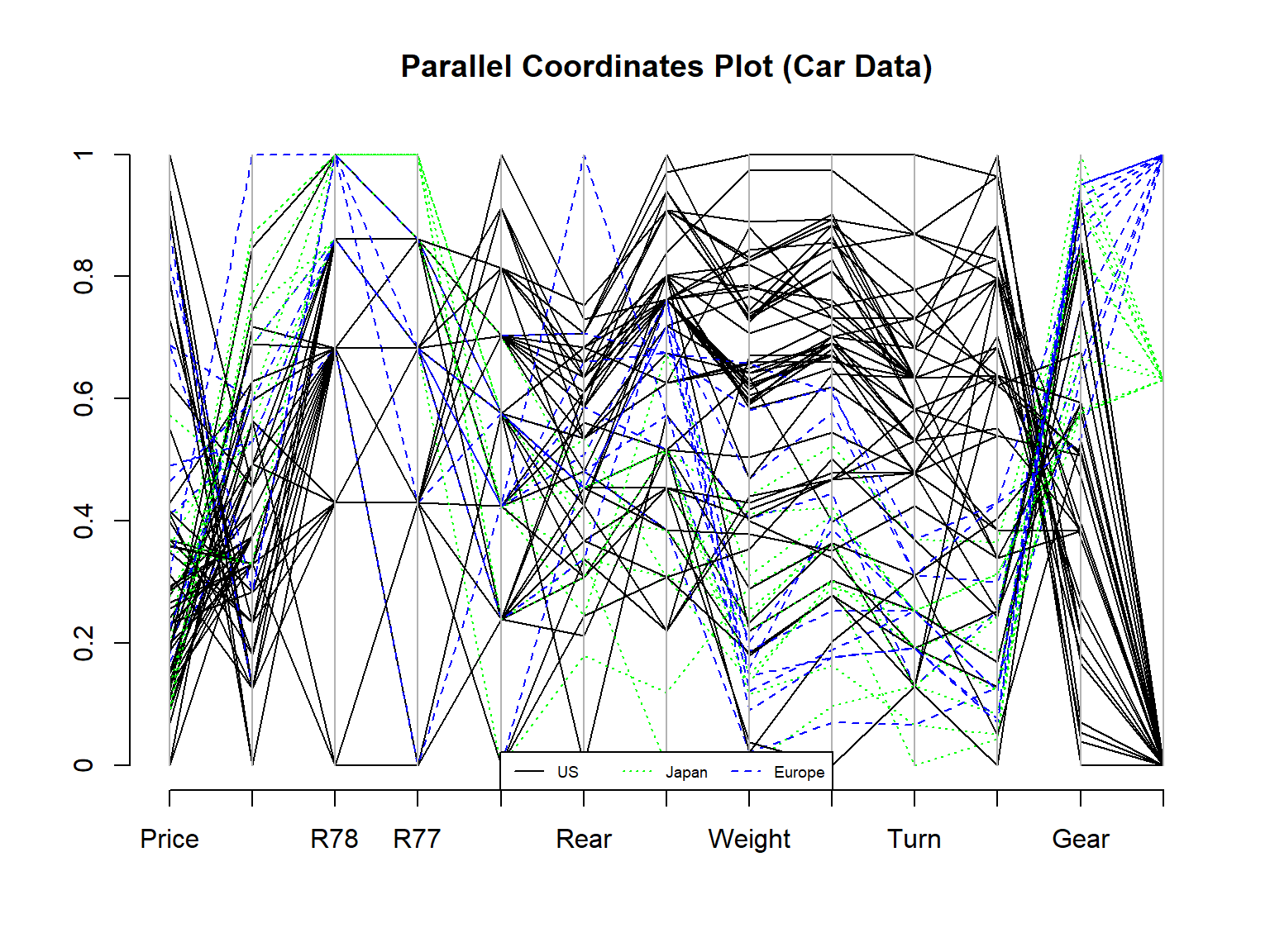

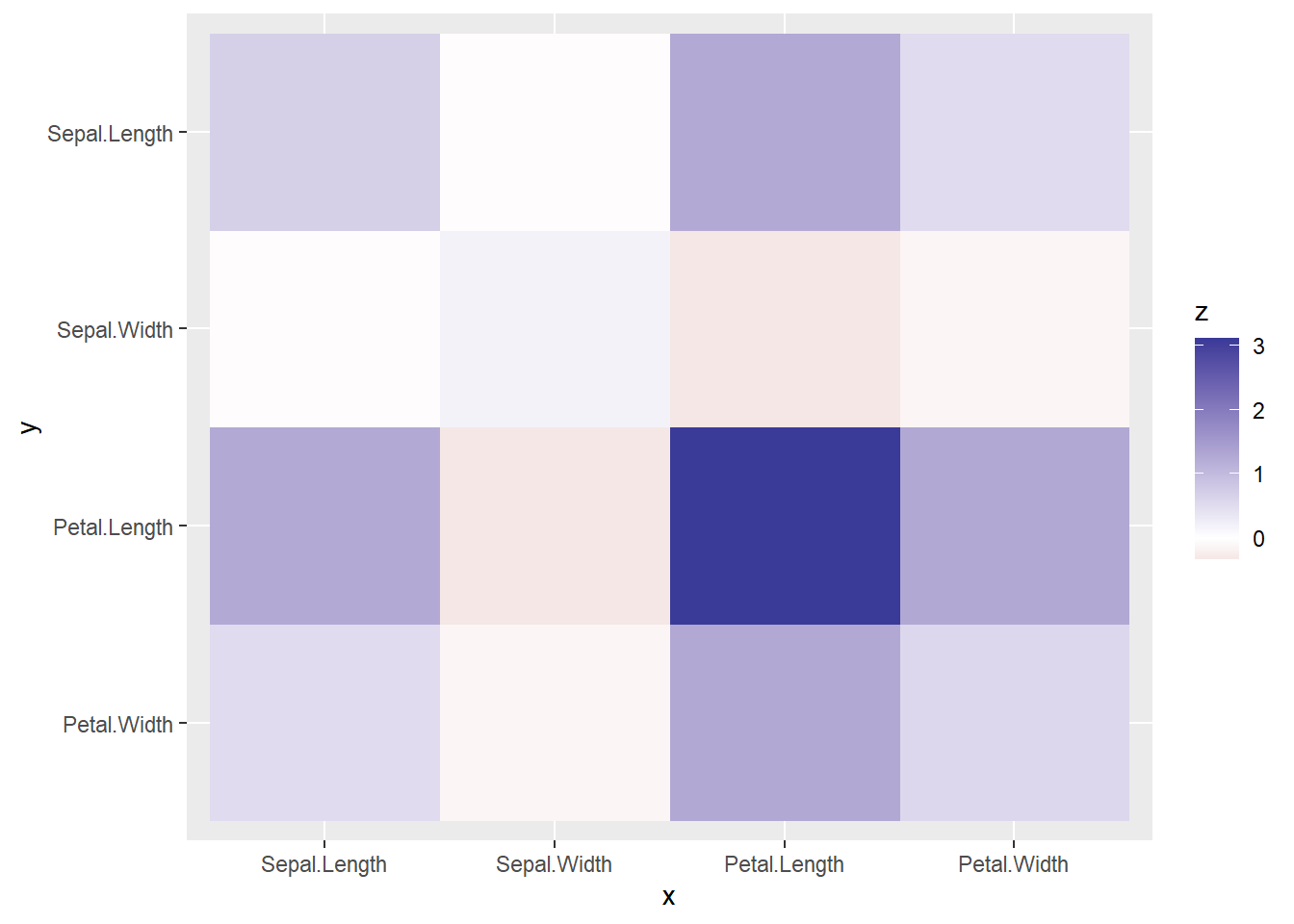
2.5.8 矩阵数据的图形

对于矩阵， 将其行号作为纵坐标\(y\)，列号作为横坐标\(x\)， 元素值作为\(z\)坐标， 可以看成是\(z = f(x,y)\)的数据， 可以用色块代表\(z\)的值， 色块位置代表\(x, y\)坐标。

例如，我们计算iris数据集中四个数值型列的协方差阵， 用色块图表示协方差阵：

dv <- as.data.frame(var(iris[,1:4]))
knitr::kable(dv, digits=2)

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
Sepal.Length	0.69	-0.04	1.27	0.52
Sepal.Width	-0.04	0.19	-0.33	-0.12
Petal.Length	1.27	-0.33	3.12	1.30
Petal.Width	0.52	-0.12	1.30	0.58

library(pheatmap)

pheatmap(dv)

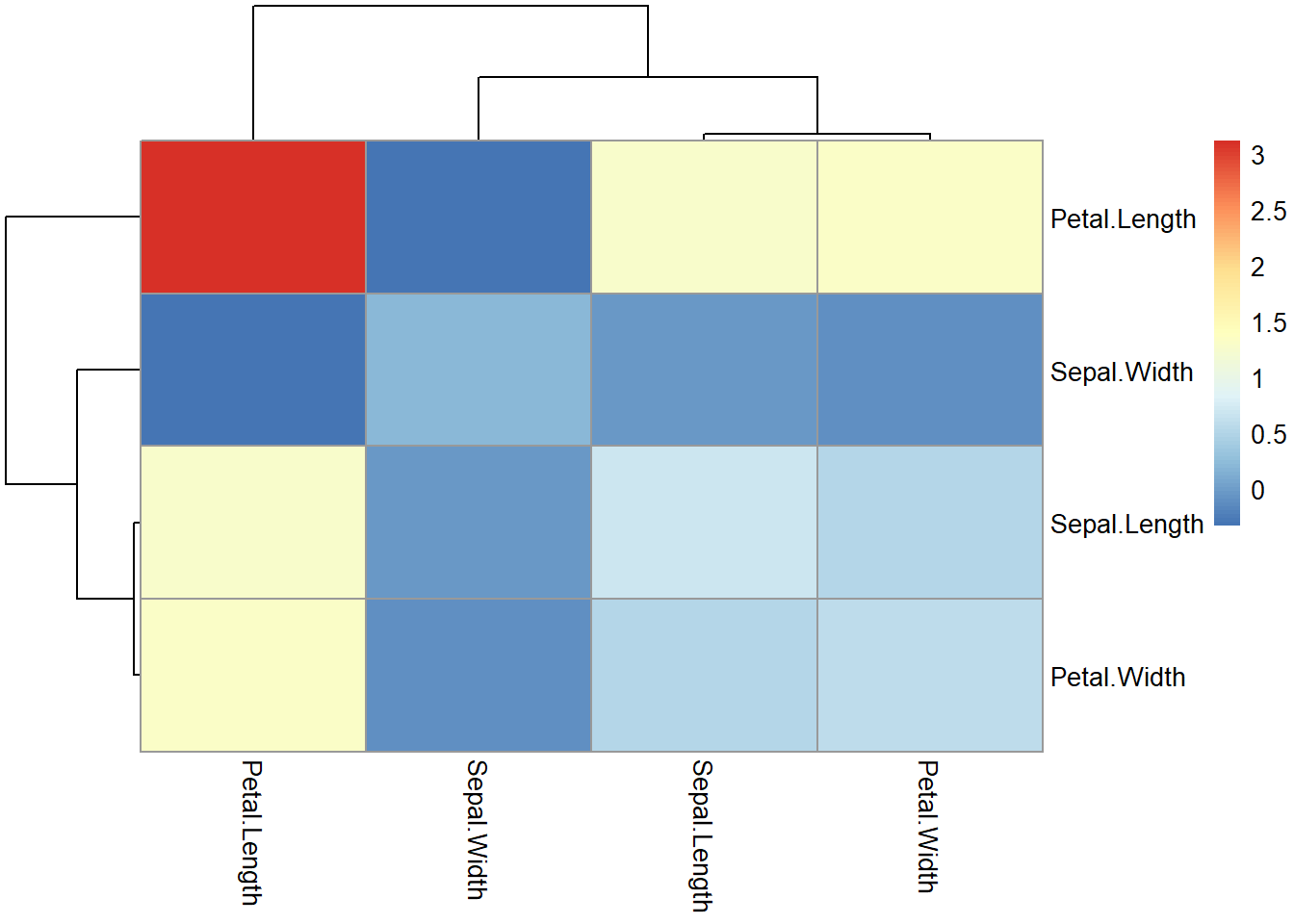
pheatmap()会自动对矩阵的各行、各列用谱系聚类法分类并作图表现出来。 这样的聚类对方差阵、相关系数阵意义不大。

也可以自己用ggplot2包绘图：

vn <- names(dv)
dvlong <- tibble(
  y = factor(rep(vn, 4), levels=rev(vn)),
  x = factor(rep(vn, each=4), levels=vn),
  z = c(as.matrix(dv)))
ggplot(data=dvlong, mapping=aes(
  x=x, y=y, fill=z)) +
  geom_raster() + 
  scale_fill_gradient2()