8 主成分分析
8.1 主成分分析的基本思想
主成分分析(Principal Component Analysis, PCA)由Hotelling于1933年首先提出。 目的是把多个变量压缩为少数几个综合指标(称为主成分), 使得综合指标能够包含原来的多个变量的主要的信息。
如何度量变量中包含的信息? 如果变量取常数,就没有信息。 变量变化范围越大,越不容易预知其取值, 得到变量的观测值时获得的信息量就大。 所以,用方差衡量综合指标包含的信息多少。 寻找原始变量的线性组合作为综合指标, 使得综合指标的方差最大; 各个综合指标之间不相关。
主成分分析是变量降维的最主要方法之一。 实际中也经常对多个变量作主成分分析, 获得更有意义的指标。 比如, 许多学生的若干门课程的考试分数, 如果直接计算平均分或者总分, 会收到各门课程分数高低、区分程度的影响, 用主成分分析方法计算线性组合作为第一主成分, 是比较合理的多门课程的综合指标。 在经济研究中也涉及多个指数, 如物价、工资、居住等, 可以计算第一主成分作为综合指标。
有时第二、第三主成分更有用。 比如, 研究动物特征时, 测量了动物的多个长度指标, 这时第一主成分仅反映动物的大小, 而第二、第三主成分则可以用来区分动物的不同样貌。
多维数据很难用图形表示, 用主成分分析降维后, 可以用通常的散点图、三维散点图等方法作图显示。
在回归分析中, 如果自变量高度相关, 会引起多重共线性问题, 使得计算不稳定, 参数估计的标准误差变大, 用变量选择方法则会损失一定的信息, 可以计算自变量的主成分, 用前几个主成分作为回归自变量进行回归建模。
8.2 总体主成分
8.2.1 二维情形
设总体为一个\(p\)维随机向量\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)。 以二维正态分布为例。设\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\), 其中 \[\begin{aligned} \boldsymbol\mu = \left( \begin{array}{c} \mu_1 \\ \mu_2 \end{array} \right),\; \Sigma = \left(\begin{array}{cc} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{array}\right) . \end{aligned}\] 设此总体有\(n\)个观测值\((x_{i1}, x_{i2}), i=1,2,\dots,n\),
模拟一批二维正态分布的样本的散点图:
library(mvtnorm)
set.seed(101)
n <- 10000
mu <- c(0, 0)
rho <- 0.5
sigma1 <- 1.6
sigma2 <- 1
S <- rbind(c(sigma1^2, rho*sigma1*sigma2),
c(rho*sigma1*sigma2, sigma2^2))
d <- rmvnorm(n, mu, S)
colnames(d) <- c("x", "y")
##plot(d, xlab=expression(x[1]), ylab=expression(x[2]),
## xlim=c(-5,5), ylim=c(-5,5))
library(ggplot2)
ggplot(data=as.data.frame(d), mapping=aes(x=x, y=y)) +
geom_point(size=0.3, alpha=0.2)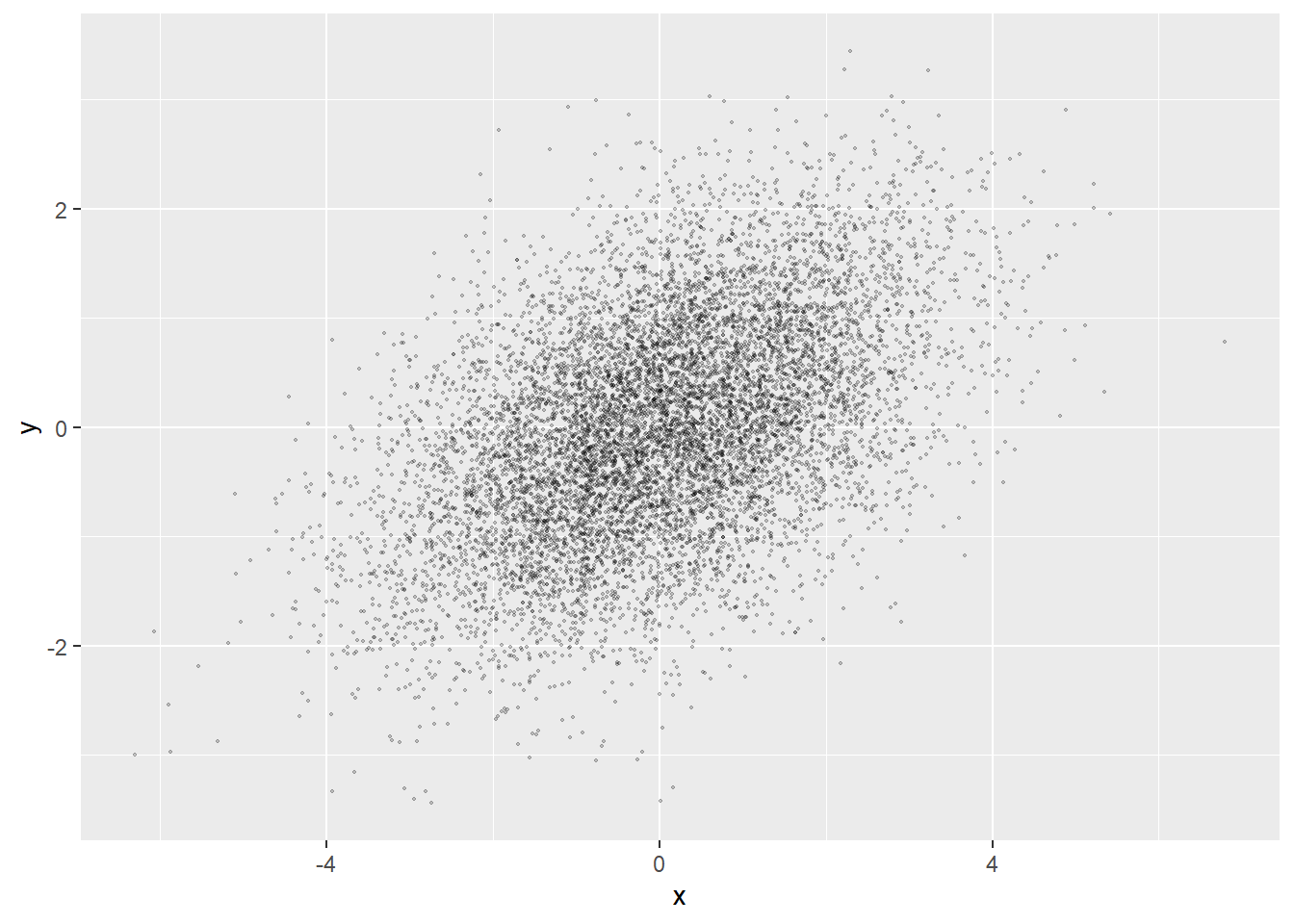
如果取散点变化最大的方向为新坐标\(y_1\)轴, 其正交方向为\(y_2\)轴, 这些点的新\(y_1\)坐标可以更好地概括观测点的信息。
设坐标变换原点不变, 仅进行逆时针\(\theta\)弧度的旋转变换,则变换后的随机向量为 \[\begin{aligned} \boldsymbol Y = \left( \begin{array}{c} Y_1 \\ Y_2 \end{array} \right) = \left( \begin{array}{cc} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{array} \right) \left( \begin{array}{c} X_1 \\ X_2 \end{array} \right) \end{aligned}\]
记变换矩阵为\(P^T\),这是一个正交阵(\(P^T P = I\))。 \(y_1\)是\(x_1, x_2\)的线性组合,线性组合系数是单位向量 (这里指欧式长度等于1的向量)。 适当选取\(\theta\)可以使得\(Y_1\)的方差最大, 而且\(Y_1\)和\(Y_2\)不相关。
考虑三种极端情况。
- 如果\(\rho=0\), \(\sigma_1 = \sigma_2\), 这时散点呈现为正圆,不需要旋转变换 (任何旋转方向都不会使得方差变大)。 取任何一个线性组合,都只能保留原来50%的信息。
- 如果\(\rho\)接近于\(\pm 1\), 这时图形呈现出一个很扁的椭圆, 变换后的\(Y_1\)可以包含主要的信息。
- 如果\(\sigma_1\)远大于\(\sigma_2\), 这时仅保留\(X_1\)就保留了\((X_1, X_2)\)的大部分信息。
设\(\boldsymbol Y = P^T \boldsymbol X\)。 考虑求\(P\)使得\(\text{Var}(Y_1)\)最大的问题。
设\(\Sigma\)有如下的特征值分解: \[\begin{aligned} \Sigma = P \Lambda P^T, \end{aligned}\] 其中\(\lambda_1 \geq \lambda_2 > 0\)是正定阵\(\Sigma\)的两个特征值, \(\Lambda=\text{diag}(\lambda_1, \lambda_2)\), \(P\)的两列分别为这两个特征值对应的特征向量。
这时, \[\begin{aligned} \text{Var}(\boldsymbol Y) =& \text{Var}(P^T \boldsymbol X) = P^T \Sigma P = \Lambda, \end{aligned}\] 且\(Y_1 = X_1 \cos\theta + X_2 \sin\theta\) 是所有单位向量作为线性组合系数的线性变换中方差最大的。 \(Y_1\)和\(Y_2\)不相关。
设\(\boldsymbol\alpha = (\alpha_1, \alpha_2)^T\)是线性组合系数, 满足\(\| \boldsymbol\alpha \| = \sqrt{\alpha_1^2 + \alpha_2^2} = 1\)。 令\(Z = \boldsymbol\alpha^T \boldsymbol X\), 则 \[\begin{aligned} \text{Var}(Z) =& \boldsymbol\alpha^T \Sigma \boldsymbol\alpha = \boldsymbol\alpha^T P \Lambda P^T \boldsymbol\alpha = (P^T \boldsymbol\alpha)^T \Lambda (P^T \boldsymbol\alpha), \end{aligned}\]
记\(\boldsymbol\beta=P^T \boldsymbol\alpha\), 则\(\| \boldsymbol\beta \| = 1\), 有 \[\begin{aligned} \text{Var}(Z) =& \boldsymbol\beta^T \Lambda \boldsymbol\beta = \lambda_1 \beta_1^2 + \lambda_2 \beta_2^2 \\ \leq& \lambda_1 \beta_1^2 + \lambda_1 \beta_2^2 = \lambda_1 (\beta_1^2 + \beta_2^2) = \lambda_1, \end{aligned}\] 所以\(\boldsymbol\beta=(1,0)^T\)使得\(\text{Var}(Z) = \lambda_1\)达到最大。 这时\(\boldsymbol\alpha = P\boldsymbol\beta\)是\(P\)的第一列, 即\(\Sigma\)的特征值\(\lambda_1\)对应的单位特征向量。
注意: \(-\boldsymbol\alpha\)也满足要求。
8.2.2 多维情形
定理6.1 设总体\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)的协方差阵为\(\Sigma\), \(\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_p \geq 0\) 为\(\Sigma\)的\(p\)个特征值, \(\Sigma\)有如下的特征值分解 \[\begin{aligned} \Sigma = P \Lambda P^T, \end{aligned}\] 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots,\lambda_p)\), \(P\)为正交阵,\(P\)的第\(j\)列是\(\lambda_j\)对应的特征向量,记为\(\boldsymbol p_j\)。 则\(X\)的第\(j\)个主成分为 \[\begin{aligned} Y_j = \boldsymbol p_j^T \boldsymbol X, \end{aligned}\] 令\(Y = (Y_1, Y_2, \dots, Y_p)^T\), 则\(\boldsymbol Y = P^T \boldsymbol X\), \(\text{Var}(\boldsymbol Y) = \Lambda\)。
在线性组合系数必须是单位向量的约束下, 这样得到的\(\text{Var}(Y_1)\)最大,\(Y_j\)在与\(Y_1, \dots, Y_{j-1}\)不相关的前提下达到最大方差。
由\(\boldsymbol Y = P^T \boldsymbol X\)得 \[ \boldsymbol X = P \boldsymbol Y = \begin{pmatrix} \boldsymbol p_1, \boldsymbol p_2, \dots, \boldsymbol p_p \end{pmatrix} \begin{pmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_p \end{pmatrix} = Y_1 \boldsymbol p_1 + Y_2 \boldsymbol p_2 + \dots + Y_p \boldsymbol p_p , \] 原始变量可以用主成分的线性组合表示, \(\boldsymbol p_1\)是主成分\(Y_1\)对原始变量\(\boldsymbol X\)的贡献, \(\boldsymbol p_2\)是主成分\(Y_2\)对原始变量\(\boldsymbol X\)的贡献, …………, 称矩阵\(P\)为主成分分析的载荷矩阵。参见节9.1.1的解释。
8.2.3 主成分的性质
设\(\boldsymbol Y = (Y_1, Y_2, \dots, Y_p)^T\)是\(\boldsymbol X\)的主成分向量。 \(\text{Var}(\boldsymbol X) = \Sigma = P \Lambda P^T\), \(\boldsymbol Y = P^T \boldsymbol X\)。
性质1 主成分向量\(\boldsymbol Y\)的协方差阵是对角阵 \(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_p)\)。
事实上, \[\begin{aligned} \text{Var}(\boldsymbol Y) =& \text{Var}(P^T \boldsymbol X) = P^T \Sigma P = P^T P \Lambda P^T P \\ =& \Lambda \end{aligned}\]
性质2 主成分\(Y_1, Y_2, \dots, Y_p\)的方差之和等于原始变量 \(X_1, X_2, \dots, X_p\)的方差之和。
事实上, \[\begin{aligned} & \sum_{j=1}^p \text{Var}(Y_j) = \text{trace}(\text{Var}(\boldsymbol Y)) = \text{trace}(\text{Var}(P^T \boldsymbol X)) \\ =& \text{trace}(P^T \Sigma P) = \text{trace}(P P^T \Sigma) = \text{trace}(\Sigma) \\ =& \sum_{j=1}^p \text{Var}(X_j). \end{aligned}\]
性质3 原始变量\(X_k\)与主成分\(Y_j\)的相关系数为 \[\begin{aligned} \rho_{kj} = \rho(X_k, Y_j) = \frac{\sqrt{\lambda_j}}{\sqrt{\sigma_{kk}}} p_{kj}, \end{aligned}\] 其中\(\boldsymbol p_j = (p_{1j}, p_{2j}, \dots, p_{pj})^T\)是\(P\)的第\(j\)列, \(p_{kj}\)是\(P\)的第\((k,j)\)元素。
证明: 记\(\boldsymbol e_k\)为单位阵\(I_p\)的第\(k\)列, 即仅第\(k\)元素为1,其它元素都为0的\(p\)维向量。 则\(X_k = \boldsymbol e_k^T \boldsymbol X\), \(Y_j = \boldsymbol p_j^T \boldsymbol X\), 于是 \[\begin{aligned} \text{Cov}(X_k, Y_j) =& \text{Cov}(\boldsymbol e_k^T \boldsymbol X, \boldsymbol p_j^T \boldsymbol X) = \boldsymbol e_k^T \Sigma \boldsymbol p_j \\ =& \boldsymbol e_k^T (\Sigma \boldsymbol p_j) = \boldsymbol e_k^T (\lambda_j \boldsymbol p_j) \quad\text{($\boldsymbol p_j$是$\lambda_j$对应的特征向量)} \\ =& \lambda_j (\boldsymbol e_k^T \boldsymbol p_j) = \lambda_j p_{kj}, \\ \rho_{kj} =& \rho(X_k, Y_j) = \frac{\text{Cov}(X_k, Y_j)}{\sqrt{\text{Var}(X_k) \cdot \text{Var}(Y_j)}} \\ =& \frac{\lambda_j p_{kj}}{\sqrt{\sigma_{kk} \lambda_j}} = \frac{\sqrt{\lambda_j}}{\sqrt{\sigma_{kk}}} p_{kj} . \end{aligned}\]
性质4 原始变量\(X_k\)与所有主成分\(\{Y_j \}\)的相关系数满足 \[\begin{aligned} \sum_{j=1}^p \rho_{kj}^2 = 1, \ k=1,2,\dots,p . \end{aligned}\]
证明: 注意到 \[\begin{aligned} \Sigma = P \Lambda P^T = \sum_{j=1}^p \lambda_j \boldsymbol p_j \boldsymbol p_j^T, \end{aligned}\] 所以 \[\begin{aligned} \sigma_{kk} = \sum_{j=1}^p \lambda_j p_{kj}^2, \end{aligned}\] 于是 \[\begin{aligned} \sum_{j=1}^p \rho_{kj}^2 = \frac{1}{\sigma_{kk}} \sum_{j=1}^p \lambda_j p_{kj}^2 = 1. \end{aligned}\] 这样,\(\rho_{kj}^2\)可以看成是在原始变量\(X_k\)的方差中, 第\(j\)主成分\(Y_j\)能够解释的方差比例。
8.3 样本主成分
实际问题中, 总体的分布通常是未知的, 需要从样本中估计。 设总体\(\boldsymbol X\)有\(n\)个独立观测, 保存为矩阵\(M = (x_{ij})_{n \times p}\), 其中第\(i\)行为第\(i\)个观测, 第\(j\)列为第\(j\)分量的所有\(n\)个观测组成的向量。 这也是统计中最常见的数据表示,常称为数据集, 在R中通常用数据框(data frame)存储。
8.3.1 R型主成分与Q型主成分
因为现在有总体的\(n\)个独立观测, 所以从\(M\)估计总体的主成分, 将得到\(n\)个第一主成分值, \(n\)个第二主成分值,……。 如果仅取前\(k\)个主成分, 则数据集\(M\)被压缩成\(n \times k\)的得分数据集, 每列为一个主成分得分(总体主成分的估计值)。 原来每行是一个\(p\)维向量,压缩为每行\(k\)个得分(\(k<p\)), 这样的主成分分析称为R型主成分分析。
对矩阵\(M\),还可以把每列的\(n\)维向量, 用类似方法压缩为\(k\)个得分, 这样的主成分分析称为Q型主成分分析。 这里仅考虑R型主成分分析。
8.3.2 标准化
主成分的组成,不仅与\(\boldsymbol X\)的相关结构有关系, 与每个分量的方差也有关系, 方差大的分量在第一主成分中贡献更大。
在变量的各分量可比的情况下(比如,都是考试分数且满分相同), 这不成为问题,而且是合理的。 但是,如果分量之间不可比,这时量纲会对主成分结果造成很大影响。 比如,某分量的量纲从千克变成了克,其方差就变大到了原来的一百万倍, 在第一主成分中的贡献就比原来大得多了。
所以,主成分分析经常对标准化的分量 \[\begin{aligned} Y_j = \frac{X_j - E(X_j)}{\sqrt{\text{Var}(X_J)}}, \ j=1,2,\dots,p, \quad \boldsymbol Y = (Y_1, Y_2, \dots, Y_p)^T \end{aligned}\] 进行。 这时\(\text{Var}(\boldsymbol Y) = R\), 其中\(R\)的\((j,j)\)元素等于1, \(R\)的\((i,j)\)元素为\(\rho(X_i, X_j)\), 是\(\boldsymbol X\)的相关阵。 对标准化的随机向量进行主成分分析, 相当于用相关阵\(R\)代替协方差阵\(\Sigma\)作特征值分解, 以\(R\)的各特征向量为主成分的线性组合系数。 对\(S\)作特征值分解与对\(R\)作特征值分解, 结果一般是不同的。 选择基于\(R\)作主成分分析, 同时也默认了所有\(p\)个变量具有相同的重要性。
为估计协方差阵\(\Sigma\), 令 \[\begin{aligned} \bar x_{\cdot j} =& \frac{1}{n} \sum_{i=1}^n x_{ij}, \ j=1,2,\dots, p, \\ s_{jk} =& \frac{1}{n} \sum_{i=1}^n (x_{ij} - \bar x_{\cdot j})(x_{ik} - \bar x_{\cdot k}), \ j, k=1,2,\dots,p, \end{aligned}\] \(S=(s_{jk})_{p \times p}\)是\(\Sigma\)的估计。 注意方差和协方差估计用了\(1/n\)而不是\(1/(n-1)\)。
为估计相关阵\(R\),令 \[\begin{aligned} r_{jk} =& \frac{s_{jk}}{\sqrt{s_{jj} \cdot s_{kk}}}, \ j, k=1,2,\dots,p, \end{aligned}\] \(\hat R = (r_{jk})_{p \times p}\), 则\(\hat R\)是相关阵\(R\)相合估计。 在不引起混淆时可简记\(\hat R\)为\(R\)。
8.3.3 样本主成分推导
从观测数据\(M\)求样本主成分, 其理论推导与总体主成分推导类似。 以使用协方差阵\(S\)为例。 令\(M_C = H M\), \[ S = \frac{1}{n} M_C^T M_C = \frac{1}{n} M^T H M . \] 考虑\(M_C\)各行都用线性组合系数\(\boldsymbol g_1\)作线性组合, 得到第一主成分得分向量\(\boldsymbol z_1 = M_C \boldsymbol g_1\), 由§4.1.5, \(\boldsymbol z_1\)的样本方差(用除以\(n\)的公式)为 \[ S_{z_1}^2 = \boldsymbol g_1^T S \boldsymbol g_1, \] 在\(\| \boldsymbol g_1 \| = 1\)约束下令\(S_{z_1}^2\)达到最大, 用与8.2同样的推理可知应取\(S\)的最大特征值\(\lambda_1\)对应的单位特征向量\(\boldsymbol g_1\)作为线性组合系数。 这时,\(S_{z_1}^2 = \lambda_1\)。
第二、第三等主成分得分的线性组合系数类似, 取为\(S\)的从大到小排列的特征值对应的单位特征向量, 第\(j\)样本主成分得分的样本方差为\(S\)的从大到小第\(j\)特征值\(\lambda_j\)。
可以证明, 第一主成分得分对应的系数\(\boldsymbol g_1\), 等价于在\(\mathbb R^p\)中求一条经过原点的直线, 使得\(M_C\)的每行对应的\(n\)个点, 到此直线的垂直距离的平方和最小。 比如, 当\(p=2\)时, 设第一样本主成分的线性组合系数\(\boldsymbol g_1 = (a_1, b_1)^T\), 则它决定一条直线\(a_1 x + b_1 y = 0\), \(M_C\)的\(n\)行对应的\(n\)个观测点到此直线的垂直距离平方和最小。
8.3.4 样本主成分计算
不论使用协方差阵还是相关阵, 样本数据\(M\)的每列都要中心化(减去列平均值\(\bar x_{\cdot j}\), \(j=1,2,\dots,p\))。
令\(H = I_n - \frac{1}{n} \boldsymbol 1_n \boldsymbol 1_n^T\), 则中心化的数据集为\(M_C = H M\)。 样本协方差阵为\(S = \frac{1}{n} M_C^T M_C = \frac{1}{n} M^T H M\)。
如果使用相关阵, \(M\)的每列要标准化, 标准化时,每列减去列平均值\(\bar x_{\cdot j}\)后除以标准差估计\(\sqrt{s_{jj}}\) (\(j=1,2,\dots,p\))。
设\(D = \text{diag}(s_{11}, s_{22}, \dots, s_{pp})\), 则标准化数据集为\(M_S = H M D^{-1/2}\), 相关系数阵估计为\(\hat R = D^{-1/2} S D^{-1/2}\)。
设样本协方差阵\(S\)(或样本相关阵\(R\))有特征值分解\(S = G L G^T\), 其中\(L = \text{diag}(l_1, l_2, \dots,l_p)\), \(G\)为正交阵。
设数据阵\(M\)已进行中心化或标准化, 记为\(\tilde M\)(\(\tilde M = M_C\)或\(M_S\)), 记\(\tilde M\)的第\(i\)行记为\((\boldsymbol x^{(i)})^T\), 则\((\boldsymbol x^{(i)})^T G\)为一个\(p\)维行向量, 第一个元素是第\(i\)个观测的第一样本主成分, 第二个元素是第\(i\)个观测的第二样本主成分,…………。 令\(Z = \tilde M G\), 则\(Z\)是一个\(n \times p\)矩阵, \(Z\)的第\(i\)行的\(p\)个元素是观测数据的第\(i\)个观测的\(p\)个样本主成分; \(Z\)的第\(j\)列是所有观测的第\(j\)主成分,称为第\(j\)主成分得分。
如果只需要前\(k\)个主成分, 则只需要计算 \[\begin{align*} Z_{n \times k} = \tilde M G_{p \times k} = (\tilde M \boldsymbol g_1, \tilde M \boldsymbol g_2, \dots, \tilde M \boldsymbol g_k), \end{align*}\] 其中\(G_{p \times k}\)表示\(G\)的前\(k\)列组成的子矩阵, \(\boldsymbol g_j\)表示\(G\)的第\(j\)列。
8.3.5 用奇异值分解计算样本主成分
设数据阵\(M\)已进行中心化或标准化, 记为\(\tilde M\)(\(\tilde M = M_C\)或\(M_S\)), 下面以中心化为例说明。 对\(\tilde M\)作如下的奇异值分解: \[ \tilde M = U L^{\frac{1}{2}} G^T \] 其中\(L\)为\(\tilde M^T \tilde M\)的特征值组成的对角阵, \(L^{\frac{1}{2}}\)为各个奇异值, \(U\)和\(G\)是\(n \times r\)和\(p \times r\)列单位正交阵, 对于样本数据, 可取\(r = \min(n, p)\)。 这时, \[ \frac{1}{n} \tilde M^T \tilde M = G (\frac{1}{n} L) G^T \] 构成协方差阵估计或相关阵估计的特征值分解。
令 \[ Z = \tilde M G \] 则\(P\)是\(n \times p\)矩阵, \(G\)是方差阵(或相关阵)的特征值分解中的各个特征向量, 所以是主成分得分矩阵。
各个主成分的方差阵估计为\(\frac{1}{n} L\)。
8.3.6 样本主成分性质
\(Z\)的每列的样本平均值都等于零;
第\(j\)个样本主成分的样本方差满足 \[\begin{align*} \frac{1}{n} \sum_{i=1}^n z_{ij}^2 = l_j, \ j=1,2,\dots, p . \end{align*}\] 证明见Zelterman(2015) §11.6 (11.30-11.31)。
由于\(S = G L G^T\), \(\text{trace}(S) = \text{trace}(L)\), 所以\(M\)中\(p\)个变量的总方差等于\(Z\)的\(p\)个主成分得分的总方差。
8.3.7 主成分个数的确定
主成分分析的主要目的是降维, 用较少的综合指标代替原来的多个变量, 所以一般只保留少数的几个主成分。
因为\(p\)个原始变量和\(p\)个主成分得分的总方差不变, 但是主成分的方差是由大到小的, 可以用\(\omega_k = \frac{l_k}{\sum_{j=1}^p l_j}\) 度量第\(k\)个主成分的贡献, 称为第\(k\)个主成分的方差贡献率。
用\(\sum_{i=1}^k w_i = \frac{\sum_{j=1}^k l_j}{\sum_{j=1}^p l_j}\) 表示前\(k\)个主成分能解释原始变量的信息的比例, 称为前\(k\)个主成分的累计贡献率。 经常取\(k\)使得累计贡献率达到\(80\%\)以上就不再增加主成分。 如果少量的主成分不能达到较好的累计贡献率, 也可以降低对累计贡献率的要求或使用更多个主成分。 常用的累计贡献率界限为\(70%\)到\(90%\)。
还可以取超过平均方差(\(p\)个原始变量的方差的平均值)的前几个主成分。 在使用相关系数阵分解计算主成分时, 平均方差是1, 可以取方差超过1的主成分, 还有人建议取方差超过\(0.7\)的主成分。
令 \[\begin{aligned} \hat{\boldsymbol X} = \sum_{j=1}^k Y_j \boldsymbol p_j, \end{aligned}\] 则 \[\begin{aligned} & E \| \boldsymbol X - \hat{\boldsymbol X} \|^2 = E \| \sum_{j=k+1}^p Y_j \boldsymbol p_j \|^2 \\ =& E \| P \; (0, \dots, 0, Y_{k+1}, \dots, Y_p)^T \|^2 \\ =& E \| (0, \dots, 0, Y_{k+1}, \dots, Y_p)^T \|^2 = E \sum_{j=k+1}^p Y_j^2 \\ =& \sum_{j=k+1}^p \lambda_j, \end{aligned}\] 可见当累计贡献率较高时, 可以用主成分较好地近似原始变量。
保留的主成分个数的变化不影响计算的主成分得分。 对因子分析, 选择不同的因子个数, 计算得到的因子得分也会有差别。
8.4 样本主成分的几何解释
前面对主成分分析的解释, 是从用原始变量的单位长度系数的线性组合最大化方差来给出的, 对样本主成分就简单地使用了样本方差阵来代替理论方差阵。 下面我们说明, 将\(n \times p\)的观测数据集\(M\)的每一行看成\(\mathbb R^p\)中的点, 样本主成分实际是将这\(p\)个点用\(\mathbb R^p\)中的子空间(或仿射集)进行最优逼近产生的降维结果。
8.4.1 已经中心化的数据
先考虑将\(M_C\)(中心化的数据)的\(n\)个点用\(\mathbb R^p\)的一维子空间中的点来逼近: \[ \mathcal S = \{ \lambda \boldsymbol u: \lambda \in \mathbb R \} . \] 其中\(\boldsymbol u \in \mathbb R^p\), \(\| \boldsymbol u \| = 1\)。 求\(\boldsymbol u\)使得这\(n\)个点到\(\mathcal S\)的总距离平方最小: \[ \min_{\boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \sum_i \| \boldsymbol x^{(i)} - \lambda_i \boldsymbol u \|^2 . \] 其中\(\boldsymbol x^{(i)}\)表示\(M_C\)的第\(i\)行的转置, \(\lambda_i \boldsymbol u\)是\(\boldsymbol x^{(i)}\)在\(\mathcal S\)中的最佳逼近, 即 \[ \lambda_i = \text{argmin}_{\lambda \in \mathbb R} \| \boldsymbol x^{(i)} - \lambda \boldsymbol u \|^2 . \] 这是一个投影问题, 因为\(\boldsymbol u\)是单位长度向量, 所以 \[ \lambda_i = \langle \boldsymbol x^{(i)}, \boldsymbol u \rangle = [\boldsymbol x^{(i)}]^T \boldsymbol u^ . \] 由投影的正交性有 \[ \| \boldsymbol x^{(i)} - \lambda_i \boldsymbol u \|^2 = \| \boldsymbol x^{(i)} \|^2 - \lambda_i^2 = \| \boldsymbol x^{(i)} \|^2 - \langle \boldsymbol x^{(i)}, \boldsymbol u \rangle^2 . \] 求最优的\(\boldsymbol u\), 问题转化为 \[ \min_{\boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \left\{ \sum_i \| \boldsymbol x^{(i)} \|^2 - \sum_i \langle \boldsymbol x^{(i)}, \boldsymbol u \rangle^2 \right\} . \] 目标函数的第一项不依赖于\(\boldsymbol u\), 所以问题为 \[ \max_{\boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \sum_i \langle \boldsymbol x^{(i)}, \boldsymbol u \rangle^2 = \max_{\boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \sum_i ([\boldsymbol x^{(i)}]^T \boldsymbol u)^2 . \] 令\(\boldsymbol y = M_C \boldsymbol u\), 则\(y_i = [\boldsymbol x^{(i)}]^T \boldsymbol u\), 目标函数为 \[ \sum_i y_i^2 = \| \boldsymbol y \|^2 = \boldsymbol y^T \boldsymbol y = \boldsymbol u^T M_C^T M_C \boldsymbol u = n \boldsymbol u^T S \boldsymbol u . \] 其中\(S\)是样本方差阵, 问题变成 \[ \max_{\boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \boldsymbol u^T S \boldsymbol u . \] 于是当数据为\(M_C\)(中心化的数据集)时, 取\(S\)的最大特征值对应的单位特征向量\(\boldsymbol u\), 得到的\(\boldsymbol y = M_c \boldsymbol u\)是将\(n\)个点用\(\mathcal S\)中的点进行最小二乘逼近的最优结果(参见1.5.3)。
可以进一步考虑用\(\mathbb R^p\)的二维子空间的\(n\)个点近似原来的\(n\)个点。 取 \[ \mathcal S = \{ \lambda_1 \boldsymbol u_1 + \lambda_2 \boldsymbol u_2: \lambda_1, \lambda_2 \in \mathbb R \} , \] 其中\(\boldsymbol u_1, \boldsymbol u_2 \in \mathbb R^p\), \(\| \boldsymbol u_1 \| = \| \boldsymbol u_2 \| = 1\), 且\(\langle \boldsymbol u_1, \boldsymbol u_2 \rangle = 0\)。 这是穿过原点的一个平面。 求\(\boldsymbol u_1, \boldsymbol u_2\)使得 \[ \min \sum_{i} \| \boldsymbol x^{(i)} - \lambda_1 \boldsymbol u_1 - \lambda_2 \boldsymbol u_2 \|^2, \] 其中 \[ (\lambda_1, \lambda_2) = \text{argmin} \| \boldsymbol x^{(i)} - \lambda_1 \boldsymbol u_1 - \lambda_2 \boldsymbol u_2 \|^2 . \] 这仍是\(\boldsymbol x^{(i)}\)向\(\mathcal S\)的正交投影, 有 \[ \lambda_j = \langle \boldsymbol x^{(i)}, \boldsymbol u_j \rangle, \ j=1, 2 . \] 可以证明优化问题的解是\(\boldsymbol u_1\)为\(S\)的最大特征值对应的单位特征向量, \(\boldsymbol u_2\)为\(S\)的次大特征值对应的单位特征向量。
8.4.2 未中心化的数据
从以上推导看出, \(M\)不需要中心化, 则这时\(\boldsymbol u\)是\(M^T M\)的最大特征值对应的单位特征向量。 但是, 这样的逼近不是\(\mathbb R^p\)的一维子集的最小二乘逼近, 当\(\mathcal S\)为一维时, 上面的方法中的\(\mathcal S\)是一条穿过原点的直线, 为了最优逼近\(\mathbb R^p\)中的\(n\)个点, 取消“穿过原点”这个要求可以得到更合理的逼近结果。 当\(\mathcal S\)为二维时, 上面的方法中的\(\mathcal S\)是穿过原点的平面, 取消“穿过原点”这个要求也可以得到更合理的逼近结果。
所以, 我们可以考虑\(\mathbb R^p\)这样的仿射子集: \[ \mathcal S = \{\boldsymbol c + \lambda \boldsymbol u: \ \lambda \in \mathbb R \}, \] 其中\(\boldsymbol c, \boldsymbol u \in \mathbb R^p\), \(\| \boldsymbol u \| = 1\)。 考虑最小化问题 \[\begin{align} \min_{\boldsymbol c, \boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \;\min_{\{ \lambda_i \}} \sum_i \| \boldsymbol x^{(i)} - \boldsymbol c - \lambda_i \boldsymbol u \|^2 . \tag{8.1} \end{align}\] 其中 \[ \lambda_i = \text{argmin}_{\lambda} \| \boldsymbol x^{(i)} - \boldsymbol c - \lambda \boldsymbol u \|^2 . \] 这又是一个投影问题, 有 \[ \lambda_i = \langle \boldsymbol x^{(i)} - \boldsymbol c, \boldsymbol u \rangle . \] 于是 \[\begin{aligned} & \| \boldsymbol x^{(i)} - \boldsymbol c - \lambda_i \boldsymbol u \|^2 \\ =& \| \boldsymbol x^{(i)} - \boldsymbol c \|^2 - \langle \boldsymbol x^{(i)} - \boldsymbol c, \boldsymbol u \rangle^2, \\ & \sum_i \| \boldsymbol x^{(i)} - \boldsymbol c - \lambda_i \boldsymbol u \|^2 \\ =& \sum_i \| \boldsymbol x^{(i)} - \boldsymbol c \|^2 - \sum_i \langle \boldsymbol x^{(i)} - \boldsymbol c, \boldsymbol u \rangle^2 . \end{aligned}\] 令 \[\begin{aligned} \bar{\boldsymbol x} =& \frac{1}{n} \sum_i \boldsymbol x^{(i)}, \\ \boldsymbol d =& \boldsymbol c - \bar{\boldsymbol x}, \\ \boldsymbol x^{(i)} - \boldsymbol c =& (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) + (\bar{\boldsymbol x} - \boldsymbol c) \\ =& (\boldsymbol x^{(i)} - \bar{\boldsymbol x}) - \boldsymbol d . \end{aligned}\] 将目标函数化为 \[\begin{align} \sum_i \| \boldsymbol x^{(i)} - \bar{\boldsymbol x} \|^2 + n \| \boldsymbol d \|^2 - \sum_i \langle \boldsymbol x^{(i)} - \bar{\boldsymbol x}, \boldsymbol u \rangle^2 - n \langle \boldsymbol d, \boldsymbol u \rangle^2 . \tag{8.2} \end{align}\] 上式的推导利用了 \[\begin{aligned} & \sum_i \langle \boldsymbol x^{(i)} - \bar{\boldsymbol x}, \;\boldsymbol d \rangle = 0, \\ & \sum_i \langle \boldsymbol x^{(i)} - \bar{\boldsymbol x}, \; \boldsymbol u \rangle \langle \boldsymbol d, \; \boldsymbol u \rangle = 0 . \end{aligned}\]
考虑(8.2)关于\(\boldsymbol d\)和\(\boldsymbol u\)的最小值问题。 前面已经证明 \[ - \sum_i \langle \boldsymbol x^{(i)} - \bar{\boldsymbol x}, \boldsymbol u \rangle^2 = -n \boldsymbol u^T S \boldsymbol u . \] 所以问题转化为 \[\begin{align} \min_{\boldsymbol d, \boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1 } \left\{ \boldsymbol d^T \boldsymbol d - \boldsymbol u^T S \boldsymbol u - (\boldsymbol u^T \boldsymbol d)^2 \right\} . \tag{8.3} \end{align}\]
如果\(\boldsymbol d = \boldsymbol 0\), 即\(\boldsymbol c = \bar{\boldsymbol x}\), 则\(\boldsymbol u\)的解为\(S\)的最大特征值对应的单位特征向量。 记\(\boldsymbol u_1\)为这个解。
如果\(\boldsymbol d \neq 0\), 约束最小问题(8.3)的Lagrange乘子函数为 \[ g(\boldsymbol u, \boldsymbol d, \alpha) = \boldsymbol d^T \boldsymbol d - \boldsymbol u^T S \boldsymbol u - (\boldsymbol u^T \boldsymbol d)^2 - \alpha (\boldsymbol u^T \boldsymbol u - 1) . \] 约束最小值点应满足 \[\begin{aligned} \boldsymbol 0 =& \frac{\partial g}{\partial \boldsymbol u} = -2 S \boldsymbol u - 2 (\boldsymbol u^T \boldsymbol d) \boldsymbol d - 2 \alpha \boldsymbol u, \\ \boldsymbol 0 =& \frac{\partial g}{\partial \boldsymbol d} = 2 \boldsymbol d - 2 (\boldsymbol u^T \boldsymbol d) \boldsymbol u, \\ 0 =& \frac{\partial g}{\partial \alpha} = 1 - \boldsymbol u^T \boldsymbol u . \end{aligned}\] 第三式要求\(\boldsymbol u^T \boldsymbol u = 1\)。 由第二式得 \[ \boldsymbol d = (\boldsymbol u^T \boldsymbol d) \boldsymbol u, \] 这是约束最小值点的必要条件。 于是初始的优化问题(8.1)变成 \[\begin{aligned} & \min_{\boldsymbol c, \boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \;\min_{\{ \lambda_i \}} \sum_i \| \boldsymbol x^{(i)} - \bar{\boldsymbol x} - \boldsymbol d - \lambda_i \boldsymbol u \|^2 \\ =& \min_{\boldsymbol c, \boldsymbol u \in \mathbb R^p, \| \boldsymbol u \| = 1} \;\min_{\{ \lambda_i \}} \sum_i \| \boldsymbol x^{(i)} - \bar{\boldsymbol x} - [\lambda_i + (\boldsymbol u^T \boldsymbol d) ] \boldsymbol u \|^2 , \end{aligned}\] 这要求 \[ \lambda_i + (\boldsymbol u^T \boldsymbol d) = \langle \boldsymbol x^{(i)} - \bar{\boldsymbol x}, \boldsymbol u \rangle , \] 且要求\(\boldsymbol u = \boldsymbol u_1\)。 这与\(\boldsymbol d = \boldsymbol 0\)的目标函数值相等, 所以原来的约束极值问题的解为:
用仿射集\(\mathcal S = \{\boldsymbol c + \lambda \boldsymbol u \}\)逼近\(M\)的各行代表的\(n\)个点时, 在最小二乘准则下的解是令\(\boldsymbol c = \bar{\boldsymbol x}\), \(\boldsymbol u\)取为\(S\)的最大特征值对应的单位特征向量。 这正是求解第一个样本主成分得分的方法。
更多的样本主成分解释类似, 比如取两个样本主成分时, 采用的子空间为: \[ \mathcal S = \{ \boldsymbol c + \lambda_1 \boldsymbol u_1 + \lambda_2 \boldsymbol u_2: \lambda_1, \lambda_2 \in \mathbb R \}, \] 其中\(\boldsymbol c, \boldsymbol u_1, \boldsymbol u_2 \in \mathbb R^p\), \(\| \boldsymbol u_1 \| = \| \boldsymbol u_2 \| = 1\), \(\langle \boldsymbol u_1, \boldsymbol u_2 \rangle = 0\)。 这时\(\boldsymbol c\)仍取为\(\bar{\boldsymbol x}\), \(\boldsymbol u_1\)是\(S\)的最大特征值对应的单位特征向量, \(\boldsymbol u_2\)是\(S\)的第二大特征值对应的单位特征向量。 解决的问题是用\(\mathbb R^p\)中的一个平面上的点对\(M\)代表的\(n\)个点在最小二乘意义下进行最优逼近。
8.5 双重散点图(biplot)
8.5.1 R型主成分分析与Q型主成分分析的对偶关系
设矩阵\(A\)为\(n^{-1/2}M_C\)或\(n^{-1/2} M_S\), 这时\(A^T A\)是协方差阵\(S\) 或相关阵\(R\)。
以\(A = n^{-1/2} M_C\)为例。样本协方差阵\(S\)有特征值分解 \[\begin{align*} S =& A^T A = \sum_{j=1}^p l_j \boldsymbol g_j \boldsymbol g_j^T, \end{align*}\] 其中\(l_j>0\)是\(A^T A\)的特征值, \(\boldsymbol g_j \in \mathbb R^p\)是矩阵\(A^T A\)对应于特征值\(l_j\)的单位特征向量(长度等于1的特征向量)。
由线性代数知识,矩阵\(A^T A\)与\(A A^T\)具有相同的正特征值, 且若\(\boldsymbol g_j\)是矩阵\(A^T A\)对应于正特征值\(l_j\)的单位特征向量, 则\(A \boldsymbol g_j \in \mathbb R^n\)是矩阵\(A A^T\)对应于正特征值\(l_j\)的特征向量, 归一化得\(\boldsymbol f_j = l_j^{-1/2} A \boldsymbol g_j\)是矩阵\(A A^T\)对应于正特征值\(l_j\)的单位特征向量。
设\(\boldsymbol f_j\)是矩阵\(A A^T\)对应于正特征值\(l_j\)的单位特征向量, 则\(\boldsymbol g_j = l_j^{-1/2} A^T \boldsymbol f_j\)是矩阵\(A^T A\)对应于正特征值\(l_j\)的特征向量。
\(A\)有奇异值分解 \[\begin{aligned} A = F \Lambda G^T = \sum_{j=1}^p l_j^{1/2} \boldsymbol f_j \boldsymbol g_j^T, \end{aligned}\] 其中\(\Lambda = \text{diag}(l_1^{1/2}, l_2^{1/2}, \dots, l_p^{1/2})\), \(G = (\boldsymbol g_1, \dots, \boldsymbol g_p)\), \(F = (\boldsymbol f_1, \dots, \boldsymbol f_p)\)。
在R型主成分分析中, 第\(j\)个R型主成分得分为 \[\begin{align*} M_C \boldsymbol g_j = n^{1/2} A \boldsymbol g_j = n^{1/2} l_j^{1/2} \boldsymbol f_j, j=1,2,\dots, p. \end{align*}\]
在根据\(M_C\)作的Q型主成分分析中, 第\(j\)个Q型主成分得分为 \[\begin{align*} M_C^T \boldsymbol f_j = n^{1/2} A^T \boldsymbol f_j = n^{1/2} l_j^{1/2} \boldsymbol g_j , j=1,2,\dots, p. \end{align*}\]
8.5.2 双重散点图
若仅取前两个R型主成分得分,得 \[\begin{aligned} M_C = n^{1/2} A \approx n^{1/2} l_1^{1/2} \boldsymbol f_1 \boldsymbol g_1^T + n^{1/2} l_2^{1/2} \boldsymbol f_2 \boldsymbol g_2^T, \end{aligned}\] 其中\(n^{1/2} l_1^{1/2} \boldsymbol f_1 = M_C \boldsymbol g_1\)是第一主成分得分\(\boldsymbol s_1\), \(n^{1/2} l_2^{1/2} \boldsymbol f_2 = M_C \boldsymbol g_2\)是第二主成分得分\(\boldsymbol s_2\), 所以 \[\begin{align*} M_C \approx \boldsymbol s_1 \boldsymbol g_1^T + \boldsymbol s_2 \boldsymbol g_2^T . \end{align*}\]
可以在\((s_{i1}, s_{i2})\)坐标画散点, 把\(n\)个观测画成散点图。
注意第\(j\)个Q型主成分\(n^{1/2} l_j^{1/2} \boldsymbol g_j\) 就是载荷阵\(G\)的第\(j\)列的伸缩。
取\((g_{j1}, g_{j2})\)为第\(j\)个变量的坐标, 在原来观测的主成分的散点图上画从原点到 \((g_{j1}, g_{j2})\)的矢量, 这样的图形叫做双重散点图(biplot)。 当某个变量与某个观测接近时, 表示该变量在该观测上取值较大。 关于这一点将在“对应分析”部分更详细地阐述。
8.6 主成分分析的做法
8.6.1 主成分分析的步骤
- 选择是否标准化数据;
- 计算样本协方差阵或相关阵;
- 求\(S\)或\(R\)的特征值分解;
- 按主成分累积贡献率超过80%(或其它满意的比例)的要求确定主成分的个数\(k\);
- 计算各个主成分得分;
- 对分析结果做统计意义和实际意义的解释。
- 实际计算时用R函数计算,这些步骤已经被整合在一些R函数中。
8.6.2 R中的有关函数
R中用princomp()函数进行主成分分析。
用cor=选择是否进行标准化,
用scores=选择是否输出主成分得分。
summary()函数显示主成分分析的概况,
用loadings=TRUE要求显示载荷,
即主成分线性组合系数,
也即特征向量。
loadings()单独输出载荷。
predict()函数用来对训练数据或新数据计算主成分得分。
注意:计算主成分得分时,都按训练数据的列均值进行中心化。
screeplot()函数显示从大到小排列的特征值的线图或条形图,
便于在特征值骤减的位置截断从而确定主成分个数。
取前两个主成分时,
用biplot()函数作双重散点图(biplot)。
8.6.3 例6.1(学生六科成绩的主成分分析)
P.83例6.1, 数据为52名学生的数学(x1)、物理(x2)、化学(x3)、语文(x4)、历史(x5)和英语(x6)的成绩。 作主成分分析。
读入数据,变量名用有意义的短名:
student6Score <- readr::read_csv("data/学生六科成绩.csv",
show_col_types = FALSE)
names(student6Score) <- c(
"数学", "物理", "化学", "语文", "历史", "英语")
d <- student6Score显示数据:
| 数学 | 物理 | 化学 | 语文 | 历史 | 英语 |
|---|---|---|---|---|---|
| 65 | 61 | 72 | 84 | 81 | 79 |
| 77 | 77 | 76 | 64 | 70 | 55 |
| 67 | 63 | 49 | 65 | 67 | 57 |
| 78 | 84 | 75 | 62 | 71 | 64 |
| 66 | 71 | 67 | 52 | 65 | 57 |
| 83 | 100 | 79 | 41 | 67 | 50 |
| 86 | 94 | 97 | 51 | 63 | 55 |
| 67 | 84 | 53 | 58 | 66 | 56 |
| 69 | 56 | 67 | 75 | 94 | 80 |
| 77 | 90 | 80 | 68 | 66 | 60 |
| 84 | 67 | 75 | 60 | 70 | 63 |
| 62 | 67 | 83 | 71 | 85 | 77 |
| 91 | 74 | 97 | 62 | 71 | 66 |
| 82 | 70 | 83 | 68 | 77 | 85 |
| 66 | 61 | 77 | 62 | 73 | 64 |
| 90 | 78 | 78 | 59 | 72 | 66 |
| 77 | 89 | 80 | 73 | 75 | 70 |
| 72 | 68 | 77 | 83 | 92 | 79 |
| 72 | 67 | 61 | 92 | 92 | 88 |
| 81 | 90 | 79 | 73 | 85 | 80 |
| 68 | 85 | 70 | 84 | 89 | 86 |
| 85 | 91 | 95 | 63 | 76 | 66 |
| 91 | 85 | 100 | 70 | 65 | 76 |
| 74 | 74 | 84 | 61 | 80 | 69 |
| 88 | 100 | 85 | 49 | 71 | 66 |
| 87 | 84 | 100 | 74 | 81 | 76 |
| 64 | 79 | 64 | 72 | 76 | 74 |
| 60 | 51 | 60 | 78 | 74 | 76 |
| 59 | 75 | 81 | 82 | 77 | 73 |
| 64 | 61 | 49 | 100 | 99 | 95 |
| 56 | 48 | 61 | 85 | 82 | 80 |
| 62 | 45 | 67 | 78 | 76 | 82 |
| 86 | 78 | 92 | 87 | 87 | 77 |
| 80 | 98 | 83 | 58 | 66 | 66 |
| 83 | 71 | 81 | 63 | 77 | 73 |
| 67 | 83 | 65 | 68 | 74 | 60 |
| 71 | 58 | 45 | 83 | 77 | 73 |
| 90 | 83 | 91 | 58 | 60 | 59 |
| 73 | 80 | 64 | 75 | 80 | 78 |
| 87 | 98 | 87 | 68 | 78 | 64 |
| 69 | 72 | 79 | 89 | 82 | 73 |
| 79 | 73 | 69 | 65 | 73 | 73 |
| 87 | 86 | 88 | 70 | 73 | 70 |
| 76 | 61 | 73 | 63 | 60 | 70 |
| 99 | 100 | 99 | 53 | 63 | 60 |
| 78 | 68 | 52 | 75 | 74 | 66 |
| 72 | 90 | 73 | 76 | 80 | 79 |
| 69 | 64 | 60 | 68 | 74 | 80 |
| 52 | 62 | 65 | 100 | 96 | 100 |
| 70 | 72 | 56 | 74 | 82 | 74 |
| 72 | 74 | 75 | 88 | 91 | 86 |
| 68 | 74 | 70 | 87 | 87 | 83 |
每列中心化:
每列标准化:
8.6.3.1 用方差阵作主成分分析
因为是分数,是可比的,所以可以用样本方差阵, 方差阵估计:
| 数学 | 物理 | 化学 | 语文 | 历史 | 英语 | |
|---|---|---|---|---|---|---|
| 数学 | 108.63 | 92.46 | 100.64 | -74.69 | -44.72 | -48.67 |
| 物理 | 92.46 | 188.23 | 109.00 | -88.13 | -45.33 | -66.87 |
| 化学 | 100.64 | 109.00 | 192.46 | -67.30 | -35.75 | -35.99 |
| 语文 | -74.69 | -88.13 | -67.30 | 163.38 | 97.88 | 113.57 |
| 历史 | -44.72 | -45.33 | -35.75 | 97.88 | 88.64 | 82.05 |
| 英语 | -48.67 | -66.87 | -35.99 | 113.57 | 82.05 | 113.30 |
用图形方式显示方差阵:
library(tidyverse)
dgg <- tibble(
x = rep(1:6, 6),
y = rep(1:6, each=6),
Cov = c(as.matrix(var(d)))) %>%
mutate(
x = factor(x, levels=1:6, labels=names(d)),
y = factor(y, levels=6:1, labels=rev(names(d))))
ggplot(data=dgg, mapping=aes(x=x, y=y, fill=Cov)) +
geom_raster() +
scale_fill_gradient2() +
labs(x=NULL, y=NULL)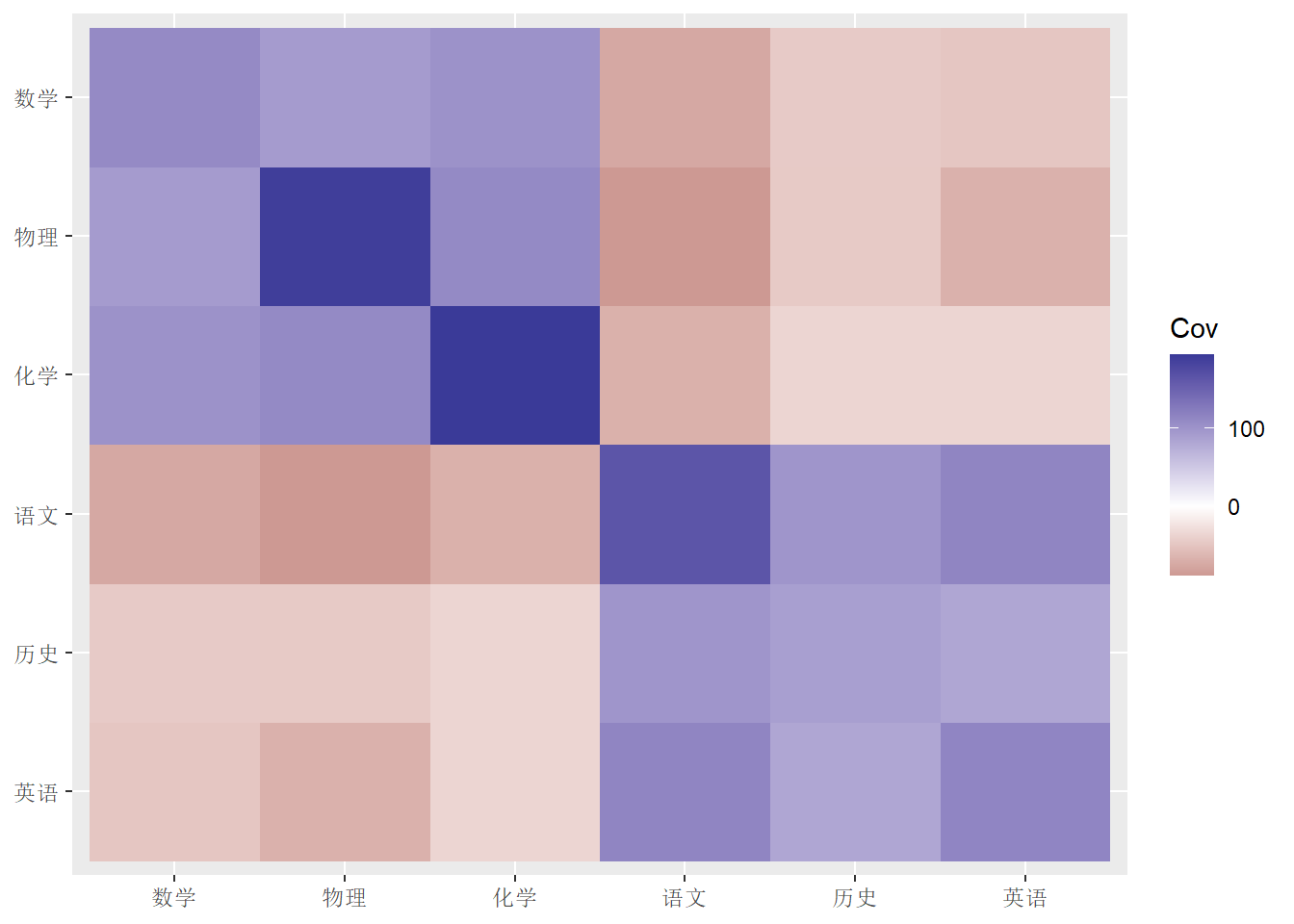
计算主成分分析:
用方差阵得到的主成分结果:
## Call:
## princomp(x = d, cor = FALSE)
##
## Standard deviations:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 22.636 13.326 8.807 5.790 4.610 3.985
##
## 6 variables and 52 observations.## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## Standard deviation 22.6360 13.3263 8.80699 5.7900 4.61027 3.98464
## Proportion of Variance 0.6113 0.2119 0.09254 0.0400 0.02536 0.01894
## Cumulative Proportion 0.6113 0.8232 0.91570 0.9557 0.98106 1.00000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 数学 0.373 0.205 0.121 0.882 0.112 0.120
## 物理 0.482 0.288 -0.802 -0.143 -0.147
## 化学 0.440 0.588 0.541 -0.407
## 语文 -0.471 0.432 -0.125 0.759
## 历史 -0.298 0.383 -0.184 -0.458 0.721
## 英语 -0.352 0.444 0.190 -0.448 -0.664结果中有各主成分的标准差,贡献率,累积贡献率。 可以看出前两个主成分累积贡献率达到82%, 第一主成分贡献率为61%。 从载荷看, 第一主成分在理科上系数为正,在文科上系数为负,反映了学生理科相对于文科的优势。 第二主成分都为正数且值相近,反映学生所有六科的整体水平。
注意:得到载荷阵后, 经常可以用每一列的系数来解释每一个对应的主成分含义。 当数据确实有很强的变量分类时, 这可能是有意义的。 但是, 大多数情况下, 这些系数只是数学上矩阵特征值分解的结果, 并不保证能够有实际解释, 及时能有听起来合理的解释, 也可能仅是巧合, 数据的随机扰动就有可能修改系数造成不同的解释。
单独用loadings()函数显示载荷阵:
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 数学 0.373 0.205 0.121 0.882 0.112 0.120
## 物理 0.482 0.288 -0.802 -0.143 -0.147
## 化学 0.440 0.588 0.541 -0.407
## 语文 -0.471 0.432 -0.125 0.759
## 历史 -0.298 0.383 -0.184 -0.458 0.721
## 英语 -0.352 0.444 0.190 -0.448 -0.664
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.167 0.167 0.167 0.167 0.167 0.167
## Cumulative Var 0.167 0.333 0.500 0.667 0.833 1.000loadings函数显示的第二部分没有什么用处。
screeplot()用于帮助确定主成分个数:
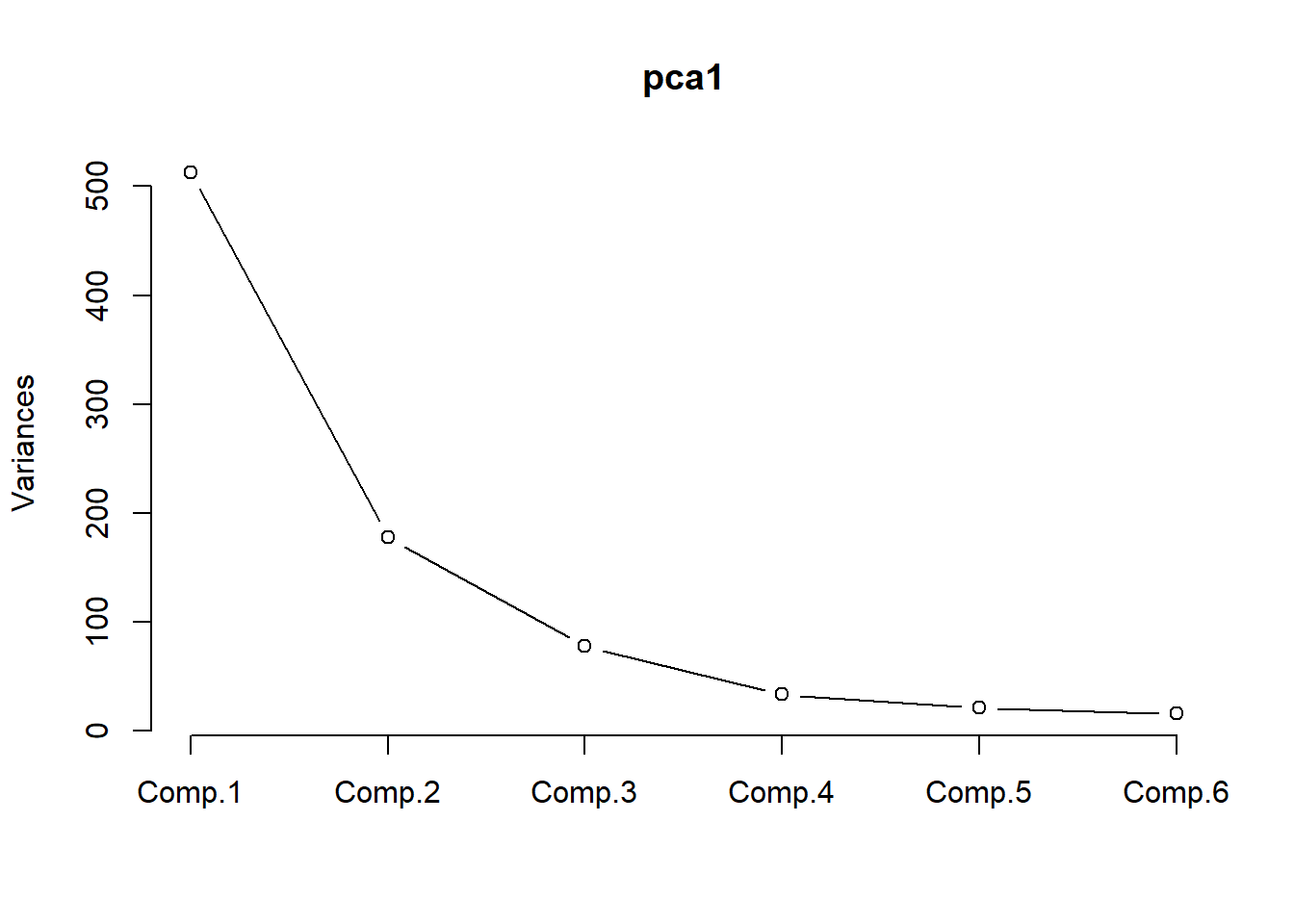
或者:
library(tidyverse)
dgg <- tibble(
`主成分` = seq(length(summary(pca1)$sdev)),
`方差` = summary(pca1)$sdev^2,
`方差比例` = `方差` / sum(`方差`),
`累计方差比例` = cumsum(`方差比例`))
ggplot(data=dgg, mapping=aes(
x=`主成分`, y = `方差`)) +
geom_line() +
geom_point()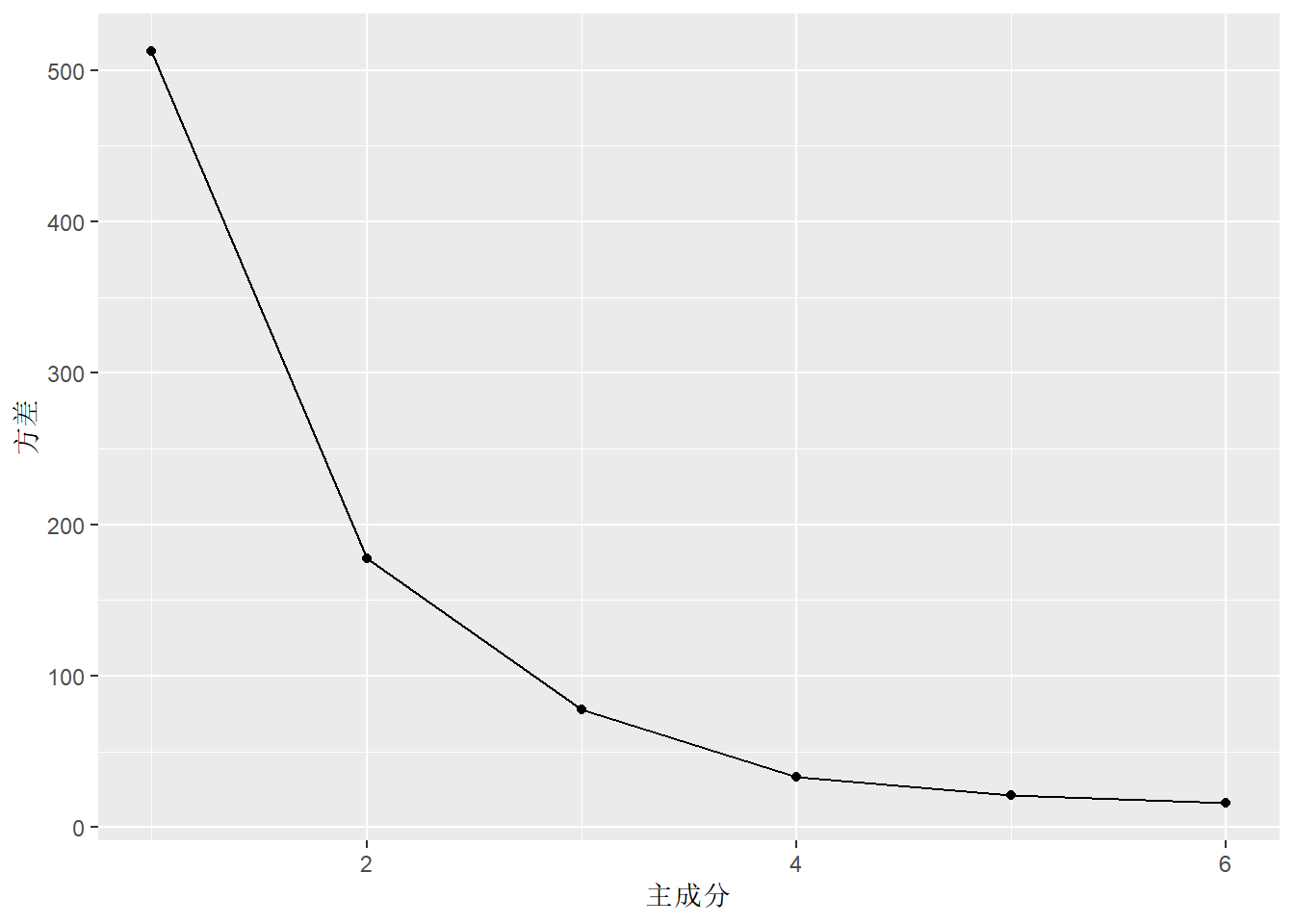
也可以画成百分比:
ggplot(data=dgg, mapping=aes(
x=`主成分`, y = `方差比例`)) +
geom_line() +
geom_point() +
scale_y_continuous(labels = scales::percent)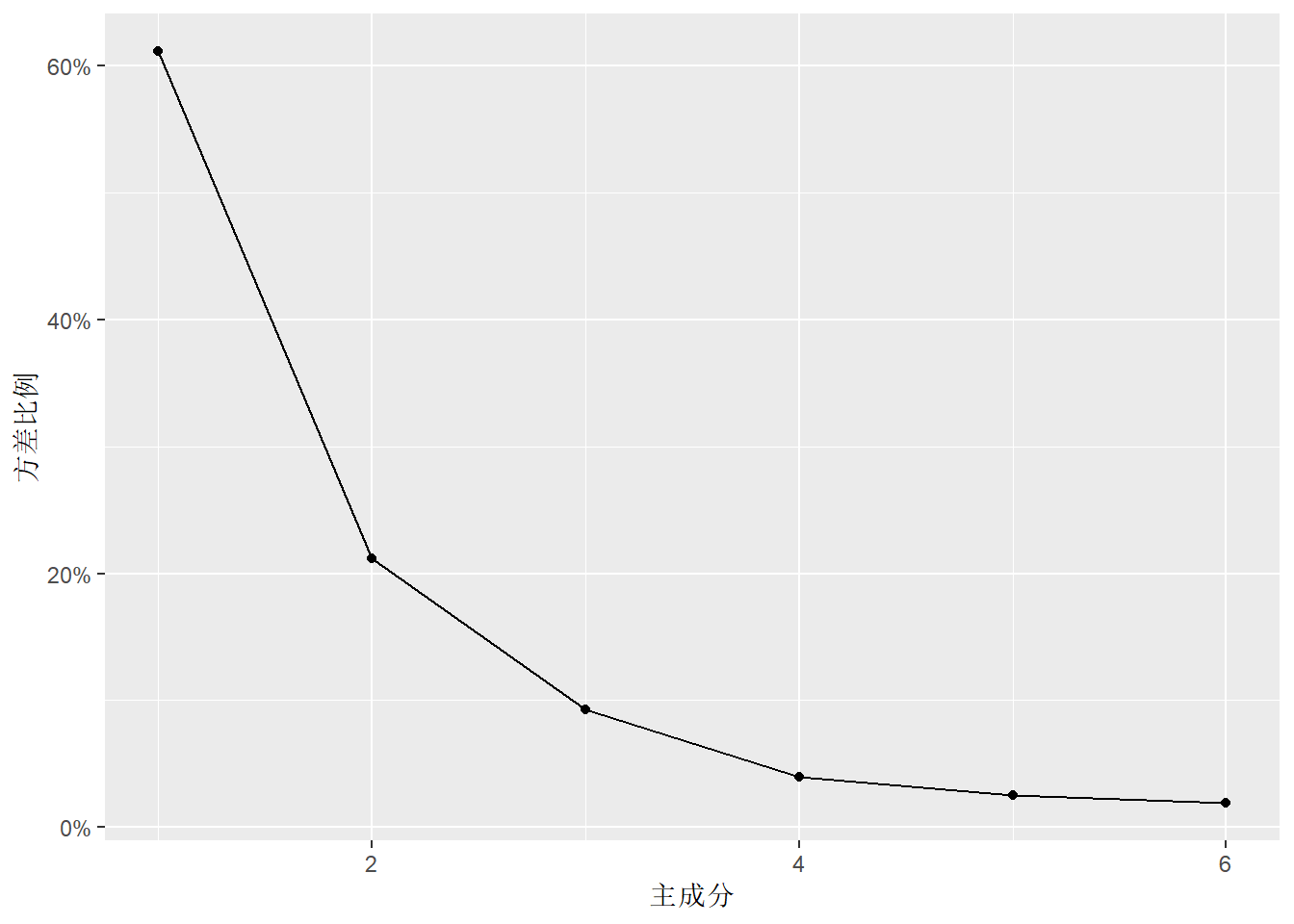
也可以做方差累计比例图:
ggplot(data=dgg, mapping=aes(
x=`主成分`, y = `累计方差比例`)) +
geom_line() +
geom_point() +
scale_y_continuous(
limits=c(0, NA),
labels = scales::percent)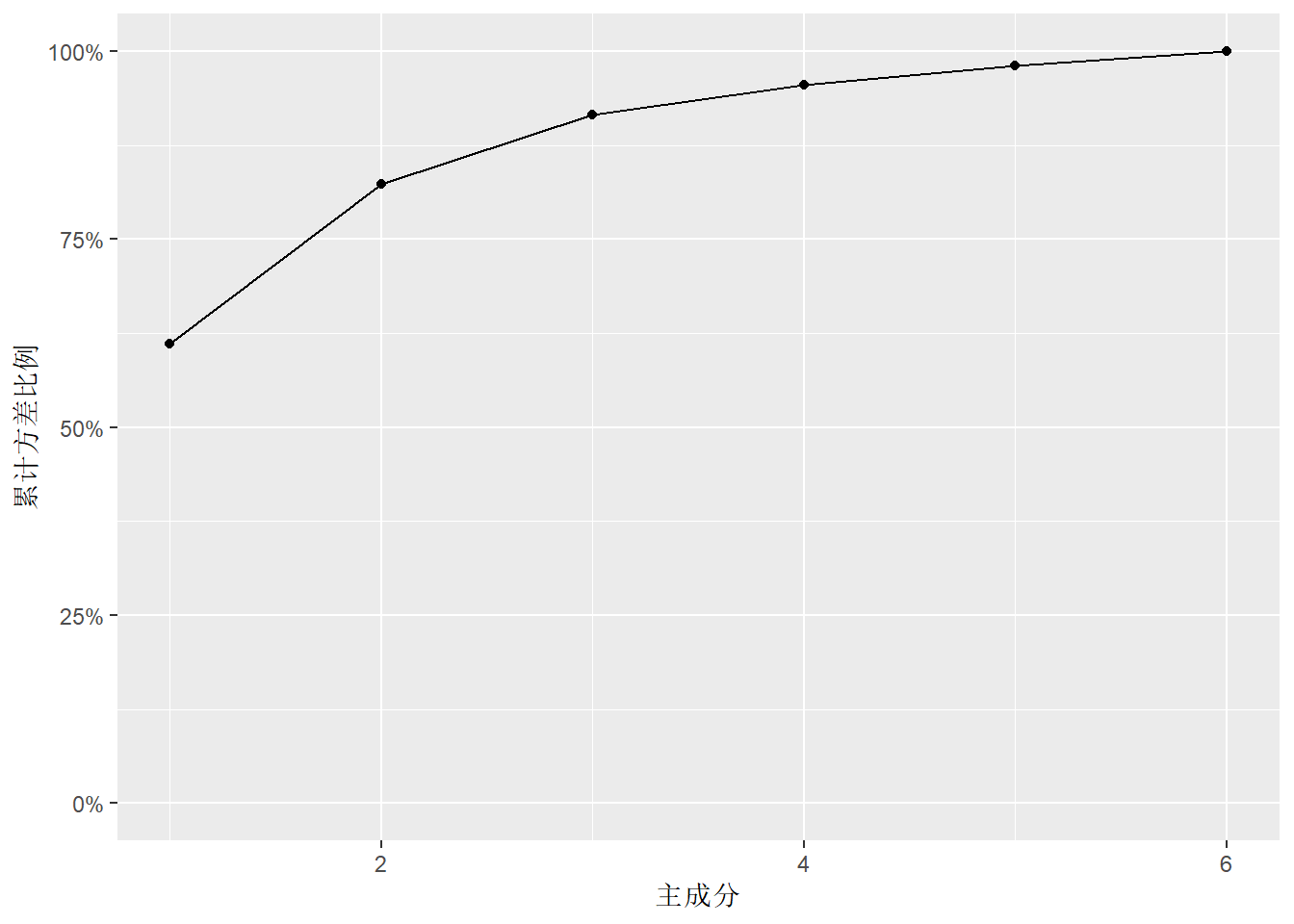
计算前两个主成分的主成分得分:
| id | 数学 | 物理 | 化学 | 语文 | 历史 | 英语 | Comp.1 | Comp.2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 65 | 61 | 72 | 84 | 81 | 79 | -22.02 | 2.65 |
| 2 | 77 | 77 | 76 | 64 | 70 | 55 | 13.09 | -11.42 |
| 3 | 67 | 63 | 49 | 65 | 67 | 57 | -9.55 | -33.20 |
| 4 | 78 | 84 | 75 | 62 | 71 | 64 | 13.87 | -6.28 |
| 5 | 66 | 71 | 67 | 52 | 65 | 57 | 8.57 | -26.90 |
| 6 | 83 | 100 | 79 | 41 | 67 | 50 | 41.22 | -15.10 |
| 7 | 86 | 94 | 97 | 51 | 63 | 55 | 42.09 | -0.63 |
| 8 | 67 | 84 | 53 | 58 | 66 | 56 | 6.28 | -28.65 |
| 9 | 69 | 56 | 67 | 75 | 94 | 80 | -25.12 | 0.63 |
| 10 | 77 | 90 | 80 | 68 | 66 | 60 | 18.66 | -2.92 |
| 11 | 84 | 67 | 75 | 60 | 70 | 63 | 9.51 | -11.64 |
| 12 | 62 | 67 | 83 | 71 | 85 | 77 | -9.77 | 5.26 |
| 13 | 91 | 74 | 97 | 62 | 71 | 66 | 22.87 | 7.32 |
| 14 | 82 | 70 | 83 | 68 | 77 | 85 | 0.12 | 9.41 |
| 15 | 66 | 61 | 77 | 62 | 73 | 64 | -1.41 | -13.42 |
| 16 | 90 | 78 | 78 | 59 | 72 | 66 | 17.18 | -3.81 |
| 17 | 77 | 89 | 80 | 73 | 75 | 70 | 9.61 | 6.84 |
| 18 | 72 | 68 | 77 | 83 | 92 | 79 | -16.64 | 12.82 |
| 19 | 72 | 67 | 61 | 92 | 92 | 88 | -31.57 | 11.00 |
| 20 | 81 | 90 | 79 | 73 | 85 | 80 | 4.64 | 15.62 |
| 21 | 68 | 85 | 70 | 84 | 89 | 86 | -15.07 | 15.17 |
| 22 | 85 | 91 | 95 | 63 | 76 | 66 | 25.98 | 12.16 |
| 23 | 91 | 85 | 100 | 70 | 65 | 76 | 23.99 | 17.84 |
| 24 | 74 | 74 | 84 | 61 | 80 | 69 | 7.54 | 0.54 |
| 25 | 88 | 100 | 85 | 49 | 71 | 66 | 35.13 | 1.53 |
| 26 | 87 | 84 | 100 | 74 | 81 | 76 | 15.36 | 24.59 |
| 27 | 64 | 79 | 64 | 72 | 76 | 74 | -8.33 | -6.39 |
| 28 | 60 | 51 | 60 | 78 | 74 | 76 | -28.01 | -14.91 |
| 29 | 59 | 75 | 81 | 82 | 77 | 73 | -9.31 | 5.68 |
| 30 | 64 | 61 | 49 | 100 | 99 | 95 | -51.05 | 9.82 |
| 31 | 56 | 48 | 61 | 85 | 82 | 80 | -37.61 | -8.15 |
| 32 | 62 | 45 | 67 | 78 | 76 | 82 | -29.79 | -8.69 |
| 33 | 86 | 78 | 92 | 87 | 87 | 77 | 0.31 | 26.30 |
| 34 | 80 | 98 | 83 | 58 | 66 | 66 | 27.55 | 0.11 |
| 35 | 83 | 71 | 81 | 63 | 77 | 73 | 6.68 | 1.25 |
| 36 | 67 | 83 | 65 | 68 | 74 | 60 | 2.57 | -12.73 |
| 37 | 71 | 58 | 45 | 83 | 77 | 73 | -29.32 | -17.48 |
| 38 | 90 | 83 | 91 | 58 | 60 | 59 | 31.83 | -2.86 |
| 39 | 73 | 80 | 64 | 75 | 80 | 78 | -8.51 | 0.35 |
| 40 | 87 | 98 | 87 | 68 | 78 | 64 | 24.34 | 11.92 |
| 41 | 69 | 72 | 79 | 89 | 82 | 73 | -12.69 | 10.63 |
| 42 | 79 | 73 | 69 | 65 | 73 | 73 | 1.12 | -6.72 |
| 43 | 87 | 86 | 88 | 70 | 73 | 70 | 17.43 | 10.66 |
| 44 | 76 | 61 | 73 | 63 | 60 | 70 | 1.85 | -15.61 |
| 45 | 99 | 100 | 99 | 53 | 63 | 60 | 48.01 | 8.01 |
| 46 | 78 | 68 | 52 | 75 | 74 | 66 | -11.68 | -16.76 |
| 47 | 72 | 90 | 73 | 76 | 80 | 79 | -0.93 | 9.19 |
| 48 | 69 | 64 | 60 | 68 | 74 | 80 | -15.09 | -11.86 |
| 49 | 52 | 62 | 65 | 100 | 96 | 100 | -48.88 | 18.12 |
| 50 | 70 | 72 | 56 | 74 | 82 | 74 | -15.72 | -8.71 |
| 51 | 72 | 74 | 75 | 88 | 91 | 86 | -19.16 | 18.25 |
| 52 | 68 | 74 | 70 | 87 | 87 | 83 | -20.13 | 11.20 |
用前两个主成分作散点图:
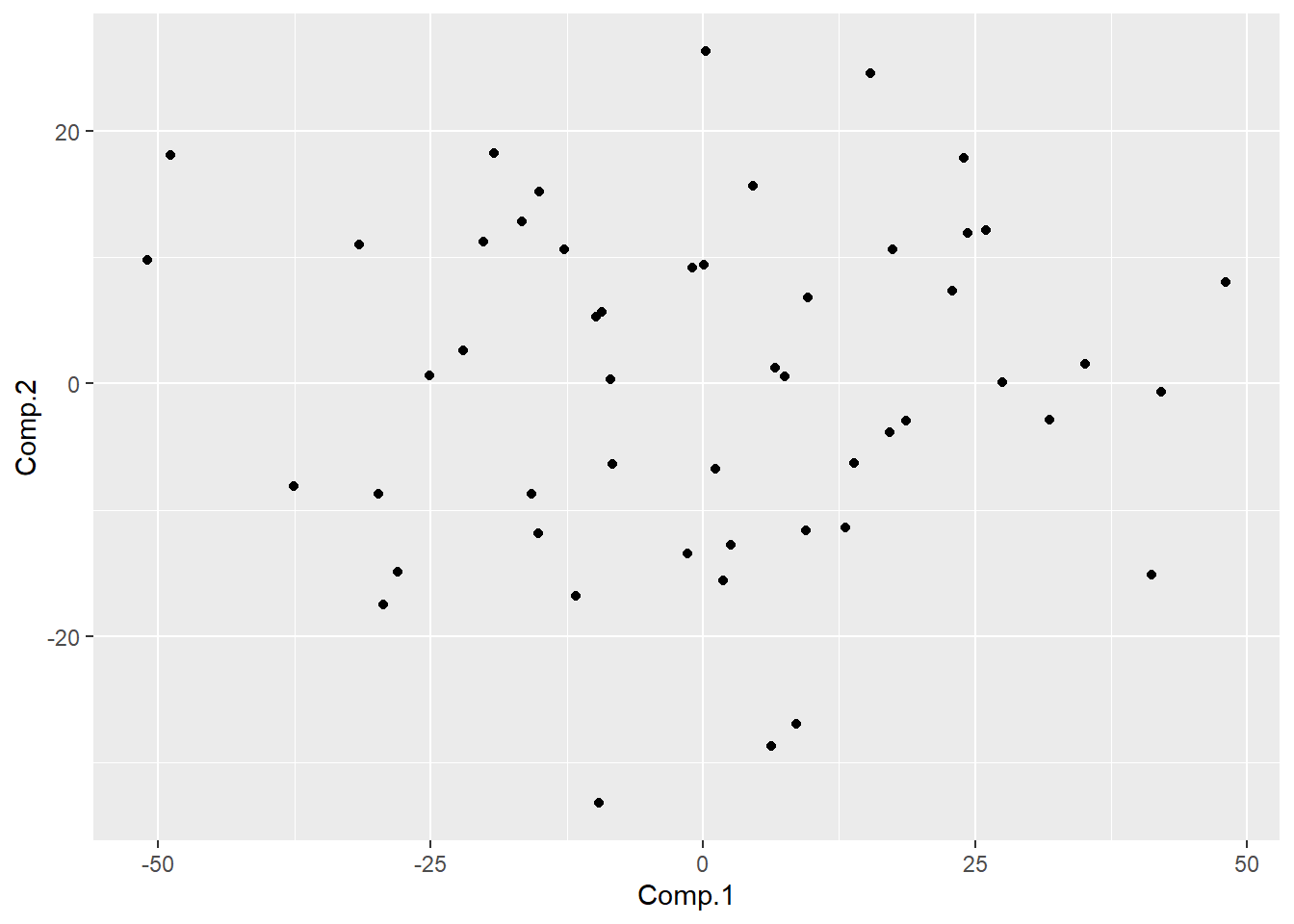
显示编号:
library(ggplot2)
library(ggrepel)
ggplot(data=da1, mapping=aes(
x = Comp.1, y = Comp.2, label=id)) +
geom_text_repel() +
geom_point(alpha=0.5, color="blue")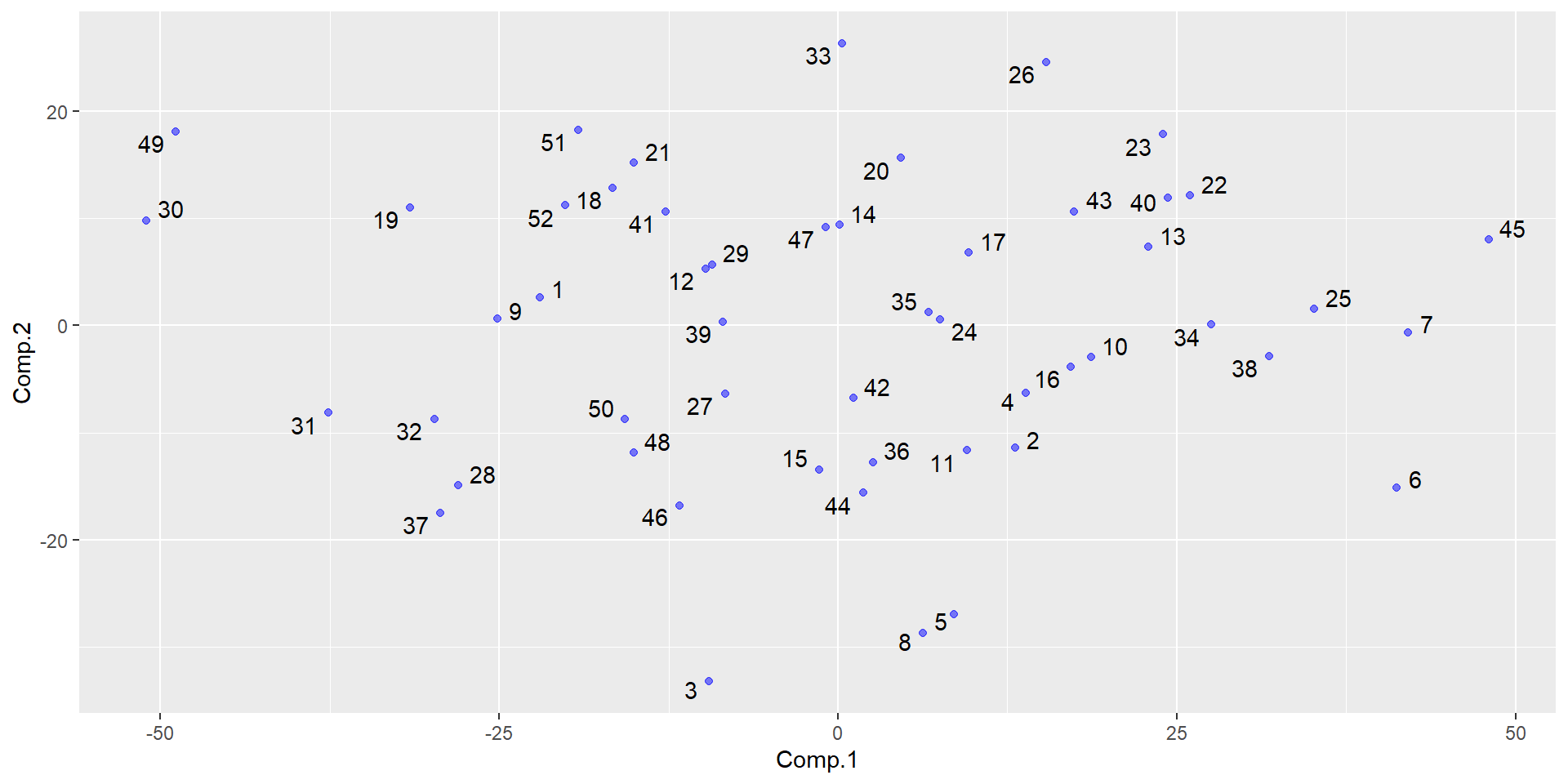
为了验证主成分得分的计算公式, 自己用载荷和中心化数据计算第二主成分:
## [1] 2.65 -11.42 -33.20 -6.28 -26.90 -15.10 -0.63 -28.65 0.63 -2.92
## [11] -11.64 5.26 7.32 9.41 -13.42 -3.81 6.84 12.82 11.00 15.62
## [21] 15.17 12.16 17.84 0.54 1.53 24.59 -6.39 -14.91 5.68 9.82
## [31] -8.15 -8.69 26.30 0.11 1.25 -12.73 -17.48 -2.86 0.35 11.92
## [41] 10.63 -6.72 10.66 -15.61 8.01 -16.76 9.19 -11.86 18.12 -8.71
## [51] 18.25 11.20与predict()结果一致。
显示载荷阵的前两列,作为变量压缩结果(R型主成分分析):
dgl <- loadings(pca1)[,1:2]
plot(dgl, type='n',
xlab='PCA1', ylab='PCA2',
main='Loadings')
text(dgl, rownames(dgl))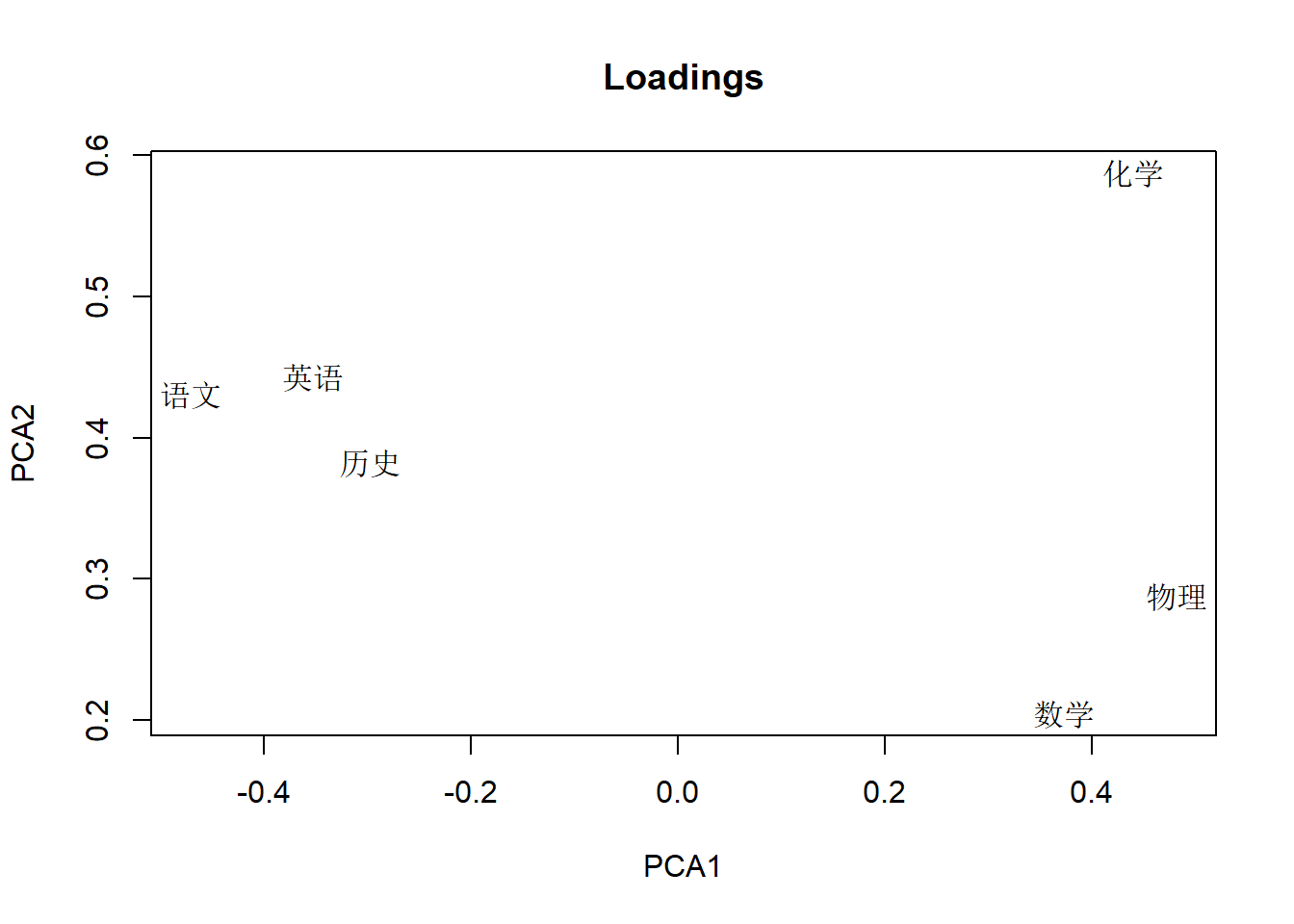
或:
dgl <- as.data.frame(loadings(pca1)[,1:2])
dgl[["varnames"]] <- rownames(dgl)
ggplot(data=dgl, mapping=aes(
x=Comp.1, y=Comp.2, label=varnames)) +
geom_text()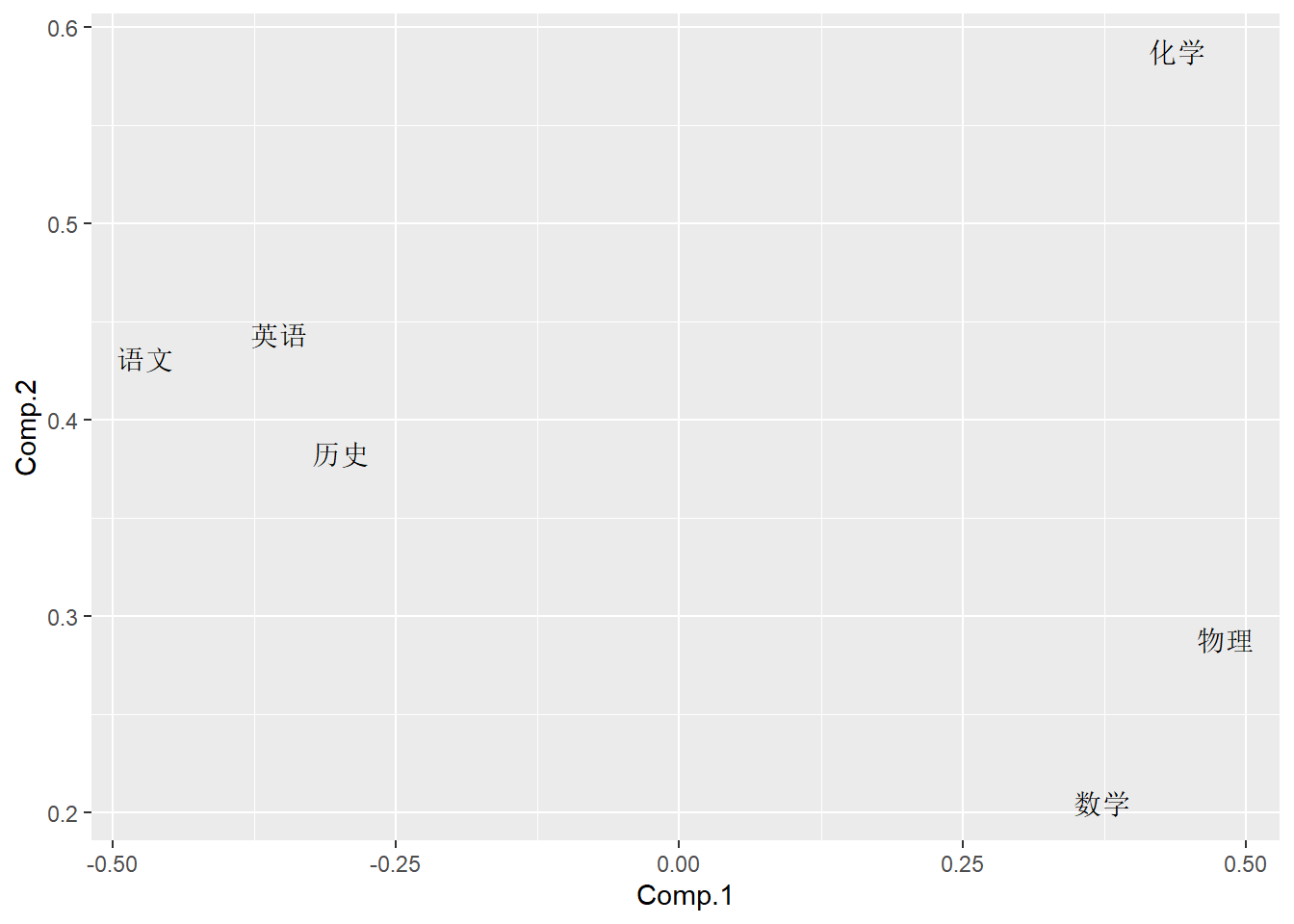
制作双重散点图:
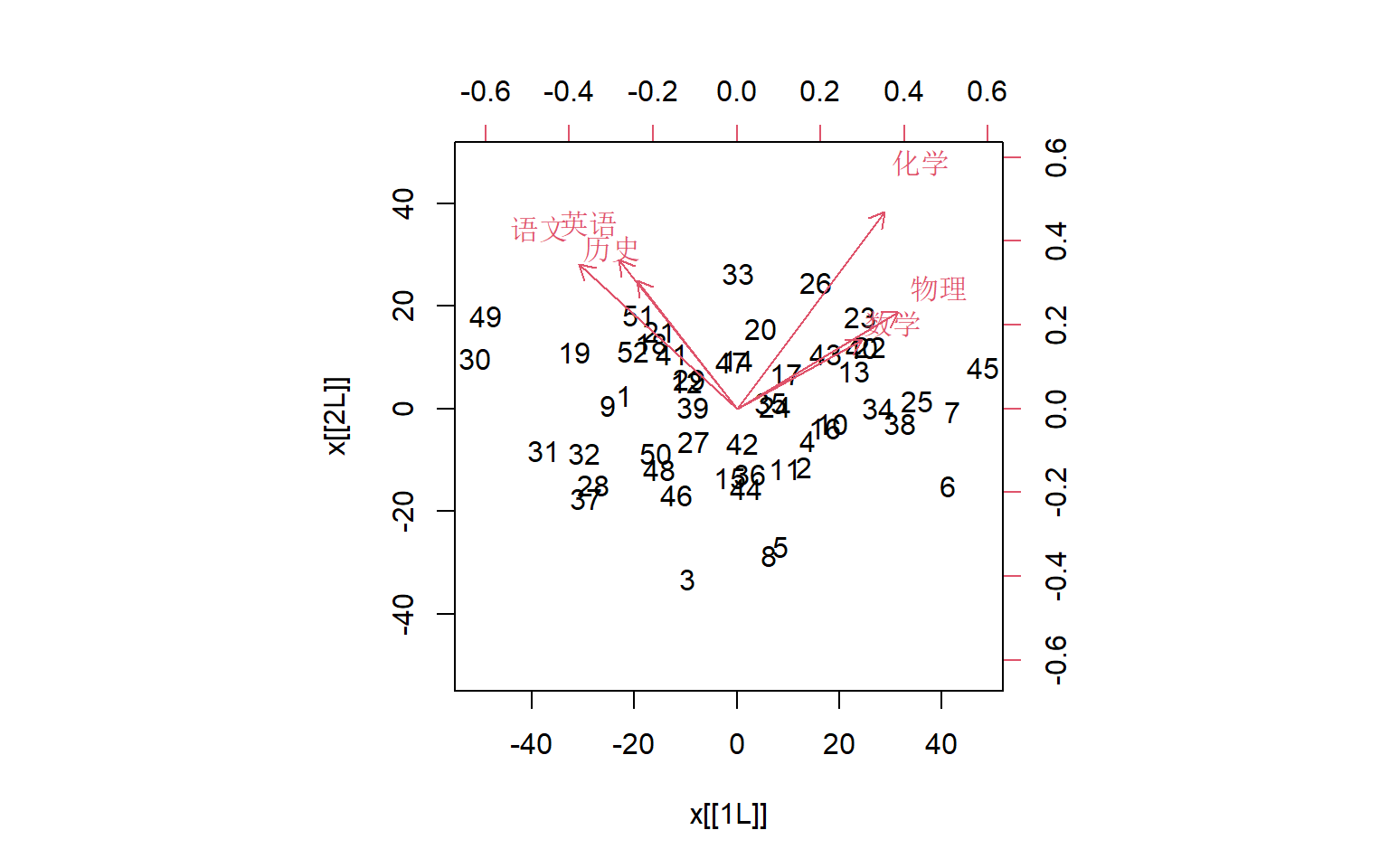
或:
library(ggfortify)
dggd <- as.data.frame(da1[,c("Comp.1", "Comp.2")])
dggl <- as.data.frame(loadings(pca1)[,1:2])
dggl[["varnames"]] <- rownames(loadings(pca1))
ggbiplot(
dggd, dggl,
loadings=TRUE,
loadings.label=TRUE,
loadings.label.label="varnames")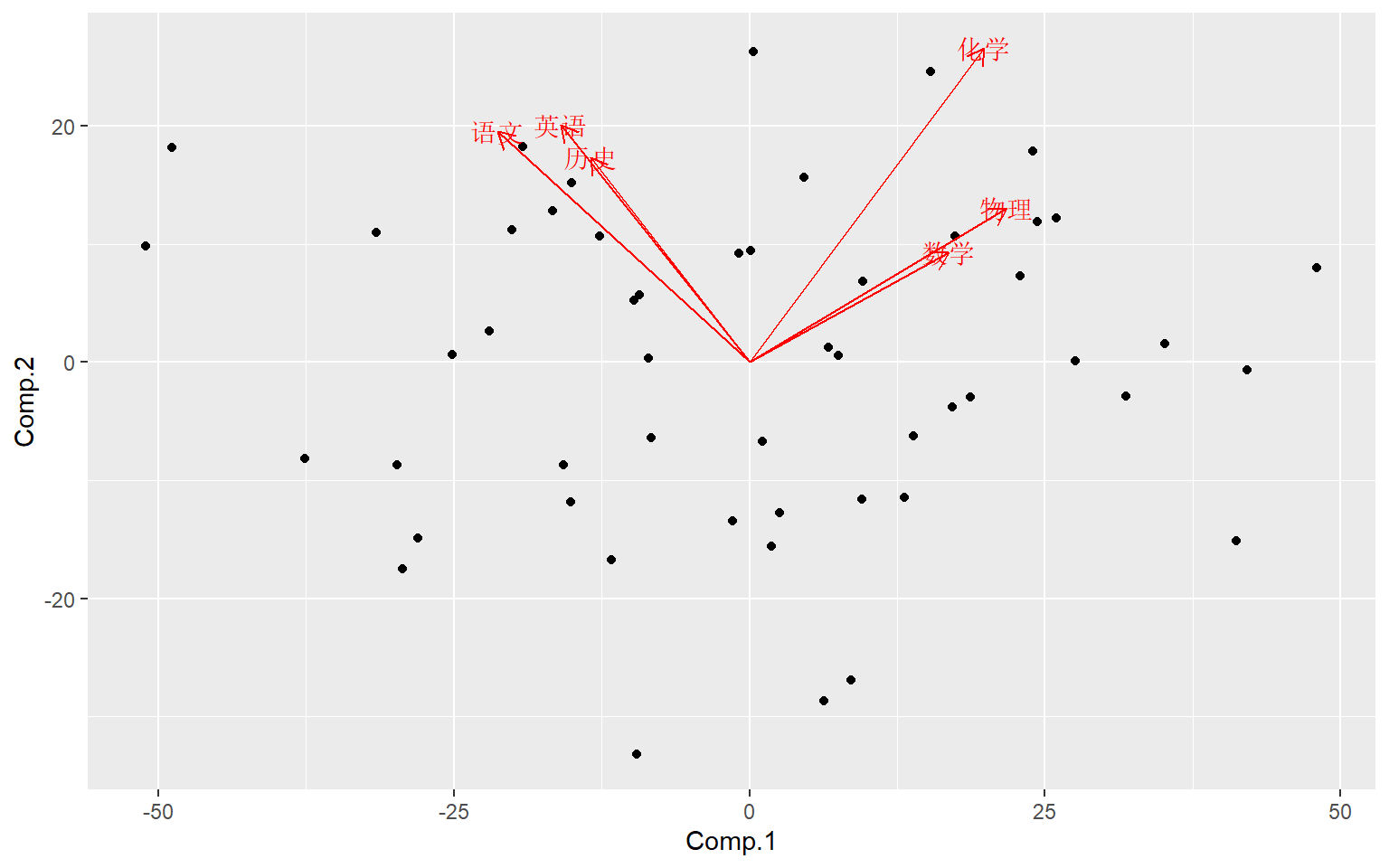
8.6.3.2 用相关阵作主成分分析
上述分析用相关阵重做一遍。 相关阵为:
## 数学 物理 化学 语文 历史 英语
## 数学 1.000 0.647 0.696 -0.561 -0.456 -0.439
## 物理 0.647 1.000 0.573 -0.503 -0.351 -0.458
## 化学 0.696 0.573 1.000 -0.380 -0.274 -0.244
## 语文 -0.561 -0.503 -0.380 1.000 0.813 0.835
## 历史 -0.456 -0.351 -0.274 0.813 1.000 0.819
## 英语 -0.439 -0.458 -0.244 0.835 0.819 1.000相关阵图形:

计算主成分分析结果:
## Call:
## princomp(x = d, cor = TRUE, scores = TRUE)
##
## Standard deviations:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 1.9261112 1.1236019 0.6639552 0.5200978 0.4117231 0.3830929
##
## 6 variables and 52 observations.主成分分析结果pca2中,有如下变量:
- sdev: 主成分的标准差,即各个特征值的平方根
- loadings: 载荷阵,每列是一个特征向量
- center: 中心化所用的中心,应为各列平均值
- scale: 如果做了标准化,所用的除数,应为各列标准差但使用1/n而非1/(n-1)的公式
- n.obs: 观测个数
- scores: 输出的主成分得分(需要scores=TRUE选项)
用summary()输出更详细的结果:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.9261112 1.1236019 0.66395522 0.52009785 0.41172308
## Proportion of Variance 0.6183174 0.2104135 0.07347275 0.04508363 0.02825265
## Cumulative Proportion 0.6183174 0.8287309 0.90220369 0.94728732 0.97553997
## Comp.6
## Standard deviation 0.38309295
## Proportion of Variance 0.02446003
## Cumulative Proportion 1.00000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 数学 0.412 0.376 0.216 0.788 0.145
## 物理 0.381 0.357 -0.806 -0.118 -0.212 -0.141
## 化学 0.332 0.563 0.467 -0.588
## 语文 -0.461 0.279 -0.599 0.590
## 历史 -0.421 0.415 -0.250 0.738 0.205
## 英语 -0.430 0.407 0.146 0.134 -0.222 -0.749结果中有各主成分的标准差,贡献率,累积贡献率。 可以看出前两个主成分累积贡献率达到82%, 第一主成分贡献率为61%。 从载荷看, 第一主成分在理科上系数为负,在文科上系数为正,反映了学生在文理科的相对优势; 第二主成分都为负数且值相近,可以把系数都取相反数,反映学生所有六科的整体水平。
用loadings()函数单独求载荷。pca2$loadings也是:
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 数学 0.412 0.376 0.216 0.788 0.145
## 物理 0.381 0.357 -0.806 -0.118 -0.212 -0.141
## 化学 0.332 0.563 0.467 -0.588
## 语文 -0.461 0.279 -0.599 0.590
## 历史 -0.421 0.415 -0.250 0.738 0.205
## 英语 -0.430 0.407 0.146 0.134 -0.222 -0.749
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.167 0.167 0.167 0.167 0.167 0.167
## Cumulative Var 0.167 0.333 0.500 0.667 0.833 1.000loadings函数的第二部分输出没有什么用处。
用predict()计算前两个主成分的主成分得分, 数据是标准化过的,
pca2$scores也是得分:
| id | 数学 | 物理 | 化学 | 语文 | 历史 | 英语 | Comp.1 | Comp.2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 65 | 61 | 72 | 84 | 81 | 79 | -1.85 | -0.10 |
| 2 | 77 | 77 | 76 | 64 | 70 | 55 | 1.38 | -0.93 |
| 3 | 67 | 63 | 49 | 65 | 67 | 57 | -0.04 | -2.80 |
| 4 | 78 | 84 | 75 | 62 | 71 | 64 | 1.26 | -0.41 |
| 5 | 66 | 71 | 67 | 52 | 65 | 57 | 1.14 | -2.27 |
| 6 | 83 | 100 | 79 | 41 | 67 | 50 | 3.52 | -0.82 |
| 7 | 86 | 94 | 97 | 51 | 63 | 55 | 3.52 | 0.10 |
| 8 | 67 | 84 | 53 | 58 | 66 | 56 | 0.98 | -2.33 |
| 9 | 69 | 56 | 67 | 75 | 94 | 80 | -2.25 | 0.13 |
| 10 | 77 | 90 | 80 | 68 | 66 | 60 | 1.68 | -0.32 |
| 11 | 84 | 67 | 75 | 60 | 70 | 63 | 1.18 | -0.76 |
| 12 | 62 | 67 | 83 | 71 | 85 | 77 | -1.16 | 0.21 |
| 13 | 91 | 74 | 97 | 62 | 71 | 66 | 1.94 | 0.78 |
| 14 | 82 | 70 | 83 | 68 | 77 | 85 | -0.13 | 0.91 |
| 15 | 66 | 61 | 77 | 62 | 73 | 64 | 0.09 | -1.28 |
| 16 | 90 | 78 | 78 | 59 | 72 | 66 | 1.62 | 0.05 |
| 17 | 77 | 89 | 80 | 73 | 75 | 70 | 0.65 | 0.55 |
| 18 | 72 | 68 | 77 | 83 | 92 | 79 | -1.71 | 1.01 |
| 19 | 72 | 67 | 61 | 92 | 92 | 88 | -2.82 | 0.88 |
| 20 | 81 | 90 | 79 | 73 | 85 | 80 | -0.04 | 1.51 |
| 21 | 68 | 85 | 70 | 84 | 89 | 86 | -1.75 | 1.18 |
| 22 | 85 | 91 | 95 | 63 | 76 | 66 | 1.87 | 1.17 |
| 23 | 91 | 85 | 100 | 70 | 65 | 76 | 1.90 | 1.49 |
| 24 | 74 | 74 | 84 | 61 | 80 | 69 | 0.46 | 0.13 |
| 25 | 88 | 100 | 85 | 49 | 71 | 66 | 2.74 | 0.58 |
| 26 | 87 | 84 | 100 | 74 | 81 | 76 | 0.84 | 2.12 |
| 27 | 64 | 79 | 64 | 72 | 76 | 74 | -0.71 | -0.67 |
| 28 | 60 | 51 | 60 | 78 | 74 | 76 | -1.96 | -1.59 |
| 29 | 59 | 75 | 81 | 82 | 77 | 73 | -0.98 | -0.03 |
| 30 | 64 | 61 | 49 | 100 | 99 | 95 | -4.49 | 0.69 |
| 31 | 56 | 48 | 61 | 85 | 82 | 80 | -2.96 | -1.11 |
| 32 | 62 | 45 | 67 | 78 | 76 | 82 | -2.21 | -1.07 |
| 33 | 86 | 78 | 92 | 87 | 87 | 77 | -0.35 | 2.19 |
| 34 | 80 | 98 | 83 | 58 | 66 | 66 | 2.21 | 0.13 |
| 35 | 83 | 71 | 81 | 63 | 77 | 73 | 0.56 | 0.32 |
| 36 | 67 | 83 | 65 | 68 | 74 | 60 | 0.36 | -1.13 |
| 37 | 71 | 58 | 45 | 83 | 77 | 73 | -1.88 | -1.50 |
| 38 | 90 | 83 | 91 | 58 | 60 | 59 | 2.94 | -0.11 |
| 39 | 73 | 80 | 64 | 75 | 80 | 78 | -0.77 | 0.08 |
| 40 | 87 | 98 | 87 | 68 | 78 | 64 | 1.76 | 1.22 |
| 41 | 69 | 72 | 79 | 89 | 82 | 73 | -1.19 | 0.55 |
| 42 | 79 | 73 | 69 | 65 | 73 | 73 | 0.28 | -0.40 |
| 43 | 87 | 86 | 88 | 70 | 73 | 70 | 1.36 | 1.00 |
| 44 | 76 | 61 | 73 | 63 | 60 | 70 | 0.70 | -1.40 |
| 45 | 99 | 100 | 99 | 53 | 63 | 60 | 3.97 | 1.05 |
| 46 | 78 | 68 | 52 | 75 | 74 | 66 | -0.44 | -1.27 |
| 47 | 72 | 90 | 73 | 76 | 80 | 79 | -0.39 | 0.74 |
| 48 | 69 | 64 | 60 | 68 | 74 | 80 | -1.03 | -0.99 |
| 49 | 52 | 62 | 65 | 100 | 96 | 100 | -4.62 | 1.00 |
| 50 | 70 | 72 | 56 | 74 | 82 | 74 | -1.20 | -0.65 |
| 51 | 72 | 74 | 75 | 88 | 91 | 86 | -2.01 | 1.42 |
| 52 | 68 | 74 | 70 | 87 | 87 | 83 | -1.95 | 0.76 |
pca2中scale的值,是\(1/n\)版本的各列标准差:
## 数学 物理 化学 语文 历史 英语
## 10.321675 13.587161 13.738793 12.658624 9.323969 10.541198数据各列样本标准差:
## 数学 物理 化学 语文 历史 英语
## 10.422377 13.719722 13.872833 12.782125 9.414936 10.644042数据各列样本标准差,用\(1/n\)版本:
## 数学 物理 化学 语文 历史 英语
## 10.321675 13.587161 13.738793 12.658624 9.323969 10.541198自己用载荷和标准化数据计算的第二主成分(方差公式修正后):
## [1] -0.09869937 -0.93264526 -2.80445313 -0.40584893 -2.26874265 -0.81974747
## [7] 0.10402783 -2.32640027 0.12983805 -0.32466680 -0.76065098 0.21478424
## [13] 0.78320441 0.90867535 -1.27591036 0.05220103 0.54509667 1.01214990
## [19] 0.87577409 1.50659205 1.18458088 1.17348168 1.48958061 0.12565877
## [25] 0.57906315 2.11740575 -0.66945216 -1.59387782 -0.03447987 0.69279938
## [31] -1.11323328 -1.07153767 2.18736513 0.12884205 0.31668122 -1.13107716
## [37] -1.49590296 -0.10994465 0.08283856 1.22435661 0.54556585 -0.40186537
## [43] 1.00322527 -1.40038695 1.05380785 -1.27115334 0.73806851 -0.99052635
## [49] 0.99651436 -0.65135618 1.42323676 0.75714295screeplot(),用于帮助确定主成分个数:
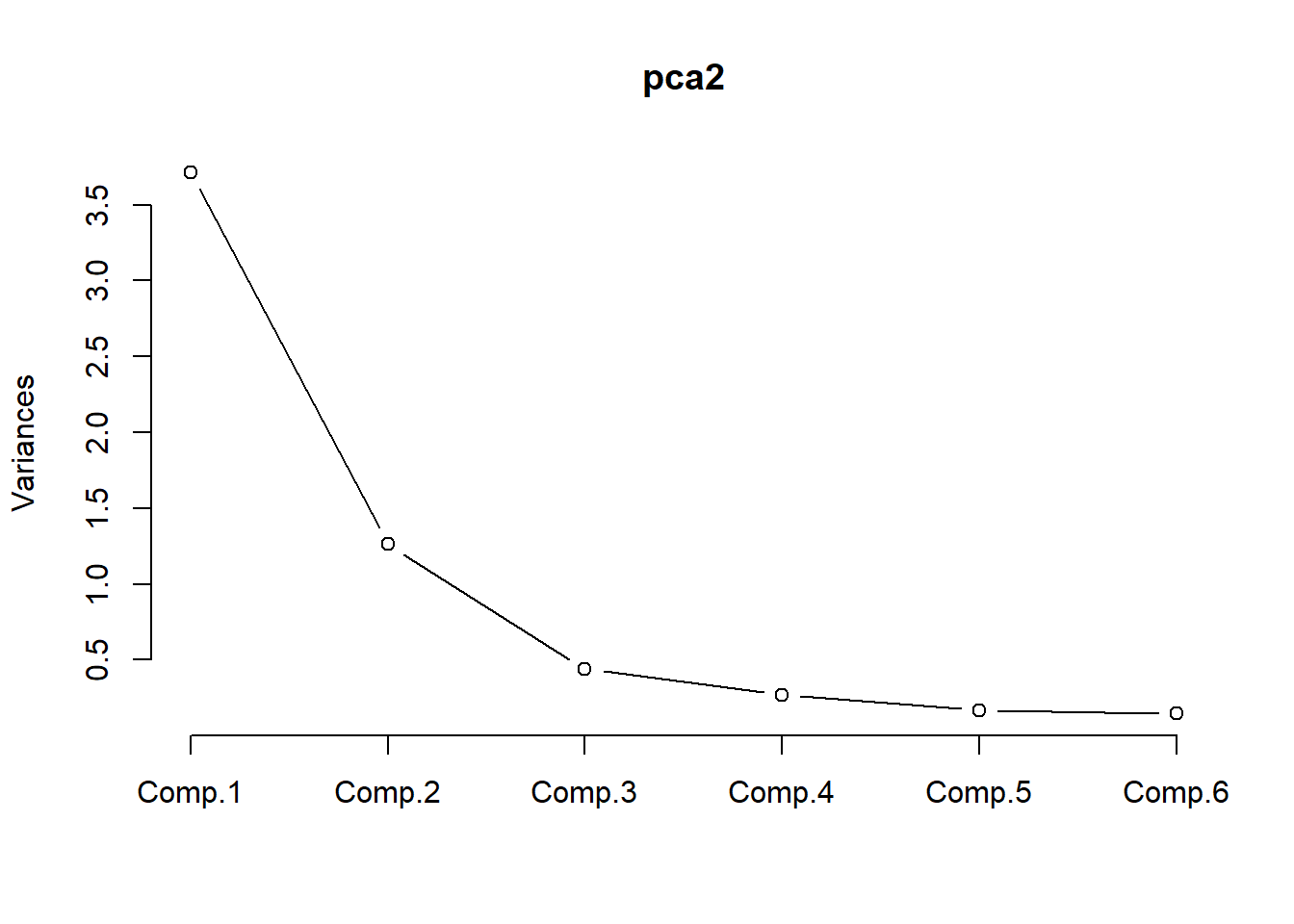
前两个主成分载荷的散点图,可以看出前两个主成分使用各个变量的多少:
load2 <- loadings(pca2)
plot(load2[,1:2], type='n',
xlab='PCA1', ylab='PCA2',
main='Loadings')
text(load2[,1:2], rownames(load2))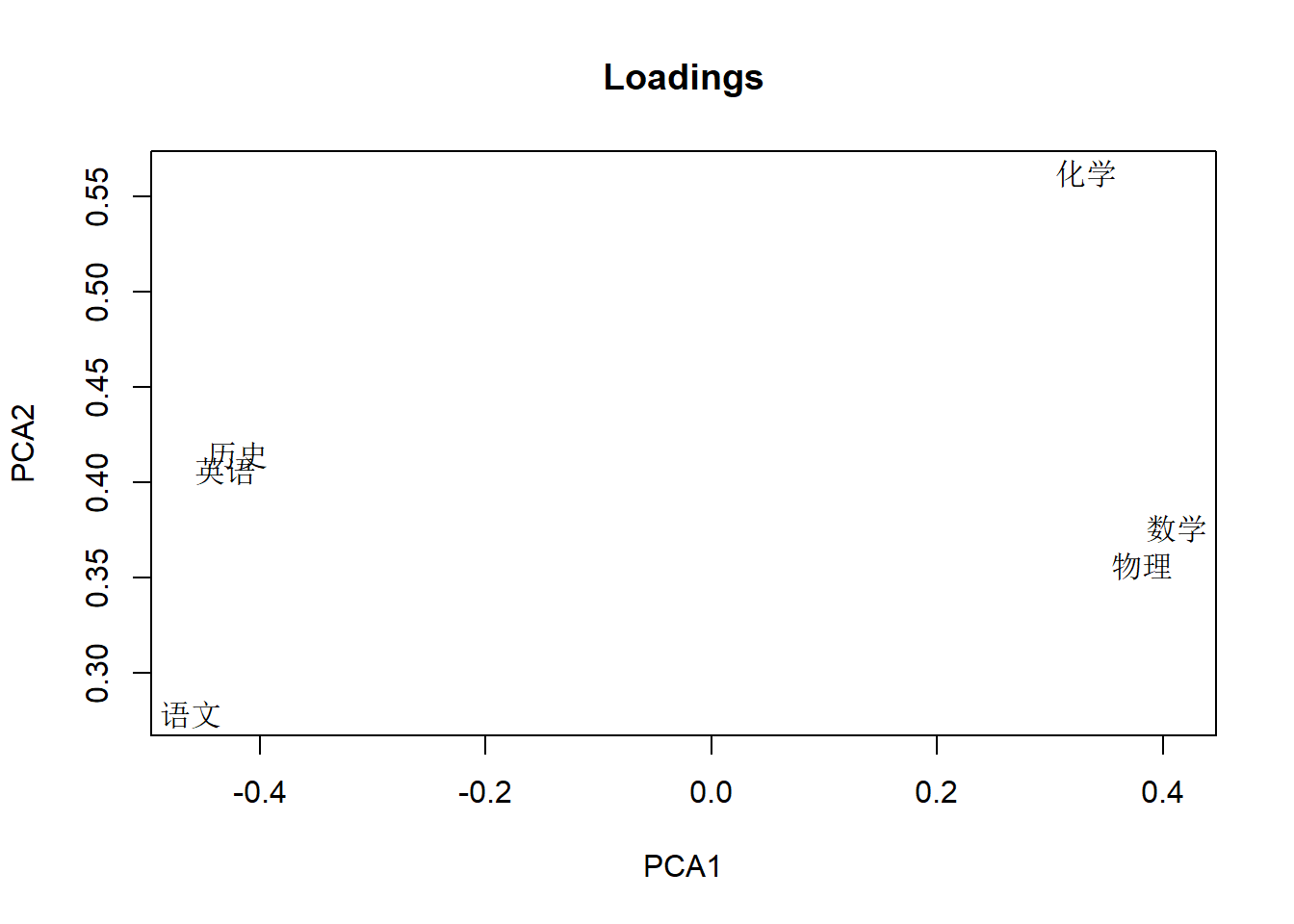
可以看出PCA1受到所有变量的影响,其中x1,x2,x3是负系数,x4,x5,x6是正系数。 PCA2主要受到x3影响,其它几个变量也有影响。
计算corr(PCA[k], X[j]),
在princomp的输出结果中,
元素sdev是各主成分的标准差,即特征值的平方根。
因为用了相关阵,所以sigma[k,k]=1。
rhoxy <- loadings(pca2) %*% diag(pca2$sdev)
plot(rhoxy[,1:2], type='n',
xlim=c(-1,1), ylim=c(-1,1),
asp=1,
xlab='PCA1', ylab='PCA2',
main='Correlations')
tmpx <- seq(0, 2*pi, length=50)
lines(cos(tmpx), sin(tmpx))
text(rhoxy[,1:2], rownames(rhoxy), pty="s")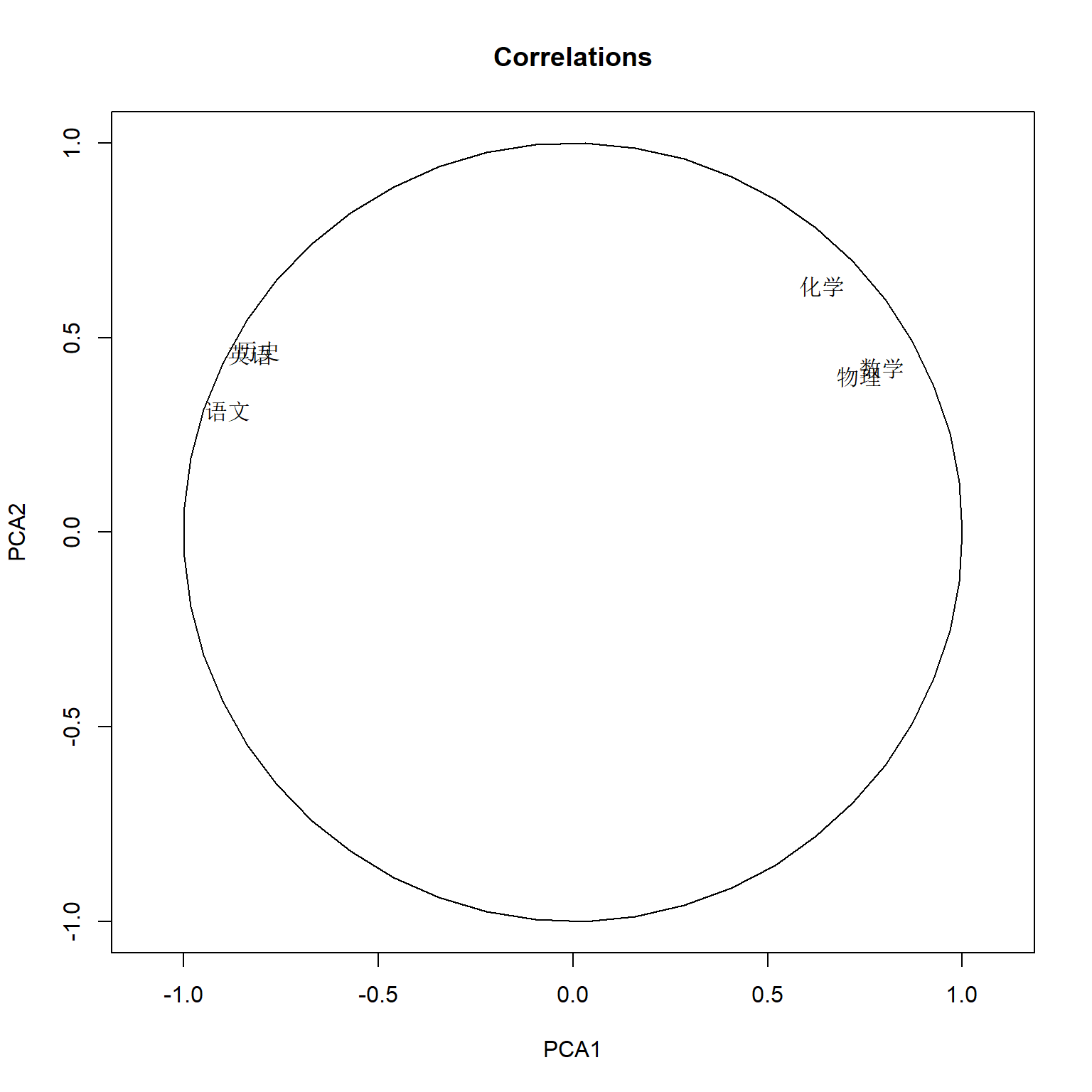 或:
或:
library(tidyverse)
library(ggrepel)
rhoxy <- as.data.frame(loadings(pca2) %*% diag(pca2$sdev))[,1:2]
names(rhoxy) <- c("Comp.1", "Comp.2")
rhoxy[["varnames"]] <- rownames(rhoxy)
dcirc <- tibble(
theta = seq(0, 2*pi, length=100),
x = cos(theta),
y = sin(theta))
ggplot() +
geom_text_repel(data=rhoxy, mapping=aes(
x = Comp.1, y = Comp.2, label=varnames)) +
geom_point(data=rhoxy, mapping=aes(
x = Comp.1, y = Comp.2),
alpha=0.5, color="blue") +
geom_path(data=dcirc, mapping=aes(
x=x, y=y)) +
coord_fixed() 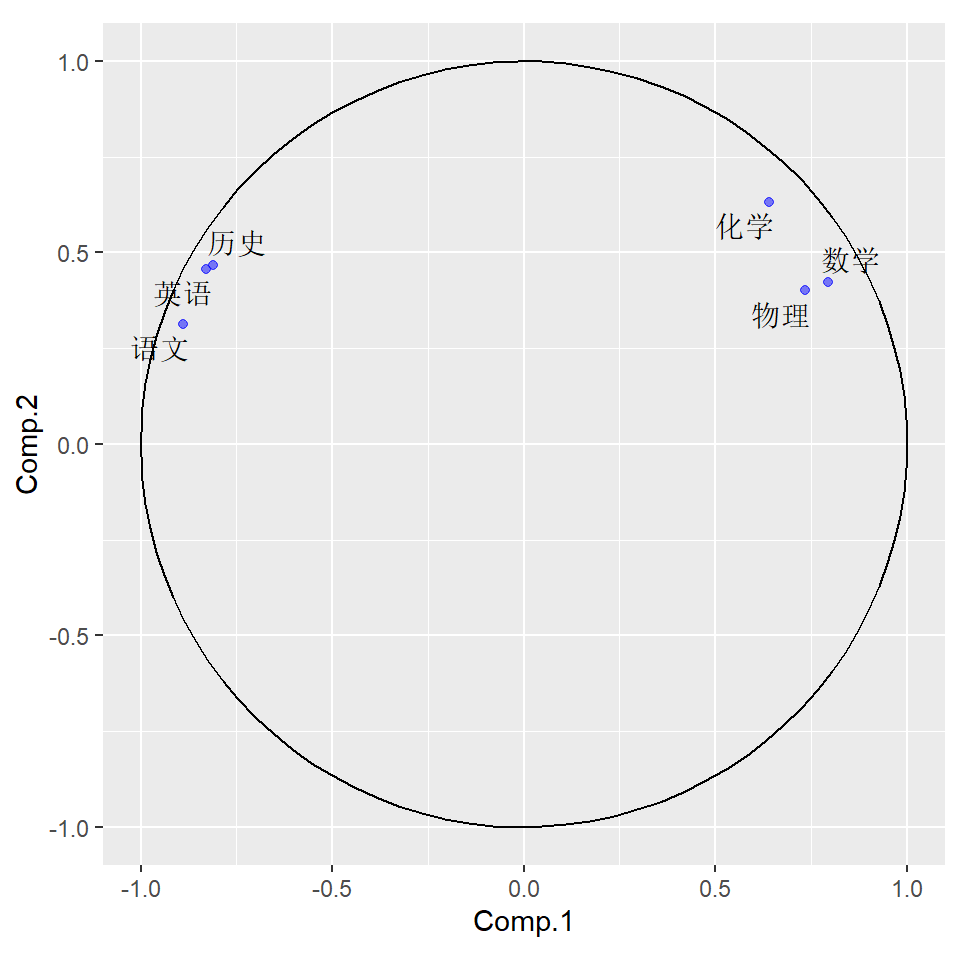
相关系数矩阵的每行的平方和等于1,前两个元素的平方和小于等于1,都在单位圆内。 六个变量的方差都得到了很好的解释。 这个图中代表变量的点的夹角可以近似表示变量间的相关,锐角正相关,直角不相关,钝角负相关。
biplot, 同时画出前两个主成分得分和前两个载荷:
library(ggfortify)
dggd <- as.data.frame(pca2$scores[,1:2])
dggl <- as.data.frame(loadings(pca2)[,1:2])
dggl[["varnames"]] <- rownames(loadings(pca2))
ggbiplot(
dggd, dggl,
loadings=TRUE,
loadings.label=TRUE,
loadings.label.label="varnames")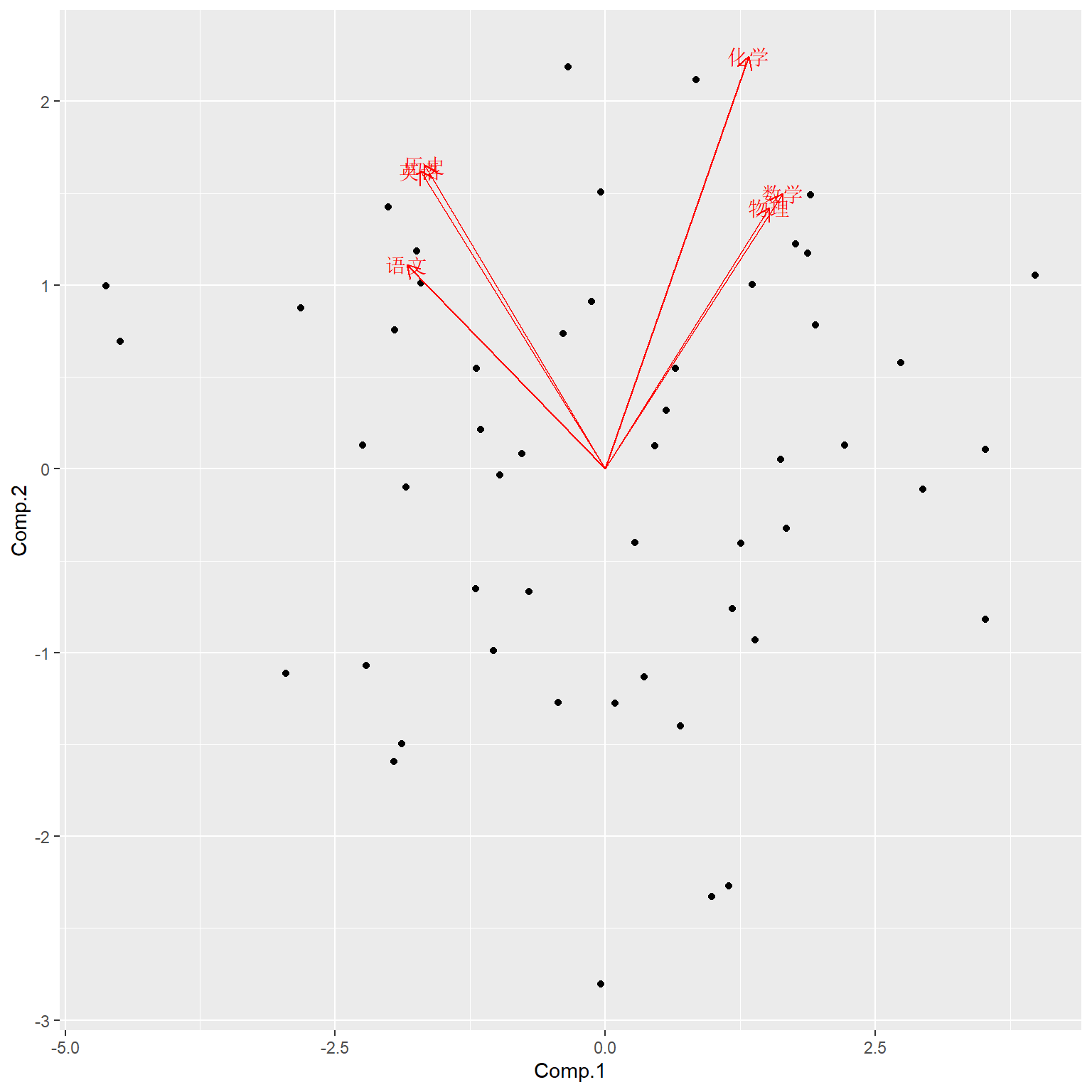
8.7 FactoMineR例子
例子来自FactoMineR文档。
## Warning: ggrepel: 3 unlabeled data points (too many overlaps). Consider
## increasing max.overlaps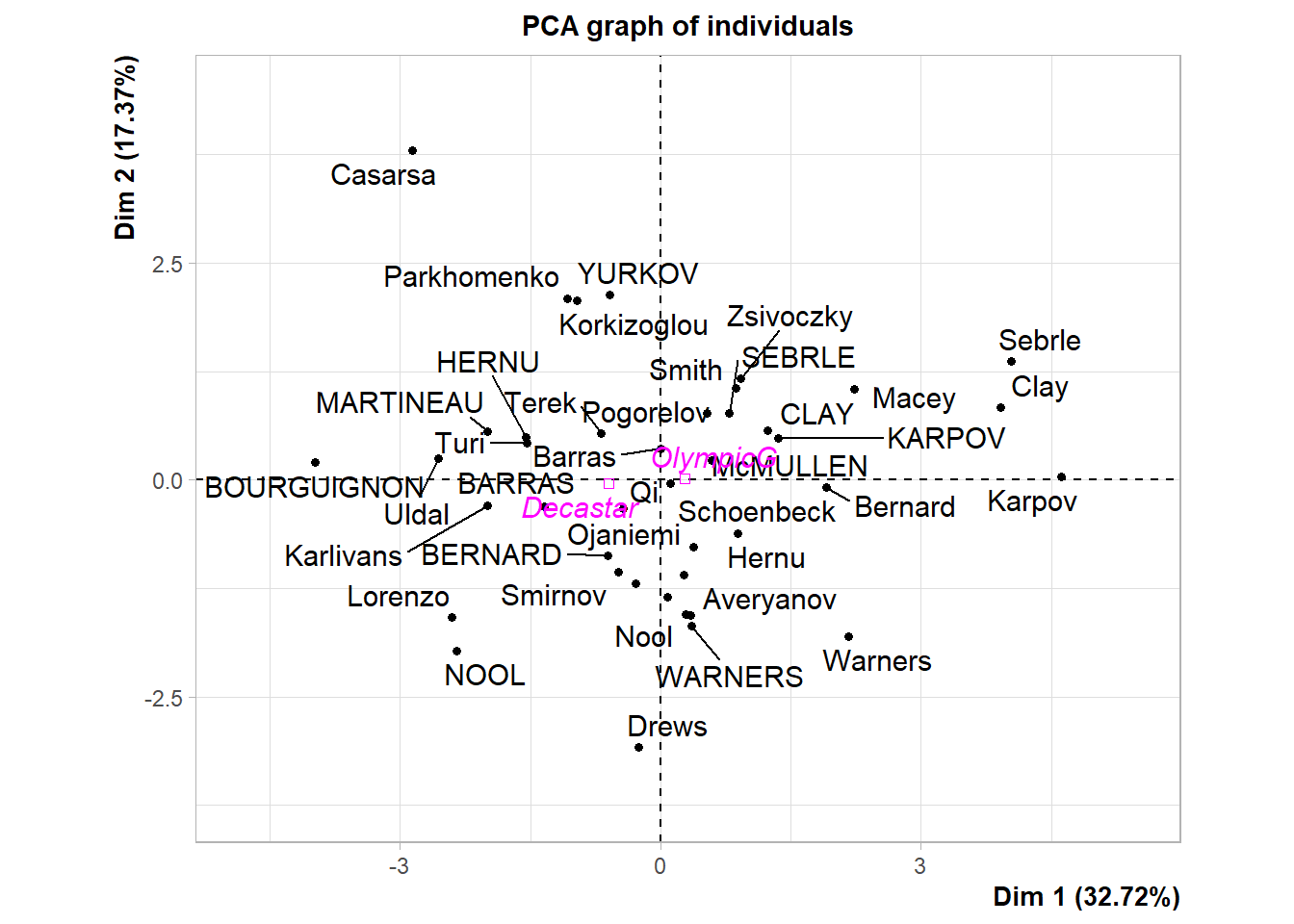
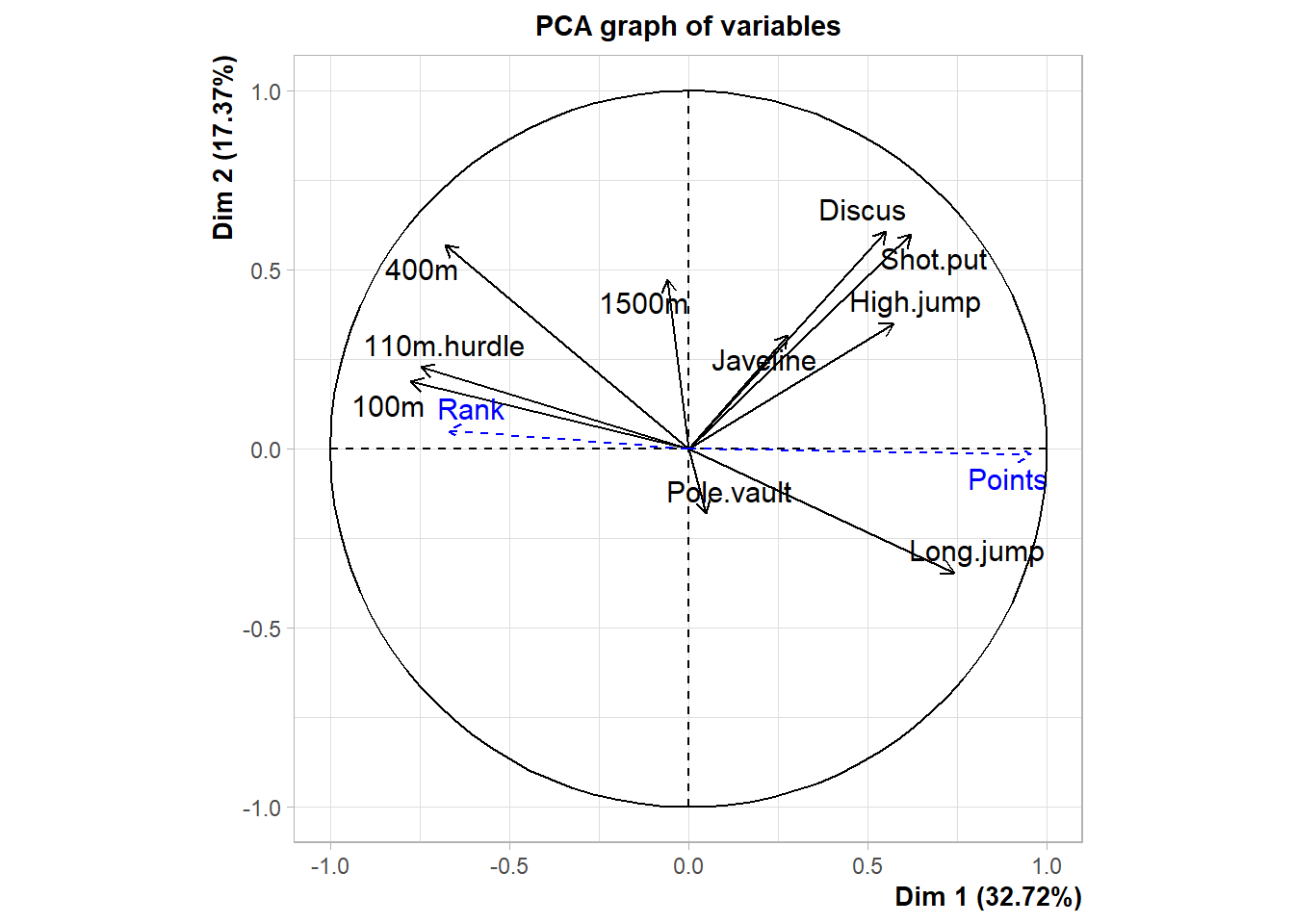
## plot of the eigenvalues
## barplot(res.pca$eig[,1],main="Eigenvalues",names.arg=1:nrow(res.pca$eig))
summary(res.pca)##
## Call:
## PCA(X = decathlon, quanti.sup = 11:12, quali.sup = 13)
##
##
## Eigenvalues
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
## Variance 3.272 1.737 1.405 1.057 0.685 0.599 0.451
## % of var. 32.719 17.371 14.049 10.569 6.848 5.993 4.512
## Cumulative % of var. 32.719 50.090 64.140 74.708 81.556 87.548 92.061
## Dim.8 Dim.9 Dim.10
## Variance 0.397 0.215 0.182
## % of var. 3.969 2.148 1.822
## Cumulative % of var. 96.030 98.178 100.000
##
## Individuals (the 10 first)
## Dist Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3
## SEBRLE | 2.369 | 0.792 0.467 0.112 | 0.772 0.836 0.106 | 0.827
## CLAY | 3.507 | 1.235 1.137 0.124 | 0.575 0.464 0.027 | 2.141
## KARPOV | 3.396 | 1.358 1.375 0.160 | 0.484 0.329 0.020 | 1.956
## BERNARD | 2.763 | -0.610 0.277 0.049 | -0.875 1.074 0.100 | 0.890
## YURKOV | 3.018 | -0.586 0.256 0.038 | 2.131 6.376 0.499 | -1.225
## WARNERS | 2.428 | 0.357 0.095 0.022 | -1.685 3.986 0.482 | 0.767
## ZSIVOCZKY | 2.563 | 0.272 0.055 0.011 | -1.094 1.680 0.182 | -1.283
## McMULLEN | 2.561 | 0.588 0.257 0.053 | 0.231 0.075 0.008 | -0.418
## MARTINEAU | 3.742 | -1.995 2.968 0.284 | 0.561 0.442 0.022 | -0.730
## HERNU | 2.794 | -1.546 1.782 0.306 | 0.488 0.335 0.031 | 0.841
## ctr cos2
## SEBRLE 1.187 0.122 |
## CLAY 7.960 0.373 |
## KARPOV 6.644 0.332 |
## BERNARD 1.375 0.104 |
## YURKOV 2.606 0.165 |
## WARNERS 1.020 0.100 |
## ZSIVOCZKY 2.857 0.250 |
## McMULLEN 0.303 0.027 |
## MARTINEAU 0.925 0.038 |
## HERNU 1.227 0.091 |
##
## Variables
## Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr
## 100m | -0.775 18.344 0.600 | 0.187 2.016 0.035 | -0.184 2.420
## Long.jump | 0.742 16.822 0.550 | -0.345 6.869 0.119 | 0.182 2.363
## Shot.put | 0.623 11.844 0.388 | 0.598 20.607 0.358 | -0.023 0.039
## High.jump | 0.572 9.998 0.327 | 0.350 7.064 0.123 | -0.260 4.794
## 400m | -0.680 14.116 0.462 | 0.569 18.666 0.324 | 0.131 1.230
## 110m.hurdle | -0.746 17.020 0.557 | 0.229 3.013 0.052 | -0.093 0.611
## Discus | 0.552 9.328 0.305 | 0.606 21.162 0.368 | 0.043 0.131
## Pole.vault | 0.050 0.077 0.003 | -0.180 1.873 0.033 | 0.692 34.061
## Javeline | 0.277 2.347 0.077 | 0.317 5.784 0.100 | -0.390 10.807
## 1500m | -0.058 0.103 0.003 | 0.474 12.946 0.225 | 0.782 43.543
## cos2
## 100m 0.034 |
## Long.jump 0.033 |
## Shot.put 0.001 |
## High.jump 0.067 |
## 400m 0.017 |
## 110m.hurdle 0.009 |
## Discus 0.002 |
## Pole.vault 0.479 |
## Javeline 0.152 |
## 1500m 0.612 |
##
## Supplementary continuous variables
## Dim.1 cos2 Dim.2 cos2 Dim.3 cos2
## Rank | -0.671 0.450 | 0.051 0.003 | -0.058 0.003 |
## Points | 0.956 0.914 | -0.017 0.000 | -0.066 0.004 |
##
## Supplementary categories
## Dist Dim.1 cos2 v.test Dim.2 cos2 v.test Dim.3
## Decastar | 0.946 | -0.600 0.403 -1.430 | -0.038 0.002 -0.123 | 0.289
## OlympicG | 0.439 | 0.279 0.403 1.430 | 0.017 0.002 0.123 | -0.134
## cos2 v.test
## Decastar 0.093 1.050 |
## OlympicG 0.093 -1.050 |## Warning: ggrepel: 3 unlabeled data points (too many overlaps). Consider
## increasing max.overlaps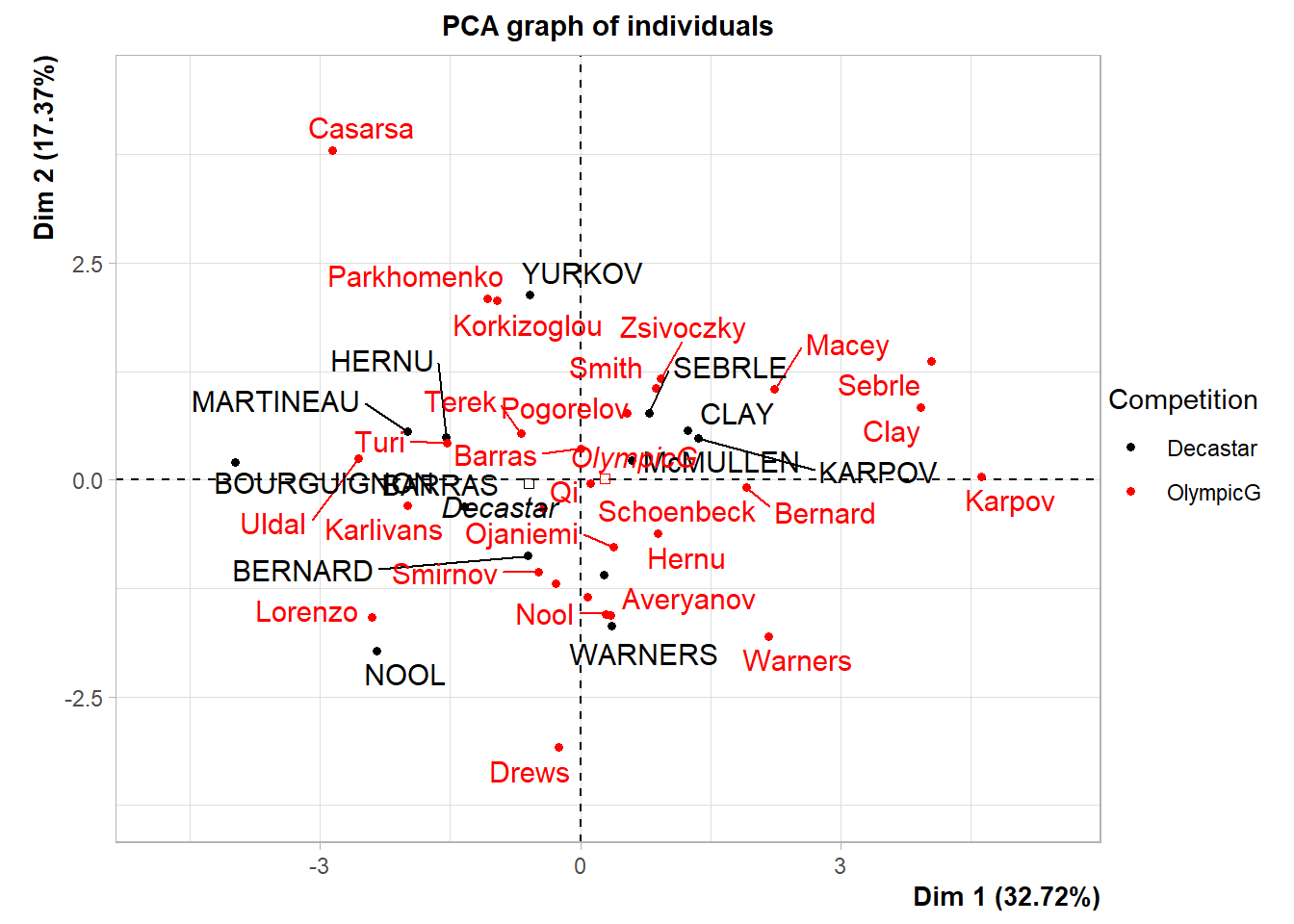
## $Dim.1
##
## Link between the variable and the continuous variables (R-square)
## =================================================================================
## correlation p.value
## Points 0.9561543 2.099191e-22
## Long.jump 0.7418997 2.849886e-08
## Shot.put 0.6225026 1.388321e-05
## High.jump 0.5719453 9.362285e-05
## Discus 0.5524665 1.802220e-04
## Rank -0.6705104 1.616348e-06
## 400m -0.6796099 1.028175e-06
## 110m.hurdle -0.7462453 2.136962e-08
## 100m -0.7747198 2.778467e-09
##
## $Dim.2
##
## Link between the variable and the continuous variables (R-square)
## =================================================================================
## correlation p.value
## Discus 0.6063134 2.650745e-05
## Shot.put 0.5983033 3.603567e-05
## 400m 0.5694378 1.020941e-04
## 1500m 0.4742238 1.734405e-03
## High.jump 0.3502936 2.475025e-02
## Javeline 0.3169891 4.344974e-02
## Long.jump -0.3454213 2.696969e-02## To draw ellipses around the categories of the 13th variable (which is categorical)
plotellipses(res.pca,13)## Warning: ggrepel: 3 unlabeled data points (too many overlaps). Consider
## increasing max.overlaps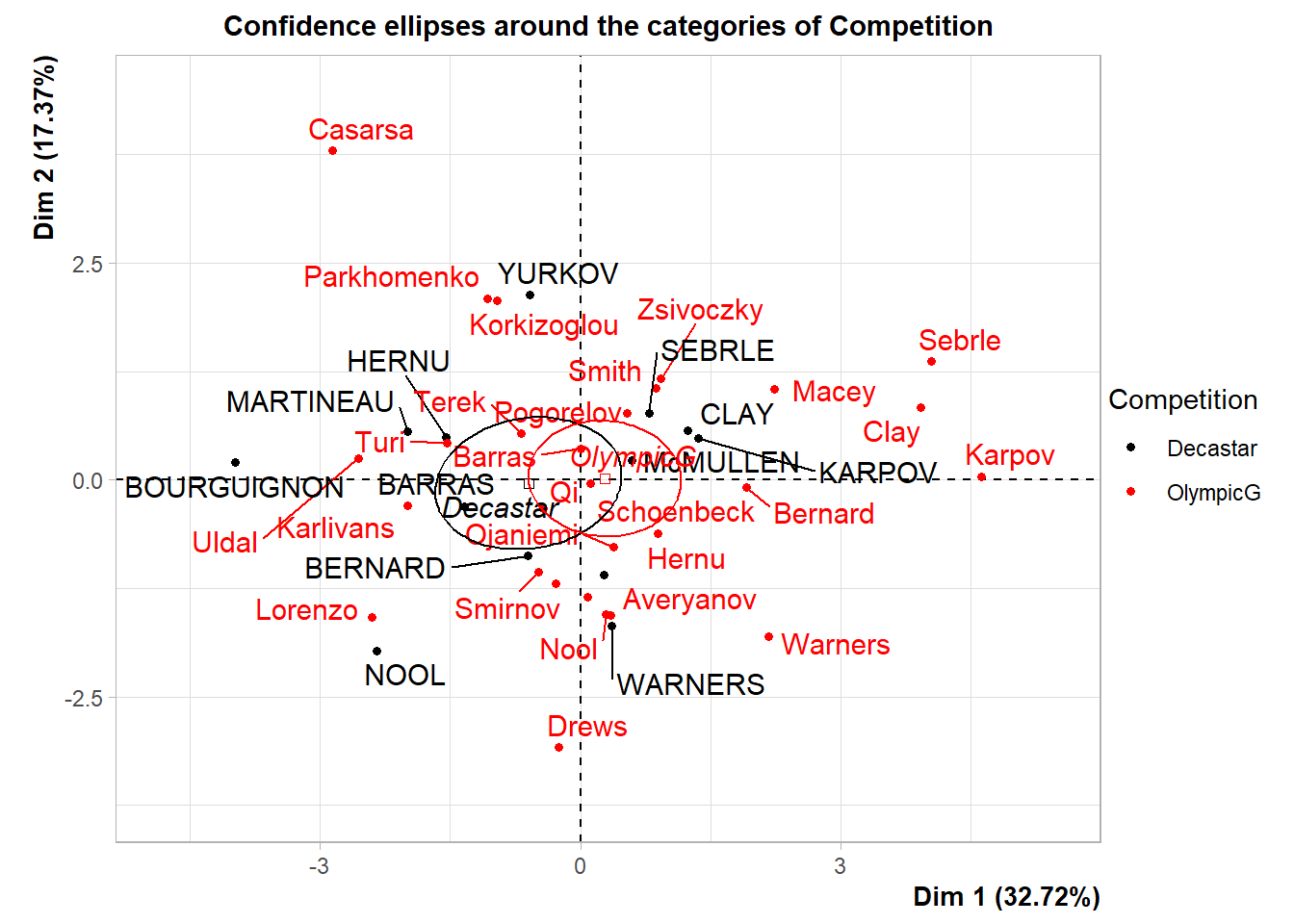
8.8 factoMineR包和factoextra包
参见factoMineR包介绍文档。
例子来自factoextra包文档。
## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa# Principal component analysis
# ++++++++++++++++++++++++++++++
data(iris)
res.pca <- prcomp(iris[, -5], scale = TRUE)
# Graph of individuals
# +++++++++++++++++++++
# Default plot
# Use repel = TRUE to avoid overplotting (slow if many points)
fviz_pca_ind(res.pca, col.ind = "#00AFBB",
repel = TRUE)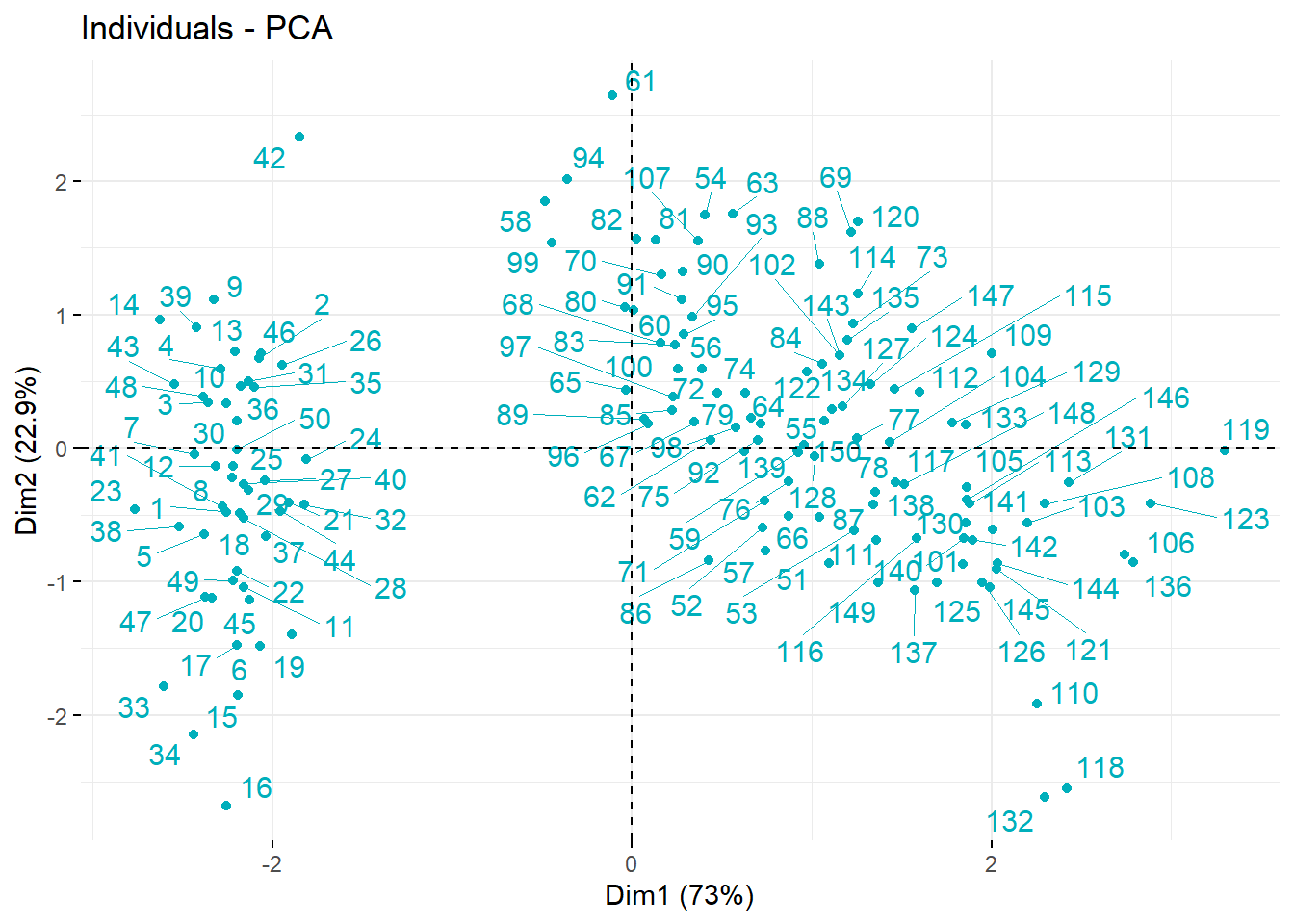
# 1. Control automatically the color of individuals
# using the "cos2" or the contributions "contrib"
# cos2 = the quality of the individuals on the factor map
# 2. To keep only point or text use geom = "point" or geom = "text".
# 3. Change themes using ggtheme: http://www.sthda.com/english/wiki/ggplot2-themes
fviz_pca_ind(res.pca, col.ind="cos2", geom = "point",
gradient.cols = c("white", "#2E9FDF", "#FC4E07" ))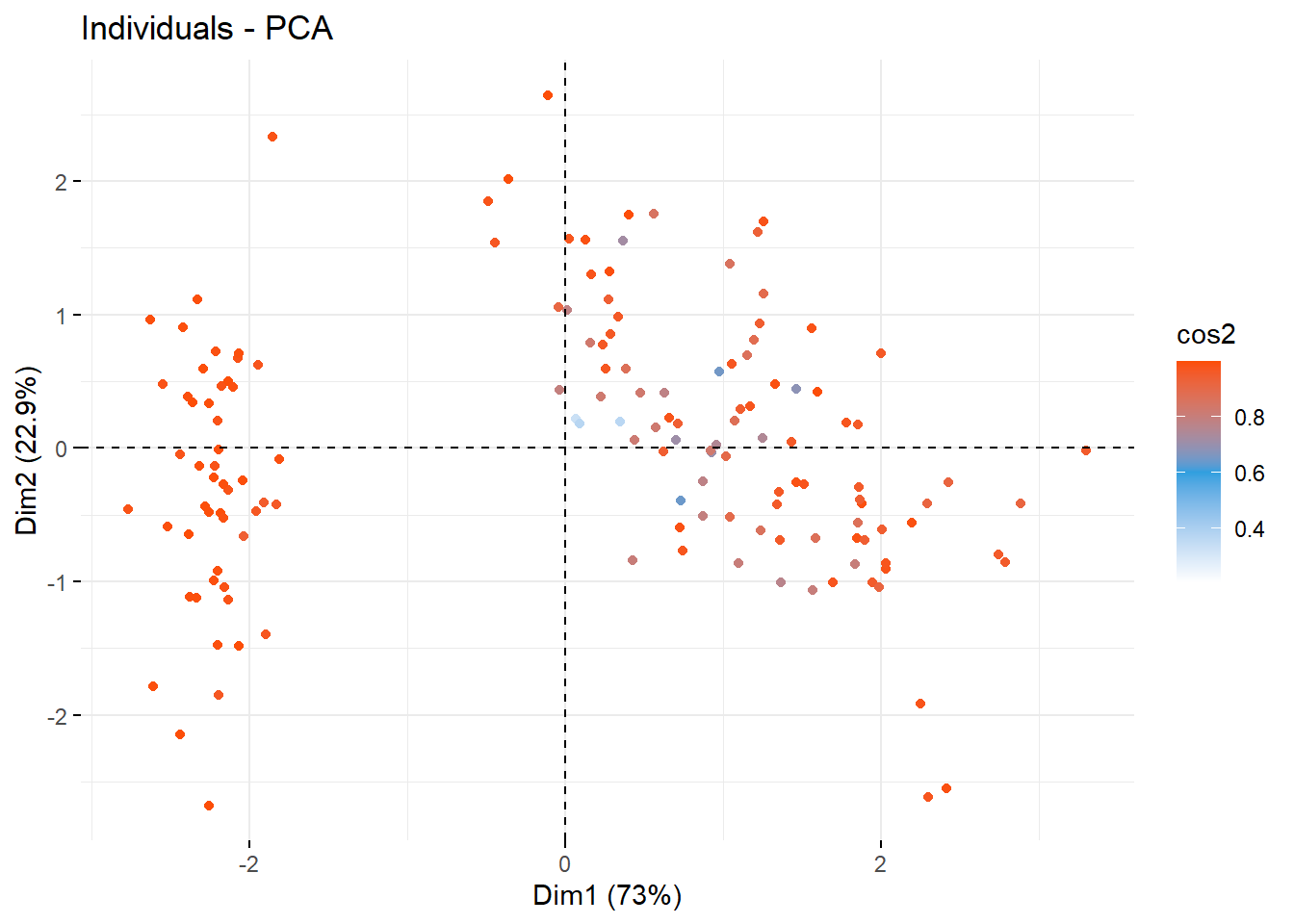
# Color individuals by groups, add concentration ellipses
# Change group colors using RColorBrewer color palettes
# Read more: http://www.sthda.com/english/wiki/ggplot2-colors
# Remove labels: label = "none".
fviz_pca_ind(res.pca, label="none", habillage=iris$Species,
addEllipses=TRUE, ellipse.level=0.95, palette = "Dark2")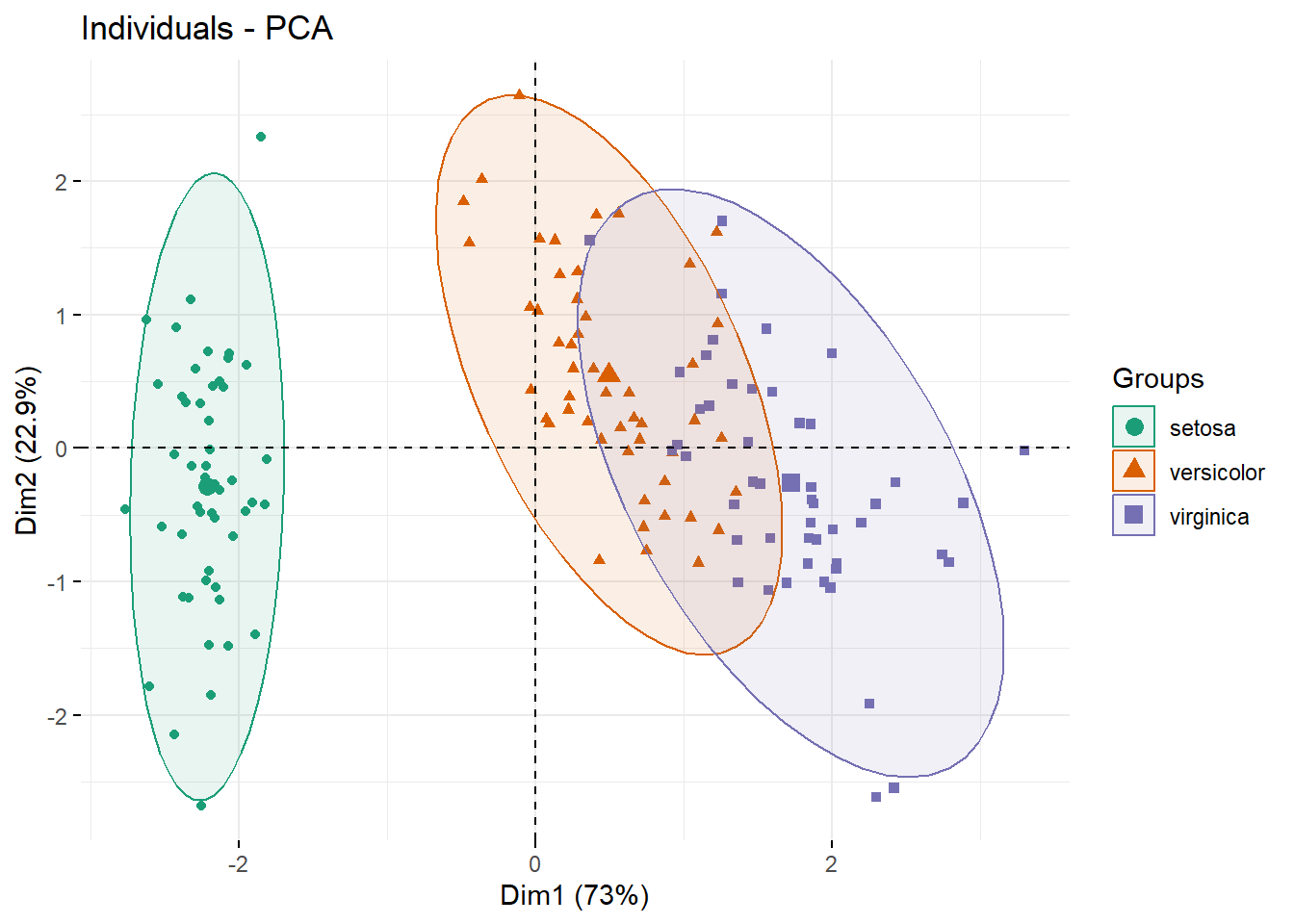
# Change group colors manually
# Read more: http://www.sthda.com/english/wiki/ggplot2-colors
fviz_pca_ind(res.pca, label="none", habillage=iris$Species,
addEllipses=TRUE, ellipse.level=0.95,
palette = c("#999999", "#E69F00", "#56B4E9"))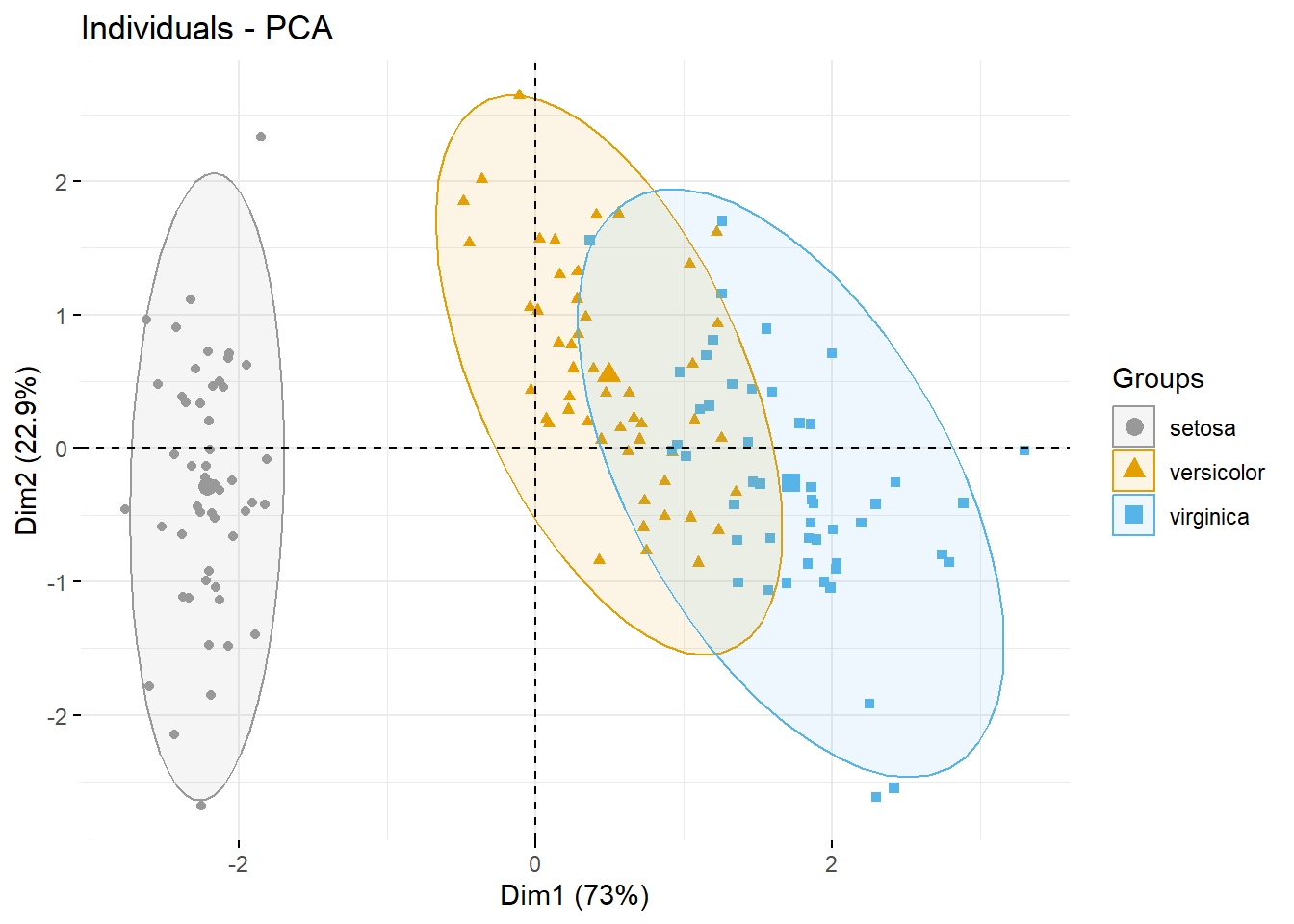
# Select and visualize some individuals (ind) with select.ind argument.
# - ind with cos2 >= 0.96: select.ind = list(cos2 = 0.96)
# - Top 20 ind according to the cos2: select.ind = list(cos2 = 20)
# - Top 20 contributing individuals: select.ind = list(contrib = 20)
# - Select ind by names: select.ind = list(name = c("23", "42", "119") )
# Example: Select the top 40 according to the cos2
fviz_pca_ind(res.pca, select.ind = list(cos2 = 40))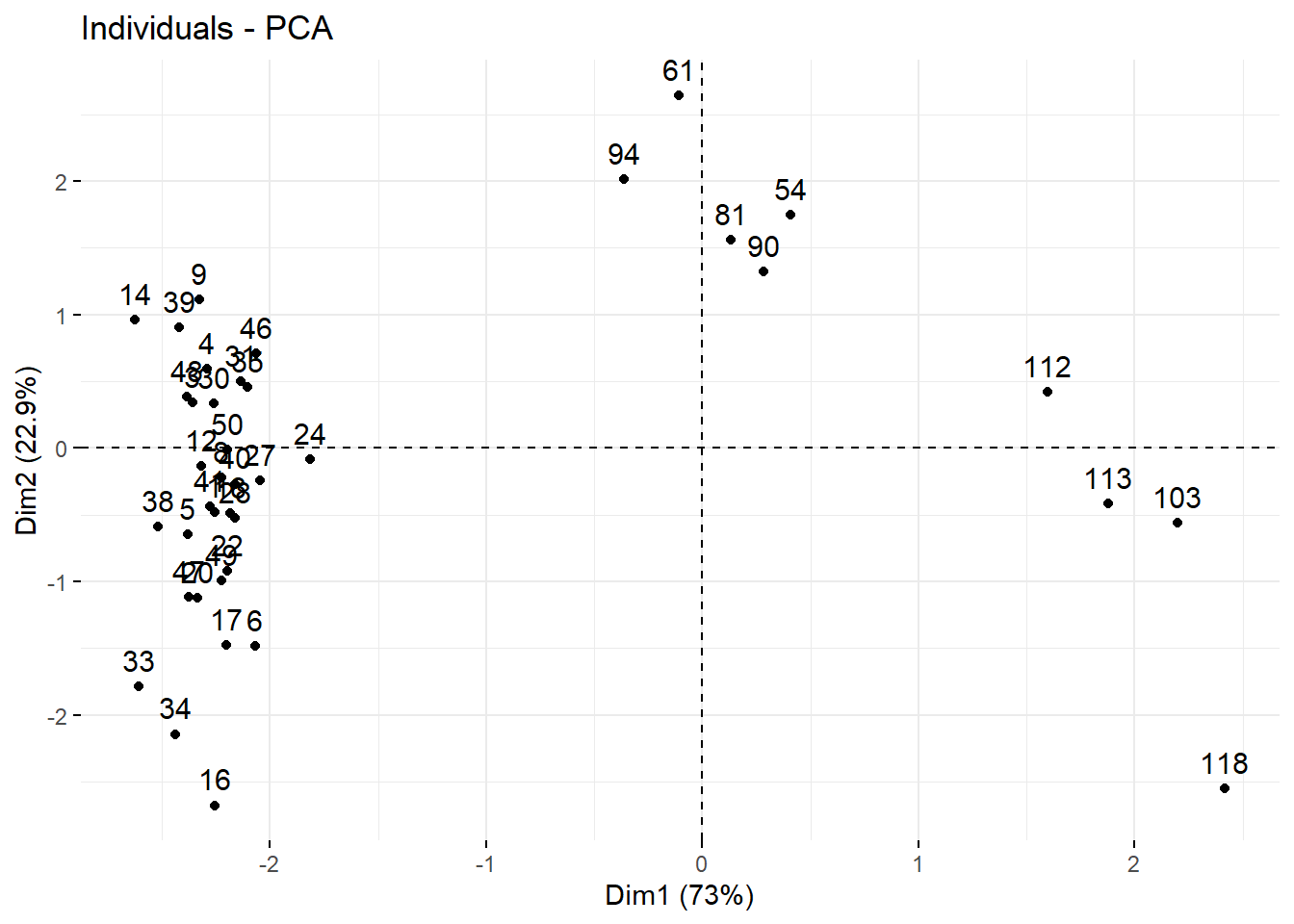
# Graph of variables
# ++++++++++++++++++++++++++++
# Default plot
fviz_pca_var(res.pca, col.var = "steelblue")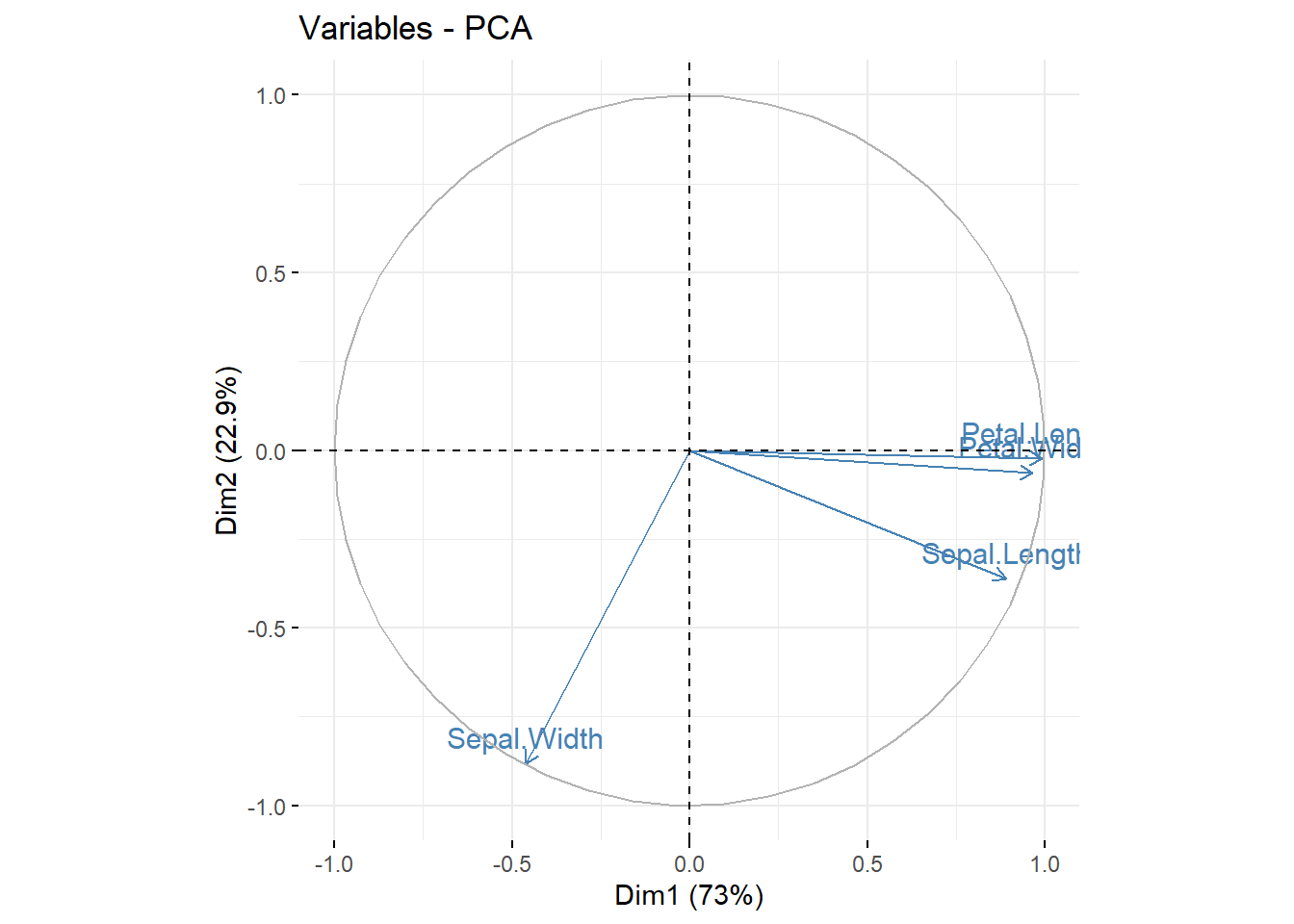
# Control variable colors using their contributions
fviz_pca_var(res.pca, col.var = "contrib",
gradient.cols = c("white", "blue", "red"),
ggtheme = theme_minimal())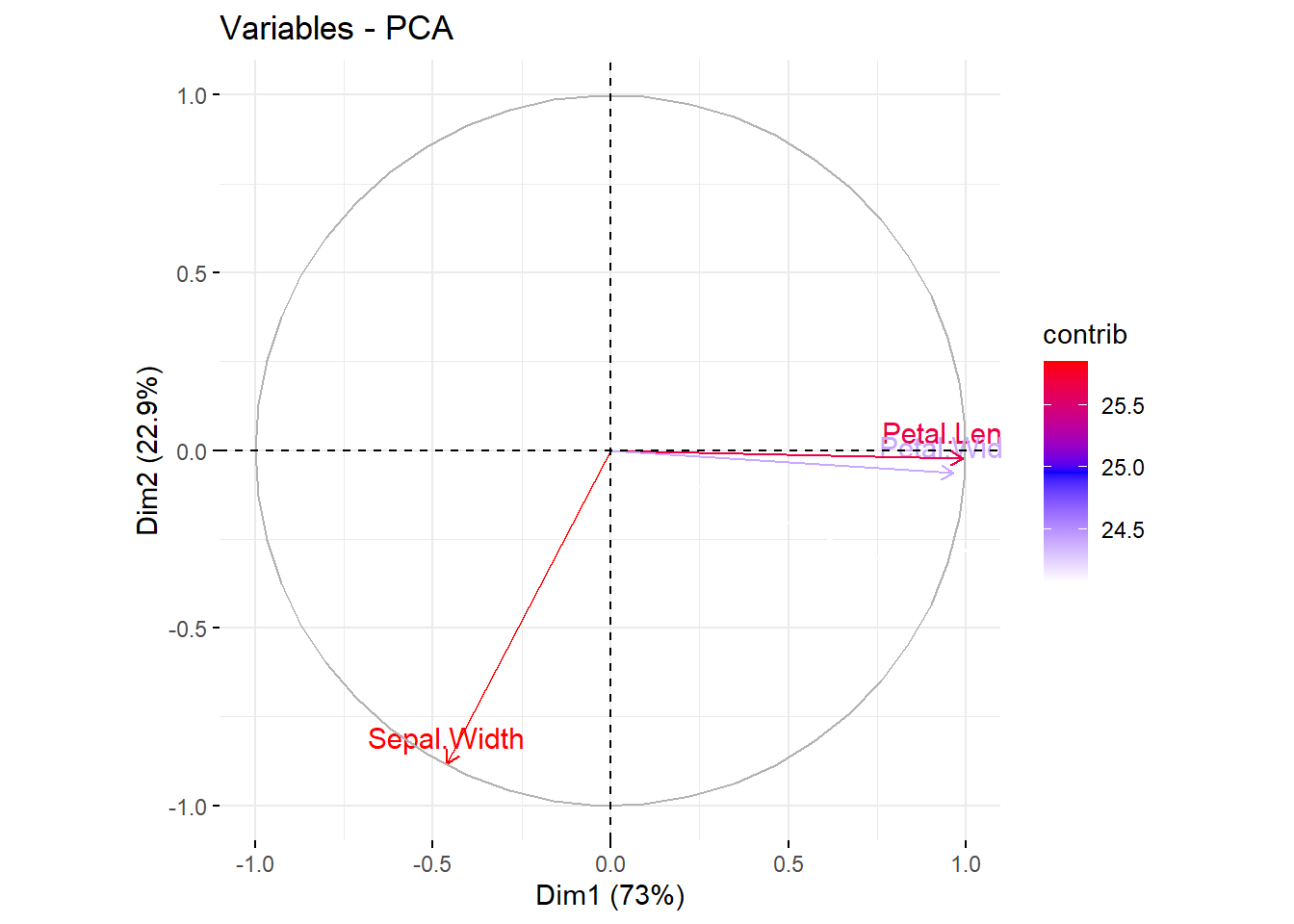
# Biplot of individuals and variables
# ++++++++++++++++++++++++++
# Keep only the labels for variables
# Change the color by groups, add ellipses
fviz_pca_biplot(res.pca, label = "var", habillage=iris$Species,
addEllipses=TRUE, ellipse.level=0.95,
ggtheme = theme_minimal())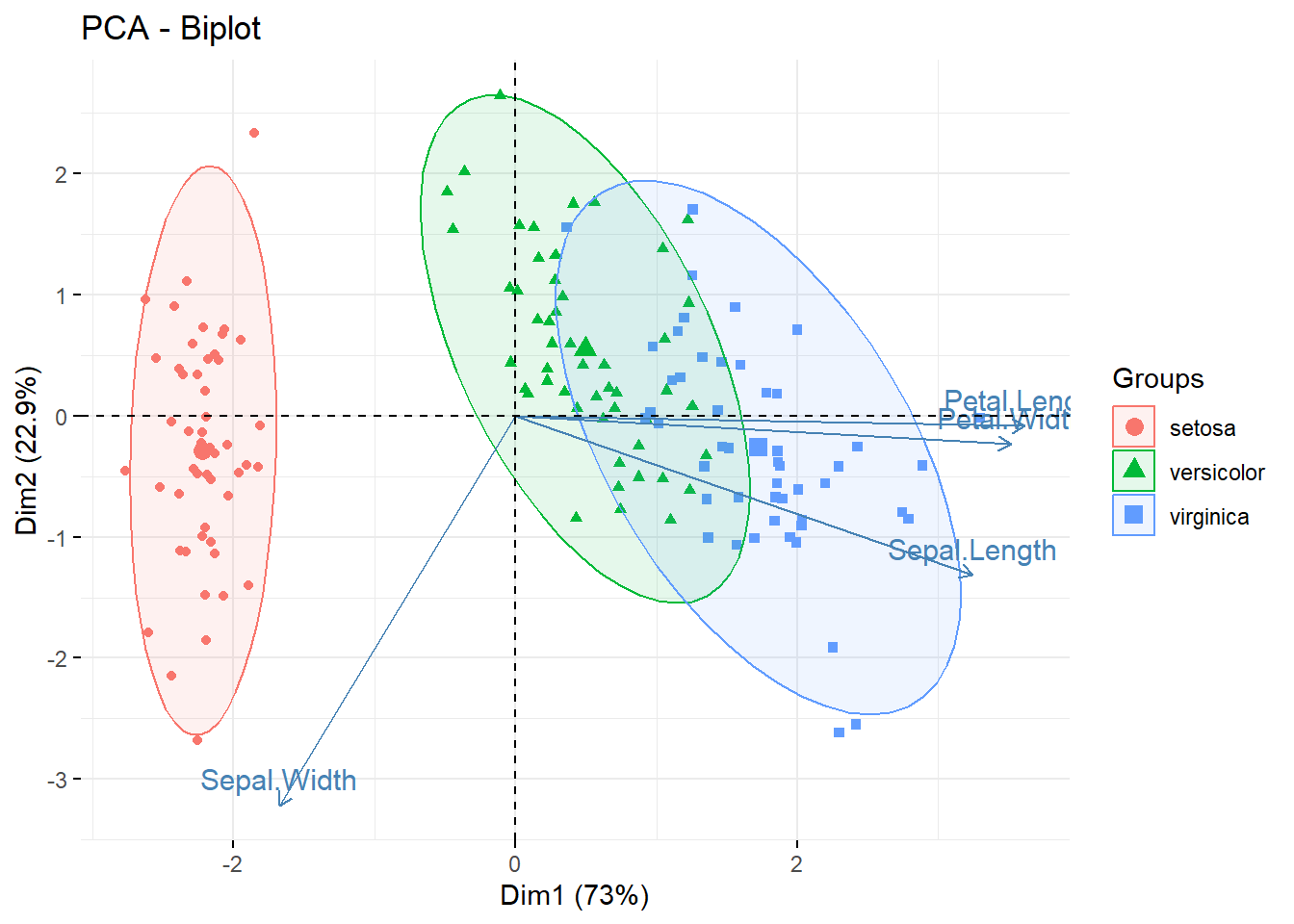
8.9 节6.4案例:主成分综合分析
P.88 节6.4案例:主成分综合分析。 数据为某市工业部门13个行业8项重要经济指标数据。
- x1为年末固定资产净值,
- x2为职工人数(单位:人),
- x3为工业总产值,
- x4为全员劳动生产率(单位:元/年),
- x5为百元固定资产原值实现产值,
- x6为资金利税率(%),
- x7为标准燃料消费量(单位:吨),
- x8为能源利用效率(单位:万元/吨)。
industryPCA <- read_csv(
"data/十三行业主成分.csv",
locale=locale(encoding = "GB18030"),
show_col_types = FALSE)## New names:
## • `` -> `...1`| 行业 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
|---|---|---|---|---|---|---|---|---|
| 冶金 | 90342 | 52455 | 101091 | 19272 | 82.0 | 16.1 | 197435 | 0.172 |
| 电力 | 4903 | 1973 | 2035 | 10313 | 34.2 | 7.1 | 592077 | 0.003 |
| 煤炭 | 6735 | 21139 | 3767 | 1780 | 36.1 | 8.2 | 726396 | 0.003 |
| 化学 | 49454 | 36241 | 81557 | 22504 | 98.1 | 25.9 | 348226 | 0.985 |
| 机器 | 139190 | 203505 | 215898 | 10609 | 93.2 | 12.6 | 139572 | 0.628 |
| 建材 | 12215 | 16219 | 10351 | 6382 | 62.5 | 8.7 | 145818 | 0.066 |
| 森工 | 2372 | 6572 | 8103 | 12329 | 184.4 | 22.2 | 20921 | 0.152 |
| 食品 | 11062 | 23078 | 54935 | 23804 | 370.4 | 41.0 | 65486 | 0.263 |
| 纺织 | 17111 | 23907 | 52108 | 21796 | 221.5 | 21.5 | 63806 | 0.276 |
| 缝纫 | 1206 | 3930 | 6126 | 15586 | 330.4 | 29.5 | 1840 | 0.437 |
| 皮革 | 2150 | 5704 | 6200 | 10870 | 184.2 | 12.0 | 8913 | 0.274 |
| 造纸 | 5251 | 6155 | 10383 | 16875 | 146.4 | 27.5 | 78796 | 0.151 |
| 文教 | 14341 | 13203 | 19396 | 14691 | 94.6 | 17.8 | 6354 | 1.574 |
各列不可比,用样本相关阵。 样本相关阵:
## x1 x2 x3 x4 x5 x6 x7 x8
## x1 1.000 0.920 0.962 0.109 -0.289 -0.166 0.007 0.214
## x2 0.920 1.000 0.947 -0.055 -0.197 -0.171 -0.015 0.186
## x3 0.962 0.947 1.000 0.233 -0.104 0.004 -0.078 0.247
## x4 0.109 -0.055 0.233 1.000 0.560 0.781 -0.450 0.301
## x5 -0.289 -0.197 -0.104 0.560 1.000 0.827 -0.609 -0.030
## x6 -0.166 -0.171 0.004 0.781 0.827 1.000 -0.492 0.174
## x7 0.007 -0.015 -0.078 -0.450 -0.609 -0.492 1.000 -0.300
## x8 0.214 0.186 0.247 0.301 -0.030 0.174 -0.300 1.000前三个指标相关性强,代表规模。
用相关阵作主成分分析:
## Call:
## princomp(x = d, cor = TRUE)
##
## Standard deviations:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## 1.76207620 1.70218731 0.96447683 0.80132532 0.55143824 0.29427497 0.17940006
## Comp.8
## 0.04941432
##
## 8 variables and 13 observations.## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.7620762 1.7021873 0.9644768 0.80132532 0.55143824
## Proportion of Variance 0.3881141 0.3621802 0.1162769 0.08026528 0.03801052
## Cumulative Proportion 0.3881141 0.7502943 0.8665712 0.94683649 0.98484701
## Comp.6 Comp.7 Comp.8
## Standard deviation 0.29427497 0.179400062 0.0494143207
## Proportion of Variance 0.01082472 0.004023048 0.0003052219
## Cumulative Proportion 0.99567173 0.999694778 1.0000000000
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## x1 0.477 0.296 0.104 0.184 0.758 0.245
## x2 0.473 0.278 0.163 -0.174 -0.305 -0.518 0.527
## x3 0.424 0.378 0.156 -0.174 -0.781
## x4 -0.213 0.451 0.516 0.539 -0.288 -0.249 0.220
## x5 -0.388 0.331 0.321 -0.199 -0.450 -0.582 0.233
## x6 -0.352 0.403 0.145 0.279 -0.317 0.714
## x7 0.215 -0.377 0.140 0.758 -0.418 -0.194
## x8 0.273 -0.891 -0.322 -0.122要三个主成分才能达到累积贡献率86%, 两个只有75%。
- 第一主成分在x1,x2,x3,x7上为正,这四个指标代表了规模, 在x4, x5, x6上为负,这三个指标代表了效率, 所以第一主成分可以认为是效率与规模的对比因素。 第一主成分为负,是效率好而规模小的行业; 第一主成分为正,是规模大而效率差的行业。
- 第二主成分在除x7之外所有指标上载荷为正,在x7上为负, x7是燃料消费量,第二主成分没有太好的解释。
- 第三主成分在除了x8之外的指标上载荷为小的正数, 在x8(能源利用效率)上是较大负数, 可认为主要代表了能源利用效率反面。
为了得到更好的解释,可以用带因子旋转的因子分析。
用loadings()计算载荷:
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## x1 0.477 0.296 0.104 0.184 0.758 0.245
## x2 0.473 0.278 0.163 -0.174 -0.305 -0.518 0.527
## x3 0.424 0.378 0.156 -0.174 -0.781
## x4 -0.213 0.451 0.516 0.539 -0.288 -0.249 0.220
## x5 -0.388 0.331 0.321 -0.199 -0.450 -0.582 0.233
## x6 -0.352 0.403 0.145 0.279 -0.317 0.714
## x7 0.215 -0.377 0.140 0.758 -0.418 -0.194
## x8 0.273 -0.891 -0.322 -0.122
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125
## Cumulative Var 0.125 0.250 0.375 0.500 0.625 0.750 0.875 1.000screeplot()帮助确定主成分个数:
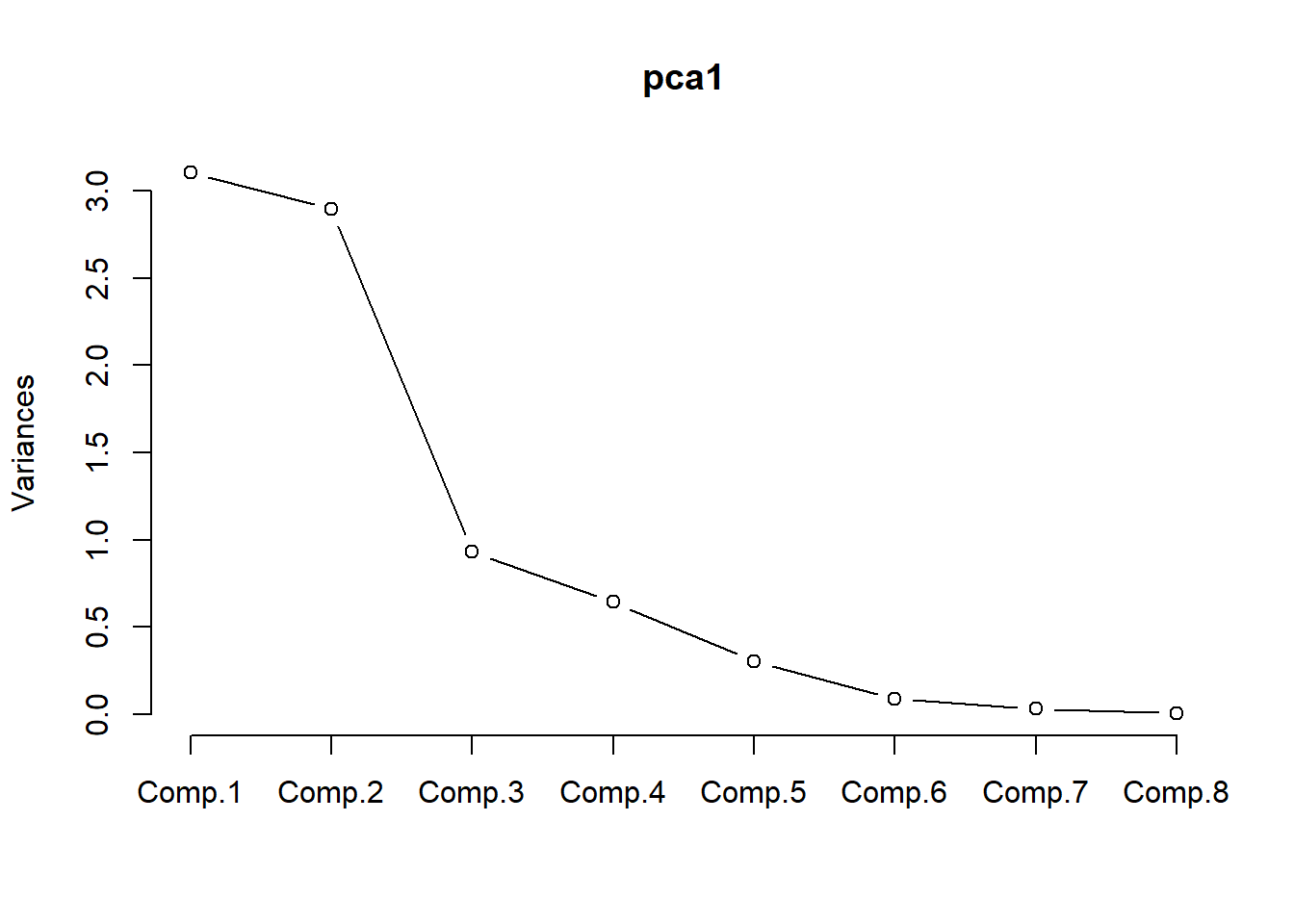
前三个主成分得分:
| 行业 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | Comp.1 | Comp.2 | Comp.3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 冶金 | 90342 | 52455 | 101091 | 19272 | 82.0 | 16.1 | 197435 | 0.172 | 1.535 | 0.790 | 0.560 |
| 电力 | 4903 | 1973 | 2035 | 10313 | 34.2 | 7.1 | 592077 | 0.003 | 0.519 | -2.697 | 0.238 |
| 煤炭 | 6735 | 21139 | 3767 | 1780 | 36.1 | 8.2 | 726396 | 0.003 | 1.100 | -3.357 | 0.426 |
| 化学 | 49454 | 36241 | 81557 | 22504 | 98.1 | 25.9 | 348226 | 0.985 | 0.479 | 1.232 | -1.038 |
| 机器 | 139190 | 203505 | 215898 | 10609 | 93.2 | 12.6 | 139572 | 0.628 | 4.713 | 2.355 | 0.487 |
| 建材 | 12215 | 16219 | 10351 | 6382 | 62.5 | 8.7 | 145818 | 0.066 | 0.343 | -1.846 | 0.032 |
| 森工 | 2372 | 6572 | 8103 | 12329 | 184.4 | 22.2 | 20921 | 0.152 | -1.148 | -0.331 | 0.293 |
| 食品 | 11062 | 23078 | 54935 | 23804 | 370.4 | 41.0 | 65486 | 0.263 | -2.285 | 2.336 | 1.144 |
| 纺织 | 17111 | 23907 | 52108 | 21796 | 221.5 | 21.5 | 63806 | 0.276 | -0.876 | 0.932 | 0.367 |
| 缝纫 | 1206 | 3930 | 6126 | 15586 | 330.4 | 29.5 | 1840 | 0.437 | -2.115 | 0.859 | 0.240 |
| 皮革 | 2150 | 5704 | 6200 | 10870 | 184.2 | 12.0 | 8913 | 0.274 | -0.742 | -0.786 | -0.128 |
| 造纸 | 5251 | 6155 | 10383 | 16875 | 146.4 | 27.5 | 78796 | 0.151 | -1.250 | 0.032 | 0.299 |
| 文教 | 14341 | 13203 | 19396 | 14691 | 94.6 | 17.8 | 6354 | 1.574 | -0.274 | 0.483 | -2.921 |
食品、缝纫是典型的效率高、规模小的行业; 机器是典型的规模大、效率低的行业。
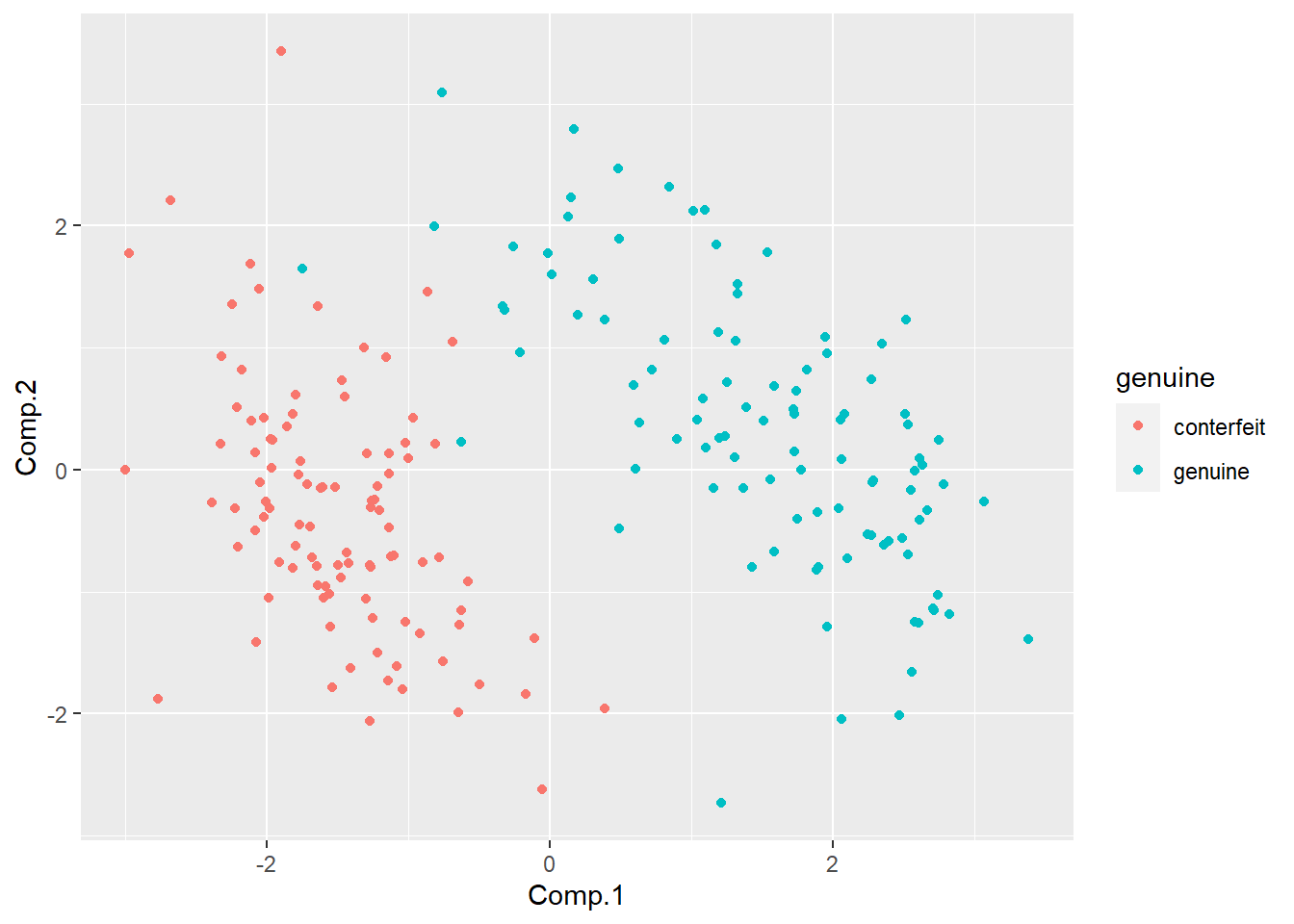
8.10 瑞士银行真假钞数据主成分分析
## tibble [200 × 7] (S3: tbl_df/tbl/data.frame)
## $ length : num [1:200] 215 215 215 215 215 ...
## $ left : num [1:200] 131 130 130 130 130 ...
## $ right : num [1:200] 131 130 130 130 130 ...
## $ bottom : num [1:200] 9 8.1 8.7 7.5 10.4 9 7.9 7.2 8.2 9.2 ...
## $ top : num [1:200] 9.7 9.5 9.6 10.4 7.7 10.1 9.6 10.7 11 10 ...
## $ diag : num [1:200] 141 142 142 142 142 ...
## $ genuine: Factor w/ 2 levels "conterfeit","genuine": 2 2 2 2 2 2 2 2 2 2 ...pca结果:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.7162629 1.1305237 0.9322192 0.67064796 0.51834053
## Proportion of Variance 0.4909264 0.2130140 0.1448388 0.07496145 0.04477948
## Cumulative Proportion 0.4909264 0.7039403 0.8487791 0.92374054 0.96852002
## Comp.6
## Standard deviation 0.43460313
## Proportion of Variance 0.03147998
## Cumulative Proportion 1.00000000##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## length 0.815 0.575
## left -0.468 0.342 -0.103 -0.395 -0.639 -0.298
## right -0.487 0.252 -0.123 -0.430 0.614 0.349
## bottom -0.407 -0.266 -0.584 0.404 0.215 -0.462
## top -0.368 0.788 0.110 0.220 -0.419
## diag 0.493 0.274 -0.114 -0.392 0.340 -0.632
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.167 0.167 0.167 0.167 0.167 0.167
## Cumulative Var 0.167 0.333 0.500 0.667 0.833 1.000主成分得分:
res1 <- predict(pca1)[,1:3]
d2 <- cbind(bankNotes, res1)
knitr::kable(head(cbind(bankNotes, round(res1,3)), 5))| length | left | right | bottom | top | diag | genuine | Comp.1 | Comp.2 | Comp.3 |
|---|---|---|---|---|---|---|---|---|---|
| 214.8 | 131.0 | 131.1 | 9.0 | 9.7 | 141.0 | genuine | -1.747 | 1.651 | -1.424 |
| 214.6 | 129.7 | 129.7 | 8.1 | 9.5 | 141.7 | genuine | 2.274 | -0.539 | -0.533 |
| 214.8 | 129.7 | 129.7 | 8.7 | 9.6 | 142.2 | genuine | 2.277 | -0.108 | -0.717 |
| 214.8 | 129.7 | 129.6 | 7.5 | 10.4 | 142.0 | genuine | 2.284 | -0.088 | 0.606 |
| 215.0 | 129.6 | 129.7 | 10.4 | 7.7 | 141.8 | genuine | 2.632 | 0.039 | -3.196 |
用前两个主成分作图,区分真假钞: