14 资产组合应用

14.1 介绍

金融学中的最优资产组合问题， 虽然不是多元分析问题， 但其中所用到的数学方法， 与多元分析中的主成分分析、对应分析等问题的的求解方法类似。 这里以最优资产组合为多元分析的应用示例进行介绍。 参见(Wolfgang Härdle 2015)第19章。

设共有\(p\)项资产， 第\(j\)资产在时刻\(t\)的价格为\(p_{tj}\)， 则此资产在\(t\)时刻的单期简单收益率（每期为1天，月，年等）为 \[ x_{tj} = \frac{p_{tj} - p_{t-1,j}}{p_{t-1,j}} \] 设有若干个\(\boldsymbol x_t = (x_{t1}, x_{t2}, \dots, x_{tp})\)的观测\(t=1,2,\dots,T\)。 将\(x_{tj}, j=1,\dots,p, t=1,\dots,T\)排列成一个矩阵\(M\)， 其中每一行对应一个时间\(t\)， 每一列对应一个资产的收益率。

设\(\boldsymbol x_t, t=1,2,\dots,T\)是来自\(\text{N}(\boldsymbol\mu, \Sigma)\)的独立同分布样本， \(\boldsymbol c = (c_1, \dots, c_p)\)是\(p\)个加权平均系数， 满足\(\sum_{j=1}^p c_j = 1\)， 按照\(\boldsymbol c\)的元素分配资产， 则投资组合的收益率为\(Q = \boldsymbol c^T \boldsymbol x_t\)（这里忽略时间）。 投资组合的期望收益为\(EQ = \boldsymbol c^T \boldsymbol\mu\)， 投资组合的风险用其收益率方差度量， 其标准差称为波动率(volatility)， 方差为 \[ \text{Var}(Q)= \text{Var}(\boldsymbol c^T \boldsymbol x_t) = \boldsymbol c^T \text{Var}(\boldsymbol x_t) \boldsymbol c = \boldsymbol c^T \Sigma \boldsymbol c \] 其中\(\Sigma=\text{Var}(\boldsymbol x_t)\)是各个资产的收益率的协方差阵。 在后续使用\(\frac12 c^T \Sigma \boldsymbol c\)， 这样得到的结果表达式较简单。

最优投资组合， 一般是给定了风险上界后求平均收益最大的投资组合， 或者等价地， 给定了平均收益下界后求风险最小的投资组合。

14.2 有效组合(Efficient Portfolio)

方差有效投资组合， 是在\(\boldsymbol 1^T \boldsymbol c=1\)的约束下使得风险度量 \(\frac12 \boldsymbol c^T \Sigma \boldsymbol c\)最小的\(\boldsymbol c\)取值。 为求解 \[\begin{align} & \min_{\boldsymbol c} \frac12 \boldsymbol c^T \Sigma \boldsymbol c, \ \text{s.t.} \\ & \boldsymbol 1^T \boldsymbol c=1 \tag{14.1} \end{align}\] 只要对如下拉格朗日函数求偏导，令偏导数等于零 \[\begin{aligned} \mathcal L = \frac12 \boldsymbol c^T \Sigma \boldsymbol c - \lambda(\boldsymbol 1^T \boldsymbol c - 1) \end{aligned}\] 用多元函数的运算规则得 \[\begin{aligned} \frac{\partial \mathcal L}{\partial \boldsymbol c} =& \Sigma \boldsymbol c - \lambda \boldsymbol 1 = 0 \\ \frac{\partial \mathcal L}{\partial \lambda} =& \boldsymbol 1^T \boldsymbol c - 1 = 0 \end{aligned}\] 从第一式可得\(\boldsymbol c = \lambda \Sigma^{-1} \boldsymbol 1\), 代入第二式可求得\(\lambda\)， 最后得到\(\boldsymbol c\)的最优解为 \[\begin{align} \boldsymbol c = \frac{\Sigma^{-1} \boldsymbol 1}{\boldsymbol 1^T \Sigma^{-1} \boldsymbol 1} \tag{14.2} \end{align}\]

均值方差有效投资组合， 是在所有期望收益相同的投资组合中风险最小的。 设\(\bar\mu\)为预期的收益率， 均值方差有效投资组合需对\(\boldsymbol c\)求解如下优化问题 \[\begin{align} & \min_{\boldsymbol c} \frac12 \boldsymbol c^T \Sigma \boldsymbol c, \ \text{s.t.} \\ & \boldsymbol\mu^T \boldsymbol c = \bar\mu \\ & \boldsymbol 1^T \boldsymbol c=1 \tag{14.3} \end{align}\] 这只要令如下的拉格朗日函数偏导数等于零： \[\begin{align} \mathcal L = \frac12 \boldsymbol c^T \Sigma \boldsymbol c + \lambda_1(\bar\mu - \boldsymbol\mu^T \boldsymbol c) + \lambda_2(1 - \boldsymbol 1^T \boldsymbol c) \tag{14.4} \end{align}\]

令关于\(\boldsymbol c\)的偏导等于零，有 \[\begin{align} \frac{\partial \mathcal L}{\partial \boldsymbol c} =& \Sigma \boldsymbol c - \lambda_1 \boldsymbol\mu - \lambda_2 \boldsymbol 1 = 0 \tag{14.5} \end{align}\]

14.2.1 组合中不包含无风险资产的情形

当\(\Sigma\)可逆时 \[\begin{aligned} \boldsymbol c =& \lambda_1 \Sigma^{-1} \boldsymbol\mu + \lambda_2 \Sigma^{-1} \boldsymbol 1 \end{aligned}\]

\(\Sigma\)可逆即要求其为正定阵， 不存在组合\(\boldsymbol c\)使得 \(\boldsymbol c^T \Sigma \boldsymbol c = 0\)。 如果存在一个无风险资产，其收益率为固定的常数\(r_0\)， 则此资产收益率与其它资产收益率的协方差等于零， 其方差也等于零， 这使得\(\Sigma\)不满秩， 所以\(\Sigma\)可逆要求考虑的资产中没有固定收益率的无风险资产。

将上式分别代入约束\(\boldsymbol\mu^T \boldsymbol c=\bar\mu\) 和约束\(\boldsymbol 1^T \boldsymbol c = 1\)，得如下方程组 \[\begin{aligned} \left(\begin{array}{cc} \boldsymbol\mu^T \Sigma^{-1} \boldsymbol\mu & \boldsymbol\mu^T \Sigma^{-1} \boldsymbol 1 \\ \boldsymbol\mu^T \Sigma^{-1} \boldsymbol 1 & \boldsymbol 1^T \Sigma^{-1} \boldsymbol 1 \end{array}\right) \left(\begin{array}{c} \lambda_1 \\ \lambda_2 \end{array}\right) = \left(\begin{array}{c} \bar\mu \\ 1 \end{array}\right) \end{aligned}\] 求解此关于\(\lambda_1, \lambda_2\)的方程组， 代入 \[ \boldsymbol c = \lambda_1 \Sigma^{-1} \boldsymbol\mu + \lambda_2 \Sigma^{-1} \boldsymbol 1 \] 就得到了均值方差有效的最优投资组合系数\(\boldsymbol c\)。

例

考虑卡特彼勒公司和IBM公司股票2010年的日简单收益率数据。

library(quantmod)
load("xts-d0110.RData")
xts.catibm <- xts.d0110["2010",c("CAT", "IBM")]*100

这两个序列的图形：

plot(xts.catibm, type="l", multi.panel=TRUE, theme="white",
     main="卡特彼勒和IBM日简单收益率（%）",
     major.ticks="months",
     grid.ticks.on = "months")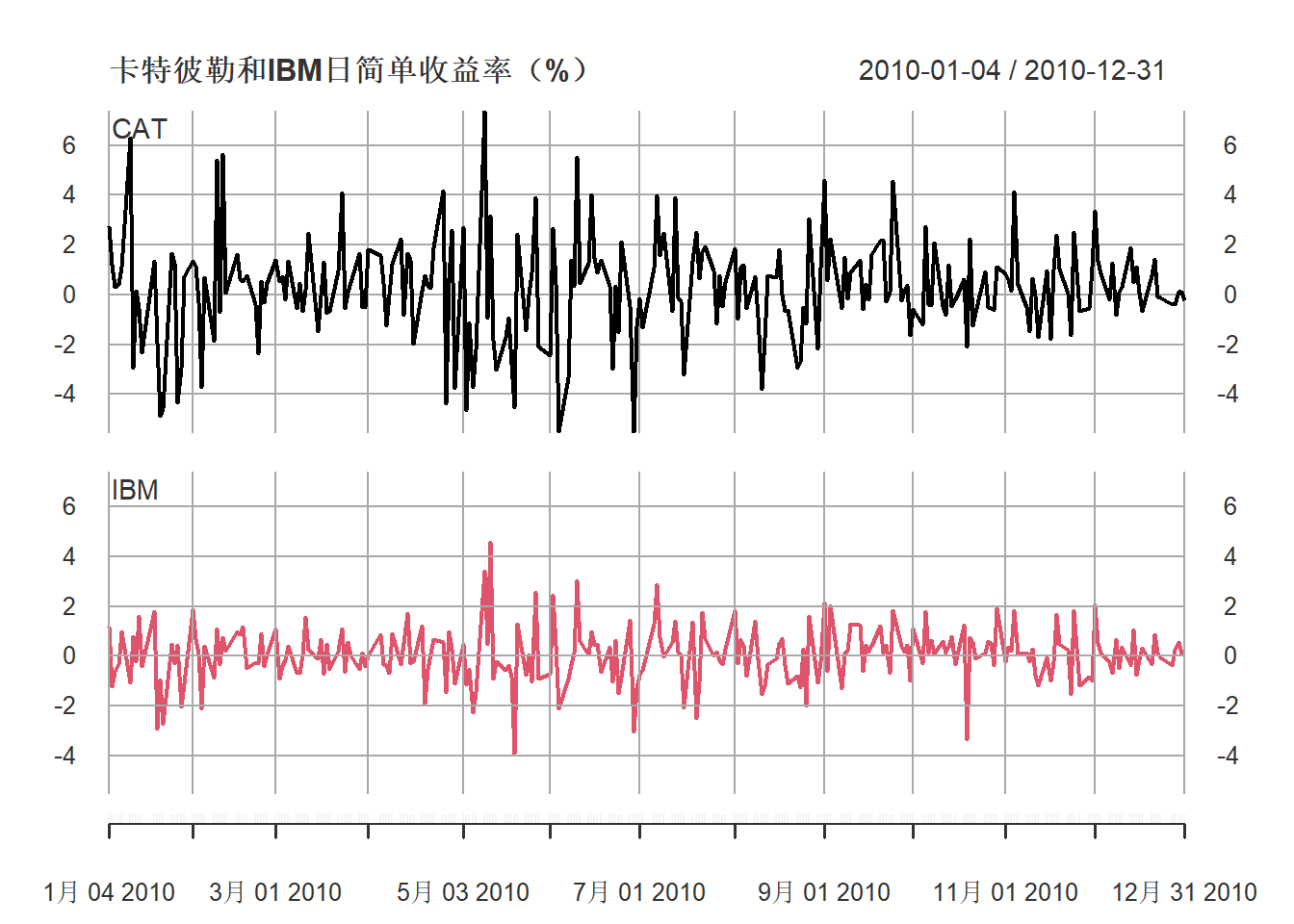

图14.1: 2010年卡特彼勒和IBM日简单收益率（%）

可以按各50%配置资产， 称为等权组合，其收益率序列为：

M <- coredata(xts.catibm)
ew.catibm <- M %*% c(0.5, 0.5)

用方差有效投资组合计算权重：

M <- coredata(xts.catibm)
hatSig <- var(M)
w.bestvar <- solve(hatSig, c(1,1))
w.bestvar[] <- w.bestvar / sum(w.bestvar)
w.bestvar

##         CAT         IBM 
## -0.08905226  1.08905226

bw.catibm <- M %*% w.bestvar

这里负权重表示卖空。 求等权资产与方差有效资产的收益率方差：

var(ew.catibm)

##          [,1]
## [1,] 2.041152

var(bw.catibm)

##          [,1]
## [1,] 1.234504

第二个方差小得多。 作两个投资组合收益率序列的图形：

plot(xts(cbind(ew.catibm, bw.catibm), index(xts.catibm)), 
     type="l", multi.panel=TRUE, theme="white",
     main="卡特彼勒和IBM等权与方差有效组合日简单收益率（%）",
     major.ticks="months",
     grid.ticks.on = "months")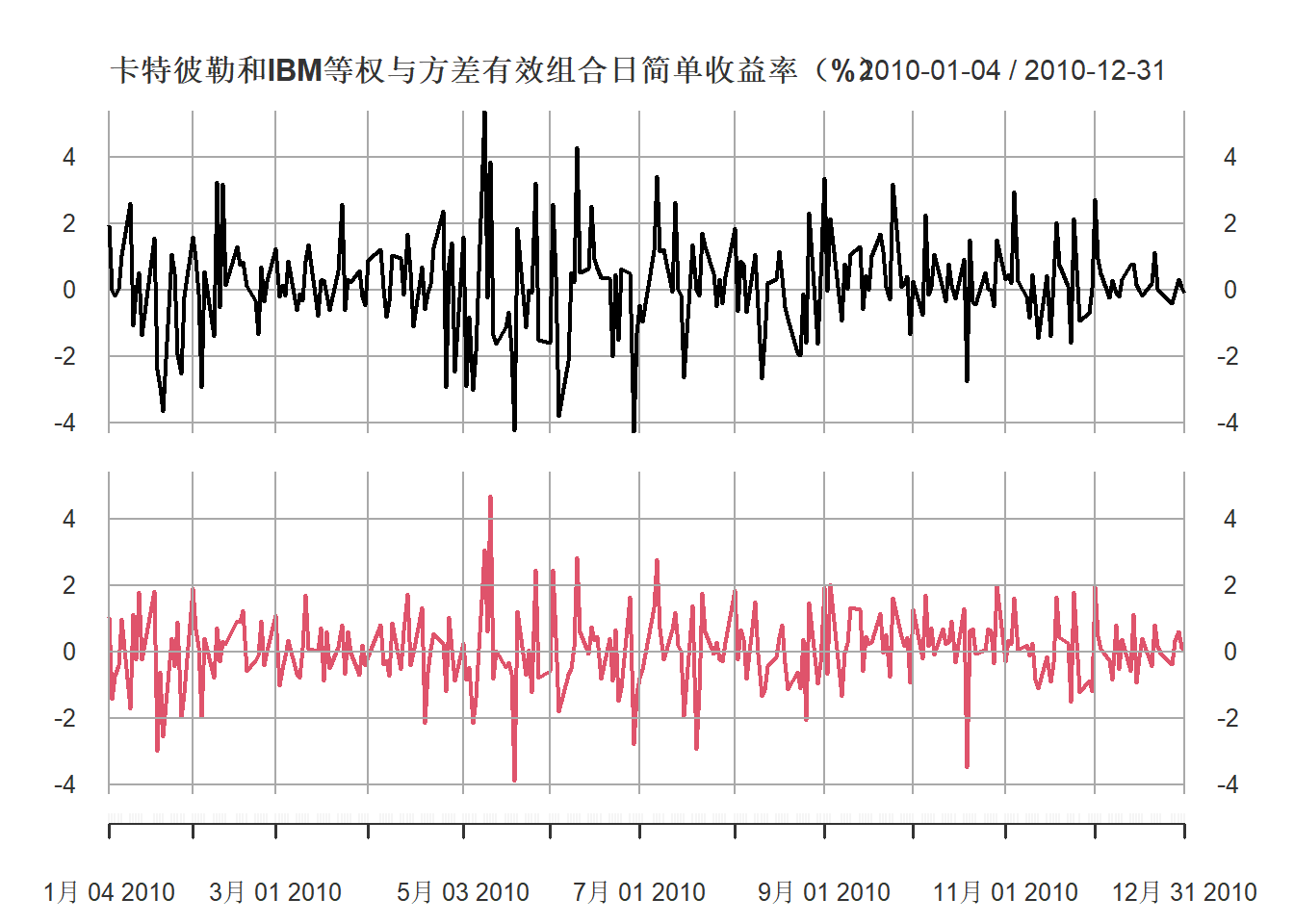

图14.2: 2010年卡特彼勒和IBM等权与方差有效组合日简单收益率（%）

14.2.2 组合中包含无风险资产的情形

如果投资组合中包含一个收益率为常数\(r\)的资产， 则\(\Sigma\)不可逆。 设\(p\)个风险资产为\(\boldsymbol x_t\)， 记\(\text{Var}(\boldsymbol x_t)=\Sigma\)， 设\(\Sigma\)正定。 设固定收益率资产是第\(p+1\)个资产， 资产组合系数为\((\boldsymbol c^T, c_0)\)， 则\(c_0 = 1 - \boldsymbol 1^T \boldsymbol c\)。 因为常数与任何随机变量的协方差等于零， 于是求解拉格朗日偏导数等于零的方程变成 \[\begin{aligned} \left(\begin{array}{cc} \Sigma & \boldsymbol 0 \\ \boldsymbol 0^T & 0 \end{array}\right) \left(\begin{array}{c} \boldsymbol c \\ c_0 \end{array}\right) - \lambda_1 \left(\begin{array}{c} \boldsymbol\mu \\ r \end{array}\right) - \lambda_2 \boldsymbol 1_{p+1} = 0 \end{aligned}\] 由其中最后一个方程可得\(\lambda_2 = -\lambda_1 r\)， 代入到前\(p\)个方程得 \[\begin{aligned} & \Sigma \boldsymbol c - \lambda_1 \boldsymbol\mu + \lambda_1 r \boldsymbol 1_p = 0 \\ & \boldsymbol c = \lambda_1 \Sigma^{-1} (\boldsymbol\mu - r \boldsymbol 1_p) \end{aligned}\] 代入约束 \[\begin{aligned} \left(\begin{array}{c} \boldsymbol\mu \\ r \end{array}\right)^T \left(\begin{array}{c} \boldsymbol c \\ 1 - \boldsymbol 1^T \boldsymbol c \end{array}\right) = \bar\mu \end{aligned}\] 中，即 \[\begin{aligned} & \boldsymbol\mu^T \boldsymbol c + r(1 - \boldsymbol 1^T \boldsymbol c) = \bar\mu \\ & (\boldsymbol\mu - r \boldsymbol 1)^T \boldsymbol c = \bar\mu - r \end{aligned}\] 解得 \[\begin{aligned} \lambda_1 =& \frac{\bar\mu - r}{ (\boldsymbol\mu - r \boldsymbol 1)^T \Sigma^{-1} (\boldsymbol\mu - r \boldsymbol 1)} \end{aligned}\] 于是 \[\begin{aligned} \boldsymbol c =& \frac{(\bar\mu - r) \Sigma^{-1} (\boldsymbol\mu - r \boldsymbol 1)}{ (\boldsymbol\mu - r \boldsymbol 1)^T \Sigma^{-1} (\boldsymbol\mu - r \boldsymbol 1)} \end{aligned}\] 而\(c_0 = 1 - \boldsymbol 1^T \boldsymbol c\)是无风险资产的权重。

14.2.3 一些特殊的有效组合

考虑没有无风险资产的情形。

特例1 如果\(\Sigma = \sigma^2 I\)， 即各资产收益率不相关且方差相等， 则最小方差资产组合的权重为等权 \[ \boldsymbol c_{\text{opt}} = \frac{1}{p} \boldsymbol 1_p \]

证明： 按公式\(\boldsymbol c_{\text{opt}} = \lambda \Sigma^{-1} \boldsymbol 1_p\)， 现在\(\Sigma^{-1} = \frac{1}{\Sigma^2} I\)， 所以\(\boldsymbol c_{\text{opt}} = \lambda1 \sigma^{-2} \boldsymbol 1_p\)， 由\(\boldsymbol 1^T \boldsymbol c=1\)可得上面的等权公式。

特例2 如果 \[\begin{aligned} \Sigma = \sigma^2 \left(\begin{array}{cccc} 1 & \rho & \cdots & \rho \\ \rho & 1 & \cdots & \rho \\ \vdots & \vdots & \ddots & \vdots \\ \rho & \rho & \cdots & 1 \end{array}\right) \end{aligned}\] 则方差最小权重也是等权。

事实上，这时有 \[\begin{aligned} \Sigma = \sigma^2 \left\{ (1 - \rho) I_p + \rho \boldsymbol 1_p \boldsymbol 1^T \right\} \end{aligned}\] 利用如下的矩阵求逆公式： \[\begin{aligned} A =& (a - b) I_p + b \boldsymbol 1 \boldsymbol 1^T \\ A^{-1} =& \frac{1}{a-b} I_p - \frac{b}{(a-b)[a + (p-1) b]} \boldsymbol 1 \boldsymbol 1^T \end{aligned}\] 可得 \[\begin{aligned} \Sigma^{-1} \boldsymbol 1 =& \sigma^{-2} \left\{ \frac{1}{1-\rho} I_p - \frac{\rho}{(1-\rho)[1 + (p-1)\rho]} \boldsymbol 1_p \boldsymbol 1_p^T \right\} \boldsymbol 1 \\ =& \frac{1}{\sigma^2 (1 - \rho)} \left\{ \boldsymbol 1_p - \frac{p \rho}{1 + (p-1) \rho} \boldsymbol 1 \right\} \\ =& \frac{1}{\sigma^2[1 + (p-1) \rho]} \boldsymbol 1 \end{aligned}\] 由约束\(\boldsymbol 1^T \boldsymbol c=1\)可知\(\boldsymbol c\)为等权。

特例3 如果\(\Sigma=\text{diag}(\sigma_1^2, \dots, \sigma_p^2)\), 则 \[ \boldsymbol c_{\text{opt}} = (\sum_{l=1}^p \sigma_l^{-2}) (\sigma_1^{-2}, \dots, \sigma_p^{-2})^T \]

事实上，这时 \(\Sigma^{-1} = \text{diag}(\sigma_1^{-2}, \dots, \sigma_p^{-2})\)， 于是 \(\Sigma^{-1} \boldsymbol 1 = (\sigma_1^{-2}, \dots, \sigma_p^{-2})^T\)。

特例4 如果各个资产分成了\(k\)个组， 不同组的资产收益率不相关， 第\(j\)组的资产收益率协方差阵为\(\Sigma_j\)， 则方差最小投资组合系数为 \[\begin{aligned} \boldsymbol c_{\text{opt}} = \lambda \left(\begin{array}{c} \Sigma_1^{-1} \boldsymbol 1 \\ \vdots \\ \Sigma_k^{-1} \boldsymbol 1 \end{array}\right) \end{aligned}\] 其中\(\lambda^{-1} = \sum_{j=1}^k \boldsymbol 1^T \Sigma_j^{-1} \boldsymbol 1\)。

14.3 CAPM 模型

CAPM模型研究个股与市场的关系。 设考虑投资的资产有\(p\)个， 另外有一个资产与这\(p\)个资产不相关（收益率不相关）。 与其他资产不相关的最典型情况是无风险资产， 其收益率为常数\(r\)， 常数与任何随机变量都不相关。

均值方差有效投资组合的方程为(14.5)，即 \[\begin{aligned} \Sigma \boldsymbol c - \lambda_1 \boldsymbol\mu - \lambda_2 \boldsymbol 1_p = 0 \end{aligned}\] 为了消去\(\lambda_1\)，左乘\(\boldsymbol c^T\)， 利用\(\boldsymbol c^T \boldsymbol\mu = \bar\mu\)约束条件可得 \[\begin{aligned} \boldsymbol c^T \Sigma \boldsymbol c - \lambda_1 \bar\mu = \lambda_2 \end{aligned}\] 将\(\lambda_2\)代入(14.5)中， 得 \[\begin{aligned} \Sigma \boldsymbol c - \lambda_1 \boldsymbol\mu = \boldsymbol c^T \Sigma \boldsymbol c \boldsymbol 1_p - \lambda_1 \bar\mu \boldsymbol 1_p \end{aligned}\] 于是 \[\begin{align} \boldsymbol\mu =& \bar\mu \boldsymbol 1_p + \frac{1}{\lambda_1} [\Sigma \boldsymbol c - (\boldsymbol c^T \Sigma \boldsymbol c) \boldsymbol 1_p] \tag{14.6} \end{align}\]

在有\(p\)个资产的收益率协方差阵为\(\Sigma>0\)， 有第\(p+1\)个资产为无风险资产\(r\)时， 设均值方差有效组合为\((\boldsymbol c^T, c_0)^T\)， (14.6)变成 \[\begin{aligned} \left(\begin{array}{c} \boldsymbol\mu \\ r \end{array}\right) =& \bar\mu \boldsymbol 1_{p+1} + \frac{1}{\lambda_1}\left[ \left(\begin{array}{cc} \Sigma & \boldsymbol 0 \\ \boldsymbol 0^T & 0 \end{array}\right) \left(\begin{array}{c} \boldsymbol c \\ c_0 \end{array}\right) - (\boldsymbol c^T, c_0) \left(\begin{array}{cc} \Sigma & \boldsymbol 0 \\ \boldsymbol 0^T & 0 \end{array}\right) \left(\begin{array}{c} \boldsymbol c \\ c_0 \end{array}\right) \boldsymbol 1_{p+1} \right] \\ =& \bar\mu \boldsymbol 1_{p+1} + \frac{1}{\lambda_1}\left[ \left(\begin{array}{c} \Sigma \boldsymbol c \\ 0 \end{array}\right) - (\boldsymbol c^T \Sigma \boldsymbol c) \boldsymbol 1_{p+1} \right] \end{aligned}\] 上式的最后一个方程为 \[ r = \bar\mu - \frac{1}{\lambda_1} (\boldsymbol c^T \Sigma \boldsymbol c) \] 从中解出\(\lambda_1\)： \[\begin{aligned} \lambda_1 = \frac{\boldsymbol c^T \Sigma \boldsymbol c}{\bar\mu - r} \end{aligned}\] 将解除的\(\lambda_1\)代入(14.6)中， 得 \[\begin{align} \boldsymbol\mu =& \bar\mu \boldsymbol 1_p + \frac{\bar\mu - r}{\boldsymbol c^T \Sigma \boldsymbol c}\left[ \Sigma \boldsymbol c - (\boldsymbol c^T \Sigma \boldsymbol c) \boldsymbol 1_p \right] \\ =& \bar\mu \boldsymbol 1_p + \frac{\bar\mu - r}{\boldsymbol c^T \Sigma \boldsymbol c} \cdot \Sigma \boldsymbol c - (\bar\mu - r) \boldsymbol 1_p \\ =& r \boldsymbol 1_p + (\boldsymbol c^T \Sigma \boldsymbol c)^{-1} \Sigma\boldsymbol c \cdot(\bar\mu - r) \\ =& r \boldsymbol 1_p + \boldsymbol\beta (\bar\mu - r) \tag{14.7} \end{align}\] 其中\(\boldsymbol\beta = (\boldsymbol c^T \Sigma \boldsymbol c)^{-1} \Sigma\boldsymbol c\)。

最后一个式子 \[ \boldsymbol\mu - r \boldsymbol 1_p = \boldsymbol\beta (\bar\mu - r) \] 这称为CAPM模型（Capital asset pricing model）， 左边是每个资产的平均超额收益率（\(r\)是无风险资产收益率）， 右边的\(\bar\mu - r\)是所有风险资产的均值方差有效投资组合的超额收益率， 公式描述了单个资产与投资组合的关系的强弱， \(\boldsymbol\beta\)每个分量代表一项资产， \(\boldsymbol\beta\)分量一般接近于1。 大于1时比市场变化更剧烈， 小于1时可能是波动较小也可能是与其他资产的相关性较弱。 关于CAPM模型参见(Franke, Härdle, and Hafner 2011)。

References

Franke, J., W. Härdle, and C. Hafner. 2011. Introduction to Statistics of Financial Markets. 3rd edition. Heidelberg: Springer.

Wolfgang Härdle, Léopold Simar. 2015. Applied Multivariate Statistical Analysis. 4th Edition. Springer.