3 多元分布

本章内容主要参考 (Zelterman 2015) Applied Multivariate Statistics with R, Springer.

需要额外安装的软件包：

options(repos=c(CRAN="https://mirrors.tuna.tsinghua.edu.cn/CRAN/"))
install.packages(c("fBasics", "mvtnorm", "ICSNP", "rrcov"))

3.1 一元正态分布及其统计推断

3.1.1 密度

一元标准正态分布N(0,1)密度函数:

\[\begin{aligned} \phi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac12 x^2}, \ x \in \mathbb R . \end{aligned}\]

N(\(\mu, \sigma^2\))密度：

\[\begin{aligned} \phi(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} \exp\left\{-\frac12 \left(\frac{x-\mu}{\sigma} \right)^2 \right\}, \ x \in \mathbb R . \end{aligned}\]

R中: dnorm(x, mean, sd)

R程序示例：作不同mu的密度图；作不同sigma的密度图。

## 正态分布密度的图形
demo.normal.den <- function(){
    opar <- par(mar=c(5,5,3,1)); on.exit(opar)
    x <- seq(-5, 5, length=100)
    ## 不同mu的密度
    mus <- c(-1, 0, 1); sigma <- 1
    ys <- lapply(mus, function(mu) dnorm(x, mu, sigma))
    ylim <- range(unlist(ys))
    ylim[2] <- 1.1*ylim[2]
    plot(x, ys[[1]], type='l', lwd=2,
         ylim=ylim,
         xlab='x', ylab='f(x)',
         main='Normal Densities')
    lines(x, ys[[2]], lwd=2)
    lines(x, ys[[3]], lwd=2)
    text(-1, ylim[2]*0.98,
         expression(mu==-1))
    text(0, ylim[2]*0.98,
         expression(mu==0))
    text(1, ylim[2]*0.98,
         expression(mu==1))

    ## 不同sigma的密度
    mu <- 0
    sigmas <- c(0.5, 1, 2)
    ys <- lapply(sigmas, function(sigma) dnorm(x, 0, sigma))
    ylim <- range(unlist(ys))
    ylim[2] <- 1.1*ylim[2]
    plot(x, ys[[1]], type='l', lwd=2,
         ylim=ylim,
         xlab='x', ylab='f(x)',
         main='Normal Densities')
    lines(x, ys[[2]], lwd=2)
    lines(x, ys[[3]], lwd=2)
    text(0, 0.84, expression(sigma==0.5))
    text(1.3, 0.28, expression(sigma==1))
    text(3.2, 0.11, expression(sigma==2))
}
demo.normal.den()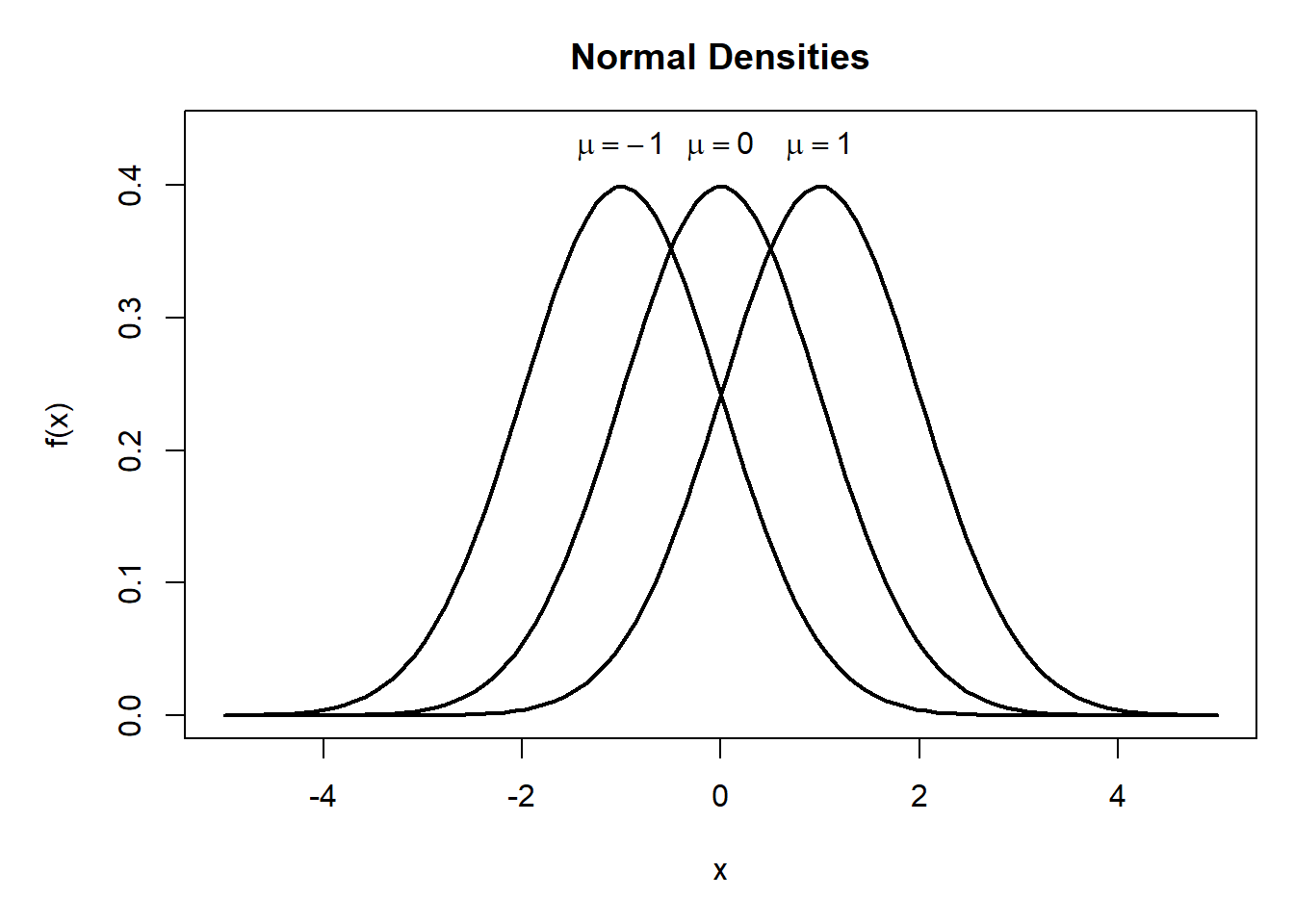

图3.1: 一元正态密度图形

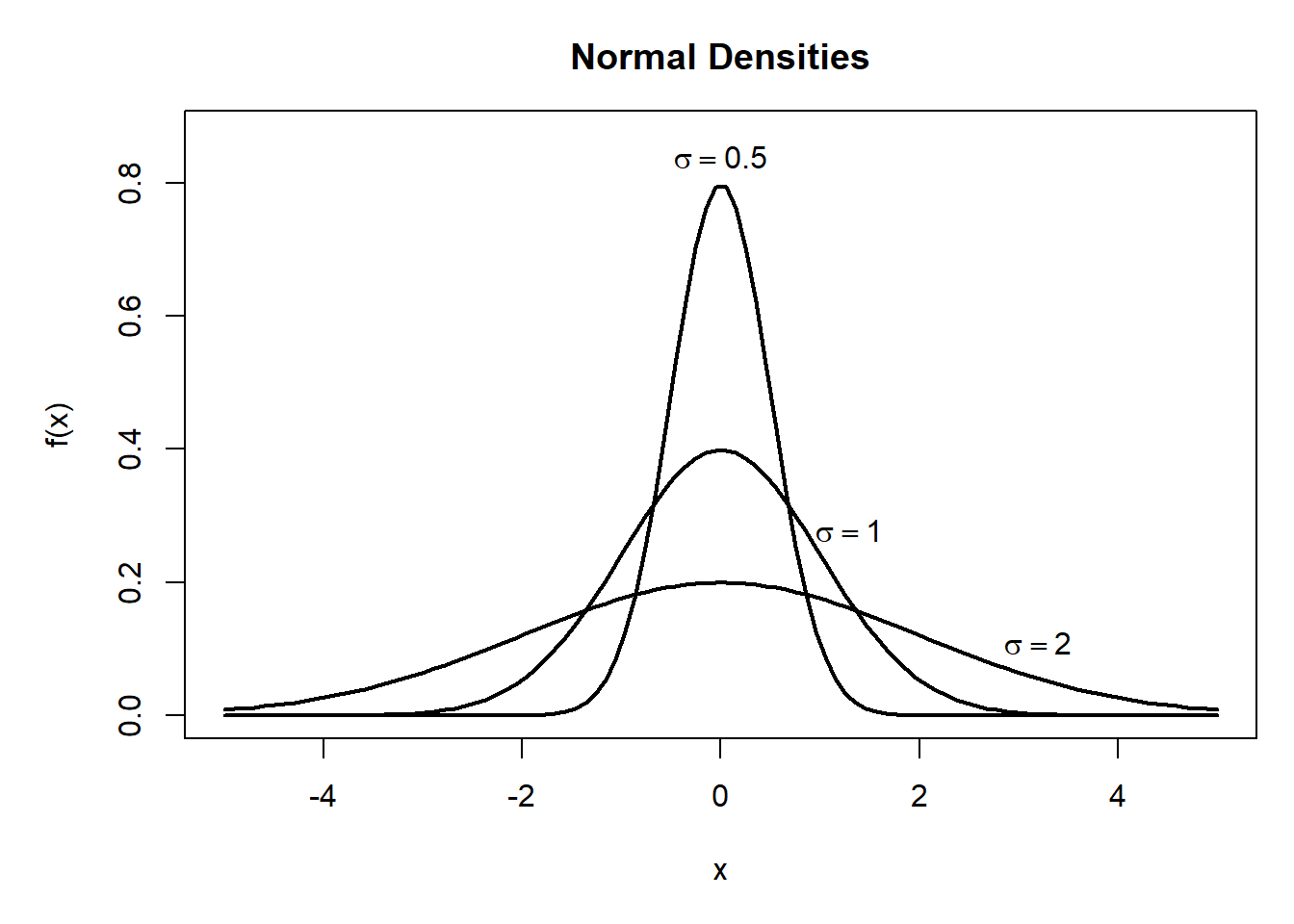
图3.2: 一元正态密度图形

3.1.2 分布函数和分位数函数

N(0,1)分布函数:

\[\begin{aligned} \Phi(x) = \int_{-\infty}^x \phi(t) \,dt . \end{aligned}\]

N(\(\mu, \sigma^2\))分布函数: \(\Phi(\frac{x - \mu}{\sigma})\)。

R中pnorm(x, mean, sd)。

R程序示例：作不同mu的分布函数；作不同sigma的分布函数。

## 正态分布函数的图形
demo.normal.cdf <- function(){
    opar <- par(mar=c(5,5,3,1)); on.exit(opar)
    x <- seq(-5, 5, length=100)
    ## 不同mu的分布函数
    mus <- c(-1, 0, 1); sigma <- 1
    ys <- lapply(mus, function(mu) pnorm(x, mu, sigma))
    ylim <- c(0, 1.1)
    plot(x, ys[[1]], type='l', lwd=2,
         ylim=ylim,
         xlab='x', ylab='f(x)',
         main='Normal CDF')
    abline(v=0)
    lines(x, ys[[2]], lwd=2)
    lines(x, ys[[3]], lwd=2)
    text(0.2, 1.0, expression(mu == -1), pos=4)
    text(0.46, 0.65, expression(mu == 0), pos=4)
    text(0.9, 0.4, expression(mu == 1), pos=4)
    locator(1)

    ## 不同sigma的分布函数
    mu <- 0
    sigmas <- c(0.5, 1, 2)
    ys <- lapply(sigmas, function(sigma) pnorm(x, 0, sigma))
    ylim <- c(0, 1.1)
    plot(x, ys[[1]], type='l', lwd=2,
         ylim=ylim,
         xlab='x', ylab='f(x)',
         main='Normal CDF')
    lines(x, ys[[2]], lwd=2)
    lines(x, ys[[3]], lwd=2)
    text(0.76, 1.00, expression(sigma==0.5), pos=3)
    text(1.48, 0.91, expression(sigma==1), pos=4)
    text(2.36, 0.85, expression(sigma==2), pos=4)
    locator(1)
}
demo.normal.cdf()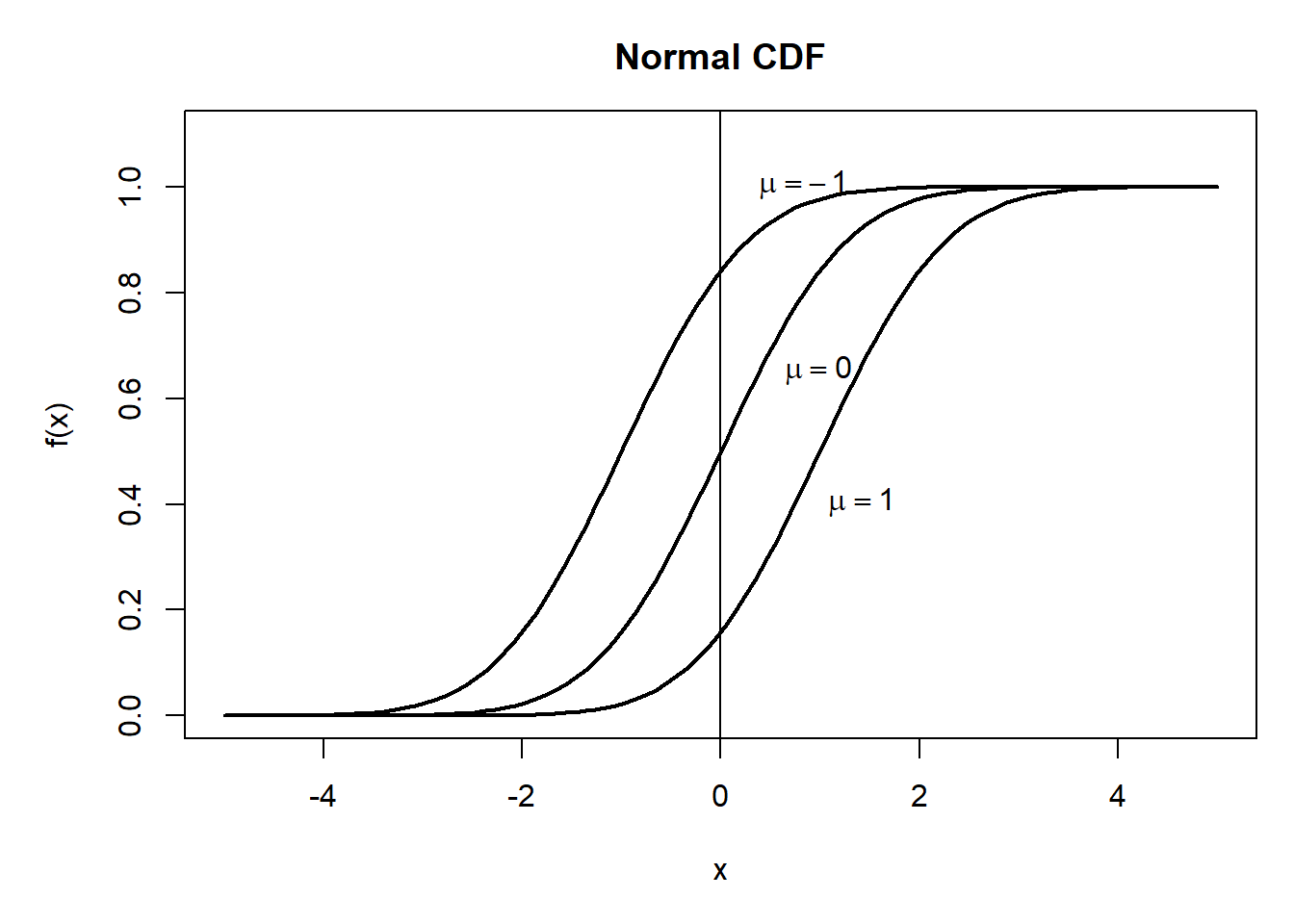

图3.3: 一元正态分布函数图形

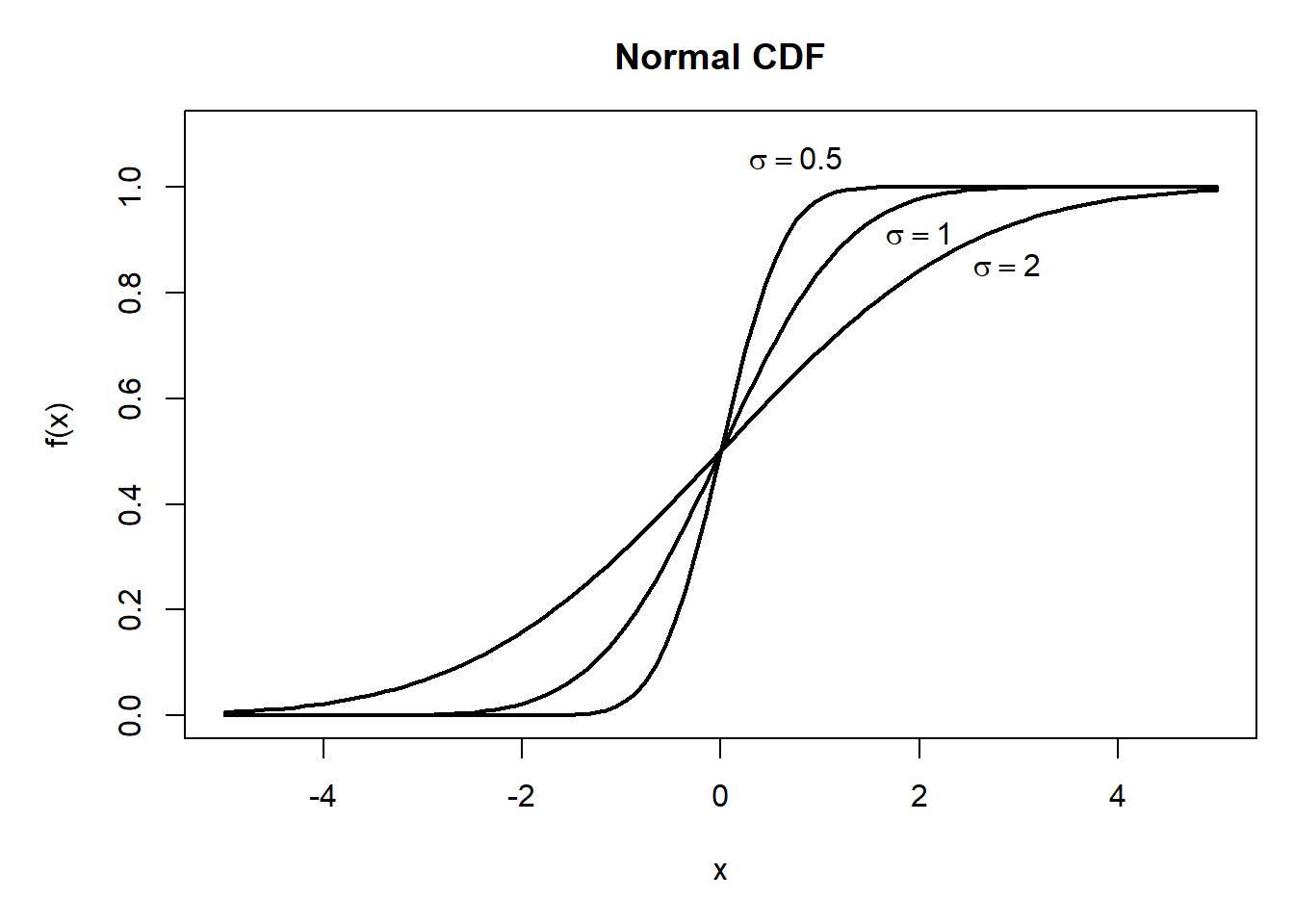
图3.4: 一元正态分布函数图形

\(\Phi^{-1}(p), p \in (0,1)\)是标准正态分布的分位数函数，又称为下侧（左侧）\(p\)分位数。

R中qnorm(p)为\(\Phi^{-1}(p)\)。

上侧（右侧）\(\alpha\)分位数即\(\Phi^{-1}(1-\alpha)\)。

双侧\(\alpha\)分位数为\(\Phi^{-1}(1-\frac{\alpha}{2})\)。

## 正态分位数函数的图形
demo.normal.quantile <- function(){
    opar <- par(mar=c(5,5,3,1)); on.exit(opar)

    ## 标准正态分位数函数
    x <- (1:99)/100
    y <- qnorm(x)
    plot(x, y, type='l', lwd=2,
         xlim=c(0,1),
         xlab='p', ylab=expression({Phi^{-1}} (p)),
         main='N(0,1) Quantile Function')
    abline(h=0)
}
demo.normal.quantile()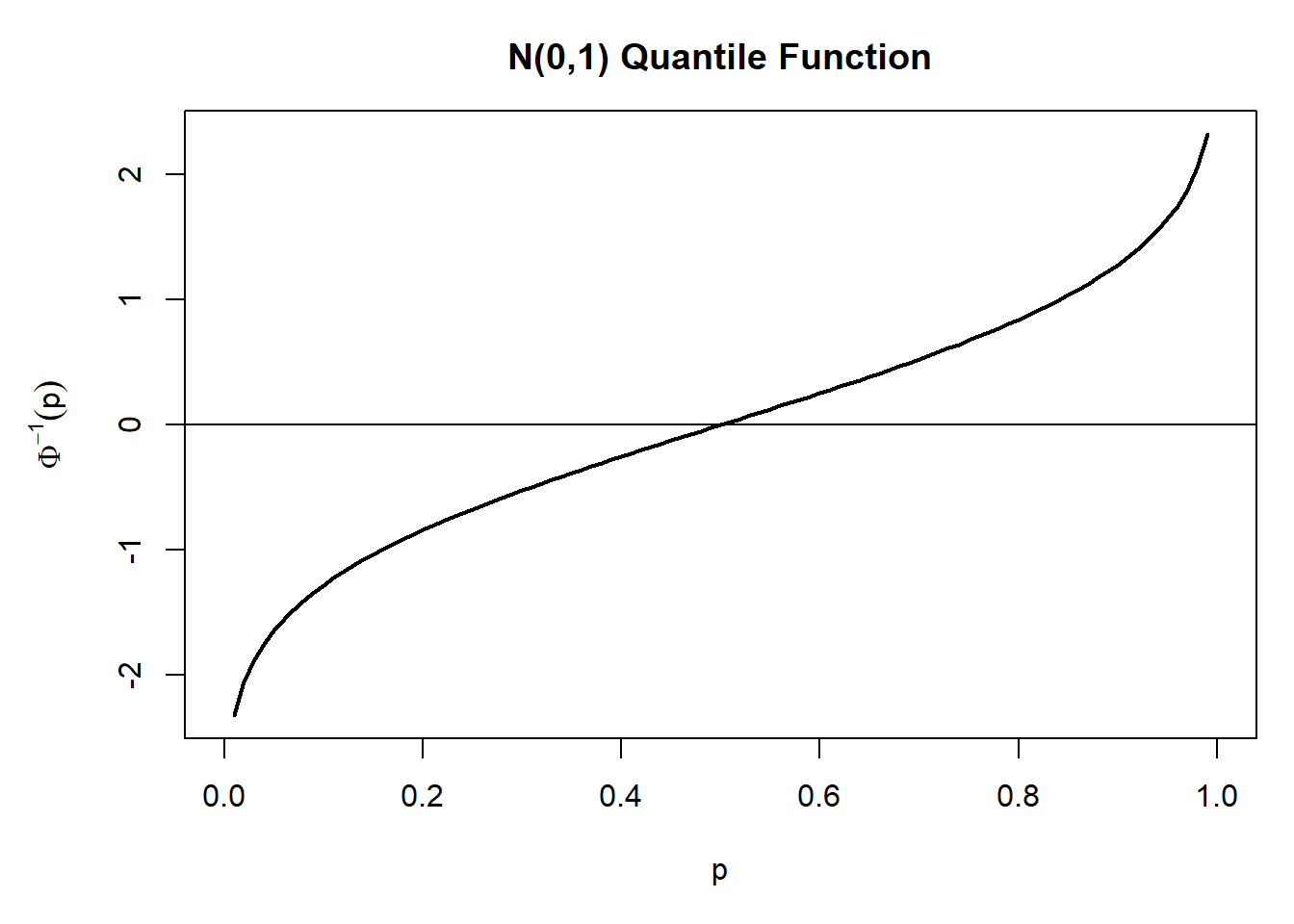

图3.5: 一元正态分位数函数图形

3.1.3 正态随机数函数

随机数解释。

rnorm(n)。

设置开始点：set.seed(1)。

正态分布随机数演示：

set.seed(1)
x <- round(rnorm(100), 2)
print(x)

##   [1] -0.63  0.18 -0.84  1.60  0.33 -0.82  0.49  0.74  0.58 -0.31  1.51  0.39
##  [13] -0.62 -2.21  1.12 -0.04 -0.02  0.94  0.82  0.59  0.92  0.78  0.07 -1.99
##  [25]  0.62 -0.06 -0.16 -1.47 -0.48  0.42  1.36 -0.10  0.39 -0.05 -1.38 -0.41
##  [37] -0.39 -0.06  1.10  0.76 -0.16 -0.25  0.70  0.56 -0.69 -0.71  0.36  0.77
##  [49] -0.11  0.88  0.40 -0.61  0.34 -1.13  1.43  1.98 -0.37 -1.04  0.57 -0.14
##  [61]  2.40 -0.04  0.69  0.03 -0.74  0.19 -1.80  1.47  0.15  2.17  0.48 -0.71
##  [73]  0.61 -0.93 -1.25  0.29 -0.44  0.00  0.07 -0.59 -0.57 -0.14  1.18 -1.52
##  [85]  0.59  0.33  1.06 -0.30  0.37  0.27 -0.54  1.21  1.16  0.70  1.59  0.56
##  [97] -1.28 -0.57 -1.22 -0.47

hist(x, prob=TRUE)
lines(density(x), col='red', lwd=2)

图3.6: 一元正态随机数

3.1.4 与其它分布的关系

中心极限定理说明许多分布可以用正态分布近似。

\(X \sim \text{N}(0,1)\)则\(X^2 \sim \chi^2(1)\)。

\(X_1, X_2, \dots, X_n \text{iid}\ \text{N}(0,1)\)则 \(X_1^2 + X_2^2 + \dots + X_n^2 \sim \chi^2(n)\)。

\(X_1, X_2\ \text{iid}\ \text{N}(0,1)\)则 \(X_1/X_2\)服从t(1)分布，也是柯西分布(Cauchy)。

3.1.5 正态化变换

明显偏态的分布可以通过函数变换变得比较对称，接近于正态。

取正值的数据样本有偏斜分布，想要变得比较对称，常用Box-Cox变换:

\[\begin{aligned} G(x) = \begin{cases} - x^\lambda, & \lambda < 0 \\ \log(x), & \lambda = 0 \\ x^\lambda, & \lambda > 0 \end{cases} \end{aligned}\]

自定义的Box-Cox变换函数：

## 给定正值观测向量y和变换参数lambda作Box-Cox变换。
bct <- function(y,lambda){
    gm <- exp( mean( log(y) ) )
    if(lambda==0) return( log(y)*gm )
    yt <- (y^lambda - 1)/( lambda * gm^(lambda-1) )
    return(yt)
}

城市居民可支配收入的正态化变换：

## 正态化变换演示
cityIncomeConsume <- read_csv(
  "data/居民收入支出.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
x <- cityIncomeConsume[["可支配收入"]]
hist(x, main='可支配收入')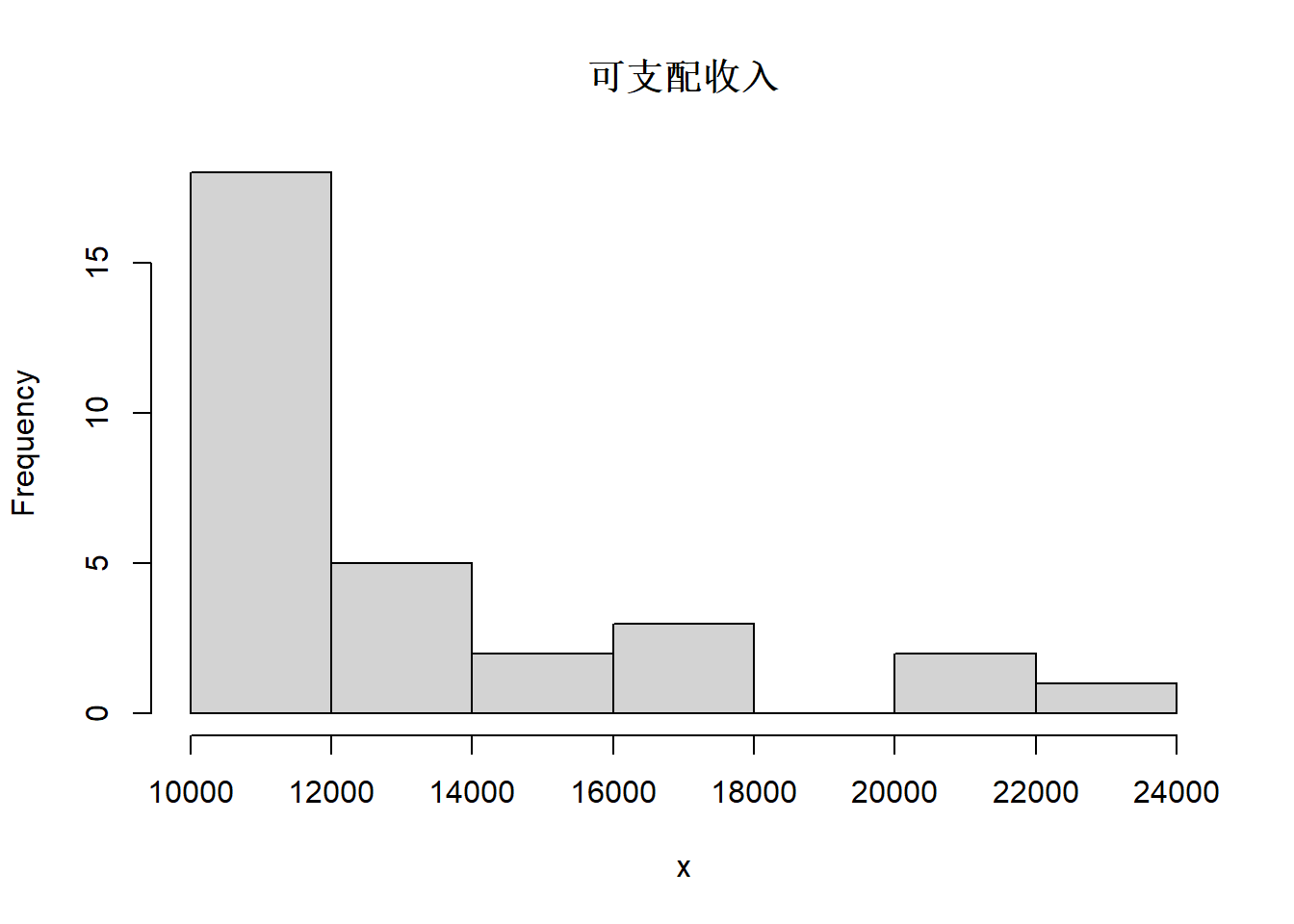

图3.7: 城市居民可支配收入

x <- cityIncomeConsume[["可支配收入"]]
y <- log10(x)
hist(y, main='可支配收入常用对数值')

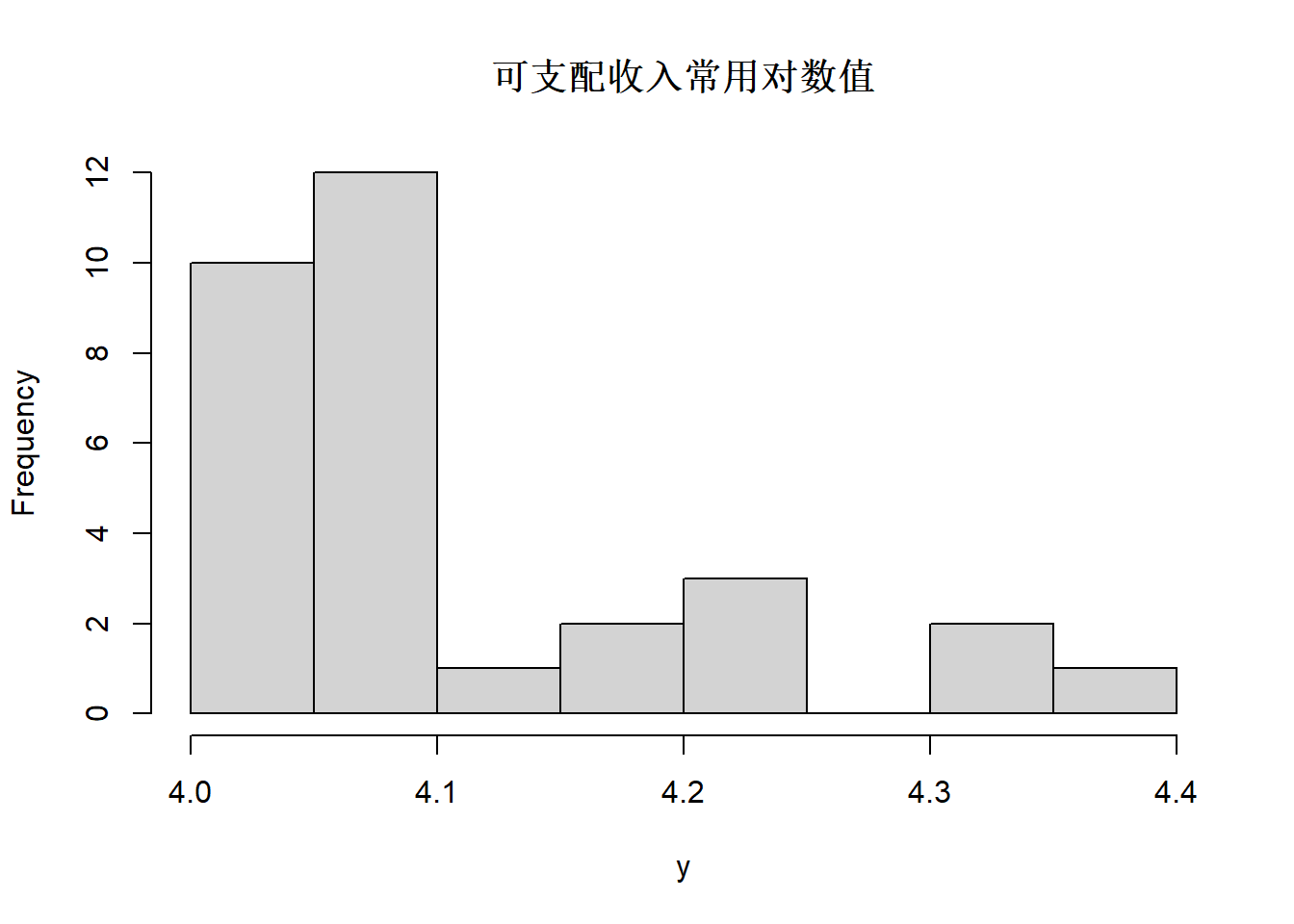
图3.8: 城市居民可支配收入的对数值

收入分布原来严重右偏，取对数后仍然右偏明显。

正态化变换：血糖数据glycemia中甘油数值的变换

glycemia <- read_csv(
  "data/血糖数据.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
x <- glycemia[["甘油"]]
hist(x, main='糖尿病人甘油值')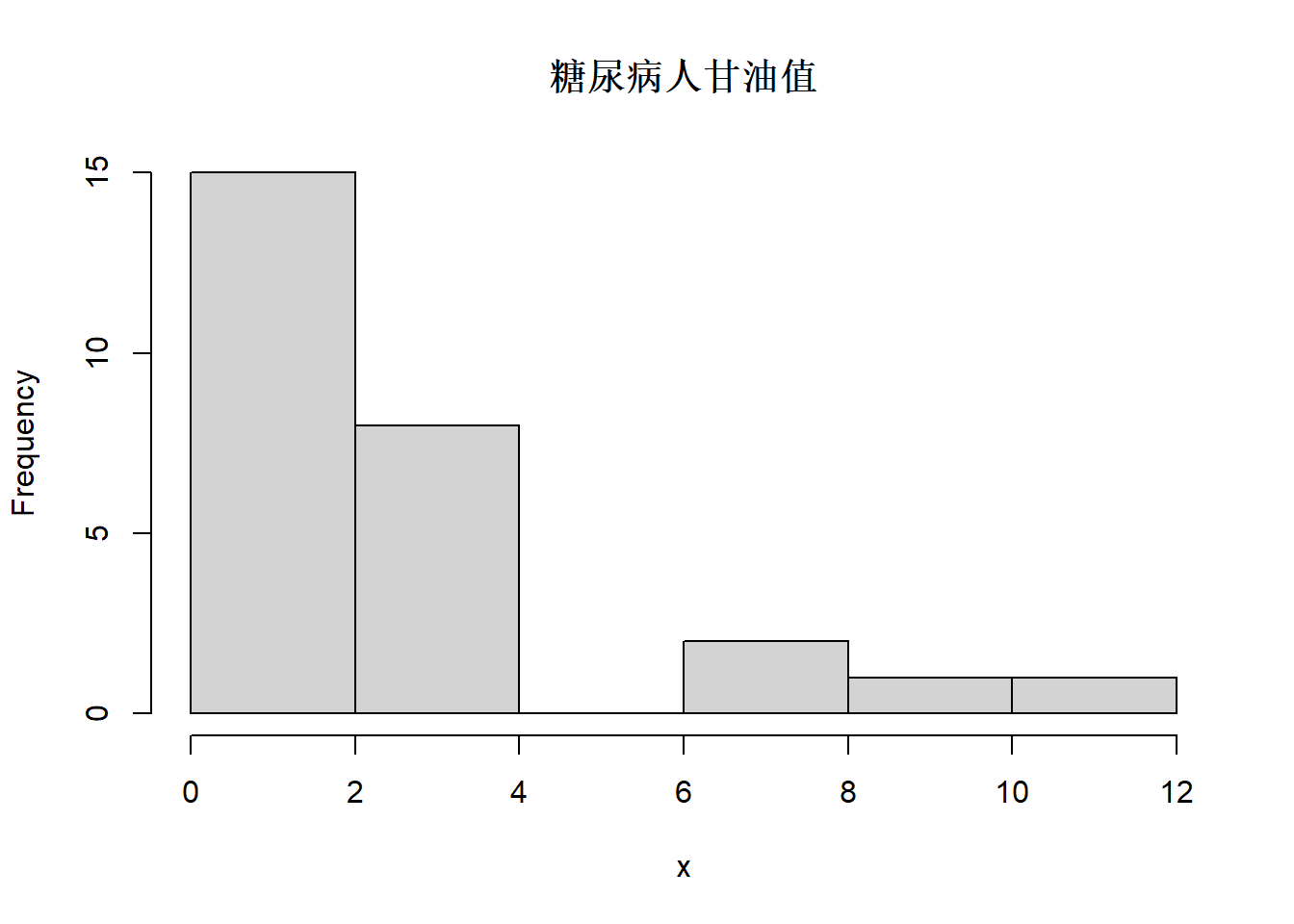

图3.9: 血糖数据glycemia中甘油数值直方图

x <- glycemia[["甘油"]]
qqnorm(x); qqline(x)

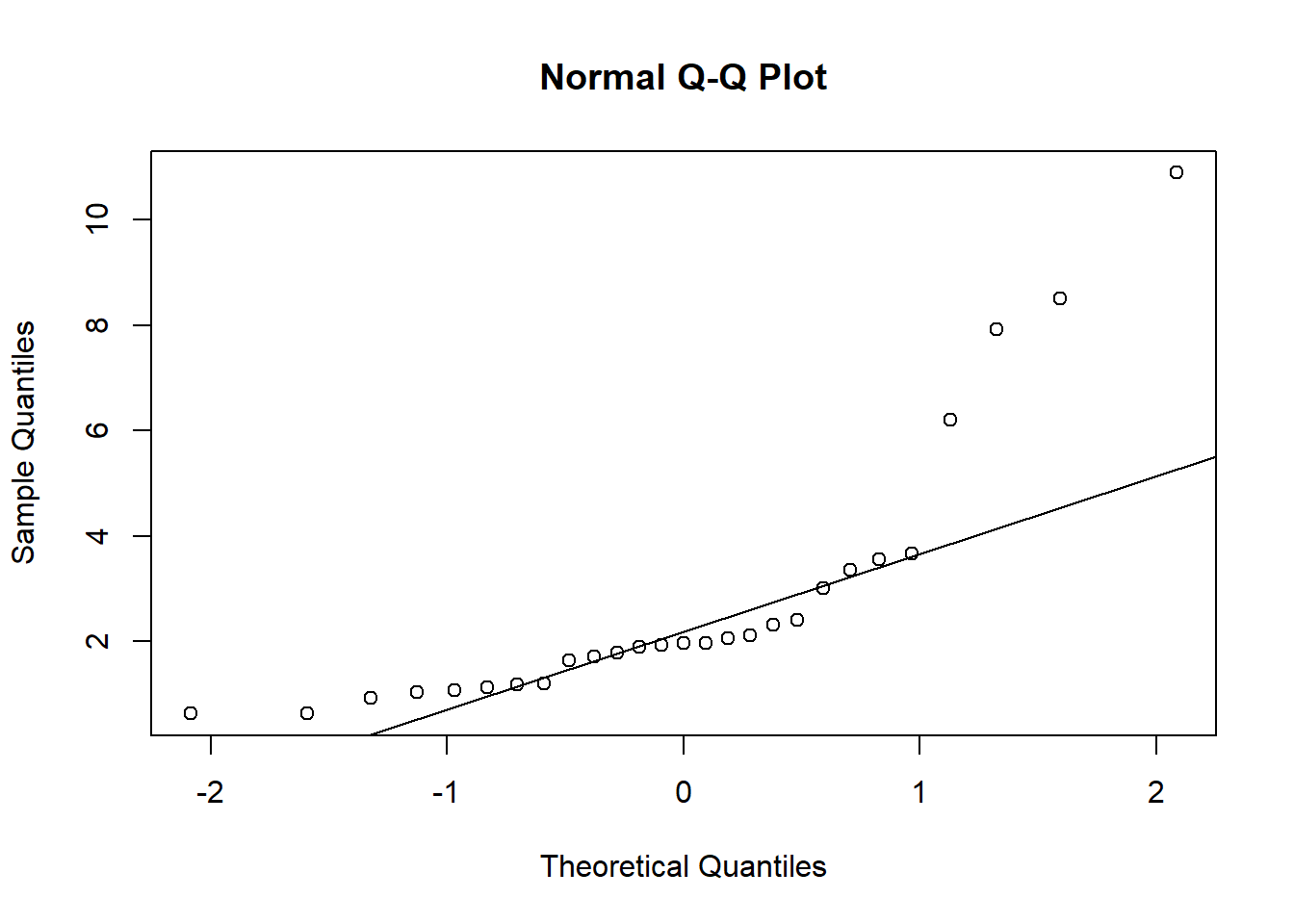
图3.10: 血糖数据glycemia中甘油数值QQ图

正态QQ图解释:

设\(Y_1, Y_2, \dots, Y_n\)是来自N(\(\mu, \sigma^2\))的简单随机样本，从小到大排列为

\[\begin{aligned} Y_{(1)} \leq Y_{(2)} \leq \dots Y_{(n)} \end{aligned}\]
因为\(\frac{Y_i - \mu}{\sigma}\) iid N(0,1), 所以\(\frac{Y_{(i)} - \mu}{\sigma}\)可以看成是标准正态分布的\(\frac{i}{n+1}\)分位数的估计值。
令\(x_i = \Phi^{-1}(\frac{i}{n+1})\)，\(i=1,2,\dots,n\)，则

\[\begin{aligned} \frac{Y_{(i)} - \mu}{\sigma} \approx& x_i, \ i=1,2,\dots,n \\ Y_{(i)} \approx& \mu + \sigma x_i, \ i=1,2,\dots,n \end{aligned}\]
作\((x_i, Y_{(i)}), i=1,2,\dots,n\)的散点图，散点应该落在一条直线附近。

x <- glycemia[["甘油"]]
y <- log10(x)
hist(y, main='糖尿病人甘油值常用对数')

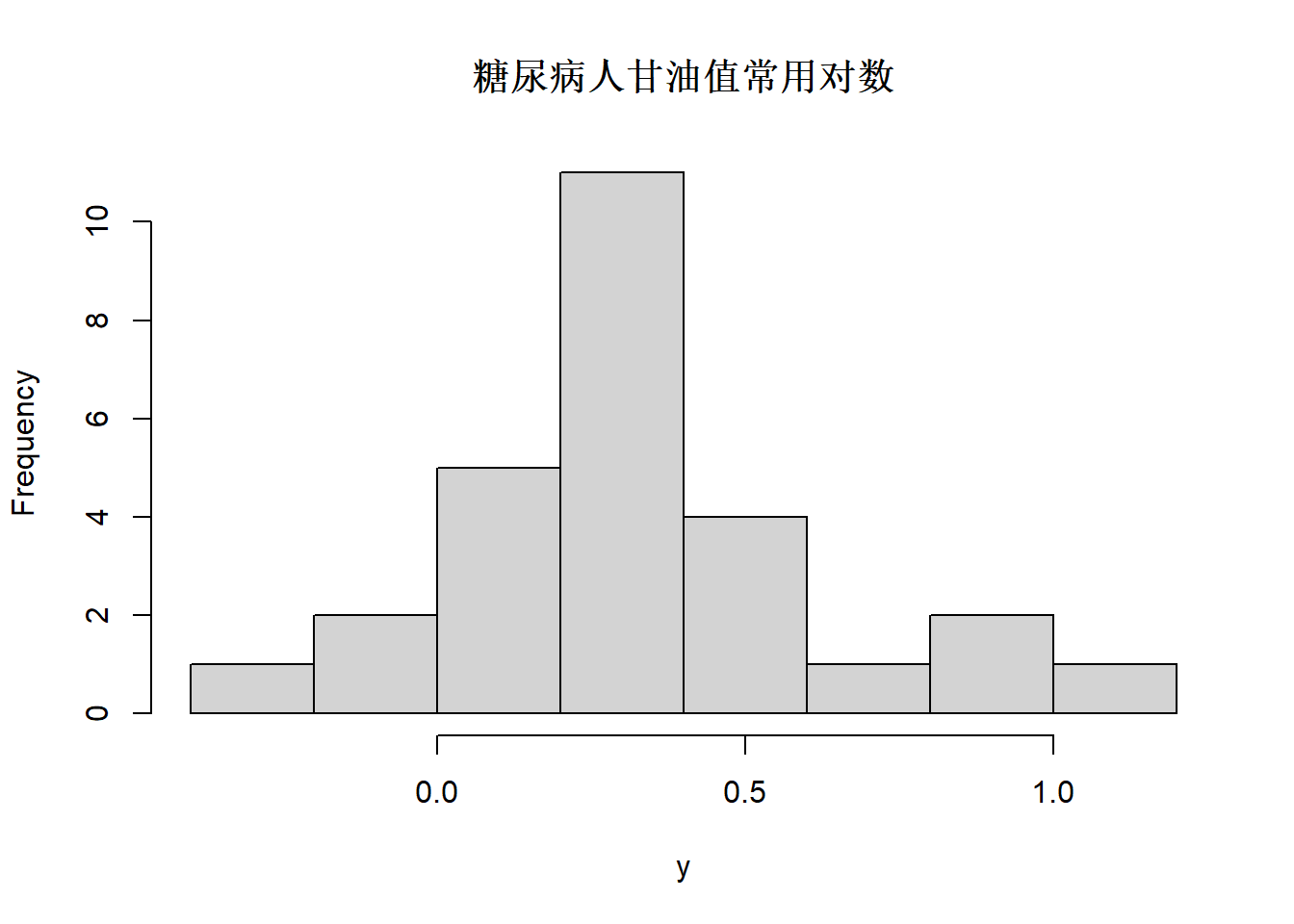
图3.11: 血糖数据glycemia中甘油数值对数值的直方图

x <- glycemia[["甘油"]]
y <- log10(x)
qqnorm(y, main='糖尿病人甘油值常用对数'); qqline(y)

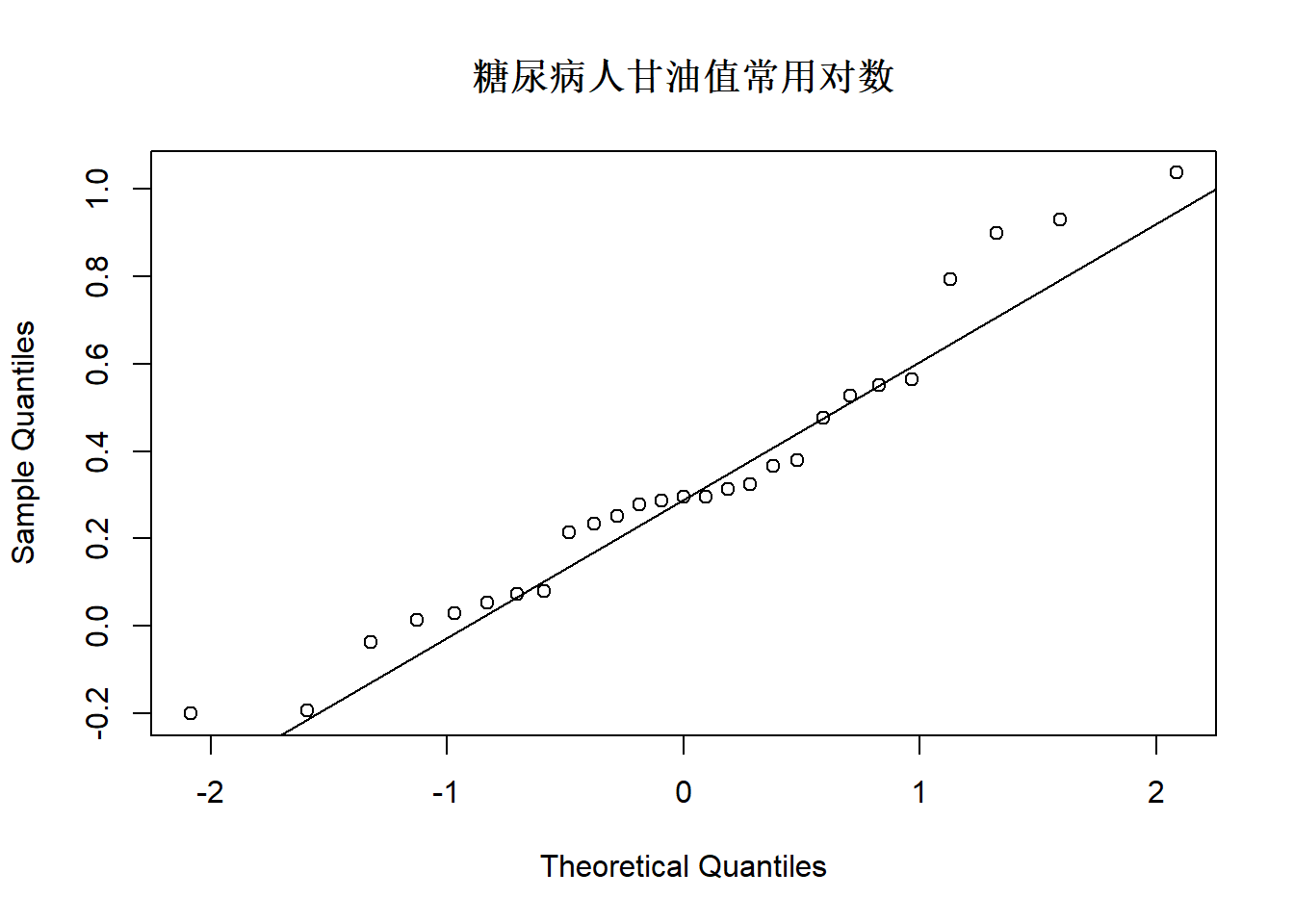
图3.12: 血糖数据glycemia中甘油数值对数值的QQ图

x <- glycemia[["甘油"]]
y <- sqrt(x)
hist(y, main='糖尿病人甘油值平方根')

图3.13: 血糖数据glycemia中甘油数值平方根的直方图

x <- glycemia[["甘油"]]
y <- sqrt(x)
qqnorm(y, main='糖尿病人甘油值平方根'); qqline(y)

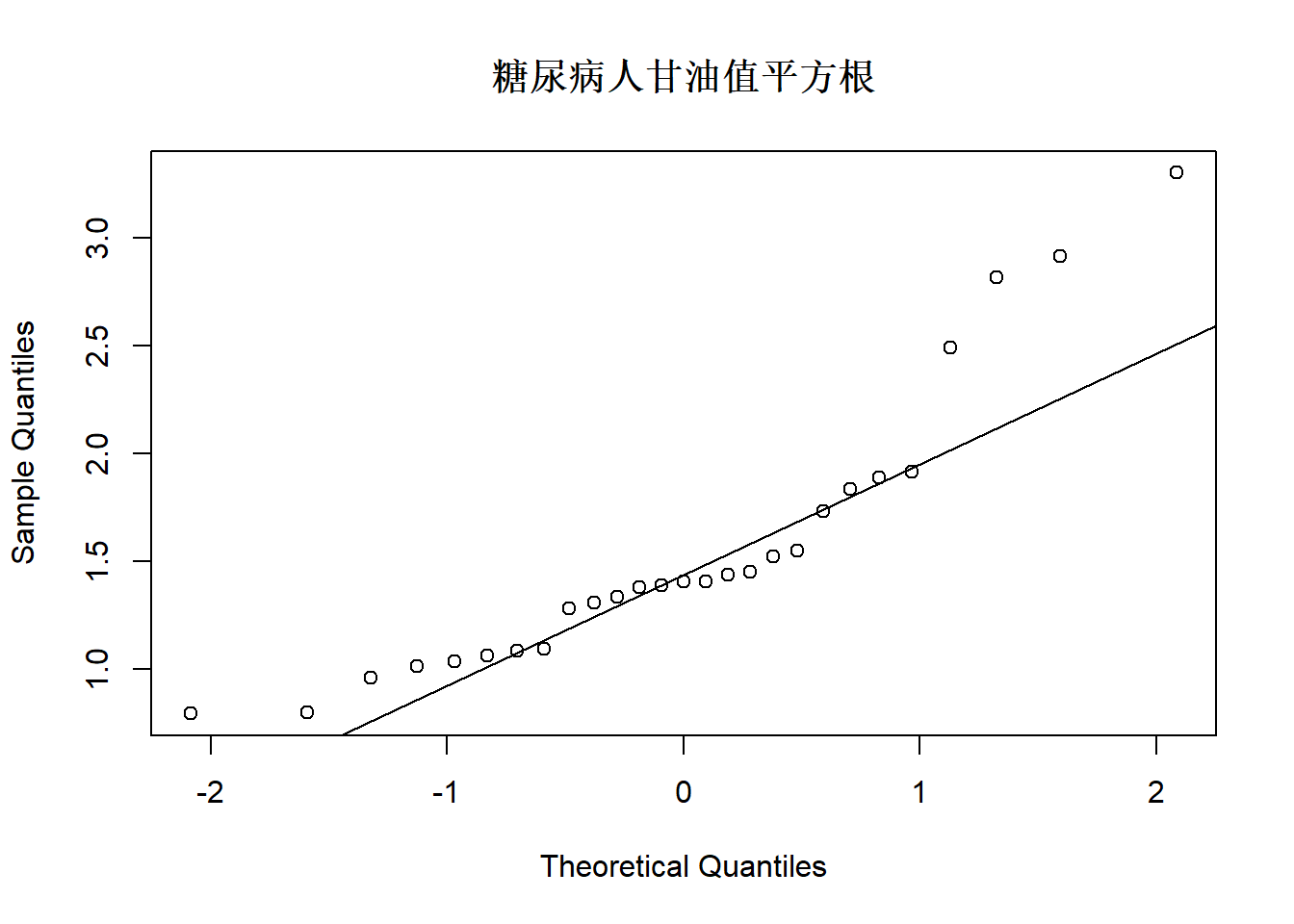
图3.14: 血糖数据glycemia中甘油数值平方根的QQ图

可以看出甘油指标数值原来是右偏分布，取对数后变成基本对称，如果取平方根则仍右偏。

3.1.6 正态性检验

\(H_0\)：样本来自正态总体。
偏离正态则有许多不同的可能性，针对不同的可能性可以提出不同的对立假设，构造不同针对性的正态性检验方法。
拟合优度卡方检验: 分段后比较观测频数和理论期望频数。 R中fBasics::pchiTest()。
Jarque-Bera偏度峰度检验:

\[\begin{aligned} \text{JB} = \frac{n}{6}( \text{偏度}^2 + \frac14 \text{峰度}^2 ) . \end{aligned}\]

在\(H_0\)下近似\(\chi^2(2)\), 右侧临界值。 R中fBasics::jbTest()。

Kolmogorov-Smirnov检验：比较经验分布函数与理论分布函数的最大差。 R中ksnormTest()。
Shapiro-Wilk检验: 基于QQ图思想。 R中shapiro.test()。

例：血糖数据glycemia中甘油数值的正态性检验

拟合优度卡方检验：

x <- glycemia[["甘油"]]

## 拟合优度卡方检验, 自动分组
fBasics::pchiTest(x, description='糖尿病人甘油原始值')

## 
## Title:
##  Pearson Chi-Square Normality Test
## 
## Test Results:
##   PARAMETER:
##     Number of Classes: 8
##   STATISTIC:
##     P: 22.4815
##   P VALUE:
##     Adhusted: 0.000424 
##     Not adjusted: 0.002097 
## 
## Description:
##  糖尿病人甘油原始值

零假设是服从正态分布，在\(\alpha=0.05\)水平下因为p值0.000424小于\(\alpha\)所以拒绝零假设，认为甘油值分布非正态。

Jarque-Bera偏度峰度检验:

fBasics::jbTest(x, title='糖尿病人甘油原始值JB检验')

## 
## Title:
##  糖尿病人甘油原始值JB检验
## 
## Test Results:
##   PARAMETER:
##     Sample Size: 27
##   STATISTIC:
##     LM: 23.042
##     ALM: 34.445
##   P VALUE:
##     LM p-value: 0.002 
##     ALM p-value: 0.002 
##     Asymptotic: < 2.2e-16

Kolmogorov-Smirnov检验:

fBasics::ksnormTest( (x - mean(x))/sd(x) )

## Warning in ks.test.default(x, "pnorm", alternative = "two.sided"): ties should
## not be present for the one-sample Kolmogorov-Smirnov test

## Warning in ks.test.default(x, "pnorm", alternative = "less"): ties should not
## be present for the one-sample Kolmogorov-Smirnov test

## Warning in ks.test.default(x, "pnorm", alternative = "greater"): ties should
## not be present for the one-sample Kolmogorov-Smirnov test

## 
## Title:
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## Test Results:
##   STATISTIC:
##     D: 0.2717
##   P VALUE:
##     Alternative Two-Sided: 0.03718 
##     Alternative      Less: 0.1276 
##     Alternative   Greater: 0.01859

Shapiro-Wilk检验:

shapiro.test(x)

## 
##  Shapiro-Wilk normality test
## 
## data:  x
## W = 0.73182, p-value = 1.11e-05

考虑糖尿病人甘油数值取常用对数后分布，作正态性检验。

y <- log10(x)
print(fBasics::pchiTest(y))

## 
## Title:
##  Pearson Chi-Square Normality Test
## 
## Test Results:
##   PARAMETER:
##     Number of Classes: 8
##   STATISTIC:
##     P: 12.4074
##   P VALUE:
##     Adhusted: 0.02961 
##     Not adjusted: 0.08793

print(fBasics::jbTest(y))

## 
## Title:
##  Jarque - Bera Normality Test
## 
## Test Results:
##   PARAMETER:
##     Sample Size: 27
##   STATISTIC:
##     LM: 1.327
##     ALM: 1.591
##   P VALUE:
##     LM p-value: 0.318 
##     ALM p-value: 0.33 
##     Asymptotic: 0.515

print(fBasics::ksnormTest( (y - mean(y))/sd(y) ))

## Warning in ks.test.default(x, "pnorm", alternative = "two.sided"): ties should
## not be present for the one-sample Kolmogorov-Smirnov test

## Warning in ks.test.default(x, "pnorm", alternative = "less"): ties should not
## be present for the one-sample Kolmogorov-Smirnov test

## Warning in ks.test.default(x, "pnorm", alternative = "greater"): ties should
## not be present for the one-sample Kolmogorov-Smirnov test

## 
## Title:
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## Test Results:
##   STATISTIC:
##     D: 0.138
##   P VALUE:
##     Alternative Two-Sided: 0.6828 
##     Alternative      Less: 0.7408 
##     Alternative   Greater: 0.3577

print(shapiro.test(y))

## 
##  Shapiro-Wilk normality test
## 
## data:  y
## W = 0.95074, p-value = 0.2235

可见取对数以后分布基本可以认为服从正态分布。

3.1.7 偏度和峰度

设\(EX=\mu\), \(\text{Var}(X)=\sigma^2\)。

偏度 \[\begin{aligned} \gamma_3 = E \left[ \left( \frac{X - \mu}{\sigma} \right)^3 \right] . \end{aligned}\]

峰度 \[\begin{aligned} \gamma_4 = E \left[ \left( \frac{X - \mu}{\sigma} \right)^4 \right] . \end{aligned}\]

正态分布峰度等于3。有些教材将峰度定义为\(\gamma_4-3\)，也称为超额峰度。

3.1.8 重尾分布

密度在\(\pm\infty\)处比期望和方差与其相等的正态密度高的分布称为重尾分布。

如t(\(n\))分布，密度为 \[\begin{aligned} f_t(x; n) = \frac{\Gamma(\frac{n+1}{2})} {\sqrt{n\pi} \Gamma(\frac{n}{2})} \left( 1 + \frac{x^2}{n} \right)^{-\frac{n+1}{2}}, \ t \in (-\infty, \infty) . \end{aligned}\] 尾部渐近阶为\(O(|x|^{-(n+1)})\)。 \(\mu=0\)(当\(n>1\)), \(\sigma=\frac{n}{n-2}\)(当\(n>2\)), 偏度0(当\(n>3\))，峰度\(3 + \frac{t}{n-4}\)(当\(n>4\))。

如Laplace分布 \[\begin{aligned} f_{\text{Laplace}}(x; \mu, \theta) = \frac{1}{2\theta} e^{-\frac{|x-\mu|}{\theta}}, \ x \in (-\infty, \infty) \end{aligned}\] \(EX=\mu\), \(\text{Var}(X)=2\theta^2\), 偏度0，峰度6。

如柯西(Cauchy)分布 \[\begin{aligned} f_{\text{Cauchy}}(x; m, s) = \frac{1}{\pi s} \frac{1}{1 + \left(\frac{x-m}{s} \right)^2}, \ x \in (-\infty, \infty) . \end{aligned}\] 没有一阶矩。

3.1.9 混合模型分布

设\(p_k, k=1,2,\dots,K\)是\(K\)个密度函数， \(w_k \in [0, 1]\), \(\sum_{i=1}^K w_k=1\), 则 \[\begin{aligned} f(x) = \sum_{k=1}^K w_k p_k(x) \end{aligned}\] 是一个密度，称为混合模型分布密度。

设\(p_k\)的期望为\(\mu_k\), 方差为\(\sigma_k^2\)，则 \[\begin{aligned} \mu =& \sum_{k=1}^K w_k \mu_k, \\ \sigma^2 =& \sum_{k=1}^K w_k \left[ \sigma_k^2 + (\mu_k - \mu)^2 \right] . \end{aligned}\] 峰度和偏度也可以类似计算。

期望都为零的\(K\)个正态分布的混合密度为

\[\begin{aligned} f(x) = \sum_{k=1}^K \frac{w_k}{\sqrt{2\pi} \sigma_k} e^{-\frac{x^2}{2\sigma_k^2}}, \ x \in (-\infty, \infty) . \end{aligned}\]

期望为零，偏度为零， \[\begin{aligned} \sigma^2 =& \sum_{k=1}^K w_k \sigma_k^2, \\ \text{峰度} =& 3 \sum_{k=1}^K w_k (\sigma_k / \sigma)^4 . \end{aligned}\]

3.1.10 单样本t检验

一元正态总体的均值比较用单样本t检验。

例如，检验零假设：糖尿病人甘油平均值是否1.70?

x <- glycemia[["甘油"]]
t.test(x, mu=1.70)

## 
##  One Sample t-test
## 
## data:  x
## t = 2.3021, df = 26, p-value = 0.02959
## alternative hypothesis: true mean is not equal to 1.7
## 95 percent confidence interval:
##  1.822198 3.859284
## sample estimates:
## mean of x 
##  2.840741

结果在0.05水平下显著，应拒绝零假设，结论是在0.05水平下糖尿病人的甘油值与1.70有显著差异。

注意，如果分布非正态，当样本量较大时也可以用t检验法。

3.1.11 两样本t检验

为比较独立的两个总体的均值，用两样本t检验。

例如，对高管年薪数据，比较有无MBA的两组的销售额增量。

ceoSalary <- read_csv(
  "data/高管年薪.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
sample1 <- ceoSalary |>
  dplyr::filter(MBA == 1) |>
  select(`销售涨幅`) |>
  pull()
sample2 <- ceoSalary |>
  dplyr::filter(MBA == 0) |>
  select(`销售涨幅`) |>
  pull()
t.test(sample1, sample2)

## 
##  Welch Two Sample t-test
## 
## data:  sample1 and sample2
## t = 0.31924, df = 38.038, p-value = 0.7513
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -22.74446  31.26139
## sample estimates:
## mean of x mean of y 
##  15.78788  11.52941

结果p值在0.05水平下不显著，结论是有无MBA的高管的销售涨幅没有显著差异。

又例如，对汽车与收入数据，比较有无汽车的两组家庭年收入：

carIncome <- read_csv(
  "data/汽车与收入.csv",
  locale=locale(encoding = "GB18030"),
  show_col_types = FALSE)
sample1 <- carIncome |>
  dplyr::filter(`拥有汽车` == 1) |>
  select(`家庭年收入`) |>
  pull()
sample2 <- carIncome |>
  dplyr::filter(`拥有汽车` == 0) |>
  select(`家庭年收入`) |>
  pull()
t.test(sample1, sample2)

## 
##  Welch Two Sample t-test
## 
## data:  sample1 and sample2
## t = 9.4061, df = 28.255, p-value = 3.345e-10
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##   9.395514 14.624249
## sample estimates:
## mean of x mean of y 
## 20.782609  8.772727

结果表明是否拥有汽车的两种家庭的年收入有显著差异。

3.1.12 均值的置信区间

R的t.test()函数可以给出置信区间。用法如

t.test(x, conf.level=0.95)

下面模拟生成50组来自\(\text{N}(2, 5^2)\) 的样本量\(n=25\)的样本，分别计算95%置信区间，作图演示：

## Zelterman(2015)中置信区间的模拟演示画图程序
demo.ci <- function(){
    opar <- par(mfrow=c(1,2)); on.exit(par(opar))

    n <- 25       # 样本量
    reps <- 50    # 模拟重复次数
    sim.mean <- 2 # 真实期望值
    sigma <- 5    # 真实标准差，已知
    
    ints <- matrix(0, nrow=reps, ncol=2)
    for(i in seq(reps)){
        x <- rnorm(n, mean=sim.mean, sd=sigma)
        ints[i,] <- t.test(x)$conf.int[1:2]
    }
    cover <- mean(ints[,1] <= sim.mean & ints[,2] >= sim.mean)
    cat('模拟', reps, '次的覆盖率为', cover, '\n')

    ## 作各次重复模拟得到的置信区间的图形
    ## 下面type='n'仅生成空坐标系
    plot(sim.mean, 0,
         xlim = c(min(ints[,1])-0.5, max(ints[,2])+0.5),
         ylim=c(0, reps),
         type='n',
         xlab='Confidence intervals',
         ylab='Simulation number')
    for(i in seq(reps)){
        lines(ints[i,], c(i,i), col=rainbow(6)[4], lwd=3.5)
        points(ints[i,], c(i,i),
               col='red', pch=16, cex=0.5)
    }
    lines(rep(sim.mean,2), c(-5, reps+5), lty=3, col='blue')

    ## 各次模拟置信区间长度
    diam <- ints[,2] - ints[,1]
    hist(diam, xlab='置信区间长度',
         main='', breaks=10, col=rainbow(7)[5])

    invisible()
}
demo.ci()

## 模拟 50 次的覆盖率为 0.96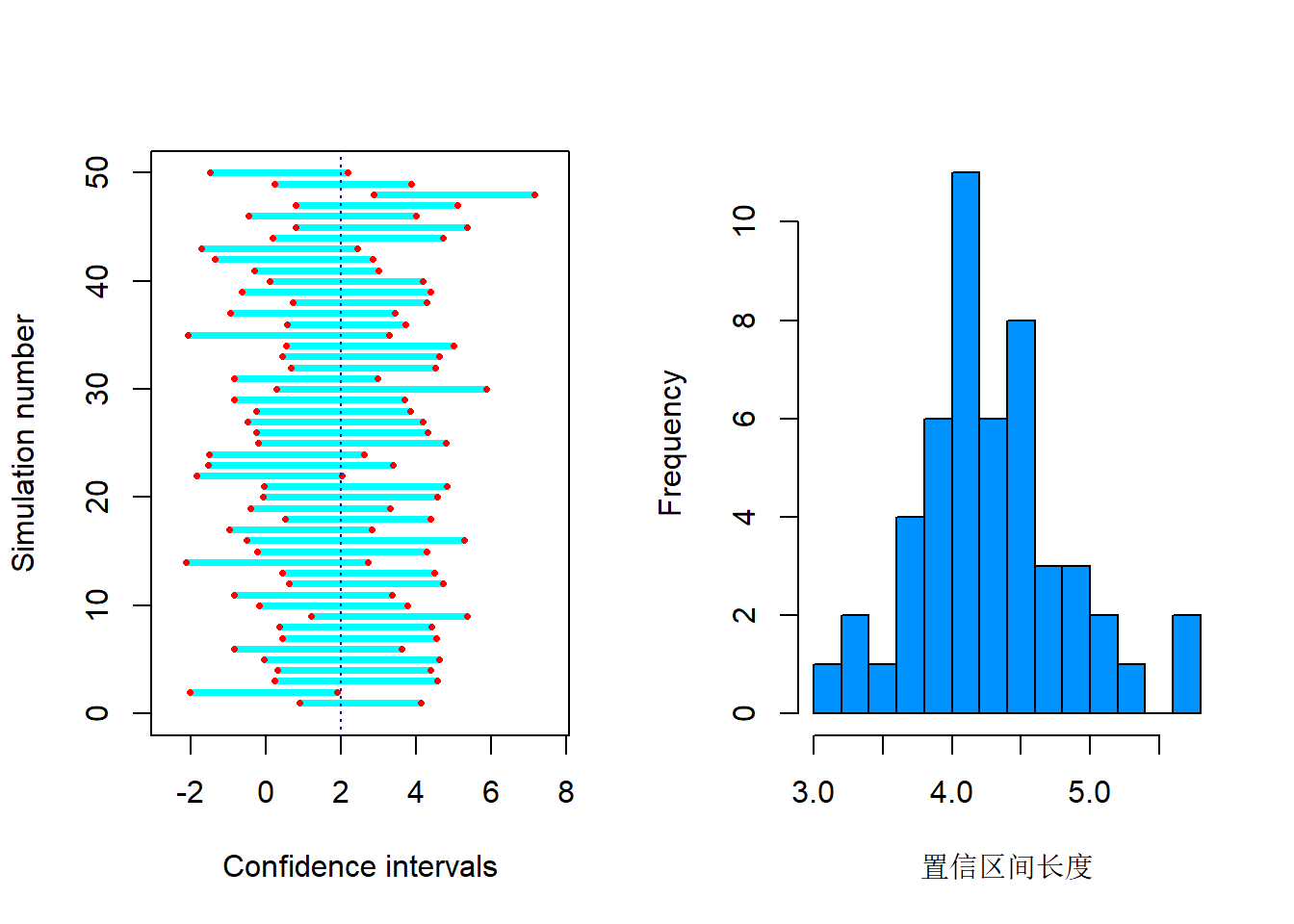

图3.15: 均值的置信区间演示

其实，这个模拟可以直接生成nreps个mean和sd，然后算出区间端点。

3.1.13 最大似然估计

一元正态分布的最大似然估计可以解出表达式， \(\mu\)的MLE即样本均值， \(\sigma^2\)的MLE为 \[ \hat\sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar x)^2 . \]

对于一般的分布，最大似然估计可能需要数值求解。下面对模拟样本作正态分布对数似然函数曲面图:

norm1d.loglike <- function(){
    set.seed(1)
    z <- rnorm(100, mean=5, sd=10)
    logL <- function(parm) {
        sum( dnorm(z, mean=parm[1],
                   sd=parm[2], log=TRUE) )
    }

    ## 作曲面图
    mus <- seq(0, 10, length=25)
    sigs <- seq(6, 14, length=25)
    zvals <- matrix(0, nrow=length(mus),
                    ncol=length(sigs))
    for(i in seq(along=mus))
        for(j in seq(along=sigs))
            zvals[i,j] <- logL(c(mus[i], sigs[j]))
    
    persp(mus, sigs, zvals,
          cex.lab=1.2,
          zlim=c(min(zvals), max(zvals)+0.5),
          xlab='mean', ylab='std dev',
          zlab='logL',
          col=rainbow(6)[3],
          axes=TRUE, box=TRUE,
          theta=-30, shade=0.3)

    invisible()
}
norm1d.loglike()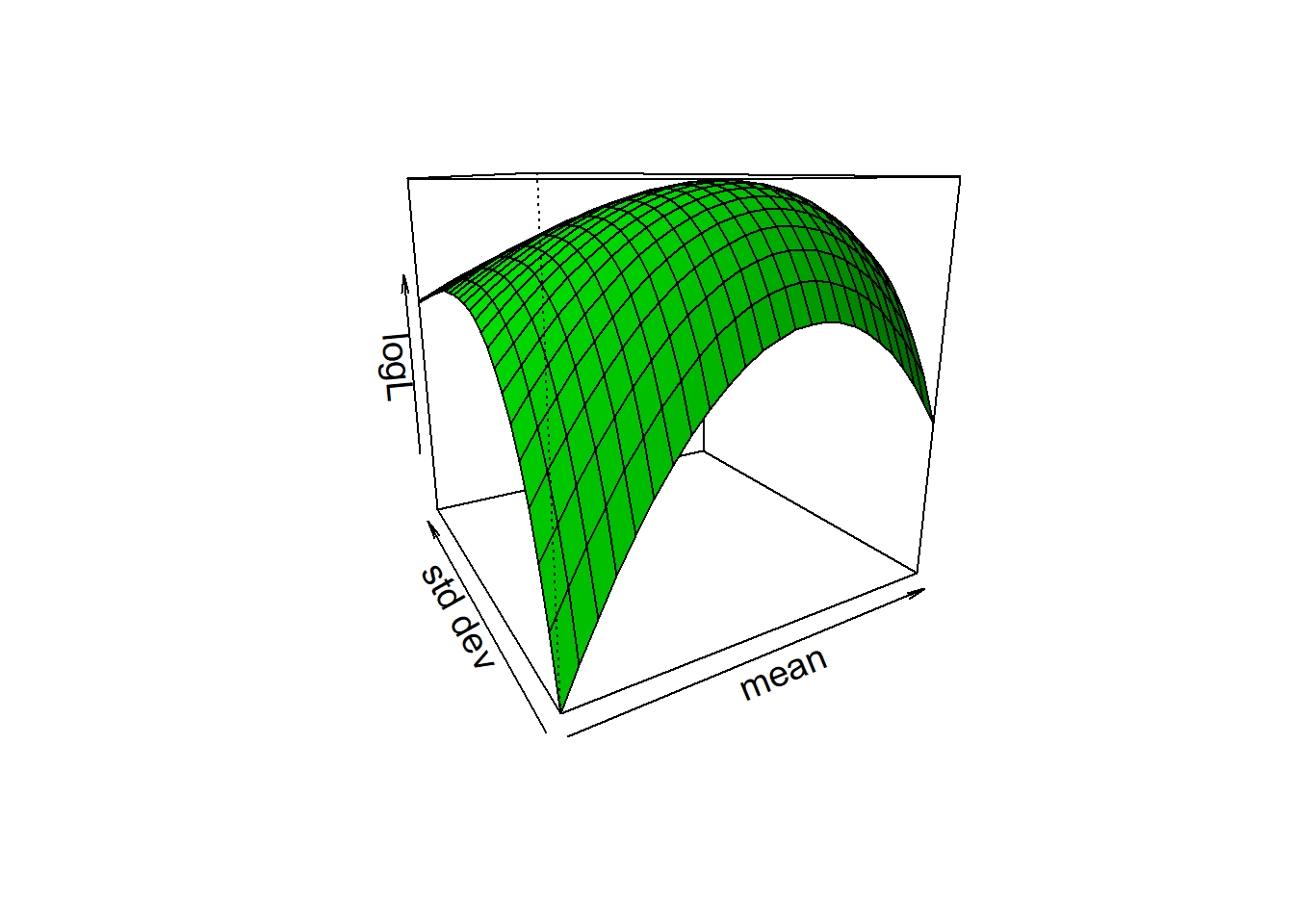

图3.16: 正态分布对数似然函数曲面图

R函数nlm()可以用来求对数似然函数的最大值点。例如，对模拟的正态样本用nlm()函数求最大似然估计，并与理论公式结果比较：

norm1d.mledemo2 <- function(){
    set.seed(1)
    n <- 20
    mu <- 5
    sig <- 10
    z <- rnorm(n, mean=mu, sd=sig)
    neglogL <- function(parm) {
        -sum( dnorm(z, mean=parm[1],
                    sd=parm[2], log=TRUE) )
    }

    res <- nlm(neglogL, c(10, 10))
    print(res)
    cat('真实mu=', mu, ' 公式估计mu=', mean(z), 
        ' 数值优化估计mu=', res$estimate[1], '\n')
    cat('真实sigma=', sig, 
        '公式估计sigma=', sqrt(var(z)*(n-1)/n), 
        ' 数值优化估计sigma=', res$estimate[2], '\n')
    invisible()
}
norm1d.mledemo2()

## $minimum
## [1] 72.10271
## 
## $estimate
## [1] 6.905234 8.901292
## 
## $gradient
## [1] -2.819437e-07 -7.822818e-08
## 
## $code
## [1] 1
## 
## $iterations
## [1] 7
## 
## 真实mu= 5  公式估计mu= 6.905239  数值优化估计mu= 6.905234 
## 真实sigma= 10 公式估计sigma= 8.901296  数值优化估计sigma= 8.901292

以上程序没有加sigma>0的限制，有可能搜索到运行参数空间之外。取log(sigma)=lsig。

norm1d.mledemo2b <- function(){
    set.seed(1)
    n <- 20
    mu <- 5
    sig <- 10
    z <- rnorm(n, mean=mu, sd=sig)
    neglogL <- function(parm) {
        -sum( dnorm(z, mean=parm[1],
                    sd=exp(parm[2]), log=TRUE) )
    }

    res <- nlm(neglogL, c(10, log(10)))
    print(res)
    sig2 <- exp(res$estimate[2])
    cat('真实mu=', mu, ' 公式估计mu=', mean(z), 
        ' 数值优化估计mu=', res$estimate[1], '\n')
    cat('真实sigma=', sig, 
        '公式估计sigma=', sqrt(var(z)*(n-1)/n), 
        ' 数值优化估计sigma=', sig2, '\n')
    invisible()
}
norm1d.mledemo2b()

## $minimum
## [1] 72.10271
## 
## $estimate
## [1] 6.905247 2.186195
## 
## $gradient
## [1]  3.006708e-06 -2.761964e-05
## 
## $code
## [1] 1
## 
## $iterations
## [1] 11
## 
## 真实mu= 5  公式估计mu= 6.905239  数值优化估计mu= 6.905247 
## 真实sigma= 10 公式估计sigma= 8.901296  数值优化估计sigma= 8.90128

下面的例子中假定\(\mu>0\)，对一元正态分布样本，估计\(\mu\)和\(\alpha=\sigma/\mu\)。当然，先求得最大似然估计再变换也是最大似然估计。

norm1d.mledemo3 <- function(){
    set.seed(1)
    n <- 20
    z <- rnorm(n, mean=5, sd=10)
    set.seed(1)
    n <- 20
    z <- rnorm(n, mean=5, sd=10)
    
    ## parm[1]: log(mu)
    ## parm[2]: log(sigma/mu)
    ## mu = exp(par[1])
    ## sigma = exp(par[1]+par[2])
    neglogL <- function(parm) {
        -sum( dnorm(z, mean=exp(parm[1]),
                    sd=exp(parm[1] + parm[2]), log=TRUE) )
    }

    res <- nlm(neglogL, c(log(10), log(10)))
    print(res)
    print(exp(res$estimate))

    ## 直接从参数MLE变换计算:
    hat.mu <- mean(z)
    hat.sigma <- sqrt((n-1)/n)*sd(z)
    hat.alpha <- hat.sigma/hat.mu
    cat('直接从MLE变换得到mu=', hat.mu,
        ' alpha=', hat.alpha, '\n')
    invisible()
}
norm1d.mledemo3()

## $minimum
## [1] 72.10271
## 
## $estimate
## [1] 1.9322804 0.2539165
## 
## $gradient
## [1] 2.423290e-07 3.407763e-07
## 
## $code
## [1] 1
## 
## $iterations
## [1] 11
## 
## [1] 6.905239 1.289064
## 直接从MLE变换得到mu= 6.905239  alpha= 1.289064

3.2 二元正态分布及其统计推断

3.2.1 二元正态分布概念

二元随机变量:

\((X, Y)\)的值是直角坐标平面上的点。
协方差\(\text{Cov}(X, Y) = E[(X - EX)(Y - EY)]\)。
相关系数

\[\begin{aligned} \rho(X, Y) = \frac{\text{Cov}(X, Y)}{ \sqrt{\text{Var}(X) \text{Var}(Y)}} . \end{aligned}\]
相关系数等于零称为不相关，独立一定是不相关的。
相关系数度量的是线性的相关程度。

二元正态分布 N(\(\mu_X, \mu_Y, \sigma_X^2, \sigma_Y^2, \rho\)):

\[\begin{aligned} & \phi(x, y | \mu_X, \mu_Y, \sigma_X^2, \sigma_Y^2, \rho) \\ =& \frac{1}{2\pi \sigma_X \sigma_Y \sqrt{1 - \rho^2}} \\ & \exp\left\{ -\frac12 \frac{1}{1-\rho^2} \right. \\ & \left. \left[ \left( \frac{x - \mu_X}{\sigma_X} \right)^2 + \left( \frac{y - \mu_Y}{\sigma_Y} \right)^2 - 2 \rho \frac{x - \mu_X}{\sigma_X} \frac{y - \mu_Y}{\sigma_Y} \right] \right\} . \end{aligned}\]

令 \[\begin{aligned} \boldsymbol\mu =\left(\begin{array}{c} \mu_X \\ \mu_Y \end{array}\right), \quad \Sigma = \left(\begin{array}{cc} \sigma_X^2 & \rho\sigma_X\sigma_Y \\ \rho\sigma_X\sigma_Y & \sigma_Y^2 \end{array}\right), \end{aligned}\] 则 \[\begin{aligned} \phi(\boldsymbol x | \boldsymbol\mu, \Sigma) = (2\pi)^{-1} \text{det}(\Sigma)^{-1/2} \exp \left( -\frac12 (\boldsymbol x - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol\mu) \right), \end{aligned}\] 其中\(\boldsymbol x = (x, y)^T\)。

二元正态分布性质：

边缘分布正态。
条件分布也正态：\(Y \,|\, X=x\)服从

\[\begin{aligned} \text{N}\left(\mu_Y + \rho \frac{\sigma_Y}{\sigma_X} (x - \mu_X), \; (1-\rho^2)\sigma_Y^2 \right) . \end{aligned}\]
线性组合正态。
二元正态标准化: 存在矩阵\(A\)使得\(A A^T = \Sigma\), \(\boldsymbol Z = A^{-1} (\boldsymbol X - \boldsymbol\mu)\)服从标准二元正态分布 (\(Z_1, Z_2\)独立同标准正态分布)。

3.2.2 参数估计

均值（R: colMeans(x), x是两列的矩阵）；
协方差阵(R: var(x))；
相关系数阵(R: cor(x), 相关系数矩阵)。

3.2.3 相关性假设检验

相关系数检验: 在R中使用cor.test(x, y)。

当总体为二元正态分布且两个分量相互独立时，统计量 \[\begin{aligned} t = \hat\rho \sqrt{\frac{n-2}{1 - \hat\rho^2}} \end{aligned}\] 服从t(\(n-2\))分布。 R中用cor.test()进行相关系数检验并用如下Fisher Z变换计算近似置信区间。

如果不假定总体为二元正态分布，为了检验相关系数是否等于零，在大样本情况下可以使用Fisher的Z变换： \[ W = \frac{1}{2} \log \left( \frac{1 + \hat\rho}{1 - \hat\rho} \right), \] 当相关系数等于0时\(W\)渐近分布为\(\text{N}(0, \frac{1}{n-3})\)。

当\(n\)较小时(\(n \leq 25\))，可以用Hotelling的变换： \[ W^* = W - \frac{3 W - \tanh(W)}{4(n-1)}, \] 近似分布为\(\text{N}(0, \frac{1}{n-1})\)。

3.2.4 均值的联立置信区间

设二元正态分布样本均值为 \(\bar{\boldsymbol x}\), 样本协方差阵为\(\hat\Sigma\), 理论期望值为\(\boldsymbol\mu\), 则置信度为\(1-\alpha\)的联合置信区间的边界为 \[\begin{aligned} (\bar{\boldsymbol x} - \boldsymbol\mu)^T \hat\Sigma^{-1} (\bar{\boldsymbol x} - \boldsymbol\mu) = \frac{1}{n}\chi^2_{1-\alpha}(2), \end{aligned}\] 其中\(\chi^2_{1-\alpha}(2)\)是\(\chi^2(2)\)的\(1-\alpha\)分位数。

3.2.5 程序例子

3.2.5.1 瑞士各省农业人口比例与考试高分比例

用图形方法研究1888年瑞士的47个法语省份的各省考试高分比例与农业人口比例的关系。 datasets::swiss数据框包含1888年瑞士的47个法语省份的人口学数据。

用str()获得数据的基本情况。

str(swiss)

## 'data.frame':    47 obs. of  6 variables:
##  $ Fertility       : num  80.2 83.1 92.5 85.8 76.9 76.1 83.8 92.4 82.4 82.9 ...
##  $ Agriculture     : num  17 45.1 39.7 36.5 43.5 35.3 70.2 67.8 53.3 45.2 ...
##  $ Examination     : int  15 6 5 12 17 9 16 14 12 16 ...
##  $ Education       : int  12 9 5 7 15 7 7 8 7 13 ...
##  $ Catholic        : num  9.96 84.84 93.4 33.77 5.16 ...
##  $ Infant.Mortality: num  22.2 22.2 20.2 20.3 20.6 26.6 23.6 24.9 21 24.4 ...

用summary()对各列作概括统计。

summary(swiss)

##    Fertility      Agriculture     Examination      Education    
##  Min.   :35.00   Min.   : 1.20   Min.   : 3.00   Min.   : 1.00  
##  1st Qu.:64.70   1st Qu.:35.90   1st Qu.:12.00   1st Qu.: 6.00  
##  Median :70.40   Median :54.10   Median :16.00   Median : 8.00  
##  Mean   :70.14   Mean   :50.66   Mean   :16.49   Mean   :10.98  
##  3rd Qu.:78.45   3rd Qu.:67.65   3rd Qu.:22.00   3rd Qu.:12.00  
##  Max.   :92.50   Max.   :89.70   Max.   :37.00   Max.   :53.00  
##     Catholic       Infant.Mortality
##  Min.   :  2.150   Min.   :10.80   
##  1st Qu.:  5.195   1st Qu.:18.15   
##  Median : 15.140   Median :20.00   
##  Mean   : 41.144   Mean   :19.94   
##  3rd Qu.: 93.125   3rd Qu.:21.70   
##  Max.   :100.000   Max.   :26.60

各省考试高分比例对农业人口比例的散点图：

with(swiss,
  plot(Agriculture, Examination,
    pch=16, col='blue',
    xlab='%algriculture',
    ylab='%with high exam'))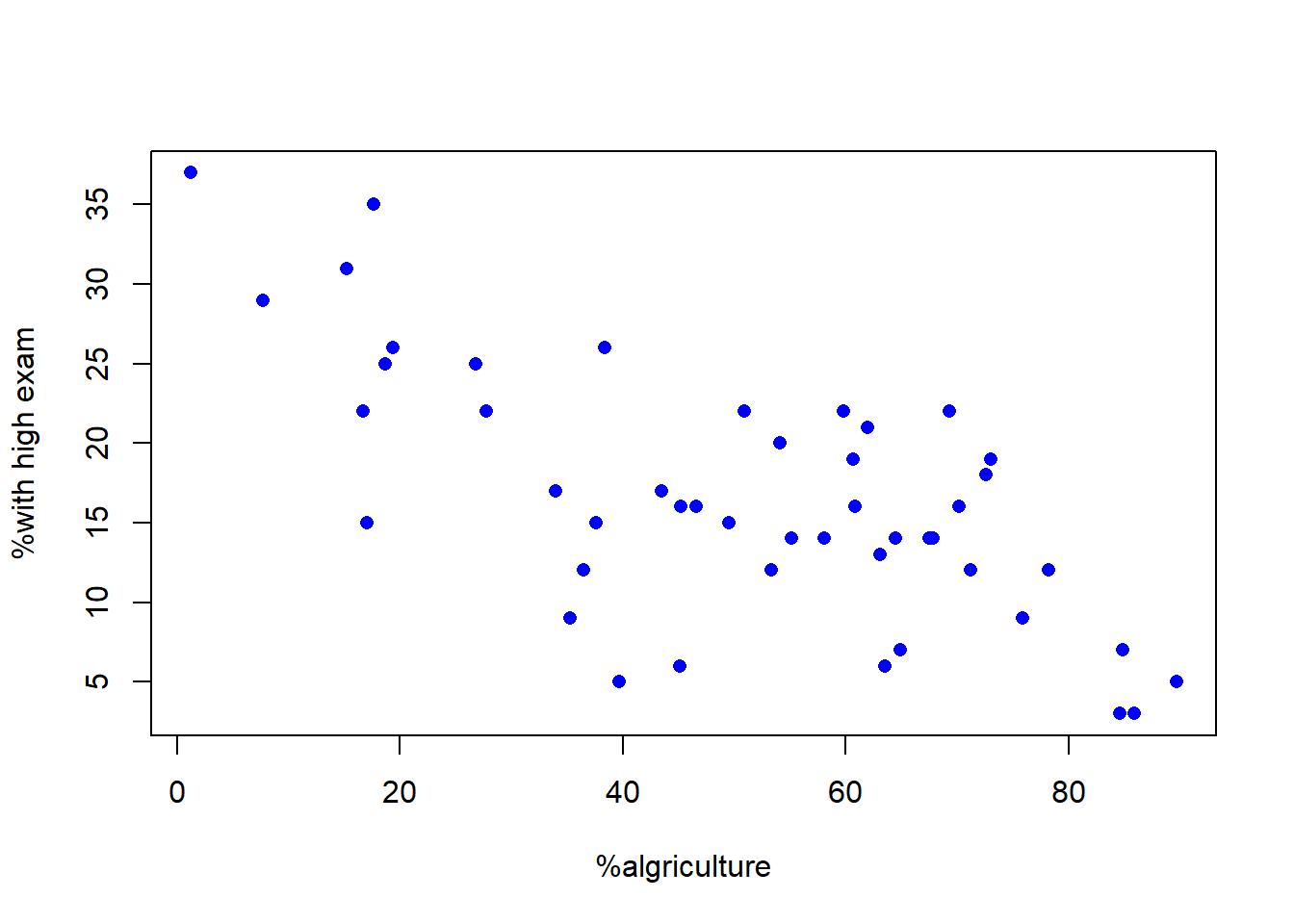

图3.17: 各省考试高分比例对农业人口比例

农业人口比例与各省考试高分比例的二维盒形图：

MVA::bvbox(
  swiss[,c('Agriculture', 'Examination')],
  pch=16, col='blue',
  xlab='%algriculture',
  ylab='%with high exam')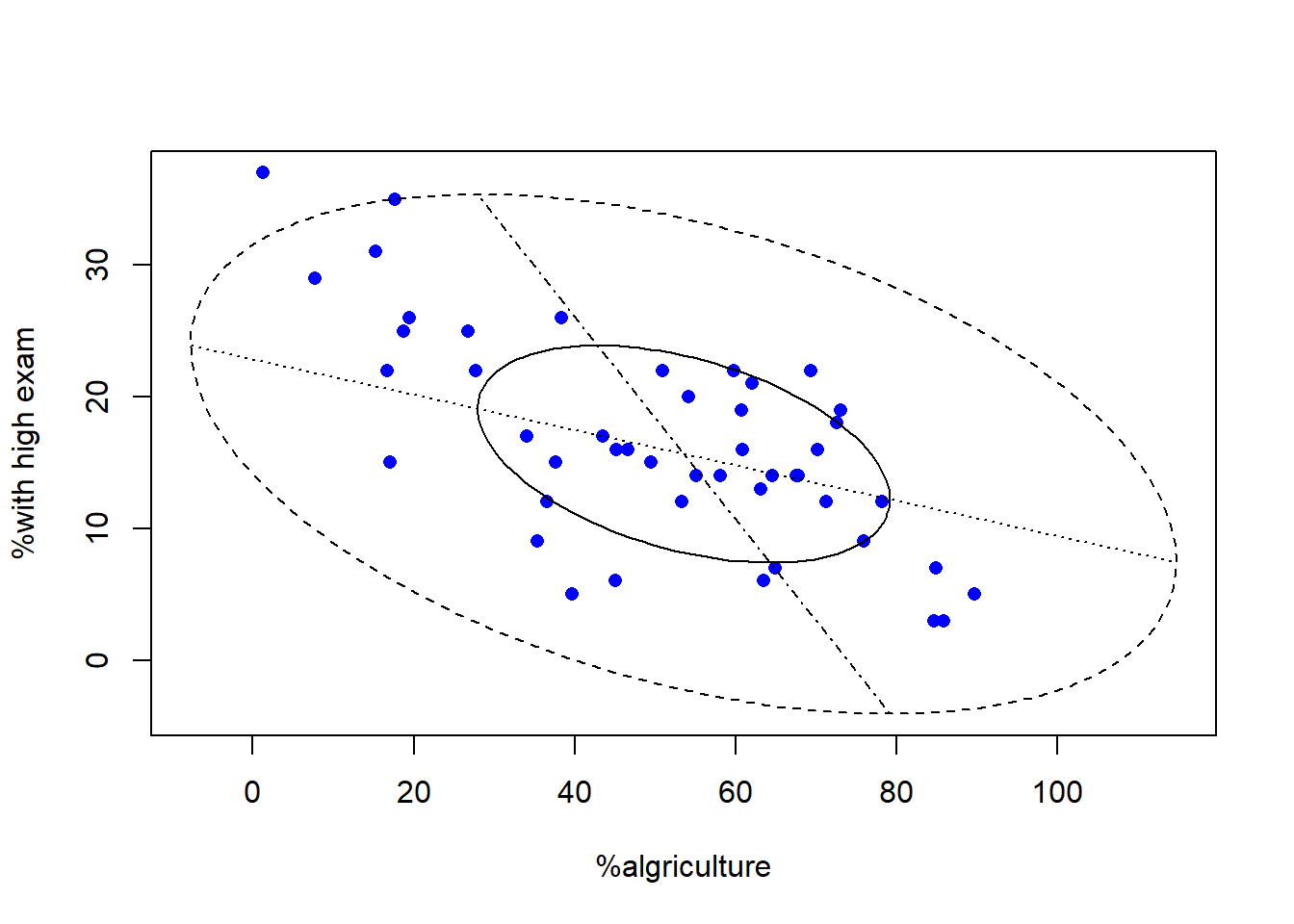

图3.18: 农业人口比例与各省考试高分比例的二维盒形图

nlev <- 5
cols <- heat.colors(9)[3:(nlev+2)]
aplpack::plothulls(
  swiss[,c('Agriculture', 'Examination')],
  n.hull=nlev,
  col.hull=cols,
  xlab='%algriculture', ylab='%with high exam',
  density=NA, col=0, main='')

## [[1]]
##       x.hull y.hull
##  [1,]   89.7      5
##  [2,]   85.9      3
##  [3,]   84.6      3
##  [4,]   39.7      5
##  [5,]   17.0     15
##  [6,]    1.2     37
##  [7,]   17.6     35
##  [8,]   69.3     22
##  [9,]   73.0     19
## 
## [[2]]
##       x.hull y.hull
##  [1,]   84.9      7
##  [2,]   63.5      6
##  [3,]   45.1      6
##  [4,]   35.3      9
##  [5,]   16.7     22
##  [6,]    7.7     29
##  [7,]   15.2     31
##  [8,]   59.8     22
##  [9,]   72.6     18
## 
## [[3]]
##      x.hull y.hull
## [1,]   78.2     12
## [2,]   75.9      9
## [3,]   64.9      7
## [4,]   36.5     12
## [5,]   18.7     25
## [6,]   19.4     26
## [7,]   38.4     26
## [8,]   62.0     21
## 
## [[4]]
##       x.hull y.hull
##  [1,]   70.2     16
##  [2,]   71.2     12
##  [3,]   53.3     12
##  [4,]   37.6     15
##  [5,]   34.0     17
##  [6,]   27.7     22
##  [7,]   26.8     25
##  [8,]   50.9     22
##  [9,]   60.7     19
## 
## [[5]]
##      x.hull y.hull
## [1,]   67.8     14
## [2,]   63.1     13
## [3,]   55.1     14
## [4,]   49.5     15
## [5,]   45.2     16
## [6,]   43.5     17
## [7,]   54.1     20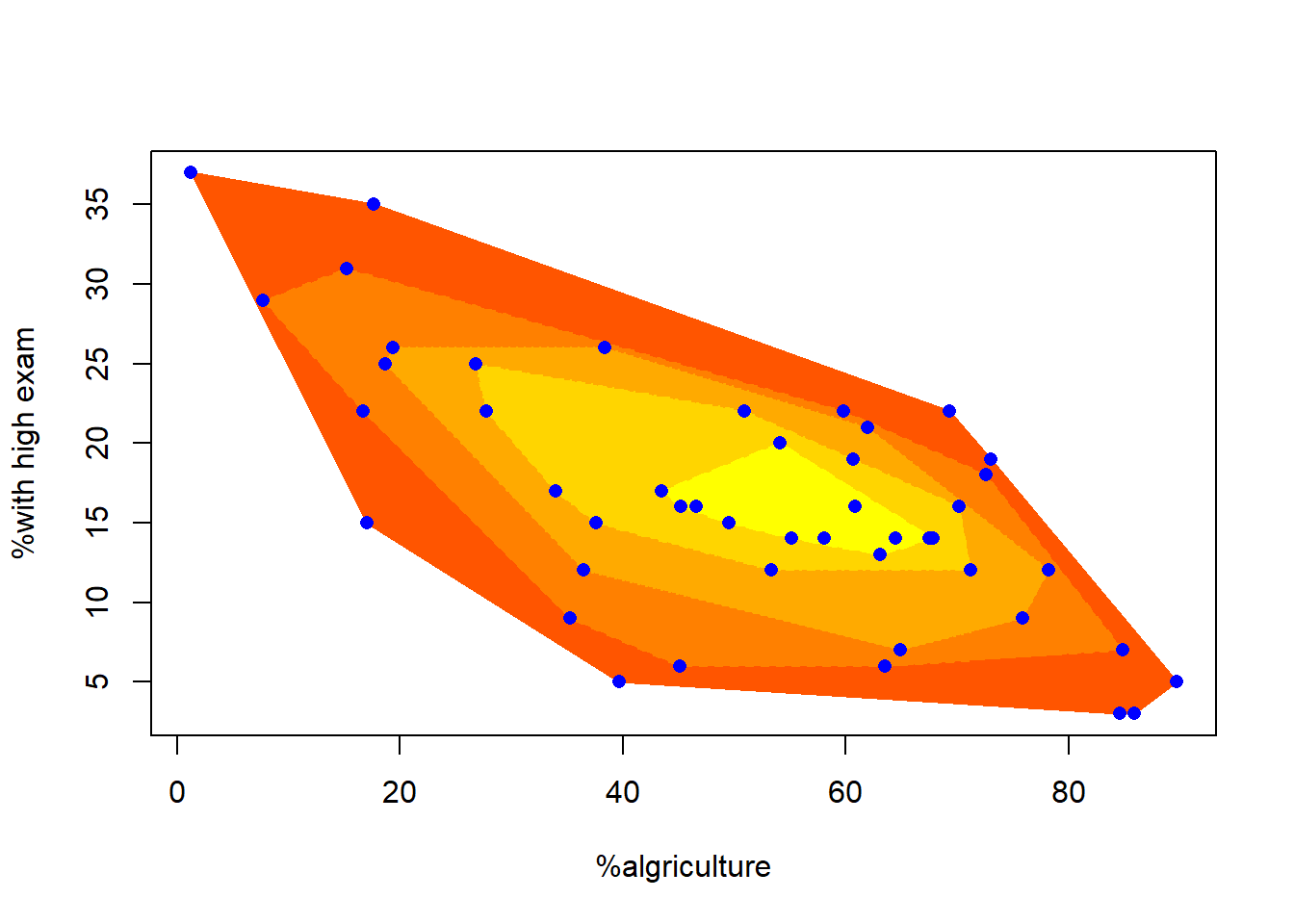

with(swiss,
     points(Agriculture, Examination,
            pch=16, col='blue'))

图3.19: 农业人口比例与各省考试高分比例的洋葱图

3.2.5.2 二元正态密度函数作图

下面的R程序作二元正态密度的等高线图、密度图、颜色图。

demo.2dnorm.den <- function(){

  rho <- 0.8
  Sig <- rbind(c(1, rho), c(rho, 1))
  ng <- 25
  x <- seq(-2, 2, length=ng)
  y <- x
  z <- cbind(rep(x, each=ng),
             rep(y, ng))
  dens <- matrix(mvtnorm::dmvnorm(z, sigma=Sig),
                 ng, ng)
  nlev <- 6
  contour(x, y, dens,
          nlevels=nlev,
          drawlabels=FALSE, 
          col=rainbow(nlev)
  )

  image(x, y, dens)
  
  persp(x, y, dens)
}
demo.2dnorm.den()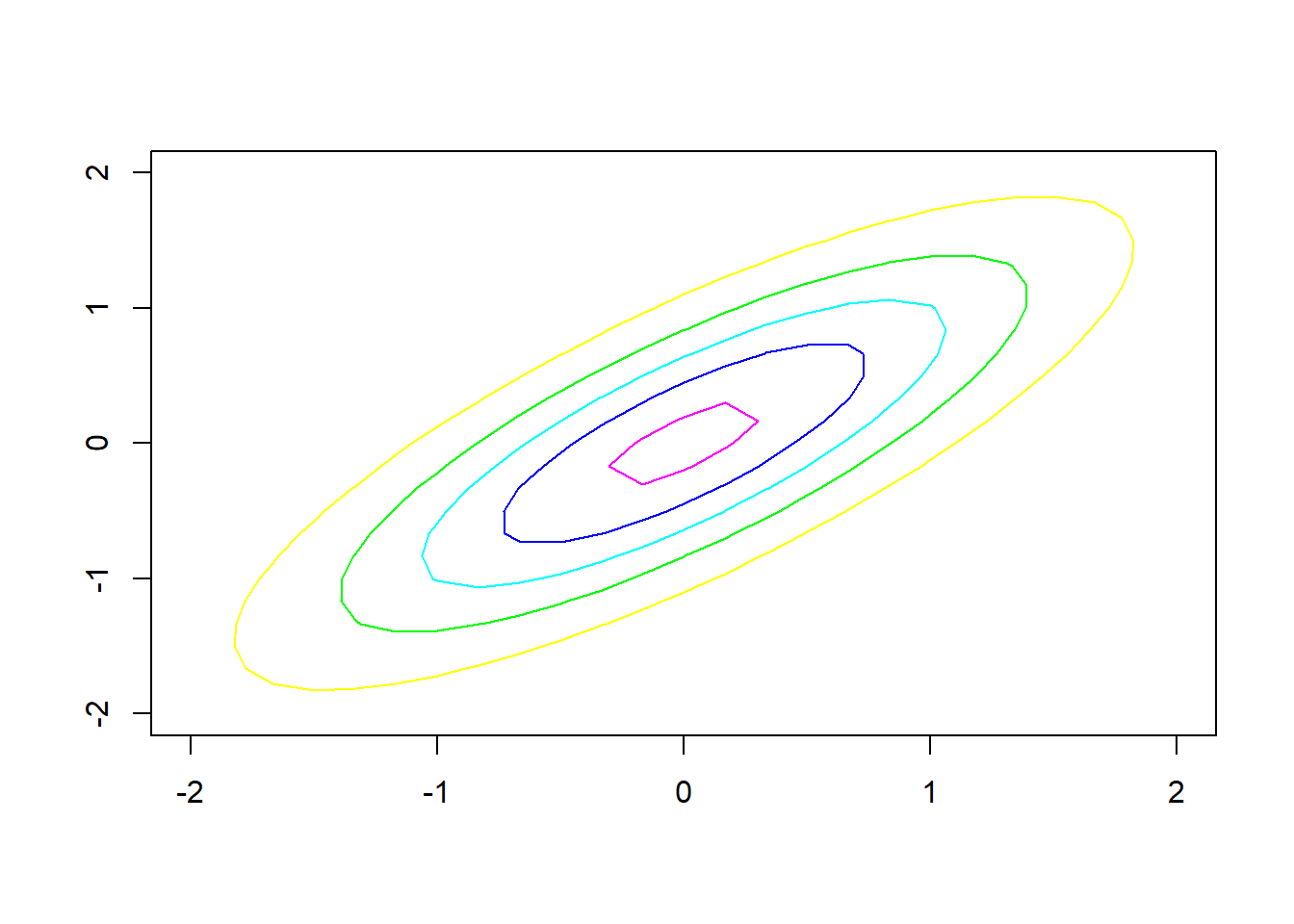

图3.20: 二元正态分布密度函数

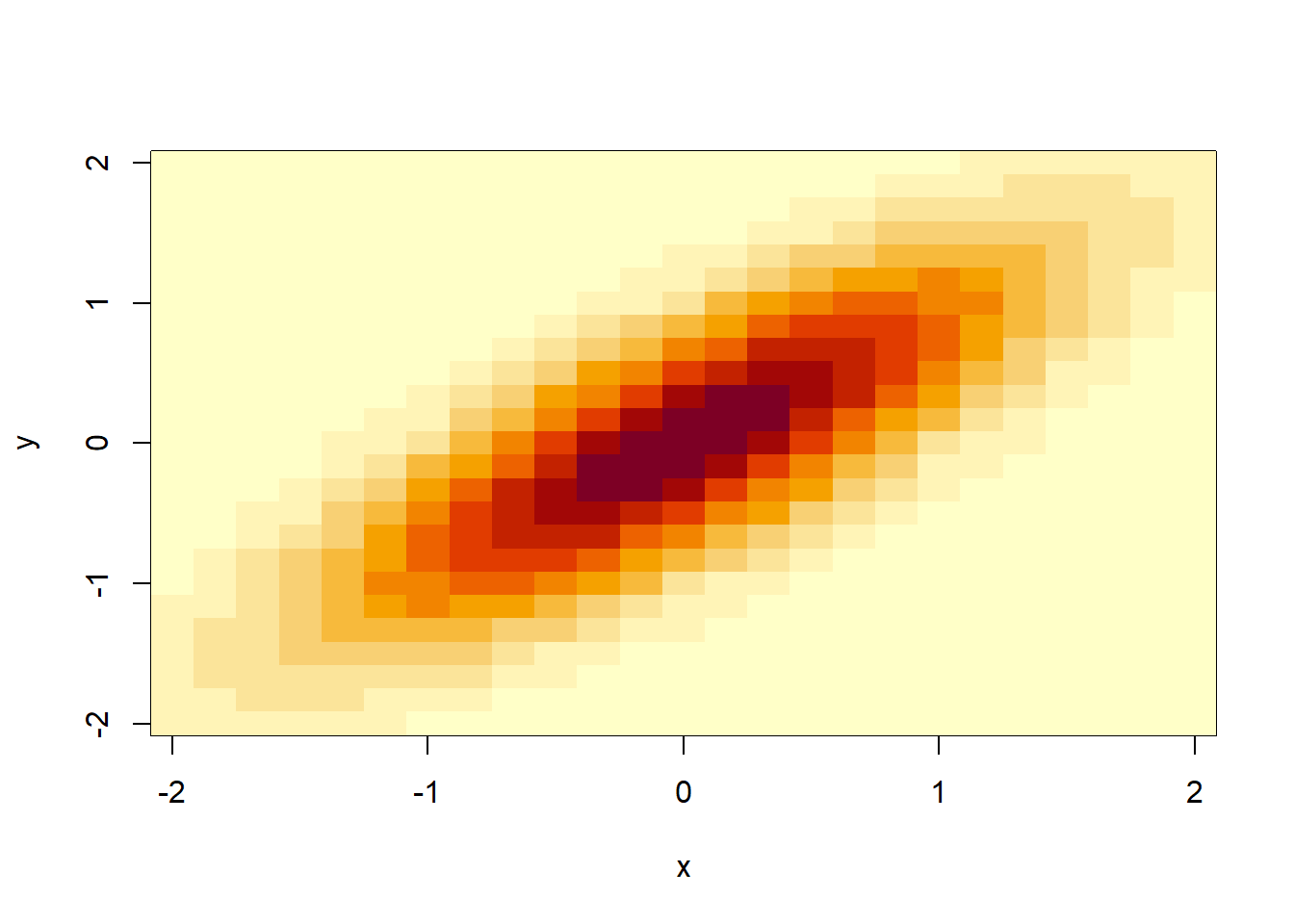
图3.21: 二元正态分布密度函数

图3.22: 二元正态分布密度函数

3.2.5.3 相关系数检验

对城镇居民收入和消费数据，进行相关系数检验。用cor.test()函数。

x <- cityIncomeConsume[["可支配收入"]]
y <- cityIncomeConsume[["消费性支出"]]
cor.test(x, y)

## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = 24.148, df = 29, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.9503637 0.9884983
## sample estimates:
##       cor 
## 0.9760254

检验结果显著，说明相关系数与零有显著差异。

3.2.5.4 联立置信区间

估计swiss数据中各省农业人口比例和考试高分比例这两个变量的均值的联立置信区间并作图。

demo.ci2.swiss <- function(){
    ## 给定二元正态样本估计的样本量n，两个均值xbar,
    ## 协方差阵估计hatSigma, 置信度1-alpha,
    ## 返回m个均匀布点的联立置信区间的x,y 坐标点（两列矩阵）
    bivCI <- function(n, xbar, hatSigma, alpha, m=100){
        x <- sin(2*pi*(0:(m-1))/(m-1)) # 先在圆上布点
        y <- cos(2*pi*(0:(m-1))/(m-1)) # 先在圆上布点
        crit <- qchisq(1-alpha, 2) / n
        resm <- matrix(0, m, 2)
        for(i in seq(m)){
            pair <- c(x[i], y[i])
            ## 二次型的值
            q <- pair %*% solve(hatSigma, pair)
            x[i] <- x[i] * sqrt(crit/q) + xbar[1]
            y[i] <- y[i] * sqrt(crit/q) + xbar[2]
        } # for i

        cbind(x, y)
    }

    ## 数据
    biv <- as.matrix(swiss[,c('Agriculture', 'Examination')])
    ## 散点图
    plot(biv, col='red', pch=16, cex.lab=1.5)
    lines(bivCI(n=nrow(biv),
                xbar=colMeans(biv),
                hatSigma=var(biv),
                alpha=0.01),
          col='blue')
    lines(bivCI(n=nrow(biv),
                xbar=colMeans(biv),
                hatSigma=var(biv),
                alpha=0.05),
          col='green')
    points(rbind(colMeans(biv)),
           pch=3, cex=0.8)
}
demo.ci2.swiss()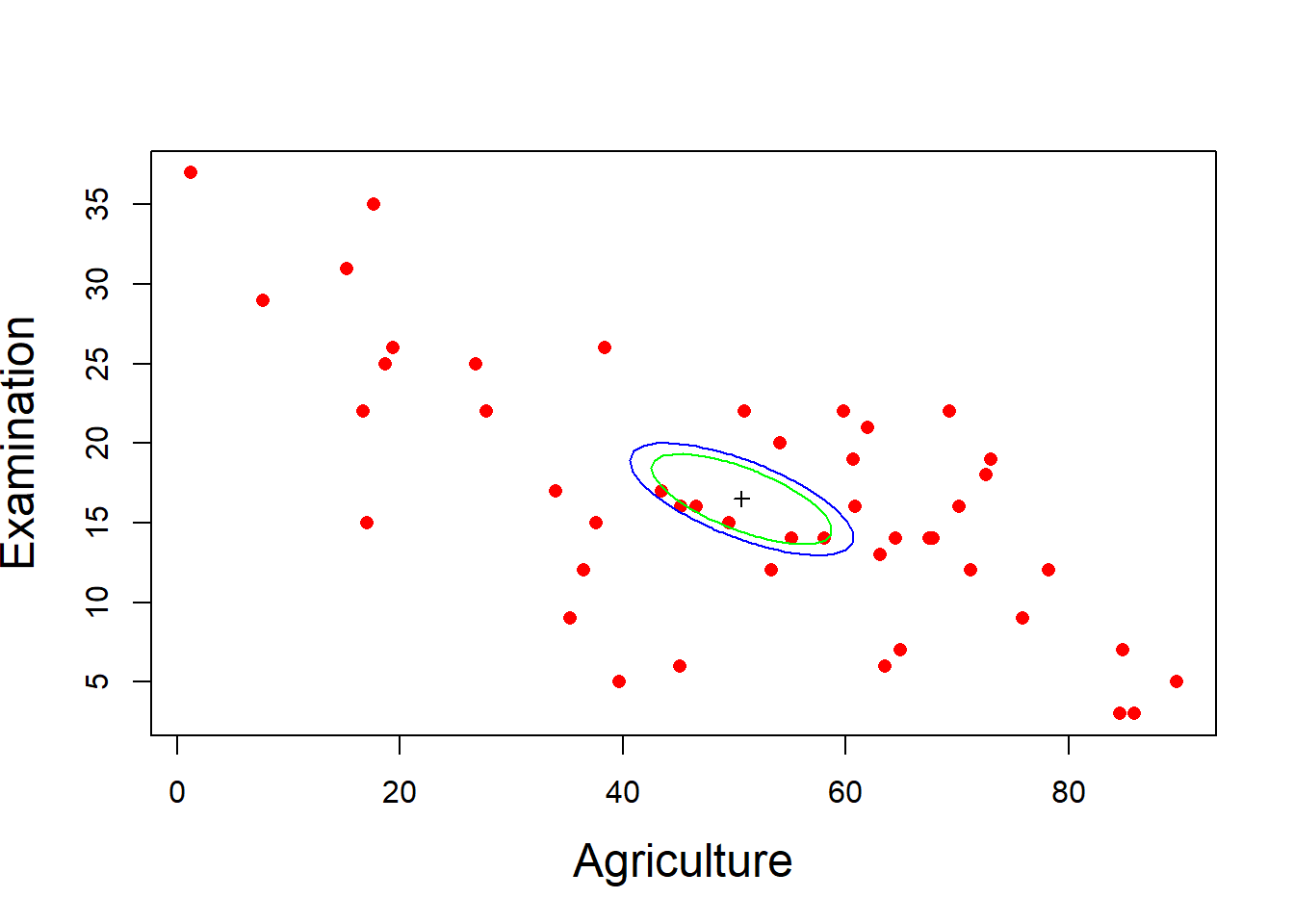

图3.23: 农业人口比例与各省考试高分比例的均值联立置信区间

3.2.5.5 二元正态分布参数最大似然估计的数值优化方法

二元正态分布参数的最大似然估计可以得到显示表达式。一般分布的最大似然估计可能需要用数值优化方法， R的nlm()函数可以执行最大似然估计。

下面对swiss数据框中各省农业人口比例与考试高分比例的数据估计其二元正态分布参数。用nlm()估计。

demo.mle2d.swiss <- function(){
  d <- as.matrix(swiss[,c('Agriculture', 'Examination')])
  n <- nrow(d)
  cat('公式得到的MLE为:\n')
  cat('mu1=', mean(d[,1]),
      ' mu2=', mean(d[,2]), '\n')
  cat('sigma1=', sqrt((n-1)/n)*sd(d[,1]),
      ' sigma2=', sqrt((n-1)/n)*sd(d[,2]), '\n')
  cat('rho=', cor(d)[1,2], '\n\n')
  
  ## 定义似然函数，参数包括mu1, mu2, log(sigma1), log(sigma2),
  ## 和rho=sin(parm[5])
  neglogL <- function(parm){
    u <- (d[,1] - parm[1])/exp(parm[3])
    v <- (d[,2] - parm[2])/exp(parm[4])
    -( -n*(parm[3] + parm[4] + log(abs(cos(parm[5]))))
       - 0.5 / cos(parm[5])^2 *
         sum( u^2 + v^2 - 2*sin(parm[5])*u*v ) )
  }
  ## 初值用矩估计和rho=0, 结果不收敛
  ##parm0 <- c(mean(d[,1]), mean(d[,2]), log(sd(d[,1])), log(sd(d[,2])), 0)
  ## 初值用矩估计和rho=-0.5
  parm0 <- c(mean(d[,1]), mean(d[,2]), log(sd(d[,1])), log(sd(d[,2])), -0.5)
  nlm.res <- nlm(neglogL, parm0, hessian=TRUE)
  print(nlm.res)
  pare <- nlm.res$estimate
  cat('估计mu1=', pare[1],
      ' mu2=', pare[2],
      'sigma1=', exp(pare[3]),
      'sigma2=', exp(pare[4]),
      'rho=', sin(pare[5]), '\n')
  ## 因为参数是变换过的，
  ## 负对数似然函数在极小值点处的海色阵逆矩阵不能直接得到参数的抽样协方差阵估计
  ## 可以用非参数bootstrap方法获得标准误差估计
}
demo.mle2d.swiss()

## 公式得到的MLE为:
## mu1= 50.65957  mu2= 16.48936 
## sigma1= 22.46831  sigma2= 7.892556 
## rho= -0.6865422 
## 
## $minimum
## [1] 275.3881
## 
## $estimate
## [1] 50.6595741 16.4893608  3.1121036  2.0659176 -0.7567212
## 
## $gradient
## [1]  4.103398e-06  1.041423e-05  6.599243e-05 -2.823024e-05  5.053380e-05
## 
## $hessian
##               [,1]         [,2]          [,3]          [,4]          [,5]
## [1,]  1.761090e-01  0.344192086 -8.914581e-04  3.258794e-07 -8.411012e-04
## [2,]  3.441921e-01  1.427207499  0.000000e+00 -2.350283e-03 -2.219013e-03
## [3,] -8.914581e-04  0.000000000  1.358068e+02 -4.189322e+01  4.433481e+01
## [4,]  3.258794e-07 -0.002350283 -4.189322e+01  1.358396e+02  4.434595e+01
## [5,] -8.411012e-04 -0.002219013  4.433481e+01  4.434595e+01  1.307285e+02
## 
## $code
## [1] 1
## 
## $iterations
## [1] 6
## 
## 估计mu1= 50.65957  mu2= 16.48936 sigma1= 22.46826 sigma2= 7.892537 rho= -0.6865411

3.3 多元随机变量

3.3.1 多元随机变量概念

\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)取值于\(\mathbb R^p\)中。

期望向量\(E\boldsymbol X = (E X_1, E X_2, \dots, E X_p)^T\)。协方差阵 \[\begin{aligned} \text{Var}(\boldsymbol X) = E[ (\boldsymbol X - E \boldsymbol X) (\boldsymbol X - E \boldsymbol X)^T ], \end{aligned}\] 是\(p \times p\)对称半正定矩阵，第\((i,i)\)元素等于\(\text{Var}(X_i)\)，第\((i,j)\)元素等于\(\text{Cov}(X_i, X_j)\)。

设\(\boldsymbol X\)为\(p\)维随机向量， \(\boldsymbol Y\)为\(q\)维随机向量，则 \[ \text{Cov}(\boldsymbol X, \boldsymbol Y) = E[ (\boldsymbol X - \boldsymbol\mu_X) (\boldsymbol Y - \boldsymbol\mu_Y)^T] = [ \text{Cov}(\boldsymbol Y, \boldsymbol X) ]^T . \]

估计：均值为各分量的样本矩阵（R: colMeans(x), x是\(p\)列的矩阵）；协方差阵(R: var(x))；相关系数阵(R: cor(x), 相关系数矩阵)。

3.3.2 多元期望和方差阵的性质

设\(A, B, C\)为矩阵，\(\boldsymbol M\)为随机矩阵，有 \[\begin{aligned} E( A \boldsymbol M B + C) = A E(\boldsymbol M) B + C . \end{aligned}\]

设\(\boldsymbol a, \boldsymbol b\)为向量， \(A, B\)为矩阵，\(\boldsymbol X, \boldsymbol Y, \boldsymbol Z\)为随机向量，则 \[\begin{aligned} \text{Var}(\boldsymbol a^T \boldsymbol X) =& \boldsymbol a^T \text{Var}(\boldsymbol X) \boldsymbol a \\ \text{Var}(A \boldsymbol X + \boldsymbol b) =& A \text{Var}(\boldsymbol X) A^T \\ \text{Cov}(\boldsymbol X + \boldsymbol Y, \boldsymbol Z) =& \text{Cov}(\boldsymbol X, \boldsymbol Z) + \text{Cov}(\boldsymbol Y, \boldsymbol Z) \\ \text{Var}(\boldsymbol X + \boldsymbol Y) =& \text{Var}(\boldsymbol X) + \text{Var}(\boldsymbol Y) + \text{Cov}(\boldsymbol X, \boldsymbol Y) + \text{Cov}(\boldsymbol Y, \boldsymbol X) \\ \text{Cov}(A \boldsymbol X, B \boldsymbol Y) =& A \text{Cov}(\boldsymbol X, \boldsymbol Y) B^T . \end{aligned}\]

3.3.3 一元随机变量变换的分布

设\(X\)有密度\(f(x)\)，密度支集为区间\(I\)，变换\(g(\cdot)\)为区间\(I\)到区间\(J\)的一一变换，对\(h(y) = g^{-1}(y)\)，设\(h(y)\)连续可导，则\(Y = g(X)\)有密度 \[ f_Y(y) = f(h(y)) |h'(y)|, \ y \in J . \]

例如，设\(g(x) = e^x\)，则\(h(y) = \log y\)，于是 \[ f_Y(y) = f(\log y) y^{-1}, \ y > 0 . \] 若其中\(X\)为\(\text{N}(\mu, \sigma^2)\)，则\(Y\)的分布密度为 \[ \frac{1}{\sqrt{2\pi \sigma^2}} \frac{1}{y} \exp\left\{ -\frac{1}{2} \frac{(\log y - \mu)^2}{\sigma^2} \right\} . \] 即对数正态分布密度。

3.3.4 多元随机变量变换的分布

设\(\boldsymbol X\)有联合密度\(f(\boldsymbol x)\)， \(g(\cdot)\)是\(\mathbb R^p\)到\(\mathbb R^p\)的一一变换，有反变换\(\boldsymbol x = h(\boldsymbol y)\)， \(h\)的Jacobi矩阵为 \[ J = (\frac{\partial x_j}{\partial y_i})_{p \times p}, \] \(J\)的\((i,j)\)元为\(\frac{\partial x_j}{\partial y_i}\)，则\(\boldsymbol Y = g(\boldsymbol X)\)有联合密度 \[ f_{\boldsymbol Y}(\boldsymbol y) = f(h(\boldsymbol y)) \, |\text{det}(J)| . \]

例如，设 \[ g(\boldsymbol x) = A \boldsymbol x + \boldsymbol b, \] 则\(h(\boldsymbol y) = A^{-1}(\boldsymbol y - \boldsymbol b)\)， Jacobi矩阵为\(A^{-1}\)，于是\(\boldsymbol Y\)的联合密度为 \[ f(A^{-1}(\boldsymbol y - \boldsymbol b)) |\text{det}(A))|^{-1} . \]

3.3.5 随机向量的标准化

类似于一元随机变量\(X\)的标准化\(Y = \frac{X - EX}{\sqrt{\text{Var}(X)}}\), 可以把随机向量标准化为零均值和单位阵协方差阵。设随机向量\(\boldsymbol X\)满足\(E \boldsymbol X=\boldsymbol\mu\), \(\text{Var}(\boldsymbol X) = \Sigma>0\), 若\(\Sigma = (\Sigma^{1/2})^2\), 记\(\Sigma^{-1/2} = (\Sigma^{1/2})^{-1}\), 令\(\boldsymbol Z = \Sigma^{-1/2} (\boldsymbol X - \boldsymbol\mu)\)，则\(\boldsymbol Z\)满足\(E\boldsymbol Z=\boldsymbol 0\), \(\text{Var}(\boldsymbol Z) = I\)。

设\(\Sigma\)有特征值分解\(\Sigma = \Gamma \Lambda \Gamma^T\), 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_p)\) 是\(\Sigma\)的所有特征值为对角元素的对角阵， \(\Gamma\)为正交阵，则可以取\(\Sigma^{1/2} = \Gamma \Lambda^{1/2} \Gamma^T\), 其中\(\Lambda^{1/2} = \text{diag}(\sqrt{\lambda_1}, \sqrt{\lambda_2}, \dots, \sqrt{\lambda_p})\)。 \(\Sigma^{-1/2} = \Gamma \Lambda^{-1/2} \Gamma^T\)，其中\(\Lambda^{-1/2} = \text{diag}(\frac{1}{\sqrt{\lambda_1}}, \frac{1}{\sqrt{\lambda_2}}, \dots, \frac{1}{\sqrt{\lambda_p}})\)。

另外，对于正定阵\(\Sigma\)，存在对角线元素都为正值的下三角阵\(B\)使得\(\Sigma = B B^T\)，这称为\(\Sigma\)的Cholesky分解；令\(\boldsymbol Z = B^{-1} (\boldsymbol X - \boldsymbol\mu)\)，则\(E \boldsymbol Z = \boldsymbol 0\)， \(\text{Var}(\boldsymbol Z) = I\)。

3.4 多元正态分布

3.4.1 多元正态分布概念

多元正态分布是理论性质比较优良的分布，其线性变换仍保持多元正态分布不变，边缘分布和条件分布仍为正态分布，分布完全由一二阶矩决定，在大样本下许多统计量近似分布为正态分布。

多元正态分布密度: \[\begin{aligned} f(\boldsymbol x | \boldsymbol\mu, \Sigma) =& (2\pi)^{-n/2} [\text{det}(\Sigma)]^{-1/2} \\ & \exp\left\{-\frac12 (\boldsymbol x - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol\mu) \right\} , \end{aligned}\] 其中\(\Sigma\)是正定矩阵，是分布的协方差矩阵。 \(\boldsymbol\mu\)是分布的期望向量。

R中mvtnorm::dvtnorm()函数计算多元正态密度函数。

3.4.2 多元正态密度的等值集

给定\(z>0\)，考虑集合 \[\begin{aligned} & \{ \boldsymbol x \in \mathbb R^p \,|\, f(\boldsymbol x | \boldsymbol\mu, \Sigma) = z \} \\ =& \{ \boldsymbol x \in \mathbb R^p \,|\, (\boldsymbol x - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol\mu) = d^2 \} , \end{aligned}\] 其中\(d>0\)与\(z\)一一对应。这个集合是一个超椭球面。适当的正交变换和坐标伸缩可以将其变换为球面。

3.4.3 （广义）多元正态分布

若随机向量\(\boldsymbol X\)的特征函数为 \[\begin{aligned} \phi(\boldsymbol t) = E e^{i \boldsymbol t^T \boldsymbol X} = \exp\left( i \boldsymbol t^T \boldsymbol\mu - \frac12 \boldsymbol t^T \Sigma \boldsymbol t \right) , \end{aligned}\] 其中\(\Sigma\)为半正定矩阵，则称\(\boldsymbol X\)服从（广义）多元正态分布。

当\(\Sigma\)为正定阵时，以上（广义）多元正态分布就是多元正态分布\(\text{N}(\boldsymbol\mu, \Sigma)\)。

（广义）多元正态分布的等价定义：设\(\boldsymbol Z\)服从标准多元正态分布， \(A\)是矩阵， \(\boldsymbol X = \boldsymbol\mu + A \boldsymbol Z\), 则\(\boldsymbol X\)服从（广义）多元正态分布 \(\text{N}(\boldsymbol\mu, A A^T)\)。

性质：

设\(\boldsymbol X\)服从（广义）多元正态分布\(\text{N}(\boldsymbol\mu, \Sigma)\)， \(\boldsymbol\beta\)是向量， \(B\)是矩阵，则\(\boldsymbol Y = \boldsymbol\beta + B \boldsymbol X\)也服从（广义）多元正态分布 \(\text{N}(\boldsymbol\beta + B\boldsymbol\mu, B \Sigma B^T)\)。
（广义）多元正态分布的一元边缘分布是（广义）一元正态分布：或者服从一元正态分布，或者等于一个常数。
（广义）多元正态分布的边缘分布也是（广义）多元正态分布。
设\((\boldsymbol X, \boldsymbol Y)\)服从多元正态分布，则\(\boldsymbol X\)与\(\boldsymbol Y\)相互独立的充分必要条件是\(\text{Cov}(\boldsymbol X, \boldsymbol Y) = \boldsymbol 0\)。

3.4.4 多元正态标准化

设\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\), \(\Sigma>0\)，令\(\boldsymbol Z = \Sigma^{-1/2} (\boldsymbol X - \boldsymbol\mu)\)，则\(\boldsymbol Z\)服从标准多元正态分布\(\text{N}(\boldsymbol 0, I)\)。

\(Y = \boldsymbol Z^T \boldsymbol Z = (\boldsymbol X - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol X - \boldsymbol\mu) \sim \chi^2(p)\)。

若\(\Sigma\)有Cholesky分解\(\Sigma = G G^T\), \(G\)为下三角阵且对角线元素都为正值，则\(\boldsymbol Z = G^{-1} (\boldsymbol X - \boldsymbol\mu)\)服从标准多元正态分布。

3.4.5 条件分布

设\(\boldsymbol X = (X_1, X_2)^T\)有联合密度\(f(x_1, x_2)\)，则\(X_1=x_1\)条件下\(X_2\)的条件密度为 \[\begin{aligned} f_{2|1}(x_2|x_1) = \frac{f(x_1, x_2)}{f_1(x_1)}. \end{aligned}\]

\(X_1=x_1\)条件下\(g(X_2)\)的条件期望为 \[\begin{aligned} h(x_1) = E(g(X_2) | X_1=x_1)=\int g(x_2) f_{2|1}(x_2 | x_1) \,dx_2, \end{aligned}\] 记\(h(X_1)\)为\(E(g(X_2)|X_1)\)。

令 \[\begin{aligned} \text{Var}(X_2 | X_1) = E\left\{ \left[ X_2 - E(X_2|X_1) \right]^2 \,|\, X_1 \right\} . \end{aligned}\]

条件期望性质： \[\begin{aligned} E(X_2) =& E \left\{ E(X_2|X_1) \right\} \\ \text{Var}(X_2) =& E \left\{ \text{Var}(X_2|X_1) \right\} + \text{Var}\left\{ E(X_2|X_1) \right\} . \end{aligned}\]

3.4.6 正态条件分布

设 \[\begin{aligned} \boldsymbol X = \left(\begin{array}{c} \boldsymbol X_1 \\ \boldsymbol X_2 \end{array}\right) \sim \text{N}(\boldsymbol\mu, \Sigma), \ \boldsymbol \mu = \left(\begin{array}{c} \boldsymbol \mu_1 \\ \boldsymbol \mu_2 \end{array}\right) , \ \Sigma = \left(\begin{array}{cc} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array}\right) , \end{aligned}\] 则\(\boldsymbol X_1 = \boldsymbol x_1\)条件下\(\boldsymbol X_2\)的条件分布为 \[\begin{aligned} \text{N}\big(\boldsymbol\mu_2 + \Sigma_{21}\Sigma_{11}^{-1}(\boldsymbol x_1 - \boldsymbol\mu_1), \; \Sigma_{22} - \Sigma_{21} \Sigma_{11}^{-1} \Sigma_{12} \big). \end{aligned}\] 条件方差不依赖于\(\boldsymbol x_1\)的值。令 \[\begin{aligned} \boldsymbol X_{2\cdot 1} =& \boldsymbol X_2 - E(\boldsymbol X_2 | \boldsymbol X_1) = \boldsymbol X_2 - \boldsymbol\mu_2 + \Sigma_{21}\Sigma_{11}^{-1}(\boldsymbol X_1 - \boldsymbol\mu_1), \\ \Sigma_{22\cdot 1} =& \Sigma_{22} - \Sigma_{21} \Sigma_{11}^{-1} \Sigma_{12}, \end{aligned}\] 则\((\boldsymbol X_1, \boldsymbol X_{2\cdot 1})\)独立， \(\boldsymbol X_{2\cdot 1} \sim \text{N}(\boldsymbol 0, \Sigma_{22\cdot 1})\)。

3.4.7 多元正态与卡方分布

设\(\boldsymbol X \sim \text{N}(\boldsymbol\mu, \Sigma)\), 则\((\boldsymbol X - \boldsymbol\mu)^T \Sigma^{-1} (\boldsymbol X - \boldsymbol\mu) \sim \chi^2(p)\)。

3.5 随机矩阵

设矩阵\(\boldsymbol M = (X_{ij})_{n \times p}\)，其中每一个\(X_{ij}\)是随机变量，称\(\boldsymbol M\)为随机矩阵。

随机矩阵本质上是随机向量，可以用拉直运算将随机矩阵表示为随机向量。

3.5.1 拉直运算

记\(\boldsymbol M\)的各个列向量为\(\boldsymbol x_j \in \mathbb R^n\), \(j=1,2,\dots, p\)；记\(\boldsymbol M\)的各个行向量为\([\boldsymbol x^{(i)}]^T \in \mathbb R^p\)， \(i=1,2,\dots,n\)。则 \[\begin{aligned} \boldsymbol M =& (\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_p) = \begin{pmatrix} [\boldsymbol x^{(1)}]^T \\ [\boldsymbol x^{(2)}]^T \\ \vdots \\ [\boldsymbol x^{(n)}]^T \end{pmatrix}, \\ \boldsymbol M^T =& (\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \dots, \boldsymbol x^{(n)}) . \end{aligned}\]

记 \[ \text{vec}(\boldsymbol M) = \begin{pmatrix} \boldsymbol x_1 \\ \boldsymbol x_2 \\ \vdots \\ \boldsymbol x_p \end{pmatrix}, \] 称为\(\boldsymbol M\)的（按列）拉直向量，则\(\text{vec}(M)\)为\(n p\)维随机向量。令 \[ \text{vec}(\boldsymbol M^T) = \begin{pmatrix} \boldsymbol x^{(1)} \\ \boldsymbol x^{(2)} \\ \vdots \\ \boldsymbol x^{(n)} \end{pmatrix}, \] 称为\(\boldsymbol M\)的按行拉直向量。

若\(\boldsymbol S = (S_{ij})_{p \times p}\)为对称矩阵，则令 \[ \text{Svec}(S) = (S_{11}, S_{21}, \dots, S_{p1}, S_{22}, \dots, S_{p2}, \dots, S_{pp})^T, \] 即将矩阵的下三角阵按列拉直，称为对称阵\(S\)的对称拉直向量。

拉直运算满足线性性质： \[\begin{aligned} \text{vec}(A + B) =& \text{vec}(A) + \text{vec}(B), \\ \text{vec}(\lambda \, A) =& \lambda \,\text{vec}(A) \quad(\lambda \in \mathbb R). \end{aligned}\]

3.5.2 Kronecker积

设\(A\)为\(m \times n\)矩阵， \(B\)为\(p \times q\)矩阵，将\(A\)的每一个元素和\(B\)的每一个元素相乘，将产生\(mnpq\)个乘积，将这些乘积写成一个\((mp) \times (nq)\)矩阵： \[ A \otimes B = \begin{pmatrix} a_{11} B & a_{12} B & \cdots & a_{1n} B \\ a_{21} B & a_{22} B & \cdots & a_{2n} B \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} B & a_{n2} B & \cdots & a_{nn} B \end{pmatrix} . \] 称为\(A\)和\(B\)的Kronecker乘积。

Kronecker积满足线性性质： \[\begin{aligned} & (a A + b B) \otimes C = a(A \otimes C) + b(B \otimes C), \\ & A \otimes (a B + b C) = a (A \otimes B) + b(A \otimes C) . \end{aligned}\]

Kronecker积满足结合律： \[ (A \otimes B) \otimes C = A \otimes (B \otimes C) . \] 还满足 \[\begin{aligned} (A \otimes B) (C \otimes D) =& (A C) \otimes (B D), \\ (A \otimes B)^T =& A^T \otimes B^T . \end{aligned}\]

在R中用A %x% B或kronecker(A, B)计算Kronecker乘积。

例如： \[ A = \boldsymbol 1_3 = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, \quad B = \begin{pmatrix} 11 \\ 21 \end{pmatrix}, \quad \] 则\(A \otimes B\)为：

A %x% B

##      [,1]
## [1,]   11
## [2,]   21
## [3,]   11
## [4,]   21
## [5,]   11
## [6,]   21

又如： \[ A = \begin{pmatrix} 1 & 0 \\ 0 & 10 \end{pmatrix}, \quad B = \begin{pmatrix} 11 & 12 \\ 21 & 22 \end{pmatrix}, \quad \] 则\(A \otimes B\)为：

A %x% B

##      [,1] [,2] [,3] [,4]
## [1,]   11   12    0    0
## [2,]   21   22    0    0
## [3,]    0    0  110  120
## [4,]    0    0  210  220

3.5.3 随机矩阵的均值和方差阵

设\(\boldsymbol M\)为\(n \times p\)随机矩阵，则\(E \boldsymbol M\)也是\(n \times p\)矩阵，其\((i,j)\)元素等于\(\boldsymbol M\)的第\((i,j)\)元素的期望值。

若\(A, B, C\)为普通矩阵，有 \[ E(A \boldsymbol M B^T + C) = A E(\boldsymbol M) B^T + C . \]

设\(\boldsymbol X\)为\(p \times 1\)随机向量， \(\boldsymbol a\)为\(n \times 1\)向量，则\(\boldsymbol a \boldsymbol X^T\)为\(n \times p\)随机矩阵。将\(\boldsymbol a \boldsymbol X^T\)按行拉直，有 \[\begin{aligned} & \text{Var}\left\{ \text{vec}( [\boldsymbol a \boldsymbol X^T]^T) \right\} = \text{Var}\left\{ \text{vec}( \boldsymbol X \boldsymbol a^T) \right\} \\ =& \text{Var}\left\{ \begin{pmatrix} a_1 \boldsymbol X \\ a_2 \boldsymbol X \\ \vdots \\ a_n \boldsymbol X \end{pmatrix} \right\} \\ =& \begin{pmatrix} a_1^2 \Sigma & a_1 a_2 \Sigma & \cdots & a_1 a_n \Sigma \\ a_2 a_1 \Sigma & a_2^2 \Sigma & \cdots & a_2 a_n \Sigma \\ \vdots & \vdots & \ddots & \vdots \\ a_n a_1 \Sigma & a_n a_2 \Sigma & \cdots & a_n^2 \Sigma \end{pmatrix} \\ =& (\boldsymbol a \boldsymbol a^T) \otimes \Sigma . \end{aligned}\] 即： \[\begin{align} \text{Var}\left\{ \text{vec}( [\boldsymbol a \boldsymbol X^T]^T) \right\} = \text{Var}\left\{ \text{vec}( \boldsymbol X \boldsymbol a^T) \right\} = (\boldsymbol a \boldsymbol a^T) \otimes \Sigma . \tag{3.1} \end{align}\]

若\(\boldsymbol M\)的各行\([\boldsymbol x^{(i)}]^T\), \(i=1,2,\dots,n\)相互独立同分布， \[ E(\boldsymbol x^{(i)}) = \boldsymbol\mu, \quad \text{Var}(\boldsymbol x^{(i)}) = \Sigma, \] 则\(\boldsymbol M\)按行拉直后，有 \[\begin{aligned} E[\text{vec}(\boldsymbol M^T)] =& \boldsymbol 1_n \otimes \boldsymbol \mu, \\ \text{Var}[\text{vec}(\boldsymbol M^T)] =& I_n \otimes \boldsymbol \Sigma . \end{aligned}\] 这时令随机矩阵\(N\)定义为 \[\begin{aligned} \boldsymbol N = \boldsymbol M B^T + C, \end{aligned}\] 其中\(B\)为\(q \times p\)矩阵，则\(N\)的第\(i\)行\([\boldsymbol y^{(i)}]^T\)完全由\([\boldsymbol x^{(i)}]^T\)决定： \[\begin{aligned} \; [\boldsymbol y^{(i)}]^T =& [\boldsymbol x^{(i)}]^T B^T + [\boldsymbol c^{(i)}]^T, \\ \boldsymbol y^{(i)} =& B \boldsymbol x^{(i)} + \boldsymbol c^{(i)} . \end{aligned}\] 其中\([\boldsymbol c^{(i)}]^T\)是\(C\)的第\(i\)行。于是，各\(\boldsymbol y^{(i)}\), \(i=1,2,\dots,n\)独立， \[ \text{Var}(\boldsymbol y^{(i)}) = \text{Var}(B \boldsymbol x^{(i)}) = B \Sigma B^T, \] 于是 \[\begin{align} E(\boldsymbol N) =& E(\boldsymbol M) B^T + C, \tag{3.2} \\ \text{Var}(\text{vec}(\boldsymbol N^T)) =& I_n \otimes (B \Sigma B^T) . \tag{3.3} \end{align}\]

进一步地，仍设\(\boldsymbol M\)的各行独立同分布，令 \[\begin{aligned} \boldsymbol N = A \boldsymbol M B^T + C, \end{aligned}\] 则有 \[\begin{align} E(\boldsymbol N) =& A E(\boldsymbol M) B^T + C, \tag{3.4} \\ \text{Var}(\text{vec}(\boldsymbol N^T)) =& (A A^T) \otimes (B \Sigma B^T) . \tag{3.5} \end{align}\] (3.4)由期望的线性性质可得。下面证明(3.5)。

因为\(C\)不影响方差和协方差计算，在证明(3.5)时设\(C = 0\)。令\(\boldsymbol z^{(i)} = B \boldsymbol x^{(i)}\)，则各\(\boldsymbol z^{(i)}\)独立同分布， \[ \text{Var}(\boldsymbol z^{(i)}) = B \Sigma B . \] 且\(M B^T\)的各行为\([\boldsymbol z^{(i)}]^T\)。设\(A\)为\(m \times n\)矩阵，各个列向量为\(\boldsymbol a_i\), \(i=1,2,\dots, n\)，则 \[\begin{aligned} \boldsymbol N =& A \boldsymbol M B^T \\ =& (\boldsymbol a_1, \boldsymbol a_2, \dots, \boldsymbol a_n) \begin{pmatrix} [\boldsymbol z^{(1)}]^T \\ [\boldsymbol z^{(2)}]^T \\ \vdots \\ [\boldsymbol z^{(n)}]^T \\ \end{pmatrix} \\ =& \sum_{i=1}^n \boldsymbol a_i [\boldsymbol z^{(i)}]^T , \end{aligned}\] 其按行拉直的协方差阵为 \[\begin{aligned} & \text{Var}\left\{ \text{vec}( \boldsymbol N^T) \right\} = \text{Var}\left\{ \text{vec} \left[ \left( \sum_{i=1}^n \boldsymbol a_i [\boldsymbol z^{(i)}]^T \right)^T \right] \right\} \\ =& \text{Var}\left\{ \text{vec} \left[ \sum_{i=1}^n \boldsymbol z^{(i)} \boldsymbol a_i^T \right] \right\} = \text{Var}\left\{ \sum_{i=1}^n \text{vec} \left[ \boldsymbol z^{(i)} \boldsymbol a_i^T \right] \right\} \\ =& \sum_{i=1}^n \text{Var}\left\{ \boldsymbol z^{(i)} \boldsymbol a_i^T \right\} \\ =& \sum_{i=1}^n (\boldsymbol a_i \boldsymbol a_i^T) \otimes (B \Sigma B) \\ =& (A A^T) \otimes (B \Sigma B) , \end{aligned}\] 证明中用到不同的\(\boldsymbol z^{(i)}\)的不相关性，拉直运算的线性性质， Kronecker乘积的线性性质，和式(3.1)。 (3.5)式证毕。

3.6 Copula

参考：(Wolfgang Härdle 2015)节4.1和节4.7。

3.6.1 Copula介绍

联合分布决定边缘分布，反过来，边缘分布不能决定联合分布，相同的边缘分布可能对应于完全不同的联合分布。

例3.1 考虑如下两个联合分布。设第一个联合密度为 \[ f(x, y) = 1, \ x, y \in (0, 1), \] 边缘分布都是\(\text{U}(0,1)\)。

设第二个联合密度为 \[ g(x, y) = 1 + \alpha(2x-1)(2y-1), \ x, y \in (0, 1), \] 则边缘分布仍然都是\(\text{U}(0,1)\)。其中\(\alpha \in [-1,1]\)为分布参数。

○○○○○○

如果联合分布是正态分布，有了边缘分布后只要用相关系数就可以完全确定联合分布。对一般的分布，如何从边缘分布产生一个联合分布？ Copula是这样的一种工具。

注意若\(X\)为连续型随机变量，在区间\(I\)上有正密度，分布函数为\(F(x)\)，则\(U = F(X)\)服从\(\text{U}(0,1)\)。反过来，如果\(U\)服从\(\text{U}(0,1)\)，则\(X = F^{-1}(U)\)服从\(F(x)\)。

考虑二元的联合分布。设函数 \[ C: [0,1]^2 \to [0,1], \] 称\(C\)是一个二元的Copula，若其满足

\(C(0, u) = C(u, 0) = 0\), \(\forall u \in [0, 1]\)；
\(C(1, u) = C(u, 1) = u\), \(\forall u \in [0, 1]\)。
对\((u_1, u_2), (v_1, v_2) \in [0,1]^2\)，若\(u_1 \leq v_1\), \(u_2 \leq v_2\)，则\(C(v_1, v_2) - C(v_1, u_2) - C(u_1, v_2) + C(u_1, u_2) \geq 0\)。

可以看出， \(C\)是一个\([0,1]^2\)的联合分布函数，且两个边缘分布均为\(\text{U}(0,1)\)。 \(C(v_1, v_2) - C(v_1, u_2) - C(u_1, v_2) + C(u_1, u_2)\)是随机向量在左下角为\((u_1,u_2)\)，右上角为\((v_1, v_2)\)的矩形中取值的概率。注意取\(u_1 = 0\)，则 \[ C(v_1, v_2) - C(v_1, u_2) \geq 0, \ \forall u_2 \leq v_2 , v_1 \in [0, 1] . \] 类似地取\(u_2=0\)有 \[ C(v_1, v_2) - C(u_1, v_2) \geq 0, \ \forall u_1 \leq v_1 , v_2 \in [0, 1] . \] \(C(u_1, 1) = u_1\)即第一分量的边缘分布， \(C(1, u_2) = u_2\)即第二分量的边缘分布。

定理3.1 (Sklar定理) 设\(F(\cdot,\cdot)\)是一个联合分布函数，边缘分布函数为\(F_{X_1}\)和\(F_{X_2}\)。则存在函数C为Copula，满足 \[\begin{align} F(x_1, x_2) = C(F(x_1), F(x_2)), \ \forall (x_1, x_2) \in \mathbb R^2 . \tag{3.6} \end{align}\] 如果\(F_{X_1}\)和\(F_{X_2}\)都连续，则\(C\)唯一。反过来，如果\(C\)是二元Copula， \(F_{X_1}\)和\(F_{X_2}\)是两个分布函数，则(3.6)定义的\(F(\cdot,\cdot)\)是以\(F_{X_1}\)和\(F_{X_2}\)为边缘分布函数的联合分布函数。

从Sklar定理可以看出，联合分布都可以用Copula函数和边缘分布表示；在不知道随机向量各分量之间的关系时，可以选择某个Copula函数用来表示分量之间的关系。

例3.2 若两个分量独立，则 \[ C(u_1, u_2) = u_1 u_2, \ u_1, u_2 \in [0, 1] . \] 这称为独立Copula。可以推广到\(n\)个分量情形。

○○○○○○

定理3.2 设随机变量\(X_1\)和\(X_2\)的分布函数\(F_{X_1}\)和\(F_{X_2}\)连续，联合分布函数为\(F\)，则存在唯一的copula \(C\)使得\(F(x_1, x_2) = C(F_{X_1}(x_1), F_{X_2}(x_2))\)；这时，\(X_1\)和\(X_2\)相互独立的充分必要条件是\(C(u_1, u_2) = u_1 u_2\)。

例3.3 Gumbel-Hougaard copula族定义为 \[ C_{\theta}(u, v) = \exp\left\{ -\left[ (-\log u)^\theta + (-\log v)^\theta . \right]^{1/\theta} \right\} \] 其中\(\theta \geq 1\)。适用于描述二元的有极端值的分布。当\(\theta=1\)时即独立copula。当\(\theta \to \infty\)时变成: \[ M(u, v) = \min(u, v) . \] \(M(u,v)\)称为Fréchet–Hoeffding上界，对任意的copula \(C\)都有 \[ C(u,v) \leq M(u,v), \ \forall u, v \in [0, 1] . \]

事实上， \[ C(u, v) \leq C(u, 1) = u, \ C(u, v) \leq C(1, v) = v . \]

例3.4 设\((Z_1, Z_2)\)服从联合正态分布，联合分布函数为\(G_{\rho}(\cdot, \cdot)\)，边缘分布都是标准正态分布，相关系数为\(\rho\)。则 \[ C(u, v) = G(\Phi^{-1}(u), \Phi^{-1}(v)), \ u, v \in [0, 1] \] 称为高斯copula。 \(\rho=0\)时为独立copula。

3.6.2 二元copula的理论

设\(U_1\), \(U_2\)是\(\bar{\mathbb R} = \mathbb R \cup \{+\infty, -\infty \}\)中的两个集合， \(F\)是\(U_1 \times U_2 \to \bar{\mathbb R}\)的函数。

\(U_1 \times U_2\)中的一个子集\(B = [x_1, x_2] \times [y_1, y_2]\)的\(F\)体积定义为 \[ V_F(B) = F(x_2, y_2) - F(x_1, y_2) - F(x_2, y_1) + F(x_1, y_1) . \] 若\(F\)是二元的联合密度，则\(F\)体积就是将\(F\)看作一个测度，在矩形\(B\)上的测度值。如果对任意的\(B\)都有\(V_F(B) \geq 0\)，则称函数\(F\)是“二元增函数”。但二元增函数不能保证关于每个分量都是增函数。

设\(U_1\)和\(U_2\)以及\(x_1, x_2, y_1, y_2\)如上定义，则对给定\(y_1, y_2\)， \(F(t, y_2) - F(t, y_1)\)关于\(t\)是增函数；对给定\(x_1, x_2\)， \(F(x_2, t) - F(x_1, t)\)关于\(t\)是增函数。

为了使得\(F\)关于每个分量是增函数，还需要增加条件。

设\(U_1\)和\(U_2\)都有最小元素。称\(F: U_1 \times U_2 \to \mathbb R\)是触底的(grounded)，如果 \[\begin{aligned} & F(x, \min U_2) = 0, \ \forall x \in U_1; \\ & F(\min U_1, y) = 0, \ \forall y \in U_2 . \end{aligned}\]

定义3.1 称\(F\)是二维的分布函数，如果

(1) \(F\)是触底的;

(2) \(F\)是二维增函数；

(3) \(F(+\infty, +\infty) = 1\)。

若\(F\)是触底的二维增函数，则\(F\)对每个分量都是增函数。

如果\(U_1\)和\(U_2\)都有最大元素，则称\(F\)有边缘，其边缘分别为\(F_1(x) = F(x, \max U_2)\)和\(F_2(y) = F(\max U_1, y)\)。

若\(F\)触底、有边缘、二维增，则 \[ | F(x_2, y_2) - F(x_1, y_1) | \leq |F_1(x_2) - F_1(x_1)| + | F_2(y_2) - F_2(y_1) | . \]

于是，Copula是一个\([0,1] \times [0,1]\)上的二维分布函数且边缘分布都是标准均匀分布。实际定义如下：

定义3.2 二维copula是\([0,1] \times [0,1]\)上定义的函数，满足

(1) 对任意\(u \in [0,1]\), \(C(u, 0) = C(0, u) = 0\);

(2) 对任意\(u \in [0,1]\), \(C(u, 1) = u\), 对任意\(v \in [0,1]\), \(C(1, v) = v\);

(3) 对任意\(u_1, u_2, v_1, v_2 \in [0, 1]\)且\(u_1 \leq u_2\), \(v_1 \leq v_2\)，都有 \[ C(u_2, v_2) - C(u_2, v_1) - C(u_1, v_2) + C(u_1, v_1) \geq 0 . \]

例3.5 \(\max(u+v-1, 0)\)称为最小copula。 \(uv\)称为乘积copula(独立copula)。 \(\min(u, v)\)称为最大copula。

例3.6 二维的高斯copula见例3.4。

如果对边缘分布进行连续单调增变换，联合分布对应的copula保持不变。

定理3.3 设随机向量\((X_1, X_2)\)对应于copula \(C\)， \(g_1(\cdot)\), \(g_2(\cdot)\)是两个连续的单调增变换，则\((g_1(X_1), g_2(X_2))\)也对应于copula \(C\)。

见(Wolfgang Härdle 2015) P.172定理4.13。

定理3.4 设\(X_1\)和\(X_2\)分别有连续的分布函数\(F_1\)和\(F_2\)，则\(X_1\)与\(X_2\)独立的充要条件是其对应的copula \(C_{X_1, X_2}\)是独立copula(乘积copula)。

定理3.5 设\(C\)是二维copula，则对任意\(u_1, v_1, u_2, v_2 \in [0, 1]\)，有 \[\begin{align} |C(u_2, v_2) - C(u_1, v_1)| \leq |u_2 - u_1| + |v_2 - v_1| . \tag{3.7} \end{align}\]

(3.7)说明copula在考虑一个分量的变换时，关于另一个分量是一致连续的。

定理3.6 设\(C(u,v)\)是copula， \(\frac{\partial C(u,v)}{\partial v}\)对几乎处处的\(u \in [0,1]\)存在，存在时\(\frac{\partial C(u,v)}{\partial v} \in [0, 1]\); \(\frac{\partial C(u,v)}{\partial u}\)对几乎处处的\(v \in [0,1]\)存在，存在时\(\frac{\partial C(u,v)}{\partial u} \in [0, 1]\)。考虑函数 \[\begin{aligned} & u \mapsto C_v(u) = \frac{\partial C(u,v)}{\partial v}, \\ & v \mapsto C_u(v) = \frac{\partial C(u,v)}{\partial u}, \end{aligned}\] 这两个函数在\([0,1]\)上几乎处处有定义，且为单调增函数。

见(Wolfgang Härdle 2015) P.172定理4.15。

3.6.3 多元copula

考虑\(\mathbb R^d\)值随机向量。

设\(U_1, \dots, U_d\)是\(\bar{\mathbb R}\)的非空集合。 \(F\)是\(U_1 \times U_d \to \bar{\mathbb R}\)函数。设\(a_k \leq b_k\)，\([a_k, b_k] \subset U_k\), \(k=1,\dots,d\)。 \(B = [a_1,b_1] \times [a_d,b_d]\)构成\(\mathbb R^d\)的超矩形，设其\(2^d\)个顶点中的一个记为\([c_1, \dots, c_d]\)，则\(c_k\)等于\(a_k\)或者\(b_k\)。

内容待完成。

References

Wolfgang Härdle, Léopold Simar. 2015. Applied Multivariate Statistical Analysis. 4th Edition. Springer.

Zelterman, Daniel. 2015. Applied Multivariate Statistics with r. Springer.