11 典型相关分析
《多元统计分析—基于R》课程的R示例， 主要参考书: 费宇《多元统计分析-基于R》，人民大学出版社，2012。
11.1 典型相关分析介绍
变量之间的相关性的研究方法包括：
- 用相关系数衡量两个随机变量（或其样本）的线性相关性的方向和强弱。
- 对于一个因变量与多个自变量的样本的情形， 用回归分析建立自变量的线性组合使其最好地描述因变量， 用复相关系数平方(\(R^2\))描述因变量与自变量线性组合的相关性强弱。
在线性回归分析中， 可以用主成分分析方法把\(p\)多个自变量降维到\(k\)个自变量的线性组合（主成分）， 但是这些主成分并没有最好地解释因变量。 可以考虑找自变量的若干线性组合使其互不相关但与因变量的相关最强。
把线性回归和主成分分析问题推广到多个因变量和多个自变量。 同时找因变量的若干线性组合与自变量的若干线性组合， 使其因变量组和自变量组之间成对的线性组合的相关性最强， 因变量组内、自变量组内的线性组合不相关， 且尽可能保存原始变量信息， 这就是典型相关分析。
典型相关分析与其它多元分析方法相比使用不够广泛， 因为其结果常常不易解释。
11.2 总体典型相关
11.2.1 第一对典型变量的求解
设有两组变量\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\) 和\(\boldsymbol Y = (Y_1, Y_2,\dots, Y_q)^T\) 设\(p \leq q\)。 变量\(\boldsymbol Z = (\boldsymbol X^T, \boldsymbol Y^T)^T\)的协方差矩阵为 \[\begin{aligned} \Sigma = \left(\begin{array}{cc} \text{Var}(\boldsymbol X) & \text{Cov}(\boldsymbol X, \boldsymbol Y) \\ \text{Cov}(\boldsymbol Y, \boldsymbol X) & \text{Var}(\boldsymbol Y) \end{array}\right) = \left(\begin{array}{cc} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array}\right) \end{aligned}\] (其中\(\Sigma_{21} = \Sigma_{12}^T\))。 设\(\Sigma\)正定，从而\(\Sigma_{11}\)和\(\Sigma_{22}\)都正定。 找\(\boldsymbol X\)的线性组合\(U = \boldsymbol a^T \boldsymbol X\) 与\(\boldsymbol Y\)的线性组合\(V = \boldsymbol b^T \boldsymbol Y\)使得 \(U\)与\(V\)的相关系数最大。
这里 \[\begin{aligned} \text{Var}(U) =& \text{Var}(\boldsymbol a^T \boldsymbol X) = \boldsymbol a^T \Sigma_{11} \boldsymbol a, \\ \text{Var}(V) =& \text{Var}(\boldsymbol b^T \boldsymbol Y) = \boldsymbol b^T \Sigma_{22} \boldsymbol b, \\ \text{Cov}(U, V) =& \text{Cov}(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y) = \boldsymbol a^T \Sigma_{12} \boldsymbol b, \\ \rho(U, V) =& \frac{\text{Cov}(U, V)}{\sqrt{\text{Var}(U) \text{Var}(V)}} = \frac{ \boldsymbol a^T \Sigma_{12} \boldsymbol b } {\sqrt{ ( \boldsymbol a^T \Sigma_{11} \boldsymbol a ) ( \boldsymbol b^T \Sigma_{22} \boldsymbol b ) } } . \end{aligned}\] 当\(\Sigma_{12}=0\)即\(\boldsymbol Y\)与\(\boldsymbol X\)不相关时恒有\(\rho(U, V)=0\)， 所以下面设\(\Sigma_{12} \neq 0\)。
注意\(\rho(\alpha U , \beta V) = \rho(U, V)\)对任意的\(\alpha \beta > 0\)成立， 所以需要对系数\(\boldsymbol a, \boldsymbol b\)加上约束， 假定 \[\begin{align} \begin{cases} \text{Var}(U) = \boldsymbol a^T \Sigma_{11} \boldsymbol a = 1, \\ \text{Var}(V) = \boldsymbol b^T \Sigma_{22} \boldsymbol b = 1. \tag{11.1} \end{cases} \end{align}\] 显然当\(\boldsymbol a, \boldsymbol b\)满足以上约束时， 对任意\(k \neq \pm 1\)都有\(\text{Var}((k \boldsymbol a)^T \boldsymbol X) = k^2 \text{Var}(U) = k^2 \neq 1\), \(\text{Var}((k \boldsymbol b)^T \boldsymbol Y) \neq 1\)。 对满足(11.1)的\(\boldsymbol a, \boldsymbol b\)， 为使得\(\rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y)\)不变， 只有\(-\boldsymbol a, -\boldsymbol b\)才满足要求。
于是，考虑如下的问题：在约束 \[\begin{aligned} &\text{Var}(\boldsymbol a^T \boldsymbol X) = \boldsymbol a^T \Sigma_{11} \boldsymbol a = 1, \\ &\text{Var}(\boldsymbol b^T \boldsymbol Y) = \boldsymbol b^T \Sigma_{22} \boldsymbol b = 1 \end{aligned}\] 下，求\(\boldsymbol a, \boldsymbol b\)使得 \[\begin{aligned} \rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y) = \frac{ \boldsymbol a^T \Sigma_{12} \boldsymbol b } {\sqrt{ ( \boldsymbol a^T \Sigma_{11} \boldsymbol a ) ( \boldsymbol b^T \Sigma_{22} \boldsymbol b ) } } = \boldsymbol a^T \Sigma_{12} \boldsymbol b \end{aligned}\] 达到最大。
\(\boldsymbol a^T \Sigma_{11} \boldsymbol a=1\)这样的约束不易使用。 令\(\boldsymbol\gamma = \Sigma_{11}^{1/2} \boldsymbol a\), \(\boldsymbol\delta = \Sigma_{22}^{1/2} \boldsymbol b\), 则\(\boldsymbol\gamma\)与\(\boldsymbol a\)一一对应， \(\boldsymbol\delta\)与\(\boldsymbol b\)一一对应， 约束\(\boldsymbol a^T \Sigma_{11} \boldsymbol a = 1\)等价于\(\| \boldsymbol\gamma \| = 1\), 约束\(\boldsymbol b^T \Sigma_{22} \boldsymbol b = 1\)等价于\(\| \boldsymbol\delta \| = 1\)。 目标函数变成 \[\begin{aligned} \boldsymbol a^T \Sigma_{12} \boldsymbol b = \boldsymbol\gamma^T \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2} \boldsymbol \delta . \end{aligned}\] 记 \[\begin{aligned} K =& \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2}, \end{aligned}\] 目标函数变成\(\boldsymbol\gamma^T K \boldsymbol\delta\)。
求第一对典型变量的问题， 变成了在\(\| \boldsymbol\gamma \|=1\), \(\| \boldsymbol\delta \|=1\)条件下求 \[\begin{align} \boldsymbol\gamma^T K \boldsymbol\delta \end{align}\] 的最大值， 其中\(K = \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2}\)。
先固定\(\boldsymbol\gamma\), 求满足\(\| \boldsymbol\delta \| = 1\)的\(\boldsymbol\delta\)使得 \[\begin{aligned} \boldsymbol\gamma^T K \boldsymbol\delta \end{aligned}\] 最大。
注意\(\boldsymbol\gamma^T K\)是一个行向量， \(\boldsymbol\gamma^T K \boldsymbol\delta\)是向量\(K^T \boldsymbol\gamma\)与向量\(\boldsymbol\delta\)的内积。
由内积不等式， \[\begin{aligned} \boldsymbol\gamma^T K \boldsymbol\delta \leq \| \boldsymbol\gamma^T K \| \,\cdot \| \boldsymbol\delta \| = \| \boldsymbol\gamma^T K \|, \end{aligned}\] 等号成立当且仅当存在常数\(c\)使得\(\boldsymbol\delta = c K^T \boldsymbol\gamma\)。
由\(\| \boldsymbol\delta \| = 1\)解得最大值点 \(\boldsymbol\delta = K^T \boldsymbol\gamma / \| K^T \boldsymbol\gamma \|\), 最大值为 \[\begin{aligned} \frac{\boldsymbol\gamma^T K K^T \boldsymbol\gamma}{\| K^T \boldsymbol\gamma \|} = \left( \boldsymbol\gamma^T K K^T \boldsymbol\gamma \right)^{1/2} . \end{aligned}\]
下一步只要求满足\(\| \boldsymbol\gamma \| = 1\)的\(\boldsymbol\gamma\) 使得\(\boldsymbol\gamma^T K K^T \boldsymbol\gamma\)最大。
注意\(K K^T\)是一个半正定矩阵， 由线性代数中熟知的结论， 最大值为\(K K^T\)的最大特征值\(\lambda_1^2\)， 在\(K K^T\)对应于\(\lambda_1^2\)的单位特征向量\(\boldsymbol\gamma_1\)处取到。 这时\(\boldsymbol\delta\)应取为 \[\begin{aligned} \boldsymbol\delta_1 = K^T \boldsymbol\gamma_1 / \| K^T \boldsymbol\gamma_1 \| . \end{aligned}\]
事实上，\(K K^T\)与\(K^T K\)一定有相同的正特征值 \(\lambda_1^2, \lambda_2^2, \dots, \lambda_r^2\), \(\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_r\), \(r = \text{rank}(K) = \text{rank}(\Sigma_{12})\), 且若\(\boldsymbol\gamma_i\)是\(K K^T\)对应于特征值\(\lambda_i^2\)的单位特征向量， 则\(\boldsymbol\delta_i = K^T \boldsymbol\gamma_i / \| K^T \boldsymbol\gamma_i \|\) 是\(K^T K\)对应于特征值\(\lambda_i^2\)的单位特征向量; 若\(\boldsymbol\delta_i\)是\(K^T K\)对应于特征值\(\lambda_i^2\)的单位特征向量， 则\(\boldsymbol\gamma_i = K \boldsymbol\delta_i / \| K \boldsymbol\delta_i \|\) 是\(K K^T\)对应于特征值\(\lambda_i^2\)的单位特征向量。
对任意的\(p \times q\)矩阵\(K\)， 设\(\text{rank}(K)=r\), 一定存在\(\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_r > 0\)， \(p \times r\)矩阵 \(\Gamma = (\boldsymbol\gamma_1, \boldsymbol\gamma_2, \dots, \boldsymbol\gamma_r)\)满足 \(\Gamma^T \Gamma = I_r\), \(q \times r\)矩阵 \(\Delta = (\boldsymbol\delta_1, \boldsymbol\delta_2, \dots, \boldsymbol\delta_r)\)满足 \(\Delta^T \Delta = I_r\)，使得 \[\begin{align} K = \Gamma \Lambda \Delta^T = \sum_{i=1}^r \lambda_i \boldsymbol\gamma_i \boldsymbol\delta_i^T, \tag{11.2} \end{align}\] 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_r)\)。 \(\lambda_1^2, \lambda_2^2, \dots, \lambda_r^2\)是\(K K^T\)和\(K^T K\)的共同的正特征值， \(\boldsymbol\gamma_i\)是\(K K^T\)对应于特征值\(\lambda_i^2\)的单位特征向量， \(\boldsymbol\delta_i\)是\(K^T K\)对应于特征值\(\lambda_i^2\)的单位特征向量。
所以，第一对典型变量的系数由 \(K = \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2}\)的奇异值分解(11.2)给出。 令 \[\begin{aligned} \boldsymbol a_1 =& \Sigma_{11}^{-1/2} \boldsymbol\gamma_1, \quad \boldsymbol b_1 = \Sigma_{22}^{-1/2} \boldsymbol\delta_1, \end{aligned}\] 则在\(\boldsymbol a^T \Sigma_{11} \boldsymbol a = 1\)和 \(\boldsymbol b^T \Sigma_{22} \boldsymbol b = 1\)条件下， \(\rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y)\) 的最大值当\(\boldsymbol a = \boldsymbol a_1\), \(\boldsymbol b = \boldsymbol b_1\)时取到， 相关系数的最大值为\(\lambda_1\)。 称\(U_1 = \boldsymbol a_1^T \boldsymbol X\)和\(V_1 = \boldsymbol b_1^T \boldsymbol Y\)为第一对典型变量， \(\lambda_1\)为第一典型相关系数。
第一对典型变量具有如下性质：
- \(\text{Var}(U_1) = \boldsymbol a_1^T \Sigma_{11} \boldsymbol a = 1\), \(\text{Var}(V_1) = \boldsymbol b_1^T \Sigma_{22} \boldsymbol b = 1\)。
- \(\rho(U_1, V_1) = \text{Cov}(U_1, V_1) = \lambda_1\), 所以\(0 < \lambda_1 < 1\)。
11.2.2 其它对典型变量的求解
假设已经有了\(j-1\)对典型变量\(\boldsymbol a_i^T \boldsymbol X\) 和\(\boldsymbol b_i^T \boldsymbol Y\)，\(i=1,2,\dots, j-1\), 其中\(\boldsymbol a_i = \Sigma_{11}^{-1/2} \boldsymbol\gamma_i\), \(\boldsymbol b_i = \Sigma_{22}^{-1/2} \boldsymbol\delta_i\)。 求\(\boldsymbol a^T\)和\(\boldsymbol b\)，使得在条件 \[\begin{align} & \text{Var}(\boldsymbol a^T \boldsymbol X) = \boldsymbol a^T \Sigma_{11} \boldsymbol a = 1, \tag{11.3}\\ & \text{Var}(\boldsymbol b^T \boldsymbol Y) = \boldsymbol b^T \Sigma_{22} \boldsymbol b = 1, \tag{11.4}\\ & \text{Cov}(\boldsymbol a^T \boldsymbol X, \boldsymbol a_i^T \boldsymbol X) = 0, \ i=1,2,\dots, j-1, \tag{11.5}\\ & \text{Cov}(\boldsymbol a^T \boldsymbol X, \boldsymbol b_i^T \boldsymbol Y) = 0, \ i=1,2,\dots, j-1 , \tag{11.6} \\ & \text{Cov}(\boldsymbol b^T \boldsymbol Y, \boldsymbol b_i^T \boldsymbol Y) = 0, \ i=1,2,\dots, j-1 , \tag{11.7} \\ & \text{Cov}(\boldsymbol b^T \boldsymbol Y, \boldsymbol a_i^T \boldsymbol X) = 0, \ i=1,2,\dots, j-1 . \tag{11.8} \end{align}\] 下目标函数 \[\begin{align} \rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y) = \frac{ \boldsymbol a^T \Sigma_{12} \boldsymbol b } {\sqrt{ ( \boldsymbol a^T \Sigma_{11} \boldsymbol a ) ( \boldsymbol b^T \Sigma_{22} \boldsymbol b ) } } = \boldsymbol a^T \Sigma_{12} \boldsymbol b \end{align}\] 达到最大。
仍进行变量替换\(\boldsymbol\gamma = \Sigma_{11}^{1/2} \boldsymbol a\), \(\boldsymbol\delta = \Sigma_{22}^{1/2} \boldsymbol b\), 则\(\boldsymbol\gamma\)与\(\boldsymbol a\)一一对应， \(\boldsymbol\delta\)与\(\boldsymbol b\)一一对应。 易见约束条件(11.3)变成\(\| \boldsymbol\gamma \| = 1\), 约束条件(11.4)变成\(\| \boldsymbol\delta \| = 1\)。 约束条件(11.5)变成 \[\begin{aligned} \boldsymbol\gamma^T \Sigma_{11}^{-1/2} \Sigma_{11} \Sigma_{11}^{-1/2} \boldsymbol\gamma_i = \boldsymbol\gamma^T \boldsymbol\gamma_i = 0, \ i=1,2,\dots,j-1 . \end{aligned}\] 约束条件(11.7)变成 \[\begin{aligned} \boldsymbol\delta^T \boldsymbol\delta_i = 0, \ i=1,2,\dots, j-1. \end{aligned}\]
约束条件(11.6)变成 \[\begin{aligned} \boldsymbol\gamma^T \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2} \boldsymbol\delta_i = \boldsymbol\gamma^T K \boldsymbol\delta_i = 0, \ i=1,2,\dots, j-1, \end{aligned}\] 约束条件(11.8)变成 \[\begin{aligned} \boldsymbol\delta^T K^T \boldsymbol\gamma_i = 0, \ i=1,2,\dots, j-1 . \end{aligned}\]
求第\(j\)对典型变量问题，转化为在如下约束 \[\begin{align} & \| \boldsymbol\gamma \| = 1, \tag{11.9}\\ & \| \boldsymbol\delta \| = 1, \tag{11.10}\\ & \boldsymbol\gamma^T \boldsymbol\gamma_i = 0, \ i=1,2,\dots, j-1, \tag{11.11}\\ & \boldsymbol\gamma^T K \boldsymbol\delta_i = 0, \ i=1,2,\dots, j-1, \tag{11.12}\\ & \boldsymbol\delta^T \boldsymbol\delta_i = 0, \ i=1,2,\dots, j-1, \tag{11.13}\\ & \boldsymbol\delta^T K^T \boldsymbol\gamma_i = 0, i=1,2,\dots, j-1 \tag{11.14} \end{align}\] 下求\(\boldsymbol\gamma^T K \boldsymbol\delta\)的最大值的问题。
先求约束(11.9)—(11.11)下\(\boldsymbol\gamma^T K \boldsymbol\delta\)的最大值。 后面将指出，在约束(11.9)—(11.11)下求得的\(\boldsymbol\gamma^T K \boldsymbol\delta\) 最大值点也满足约束(11.12)—(11.14)。
先固定\(\boldsymbol\gamma\), 求满足\(\| \boldsymbol\delta \| = 1\)的\(\boldsymbol\delta\)使\(\boldsymbol\gamma^T K \boldsymbol\delta\)最大。
如前，应取 \[\begin{aligned} \boldsymbol\delta = \frac{K^T \boldsymbol\gamma}{\| K^T \boldsymbol\gamma \|}, \end{aligned}\] 这时最大值为 \[\begin{aligned} \left( \boldsymbol\gamma^T K K^T \boldsymbol\gamma \right)^{1/2}, \end{aligned}\] 只要在约束 \[\begin{aligned} & \| \boldsymbol\gamma \| = 1, \\ & \boldsymbol\gamma^T \boldsymbol\gamma_i = 0, \ i=1,2,\dots, j-1 \end{aligned}\] 下求\(\boldsymbol\gamma^T K K^T \boldsymbol\gamma\)的最大值。
由\(K\)的奇异值分解可知 \[\begin{aligned} K K^T = \sum_{\ell=1}^r \lambda_{\ell}^2 \boldsymbol\gamma_{\ell} \boldsymbol\gamma_{\ell}^T, \end{aligned}\] 于是 \[\begin{aligned} \boldsymbol\gamma^T K K^T \boldsymbol\gamma =& \sum_{\ell=1}^r \lambda_{\ell}^2 ( \boldsymbol\gamma^T \boldsymbol\gamma_{\ell}) (\boldsymbol\gamma_{\ell}^T \boldsymbol\gamma) \\ =& \sum_{\ell=j}^r \lambda_{\ell}^2 ( \boldsymbol\gamma^T \boldsymbol\gamma_{\ell}) (\boldsymbol\gamma_{\ell}^T \boldsymbol\gamma) \\ =& \boldsymbol\gamma^T \left( \sum_{\ell=j}^r \lambda_{\ell}^2 \boldsymbol\gamma_{\ell} \boldsymbol\gamma_{\ell}^T \right) \boldsymbol\gamma \end{aligned}\] 括号中的矩阵是半正定矩阵，最大特征值为\(\lambda_j^2\)， 在约束\(\| \boldsymbol\gamma \| = 1\)下的最大值点为\(\boldsymbol\gamma = \boldsymbol\gamma_j\)， 这时\(\boldsymbol\gamma\)也满足约束(11.11)。
这时，需取 \[\begin{aligned} \boldsymbol\delta = \frac{K^T \boldsymbol\gamma_j}{\| K^T \boldsymbol\gamma_j \|}, \end{aligned}\] 由前面关于\(K K^T\)和\(K^T K\)的特征向量对应关系的讨论可知\(\boldsymbol\delta = \boldsymbol\delta_j\)。
所以， 当\(\boldsymbol\gamma = \boldsymbol\gamma_j\), \(\boldsymbol\delta=\boldsymbol\delta_j\), \(\boldsymbol a = \boldsymbol a_j = \Sigma_{11}^{-1/2} \boldsymbol\gamma_j\), \(\boldsymbol b = \boldsymbol b_j = \Sigma_{22}^{-1/2} \boldsymbol\delta_j\) 时\(\rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y)\)达到最大值\(\lambda_j\)。
以上最大值是在约束(11.9)—(11.11)下求得的。 来验证这样的取法也满足约束(11.12)—(11.14)。
对约束(11.12)即\(\gamma^T K \boldsymbol\delta_i = 0\), \(i=1,2,\dots, j-1\)条件， 取\(\boldsymbol\gamma = \boldsymbol\gamma_j\)时，由\(K\)的奇异值分解可知 \[\begin{aligned} \boldsymbol\gamma_j^T K \boldsymbol\delta_i =& \sum_{\ell=1}^r \lambda_{\ell} \boldsymbol\gamma_j^T \boldsymbol\gamma_{\ell} \boldsymbol\delta_{\ell}^T \boldsymbol\delta_i \\ =& 0 \quad(\text{只有} j=\ell=i \text{时才可能有非零项}) \end{aligned}\]
对约束(11.13)即\(\boldsymbol\delta^T \boldsymbol\delta_i = 0\), \(i=1,2,\dots, j-1\), 取\(\boldsymbol\delta = \boldsymbol\delta_j\)时由\(\Delta^T \Delta = I_r\)即知约束成立。
对约束(11.14)即\(\boldsymbol\delta^T K^T \boldsymbol\gamma_i = 0\), \(i=1,2,\dots, j-1\)， 可以类似对约束(11.12)的证明那样证明\(\boldsymbol\delta=\boldsymbol\delta_j\)时约束满足。
所以，\(\boldsymbol a_j = \Sigma_{11}^{-1/2} \boldsymbol\gamma_j\), \(\boldsymbol b_j = \Sigma_{22}^{-1/2} \boldsymbol\delta_j\) 是在约束条件(11.9)—(11.14)下使得\(\rho(\boldsymbol a^T \boldsymbol X, \boldsymbol b^T \boldsymbol Y)\)最大的解， 最大值是\(K\)的第\(j\)个奇异值\(\lambda_j\)。 \(U_j = \boldsymbol a_j^T \boldsymbol X\), \(V_j = \boldsymbol b_j^T \boldsymbol Y\)称为第\(j\)对典型变量， 其相关系数\(\lambda_j\)称为第\(j\)典型相关系数。
11.2.3 总体典型相关性质
- \(\text{Var}(U_j) = \text{Var}(V_j) = 1\), \(j=1,2, \dots, r\);
- \(U_1, U_2, \dots, U_r\)互不相关； \(V_1, V_2, \dots, V_r\)互不相关；
- 对\(i \neq j\), \(U_i\)与\(V_j\)不相关;
- \(\rho(U_j, V_j) = \text{Cov}(U_j, V_j) = \lambda_j\), \(\lambda_j\)是\(K=\Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2}\)的第\(j\)个奇异值。
- \((U_1, V_1)\)是所有\(\boldsymbol a^T \boldsymbol X\)与\(\boldsymbol b^T \boldsymbol Y\) 这样的线性组合中相关系数最大的；
- \((U_j, V_j)\)(\(2 \leq j \leq r\))是在\((U_j, V_j)\) 与\(U_1, \dots, U_{j-1}, V_1, \dots, V_{j-1}\) 不相关的前提下， 在所有\(\boldsymbol a^T \boldsymbol X\)与\(\boldsymbol b^T \boldsymbol Y\)这样的线性组合中找到的相关系数最大的。
线性变换不变性：
设\(A, B\)为满秩矩阵，做变换 \(\boldsymbol\xi=A \boldsymbol X + \boldsymbol\mu\), \(\boldsymbol\eta = B \boldsymbol Y + \boldsymbol\beta\), 则\(\boldsymbol\xi\)与\(\boldsymbol\eta\)的典型相关系数不变。
\(\boldsymbol X\), \(\boldsymbol Y\)的第\(j\)对典型变量是 \(\boldsymbol a_j^T \boldsymbol X\)和\(\boldsymbol b_j^T \boldsymbol Y\)。 以\(\boldsymbol X = A^{-1}(\boldsymbol\xi - \boldsymbol\mu)\), \(\boldsymbol Y = B^{-1}(\boldsymbol\eta - \boldsymbol\beta)\)代入， 即\((A^{-T} \boldsymbol a_j)^T (\boldsymbol\xi - \boldsymbol\mu)\) 和\((B^{-T} \boldsymbol b_j)^T (\boldsymbol\eta - \boldsymbol\beta)\)， 这里\(A^{-T} = (A^{-1})^T = (A^T)^{-1}\)。
由于方差、协方差与均值无关， 所以\(\boldsymbol\xi, \boldsymbol\eta\)的第\(j\)对典型变量可取为 \((A^{-T} \boldsymbol a_j)^T \boldsymbol\xi =\boldsymbol a_j^T A^{-1} \boldsymbol\xi\) 和\((B^{-T} \boldsymbol b_j)^T \boldsymbol\eta = \boldsymbol b_j^T B^{-1} \boldsymbol\eta\)。
线性变换不变性的证明：
记\(\tilde{\boldsymbol a}_j = A^{-T} \boldsymbol a_j\), \(\tilde{\boldsymbol b}_j = B^{-T} \boldsymbol b_j\), 来证明\(\tilde{\boldsymbol a}_j^T \boldsymbol\xi\) 和\(\tilde{\boldsymbol b}_j^T \boldsymbol\eta\) 是\(\boldsymbol\xi\)和\(\boldsymbol\eta\)的第\(j\)对典型变量。
显然\(\tilde{\boldsymbol a}_j^T \boldsymbol\xi\) 和\(\tilde{\boldsymbol b}_j^T \boldsymbol\eta\)相关系数仍为\(\lambda_j\)。
注意 \[ \text{Var}\left[ \begin{pmatrix} \boldsymbol \xi \\ \boldsymbol \eta \end{pmatrix}\right] = \begin{pmatrix} A \Sigma_{11} A^T & A \Sigma_{12} B^T \\ B \Sigma_{21} A^T & B \Sigma_{22} B^T \end{pmatrix} . \] 令 \[\begin{aligned} \tilde K =& (A \Sigma_{11} A^T)^{-1/2} A \Sigma_{12} B^T (B \Sigma_{22} B^T)^{-1/2} \\ =& (A \Sigma_{11} A^T)^{-1/2} A \Sigma_{11}^{1/2} \Sigma_{11}^{-1/2} \Sigma_{12} \Sigma_{22}^{-1/2} \Sigma_{}^{1/2} B^T (B \Sigma_{22} B^T)^{-1/2} \\ =& (A \Sigma_{11} A^T)^{-1/2} A \Sigma_{11}^{1/2} K \Sigma_{22}^{1/2} B^T (B \Sigma_{22} B^T)^{-1/2} \\ =& \sum_{i=1}^r \lambda_i (A \Sigma_{11} A^T)^{-1/2} A \Sigma_{11}^{1/2} \boldsymbol\gamma_i \boldsymbol\delta_i^T \Sigma_{22}^{1/2} B^T (B \Sigma_{22} B^T)^{-1/2} \\ =& \sum_{i=1}^r \lambda_i \tilde{\boldsymbol\gamma_i} \tilde{\boldsymbol\delta_i}^T, \end{aligned}\] 容易证明\(\tilde{\boldsymbol\gamma}_i^T \tilde{\boldsymbol\gamma}_i = 1\), \(\tilde{\boldsymbol\delta}_i^T \tilde{\boldsymbol\delta}_i = 1\), \(\tilde{\boldsymbol\gamma}_i^T \tilde{\boldsymbol\gamma}_j = 0\)(\(i\neq j\)), \(\tilde{\boldsymbol\delta}_i^T \tilde{\boldsymbol\delta}_j = 0\)， 所以上式为\(\tilde K\)的奇异值分解。 因此应取\(\boldsymbol\xi\)的系数为 \[\begin{aligned} \tilde{\boldsymbol a}_i =& (A \Sigma_{11} A^T)^{-1/2} \tilde{\boldsymbol\gamma}_i \\ =& (A \Sigma_{11} A^T)^{-1/2} (A \Sigma_{11} A^T)^{-1/2} A \Sigma_{11}^{1/2} \boldsymbol\gamma_i \\ =& A^{-T} \boldsymbol a_i , \end{aligned}\] 类似地有\(\boldsymbol\eta\)的系数为\(\tilde{\boldsymbol b}_i = B^{-T} \boldsymbol b_i\)。
特别地， 令\(\boldsymbol{\xi} = \Sigma_{11}^{-\frac{1}{2}} (\boldsymbol{X} - E\boldsymbol{X})\), \(\boldsymbol{\eta} = \Sigma_{22}^{-\frac{1}{2}} (\boldsymbol{Y} - E\boldsymbol{Y})\), 则\(\text{Var}(\boldsymbol{\xi}) = I_p\), \(\text{Var}(\boldsymbol{\eta}) = I_q\)， 而\(K = \text{Cov}(\boldsymbol{\xi}, \boldsymbol{\eta})\)。 所以\(K\)是将\(\boldsymbol{X}\)和\(\boldsymbol{Y}\)分别进行严格标准化后的相关阵。
11.3 样本典型相关
假设得到了\(\boldsymbol X\)和\(\boldsymbol Y\)的\(n\)次独立观测数据。 从数据可以估计\(\boldsymbol X\)的方差阵\(\Sigma_{11}\), \(\boldsymbol Y\)的方差阵\(\Sigma_{22}\), 以及\(\boldsymbol X\)与\(\boldsymbol Y\)的协方差阵\(\Sigma_{12}\)。
如果从估计的方差和协方差去计算典型相关， 可能出现特征值不小于1的现象， 所以通常把每个分量的\(n\)个数据进行标准化， 然后基于\(\boldsymbol X\)的相关阵估计\(R_{11}\)， \(\boldsymbol Y\)的相关阵估计\(R_{22}\) 和\(\boldsymbol X\)与\(\boldsymbol Y\)的相关系数阵的估计\(R_{12}\)来进行典型相关分析。 根据典型相关的线性变换不变性， 理论上与用原始数据的结果是一样的。
在计算中，数据每个分量认为已经标准化。
令 \[\begin{aligned} K =& R_{11}^{-1/2} R_{12} R_{22}^{-1/2} . \end{aligned}\] 求\(K\)的奇异值分解 \[\begin{aligned} K = \sum_{i=1}^r l_i \boldsymbol\gamma_i \boldsymbol\delta_i^T . \end{aligned}\] 由于随机性，矩阵很少严格不满秩， 所以一般有\(r = \min(p,q)\)。 称\(l_1, l_2, \dots, l_r\)为样本典型相关系数。 令 \[\begin{aligned} \hat{\boldsymbol a}_i =& R_{11}^{-1/2} \boldsymbol\gamma_i, \quad \hat{\boldsymbol b}_i = R_{22}^{-1/2} \boldsymbol\delta_i . \end{aligned}\] 设\(\boldsymbol X\)的观测数据标准化后为\(n \times p\)矩阵\(M_X\), \(\boldsymbol Y\)的观测数据标准化后为\(n \times q\)矩阵\(M_Y\)， 令 \[\begin{aligned} \boldsymbol u_i =& M_X \hat{\boldsymbol a}_i, \quad \boldsymbol v_i = M_Y \hat{\boldsymbol b}_i, \ i=1,2,\dots, r, \end{aligned}\] 则\(\boldsymbol u_i\)和\(\boldsymbol v_i\)都是\(n\)维向量， 是第\(i\)对典型变量的得分， 也称为样本典型相关变量。
样本典型相关变量的解释， 与主成分解释类似， 只不过变成了因变量组和自变量组的某些特性之间的关系。 典型相关也有标准化问题， 如果因变量组内、自变量组内的方差变化很大， 可能也需要对每个变量进行标准化变换。
11.4 典型相关系数的显著性检验
典型相关系数\(\lambda_i\)的个数\(r\)实际是\(\Sigma_{12}\)的秩。 当\(\Sigma_{12}=0\)即\(\boldsymbol X\)与\(\boldsymbol Y\)不相关时， 典型相关系数不存在。
从样本中估计协方差阵或者相关系数阵时， 由于随机性， 一般不会严格不满秩， 需要用假设检验方法确定\(r\)的值。 对假设 \[\begin{aligned} H_0: \lambda_1 = \dots = \lambda_p = 0 \Longleftrightarrow H_1: \lambda_1 \neq 0 \end{aligned}\] 可以采用Bartlett大样本卡方统计量检验法。 检验统计量为 \[\begin{aligned} Q_1 = - \left[ n-1 - \frac12 (p+q+1) \right] \ln\Lambda_1 \stackrel{H_0}{\sim} \chi^2(pq) \end{aligned}\] 其中\(\Lambda_j = \prod_{i=j}^p (1 - \lambda_i^2)\)。 设\(Q_1\)的值为\(c\), 则检验的p值为\(P(\chi^2(pq) > c)\)。
为检验 \[\begin{aligned} H_0: \lambda_j = \dots = \lambda_p = 0 \Longleftrightarrow H_1: \lambda_j \neq 0 \end{aligned}\] 使用检验统计量 \[\begin{aligned} Q_j = - \left[ n - j - \frac12 (p+q+1) \right] \ln\Lambda_j \stackrel{H_0}{\sim} \chi^2((p-j+1)(q-j+1)) \end{aligned}\] 设\(Q_j\)的值为\(c\), 则检验的p值为\(P(\chi^2((p-j+1)(q-j+1)) > c)\)。
可以用这样的检验方法决定最好保留多少对典型变量， 即确定\(r\)的值。 保留的典型变量个数越少越好， 最好能只保留一对典型变量。 如果一对也没有，说明两组变量之间不存在线性相关关系。
11.5 案例：家庭长子、次子头部测量
数据集headsize中包含了25个家庭的长子、次子的头高、宽的测量值。 可以用典型相关分析方法研究长子与次子的头高、宽的关系。
| head1 | breadth1 | head2 | breadth2 |
|---|---|---|---|
| 191 | 155 | 179 | 145 |
| 195 | 149 | 201 | 152 |
| 181 | 148 | 185 | 149 |
| 183 | 153 | 188 | 149 |
| 176 | 144 | 171 | 142 |
计算4个变量的相关系数矩阵：
| head1 | breadth1 | head2 | breadth2 | |
|---|---|---|---|---|
| head1 | 1.00 | 0.73 | 0.71 | 0.70 |
| breadth1 | 0.73 | 1.00 | 0.69 | 0.71 |
| head2 | 0.71 | 0.69 | 1.00 | 0.84 |
| breadth2 | 0.70 | 0.71 | 0.84 | 1.00 |
用stats::cancor()进行典型相关分析：
## $cor
## [1] 0.7885079 0.0537397
##
## $xcoef
## [,1] [,2]
## head1 0.1127152 -0.2789099
## breadth1 0.1064583 0.2813576
##
## $ycoef
## [,1] [,2]
## head2 0.1029701 -0.3610078
## breadth2 0.1098775 0.3589657
##
## $xcenter
## head1 breadth1
## 1.243450e-16 -6.049328e-16
##
## $ycenter
## head2 breadth2
## -3.380629e-16 -1.359746e-15第一对典型变量可以写成：
\[\begin{aligned} U_1 =& 0.11 (X_1 - \bar X_1) / S_1 + 0.11 (X_2 - \bar X_2) / S_2, \\ V_1 =& 0.10 (X_3 - \bar X_3) / S_3 + 0.11 (X_4 - \bar X_4) / S_4, \end{aligned}\]
这分别度量了长子、次子头部的大小， 第一典型相关系数为\(0.7885\)。 其中\(\bar X_j\)和\(S_j\)分别表示第\(j\)个变量的样本均值和样本标准差。
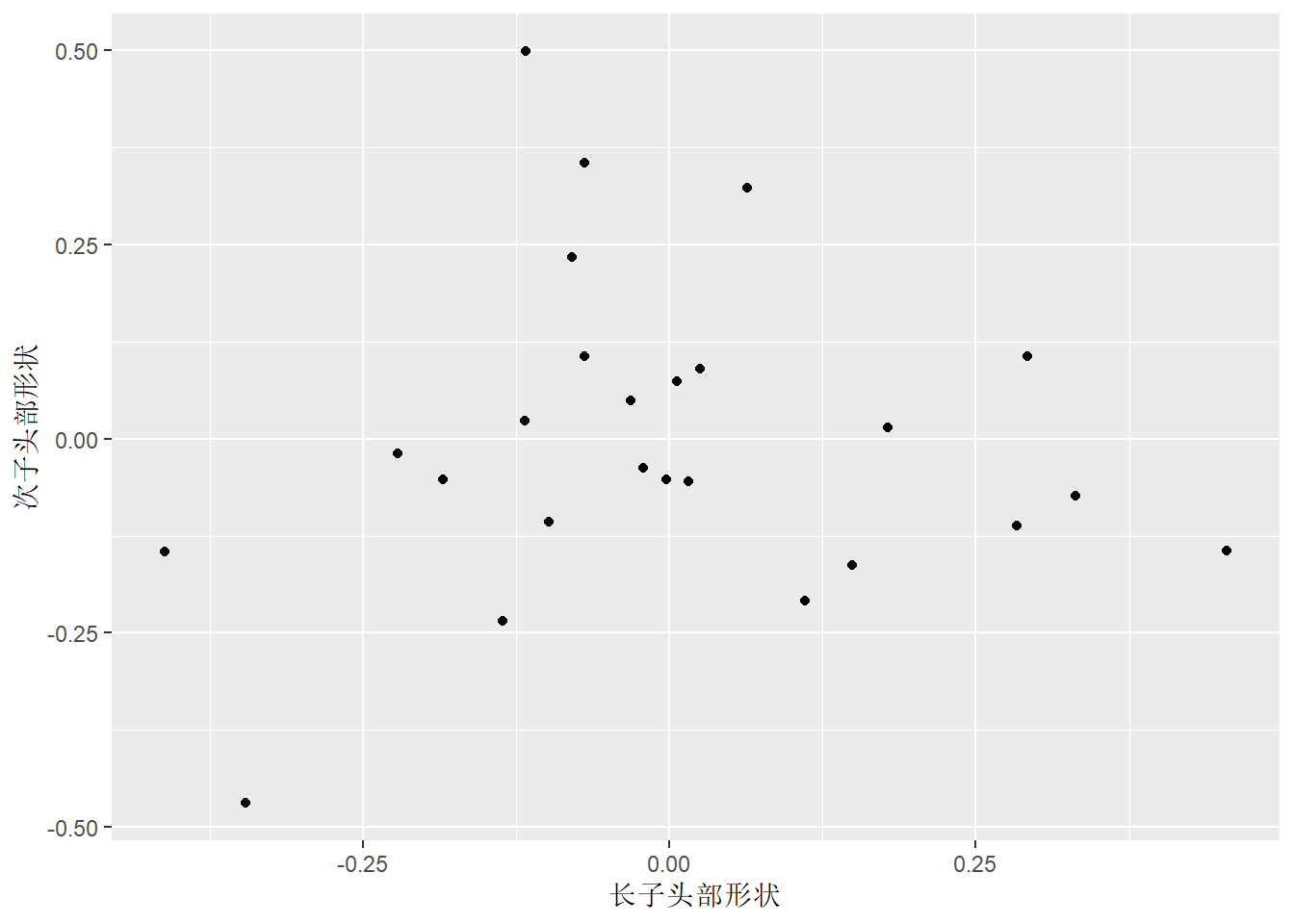
第二对典型变量可以写成：
\[\begin{aligned} U_2 =& -0.28 (X_1 - \bar X_1) / S_1 + 0.28 (X_2 - \bar X_2) / S_2, \\ V_2 =& -0.36 (X_3 - \bar X_3) / S_3 + 0.36 (X_4 - \bar X_4) / S_4, \end{aligned}\]
这分别度量了长子、次子头部高、宽差异， 可以理解为头部形状。 第二典型相关系数为\(0.0537\)， 所以长子、次子的头部测量值的关系主要体现在头部大小的相关性， 此相关性较强（系数为\(0.7885\)）。
第一典型变量之间的散点图：
mat_hs <- as.matrix(ds)
d_cc_hs <- tibble(
u1 = mat_hs[,1:2] %*% cc.hs$xcoef[,1],
v1 = mat_hs[,3:4] %*% cc.hs$ycoef[,1],
u2 = mat_hs[,1:2] %*% cc.hs$xcoef[,2],
v2 = mat_hs[,3:4] %*% cc.hs$ycoef[,2]
)
ggplot(d_cc_hs, aes(x = u1, y = v1)) +
geom_point() +
labs(x = "长子头部大小", y = "次子头部大小")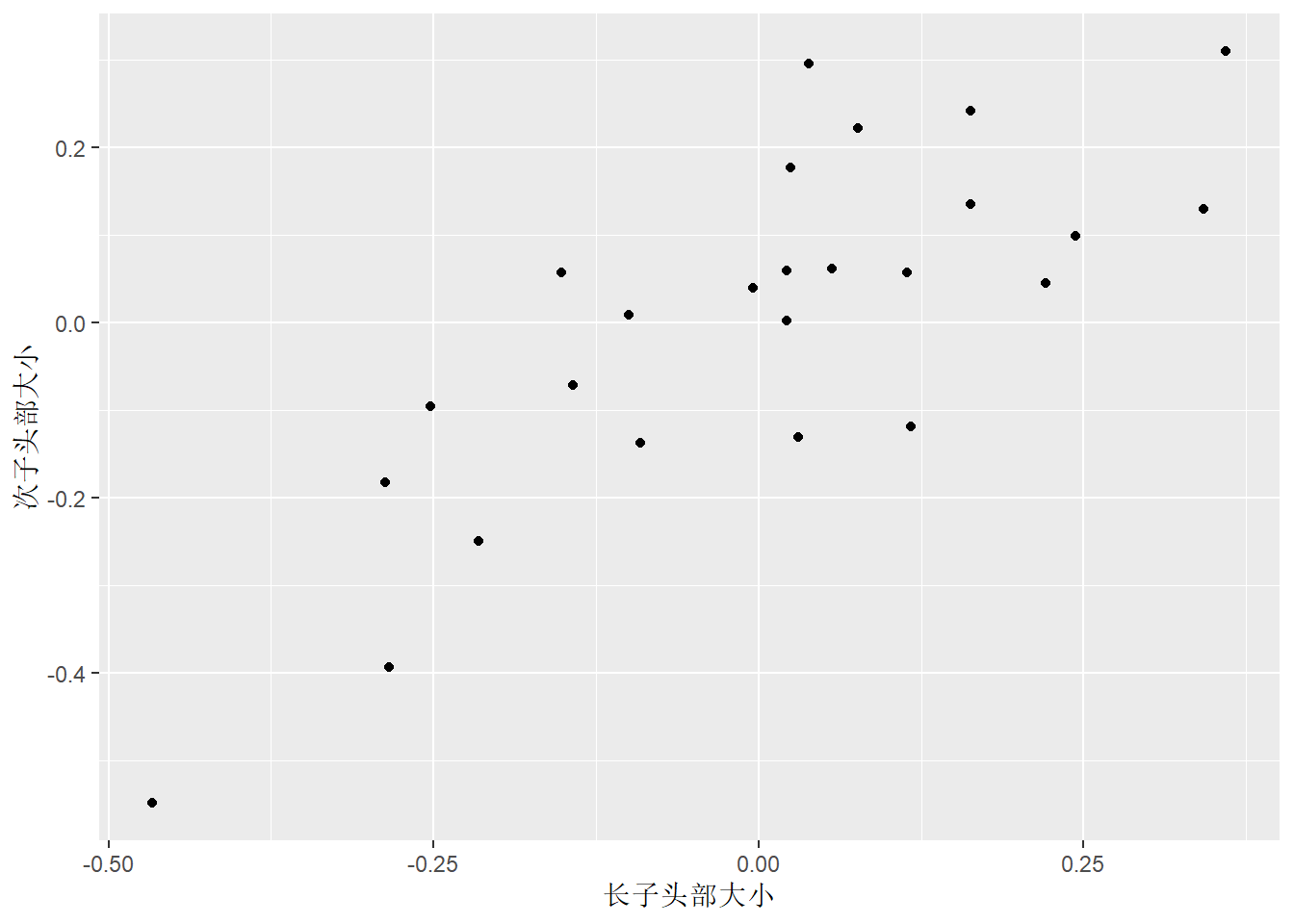
第二典型变量之间的散点图：
11.6 案例：科技投入与产出的典型相关分析
11.6.1 数据和基本概括
科技产出变量:
- 发表科技论文篇数\(Y_1\),
- 专利申请受理数\(Y_2\),
- 发明专利件数\(Y_3\)。
科技投入变量:
- 研发人员全时当量（单位：万人年）\(X_1\),
- 研发经费支出\(X_2\)（单位：亿元）,
- 政府资金\(X_3\)（单位：亿元），
- 企业资金\(X_4\)（单位：亿元）。
研究科技投入与产出的关系。 仅分析相关性，而非因果关系。
techProduct <- readr::read_csv(
"data/科技投入产出.csv",
locale=locale(encoding = "GB18030"),
show_col_types = FALSE)
d <- techProduct数据已读入到techProduct数据框，变量为
year, X1-X4, Y1-Y3。
数据如下：
| 年份 | R&D人员全时当量 | R&D经费支出 | 政府资金 | 企业资金 | 发表科技论文 | 专利申请受理数 | 发明专利 |
|---|---|---|---|---|---|---|---|
| 2003 | 20.4000 | 399.000 | 320.300 | 20.8000 | 97500 | 4836 | 1393 |
| 2004 | 20.3000 | 431.700 | 344.300 | 22.4000 | 104699 | 5464 | 1972 |
| 2005 | 21.5000 | 513.100 | 424.700 | 17.6000 | 109995 | 6814 | 2088 |
| 2006 | 23.1000 | 567.300 | 481.200 | 17.3000 | 118211 | 8026 | 2191 |
| 2007 | 25.5000 | 687.900 | 592.900 | 26.2000 | 126527 | 9802 | 2467 |
| 2008 | 26.0000 | 811.300 | 699.700 | 28.2000 | 132072 | 12536 | 3102 |
| 2009 | 27.7000 | 996.000 | 849.500 | 29.8000 | 138119 | 15773 | 4077 |
| 2010 | 29.3000 | 1186.400 | 1036.500 | 34.2000 | 140818 | 19192 | 5249 |
| 2011 | 31.5679 | 1306.742 | 1106.115 | 39.8776 | 148039 | 24059 | 7862 |
| 2012 | 34.3978 | 1548.933 | 1292.706 | 47.4115 | 158647 | 30418 | 10935 |
计算7个变量的相关系数阵:
| R&D人员全时当量 | R&D经费支出 | 政府资金 | 企业资金 | 发表科技论文 | 专利申请受理数 | 发明专利 | |
|---|---|---|---|---|---|---|---|
| R&D人员全时当量 | 1.00 | 0.99 | 0.99 | 0.95 | 0.98 | 0.98 | 0.94 |
| R&D经费支出 | 0.99 | 1.00 | 1.00 | 0.96 | 0.97 | 0.99 | 0.95 |
| 政府资金 | 0.99 | 1.00 | 1.00 | 0.95 | 0.97 | 0.99 | 0.94 |
| 企业资金 | 0.95 | 0.96 | 0.95 | 1.00 | 0.90 | 0.97 | 0.95 |
| 发表科技论文 | 0.98 | 0.97 | 0.97 | 0.90 | 1.00 | 0.95 | 0.88 |
| 专利申请受理数 | 0.98 | 0.99 | 0.99 | 0.97 | 0.95 | 1.00 | 0.98 |
| 发明专利 | 0.94 | 0.95 | 0.94 | 0.95 | 0.88 | 0.98 | 1.00 |
所有的相关系数都很大。
相关系数图形：
## Warning: package 'ggcorrplot' was built under R version 4.2.2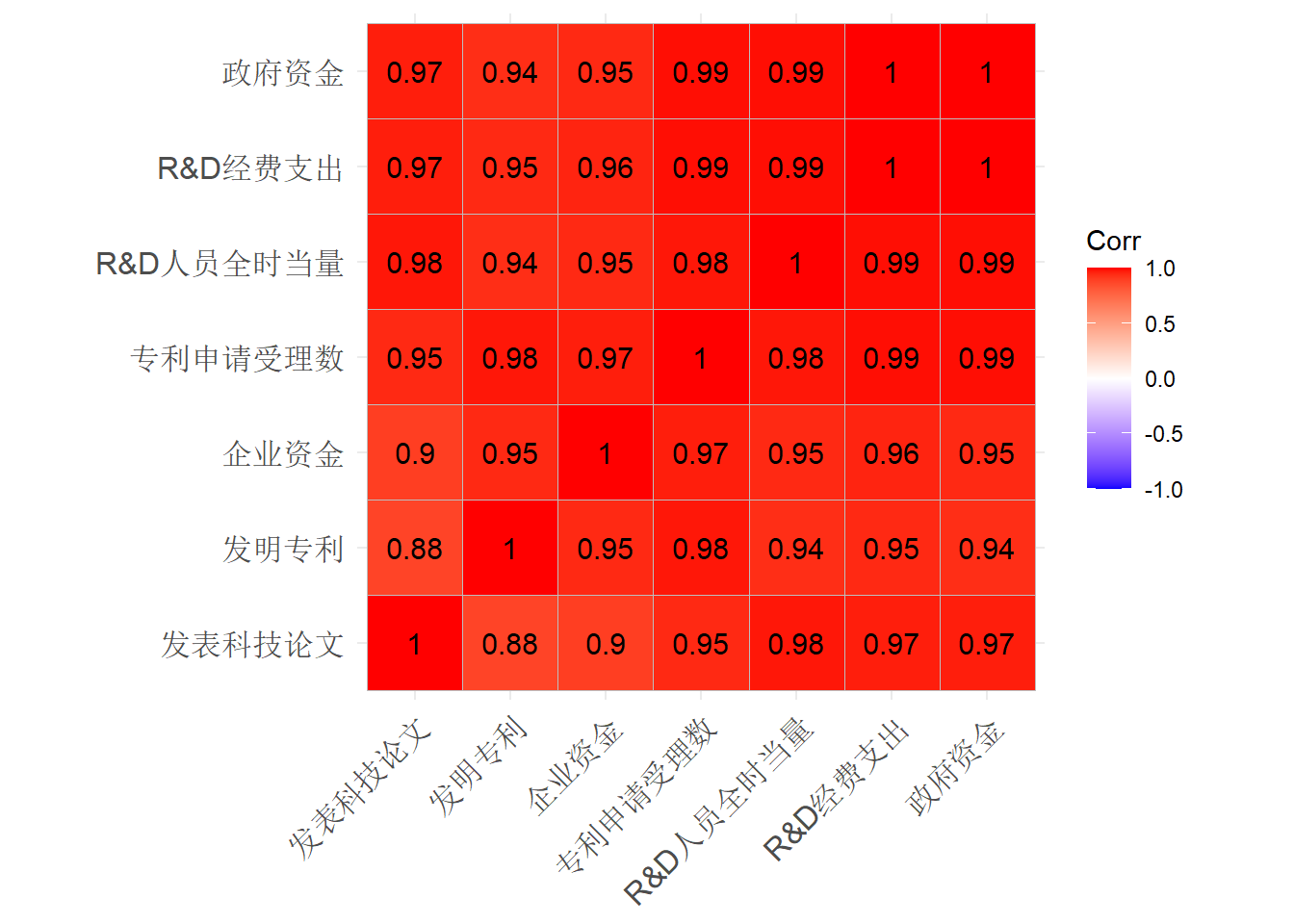
变量之间具有强相关性， 这很可能是由于时间序列效应， 即这些变量都是与经济增长强相关的， 如果扣除时间序列增长因素， 相关性可能就没有这么强。 这也说明了我们分析的仅是相关性而不是因果性。
论文篇数的时间序列图：
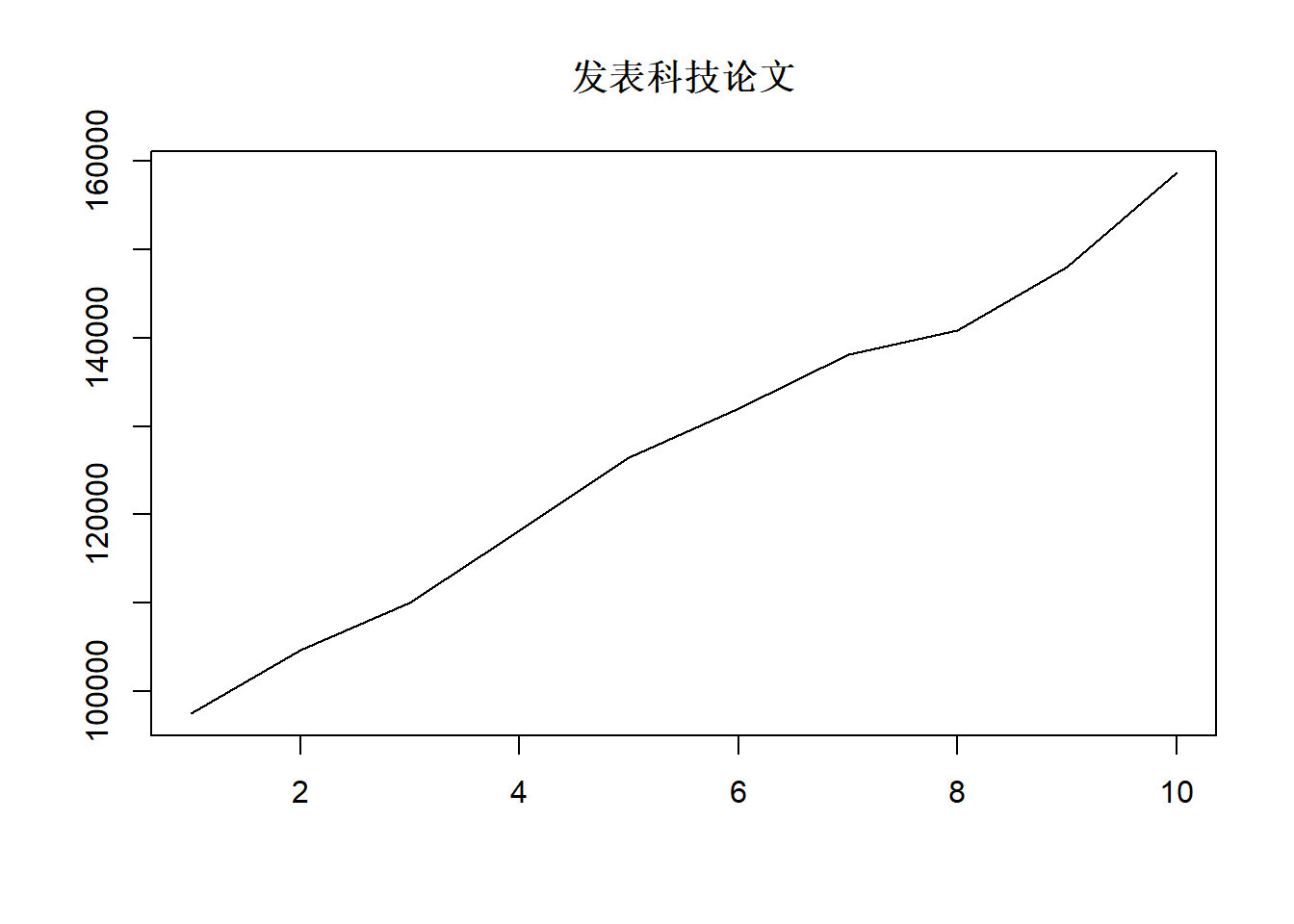
可见数据可能有很强的序列相关性， 可能有单位根， 这时计算的相关系数是没有严格定义的。
为了解决这个问题， 我们将各个变量改成年增量， 研究年增量之间的关系：
| R.D人员全时当量 | R.D经费支出 | 政府资金 | 企业资金 | 发表科技论文 | 专利申请受理数 | 发明专利 |
|---|---|---|---|---|---|---|
| -0.10 | 32.70 | 24.00 | 1.60 | 7199 | 628 | 579 |
| 1.20 | 81.40 | 80.40 | -4.80 | 5296 | 1350 | 116 |
| 1.60 | 54.20 | 56.50 | -0.30 | 8216 | 1212 | 103 |
| 2.40 | 120.60 | 111.70 | 8.90 | 8316 | 1776 | 276 |
| 0.50 | 123.40 | 106.80 | 2.00 | 5545 | 2734 | 635 |
| 1.70 | 184.70 | 149.80 | 1.60 | 6047 | 3237 | 975 |
| 1.60 | 190.40 | 187.00 | 4.40 | 2699 | 3419 | 1172 |
| 2.27 | 120.34 | 69.62 | 5.68 | 7221 | 4867 | 2613 |
| 2.83 | 242.19 | 186.59 | 7.53 | 10608 | 6359 | 3073 |
增量的相关系数阵：
| R.D人员全时当量 | R.D经费支出 | 政府资金 | 企业资金 | 发表科技论文 | 专利申请受理数 | 发明专利 | |
|---|---|---|---|---|---|---|---|
| R.D人员全时当量 | 1.00 | 0.64 | 0.55 | 0.60 | 0.45 | 0.68 | 0.57 |
| R.D经费支出 | 0.64 | 1.00 | 0.95 | 0.53 | 0.05 | 0.84 | 0.66 |
| 政府资金 | 0.55 | 0.95 | 1.00 | 0.43 | -0.13 | 0.67 | 0.44 |
| 企业资金 | 0.60 | 0.53 | 0.43 | 1.00 | 0.40 | 0.57 | 0.57 |
| 发表科技论文 | 0.45 | 0.05 | -0.13 | 0.40 | 1.00 | 0.27 | 0.37 |
| 专利申请受理数 | 0.68 | 0.84 | 0.67 | 0.57 | 0.27 | 1.00 | 0.94 |
| 发明专利 | 0.57 | 0.66 | 0.44 | 0.57 | 0.37 | 0.94 | 1.00 |
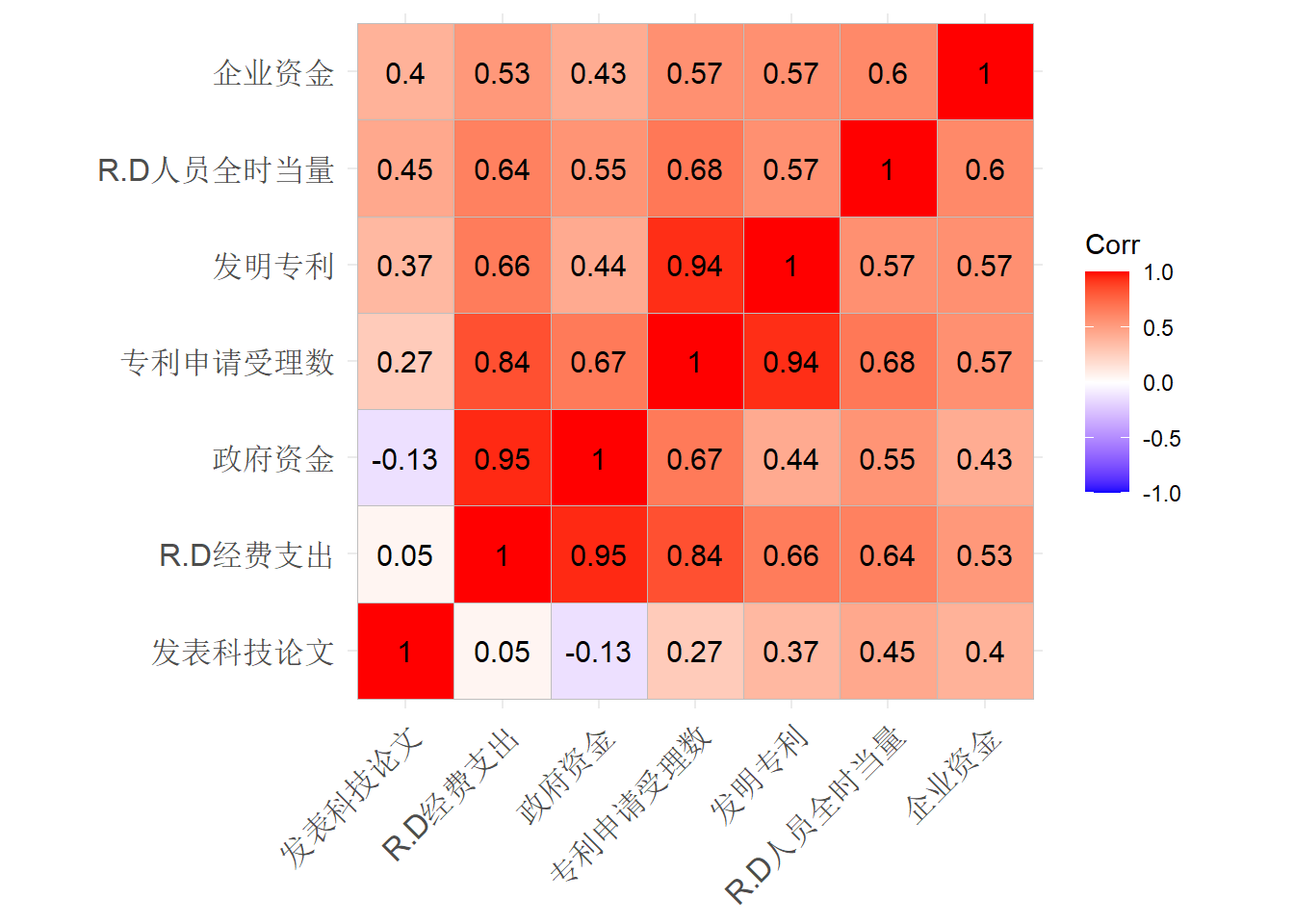
这些增量的相关系数已经没有那么接近于1。
11.6.2 用stats::cancor()计算典型相关
计算时对每个变量进行标准化。
## ==== 典型相关:## $cor
## [1] 0.9667595 0.8159978 0.4611396
##
## $xcoef
## [,1] [,2] [,3] [,4]
## R.D人员全时当量 0.074275186 0.01017197 -0.46693840 0.1779072
## R.D经费支出 0.724418960 0.57644286 0.79913200 0.5941000
## 政府资金 -0.477622788 -0.85388795 -0.50646962 -0.5575717
## 企业资金 -0.006927141 0.14769849 0.01215391 -0.4386271
##
## $ycoef
## [,1] [,2] [,3]
## 发表科技论文 0.0524833 0.1653323 -0.3506258
## 专利申请受理数 0.4698818 -0.7761834 -0.5769901
## 发明专利 -0.1437149 0.7858189 0.7744999
##
## $xcenter
## R.D人员全时当量 R.D经费支出 政府资金 企业资金
## 4.934325e-17 4.471732e-17 -6.630499e-17 -2.158767e-17
##
## $ycenter
## 发表科技论文 专利申请受理数 发明专利
## -7.709882e-17 6.553400e-17 4.009139e-17前两对典型相关系数都很大。
作为降维结果的各个典型变量的含义没有很好的解释。
11.6.3 用CCA包和CCP计算典型相关分析
## 载入需要的程辑包：fda## Warning: 程辑包'fda'是用R版本4.1.2 来建造的## 载入需要的程辑包：splines## 载入需要的程辑包：Matrix## Warning: 程辑包'Matrix'是用R版本4.1.2 来建造的## 载入需要的程辑包：fds## 载入需要的程辑包：rainbow## 载入需要的程辑包：MASS## Warning: 程辑包'MASS'是用R版本4.1.2 来建造的## 载入需要的程辑包：pcaPP## 载入需要的程辑包：RCurl## 载入需要的程辑包：deSolve##
## 载入程辑包：'fda'## The following object is masked from 'package:graphics':
##
## matplot## 载入需要的程辑包：fields## Warning: 程辑包'fields'是用R版本4.1.2 来建造的## 载入需要的程辑包：spam## Warning: 程辑包'spam'是用R版本4.1.2 来建造的## Spam version 2.8-0 (2022-01-05) is loaded.
## Type 'help( Spam)' or 'demo( spam)' for a short introduction
## and overview of this package.
## Help for individual functions is also obtained by adding the
## suffix '.spam' to the function name, e.g. 'help( chol.spam)'.##
## 载入程辑包：'spam'## The following object is masked from 'package:Matrix':
##
## det## The following objects are masked from 'package:base':
##
## backsolve, forwardsolve## 载入需要的程辑包：viridis## 载入需要的程辑包：viridisLite##
## Try help(fields) to get started.计算典型相关:
## $cor
## [1] 0.9667595 0.8159978 0.4611396
##
## $names
## $names$Xnames
## [1] "R.D人员全时当量" "R.D经费支出" "政府资金" "企业资金"
##
## $names$Ynames
## [1] "发表科技论文" "专利申请受理数" "发明专利"
##
## $names$ind.names
## NULL
##
##
## $xcoef
## [,1] [,2] [,3]
## R.D人员全时当量 -0.21008195 0.02877069 -1.32070124
## R.D经费支出 -2.04896624 1.63042662 2.26028662
## 政府资金 1.35092125 -2.41515984 -1.43251240
## 企业资金 0.01959291 0.41775442 0.03437646
##
## $ycoef
## [,1] [,2] [,3]
## 发表科技论文 -0.1484452 0.4676304 -0.9917195
## 专利申请受理数 -1.3290264 -2.1953781 -1.6319744
## 发明专利 0.4064872 2.2226314 2.1906165
##
## $scores
## $scores$xscores
## [,1] [,2] [,3]
## [1,] 1.24758559 1.08593445 1.2977193
## [2,] 0.78833209 -0.72610725 -0.4048953
## [3,] 0.97319429 0.09177845 -1.2440306
## [4,] 0.13845044 0.29096414 -1.4868758
## [5,] 0.33738124 -0.18015583 1.3842180
## [6,] -0.76767780 -0.53004000 0.6282203
## [7,] -0.02425211 -1.69021362 0.0507943
## [8,] -0.83372912 1.73886336 -0.2782949
## [9,] -1.85928463 -0.08102370 0.0531446
##
## $scores$yscores
## [,1] [,2] [,3]
## [1,] 1.3681682365 1.69685407 0.77989371
## [2,] 0.8056415399 -0.50178311 0.04923073
## [3,] 0.7059931005 0.24161026 -1.14576363
## [4,] 0.3631058492 -0.04440056 -1.33169762
## [5,] -0.0004236445 -1.00830036 -0.21685592
## [6,] -0.2635584881 -0.79495838 -0.18797789
## [7,] -0.0976377193 -1.30023865 1.53102057
## [8,] -0.8843728749 0.90646459 1.19393161
## [9,] -1.9969159992 0.80475214 -0.67178156
##
## $scores$corr.X.xscores
## [,1] [,2] [,3]
## R.D人员全时当量 -0.7587258 -0.01566518 -0.650265650
## R.D经费支出 -0.8843034 -0.43358937 0.071020148
## 政府资金 -0.7102524 -0.66369524 0.009194226
## 企业资金 -0.6026320 0.25004224 -0.179241725
##
## $scores$corr.Y.xscores
## [,1] [,2] [,3]
## 发表科技论文 -0.3493144 0.56077001 -0.29061782
## 专利申请受理数 -0.9541874 0.01944097 0.07330842
## 发明专利 -0.8689934 0.26835082 0.13355405
##
## $scores$corr.X.yscores
## [,1] [,2] [,3]
## R.D人员全时当量 -0.7335054 -0.01278275 -0.299863250
## R.D经费支出 -0.8549087 -0.35380797 0.032750203
## 政府资金 -0.6866433 -0.54157386 0.004239822
## 企业资金 -0.5826002 0.20403392 -0.082655460
##
## $scores$corr.Y.yscores
## [,1] [,2] [,3]
## 发表科技论文 -0.3613250 0.68722000 -0.6302166
## 专利申请受理数 -0.9869955 0.02382478 0.1589723
## 发明专利 -0.8988723 0.32886219 0.2896174作第一对典型变量的散点图：
plot(cc2$scores$xscores[, 1],
cc2$scores$yscores[, 1],
xlab="自变量第一典型变量",
ylab="因变量第一典型变量",
pch=16, col="red")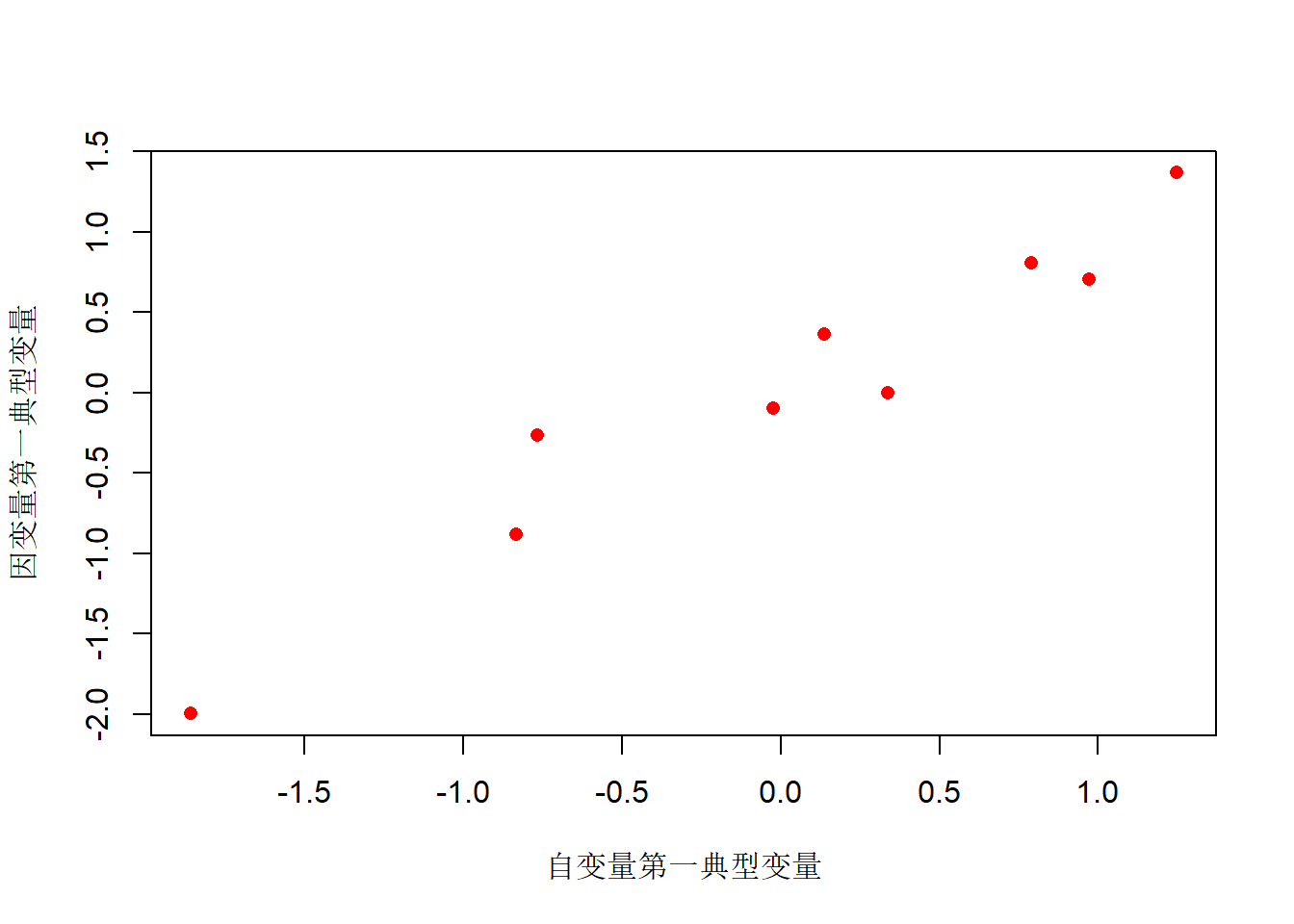
典型相关系数和第一对典型变量得分的样本相关系数：
## [1] 0.9667595 0.8159978 0.4611396## [1] 0.9667595作第二对典型变量的散点图：
xcc1 <- cc2$scores$xscores[, 2]
ycc1 <- cc2$scores$yscores[, 2]
plot(cc2$scores$xscores[, 2],
cc2$scores$yscores[ , 2],
xlab="自变量第二典型变量",
ylab="因变量第二典型变量",
pch=16, col="red")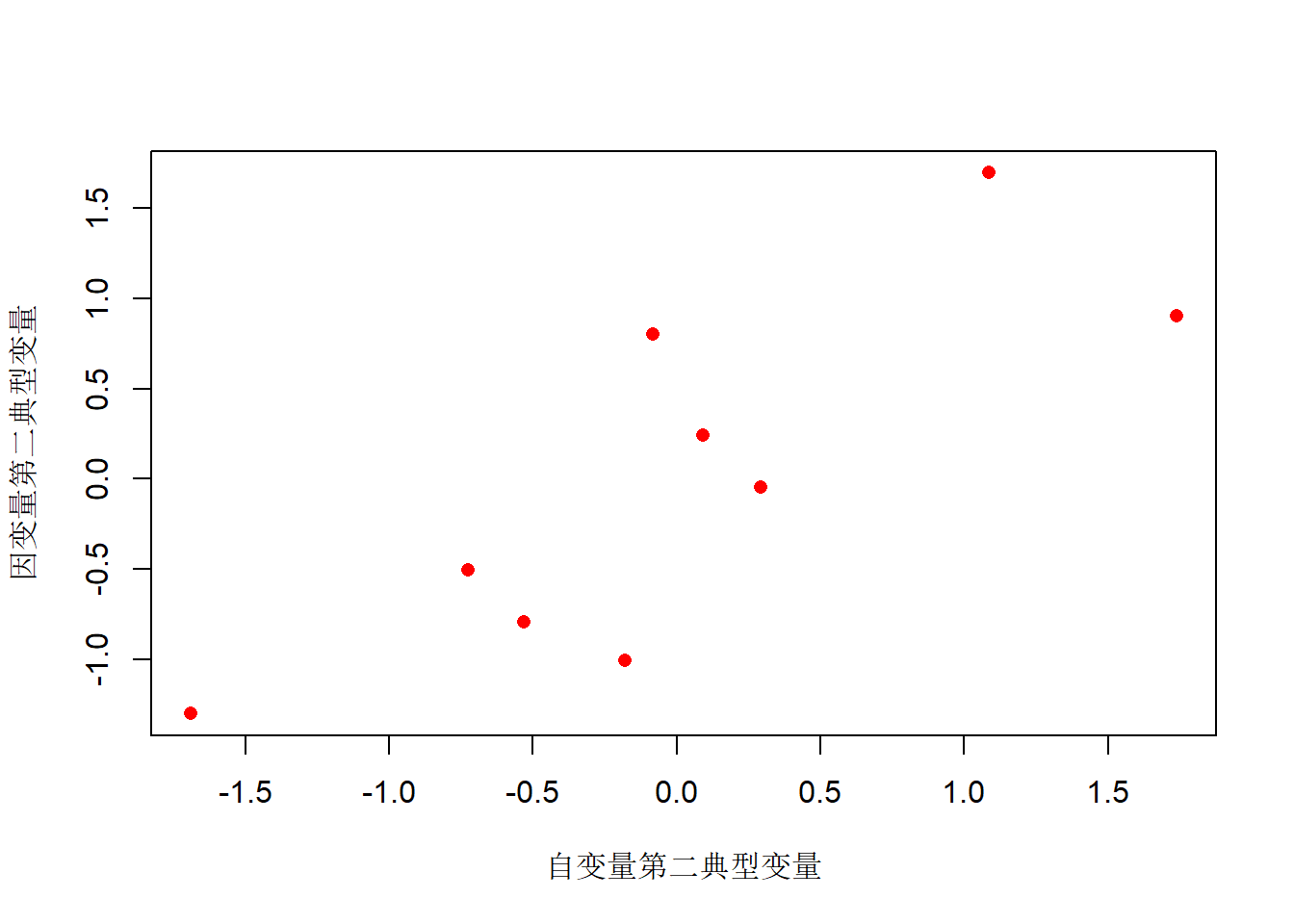
典型相关系数和第二对典型变量得分的样本相关系数：
## [1] 0.9667595 0.8159978 0.4611396## [1] 0.8159978作所有原始变量与前两对典型变量得分的相关系数的散点图， 横坐标是各个原始变量与所属组的第一典型变量的相关系数， 纵坐标是则是与第二典型变量。 自变量为红色，因变量为蓝色。
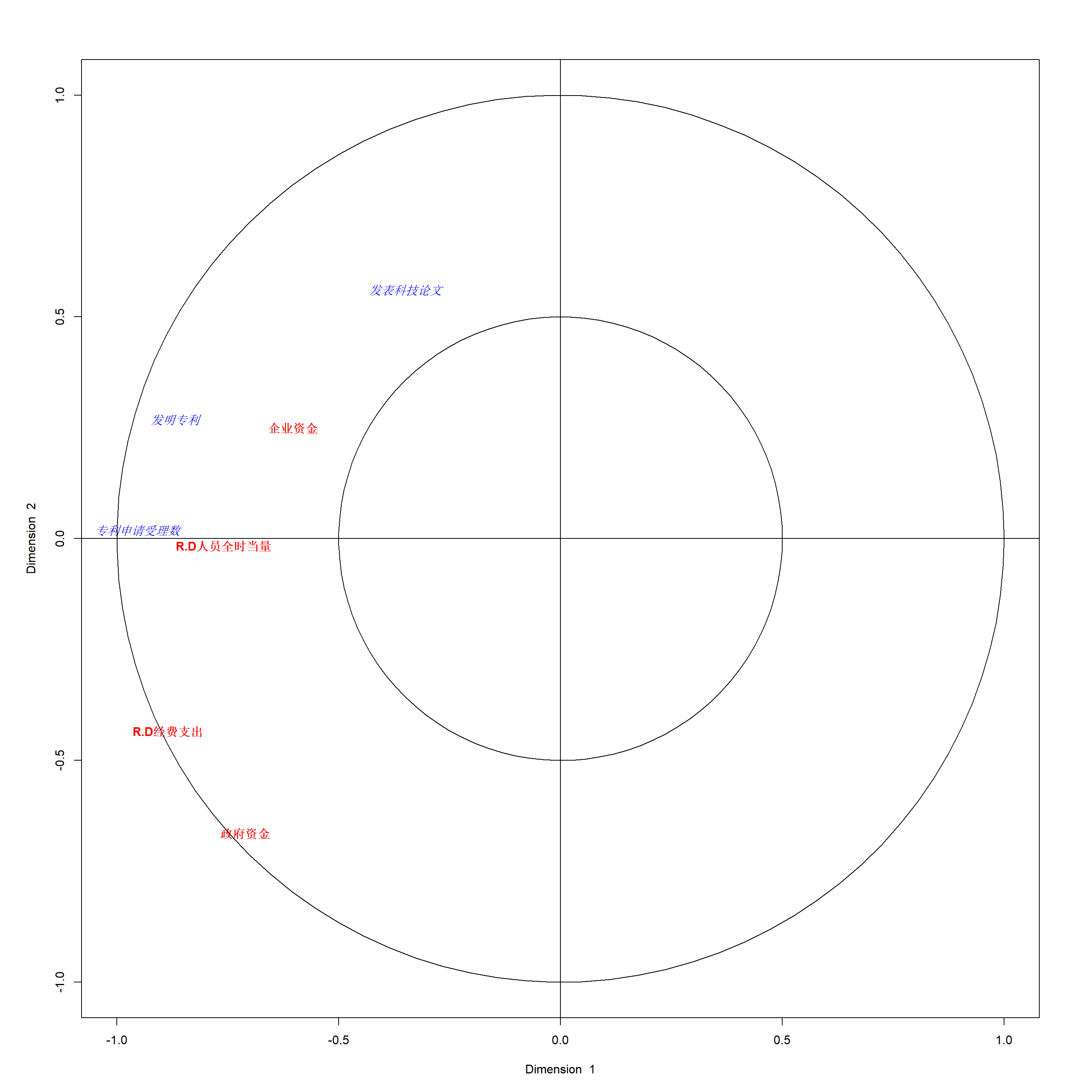
计算作为上图横纵坐标的相关系数：
## [,1] [,2]
## R.D人员全时当量 -0.7587258 -0.01566518
## R.D经费支出 -0.8843034 -0.43358937
## 政府资金 -0.7102524 -0.66369524
## 企业资金 -0.6026320 0.25004224## [,1] [,2]
## 发表科技论文 -0.3613250 0.68722000
## 专利申请受理数 -0.9869955 0.02382478
## 发明专利 -0.8988723 0.32886219将每个观测用第一和第二典型变量表示：
相关系数检验，用Pillai-Bartlett 迹方法:
## Pillai-Bartlett Trace, using F-approximation:
## stat approx df1 df2 p.value
## 1 to 3: 1.8131261 1.527649 12 12 0.2369332
## 2 to 3: 0.8785021 1.242286 6 18 0.3314555
## 3 to 3: 0.2126497 0.915492 2 24 0.4138505
## $id
## [1] "Pillai"
##
## $stat
## [1] 1.8131261 0.8785021 0.2126497
##
## $approx
## [1] 1.527649 1.242286 0.915492
##
## $df1
## [1] 12 6 2
##
## $df2
## [1] 12 18 24
##
## $p.value
## [1] 0.2369332 0.3314555 0.4138505CCP::p.asym()函数中第一自变量是获得的各个典型相关系数，
N是观测数据样本量，
p是自变量(\(X\)变量)个数，
q是因变量(\(Y\)变量)个数。
从结果看出， 两组增长率变量之间没有显著的线性相关性。 因为第一典型相关系数很大， 所以这个检验结果可能与样本量很小有关。 统计假设检验在小样本时不容易产生显著结果。 另外， Bartlett大样本检验要求数据服从多元正态分布， 或者样本量充分大。