9 因子分析

因子分析最早起源于Karl Pearson和Charles Spearman 等人关于智力的定义和测量工作。因子分析的目的与主成分分析类似，要把多个变量的信息压缩到少数几个变量中，压缩的结果称为“因子”，因子需要起到把变量分组的作用，需要有比较好的实际解释。

理论上，少数的因子能够概括原始变量中大部分的协方差信息。

把多个变量压缩成因子的方法称为R型因子分析。 R型因子分析保持数据集的观测个数不变，把变量个数降维表示。

如果把数据观测和变量之间的关系颠倒过来，希望得到少数几个概括观测的因子，这样的方法称为Q型因子分析。 Q型因子保持数据集的变量个数（列数）不变，把观测个数降维。

9.1 正交因子分析

9.1.1 模型

设有\(p\)维随机向量\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)， \(E \boldsymbol X = \boldsymbol\mu\), \(\text{Var}(\boldsymbol X) = \Sigma\)。假定\(\boldsymbol X\)可以用少数几个不可观测的随机变量 \(F_1, F_2, \dots, F_m\)(\(m < p\))比较好地线性近似，写出类似如下回归模型的因子模型： \[\begin{align} \begin{cases} X_1 = \mu_1 + a_{11} F_1 + a_{12} F_2 + \dots + a_{1m} F_m + \varepsilon_1 \\ X_2 = \mu_2 + a_{21} F_1 + a_{22} F_2 + \dots + a_{2m} F_m + \varepsilon_2 \\ \qquad\qquad \vdots \\ X_p = \mu_p + a_{p1} F_1 + a_{p2} F_2 + \dots + a_{pm} F_m + \varepsilon_p \end{cases} \end{align}\] 其中\(F_1, F_2, \dots, F_m\)称为公共因子， \(\varepsilon_1, \varepsilon_2, \dots, \varepsilon_p\)称为特殊因子。 \(a_{ij}\)称为第\(i\)个变量在第\(j\)个因子上的载荷(loading), 矩阵\(A=(a_{ij})_{p \times m}\)称为载荷矩阵。

记\(\boldsymbol F = (F_1, F_2, \dots, F_m)^T\), \(\boldsymbol\varepsilon = (\varepsilon_1, \varepsilon_2, \dots, \varepsilon_p)^T\)，因子模型可以写成 \[\begin{align} \boldsymbol X = \boldsymbol\mu + A \boldsymbol F + \boldsymbol\varepsilon . \end{align}\]

9.1.2 与线性模型的比较

因子分析的模型与线性模型 \[\begin{align*} \boldsymbol Y = M \boldsymbol\beta + \boldsymbol\varepsilon \end{align*}\] (\(M\)是设计阵) 很相似，但是有如下差别：

因子模型中的系数\(A\)是未知的，线性模型中的设计阵\(M\)是已知的；
因子模型中\(\boldsymbol F\)是未知的随机向量，线性模型中的\(\boldsymbol\beta\)是未知的非随机参数向量。

9.1.3 模型假定

对公共因子和特殊因子，假定 \[\begin{align*} & E(\boldsymbol F) = 0, \ \text{Var}(\boldsymbol F) = I, \\ & E(\boldsymbol\varepsilon) = 0, \ \text{Var}(\boldsymbol\varepsilon) = \Phi = \text{diag}(\phi_1, \phi_2, \dots, \phi_p) \\ & \text{Cov}(\boldsymbol F, \boldsymbol\varepsilon) = E(\boldsymbol F \boldsymbol\varepsilon^T) = 0. \end{align*}\] 即：

公共因子和特殊因子都是零均值的，它们都用来解释原始变量的协方差结构而与原始变量均值无关；
各公共因子之间不相关；各特殊因子之间不相关；公共因子与特殊因子之间不相关；
公共因子都是单位方差的。如果不这样假设，系数\(\{ a_{ij} \}\)就无法唯一确定。
\(p\)个特殊因子可以有自己单独的方差。

称这样的因子模型为正交因子模型。如果允许公共因子之间有相关，相应的因子模型称为斜交因子模型。

9.1.4 正交因子模型的协方差结构

对正交因子模型， \[\begin{align} \Sigma =& \text{Var}(\boldsymbol X) = E\left[ (\boldsymbol X - \boldsymbol\mu) (\boldsymbol X - \boldsymbol\mu)^T \right] \nonumber\\ =& E \left[ ( A \boldsymbol F + \boldsymbol\varepsilon ) ( A \boldsymbol F + \boldsymbol\varepsilon )^T \right] \nonumber\\ =& E \left[ A F F^T A^T + \boldsymbol\varepsilon \boldsymbol F^T A^T + A \boldsymbol F \boldsymbol\varepsilon^T + \boldsymbol\varepsilon \boldsymbol\varepsilon^T \right] \nonumber\\ =& A\; E(\boldsymbol F \boldsymbol F^T) \; A^T + E( \boldsymbol\varepsilon \boldsymbol F^T ) A^T + A E( \boldsymbol F \boldsymbol\varepsilon^T ) + E( \boldsymbol\varepsilon \boldsymbol\varepsilon^T ) \nonumber\\ =& A A^T + \Phi \tag{9.1} \\ \text{Cov}(\boldsymbol X, \boldsymbol F) =& E\left[ (\boldsymbol X - \boldsymbol\mu) \boldsymbol F^T \right] = E\left[ (A \boldsymbol F + \boldsymbol\varepsilon) F^T \right] \nonumber\\ =& A \tag{9.2} \\ \text{Var}(X_i) =& \sigma_{ii} = a_{i1}^2 + a_{i2}^2 + \dots + a_{im}^2 + \phi_i, \ i=1,2,\dots, p \tag{9.3} \end{align}\]

从(9.3)看出, \(X_i\)的方差由两部分构成: \(m\)个公共因子和一个特殊因子的贡献，其中\(a_{ij}^2\)表示第\(j\)个公共因子对第\(i\)个原始变量的方差贡献， \(\phi_i\)是特殊因子对第\(i\)个原始变量的方差贡献。

记\(h_i^2 = a_{i1}^2 + a_{i2}^2 + \dots + a_{im}^2\), 表示\(m\)个公共因子对原始变量\(X_i\)的方差贡献总和，称为第\(i\)个共同度, 是载荷矩阵\(A\)的第\(i\)行的平方和。

\(\phi_i\)称为第\(i\)个特殊度。

因为特殊方差阵\(\Phi\)是对角阵，所以两个变量\(X_i\), \(X_j\)(\(i\neq j\))的协方差为 \[ \text{Cov}(X_i, X_j) = \sum_{\ell=1}^m a_{i\ell} a_{j\ell}, \] 仅由公共因子决定，不含特殊因子影响。

由(9.2)知 \[\begin{align} \text{Cov}(X_i, F_j) = a_{ij}, i=1,2,\dots, p;\ j=1,2,\dots,m . \end{align}\] 即\(a_{ij}\)是原始变量\(X_i\)与公共因子\(F_j\)的协方差。

考虑单个的公共因子\(F_j\)对所有原始变量的影响，令 \[\begin{align} b_j^2 = a_{1j}^2 + a_{2j}^2 + \dots + a_{pj}^2, \end{align}\] \(b_j^2\)越大，第\(j\)因子的影响也越大。 \(b_j^2\)是载荷矩阵第\(j\)列的平方和。

9.1.5 模型的伸缩不变性

正交因子模型中因子\(\boldsymbol F\)是零均值、方差阵为单位阵的随机向量，所以如果对输入的变量\(\boldsymbol X\)的分量作伸缩变换，因子不变。

设\(C\)为对角阵，对\(\boldsymbol X\)作伸缩变换\(C \boldsymbol X\)，有 \[ C \boldsymbol X = C A \boldsymbol F + C \boldsymbol\varepsilon . \] 令\(\boldsymbol Y = C \boldsymbol X\), \(\tilde A = C A\), \(\tilde{\boldsymbol\varepsilon} = C \boldsymbol\varepsilon\)，则\(\boldsymbol Y\)仍服从正交因子模型，因子\(\boldsymbol F\)不变，载荷阵仅每行乘以不同系数，特殊因子也仅是方差有变化。

于是，令\(C = \text{diag}(\sigma_{ii}^{-1/2}, i=1,2,\dots, p)\)，则\(\boldsymbol Y\)的协方差阵是\(\boldsymbol X\)的相关阵。所以，正交因子分析从\(\boldsymbol X\)的协方差阵和从\(\boldsymbol X\)的相关阵计算，得到的公共因子是相同的。与之成对比的是，主成分分析中，从协方差阵阵出发与从相关阵出发得到的主成分是不同的。

9.1.6 因子表示的不唯一性

设\(T\)为\(m \times m\)正交阵，即\(T^T T = T T^T = I_m\), 则 \[\begin{align*} \boldsymbol X =& \boldsymbol\mu + A \boldsymbol F + \boldsymbol\varepsilon \nonumber\\ =& \boldsymbol\mu + A T T^T \boldsymbol F + \boldsymbol\varepsilon \end{align*}\]

记\(\tilde A = A T\), \(\tilde{\boldsymbol F} = T^T \boldsymbol F\), 则因子模型变成了 \[\begin{align} \boldsymbol X =& \boldsymbol\mu + \tilde A \tilde{\boldsymbol F} + \boldsymbol\varepsilon, \end{align}\] 其中\(\tilde{\boldsymbol F}\)仍满足\(E(\tilde{\boldsymbol F})=\boldsymbol 0\), \(\text{Var}(\tilde{\boldsymbol F}) = I\)， \(\text{Cov}(\tilde{\boldsymbol F}, \boldsymbol\varepsilon) = 0\)。

新的公共因子可以得到相同的方差结构： \[\begin{align} \Sigma = A A^T + \Phi = \tilde A \tilde A^T + \Phi . \end{align}\] 共同度\(h_i^2\)也不变（\(\tilde A = A T\), 正交变换不改变行向量长度）。

这种性质可以用来获得更容易解释的因子。

9.1.7 与主成分分析的比较

在主成分分析中， \(\boldsymbol X\)是原始变量，主成分\(\boldsymbol Y = P^T \boldsymbol X\)，于是 \[ \boldsymbol X = P \boldsymbol Y, \] 如果前\(m\)个主成分累计贡献率足够大，记\(\boldsymbol Y_{m\times 1}\)为\(\boldsymbol Y\)的前\(m\)元素组成的向量， \(G_{p\times m}\)为\(P\)的前\(m\)列组成的矩阵，有 \[ \boldsymbol X \approx G \boldsymbol Y_{m\times 1} \] 这个式子与因子分析的模型 \[ \boldsymbol X = \boldsymbol\mu + A \boldsymbol F + \boldsymbol\varepsilon \] 很接近。因为主成分分析的数据都要中心化或者标准化，所以主成分分析的模型中没有\(\boldsymbol\mu\)项。

主成分分析与因子分析的异同点：

都能起到压缩数据的作用，主成分得分或者因子得分可以概括多个变量中的某些潜在影响因素。
主成分分析中的\(G_{p \times m}\)和因子分析中的\(A\)都称为载荷阵，主成分分析中\(G\)的每一列可以作为\(\boldsymbol X\)的线性组合系数产生一个主成分，而因子分析中的载荷阵的列向量不能作为\(\boldsymbol X\)的线性组合系数。
主成分分析中\(\boldsymbol Y_{m \times 1}\)是\(\boldsymbol X\)的线性组合，而因子分析中\(\boldsymbol F\)不是。
主成分分析中\(\text{Var}(\boldsymbol Y_{m \times 1}) = \text{diag}(\lambda_1, \dots, \lambda_m)\)，其中\(\lambda_1, \dots, \lambda_m\)是\(\text{Var}(\boldsymbol X)\)的从大到小的\(m\)个最大特征值，而因子分析中\(\text{Var}(\boldsymbol F) = I_m\)。
选择不同的因子个数，得到的因子是不同的，而主成分分析中得到的主成分是相同的。
主成分得分可以很容易用原始变量值的线性组合计算，而因子得分则比较复杂，计算方法也有多种。
主成分分析中 \(\text{Var}(\boldsymbol X) = P \Lambda P^T \approx G \Lambda_{m\times m} G^T\)，而因子分析中\(\text{Var}(\boldsymbol X) = A A^T + \Phi\)。
因子分析具有伸缩不变性，主成分分析当使用相关阵时才有伸缩不变性。
因子分析从协方差阵计算与从相关阵计算可以得到相同的公共因子，主成分分析从协方差阵计算与从相关阵计算得到的主成分不同。

9.2 因子模型的估计

因子模型的未知参数是载荷矩阵\(A\)和特殊方差\(\phi_i, i=1,2,\dots,p\)。先估计未知参数。可以用主成分法、极大似然法、主因子法。这里介绍主成分法。

9.2.1 主成分法

设\(\Sigma\)的特征值为 \(\lambda_1 \geq \lambda_1 \geq \dots \lambda_p\)，有如下的特征值分解 \[\begin{align} \Sigma =& P \Lambda P^T = \sum_{i=1}^p \lambda_i \boldsymbol p_i \boldsymbol p_i^T \nonumber\\ =& \left(\sqrt{\lambda_1} \boldsymbol p_1, \sqrt{\lambda_2} \boldsymbol p_2, \dots, \sqrt{\lambda_p} \boldsymbol p_p \right) \left(\begin{array}{c} \sqrt{\lambda_1} \boldsymbol p_1^T \\ \sqrt{\lambda_2} \boldsymbol p_2^T \\ \vdots \\ \sqrt{\lambda_p} \boldsymbol p_p^T \end{array}\right) \nonumber\\ =& (P \Lambda^{1/2}) (P \Lambda^{1/2})^T \stackrel{\triangle}{=} A A^T, \tag{9.4} \end{align}\] 其中\(\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_p)\), \(P\)为正交阵，\(P\)的第\(i\)列\(\boldsymbol p_i\)是特征值\(\lambda_i\)对应的单位特征向量， \(A = P \Lambda^{1/2}\)。

这样得到\(A\)有\(p\)列而不是\(m < p\)列，没有实际意义。需要较少的公因子。

如果\(\Sigma\)的最后\(p-m\)个特征值较小，则可以在(9.4)略去求和中最后\(p-m\)项，得 \[\begin{align} \Sigma \approx& \sum_{i=1}^m \lambda_i \boldsymbol p_i \boldsymbol p_i^T \nonumber\\ =& \left(\sqrt{\lambda_1} \boldsymbol p_1, \sqrt{\lambda_2} \boldsymbol p_2, \dots, \sqrt{\lambda_m} \boldsymbol p_m \right) \left(\begin{array}{c} \sqrt{\lambda_1} \boldsymbol p_1^T \\ \sqrt{\lambda_2} \boldsymbol p_2^T \\ \vdots \\ \sqrt{\lambda_m} \boldsymbol p_m^T \end{array}\right) \nonumber\\ \stackrel{\triangle}{=}& A A^T, \end{align}\] 这里\(A\)是\(p \times m\)矩阵，各列为\(P\)的前\(m\)列分别乘以相应的特征值平方根。

\(\Sigma\)与\(A A^T\)的差由特殊因子\(\varepsilon\)来解释，取\(\Phi\)为\(\Sigma - A A^T\)的主对角线元素组成的对角阵。这时有近似分解 \[\begin{align} \Sigma \approx A A^T + \Phi, \end{align}\] 其中\(A\)是\(m \times p\)矩阵，各列为\(P\)的前\(m\)列分别乘以相应的特征值平方根; \(\Phi\)为\(\Sigma - A A^T\)的主对角线元素组成的对角阵。

这样分解有可能得到\(\Phi\)中有负值方差的结果。所以，更实际的方法是，从相关阵估计\(R\)出发，将\(R\)中对角线元素\(1\)，替换成估计的共同度\(h_i^2\)，得到修正的相关阵\(R^*\)，对\(R^*\)作特征值分解得到载荷阵\(A\)，从载荷阵\(A\)得到新的共同度估计，再修正\(R^*\)，如此迭代计算直到收敛。

初始时为了估计共同度，可以估计\(h_i^2\)为\(X_i\)与其它的\(X_j\)的相关系数平方的和，或者\(X_i\)与其它的\(X_j\)的相关系数平方中最大的一个，这样会高估共同度，一般能保证\(R^*\)的非负定性。

如果最后结果还使得\(\Phi\)中有负值的方差，则结果是不可取的。

9.2.2 最大似然估计法

设\(\boldsymbol X\)服从多元正态分布，可以用\(A\)和\(\Phi\)表示似然函数。可以先给出\(A\)和\(\Phi\)的初值，然后用数值优化算法求最大似然估计。这种方法也不能保证得到的\(\Phi\)不包含负值。

9.2.3 样本的因子分解

实际中，总体的\(\Sigma\)是未知的，可以从观测样本中估计, 用样本协方差阵\(S\)代替\(\Sigma\)。

在各个变量不可比的情况下，通常需要对数据进行标准化，这样，变量的协方差阵实际是原始变量的相关阵\(R\)。所以经常选择用相关阵来估计因子载荷阵\(A\)和特殊因子方差\(\Phi\)。

考虑使用样本相关阵\(R\)计算正交因子分析的问题。设\(R\)的特征值为\(\lambda_1 \geq \lambda_2 \geq \dots \lambda_p > 0\)， \(\boldsymbol p_i\)是\(\lambda_i\)对应的单位特征向量， \(P = (\boldsymbol p_1, \dots, \boldsymbol p_p)\)是正交阵。

由\(R\)出发的因子模型的载荷矩阵\(A\)估计为 \[\begin{align} \hat A =& (\sqrt{\lambda_1} \boldsymbol p_1, \sqrt{\lambda_2} \boldsymbol p_2, \dots, \sqrt{\lambda_m} \boldsymbol p_m) \nonumber\\ \stackrel{\triangle}{=}& (\hat a_{ij})_{p \times m} \quad (p > m), \end{align}\]

特殊因子的方差\(\phi_i\)的估计为 \[\begin{align} \hat\phi_i = 1 - \sum_{j=1}^m \hat a_{ij}^2, \ i=1,2,\dots,p . \end{align}\]

共同度\(h_i^2\)的估计为 \[\begin{align} \hat h_i^2 = \sum_{j=1}^m \hat a_{ij}^2, \ i=1,2,\dots,p . \end{align}\]

变量\(X_i\)与因子\(F_j\)的协方差估计为\(\hat a_{ij}\)。

公共因子\(F_j\)对所有\(p\)个原始变量的方差贡献估计为 \[\begin{align} \hat b_j^2 = \sum_{i=1}^p \hat a_{ij}^2 = \| \sqrt{\lambda_j} \boldsymbol p_j \|^2 = \lambda_j, \ j=1,2,\dots,m . \end{align}\]

9.2.4 因子个数的选择

因子个数不同，得到的公共因子也不同。因子个数太少，会使得高载荷\(a_{ij}\)个数太多。因子个数太多，会使得载荷取值过于分散，不易解释，也起不到压缩数据作用。

选择因子个数\(m\)，一种方法是尝试不同的\(m\)值，看哪一种得到的因子可解释性更好。

另外，
仿照主成分分析的想法，求\(m\)使得 \[\begin{aligned} \frac{\sum_{j=1}^m \lambda_j}{\sum_{j=1}^p \lambda_j} = \frac{\sum_{j=1}^m \lambda_j}{p} \geq 80\% . \end{aligned}\]

注：对正定阵\(D\), \(\text{trace(D)}\)等于其所有特征值之和。事实上，若\(D\)有特征值分解\(D = P \Lambda P^T\), 则\(\text{trace}(D) = \text{trace}(\Lambda P^T P) = \text{trace}(\Lambda)\)。

使用最大似然法估计参数时，还可以用假设检验法确定参数个数，零假设是\(m\)个主因子能拟合数据，对立假设是\(\boldsymbol X\)的协方差阵没有任何约束。可以从\(m=1\)开始尝试，直到零假设被接受为止。

9.3 因子旋转

满足因子模型的方差结构\(\Sigma = A A^T + \Phi\)的载荷矩阵\(A\)并不唯一。相应地，公共因子也不唯一。

如果\(\boldsymbol F\)是\(\boldsymbol X\)的公共因子， \(T\)是\(m \times m\)正交阵，则\(\tilde{\boldsymbol F} = T^T \boldsymbol F\)也是公共因子，相应的载荷阵为\(\tilde A = A T\), \(\tilde A\)也满足\(\Sigma = \tilde A \tilde A^T + \Phi\)，正交因子模型变成 \[ \boldsymbol X = \tilde A\tilde{\boldsymbol F} + \boldsymbol\varepsilon . \]

这造成了正交因子模型解的不唯一性。为了唯一确定\(A\)和\(\boldsymbol F\)，可以添加一些约束条件。比如，可以要求矩阵 \[ G = A \Phi^{-1} A^T \] 为对角阵，且各对角元素从大到小排列，这使得产生的第一公共因子对所有原始变量的共同方差贡献最大，第二公共因子在与第一公共因子不相关的前提下贡献次大，等等，类似于主成分分析中的主成分排序。这样可以唯一确定载荷阵\(A\)（各列可以有正负号的变化），从而确定公共因子。

上述做法能够确保因子模型有唯一解，但并不是因子模型必要的约束条件，得到的结果可能并不容易解释。所以，因子模型解的不唯一性应该看成一个优点而不是一个缺陷，可以寻找适当的正交变换\(T\)，使得变换后的载荷阵\(\tilde A\)的每列的\(p\)个元素或者绝对值比较大，或者接近于零，尽量不要出现绝对值不大也不接近于零的元素。这样的载荷阵对应的因子构成了对变量的分组，某个因子的载荷列那些绝对值比较大的元素对应的原始变量为一组，可以用来解释这个因子的含义。

称因子载荷的正交变换和伴随的因子正交变换为因子正交旋转。进一步地，可以修改正交因子模型，允许共同因子\(\boldsymbol F\)之间相关，称这样的变换为因子斜交旋转(oblique rotation)。如果\(\tilde A = A T\)中的矩阵\(T\)不是正交阵，则\(\tilde{\boldsymbol F}\)中的各个公共因子可能相关，公共因子的方差仍要求等于1。

斜交因子模型比较灵活，适用于更好地拟合所用的数据；正交因子模型约束更严格，模型在类似问题中的适用性更好。

因子分析中常用的正交旋转和斜交旋转方法有：

varimax旋转：正交旋转方法，要求每个因子仅有少数绝对值较大的载荷，多数载荷接近0。通过迭代最小化载荷系数的一个二次函数实现。结果使得每个因子仅与少数原始变量有强相关，而与其余原始变量近似不相关。
quartimax旋转：正交旋转方法，要求每个原始变量仅与一个公共因子强相关，而与其余公共因子近似不相关。不如varimax接受程度高。
oblimin旋转：斜交旋转方法，追求载荷阵中0尽可能多，设置公共因子之间的相关系数在较小值。
promax旋转：斜交旋转方法，追求载荷阵中0尽可能多，方法是取正交旋转得到的载荷阵元素的幂次。要求幂次尽可能低，公共因子间的相关性尽可能低。

9.4 因子得分

因子分析中，首要地是得到因子载荷阵，从而得到变量的适当分组，对因子进行解释。

其次，可以从数据中估计因子的取值（注意因子在模型中是不可观测的）。公共因子的观测值的估计称为因子得分。因子得分起到了数据压缩的作用，比原始更能体现个体的特点，更能代表个体特性。

可以用加权最小二乘法估计因子得分。

9.4.1 用加权最小二乘法计算因子得分

设\(\boldsymbol X\)已知且已标准化, \(A\), \(\Phi\)已知，在因子模型 \[\begin{align} \boldsymbol X = A \boldsymbol F + \boldsymbol\varepsilon \end{align}\] 中要估计公共因子\(\boldsymbol F\)。

在模型两边左乘\(\Phi^{-1/2}\), 得 \[\begin{align} \Phi^{-1/2} \boldsymbol X = (\Phi^{-1/2} A) \boldsymbol F + \Phi^{-1/2} \boldsymbol\varepsilon \end{align}\]

记\(\boldsymbol X^* = \Phi^{-1/2} \boldsymbol X\), \(\boldsymbol A^* = \Phi^{-1/2} A\), \(\boldsymbol\varepsilon^* = \Phi^{-1/2} \boldsymbol\varepsilon\), 得到关于新的随机向量\(\boldsymbol X^*\)的模型 \[\begin{align} \boldsymbol X^* = A^* \boldsymbol F + \boldsymbol\varepsilon^*, \end{align}\] 其中的因子\(\boldsymbol\varepsilon^*\)相当于误差项，满足\(\text{Var}(\boldsymbol\varepsilon^*)=I\)。

在已知\(\boldsymbol X\)且已标准化, \(A\), \(\Phi\)已知时，\(\boldsymbol X^*\), \(A^*\)也已知，只要最小化\(\| \boldsymbol X^* - A^* \boldsymbol F \|^2\)就可以得到\(\boldsymbol F\)的估计值，即最小二乘估计。

\(\boldsymbol F\)的最小二乘估计（实际是加权最小二乘估计）为 \[\begin{align} \hat{\boldsymbol F} =& (A^{*T} A^*)^{-1} A^{*T} \boldsymbol X^* = (A^T \Phi^{-1} A)^{-1} A^T \Phi^{-1} \boldsymbol X . \end{align}\]

9.4.2 样本因子得分

实际应用时， \(\boldsymbol\mu\), \(R\), \(A\), \(\Phi\)都是未知的。设\(\boldsymbol X\)有\(n\)组观测(\(n>p\))，记为\(M = (x_{ki})_{n \times p}\)，第\(k\)行记为\([\boldsymbol x^{(k)}]^T\), 是\(\boldsymbol X\)的第\(k\)个观测。设\(M\) 的每列已经标准化。可以从\(M\)中用样本相关阵估计\(R\), 然后用\(R\)的特征值分解估计\(A\)和\(\Phi\)。

设得到了\(\hat A\)和\(\hat\Phi\)，则\(\boldsymbol X\)的第\(k\)个观测\([\boldsymbol x^{(k)}]^T\) 的因子得分的计算公式为 \[\begin{align} \hat f^{(k)} =& (A^T \Phi^{-1} A)^{-1} A^T \Phi^{-1} \boldsymbol x^{(k)}, \nonumber\\ [\hat f^{(k)}]^T =& [\boldsymbol x^{(k)}]^T \Phi^{-1} A (A^T \Phi^{-1} A)^{-1} \end{align}\]

所有\(n\)个观测的因子得分可以写成如下矩阵: \[\begin{align} \hat C = M \Phi^{-1} A (A^T \Phi^{-1} A)^{-1} . \end{align}\] 这是一个\(n \times m\)矩阵，每一行是一个观测对应的因子得分，每一列是某个因子的所有观测值估计。

9.5 例：学生六科成绩的因子分析

9.5.1 问题介绍

P.102例7.1, 52个学生的六科成绩的因子分析。

前一章的主成分分析对52个学生的六科成绩计算了主成分，得到了具有良好解释的两个主成分。用因子分析方法重新进行分析。

R函数factanal(), 用rotation=指定旋转方法，常用有varimax和promax。

用scores=指定是否估计得分以及估计计算方法，用scores='regression'指定使用加权最小二乘法估计得分。

factanal()结果列表中元素loadings是载荷阵， scores是估计的得分。

可以做载荷矩阵的前两个因子的散点图查看载荷分配。可以用biplot()同时查看载荷和得分。

9.5.2 数据预处理

载入数据：

student6Score <- readr::read_csv(
  "data/学生六科成绩.csv", 
  show_col_types = FALSE)
d <- student6Score

产生中心化与标准化的数据集：

d2 <- sweep(d, 2, colMeans(d)) # 每列中心化
d3 <- scale(d) # 每列标准化

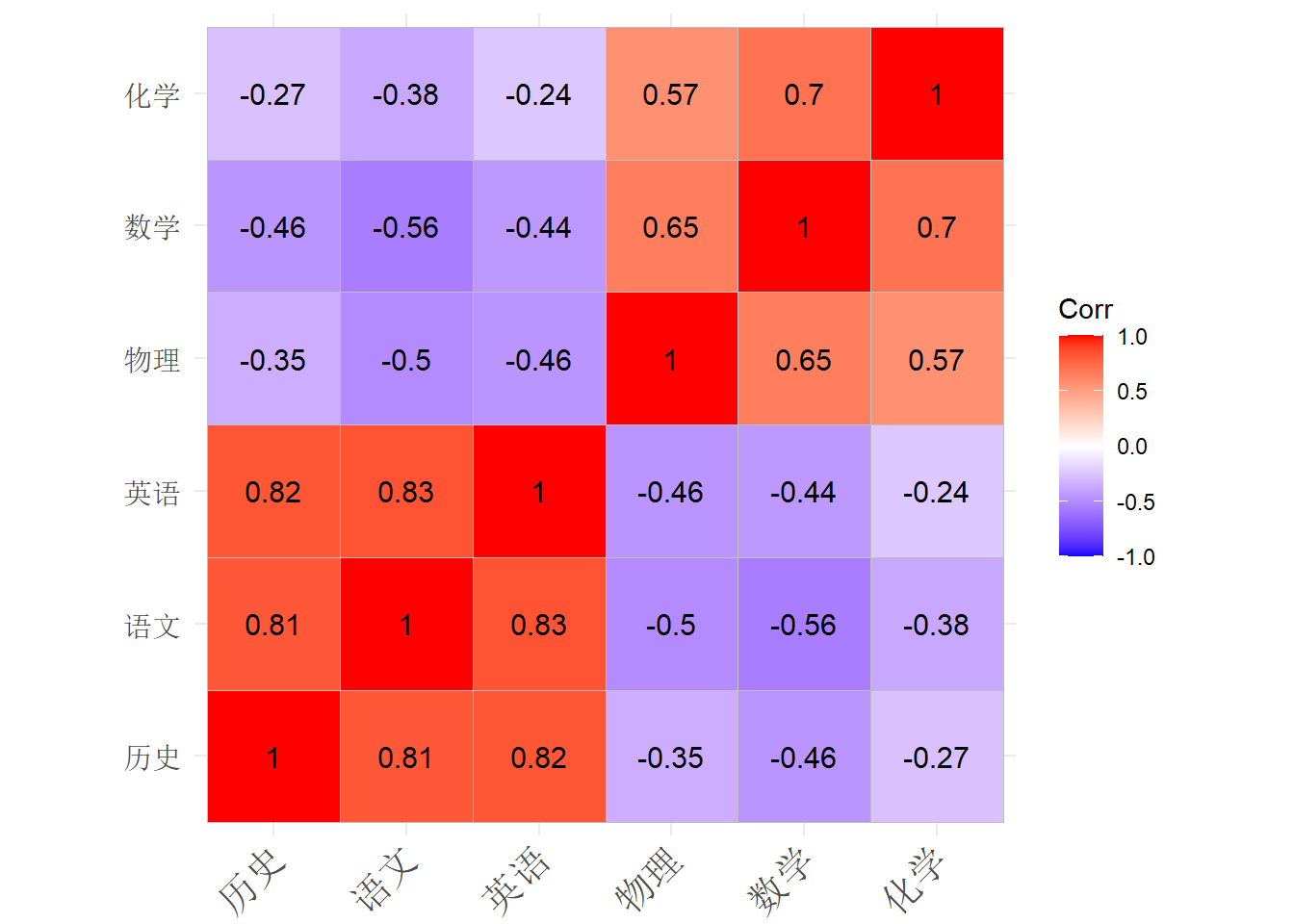
9.5.3 主成分分析

用相关阵作的主成分分析：

pca1 <- princomp(d, cor=TRUE)
print(pca1)

## Call:
## princomp(x = d, cor = TRUE)
## 
## Standard deviations:
##    Comp.1    Comp.2    Comp.3    Comp.4    Comp.5    Comp.6 
## 1.9261112 1.1236019 0.6639552 0.5200978 0.4117231 0.3830929 
## 
##  6  variables and  52 observations.

print(summary(pca1, loadings=TRUE))

## Importance of components:
##                           Comp.1    Comp.2     Comp.3     Comp.4     Comp.5
## Standard deviation     1.9261112 1.1236019 0.66395522 0.52009785 0.41172308
## Proportion of Variance 0.6183174 0.2104135 0.07347275 0.04508363 0.02825265
## Cumulative Proportion  0.6183174 0.8287309 0.90220369 0.94728732 0.97553997
##                            Comp.6
## Standard deviation     0.38309295
## Proportion of Variance 0.02446003
## Cumulative Proportion  1.00000000
## 
## Loadings:
##    Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## x1  0.412  0.376  0.216  0.788         0.145
## x2  0.381  0.357 -0.806 -0.118 -0.212 -0.141
## x3  0.332  0.563  0.467 -0.588              
## x4 -0.461  0.279               -0.599  0.590
## x5 -0.421  0.415 -0.250         0.738  0.205
## x6 -0.430  0.407  0.146  0.134 -0.222 -0.749

结果中有各主成分的标准差，贡献率，累积贡献率。可以看出前两个主成分累积贡献率达到82%, 第一主成分贡献率为61%。从载荷看，第一主成分在理科上系数为负，在文科上系数为正，反映了学生在文理科的相对优势。第二主成分都为负数且值相近，可以把系数都取相反数，反映学生所有六科的整体水平。

计算前两个主成分的主成分得分, 数据是标准化过的:

print(cbind(d, round( predict(pca1)[,1:2], 3)))

##    x1  x2  x3  x4 x5  x6 Comp.1 Comp.2
## 1  65  61  72  84 81  79 -1.846 -0.099
## 2  77  77  76  64 70  55  1.383 -0.933
## 3  67  63  49  65 67  57 -0.044 -2.804
## 4  78  84  75  62 71  64  1.256 -0.406
## 5  66  71  67  52 65  57  1.139 -2.269
## 6  83 100  79  41 67  50  3.518 -0.820
## 7  86  94  97  51 63  55  3.516  0.104
## 8  67  84  53  58 66  56  0.982 -2.326
## 9  69  56  67  75 94  80 -2.247  0.130
## 10 77  90  80  68 66  60  1.675 -0.325
## 11 84  67  75  60 70  63  1.177 -0.761
## 12 62  67  83  71 85  77 -1.157  0.215
## 13 91  74  97  62 71  66  1.944  0.783
## 14 82  70  83  68 77  85 -0.130  0.909
## 15 66  61  77  62 73  64  0.089 -1.276
## 16 90  78  78  59 72  66  1.621  0.052
## 17 77  89  80  73 75  70  0.651  0.545
## 18 72  68  77  83 92  79 -1.709  1.012
## 19 72  67  61  92 92  88 -2.819  0.876
## 20 81  90  79  73 85  80 -0.045  1.507
## 21 68  85  70  84 89  86 -1.748  1.185
## 22 85  91  95  63 76  66  1.871  1.173
## 23 91  85 100  70 65  76  1.896  1.490
## 24 74  74  84  61 80  69  0.459  0.126
## 25 88 100  85  49 71  66  2.737  0.579
## 26 87  84 100  74 81  76  0.841  2.117
## 27 64  79  64  72 76  74 -0.707 -0.669
## 28 60  51  60  78 74  76 -1.959 -1.594
## 29 59  75  81  82 77  73 -0.977 -0.034
## 30 64  61  49 100 99  95 -4.490  0.693
## 31 56  48  61  85 82  80 -2.958 -1.113
## 32 62  45  67  78 76  82 -2.214 -1.072
## 33 86  78  92  87 87  77 -0.345  2.187
## 34 80  98  83  58 66  66  2.211  0.129
## 35 83  71  81  63 77  73  0.561  0.317
## 36 67  83  65  68 74  60  0.356 -1.131
## 37 71  58  45  83 77  73 -1.882 -1.496
## 38 90  83  91  58 60  59  2.939 -0.110
## 39 73  80  64  75 80  78 -0.773  0.083
## 40 87  98  87  68 78  64  1.763  1.224
## 41 69  72  79  89 82  73 -1.191  0.546
## 42 79  73  69  65 73  73  0.275 -0.402
## 43 87  86  88  70 73  70  1.359  1.003
## 44 76  61  73  63 60  70  0.697 -1.400
## 45 99 100  99  53 63  60  3.975  1.054
## 46 78  68  52  75 74  66 -0.440 -1.271
## 47 72  90  73  76 80  79 -0.392  0.738
## 48 69  64  60  68 74  80 -1.034 -0.991
## 49 52  62  65 100 96 100 -4.622  0.997
## 50 70  72  56  74 82  74 -1.201 -0.651
## 51 72  74  75  88 91  86 -2.012  1.423
## 52 68  74  70  87 87  83 -1.953  0.757

9.5.4 因子分析不旋转

用相关阵不旋转做因子分析。用极大似然估计，没有旋转：

fac1 <- factanal(d, 
  factors=2, rotation='none', 
  method="mle")
print(fac1)

## 
## Call:
## factanal(x = d, factors = 2, rotation = "none", method = "mle")
## 
## Uniquenesses:
##    x1    x2    x3    x4    x5    x6 
## 0.228 0.459 0.333 0.148 0.210 0.150 
## 
## Loadings:
##    Factor1 Factor2
## x1 -0.676   0.562 
## x2 -0.599   0.427 
## x3 -0.487   0.656 
## x4  0.917   0.104 
## x5  0.856   0.239 
## x6  0.883   0.266 
## 
##                Factor1 Factor2
## SS loadings      3.404   1.068
## Proportion Var   0.567   0.178
## Cumulative Var   0.567   0.745
## 
## Test of the hypothesis that 2 factors are sufficient.
## The chi square statistic is 3.64 on 4 degrees of freedom.
## The p-value is 0.457

第一因子代表了文科对理科的优势，第二因子主要代表理科成绩。

用因子载荷阵前两个因子作图:

load1 <- loadings(fac1)
plot(load1, type='n', main='不旋转的因子分析载荷')
text(load1, rownames(load1))

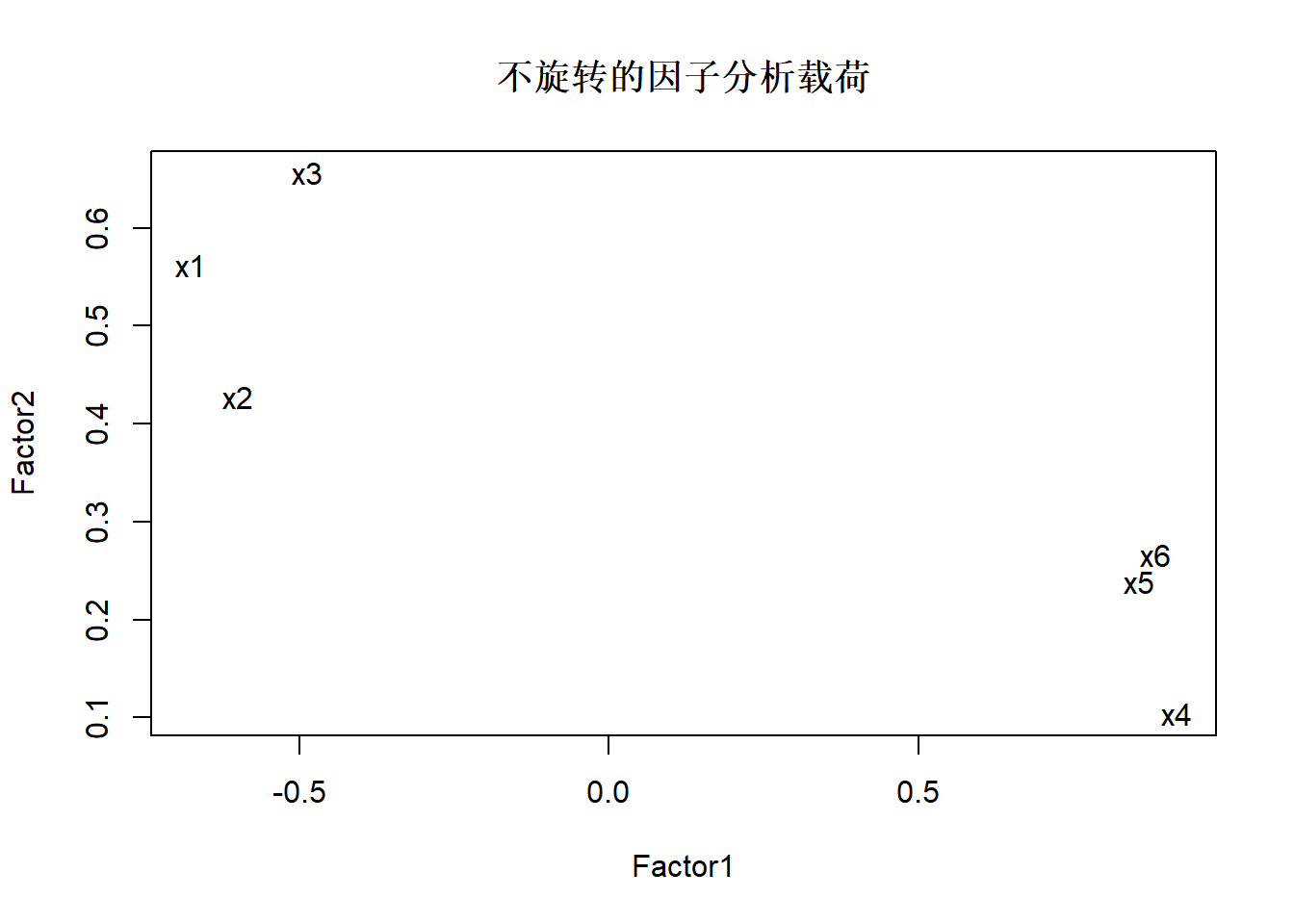
9.5.5 因子个数

可以用假设检验方法获得合适的公共因子个数选择。在上面的结果中给出了p值为0.457，以0.05为阈值，则可以认为公共因子取两个是合适的。

公共因子取一个是否合适？

fac1a <- factanal(d, 
  factors=1, rotation='none', 
  method="mle")
print(fac1a)

## 
## Call:
## factanal(x = d, factors = 1, rotation = "none", method = "mle")
## 
## Uniquenesses:
##    x1    x2    x3    x4    x5    x6 
## 0.657 0.715 0.842 0.121 0.243 0.204 
## 
## Loadings:
##    Factor1
## x1 -0.586 
## x2 -0.534 
## x3 -0.397 
## x4  0.937 
## x5  0.870 
## x6  0.892 
## 
##                Factor1
## SS loadings      3.217
## Proportion Var   0.536
## 
## Test of the hypothesis that 1 factor is sufficient.
## The chi square statistic is 48.94 on 9 degrees of freedom.
## The p-value is 1.7e-07

检验p值为1.7e-07即\(1.7 \times 10^{-7}\)，在0.05水平下显著，说明模型不充分，一个公共因子不足以拟合原始变量的方差结构。

实际应用中，如果检验方法提示的公共因子个数太大，也可以人为减少因子个数，提示的个数可以看成是一个上限值。

9.5.6 因子分析用varimax旋转

fac2 <- factanal(d, factors=2, rotation='varimax')
print(fac2)

## 
## Call:
## factanal(x = d, factors = 2, rotation = "varimax")
## 
## Uniquenesses:
##    x1    x2    x3    x4    x5    x6 
## 0.228 0.459 0.333 0.148 0.210 0.150 
## 
## Loadings:
##    Factor1 Factor2
## x1 -0.309   0.823 
## x2 -0.309   0.668 
## x3          0.811 
## x4  0.848  -0.363 
## x5  0.862  -0.216 
## x6  0.899  -0.206 
## 
##                Factor1 Factor2
## SS loadings      2.471   2.001
## Proportion Var   0.412   0.333
## Cumulative Var   0.412   0.745
## 
## Test of the hypothesis that 2 factors are sufficient.
## The chi square statistic is 3.64 on 4 degrees of freedom.
## The p-value is 0.457

第一因子代表文科对理科优势；第二因子代表理科对文科优势。旋转效果不强。

load2 <- loadings(fac2)
plot(load2, type='n', main='varimax旋转的因子分析载荷')
text(load2, rownames(load2))

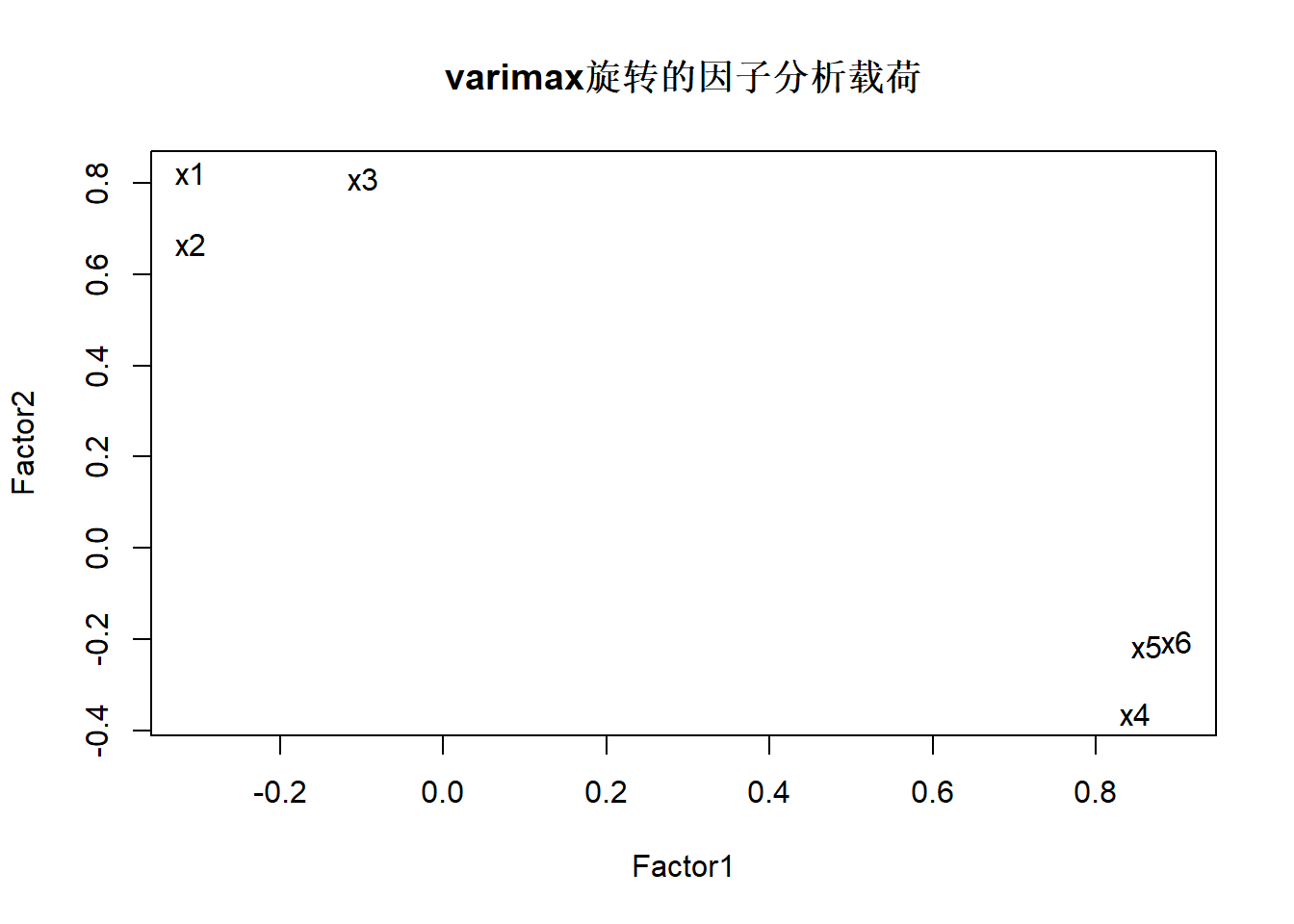
9.5.7 因子分析用promax旋转

fac3 <- factanal(d, factors=2,
  rotation='promax',
  scores='regression')
print(fac3)

## 
## Call:
## factanal(x = d, factors = 2, scores = "regression", rotation = "promax")
## 
## Uniquenesses:
##    x1    x2    x3    x4    x5    x6 
## 0.228 0.459 0.333 0.148 0.210 0.150 
## 
## Loadings:
##    Factor1 Factor2
## x1          0.833 
## x2 -0.132   0.657 
## x3  0.156   0.890 
## x4  0.845  -0.133 
## x5  0.909         
## x6  0.954         
## 
##                Factor1 Factor2
## SS loadings      2.500   1.940
## Proportion Var   0.417   0.323
## Cumulative Var   0.417   0.740
## 
## Factor Correlations:
##         Factor1 Factor2
## Factor1   1.000   0.535
## Factor2   0.535   1.000
## 
## Test of the hypothesis that 2 factors are sufficient.
## The chi square statistic is 3.64 on 4 degrees of freedom.
## The p-value is 0.457

第一因子是文科成绩，第二因子是理科成绩，旋转效果很好。

load3 <- loadings(fac3)
plot(load3, type='n', main='promax旋转的因子分析载荷')
text(load3, rownames(load3))

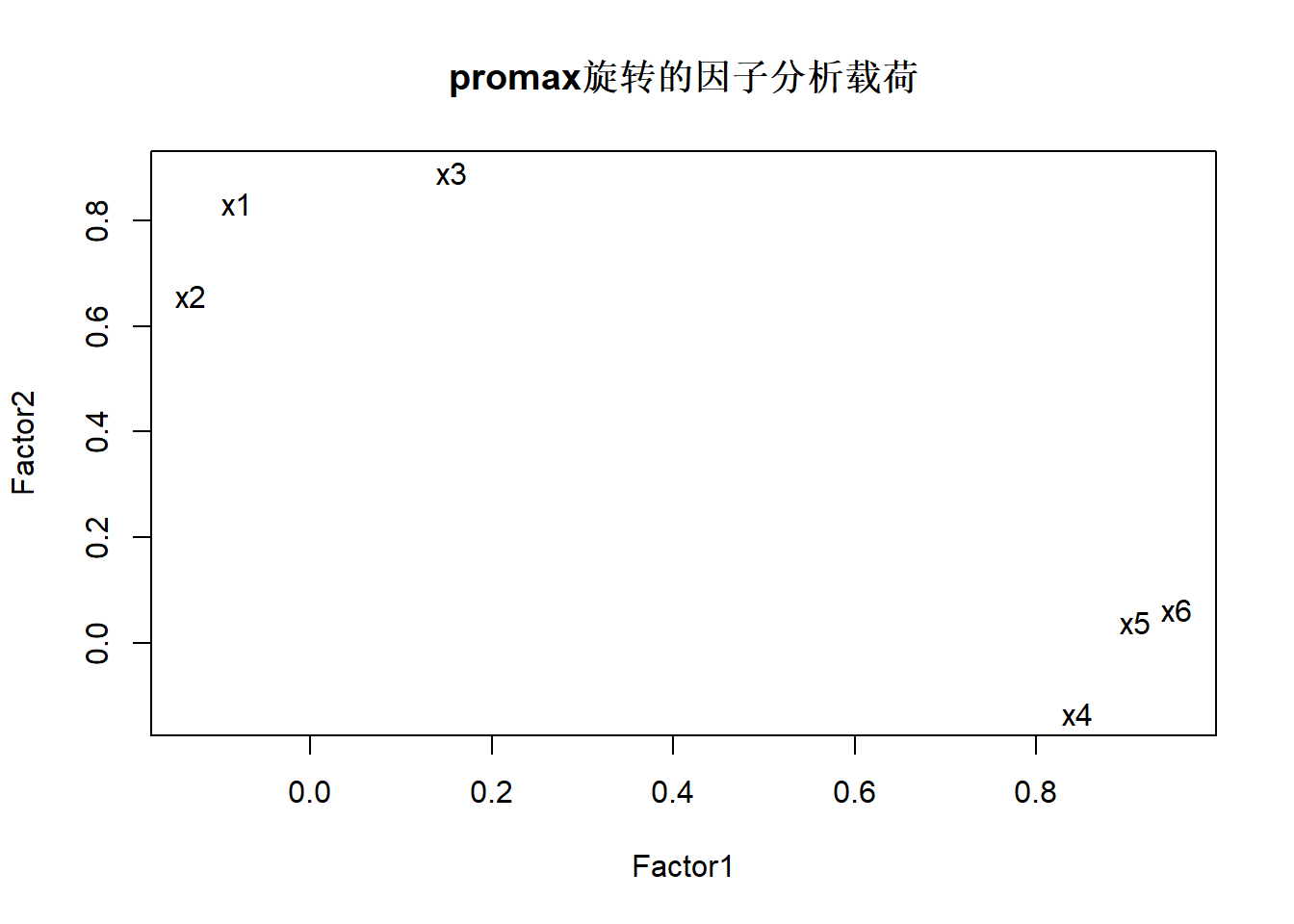
从图上看出，第一主因子载荷高的x4, x6, x6三个变量在第二主因子上载荷接近0，第二主因子载荷高的x1,x2,x3三个变量在第一主因子上载荷接近0，实现了比较好的原始变量分组效果。

用相关阵及promax旋转得到的因子得分:

print(cbind(d, round(fac3$scores, 2)))

##    x1  x2  x3  x4 x5  x6 Factor1 Factor2
## 1  65  61  72  84 81  79    0.51   -0.55
## 2  77  77  76  64 70  55   -1.27   -0.52
## 3  67  63  49  65 67  57   -2.19   -2.31
## 4  78  84  75  62 71  64   -0.76   -0.08
## 5  66  71  67  52 65  57   -2.28   -1.72
## 6  83 100  79  41 67  50   -1.96   -0.01
## 7  86  94  97  51 63  55   -1.14    0.82
## 8  67  84  53  58 66  56   -2.26   -1.89
## 9  69  56  67  75 94  80    0.78   -0.31
## 10 77  90  80  68 66  60   -0.87   -0.06
## 11 84  67  75  60 70  63   -0.87   -0.09
## 12 62  67  83  71 85  77    0.34   -0.29
## 13 91  74  97  62 71  66    0.09    1.35
## 14 82  70  83  68 77  85    0.95    1.01
## 15 66  61  77  62 73  64   -1.15   -1.09
## 16 90  78  78  59 72  66   -0.34    0.70
## 17 77  89  80  73 75  70    0.17    0.46
## 18 72  68  77  83 92  79    1.27    0.40
## 19 72  67  61  92 92  88    1.70    0.16
## 20 81  90  79  73 85  80    1.20    1.21
## 21 68  85  70  84 89  86    1.43    0.37
## 22 85  91  95  63 76  66    0.23    1.33
## 23 91  85 100  70 65  76    0.77    1.87
## 24 74  74  84  61 80  69   -0.17    0.17
## 25 88 100  85  49 71  66   -0.44    1.13
## 26 87  84 100  74 81  76    1.41    1.99
## 27 64  79  64  72 76  74   -0.38   -0.91
## 28 60  51  60  78 74  76   -0.57   -1.72
## 29 59  75  81  82 77  73    0.08   -0.64
## 30 64  61  49 100 99  95    2.08   -0.42
## 31 56  48  61  85 82  80    0.06   -1.64
## 32 62  45  67  78 76  82   -0.02   -1.23
## 33 86  78  92  87 87  77    1.86    1.79
## 34 80  98  83  58 66  66   -0.65    0.49
## 35 83  71  81  63 77  73    0.16    0.62
## 36 67  83  65  68 74  60   -1.19   -1.13
## 37 71  58  45  83 77  73   -0.39   -1.47
## 38 90  83  91  58 60  59   -0.93    0.75
## 39 73  80  64  75 80  78    0.35   -0.13
## 40 87  98  87  68 78  64    0.31    1.31
## 41 69  72  79  89 82  73    0.72   -0.01
## 42 79  73  69  65 73  73   -0.28   -0.08
## 43 87  86  88  70 73  70    0.42    1.22
## 44 76  61  73  63 60  70   -1.12   -0.72
## 45 99 100  99  53 63  60   -0.36    1.94
## 46 78  68  52  75 74  66   -0.71   -0.96
## 47 72  90  73  76 80  79    0.66    0.34
## 48 69  64  60  68 74  80   -0.31   -0.89
## 49 52  62  65 100 96 100    2.21   -0.47
## 50 70  72  56  74 82  74   -0.12   -0.81
## 51 72  74  75  88 91  86    1.76    0.66
## 52 68  74  70  87 87  83    1.20    0.06

把因子载荷矩阵前两列用箭头画出；把前两个因子得分用散点画出，称为biplot:

biplot(fac3$scores, fac3$loadings)

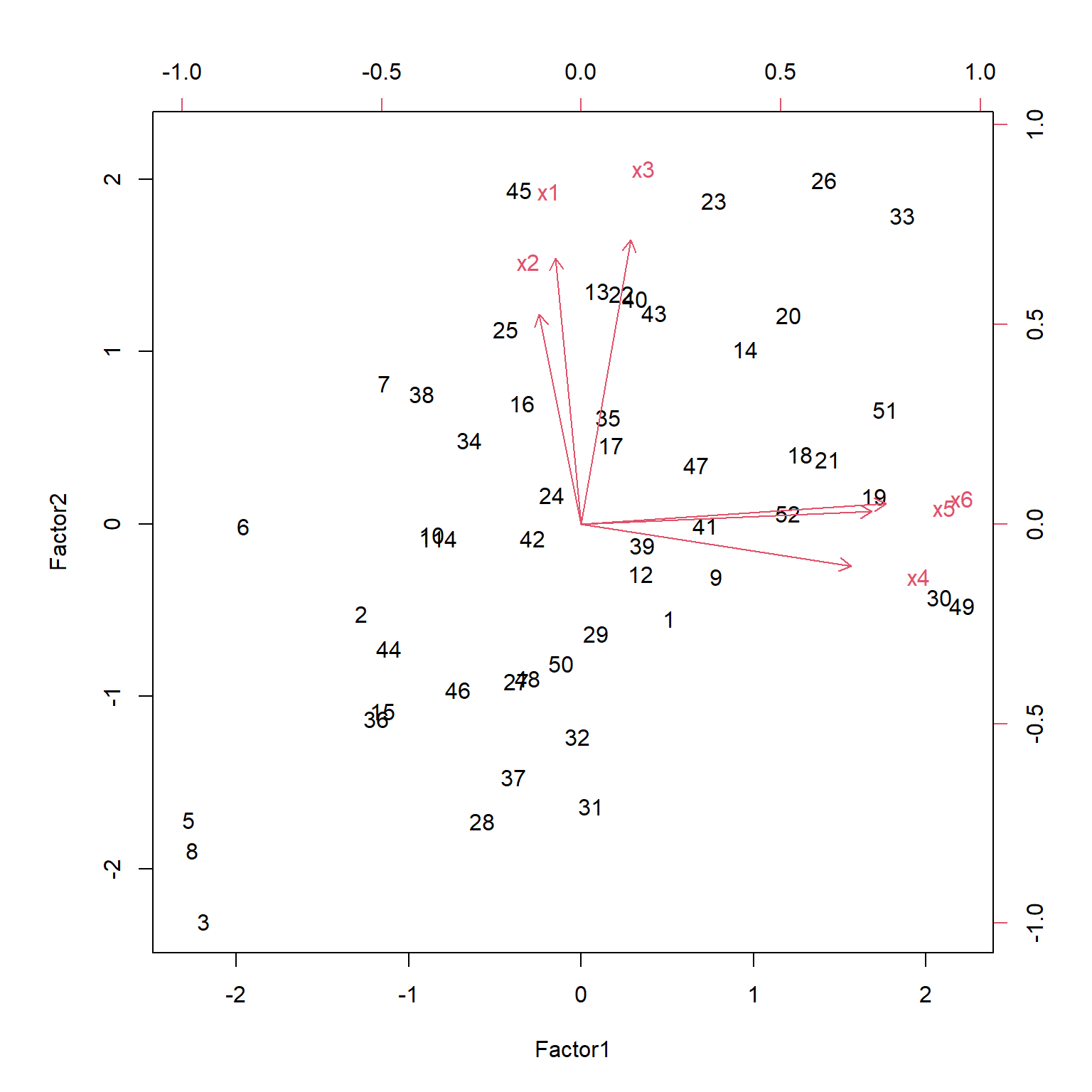
49, 30号学生文科偏科； 45号学生理科偏科。

9.6 例：各国期望寿命

9.6.1 数据

life <- read_csv("data/life.csv",
  show_col_types = FALSE)
knitr::kable(life)

country	m0	m25	m50	m75	w0	w25	w50	w75
Algeria	63	51	30	13	67	54	34	15
Cameroon	34	29	13	5	38	32	17	6
Madagascar	38	30	17	7	38	34	20	7
Mauritius	59	42	20	6	64	46	25	8
Reunion	56	38	18	7	62	46	25	10
Seychelles	62	44	24	7	69	50	28	14
South Africa (C)	50	39	20	7	55	43	23	8
South Africa (W)	65	44	22	7	72	50	27	9
Tunisia	56	46	24	11	63	54	33	19
Canada	69	47	24	8	75	53	29	10
Costa Rica	65	48	26	9	68	50	27	10
Dominican Rep.	64	50	28	11	66	51	29	11
El Salvador	56	44	25	10	61	48	27	12
Greenland	60	44	22	6	65	45	25	9
Grenada	61	45	22	8	65	49	27	10
Guatemala	49	40	22	9	51	41	23	8
Honduras	59	42	22	6	61	43	22	7
Jamaica	63	44	23	8	67	48	26	9
Mexico	59	44	24	8	63	46	25	8
Nicaragua	65	48	28	14	68	51	29	13
Panama	65	48	26	9	67	49	27	10
Trinidad (62)	64	63	21	7	68	47	25	9
Trinidad (67)	64	43	21	6	68	47	24	8
United States (66)	67	45	23	8	74	51	28	10
United States (NW66)	61	40	21	10	67	46	25	11
United States (W66)	68	46	23	8	75	52	29	10
United States (67)	67	45	23	8	74	51	28	10
Argentina	65	46	24	9	71	51	28	10
Chile	59	43	23	10	66	49	27	12
Colombia	58	44	24	9	62	47	25	10
Ecuador	57	46	28	9	60	49	28	11

life数据框包含了各国人口不同性别、不同年龄时的期望剩余寿命数据。我们不从回归角度看待这个数据，直接将m0,m25,m50,m75,w0,w25,w50,w75这8个变量看成原始变量，进行因子分析，希望能得出能反映各国人口在不同性别、不同年龄的期望剩余寿命的潜在因子。

9.6.2 因子分析不旋转

l_fac1 <- factanal(life[,-1], 
  factors=3, method="mle")
l_fac1

## 
## Call:
## factanal(x = life[, -1], factors = 3, method = "mle")
## 
## Uniquenesses:
##    m0   m25   m50   m75    w0   w25   w50   w75 
## 0.005 0.362 0.066 0.288 0.005 0.011 0.020 0.146 
## 
## Loadings:
##     Factor1 Factor2 Factor3
## m0  0.964   0.122   0.226  
## m25 0.646   0.169   0.438  
## m50 0.430   0.354   0.790  
## m75         0.525   0.656  
## w0  0.970   0.217          
## w25 0.764   0.556   0.310  
## w50 0.536   0.729   0.401  
## w75 0.156   0.867   0.280  
## 
##                Factor1 Factor2 Factor3
## SS loadings      3.375   2.082   1.640
## Proportion Var   0.422   0.260   0.205
## Cumulative Var   0.422   0.682   0.887
## 
## Test of the hypothesis that 3 factors are sufficient.
## The chi square statistic is 6.73 on 7 degrees of freedom.
## The p-value is 0.458

三个公共因子是充分的。从载荷看，第一公共因子主要反映了出生时不论男女的期望寿命；第二公共因子主要反映中老年时的期望寿命，第三公共因子则主要反映中老年男性的期望寿命。载荷阵中系数不大不小的元素较多，不利于因子的解释。

9.6.3 用promax旋转

l_fac2 <- factanal(life[,-1], 
  factors=3, method="mle", rotation="promax",
  scores="regression")
l_fac2

## 
## Call:
## factanal(x = life[, -1], factors = 3, scores = "regression",     rotation = "promax", method = "mle")
## 
## Uniquenesses:
##    m0   m25   m50   m75    w0   w25   w50   w75 
## 0.005 0.362 0.066 0.288 0.005 0.011 0.020 0.146 
## 
## Loadings:
##     Factor1 Factor2 Factor3
## m0   1.015  -0.135         
## m25  0.533  -0.129   0.443 
## m50                  0.937 
## m75 -0.298   0.332   0.730 
## w0   1.073          -0.192 
## w25  0.665   0.438         
## w50  0.323   0.662   0.147 
## w75          0.980         
## 
##                Factor1 Factor2 Factor3
## SS loadings      3.118   1.742   1.673
## Proportion Var   0.390   0.218   0.209
## Cumulative Var   0.390   0.608   0.817
## 
## Factor Correlations:
##         Factor1 Factor2 Factor3
## Factor1   1.000   0.505   0.620
## Factor2   0.505   1.000   0.724
## Factor3   0.620   0.724   1.000
## 
## Test of the hypothesis that 3 factors are sufficient.
## The chi square statistic is 6.73 on 7 degrees of freedom.
## The p-value is 0.458

第一公共因子仍反映出生时的剩余寿命，第二公共因子反映成年后的女性寿命，第三公共因子反映成年后的男性寿命。经promax旋转后得到的三个因子的可解释性很好。

生成因子得分，按第一因子从大到小排列：

l_fac2$scores |>
  as_tibble() |>
  mutate(country = life[["country"]]) |>
  select(country, everything()) |>
  arrange(desc(Factor1)) |>
  knitr::kable(digits=2)

country	Factor1	Factor2	Factor3
United States (W66)	1.69	0.70	-1.51
United States (66)	1.62	0.39	-1.36
United States (67)	1.62	0.39	-1.36
Canada	1.55	0.32	-0.83
South Africa (W)	1.53	0.41	-1.63
Trinidad (67)	1.36	-1.34	-0.44
Trinidad (62)	1.11	-1.30	-0.03
Argentina	0.88	0.27	-0.47
United States (NW66)	0.88	-0.15	-1.04
Mauritius	0.61	0.05	-1.20
Jamaica	0.60	-0.82	0.27
Greenland	0.57	-0.76	-0.31
Seychelles	0.55	1.34	-1.31
Reunion	0.40	1.51	-2.53
Honduras	0.23	-2.66	1.33
Costa Rica	0.22	-1.32	1.66
Grenada	0.18	0.40	-0.38
Chile	0.11	1.27	-1.10
Panama	0.07	-1.75	2.15
Mexico	-0.14	-1.20	1.02
Colombia	-0.43	-0.59	0.84
Nicaragua	-0.48	-0.86	2.49
Dominican Rep.	-0.72	-1.00	2.76
South Africa (C)	-0.90	0.43	-0.73
El Salvador	-1.06	0.72	0.57
Tunisia	-1.47	5.17	-2.06
Algeria	-1.52	1.55	2.06
Ecuador	-1.67	-0.14	2.36
Guatemala	-1.90	-1.00	1.64
Cameroon	-2.31	0.54	-1.85
Madagascar	-3.17	-0.57	0.98

9.7 确认性因子分析

9.7.1 介绍

一般的因子分析模型对哪些原始变量和那些公共因子最相关，并没有约束。确认性(confirmatory)因子分析则可以预先确定哪些原始变量与那些公共因子相关，直接设置载荷阵的某些元素为0。这些约束可能来自理论假设，或者来自一般因子分析的结果，然后希望将结果作为类似数据的可推广的模型。虽然可以先进行一般因子分析，再对同一组数据进行确认性因子分析，但是为了测试模型，必须使用新的数据进行测试，而不应该先建立一般因子模型后，用同一组数据建立确认性因子模型并测试模型。

因为因子分析模型是对原始变量的协方差阵结构的一种模型，所以与线性混合模型有相近的地方，确认性因子分析，则是一种潜在(latent)变量建模的一个分支，这种建模方法称为结构方程模型或者协方差结构模型，该模型允许原始变量与潜在变量通过一系列线性方程联系在一起。结构方程模型比因子分析更复杂，但是研究目的也是对原始变量的协方差结构进行简化描述，方法是将原始变量与潜在变量关联，潜在变量之间也可以有关联。

确认性因子模型会设置载荷阵的某些元素等于零，还可能设置公共因子之间的某些相关系数等于零。其它没有设置为零的参数以及特殊因子方差作为自由参数，估计自由参数并建模。

9.7.2 估计、辨识、评估

9.7.2.1 估计

结构方程模型的参数估计，可以先定义实际的原始变量方差阵\(S\)与参数化模型所蕴含的方差阵\(\Sigma(\boldsymbol\theta)\)之间的一个损失函数，比如使用最小二乘损失： \[ \text{FLS}(S, \Sigma(\boldsymbol\theta)) = \sum_{i<j} [s_{ij} - \sigma_{ij}(\boldsymbol\theta)]^2 . \] 这个损失函数有一些缺陷，比如依赖于原始变量的量纲。

实际中估计确认性因子分析和结构方程模型参数的方法，更多是假定原始变量服从多元正态分布，然后利用最大似然估计方法估计模型参数。这等价于最小化如下的损失函数： \[ \text{FML}(S, \Sigma(\boldsymbol\theta)) = \log|\Sigma(\boldsymbol\theta)| - \log|S| + \text{tr}(S \Sigma(\boldsymbol\theta)^{-1}) - p, \] 其中\(p\)是原始变量个数。用数值优化方法求最小值点。

9.7.2.2 可辨识性

如果有不同的参数值，使得最终得到的模型中原始变量协方差阵相同，则模型不可辨识。

考虑如下简单模型： \[\begin{aligned} x =& u + \epsilon\\ y =& v + \delta \\ y' =& v + \delta' . \end{aligned}\] 如果假设\(\delta, \delta', \epsilon\)互相不相关，且与\(u, v\)互不相关，即仅\(u, v\)有相关性。记\(\sigma_{uv} = \text{Cov}(u, v)\)并使用类似记号，则 \[ \Sigma(\boldsymbol\theta) = \begin{pmatrix} \sigma_{uu} + \sigma_{\epsilon\epsilon} \\ \sigma_{uv} & \sigma_{vv} + \sigma_{\delta\delta} \\ \sigma_{uv} & \sigma_{vv} & \sigma_{vv} + \sigma_{\delta'\delta'} \end{pmatrix} . \] 易见其中的\(\sigma_{uu} + \sigma_{\epsilon\epsilon}\)可辨识，但是单独的\(\sigma_{uu}\)和\(\sigma_{\epsilon\epsilon}\)不可辨识。这是因为潜在变量\(u\)仅出现在一个原始变量\(x\)的方程中，所以公共因子\(u\)与特殊因子\(\epsilon\)无法区分。

一般的因子分析模型是不可辨识的，因为正交旋转可以修改载荷阵而不改变原始变量方差阵。

更一般地，结构方程模型并没有普适可用的方法判断模型是否参数可辨识。但是，可辨识的必要条件是自由参数个数不能超过\(p(p+1)/2\)，即\(\Sigma\)中的自由参数个数。

9.7.2.3 模型拟合的评估

先确认模型参数可辨识，然后估计模型参数，后续需要评估模型对原始变量方差阵的拟合程度。可以使用似然比统计量\(\chi^2 = (n-1) \text{FML}_{\min}\)，其中\(n\)是样本量，\(\text{FML}_{\min}\)是最大似然估计对应的FML指标值。取零假设为模型充分拟合原始变量方差阵，对立假设是原始变量方差阵不具有这样的约束， \(n\)充分大时在零假设下\(\chi^2\)服从自由度为\(\nu = \frac{1}{2} p(p+1) - t\)的卡方分布， \(p\)为原始变量维数， \(t\)是模型中自由参数个数。

当\(n\)很大时，及时线性结构方程模型对原始变量方差阵拟合误差很小，检验结果也可能是显著的，所以单独使用这个检验意义不大。如果有嵌套的模型，则可以计算两个嵌套模型的卡方统计量的差，当这个差值很大时，就说明精简的模型不如复杂的模型，否则就应该采用精简的模型。

如果原始变量不服从多元正态分布，这个统计量可能与卡方分布差别较大。

除了使用卡方检验，还应该进行如下的评估：

直接计算原始变量方差阵与模型拟合得到的方差阵之间的差别是否足够小；
计算参数估计的标准误差，以及参数估计之间的相关系数。如果相关系数很大，提示参数可能不可辨识。
如果参数值超出合理范围，比如，负值的方差，超过1的相关系数，这意味着模型拟合错误。

还可以计算拟合优度指标GFI，定义为 \[ \text{GFI} = 1 - \frac{\text{tr}(S \hat\Sigma^{-1} - I) \cdot (S \hat\Sigma^{-1} - I)}{ \text{tr}(S \hat\Sigma^{-1} S \hat\Sigma^{-1})} . \] 其中\(S\)表示原始变量方差阵估计， \(\hat\Sigma\)为模型拟合的原始变量方差阵。取值在0到1之间， 0表示没有拟合， 1表示完全拟合，一般在0.90或0.95以上才算是较好拟合。

修正的GFI指标(AGFI)针对自由参数个数进行修正，公式为 \[ \text{AGFI} = 1 - \frac{k}{\text{df}}(1 - \text{GFI}) . \] 其中\(k\)是矩阵\(S\)中不同元素个数（考虑到对称性影响）， df是模型自由度。

可以用GFI、AGFI指标比较同一数据的不同模型，或者比较用于不同数据的结果。

还有类似的根均方残差(RMSR，root mean square residual)指标，指标小于0.05时认为是较好拟合结果。

9.7.3 示例：能力与志向

Calsyn and Kenny (1977)研究了学生能力与志向的问题。数据是556位美国八年级白人学生的6个评测指标：

SCA：能力的自我评价；
PPE：感知的父母评价；
PTE：感知的教师评价；
PFE：感知的朋友评价；
EA：教育方面的志向；
CP：读大学的计划。

确认性因子模型仍从方差阵或相关阵出发建模，这6个指标的相关系数如下：

library("sem")

## Warning: package 'sem' was built under R version 4.2.2

d <- read_csv("data/ability.csv",
  show_col_types = FALSE)
d <- as.data.frame(d)
rownames(d) <- d[["var"]]
ability <- as.matrix(d[,-1])
knitr::kable(ability)

	SCA	PPE	PTE	PFE	EA	CP
SCA	1.00	0.73	0.70	0.58	0.46	0.56
PPE	0.73	1.00	0.68	0.61	0.43	0.52
PTE	0.70	0.68	1.00	0.57	0.40	0.48
PFE	0.58	0.61	0.57	1.00	0.37	0.41
EA	0.46	0.43	0.40	0.37	1.00	0.72
CP	0.56	0.52	0.48	0.41	0.72	1.00

相关系数矩阵作图，将相关性强的凑在一起：

library(ggcorrplot)
ggcorrplot(ability, hc.order=TRUE,
  lab = TRUE)

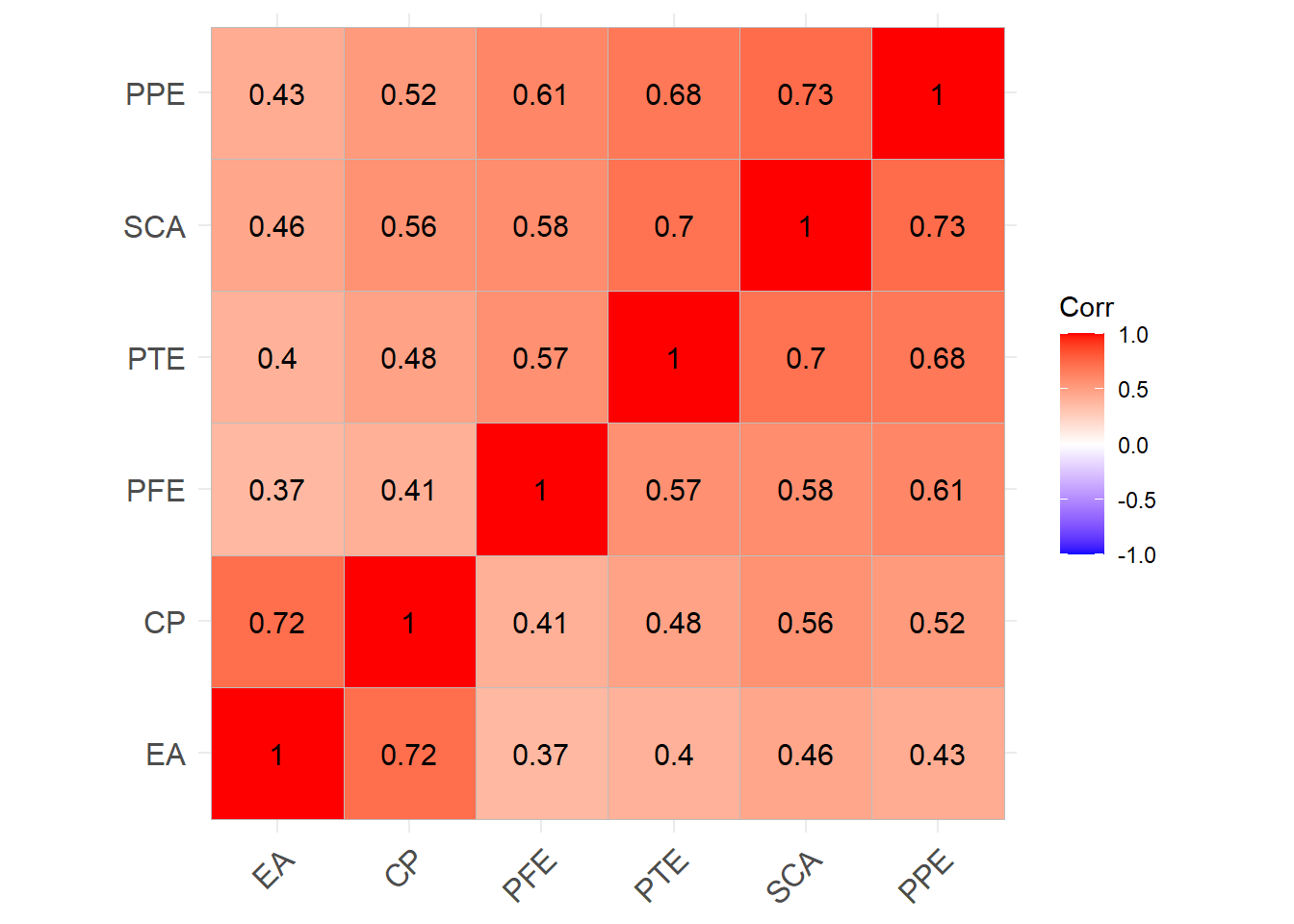
建立确认性因子分析模型，考虑两个潜在因子：

\(f_1\)：Ability, 能力；
\(f_2\)：Aspiration，志向。

认为\(f_1\)和\(f_2\)相关，方差都等于1， SCA, PPE, PTE, PFE是反映能力的指标，载荷阵中仅与Ability相关， EA, CP是反映志向的指标，载荷阵中仅与Aspiration相关。模型为 \[\begin{aligned} \text{SCA} =& \lambda_1 f_1 + 0\, f_2 + u_1, \\ \text{PPE} =& \lambda_2 f_1 + 0\, f_2 + u_2, \\ \text{PTE} =& \lambda_3 f_1 + 0\, f_2 + u_3, \\ \text{PFE} =& \lambda_4 f_1 + 0\, f_2 + u_4, \\ \text{EA} =& 0\, f_1 + \lambda_5 f_2 + u_5, \\ \text{CP} =& 0\, f_1 + \lambda_6 f_2 + u_6 . \end{aligned}\]

其中\(\lambda_1, \dots, \lambda_6\)是6个载荷阵参数， \(u_1, \dots, u_6\)的6个特殊因子方差是方差参数， \(f_1, f_2\)的相关系数\(\rho\)也是一个参数，共有13个要估计的参数。

这是确认性因子分析模型，和正常因子分析模型相比，其中的某些载荷阵系数固定为0，并允许公因子（隐含变量）之间有相关性。确认性因子分析模型属于结构方程模型，结构方程模型则还允许隐含变量出现在方程左侧。

R的sem包可以建立结构方程模型，指定模型如下：

ab_mt <- c(
  "Ability     -> SCA, lambda1, NA",
  "Ability     -> PPE, lambda2, NA",
  "Ability     -> PTE, lambda3, NA",
  "Ability     -> PFE, lambda4, NA",
  "Aspiration  -> EA, lambda5, NA",
  "Aspiration  -> CP, lambda6, NA",
  "Ability    <-> Aspiration, rho, NA",
  "SCA        <-> SCA, theta1, NA",
  "PPE        <-> PPE, theta2, NA",
  "PTE        <-> PTE, theta3, NA",
  "PFE        <-> PFE, theta4, NA",
  "EA         <-> EA, theta5, NA",
  "CP         <-> CP, theta6, NA",
  "Ability    <-> Ability, NA, 1",
  "Aspiration <-> Aspiration, NA, 1")
ab_mod <- specifyModel(text = ab_mt)

## NOTE: it is generally simpler to use specifyEquations() or cfa()
##       see ?specifyEquations

用specifyModel()输入用字符串向量表示的RAM(网状动作模型，reticular action model)格式模型。其中的每一项都有单向箭头或者双向箭头，单向箭头表示载荷阵参数，双向箭头表示方差参数。前6项给出了两个潜在因子(Ability和Aspiration)与6个原始变量之间的载荷参数，给出了参数名(lambda1到lambda6)，最后的NA表示没有设置固定值。第7项给出了两个潜在因子的相关系数（也是方差，因为都标准化了）参数rho。第8到第13项给出了6个特殊因子参数名(theta1到theta6)。第14到第15项给出了两个潜在因子(Ability和Aspiration)的方差参数，没有方差参数，而是固定为常数1。

用sem()函数建立模型：

(ab_sem <- sem(ab_mod, S = ability, N = 556))

## 
##  Model Chisquare =  9.255732   Df =  8 
## 
##   lambda1   lambda2   lambda3   lambda4   lambda5   lambda6       rho    theta1 
## 0.8632049 0.8493226 0.8050861 0.6952671 0.7750850 0.9289304 0.6663697 0.2548772 
##    theta2    theta3    theta4    theta5    theta6 
## 0.2786512 0.3518366 0.5166036 0.3992432 0.1370884 
## 
##  Iterations =  29

sem()中第一个参数是模型， S是输入的协方差阵或相关系数阵， N是原始样本量。

用summary()显示参数估计和检验结果：

(ab_summ <- summary(ab_sem, fit.indices=c(
  "GFI", "AGFI", "RMSEA", 
  "AIC", "BIC")))

## 
##  Model Chisquare =  9.255732   Df =  8 Pr(>Chisq) = 0.3211842
##  Goodness-of-fit index =  0.9944253
##  Adjusted goodness-of-fit index =  0.9853663
##  RMSEA index =  0.01681733   90% CI: (NA, 0.05432054)
##  AIC =  35.25573
##  BIC =  -41.31041
## 
##  Normalized Residuals
##       Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
## -0.4409685 -0.1870306 -0.0000018 -0.0130992  0.2107128  0.5333068 
## 
##  R-square for Endogenous Variables
##    SCA    PPE    PTE    PFE     EA     CP 
## 0.7451 0.7213 0.6482 0.4834 0.6008 0.8629 
## 
##  Parameter Estimates
##         Estimate  Std Error  z value   Pr(>|z|)                             
## lambda1 0.8632049 0.03514508 24.561188 3.284552e-133 SCA <--- Ability       
## lambda2 0.8493226 0.03545022 23.958178 7.593661e-127 PPE <--- Ability       
## lambda3 0.8050861 0.03640470 22.114892 2.272503e-108 PTE <--- Ability       
## lambda4 0.6952671 0.03863370 17.996387  2.079489e-72 PFE <--- Ability       
## lambda5 0.7750850 0.04035675 19.205834  3.307658e-82 EA <--- Aspiration     
## lambda6 0.9289304 0.03940959 23.571177 7.615270e-123 CP <--- Aspiration     
## rho     0.6663697 0.03095414 21.527645 8.578257e-103 Aspiration <--> Ability
## theta1  0.2548772 0.02336722 10.907470  1.061704e-27 SCA <--> SCA           
## theta2  0.2786512 0.02412754 11.549097  7.460043e-31 PPE <--> PPE           
## theta3  0.3518366 0.02691875 13.070321  4.865973e-39 PTE <--> PTE           
## theta4  0.5166036 0.03472534 14.876847  4.659431e-50 PFE <--> PFE           
## theta5  0.3992432 0.03819583 10.452535  1.426604e-25 EA <--> EA             
## theta6  0.1370884 0.04350459  3.151126  1.626425e-03 CP <--> CP             
## 
##  Iterations =  29

其中fit.indices用来指定要计算的拟合优度指标。从拟合优度指标看，模型拟合是很好的。