40 随机模拟
40.1 随机数
随机模拟是统计研究的重要方法, 另外许多现代统计计算方法(如MCMC)也是基于随机模拟的。 R中提供了多种不同概率分布的随机数函数, 可以批量地产生随机数。 一些R扩展包利用了随机模拟方法,如boot包进行bootstrap估计。
所谓随机数,实际是“伪随机数”, 是从一组起始值(称为种子), 按照某种递推算法向前递推得到的。 所以,从同一种子出发,得到的随机数序列是相同的。
为了得到可重现的结果, 随机模拟应该从固定不变的种子开始模拟。
用set.seed(k)指定一个编号为k的种子,
这样每次从编号k种子运行相同的模拟程序可以得到相同的结果。
还可以用set.seed()加选项kind=指定后续程序要使用的随机数发生器名称,
用normal.kind=指定要使用的正态分布随机数发生器名称。
R提供了多种分布的随机数函数,如runif(n)产生n个标准均匀分布随机数,
rnorm(n)产生n个标准正态分布随机数。
例如:
round(runif(5), 2)
## [1] 0.44 0.56 0.93 0.23 0.22
round(rnorm(5), 2)
## [1] -0.20 1.10 -0.02 0.16 2.02注意因为没有指定种子,每次运行会得到不同的结果。
在R命令行运行
可以查看R中提供的不同概率分布。
40.2 sample()函数
sample()函数从一个有限集合中无放回或有放回地随机抽取,
产生随机结果。
例如,为了设随机变量\(X\)取值于\(\{\text{正面}, \text{反面} \}\), 且\(P(X=\text{正面}) = 0.7 = 1 - P(X = \text{反面})\), 如下程序产生\(X\)的10个随机抽样值:
sample(c('正面', '反面'), size=10,
prob=c(0.7, 0.3), replace=TRUE)
## [1] "反面" "反面" "反面" "反面" "正面"
## [6] "正面" "正面" "正面" "反面" "反面"sample()的选项size指定抽样个数,
prob指定每个值的概率,
replace=TRUE说明是有放回抽样。
如果要做无放回等概率的随机抽样,
可以不指定prob和replace(缺省是FALSE)。
比如,下面的程序从1:10随机抽取4个:
如果要从\(1:n\)中等概率无放回随机抽样直到每一个都被抽过,只要用如:
这实际上返回了\(1:10\)的一个重排。
dplyr包的sample_n()函数与sample()类似,
但输入为数据框,
输出为随机抽取的数据框行子集。
40.3 随机模拟示例
40.3.1 估计期望值
设随机变量或随机向量\(X\)有复杂的分布, 使得期望\(\theta = E h(X)\)很难计算。 如果可以得到\(X\)的\(N\)个独立同分布抽样值\(X_1, X_2, \dots, X_N\), 则可估计\(\theta\)为: \[ \hat\theta = \frac{1}{N} \sum_{i=1}^N h(X_i) , \] 这时\(E \hat\theta = \theta\), 估计无偏; 均方误差为 \[\begin{aligned} \text{MSE} =& E|\hat\theta - \theta|^2 = \text{Var}(\hat\theta) = \text{SE}^2 \\ =& \frac{\text{Var}(h(X))}{N} \approx \frac{S_N^2}{N} , \end{aligned}\] 其中 \[ S_N^2 = \frac{1}{N-1} \sum_{i=1}^N (h(X_i) - \hat\theta)^2 \] 是样本方差。 由强大数律可知\(N\to\infty\)时\(\hat\theta\)以概率1收敛到\(\theta\), 由中心极限定理可知\(N\)充分大时\(\hat\theta\)有近似正态分布 \[ \text{N}(\theta, \text{SE}^2) . \]
例如,考虑正方形区域\(\Omega = \{(x,y): x \in [0,1], y \in [0,1] \}\), 以及其中的四分之一扇形\(A = \{(x,y): (x,y) \in \Omega, x^2 + y^2 \leq 1 \}\)。 设\(\boldsymbol X\)服从\(\Omega\)上的均匀分布, 令 \[ Y = \begin{cases} 1, & \text{当} \boldsymbol X \in A, \\ 0, & \text{其它} \end{cases} \] 则\(Y\)服从两点分布, 概率为 \[ p = E Y = \frac{\frac{1}{4} \pi 1^2}{1^2} = \frac{\pi}{4} . \]
在\(\Omega\)中投入\(N=10000\)个点, 得到\(N\)个\(Y_i, i=1,2,\dots,N\)的值,估计\(\pi\)为 \[ \hat\pi = 4 \bar Y = \frac{4}{N} \sum_{i=1}^N Y_i . \] \(E \hat\pi = \pi\), 估计的根均方误差可估计为 \[ \text{RMSE} = \sqrt{E | \hat\pi - \pi |^2} = 4 \frac{\sqrt{\text{Var}(Y)}}{\sqrt{N}} \approx 4 \frac{S_N}{\sqrt{N}} . \]
程序如下:
est_pi <- function(N){
set.seed(101)
x1 <- runif(N, 0, 1)
x2 <- runif(N, 0, 1)
y <- as.numeric(x1^2 + x2^2 <= 1)
hat_pi <- 4*mean(y)
se <- 4 * sd(y) / sqrt(N)
cat("N = ", N, " pi估计值 =", hat_pi, " SE =", se, "\n")
invisible(list(N=N, hat_pi = hat_pi, SE = se))
}
est_pi(1E4)
## N = 10000 pi估计值 = 3.14 SE = 0.01643372 估计的标准误差(SE)还是比较大, 提高到\(N=10^6\),精度可以增加一位小数:
40.3.2 线性回归模拟
考虑如下线性回归模型
\[\begin{aligned}
y = 10 + 2 x + \varepsilon,
\ \varepsilon \sim \text{N}(0, 0.5^2) .
\end{aligned}\]
假设有样本量\(n=10\)的一组样本, R函数lm()可以 可以得到截距\(a\),
斜率\(b\)的估计\(\hat a, \hat b\),
以及相应的标准误差\(\text{SE}(\hat a)\), \(\text{SE}(\hat b)\)。
样本可以模拟产生。
模型中的自变量\(x\)可以用随机数产生,
比如,用sample()函数从\(1:10\)中随机有放回地抽取\(n\)个。
模型中的随机误差项\(\varepsilon\)可以用rnorm()产生。
产生一组样本的程序如:
n <- 10; a <- 10; b <- 2
x <- sample(1:10, size=n, replace=TRUE)
eps <- rnorm(n, 0, 0.5)
y <- a + b * x + eps如下程序计算线性回归:
##
## Call:
## lm(formula = y ~ x)
##
## Coefficients:
## (Intercept) x
## 10.133 2.036如下程序计算线性回归的多种统计量:
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.34460 -0.17868 -0.02952 0.12797 0.49934
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.13297 0.16058 63.10 4.42e-12 ***
## x 2.03556 0.03258 62.49 4.78e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2819 on 8 degrees of freedom
## Multiple R-squared: 0.998, Adjusted R-squared: 0.9977
## F-statistic: 3905 on 1 and 8 DF, p-value: 4.783e-12如下程序返回一个矩阵, 包括\(a, b\)的估计值、标准误差、t检验统计量、检验p值:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.132970 0.16058073 63.10203 4.423167e-12
## x 2.035564 0.03257544 62.48768 4.782587e-12如下程序把上述矩阵的前两列拉直成一个向量返回:
## [1] 10.13296972 2.03556360 0.16058073 0.03257544这样得到 \(\hat a, \hat b, \text{SE}(\hat a), \text{SE}(\hat b)\)这四个值。
用replicate(, 复合语句)执行多次模拟, 返回向量或矩阵结果,
返回矩阵时,每列是一次模拟的结果。
下面是线性回归整个模拟程序,写成了一个函数。
reg.sim <- function(
a=10, b=2, sigma=0.5,
n=10, B=1000){
set.seed(1)
resm <- replicate(B, {
x <- sample(1:10, size=n, replace=TRUE)
eps <- rnorm(n, 0, 0.5)
y <- a + b * x + eps
c(summary(lm(y ~ x))$coefficients[,1:2])
})
resm <- t(resm)
colnames(resm) <- c('a', 'b', 'SE.a', 'SE.b')
cat(B, '次模拟的平均值:\n')
print( apply(resm, 2, mean) )
cat(B, '次模拟的标准差:\n')
print( apply(resm, 2, sd) )
}运行测试:
## 1000 次模拟的平均值:
## a b SE.a SE.b
## 9.9970476 1.9994490 0.3639505 0.0592510
## 1000 次模拟的标准差:
## a b SE.a SE.b
## 0.37974881 0.06297733 0.11992515 0.01795926可以看出,标准误差作为\(\hat a, \hat b\)的标准差估计, 与多次模拟得到多个\(\hat a, \hat b\)样本计算得到的标准差估计是比较接近的。 结果中\(\text{SE}(\hat a)\)的平均值为0.364, 1000次模拟的\(\hat a\)的样本标准差为0.380,比较接近; \(\text{SE}(\hat b)\)的平均值为0.0593, 1000次模拟的\(\hat b\)的样本标准差为0.0630,比较接近。
40.4 bootstrap
随机模拟研究中, 可以从理论模型生成许多组独立样本, 对每一组样本进行估计, 最后评估估计效果。
实际问题中, 仅有一组样本, 能否利用随机模拟方法评估对这组样本的估计效果? bootstrap就是这样一种方法, 对原始样本进行“再抽样”, 得到与原始样本分布相近的许多组样本, 称为bootstrap样本, 对每一个bootstrap样本进行估计, 用多个样本的估计结果来评估估计效果。
再抽样分为非参数和参数两种方法, 其中非参数bootstrap对原始数据集进行多次(如\(B=1000\))重复有放回抽样, 每次得到一个同样大小的bootstrap数据集, 对每个bootstrap数据集进行相同的估计过程, 用得到的多次估计结果评估参数估计的精度、分布等。 参数方法是对原始数据集利用参数方法建模, 然后把估计出来的参数当作真实模型参数产生新的多组样本。
40.4.1 boot扩展包
基本R内嵌的boot包可以用来对数据集进行bootstrap抽样, 输入数据集和对数据集进行处理的函数, 直接输出对多个bootstrap数据集分析的结果。
作为示例,
考虑肺癌放疗研究中放疗前后的肿瘤大小(v0, v1)的线性回归模型估计参数\(\hat\beta_0\), \(\hat\beta_1\)的评估问题。
得到的回归方程是:
\[
v_1 \approx \hat\beta_0 + \hat\beta_1 v_0 .
\]
library(tidyverse)
library(boot)
d.cancer <- read_csv(
"data/cancer.csv",
locale=locale(encoding="GBK"),
show_col_types=FALSE)
fa <- function(d, inds){
dd <- d[inds,]
lm1 <- lm(v1 ~ v0, data=dd)
unname(coef(lm1))
}
lm0 <- lm(v1 ~ v0, data=d.cancer)
print(summary(lm0))##
## Call:
## lm(formula = v1 ~ v0, data = d.cancer)
##
## Residuals:
## Min 1Q Median 3Q Max
## -61.536 -10.582 -5.011 11.750 58.621
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.33079 7.26335 0.459 0.65
## v0 0.37576 0.05376 6.990 6.4e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24.56 on 32 degrees of freedom
## Multiple R-squared: 0.6042, Adjusted R-squared: 0.5919
## F-statistic: 48.86 on 1 and 32 DF, p-value: 6.401e-08set.seed(101)
btr <- boot(d.cancer, fa, R=1000)
cat("Intercept: bias = ", btr$t0[1] - mean(btr$t[,1]),
" SE = ", sd(btr$t[,1]), "\n")## Intercept: bias = 0.2877853 SE = 4.78422## v0 slope: bias = -0.003612172 SE = 0.05450733boot()函数的第一个自变量是data,
为原始数据集,
第二个自变量是statistic,
是统计估计函数,
该函数第一个自变量为原始数据,
第二个自变量是每次重抽样的下标向量,
R是重复抽样次数,
函数输出要考察的参数估计。
boot()的结果(上面程序中的btr)是一个列表,
列表元素t0是对原始数据集的参数估计,
而t是对每一个重抽样数据集的参数估计,
每个重抽样的数据集占据矩阵t的一行,
每个估计量占据一列。
在这个例子中, bootstrap对斜率项的参数估计的标准误差估计与参数模型结果相近, 但对截距项的标准误差估计与参数模型结果相差较大。 还利用bootstrap方法估计了偏度, 但是注意线性回归模型的最小二乘估计在理论上是无偏估计。
利用得到的bootstrap样本计算\(\beta_0\)和\(\beta_1\)的置信区间:
ci_b0 <- quantile(btr$t[,1], c(0.025, 0.975))
ci_b1 <- quantile(btr$t[,2], c(0.025, 0.975))
cat("95% CI for beta0: (",
ci_b0[1], ", ", ci_b0[2], ")\n")## 95% CI for beta0: ( -5.944525 , 12.44923 )## 95% CI for beta1: ( 0.277491 , 0.4920218 )40.4.2 rsample扩展包
boot扩展包的功能比较固定, 另一个rsample扩展包则与函数式编程风格比较接近, 可以比较灵活地进行各种重抽样, 包括bootstrap、交叉验证、重要性抽样等。
bootstraps函数输入一个数据集,
输出多个bootstrap数据集并将其存放在一个tibble数据框的列表类型的列splits中,
每个元素是rsplit类型,
可以用as.data.frame()或者analysis()函数将其转换成数据框。
利用tibble的列表列,我们可以实现管道形式的bootstrap分析。 如:
library(rsample)
fb <- function(dd){
lm1 <- lm(v1 ~ v0, data=dd)
as_tibble(rbind(coef(lm1)))
}
btr2 <- d.cancer |>
bootstraps(times=1000) |>
pull(splits) |>
map_dfr( \(df) fb(analysis(df)) )
cat("Intercept: bias = ", coef(lm0)[1] - mean(btr2[[1]]),
" SE = ", sd(btr2[[1]]), "\n")## Intercept: bias = 0.1611144 SE = 4.905335## v0 slope: bias = -0.001650511 SE = 0.05649049ci_b0 <- quantile(btr2[[1]], c(0.025, 0.975))
ci_b1 <- quantile(btr2[[2]], c(0.025, 0.975))
cat("95% CI for beta0: (",
ci_b0[1], ", ", ci_b0[2], ")\n")## 95% CI for beta0: ( -6.250138 , 12.52947 )## 95% CI for beta1: ( 0.2667938 , 0.4824034 )结果的btr2是一个两列的数据框,
每一行包含对一个重抽样数据集的两个回归系数估计。
40.4.3 例:核密度的bootstrap置信区间
R自带的数据框faithful内保存了美国黄石国家公园Faithful火山的272次爆发持续时间和间歇时间。
为估计爆发持续时间的密度,可以用核密度估计方法,
R函数density可以执行此估计,
返回\(N\)个格子点上的密度曲线坐标:
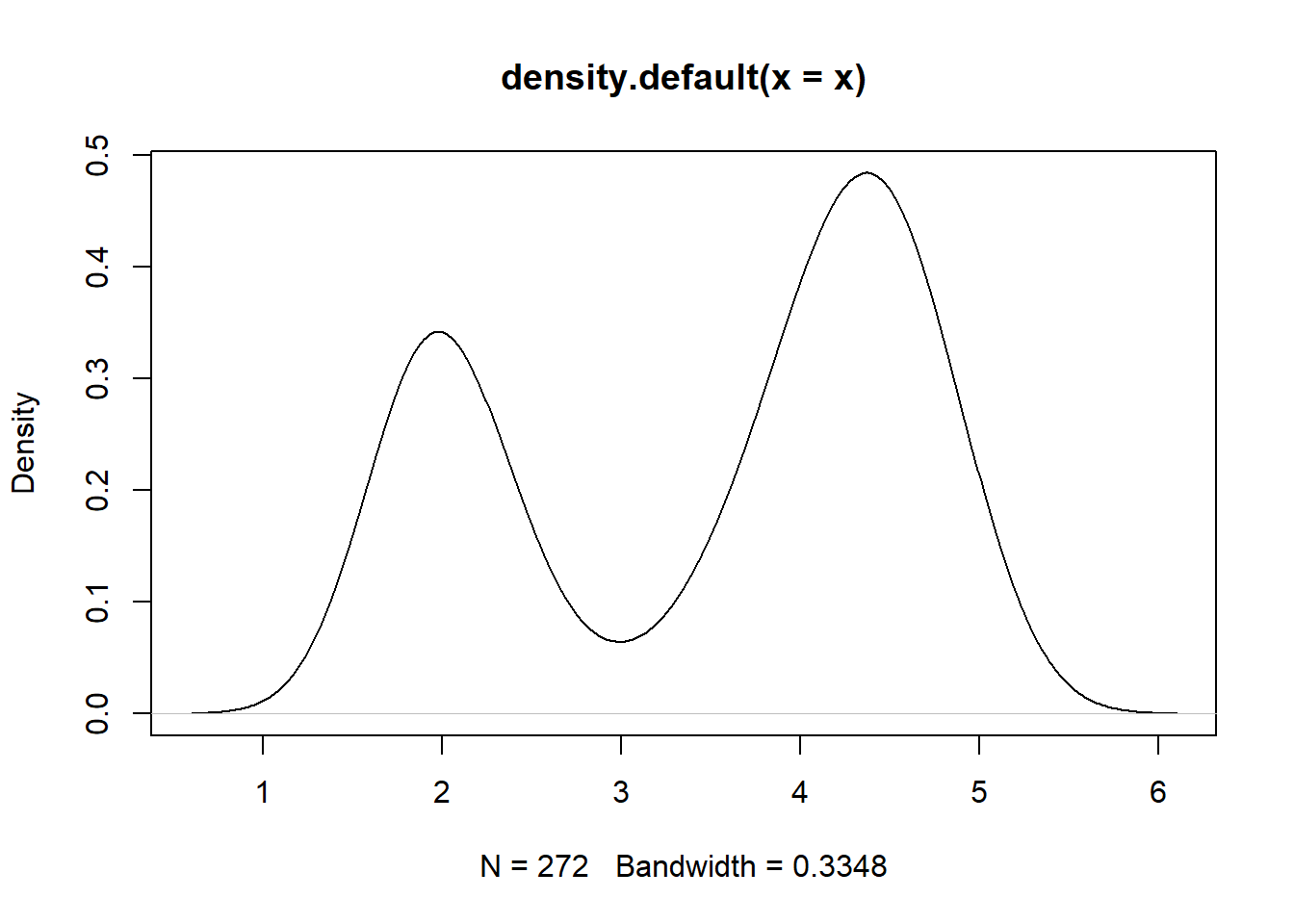
这个密度估计明显呈现出双峰形态。
核密度估计是统计估计, 为了得到其置信区间(给定每个\(x\)坐标,真实密度\(f(x)\)的单点的置信区间), 采用如下非参数bootstrap方法:
重复\(B=10000\)次, 每次从原始样本中有重复地抽取与原来大小相同的一组样本, 对这组样本计算核密度估计, 结果为\((x_i, y_i^{(j)}), i=1,2,\dots,N, j=1,2,\dots, B\), 每组样本估计\(N\)个格子点的密度曲线坐标, 横坐标不随样本改变。
对每个横坐标\(x_i\), 取bootstrap得到的\(B\)个\(y_i^{(j)}, j=1,2,\dots,B\)的0.025和0.975样本分位数, 作为真实密度\(f(x_i)\)的bootstrap置信区间。
在R中利用replicate()函数实现:
set.seed(1)
resm <- replicate(10000, {
x1 <- sample(x, replace=TRUE)
density(x1, from=min(est0$x),
to=max(est0$x))$y
})
CI <- apply(resm, 1, quantile, c(0.025, 0.975))
plot(est0, ylim=range(CI), type='n')
polygon(c(est0$x, rev(est0$x)),
c(CI[1,], rev(CI[2,])),
col='grey', border=FALSE)
lines(est0, lwd=2)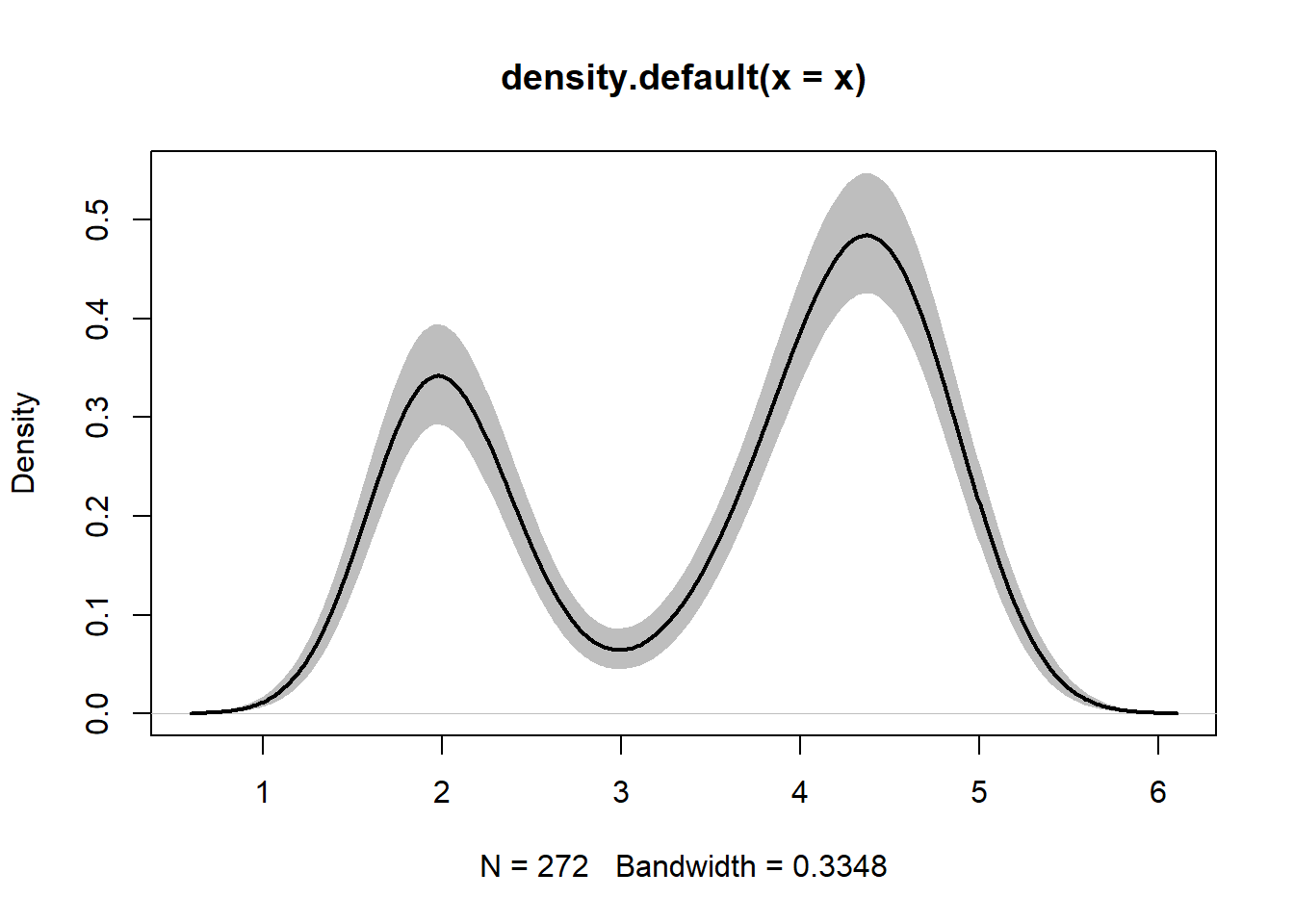
程序中用set.seed(1)保证每次运行得到的结果是不变的,
replicate()函数第一参数是重复模拟次数,
第二参数是复合语句,
这些语句是每次模拟要执行的计算。
在每次模拟中,
用带有replace=TRUE选项的sample()函数从样本中有放回地抽样得到一组bootstrap样本,
每次模拟的结果是在指定格子点上计算的核密度估计的纵坐标。
replicate()的结果为一个矩阵,
每一列是一次模拟得到的纵坐标集合。
对每个横坐标格子点,用quantile()函数计算\(B\)个bootstrap样本的2.5%和97.5%分位数,
循环用apply()函数表示。
polygon()函数指定一个多边形的顺序的顶点坐标用col=指定的颜色填充,
本程序中实现了置信下限与置信上限两条曲线之间的颜色填充。
lines()函数绘制了与原始样本对应的核密度估计曲线。
40.5 附录:完全试验方案设计函数
最简单的模拟试验设计, 是将考虑的所有因素的所有水平组合都执行, 比如,分别有2、3、4个水平的三个因素要进行完全试验, 需要\(2 \times 3 \times 4 = 24\)个方法。 下面的函数可以用来产生这样的试验方案, 输出为一个数据框, 数据框的每一行是一次试验的方法。
tidyr包的expand_grid()函数可以实现这样的功能,
基本R的expand.grid()函数有类似功能。
这两个函数输入因子,产生完全试验组合。
参见23.17。
下面的程序直接实现了略强一些的功能, 支持以数据框为输入。
## 生成完全试验设计方案的函数。
## 输入:
## varlist: 列表,元素可以是正整数、向量或数据框,
## 每个元素代表一个单纯的或者组合的因素。
## 元素取正整数时,表示仅用编号表示的因素的水平数。
## 元素取数值型或字符型向量时,表示因素的各个水平;
## 元素取多列的数据框时,每一行是一种因素组合,
## 数据框的每一列仍看作一个因素,但只允许数据框的各行出现的因素组合。
## numbering: 真值表示输出中增加一列expNumber表示互不相同的试验方案的编号,
## 假值则不增加这一列。
## size: 每种试验方案重复多少行。
## 输出:一个R数据框,每一行代表一次试验,每一列代表一个因素取值。
complete.design <- function(
varlist,
numbering=TRUE, # 是否为试验方案编号
size=1){ # 每个方案的重复次数
nf <- length(varlist)
vl <- vector(mode="list", length=nf)
tf <- character(nf)
for(i in seq_along(varlist)){
if(length(varlist[[i]])==1){
if(varlist[[i]]==as.integer(varlist[[i]]) && varlist[[i]] > 0){
# 用一个正整数表示的因子,就只需要用编码表示各个水平
vl[[i]] <- factor(seq(varlist[[i]]))
tf[i] <- "factor"
} else {
stop("非法输入!")
}
} else if(is.data.frame(varlist[[i]])){
# 数据框,可以有一到多列,但是不可拆分,看作固定的组合
vl[[i]] <- seq(nrow(varlist[[i]]))
tf[i] <- "df"
} else {
# 普通向量,元素为因素水平
stopifnot(!any(duplicated(varlist[[i]])))
vl[[i]] <- factor(varlist[[i]])
tf[i] <- "factor"
}
}
## 每个因素的水平数
nlev <- vapply(vl, length, 1)
## 总试验次数
ne <- prod(nlev) * size
## 每个因子的重复数
nr <- rev(cumprod(rev(c(nlev, size))))[-1]
## 每个因子的循环次数
nc <- ne / nr
## 产生作为数据集草稿的列表
dl <- list()
for(i in seq_along(vl)){
idl <- as.integer(gl(nlev[i], nr[i], ne))
if(tf[i]=="factor"){
## 单个因素
dl[[i]] <- data.frame(
factor(idl, labels=levels(vl[[i]])))
names(dl[[i]]) <- names(varlist)[[i]]
} else {
## 数据框,要恢复数据框
dl[[i]] <- varlist[[i]][idl,]
}
}
## 合并数据框得到最终结果
d <- dl[[1]]
if(nf>1){
for(i in seq(2, nf)){
d <- cbind(d, dl[[i]])
}
}
if(numbering){
d <- cbind(d, data.frame(
expNumber = rep(seq(ne/size), each=size)))
}
d
}
## 测试程序
test1 <- function(){
complete.design(list(f1=3, f2=c("a", "b"), f3=4))
}
print(test1())
test2 <- function(){
complete.design(list(f1=3, f2=c("a", "b"), f3=4), size=2)
}
print(test2())
test3 <- function(){
complete.design(list(f1=3, f2=c("a", "b"), f3=data.frame(
fa=c(0.01, 0.05, 0.1), fb = c("x", "x", "y"))), size=2)
}
print(test3())