21 Julia编程示例–科学计算问题
21.1 用迭代计算平方根
求某个正数\(x\)的平方根, 相当于求解方程\(f(u) = u^2 - x = 0\)。 利用一阶泰勒展开式\(f(u) = f(u_0) + f'(u_0)(u - u_0) + o(u-u_0)\), 其中\(f'(u) = 2u\), 令\(f(u)=0\)得 \[ u \approx u_0 - \frac{f(u_0)}{f'(u_0)}, \] 将其作为迭代公式 \[\begin{aligned} u_n =& u_{n-1} - \frac{f(u_{n-1})}{f'(u_{n-1})} \\ =& u_{n-1} - \frac{u_{n-1}^2 - x}{2 u_{n-1}} \\ =& \frac12 \left( u_{n-1} + \frac{x}{u_{n-1}} \right), n=1,2,\dots \end{aligned}\] 给定一个初始值\(u_0\), 迭代直到\(|u_{n} - u_{n-1}| < \epsilon\)为止, \(\epsilon\)是预先给定的精度如\(10^{-6}\)。
程序如下:
function mysqrt(x, eps=1E-6)
u = 1.0
u1 = 0.0
while abs(u - u1) >= eps
u1 = u
u = 0.5*(u + x/u)
end
return u
end
mysqrt(2)
## 1.41421356237309521.2 圆周率
21.2.1 割圆术
公元3世纪北魏时期科学家刘徽在《九章算术注》中记载了割圆术估计圆周率的方法。
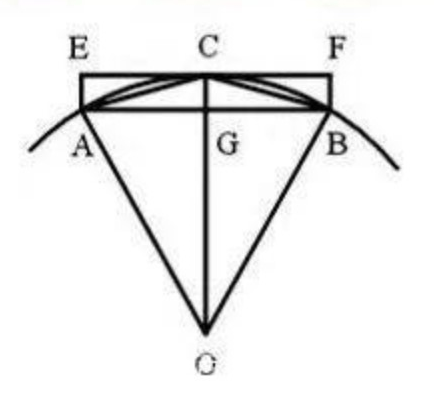
很容易算出内接6六边形等低阶内接正\(n\)边形的弦边长和面积。 比如, 设圆半径为1, 则内接正六边形可等分为6个正三角形, 其弦边的长为1, 面积为\(\frac{\sqrt{2}}{4}\), 六边形面积为\(\frac{3\sqrt{2}}{2} \approx 2.12\)。
设内接正\(n\)边形的弦边(靠近圆周的边)长为\(l_n\), 面积为\(S_n\), 可以分解为\(n\)个等腰三角形, 腰长为1, 底边长为\(l_n\)。 如图中的三角形OAB。 将这个三角形的顶角等分, 设与圆周的交点为C, 则三角形OAC构成正\(2n\)边形的一部分。 如此细分令\(n \to \infty\)则\(\frac{1}{2} n l_n \to \pi\), \(S_n \to \pi\)。
如何递推计算\(l_{2n}\)和\(S_{2n}\)? 设角平分线OC和弦AB的交点为G, 设CG=\(x\), 则OG=\(1-x\), AG = \(\frac{l_n}{2}\), AC = \(l_{2n}\), 于是由勾股定理得 \[\begin{aligned} l_{2n}^2 =& \left( \frac{l_n}{2} \right)^2 + x^2, \\ 1 =& \left( \frac{l_n}{2} \right)^2 + (1-x)^2 . \end{aligned}\] 从第二个方程解出\(x\),代入第一个方程,得 \[ l_{2n} = \sqrt{ \left( 1 - \sqrt{1 - \left( \frac{l_n}{2} \right)^2} \right)^2 + \left( \frac{l_n}{2} \right)^2} . \] 递推过程仅需要使用开平方根运算, 所以在古代的研究条件下是可以手工计算的。 从\(l_n\), 可知三角形OAB面积为\(\frac{1}{2} l_n \sqrt{1 - (\frac{l_n}{2})^2}\), 从而正\(n\)边形面积为 \[ n \frac{l_n}{2}\sqrt{1 - (\frac{l_n}{2})^2} . \]
可以看出,\(n\to \infty\)时\(l_n \to 0\), 上述\(l_{2n}\)的递推公式出现相近数相减, 误差较大。 为避免相近数相减的误差,将\(l_{2n}\)公式转换为 \[ l_{2n} = \frac{l_n}{\sqrt{2 + \sqrt{4 + l_n^2}}} . \]
using Printf
area(s, n) = n*s/2*sqrt(1-s^2/4)
side_next(s) = s / sqrt(2 + sqrt(4 - s^2))
function pi_secant(niter = 10)
n = 6
s = big(1.0)
ns = [n]
sides = [s]
for i=1:niter
n *= 2
s = side_next(s)
push!(ns, n)
push!(sides, s)
end
pi_vec_side = [0.5*n*s for (n,s) in zip(ns, sides)]
pi_vec_area = [area(big(s), n) for (n,s) in zip(ns, sides)]
println(" d n side pi_side pi_area")
for i=1:(niter+1)
println( @sprintf("%2d", i-1),
@sprintf("%10d", ns[i]),
@sprintf("%12.8f", sides[i]),
@sprintf("%16.12f", pi_vec_side[i]),
@sprintf("%16.12f", pi_vec_area[i]))
end
[0:niter ns sides pi_vec_side pi_vec_area]
end
pi_secant(20); d n side pi_side pi_area
0 6 1.00000000 3.000000000000 2.598076211353
1 12 0.51763809 3.105828541230 3.000000000000
2 24 0.26105238 3.132628613281 3.105828541230
3 48 0.13080626 3.139350203047 3.132628613281
4 96 0.06543817 3.141031950891 3.139350203047
5 192 0.03272346 3.141452472285 3.141031950891
6 384 0.01636228 3.141557607912 3.141452472285
7 768 0.00818121 3.141583892148 3.141557607912
8 1536 0.00409061 3.141590463228 3.141583892148
9 3072 0.00204531 3.141592105999 3.141590463228
10 6144 0.00102265 3.141592516692 3.141592105999
11 12288 0.00051133 3.141592619365 3.141592516692
12 24576 0.00025566 3.141592645034 3.141592619365
13 49152 0.00012783 3.141592651451 3.141592645034
14 98304 0.00006392 3.141592653055 3.141592651451
15 196608 0.00003196 3.141592653456 3.141592653055
16 393216 0.00001598 3.141592653556 3.141592653456
17 786432 0.00000799 3.141592653581 3.141592653556
18 1572864 0.00000399 3.141592653588 3.141592653581
19 3145728 0.00000200 3.141592653589 3.141592653588
20 6291456 0.00000100 3.141592653590 3.141592653589结果中最后的边数已经达到六百万以上, 用面积的方法精确到了第12位有效数字。 21.5用递推(滤波)的方法从面积序列进行了改进, 大大提高了精度。
21.2.2 用有理数近似π
π是一个无理数, 大家常用的近似值是小数表示的\(3.1415926\), 精度是小数点后7位小数, 误差为\(5.4 \times 10^{-8}\)。
历史上多位数学家研究过用有理数近似圆周率。 我们在已知圆周率比较精确的近似值的基础上找到最优的有理数逼近。
function pi_rational(n=2)
dens = 10^(n-1):10^n-1
nums = round.(Int, pi .* dens)
pirs = nums ./ dens
errs = abs.(pirs .- pi)
i = argmin(errs)
pir = pirs[i]
# 返回近似有理数,近似实数,误差绝对值
return nums[i]//dens[i], pir, errs[i]
end
pi_rational(2)
# (22//7, 3.142857142857143, 0.0012644892673496777)
pi_rational(2)
# (311//99, 3.1414141414141414, 0.00017851217565167943)
pi_rational(3)
# (355//113, 3.1415929203539825, 2.667641894049666e-7)
pi_rational(4)
# (355//113, 3.1415929203539825, 2.667641894049666e-7)
pi_rational(5)
(312689//99532, 3.1415926536189365, 2.914335439641036e-11)其中分母为1位数的近似值\(22/7\)是祖冲之得到的“约率”近似, 有小数点后2位精度; 分母为3位数的近似值\(355/113\)是很好的近似值, 精确到了小数点后第6位, 这正是祖冲之得到的“密率”近似, 分母更多位数的近似已经是分母为5位数的\(312689/99532\), 其精度达到小数点后9位。
21.2.3 用级数计算π
此问题来自Ben Lauwens和Allen B. Downey(2019) 《Julia语言编程入门》,中国电力出版社, 肖斌、王磊等译。
数学家Srinivasa Ramanujan提出了如下的计算\(\frac{1}{\pi}\)的级数: \[ \frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}} \]
k = 0
x = 2*sqrt(2)/9801
y = 1103
z = x*y
s = z
while z > 1E-15
k += 1
k4 = 4*k
x *= k4*(k4-1)*(k4-2)*(k4-3)/k^4/396^4
y += 26390
z = x*y
s += z
end
println("k=", k, " estimate = ", s)
println("Error = ", s - 1/π)
## k=2 estimate = 0.3183098861837907
## Error = 0.0只算了3项就达到了\(10^{-15}\)的精度。
21.3 卷积
21.3.1 离散卷积
令\(\mathbb Z\)表示整数集\(\{ \ldots, -2, -1, 0, 1, 2, \ldots \}\), 设\(x = \{ x_n, n \in \mathbb Z \}\)是一个数列。 若\(x, y\)是两个数列,定义数列\(z\)为 \[ z_n = \sum_{k=-\infty}^\infty x_k y_{n-k}, \ n \in \mathbb Z , \] 称\(z = \{ x_n, n \in \mathbb Z \}\)为\(x\)和\(y\)的离散卷积,记作\(x * y\)。
21.3.1.1 交换律
\[ x * y = y * x . \]
证明: \[\begin{aligned} (x * y)_n =& \sum_k x_k y_{n-k} \quad (\text{令} s = n-k, \ k=n-s) \\ =& \sum_s x_{n-s} y_s = (y * x)_n . \end{aligned}\]
21.3.1.2 结合律
\[ (x * y) * z = x * (y * z) . \]
证明: 记\(v = x*y\), \(w = y*z\)。 \[\begin{aligned} v_n =& (x * y)_n = \sum_k x_k y_{n-k}, \\ w_n =& (y * z)_n = (z * y)_n = \sum_s z_s y_{n-s}, \end{aligned}\] 有 \[\begin{aligned} \;[(x * y) * z]_m =& [z * (x * y)]_m = \sum_s z_s v_{m-s} \\ =& \sum_s z_s \sum_k x_k y_{m-s-k} \\ =& \sum_s \sum_k z_s x_k y_{m-s-k}, \end{aligned}\] 而 \[\begin{aligned} \;[x * (y*z)]_m=& \sum_k x_k w_{m-k} \\ =& \sum_k x_k \sum_s z_s y_{m-k-s} \\ =& \sum_k \sum_s z_s x_k y_{m-s-k} . \end{aligned}\] 在一定收敛性条件下(如上面的二重级数绝对收敛)结合律成立。
21.3.2 有限离散卷积
设\(x\)仅有\(A\)个元素, 记为\(x_n, n=0,1,\ldots,A-1\); 设\(y\)仅有\(B\)个元素, 记为\(y_n, n=0,1,\ldots,B-1\)。 记\(x_n=0\)当\(n<0\)或\(n > A-1\), \(y_n\)类似, 则可定义 \[ z_n = (x * y)_n, \ n \in \mathbb Z . \]
显然,这样的卷积仍服从交换律、结合律、分配律。 \[\begin{aligned} z_n =& \sum_{k = -\infty}^\infty x_k y_{n-k}, \end{aligned}\] 为使得\(x_k y_{n-k} \neq 0\), 必须有 \[ 0 \leq k \leq A-1, \ 0 \leq n-k \leq B-1, \] 这等价于 \[ 0 \leq k \leq A-1, \ n+1-B \leq k \leq n, \] 于是 \[ z_n = \sum_{k = \max(0, n+1-B)}^{\min(A-1, n)} x_k y_{n-k}, \] 为使得\(z_n \neq 0\)必须有 \[ \max(0, n+1-B) \leq \min(A-1, n), \] 这等价于 \[ 0 \leq n \leq A + B - 2 . \] 可见结果的非零元素最多有\(A+B-1\)个。
在Julia中,
将x的下标用1:A代替,
y的下标用1:B代替,
x*y的下标用1:(A+B-1)代替。
两个向量卷积的Julia程序:
function convolve_zero(x, y)
A = length(x)
B = length(y)
z = similar(x, (A+B-1,))
z .= 0
i0 = firstindex(x)
j0 = firstindex(y)
for i in eachindex(x)
for j in eachindex(y)
z[1 + (i-i0) + (j-j0)] += x[i] * y[j]
end
end
return z
end # functionconvolve_zero([1, -1], [2, 3, 5, 11]) |> show
## [2, 1, 2, 6, -11]21.4 滤波与推移算子
21.4.1 下标非有限情形
设\(\{a_j, j \in \mathbb Z \}\)满足\(\sum_{j=-\infty}^\infty |a_j| < \infty\), 称这个条件为\(\{ a_j \} \in l_1\)。
设\(\{x_t, t \in \mathbb Z \}\)有界, 定义 \[ y_t = \sum_{j=-\infty}^\infty a_j x_{t-j} = (a * x)_t, \ t \in \mathbb Z, \] 称\(\{ a_j \}\)为一个保时线性滤波器, 称\(\{ y_t \}\)为\(\{ x_t \}\)的滤波。 实际上是\(a\)和\(x\)的离散卷积。
记\(\mathbb C\)为复数域, 其元素\(z\)为复平面上的点。 定义 \[ P(z) = \sum_{j=-\infty}^\infty a_j z^j, \] 则存在\(0 < \rho_1 < 1 < \rho_2\)使得\(P(z)\)在\(\rho_1 < |z| < \rho_2\)的\(z \in \mathbb C\)子集上收敛, 还是解析函数。
定义\(L x_t = x_{t-1}\), 称\(L\)为推移算子。 定义 \[\begin{aligned} P(L) =& \sum_{j=-\infty}^\infty a_j L^j, \\ y_t =& P(L) x_t = \sum_{j=-\infty}^\infty a_j x_{t-j} , \end{aligned}\] 称\(P(L)\)为推移算子多项式。
关于推移算子多项式, 有如下结论。 这也是下标取所有整数\(\mathbb Z\)情况下的离散卷积的性质。
性质1(交换律):对\(\{ a_j \} \in l_1\), \(\{ b_j \} \in l_1\), \(P(z) = \sum a_j z^j\), \(Q(z) = \sum_j b_j z^j\), 令\(U(z) = P(z) Q(z)\):
令\(c = a*b\), 则\(U(z) = \sum_{j=-\infty}^\infty c_j z^j\).
对\(\{ x_t \}\)有\(P(L) (Q(L) x_t) = Q(L) (P(L) x_t) = U(L) x_t\).
证明略。
性质2(线性):若\(P(L), Q(L)\)为推移算子多项式,\(a, b\)为实数或复数, 则\(a P(L) + b Q(L)\)也是推移算子多项式。
性质3(分配律):设\(P, Q, U\)是推移算子多项式, 则\(P(Q + U) = P Q + P U\), \((P + Q) U = P U + Q U\)。
关于推移算子的性质,参见:
- 何书元(2003) 《应用时间序列分析》, 北京大学出版社
- 李东风的时间序列分析讲义
上面的做法将有限的离散卷积看成是无穷长数列卷积的特例。 在作为滤波计算时, 设\(a_0, a_1, \ldots, a_{m-1}\)看成滤波器, \(x_0, x_1, \ldots, x_{n-1}\)看成信号, \(m < n\), 为了不使用\(t < 0\)和\(t > n-1\)时的信号作为输入, 可定义滤波结果 \[ y_t = \sum_{j=0}^{m-1} a_j x_{t-j}, \ t=m-1, m, \ldots, n-1, \] 仅输出这\(n-m+1\)个元素。 这样的卷积不再服从交换律。
21.4.2 下标有限情形
设\(\{ a_j \}\)仅有有限个非零, 仅有\(\{ a_j, j=j_0, j_0 + 1, \ldots, j_1 \}\)。
21.4.2.1 输入序列无限情形
若\(\{ x_t \}\)仍定义在\(t \in \mathbb Z\), 则 \[\begin{aligned} P(z) =& \sum_{j=j_0}^{j_1} a_j z^j, \\ y_t =& P(L) x_t = \sum_{j=j_0}^{j_1} a_j x_{t-j} , \ t \in \mathbb Z . \end{aligned}\] 这时卷积运算和推移算子多项式的性质与下标非有限时相同。
21.4.2.2 两侧补零的做法
如果\(\{ a_j \} = \{ a_j, j=j_0, j_0 + 1, \ldots, j_1 \}\), \(\{ x_t \}\)也仅有有限个观测值\(\{ x_t , t = 1,2,\dots,n \}\), 则情况比较复杂。
下面都定义\(a_j = 0\)对\(j < j_0\)或\(j > j_1\)。
一种方法是定义\(x_t = 0\)对\(t < 1\)或\(t > n\)。
这时为了\(y_t \neq 0\),
必须满足\(j_0 + 1 \leq t \leq j_1 + n\),
共输出\(m = n + j_1 - j_0\)个非零元素。
这时仍满足
\[
y_t = (a * x)_t,
\ t=j_0+1, j_0 + 2, \ldots, j_1 + n .
\]
如果将\(y_t, t=j_0+1, j_0 + 2, \ldots, j_1 + n\)仍放到下标为1:m的数组中,
这个结果与向量a和z的有限离散卷积的结果完全相同。
比如, 令\(a = [-1, 2, -1]\)。 若\(j_0 = -1, j_1 = 1\), 则\(y_t = - x_{t+1} + 2 x_t - x_{t-1}\), \(t=0, 1, \ldots, n+1\)。
using OffsetArrays
function test_finfilt1(;j0=-1, j1=1)
a = [-1, 2, -1]
a = OffsetArray(a, j0:j1)
x = [2, 3, 7, 11, 13, 17]
n = length(x)
get(x, s) = 1 <= s <= n ? x[s] : 0
y = [ sum(a[j] * get(x, t-j) for j=j0:j1) for t = j0+1:j1+n]
return y
endtest_finfilt1(j0=-1, j1=1)'
## -2 1 -3 0 2 -2 21 -17
test_finfilt1(j0=0, j1=2)'
## -2 1 -3 0 2 -2 21 -17
test_finfilt1(j0=1, j1=3)'
## -2 1 -3 0 2 -2 21 -17
convolve_zero([-1,2,-1], [2, 3, 7, 11, 13, 17])'
## -2 1 -3 0 2 -2 21 -1721.4.2.3 不补零的做法
如果要求\(y_t = \sum_{j=j_0}^{j_1} a_j x_{t-j}\)中每一个\(x_{t-j}\)都是观测值而不是补的0,
就要求
\[
1 \leq t-j \leq n, \ \forall j_0 \leq j \leq j_1 .
\]
这等价于\(j_1 + 1 \leq t \leq j_0 + n\),
滤波后元素个数减少到了\(n - (j_1 - j_0)\)个。
比如,\(j_0 = 0, j_1=2\),则元素个数减少了2个。
即减少的元素个数等于a的长度减1。
这时,具体使用的边界\(t=1\)和\(t=n\)处的值的个数不同, 这实际上是抛弃了补零的结果中\(j_0 + 1 \leq t \leq j_1\)部分和\(n + j_0 + 1 \leq t \leq n + j_1\)部分, 即在左端和右端都抛弃了\(j_1 - j_0\)个, 因此结果仍与\(a\)的下标从几开始无关。
常用的\(j_0\)和\(j_1\)有两种,
一种是\(j_0 = 0\),
\(j_1 = m-1\), (\(m\)是a的长度),
这时
\[\begin{aligned}
y_t =& \sum_{j=0}^{j_1} a_j x_{t-j} \\
=& a_0 x_t + a_1 x_{t-1} + \cdots + a_{j_1} x_{t-j_1} ,
\ t = m, m+1, \ldots, n .
\end{aligned}\]
称为单边滤波,
输出\(y_{m}, y_{m+1}, \ldots, y_n\), 长度为\(n-(m-1)\)。
另一种是\(j_0 = -j_1\), \(m = 2 j_1 + 1\), 这时 \[\begin{aligned} y_t =& \sum_{j=-j_1}^{j_1} a_j x_{t-j} \\ =& a_{-j_1} x_{t+j_1} + \cdots + a_0 x_t + \cdots + a_{j_1} x_{t-j_1}, \ t=j_1 + 1, \ldots, n-j_1, \end{aligned}\] 输出\(n-(m-1)\)个值, 称为双侧滤波。
只要结果的下标仍统一为1到\(n-(m-1)\),则不论\(j_0\)和\(j_1\)如何取, 这种方法得到的结果都是相同的。
例:
function test_finfilt2(;j0=-1, j1=1)
a = [-1, 2, -1]
a = OffsetArray(a, j0:j1)
x = [2, 3, 7, 11, 13, 17]
n = length(x)
get(x, s) = 1 <= s <= n ? x[s] : 0
y = [ sum(a[j] * x[t-j] for j=j0:j1) for t = j1+1:j0+n]
return y
end
convolve_zero([-1,2,-1], [2, 3, 7, 11, 13, 17])'
## -2 1 -3 0 2 -2 21 -17
test_finfilt2(j0=-1, j1=1)'
## -3 0 2 -2
test_finfilt2(j0=0, j1=2)'
## -3 0 2 -221.4.2.4 结合律
对于补零的做法,
设a, b是两个一维数组,
用作滤波器,
x是一个观测值向量,
由离散卷积的性质可知
\[
a * (b * x) = (a*b) * x .
\]
即分别进行两次滤波,
可以用两个滤波器的卷积(补零做法)\(a * b\)作为滤波器进行一次滤波。
如:
function test_finfilt3()
a = [-1, 2, -1]
b = [3, 1]
x = [2, 3, 7, 11, 13, 17]
y1 = convolve_zero(b, x)
y2 = convolve_zero(a, y1)
c = convolve_zero(a, b)
y3 = convolve_zero(c, x)
[y2 y3]
end
test_finfilt3()'
## -6 1 -8 -3 6 -4 61 -30 -17
## -6 1 -8 -3 6 -4 61 -30 -17对于不补零的做法, 将不补零的卷积记为\(a \star x\), 这个运算不满足交换律, 仍满足如下的结合律:
\[ a \star (b \star x) = (a * b) \star x , \] 其中\(a * b\)仍是补零的卷积。
证明: 设\(a, b, x\)的长度分别为\(n_a, n_b, n_x\), 且\(n_a + n_b - 1 \leq n_x\)。 这三个向量的下标都从0开始计数。
令\(z = b \star x\), 则\(z\)的元素为 \[ z_t = \sum_{s=0}^{n_b - 1} b_s x_{t-s}, \ t=n_b-1, n_b, \ldots, n_x - 1, \] 共有\(n_x - n_b + 1\)个元素。
令\(y = a \star z\), 则 \[\begin{aligned} y_t =& \sum_{j=0}^{n_a - 1} a_j z_{t-j}, \ t = n_a + n_b - 2, n_a + n_b - 1, \ldots, n_x - 1, \end{aligned}\] 有\(n_x - (n_a + n_b - 2)\)个元素。以\(z_{t-j}\)的公式代入得 \[\begin{aligned} y_t =& \sum_{j=0}^{n_a - 1} a_j \sum_{s=0}^{n_b - 1} b_s x_{t-j-s} \\ =& \sum_{j=0}^{n_a - 1} \sum_{s=0}^{n_b - 1} a_j b_s x_{t - (j+s)} \\ & (\text{令}k = j+s, \ s = k-j) \\ =& \sum_{j=0}^{n_a - 1} \sum_{k=j}^{j + n_b - 1} a_j b_{k-j} x_{t-k} \\ =& \sum_{k=0}^{n_a + n_b - 2} \left( \sum_{j=0}^{n_a - 1} a_j b_{k-j} \right) x_{t-k}, \ t = n_a + n_b - 2, n_a + n_b - 1, \ldots, n_x - 1. \end{aligned}\]
记\(c = a * b\),则\(c\)有\(n_a + n_b - 1\)个元素,且 \[ c_k = \sum_{j=0}^{n_a - 1} a_j b_{k-j}, \ k=0,1,\ldots, n_a + n_b - 2 . \] 于是 \[ y_t = (c \star x)_t, \ t = n_a + n_b - 2, n_a + n_b - 1, \ldots, n_x - 1. \] 即\(y = a \star (b \star x) = c \star x = (a * b) \star x\), 得证。
为了验证, 先写一个一般的滤波函数, 注意这是不满足交换律的:
function convolve_nz(a, x)
# a 是滤波器,x是输入信号
m = length(a)
# 两侧分别去掉m-1个
convolve_zero(a, x)[m:end-m+1]
end不补零做法结合律测试:
function test_finfilt4()
a = [-1, 2, -1]
b = [3, 1]
x = [2, 3, 7, 11, 13, 17]
y1 = convolve_nz(b, x)
y2 = convolve_nz(a, y1)
c = convolve_zero(a, b)
y3 = convolve_nz(c, x)
[y2 y3]
end
test_finfilt4()'
## -3 6 -4
## -3 6 -421.5 卷积与圆周率割圆法改进
21.5.1 推导
割圆法是用内接正多边形的面积估计圆面积从而逼近圆周率的方法, 从边数等于3或者等于6开始(可以很容易地仅用平方根计算面积), 然后每次从分\(n\)块增加到分\(2n\)块, 仍可以仅用开平方根递推地计算内接正多边形面积。 见21.2。
为了演示, 这里不使用初等的平方根递推方法, 而是直接用三角函数求面积, 令\(f_0(s)\)为半径等于1的内接正\(s\)边形面积, 则 \[ f_0(s) = \frac{s}{2} \sin \frac{2\pi}{s} . \]
利用sin函数的泰勒展开,
可以从割圆法得到的逐次逼近序列仅用简单的卷积(滤波)方法得到高精度的圆周率逼近。
为了得到更多有效数字(Float64只有约16位有效数字),
下面的计算用了Julia的BigFloat类型,
只要用big()说明某个数,
则从这个数计算的结果也会用BigFloat保存。
\(\sin(x)\)的泰勒展开为 \[ \sin(x) = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 - \cdots = \sum_{j=0}^\infty (-1)^{j} \frac{x^{2j+1}}{(2j+1)!} . \] 于是 \[\begin{aligned} f_0(s) =& \frac{s}{2} \sin \frac{2\pi}{s} \\ =& \pi - \frac{2\pi^3}{3} s^{-2} + \frac{2 \pi^5}{15} s^{-4} - \frac{4 \pi^7}{315} s^{-6} + \cdots \\ =& \pi + \sum_{k=1}^\infty c_k s^{-2k} = \pi + c_1 s^{-2} + O(s^{-4}) . \end{aligned}\]
所以当\(s \to \infty\)时这个估计\(\pi\)的近似公式有\(O(s^{-2})\)阶精度。
如果使用内接正多边形周长来估计\(2\pi\), \(\pi\)可估计为 \[ p_0(s) = \frac{1}{2} \cdot s \cdot 2 \cdot \sin\frac{\pi}{s} = s \sin\frac{\pi}{s} . \] 作泰勒展开得 \[ p_0(s) = s \left[ \frac{\pi}{s} - \frac{1}{3!} (\frac{\pi}{s})^3 + \frac{1}{5!} (\frac{\pi}{s})^5 + \cdots \right] = \pi - \frac{\pi^3}{6} s^{-2} + O(s^{-4}) . \]
考虑联合使用面积序列的\(f_0(s)\)和\(f_0(2s)\)来改进精度。 \[\begin{aligned} f_0(2s) =& \pi - \left(\frac{1}{4}\right) \frac{2}{3 \pi^3} s^{-2} + \left(\frac{1}{4}\right)^2 \frac{2 \pi^5}{15} s^{-4} - \left(\frac{1}{4}\right)^3 \frac{4 \pi^7}{315} s^{-6} + \cdots \\ =& \pi + \sum_{k=1}^\infty \left(\frac{1}{4}\right)^k c_k s^{-2k} = \pi + \frac{1}{4} c_1 s^{-2} + O(s^{-4}), \end{aligned}\]
注意\(f_0(s)\)和\(f_0(2s)\)误差部分的\(s^{-2}\)项系数分别为\(c_1\)和\(\frac{1}{4} c_1\), 于是\(4 f_0(2s) - f_0(s)\)的\(s^{-2}\)系数为0, 常数项\(\pi\)变成了\(3 \pi\), 于是 \[\begin{aligned} 4 f_0(2s) - f_0(s) =& 3\pi + O(s^{-4}) , \\ \frac{4}{3} f_0(2s) - \frac{1}{3} f_0(s) =& \pi + O(s^{-4}) . \end{aligned}\]
所以\(\frac{4}{3} f_0(2s) - \frac{1}{3} f_0(s)\)可以获得\(O(s^{-4})\)阶精度的\(\pi\)近似公式。 令 \[\begin{aligned} f_1(s) =& \frac{4}{3} f_0(2s) - \frac{1}{3} f_0(s) \\ =& \pi + O(s^{-4}) \\ =& \pi + c_2^{(1)} s^{-4} + \sum_{k=3}^\infty c_k^{(1)} s^{-2k} . \end{aligned}\]
易见\(f_1(2s)\)与\(f_1(s)\)的\(s^{-4}\)项系数为\(2^4 = 16\)倍关系, 所以 \[\begin{aligned} f_2(s) =& \frac{16}{15} f_1(2s) - \frac{1}{15} f_1(s) \\ =& \pi + O(s^{-6}) \\ =& \pi + c_3^{(2)} s^{-6} + \sum_{k=4}^\infty c_k^{(2)} s^{-2k} . \end{aligned}\]
以此类推,\(f_2(2s)\)和\(f_2(s)\)的主要误差项系数相差\(2^6 = 64\)倍, 于是 \[\begin{aligned} f_3(s) =& \frac{64}{63} f_2(2s) - \frac{1}{63} f_2(s) \\ =& \pi + O(s^{-8}) \\ =& \pi + c_4^{(3)} s^{-8} + \sum_{k=4}^\infty c_k^{(3)} s^{-2k} . \end{aligned}\]
一般地,\(f_m(s)\)的精度为\(s^{-(2m+2)}\), \(f_m(2s)\)与\(f_m(s)\)的误差项的倍数为\(2^{2m+2}\), 有 \[\begin{aligned} f_{m+1}(s) = \frac{2^{2m+2}}{2^{2m+2} - 1} f_m(2s) - \frac{1}{2^{2m+2} - 1} f_m(s) , \ m=0, 1, 2, 3, \ldots. \end{aligned}\]
设从某个基础的\(s\)(如\(s=6\))出发, 每次边数加倍计算精确的内接正多边形面积, 得到一个序列\(S_n^{(0)}, n=0, 1, 2, \dots, M\), 其中\(S_{n+1}^{(0)}\)对应的边数等于\(S_n^{(0)}\)对应的边数的二倍。 则令 \[ a^{(m)} = \left(\frac{2^{2m+2}}{2^{2m+2} - 1}, -\frac{1}{2^{2m+2} - 1} \right), m=0,1,2,\ldots, \] 计算\(S^{(1)} = a^{(0)} \star S^{(0)}\)就可以从\(O(s^{-2})\)精度提高到\(O(s^{-4})\)精度, 计算\(S^{(2)} = a^{(1)} \star S^{(1)}\)就可以从\(O(s^{-4})\)精度提高到\(O(s^{-6})\)精度, 可以反复卷积, 令 \[ S^{(m+1)} = a^{(m)} \star S^{(m)}, m=0,1,\ldots, M-1, \] 则\(S^{(M)}\)有\(O(s^{-2M-2})\)精度。
这种改进方法也适用于用内接正多边形周长的二分之一近似估计\(\pi\)的序列。
下面是改进的几种不同的编程实现。
21.5.2 递归方法
因为改进是逐次进行的, 所以如果需要进行\(M\)次改进, 可以先生成第\(M-1\)次改进, 如此递归调用, 直到第\(0\)次计算为\(f_0(s) = \frac{s}{2} \sin \frac{2\pi}{s}\)。
using Printf
f0(s) = s/2*sin(big(2.0)*big(pi)/s)
function show_precision(pi_est)
pi_str = @sprintf("%.50f", big(π))
pi_est_str = @sprintf("%.50f", pi_est)
ind = findfirst(x -> x[1] ≠ x[2],
collect(zip(collect(pi_est_str)[3:end], collect(pi_str)[3:end]) ))
@sprintf("%2i : %.50f", ind, pi_est)
end
function test_pi01(s=6, m=6)
# 递归算法
function pi_sin_improve(s=6, m=0)
# m: 改进次数
# s: 从m=0开始所用的边数,每改进一次边数自动加倍
if m==0
return f0(s)
else # m > 0
m1 = m - 1
a0 = 2^(2*m1 + 2)
a1 = a0 - 1
return (a0*pi_sin_improve(2*s, m1) -
pi_sin_improve(s, m1)) / a1
end
end
pi_str = @sprintf "%.50f" big(π)
est_vec = map(i -> pi_sin_improve(s,i), 1:6)
println(" ", pi_str)
map(est_vec) do est
println(show_precision(est))
end
end # function test_pi01
test_pi01(6, 6); 3.14159265358979323846264338327950288419716939937511
2 : 3.13397459621556135323627682924706381652859737309481
5 : 3.14158006333531692053878837350062054938886942432049
9 : 3.14159265057324285166532423432989114988405248587089
13 : 3.14159265358967531032793304529670698783308976448951
18 : 3.14159265358979323765113602412171302806878023573296
24 : 3.14159265358979323846264234704427340360292693968997第一行是\(\pi\)的真值, 后面是\(m=1,2,\dots,6\)的改进结果, 冒号前面是与\(\pi\)真值首次在小数点后出现不同的位置。 注意改进了6次, 用到的最大边数就是\(6 \times 2^6 = 384\), 精度是小数点后23位, 如果直接用384边的正多边形, 误差大得多:
@sprintf "%.50f" big(pi)
@sprintf "%.50f" big(f0(384))
## "3.14159265358979323846264338327950288419716939937511"
## "3.14145247228546207545060930896122564524766230454968"结果在小数点后第4位出现错误。
注意程序中用了big()使得计算用高精度浮点数进行计算,
否则会因为浮点误差使得迭代改进的效果无法显现。
若\(m=0\)时边数改为\(6 \times 16\),结果为:
test_pi01(6*16, 6);结果:
3.14159265358979323846264338327950288419716939937511
7 : 3.14159253350505711510342162821007307966509942509625
13 : 3.14159265358902771719437964590074800765049986127300
18 : 3.14159265358979323775098181637016594094919795366774
25 : 3.14159265358979323846264327502032881036367294118752
31 : 3.14159265358979323846264338327949998110047544876416
41 : 3.14159265358979323846264338327950288419715494157489最多用了6114正多边形, 有小数点后40位精度。
21.5.3 利用多次卷积
递归算法明显地有许多重复计算, 下面的程序直接生成多个卷积核(即\(\{a_j\}\)), 然后逐次对\(S^{(0)}\)序列进行不补零的卷积。
function test_pi02(s=6, m=6)
# s: 最少边长,m:改进次数
# 设边数取2的倍数:
svec = s .* (2 .^ (0:m))
# 求对应的内接正多边形逼近估计的pi
# 注意这里用了`big(2)`保证精度
x = [f0(s) for s in svec]
# 产生多个卷积核:
kervec = [ let
a0 = big(2.0)^(2*m + 2)
a1 = a0 - 1
[a0, -1.0] ./ a1
end
for m=0:(m-1)]
y = copy(x)
for ker in kervec
y = convolve_nz(ker, y)
end
pi_str = @sprintf "%.50f" big(π)
println(" ", pi_str)
println(show_precision(last(y)))
return
end # function test_pi02
test_pi02(6, 6);结果:
3.14159265358979323846264338327950288419716939937511
24 : 3.14159265358979323846264234704427340360292693968997从\(96\)边开始改进:
test_pi02(6*16, 6);结果:
3.14159265358979323846264338327950288419716939937511
41 : 3.1415926535897932384626433832795028841971549415748921.5.4 利用卷积结合律
上一小节用了多次卷积迭代。 前面证明了\(a \star (b \star x) = (a*b) \star x\), 所以多次卷积(滤波)可以先计算各个滤波器的补零卷积作为汇总的滤波器, 然后对输入序列\(S^{(0)}\)作不补零的卷积:
function test_pi03(s=6, m=6)
# s: 最少边长,m:改进次数
# 设边数取2的倍数:
svec = s .* 2 .^ (0:m)
# 求对应的内接多边形逼近
# 注意这里用了`big(2)`保证精度
x = [f0(s) for s in svec]
# 产生多个卷积核:
kervec = [ let
a0 = big(2)^(2*m + 2)
a1 = a0 - 1
[a0, -1.0] ./ a1
end
for m=0:(m-1)]
# 汇总的卷积
ker = reduce(convolve_zero, kervec)
y = convolve_nz(ker, x)
pi_str = @sprintf "%.50f" big(π)
println(" ", pi_str)
println(show_precision(last(y)))
return
end # function test_pi03
test_pi03(6*16, 6); 3.14159265358979323846264338327950288419716939937511
41 : 3.14159265358979323846264338327950288419715494157489这里用了reduce和convolve_zero配合,
获得了6个卷积核的卷积。
逐次卷积与先生成卷积核的卷积结果相同,
当输入序列很长时,
先生成所有卷积核的卷积会提高效率。
21.6 一维卷积在图像处理中应用
在信号处理、时间序列分析中经常对一个向量\(\{ x_t, t=1,2,\dots,n \}\)计算这样的运算: \[\begin{aligned} y_t = \sum_j a_j x_{t-j}, \end{aligned}\] 其中\(\{ a_j \}\)是一个较短的数列。 比如,\(a_0 = 1, a_1 = -1\), 则\(y_t = -x_{t-1} + x_t\), 这可以看成是\(a\)的倒序\((-1, 1)\)与\((x_{t-1}, x_t)\)的内积。
这样的卷积在\(t=1\)和\(t=n\)这样的位置可能会用到下标边界以外的值, 前面的做法是将正常下标以外的的值都用0代替,或不允许使用下标以外的值。
在图像处理中用0代替或者减小图像大小都不可取, 所以一般将\(t \leq 0\)的\(x_t\)值用\(x[1]\)代替, 将\(t > n\)的\(x_t\)值用\(x[n]\)代替。 写出如下的下标函数:
function extend(v::AbstractVector, i)
i0 = firstindex(v)
i1 = lastindex(v)
ii = min(max(i, i0), i1)
return v[ii]
end卷积中的系数列\(\{ a_j \}\)称为“核”, 常常是看成下标\(-l:l\)的长度为\(2l+1\)的数列。 这相当于上面的双侧滤波器。 针对这样的数列的卷积可以写成如下函数:
function convolve_win(v::AbstractVector, ker)
l = (length(ker)-1) ÷ 2
[ sum([extend(v, t+j) for j=(-l):l] .* reverse(ker)) for t in eachindex(v) ]
end可以从一些函数产生核,程序如:
function make_kernel(kernel_fun, n)
x = kernel_fun.(-n:n)
x ./= sum(x)
return x
end高斯核,有参数sigma:
function make_gaussian_kernel(n; sigma=1)
pdf(x; sigma=sigma) = 1/sqrt(2*pi)*exp(-0.5*x^2 / sigma^2)
make_kernel(pdf, n)
end
ker_gau = make_gaussian_kernel(2)
x = rand(20)
y = convolve_win(x, ker_gau)21.7 二维卷积在图像处理中应用
在图像处理中也普遍使用卷积, 各种滤镜往往是某种卷积, 比如高斯模糊、边界探查等。
设\(M_{ij}, i=1,\ldots,m, j=1,\ldots,n\)是矩阵, \(K_{ij}, i=-l, \ldots, l, j=-l, \ldots, l\)为\((2 l + 1)\times (2 l+1)\)矩阵, 令 \[ G_{ij} = \sum_{s=-l}^l \sum_{t=-l}^l K_{st} M_{i-s, j-t}, \] 则\(G_{ij}\)称为\(K\)和\(M\)的二维卷积, \(K\)称为“核”。 记\(G = K * M\)。
在下标边界处, 一般也用\(M\)的四个边界的元素代替超出边界的值。 扩展下标的函数:
function extend(M::AbstractMatrix, i, j)
i0 = firstindex(M, 1)
i1 = lastindex(M,1)
j0 = firstindex(M, 2)
j1 = lastindex(M,2)
ii = min(max(i, i0), i1)
jj = min(max(j, j0), j1)
return M[ii,jj]
end计算卷积的函数为:
function convolve(M::AbstractMatrix, K::AbstractMatrix)
l = (size(K,1)-1) ÷ 2
[ sum([extend(M, s-i, t-j) for i=(-l):l, j=(-l):l] .* K)
for s in axes(M,1), t in axes(M,2)]
end其中用了axes(M,1)获取矩阵M行下标迭代器,
用了axes(M,2)获取矩阵M列下标迭代器,
这是为了在M下标不从1开始的情况下也能正常工作。
仍可以用二维正态密度制作模糊滤镜,如:
gauss(x, y; σ=1) = gauss(x; σ=σ) * gauss(y; σ=σ)
function with_gaussian_blur(image; σ=3, l=5)
K = [gauss(x, y; σ=σ) for x=-l:l, y=-l:l]
K ./= sum(K)
convolve(image, K)
end可以用“Sobel”核进行边缘检测。 令: \[\begin{aligned} K_x =& \begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \\ \end{bmatrix}; \qquad K_y = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \\ \end{bmatrix} \end{aligned}\] 令 \[ G_x = K_x * M,\ G_y = K_y * M, \ G_{ij} = \sqrt{G_{x,ij}^2 + G_{y,ij}^2} . \] \(G_{ij}\)的值越大, 这个点越有可能是边界点, 值越小,这个点与周围点越相近。
Sobel边界检测滤镜的函数:
function with_sobel_edge_detect(image)
Kx = [1 0 -1; 2 0 -2; 1 0 -1]
Ky = Kx'
Gx = convolve(image, Kx)
Gy = convolve(image, Ky)
G = sqrt.(Gx .^2 + Gy .^2)
return G
end