14 统计学习介绍
这一部分介绍一些机器学习(统计学习)方法。
参考:
- McNicholas and Tait(2019) Data Science Using Julia, CRC Press.
- Jose Storopoli, Rik Huijzer, Lazaro Alonso(2022) Julia Data Science. https://cn.julialang.org/JuliaDataScience/
using DataFrames, CSV, DataFramesMeta
using CategoricalArrays
using Statistics14.1 Julia中与机器学习有关的库
Flux:基于纯Julia语言,利用Julia对GPU和AD的支持。
Gen: 通用的概率编程系统,支持可编程的推断方法, 把利用概率模型进行推断的编程自动化, 支持随机模拟、神经网络、变分推断、序贯随机模拟抽样、MCMC等方法, 支持机器学习方法。 感觉是对BUGS这种随机模拟系统的改进。 当前版本0.3.5。
Knet: Koç大学的深度学习框架。 支持GPU,可以自动计算微分。
Turing: 用概率编程(probabilistic programming)进行贝叶斯推断。
TensorFlow: Julia中TensorFlow的调用库。
14.2 概率建模与推断介绍
14.2.1 概念
概率建模与推断, 涵盖了一些传统的统计模型方法, 比如贝叶斯推断, 使用MCMC方法计算。 但是不限于贝叶斯和MCMC计算方法。
首先, 要有一个所谓生成模型(generative model)。 生成模型中包括可观测变量和潜在变量(没有观测值), 模型是对联合分布的设定, 可以利用学科知识、先验知识、对数据的探索性分析经验设置模型。
有了生成模型和观测数据后, 可以用概率论进行推断, 比如贝叶斯后验推断。 潜在变量可以是数值型的(称为参数), 也可以是分类的(称为结构)。 关于潜在变量的推断结果可以表达为:
- 从后验分布抽取的随机样本;
- 后验分布的精确数学表示;
- 后验分布的数字特征,如后验最大(MAP)估计,后验均值等。
14.2.3 计算方法
有了生成模型后, 仅有少数的模型的推断是有精确数学表达式或有明确的数值算法的, 比如回归问题, 线性高斯状态空间滤波与平滑问题, 离散变量的树状模型, 有对数似然函数为凸函数的模型, 等等。
其它的大多数模型需要用某种逼近算法进行推断。 可用的方法如随机模拟,EM算法,变分推断,随机梯度算法, 各种有监督机器学习算法,等等。
14.3 有监督学习
有监督学习是利用有标签(因变量值)的训练数据建立预报模型, 对新数据进行预报, 统计学的回归分析、判别分析等属于这类方法。
参考:
- McNicholas and Tait(2019) Data Science Using Julia, CRC Press. 源程序网址https://github.com/paTait/dswj
14.3.1 误差指标
在训练数据中, 如果因变量是连续取值的, 误差评判指标包括: \[\begin{aligned} \text{MSE} =& \frac{1}{n} \sum_{i=1}^n (y_i - f(x_i))^2 \\ \text{RMSE} =& \sqrt{\text{MSE}} \\ \text{MAE} =& \frac{1}{n} \sum_{i=1}^n | y_i - f(x_i) | \end{aligned}\] 其中RMSE比较常用, 但是易受极端值影响, 而MAE较稳健。
对分类的因变量, 误差指标包括误判率、二项偏差(或偏差, deviance,对二值因变量)等: \[\begin{aligned} \text{MCR} =& \frac{1}{n} \sum_{i=1}^n I(y_i \neq f(x_i)) \\ \text{Deviance} =& -2 \left\{ y_i \log(\hat\pi_i) + (1 - y_i) \log(1 - \hat\pi_i) \right\} \end{aligned}\] 其中\(\hat\pi_i\)表示对0-1值的因变量值取1的概率的预测(拟合)。 二项偏差是二项分布对数似然最大值估计的负二倍。
14.3.2 训练集和测试集
仅用训练数据上的错误率指标评判模型优劣, 容易造成过度拟合, 在训练集上效果很好, 但是对无标签(因变量值)的新数据则预测很差。 普遍的做法是将有标签的数据也划分为两部分, 训练集和测试集, 在训练集上建模, 用测试集上的预测误差评判。
14.3.3 交叉验证
在训练集上建模, 用测试集评估效果, 就是用测试集选择模型, 也可能会出现模型对某个测试集效果很好, 但是换一个测试集效果就变差的可能性。
于是, 保留测试集仅用来评估模型效果, 但不用来比较和选择模型; 将训练集继续划分为用来拟合的部分和用来比较不同模型的部分, 这种划分可以是随机的, 比如, 将训练集随机等分为5份, 用其中1份比较模型, 其它4份估计模型; 这样轮流用1份作为比较,而其它4份估计模型, 用5次的预测结果比较不同的模型和同一模型的不同参数选择, 这种方法称为5折交叉验证(five-fold cross valication), 也常用10折。 折数的选择与方差-偏差折衷有关系, 折数很多(如每折一个点)会有小偏差、大方差, 常用5折或10折。
14.3.3.1 交叉验证的Julia代码
Julia中许多统计学习(机器学习)方法已经自带了交叉验证功能。 这里摘录McNicholas and Tait(2019)的生成交叉验证数据结构的代码。
# 要设置随机数种子需要调用Random标准库
using Random
# 设置随机数种子使得随机模拟可重复
Random.seed!(35)
# 将1到N的下标,划分为大致相同大小的k个组
# 输出为K个下标数组组成的数组
function cvind(N, k)
## 每组的大致点数
gs = N ÷ k
## 将1到N下标随机乱序
index = shuffle(collect(1:N))
## 指定组规模分组,这可能会使得最后一个组仅有几个点
folds = collect(Iterators.partition(index, gs))
## 如果gs*k不等于N,将最后一个点很少的组与倒数第二个组合并
if length(folds) > k
folds[k] = vcat(folds[k], folds[k+1])
deleteat!(folds, k+1)
end
return folds
end # function cvind
## 输入数据框dat, cvind函数的输出结果ind,
## 产生交叉验证的k个自数据框的数组
function kfolds(dat, ind)
## 折数
k = length(ind)
## 所有数据的下标
ind1 = collect(1:size(dat, 1))
## 用字典形式返回结果,每一项是编号到字典的映射,
## 每一折有留出的用来评估的折以及其余折合并的数据集
res = Dict{Int, Dict}()
for i = 1:k
## 对第i折的产生训练集和测试集
res2 = Dict{String, DataFrame}()
## 去掉第i折作为测试集,其余k-1折皆为训练集
tr = setdiff(ind1, ind[i])
res2["training"] = dat[tr, :]
res2["testing"] = dat[ind[i], :]
res[i] = res2
end
return res
end14.4 k近邻判别法
k近邻是一种基于例子的判别方法, 对于一个待判样品, 在训练集中找到距离最近的k个样品, 用这k个样品的类别投票决定此待判样品类别。 k的选择可以对偏差和方差进行折衷, 可以用交叉核实方法选择k。 如果不同的k效果相近, 则应选取较小的k值。
McNicholas and Tait(2019)中给出了如下的knn示例Julia程序。
using StatsBase, Distances
# 多数投票。输入一系列类别标签,输出多数类别的标签与比例
function maj_vote(yn)
# StatsBase.countmap是输入整数值,返回频数表的函数
cm = countmap(yn)
mv = -999
lab = nothing
tot = 1e-8
for (k, v) in cm
tot += v
if v > mv
mv = v
lab = k
end
end
prop = mv / tot
return [lab, prop]
end
# 用k近邻方法决定待判样品类别
# 输入:x是训练样本自变量矩阵,y是训练样本类别,
# x_new是输入的待判样本自变量矩阵,k是近邻个数
function knn(x, y, x_new, k)
n, p = size(x)
n2, p2 = size(x_new)
ynew = zeros(n2, 2)
for i in 1:n2
# 对每个新样品
res = zeros(n, 2)
for j in 1:n
# 与每个训练样品计算曼哈顿距离, 库Distances.cityblock
res[j, :] = [j, cityblock(x[j, :], x_new[i, :])]
end
# 按距离和序号排序
# sortslices对多维数组的某一维排序
res2 = sortslices(res, dims = 1, by = x -> (x[2], x[1]))
# 取最小的k个距离对应的训练样本序号
ind = convert(Array{Int}, res2[1:k, 1])
# 按这k个训练样本的因变量值(标签)进行多数投票
ynew[i,:] = maj_vote(y[ind])
end # for i
return ynew
end
# 计算错判率
function knnmcr(yp, ya)
disagree = Array{Int8}(ya .!= yp)
mcr = mean(disagree)
return mcr
end用前面自己定义的交叉验证函数进行交叉验证选择k的程序:
using Distributions, StatsBase, DataFrames, Distances
## 生成模拟数据
df_3 = DataFrame(
y = [0,1],
size = [250,250],
x1 =[2.,0.],
x2 =[-1.,-2.])
df_knn = by(df_3, :y) do df
DataFrame(
x_1 = rand(Normal(df[1,:x1],1), df[1,:size]),
x_2 = rand(Normal(df[1,:x2],1), df[1,:size]))
end
## 设置交叉验证的参数
N = size(df_knn)[1]
kcv = 5
## 生成交叉验证用的下标分组
a_ind = cvind(N, kcv)
## 生成交叉验证用的5折的轮流的训练集和测试集
d_cv = kfolds(df_knn, a_ind)
## 设置knn的参数
k = 15 # 最大近邻个数
knnres = zeros(k,3)
## 尝试不同的尽量个数i,用CV比较错判率
for i = 1:k
cv_res = zeros(kcv)
for j = 1:kcv # 对每一折
tr_a = convert(Matrix, d_cv[j]["training"][[:x_1, :x_2]])
ytr_a = convert(Vector, d_cv[j]["training"][:y])
tst_a = convert(Matrix, d_cv[j]["testing"][[:x_1, :x_2]])
ytst_a = convert(Vector, d_cv[j]["testing"][:y])
pred = knn(tr_a, ytr_a, tst_a, i)[:,1]
cv_res[j] = knnmcr(pred, ytst_a)
end
# 结果第一列:近邻数
knnres[i, 1] = i
# 结果第二列:CV错判率
knnres[i, 2] = mean(cv_res)
# 结果第三列:错判率的标准误差
knnres[i, 3] = std(cv_res) / sqrt(kcv)
end
knnres14.5 判别回归树(CART)
14.5.1 方法介绍
分类树用一个二叉树表示判决过程, 对训练样本, 找到一个适当的自变量和自变量的一个适当阈值(对分类自变量是找到自变量类别的适当两组分组), 使得分成的两组的混杂程度指标尽可能最低; 然后, 从两组中选一组进行分叉, 如此重复, 一直到每一组都比较均质(所有样品属于同一类)或者很小为止。
这样得到的判别树容易过度拟合, 所以一般向减小树的方向剪枝, 剪枝的程度可以用交叉验证或测试集确定。
对于待判样品, 先按自变量值分到某个叶子上, 再利用该叶子对应的样品的因变量值(类别)进行多数投票, 以确定待判样品类别标签。
在生成判别树分叉时, 对于某个组的混杂程度, 可以用该组最大比例类别以外的其它类别的比例(即错判率)作为度量, 也可以用该组各个类别的Gini系数度量: \[ \sum_{g=1}^G \hat p_{g} (1 - \hat p_g) \] 易见当比例中一个接近于1,其余都接近于0时很小, 这时该组基本上都属于因变量的同一类别。 所以这个指标可以作为是某个组的类混杂程度的度量, 很小时此区域的类是纯一的, 很大时,此区域的类别比较混杂,应进一步分割。 或用互熵(cross entropy)度量: \[ -\sum_{g=1}^G \hat p_g \log \hat p_g . \] 它也是当比例中一个接近于1,其余都接近于0时很小, 代表组内样品基本属于同一因变量标签。
回归树的因变量是连续取值的变量, 在分叉时, 可以用类似方差分析的思想, 使得组内的离差平方和最小, 组间距离较大。
树方法容易解释, 符合许多人的决策思维, 容易图示, 但预测效果不如其他方法。 改进方法有:
- 装袋法(bagging),取许多的随机抽取的训练集,生成许多棵不剪枝的树,对结果进行平均;
- 随机森林(random forest),在装袋法中,每一棵树,仅允许使用数目受限的随机选取的自变量子集;
- 提升法(boosting),不断对错判或误差大的案例重新用简单树改进,将所有改进叠加起来。
14.5.2 例子
McNicholas and Tait(2019) 中回归树用于food数据的程序例子如下。 food数据是126个学生的食物选择和偏好的数据。 因变量是gpa,是数值型数据。
using DecisionTree, Random
Random.seed!(35)
## food training data from chapter 3
y = df_food[:gpa]
tmp = convert(Array, df_food[setdiff(names(df_food), [:gpa])] )
xmat = convert(Array{Float64}, collect(Missings.replace(tmp, 0)))
names_food = setdiff(names(df_food), [:gpa])
# defaults to regression tree if y is a Float array
model = build_tree(y, xmat)
# prune tree: merge leaves having >= 85% combined purity (default: 100%)
modelp = prune_tree(model, 0.85)
# tree depth is 9
depth(modelp)
# print the tree to depth 3
print_tree(modelp, 3)
#=
Feature 183, Threshold 0.5
L-> Feature 15, Threshold 0.5
L-> Feature 209, Threshold 0.5
L->
R->
R-> Feature 209, Threshold 0.5
L->
R->
R-> Feature 15, Threshold 0.5
L-> Feature 8, Threshold 0.5
L->
R->
R-> Feature 23, Threshold 0.5
L->
R->
=#
# print the variables in the tree
for i in [183, 15, 209, 8, 23]
println("Variable number: ", i, " name: ", names_food[i])
end
#=
Variable number: 183 name: self_perception_wgt3
Variable number: 15 name: cal_day3
Variable number: 209 name: waffle_cal1315
Variable number: 8 name: vitamins
Variable number: 23 name: comfoodr_code11
=#14.6 自助法(bootstrap)
在仅有\(n\)个样本点的情况下, 为了研究统计量\(\hat\theta\)的分布, 从样本中随机有放回地抽取\(n\)次组成一个新的自助样本, 如此可以得到\(B\)组自助样本, 得到\(B\)个\(\hat\theta\)值, 用这些\(\hat\theta\)样本近似其抽样分布。 这相当于总体分布是以\(n\)个样本点为离散均匀分布总体的分布。
例如, 用自助法估计中位数的标准误差,取重复次数为10万次:
using StatsBase, Random, Statistics
Random.seed!(46)
A1 = [10,27,31,40,46,50,52,104,146]
median(A1)
# 46.0
n = length(A1)
m = 100000
theta = zeros(m)
for i = 1:m
theta[i] = median(sample(A1, n, replace=true))
end
mean(theta)
# 45.767
std(theta)
#12.918
## function to compute the bootstrap SE, i.e., an implementation of (5.11)
function boot_se(theta_h)
m = length(theta_h)
c1 = 1.0 / (m - 1)
c2 = mean(theta_h)
res = map(x -> (x-c2)^2, theta_h)
return(sqrt(c1*sum(res)))
end
## 标准误差
boot_se(theta)
## 12.918
## 偏差
mean(theta) - median(A1)
## -0.233
## 置信区间
quantile(theta, [0.025, 0.975])
#=
2-element Array{Float64,1}:
27.0
104.0
=#14.7 随机森林
比随机森林简单一些的做法是装袋法, 从原始训练数据集进行自助法抽样产生许多组重抽样的训练数据集, 对每个训练数据集拟合不进行剪枝的CART, 然后平均结果。 这能改善预报, 但是损失了CART的可解释性和图示能力。 可以用所谓袋外观测(OOB)来估计预测误差, 可以用单个变量对某种误差指标(如根均方误差)的改善值评估变量重要程度。
装袋法的缺点是所有的参与平均的树可能都很相像, 这使得平均降低方差的效果降低。 随机森林方法在每次分叉时仅从随机选择的较少个数的自变量子集选择分叉用的变量, 这使得参与平均的树差异较大。 但是,从实际效果看, 装袋法与随机森林效果相近, 随机森林可能计算复杂度要低一些。
14.8 梯度提升(gradient boosting)
提升法每次用一个较简单的回归(判别)函数, 如一次分叉或两次分叉的树, 然后每次获得上一次的残差, 对残差再次拟合, 将多次拟合的结果乘上一个小的加权系数加起来。
Julia第三方库XGBoost实现了超级梯度提升(Extreme Gradient Boosting)算法, 基于Friedman(2001)的提升学习器, Chen and Guestrin(2016)提供了较好的描述。 R的gbm包也提供了梯度提升方法。
- Chen, T. & Guestrin, C. (2016) XGBoost: A Scalable Tree Boosting System.
McNicholas and Tait(2019) 中的示例程序:
14.8.1 XGBoost处理分类问题的交叉验证函数
对XGBoost算法用5折交叉验证进行分类学习的程序。
tunegrid_xgb产生用来训练模型的参数和结果的数组,
前两列是候选参数搭配,学习速度eta和分叉次数d的两两搭配,
后两列存储误差均值和标准差。
迭代学习次数\(M\)也应该进行选择,
这里为简单起见固定为1000次。
using Statistics, StatsBase
function tunegrid_xgb(eta, maxdepth)
n_eta = size(eta)[1]
md = collect(1:maxdepth)
n_md = size(md)[1]
## 2 cols to store the CV results
res = zeros(*(maxdepth, n_eta), 4)
n_res = size(res)[1]
## populate the res matrix with the tuning parameters
res[:,1] = repeat(md, inner = Int64(/(n_res, n_md)))
res[:,2] = repeat(eta, outer = Int64(/(n_res, n_eta)))
return(res)
endbinary_mcr函数用来计算判别问题的错判率。
function binary_mcr(yp, ya; trace = false)
yl = Array{Int8}(yp .> 0.5)
disagree = Array{Int8}(ya .!= yl)
mcr = mean(disagree)
if trace
#print(countmap(yl))
println("yl: ", yl[1:4])
println("ya: ", ya[1:4])
println("disagree: ", disagree[1:4])
println("mcr: ", mcr)
end
return( mcr )
endbinomial_dev函数用来计算二值偏差(binomial deviance),
是判别问题的一种错误率度量,
在比较不同调节参数时用了这种度量。
## 计算二值偏差的辅助函数
function bd_helper(yp, ya)
e_const = 1e-16
pneg_const = 1.0 - yp
if yp < e_const
res = +(*(ya, log(e_const)), *( -(1.0, ya), log(-(1.0, e_const))))
elseif pneg_const < e_const
res = +(*(ya, log(-(1.0, e_const))), *( -(1.0, ya), log(e_const)))
else
res = +(*(ya, log(yp)), *( -(1.0, ya), log(pneg_const)))
end
return res
end
## Binomial Deviance(二值偏差)
function binomial_dev(yp, ya) #::Vector{T}) where {T <: Number}
res = map(bd_helper, yp, ya)
dev = *(-2, sum(res))
return(dev)
end第三方库MLBase提供了对各种有监督学习方法进行交叉验证的一般性框架,
函数cvERR_xgb作为MLBase的cross_validate函数的输入,
在每次重抽样迭代时返回选定的误差度量值,
cvERR_xgb也用一个函数来输入某种度量计算函数。
function cvERR_xgb(model, Xtst, Ytst, error_fun; trace = false)
y_p = XGBoost.predict(model, Xtst)
if(trace)
println("cvERR: y_p[1:5] ", y_p[1:5])
println("cvERR: Ytst[1:5] ", Ytst[1:5])
println("cvERR: error_fun(y_p, Ytst) ", error_fun(y_p, Ytst))
end
return(error_fun(y_p, Ytst))
endcvResult_xgb是执行整个交叉验证参数选择的主控函数,
调用了MLBase库的cross_validate函数和StratifiedKfold函数进行分层k折交叉验证。
用来进行交叉验证的下标传递给xgboost函数,
在对应的训练集上估计模型并在对应的测试集上计算误差度量。
function cvResult_xgb(
Xmat,
Yvec,
cvparam,
tunegrid;
k = 5,
n = 50,
trace = false )
## tunegrid could have two columns on input
result = deepcopy(tunegrid)
n_tg = size(result)[1]
## k-Fold CV for each combination of parameters
for i = 1:n_tg
scores = cross_validate(
trind -> xgboost(
Xmat[trind,:], 1000,
label = Yvec[trind],
param = cvparam,
max_depth = Int(tunegrid[i,1]),
eta = tunegrid[i,2]),
(c, trind) -> cvERR_xgb(
c, Xmat[trind,:], Yvec[trind],
binomial_dev, trace = true),
## total number of samples
n,
## Stratified CV on the outcome
StratifiedKfold(Yvec, k)
) # cross_validate()
if(trace)
println("cvResult_xgb: scores: ", scores)
println("size(scores): ", size(scores))
end
result[i, 3] = mean(scores)
result[i, 4] = std(scores)
end
return(result)
end14.8.2 对啤酒数据分析的示例程序
先进行80:20的训练集、测试集划分,
划分时按因变量标签等比例地分层抽样。
需要给训练用的函数传送一系列参数,
包括学习速度、树分叉次数的组合,
其它一些参数采用固定值。
用了tunegrid_xgb()函数生成调节参数网格,
用了cvResult_xgb()计算交叉验证选择调节参数的结果。
结果显示0.1速度、2分叉次数较好。
在测试集上产生了8.2%错判率,
偏差4458。
在选择参数时, 选找到误差度量最小的调节参数, 然后将误差度量减去1倍标准误差, 取在此标准以上的最简单(更偏向于减小方差的)的调节参数。
还可以在全集上运行, 得到自变量重要程度的排序。 其中一种指标是增加一个变量的分叉造成的误差减少。
## 80/20 split
splt = 0.8
y_1_ind = N_array[df_recipe[:y] .== 1]
y_0_ind = N_array[df_recipe[:y] .== 0]
tr_index = sort(
vcat(
sample(y_1_ind, Int64(floor(*(N_y_1, splt))), replace = false),
sample(y_0_ind, Int64(floor(*(N_y_0, splt))), replace = false)
)
)
tst_index = setdiff(N_array, tr_index)
df_train = df_recipe[tr_index, :]
df_test = df_recipe[tst_index, :]
## Check proportions
println("train: n y: $(sum(df_train[:y]))")
println("train: % y: $(mean(df_train[:y]))")
println("test: n y: $(sum(df_test[:y]))")
println("test: % y: $(mean(df_test[:y]))")
## Static boosting parameters
param_cv = [
"silent" => 1,
"verbose" => 0,
"booster" => "gbtree",
"objective" => "binary:logistic",
"save_period" => 0,
"subsample" => 0.75,
"colsample_bytree" => 0.75,
"alpha" => 0,
"lambda" => 1,
"gamma" => 0
]
## training data: predictors are sparse matrix
tmp = convert(Array, df_train[setdiff(names(df_train), [:y])] )
xmat_tr = convert(SparseMatrixCSC{Float64,Int64},
collect(Missings.replace(tmp, 0)))
## CV Results
## eta shrinks the feature weights to help prevent overfilling by making
## the boosting process more conservative
## max_depth is the maximum depth of a tree; increasing this value makes
## the boosting process more complex
tunegrid = tunegrid_xgb([0.1, 0.25, 0.5, 0.75, 1], 5)
N_tr = size(xmat_tr)[1]
cv_res = cvResult_xgb(xmat_tr, y_tr, param_cv, tunegrid,
k = 5, n = N_tr, trace = true )
## dataframe for plotting
cv_df = DataFrame(tree_depth = cv_res[:, 1],
eta = cv_res[:, 2],
mean_error = cv_res[:, 3],
sd_error = cv_res[:, 4],
)
cv_df[:se_error] = map(x -> x / sqrt(5), cv_df[:sd_error])
cv_df[:mean_min] = map(-, cv_df[:mean_error], cv_df[:se_error])
cv_df[:mean_max] = map(+, cv_df[:mean_error], cv_df[:se_error])
## configurations within 1 se
min_dev = minimum(cv_df[:mean_error])
min_err = filter(row -> row[:mean_error] == min_dev, cv_df)
one_se = min_err[1, :mean_max]
possible_models = filter(row -> row[:mean_error] <= one_se, cv_df)
#####
## Test Set Predictions
tst_results = DataFrame(
eta = Float64[],
tree_depth = Int64[],
mcr = Float64[],
dev = Float64[])
## using model configuration selected above
pred_tmp = XGBoost.predict(xgboost(xmat_tr, 1000, label = y_tr,
param = param_cv, eta =0.1 , max_depth = 2), xmat_tst)
tmp = [0.1, 2, binary_mcr(pred_tmp, y_tst), binomial_dev(pred_tmp, y_tst)]
push!(tst_results, tmp)
#####
## Variable importance from the overall data
fit_oa = xgboost(xmat_oa, 1000, label = y_oa, param = param_cv, eta = 0.1,
max_depth = 2)
## names of features
names_oa = map(string, setdiff(names(df_recipe), [:y]))
fit_oa_imp = importance(fit_oa, names_oa)
## DF for plotting
N_fi = length(fit_oa_imp)
imp_df = DataFrame(fname = String[], gain = Float64[], cover = Float64[])
for i = 1:N_fi
tmp = [fit_oa_imp[i].fname, fit_oa_imp[i].gain, fit_oa_imp[i].cover]
push!(imp_df, tmp)
end
sort!(imp_df, :gain, rev=true)14.8.3 XGBoost处理回归问题的交叉验证函数
先给出因变量为连续取值的XGBoost用交叉验证选择调节参数的一系列函数。
tunegrid_xgb_reg生成调节参数网格和保存误差均值、标准差的数组,
参数增加了一列alpha值。
function tunegrid_xgb_reg(eta, maxdepth, alpha)
n_eta = size(eta)[1]
md = collect(1:maxdepth)
n_md = size(md)[1]
n_a = size(alpha)[1]
## 2 cols to store the CV results
res = zeros(*(maxdepth, n_eta, n_a), 5)
n_res = size(res)[1]
println("N:", n_res, " e: ", n_eta, " m: ", n_md, " a: ", n_a)
## populate the res matrix with the tuning parameters
n_md_i = Int64(/(n_res, n_md))
res[:,1] = repeat(md, outer=n_md_i)
res[:,2] = repeat(eta, inner = Int64(/(n_res, n_eta)))
res[:,3] = repeat(repeach(alpha, (n_md)), outer=n_a)
return(res)
end函数medae计算平均绝对误差,
rmse计算根均方误差。
function medae(yp, ya)
## element wise operations
res = map(yp, ya) do x,y
dif = -(x, y)
return(abs(dif))
end
return(median(res))
end
function rmse(yp, ya)
## element wise operations
res = map(yp, ya) do x,y
dif = -(x, y)
return(dif^2)
end
return(sqrt(mean(res)))
end函数cvResult_xgb_reg是用交叉验证选调节参数整个过程的主控程序。
用不分层的再抽样方法,
以平均绝对误差为误差度量。
function cvResult_xgb_reg(
Xmat, Yvec, cvparam, tunegrid;
k = 5, n = 50, trace = false )
result = deepcopy(tunegrid)
n_tg = size(result)[1]
## k-Fold CV for each combination of parameters
for i = 1:n_tg
scores = cross_validate(
## num_round investigate
trind -> xgboost(
Xmat[trind,:], 1000, label = Yvec[trind],
param = cvparam, max_depth = Int(tunegrid[i,1]),
eta = tunegrid[i,2], alpha = tunegrid[i,3]),
(c, trind) -> cvERR_xgb(
c, Xmat[trind,:], Yvec[trind], medae,
trace = true),
n, ## total number of samples
Kfold(n, k)
)
if(trace)
println("cvResult_xgb_reg: scores: ", scores)
println("size(scores): ", size(scores))
end
result[i, 4] = mean(scores)
result[i, 5] = std(scores)
end
return(result)
end14.8.4 处理食品评分数据的示例程序
对食品评分数据进行了XGBoost交叉验证训练, 调节参数包括学习速度eta、树深度(分叉次数)d、正则化系数alpha, 在自变量个数较多时alpha可以大大改善预测精度。 最终选了eta=0.1, alpha=0.1,树桩(d=1, 仅一次分叉)。
计算了自变量重要度指标。
## 80/20 train test split
splt = 0.8
tr_index = sample(N_array, Int64(floor(*(N, splt))), replace = false)
tst_index = setdiff(N_array, tr_index)
df_train = df_food[tr_index, :]
df_test = df_food[tst_index, :]
## train data: predictors are sparse matrix
y_tr = convert(Array{Float64}, df_train[:gpa])
tmp = convert(Array, df_train[setdiff(names(df_train), [:gpa])] )
xmat_tr = convert(SparseMatrixCSC{Float64,Int64},
collect(Missings.replace(tmp, 0)))
## Static boosting parameters
param_cv_reg = [
"silent" => 1,
"verbose" => 0,
"booster" => "gbtree",
"objective" => "reg:linear",
"save_period" => 0,
"subsample" => 0.75,
"colsample_bytree" => 0.75,
"lambda" => 1,
"gamma" => 0
]
## CV Results
## eta shrinks the feature weights to help prevent overfilling by making
## the boosting process more conservative
## max_depth is the maximum depth of a tree; increasing this value makes
## the boosting process more complex
## alpha is an L1 regularization term on the weights; increasing this value
## makes the boosting process more conservative
tunegrid = tunegrid_xgb_reg([0.1, 0.3, 0.5], 5, [0.1, 0.3, 0.5])
N_tr = size(xmat_tr)[1]
cv_res_reg = cvResult_xgb_reg(xmat_tr, y_tr, param_cv_reg, tunegrid,
k = 5, n = N_tr, trace = true )
## add the standard error
cv_res_reg = hcat(cv_res_reg, ./(cv_res_reg[:,5], sqrt(5)))
## dataframe for plotting
cv_df_r = DataFrame(tree_depth = cv_res_reg[:, 1],
eta = cv_res_reg[:, 2],
alpha = cv_res_reg[:, 3],
medae = cv_res_reg[:, 4],
medae_sd = cv_res_reg[:, 5]
)
cv_df_r[:medae_se] = map(x -> /(x , sqrt(5)), cv_df_r[:medae_sd])
cv_df_r[:medae_min] = map(-, cv_df_r[:medae], cv_df_r[:medae_se])
cv_df_r[:medae_max] = map(+, cv_df_r[:medae], cv_df_r[:medae_se])
min_medae = minimum(cv_df_r[:medae])
min_err = filter(row -> row[:medae] == min_medae, cv_df_r)
one_se = min_err[1, :medae_max]
#######
## Test Set Predictions
tst_results = DataFrame(
eta = Float64[],
alpha = Float64[],
tree_depth = Int64[],
medae = Float64[],
rmse = Float64[])
## using configuration chosen above
pred_tmp = XGBoost.predict(xgboost(xmat_tr, 1000, label = y_tr,
param = param_cv_reg, eta =0.1 , max_depth = 1, alpha = 0.1), xmat_tst)
tmp = [0.1, 0.1, 1, medae(pred_tmp, y_tst), rmse(pred_tmp, y_tst)]
push!(tst_results, tmp)
#####
## Variable Importance from the overall data
fit_oa = xgboost(xmat_oa, 1000, label = y_oa, param = param_cv_reg,
eta = 0.1, max_depth = 1, alpha = 0.1)
## names of features
# names_oa = convert(Array{String,1}, names(df_food))
names_oa = map(string, setdiff(names(df_train), [:gpa]))
fit_oa_imp = importance(fit_oa, names_oa)
## DF for plotting
N_fi = length(fit_oa_imp)
imp_df = DataFrame(fname = String[], gain = Float64[], cover = Float64[])
for i = 1:N_fi
tmp = [fit_oa_imp[i].fname, fit_oa_imp[i].gain, fit_oa_imp[i].cover]
push!(imp_df, tmp)
end
sort!(imp_df, :gain, rev=true)14.9 无监督学习
无监督学习的训练样本没有标签, 目标不是预测。 这样, 无监督学习的方法可以更多采用概率模型, 用概率模型描述数据的关系和不确定性。
随机向量有一些常用的公式, 如期望公式, 方差阵公式, 线性变换的期望和协方差阵公式。 方差阵的特征值分解。 参见作者的《多元统计分析》授课笔记。
参考:
- McNicholas and Tait(2019) Data Science Using Julia, CRC Press. 源程序网址https://github.com/paTait/dswj
14.10 主成分分析(PCA)
可以比较简单地用矩阵代数方法计算主成分分析所需的方差阵估计、 特征值、特征向量, 并计算主成分得分。 的输入数据集矩阵\(X\), 设每一行是\(p\)维的一个观测, \(n\)行为\(n\)个观测, 设\(X\)的每列都已经标准化(减去列平均值), 用LinearAlgebra的svd函数对\(X\)进行奇异值分解, 这相当于对协方差阵估计做特征值分解。
\[ \text{svd}(X) = U \text{diag}(S) V^T \]
其中\(X\)是\(n\times p\)阵, \(U\)是\(n \times k\)列单位正交阵, \(V\)是\(p \times k\)列单位正交阵, \(k = \min(n, p)\)。 则 \[ X V = U \text{diag}(S) \] 是\(n \times k\)矩阵, 每一列是\(X\)的一个线性组合, 且 \[ \text{Var}(X V) = \frac{1}{n-1} \text{diag}(S^2) . \] 这说明\(X V\)的每一列是一个主成分得分列。
using LinearAlgebra
## 通过奇异值分解计算主成分分析
## 输入: $n \times p$数据集矩阵
function pca_svd(X)
n, p = size(X)
k = min(n,p)
S = svd(X)
## 奇异值向量
D = S.S[1:k]
## 右特征向量
V = transpose(S.Vt)[:,1:k]
## 主成分的标准差
sD = D ./ sqrt(n-1)
rotation = V
## 主成分得分矩阵
projection = X * V
return(Dict(
"sd" => sD, # 主成分的标准差
"rotation" => rotation, # 右乘观测数据阵用的矩阵
"projection" => projection # 主成分得分矩阵
))
end用R的MASS包的crabs数据集演示主成分分析。 可以用RDatasets包获取R的许多样例数据集。 crabs有两个分类变量Sp(两个品种)、Sex(性别), 5个测量值变量,Index是序号。
using RDatasets, DataFrames, Statistics
df_crabs = RDatasets.dataset("MASS", "crabs")
first(df_crabs, 3)| Sp | Sex | Index | FL | RW | CL | CW | BD | |
|---|---|---|---|---|---|---|---|---|
| Cat… | Cat… | Int32 | Float64 | Float64 | Float64 | Float64 | Float64 | |
| 1 | B | M | 1 | 8.1 | 6.7 | 16.1 | 19.0 | 7.0 |
| 2 | B | M | 2 | 8.8 | 7.7 | 18.1 | 20.8 | 7.4 |
| 3 | B | M | 3 | 9.2 | 7.8 | 19.0 | 22.4 | 7.7 |
提取其中的5个测量值列,
将数据框用convert函数转换成浮点值矩阵,
对每列减去均值:
crab_mat = convert(Array{Float64}, df_crabs[:, [:FL, :RW, :CL, :CW, :BD]])
mean_crab = mean(crab_mat, dims = 1)
crab_mat_c = crab_mat .- mean_crab;mean()函数的dims=1是指定了计算均值的轴向,
这是沿第一下标(行下标)变化的方向计算均值,
即对每列计算均值。
后面的\(200 \times 5\)矩阵“.-”一个\(1 \times 5\)矩阵,
根据广播规则,
某一维长度为1时,
可以重复使用该维的元素与对应维的每个下标遍历运算。
下面用奇异值分解方法对中心化的数据集作奇异值分解,
生成作图用的数据框,
变量label用来获得品种和性别的四个类型:
pca1 = pca_svd(crab_mat_c)
pca_df2 = DataFrame(
pc1 = pca1["projection"][:,1],
pc2 = pca1["projection"][:,2],
pc3 = pca1["projection"][:,3],
pc4 = pca1["projection"][:,4],
pc5 = pca1["projection"][:,5],
label = map(string, repeat(1:4, inner = 50))
);前两个主成分的方差解释比例:
cumsum(pca1["sd"][1:2] .^ 2) ./ sum(pca1["sd"] .^ 2)2-element Array{Float64,1}:
0.9824717995023747
0.9915269079375648前两个主成分的图形:
using Gadfly
Gadfly.plot(pca_df2, x = :pc1, y = :pc2, color = :label)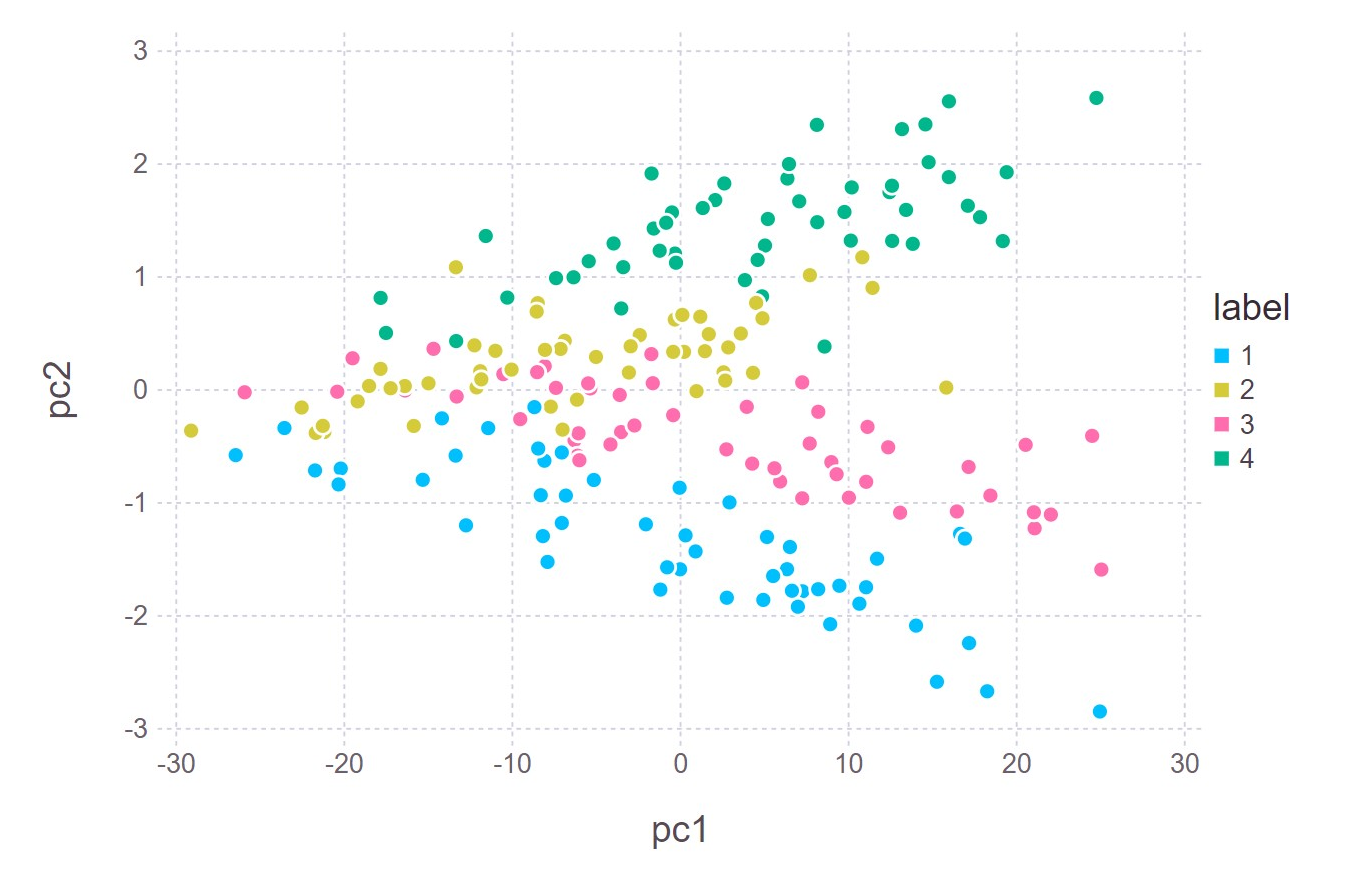
第二和第三主成分的图形:
Gadfly.plot(pca_df2, x = :pc2, y = :pc3, color = :label)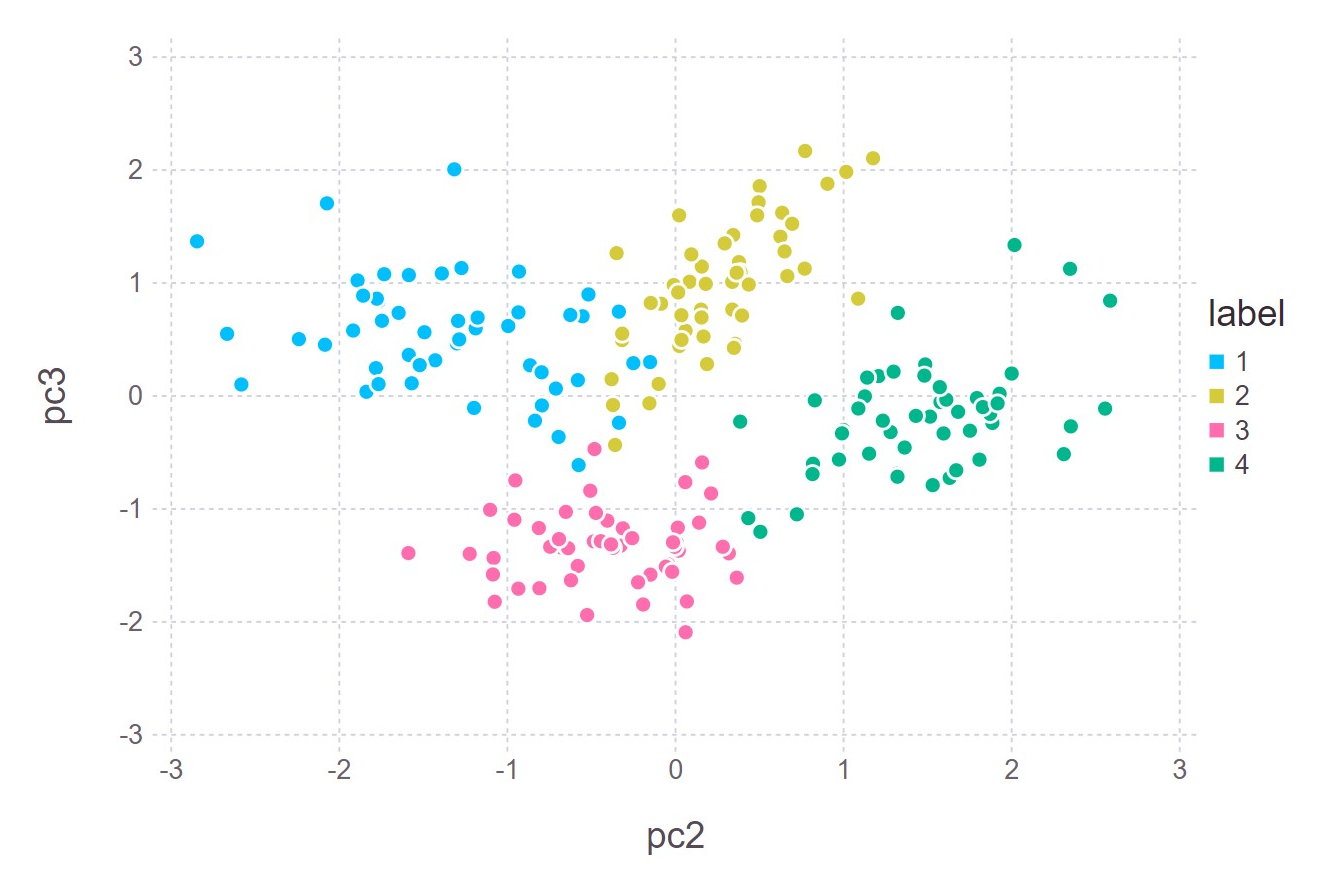
很奇怪的是, 尽管第一主成分占了98%以上的解释比例, 但是第二和第三主成分对四个类别区分得更明显。
14.11 概率主成分分析(PPCA)
14.11.1 模型
概率主成分分析与主成分分析和因子分析有深刻的关系, 也是变量降维方法, 有时可以将维数剧烈减少。 PPCA模型为 \[ \boldsymbol X_i = \boldsymbol\mu + \boldsymbol\Lambda \boldsymbol U_i + \boldsymbol\epsilon_i, \ i=1,2,\dots,n \] 其中\(\boldsymbol X_i\)为\(p\)维向量, \(\boldsymbol\Lambda\)为\(p \times q\)的载荷阵, \(\boldsymbol U_i\)为潜在变量(因子), \(\boldsymbol U_i \sim \text{N}_q(\boldsymbol 0, \boldsymbol I_q)\), \(\boldsymbol\epsilon_i \sim \text{N}_p(\boldsymbol 0, \psi \boldsymbol I_p)\)是因子分析中的特殊因子, \(\psi>0\), 各 \(\boldsymbol U_1, \dots, \boldsymbol U_n, \boldsymbol\epsilon_1, \dots, \boldsymbol\epsilon_n\)相互独立。 则\(\boldsymbol X_i\)分布为 \[ \text{N}(\boldsymbol\mu, \boldsymbol\Lambda \boldsymbol\Lambda^T + \psi \boldsymbol I_p) . \]
可以写出模型的对数似然函数: \[\begin{aligned} & \ell(\boldsymbol \mu, \boldsymbol \Lambda, \psi) \\ =& \sum_{i=1}^n \log \phi(\boldsymbol x_i | \boldsymbol \mu, \boldsymbol \Lambda \boldsymbol \Lambda^T + \psi \boldsymbol I_p) \\ =& -\frac{np}{2} \log(2\pi) - \frac{n}{2} \log \text{det}(\boldsymbol \Lambda \boldsymbol \Lambda^T + \psi \boldsymbol I_p) \\ & - \frac{n}{2} \text{tr} \{ \boldsymbol S ( \boldsymbol \Lambda \boldsymbol \Lambda^T + \psi \boldsymbol I_p )^{-1} \} \\ \boldsymbol S =& \frac{1}{n} \sum_{i=1}^n (\boldsymbol x_i - \boldsymbol \mu)(\boldsymbol x_i - \boldsymbol \mu)^T . \end{aligned}\]
先用均值得到\(\boldsymbol\mu\)的估计, 然后用EM算法求方差阵参数的估计。
14.11.2 EM算法
EM算法时最大似然估计的迭代方法, 每次迭代对参数估计值进行更新。 在E步, 基于当前的参数估计值, 计算完全数据对数似然函数在观测数据条件下的条件期望值, 求期望时,将已有的参数估计值和观测数据看作是已知的, 对潜在变量取条件期望。 在M步, 将上一步的期望值作为未知参数的函数求最大值点, 得到参数估计的更新值。
在PPCA模型中, 完全数据设定为\((\boldsymbol X_i, \boldsymbol U_i)\), \(i=1,2,\dots,n\), 注意实际上\(\boldsymbol U_i\)是不可观测的, 但在\(\boldsymbol U_i\)已知条件下\(\boldsymbol X_i\)的条件分布可以变得很简单, 从而用乘法法则写出完全似然。 易见在\(\boldsymbol U_i\)条件下, \(\boldsymbol X_i\)服从 \[ \text{N}(\boldsymbol \mu + \boldsymbol \Lambda, \psi \boldsymbol I_p) \] 分布, 而\(\boldsymbol U_i\)服从N(0,1)分布, 可以写出完全数据的对数似然函数, 然后利用\((\boldsymbol X_i, \boldsymbol U_i)\)的联合正态密度求出 \(E(\boldsymbol U_i | \boldsymbol X_i)\)和\(E(\boldsymbol U_i \boldsymbol U_i^T | \boldsymbol X_i)\), 并预先取\(\boldsymbol \mu = \bar{\boldsymbol X}\), 可以求出在各\(\boldsymbol X_i\)条件下完全对数似然的期望值, 作为未知参数\(\boldsymbol \Lambda\)和\(\psi\)的函数\(Q(\boldsymbol \Lambda, \psi)\)。
在M步对此函数求最大值点。 关于两个参数求偏导数, 得到得分函数, 令得分函数等于零, 可以解出新的参数估计的表达式。
为了给参数初值, 可以对\(\boldsymbol X\)的协方差阵估计作特征值分解, 从中得到\(\boldsymbol \Lambda\)和\(\psi\)的初值。
关于迭代的停止法则, 可以用两次的对数似然函数值的变化量小于某个阈值\(\epsilon\)作为准则, 更可靠的是用Aitken加速法则, 用 \[\begin{aligned} a^{(k)} = \frac{\ell^{(k+1)} - \ell^{(k)}}{\ell^{(k)} - \ell^{(k-1)}} \end{aligned}\] 估计变化速度,从而获得\(k+1\)步的渐近对数似然值 \[ \ell_{\infty}^{(k+1)} = \ell^{(k)} + \frac{\ell^{(k+1)} - \ell^{(k)}}{1 - a^{(k)}}, \] 当 \[ 0 < \ell_{\infty}^{(k+1)} - \ell^{(k)} < \epsilon \] 时停止。
14.11.3 PPCA的Julia实现
先给出一些辅助函数。
## EM Algorithm for PPCA -- Helper functions
## 用Woodbury公式求逆
function wbiinv(q, p, psi, L)
## Woodbury Indentity eq 6.13
Lt = transpose(L)
Iq = Matrix{Float64}(I, q, q)
Ip = Matrix{Float64}(I, p, p)
psi2 = /(1, psi)
m1 = *(psi2, Ip)
m2c = +( *(psi, Iq), *(Lt, L) )
m2 = *(psi2, L, inv(m2c), Lt)
return( -(m1, m2) )
end
## 用Woodbury公式求行列式
function wbidet(q, p, psi, L)
## Woodbury Indentity eq 6.14
Iq = Matrix{Float64}(I, q, q)
num = psi^p
den1 = *(transpose(L), wbiinv(q, p, psi, L), L)
den = det(-(Iq, den1))
return( /(num, den) )
end
## 似然函数
function ppca_ll(n, q, p, psi, L, S)
## log likelihood eq 6.8
n2 = /(n, 2)
c = /( *(n, p, log(*(2, pi))), 2)
l1 = *(n2, log(wbidet(q, p, psi, L)))
l2 = *(n2, tr(*(S, wbiinv(q, p, psi, L))))
return( *(-1, +(c, l1, l2)) )
end
## 计算协方差阵
function cov_mat(X)
n,p = size(X)
mux = mean(X, dims = 1)
X_c = .-(X, mux)
res = *( /(1,n), *(transpose(X_c), X_c))
return(res)
end
## 用Aitken加速判断是否收敛
function aitkenaccel(l1, l2, l3, tol)
## l1 = l(k+1), l2 = l(k), l3 = l(k-1)
conv = false
num = -(l1, l2)
den = -(l2, l3)
## eq 6.16
ak = /(num, den)
if ak <= 1.0
c1 = -(l1, l2)
c2 = -(1.0, ak)
## eq 6.17
l_inf = +(l2, /(c2, c1))
c3 = -(l_inf, l2)
if 0.0 < c3 < tol
conv = true
end
end
return conv
end
## 计算自由参数个数
function ppca_fparams(p, q)
## number of free parameters in the ppca model
c1 = *(p, q)
c2 = *(-1, q, -(q, 1), 0.5)
return( +(c1, c2, 1) )
end
## 计算BIC准则值
function BiC(ll, n, q, ρ)
## name does not conflict with StatsBase
## eq 6.19
c1 = *(2, ll)
c2 = *(ρ, log(n))
return( -(c1, c2) )
endPPCA的EM算法的主要程序如下:
using LinearAlgebra, Random
Random.seed!(429)
## EM Function for PPCA
function ppca(X; q = 2, thresh = 1e-5, maxit = 1e5)
Iq = Matrix{Float64}(I, q, q)
qI = *(q, Iq)
n,p = size(X)
## eigfact has eval/evec smallest to largest
ind = p:-1:(p-q+1)
Sx = cov_mat(X)
D = eigen(Sx)
d = diagm(0 => map(sqrt, D.values[ind]))
P = D.vectors[:, ind]
## initialize parameters
L = *(P, d) ## pxq
psi = *( /(1, p), tr( -( Sx, *(L, transpose(L)) ) ) )
B = zeros(q,p)
T = zeros(q,q)
conv = true
iter = 1
ll = zeros(100)
ll[1] = 1e4
## while not converged
while(conv)
## above eq 6.12
B = *(transpose(L), wbiinv(q, p, psi, L)) ## qxp
T = -(qI, +( *(B,L), *(B, Sx, transpose(B)) ) ) ## qxq
## sec 6.4.3 - update Lambda_new
L_new = *(Sx, transpose(B), inv(T)) ## pxq
## update psi_new
psi_new = *( /(1, p), tr( -(Sx, *(L_new, B, Sx) ) )) #num
iter += 1
if iter > maxit
conv = false
println("ppca() while loop went over maxit parameter. iter = $iter")
else
## stores at most the 100 most recent ll values
if iter <= 100
ll[iter]=ppca_ll(n, q, p, psi_new, L_new, Sx)
else
ll = circshift(ll, -1)
ll[100] = ppca_ll(n, q, p, psi_new, L_new, Sx)
end
if 2 < iter < 101
## scales the threshold by the latest ll value
thresh2 = *(-1, ll[iter], thresh)
if aitkenaccel(ll[iter], ll[(iter-1)], ll[(iter-2)], thresh2)
conv = false
end
else
thresh2 = *(-1, ll[100], thresh)
if aitkenaccel(ll[100], ll[(99)], ll[(98)], thresh2)
conv = false
end
end
end ## if maxit
L = L_new
psi = psi_new
end ## while
## orthonormal coefficients
coef = svd(L).U
## projections
proj = *(X, coef)
if iter <= 100
resize!(ll, iter)
end
fp = ppca_fparams(p, q)
bic_res = BiC(ll[end], n, q, fp)
return(Dict(
"iter" => iter,
"ll" => ll,
"beta" => B,
"theta" => T,
"lambda" => L,
"psi" => psi,
"q" => q,
"sd" => diag(d),
"coef" => coef,
"proj" => proj,
"bic" => bic_res
))
end
ppca1 = ppca(crab_mat_c, q=3, maxit = 1e3)Dict{String,Any} with 11 entries:
"psi" => -1.45759
"coef" => [-0.288981 0.32325 0.50717; -0.197282 0.864716 -0.414136; … ; -0.…
"theta" => [0.980799 9.80988e-13 1.25678e-12; 9.8144e-13 2.21372 -8.98728e-1…
"lambda" => [-3.57065 -0.0431202 0.0289235; -2.43762 -0.11535 -0.0236179; … ;…
"q" => 3
"bic" => -3048.97
"ll" => [10000.0, -1504.4, -1513.29, -1504.07, -1520.18, 3833.21, -290.70…
"iter" => 9
"sd" => [11.8323, 1.13594, 0.997631]
"beta" => [-0.0250145 -0.017077 … -0.0572736 -0.0245601; -0.0739769 -0.1978…
"proj" => [26.4646 -0.576534 0.611568; 23.5617 -0.33642 0.237388; … ; -19.1…结果有问题,psi应该是正值, 似然函数应该单调下降。
为了选择潜在变量个数, 可以用BIC准则: \[ \text{BIC}(q) = 2 \hat\ell_{\max} - \rho n \] 找BIC最大的个数, 其中\(\rho\)是模型中自由参数个数。 \(\hat\ell_{\max}\)是在最大似然估计处计算的对数似然函数值。
PPCA并不一定比PCA结果更好, 但是这个模型的可扩展性强, 也可以与其他的基于概率模型的方法进行比较。 扩展如, 可以容纳缺失数据, 可以转为贝叶斯体系。 当\(\psi \to 0\)时, 结果趋近于PCA结果。
14.12 k均值聚类
k均值聚类的每个类中心是均值, 这相当于画了k个圈, 每个圈都是相同大小的正圆形(超球面)。 Clustering库的kmeans函数提供了k均值聚类功能。
考虑x2数据集, 这是模拟生成的三个二元正态样本混合的数据。 在R的mixture包的x2数据集中。
为了选择类个数k, 可以对多个k计算并做出类内离差平方和的总和对k的散点图, 找到随k增加减少速度变缓的拐点(肘部)。
using CSV, DataFrames, Statistics, Clustering, Gadfly, Random
Random.seed!(429)
x2_df = DataFrame!(CSV.File("x2.csv"))
Gadfly.plot(
x2_df, x = :V1, y = :V2,
Geom.point)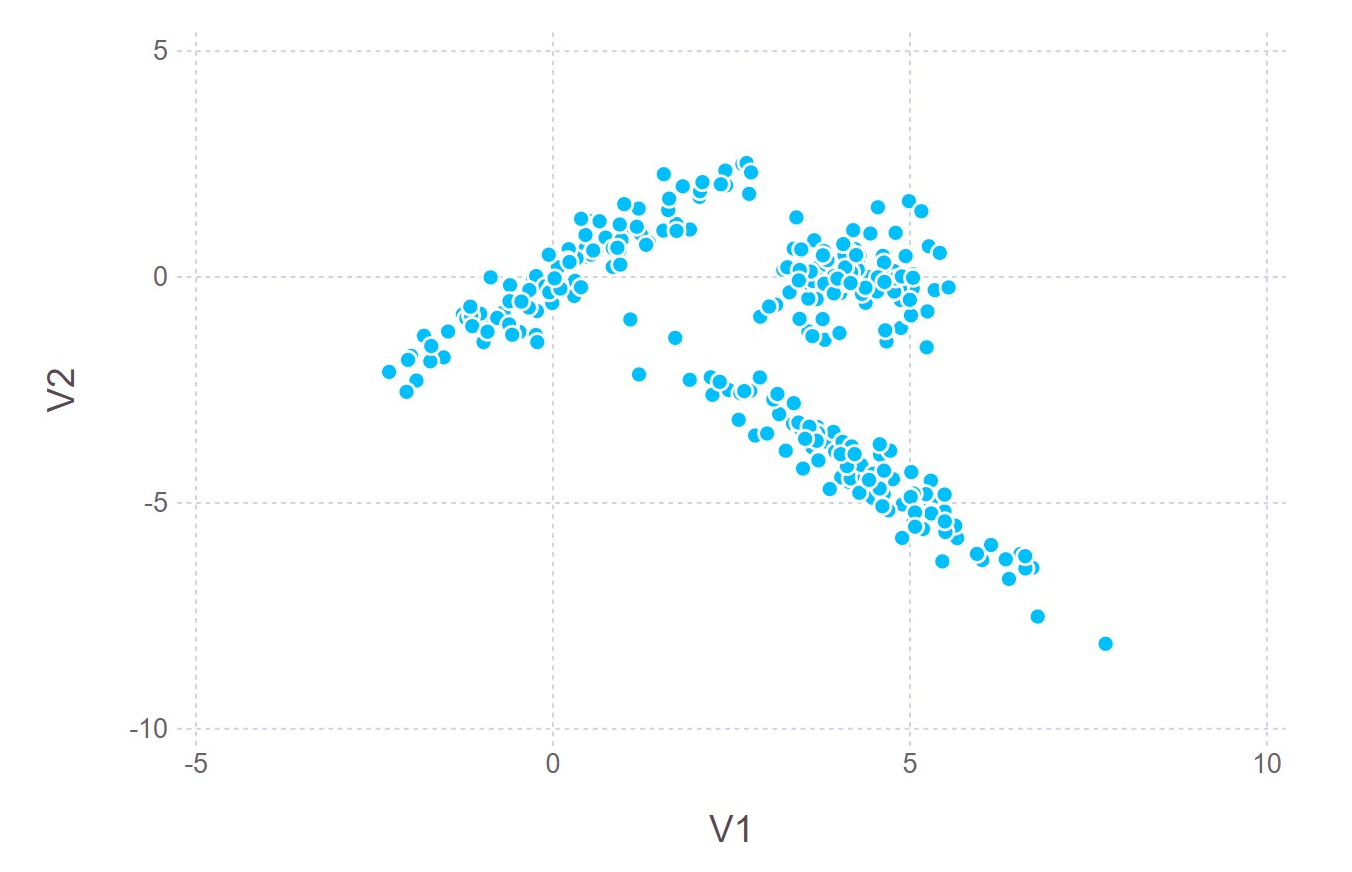
x2_mat = convert(Matrix{Float64}, x2_df)
## 数据中心化
mean_x2 = mean(x2_mat, dims=1)
x2_mat_c = x2_mat .- mean_x2
## 样本量
N = size(x2_mat_c)[1]
## kmeans()函数需要每一列是一个样品
##x2_mat_t = reshape(x2_mat_c, (2,N))
x2_mat_t = x2_mat_c'
## 对多个类数尝试,作肘部图
k = 2:8
df_elbow = DataFrame(k = Vector{Int64}(), tot_cost = Vector{Float64}())
for i in k
tmp = [i, kmeans(x2_mat_t, i; maxiter=10, init=:kmpp).totalcost ]
push!(df_elbow, tmp)
end
## 画肘部图
p_km_elbow = Gadfly.plot(
df_elbow, x = :k, y = :tot_cost,
Geom.point, Geom.line,
Guide.xlabel("k"),
Guide.ylabel("Total Within Cluster SS"),
Coord.Cartesian(xmin = 1.95),
Guide.xticks(ticks = collect(2:8)))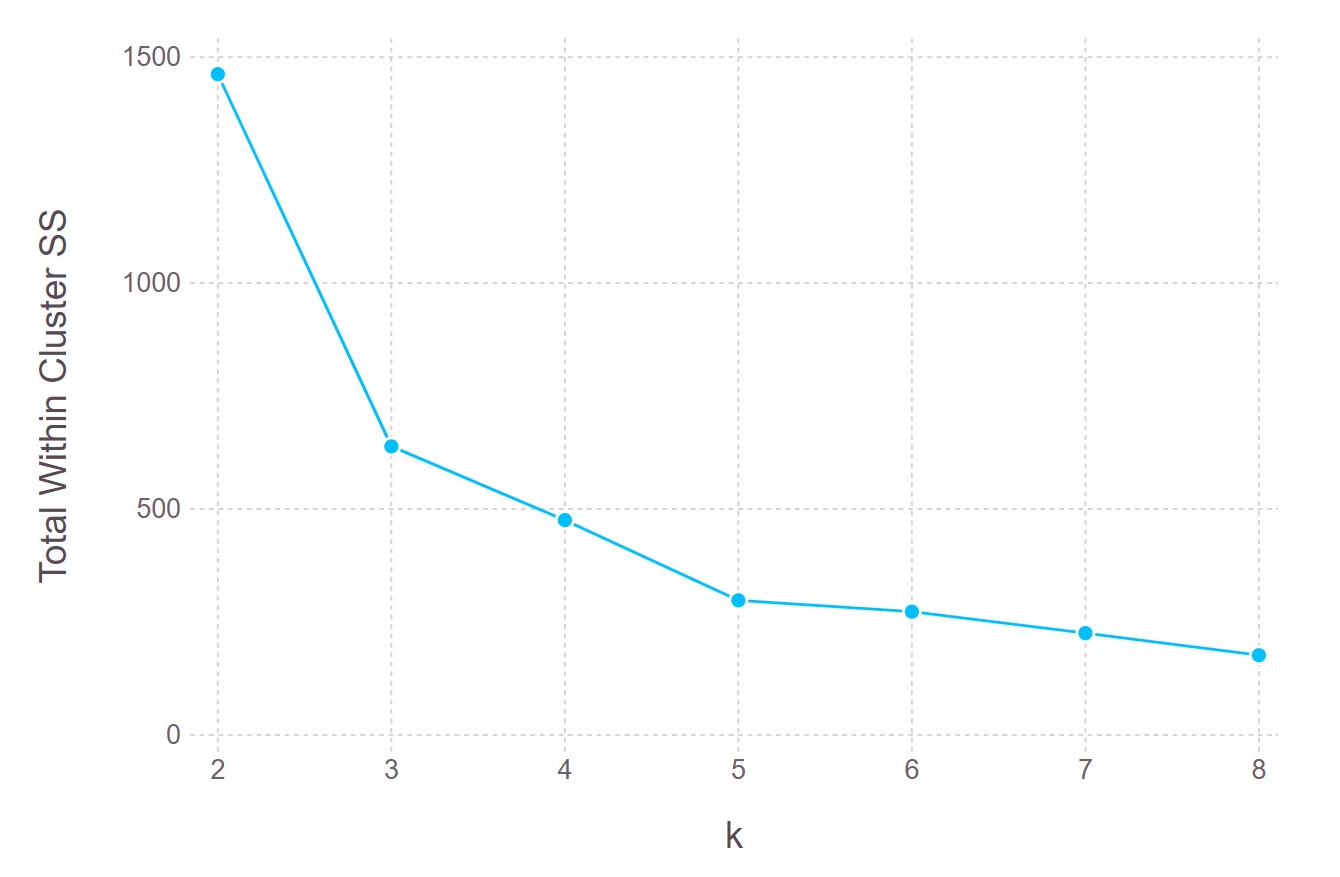
从图形看, 明显的拐点在k=3。 这个数据实际有三个类, 但是其中两个类为扁长形, 使得等大小圆形的类的效果不够好。
14.13 混合概率主成分分析(MPPCA)模型
14.13.1 模型
混合分布可以用来表示聚类, PPCA可以用来对高维数据降维, 将两者结合, 可以用来在高维数据中进行聚类、分布密度估计、判别分析。
模型假定为 \[ \boldsymbol X_i = \boldsymbol\mu_g + \boldsymbol\Lambda_g \boldsymbol U_{ig} + \boldsymbol\epsilon_{ig}, \ i=1,2,\dots,n \] 其中\(g\)是在\(\{ 1, 2, \dots, G \}\)中取值的离散随机变量, 在已知\(g\)时分布于PPCA相同, 但\(\boldsymbol X_i\)的边缘分布为 \[ f(\boldsymbol x_i | \boldsymbol \vartheta) = \sum_{g=1}^G \pi_g \phi(\boldsymbol x_i | \boldsymbol \mu_g, \boldsymbol \Lambda_g \boldsymbol \Lambda_g^T + \psi_g \boldsymbol I_p) . \]
14.13.2 参数估计
可以用交替期望与条件最大化(AECM, alternating expectation-conditional maximization)方法估计参数。 ECM是EM方法的变种, 在M不用若干次条件最大化代替最大化。 AECM则允许在每一次条件最大化时使用不同的完全数据设定。
在MPPCA模型中有两种缺失值, 即PPCA中的潜在变量, 和混合分布中的未知组别。 这样,使用AECM算法是合适的。
辅助函数:
## MPPCA helper functions
using LinearAlgebra
function sigmaG(mu, xmat, Z)
res = Dict{Int, Array}()
N,g = size(Z)
c1 = ./(1, sum(Z, dims = 1))
for i = 1:g
xmu = .-(xmat, transpose(mu[:,i]))
zxmu = .*(Z[:,i], xmu)
res_g = *(c1[i], *(transpose(zxmu), zxmu))
push!(res, i=>res_g)
end
return res
end
function muG(g, xmat, Z)
N, p = size(xmat)
mu = zeros(p, g)
for i in 1:g
num = sum(.*(Z[:,i], xmat), dims = 1)
den = sum(Z[:, i])
mu[:, i] = /(num, den)
end
return mu
end
## initializations
function init_LambdaG(q, g, Sx)
res = Dict{Int, Array}()
for i = 1:g
p = size(Sx[i], 1)
ind = p:-1:(p-q+1)
D = eigen(Sx[i])
d = diagm(0 => map(sqrt, D.values[ind]))
P = D.vectors[:, ind]
L = *(P,d)
push!(res, i => L)
end
return res
end
function init_psi(g, Sx, L)
res = Dict{Int, Float64}()
for i = 1:g
p = size(Sx[i], 1)
psi = *(/(1, p), tr(-(Sx[i], *(L[i], transpose(L[i])))))
push!(res, i=>psi)
end
return res
end
function init_dict0(g, r, c)
res = Dict{Int, Array}()
for i = 1:g
push!(res, i=> zeros(r, c))
end
return res
end
## Updates
function update_B(q, p, psig, Lg)
res = Dict{Int, Array}()
g = length(psig)
for i=1:g
B = *(transpose(Lg[i]), wbiinv(q, p, psig[i], Lg[i]))
push!(res, i=>B)
end
return res
end
function update_T(q, Bg, Lg, Sg)
res = Dict{Int, Array}()
Iq = Matrix{Float64}(I, q, q)
qI = *(q, Iq)
g = length(Bg)
for i =1:g
T = -(qI, +(*(Bg[i], Lg[i]), *(Bg[i], Sg[i], transpose(Bg[i]))))
push!(res, i=>T)
end
return res
end
function update_L(Sg, Bg, Tg)
res = Dict{Int, Array}()
g = length(Bg)
for i = 1:g
L = *(Sg[i], transpose(Bg[i]), inv(Tg[i]))
push!(res, i=>L)
end
return res
end
function update_psi(p, Sg, Lg, Bg)
res = Dict{Int, Float64}()
g = length(Bg)
for i = 1:g
psi = *( /(1, p), tr( -(Sg[i], *(Lg[i], Bg[i], Sg[i]) ) ) )
push!(res, i=>psi)
end
return res
end
function update_zmat(xmat, mug, Lg, psig, pig)
N,p = size(xmat)
g = length(Lg)
res = Matrix{Float64}(undef, N, g)
Ip = Matrix{Float64}(I, p, p)
for i = 1:g
pI = *(psig[i], Ip)
mu = mug[:, i]
cov = +( *( Lg[i], transpose(Lg[i]) ), pI)
pi_den = *(pig[i], pdf(MvNormal(mu, cov), transpose(xmat)))
res[:,i] = pi_den
end
return ./(res, sum(res, dims = 2))
end
function mapz(Z)
N,g = size(Z)
res = Vector{Int}(undef, N)
for i = 1:N
res[i] = findmax(Z[i,:])[2]
end
return res
end
function mppca_ll(N, p, pig, q, psig, Lg, Sg)
g = length(Lg)
l1,l2,l3 = (0,0,0)
c1 = /(N,2)
c2 = *(-1, c1, p, g, log( *(2,pi) ))
for i = 1:g
l1 += log(pig[i])
l2 += log(wbidet(q, p, psig[i], Lg[i]))
l3 += tr(*(Sg[i], wbiinv(q, p, psig[i], Lg[i])))
end
l1b = *(N, l1)
l2b = *(-1, c1, l2)
l3b = *(-1, c1, l3)
return(+(c2, l1b, l2b, l3b))
end
function mppca_fparams(p, q, g)
## number of free parameters in the ppca model
c1 = *(p, q)
c2 = *(-1, q, -(q, 1), 0.5)
return(+( *( +(c1, c2), g), g))
end
function mppca_proj(X, G, map, L)
res = Dict{Int, Array}()
for i in 1:G
coef = svd(L[i]).U
sel = map .== i
proj = *(X[sel, :], coef)
push!(res, i=>proj)
end
return(res)
endAECM算法主体, 用聚类算法初始化类别:
using Clustering
include("chp6_ppca_functions.jl")
include("chp6_mixppca_functions.jl")
## MPPCA function
function mixppca(X; q = 2, G = 2, thresh = 1e-5, maxit = 1e5, init = 1))
## initializations
N, p = size(X)
## z_ig
if init == 1
## random
zmat = rand(Uniform(0,1), N, G)
## row sum to 1
zmat = ./(zmat, sum(zmat, dims = 2))
elseif init == 2
# k-means
kma = kmeans(permutedims(X), G; init=:rand).assignments
zmat = zeros(N,G)
for i in 1:N
zmat[i, kma[i]] = 1
end
end
n_g = sum(zmat, dims = 1)
pi_g = /(n_g, N)
mu_g = muG(G, X, zmat)
S_g = sigmaG(mu_g, X, zmat)
L_g = init_LambdaG(q, G, S_g)
psi_g = init_psi(G, S_g, L_g)
B_g = init_dict0(G, q, p)
T_g = init_dict0(G, q, q)
conv = true
iter = 1
ll = zeros(100)
ll[1] = 1e4
# while not converged
while(conv)
## update pi_g and mu_g
n_g = sum(zmat, dims = 1)
pi_g = /(n_g, N)
mu_g = muG(G, X, zmat)
if iter > 1
## update z_ig
zmat = update_zmat(X, mu_g, L_g, psi_g, pi_g)
end
## compute S_g, Beta_g, Theta_g
S_g = sigmaG(mu_g, X, zmat)
B_g = update_B(q, p, psi_g, L_g)
T_g = update_T(q, B_g, L_g, S_g)
## update Lambda_g psi_g
L_g_new = update_L(S_g, B_g, T_g)
psi_g_new = update_psi(p, S_g, L_g, B_g)
## update z_ig
zmat = update_zmat(X, mu_g, L_g_new, psi_g_new, pi_g)
iter += 1
if iter > maxit
conv = false
println("mixppca() while loop went past maxit parameter. iter =
$iter")
else
## stores at most the 100 most recent ll values
if iter <= 100
ll[iter] = mppca_ll(N, p, n_g, pi_g, q, psi_g, L_g, S_g)
else
ll = circshift(ll, -1)
ll[100] = mppca_ll(N, p, n_g, pi_g, q, psi_g, L_g, S_g)
end
if 2 < iter < 101
## scales the threshold by the latest ll value
thresh2 = *(-1, ll[iter], thresh)
if aitkenaccel(ll[iter], ll[(iter-1)], ll[(iter-2)], thresh2)
conv = false
end
else
thresh2 = *(-1, ll[100], thresh)
if aitkenaccel(ll[100], ll[(99)], ll[(98)], thresh2)
conv = false
end
end
end ## if maxit
L_g = L_g_new
psi_g = psi_g_new
end ## while
map_res = mapz(zmat)
proj_res = mppca_proj(X, G, map_res, L_g)
if iter <= 100
resize!(ll, iter)
end
fp = mppca_fparams(p, q, G)
bic_res = BiC(ll[end], N, q, fp)
return Dict(
"iter" => iter,
"ll" => ll,
"beta" => B_g,
"theta" => T_g,
"lambda" => L_g,
"psi" => psi_g,
"q" => q,
"G" => G,
"map" => map_res,
"zmat" => zmat,
"proj" => proj_res,
"bic" => bic_res
)
end
mixppca_12k = mixppca(cof_mat_c, q=1, G=2, maxit = 1e6, thresh = 1e-3,
init=2)最终产生的分类是[0,1]中的概率, 但可以用投票法变成0-1值。