16 随机模拟
16.1 介绍
在用数学模型, 包括概率统计模型处理实际应用中的问题时, 我们希望建立的模型能够尽可能地符合实际情况。 但是,实际情况是错综复杂的, 如果一味地要求模型与实际完全相符, 会导致模型过于复杂, 以至于不能进行严格理论分析, 结果导致模型不能使用。 所以,实际建模时会忽略许多细节, 增加一些可能很难验证的理论假设, 使得模型比较简单,可以用数学理论进行分析研究。
这样,简化的模型就可以与实际情况有较大的差距, 即使我们对模型进行了完美的理论分析, 也不能保证分析结果是可信的。 这一困难可以用随机模拟的方法解决。
模拟是指把某一现实的或抽象的系统的某种特征或部分状态, 用另一系统(称为模拟模型)来代替或模拟。 为了解决某问题, 把它变成一个概率模型的求解问题, 然后产生符合模型的大量随机数, 对产生的随机数进行分析从而求解问题, 这种方法叫做随机模拟方法, 又称为蒙特卡洛(Monte Carlo)方法。
例如,一个交通路口需要找到一种最优的控制红绿灯信号的办法, 使得通过路口的汽车耽搁的平均时间最短, 而行人等候过路的时间不超过某一给定的心理极限值。 十字路口的信号共有四个方向, 每个方向又分直行、左转、右转。 因为汽车和行人的到来是随机的, 我们要用随机过程来描述四个方向的汽车到来和路口的行人到来过程。 理论建模分析很难解决这个最优化问题。 但是, 我们可以采集汽车和行人到来的频率, 用随机模拟方法模拟汽车和行人到来的过程, 并模拟各种控制方案,记录不同方案造成的等待时间, 通过统计比较找出最优的控制方案。
随机模拟中的随机性可能来自模型本身的随机变量, 比如上面描述的汽车和行人到来, 也可能是把非随机的问题转换为概率模型的特征量估计问题从而用随机模拟方法解决。 例如, 用随机模拟计算积分。
16.2 随机模拟计算定积分
16.2.1 平均值法
随机模拟的基本思想可以用随机模拟积分来介绍, 考虑积分问题\(\int_0^1 h(x) \,dx\), 若取\(X \sim \text{U}(0, 1)\), 产生\(X_1, X_2, \dots, X_N\)独立同\(\text{U}(0, 1)\)分布, 则因为\(E[h(X)] = \int_0^1 h(x) \,dx\),而 \[ E[h(X)] \approx \frac{1}{N} \sum_{i=1}^N h(X_i), \] 所以可以用方程的右侧公式来估计积分\(\int_0^1 h(x) \,dx\)。
例如,\(\int_0^1 e^x \,dx = e - 1 \approx 1.718282\), 用Julia程序模拟估计,取\(N=10^6\):
using Random
using Statistics
Random.seed!(101)
mean(exp.(rand(1_000_000)))
## 1.7178412037826383为了计算\(\int_a^b h(x) \,dx\), 设\(X \sim \text{U}(a,b)\), 即\(X\)服从\((a,b)\)上的均匀分布, 因为 \[ E[h(X)] = \int_a^b h(x) \frac{1}{b-a} \,dx = \frac{1}{b-a} \int_a^b h(x) \,dx, \] 所以可以生成服从\((a,b)\)上均匀分布的随机变量\(X_i\), \(i=1,2,\ldots,N\), 计算\(\frac{b-a}{N}\sum_{i=1}^N h(X_i)\)作为\(\int_a^b h(x) \,dx\)的估计值。
16.2.1.1 随机模拟编程常见错误
使用随机数时一定要注意, 每次调用随机数函数都会产生新的结果, 这是随机模拟时很容易犯错误的地方。 比如, 设 \[ h(x) = \begin{cases} x, & x \leq \frac{1}{2}, \\ 1 - x, & x > \frac{1}{2} . \end{cases} \] 易见积分结果是底边长度为1、高为\(\frac{1}{2}\)的三角形面积, 等于\(\frac{1}{4}\)。 下面的Julia程序模拟估计\(\int_0^1 h(x) \,dx\), 但是有难以察觉的逻辑错误:
# 重复调用随机数函数的错误
function sim_demo(N=1_000_000)
s = 0.0
for i=1:N
if rand() < 0.5
s += rand()
else
s += 1 - rand()
end
end
s / N
end
using Random
Random.seed!(101)
sim_demo()
## 0.5001518755483094正确结果是\(0.25\),估计值却等于\(0.50\)。
上述程序的错误在于在每轮循环中,
调用了3次rand()函数,
结果生成了3个不同的随机数,
而我们的本意应该是生成一个随机数,
然后根据这个随机数的值小于\(\frac{1}{2}\)还是大于\(\frac{1}{2}\)决定函数函数值,
现在判断是否小于\(\frac{1}{2}\)的地方使用了一个随机数,
但是计算函数值的地方使用了新的随机数而不是已经生成的\(X_i\)的值。
正确的版本为:
function sim_demo(N=1_000_000)
s = 0.0
for i=1:N
u = rand()
if u < 0.5
s += u
else
s += 1 - u
end
end
s / N
end
sim_demo()
## 0.24983656295114867程序也可以简化为:
function sim_demo(N=1_000_000)
sum(x -> x < 0.5 ? x : 1-x, rand(N)) / N
end
sim_demo()
## 0.2501955324872404716.2.2 重要抽样法
产生均匀分布随机数估计定积分的方法无法计算无穷区间的积分\(\int_{-\infty}^\infty f(x) \,dx\); 另外, 在计算有限区间积分\(\int_0^1 f(x) \,dx\)时, 如果\(f(x)\)在\([0,1]\)中某一段的绝对值很大, 其它位置的绝对值很小, 则当\(X_i\)落入\(f(x)\)绝对值很小的区间时, \(X_i\)对最后估计结果的贡献很小。 所以, 希望不使用均匀分布抽样, 而是抽取随机数\(X_i\)使得\(X_i\)的取值在\(f(x)\)绝对值大的位置出现更密集, 在\(f(x)\)绝对值小的位置出现较稀疏, 这样能够合理利用所有的抽样点\(X_i\)。
设\(X \sim g(\cdot)\), \(g(x)\)是区间\((a,b)\)上的一个分布密度(\((a,b)\)可以是无穷区间), \(i=1,2,\ldots,N\), 为了计算\(\int_a^b h(x) \,dx\), 注意 \[ \int_a^b h(x) \,dx = \int_a^b \frac{h(x)}{g(x)}\, g(x)\,dx = E\left[\frac{h(X)}{g(X)} \right], \] 所以可以取\(X_i \sim g(\cdot)\), \(i=1,2,\ldots,N\), 估计\(\int_a^b h(x) \,dx\)为 \[ \frac{1}{N} \sum_{i=1}^N \frac{h(X_i)}{g(X_i)} . \] 这种方法称为重要抽样法(importance sampling), 其中\(g(x)\)称为试抽样密度(trial density), 应取\(g(x)\)使其形状与\(|h(x)|\)尽可能接近。
例如,仍考虑\(\int_0^1 e^x \,dx = 1.718282\)的问题。 函数\(h(x) = e^x\)是增函数, 所以应取试抽样密度\(g(x)\)在左边较小, 在右边较大。 对\(e^x\)用一阶泰勒展开近似有\(e^x \approx 1 + x\), 所以取试抽样密度为 \[\begin{aligned} g(x)=c(1+x) = \frac{2}{3}(1+x), \end{aligned}\] 要产生\(g(x)\)的随机数可以用逆变换法, 密度\(g(x)\)的分布函数\(G(x)\)的反函数为 \[\begin{aligned} G^{-1}(y) = \sqrt{1+3y}-1, \ 0<y<1 . \end{aligned}\] 因此,取\(U_i\) iid U(0,1), 令\(X_i = \sqrt{1+3U_i}-1\), \(i=1,2,\ldots,N\), 则重要抽样法的积分公式为 \[\begin{aligned} \hat I = \frac{1}{N} \sum_{i=1}^N \frac{e^{X_i}}{\frac{2}{3}(1+X_i)} . \end{aligned}\]
Julia程序实现:
g(x) = 2/3*(1+x)
Ginv(p) = sqrt(1 + 3p) - 1
Random.seed!(101)
mean(map((x -> exp(x) / g(x)) ∘ Ginv, rand(1_000_000)))
## 1.7181425608987528其中\(\circ\)表示两个函数的复合运算。
map函数将某个一元函数作用到一个序列的每个元素,
上面的程序如果写成广播格式则会比较繁琐,
难以阅读。
注意, 如果将程序写成下面这样就又犯了使用不同随机数的错误:
mean(exp(Ginv(rand())) / g(Ginv(rand)) for _=1:1_000_000)这时分子和分母使用了不同的随机数, 结果错误。
16.3 随机向量抽样
16.3.1 条件分布法
产生随机向量的一种方法是条件分布法。 设\(\boldsymbol X = (X_1, X_2, \dots, X_r)\)的分布密度或分布概率 \(p(x_1, x_2, \dots, x_r)\)可以分解为 \[\begin{aligned} p(x_1, x_2, \dots, x_r) = p(x_1) p(x_2 | x_1) p(x_3 | x_1, x_2) \cdots p(x_r | x_1, x_2, \dots, x_{r-1}) \end{aligned}\] 则可以先生成\(X_1\), 由已知的\(X_1\)的值从条件分布\(p(x_2 | x_1)\)产生\(X_2\), 再从已知的\(X_1, X_2\)的值从条件分布\(p(x_3 | x_1, x_2)\)产生\(X_3\), 如此重复直到产生\(X_r\)。
16.3.2 变换法
设随机向量\(\boldsymbol X = (X_1, X_2, \dots, X_p)^T\)服从多元正态分布 \(\text{N}(\boldsymbol \mu, \Sigma)\), 联合密度函数为 \[\begin{aligned} p(\boldsymbol x) = (2\pi)^{-\frac{p}{2}} |\Sigma|^{-\frac12} \exp\left\{ -\frac12 (\boldsymbol x - \boldsymbol \mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol \mu) \right\}, \ \boldsymbol x \in R^p \end{aligned}\] 正定矩阵\(\Sigma\)有Cholesky分解\(\Sigma = L L^T\), 其中\(L\)为下三角矩阵。 设\(\boldsymbol Z = (Z_1, Z_2, \dots, Z_p)^T\)服从\(p\)元标准正态分布 \(\text{N}(\boldsymbol 0, I)\)(\(I\)表示单位阵), 则\(\boldsymbol X = \boldsymbol\mu + L \boldsymbol Z\) 服从\(\text{N}(\boldsymbol \mu, \Sigma)\)分布。
Julia的LinearAlgebra包提供了chol函数。
chol(A).L返回的矩阵\(L\)使得\(L^T L = A\)。
16.4 泊松过程抽样
参数为\(\lambda\)的泊松过程\(N(t), t\geq 0\)是取整数值的随机过程, \(N(t)\)表示到时刻\(t\)为止到来的事件个数, 两次事件到来的时间间隔相互独立, 都服从指数分布Exp(\(\lambda\))。
所以,如果要生成泊松过程前\(n\)个事件到来的时间, 只要生成\(n\)个独立的Exp(\(\lambda\))随机数\(X_1, X_2, \dots, X_n\), 则\(S_k = \sum_{i=1}^k X_i, k=1,2,\dots,n\)为各个事件到来的时间。
如果要生成泊松过程在时刻\(T\)之前的状态, 只要知道发生在\(T\)之前的所有事件到来时间就可以了。
如下的Julia程序输入需要模拟的时间\(T\), 速率参数\(\lambda\), 输出\(T\)之前各个事件的发生时间的序列。
# 泊松过程模拟
function randpproc(T=100.0, λ=1.0)
local xs, S, nev, X
xs = Float64[]
S = 0.0 # 当前时刻
nev = 0 # 已发生事件个数
while true
X = -log(rand()) / λ
S += X
if S <= T
nev += 1
push!(xs, S)
else
break
end
end # while true
return xs
end测试:
using Random, Distributions
using CairoMakie, AlgebraOfGraphics
CairoMakie.activate!()
Random.seed!(101)
x = randpproc(50, 1)
plt = data((; x=x)) * mapping(:x) * visual(VLines)
draw(plt)
## 估计速率
mean(x[2:end] .- x[begin:end-1])
## 0.8870887289991723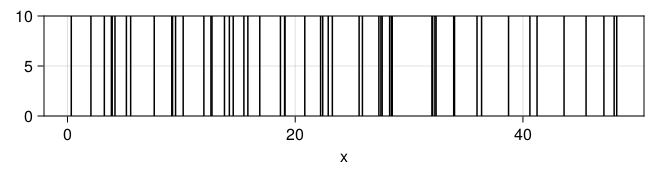
生成泊松过程在时刻\(T\)之前的状态的另外一种方法是先生成\(N(T) \sim \text{Poisson}(\lambda)\), 设\(N(T)\)的值为\(n\), 再生成\(n\)个独立的U(0,1)随机变量\(U_1, U_2, \dots, U_n\), 从小到大排序为\(U_{(1)} \leq U_{(2)} \leq \dots U_{(n)}\), 则\((T U_{(1)} , T U_{(2)} , \dots, T U_{(n)})\)为时刻\(T\)之前的所有事件到来时间。
为了生成强度函数为\(\lambda(t), t\geq 0\)的非齐次泊松过程到时刻\(T\)为止的状态, 如果\(\lambda(t)\)满足 \[\begin{aligned} \lambda(t) \leq M, \ \forall t \geq 0, \end{aligned}\] 则可以按照生成参数为\(M\)的齐次泊松过程的方法去生成各个事件到来时刻, 但是以\(\lambda(t)/M\)的概率实际记录各个时刻。 Julia程序如下:
function randnhpproc(T, λ = x -> 1.0, M=1.0)
local xs
xs = randpproc(T, M)
xs = [t for t in xs if rand() < λ(t) / M]
return xs
end 测试。假设前50分钟速率为0.2, 后50分钟速率为1。
fl(t) = t <= 50 ? 0.2 : 1.0
Random.seed!(101)
x = randnhpproc(100.0, fl, 1.0)
plt = data((; x=x)) * mapping(:x) * visual(VLines)
dr = draw(plt; axis = (; width=600, height=100))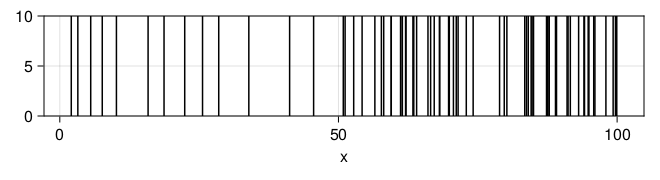
16.5 高斯过程模拟
16.5.1 布朗运动模拟
布朗运动是具有独立增量的高斯过程, 其模拟比较简单。
时间区间\([0, T]\)上的一维的标准布朗运动为随机过程\(\{ W(t), 0 \leq t \leq T \}\), 满足:
- \(W(0)=0\);
- 以概率1地,\(W(t)\)作为\(t\)的函数,(每条轨道)在\([0,T]\)连续;
- 独立增量;
- \(W(t) - W(s) \sim \text{N}(0, t-s)\), 对任意\(0 \leq s < t \leq T\)。
\(W(t)\)分布为 \[ W(t) \sim \text{N}(0, t), \ 0 < t \leq T. \]
对标准布朗运动\(W(t)\),令 \[ X(t) = \mu t + \sigma W(t), 0 \leq t \leq T, \] 称\(X(t)\)为有漂移\(\mu\)和扩散系数\(\sigma^2\)的布朗运动, 简记为BM(\(\mu, \sigma^2\))。 其中\(\mu\),\(\sigma\)为常数,\(\sigma>0\)。 \(X(t)\)仍是高斯过程, 从0出发, 有独立增量, 轨道连续, 边缘分布为 \[ X(t) \sim \text{N}(\mu t, \sigma^2 t) . \]
也可以构造\(X(0)=x\)的解, 只要给每个\(X(t)\)加\(x\)即可。
可以定义漂移和扩散系数时变的布朗运动, 存在时变的函数\(\mu(t)\)和\(\sigma(t)\), 使得增量\(X(t) - X(s)\)(\(0 \leq s < t \leq T\))服从正态分布,期望为 \[ E[X(t) - X(s)] = \int_s^t \mu(u) \,du, \] 方差为 \[ \text{Var}[X(t) - X(s)] = \int_s^t \sigma^2(u) \,du . \]
设\(0 < t_1 < t_2 < \dots < t_n \leq T\), 要生成\((W(t_1), \dots, W(t_n))\)或者\((X(t_1), \dots, X(t_n))\)的抽样, 最简单的方法是利用布朗运动的独立增量性和正态性。 设\(Z_1, \dots, Z_n\)是独立同标准正态分布的随机变量(随机数), \(t_0=0\), \(W(0)=0\), \(X(0)=0\)。
令 \[\begin{align} W(t_{i+1}) = W(t_i) + \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{16.1} \end{align}\]
对\(X(t) \sim \text{BM}(\mu, \sigma^2)\),令 \[\begin{align} X(t_{i+1}) = X(t_i) + \mu \cdot (t_{i+1} - t_i) + \sigma \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{16.2} \end{align}\]
对于漂移和扩散系数时变的\(X(t)\),令 \[\begin{align} X(t_{i+1}) = X(t_i) + \int_{t_i}^{t_{i+1}}\mu(u) \,du + \left( \int_{t_i}^{t_{i+1}}\sigma^2(u) \,du \right)^{1/2} Z_{i+1}, \ i=0,1,\dots, n-1 . \tag{16.3} \end{align}\]
只要输入的\(Z_1, \dots, Z_n\)的联合分布正确, 则输出的\((W(t_1), \dots, W(t_n))\)和\((X(t_1), \dots, X(t_n))\)的联合分布也是正确的, 没有离散化误差。
这只输出了\(t_1, t_2, \dots, t_n\)这有限个点上的轨道的值, 中间的值未知, 如果用通常的线性插值等方法近似, 就会产生离散化误差, 分布也不准确。
在漂移和扩散系数时变时, 如果将(16.3)中的积分替换成如下的欧拉(Euler)近似: \[ X(t_{i+1}) = X(t_i) + \mu(t_i) \cdot (t_{i+1} - t_i) + \sigma(t_i) \sqrt{t_{i+1} - t_i} Z_{i+1}, \ i=0,1,\dots, n-1 , \] 则输出的\((X(t_1), \dots, X(t_n))\)的联合分布也是近似的, 带有离散化误差(discretization error), 而且这种误差是累积的, 时间越往后误差越大。
如下的函数输入时间点的数组, 输出模拟的标准布朗运动轨道在这些时间点的值:
function sim_bm(ts::Vector)
xs = zeros(length(ts))
t0 = 0
x0 = 0.0
for i in eachindex(ts)
x1 = x0 + sqrt(ts[i] - t0)*randn()
xs[i] = x1
t0 = ts[i]
x0 = x1
end
return (ts, xs)
end
function sim_bm(T::Real, n::Integer)
ts = collect(1:n) .* (T/n)
return sim_bm(ts)
end测试:
using Random
using CairoMakie
CairoMakie.activate!()
Random.seed!(101)
n = 100
ts, xs = sim_bm(10.0, 100)
lines(ts, xs)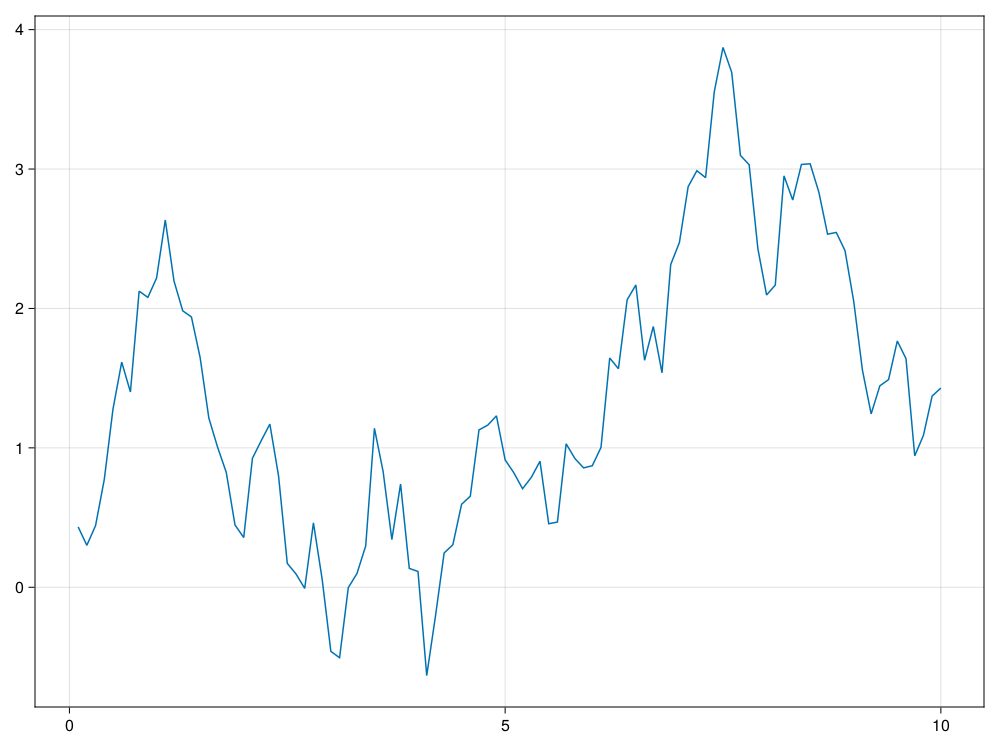
16.5.2 采样点较少情形
布朗运动是正交增量过程, 所以只要在新的时间点模拟出独立的增量即可。 一般的高斯过程不一定有独立增量。
比如, 设随机过程\(X(t), t \geq 0\)满足: \(X(0)=0\), \(E[X(t)]=0\), \[ \text{Cov}[X(t), X(s)] = \exp\left(-\frac{(t-s)^2}{2 \ell^2}\right) , \] 记右侧的函数为\(\sigma(t, s)\), 称其为高斯核函数, 这是一个对称正定核,即: \[ \sigma(t, s) = \sigma(s, t); \quad\forall n \geq 1, \ t_1, \dots, t_n, (\sigma(t_i, t_j))_{n \times n} \geq 0 . \]
高斯核函数中的参数\(\ell\)代表不同时间的状态的相关性随时间距离衰减的平均时间, 各\(X_t, X_s\)之间都是正相关, \(\ell\)越大, 相关性随时间距离衰减越慢, 不同时刻的状态的相关性越强, 这时轨道也越光滑; \(\ell\)越小, 轨道的局部变动也越剧烈。
实际上, 因为\(\sigma(s, t)\)是\(s-t\)的函数, 所以这是一个高斯平稳过程, 即任意的有限维分布都服从多元正态分布, 均值为常数, 协方差函数\(\sigma(s, t)\)仅依赖于\(t-s\)的随机过程。
为了模拟这个过程在时间点\(t_1, \dots, t_n\)上的值, 当\(n\)较小时, 因为\((X(t_1), \dots, X(t_n))\)服从多元正态分布, 均值向量为\(\boldsymbol 0\), 协方差阵为 \[ \Sigma = (\sigma(t_i, t_j))_{n \times n}, \] 所以可以对\(\Sigma\)作Cholesky分解得\(\Sigma = L L^T\), 其中\(L\)为满秩下三角阵, 令\(\boldsymbol Z\)为\(n\)元标准正态分布随机向量, 则\(L \boldsymbol Z\)服从多元正态分布\(\text{N}(\boldsymbol 0, \Sigma)\)。
Julia的Distributions包的MvNormal(mu, Sigma)函数可以用来表示多元正态分布。
为了生成\(m\)条轨道,方法如:
dist = MvNormal(zeros(n), Sigma)
sampmat = rand(dist, m)结果是一个\(n \times m\)矩阵, 每列是随机过程一条轨道。
但是,这样做法有一个问题, 就是虽然在理论上\(\Sigma\)矩阵是正定矩阵, 但是当采样点个数\(n\)较大时, 这个矩阵很接近于不满秩, 使得Cholesky分解的数值算法出错。 为此,借鉴(Kochenderfer 2019)中的做法, 将\(\Sigma\)替换成\(\Sigma + \epsilon I\), 其中\(\epsilon\)是较小的正常数,如\(10^{-6}\)。
生成高斯核的高斯过程的Julia函数如下:
using Distributions
# 给定表示时间点的向量ts, 需要的轨道条数npath,
# 高斯核参数decay, 保证Cholesky分解可行的扰动量inflate,
# 输出模拟结果为n*m矩阵,每列为一条轨道.
function sim_Gauss(ts::Vector, npath::Integer,
decay=1.0; inflate = 1e-6)
n = length(ts)
ker(t, s) = exp(-(t-s)^2 / (2*decay^2))
Sig = [ker(ts[i], ts[j]) for i=1:n, j=1:n]
dist = MvNormal(zeros(n), Sig + inflate .* I)
xs = rand(dist, npath)
return ts, xs
end
# 输入要生成的时间长度T,等分时间点点数n的模拟函数
function sim_Gauss(T::Real, n::Integer, npath=1,
decay=1.0; inflate=1e-6)
ts = collect(1:n) .* (T/n)
return sim_Gauss(ts, npath, decay; inflate=inflate)
end测试,模拟100个时间点,取\(\ell=2.0\), 模拟5条轨道:
using CairoMakie
CairoMakie.activate!()
ts, xs = sim_Gauss(10.0, 100, 5, 2.0)
fig = lines(ts, xs[:,1])
for i=2:5 ; lines!(ts, xs[:,i]); end
fig 结果图形:
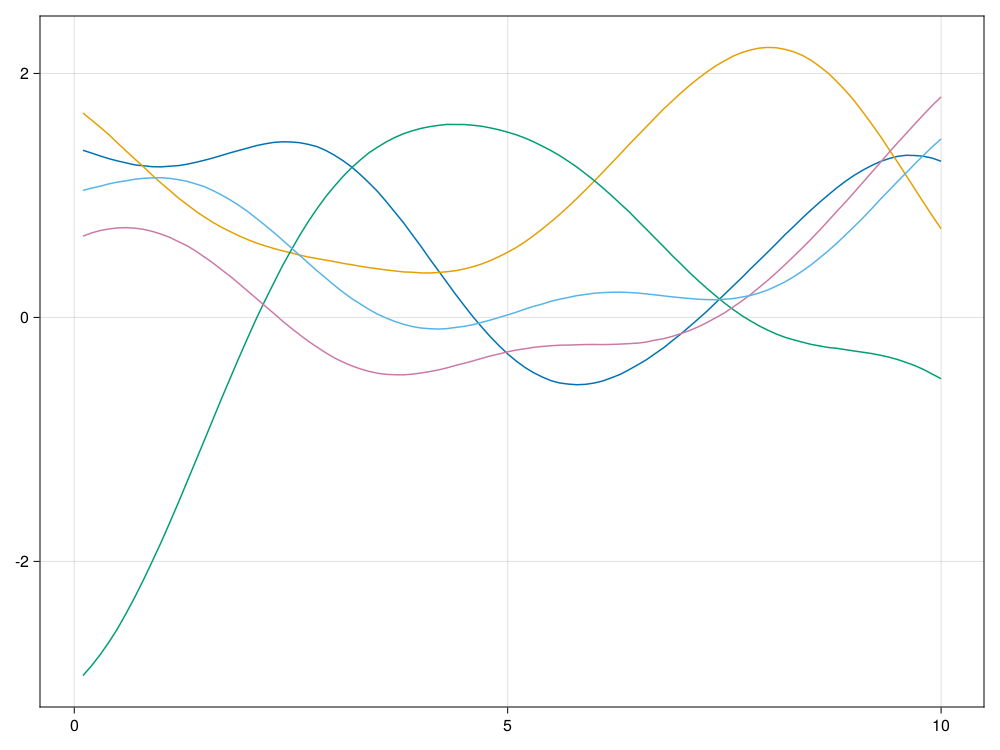
因为取的相关性衰减时间参数\(\ell=2.0\)的值较大, 所以每条轨道都很光滑。
下面取\(\ell=0.2\):
ts, xs = sim_Gauss(10.0, 100, 5, 0.2)结果图形:
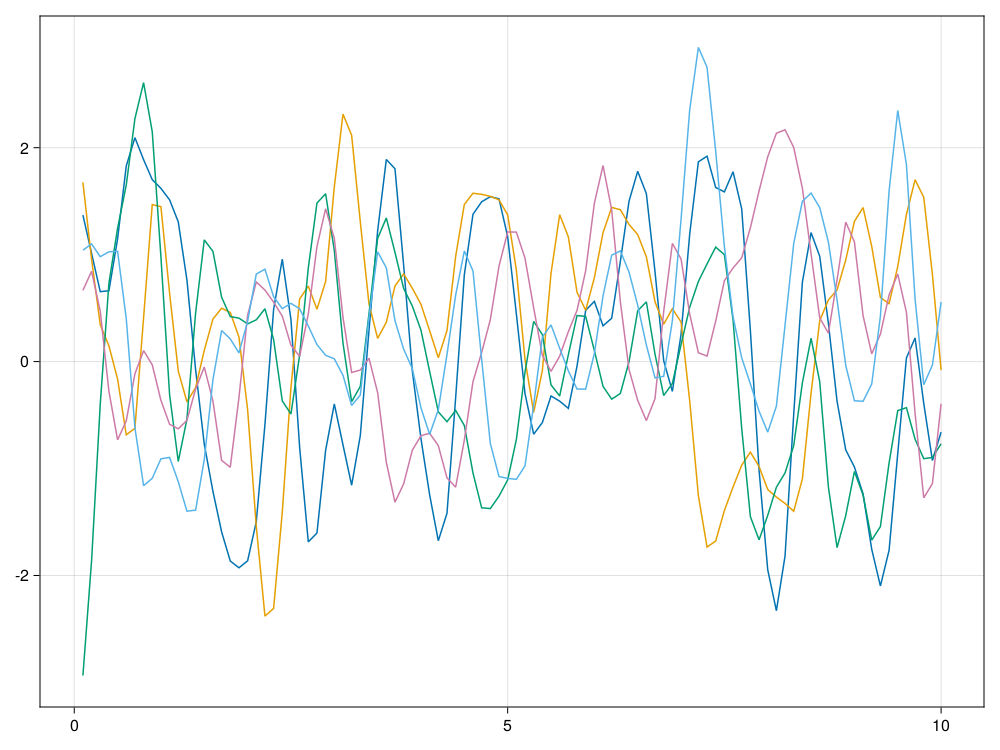
因为相关性减弱, 所以轨道变得不那么光滑。
16.5.3 平稳高斯列
若\(X(t)\)为平稳高斯列, 均值为0, 协方差函数为\(\gamma_k, k=0,1,2,\dots\), 则有限维分布完全由\(\{\gamma_k \}\)决定。 为了生成\(X(t)\)的一条长度为\(n\)的轨道, 可以递推地进行抽样。 抽取\(X(1) \sim \text{N}(0, \gamma_0)\), 然后, 对\(X(t+1)\), \(t=1,\dots, n-1\), 因为\(X(t+1) | X(t), \dots, X(1)\)是条件正态分布, 有
\[\begin{aligned} E(X(t+1) | X(t), \dots, X(1)) &= \sum_{j=1}^t a_{t,j} X(t+1-j) \\ =& a_{t,1} X(t) + a_{t,2} X(t-1) + \dots + a_{t,t} X(1), \\ \text{Var}(X(t+1) | X(t), \dots, X(1)) =& \sigma_t^2, \end{aligned}\] 其中\(\sigma_0^2, \sigma_1^2, \dots\)和\(a_{t,j}, j=1,\dots, t\), \(t=1,2,\dots\)可以用如下的Levinson递推公式从\(\{\gamma_k \}\)序列计算得到: \[\begin{align} \sigma_0^2 =& \gamma_0 \\ a_{1,1} =& \gamma_1 / \gamma_0 \\ \sigma_k^2 =& \sigma_{k-1}^2 (1 - a_{k,k}^2) \\ a_{k+1,k+1} =& \frac{\gamma_{k+1} - a_{k,1} \gamma_k - a_{k,2} \gamma_{k-1} - \dots - a_{k,k} \gamma_1}{ \gamma_0 - a_{k,1} \gamma_1 - a_{k,2} \gamma_2 - \dots - a_{k,k} \gamma_k } \\ a_{k+1,j} =& a_{k,j} - a_{k+1,k+1} a_{k,k+1-j}, \quad 1 \leq j \leq k \tag{16.4} \end{align}\]
这样,就可以递推地计算出\(X(t+1) | X(t), \dots, X(1)\)的条件期望和条件方差, 从这个条件分布抽样得到\(X(t+1)\)。
在递推过程中, 如果平稳高斯序列\(\{ X(t) \}\)相关性较强, 有可能出现\(\sigma_k^2 \to 0\)(\(k\to\infty\))的情况。 这时, 可以设置一个阈值\(\epsilon\), 当\(\sigma_p^2 < \epsilon\)时, 对\(t > p\)就不再用所有的\(X(1), \dots, X(t-1)\)计算条件分布, 而是仅使用\(X(t-1), \dots, X(t-p)\)这\(p\)个, 递推预测系数统一使用\(a_{p,j}\), \(j=1,\dots,p\)。
下面的函数gauss_levinson函数输入长度为\(n\)的自协方差函数序列\(\{ \gamma_k, k=0,1,\dots,n-1 \}\),
要求的轨道条数npath,
输出一个结果矩阵,
每行为一条轨道的\(n\)个观测值。
也可以输入一个计算\(\gamma_k\)的函数,
此函数输入非负整数值\(k\),
返回\(\gamma_k\)的值,
用这个函数规定自协方差函数,
进行模拟。
function gauss_levinson(gam_vec::Vector{Float64}, npath=1; eps=1e-6)
n = length(gam_vec)
x = zeros(npath, n)
a1 = zeros(n)
a2 = zeros(n)
S2 = zeros(n)
S2[1+0] = gam_vec[0+1] # 用0个去预报下一个的方差
x[:,1] .= rand_norm(zeros(npath), sqrt(S2[1]), npath)
a1[1] = gam_vec[1+1]/gam_vec[0+1] # a_{1,1},用X_1预报X_2的系数
# 下面是Levinson递推计算条件分布的条件期望的线性组合系数,
# 与条件分布的方差,
# 并从条件分布抽样
p = -1
for k=1:(n-1)
# 从前k个预报第k+1个的方差
S2[1+k] = S2[k] * (1 - a1[k]^2)
#@show S2[1+k]
# 如果基本可完全线性预报,不需要更多预报系数
if S2[1+k] < eps
p = k
break
end
# 从前k个给出条件期望和条件方差,抽取第k+1个
cond_mean = sum(a1[j] .* x[:,k+1-j] for j=1:k)
x[:,1+k] .= rand_norm(cond_mean, sqrt(S2[1+k]), npath)
# 不需要计算用n个预报n+1个的公式
k == n-1 && break
# 继续计算从前k+1个预报第k+2个的系数
a2[1+k] = (gam_vec[1+(k+1)] -
sum(a1[1:k] .* gam_vec[(1+k):-1:(1+1)])) /
S2[1+k]
#println("a[",k+1,", ", k+1, "]=", a2[1+k])
a2[1:k] .= a1[1:k] .- a2[1+k] .* a1[k:-1:1]
# 重复利用a1, a2的空间,用a1表示当前可用的预报系数
a1, a2 = a2, a1
end # for k
if p > 0 # 用p个可完全线性预报
for k=(p+1):n
cond_mean = sum(a1[j] .* x[:,k-j] for j=1:p)
x[:,k] .= rand_norm(cond_mean, sqrt(S2[1+p]), npath)
end
end # if p>0
#show(round.(S2, digits=4))
return x
end
# 输入:自协方差函数gam(k),以函数形式输入
# n是需要输出的长度
function gauss_levinson(gam::Function,
n::Int = 100, npath=1; eps=1e-6)
gam_vec = gam.(0:(n-1))
#@show gam_vec
return gauss_levinson(gam_vec, npath;
eps = eps)
end设某个高斯平稳列的协方差函数\(\{\gamma_k \}\)满足 \[ \gamma_k = \exp(-k^2 / (2 \ell^2)), \] 其中\(\ell>0\)描述了前后相关性持续的时间长度, \(\ell\)越大相关性越强, 结果的轨道越光滑。 测试,生成5条轨道:
using CairoMakie
CairoMakie.activate!()
using Random
n, npath, ell = 200, 5, 5.0
Random.seed!(101)
x = gauss_levinson(k -> exp(-k^2 / (2*ell^2)), n, npath);
fig = series(1:n, x)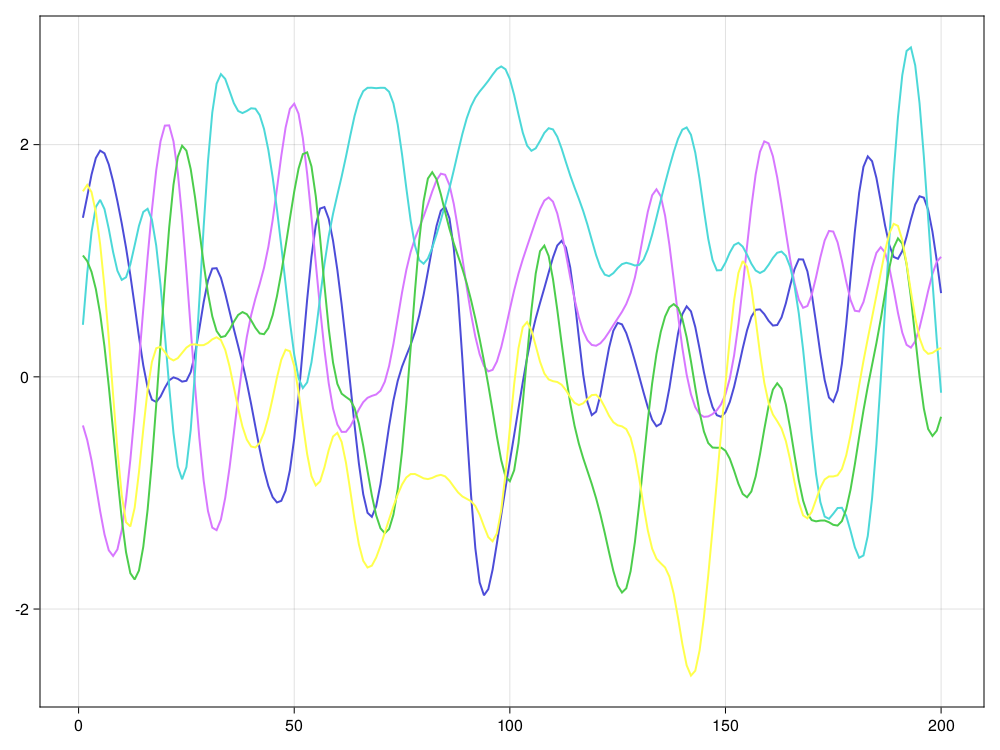
16.6 置换检验
设有两个独立的总体\(X \sim F(\cdot)\)和\(Y \sim G(\cdot)\), 分别有简单随机样本\(X_1, \dots, X_{n_1}\)和\(Y_1, \dots, Y_{n_2}\), \(n = n_1 + n_2\)。 要检验如下零假设: \[ H_0:\; F = G . \]
两个分布相同的检验有许多, 比如, 在假定两个总体都服从正态分布的情况下, 可以检验其方差和均值都相等的两个假设。 非参数检验方法有适用于连续分布的Kolmogorov-Smirnov检验。 对于更一般的分布, 已有的检验统计量没有零假设的理论分布或者渐近分布, 无法使用已有的方法。
置换检验是基于对称性的一种计算密集型检验方法, 可以利用已有的检验统计量进行检验, 检验p值通过零假设下样本值的对称性进行计算。
我们用一个案例来讲解置换检验的做法。
有22个肺癌病人的肿瘤大小数据, 其中10个为腺癌,12个为鳞癌,数据为: \[ \begin{array}{l*{12}r} X: & 13 & 27 & 33 & 40 & 43 & 61 & 125 & 135 & 161 & 330 & & \\ Y: & 2 & 3 & 6 & 7 & 9 & 12 & 24 & 35 & 35 & 74 & 112 & 122 \end{array} \] 从这组数据比较这两种类型的肿瘤大小有无显著差异。
两个变量的大小比较, 常用独立两样本t检验, 但是该检验要求两个样本都服从正态分布或者样本量充分大, 而这两个样本都有明显的右偏,不服从正态分布,样本量也不够大, 下面是R程序计算t检验的程序和结果, 其结果不完全可信:
dc <- data.frame(
x = c(c(13, 27, 33, 40, 43, 61, 125, 135, 161, 330),
c(2, 3, 6, 7, 9, 12, 24, 35, 35, 74, 112, 122)),
type = factor(rep(c("腺癌", "鳞癌"), c(10, 12)),
levels=c("腺癌", "鳞癌")))
ttc <- t.test(x ~ type, data = dc,
var.equal=TRUE); ttc##
## Two Sample t-test
##
## data: x by type
## t = 1.9433, df = 20, p-value = 0.06619
## alternative hypothesis: true difference in means between group 腺癌 and group 鳞癌 is not equal to 0
## 95 percent confidence interval:
## -4.409599 124.509599
## sample estimates:
## mean in group 腺癌 mean in group 鳞癌
## 96.80 36.75取零假设\(H_0\)为两种类型的肿瘤大小分布相同。 考虑零假设成立时两样本t统计量的分布, t统计量为: \[ t = \frac{\bar x - \bar y}{\sqrt{\frac{1}{n_1+n_2-2} \left[ \sum_{i=1}^{n_1} (x_i - \bar x)^2 + \sum_{i=1}^{n_2}(y_i - \bar y)^2 \right] \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} . \]
记\(n = n_1 + n_2\), \[ Z_i = \begin{cases} X_i, & i=1,2,\dots, n_1; \\ Y_{i-n_1}, & i=n_1+1, \dots, n . \end{cases} \] 则在\(H_0\)下\(Z_i, i=1,2,\dots,n\)是来自于同一总体的简单随机样本, 这样, \(Z_i, i=1,2,\dots,n\)任意打乱次序, 重新计算t统计量, 新的t统计量的分布应该是不变的。 因为如果仅在\(\{1,\dots,n_1\}\)或者\(\{n_1+1, \dots, n\}\)集合内部打乱次序并不改变t统计量的值, 所以仅需考虑\(\{1, \dots, n \}\)的\(n!\)个排列中, \(K = \binom{n}{n_1}\)种不同的将\(n\)个样本值划分为前\(n_1\)个与后\(n_2\)个的划分方法, 根据对称性, 在\(H_0\)下这\(K\)种划分是概率相等的, 每一种的概率都等于\(\frac{1}{K}\)。 如果我们将这\(K\)种划分穷举出来, 每一种划分可以计算一个t统计量值, 就可以计算\(K\)个t统计量的值\(\{ t_1, \dots, t_K \}\), 可以认为当零假设成立时我们从当前样本得到的t统计量的值是从离散均匀分布\(\{ t_1, \dots, t_K \}\)随机抽取出来的, 称这个分布为置换分布, 利用置换分布可以计算t统计量的双侧或者单侧p值。
用\(T\)表示服从置换分布的随机变量, 定义检验的右侧p值为\(P(T \geq t_0)\)(\(t_0\)表示t统计量的值, 如本例中\(t_0=1.9433\)), 左侧p值为\(P(T \leq t_0)\), 双侧p值为 \[ 2 \min\{ P(T \leq t_0), \; P(T \geq t_0) \} . \] 如果穷举了所有\(K\)个置换分布的取值\(\{t_1, \dots, t_K\}\), 就可以计算p值, 比如,右侧p值可以计算为 \[ \frac{1}{K} \sum_{j=1}^K I_{\{t_j \geq t_0 \}}, \] 其中\(I_A\)表示事件\(A\)的示性函数。
\(\binom{22}{10}\)约为64万种组合。
Julia的Combinatorics包的combinations(a, n)可以对序列a罗列所有取出n个的组合结果。
下面用Julia程序罗列所有组合, 计算置换检验的p值:
using Combinatorics
# 两样本t统计量计算函数
function tstat(x, y)
n1 = length(x)
n2 = length(y)
mx = mean(x)
my = mean(y)
S2p = 1/(n1+n2-2)*(
sum((x .- mx) .^ 2) +
sum((y .- my) .^ 2))
tstat = (mx - my) / sqrt(S2p * (1/n1 + 1/n2))
return tstat
end
xv = [13, 27, 33, 40, 43, 61, 125, 135, 161, 330]
yv = [2, 3, 6, 7, 9, 12, 24, 35, 35, 74, 112, 122]
n1 = length(xv)
n2 = length(yv)
mixedxy = [xv; yv]
# 真实样本的统计量值
t0 = tstat(xv, yv)
# 所有的从n1+n2个样本点中取出n1个的罗列,
# 其中每一个是1:(n1+n2)的n1个下标的集合
allcomb = Combinatorics.combinations(1:(n1+n2), n1)
# 计算每一个的置换样本的统计量
tstats = map(allcomb) do ix
xv1 = mixedxy[ix]
yv1 = mixedxy[setdiff(1:(n1+n2), ix)]
tstat(xv1, yv1)
end
# 双侧检验p值
pvalue = 2*min(mean(tstats .> t0),
mean(tstats .< t0))
@show pvalue;
## pvalue = 0.0577472063540175结果p值为0.58, 与t检验结果给出的p值相近。
因为罗列所有的组合计算量过大, 所以可以从上述的\(K\)个组合种随机有放回地抽取\(M\)个(\(M<K\)), 设这些组合对应的统计量值为\(\{ t_1, t_2, \dots, t_M \}\), 估计双侧p值为 \[ \hat p = 2 \min \left[ \frac{1}{M+1} \sum_{i=0}^M I_{\{t_i \geq t_0 \}},\; \frac{1}{M+1} \sum_{i=0}^M I_{\{t_i \leq t_0 \}} \right] . \] 其中\(t_0\)是用原始数据计算的统计量值。
Julia函数randperm(n)生成\(1:n\)的随机排列。
随机抽样方法计算置换检验双侧p值程序和结果如下:
Random.seed!(101)
M = 10_000
tstats = map(1:M) do _
rp = Random.randperm(n1+n2)
xv1 = mixedxy[rp[1:n1]]
yv1 = mixedxy[rp[n1+1:end]]
tstat(xv1, yv1)
end
pvalue = 2*min(mean([t0; tstats] .>= t0),
mean([t0; tstats] .<= t0))
@show pvalue;
## pvalue = 0.0613938606139386置换检验也适用于比较两个分布的其它检验统计量的p值计算, 包括两个多元分布的比较问题, 也可以推广到多个分布的比较问题。