22 Julia编程示例–自然数处理
在Julia中用Int64保存整数, 如果需要许多位的整数就用BigInt类型。
22.1 从整数值拆分各个数字
编写一个函数,
从一个正整数如12345,
拆分成各个数字的数组[1,2,3,4,5]。
输入:
- n: 要拆分的值。
- base: n的进制。
- ndigits: 输出的位数,不足时在左边添加0,超过时出错。
function todigits(n, base = 10; ndigits=0)
x = Int[]
while n > 0
(n, d) = divrem(n, base)
push!(x, d)
end
x = reverse(x)
nx = length(x)
if ndigits > 0
if nx < ndigits
x = [zeros(Int, ndigits - nx); x]
elseif nx > ndigits
error("ndigits too small!")
end
end
x
end
todigits(12345, ndigits=8)'
## 0 0 0 1 2 3 4 5这个问题Base库已经提供了digits函数,结果从个位倒序输出:
digits(12345)'
## 5 4 3 2 122.2 素因子分解
素数是大于等于2的整数中, 只能被自己和1整除的数。 等于两个大于1的数的乘积的数称为合数。 1既不是素数,也不是合数。 前几个素数为2,3,5,7,11,13,19, 除了2以外都是奇数。
设n为正整数, 将其分解为各个素数因子的乘积, 如 \[ 60 = 2 \times 2 \times 3 \times 5 \]
先写一个不利用保存的素数序列的版本。 输入正整数,输出从小到大素因子组成的数组,元素可重复。
function prime_factors(n::Integer)
x = Int[]
d = BigInt(2)
while n > 1
# 如果d是因子,则从n中都除掉
while n > 1 && n % d == 0
n = n ÷ d
push!(x, d)
end
if n == 1 # 已经没有素因子
break
else
# 考虑下一个可能的因子,所有因子都>d了
d += (d == 2 ? 1 : 2)
if n < d^2
# 如果n还是合数,n=ab, 则a>=d, b>=d, n >= d^2
# 所以n < d^2时n为素数
push!(x, n)
break
end
# 这里n还有可能是合数,继续用d尝试能否除尽
end # if - else
end # while n > 1
x
end
prime_factors(60)'
2 2 3 5设已经有m个素数保存在一维数组primes中。 在素因子分解时可以利用这些已有的素数, 这样在考虑因子时,就不必考虑所有的奇数了。 程序会复杂一些, 但是速度应该能提高。
输入正整数,和素数表的开头若干个组成的数组, 输出从小到大素因子组成的数组,元素可重复。 注意下面的函数与前面的函数名称相同, 但位置参数不同, 所以算是同一函数的不同方法。
function prime_factors(n::Integer, primes=[2])
x = Int[]
np = length(primes)
if np <= 8
primes = Int[2, 3, 5, 7, 11, 13, 17, 19]
np = 8
end
ip = 1
d = primes[ip]
# 循环继续的条件,是n还有大于1的因子
while n > 1
# 把当前考虑的因子都除去
while n > 1 && n % d == 0
n = n ÷ d
push!(x, d)
end
if n == 1
# 所有素因子都已经找到
break
else # n > 1
# 考虑下一个可能的因子
if ip < np
ip += 1
d = primes[ip]
else
d += 2
end
if d^2 > n
# n是合数要求n至少是d*d,即 n >= d^2,
# 所以d^2>n时n不是合数,又有n>1, 所以n是素数
push!(x, n)
break
end
# 进入下一轮循环尝试用d作为因子
end # if n==1
end # while n>1
x
end比较两个版本:
using BenchmarkTools
@btime prime_factors(12345678901234567890)
@btime prime_factors(12345678901234567890, [2])发现运算速度相近。
分解结果为[2, 3, 3, 5, 101, 3541, 3607, 3803, 27961]。
在\(n\)很大时会很慢,
如n = BigInt(2)^100 + 5。
有可能输入一个很大的素数表可以帮助。
22.4 求素数表
22.4.1 用逐个试验能否除尽的方法
前面进行素因子分解的程序,只要化简一下就可以变成判断素数的程序: 如果找到了任何一个小于n的因子, 就不是素数, 否则是素数。 程序如下:
# 用逐个除数试除的方法判断是否素数。
function isprime(n::Integer)
@assert n >= 1
if n==1
return false
elseif n==2
return true
end
prime = false
d = 2
while n % d != 0 && d^2 < n
# 只要当前除数不能整除n,就考虑下一个除数
if d==2
d = 3
else
d += 2
end
end
# 退出while循环时,如果不是因为d^2 > n退出,就是被中途
# 两种退出原因就决定了是素数还是合数
if n % d == 0
return false
else
return true
end
end
show(filter(isprime, [1:100;]))
## [2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
## 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
## 73, 79, 83, 89, 97]22.4.2 筛法求素数表
为了获得\(N\)以内的素数表, 可以用如下的方法: 将\(1:N\)罗列出来, 划去1, 然后划去2除本身以外的倍数, 再划去3除本身以外的倍数, 然后划去下一个没有被划去的数的2倍及以上的倍数, 如此重复一直到找不到下一个未被划去的数为止。 最后输出没有被划去的数。
用Julia实现,
输入上限n,
设置一个布尔型数组x[1:n],
初值为true,
数k被划去,
就设x[k]=false。
md"""
筛法求素数表。
输入上限n,输出n以内的素数的数组。
"""
function primes_sieve(n)
x = Array{Bool}(undef, n)
x .= true
x[1] = false
d = BigInt(2)
while d <= n
pos = d * 2
## 各个倍数
while pos <= n
x[pos] = false
pos += d
end
## 找到下一个未被划去的数
while true
d += 1
if d > n || x[d]
break
end
end
end
[i for i=1:n if x[i]]
end
string(primes_sieve(100))
## [2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
## 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
## 73, 79, 83, 89, 97]22.5 水仙花数和兰德尔数
如果十进制的\(\text{abc}_{10}\)等于其三个数字的立方和, 称为水仙花数。 如果十进制的\(n\)位数等于其数字的\(n\)次方的和, 称为兰德尔数。
下面用Julia求出\(n\)位数的兰德尔数。
function randle(ndigits)
res = Int[]
for x = (10^(ndigits-1)):(10^ndigits - 1)
ds = digits(x)
if x == sum(ds .^ ndigits)
push!(res, x)
end
end
return res
end
show(randle(3)) ## [153, 370, 371, 407]
show(randle(4)) ## [1634, 8208, 9474]
show(randle(5)) ## [54748, 92727, 93084]
show(randle(6)) ## [548834]
show(randle(7)) ## [1741725, 4210818, 9800817, 9926315]
show(randle(8)) ## [24678050, 24678051, 88593477]22.6 勾股数
当勾股定理中三个边长都是整数的时候, 称这三个数为勾股数, 如3, 4, 5: \[ 3^2 + 4^2 = 5^2 \]
查找斜边在\(n\)以下的勾股数,去掉三个边有大于1的公因子的情况。 对两个直角边长做二重循环查找。
md"""
斜边长在n以下的勾股数。
"""
function pythagoras_numbers(n)
res = [(0,0,0)]
for a in 1:(n ÷ 2)
for b in a:(n-1)
x = a*a + b*b
c = round(Int, sqrt(x))
if x == c*c && c ≤ n && gcd(a, b, c)==1
push!(res, (a, b, c))
end
end
end
return res[2:end]
end
print(pythagoras_numbers(100))
## [(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17),
## (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85),
## (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65),
## (36, 77, 85), (39, 80, 89), (48, 55, 73)]22.7 角谷猜想
考虑如下的自然数递推序列: \[ x_{n+1} = \begin{cases} x_n/2, & \text{若} x_n \text{为偶数}, \\ 3x_n + 1, & \text{若} x_n \text{为奇数}. \end{cases} \]
比如, \(x_0=5\), 序列为\(5, 16, 8, 4, 2, 1\), 从这里开始就会不停重复\(4, 2, 1\)。 称这样的序列为“冰雹序列”。 角谷猜想是, 从任何正整数出发这样递推都会回到1, 现在还没有发现任何反例,也没有数学证明。 将从\(x_0\)出发到1为止的步数称为此\(x_0\)对应的冰雹序列长度。 作图显示冰雹序列长度分布。
我们对\(1:n\)的所有\(x_0\)都计算长度, 并用直方图表示长度分布。
计算冰雹序列长度的函数:
function hailstone(n::Int)
len = 0
while n ≠ 1
if iseven(n)
n = n ÷ 2
else
n = 3n + 1
end
len += 1
end
return len
end作直方图测试的程序:
using CairoMakie
CairoMakie.activate!()
ys = [hailstone(n) for n=2:10_000_000];
hist(ys, bins=1000) |> displayknitr::include_graphics("figs/exa-numbers-hail001.png")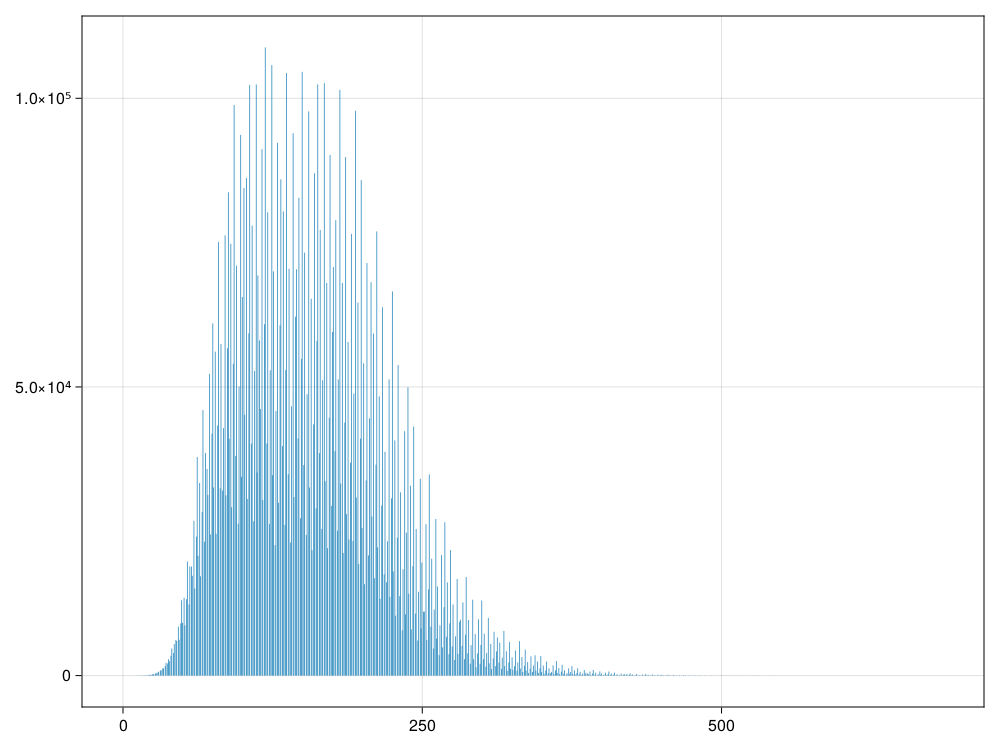
对前一千万个自然数计算了冰雹序列长度, 用时仅几秒钟。