5 移动平均模型

5.1 移动平均模型的概念

移动平均模型是具有\(q\)步外不相关性质的平稳列的模型； 对于高阶的AR模型， 有些可以用低阶的MA模型更好地描述。 一般的AR模型也可以用高阶MA模型近似。

理论上，AR模型也可以是无穷阶的： \[ X_t = \phi_0 + \sum_{j=1}^\infty \phi_j X_{t-j} + \varepsilon_t . \] 其中\(\{ \phi_j \}\)应绝对可和。 一个特例为 \[ X_t = \phi_0 - \sum_{j=1}^\infty (-\theta_1)^j X_{t-j} + \varepsilon_t . \] 其中\(0 < |\theta| < 1\)。 将模型写成： \[ X_t + \sum_{j=1}^\infty (-\theta_1)^j X_{t-j} = \phi_0 + \varepsilon_t . \tag{*} \] 以\(t-1\)代入，并乘以\(-\theta_1\)，有 \[ \sum_{j=1}^\infty (-\theta_1)^j X_{t-j} = -\phi_0 \theta_1 - \theta_1 \varepsilon_{t-1} . \] 代入到(*)式中得 \[ X_t = \phi_0(1+\theta_1) + \varepsilon_t + \theta_1 \varepsilon_{t-1} . \] 这样的模型称为MA(1)模型。

一般地，若\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声， 方差为\(\sigma^2\)，\(|\theta_1| < 1\)， 令 \[ X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} , \] 易见\(\{ X_t \}\)为线性时间序列形式的弱平稳列， 称为MA(1)序列。

类似地，MA(2)序列的模型为 \[ X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2} . \]

MA(\(q\))序列的模型为 \[ X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} . \] 此模型也有特征多项式 \[ 1 + \theta_1 z + \dots + \theta_q z^q . \] 特征方程的根称为特征根， 特征根都在单位圆外的条件称为MA模型的可逆条件。 平稳性并不需要特征根的条件。

上面从AR(\(\infty\))导出MA(1)的过程， 实际用了滞后算子的一些运算法则： 设\(P(z)=\sum_{j=0}^\infty \phi_j z^j\)和\(Q(z)=\sum_{j=0}^\infty \theta_j z^j\)， \(\sum_{j=0}^\infty |\phi_j| < \infty\), \(\sum_{j=0}^\infty |\theta_j| < \infty\), 则 \[ P(z)Q(z) = R(z) = \sum_{j=0}^\infty r_j z^j , \] 其中 \[ r_j = \sum_{i=0}^j \phi_i \theta_{j-i}, \] 且对弱平稳列\(\{ \xi_t \}\)有 \[ P(B)Q(B) \xi_t = R(B) \xi_t . \]

详见(何书元 2003)§2.1，以及李东风“应用时间序列分析课堂演示”。

5.2 移动平均模型的性质

以MA(1)和MA(2)为例讨论MA序列的性质，一般MA(\(q\))序列类似讨论即可。

5.2.1 平稳性与自相关函数性质

以MA(1)为例。\(X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1}\)， 其中\(\{ \varepsilon_t \}\)是零均值独立同分布白噪声， \(\theta_0\), \(\theta_1\)是任意实数， 平稳性不需要特征根的条件。

易见 \[ E X_t = \theta_0, \ \forall t , \quad \text{Var}(X_t) = \sigma^2(1 + \theta_1^2) = \gamma_0 . \] 而 \[ \gamma_1 = E[(X_t - \theta_0)(X_{t-1}-\theta_0)] = E[(\varepsilon_t + \theta_1 \varepsilon_{t-1}) (\varepsilon_{t-1} + \theta_1 \varepsilon_{t-2})] = \theta_1 E \varepsilon_{t-1}^2 = \sigma^2 \theta_1 . \] 对\(k > 1\)有 \[ \gamma_k = E[(\varepsilon_t + \theta_1 \varepsilon_{t-1}) (\varepsilon_{t-k} + \theta_1 \varepsilon_{t-k-1})] = 0 \ (k>1) . \] 因为\(k>1\)，所以\(t-k-1 < t-k < t-1 < t\)， 求协方差时均不相关。

所以，对于MA(1)序列，有 \[ \gamma_k = \begin{cases} \sigma^2(1 + \theta_1^2), & k=0, \\ \sigma^2 \theta_1, & k=1, \\ 0, & k>1 . \end{cases} \] 相应地，MA(1)的自相关函数为 \[ \rho_k = \begin{cases} 1, & k=0, \\ \frac{\theta_1}{1 + \theta_1^2}, & k=1, \\ 0, & k>1 . \end{cases} \]

这就验证了MA(1)序列是弱平稳列。 MA(1)的自相关函数在\(k>1\)后为零的性质叫做MA序列的自相关函数截尾性。

对于MA(\(q\))序列 \[ X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} , \] 易见 \[ EX_t = \theta_0, \quad \text{Var}(X_t) = \sigma^2(1 + \theta_1^2 + \dots + \theta_q^2) = \gamma_0 . \] 其自相关函数\(\rho_k\)也满足\(q\)后截尾性， 即\(\rho_{k}=0\), \(\forall k > q\)。 如果\(\theta_q \neq 0\)， 则\(\rho_q \neq 0\)。 这样， MA(\(q\))序列的两个时间点的观测\(X_s\)和\(X_t\)当\(|s-t|>q\)时不相关， 代表了一种特殊的“有限记忆”的模型。 MA序列的自相关函数截尾性也是在模型识别和定阶时的重要依据。

5.2.2 可逆性

对MA(1)模型， 当\(|\theta_1|<1\)时， 根据本章开始的推导可得 \[ \varepsilon_t = -\phi_0 + X_t + \sum_{j=1}^\infty (-\theta_1)^j X_{t-j} . \] 其中的级数是可以在a.s.意义和均方意义下收敛的。 这表明新息\(\varepsilon_t\)可以用当前的观测\(X_t\)以及历史观测\(X_{t-j}, j=1,2,\dots\)的线性组合表示， 而且历史观测\(X_{t-j}\)所在时刻离\(t\)时刻越远， 其作用越小。 这种性质叫做模型的可逆性。 MA模型的平稳性不需要可逆性条件， 但是从理论讨论的角度， 可逆的线性时间序列更合理： \(\{ X_t, X_{t-1}, \dots \}\)与\(\{\varepsilon_t, \varepsilon_{t-1}, \dots \}\)可以互相线性表示， 对任意\(t \in \mathbb Z\)成立。

5.3 移动平均模型定阶

MA(\(q\))序列的理论自相关函数\(\rho_k\)在\(q\)后截尾， \(\rho_q\neq 0\), \(\rho_k=0\), \(k>q\)。

在\(\{ X_t \}\)为独立同分布白噪声列的条件下， \(k>0\)的\(\hat\rho_k\)渐近\(\text{N}(0, \frac{1}{T})\)分布， 所以查看ACF图， 最后一个显著不等于零的\(\hat\rho_k\)的位置可以暂定为MA模型的阶。

实际上，如\(\{ X_t \}\)是MA(\(q\))序列， 则对\(k>q\)，\(\sqrt{T}\hat\rho_k\)渐近服从正态分布， 渐近均值为零，渐近方差为 \[ 1 + 2\rho_1^2 + \dots + 2\rho_q^2 . \]

也可以用AIC定阶：

\[ \text{AIC}(k) = \ln \hat\sigma_k^2 + \frac{2k}{T} . \] 其中\(\hat\sigma_k^2\)是用MA(\(k\))建模时新息方差的最大似然估计。

例5.1 考虑CRSP等权指数月度收益率，时间从1926-1到2008-12。

d <- read_table2(
  "m-ibm3dx2608.txt",
  col_types=cols(.default=col_double(),
                 date=col_date(format="%Y%m%d")))
## Warning: `read_table2()` was deprecated in readr 2.0.0.
## ℹ Please use `read_table()` instead.
ibmind <- xts(as.matrix(d[,-1]), d$date)
rm(d)
tclass(ibmind) <- "yearmon"
ew <- ts(coredata(ibmind)[,"ewrtn"], start=c(1926,1), frequency=12)
head(ibmind)
##             ibmrtn     vwrtn     ewrtn     sprtn
## 1月 1926 -0.010381  0.000724  0.023174  0.022472
## 2月 1926 -0.024476 -0.033374 -0.053510 -0.043956
## 3月 1926 -0.115591 -0.064341 -0.096824 -0.059113
## 4月 1926  0.089783  0.038358  0.032946  0.022688
## 5月 1926  0.036932  0.012172  0.001035  0.007679
## 6月 1926  0.068493  0.056888  0.050487  0.043184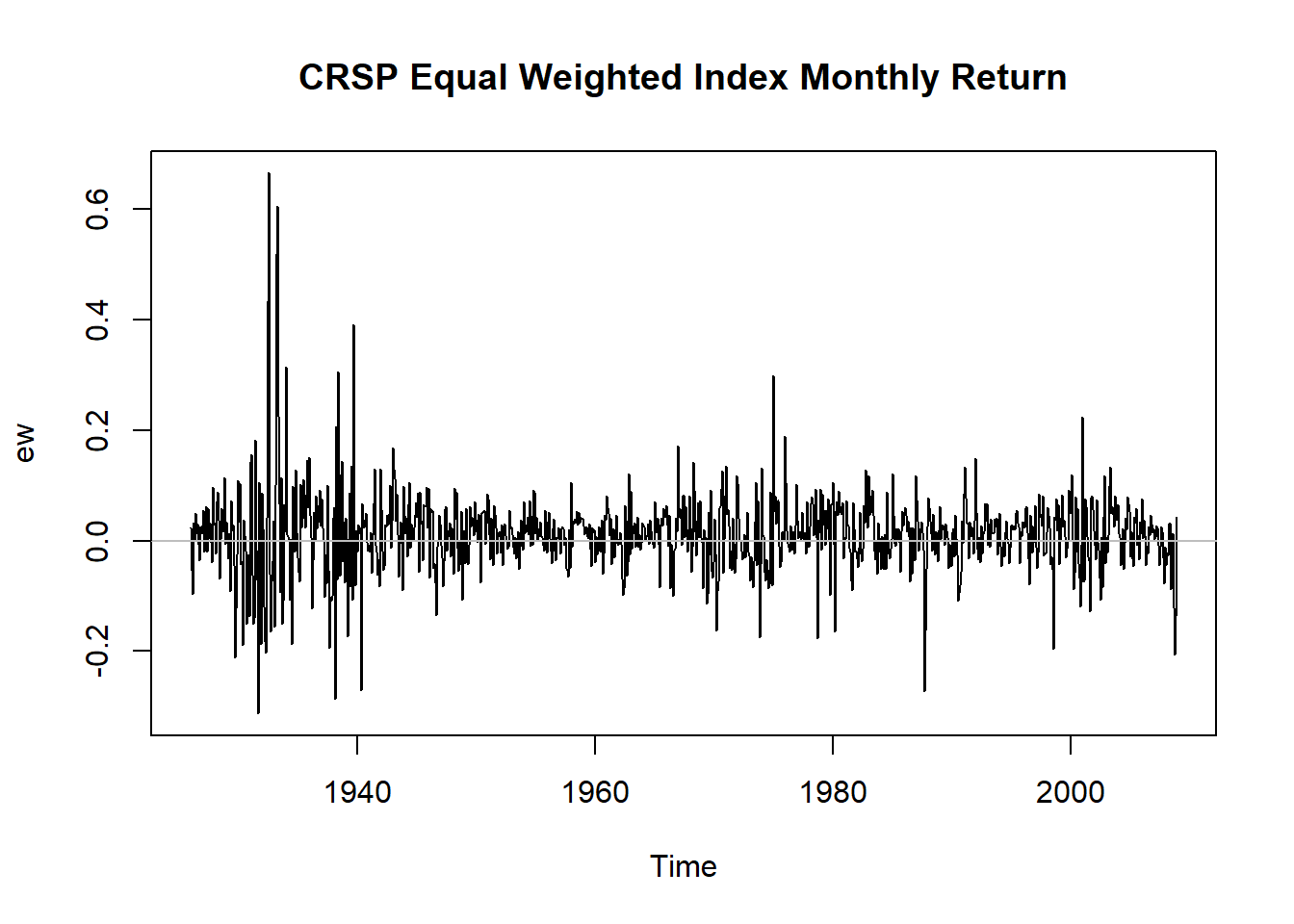
plot(ew, main="CRSP Equal Weighted Index Monthly Return")
abline(h=0, col="gray")
CRSP等权指数月度收益率

图5.1: CRSP等权指数月度收益率 

forecast::Acf(ew, main="")
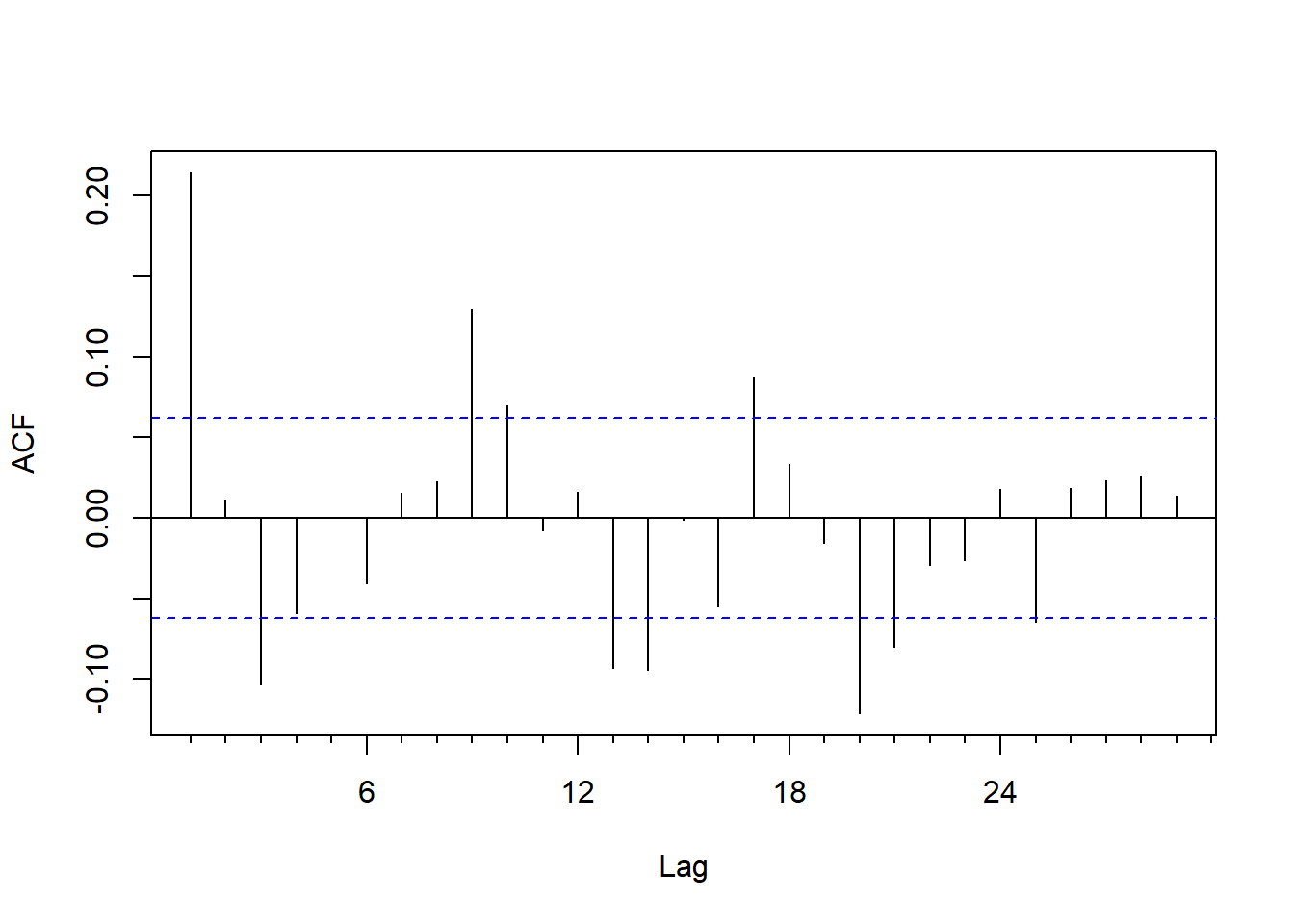
CRSP等权指数月收益率的ACF

图5.2: CRSP等权指数月收益率的ACF

ACF在\(k=1\)很大，在\(k=3\)和\(k=9\)也比较明显。 可以考虑拟合MA(3)或MA(9)。

○○○○○

5.4 移动平均模型的估计

MA模型参数的估计方法有：

  • 矩估计法，利用\(\{\gamma_k \}\)与\(\{\theta_k\}\)、\(\sigma^2\)的关系求非线性方程组解；
  • 逆相关函数法，将MA模型转换为长阶自回归模型，用估计自回归模型的方法估计，能保证可逆性；
  • 新息估计法；
  • 条件最大似然估计法；
  • 精确最大似然估计法。

前面三种方法见(何书元 2003)§6.2。

条件最大似然估计法和完全最大似然估计法都假定\(\{\varepsilon_t \}\)为高斯白噪声， 计算似然函数。 在条件最大似然估计法中， 近似假定\(\varepsilon_t=0, t \leq 0\)， 这样就可以得到\(\varepsilon_1 = x_1 - \theta_0\), \(\varepsilon_{2} = x_2 - \theta_0 - \theta_1 \varepsilon_1\)等递推表示， 将其代入\(\varepsilon_t, t=1,2,\dots,T\)的独立联合正态分布密度中就得到了条件似然函数， 求其关于\(\sigma^2\)和\(\theta_0, \theta_1, \dots, \theta_q\)的最大值点。

在精确最大似然估计中，将\(\varepsilon_t, t=1-q, 2-q, \dots, -1, 0\)也作为未知参数， 与其它模型参数一起估计。

条件最大似然估计更容易计算，在\(T\)充分大时两者的结果趋于相同。 在样本量较小时精确最大似然估计结果更为精确。 见(Tsay 2010)第8章。

例5.2 考虑例5.1中的CRSP等权指数月度收益率用MA建模， 时间从1926-1到2008-12。

例5.1提示建立MA(9)。 在R中用arima()函数可以建立AR模型和MA模型。

resm1 <- arima(ew, order=c(0,0,9)); resm1
## 
## Call:
## arima(x = ew, order = c(0, 0, 9))
## 
## Coefficients:
##          ma1     ma2      ma3      ma4     ma5      ma6     ma7      ma8
##       0.2144  0.0374  -0.1203  -0.0425  0.0232  -0.0302  0.0482  -0.0276
## s.e.  0.0316  0.0321   0.0328   0.0336  0.0319   0.0318  0.0364   0.0354
##          ma9  intercept
##       0.1350     0.0122
## s.e.  0.0323     0.0028
## 
## sigma^2 estimated as 0.005043:  log likelihood = 1220.86,  aic = -2419.72

对残差作Ljung-Box白噪声检验:

Box.test(resm1$residuals, type="Ljung", lag=12, fitdf=9)
## 
##  Box-Ljung test
## 
## data:  resm1$residuals
## X-squared = 6.0921, df = 3, p-value = 0.1072

结果不显著，检验结果支持所建立的模型。

从结果的标准误差构造近似95%置信区间， 可以看出\(\theta_k\)在\(k=2, 4, 5, 6, 7, 8\)处不显著。 所以，可以用arima()函数的fixed=指定这些参数固定为0：

resm1b <- arima(ew, order=c(0,0,9), 
                fixed=c(NA,0,NA,0,0,0,0,0,NA,NA))
resm1b
## 
## Call:
## arima(x = ew, order = c(0, 0, 9), fixed = c(NA, 0, NA, 0, 0, 0, 0, 0, NA, NA))
## 
## Coefficients:
##          ma1  ma2      ma3  ma4  ma5  ma6  ma7  ma8     ma9  intercept
##       0.1909    0  -0.1199    0    0    0    0    0  0.1227     0.0122
## s.e.  0.0293    0   0.0338    0    0    0    0    0  0.0312     0.0027
## 
## sigma^2 estimated as 0.005097:  log likelihood = 1215.61,  aic = -2421.22

没有限定之前，AIC为\(-2419.72\)； 限定后，AIC为\(-2421.22\)，限定后的AIC更优。

为了比较不同的模型， 可以逐个尝试不同的模型并比较AIC的值。

○○○○○

注意，R的stats::arima()函数在估计ARMA(\(p,q\))模型时， 输出结果的对应模型格式为 \[ (1 - \phi_1 B - \dots - \phi_p B^p) (X_t - \mu) = (1 + \theta_1 B + \dots + \theta_q B^q) \varepsilon_t \] 其中\(\mu\)对应于输出中的截距项(intercept)。 系数会输出为ar1, ……, arp, ma1, ……, maq, intercept的次序， ar\(k\)对应\(\phi_k\)，ma\(k\)对应\(\theta_k\)， intercept对应\(\mu\)。

5.5 移动平均模型的预测

因为MA(\(q\))序列在间隔超过\(q\)步以后就独立， 所以超前多步预测， 只能预测到\(q\)步， 从\(q+1\)步开始就只能用均值\(\mu\)预测了。

以MA(1)为例， \[ X_t = \theta_0 + \varepsilon_t + \theta_1 \varepsilon_{t-1} . \]

超前一步： \[ \hat x_h(1) = E(X_{h+1}|x_1, \dots, x_h) = \theta_0 + \theta_1 \varepsilon_{h} . \] 这里利用了\(E(\varepsilon_{h+1}|x_1, \dots, x_h)=0\)。 \(\varepsilon_h\)是第\(h\)个新息， 可以作为模型的残差计算， 或者通过将MA模型表达为AR模型来计算。 较精确的做法是“递推预报”， 参见(何书元 2003)§5.3。

超前两步: \[ \hat x_h(2) = E(\theta_0 + \varepsilon_{h+2} + \theta_1 \varepsilon_{h+1} | x_1, \dots, x_h) = \theta_0 \] 从两步开始的超前多步预报就变成\(EX_t=\theta_0\)了。

类似地，对于MA(2)序列， \[ \hat x_h(1) = \theta_0 + \theta_1 \varepsilon_h + \theta_2 \varepsilon_{h-1}, \ \hat x_h(2) = \theta_0 + \theta_2 \varepsilon_{h} . \] 对\(k=3,4,\dots\)则有\(\hat x_h(k) = \theta_0 = EX_t\)。

在R软件中， 用stats::arima()函数建模后， 对建模结果用predict()函数计算预测值和对应的近似标准误差。

例5.3 考虑例5.2中的CRSP等权指数月度收益率用稀疏系数的MA(9)建模， 但保留最后10个月的数据作为验证。 原始数据中时间从1926-1到2008-12。

resm1c <- arima(ew[1:986], order=c(0,0,9), 
                fixed=c(NA,0,NA,0,0,0,0,0,NA,NA))
resm1c
## 
## Call:
## arima(x = ew[1:986], order = c(0, 0, 9), fixed = c(NA, 0, NA, 0, 0, 0, 0, 0, 
##     NA, NA))
## 
## Coefficients:
##          ma1  ma2      ma3  ma4  ma5  ma6  ma7  ma8     ma9  intercept
##       0.1844    0  -0.1206    0    0    0    0    0  0.1218     0.0128
## s.e.  0.0295    0   0.0338    0    0    0    0    0  0.0312     0.0027
## 
## sigma^2 estimated as 0.005066:  log likelihood = 1206.44,  aic = -2402.88
pred1c <- predict(resm1c, n.ahead=10, se.fit=TRUE)
tmp.tab <- cbind(Observed=round(c(ew[987:996]), 4), 
                 Predicted=round(c(pred1c$pred), 4), 
                 SE=round(c(pred1c$se), 4))
row.names(tmp.tab) <- sprintf("2008-%02d", 3:12)
tmp.tab
##         Observed Predicted     SE
## 2008-03  -0.0260    0.0043 0.0712
## 2008-04   0.0312    0.0136 0.0724
## 2008-05   0.0322    0.0150 0.0724
## 2008-06  -0.0871    0.0145 0.0729
## 2008-07  -0.0010    0.0120 0.0729
## 2008-08   0.0141    0.0018 0.0729
## 2008-09  -0.1209    0.0122 0.0729
## 2008-10  -0.2060    0.0055 0.0729
## 2008-11  -0.1366    0.0085 0.0729
## 2008-12   0.0431    0.0128 0.0734

因为次贷危机影响，实际收益率不如预测的那么好。 可以看出当\(k=10\)的时候（模型\(q=9\)）预测等于序列均值。 超前多步预测的标准误差逐渐增加到等于序列的样本标准差：

sd(c(ew[1:986]))
## [1] 0.07368157

○○○○○

5.6 AR和MA的小结

  • 对MA(\(q\))模型，ACF对定阶有意义，因为其\(q\)后截尾；
  • 对AR(\(p\))模型，PACF对定阶有意义，因为其\(p\)后截尾；
  • MA模型的序列不管系数如何总是平稳的， 实际上还是因果线性时间序列， 当特征根都在单位圆外时是可逆的；
  • AR模型只有当特征根都在单位圆外时才有\(\epsilon_t\) 与\(X_{t-1}, X_{t-2}, \dots\)独立的弱平稳解；
  • 对AR和MA序列，超前多步预测趋于序列的均值， 预测均方误差趋于序列的方差。

B 参考文献

Tsay, Ruey S. 2010. Analysis of Financial Time Series. 3rd Ed. John Wiley & Sons, Inc.
何书元. 2003. 应用时间序列分析. 北京大学出版社.