11 长记忆模型
11.1 长记忆模型介绍
ACF是时间序列建模的重要参考。 对于ARMA序列, 当滞后\(k\to\infty\)时其样本ACF是负指数速度趋于零的。 对于单位根非平稳列, 其理论ACF无定义(因为自协方差是针对弱平稳列定义的), 其样本ACF在样本量\(T \to \infty\)时每个\(\hat\rho_k\)都趋于1 (\(k>0\))。
有一些平稳时间序列的ACF虽然也随滞后\(k\to\infty\)趋于零, 但是收敛到零的速度比较慢, 只有负幂次\(k^{-\alpha}\)这样的速度。 这代表着序列的自相关性随着距离变远而减小得比较慢, 称这样的序列是长记忆时间序列。 注意, 长记忆时间序列仍是弱平稳的, 单位根非平稳列虽然远距离的自相关性很强但不称为长记忆。
长记忆时间序列的典型模型是分数差分弱平稳列,模型为
\[\begin{align} (1-B)^d X_t = \xi_t, \ -0.5 < d < 0.5 \tag{11.1} \end{align}\]
其中\(\{ \xi_t \}\)是零均值独立同分布白噪声。
类似于ARMA序列平稳解的讨论, 对算子多项式使用复变多项式的泰勒展开来求解。 函数\(f(z) = (1-z)^{-d}\)在\(z=0\)有如下的泰勒展开:
\[ (1-z)^{-d} = \sum_{k=0}^\infty \psi_k z^k \] 其中 \[ \psi_0=1, \ \psi_k = \frac{d(d+1)\dots(d+k-1)}{k!} \] 类似地有 \[ (1-z)^d = \sum_{k=0}^\infty \pi_k z^k \] 其中 \[ \pi_0=1, \quad \pi_k = (-1)^k \frac{d(d-1)\dots (d-k+1)}{k!} \]
若对实数\(d\)推广记号 \[ \binom{d}{k} = \frac{d(d-1)(d-2)\dots (d-k+1)}{k!} \] 则有 \[ \begin{aligned} (1 - z)^{-d} =& \sum_{j=0}^\infty \binom{-d}{k} (-z)^k = \sum_{k=0}^\infty \frac{(-d)(-d-1)\dots(-d-k+1)}{k!} (-z)^k \\ =& \sum_{k=0}^\infty \frac{d(d+1)\dots(d+k-1)}{k!} (+z)^k = \sum_{k=0}^\infty \psi_k z^k \end{aligned} \] 也有 \[ (1-z)^d = \sum_{j=0}^\infty \binom{d}{k} (-z)^k = \sum_{k=0}^\infty (-1)^k \frac{d(d-1)\dots(d-k+1)}{k!} z^k = \sum_{k=0}^\infty \pi_k z^k \]
11.2 长记忆模型性质
模型(11.1)有如下性质:
11.2.1 MA表示
若\(d<0.5\),则模型中的\(\{ X_t \}\)有弱平稳列解,并有无穷阶MA表示:
\[ x_t = \sum_{k=0}^\infty \psi_k \xi_{t-k} \]
11.2.2 AR表示
若\(d > -0.5\),则模型中的\(\{ \xi_t \}\)可以用\(\{ X_t \}\)表示为如下的无穷阶AR形式:
\[ X_t + \sum_{k=1}^\infty \pi_k X_{t-k} = \xi_t \]
11.2.3 ACF衰减速率
若\(-0.5<d<0.5\), 则平稳解\(\{ X_t \}\)的ACF为 \[ \rho_k = \frac{d(d+1)\dots(d+k-1)}{(-d+1)(-d+2)\dots(-d+k)}, k=1,2,\dots \] \(\rho_1 = \frac{d}{1-d}\), 当\(k\to\infty\)时 \[ \rho_k = c k^{2d-1} + o(k^{2d-1}) \]
是以负幂律缓慢衰减的(\(c\)为与\(k\)无关的常数)。 注意ARMA序列的\(\rho_k\)以负指数速度快速衰减。
11.2.4 PACF
若\(-0.5<d<0.5\), 则平稳解\(\{ X_t \}\)的PACF为
\[ \phi_{kk} = \frac{d}{k-d}, \ k=1,2,\dots \] 以\(k^{-1}\)速度衰减。
11.2.5 谱密度性质
弱平稳时间序列的谱密度\(f(\omega)\), \(\omega \in [0,\pi]\)是序列在不同的随机振动频率上的能量分布, 是一个非负可积函数。 若\(-0.5<d<0.5\), 若平稳解的谱密度满足 \[ f(\omega) \sim \omega^{-2d}, \ \omega \to 0 \] 这样,则\(0<d<0.5\)时谱密度在\(\omega=0\)频率附近趋于正无穷, 这在实际数据中的表现是数据存在缓慢的长期水平波动。 ARAM序列的谱密度是有界的。
如果将模型(11.1)中的白噪声\(\{\xi_t \}\)推广为可以取ARMA(\(p,q\))序列, 这样的模型称为 ARFIMA(\(p,d,q\))模型, 称为分数阶差分ARMA模型。 参见(Geweke and Porter-Hudak 1983)。
R的fracdiff软件包用来构建分数阶差分ARMA模型。
在金融时间序列建模中, 如果样本ACF数值不大但是衰减特别缓慢, 可以考虑长记忆模型。 如果数值很大同时衰减慢则可能是单位根非平稳, 或者具有很接近1的特征根的ARMA序列。
11.3 长记忆模型建模实例
例11.1 对CRSP价值加权指数和等权指数的日简单收益率数据, 时间从1970-01-02到2008-12-31, 考虑日收益率的绝对值。
读入数据,计算日收益率的绝对值:
da <- read_table(
"d-ibm3dx7008.txt",
col_types=cols(.default=col_double(),
Date=col_date("%Y%m%d"))
)
xts.crspw <- xts(da[,-1], da$Date)
vw <- abs(da$vwretd)
ew <- abs(da$ewretd)
rm(da)价值加权日收益率绝对值序列的ACF:
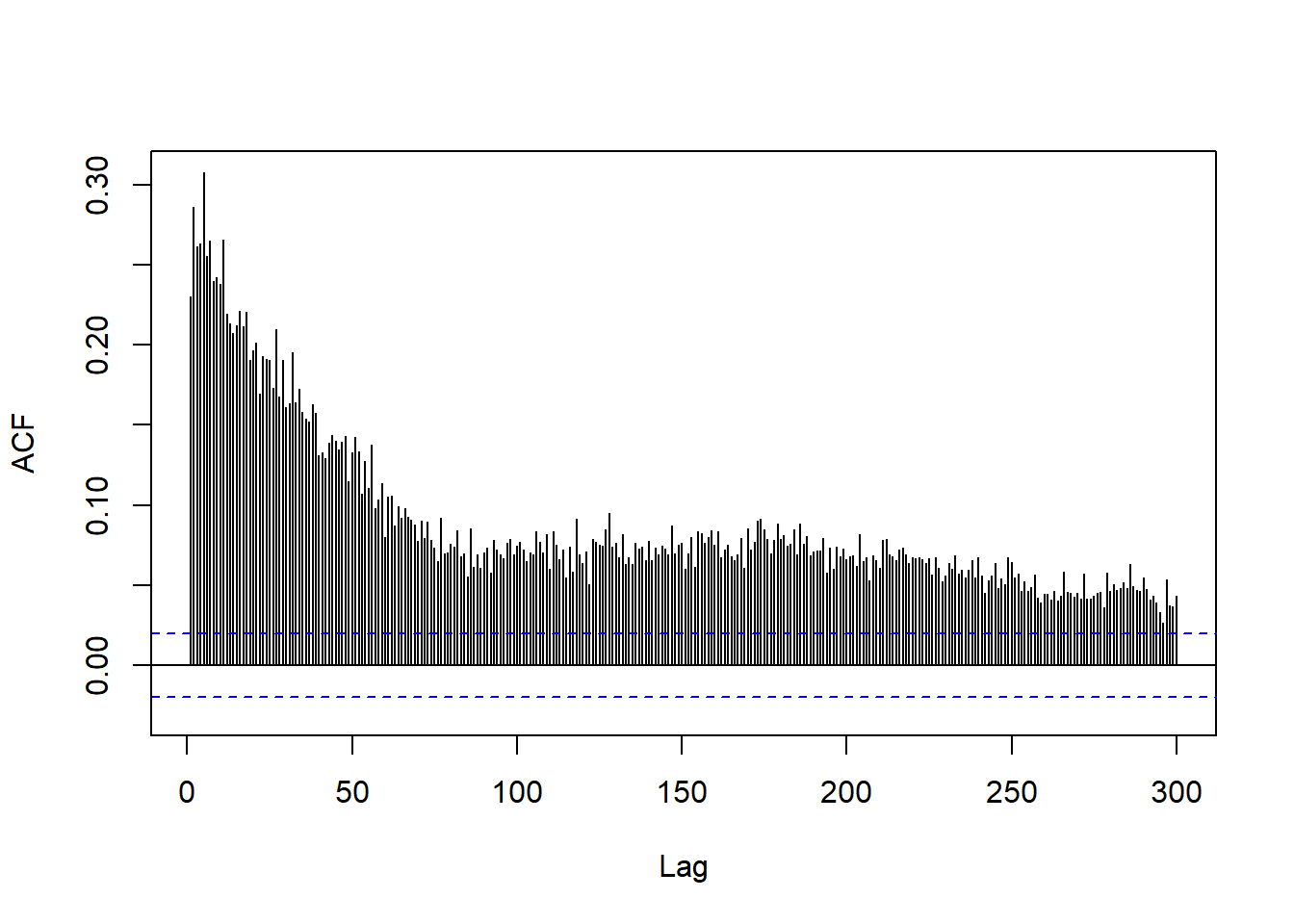
图11.1: 价值加权日收益率绝对值序列的ACF
等加权日收益率绝对值序列的ACF:
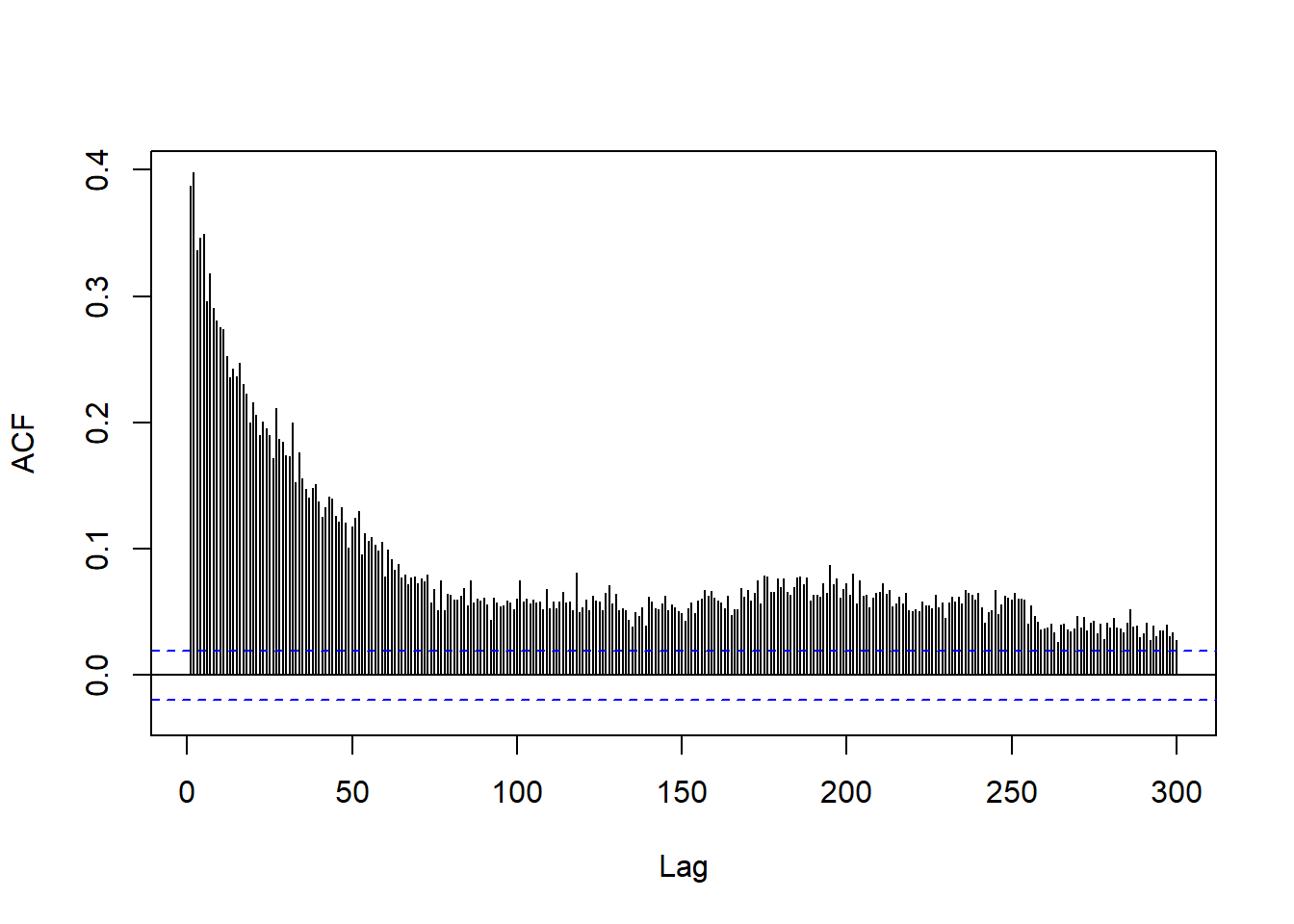
图11.2: 等加权日收益率绝对值序列的ACF
这两个序列的ACF都比较小但是衰减缓慢,到之后300时仍显著不为零。 都是正相关。
函数fracdiff::fdGPH()计算差分阶的Geweke-Porter-Hudak估计值:
## $d
## [1] 0.372226
##
## $sd.as
## [1] 0.0698385
##
## $sd.reg
## [1] 0.06868857估计的差分阶为\(d=0.372\)。
用fracdiff::fracdiff()函数进行ARFIMA模型估计:
##
## Call:
## fracdiff::fracdiff(x = vw, nar = 1, nma = 1)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## d 0.490938 0.007997 61.39 <2e-16 ***
## ar 0.113389 0.005988 18.94 <2e-16 ***
## ma 0.575895 0.005946 96.85 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## sigma[eps] = 0.0065619
## [d.tol = 0.0001221, M = 100, h = 0.0003742]
## Log likelihood: 3.551e+04 ==> AIC = -71021.02 [4 deg.freedom]其中选项nar和nma用来指定AR阶和MA阶。
模型为
\[
(1 - 0.1133 B)(1 - B)^{0.4909} X_t
= \varepsilon_t - 0.5759 \varepsilon_{t-1},
\ \sigma_{\varepsilon} = 0.006562
\]
估计结果中差分阶\(d=0.4909\)已经接近非平稳的边缘0.5了。
注意:fracdiff::fracdiff()的输出与arima()输出有差别,
其MA系数的输出是\(1 - \theta_1 B - \dots - \theta_q B^q\)格式的。