26 格兰格因果性

26.1 介绍

前面已经在VAR部分简单介绍了格兰格因果性的概念，以及用VAR模型检验格兰格因果性的方法。这里对格兰格因果性的概念与检验方法进行更详细的阐述。这一章的内容主要参考(Gebhard Kirchgässner 2013)，(C. W. J. Granger 1969)。

考虑两个时间序列之间的因果性。这里的因果性指的是时间顺序上的关系，如果\(X_{t-1}, X_{t-2}, \dots\)对\(Y_t\)有额外的预测作用，而\(Y_{t-1}, Y_{t-2}, \dots\)对\(X_t\)没有额外的预测作用，则称\(\{X_t \}\)是\(\{ Y_t \}\)的格兰格原因，而\(\{ Y_t \}\)不是\(\{ X_t \}\)的格兰格原因。如果\(X_{t-1}, X_{t-2}, \dots\)对\(Y_t\)有额外的预测作用， \(Y_{t-1}, Y_{t-2}, \dots\)对\(X_t\)也有额外的预测作用，则在没有进一步信息的情况下无法确定两个时间序列的因果性关系。

注意这种因果性与采样频率有关系，在日数据或者月度数据中能发现的领先——滞后性质的因果关系，到年度数据可能就以及混杂在以前变成同步的关系了。

(C. W. J. Granger 1969)首先提出了时间序列之间因果关系的概念。时间序列因果关系可以是假设没有因果关系，然后检验能否拒绝假设，这是(C. W. J. Granger 1969)的方法；也可以是首先建立包含因果关系的模型，然后检验其中表示因果关系的参数是否不显著，这是利用VAR和VECM的方法。后一种方法首先提出于(Sims 1972)。

在具有格兰杰因果性的情况下，可以用来改善预测。比如，如果\(\{X_t \}\)是\(\{ Y_t \}\)的格兰格原因，则可以利用\(\{Y_t \}\)的过去值、 \(\{ X_t \}\)的过去值去预测\(\{Y_t \}\)的当前值，会比仅利用\(\{ Y_t \}\)的过去值预测要好，这是认为\(\{ X_t \}\)的过去值中包含了\(\{ Y_t \}\)的过去值中缺少的信息，而这些信息对预测\(\{ Y_t \}\)的当前值是有作用的。 (C. W. J. Granger 1969)的检验方法就是针对这一点进行检验。

在经济与金融时间序列建模中考虑\(X_{t-1}\)对\(Y_t\)影响的另一个原因是，许多时间序列具有较强的正自相关性，比如单位根过程或者特征根接近于单位圆的ARMA模型，对于这样的两个时间序列\(\{(X_t, Y_t) \}\)，如果以\(Y_t\)为因变量， \(X_t\)为自变量作线性回归，可能发生虚假的回归，即使两个序列之间独立，但是回归结果可以是显著的。这是因为，\(Y_t\)与\(Y_{t-1}\)之间的强序列相关性。如果在回归中引入滞后项，这样的虚假回归就可以被消除。参见(Clive W. J. Granger and Newbold 1974)。

从因果性的角度讲，只有两个序列的新息（innovation）对另一个序列的影响才是有意义的。参见(Schwert 1979)。

26.2 格兰格因果性的定义

设\(\{ \xi_t \}\)为一个时间序列， \(\{ \boldsymbol{\eta}_t \}\)为向量时间序列，记 \[\begin{aligned} \bar{\boldsymbol{\eta}}_t =& \{ \boldsymbol{\eta}_{t-1}, \boldsymbol{\eta}_{t-2}, \dots \} \end{aligned}\]

记 \(\text{Pred}(\xi_t | \bar{\boldsymbol{\eta}}_t)\)为基于 \(\boldsymbol{\eta}_{t-1}, \boldsymbol{\eta}_{t-2}, \dots\) 对\(\xi_t\)作的最小均方误差无偏预报，其解为条件数学期望\(E(\xi_t | \boldsymbol{\eta}_{t-1}, \boldsymbol{\eta}_{t-2}, \dots)\)，在一定条件下可以等于\(\xi_t\)在\(\boldsymbol{\eta}_{t-1}, \boldsymbol{\eta}_{t-2}, \dots\)张成的线性Hilbert空间的投影（比如，\((\xi_t, \boldsymbol{\eta}_t)\)为平稳正态多元时间序列），即最优线性预测。直观理解成基于过去的\(\{\boldsymbol{\eta}_{t-1}, \boldsymbol{\eta}_{t-2}, \dots \}\)的信息对当前的\(\xi_t\)作的最优预测。 (C. W. J. Granger 1969)允许最优预测与最优线性预测，实际检验方法用了谱和互谱来分析，因为谱和互谱仅涉及二阶性质，所以(C. W. J. Granger 1969)实际是用最优线性预测定义因果性。

令一步预测误差为 \[ \varepsilon(\xi_t | \bar{\boldsymbol{\eta}}_t) = \xi_t - \text{Pred}(\xi_t | \bar{\boldsymbol{\eta}}_t) \] 令一步预测误差方差，或者均方误差，为 \[ \sigma^2(\xi_t | \bar{\boldsymbol{\eta}}_t) = \text{Var}(\varepsilon_t(\xi_t | \bar{\boldsymbol{\eta}}_t) ) = E \left[ \xi_t - \text{Pred}(\xi_t | \bar{\boldsymbol{\eta}}_t) \right]^2 \]

考虑两个时间序列\(\{ X_t \}\)和\(\{ Y_t \}\)， \(\{(X_t, Y_t) \}\)宽平稳或严平稳。

如果 \[ \sigma^2(Y_t | \bar Y_t, \bar X_t) < \sigma^2(Y_t | \bar Y_t) \] 则称\(\{ X_t \}\)是\(\{ Y_t \}\)的格兰格原因，记作\(X_t \Rightarrow Y_t\)。这不排除\(\{ Y_t \}\)也可以是\(\{ X_t \}\)的格兰格原因。
如果\(X_t \Rightarrow Y_t\)，而且\(Y_t \Rightarrow X_t\)，则称互相有反馈关系，记作\(X_t \Leftrightarrow Y_t\)。
如果 \[ \sigma^2(Y_t | \bar Y_t, X_t, \bar X_t) < \sigma^2(Y_t | \bar Y_t, \bar X_t) \] 即除了过去的信息，增加同时刻的\(X_t\)信息后对\(Y_t\)预测有改进，则称\(\{X_t \}\)对\(\{Y_t \}\)有瞬时因果性。这时\(\{Y_t \}\)对\(\{X_t \}\)也有瞬时因果性。
如果\(X_t \Rightarrow Y_t\)，则存在最小的正整数\(m\)，使得 \[ \sigma^2(Y_t | \bar Y_t, X_{t-m}, X_{t-m-1}, \dots) < \sigma^2(Y_t | \bar Y_t, X_{t-m-1}, X_{t-m-2}, \dots) \] 称\(m\)为因果性滞后值(causality lag)。如果\(m>1\)，这意味着在已有\(Y_{t-1}, Y_{t-2}, \dots\)和\(X_{t-m}, X_{t-m-1}, \dots\)的条件下，增加\(X_{t-1}\), , \(X_{t-m+1}\)不能改进对\(Y_t\)的预测。

例26.1 设\(\{ \varepsilon_t, \eta_t \}\)是相互独立的零均值白噪声列， \(\text{Var}(\varepsilon_t)=1\), \(\text{Var}(\eta_t)=1\), 考虑 \[\begin{aligned} Y_t =& X_{t-1} + \varepsilon_t \\ X_t =& \eta_t + 0.5 \eta_{t-1} \end{aligned}\]

用\(L(\cdot|\cdot)\)表示最优线性预测，则 \[\begin{aligned} & L(Y_t | \bar Y_t, \bar X_t) \\ =& L(X_{t-1} | X_{t-1}, \dots, Y_{t-1}, \dots) + L(\varepsilon_t | \bar Y_t, \bar X_t) \\ =& X_{t-1} + 0 \\ =& X_{t-1} \\ \sigma^2(Y_t | \bar Y_t, \bar X_t) =& \text{Var}(\varepsilon_t) = 1 \end{aligned}\] 而 \[ Y_t = \eta_{t-1} + 0.5\eta_{t-2} + \varepsilon_t \] 有 \[\begin{aligned} \gamma_Y(0) = 2.25, \gamma_Y(1) = 0.5, \gamma_Y(k) = 0, k \geq 2 \end{aligned}\] 所以\(\{Y_t \}\)是一个MA(1)序列，设其方程为 \[ Y_t = \zeta_t + b \zeta_{t-1}, \zeta_t \sim \text{WN}(0, \sigma_\zeta^2) \] 可以解出 \[\begin{aligned} \rho_Y(1) =& \frac{\gamma_Y(1)}{\gamma_Y(0)} = \frac{2}{9} \\ b =& \frac{1 - \sqrt{1 - 4 \rho_Y^2(1)}}{2 \rho_Y(1)} \approx 0.2344 \\ \sigma_\zeta^2 =& \frac{\gamma_Y(1)}{b} \approx 2.1328 \end{aligned}\] 于是 \[\begin{aligned} \sigma^2(Y_t | \bar Y_t) =& \sigma_\zeta^2 = 2.1328 \end{aligned}\] 所以 \[\begin{aligned} \sigma^2(Y_t | \bar Y_t, \bar X_t) = 1 < 2.1328 = \sigma^2(Y_t | \bar Y_t) \end{aligned}\] 即\(X_t\)是\(Y_t\)的格兰格原因。

反之， \(X_t\)是MA(1)序列，有 \[ \eta_t = \frac{1}{1 + 0.5 B} X_t = \sum_{j=0}^\infty (-0.5)^j X_{t-j} \] 其中\(B\)是推移算子（滞后算子）。于是 \[\begin{aligned} L(X_t | \bar X_t) =& L(\eta_t | \bar X_t) + 0.5 L(\eta_{t-1} | \bar X_t) \\ =& 0.5 \sum_{j=0}^\infty (-0.5)^j X_{t-1-j} \\ =& - \sum_{j=1}^\infty (-0.5)^j X_{t-j} \\ \sigma^2(X_t | \bar X_t) =& \text{Var}(X_t - L(X_t | \bar X_t)) \\ =& \text{Var}(\eta_t) = 1 \end{aligned}\] 而 \[\begin{aligned} L(X_t | \bar X_t, \bar Y_t) =& L(\eta_t | \bar X_t, \bar Y_t) + 0.5 L(\eta_{t-1} | \bar X_t, \bar Y_t) \\ =& 0 + 0.5 L(\sum_{j=0}^\infty (-0.5)^j X_{t-1-j} | \bar X_t, \bar Y_t) \\ =& -\sum_{j=1}^\infty (-0.5)^j X_{t-j} \\ =& L(X_t | \bar X_t) \end{aligned}\] 所以\(Y_t\)不是\(X_t\)的格兰格原因。

考虑瞬时因果性。 \[\begin{aligned} L(Y_t | \bar X_t, \bar Y_t, X_t) =& X_{t-1} + 0 (\text{注意}\varepsilon_t\text{与}\{X_s, \forall s\}\text{不相关} \\ =& L(Y_t | \bar X_t, \bar Y_t) \end{aligned}\] 所以\(X_t\)不是\(Y_t\)的瞬时格兰格原因。

○○○○○

例26.2 在例26.1中，如果模型改成 \[\begin{aligned} Y_t =& X_{t} + \varepsilon_t \\ X_t =& \eta_t + 0.5 \eta_{t-1} \end{aligned}\] 有怎样的结果？

这时 \[ Y_t = \varepsilon_t + \eta_t + 0.5 \eta_{t-1} \] 仍有 \[\begin{aligned} \gamma_Y(0) = 2.25, \gamma_Y(1) = 0.5, \gamma_Y(k) = 0, k \geq 2 \end{aligned}\] 所以\(Y_t\)还服从MA(1)模型 \[ Y_t = \zeta_t + b \zeta_{t-1}, b \approx 0.2344, \sigma^2_\zeta \approx 2.1328 \]

\[\begin{aligned} L(Y_t | \bar Y_t, \bar X_t) =& L(X_t | \bar Y_t, \bar X_t) + 0 \\ =& L(\eta_t | \bar Y_t, \bar X_t) + 0.5 L(\eta_{t-1} | \bar Y_t, \bar X_t) \\ =& 0 + 0.5 L(\sum_{j=0}^\infty (-0.5)^j X_{t-1-j} | \bar Y_t, \bar X_t) \\ =& - \sum_{j=1}^\infty (-0.5)^j X_{t-j} \\ =& X_t - \eta_t \\ \sigma^2(Y_t | \bar Y_t, \bar X_t) =& \text{Var}(\varepsilon_t + \eta_t) = 2 \end{aligned}\] 而 \[ \sigma^2(Y_t | \bar Y_t) = \sigma^2_\zeta \approx 2.1328 > \sigma^2(Y_t | \bar Y_t, \bar X_t) = 2 \] 所以\(X_t\)是\(Y_t\)的格兰格原因。

反之， \[\begin{aligned} L(X_t | \bar X_t, \bar Y_t) =& - \sum_{j=1}^\infty (-0.5)^j X_{t-j} \\ =& L(X_t | \bar X_t) \end{aligned}\] 所以\(Y_t\)不是\(X_t\)的格兰格原因。

考虑瞬时因果性。 \[\begin{aligned} L(Y_t | \bar X_t, \bar Y_t, X_t) =& X_{t} + 0 (\text{注意}\varepsilon_t\text{与}\{X_s, \forall s\}\text{不相关} \\ =& X_t \\ \sigma^2(Y_t | \bar X_t, \bar Y_t, X_t) =& \text{Var}(\varepsilon) \\ =& 1 < 2 = \sigma^2(Y_t | \bar X_t, \bar Y_t) \end{aligned}\] 所以\(X_t\)是\(Y_t\)的瞬时格兰格原因。

○○○○○

例26.3 设 \[\begin{aligned} X_t =& 0.5 X_{t-1} + \varepsilon_t \\ Y_t =& 0.1 X_{t-1} + 0.5 Y_{t-1} + \eta_t \end{aligned}\] 其中 \[ \left(\begin{matrix} \varepsilon_t \\ \eta_t \end{matrix}\right) \sim \text{N}\left( \left(\begin{matrix} 0 \\0 \end{matrix}\right), \left(\begin{matrix} 1 & \rho \\ \rho & 1 \end{matrix}\right) \right) \] 为独立同分布的向量白噪声列，\(|\rho|<1\)。

易见 \[\begin{aligned} E(X_t | \bar X_t) =& 0.5 X_{t-1} \\ \sigma^2(X_t | \bar X_t) =& \text{Var}(\varepsilon_t) = 1 \\ E(X_t | \bar X_t, \bar Y_t) =& 0.5 X_{t-1} = E(X_t | \bar X_t)\\ \sigma^2(X_t | \bar X_t, \bar Y_t) =& 1 = \sigma^2(X_t | \bar X_t) \end{aligned}\] 所以\(Y_t\)不是\(X_t\)的格兰格原因。

反过来， \[\begin{aligned} E(Y_t | \bar X_t, \bar Y_t) =& 0.1 X_{t-1} + 0.5 Y_{t-1} \\ \sigma^2(Y_t | \bar X_t, \bar Y_t) =& \text{Var}(\eta_t) = 1 \\ E(Y_t | \bar Y_t) =& 0.1 E(X_{t-1} | \bar Y_t) + 0.5 Y_{t-1} \\ \sigma^2(Y_t | \bar Y_t) =& E \left[ Y_t - E(Y_t | \bar Y_t) \right]^2 \\ =& E \left[ \eta_t + 0.1(X_{t-1} - E(X_{t-1} | \bar Y_t)) \right]^2 \\ =& 1 + 0.1^2 \sigma^2(X_{t-1} | \bar Y_t) \\ >& 1 = E(Y_t | \bar X_t, \bar Y_t) \end{aligned}\] 所以\(X_t\)是\(Y_t\)的格兰格原因。

○○○○○

这些概念可以推广到有多个序列的情况。设所有构成互相影响的序列为\(Y_t^D = \{ Y_t^{(i)}, i \in D \}\)，如\(D = \{ 1, 2, \dots, K \}\)。记\(D(j) = D \backslash \{j \}\)， \(Y_t^{D(j)} = \{ Y_t^{(i)}, i \in D(j) \}\)。这时，称\(Y_t^{(j)}\)是\(Y_t^{(i)}\)的格兰格原因，如果 \[ \sigma^2(Y_t^{(i)} | Y_{t-1}^D, Y_{t-2}^D, \dots) < \sigma^2(Y_t^{(i)} | Y_{t-1}^{D(j)}, Y_{t-2}^{D(j)}, \dots) . \]

这样定义的因果性在用到实际问题时，需要假定可能造成因果关系的数据都已经在\(\{ Y_t^D \}\)中，如果存在外面的序列\(\{ A_t \}\)，使得\(A_t\)影响了所有\(Y_t^{(i)}\)，则仅有\(\{ Y_t^D \}\)数据时得到的因果性可能是虚假的， (C. W. J. Granger 1969)第4节给出了一个例子。

例26.4 设 \[\begin{aligned} Y_t =& A_{t-1} + \xi_t \\ X_t =& A_t + \eta_t \end{aligned}\] 其中\(\{ A_t \}\)是一个宽平稳时间序列， \(\{\varepsilon_t \}\), \(\{ \xi_t \}\)是两个相互独立的标准白噪声列，且都与\(\{ A_t \}\)独立。

则数据仅有\(Y_t^D = \{ X_t, Y_t \}\)时， \(X_t\)是\(Y_t\)的格兰格原因。以\(\{A_t \}\)是独立同分布白噪声列来证明。设\(\{A_t\}\), \(\{\xi_t\}\), \(\{\eta_t\}\)相互独立，都是独立同分布白噪声列WN(0,1)。这时 \[\begin{aligned} \text{Pred}(Y_t | \bar Y_t) =& \text{Pred}(A_{t-1} | \bar Y_t) = 0, \end{aligned}\] 这是因为\(\xi_t\)与\(\bar Y_t\)独立， \(A_{t-1}\)与\(\bar Y_t\)独立。于是 \[\begin{aligned} \varepsilon(Y_t | \bar Y_t) =& Y_t - \text{Pred}(Y_t | \bar Y_t) = Y_t = A_{t-1} + \xi_t, \\ \sigma^2(Y_t | \bar Y_t) =& \text{Var}[\varepsilon(Y_t | \bar Y_t)] = 2; \end{aligned}\] 而 \[\begin{aligned} \text{Pred}(Y_t | \bar Y_t, \bar X_t) =& \text{Pred}(A_{t-1} | \bar Y_t, \bar X_t) = \text{Pred}(X_{t-1} - \eta_{t-1} | \bar Y_t, \bar X_t) \\ =& X_{t-1} - \text{Pred}(\eta_{t-1} | \bar Y_t, \bar X_t) , \\ \varepsilon(Y_t | \bar Y_t, \bar X_t) =& Y_t - \text{Pred}(Y_t | \bar Y_t, \bar X_t) \\ =& \xi_t + X_{t-1} - \eta_{t-1} - [X_{t-1} - \text{Pred}(\eta_{t-1} | \bar Y_t, \bar X_t)] \\ =& \xi_t - [\eta_{t-1} - \text{Pred}(\eta_{t-1} | \bar Y_t, \bar X_t)], \\ \sigma^2(Y_t | \bar Y_t, \bar X_t) =& \text{Var}[\varepsilon(Y_t | \bar Y_t, \bar X_t)] \\ =& 1 + E \{ [\eta_{t-1} - \text{Pred}(\eta_{t-1} | \bar Y_t, \bar X_t)]^2 \} < 2, \end{aligned}\] 所以\(\{X_t \}\)是\(\{Y_t \}\)的格兰格原因。证明中利用了 \[ E \{ [\eta_{t-1} - \text{Pred}(\eta_{t-1} | \bar Y_t, \bar X_t)]^2 \} < \text{Var}(\eta_{t-1}) = 1, \] 这是因为 \[\begin{aligned} \text{Cov}(\eta_{t-1}, X_{t-1}) = \text{Cov}(\eta_{t-1}, A_{t-1} + \eta_{t-1}) = 1 \neq 0, \end{aligned}\] 所以上式成立。

另一方面，如果数据为\(Y_t^{D'} = \{ A_t, X_t, Y_t \}\)，则\(A_t\)是\(Y_t\)的格兰格原因，而\(X_t\)不是\(Y_t\)的格兰格原因。事实上， \[\begin{aligned} E(Y_t | \bar A_t, \bar X_t, \bar Y_t) =& E(A_{t-1} | \bar A_t, \bar X_t, \bar Y_t) + E(\xi_{t} | \bar A_t, \bar X_t, \bar Y_t) \\ =& A_{t-1} + 0 \\ =& E(Y_t | \bar A_t, \bar Y_t) = E(Y_t | \bar A_t), \end{aligned}\] 即增加\(\bar X_t\)的信息不能改进预测。所以，当\(Y_t^D = (X_t, Y_t)\)时得到的因果性是虚假的。

○○○○○

26.3 两变量VAR情形

\[\begin{aligned} X_t = a(B) X_t + b(B) Y_t + \xi_t \\ Y_t = c(B) X_t + d(B) Y_t + \eta_t \end{aligned}\] 其中\(a(z) = a_1 z + \dots + a_m z^m\)， \(b(z), c(z), d(z)\)类似定义， \(B\)为推移算子。 \(\{\xi_t \}\), \(\{\eta_t \}\)为零均值白噪声，两者可以有同步相关性。当且仅当\(b(z) \equiv 0\)时， \(Y_t\)不是\(X_t\)的格兰格原因。

上述模型应该满足VAR的平稳性条件。这时，存在平稳解\((X_t, Y_t)\)且 \((\xi_t, \eta_t)\)与\((X_{t-j}, Y_{t-j}), j=1,2,\dots\)不相关。

当\(\xi_t\)和\(\eta_t\)有同步相关性时， \(X_t\)与\(Y_t\)有瞬时因果性。但当\(b(z) \equiv 0\)时，仍有\(Y_t\)不是\(X_t\)的格兰格原因。

如果\(\xi_t\)和\(\eta_t\)没有同步相关性，则\(X_t\)与\(Y_t\)没有瞬时因果性。

26.4 两变量VMA情形

考虑如下二元时间序列模型： \[\begin{aligned} X_t = a(B) \xi_t + b(B) \eta_t \\ Y_t = c(B) \xi_t + d(B) \eta_t \end{aligned}\] 其中 \[\begin{aligned} a(z) =& 1 + a_1 z + \dots + a_m z^m \\ b(z) =& b_1 z + \dots + b_m z^m \\ c(z) =& c_1 z + \dots + c_m z^m \\ d(z) =& 1 + d_1 z + \dots + d_m z^m \end{aligned}\] \(B\)为推移算子。 \(\{\xi_t \}\), \(\{\eta_t \}\)为零均值白噪声，可以存在同步相关性。

如果\(\xi_t\)是\(\{X_t\}\)的新息且\(b(z) \equiv 0\)，则\(Y_t\)不是\(X_t\)的格兰格原因。

\(Y_t\)与\(X_t\)有瞬时因果关系，当且仅当\(\xi_t\)与\(\eta_t\)有同步相关性。

例26.5 当\(m=1\)时，模型为 \[\begin{aligned} X_t =& \xi_t + a_1 \xi_{t-1} + b_0 \eta_t + b_1 \eta_{t-1} \\ Y_t =& c_0 \xi_t + c_1 \xi_{t-1} + \eta_t + d_1 \eta_{t-1} \end{aligned}\] 其中\((\xi_t, \eta_t) \sim \text{WN}(\boldsymbol 0, \text{diag}(\sigma_x^2, \sigma_\eta^2))\)。

如果\(b_0 = b_1 = 0\)，且设\(0 < |a_1| < 1\)，则模型变成 \[\begin{aligned} X_t =& \xi_t + a_1 \xi_{t-1} \\ Y_t =& c_0 \xi_t + c_1 \xi_{t-1} + \eta_t + d_1 \eta_{t-1} \end{aligned}\] 这时 \[\begin{aligned} \xi_t = \sum_{j=0}^\infty (-a_1)^j X_{t-j} \end{aligned}\] 是\(\{ X_t \}\)的新息列，有 \[\begin{aligned} L(X_t | \bar X_t, \bar Y_t) =& 0 + a_1 L(\xi_{t-1} | \bar X_t, \bar Y_t) \\ =& a_1 L(\sum_{j=0}^\infty (-a_1)^j X_{t-1-j} | \bar X_t, \bar Y_t) \\ =& - \sum_{j=1}^\infty (-a_1)^j X_{t-j} \\ =& L(X_t | \bar X_t) \end{aligned}\] 所以\(Y_t\)不是\(X_t\)的格兰格原因。

○○○○○

26.5 单变量模型表示

一个平稳可逆的VAR(m)二元时间序列可以有两种表示。简约形式的VAR表示为 \[\begin{aligned} \Phi(B) \left(\begin{matrix} X_t \\ Y_t \end{matrix}\right) =& \left(\begin{matrix} \Phi_{11}(B) & \Phi_{12}(B) \\ \Phi_{21}(B) & \Phi_{22}(B) \end{matrix}\right) \left(\begin{matrix} X_t \\ Y_t \end{matrix}\right) = \left(\begin{matrix} \xi_t \\ \eta_t \end{matrix}\right) \end{aligned}\] 其中\(\Phi(z) = I - A_1 z - \dots - A_m z^m\)是2阶方阵，每个元素是\(z\)的\(m\)次多项式，满足\(\text{det}(\Phi(\lambda) )\)的根都在单位圆外的条件。 \(\Phi_{11}(z)\)和\(\Phi_{22}(z)\)的常数项为1， \(\Phi_{12}(z)\)和\(\Phi_{21}(z)\)的常数项为0。 \(B\)是推移算子。 \((\xi_t, \eta_t)^T\)是零均值向量白噪声列，协方差阵为\(\Sigma\)。

当且仅当\(\Phi_{12}(z) \equiv 0\)时\(Y_t\)不是\(X_t\)的格兰格原因。

可以得到 \[ \Psi(z) = [\Phi(z)]^{-1} = \left(\begin{matrix} \Psi_{11}(z) & \Psi_{12}(z) \\ \Psi_{21}(z) & \Psi_{22}(z) \end{matrix}\right) = [\text{det}(\Phi(z))]^{-1} \left(\begin{matrix} \Phi_{22}(z) & -\Phi_{12}(z) \\ -\Phi_{21}(z) & \Phi_{11}(z) \end{matrix}\right) \] 其中\(\Psi(z)\)是2阶方阵，每个元素是\(z\)的无穷阶多项式且在根都在单位圆外， \(\Psi(z)\)的\((1,2)\)元素与\((2,1)\)的常数项等于0。这时有MA表示： \[\begin{aligned} \left(\begin{matrix} X_t \\ Y_t \end{matrix}\right) = \Psi(B) \left(\begin{matrix} \xi_t \\ \eta_t \end{matrix}\right) \end{aligned}\]

当且仅当\(\Psi_{12}(z) \equiv 0\)时，即\(\Phi_{12}(z) \equiv 0\)时， \(Y_t\)不是\(X_t\)的格兰格原因。

\((X_t, Y_t)\)还可以分别建立一元的Wold表示： \[\begin{aligned} \left(\begin{matrix} X_t \\ Y_t \end{matrix}\right) = \left(\begin{matrix} W_1(B) u_t \\ W_2(B) v_t \end{matrix}\right) = \left(\begin{matrix} W_1(B) & 0 \\ 0 & W_2(B) \end{matrix}\right) \left(\begin{matrix} u_t \\ v_t \end{matrix}\right) = W(B) \left(\begin{matrix} u_t \\ v_t \end{matrix}\right) \end{aligned}\] 其中\(\{u_t \}\)是\(\{ X_t \}\)的信息列，其中\(\{v_t \}\)是\(\{ Y_t \}\)的信息列。利用MA形式写成 \[\begin{aligned} \left(\begin{matrix} X_t \\ Y_t \end{matrix}\right) = W(B) \{ W(B) \}^{-1} \Psi(B) \left(\begin{matrix} \xi_t \\ \eta_t \end{matrix}\right) = W(B) V(B) \left(\begin{matrix} \xi_t \\ \eta_t \end{matrix}\right) \end{aligned}\] 其中 \[\begin{aligned} V(z) = \left(\begin{matrix} \frac{\Psi_{11}(z)}{W_1(z)} & \frac{\Psi_{12}(z)}{W_1(z)} \\ \frac{\Psi_{21}(z)}{W_2(z)} & \frac{\Psi_{22}(z)}{W_2(z)} \end{matrix}\right) \end{aligned}\] 这提示 \[\begin{aligned} \left(\begin{matrix} u_t \\ v_t \end{matrix}\right) = V(B) \left(\begin{matrix} \xi_t \\ \eta_t \end{matrix}\right) \end{aligned}\]

当\(\Psi_{12}(z) \equiv 0\)时\(Y_t\)不是\(X_t\)的格兰格原因，且这时\(\xi_t\)和\(u_t\)都是\(\{ X_t \}\)的新息，所以有\(\xi_t = u_t\)， \(V_{11}(z) \equiv 1\)，对\(k \geq 1\)有 \[\begin{aligned} \text{Cov}(u_t, v_{t-k}) = E \left\{ \xi_t V_{21}(B) \xi_{t-k} + \xi_t V_{22}(B) \eta_{t-k} \right\} = 0 \end{aligned}\] 当\(\xi_t\)与\(\eta_t\)没有同步相关时，对\(k=0\)也有\(\text{Cov}(u_t, v_{t}) = 0\)。可以根据这种性质，利用两个序列的新息的互相关系数进行因果性检验。

26.6 因果性检验

为了检验\(Y_t\)不是\(X_t\)的格兰格原因，可以检验在对\(X_t\)预测时加入\(\bar Y_t\)的信息是否改进对\(X_t\)的预测；可以在VAR或者VAR模型中检验相应的系数是否为零。

参考：(Gebhard Kirchgässner 2013)。

26.6.1 直接格兰格方法

原始文献： Sargent, Thomas J. (1976) A Classical Macroeconomic Model for the United States, Journal of Political Economy 84, pp. 207-237.

对两个平稳列\(x_t, y_t\)，直接利用增加一个序列的历史值能否改善对另一个序列的预测来判断是否有格兰格因果关系。使用普通最小二乘法估计如下的回归：

\[\begin{align} y_t = \alpha_0 + \sum_{j=1}^{k_1} \alpha_{11,j} y_{t-j} + \sum_{j=k_0}^{k_2} \alpha_{12,j} x_{t-j} + \xi_{1t} \tag{26.1} \end{align}\] 其中\(k_0=1\)。检验零假设： \[ \alpha_{12,1} = \alpha_{12,2} = \dots \alpha_{11,k_2} = 0 \] 采用多个回归系数为零的\(F\)检验。拒绝零假设时\(x_t\)是\(y_t\)的格兰格原因；不拒绝零假设时， \(x_t\)不是\(y_t\)的格兰格原因。

为检验\(y_t\)是不是\(x_t\)的格兰格原因，可以建立类似(26.1)的以\(x_t\)为因变量的回归方程。

如果两个方向都拒绝零假设，则\(x_t\)与\(y_t\)有反馈关系。

为了检验有无瞬时因果性，可以在(26.1)中取\(k_0=0\)，即在等式右侧加入\(x_t\)的同步项，并用\(t\)或者\(F\)统计量检验 \[ H_0: \alpha_{12,0} = 0 \] 拒绝零假设时有瞬时因果性，否则无瞬时因果性。当\(k_1 = k_2\)时，检验瞬时因果性的结果不依赖于以\(x_t\)还是以\(y_t\)为因变量。

这一检验方法的缺点是严重地依赖于滞后项数\(k_2\)的选择， \(k_2\)越大，能检验到的滞后影响越大，但是由于平均效应的作用检验的功效会下降。可以选取多个\(k_2\)值进行检验，如果结果一致，则检验结果比较稳定。另一种办法是计算回归的AIC或者BIC值，这里参数个数计为\(k_1 + k_2 + 1\)(\(k_0=1\))。

例26.6 英、加、美GDP季度增长率的因果关系，仅考虑英国和每国。

读入数据，并单独保存各个滞后项。

my_lag <- function(x, k){
  c(rep(NA, k), x[1:(length(x)-k)])
}
da <- read.table("q-gdp-ukcaus.txt", header=TRUE)
da2 <- da[,c("uk", "us")]
da3 <- apply(da2, 2, function(x) diff(log(x))*100)
da3 <- as.data.frame(da3)
max_lag <- 8
for(j in 1:max_lag){
  da3 <- cbind(da3, my_lag(da3[,"uk"], k=j))
  da3 <- cbind(da3, my_lag(da3[,"us"], k=j))
}
colnames(da3) <- c(
  "uk", "us",
  paste(rep(c("uk", "us"), 8), rep(1:8, each=2), sep=""))
ts.gdp2r <- ts(da3, start=c(1980,1), frequency=4)
head(round(da3[,1:10], 2), 12)

##       uk    us   uk1   us1   uk2   us2   uk3   us3   uk4   us4
## 1  -1.80 -2.07    NA    NA    NA    NA    NA    NA    NA    NA
## 2  -0.19 -0.19 -1.80 -2.07    NA    NA    NA    NA    NA    NA
## 3  -1.11  1.83 -0.19 -0.19 -1.80 -2.07    NA    NA    NA    NA
## 4  -0.68  2.06 -1.11  1.83 -0.19 -0.19 -1.80 -2.07    NA    NA
## 5   0.21 -0.80 -0.68  2.06 -1.11  1.83 -0.19 -0.19 -1.80 -2.07
## 6   1.35  1.21  0.21 -0.80 -0.68  2.06 -1.11  1.83 -0.19 -0.19
## 7   0.01 -1.25  1.35  1.21  0.21 -0.80 -0.68  2.06 -1.11  1.83
## 8   0.37 -1.66  0.01 -1.25  1.35  1.21  0.21 -0.80 -0.68  2.06
## 9   1.26  0.54  0.37 -1.66  0.01 -1.25  1.35  1.21  0.21 -0.80
## 10  0.00 -0.39  1.26  0.54  0.37 -1.66  0.01 -1.25  1.35  1.21
## 11  0.53  0.08  0.00 -0.39  1.26  0.54  0.37 -1.66  0.01 -1.25
## 12  1.45  1.24  0.53  0.08  0.00 -0.39  1.26  0.54  0.37 -1.66

建立预报英国的线性回归模型，使用英国和美国的最多4个季度的滞后变量：

lm1 <- lm(uk ~ uk1 + uk2 + uk3 + uk4 + us1 + us2 + us3 + us4, data=da3)
summary(lm1)

## 
## Call:
## lm(formula = uk ~ uk1 + uk2 + uk3 + uk4 + us1 + us2 + us3 + us4, 
##     data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.72521 -0.27778  0.05682  0.32431  1.27704 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.1858767  0.0776542   2.394  0.01834 *  
## uk1          0.4320162  0.0954924   4.524 1.52e-05 ***
## uk2         -0.0008427  0.1021392  -0.008  0.99343    
## uk3          0.1498499  0.1039568   1.441  0.15224    
## uk4         -0.0027531  0.0949600  -0.029  0.97692    
## us1          0.1201269  0.0847244   1.418  0.15901    
## us2          0.0381883  0.0845357   0.452  0.65233    
## us3          0.1363833  0.0829753   1.644  0.10305    
## us4         -0.2115821  0.0761625  -2.778  0.00641 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5293 on 112 degrees of freedom
##   (因为不存在，4个观察量被删除了)
## Multiple R-squared:  0.3966, Adjusted R-squared:  0.3535 
## F-statistic: 9.203 on 8 and 112 DF,  p-value: 1.136e-09

回归有效，\(R^2\)约为0.40。

去掉美国的滞后项再回归：

lm2 <- lm(uk ~ uk1 + uk2 + uk3 + uk4, data=da3)
summary(lm2)

## 
## Call:
## lm(formula = uk ~ uk1 + uk2 + uk3 + uk4, data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.95459 -0.28774  0.07628  0.33604  1.22413 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.22588    0.07255   3.113  0.00233 ** 
## uk1          0.47320    0.09272   5.103 1.32e-06 ***
## uk2          0.04367    0.10054   0.434  0.66486    
## uk3          0.16558    0.10093   1.641  0.10361    
## uk4         -0.07051    0.08844  -0.797  0.42692    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5528 on 116 degrees of freedom
##   (因为不存在，4个观察量被删除了)
## Multiple R-squared:  0.3183, Adjusted R-squared:  0.2948 
## F-statistic: 13.54 on 4 and 116 DF,  p-value: 4.351e-09

回归结果仍有效，\(R^2\)为0.32。比较这两个嵌套的模型：

anova(lm1, lm2)

## Analysis of Variance Table
## 
## Model 1: uk ~ uk1 + uk2 + uk3 + uk4 + us1 + us2 + us3 + us4
## Model 2: uk ~ uk1 + uk2 + uk3 + uk4
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
## 1    112 31.374                                
## 2    116 35.447 -4   -4.0736 3.6356 0.007985 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

在0.05水平下检验结果显著。这说明预报时去掉美国的滞后数据对预报是有损失的，即美国是英国的格兰格原因。

取8个滞后项重新做一遍：

lm3 <- lm(uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8 
          + us1 + us2 + us3 + us4 + us5 + us6 + us7 + us8, data=da3)
summary(lm3)

## 
## Call:
## lm(formula = uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8 + 
##     us1 + us2 + us3 + us4 + us5 + us6 + us7 + us8, data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.44719 -0.27235  0.01485  0.27273  1.05355 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.05038    0.08640   0.583 0.561138    
## uk1          0.47535    0.09551   4.977  2.7e-06 ***
## uk2         -0.22172    0.11333  -1.956 0.053204 .  
## uk3          0.28998    0.11328   2.560 0.011966 *  
## uk4         -0.15414    0.11345  -1.359 0.177294    
## uk5          0.18674    0.11190   1.669 0.098286 .  
## uk6         -0.10806    0.10047  -1.076 0.284701    
## uk7          0.13634    0.09835   1.386 0.168743    
## uk8         -0.26884    0.09081  -2.961 0.003835 ** 
## us1          0.34931    0.09453   3.695 0.000359 ***
## us2         -0.08949    0.09596  -0.933 0.353278    
## us3          0.20481    0.09643   2.124 0.036138 *  
## us4         -0.28427    0.09173  -3.099 0.002521 ** 
## us5          0.10928    0.08826   1.238 0.218559    
## us6         -0.06517    0.08760  -0.744 0.458694    
## us7          0.11906    0.08515   1.398 0.165167    
## us8          0.12681    0.07420   1.709 0.090530 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4878 on 100 degrees of freedom
##   (因为不存在，8个观察量被删除了)
## Multiple R-squared:  0.5325, Adjusted R-squared:  0.4577 
## F-statistic:  7.12 on 16 and 100 DF,  p-value: 1.12e-10

lm4 <- lm(uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8, data=da3)
summary(lm4)

## 
## Call:
## lm(formula = uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8, 
##     data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.90686 -0.25167  0.04234  0.34808  1.04474 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.21135    0.08226   2.569   0.0116 *  
## uk1          0.49539    0.09465   5.234 8.23e-07 ***
## uk2          0.07643    0.10484   0.729   0.4676    
## uk3          0.15853    0.10400   1.524   0.1304    
## uk4         -0.11202    0.10484  -1.068   0.2877    
## uk5          0.02367    0.10593   0.223   0.8236    
## uk6          0.02614    0.10293   0.254   0.8000    
## uk7          0.12883    0.10135   1.271   0.2064    
## uk8         -0.17309    0.08911  -1.942   0.0547 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5435 on 108 degrees of freedom
##   (因为不存在，8个观察量被删除了)
## Multiple R-squared:  0.3732, Adjusted R-squared:  0.3268 
## F-statistic: 8.038 on 8 and 108 DF,  p-value: 1.852e-08

anova(lm3, lm4)

## Analysis of Variance Table
## 
## Model 1: uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8 + us1 + us2 + 
##     us3 + us4 + us5 + us6 + us7 + us8
## Model 2: uk ~ uk1 + uk2 + uk3 + uk4 + uk5 + uk6 + uk7 + uk8
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    100 23.797                                  
## 2    108 31.907 -8   -8.1102 4.2602 0.0001965 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

结果说明美国是英国的格兰格原因。

取滞后4，检验英国是不是美国的格兰格原因：

lm5 <- lm(us ~ uk1 + uk2 + uk3 + uk4
          + us1 + us2 + us3 + us4, data=da3)
summary(lm5)

## 
## Call:
## lm(formula = us ~ uk1 + uk2 + uk3 + uk4 + us1 + us2 + us3 + us4, 
##     data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.00435 -0.33896  0.02654  0.39247  1.31429 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.2281998  0.0857538   2.661  0.00893 ** 
## uk1          0.5335165  0.1054525   5.059 1.66e-06 ***
## uk2         -0.2284360  0.1127926  -2.025  0.04522 *  
## uk3          0.0008313  0.1147997   0.007  0.99424    
## uk4          0.1621996  0.1048646   1.547  0.12474    
## us1          0.2199575  0.0935613   2.351  0.02047 *  
## us2          0.2403357  0.0933530   2.574  0.01134 *  
## us3         -0.0483437  0.0916298  -0.528  0.59882    
## us4         -0.1735589  0.0841065  -2.064  0.04137 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5845 on 112 degrees of freedom
##   (因为不存在，4个观察量被删除了)
## Multiple R-squared:  0.4148, Adjusted R-squared:  0.373 
## F-statistic: 9.922 on 8 and 112 DF,  p-value: 2.334e-10

lm6 <- lm(us ~ us1 + us2 + us3 + us4, data=da3)
summary(lm6)

## 
## Call:
## lm(formula = us ~ us1 + us2 + us3 + us4, data = da3)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.35757 -0.30055  0.07061  0.43079  1.51800 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.293791   0.093607   3.139  0.00215 ** 
## us1          0.341741   0.091681   3.728  0.00030 ***
## us2          0.240559   0.095254   2.525  0.01290 *  
## us3          0.004113   0.096357   0.043  0.96603    
## us4         -0.052820   0.084229  -0.627  0.53182    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6499 on 116 degrees of freedom
##   (因为不存在，4个观察量被删除了)
## Multiple R-squared:  0.2505, Adjusted R-squared:  0.2246 
## F-statistic:  9.69 on 4 and 116 DF,  p-value: 8.498e-07

anova(lm5, lm6)

## Analysis of Variance Table
## 
## Model 1: us ~ uk1 + uk2 + uk3 + uk4 + us1 + us2 + us3 + us4
## Model 2: us ~ us1 + us2 + us3 + us4
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    112 38.259                                  
## 2    116 49.002 -4   -10.742 7.8617 1.272e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

结果表明英国也是美国的格兰格原因，两者是反馈关系。

○○○○○

26.6.2 Haugh-Pierce方法

原始文献：

LARRY D. HAUGH (1976), Checking the Independence of Two Covariance Stationary Time Series: A Univariate Residual Cross-Correlation Approach, Journal of the American Statistical Association 71, pp. 378-385
DAVID A. PIERCE and LARRY D. HAUGH (1977), Causality in Temporal Systems: Characterizations and a Survey, Journal of Econometrics 5, pp. 265-293

Haugh(1976)和Pierce and Haugh(1977)提出了基于一元时间序列建模的方法。对\(x_t\)和\(y_t\)分别建立一元ARMA模型，计算分别的残差\(a_t\)和\(b_t\)，用Ljung-Box白噪声检验方法进行残差诊断，确认残差为白噪声。然后，计算两个残差之间的互相关系数\(\hat\rho_{ab}(k)\)，对\(k>0\)， \(\rho_{ab}(k)\)代表了\(y_t\)对\(x_t\)的影响。取统计量 \[ S = T \; \sum_{k=k_1}^{k_2} \hat\rho_{ab}^2(k) \] 在零假设 \[ H_0: \rho_{ab}(k)=0, k=k_1, k_1 + 1, \dots, k_2 \] 下\(S\)近似服从\(\chi^2(k_2 - k_1 + 1)\)。

可以先取\(k_1<0\), \(k_2>0\)，来检验是否存在任何方向的因果性。如果结果显著，再取\(k_1=1\), \(k_2 \geq k_1\)，检验是否有\(y_t\)对\(x_t\)序列的因果性；取\(k_2 = -1\), \(k_1 \leq k_2\)，检验是否有\(x_t\)对\(y_t\)序列的因果性；取\(k_1=k_2=0\)，检验有无瞬时因果性。

这种方法比直接格兰格方法功效较低。

例26.7 仍考虑英国和美国的季度GDP对数增长率问题。

对英国的数据建立ARMA模型：

acf(ts.gdp2r[,"uk"])

pacf(ts.gdp2r[,"uk"])

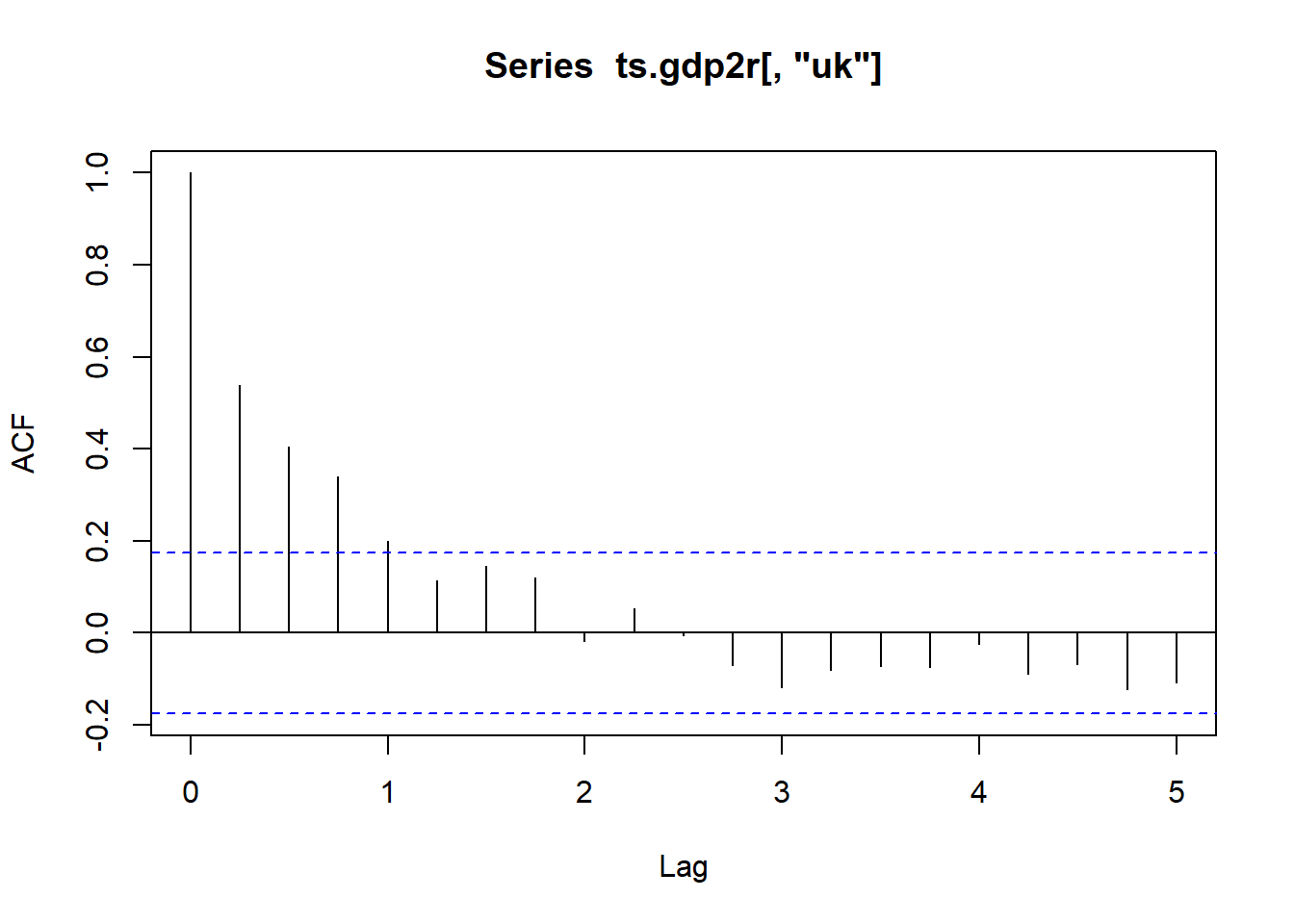
试验模型1：

mod.uk01 <- arima(ts.gdp2r[,"uk"], order=c(1,0,0)); mod.uk01

## 
## Call:
## arima(x = ts.gdp2r[, "uk"], order = c(1, 0, 0))
## 
## Coefficients:
##          ar1  intercept
##       0.5871     0.4925
## s.e.  0.0766     0.1250
## 
## sigma^2 estimated as 0.339:  log likelihood = -109.97,  aic = 225.94

试验模型2：

mod.uk02 <- arima(ts.gdp2r[,"uk"], order=c(4,0,0)); mod.uk02

## 
## Call:
## arima(x = ts.gdp2r[, "uk"], order = c(4, 0, 0))
## 
## Coefficients:
##          ar1     ar2     ar3      ar4  intercept
##       0.4897  0.0900  0.1894  -0.0773     0.4672
## s.e.  0.0920  0.1023  0.1048   0.0951     0.1635
## 
## sigma^2 estimated as 0.3218:  log likelihood = -106.8,  aic = 225.6

试验模型3：

mod.uk03 <- arima(ts.gdp2r[,"uk"], order=c(1,0,1)); mod.uk03

## 
## Call:
## arima(x = ts.gdp2r[, "uk"], order = c(1, 0, 1))
## 
## Coefficients:
##          ar1      ma1  intercept
##       0.7989  -0.3269     0.4645
## s.e.  0.0912   0.1354     0.1691
## 
## sigma^2 estimated as 0.3274:  log likelihood = -107.84,  aic = 223.68

试验模型4：

mod.uk04 <- arima(ts.gdp2r[,"uk"], order=c(1,0,1),
                  seasonal=list(order=c(1,0,1), frequency=4)); mod.uk04

## 
## Call:
## arima(x = ts.gdp2r[, "uk"], order = c(1, 0, 1), seasonal = list(order = c(1, 
##     0, 1), frequency = 4))
## 
## Coefficients:
##          ar1      ma1    sar1     sma1  intercept
##       0.8585  -0.3906  0.6290  -0.8050     0.5044
## s.e.  0.0791   0.1259  0.1735   0.1228     0.1231
## 
## sigma^2 estimated as 0.3144:  log likelihood = -105.5,  aic = 223.01

第4个模型是一个较好（从AIC看）的模型。对其进行残差诊断：

tsdiag(mod.uk04)

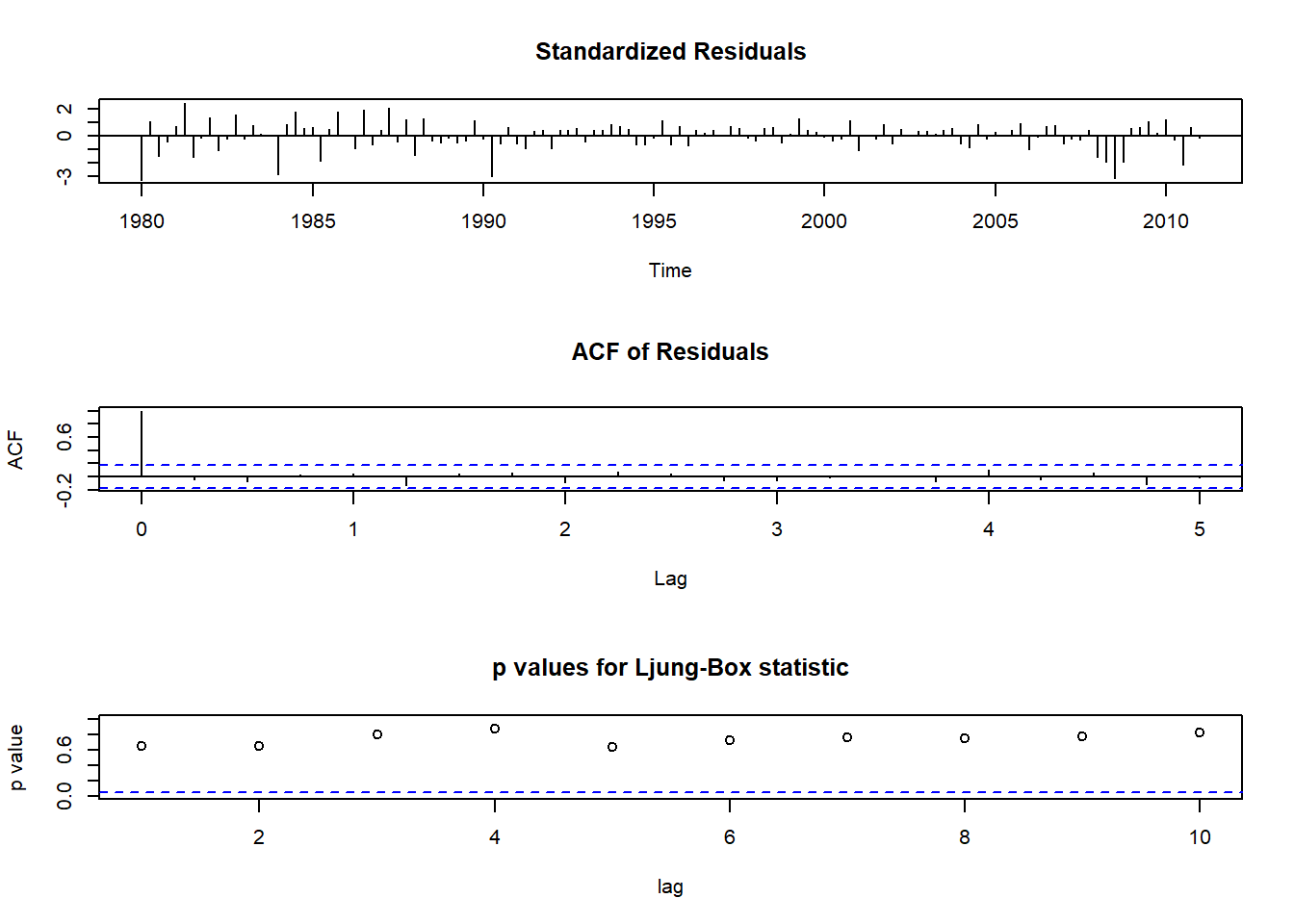
残差诊断通过。

对美国的GDP季度对数增长率建模，用类似模型：

mod.us01 <- arima(ts.gdp2r[,"us"], order=c(1,0,0)); mod.us01

## 
## Call:
## arima(x = ts.gdp2r[, "us"], order = c(1, 0, 0))
## 
## Coefficients:
##          ar1  intercept
##       0.4728     0.6259
## s.e.  0.0833     0.1180
## 
## sigma^2 estimated as 0.4887:  log likelihood = -132.74,  aic = 271.48

tsdiag(mod.us01)

残差的白噪声检验可以通过。

求两个模型的残差的互相关系数：

ccfv <- ccf(mod.uk04$residuals, mod.us01$residuals, plot=FALSE)
ccfv

## 
## Autocorrelations of series 'X', by lag
## 
##  -4.25  -4.00  -3.75  -3.50  -3.25  -3.00  -2.75  -2.50  -2.25  -2.00  -1.75 
##  0.102 -0.057  0.011 -0.061 -0.067 -0.137 -0.007  0.134 -0.030  0.013  0.074 
##  -1.50  -1.25  -1.00  -0.75  -0.50  -0.25   0.00   0.25   0.50   0.75   1.00 
##  0.076 -0.101  0.104  0.020 -0.111  0.294  0.278  0.048  0.044  0.239 -0.223 
##   1.25   1.50   1.75   2.00   2.25   2.50   2.75   3.00   3.25   3.50   3.75 
## -0.036  0.038  0.001  0.023  0.102  0.115 -0.118  0.069 -0.114 -0.046  0.112 
##   4.00   4.25 
##  0.016  0.033

R的ccf(x, y)在滞后\(k\)处计算\(\rho(x_{t+k}, y_k)\)，但是上面结果中的显示滞后阶数是除以频率的结果，单位是年，乘以4才是实际滞后阶数。

取\(k_1=-4, k_2=4\)，计算卡方统计量和p值：

stat <- ccfv$n.used * sum((ccfv$acf[
  4*ccfv$lag >= -4 - 1E-8 & 4*ccfv$lag <= 4 + 1E-8])^2)
pvalue <- 1 - pchisq(stat, df=9)
c(stat=stat, pvalue=pvalue)

##         stat       pvalue 
## 3.727209e+01 2.353255e-05

结果显著，说明存单向、反馈或者瞬时的因果性。

取\(k_1=1\), \(k_2=4\):

stat <- ccfv$n.used * sum((ccfv$acf[
  4*ccfv$lag >= 1 - 1E-8 & 4*ccfv$lag <= 4 + 1E-8])^2)
pvalue <- 1 - pchisq(stat, df=4)
c(stat=stat, pvalue=pvalue)

##         stat       pvalue 
## 13.912630659  0.007579187

结果显著，说明美国对英国有因果性影响。

反过来检验，取\(k_1=-4\), \(k_2=-1\):

stat <- ccfv$n.used * sum((ccfv$acf[
  4*ccfv$lag >= -4 - 1E-8 & 4*ccfv$lag <= -1 + 1E-8])^2)
pvalue <- 1 - pchisq(stat, df=4)
c(stat=stat, pvalue=pvalue)

##         stat       pvalue 
## 13.712136383  0.008272803

结果显著，说明英国对美国有因果性影响。

检验有无瞬时因果性：

stat <- ccfv$n.used * sum((ccfv$acf[
  4*ccfv$lag >= - 1E-8 & 4*ccfv$lag <= 1E-8])^2)
pvalue <- 1 - pchisq(stat, df=1)
c(stat=stat, pvalue=pvalue)

##        stat      pvalue 
## 9.647319356 0.001896281

结果显著，英国和美国有瞬时因果性。

○○○○○

26.6.3 Hsiao方法

原始文献：

CHENG HSIAO(1979), Autoregressive Modeling of Canadian Money and Income Data, Journal of the American Statistical Association 74, pp. 553-560.
ARNOLD ZELLNER(1962), An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias, Journal of the American Statistical Association 57, pp. 348-368.

Hsiao(1979)对直接格兰格方法进行了改进，给出了滞后项数的选取方法，步骤如下：

对\(y_t\)定阶估计一元的AR(\(k_1^*\))模型。
在对\(y_t\)的预测中加入\(x_t\)的滞后项，求出最优的滞后项数\(k_2^*\)。
固定\(k_2^*\)的值，求\(y_t\)的滞后项数的最优值\(\bar k_1^*\)。
比较第3步和第1步的模型，如果第3步AIC值优于第1步，则认为\(x_t\)对\(y_t\)有因果作用，选用第3步的模型，否则选用第1步的模型。如此得到预报\(y_t\)的初步的模型。
交换\(x_t\)和\(y_t\)的地位重复第1-4步，获得预报\(x_t\)的初步的模型。
将预测\(y_t\)的模型和预测\(x_t\)的模型联立估计，允许其随机误差项有相关性，方法采用Zellner(1962)提出的表面不相关回归(SUR)方法。

注意第4、5步就可以得到因果性的结论，第6步是为了得到更精确的预测模型。

26.7 多元情形下的因果性检验

在最原始的(C. W. J. Granger 1969)文章中定义因果性时，要求考虑到所有的到时刻\(t\)为止的信息。在仅有两个序列，考虑其相互的因果性时，如果没有其它的序列对其有影响，因果性检验的结果是可信的；如果有其他序列会有影响，因果性检验的结果可能是虚假的因果性或者虚假的无因果性。

这里考虑多个时间序列的因果性关系的检验问题。

26.7.1 直接格兰格方法

适用于二元时间序列的Haugh-Pierce方法用到两个序列之间的互相关函数，如果有三个序列，就无法计算三个序列整体的互相关，所有Haugh-Pierce方法无法推广到多于两个分量的情形。但是，仍可以利用格兰格的因果性定义来检验。在预报\(y_t\)时，如果扣除分量\(x_t\)的历史值的信息后预报误差比利用所有历史信息的预报误差显著增大，就说明\(x_t\)是\(y_t\)的格兰格原因；如果扣除若干个分量后预测误差显著增大，就说明这些分量联合起来是\(y_t\)的格兰格原因。

例如，三个序列\(x_t, y_t, z_t\)，选取适当滞后项数\(k_1\), \(k_2\), \(k_3\)，用普通最小二乘建立回归方程

\[\begin{aligned} y_t =& \beta_0 + \sum_{k=1}^{k_1} \beta_{1k} y_{t-k} + \sum_{k=1}^{k_2} \beta_{2k} x_{t-k} + \sum_{k=1}^{k_3} \beta_{3k} z_{t-k} \end{aligned}\] 则零假设 \(H_0: \beta_{21} = \dots = \beta_{2 k_2}=0\)表示\(x_t\)不是\(y_t\)的格兰格原因；零假设\(H_0: \beta_{31} = \dots = \beta_{2 k_3}=0\)表示\(z_t\)不是\(y_t\)的格兰格原因；零假设 \(H_0: \beta_{21} = \dots = \beta_{2 k_2} = \beta_{31} = \dots = \beta_{2 k_3}=0\) 表示\((x_t, z_t)\)不是\(y_t\)的格兰格原因；

可以分别建立全集模型、简约模型并用R的anova()函数比较两个模型，如果有显著差异，则说明是格兰格原因，否则不是。

这样的直接格兰格方法可以用Hsiao方法进行改进，给出滞后项数的取法和步骤。

26.7.2 缺少第三个变量的影响

设对两个变量\(x_t, y_t\)做了因果性检验，但是有可能有第三个变量\(z_t\)对其有影响。会有怎样的影响？

仅使用\(x_t, y_t\)作的瞬时因果检验可能是真实的，也可能是虚假的，只有用完全模型才能确定。
如果仅使用\(x_t, y_t\)作的因果性检验结果是反馈关系，加入\(z_t\)之后可能变成单向的因果性。
如果仅使用\(x_t, y_t\)作的因果性检验结果是单向关系，则加入\(z_t\)一般不变。以上三条见GEBHARD KIRCHGÄSSNER (1981)。
如果\(x_t, y_t\)没有因果关系，但都依赖于\(z_t\)，仅使用作\(x_t, y_t\)的因果性检验结果可能有虚假的因果性。见CHRISTOPHER A. SIMS (1977)文章。

总之，两变量的因果性检验如果结果是单向的因果性，结果相对可信；如果是反馈关系，有可能是虚假的。但是，多数情况下这种由于缺失重要变量或者测量误差引起的虚假反馈因果关系是比较弱的，也有可能会反映成单向；单向因果关系是承认\(H_0\)得到的，而承认\(H_0\)具有不可控制的第二类错误概率。所以因果性检验结果要慎重对待。

参考：

GEBHARD KIRCHGÄSSNER(1981), Einige neuere statistische Verfahren zur Erfassung kausaler Beziehungen zwischen Zeitreihen, Darstellung und Kritik, Vandenhoeck und Ruprecht, Göttingen
CHRISTOPHER A. SIMS(1977), Exogeneity and Causal Ordering in Macroeconomic Models, in: FEDERAL RESERVE BANK OF MINNEAPOLIS (ed.), New Methods in Business Cycle Research: Proceedings from a Conference, Minneapolis, pp. 23-44.

B 参考文献

Gebhard Kirchgässner, Uwe Hassler, Jürgen Wolters. 2013. Introduction to Modern Time Series Analysis. Springer.

Granger, C. W. J. 1969. “Investigating Causal Relations by Econometric Models and Cross-Spectral Methods.” Econometrica, no. 37: 424–38.

Granger, Clive W. J., and Paul Newbold. 1974. “Spurious Regressions in Econometrics.” Journal of Econometrics 2: 111–20.

Schwert, G. William. 1979. “Tests of Causality: The Message in the Innovations.” In Three Aspects of Policy and Policymaking: Knowledge, Data, and Institutions, Carnegie-Rochester Conference Series on Public Policy, Band 10, edited by K. Brunner and A. H. Meltzer, 55–96. North-Holland, Amsterdam.

Sims, Christopher A. 1972. “Money, Income, and Causality.” American Economic Review 62: 540–52.