Pingwen Zhang

Professor of Wuhan Univeristy and Peking University

Biography

Academician of Chinese Academy of Sciences
Fellow of The World Academy of Sciences(TWAS) for the advancement of science in developing countries
President of Wuhan University
Professor of Wuhan University
Boya Chair Professor of Peking University
Director of National Engineering Laboratory for Big Data Analysis and Applications
President of China Society for Industry and Applied Mathematics (CSIAM)
Fellow of Society for Industrial and Applied Mathematics (SIAM)
Vice President of the 11th Council of the Chinese Institute of Electronics

Download Resume

Research Interests

Modeling and Simulation of Soft Matter (Complex Fluids)
Applied Analysis And Numerical Analysis
Big Data Analysis and Applications

Education

Ph.D. in School of Mathematical Sciences, 1992

Peking University
B.S. in School of Mathematical Sciences, 1988

Peking University

Honors

Science and Technology Progress Award by Ho Leung Ho Lee Foundation (2021)
Fellow of China Society for Industrial and Applied Mathematics (2020)
Fellow of Society for Industrial and Applied Mathematics (2020)
Fellow of The World Academy of Sciences for the advancement of science in developing countries (2016)
Academician of Chinese Academy of Sciences (2015)
National Prize of Natural Sciences (Second-prize)(2014)
Academic leader of Science Fund for creative research groups of the National Natural Science Foundation of China (2014)
The First Prize of Natural Science Award of the Ministry of Education (2007)
National Science Foundation for Distinguished Young Scholars (2002)
Changjiang distinguished professor (2002)
Feng Kang Prize of Scientific Computing (1999)
Invited Speaker, 2018 International Congress of Mathematicians (ICM2018)
Invited Speaker, 2014 SIAM Annual Meeting (SIAM2014)
Invited Speaker, 7th International Congress on Industrial & Applied Mathematics (ICIAM 2011)
Chair of Sub-Committee of Academic, 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015)
President of China Society for Industry and Applied Mathematics (CSIAM)
Vice President (2002-2006, 2010-2014), China Society for Computational Mathematics (CSCM)

Selected Publications

Wei Si, Shifeng Li, Pingwen Zhang, An-Chang Shi, Kai Jiang

April 2025 PHYSICAL REVIEW RESEARCH

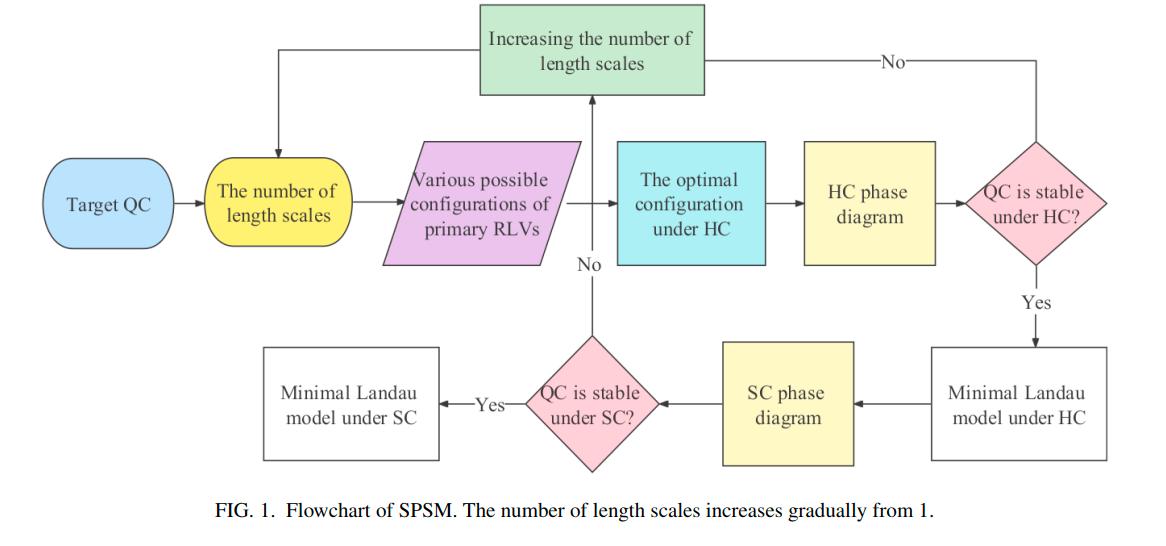
Designing a minimal Landau model to stabilize desired quasicrystals

Interparticle interactions with multiple length scales play a pivotal role in the formation and stability of quasicrystals. Choosing a minimal set of length scales to stabilize a given quasicrystal is a challenging problem. To address this challenge, we propose a symmetry-preserving screening method (SPSM) to design a Landau theory with a minimal number of length scales-referred to as the minimal Landau theory-that includes only the essential length scales necessary to stabilize quasicrystals. Based on a generalized multiple-length-scale Landau theory, SPSM first evaluates various spectral configurations of candidate structures under a hard constraint. It then identifies the configuration with the lowest free energy. Using this optimal configuration, SPSM calculates phase diagrams to explore the thermodynamic stability of desired quasicrystals. SPSM can design a minimal Landau theory capable of stabilizing the desired quasicrystals by incrementally increasing the number of length scales. Our application of SPSM has not only confirmed known behaviors in 10-and 12-fold quasicrystals but also led to a significant prediction that quasicrystals with 8-, 14-, 16-, and 18-fold symmetry could be stable within three-length-scale Landau models.

Xin Wang, An-Chang Shi, Pingwen Zhang, Kai Jiang

January 2025 Macromolecules

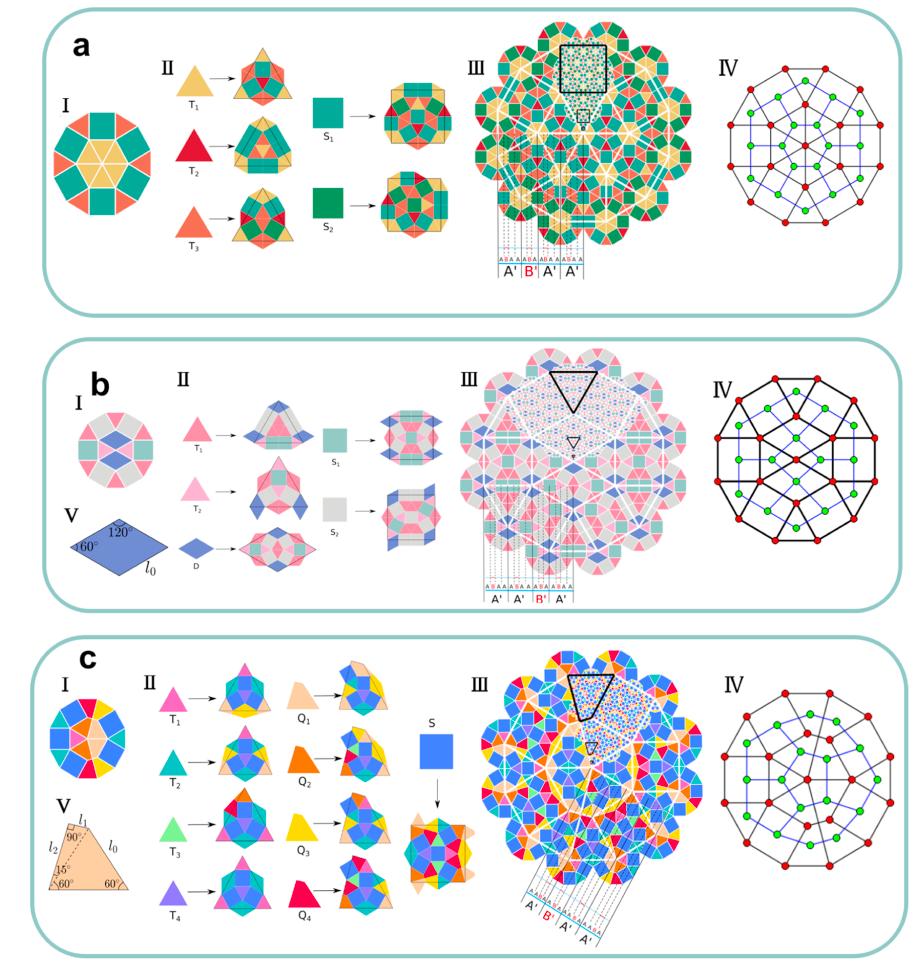
Stability of Diverse Dodecagonal Quasicrystals in T-Shaped Liquid Crystalline Molecules

Quasicrystals are intriguing ordered structures characterized by quasiperiodic translational and noncrystallographic rotational symmetry. The tiling of different geometric units such as triangles and squares in two-dimensional space can result in a great variety of quasicrystals that could be realized by the self-assembly of liquid crystalline molecules. In this study, we introduce three self-similar dodecagonal tilings, including a novel diamond–square–triangle pattern, composed of triangular and quadrangular tiles, and examine their thermodynamic stability by using the self-consistent field theory applied to T-shaped liquid crystalline molecules. Specifically, we detail the inflation rules for the construction of these dodecagonal tilings, analyze their self-similarity, and show that these tilings can be viewed as projections of higher-dimensional periodic lattice points with projection windows. Using these dodecagonal tilings as initial configurations of the SCFT results in solutions corresponding to quasicrystals that could form from T-shaped liquid crystalline molecules. The relative stability of these aperiodic phases is analyzed to obtain design rules that could stabilize quasicrystals. Meanwhile, we provide a criterion for distinguishing three dodecagonal quasicrystals and their approximants by analyzing their diffraction peaks. These findings shed new light on the discovery of new quasicrystals in soft materials.

Lei Zhang, Pingwen Zhang, Xiangcheng Zheng

January 2025 COMMUNICATIONS IN MATHEMATICAL SCIENCES

UNDERSTANDING HIGH-INDEX SADDLE DYNAMICS VIA NUMERICAL ANALYSIS

High-index saddle dynamics (HiSD) serves as a competitive instrument in searching the any-index saddle points and constructing the solution landscape of complex systems. The Lagrangian multiplier terms in HiSD ensure the Stiefel manifold constraint, which, however, are dropped in the commonly-used discrete HiSD scheme and are replaced by an additional Gram-Schmidt orthonormalization. Though this scheme has been successfully applied in various fields, it is still unclear why the above modification does not affect its effectiveness. We recover the same form as HiSD from this scheme, which not only leads to error estimates naturally, but indicates that the mechanism of Stiefel manifold preservation by Lagrangian multiplier terms in HiSD is nearly a Gram-Schmidt process (such that the above modification is appropriate). The developed methods are further extended to analyze the more complicated constrained HiSD on high-dimensional sphere, which reveals more mechanisms of the constrained HiSD in preserving several manifold properties.

Kai Jiang, Xueyang Li, Yao Ma, Juan Zhang, Pingwen Zhang, Qi Zhou

January 2025 SIAM JOURNAL ON NUMERICAL ANALYSIS

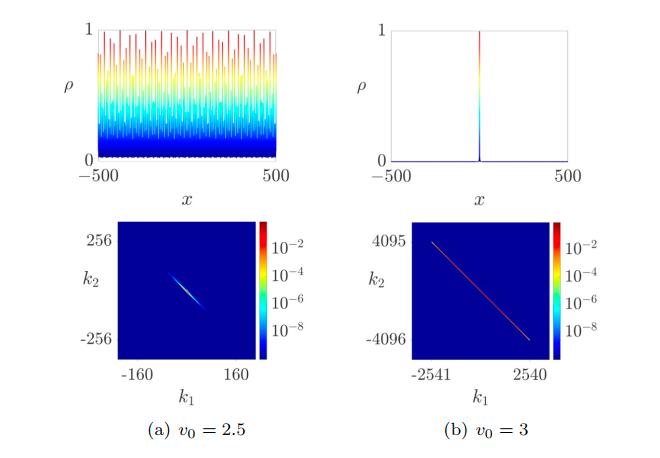
IRRATIONAL-WINDOW-FILTER PROJECTION METHOD AND APPLICATION TO QUASIPERIODIC SCHRODINGER EIGENPROBLEMS

In this paper, we propose a new algorithm, the irrational-window-filter projection method (IWFPM), for quasiperiodic systems with concentrated spectral point distribution. Based on the projection method (PM), IWFPM filters out dominant spectral points by defining an irrational window and uses a corresponding index-shift transform to make the FFT available. The error analysis on the function approximation level is also given. We apply IWFPM to one-dimensional, two-dimensional (2D), and three-dimensional (3D) quasiperiodic Schro'‘textbackslashdinger eigenproblems (QSEs) to demonstrate its accuracy and efficiency. IWFPM exhibits a significant computational advantage over PM for both extended and localized quantum states. More importantly, by using IWFPM, the existence of Anderson localization in 2D and 3D QSEs is numerically verified.

Lei Zhang, Pingwen Zhang, Xiangcheng Zheng

January 2022 SIAM Journal on Numerical Analysis

Error estimates for euler discretization of high-index saddle dynamics

High-index saddle dynamics provide an effective means to compute the any-index saddle points and construct the solution landscape. In this paper, we prove error estimates for Euler discretization of high-index saddle dynamics with respect to the time step size, which remains untreated in the literature. We overcome the main difficulties that lie in the strong nonlinearity of the saddle dynamics and the orthonormalization procedure in the numerical scheme that is uncommon in standard discretization of differential equations. The derived methods are further extended to study the generalized high-index saddle dynamics for nongradient systems and provide theoretical support for the accuracy of numerical implementations.

See all publications

Recent Publications

Zhuoyuan Li, Bin Dong, Pingwen Zhang (2025). State-observation augmented diffusion model for nonlinear assimilation with unknown dynamics. Journal of Computational Physics.

PDF DOI

Shuai Miao, Lei Zhang, Pingwen Zhang, Xiangcheng Zheng (2025). Construction and analysis for orthonormalized Runge-Kutta schemes of high-index saddle dynamics. COMMUNICATIONS IN NONLINEAR SCIENCE AND NUMERICAL SIMULATION.

PDF DOI

Dawei Wu, Baoming Shi, Yucen Han, Pingwen Zhang, Apala Majumdar, Lei Zhang (2025). A diffuse-interface Landau-de Gennes model for free-boundary problems in the theory of nematic liquid crystals. SIAM Journal on Mathematical Analysis.

PDF

Shuai Miao, Ziqi Liu, Lei Zhang, Pingwen Zhang, Xiangcheng Zheng (2025). Construction and analysis for Adams explicit discretization of high-index saddle dynamics. CSIAM Transactions on Applied Mathematics.

PDF

Yuling Jiao, Ruoxuan Li, Peiying Wu, Jerry Zhijian Yang, Pingwen Zhang (2025). DRM Revisited: A Complete Error Analysis. JOURNAL OF MACHINE LEARNING RESEARCH.

PDF

See all publications

Editors

2020 - CSIAM Transactions on Applied Mathematics (Editor in Chief)

2014 - Multiscale Modeling & Simulation, A SIAM Interdisciplinary Journal

2013 - Science China Mathematics

2012 - Discrete and Continuous Dynamical System-B

2011 - Journal of Mathematics in Industry (Coordinating Editors)

2010 - Applied Mathematics and Mechanics;(Associate Chief Editor Since 2014)

2007 - Journal of Computational Mathematics

2006 - Communications in Computational Physics

2006 - International Journal of Nonlinear Science

2005 - Communication in Mathematical Sciences

2005 - Journal of Information and Computational Science

2005 - 2013 SIAM Journal on Numerical Analysis

2002 - Applied Mathematical Research Express (AMRX)

2010 - Advances in Mathematics

2007 - Journal of Engineering Mathematics (China)

2006 - Journal of Mathematics (China)

2004 - Journal of Computational Mathematics (China)

2004 - Journal of Computational Physics (China)

2004 - Northeast Mathematical Journal (China)

Current Ph.D Students

Zhiyi Zhang

2021-

Dawei Wu

2022-

Suining Xiong

2023-

Quasicrystals; AI for mathematics

Yuyang Liu

2024-

Machine Learning;Algorithms for Solution Landscape

Wenhao Zhong

2025-

machine learning for cell-cell communication

Current Post-Doc

Leyi Wang

2023-

machine learning application in numerical model parameterization

Qihao Chen

2024-

Financial Econometrics;Volatility Modeling and Forecasting

Tianpei Cheng

2024-

Large-Scale Parallel Computing

Bing Han

2025-

Spatio-temporal reasoning;Low-altitude economy

Graduated Ph.D Students

Jun Xu

1996-1999 co-supervised with Prof. Zhenhuan Teng

Level set method

Tiejun Li

1998-2001 co-supervised with Prof. Zhenhuan Teng

Stochastic analysis and simulation stochastic modeling of complex fluids

Ruo Li

1998-2001 co-supervised with Prof. Zhenhuan Teng

Moving mesh methods based harmonic mapping and applications

Tiao Lu

2001-2004 co-supervised with Long-an Ying

High order numerical methods for Maxwell equations in dispersive media and applications

Yana Di

2000-2005

Computational fluid dynamics adaptive method

Haiyan Jiang

2002-2006

Mathematical theory of non-equilibrium Green function in MOSFET

Xia Ji

2001-2006

Numerical method for electromagnetic problem

Dan Hu

2002-2007 co-supervised with Prof. Weinan E

Dynamic modeling and simulation of fluid bio-membranes

Haijun Yu

2002-2007

Kinetic modeling and numerical simulation of liquid crystalline polymers

Dongzhuo Zhou

2002-2007 co-supervised with Prof. Weinan E

Viscoelastic phase separation in complex fluids modeling and numerical simulation

Yan Ding

2001-2007 co-supervised with Prof.Tiejun Li

Applications and algorithms of SDEs

Congmin Wu

2001-2007

Molecular dynamics simulation of nematic liquid crystals

Peng Song

2003-2008

Numerical simulations of fluid membranes

Guoxian Chen

2004-2008 co-supervised with Prof. Huazhong Tang

Adaptive unstructure moving mesh method and its application in CFD

Lingyun Zhang

2004-2008

Theoretical analysis to some kinetic models for complex fluids

Xinwei Zhang

2003-2008

Numerical simulation for the copolymer system based on mean field theory

He Wei

2003-2008

Modeling and simulations for dislocations in crystals in the framework of Peierls-Nabarro model.

Duan Wang

2004-2009 co-supervised with Prof. Ruo Li

Anisotropic adaptive refinement algorithm

Jiwei Jia

2005-2010 co-supervised with Prof. Jinchao Xu

On the adaptivity of the semi_Lagrangian methods

Kai Jiang

Xiangtan University 2006-2011 co-supervised with Prof. Yunqing Huang

Viscoelastic phase separation in complex fluids modeling and numerical simulation

Han Wang

2006-2011

Molecular dynamics simulation of liquid water Moment closure approximation of FENE dumbell model

Wei Zhang

2006-2011

Monte Carlo method in semiconductor device simulation

Kun Li

2006-2011 co-supervised with Prof. Jinchao Xu

Moment closure approximation of FENE dumbell model

Jianzhen Qian

2007-2011

Mathematical theory of complex fluids and computational methods

Yang Qu

2009-2012

Qin Liang

2008-2012

Numerical simulations on phase behaviors of semiflexible block copolymers

Jian Deng

2007-2012

Computational fluid dynamics and adaptive method

Wei Wang

2007-2013

Theoretical Analysis of Complex Fluids

Weiquan Xu

2008-2013

Numerical simulation for the copolymer system based on mean field theory

Hao Zhang

2009-2014

Theoretical and numerical study of dynamic phase transition.

Haozhe Tang

2009-2014

Shuonan Wu

2009-2014

Computational fluid dynamics and adaptive method

Jie Xu

2010-2015

Sirui Li

2010-2015

Numerical Study of Block Copolymers Based on SCFT

Shiwei Ye

2011-2016

Numerical simulation of liquid crystal dynamics

Jinglong Zhu

2012-2017

Molecular Dynamics

Yi Mo

2012-2018 co-supervised with Prof. Yunqing Huang

Yiwei Wang

2013-2018

Numerical Simulation of Liquid Crystals

Yongqiang Cai

2013-2018

Xianzhong Ma

2014-2019

Multiscale modeling and simulation

Zichao Long

2015-2020

Chen Yu

2016-2021

Jianyuan Yin

2017-2021

Multiscale modeling and simulation

Tian Tian

2015-2021

Chuansai Zhou

2018-2023

Nan Jiang

2020-2023

Data governance and application;Enterprise digital transformation

Zhuoyuan Li

2020-2025

Graduated Master Students

Zhiwu Lin

1995-1997

Partial differential equations

Xiaoming Zheng

1996-1999

Numerical studies of 2D free surface waves with fixed bottom

Ao Jiang

1998-2000 co-supervised with Prof. Zhenhuan Teng

Inversion of soil parameters from apparent resistivity in a multilayer earth structure

Zhengfu Xu

1997-2000

Boundary integral method for water wave problem

Zhijian Yang

1999-2001

A mathematical model of soil moisture spatial distribution on the hill slopes of the Loess Plateau

Jinjun Xu

1998-2001

Grounding resistance of buried electrodes in multilayer earth

Yi Sun

1999-2002

Multi-scale methods for inverse modeling in 1-D MOS capacitor

Chong Luo

2000-2003

Numerical simulation of liquid crystal polymers under shear flow

Liangda Huang

2000-2003 co-supervised with Prof. Weinan E

Bingham closure of liquid crystalline polymers

Xiang Zhou

2001-2004 co-supervised with Prof. Weinan E

Analysis of 1+1 dimensional stochastic models of liquid crystal polymer flows

Shouzheng Liu

2001-2004

Mathematical modeling of macrosegregation in the solidification process of binary alloys

Wurigen Bo

2001-2004

Finite element method of spherical shallow water equations

Na Zhou

2002-2005 co-supervised with Prof. Weinan E

Dynamical simulation of liquid crystal polymer flows

Ling Lin

2004-2007

Numerical study of nucleation of ordered phases

Xiangrui Meng

2005-2007

Moving mesh discontinuous Galerkin method for spherical shallow-water equations

Yibiao Wu

2004-2007

Multi-scale simulation of phase separation in polymer solution

Zhiling Ruan

2001-2007

Multiscale simulation of HMM

Jing Huang

2006-2009 co-supervised with Prof. Weinan E

Study the relation between birth-defect and chemical element content in Shanxi with the Institute of Population Research

Weiming Li

2008-2011

Modeling of smectic liquid crystals

Yuhui Jiang

2008-2011

Numerical study of nucleation of ordered phases

yi Luo

2011-2014

Modeling of Liquid Crystal

Hong Cheng

2011-2014

Modeling of Liquid Crystal

Renfei Gong

2012-2015

Xiaodian Kong

2014-2017

Zihan Lei

2015-2018

Fangyuan Liu

2016-2019

Wenjia Kong

2017-2020

Machine Learning

Fengwei Xu

2017-2020

Moment closure

Hening Feng

2017-2020

Machine Learning

Jun Wang

2018-2021

Data Science

Wen Yuan

2018-2021

Data Science

Jianxin Zhang

2018-2021

Lei Zhang

2020-2022

Digital Economy

Dong Xu

2019-2022

Numerical Optimization

Hongyi Shen

2019-2022

Data Science

Wenchao Zhang

2020-2022

Digital Economy

Yifan Yang

2019-2022

Machine Learning

Dingyu Wan

2020-2023

Data Science

Xuanang Li

2020-2023

Data Science

Yao Wang

2019-2023

Data Science

Mingjun Chen

2021-2024

big data analytics;machine learning;deep learning

Graduated Post-Doc

Hui Zhang

2001-2003

Mathematical theory of complex fluids

Daming Li

2002-2004

Numerical simulation of alloy solidification

Xin Zhang

2002-2004

Parallel computing and simulation

Yanze Peng

2002-2004

Exact solutions of mathematical physical equations

Lixin Feng

2003-2005

Inverse problem

Guanghua Ji

2004-2006

Multiscale modeling and simulation of the liquid crystalline polymers.

Long Wang

2004-2006

Parallel computing

Yinchuan Zhao

2006-2008

Partial differential equations

Yiran Zhang

2006-2008

The theory of adaptive finite element methods and application

Shanshan Jiang

2007-2009

Numerical analysis

Basang Tsering

2015-2017

Haochen Li

2016.07-2018.6

Computational Mathematics，Machine learning for Weather forecasts

Haiquan Fang

2017-2019

Artificial intelligence

Qiuqi Li

2018-2020

Uncertainty quantification

Qilong Zhai

2018-2020

Material science

Jianfeng Zhou

2019.07-2021.06

Fluid mechanics

Juan Wang

2019-2022

Digital Ecology Index

Jin Zhao

2020.07-2022

Machine Learning and Numerical solution of PDE

Ru Hou

2019-2022

Causal inference and machine learning

Xiangcheng Zheng

2021-2023

Algorithms and their analysis and applications in scientific computing

Angxiu Ni

2021-2023

Computational dynamical systems;numerical differentiation of chaos

Haoyang Liu

2021-2023

Numerical Software

Pengbo Xu

2021-2023

Molecular Dynamics Simulations and Deep Learning

Yingwen Guo

2019-2023

Numerical Solution of Partial Differential Equation，Computation and Simulation of Particle Fluid Dynamics

Yucong Wang

2021-2023

partial differential equations;stability of compressible gas stars

Tianyu Qiao

2021-2024

Digital Ecology Index;Computational Sociology

Wei Si

2022-2025

Modeling and computing of soft matter

Xiaofan Li

2023-2025

Dynamic Stochastic General Equilibrium Models; Data Market

Yunzhong Li

2023-2025

digital finance ;Corporate finance; risk and uncertainty

Courses

2021
- Discussion on Multiscale Physical Problems (00112510)
- Research Based Learning
2020
- Discussion on Multiscale Physical Problems (00112510)
- Big Data Modeling Method (00101819)
2019
- Discussion on Multiscale Physical Problems (00112510)
- Numerical Analysis (00130560)
2018
- Discussion on Multiscale Physical Problems (00112510)
- Numerical Analysis (00130560)
2017
- Discussion on Multiscale Physical Problems (00112510)
- Big Data Modeling Method (00101819)
2016
- Discussion on Multiscale Physical Problems (00112510)
- Research Based Learning
2015
- Discussion on Multiscale Physical Problems (00112510)
- Research Based Learning
2014
- Discussion on Multiscale Physical Problems (00112510)
- Multiscale Modeling and Computational Methods (00112690)
- Research Based Learning
2013
- Discussion on Multiscale Physical Problems (00112510)
- Research Based Learning
2012
- Discussion on Multiscale Physical Problems (00112510)
- Research Based Learning
2011
- Discussion on Multiscale Physical Problems (00112510)
- Multiscale Modeling and Computational Methods (00112690)
2010
- Discussion on Multiscale Physical Problems (00112510)
- Multiscale Modeling and Computational Methods (00112690)
2009
- Discussion on Multiscale Physical Problems (00112510)
- Multiscale Modeling and Computational Methods (00112690)
2008
- Discussion on Multiscale Physical Problems (00112510)
- Mathematical Theory of Inverse Problems (00112530)
- Finite Element Methods II (00111850)
2007
- Discussion on Multiscale Physical Problems (00112510)
- Mathematical Theory of Inverse Problems (00112530)
- Numerical Analysis (00130560)
2006
- Discussion on Multiscale Physical Problems (00112510)
- Computational Fluid Mechanics (00110820)
- Numerical Analysis (00130560)
2005
- Discussion on Multiscale Physical Problems (00112510)
- Mathematical Theory of Inverse Problems (00112530)
- Numerical Analysis (00130560)
2004
- Discussion on Multiscale Physical Problems (00112510)
- Applied PDE (00112780)
- Boundary Integral Methods (00113240)
2003
- Discussion on Multiscale Physical Problems (00112510)
- Mathematical Theory of Inverse Problems (00112530)
- Computational Methods B (00130280)
2002
- Discussion on Multiscale Physical Problems (00112510)
- Boundary Integral Methods (00113240)
2001
- Boundary Integral Methods (00113240)
- Introduction of Fluid Mechanics (00130640)
2000
- Fluid Mechanics II (00110770)
- Mathematical Theory of Inverse Problems (00112530)
- Computational Methods B (00130280)
1999
- Finite Element Methods II (00111850)
1997
- Numerical Algebra (00130550)

Contact

Ms. Ying Li

School of Mathematical Sciences, Peking University
Beijing, 100871, P. R. China
Phone: 86-10-62757147
Fax: 86-10-62757147
Email: yanyanli @ pku.edu.cn