17 Bootstrap方法(*)
17.1 标准误差
在统计建模中, 伴随着参数的估计值, 应该同时给出估计的“标准误差”。 设总体\(X \sim F(x, \theta)\), \(\theta \in \Theta\), \(\hat\phi\)是总体的一个参数\(\phi\)的估计量, 称\(\text{SE}=\sqrt{\text{Var}(\hat\phi)}\)为\(\hat\phi\)的标准误差。 实际工作中SE一般是未知的,SE的估计也称为\(\hat\phi\)的标准误差。 对有偏估计,除了标准误差外我们还希望能够估计偏差。 进一步地,我们还可能希望得到统计量\(\hat\phi\)的分布,称为抽样分布。
例17.1 设\(X_i, i=1,\ldots,n\) 是总体\(X \sim F(x)\)的样本, 样本平均值\(\hat\phi = \bar X = \frac{1}{n} \sum_i X_i\)为\(\phi=EX\)的点估计, \(\text{SE}(\bar X) = \sqrt{\text{Var}(X)/n}\), 可以用\(S / \sqrt{n}\)估计SE(\(S^2\)为样本方差)。 根据中心极限定理和强大数律,当样本量\(n\)较大时可以取\(EX\) 的近似95%置信区间为\(\bar X \pm 2 \,\text{SE}(\bar X)\)。
例17.2 线性模型参数估计的SE。
考虑线性模型中参数估计的精度。 设模型为 \[ \begin{aligned} \boldsymbol Y = \boldsymbol X \boldsymbol\beta + \boldsymbol\varepsilon, \end{aligned} \] 其中\(\boldsymbol\varepsilon \sim \text{N}(0,\sigma^2 I_n\)), \(\sigma^2\)未知, \(\boldsymbol\beta\)是未知系数向量, \(X\)是已知的\(n\times p\)数值矩阵, \(n > p\)。 在\(X\)列满秩时\(\boldsymbol\beta\)的最小二乘估计为\(\hat{\boldsymbol\beta} = (X^T X)^{-1} X^T \boldsymbol Y\), 而\(\hat{\boldsymbol\beta}\)的协方差阵为\(\text{Var}(\hat{\boldsymbol\beta}) = \sigma^2 (X^TX)^{-1}\)。 所以,第\(j\)个系数\(\beta_j\)的标准误差可估计为 \(\text{SE}(\hat\theta_j) = \hat\sigma \sqrt{a^{(jj)}}\), 其中\(\hat\sigma\)是\(\sigma\)的估计, \(a^{(ij)}\)为\((X^T X)^{-1}\)的\((i,j)\)元素。
例17.3 一维参数的信息阵与SE。
设总体\(X \sim p(x,\theta)\), \(\theta \in \Theta\), \(X_1, X_2, \dots, X_n\)为\(X\)的简单随机样本, \(\hat\theta\)是真值\(\theta\)的最大似然估计。 在适当正则性条件下,\(\hat\theta\)渐近正态分布, 渐近方差为\(\frac{1}{n}I^{-1}(\theta)\), \(I(\theta)\)为参数\(\theta\)的信息量(参见 (茆诗松, 王静龙, and 濮晓龙 2006) §2.5.2定理2.14): \[ \begin{aligned} I(\theta) = E \left[ \left(\frac{\partial \ln p(X, \theta)}{\partial \theta} \right)^2 \right] = \text{Var} \left(\frac{\partial \ln p(X, \theta)}{\partial \theta} \right) . \end{aligned} \] 在加强的条件下还有 \[ \begin{aligned} I(\theta) = -E\left(\frac{\partial^2 \ln p(X, \theta)} {\partial \theta^2} \right) . \end{aligned} \] 可以用\(\sqrt{I^{-1}(\hat\theta)/n}\)估计\(\hat\theta\)的SE。
例17.4 多维参数的信息阵与SE。
设总体\(X \sim p(x, \boldsymbol\theta)\), \(\boldsymbol\theta =(\theta_1, \ldots, \theta_m)\), 记 \[ \begin{aligned} \boldsymbol S(\theta) =& \nabla_{\boldsymbol\theta} \ln p(X, \boldsymbol\theta) = \left(\frac{\partial \ln p(X, \boldsymbol\theta)}{\partial \theta_1}, \ldots, \frac{\partial \ln p(X, \boldsymbol\theta)}{\partial \theta_m} \right)^T, \\ I(\theta) =& \text{Var}\left( \boldsymbol S(\theta) \right), \end{aligned} \] 称\(I(\theta)\)为信息量矩阵, 其\((i,j)\)元素为 \[ \begin{aligned} \text{Cov} \left( \frac{\partial \ln p(X, \boldsymbol\theta)}{\partial \theta_i}, \frac{\partial \ln p(X, \boldsymbol\theta)}{\partial \theta_j} \right) , \end{aligned} \] 在加强的条件下\(I(\theta) = -E(\nabla_{\boldsymbol\theta}^2 \ln p(X;\theta))\), \(\nabla_{\boldsymbol\theta}^2 \ln p(X;\theta)\)是\(\ln p(X, \boldsymbol\theta)\) 关于自变量\(\boldsymbol\theta\)的海色阵, 其\((i,j)\)元素为 \(\frac{\partial^2 \ln p(X, \boldsymbol\theta)}{\partial \theta_i \partial \theta_j}\)。 设\(X_1, X_2, \dots, X_n\)为\(X\)的简单随机样本, \(\hat{\boldsymbol\theta}\)为\(\boldsymbol\theta\)的最大似然估计, 在适当条件下\(\hat{\boldsymbol\theta}\)渐近正态分布\(N(\boldsymbol\theta, \frac{1}{n} I^{-1}(\boldsymbol\theta))\), 可以用\(-\frac{1}{n} [\nabla_{\boldsymbol\theta}^2 \ln p(X;\theta)]^{-1}\) 作为\(\text{Var}(\hat\theta)\)的估计。
17.2 Bootstrap方法的引入
计算参数估计的标准误差不一定总有简单的公式。 例如,需要估计的参数不一定是\(E X\)这样的简单特征, 像中位数、相关系数这样的参数估计的标准误差就比\(EX\)的估计的标准误差要困难得多。 在线性模型估计的例子中, 如果独立性、线性或者正态分布的假定不满足则求参数估计方差阵变得很困难, 比如稳健回归系数的标准误差就很难得到理论公式。 在最大似然估计问题中, 最大似然估计不一定总是渐近正态的, 信息量有时不存在或难以计算,从而无法用上面的方法给出标准误差。
设总体\(X\)服从某个未知分布\(F(x)\), \(\boldsymbol X = (x_1, x_2, \dots, x_n)\)是\(X\)的一个样本, \(\phi\)是\(F\)的一个参数, 可以把\(\phi\)看成\(F\)的一个泛函\(\phi(F)\), 用统计量\(\hat\phi = g(\boldsymbol X)\)估计\(\phi\), 设\(\psi = \psi(g, F, n)\)是统计量\(\hat\phi\)的某种分布特征(\(\hat\phi\)的抽样分布的数字特征)。 例如\(\psi = \sqrt{\text{Var}(\bar X)}\)为统计量\(\bar X\)的标准误差, 又如取\(\psi = E\hat\phi - \phi\)为统计量\(\hat\phi\)的偏差。 可以用随机模拟的方法估计\(\psi\)。
用随机模拟方法估计\(\psi\)的步骤如下。
- 从样本\(\boldsymbol X\)估计总体分布\(F\)为\(\hat F\);
- 从\(\hat F\)抽取\(B\)个独立样本\(\boldsymbol Y^{(b)}\), \(b=1, \ldots, B\), 每一个\(\boldsymbol Y^{(b)}\)样本量为\(n\), 称\(\boldsymbol Y^{(b)}\)为bootstrap样本。
- 从每个bootstrap样本\(\boldsymbol Y^{(b)}\)可以估计得到\(\hat\phi^{(b)} = g(\boldsymbol Y^{(b)})\), \(b=1,\ldots,B\)。
- \(\hat\phi^{(b)}, b=1,\ldots,B\)是\(g(\boldsymbol Y)\)在\(\hat F\)下的独立同分布样本, 可以用标准的估计方法估计关于\(g(\boldsymbol Y)\)在\(\hat F\)下的分布特征\(\hat\psi=\psi(g, \hat F, n)\), 估计结果记作\(\tilde\psi\),并以\(\tilde\psi\)作为统计量\(\hat\phi\)的抽样分布的数字特征\(\psi(g, F, n)\)的估计值。
从样本\(\boldsymbol X\)估计\(\hat F\)时,可以采用参数模型, 也可以采用经验分布函数\(F_n\)。 参数模型在模型正确时效率较高; 经验分布法使用简单,基本不依赖于模型。 从经验分布\(F_n\)抽样,相当于从\(\boldsymbol X = (x_1, \ldots, x_n)\)独立有放回抽样。
估计量的标准误差可以用bootstrap方法估计。
例17.5 设\((H,W)\)为某地小学五年级学生的身高和体重的总体,\((H,W) \sim F(\cdot,\cdot)\), 考虑\(H\)和\(W\)的相关系数\(\phi\)的估计量的标准误差估计。
设调查了\(n=10\)个学生的身高和体重的数据\((h_i, w_i), i=1,2,\dots,n\): \[ \begin{array}{*9c*9c} h_i & 144 & 166 & 163 & 143 & 152 & 169 & 130 & 159 & 160 & 175 \\ \hline w_i & 38 & 44 & 41 & 35 & 38 & 51 & 23 & 51 & 46 & 51 \end{array} \] 计算得\(\hat\phi = g(h_1,w_1, \ldots, h_{n},w_{n}) = 0.904\)。 令\(\text{SE}(\hat\phi) = \left[ \text{Var}(\hat\phi) \right]^{1/2} = \psi(g,F,n)\)。 设\(\hat F\)为\(F\)的估计,取为经验分布\(F_n\), 则bootstrap方法用随机模拟方法估计\(\psi(g, F_n, n)\), 然后当作\(\text{SE}(\hat\phi)\)的估计。 计算步骤如下:
- 从\(F_n\)中作\(n=10\)次独立抽样,即从\(\{(h_1, w_1), \ldots, (h_n,w_n) \}\) 中有放回独立抽取\(n\)次, 得到\(\hat F = F_n\)的一组样本\(\boldsymbol Y^{(1)} = ((h^{(1)}_1, w^{(1)}_1), \ldots, (h^{(1)}_n, w_n^{(1)}))\);
- 重复第(1)步, 直到获取了\(B\)组bootstrap样本\(\boldsymbol Y^{(b)}, b=1, \ldots, B\);
- 对每一样本\(\boldsymbol Y^{(b)}\)计算样本相关系数\(\hat\phi^{(b)} = g(\boldsymbol Y^{(b)})\), \(b=1,\ldots, B\);
- 把\(\hat\phi^{(b)}, b=1,\ldots,B\)作为\(\hat F\)下\(n=10\) 的样本相关系数的简单随机样本, 估计其样本标准差\(S\), 以\(S\)作为\(\psi(g,\hat F,n)\)的估计, 进而用\(S\)估计\(\hat\phi\)在真实的总体分布\(F\)下的标准误差\(\text{SE}(\hat\phi)\)。
此例非参数bootstrap用R语言直接编程实现:
rho.boot.npar <- function(B=1000, plot.samp=FALSE){
h <- c(144 , 166 , 163 , 143 , 152 , 169 , 130 , 159 , 160 , 175)
w <- c(38 , 44 , 41 , 35 , 38 , 51 , 23 , 51 , 46 , 51)
n <- length(h)
rho0 <- cor(h, w)
samp <- replicate(
B, {
ind <- sample.int(n, replace=TRUE)
cor(h[ind], w[ind]) } )
if(plot.samp) {
hist(samp, main="相关系数的非参数Bootstrap样本", xlab="")
abline(v=rho0, col="red")
}
sd(samp)
}
set.seed(1)
rho.boot.npar(B=1000, plot.samp=TRUE)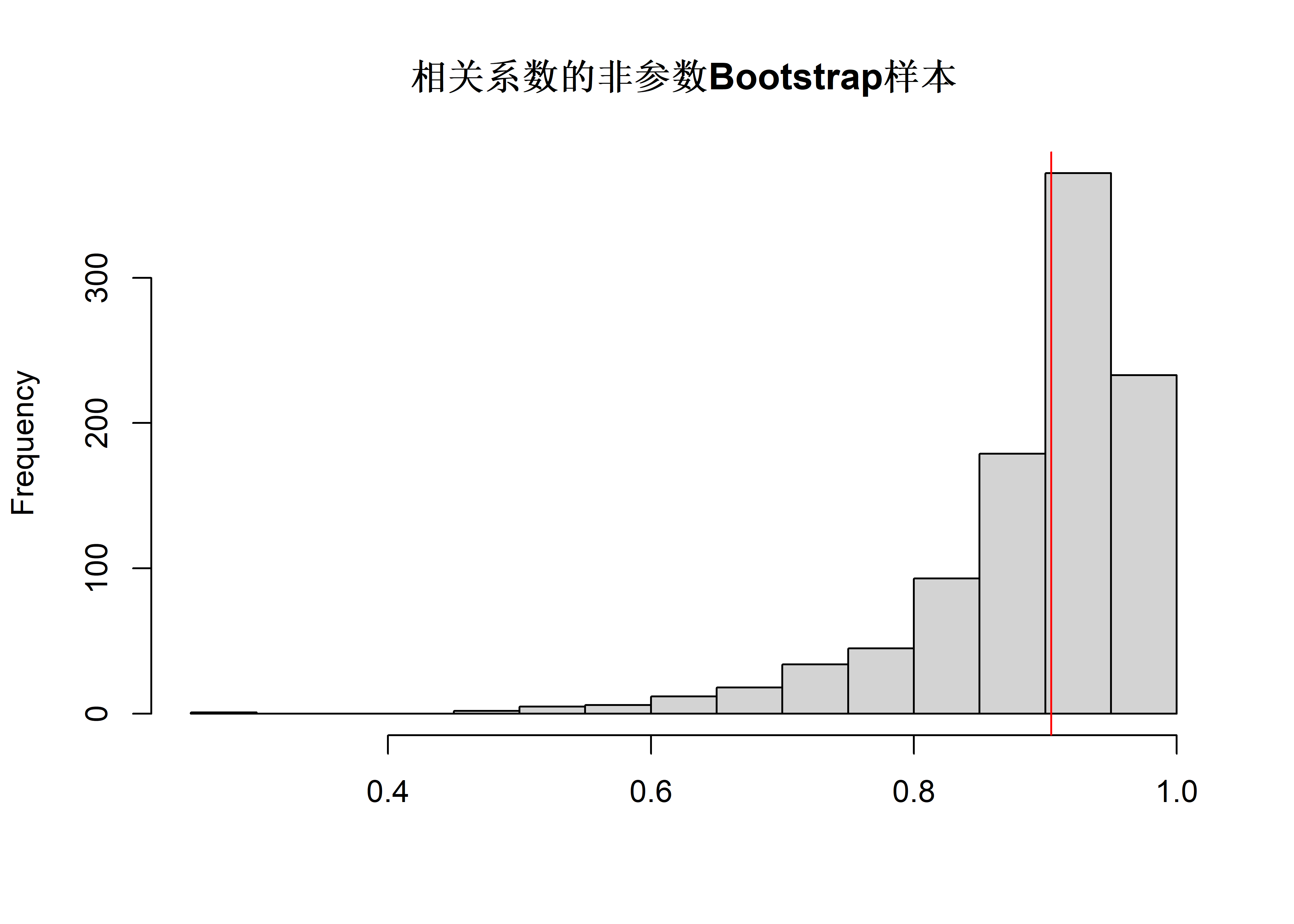
## [1] 0.08671312取\(B=1000\)的一次bootstrap计算得到的标准误差估计为\(S = 0.087\)。 当\(B \to \infty\)时\(S \to \psi(g, F_n, n)\), 但是要注意, 由于抽样误差影响, \(\psi(g, F_n, n)\)和\(\psi(g, F, n)\)之间的误差无法避免。
R中也提供了进行bootstrap估计的扩展包,
比如boot扩展包。
其中的boot()函数用来进行bootstrap估计,
默认使用非参数方法(随机有放回抽样方法)产生bootstrap样本,
需要输入原始数据,并输入一个用来计算统计量的函数,
此统计量函数以原始数据和某一次的有放回随机抽样下标向量为输入。
本例的相关系数的标准误差估计可以用如下程序计算:
da <- data.frame(
h = c(144, 166, 163, 143, 152, 169, 130, 159, 160, 175),
w = c(38, 44, 41, 35, 38, 51, 23, 51, 46, 51))
stat <- function(da, ind){
cor(da[[1]][ind], da[[2]][ind])
}
set.seed(1)
boot::boot(data = da, statistic = stat, R = 1000)
##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot::boot(data = da, statistic = stat, R = 1000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 0.9044803 -0.02006079 0.1094301估计的标准误差为0.100。
也可以用参数方法估计\(\hat F\), 比如从历史经验知道总体的身高、体重服从联合正态分布, 就可以按照联合正态总体模型从样本中得到参数最大似然估计后作为\(\hat F\)的参数, 这时\(\hat F\)是一个参数确定的二元联合正态分布N(\(156.1, 41.8, 13.78^2, 8.85^2, 0.904\))。 从\(\hat F\)中独立抽样\(n\)个得到一组样本,共生成\(B\)组这样的样本, 称为bootstrap样本。接下来的步骤只要按照上面的(3)、(4)估计\(\text{SE}(\hat\phi)\)就可以了。
参数bootstrap用R语言直接实现:
rho.boot.para <- function(B=1000, plot.samp=FALSE){
h <- c(144 , 166 , 163 , 143 , 152 , 169 , 130 , 159 , 160 , 175)
w <- c(38 , 44 , 41 , 35 , 38 , 51 , 23 , 51 , 46 , 51)
n <- length(h)
rho0 <- cor(h, w)
S1 <- var(h)
S2 <- var(w)
Sig <- rbind(c(S1^2, rho0*S1*S2), c(rho0*S1*S2, S2^2))
ch <- chol(Sig)
samp <- replicate(
B, {
xys <- matrix(rnorm(2*n), n, 2) %*% ch
cor(xys[,1], xys[,2]) } )
if(plot.samp) {
hist(samp, main="相关系数的参数Bootstrap样本", xlab="")
abline(v=rho0, col="red")
}
sd(samp)
}
set.seed(1)
rho.boot.para(B=1000, plot.samp=TRUE)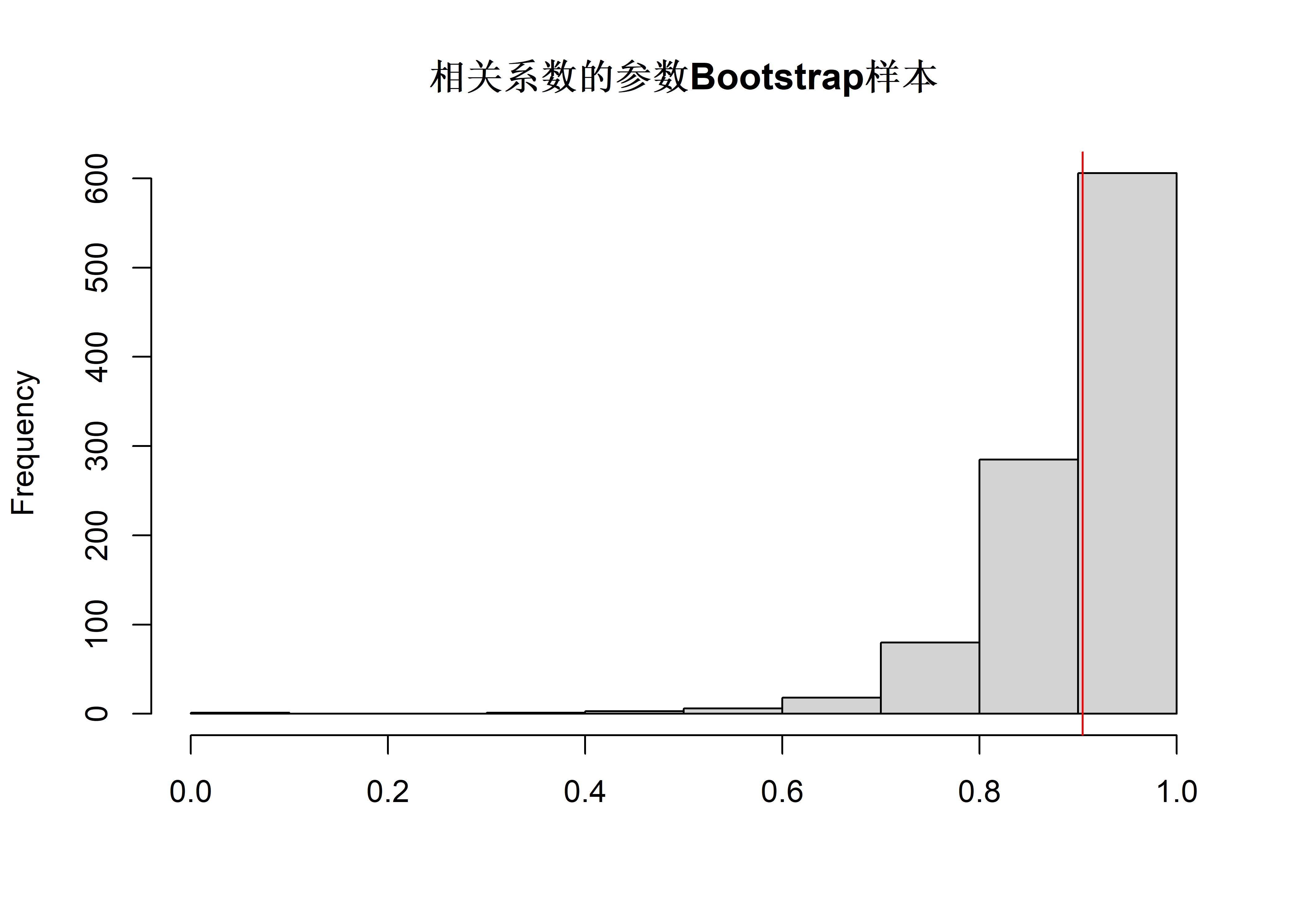
## [1] 0.08182779取\(B=1000\)的一次参数bootstrap计算得到的标准误差估计为\(0.082\)。
boot::boot()也支持参数bootstrap,
这时要加sim="parametric"选项,
还需要提供计算统计量的函数statistic,
此函数以模拟生成的数据为输入;
还需要提供一个用来从参数分布生成随机样本的函数ran.gen,
ran.gen()函数输入原始数据以及一个列表,
可以在列表中输入分布参数,
而这些分布参数用boot()函数的mle自变量提供。
例如:
get.pars <- function(da){
rho0 <- cor(da[[1]], da[[2]])
S1 <- var(da[[1]])
S2 <- var(da[[2]])
Sig <- rbind(c(S1^2, rho0*S1*S2), c(rho0*S1*S2, S2^2))
ch <- chol(Sig)
list(ch)
}
rg <- function(da, pars){
ch = pars[[1]]
n <- nrow(da)
xys <- matrix(rnorm(2*n), n, 2) %*% ch
xys
}
stat2 <- function(da){
cor(da[,1], da[,2])
}
set.seed(1)
boot::boot(data = da, sim = "parametric",
statistic = stat2,
ran.gen = rg,
mle = get.pars(da),
R=200)
##
## PARAMETRIC BOOTSTRAP
##
##
## Call:
## boot::boot(data = da, statistic = stat2, R = 200, sim = "parametric",
## ran.gen = rg, mle = get.pars(da))
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 0.9044803 -0.01153677 0.08888907也可以不提供ran.gen()参数,
而是在statistic函数中完成随机模拟,如:
stat3 <- function(da, pars){
n <- nrow(da)
ch <- pars[[1]]
xys <- matrix(rnorm(2*n), n, 2) %*% ch
cor(xys[,1], xys[,2])
}
set.seed(1)
boot::boot(data = da, sim = "parametric",
statistic = stat3,
R=200,
pars = get.pars(da))
##
## PARAMETRIC BOOTSTRAP
##
##
## Call:
## boot::boot(data = da, statistic = stat3, R = 200, sim = "parametric",
## pars = get.pars(da))
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 0.7842861 0.1095859 0.08871806这里利用了boot::boot()函数的...参数传送了模拟需要的pars列表。
※※※※※
例17.6 考虑回归模型系数估计的标准误差计算。 一般的回归模型可以写成 \[\begin{align} y_i = h(\boldsymbol x_i, \boldsymbol\beta) + \varepsilon_i, \quad i=1,2,\ldots,n \end{align}\] 其中\(h\)已知, \(\boldsymbol\beta\)是未知参数向量, \(\{\varepsilon_i\}\) iid \(F(x)\), \(F(x)\)未知, \(\{\boldsymbol x_i\}\)是确定数值向量。 可以用最小二乘等方法得到\(\boldsymbol\beta\)的估计\(\hat{\boldsymbol\beta} = g(y_1,\ldots,y_n)\), 希望估计参数估计的协方差阵\(\text{Var}(\hat{\boldsymbol\beta})\), 协方差阵主对角线元素的平方根就是单个系数估计的标准误差。
这个模型中,未知的分布信息包括\(\boldsymbol\beta\)和\(F\)。 \(\boldsymbol\beta\)可用\(\hat{\boldsymbol\beta}\)估计, \(F\)可以用回归残差的经验分布来估计或假设一个参数模型估计模型参数。
用bootstrap方法估计\(\text{Var}(\hat{\boldsymbol\beta})\)的步骤如下:
- 估计\(\boldsymbol\beta\)得到\(\hat{\boldsymbol\beta} = g(y_1, \dots, y_n)\);
- 计算残差\(e_i = y_i - h(\boldsymbol x_i, \hat{\boldsymbol\beta})\), \(i=1,\ldots,n\);
- 对\(b=1,\ldots,B\)重复: 从\(\{e_1,\ldots,e_n\}\)中有放回独立抽取\(n\)次得\(\{e_i^{(b)}, i=1,\ldots,n\}\);
- 令\(y_i^{(b)} = h(\boldsymbol x_i, \hat{\boldsymbol\beta}) + e_i^{(b)}\), \(i=1,\ldots,n\), \(b=1,2,\dots,B\);
- 对\(b=1,2,\dots,B\)重复: 从\((y_1^{(b)}, \dots, y_n^{(b)})\)中估计 \(\hat{\boldsymbol\beta}^{(b)} = g(y_1^{(b)}, \ldots, y_n^{(b)})\);
- 用\(\hat{\boldsymbol\beta}^{(b)},b=1,\ldots,B\) 的样本方差阵估计\(\text{Var}(\hat{\boldsymbol\beta})\)。
※※※※※
17.3 Bootstrap偏差校正
设\(\boldsymbol X=(x_1, x_2, \dots, x_n)\)为总体\(F(\cdot)\)的样本, 总体参数\(\phi = \phi(F)\)的估计为\(\hat\phi = g(\boldsymbol X)\), \(\beta = E \hat\phi - \phi\)为估计偏差, \(\text{Var}(\hat\phi)\)为估计方差, 估计的均方误差可以分解为 \[ \begin{aligned} E[\hat\phi - \phi]^2 = \text{Var}(\hat\phi) + \beta^2. \end{aligned} \]
如果\(\hat \beta\)是\(\beta\)的估计, 则参数\(\phi\)的一个改善的估计为\(\tilde\phi = \hat\phi - \hat \beta\), 新的估计在减小了偏差的同时一般也减小了均方误差。 设\(\beta = \psi(g, F, n)\), \(\hat F\)是总体分布\(F\)的一个估计, 这里\(\hat F\)取为经验分布\(F_n\), 则可以用\(\hat \beta = \psi(g, \hat F, n) = E g(\boldsymbol Y) - \hat\phi\)来估计偏差, 其中\(\boldsymbol Y\)是总体\(F_n\)的样本量为\(n\)的样本, \(\hat\phi\)恰好是总体分布为\(F_n\)时的参数\(\phi\), 即\(\hat\phi = \phi(F_n)\)。 如果\(\hat \beta\)不能通过理论公式计算, 可以用bootstrap方法估计\(\hat \beta\), 步骤如下:
- 从\(\{ x_1, x_2, \dots, x_n \}\)独立有放回地抽取\(n\)个,记为\(\boldsymbol Y^{(1)} = (Y_1^{(1)}, Y_2^{(1)}, \dots, Y_n^{(1)})\)。
- 重复第(1)步,直到获取了\(B\)组bootstrap样本\(\boldsymbol Y^{(b)}, b=1,2,\dots,B\);
- 从每个bootstrap样本\(\boldsymbol Y^{(b)}\)可以估计得到\(\hat\phi^{(b)} = g(\boldsymbol Y^{(b)})\), \(b=1,\ldots,B\)。
- 用\(\hat\phi^{(b)}, b=1,\ldots,B\)作为\(g(\boldsymbol Y)\)在\(F_n\)下的独立同分布样本,
估计\(\hat \beta = \psi(g, F_n, n)\)为\(\tilde \beta = \frac{1}{B} \sum_{b=1}^B \hat\phi^{(b)} - \hat\phi\)。
最后,取\(\tilde\phi = \hat\phi - \tilde b = 2 \hat\phi - \frac{1}{B} \sum_{b=1}^B \hat\phi^{(b)}\) 为参数\(\phi\)改善的估计。
例17.7 设\(X \sim \text{N}(\mu, \sigma^2)\), \(\mu, \sigma^2\)未知, \(x_1, x_2, \dots, x_n\)为\(X\)的样本。 考虑\(\phi = \mu^2\)的估计。
用最大似然估计法估计\(\phi\)为\(\hat\phi = \bar X^2\), 其中\(\bar X\)为样本平均值。 令\(Z = \sqrt{n}(\bar X - \mu)/\sigma\), 则\(Z \sim \text{N}(0,1)\)。 可以计算出估计偏差为 \[\begin{aligned} \beta =& E \bar X^2 - \mu^2 = E(\mu + \frac{\sigma}{\sqrt{n}} Z)^2 - \mu^2 = \frac{\sigma^2}{n}, \end{aligned}\] 估计的均方误差为 \[\begin{aligned} L_0 =& E( \bar X^2 - \mu^2 )^2 = E \left( \frac{2\sigma\mu}{\sqrt{n}} Z + \frac{\sigma^2}{n} Z^2 \right)^2 \nonumber\\ =& \frac{4 \sigma^2 \mu^2}{n} + \frac{3 \sigma^4}{n^2}. \end{aligned}\] 估计\(\beta\)为\(\hat \beta_1 = S^2/n\)(\(S^2\)为样本方差), 用\(\hat\phi_1 = \bar X^2 - \hat \beta_1 = \bar X^2 - \frac{S^2}{n}\)作为\(\mu^2\)的改善的估计, 则\(\hat\phi_1\)的均方误差比\(\hat\phi\)的均方误差减小了\(\frac{n-3}{n-1} \frac{\sigma^4}{n^2}\)。 (设\(n>3\))
※※※※※
如果模型更为复杂,比如,总体分布类型未知, \(\hat \beta_1\)这样的简单偏差估计很难得到, 这种情况下可以用bootstrap方法进行偏差校正, 步骤如下:
- 对\(b=1,2,\dots,B\)重复: 从\(x_1, x_2, \dots, x_n\)独立有放回地抽取\(n\)个, 组成bootstrap样本\(\boldsymbol Y^{(b)} = (y_1^{(b)}, \dots, y_n^{(b)})\);
- 对每个bootstrap样本计算\(\hat\phi^{(b)} = \left( \frac{1}{n} \sum_{i=1}^n y_i^{(b)} \right)^2\);
- 用\(\tilde\phi = 2 \bar X^2 - \frac{1}{B} \sum_{b=1}^B \hat\phi^{(b)}\)作为\(\mu^2\)的改善的估计。
R扩展包boot可以用来估计偏差,
例如例17.5中boot()函数的输出结果中包含了相关系数估计的偏差的估计。
Jacknife方法是另外一种对估计量的偏差和方差进行估计的方法, 这种方法不需要从原来的样本重新随机抽样, 而是把原来的\(n\)个样本点分为\(r\)份, 每次删去其中一份后计算统计量值, 利用\(r\)个这样的统计量值对估计量的偏差和方差进行估计。 详见(Gentle 2002) §3.3。
17.4 Bootstrap置信区间
枢轴量法是构造置信区间的最基本的方法。 设\(\phi\)是总体\(F(\cdot)\)的一个参数, 看成\(F\)的一个泛函\(\phi = \phi(F)\)。 \(\boldsymbol X = (x_1, x_2, \dots, x_n)\)为总体的样本, \(g(\boldsymbol X)\)为与\(\phi\)有关系的一个统计量, 经常是\(\phi\)的估计量。 如果有变换\(W = h(g(\boldsymbol X), \phi)\)使得\(W\)的分布不依赖于任何未知参数, 则设\(W\)的左右两侧分位数分别为\(w_{\frac{\alpha}{2}}\)和\(w_{1-\frac{\alpha}{2}}\), 有 \[ \begin{aligned} P(w_{\frac{\alpha}{2}} < h(T, \phi) < w_{1-\frac{\alpha}{2}}) = 1-\alpha, \end{aligned} \] 反解上面的不等式可以得到\(\phi\)的置信区间。
如果对枢轴量\(W\)很难求分位数时, 可以用bootstrap方法获得置信区间。 设\(\hat F\)为总体分布\(F\)的估计, 设\(\boldsymbol Y = (y_1, \dots, y_n)\)为总体\(\hat F\)的样本, \(\hat\phi = \phi(\hat F)\)为与总体\(\hat F\)对应的参数\(\phi\)的值, 实际是\(\phi\)的估计值, 则\(V = h(g(\boldsymbol Y), \hat\phi)\)与\(W\)的分布相近, 可以用\(V\)的分位数近似\(W\)的分位数。
例17.8 设总体\(X \sim F(x, \theta)\), \(\theta\)为总体的未知参数, \(\phi = E X\), \(\boldsymbol X = (x_1, x_2, \dots, x_n)\)为总体的样本, 则\(g(\boldsymbol X) = \bar X\)是\(\phi\)的估计, 若\(W = h(g(\boldsymbol X), \phi) = \bar X - E X\)的分布与\(\theta\)无关, 求\(W\)的分位数\(w_{\frac{\alpha}{2}}\)和\(w_{1-\frac{\alpha}{2}}\)就可以构造\(\phi=EX\)的置信区间 \((\bar X - w_{1-\frac{\alpha}{2}}, \; \bar X - w_{\frac{\alpha}{2}})\)。
若\(W\)的分位数无法求得, 用经验分布\(F_n\)作为总体分布\(F\)的估计, 这时\(\phi(F_n) = \bar X\), 设\(\boldsymbol Y = (Y_1, \dots, Y_n)\)为\(F_n\)的样本, \(V = h(g(\boldsymbol Y), \bar X) = \bar Y - \bar X\), 这里\(\bar X\)作为已知值, 可以用\(V\)的分位数近似代替\(W\)的分位数。 求\(V\)的分位数; 而这只要用有放回随机抽样方法从\(x_1, x_2, \dots, x_n\) 抽取\(F_n\)的\(B\)组样本\(\boldsymbol Y^{(b)}=(y_1^{(b)}, \dots, y_n^{(b)}), b=1,2,\dots,B\), 对每组样本计算平均值\(\bar Y^{(b)}\), 定义\(V^{(b)} = \bar Y^{(b)} - \bar X\), 用\(V^{(b)}, b=1,2,\dots,B\)的样本分位数估计\(V\)的分位数, 作为\(W\)的分位数\(w_{\frac{\alpha}{2}}\)和\(w_{1-\frac{\alpha}{2}}\)的近似。
R的boot扩展包的boot.ci()函数可以从boot()函数的模拟结果中计算各种bootstrap置信区间。
习题
习题2
对例17.7, 证明\(\hat\phi_1\)的均方误差为 \[\begin{aligned} L_1 = E(\hat\phi_1 - \mu^2)^2 = \frac{4 \sigma^2 \mu^2}{n} + \frac{2n}{n-1} \frac{\sigma^4}{n^2}. \end{aligned}\]
习题3
考虑下的非线性回归模型(logistic曲线) \[\begin{aligned} y = A (1 + e^{-bx}) + \varepsilon, \ \varepsilon \sim \text{N}(0, \sigma^2), \end{aligned}\] 其中\(A>0, b>0, \sigma^2>0\)是未知参数。 设有独立样本\((x_i, y_i), i=1,2,\dots, n\), 可以用最小二乘方法估计\(A, b, \sigma^2\), 估计值记为\(\hat A, \hat b, \hat \sigma^2\)。
设真实的\(A=10, b=1, \sigma=1\)。 编写程序模拟一组样本(取\(x_i=-10, -9, \dots, 9, 10\)), 计算\(\hat A, \hat b, \hat \sigma^2\), 然后用bootstrap方法估计\(\hat A, \hat b, \hat \sigma^2\)的标准误差和偏差。
重复生成\(N\)组模型的样本, 从这\(N\)组样本中分别得到估计值\(\hat A^{(j)}, \hat b^{(j)}, (\hat\sigma^{(j)})^2\), \(j=1,2,\dots,N\), 用得到的这些估计值作为\(\hat A, \hat b, \hat \sigma^2\)的抽样分布的样本, 估计其标准误差和偏差并与bootstrap方法得到的结果进行对比。