24 数值微分
24.1 三种差商方法
在没有函数微分的解析表达式时, 可以用数值方法由函数值近似计算函数的微分值。 按照微分定义, 当\(f(x)\)在点\(x\)处可微时, 对很小的\(h\)有 \[\begin{align} f'(x) =& \frac{f(x+h) - f(x)}{h} + O(h) \tag{24.1} \\ =& \frac{f(x) - f(x-h)}{h} + O(h) \tag{24.2} \\ =& \frac{f(x+h) - f(x-h)}{2h} + O(h^2) \tag{24.3} \end{align}\] 这三种近似分别称为数值微分的向前差商、 向后差商和中心差商公式, 其中中心差商公式有更好的精度。 \(h\)选取应该很小, 使得继续减小\(h\)时按差商公式计算的近似导数值不再变化或变化量小于给定误差界限。 但是,\(h\)也不能过分小, 因为计算\(f(x)\)值只能到一定精度, 当\(h\)太小时\(f(x+h)\)与\(f(x)\)的差别已经不是由\(h\)引起的而是由\(f(x)\)计算误差引起的。 如果\(f(x)\)的计算精度可以达到机器单位\(U\)量级, 取\(h\)的一个经验法则是取\(h/|x|\)为\(U^{1/2}\)左右, 对中心差商公式取\(h/|x|\)为\(U^{1/3}\)左右 (见 Monahan (2001) §8.6)。 多元函数的梯度可以类似地计算。
可以类似地计算高阶微分,如 \[\begin{align} f''(x) = \frac{[f(x+h) - f(x)] - [f(x) - f(x-h)]}{h^2} + O(h), \tag{24.4} \end{align}\] 公式分子有意地写成了两个差分的差分, 以避免有效位数损失。
公式(24.1)–(24.3)是用割线斜率近似切线斜率, 相当于用两点的函数值作线性插值后用插值函数的微分近似原始函数微分。 一般地,对函数\(f(x)\)可以计算插值多项式\(P_n(X)\), 用\(P_n'(x)\)近似\(f'(x)\)。这种计算微分的方法称为插值型求导公式。 设多项式\(P_{n-1}(x)\)满足 \[\begin{aligned} P_{n-1}(x_i) = f(x_i), \ i=1,2,\dots,n \end{aligned}\] 由定理22.2, 插值近似的余项为 \[\begin{aligned} f(x) - P_{n-1}(x) = \frac{f^{(n)}(\xi)}{n!} g(x) \end{aligned}\] 其中\(g(x)=\prod_{i=1}^n (x - x_i)\), \(\xi\)依赖于\(x\)的位置。 插值型求导公式的余项为 \[\begin{align} f'(x) - P_{n-1}'(x) = \frac{f^{(n)}(\xi)}{n!} \cdot g'(x) + \frac{g(x)}{n!} \cdot \frac{d}{dx} \frac{f^{(n)}(\xi)}{n!} \tag{24.5} \end{align}\] 因为(24.5)中的第二项中\(\xi\)与\(x\)的函数关系未知, 对任意\(x\)处用\(P_{n-1}'(x)\)近似\(f'(x)\)可能有很大误差。 如果仅在节点\(x_i, i=1,2,\dots,n\)处计算\(P_{n-1}'(x)\), 则有 \[\begin{align} f'(x_i) = P_n'(x_i) + \frac{f^{(n)}(\xi)}{n!} g'(x_i), \ i=1,2,\dots,n. \tag{24.6} \end{align}\]
根据(24.6), 我们导出对等距节点\((x_i, z_i)\)( \(i=1,2,\dots,n\))计算数值微分的公式。 设\(z_i = f(x_i)\),\(x_i - x_{i-1}=h\)。
用线性插值近似求导的公式为 \[\begin{aligned} f'(x_i) = \frac{z_{i+1} - z_i}{h} - \frac{h}{2} f''(\xi_1), \ i=1,2,\dots,n-1 \ (\xi_1 \in (x_i, x_{i+1}) \end{aligned}\] 或 \[\begin{aligned} f'(x_i) = \frac{z_i - z_{i-1}}{h} + \frac{h}{2} f''(\xi_2), \ i=2,3,\dots,n \ (\xi_2 \in (x_{i-1}, x_i) \end{aligned}\]
用二次多项式插值近似求导的公式为 \[\begin{aligned} f'(x_i) =& \frac{-3z_i + 4 z_{i+1} - z_{i+2}}{2h} + \frac{h^2}{3} f^{(3)}(\xi_1), \\ &\ i=1,2,\dots,n-2, \ \xi_1 \in (x_i, x_{i+2}) \nonumber \end{aligned}\] 或 \[\begin{aligned} f'(x_i) =& \frac{-z_{i-1} + z_{i+1}}{2h} - \frac{h^2}{6} f^{(3)}(\xi_2), \\ & \ i=2,3,\dots,n-1, \ \xi_2 \in (x_{i-1}, x_{i+1}) \nonumber \end{aligned}\] 或 \[\begin{aligned} f'(x_i) =& \frac{z_{i-2} - 4 z_{i-1} + 3z_i}{2h} + \frac{h^2}{3} f^{(3)}(\xi_3), \\ &\ i=3,4,\dots,n, \ \xi_3 \in (x_{i-2}, x_i). \end{aligned}\]
用二次多项式插值近似求二阶导数的公式为 \[\begin{aligned} f''(x_i) =& \frac{z_{i-1} - 2 z_i + z_{i+1}}{h^2} - \frac{h^2}{12} f^{(4)}(\xi_1), \\ & \ i=2,3,\dots, n-1, \ \xi_1 \in (x_{i-1}, x_{i+1}). \end{aligned}\]
用多项式插值方法近似计算函数微分, 在一般的\(x\)值处计算的误差可能很大。 可以采用样条函数来进行插值, 用样条函数的导数来计算被插值函数的导数。
Mathmatica、Maple、Maxima等软件系统支持符号运算, 可以对用数学表达式表示的函数获得数学表达式表示的微分、积分。
Julia语言的ForwardDiff包使用自动微分算法, 可以高效地对Julia程序表示的函数计算梯度、海色阵。 自动微分不是符号计算, 但也不同于简单的差商近似, 精度和效率更高。
24.2 复数差商(*)
如果函数\(f(x)\)可以对\(x \in \mathbb C\)(复数域)计算, 则由泰勒展开公式 \[\begin{aligned} f(x + ih) =& f(x) + ih f'(x) - \frac{1}{2} h^2 f''(x) - \frac{1}{6} i h^3 f'''(x) + O(h^4) , \end{aligned}\] 在两边取虚部,有 \[ \Im(f(x + ih)) = h f'(x) - \frac{1}{6} h^3 f'''(x) + O(h^4), \] 于是 \[\begin{aligned} f'(x) =& \frac{\Im(f(x + ih))}{h} + \frac{1}{6} h^2 f'''(x) + O(h^3), \end{aligned}\] 可见,不需要计算\(f(x + ih) - f(x)\)就可以用虚部得到\(O(h^2)\)精度的近似。 同时, 因为 \[ \Re(f(x + ih)) = f(x) - \frac{1}{2} h^2 f''(x) + O(h^4), \] 所以还得到了\(f(x)\)的一个精度为\(O(h^2)\)的近似值。 \(h\)的选取也不需要依赖于\(x\)的绝对值大小。 局限是\(f(x)\)必须对复数有定义且程序允许\(x\)取复数。
24.3 自动微分(*)
用计算机程序表示的函数, 在许多程序语言中可以使用“自动微分”技术, 获得微分的精确表示。 这种方法的基础是微分的链式法则 \[ \frac{d g(f(x))}{dx} = \frac{dg}{df} \cdot \frac{df}{dx} , \] 以及实数的一阶精度表示: 将函数的每个自变量\(x\)表示为\(x + h_x \epsilon\), 其中\(\epsilon\)是一个虚拟的一阶无穷小量, 将运算或者函数的结果\(y\)用运算规则计算为\(y\)和\(\epsilon\)的倍数。 对于函数\(f(x)\), 有 \[ f(x + h_x \epsilon) = f(x) + h_x f'(x) \epsilon + o(\epsilon), \] 于是只要将\(f(x + h_x \epsilon)\)忽略\(\epsilon\)的高阶项近似表示成 \[\begin{align} f(x + h_x \epsilon) = f(x) + h_x f'(x) \epsilon, \tag{24.7} \end{align}\] 就可以从\(\epsilon\)的系数中提取出\(f'(x)\)的值。 具体方法是在编程时将每个实数都编码为\((x, h_x)\)的格式, 用来表示\(x + h_x \epsilon + o(\epsilon)\)。
在四则运算中,也要对这样编码的实数进行计算。比如,两个这样的实数的乘法: \[ (a + h_a \epsilon) \times (b + h_b \epsilon) = a b + (b h_a + a h_b) \epsilon + h_a h_b \epsilon^2 \approx a b + (b h_a + a h_b) \epsilon . \]
计算机程序中计算的函数, 可以看成是四则运算、数学函数的复合。 对用程序表示的函数进行改造, 使其接受\((x, h_x)\)这样的编码格式以及运算规则, 对数学函数变换结果也用(24.7)这样的方法进行计算, 最后程序函数执行结束后的\(h_x \epsilon\)的倍数就是所需的导数值。 这样的计算不像差商方法那样受步长选取的影响, 其误差仅限于数值计算误差, 所以可以认为是精确求导。
因为只能对四则运算和常用数学函数进行这样的编码的运算, 对一般的用计算机程序表示的函数, 有程序分析工具可以将这样的计算机程序表示成有向图, 节点是运算或函数, 以及输入、输出, 连接是复合过程。 例如, \(\sin(x-1)\)就可以看成节点\(x\)和节点\(1\)用运算“\(-\)”连接, 结果可记为\(z_1\)节点, \(z_1\)节点再连接到\(\sin\)节点进行函数变换。 在进行运算和函数调用时都需要按照特殊编码\(x + h_x \epsilon\)的运算规则来计算。
自动微分的向前累积方法, 是从有向图的源头方向开始计算微分, 并利用链式法则将计算过程向结果方向传递。 在编程时, 同时保存分解后的值和微分值。 在计算梯度时, 每一个分量的微分都需要用向前累积方法分别计算一遍。
自动微分的另一种方法是向后累积方法, 计算梯度时只需要沿有向图向前和向后各一遍就可以完成多个分量微分的计算。 此方法是从计算结果方向朝源头方向应用链式法则的。
参见(Kochenderfer 2019)。
24.4 附录:误差阶的推导(*)
用泰勒展开得 \[\begin{align} f(x+h) = f(x) + h f'(x) + \frac{1}{2} h^2 f''(x) + O(h^3), \tag{24.8} \end{align}\] 可得 \[ \frac{f(x+h) - f(x)}{h} = f'(x) + \frac{1}{2} h f''(x) + O(h^2), \] 即向前差商公式的误差为\(O(h)\)阶。 向后差商公式类似。
对于中心差商公式, 因为 \[\begin{align} f(x-h) = f(x) - h f'(x) + \frac{1}{2} h^2 f''(x) + O(h^3), \tag{24.9} \end{align}\] 将(24.8)与(24.9)相减, 则\(\frac{1}{2} h^2 f''(x)\)项被约掉,于是有 \[ \frac{f(x+h) - f(x-h)}{2h} = f'(x) + O(h^2) . \]
※※※※※
24.5 附录:Julia程序(*)
24.5.1 三种差商公式的计算程序和误差演示
用三种差商公式计算数值微分的Julia函数如下:
diff_forward(f, x; h=sqrt(eps(Float64))) = (f(x+h) - f(x))/h
diff_central(f, x; h=cbrt(eps(Float64))) = (f(x+h/2) - f(x-h/2))/h
diff_backward(f, x; h=sqrt(eps(Float64))) = (f(x) - f(x-h))/h其中eps(FLoat64)给出双精度值的机器\(\varepsilon\)值,
cbrt()是立方根函数。
程序没有考虑\(x\)的大小,
实际上,
当\(x\)的绝对值很大时,
\(x + h\)会无法与\(x\)区分开来,
这时缺省的\(h\)值也不合适。
例24.1 当\(h\)太小时, 反而会因为\(f(x+h) - f(x)\)出现两个过于接近的值相减造成有效位数损失, 使得估计的微分不准确。 以\(f(x) = e^x\)在\(x=0\)处的数值微分为例查看相对误差情况。
取\(h\)为\(10\)的\(-1\)次方到\(-20\)次方, 计算误差如下:
using CairoMakie
let
f(x) = exp(x)
hvec = 10.0 .^ (-1:-1:-20)
err1 = abs.((f.(0.0 .+ hvec) .- f(0.0)) ./ hvec .- 1.0)
err2 = abs.((f.(0.0 .+ hvec) .- f.(0.0 .- hvec)) ./
(2 .* hvec) .- 1.0)
display([hvec err1 err2])
fig, ax, plt = lines(hvec, err1,
axis = (; title="数值方法估计的导数的误差",
xlabel="h", ylabel="相对误差",
xscale=log10, yscale=log10),
label = "向前差商误差" )
lines!(hvec, err2,
label = "中心差商误差" )
axislegend()
fig
end结果:
20×3 Matrix{Float64}:
0.1 0.0517092 0.0016675
0.01 0.00501671 1.66667e-5
0.001 0.000500167 1.66667e-7
0.0001 5.00017e-5 1.66689e-9
1.0e-5 5.00001e-6 1.21023e-11
1.0e-6 4.99962e-7 2.67555e-11
1.0e-7 4.94337e-8 5.26356e-10
1.0e-8 6.07747e-9 6.07747e-9
1.0e-9 8.27404e-8 2.72292e-8
1.0e-10 8.27404e-8 8.27404e-8
1.0e-11 8.27404e-8 8.27404e-8
1.0e-12 8.89006e-5 3.33894e-5
1.0e-13 0.000799278 0.000244166
1.0e-14 0.000799278 0.000799278
1.0e-15 0.110223 0.0547119
1.0e-16 1.0 0.444888
1.0e-17 1.0 1.0
1.0e-18 1.0 1.0
1.0e-19 1.0 1.0
1.0e-20 1.0 1.0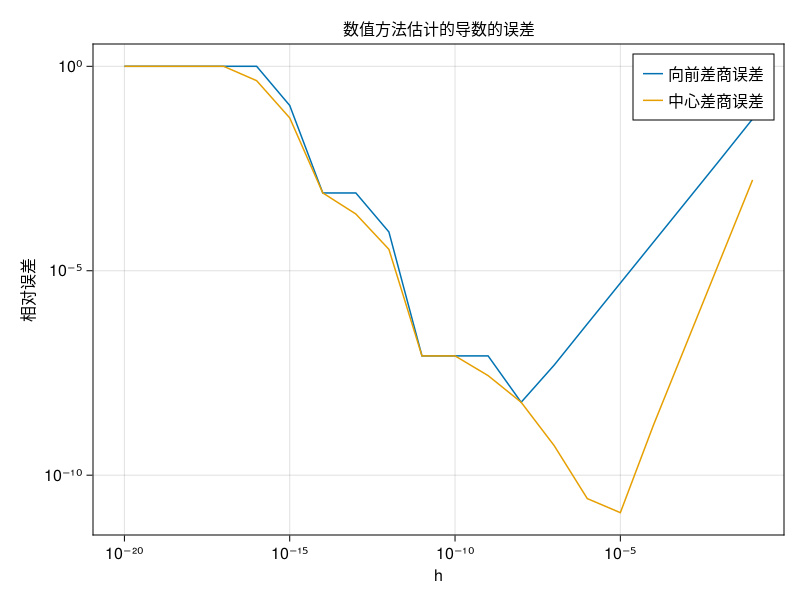
可以看出, \(h\)较大时误差较大, 减小\(h\)可以显著地减小误差, 且中心差商公式误差比向前差商公式的误差减小速度快得多; 但是,当\(h\)达到某个范围(向前差商是\(10^{-8}\), 中心差商是\(10^{-5}\))时, 误差不再减小, 反而增大。 当\(h = 10^{-16}\)时, 向前差商公式估计的\(f'(0)\)已经等于0, 这是因为这时\(x+h\)和\(x\)已经不可区分。
※※※※※
24.5.3 自动微分
Julia有许多包提供了自动微分功能, 其中ForwardDiff是功能比较完善可靠的。 使用自动微分, 要求被微分的函数允许输入一般的自变量, 而不能指定自变量类型为某种特定的浮点类型。
如:
using ForwardDiff
let
f1(x) = x^3
f1d(x) = 3 * x^2
x = [-1, 0, 1, 2]
@show f1d.(x);
@show ForwardDiff.derivative.(f1, x);
end
## f1d.(x) = [3, 0, 3, 12]
## ForwardDiff.derivative.(f1, x) = [3, 0, 3, 12]又如函数 \[ f(x) = \sum_i \sin(x_i) + \prod_i \sqrt{x_i} . \]