8 R中的随机数函数(`*`)

8.1 R语言中与分布有关的函数

R语言作为一个面向统计计算、数据分析、作图的语言，提供了丰富的与概率分布有关的函数。对一个概率分布xxx，函数dxxx()计算分布密度函数或者概率质量函数，函数pxxx()计算分布函数，函数qxxx()计算分位数函数，函数rxxx()生成该分布的若干个随机数。

在R命令行用

?Distributions

查看stats包给出的各种与分布有关的函数。

下面以正态分布为例介绍这些函数的用法。设正态分布密度为\(f(x)\), 分布函数为\(F(x)\)，分位数函数为\(F^{-1}(x)\)。密度函数\(f(x)\)用法为：

dnorm(x, mean=0, sd=1, log=FALSE)

计算标量或者向量x处的正态分布密度函数值，可以用参数mean指定分布均值参数，用参数sd指定分布的标准差参数，如果加选项log=FALSE可以返回函数值的自然对数值，这在计算对数似然函数时有用。参数缺省为mu=0, sd=1。调用时自变量x经常是向量，结果返回各个元素处的密度函数值；参数通常是标量，但是也允许取为向量，这时一般与自变量x的向量一一对应，但是也可以长度不相同，短的循环使用。

例如，计算三个不同的正态密度，并作图：

muv <- c(10, 10, 20)
sdv <- c(1, 2, 1)
np <- 200
x <- seq(0, 30, length.out=np)
ym <- matrix(0, np, 3)
for(j in 1:3){
  ym[, j] <- dnorm(x, muv[j], sdv[j])
}
matplot(x, ym, type="l", lwd=2, xlab="x", ylab="f(x)", main="Normal Densities")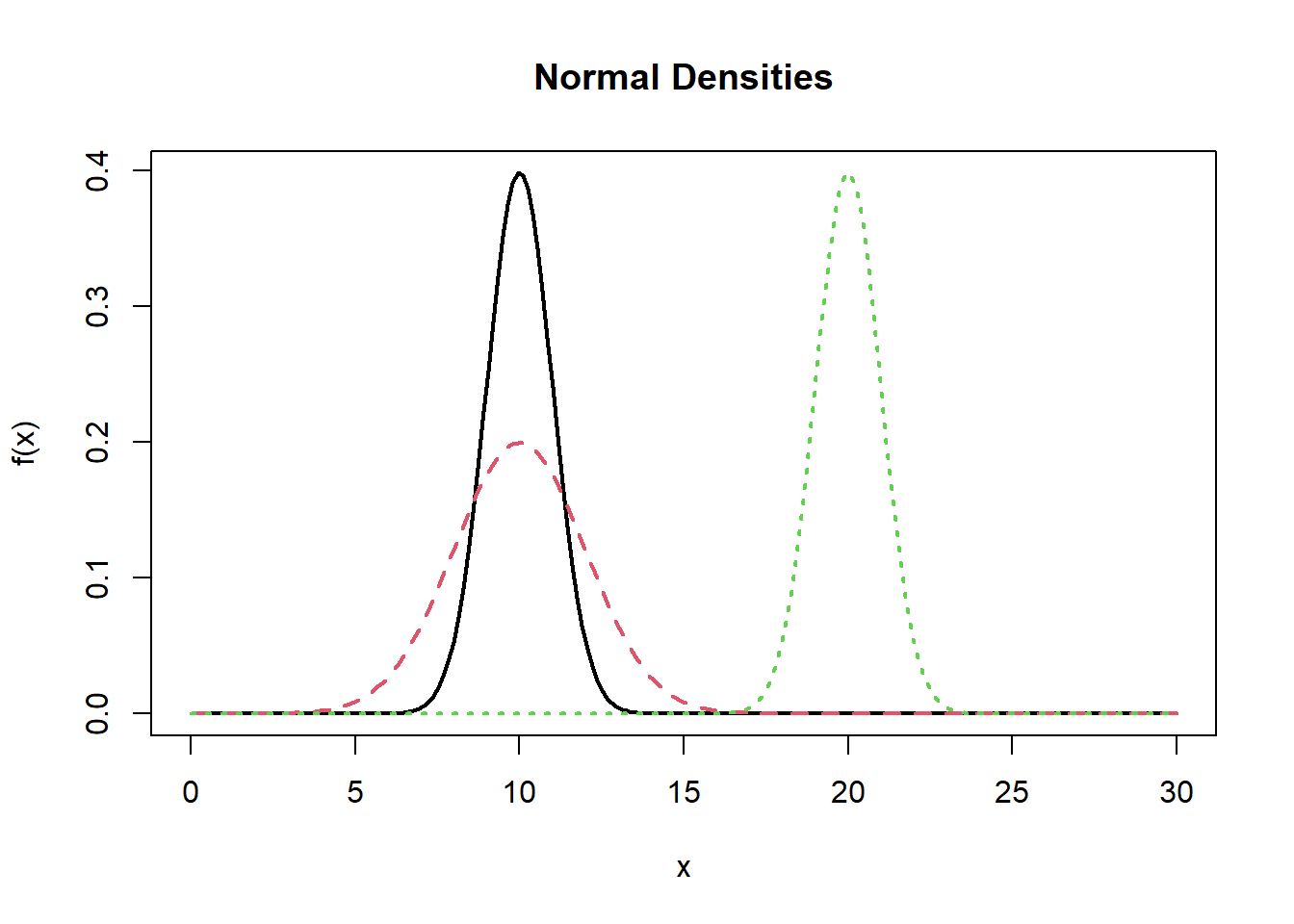

正态分布函数（\(F(x)\)）用法为：

pnorm(q, mean=0, sd=1, lower.tail=TRUE, log.p=FALSE)

其中q是要计算分布函数的自变量位置，可输入向量， mean和sd是参数，参数也允许取为向量。加选项lower.tail=FALSE可以计算\(1-F(x)\)，加选项log.p=TRUE可以输出结果的自然对数值。

正态分位数函数用法为：

qnorm(p, mean=0, sd=1, lower.tail=TRUE, log.p=FALSE)

其中p是\((0,1)\)内取值的标量或者元素在\((0,1)\)内取值的向量， mean和sd是参数。加选项lower.tail=FALSE则求的是\(F^{-1}(1-p)\)。加选项log.p=TRUE，则求\(F^{-1}(e^p)\)。

正态随机数函数用法为:

rnorm(n, mean=0, sd=1)

其中n是需要输出的随机数个数， mean和sd是分布参数。这个函数中没有指定种子的选项，要指定种子和选择不同的基础随机数发生器需要使用特殊的函数来改变。用set.seed(seed)指定一个种子的编号，其中seed是一个整数值。

下面的例子生成了100个\(\text{N}(10, 2^2)\)的随机数，将其舍入到小数点后两位精度（实际数据中并不存在真正的无限位数的实数），作直方图，并画理论的密度曲线：

set.seed(1)
x <- rnorm(100, 10, 2)
hist(x, freq=FALSE, main=expression(N(0,2^2)))
curve(dnorm(x, 10, 2), 4, 16, lwd=2, col="red", add=TRUE)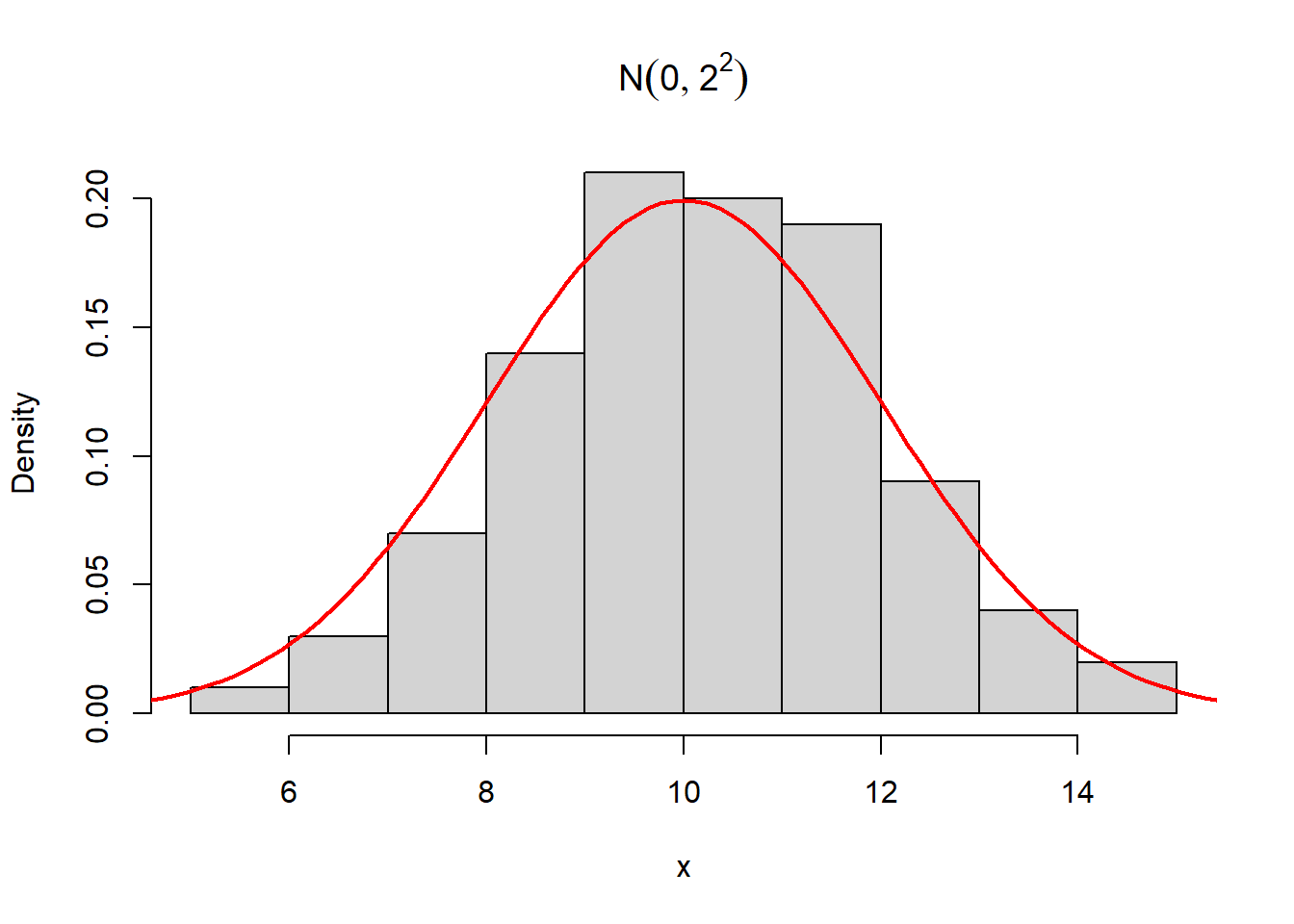

8.2 分布列表

R的stats包是默认安装的基础包，其中已经实现多种分布的有关函数，函数类型见上面以正态为例的说明。分布包括：

beta: 贝塔分布
binom: 二项分布，包括两点分布
cauchy: 柯西分布
chisq: 卡方分布
exp: 指数分布
f: F分布
gamma: 伽马分布
geom: 几何分布
hyper: 超几何分布
lnorm: 对数正态分布
multinom: 多项分布
norm: 正态分布
pois: 泊松分布
t: t分布
unif: 均匀分布
weibull: 威布尔分布

对每个上面的函数名xxx，都有对应的dxxx(), pxxx(), qxxx(), rxxx()函数。

其它的一些R扩展包中提供了更多的分布，参见R的CRAN网站的Task View中Distributions部分。

8.3 R随机数发生器

我们知道，非均匀的随机数发生器实际是通过均匀随机数发生器构造出来的。 R中内建了多种不同均匀随机数发生器算法，在R命令行用如下命令查看关于R的随机数发生器的说明：

?RNG

在调用R的产生随机数的函数如runif(), rnorm()时，随机数发生器的当前状态是随之更新的，这样，连续两次runif(5)的调用结果是不同的，如：

set.seed(1)
round(runif(5), 2)

## [1] 0.27 0.37 0.57 0.91 0.20

round(runif(5), 2)

## [1] 0.90 0.94 0.66 0.63 0.06

当前选中的随机数发生器的当前状态保存在一个整数型向量类型的全局变量.Random.seed中。直接保存这个变量的值，也可以用来保存自己的长时间模拟的中间状态；将保存的值重新赋给这个变量就可以恢复随机数发生当时的状态，但是不要直接修改这个全局变量的内容。

Random.seed需要自己保存和恢复，适用于较长时间的模拟保存中间状态，以免后续的模拟失败后还需要从头开始。对于从一开始进行的模拟，为了使得结果是可重复的，用set.seed(seed)设置一个随机数种子，即模拟的起始点，其中seed是一个整数，本身并不是真正的算法中的种子，可以看成是种子的一种编号。 set.seed()只保证结果可重复，选取不同种子时不能保证结果一定是不同的，但是不同种子给出的随机数序列一般是不同的，相同的情况及其少见。

set.seed()还可以有一个选项kind，取为一个表示不同发生器算法的字符串，当前的默认发生器算法是"Mersenne-Twister"。

随机数算法的选择有：

"Wichmann-Hill"
"Marsaglia-Multicarry"
"Super-Duper"
"Mersenne-Twister"
"Knuth-TAOCP-2002"
"Knuth-TAOCP"
"L'Ecuyer-CMRG"
"user-supplied" 由用户提供自己的随机数发生器

因为正态随机数常用，所以正态随机数发生器可以在set.seed()中用参数normal.kind指定，可取值有：

"Kinderman-Ramage"
"Ahrens-Dieter"
"Box-Muller"
"Inversion" (逆变换法，这是默认选择)

函数RNGkind(kind=NULL, normal.kind=NULL)用来选择发生器算法而不指定具体种子。调用RNGkind()可以返回当前使用的随机数发生器和正态分布随机数算法的名称。

8.4 R中使用的若干个随机数发生器的算法说明

8.4.1 Wichmann-Hill发生器

Wichmann和Hill(见 Wichmann and Hill (1982))设计了如下的线性组合发生器。

利用三个16位运算的素数模乘同余发生器: \[\begin{eqnarray*} U_n &=& 171 U_{n-1} \pmod{30269} \\ V_n &=& 172 V_{n-1} \pmod{30307} \\ W_n &=& 170 W_{n-1} \pmod{30323} \end{eqnarray*}\] 作线性组合并求余: \[\begin{align*} R_n = (U_n / 30269 + V_n / 30307 + W_n / 30323) \pmod{1} \end{align*}\] 这个组合发生器的周期约有\(7\times 10^{12}\)长, 超过\(2^{32} \approx 4\times 10^9\)。

R中使用Wichmann-Hill发生器时，全局变量.Random.seed第一个元素是对应着当前随机数发生器的一个编码，后续的三个元素是当前的\(U, V, W\)的值，因为是余数，所以分别在\(1-30268\), \(1-30306\), \(1-30322\)之间取值。

下面是R 3.4.1的源程序包中RNG.c文件中Wichmann-Hill发生器的部分C代码：

I1 = I1 * 171 % 30269;
I2 = I2 * 172 % 30307;
I3 = I3 * 170 % 30323;
value = I1 / 30269.0 + I2 / 30307.0 + I3 / 30323.0;
return fixup(value - (int) value);/* in [0,1) */

变量I1, I2, I3是C语言的32位有符号整数类型，分别代表一个素数模乘同余发生器，最后组合时取三个发生器变换到\((0,1)\)中的和的小数部分， fixup()函数用来确保不会有0和1值被返回。

8.4.2 Marsaglia-Multicarry

这是George Marsaglia提出的一种“multiply-with-carry”发生器，周期长达\(2^{60} \approx 1.2\times 10^{18}\)，种子由两个整数组成。

下面是R 3.4.1的源程序包中RNG.c文件中Marsaglia-Multicarry发生器的部分C代码：

/* 0177777(octal) == 65535(decimal)*/
I1= 36969*(I1 & 0177777) + (I1>>16);
I2= 18000*(I2 & 0177777) + (I2>>16);
return fixup(((I1 << 16)^(I2 & 0177777)) * i2_32m1); /* in [0,1) */

可以看出这也是一个混合发生器， I1和I2是两个组件发生器，变量I1, I2是C语言的32位有符号整数类型， I1 & 0177777 取I1的后16位， I1 >> 16取I1的前16位（看成无符号整数），迭代相当于I1的后16位二进制表示的无符号整数乘以36969，加上I1的前16为二进制表示的无符号整数的值。 I2的迭代类似。最后将两个发生器组合起来，组合时仅取上面迭代后的I1的32位二进制中的后16位的取反，和迭代后的I2的后16位的取反，组成一个32位二进制整数，除以\(2^{32}-1\)。

8.4.3 Super-Duper

这是Marsaglia在1970年代提出的著名算法，周期约为\(4.6 \times 10^{18}\)，种子是两个整数，第二个数是奇数。 R中使用了Reeds, J., Hubert, S. 和 Abrahams, M. 在1982-1984年的实现。

下面是R 3.4.1的源程序包中RNG.c文件中Super-Duper发生器的部分C代码：

/* This is Reeds et al (1984) implementation;
 * modified using __unsigned__  seeds instead of signed ones
 */
I1 ^= ((I1 >> 15) & 0377777); /* Tausworthe */
I1 ^= I1 << 17;
I2 *= 69069;        /* Congruential */
return fixup((I1^I2) * i2_32m1); /* in [0,1) */

也用了两个随机数发生器的混合，混合时，使用两个32位二进制整数I1和I2的按位异或运算混合在一起。关于I1的迭代，是将I1的32位二进制数右移15位，仅剩下原来高位的17位，再将这样得到的32个二进制整数与这个整数左移17位的结果按位异或，得到I1的值。 I2则是一个素数模乘同余发生器，每次乘以69069，依靠32位整数的自动溢出求余。最后输出时将I1和I2两个32位二进制整数作按位异或，除以\(2^{32}-1\)后输出。

8.4.4 Mersenne-Twister

见 Matsumoto and Nishimura (1998) 。是一个扭曲的GFSR，周期有\(2^{19937}-1\)，在623维是均匀的，种子是624个32位整数与一个当前位置。

下面是R 3.4.1的源程序包中RNG.c文件Mersenne-Twister中发生器的部分C代码：


/* ===================  Mersenne Twister ========================== */
/* From http://www.math.keio.ac.jp/~matumoto/emt.html */

/* A C-program for MT19937: Real number version([0,1)-interval)
   (1999/10/28)
     genrand() generates one pseudorandom real number (double)
   which is uniformly distributed on [0,1)-interval, for each
   call. sgenrand(seed) sets initial values to the working area
   of 624 words. Before genrand(), sgenrand(seed) must be
   called once. (seed is any 32-bit integer.)
   Integer generator is obtained by modifying two lines.
     Coded by Takuji Nishimura, considering the suggestions by
   Topher Cooper and Marc Rieffel in July-Aug. 1997.

   Copyright (C) 1997, 1999 Makoto Matsumoto and Takuji Nishimura.
   When you use this, send an email to: matumoto@math.keio.ac.jp
   with an appropriate reference to your work.

   REFERENCE
   M. Matsumoto and T. Nishimura,
   "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform
   Pseudo-Random Number Generator",
   ACM Transactions on Modeling and Computer Simulation,
   Vol. 8, No. 1, January 1998, pp 3--30.
*/

/* Period parameters */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0df   /* constant vector a */
#define UPPER_MASK 0x80000000 /* most significant w-r bits */
#define LOWER_MASK 0x7fffffff /* least significant r bits */

/* Tempering parameters */
#define TEMPERING_MASK_B 0x9d2c5680
#define TEMPERING_MASK_C 0xefc60000
#define TEMPERING_SHIFT_U(y)  (y >> 11)
#define TEMPERING_SHIFT_S(y)  (y << 7)
#define TEMPERING_SHIFT_T(y)  (y << 15)
#define TEMPERING_SHIFT_L(y)  (y >> 18)

static Int32 *mt = dummy+1; /* the array for the state vector  */
static int mti=N+1; /* mti==N+1 means mt[N] is not initialized */

/* Initializing the array with a seed */
static void
MT_sgenrand(Int32 seed)
{
    int i;

    for (i = 0; i < N; i++) {
    mt[i] = seed & 0xffff0000;
    seed = 69069 * seed + 1;
    mt[i] |= (seed & 0xffff0000) >> 16;
    seed = 69069 * seed + 1;
    }
    mti = N;
}

/* Initialization by "sgenrand()" is an example. Theoretically,
   there are 2^19937-1 possible states as an intial state.
   Essential bits in "seed_array[]" is following 19937 bits:
    (seed_array[0]&UPPER_MASK), seed_array[1], ..., seed_array[N-1].
   (seed_array[0]&LOWER_MASK) is discarded.
   Theoretically,
    (seed_array[0]&UPPER_MASK), seed_array[1], ..., seed_array[N-1]
   can take any values except all zeros.                             */

static double MT_genrand(void)
{
    Int32 y;
    static Int32 mag01[2]={0x0, MATRIX_A};
    /* mag01[x] = x * MATRIX_A  for x=0,1 */

    mti = dummy[0];

    if (mti >= N) { /* generate N words at one time */
    int kk;

    if (mti == N+1)   /* if sgenrand() has not been called, */
        MT_sgenrand(4357); /* a default initial seed is used   */

    for (kk = 0; kk < N - M; kk++) {
        y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
        mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1];
    }
    for (; kk < N - 1; kk++) {
        y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
        mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1];
    }
    y = (mt[N-1] & UPPER_MASK) | (mt[0] & LOWER_MASK);
    mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1];

    mti = 0;
    }

    y = mt[mti++];
    y ^= TEMPERING_SHIFT_U(y);
    y ^= TEMPERING_SHIFT_S(y) & TEMPERING_MASK_B;
    y ^= TEMPERING_SHIFT_T(y) & TEMPERING_MASK_C;
    y ^= TEMPERING_SHIFT_L(y);
    dummy[0] = mti;

    return ( (double)y * 2.3283064365386963e-10 ); /* reals: [0,1)-interval */
}

8.4.5 L’Ecuyer-CMRG与并行计算

是L’Ecuyer et al.在2002提出的，参见 L’Ecuyer (1999) 。是两个发生器的混合： \[ \begin{aligned} x_n =& 1403580 x_{n-2} - 810728 x_{n-3} \pmod{2^{32} - 209} \\ y_n =& 527612 y_{n-1} - 1370589 y_{n-3} \pmod{2^{32} - 22853} \\ z_n =& (x_n - y_n) \pmod{4294967087} \\ u_n =& z_n / 4294967088 \end{aligned} \] 并检查\(u_n=0\)时以接近0的正值代替。

这个随机数发生器的优点是算法相对简单，周期长达\(2^{191}\)，并可以很容易地切分成长度为\(2^{127}\)的不同段，每一段的种子容易确定，这样，在并行计算时，每个工人节点可以从不同段的种子出发进行模拟。程序如：

RNGkind("L'Ecuyer-CMRG")
set.seed(1)
## start M workers
s <- .Random.seed
for (i in 1:M) {
  s <- nextRNGStream(s)
  # send s to worker i as .Random.seed
}

参见R的parallel包的说明文档。

参考文献

L’Ecuyer, P. 1999. “Good Parameters and Implementations for Combined Multiple Recursive Random Number Generators.” Operations Research 47: 195–64. http://www.iro.umontreal.ca/ lecuyer/myftp/papers/combmrg2.ps.

Matsumoto, M., and T. Nishimura. 1998. “Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator.” ACM Transactions on Modeling and Computer Simulation 8: 3–30.

Wichmann, B. A., and I. D. Hill. 1982. “Algorithm as 183: An Efficient and Portable Pseudo-Random Number Generator.” Applied Statistics 31: 188–190. Remarks: 34, 198 and 35, 89.

8 R中的随机数函数(*)