4 更新过程
4.1 更新过程的定义及若干分布
4.1.1 定义
定义4.1 设\(\{ X_n, n = 1, 2, \dots \}\)是一列独立同分布的非负随机变量, 分布函数为\(F(x)\)。为了避免平凡的情况, 设\(F(0)=P(X_n=0) < 1\), 记\(\mu = E[X_n]\), 则\(0 < \mu \leq +\infty\). 令 \[ T_n = \sum_{i=1}^n X_i , \ n \geq 1, \ T_0 = 0 . \] 我们把由 \[ N(t) = \sup \{ n: \; T_n \leq t \} \] 定义的计数过程称为更新过程.
更新过程的一个典型例子是机器零件的更换. 在0时刻,安装上一个新零件并开始运行, 设此零件在\(X_1\)时刻损坏, 马上用一个新的来替换(假定替换不需要时间), 则第二个零件在\(X_1\)时刻开始运行, 设它在经过\(X_2\)时间后损坏, 同样马上换第三个,……. 很自然可以认为这些零件的使用寿命是独立同分布的, 那么到\(t\)时刻为止所更换的零件数目就构成一个更新过程.
注:在更新过程中我们将事件发生一次叫做一次更新, \(X_n\)就是第\(n-1\)次和第\(n\)次更新相距的时间, \(T_n\)是第\(n\)次更新发生的时刻, 而\(N(t)\)就是\(t\)时刻之前发生的总的更新次数.
更新过程\(\{N(t), t \geq 0 \}\)是泊松过程的推广, 其事件(更新)发生的时间间隔仍为独立同分布但不要求是指数分布。
注:从更新过程定义看出, 如果将某次更新时刻\(T_k\)作为新的时间原点, 则此后的计数过程仍是相同的更新过程。 即: \[ N^*(t) = N(T_k + t) - N(T_k), \ t \geq 0, \] 是与\(\{N(t), t \geq 0\}\)分布相同的更新过程。 若已知\(T_k = t_0\), 则\(N^*(t) = N(t_0+t)-N(t_0)\)是与\(\{N(t), t \geq 0\}\)分布相同的更新过程, 且与\(\{N(t), t \in [0, t_0] \}\)独立。
更新过程不再是平稳独立增量过程。 举例说明。
例4.1 设\(X_i \sim U(1, 2)\), 则两次更新之间的时间间隔至少为1,至多为2。 这时 \[\begin{aligned} & P(N(1) - N(0) = 1) = 0, \\ & P(N(2) - N(1) = 1) = 1, \end{aligned}\] 所以不是平稳增量的。
考虑\(N(1.1) - N(1)\)与\(N(2) - N(1.1)\)是否独立。 当\(N(1.1) - N(1) = 1\)时, 第一次更新\(T_1\)发生于\((1, 1.1]\), \(T_2 = T_1 + X_2 \in (2, 3.1]\), 所以 \[\begin{aligned} P(N(2) - N(1.1) = 1 \,|\, N(1.1) - N(1) = 1) = 0 ; \end{aligned}\] 当\(N(1.1) - N(1) = 0\)时, 第一次更新\(T_1\)发生于\((1.1, 2]\), \[\begin{aligned} P(N(2) - N(1.1) = 1 \,|\, N(1.1) - N(1) = 1) = 1 , \end{aligned}\] 这说明\(N(1.1) - N(1)\)与\(N(2) - N(1.1)\)不独立, 即非独立增量。
4.1.2 性质
命题4.1 \[ N(t) \geq n \Longleftrightarrow T_n \leq t . \]
下面的命题说明有限时间内不会有无穷次更新发生, 从而\(N(t)\)是普通的取非负整数值的随机变量。
命题4.2 \[ P(N(t) < \infty) = 1 . \]
证明: 令\(\mu = EX_1\), 因为\(X_1 \geq 0\)且\(P(X_1 = 0) < 1\)所以\(0 < \mu \leq +\infty\)。
如果\(0 < \mu < \infty\),由强大数律可知 \[ \frac{1}{n} T_n = \frac{1}{n} \sum_{i=1}^n X_i \to \mu, \ \text{a.s.} \] 对任意给定的\(t > 0\), 以概率1地对每一条轨道,\(T_n \to \infty\), 存在\(n_0\)使得\(n \geq n_0\)时\(T_n > t\), 即\(t\)之前仅有有限个更新发生, 即以概率1地成立\(N(t) < \infty\)。
如果\(\mu = +\infty\), 必存在\(t_0 > 0\)使得\(P(X_n \leq t_0) > 0\), 令\(Y_n = X_n I[X_n \leq t_0]\), 则\(Y_n \leq X_n\)且\(0 < E Y_n \leq t_0 < \infty\), 以\(\{Y_i\}\)为更新间隔时间的更新过程的更新次数以概率1为有限值, 而以\(\{X_i\}\)为更新间隔时间的更新过程比\(\{Y_i\}\)对应的更新过程的每次更新发生更晚, 所以更新次数以概率1为有限值。
前面的命题说明\(N(t)\)是一个取非负整数值的随机变量。 考虑\(N(t)\)的分布。 更新过程\(N(t)\)分布第一个公式:
命题4.3 \[ P(N(t)=n) = F_n(t) - F_{n+1}(t), \ t \geq 0, n=0,1,2,\dots \] 其中\(F_n(\cdot)\)是\(T_n\)的分布函数, 为\(F(\cdot)\)的\(n\)重卷积, \(F(\cdot)\)是\(X_1\)的分布函数。
证明: \[ N(t) \geq n \Longleftrightarrow T_n \leq t, \] 所以 \[\begin{aligned} & P(N(t) = n) \\ =& P(N(t) \geq n) - P(N(t) \geq n+1) \\ =& P(T_n \leq t) - P(T_{n+1} \leq t) \\ =& F_n(t) - F_{n+1}(t) . \end{aligned}\]
更新过程边缘分布的第二个公式(来自(Ross 2019) P.434):
命题4.4 \[ P(N(t) = n) = \int_0^t \overline{F}(t - y) \, dF_{n}(y) = \int_0^t \overline{F}(t - y) f_{n}(y) \,dy . \] 其中\(\overline{F}(x) = 1 - F(x)\), \(f_n(\cdot)\)是\(T_n\)的分布密度函数(如果存在)。
证明: 以\(T_n\)为条件求\(I[N(t) = n]\)的条件期望。 \[\begin{aligned} & P(N(t) = n) \\ =& E \left\{ E \left( I[N(t) = n] | T_n \right) \right\} \\ =& \int_0^\infty P(N(t) = n | T_n = y) \,d F_n(y) \\ =& \int_0^t P(N(t) = n | T_n = y) \,d F_n(y) \\ & ( \text{因为} y>t \text{从而} T_n > t \text{时必有} N(t) < n) \\ =& \int_0^t P(X_{n+1} > t-y | T_n = y) \,d F_n(y) , \end{aligned}\] 最后一式是因为在\(T_n=y\)(\(y \in (0,t]\))条件下, \(N(t) = n\)当且仅当第\(n+1\)次更新不发生在\((y, t]\)内, 即\(X_{n+1}>t-y\)。 于是 \[\begin{aligned} & P(N(t) = n) \\ =& \int_0^t P(X_{n+1} > t-y ) \,d F_n(y) \\ & (\text{因为} X_{n+1} \text{与} T_n \text{独立}) \\ =& \int_0^t \overline{F}(t-y) \,d F_n(y) . \end{aligned}\]
\(N(t) < +\infty\), a.s.并不能保证\(E N(t) < \infty\)。 下面的定理表明\(E N(t) < \infty\)且给出了一个计算公式。
定理4.1 级数 \[ M(t) = \sum_{n=1}^\infty F_n(t), \ t \geq 0 \] 收敛, \(M(t), t \geq 0\)是单调不减函数, 且 \[ M(t) = E N(t), \ t \geq 0 , \]
分段来证明这个定理。
引理4.1 设\(\{ a_n \}\)为非负数列, 则级数\(\sum_{n=1}^\infty a_n\)收敛或者等于\(+\infty\), 且结果与求和次序无关。
证明见§4.5.1。
推论4.1 正项的二重级数可以按任意次序计算, 可以交换次序计算。
引理4.2 设\(Y\)为取非负整数值的随机变量, 则 \[ E Y = \sum_{n=1}^\infty P(Y \geq n) . \]
证明
\[\begin{aligned} & \sum_{n=1}^\infty P(Y \geq n) = \sum_{n=1}^\infty \sum_{k=n}^\infty P(Y = k) \\ =& \sum_{k=1}^\infty \sum_{n=1}^k P(Y=k) = \sum_{k=1}^\infty k P(Y=k) \\ =& \sum_{k=0}^\infty k P(Y=k) = E Y . \end{aligned}\]
更新时间的序列为\(T_n, n=1,2,\dots\), 相应的分布函数为\(F_n(t), t \geq 0\)。
引理4.3 \[ E N(t) = \sum_{n=1}^\infty F_n(t) . \]
证明:因为\(N(t)\)是取非负整数值的随机变量,所以 \[\begin{aligned} E N(t) =& \sum_{n=1}^\infty P(N(t) \geq n) \\ =& \sum_{n=1}^\infty P(T_n \leq t) \\ =& \sum_{n=1}^\infty F_n(t) . \end{aligned}\] 这里用到了\(N(t) \geq n \Longleftrightarrow T_n \leq t\)。
下面证明级数\(\sum_{n=1}^\infty F_n(t)\)收敛, 而且通项是以负指数速度衰减的。 此级数定义的函数显然是单调增的。
引理4.4 对任意\(t \geq 0\), 存在\(0 < \alpha < 1\)使得 \[\begin{aligned} F_n(t) = O(\alpha^n), \end{aligned}\] 从而 \[\begin{aligned} \sum_{n=1}^{\infty} F_n(t) < \infty . \end{aligned}\]
::: {.corollary ren-prop-Mtconv-ineq} 若\(F(x)< 1\),\(\forall x \geq 0\), 则 \[ M(t) \leq \frac{F(x)}{1 - F(x)} . \]
证明: \(F_n(x) = P(X_1 + \dots + X_n \leq x)\), 若\(X_1 + \dots + X_n \leq x\)成立, 则\(X_i \leq x\), \(i=1,\dots,n\)都成立。 于是 \[\begin{aligned} F_n(x) \leq& P(X_1 \leq x, \dots, X_n \leq x) \\ =& P(X_1 \leq x) \dots P(X_n \leq x) = [F(x)]^n, \end{aligned}\] 从而 \[\begin{aligned} M(x) =& \sum_{n=1}^\infty F_n(x) \\ \leq& \sum_{n=1}^\infty [F(x)]^n \\ =& \frac{1}{1 - F(x)} - 1 \\ =& \frac{F(x)}{1 - F(x)} . \end{aligned}\]
例4.2 考虑一个时间离散的更新过程\(\{ N_j, j=1, 2, \dots\}\), 在每个时刻独立地做Bernoulli试验, 设成功的概率为\(p\), 失败的概率为\(q=1-p\). 以试验成功做为事件(更新), 求此过程的更新函数\(M(k)\)。
解: 首先, 易知更新的时间间隔\(\{X_i\}\)为独立的同几何分布 \[ P(X_i = k) = q^{k-1} p, \ k=1, 2, \dots \] 则第\(r\)次成功(更新)发生的时刻\(T_r = \sum_{i=1}^r X_i\)服从Pascal分布 \[ P(T_r = k) = \binom{k-1}{r-1} q^{k-r} p^r, \ k = r,r+1, \dots \] 因此 \[\begin{aligned} & P(N_n = r) \\ =& P(N_n \geq r) - P(N_n \geq r+1) \\ =& P(T_r \leq n) - P(T_{r+1} \leq n) \\ =& \sum_{k=r}^n \binom{k-1}{r-1} q^{k-r} p^r - \sum_{k=r+1}^n \binom{k-1}{r} q^{k-r-1} p^{r+1} \\ =& \binom{n}{r} p^r q^{n-r} , \ r=0,1,\dots,n . \end{aligned}\] 上面的最后一个等式可以直接证明, 或者注意到\(N_n\)是\(n\)次Bernoulli实验中的成功次数, 于是服从上述的二项分布B(\(n, p\))。 所以,更新函数为 \[ M(n) = E[N_n] = \sum_{r=0}^n r P(N_n=r) = n p . \]
4.2 更新方程及其应用
随机过程研究中经常以某个早期发生事件为条件导出方程, 更新方程就是其中的一个常见形式。
4.2.1 更新方程
定义4.2 在\(M(t)\)的导数存在的条件下, 其导数\(M'(t)\)称为更新密度, 记为\(m(t)\). 由\(M(t) = \sum_{n=1}^{\infty} F_n(t)\)两边求导得 \[ m(t) = \sum_{n=1}^{\infty} f_n(t) , \] 其中\(f_n(t)\)是\(F_n(t)\)的密度函数.
\(M(t)\)是到\(t\)时刻为止的平均更新次数, \(m(t)\)就是瞬时的单位时间平均更新次数。
定理4.2 \(M(t)\)和\(m(t)\)分别满足积分方程 \[\begin{align} M(t) =& F(t) + \int_0^t M(t-s) \,dF(s) \tag{4.1} \\ m(t) =& f(t) + \int_0^t m(t-s) f(s) \,ds . \tag{4.2} \end{align}\] 其中\(f(t)=F'(t)\).
证明: 只要证明第一式, 第二式由第一式两边取导数可得. 由定义可得 \[\begin{aligned} M(t) =& \sum_{n=1}^{\infty} F_n(t) = F(t) + \sum^{\infty}_{n=2} F_n(t) \\ =& F(t) + \sum^{\infty}_{n=2} \int_0^t F_{n-1}(t-s) \,dF(s) \\ =& F(t) + \int_0^t \sum^{\infty}_{n=2} F_{n-1}(t-s) \,dF(s) \quad (\text{由单调收敛定理}) \\ =& F(t) + \int_0^t M(t-s) \,dF(s) \\ =& F(t) + (F \ast M)(t) . \end{aligned}\]
定义4.3 (更新方程) 称如下形式的积分方程为更新方程 \[\begin{equation} K(t) = H(t) + \int_0^t K(t-s) \,dF(s) , \ t \geq 0 . \tag{4.3} \end{equation}\] 其中\(H(t)\), \(F(t)\)为已知, 且当\(t<0\)时\(H(t)\), \(F(t)\)均为0. 当\(H(t)\)在任意闭区间有界时, 称上述方程为适定(Proper)更新方程, 简称为更新方程.
更新方程可以用卷积记号写成 \[\begin{equation} K(t) = H(t) + (F * K)(t), \ t \geq 0 , \tag{4.4} \end{equation}\] 其中函数\(K(\cdot)\)为未知的函数。 \(H\)和\(F\)已知, 一般\(F\)为单调增有界函数。
命题4.5 假设\(B(t)\), \(B_1(t)\), \(B_2(t)\)是单调增加的右连续函数, 且\(B(0)=0\). \(C(t)\), \(C_1(t)\), \(C_2(t)\)为光滑有界函数(注:这些条件可以保证卷积有定义), 则有 \[\begin{aligned} (1)\ & \max_{0 \leq t \leq T} |(B \ast C)(t)| \leq \max_{0 \leq t \leq T} |C(t)| \cdot B(T); \\ (2)\ & (B \ast C_1)(t) + (B \ast C_2)(t) = (B \ast (C_1 + C_2))(t); \\ (3)\ & (B_1 \ast C)(t) + (B_2 \ast C)(t) = ((B_1 + B_2) \ast C)(t); \\ (4)\ & (B_1 \ast (B_2 \ast C))(t) = ((B_1 \ast B_2) \ast C)(t) . \end{aligned}\]
证明略。
定理4.3 设更新方程中\(H(t)\)为在任意闭区间有界的函数, \(F(t)\)为\([0, \infty)\)上的分布函数, 则方程在有限区间内存在唯一的闭区间有界解 \[\begin{align} K(t) = H(t) + \int_0^t H(t-s) dM(s) , \ t \geq 0 . \tag{4.5} \end{align}\] 其中\(M(t) = \sum_{n=1}^{\infty} F_n(t)\)是分布函数\(F(t)\)的更新函数.
更新方程的解又可以用卷积记号写成 \[\begin{align} K(t) = H(t) + (M*H)(t), \ t \geq 0 . \tag{4.6} \end{align}\]
证明: 我们先证(4.5) 满足闭区间有界性条件。
由\(M(t)\)是更新函数, 由定理4.1可知\(M(t)\)在任意闭区间有界且单调不减, 再由\(H(t)\)闭区间有界, 对任意\(T > 0\),有 \[\begin{aligned} \sup_{0 \leq t\leq T} |K(t)| \leq\ & |H(t)| + \int_0^T \sup_{0 \leq s \leq T} |H(T-s)| \, dM(s) \\ \leq\ & \sup_{0 \leq t\leq T}|H(t)| (1 + M(T)) < \infty . \end{aligned}\] 所以在任意闭区间上\(K(t)\)是有界的.
再来证明(4.5)确实是更新方程的解, 这只要证明\((F*K)(t) = (M*H)(t)\)。事实上, \[\begin{aligned} (F*K)(t) =& (F*(H + M*H))(t) \\ =& (F*H)(t) + (F*(M*H))(t) \\ =& (F*H)(t) + ((F*M)*H)(t) \\ =& ((F + F*M)*H)(t) \\ & \quad (\text{由卷积性质(3)}) \\ =& (M*H)(t) , \end{aligned}\] 最后一个等式利用了定理4.2。 所以,(4.5)确实是更新方程的解。
最后证明惟一性, 只需证明更新方程的任何解都有(4.5)式的形式. 设\(\tilde{K}(t)\)是更新方程的解,即 \[ \tilde K = H + F * \tilde K . \] 并且满足闭区间有界性条件。 \(\forall T > 0\), 设 \[ |K(t)| \leq B, | \tilde K(t)| \leq B, \ \forall t \in [0, T] . \] 连续代换\(\tilde{K}(t)\), 有 \[\begin{aligned} \tilde{K}(t) =& H(t) + (F \ast \tilde K)(t) \\ =& H(t) + (F\ast(H + F \ast \tilde{K}))(t) \\ =& H(t) + (F \ast H)(t) + (F \ast (F \ast \tilde{K}))(t) \\ =& H(t) + (F \ast H)(t) + (F_2 \ast \tilde{K})(t) \\ =& H(t) + (F \ast H)(t) + (F_2 \ast (H + F \ast \tilde{K}))(t) \\ =& H(t) + (F \ast H)(t) + (F_2 \ast H)(t) + (F_3 \ast \tilde{K})(t) \\ =& \cdots \cdots \\ =& H(t) + \left[\left(\sum^{n-1}_{k=1} F_k \right) \ast H \right](t) + (F_n \ast \tilde{K})(t). \end{aligned}\] 同理有 \[ K(t) = H(t) + \left[\left(\sum^{n-1}_{k=1} F_k \right) \ast H \right](t) + (F_n \ast K)(t) , \] 于是 \[ K(t) - \tilde K(t) = (F_n * (K - \tilde K))(t) . \] \(\forall t \in [0, T]\), 由\(M(T) = \sum_{n=1}^\infty F_n(T)\)收敛可知 \[ \lim_{n \to \infty} \sup_{t \in [0,T]} F_n(t) \leq \lim_{n \to \infty} F_n(T) = 0 . \] 而 \[\begin{aligned} (F_n * |K - \tilde K|)(t) =& \int_0^t |K - \tilde K|(t-s) \,dF_n(s) \\ \leq& 2 B \int_0^t \,dF_n(s) = 2 B F_n(t) \to 0 \ (n \to \infty), \end{aligned}\] 所以对\(0 \leq t \leq T\), \[\begin{aligned} |K(t) - \tilde K(t)| =& \left| F_n * (K - \tilde K)(t) \right| \\ \leq& (F_n * |K - \tilde K|)(t) \to 0 , \end{aligned}\] 即\(K(t) = \tilde K(t)\), 由\(T\)和\(t\)的任意性可知 \[ \tilde K(t) = K(t), \ t \geq 0 , \] 这就证明了闭区间有界解的唯一性。
例4.3 (Wald等式) 对更新过程设\(E X_1 < \infty\), \(i=1,2,\dots\), 证明 \[ E(T_{N(t) + 1}) = E(X_1 + X_2 + \cdots + X_{N(t)+1}) = EX_1 E(N(t)+1). \]
证明: \(N(t) + 1\)是\((t, \infty)\)区间内的首次更新的序号, \(T_{N(t) + 1}\)是\((t, \infty)\)区间内的首次更新时刻, 或\(t\)之后(不含)的首次更新时刻。
对第一次更新的时刻\(X_1\)取条件, 令\(X_1 = x\), 条件期望 \[ E(T_{N(t)+1} | X_1 = x) = \begin{cases} x & \text{若} x > t , \\ x + E(T_{N(t-x) + 1}) & \text{若} x \leq t . \end{cases} \] 事实上,如果\(X_1 = x > t\), 则\([0, t]\)内没有更新, \(N(t) + 1 = 1\), \(T_{N(t) + 1} = X_1 = x\)。 如果\(X_1 = x \leq t\), 则\([0, t]\)内至少有一次更新, \(N(t) + 1 \geq 2\), 更新过程可以从\(x\)时刻重新开始, 所以\(t\)时刻之后的首次更新时刻的条件期望等于以\(x\)为新的时间原点时的\(t-x\)之后首次更新的时间的期望。
记\(K(t) = E(T_{N(t+1)})\), 则 \[\begin{aligned} K(t) =& E[T_{N(t)+1}] = E\left[ E(T_{N(t)+1} | X_1) \right] \\ =& \int_0^{\infty} E(T_{N(t)+1} | X_1 = x) \,dF(x) \\ =& \int_t^{\infty} x \, dF(x) + \int_0^t [x + K(t-x)] \,dF(x) \\ =& \int_0^\infty x \, dF(x) + \int_0^t K(t-x) \,dF(x) \\ =& EX_1 + \int_0^t K(t-x) \, dF(x). \end{aligned}\]
这是更新方程, 由定理定理4.3知 \[\begin{aligned} K(t) =& E X_1 + \int_0^t (E X_1) \, dM(x) \\ =& E(X_1) \cdot (1+M(t)) \\ =& E(X_1) \cdot (E[N(t)+1]) . \end{aligned}\]
注:教材中给出的利用独立性的证明是错误的, 因为在\(N(t) = 1\)条件下\(X_1\)的分布有变化。 事实上,\(N(t) + 1\)是\(\{X_n, n=1,2,\dots \}\)的一个停时, 可以利用停时证明Wald等式,见6.3。
例4.4 (更新过程的余寿) 设\(\{N(t), t \geq 0 \}\)为更新过程, \(X_i\)表示第\(i\)次更新与上次更新的间隔时间(\(i=1,2,\dots\)), 比如,\(X_i\)是某产品(如电池)的寿命。 设\(X_1 \sim F(x)\)。 令\(T_n = \sum_{i=1}^n X_i\)为第\(n\)次更新的时间, 也是第\(n\)个产品的失效时间。 令 \[ r(t) = T_{N(t)+1} - t \] 为\(t\)时刻的剩余寿命, 证明\(r(t)\)的分布为 \[\begin{align} P(r(t) > y) = \bar F(t+y) + \int_0^t \bar F(t+y-x) \,d M(x) , \ y > 0 . \tag{4.7} \end{align}\]
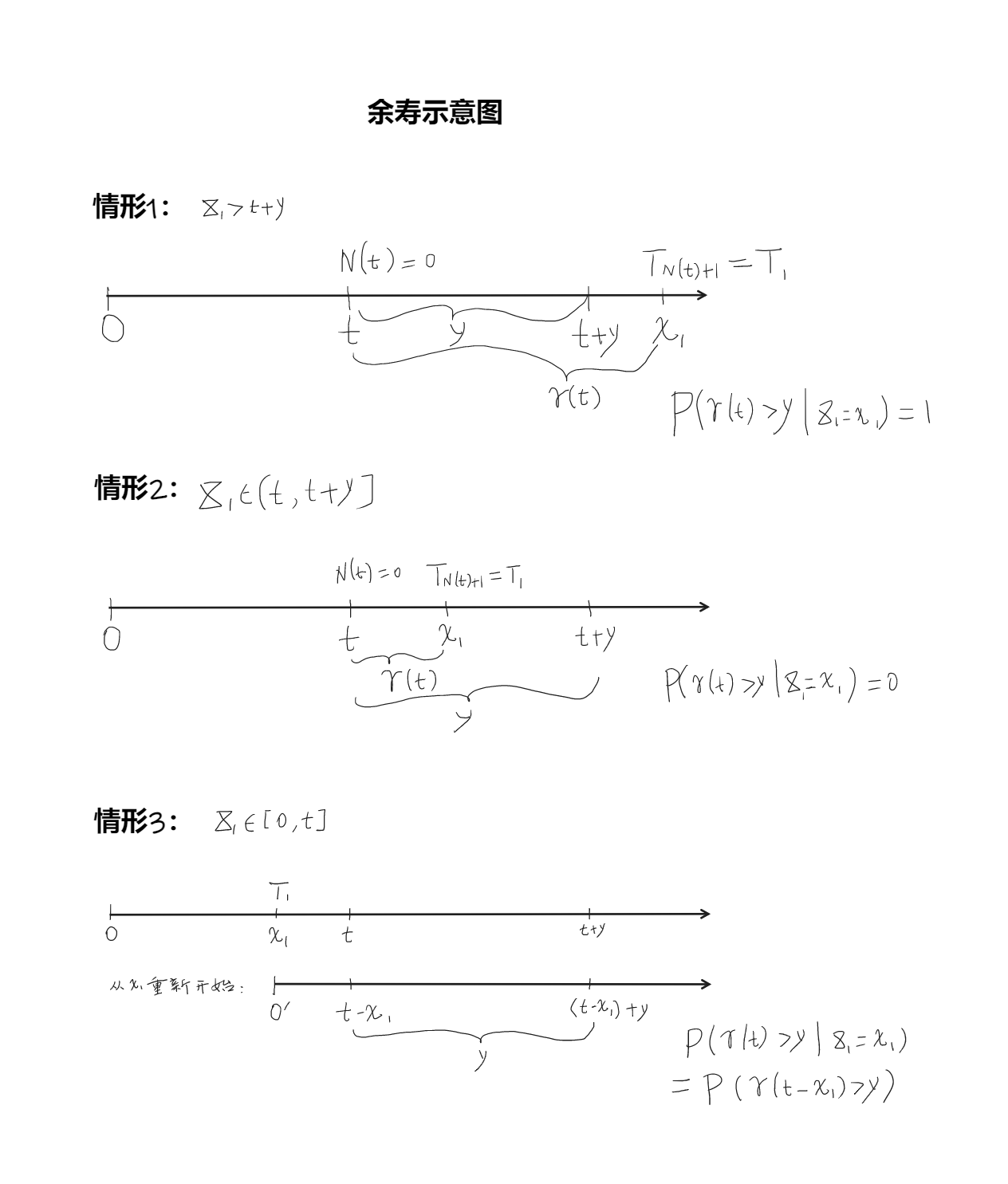
证明: 令 \[ \bar R_y(t) = P(r(t) > y), \ y > 0 . \]
对第一次更新时间\(T_1 = X_1\)取条件, 设\(X_1 = x\), 若\(x > t+y\), 则第一个产品在时刻\(t+y\)还在工作, 从\(t\)时刻开始计算的余寿\(>y\), 于是这时 \[ P(r(t) > y | X_1 = x) = 1; \] 若\(t < x \leq t + y\), 则第一个产品的更新发生在\((t, t+y]\)之间, 这时\(N(t)=0\), \(T_{N(t)+1} = T_1 = X_1 = x \leq t+y\), 从\(t\)时刻开始计算的余寿\(\leq y\), 所以这时 \[ P(r(t) > y | X_1 = x) = 0; \] 若\(0 < x \leq t\), 则\(N(t) \geq 1\), 更新过程从\(x\)时刻重新开始, 这时有 \[ P(r(t) > y | X_1 = x) = \bar R_y(t-x) . \]
总之有 \[ P(r(t) > y | X_1 = x) = \begin{cases} 1, & x > t+y, \\ 0, & t < x \leq t + y \\ \bar R_y(t-x), & 0 < x \leq t . \end{cases} \]
由全期望公式, \[\begin{aligned} \bar R_y(t) =& E \left\{ E\left( I[r(t) > y] | X_1 \right) \right\} \\ =& \int_0^\infty E\left( I[r(t) > y] | X_1 = x \right) \,dF(x) \\ =& \int_0^\infty P\left( r(t) > y | X_1 = x \right) \,dF(x) \\ =& \int_{t+y}^\infty 1 \cdot d F(x) \\ & + \int_t^{t+y} 0 \cdot d F(x) \\ & + \int_0^t \bar R_y(t-x) d F(x) \\ =& 1 - F(t+y) + \int_0^t \bar R_y(t-x) d F(x), \end{aligned}\] 记\(\bar F(x) = 1 - F(x)\), 由定理4.3得 \[ \bar R_y(t) = \bar F(t+y) + \int_0^t \bar F(t+y-x) \,d M(x) . \]
例4.5 (泊松过程的余寿) 设\(\{N(t), t \geq 0 \}\)为速率\(\lambda\)的泊松过程, \(r(t)\)为\(t\)时刻的剩余寿命, 证明\(r(t)\)服从参数为\(\lambda\)的指数分布, 这称为泊松过程的无记忆性。
证明: 由例4.4得 \[ P(r(t) > y) = \bar F(t+y) + \int_0^t \bar F(t+y-x) \,d M(x) , \ y > 0 . \]
对泊松过程, \(X_1\)服从参数\(\lambda\)的指数分布, \[\begin{aligned} \bar F(x) =& e^{-\lambda x}, x > 0, \\ M(t) =& E N(t) = \lambda t , \end{aligned}\] 所以有 \[\begin{aligned} & P(r(t) > y) \\ =& e^{-\lambda (t+y)} + \int_0^t e^{-\lambda (t+y-x)} \lambda \,dx \\ =& e^{-\lambda (t+y)} \left[ 1 + \int_0^t d e^{\lambda x} \right] \\ =& e^{-\lambda y}, \ y > 0, \end{aligned}\] 即泊松过程时刻\(t\)处的余寿分布为参数为\(\lambda\)的泊松分布, 与所处时刻和已经发生的更新次数都没有关系。
4.2.2 更新方程在人口学中的一个应用
考虑一个确定性的人口模型:
- \(B(t)\)表示在时刻\(t\)女婴的出生率, 即在\([t,t+dt]\)时间区间内有\(B(t)dt\)个女婴出生. 已知过去的\(B(t)\)(\(t \leq 0\)), 要预测未来的\(B(t)\)(\(t>0\))。
- 假定生存函数为\(S(x)\)(指一个新生女婴能够活到年龄\(x\)的概率)已知;
- 假定生育的年龄强度为\(\beta(x)(x>0)\)(指年龄为\(x\)的母亲生育女婴的速率, 即\(\beta(x)dt\)为这个母亲在长度为\(dt\)的时间区间内生下的女婴数)已知.
考虑对给定\(t > 0\)时刻, 年龄段\([x, x + dx]\)的女性, 她们出生于\([t - x - dx, t - x]\)时间段, 该时间段内有\(B(t-x)dx\)个女婴出生, 但到\(t\)时刻存活的人数为\(B(t-x) S(x) dx\), 这些人在\([t, t+dt]\)时间段将生育女婴\(B(t-x) S(x) \,dx \cdot \beta(x) \,dt\)个。 将\(t\)时刻的所有年龄的育龄妇女生出的女婴个数求和, 即求积分, 得到在\([t, t+dt]\)时间段内出生的女婴个数为 \[\begin{align} B(t) \,dt = \int_0^{\infty} B(t-x) S(x) \beta(x) \,dx \,dt . \tag{4.8} \end{align}\]
根据过去与未来的生育情况, 将上述积分分成两段 \[\begin{align} B(t) \,dt =& \int_t^{\infty} B(t-x) S(x) \beta(x) \,dx \,dt \\ + & \int_0^t B(t-x) S(x) \beta(x) \,dx \,dt . \tag{4.9} \end{align}\] (4.9)的第一个积分中\(t - x < 0\),\(B(t-x)\)已知; 第二个积分中\(t - x \geq 0\), \(B(t-x)\)未知。 消去(4.9)中的\(dt\), 记\(f(x)=S(x)\beta(x)\), \(H(t) = \int_t^{\infty} B(t-x) S(x) \beta(x) \,dx\), 则 \[ B(t) = H(t) + \int_0^t B(t-x) f(x) \,dx . \] 这是一个更新方程, 对\(H(t)\)积分作变量替换\(x=y+t\), 得 \[ H(t) = \int_0^{\infty} B(-y) S(y+t) \beta(y+t) \,dy . \]
注意\(H(t)dt\)是由年龄为\(t\)或更大的女性在时间\([t,t+dt]\)之间生育的女婴数, 此外, 每一个新生的女婴将期待在年龄\(x\)与\(x+dx\)之间生育\(f(x)dx\)个女婴. 于是,每一新生女婴在死亡或生存到年龄\(x\)之前(不论哪种情况先发生)将期待生育\(F(x) = \int_0^x f(s)ds\)个女婴, 从而在她一生中将期待生育\(F(\infty)\)个女婴.
若\(F(\infty)>1\), 可以解得\(B(t) \sim C e^{R t}\), \(t \to \infty\)(解的过程略), 其中\(C\)为常数, \(R > 0\)满足方程 \[ \int_0^{\infty} e^{-Ry} S(y) \beta(y) \, dy = 1 . \] 即出生速率(以及具有此速率的人群)将以渐近指数速度爆炸性增长. 若\(F(\infty) < 1\), 则\(B(t) \sim C e^{-R t}\), \(B(t)\)渐近负指数地趋于0, 也就是说人群最终要消亡, 只有当\(F(\infty)=1\)时, 出生速率将最终趋于一个有限的正数.
4.3 更新定理
4.3.1 Feller基础更新定理
\(N(t)\)的分布虽然可以通过\(F_n(t)\)计算, 但是很困难, 我们更关心极限情况下平均更新速率这样的问题。 在第3章中我们已经知道, 强度为\(\lambda\)的泊松过程的两次事件发生的时间间隔\(X_n\)服从参数为\(\lambda\)的指数分布, 且其更新函数 \[ M(t) = E[N(t)] = \lambda t, \] 于是 \[ \lim_{t\to\infty} \frac{M(t)}{t} = \lambda = \frac{1}{E[X_n]} . \] 那么,对于一般的更新过程是否还有这种性质呢? 有如下的极限(elementary renewal theorem)。
定理4.4 (Feller初等更新定理) 记\(\mu = EX_n\), 则 \[\begin{align} \lim_{t \to \infty} \frac{M(t)}{t} = \frac{1}{\mu} . \tag{4.10} \end{align}\] 其中\(\mu = +\infty\)时\(\frac{1}{\mu} = 0\)。
证明: 首先假设\(\mu < \infty\)。 注意到\(T_{N(t)+1}\)是\(t\)时刻之后第一次更新的时间,所以 \[ T_{N(t)+1} > t . \] 两边取期望, 利用Wald等式(见例4.3)得 \[ \mu [M(t) + 1] > t . \] 于是 \[ \frac{M(t)}{t} > \frac{1}{\mu} - \frac{1}{t} , \] 从而推出 \[\begin{align} \liminf_{t \to \infty} \frac{M(t)}{t} \geq \frac{1}{\mu}. \tag{4.11} \end{align}\]
另一方面,固定常数\(B>0\), 令 \[ X^c_n = \begin{cases} X_n, & X_n \leq B \\ B,& X_n > B, \end{cases} \] 则 \[ X^c_n \leq B, \quad X^c_n \leq X_n, \] \(X^c_n, n=1,2,\dots\)确定了一个新的更新过程,记 \[\begin{aligned} T^c_n =& \sum_{i=1}^n X^c_i , \\ N(t)^c =& \sup\{ n: T^c_n \leq t \} . \end{aligned}\] 由于\(X^c_n \leq B\), 则 \[ T^c_{N^c(t) + 1} = T^c_{N^c(t)} + X^c_{N^c(t) + 1} \leq t + B . \] 再利用Wald等式得 \[ [M^c(t) + 1] \cdot \mu_B \leq t + B, \] 其中\(\mu_B = E(X^c_n)\), \(M^c(t) = E[N^c(t)]\), 由上式得 \[ \frac{M^c(t)}{t + B} \leq \frac{1}{\mu_B} - \frac{1}{t + B}, \] 从而 \[ \limsup_{t \to \infty} \frac{M^c(t)}{t} \leq \frac{1}{\mu_B} . \] 又因为\(X^c_n \leq X_n\), 得\(T^c_n \leq T_n\), \(N^c(t) \geq N(t)\), \(M^c(t) \geq M(t)\), 于是 \[ \limsup_{t \to \infty} \frac{M(t)}{t} \leq \frac{1}{\mu_B} . \] 令\(B \to \infty\), 有\(X^c_n \to X_n\), \(E(X^c_n) \to EX_n\)(控制收敛定理), 即 \[ \mu_B \to \mu , \ (B \to \infty) , \] 所以 \[\begin{align} \limsup_{t \to \infty} \frac{M(t)}{t} \leq \frac{1}{\mu} . \tag{4.12} \end{align}\]
利用由(4.11)和(4.12)式可得\(\mu<\infty\)时 \[ \lim_{t \to \infty} \frac{M(t)}{t} = \frac{1}{\mu} . \]
当\(\mu=\infty\)时, 仍有 \[ \limsup_{t \to \infty} \frac{M(t)}{t} \leq \frac{1}{\mu_B} , \] 当\(B \to \infty\)时, \(\mu_B \to \infty\), 所以\(\limsup_{t \to \infty} \frac{M(t)}{t} = 0\), 即\(\lim_{t \to \infty} \frac{M(t)}{t} = 0\), 所以\(\mu = +\infty\)时定理结论成立.
注: 设\(X \geq 0\), \(EX = +\infty\), \(X_B = X I_{\{X \leq B\}} + B I_{\{X > B\}}\), 则\(E(X_B) \to \infty\)(\(B \to \infty\))。 事实上, 易见\(E(X_B)\)是\(B\)的单调增函数, 取\(B = n\),由单调收敛定理有 \[ \lim_{n \to \infty} E(X_n) \geq \lim_{n \to \infty} E[X I_{\{ X \leq n \}}] = E(X) = +\infty, \] 所以\(\lim_{B \to \infty} E(X_B) = +\infty\)。
考虑\(N(t)/t\)的极限。 先给出两个有关的极限。
命题4.6 若\(0 < E(X_1) < \infty\),则 \[ \lim_{n\to\infty} \frac{S_n}{n} = E(X_1) , \ \text{a.s.} \]
由强大数律直接可得此结论。
命题4.7 若\(0 < E(X_1) < \infty\),则 \[ \lim_{t \to \infty} N(t) = +\infty, \text{ a.s.} \]
证明: 因为\(E(X_1) < \infty\)所以\(X_1 < \infty\), a.s., 于是 \[\begin{aligned} & P(\lim_{t \to \infty} N(t) < \infty) \\ =& P(\text{存在} T \text{使得} t \geq T \text{时} N(t) \text{为常数}) \\ \leq& P(\text{存在} K \text{使得} X_K = +\infty) \\ \leq& \sum_{n=1}^\infty P(X_n = +\infty) = 0 . \end{aligned}\]
命题4.8 若\(0 < E(X_1) < \infty\),则 \[ \lim_{n\to\infty} \frac{N(t)}{t} = \frac{1}{E(X_1)}, \ \text{a.s.} \]
证明: 由命题4.7, \(\lim_{t\to\infty} N(t) = \infty\), a.s., 又已证明\(\lim_{n\to\infty}\frac{S_n}{n} = E(X_1)\), 由复合极限性质知 \[ \lim_{t\to\infty} \frac{S_{N(t)}}{N(t)} = E(X_1) . \] 由 \[ S_{N(t)} \leq t < S_{N(t)+1}, \] 得 \[ \frac{S_{N(t)}}{N(t)} \leq \frac{t}{N(t)} \leq \frac{S_{N(t)+1}}{N(t)+1} \frac{N(t)+1}{N(t)}, \] 于是可知 \[ \lim_{t\to\infty} \frac{t}{N(t)} = E(X_1), \ \text{a.s.}, \] 从而 \[ \lim_{t\to\infty} \frac{N(t)}{t} = \frac{1}{E(X_1)}, \ \text{a.s.} \]
例4.6 某控制器用一节电池供电, 设电池寿命\(X_i(i=1,2,\dots)\)服从均值为45小时的正态分布, 电池失效时需要去仓库领取, 领取新电池的时间\(Y_i(i=1,2,\dots)\)服从期望为0.5小时的均匀分布. 求长时间工作时, 控制器更换电池的速率.
解: 以\(N(t)\)表示到时刻\(t\)为止更换电池的次数, 平均更新时间为\(E[X_i+Y_i]=45.5\)小时.
由初等更新定理(Feller),更换电池的速率为 \[ \lim_{t \to \infty} \frac{M(t)}{t} = \frac{1}{45.5} \text{(次/小时)} . \]
例4.7 考虑离散时间的更新过程\(N(n),n=0,1,2,\dots\), 在每个时间点独立地做Bernoulli试验, 设试验成功的概率为\(p\),失败的概率为\(q=1-p\), 以试验成功作为更新事件, 以\(M(n)\)记此过程的更新函数, 求其更新率\(\lim_{n \to \infty} \frac{M(n)}{n}\).
解: 相邻两次试验成功的时间间隔\(X_i\)的分布为几何分布, \(P\{ X_i = k \} = p q^{k-1}\), \(k=1,2,\dots\),
平均更新时间为几何分布的期望值: \[\begin{aligned} E[X_1] =& \sum_{k=1}^{\infty} k p q^{k-1} = p \sum_{k=1}^{\infty} (q^{k})' \\ =& p \left(\sum_{k=1}^{+\infty}q^{k}\right)' = p (\frac{q}{1-q})' =\frac{1}{p} . \end{aligned}\]
由初等更新定理(Feller)有 \[ \lim_{n \to \infty} \frac{M(n)}{n} = \frac{1}{E[X_1]}=p . \]
这个例子不用更新定理也能解决。 实际上, \(N(n) \sim \text{B}(n, p)\), 所以\(M(n) = E[N(n)] = n p\), \(\frac{M(n)}{n} = p\)。
例4.8 某电话交换台的电话呼叫次数服从平均1分钟\(\lambda\)次的Poisson过程, 通话时间\(Y_1,Y_2,\cdots\)是相互独立且服从同一分布的随机变量序列, 满足 \(E[Y_1]<\infty\), 假定通话时电话打不进来, 用\(N(t)\)表示到时刻\(t\)为止电话打来的次数, 试证 \[ \lim_{n \to \infty} \frac{E[N(t)]}{t} = \frac{\lambda}{1 + \lambda E[Y_1]} . \]
解:
简化地考虑, 每次通话结束, 平均等待有电话打入的时间是\(1/\lambda\), 平均通话时间是\(E(Y_1)\), 所以通话结束之间的间隔\(X_1\)的期望是\(\frac{1}{\lambda} + E(Y_1)\)。 在第一次通话结束之后, 由泊松过程的无记忆性, 可以将此刻作为新的电话开始打入时刻, 所以第一次通话结束到第二次通话结束之间的间隔\(X_2\)与\(X_1\)同分布且独立, 同理可知各\(X_1, X_2, \dots\)独立同分布, 构成更新过程的间隔时间, 于是 \[ \lim_{n \to \infty} \frac{E[N(t)]}{t} = \frac{1}{\frac{1}{\lambda} + E(Y_1)} = \frac{\lambda}{1 + \lambda E[Y_1]} . \]
下面更严格第证明通话结束时刻的序列为更新过程的发生时间. 以\(X_i\)表示从第\(i-1\)次通话结束到下一次\(i\)次电话打进来并开始通话的间隔时间, \(X_1\)是第一个电话打入的时间。 用\(Z_i\)表示所有电话(接通与未接通)的间隔时间, 则\(\{ Z_i \}\)相互独立服从Exp(\(\lambda\)), 定义了一个速率参数为\(\lambda\)的泊松过程\(\{ \tilde N(t), t \geq 0 \}\), 记为PP(\(\lambda\)), 记第\(n\)个电话的到来时刻为\(\tilde T_n = \sum_{i=1}^n Z_i\)。 记\(W_i = X_i + Y_i\), 来证明\(W_i, i=1,2,\dots\)独立同分布且\(X_i \sim \text{Exp}(\lambda)\)。
第一个电话在\(X_1\)时刻到来并开始通话, 要到\(X_1 + Y_1\)时刻才能继续接听新的电话, 在\(X_1\)到\(X_1 + Y_1\)之间到来的电话被忽略。 以\(X_1 = x_1\), \(Y_1 = y_1\)为条件, 记\(t_1 = x_1 + y_1\), 则\(\tilde N(t_1) \geq 1\), 第\(\tilde N(t_1) + 1\)个电话在\(\tilde T_{\tilde N(t_1) + 1}\)时刻到来并开始通话, 是第二个被接通的电话,所以 \[ X_2 = \tilde T_{\tilde N(t_1) + 1} - t_1 \] 是PP(\(\lambda\))在\(t_1\)时刻的余寿, 服从Exp(\(\lambda\))且不依赖于\(t_1\), 因此\(X_2\)与\((X_1, Y_1)\)独立, 从而\(W_2\)与\(W_1\)独立。 类似可证明\(W_n\)与\(W_1, \dots, W_{n-1}\)独立且\(X_n\)服从Exp(\(\lambda\)), 这样, \(\{W_n = X_n + Y_n \}\)定义了一个更新过程, 平均更新时间为 \[ \mu = E[X_i + Y_i] =\frac{1}{\lambda} + E[Y_1] , \]
例4.9 设有一个单服务员银行, 顾客到达可看作速率为\(\lambda\)的Poisson过程, 服务员为每一位顾客服务的时间是随机变量, 分布为均值为\(\frac{1}{\mu}\)指数分布. 顾客到达门口只能在服务员空闲时才准进来, 服务员忙时顾客则离开不返回. 试求:
(1)顾客进银行的速率;
(2) 服务员工作的时间所占的比例.
解: 这与例4.8模型相同。 用\(X_i\)表示第\(i-1\)个顾客结束服务后下一个顾客到来的间隔, 由泊松过程的无记忆性, \(X_i\)相互独立且服从Exp(\(\lambda\))分布。
(1) 两位进入银行的顾客的平均间隔时间为\(\frac{1}{\lambda} + \frac{1}{\mu}\).
反过来,顾客进银行的速率为\(\frac{\lambda\mu}{\lambda+\mu}\).
(2)服务员工作的时间所占比例 \[ {\frac{1}{\mu}}/({\frac{1}{\lambda}+\frac{1}{\mu}})=\frac{\lambda}{\lambda+\mu} . \]
4.3.2 Blackwell更新定理
\(\mu<\infty\)时,定理4.4可以看做当\(t\to \infty\)时, \(M(t) \sim \frac{t}{\mu}\)(\(\sim\)记号含义是\(\lim_{t\to\infty} \frac{M(t)}{\frac{t}{\mu}} = 1\)). 很自然, 我们会猜想当\(t \to \infty\)时, 对于任意一个\(h\),是否有 \[ M(t+h) - M(t) \to \frac{h}{\mu} \quad (=\frac{t+h}{\mu}-\frac{t}{\mu}) . \] 由这一猜想, 引出了另一个重要的更新定理——Blackwell更新定理. 为了描述这一定理,我们先引入一个新的概念.
定义4.4 (格点分布) 若存在\(d \geq 0\), 使得 \[ \sum_{n=0}^{\infty} P(X=nd) = 1 , \] 称随机变量\(X\)服从格点分布(或称随机变量\(X\)的分布\(F\)是格点分布), 称满足上述条件的最大的\(d\)为此格点分布的周期.
注: 从上述定义只能知道格点分布在不是\(d\)的整数倍处取值的概率为0, 但并不一定所有\(nd, n=0,1,2,\dots\)都有正概率.
定理4.5 (Blackwell更新定理) 记\(\mu =E X_1\),
(1)若\(F\)不是格点分布, 则对一切\(a \geq 0\), \[ \lim_{t\to \infty} [M(t + a) - M(t)] = \frac{a}{\mu} . \]
(2)若\(F\)是格点分布,周期为\(d>0\), 则 \[ \lim_{t\to\infty} P(\text{在} nd \text{处发生更新}) = \frac{d}{\mu}. \]
证明略去。
注: Blackwell定理指出, 在远离原点的某长度为\(a\)的区间内, 更新次数的期望是\(\frac{a}{\mu}\), 直观上这是容易理解的, 因为\(\frac{1}{\mu}\)本来就可以看做长时间后更新过程发生的平均速率(见习题4.3). 但当\(F\)是格点时, \(T_n\)的分布也是格点的, 以\(d\)为周期, 由于更新只能发生在\(d\)的整数倍处, (1)就不能成立了, 因为更新次数的多少是依赖于区间上形如\(nd\)的点的数目, 而同样长度的区间内含有此类点的数目是可以不同的.
初等更新定理是Blackwell定理的特殊情形. 事实上, 令 \(b_n = M(n) - M(n-1)\), 当\(F\)是非格点时, 由(1)知 \[ b_n \to \frac{1}{\mu}, \ n \to \infty , \] 由极限的性质得 \[ \frac{M(n)}{n} = \frac{b_1 + b_2 + \cdots + b_n}{n} \to \frac{1}{\mu}, \ n\to \infty . \] 而对任何实数\(t\), \[ \frac{[t]}{t} \cdot \frac{M([t])}{[t]} \leq \frac{M(t)}{t} \leq \frac{[t]+1}{t} \cdot \frac{M([t]+1)}{[t]+1} , \] 这里\([t]\)表示\(t\)的整数部分, 即不超过\(t\)的最大整数. 令\(t \to \infty\)可得 \[ \frac{M(t)}{t} \to \frac{1}{\mu} . \] 这就是Feller定理. 当\(F\)是格点分布时,请读者自己论证.
4.3.3 关键更新定理
下面的定理结论更一般也更复杂。
定理4.6 (关键更新定理) 记\(\mu=EX_1\), 设函数\(h(t), t \in[0, \infty)\)满足 \[\begin{aligned} \text{(i)}\ & h(t) \text{非负不增}; \\ \text{(ii)}\ & \int_0^{\infty} h(t) \,dt < \infty . \end{aligned}\] \(H(t)\)是更新方程 \[ H(t) = h(t) + \int_0^t H(t-x) \,dF(x) \] 的解. 那么
(1)若\(F\)不是格点分布, 有 \[ \lim_{t \to \infty} H(t) = \begin{cases} \frac{1}{\mu} \int_0^{\infty} h(x) \,dx, & \mu < \infty ,\\ 0, & \mu = \infty . \end{cases} \]
(2)若\(F\)是格点分布,对于\(0 \leq c < d\),有 \[ \lim_{n \to \infty} H(c+nd) = \begin{cases} \frac{d}{\mu} \sum_{n=0}^{\infty} h(c+nd) , & \mu < \infty ,\\ 0, & \mu =\infty . \end{cases} \]
关键更新定理与Blackwell定理的等价性(不严格的讨论): 只考虑\(F\)不是格点的情况, 在关键更新定理中, 取满足(i),(ii)两个条件的 \(h(t)=I_{[0, a)}(t)\). 代入更新方程的解, 则有 \[\begin{aligned} H(t) =& h(t) + \int_0^t h(t-x) dM(x) \\ =& \int_{t-a}^t d M(x) = M(t) - M(t-a) . \end{aligned}\] 又 \[ \lim_{t \to \infty} H(t) = \frac{1}{\mu} \int_0^{\infty} h(x) dx = \frac{1}{\mu} \int_0^a \,dx =\frac{a}{\mu} , \] 从而有 \[ \lim_{t \to \infty} (M(t)-M(t-a)) = \frac{a}{\mu} . \]
反过来,由Blackwell定理知道, 对任意的\(a>0\), \[ \lim_{t \to \infty} \frac{M(t+a) - M(t)}{a} = \frac{1}{\mu} . \] 故 \[ \lim_{a \to 0} \lim_{t \to \infty} \frac{M(t+a) - M(t)}{a} = \frac{1}{\mu} . \] 假设极限次序可交换, 将有 \[ \lim_{t \to \infty} \frac{dM(t)}{dt} = \frac{1}{\mu} . \] 即当\(t\)很大时, 有\(dM(t) \sim \frac{1}{\mu}dt\). 又\(\int_0^{\infty} h(x)dx < \infty\), 则当\(t \to \infty\)时, \(h(t)\)将快速趋于0, 因此当\(t\)变得很大时, 对于\(h(t-x)\)主要考虑当\(t-x\)比较小也就是\(x\)比较大的情况. 则有 \[ \int_0^t h(t-x) dM(x) \approx \int_0^t h(t-x) dx \cdot \frac{1}{\mu} = \frac{1}{\mu} \int_0^t h(x) dx . \] 这正是关键更新定理的结论.
例4.10 (剩余寿命与年龄的极限分布) 以\(r(t)=T_{N(t)+1} - t\)表示更新过程在时刻\(t\)的剩余寿命, \(s(t) = t - T_{N(t)}\)为\(t\)时刻的年龄. 求\(r(t)\)和\(s(t)\)的极限分布.
解: 对给定的\(y > 0\), 记\(H(t) = P(r(t) > y)\), 由例4.4有 \[ H(t) = \bar F(t+y) + \int_0^t H(t-x) \,dF(x), \] 这是更新方程,其解为 \[ P(r(t) > y) = \bar F(t+y) + \int_0^t \bar F(t+y-x) \,d M(x) , \ y > 0 . \]
设\(\mu = EX_1 < \infty\), 则 \[ \mu = \int_0^{\infty} [1-F(x)] dx < \infty . \] 所以 \[ \int_0^{\infty} [1-F(t+y)] dt =\int_y^{\infty} [1-F(x)]dx < \infty . \] 即\(h(t) = 1-F(t+y)\)满足关键更新定理的条件, 于是 \[\begin{align} & \lim_{t \to \infty} P(r(t) > y) = \lim_{t \to \infty} H(t) \\ =& \frac{1}{\mu} \int_0^\infty h(x) \,dx = \frac{1}{\mu} \int_y^{\infty} [1-F(x)] \,dx,\ \ y>0 . \tag{4.13} \end{align}\]
年龄\(s(t)\)的分布可由(4.13)式导出. 注意到 \[ \{ r(t) > x, s(t) > y \} \iff \{ r(t-y) > x + y \}, \]
从而 \[\begin{aligned} \lim_{t \to \infty} P(r(t) > x, s(t) > y) =& \lim_{t \to \infty} P(r(t-y) > x+y) \\ =& \frac{1}{\mu} \int^{\infty}_{x+y} [1 - F(z)]dz . \end{aligned}\] 特别地 \[\begin{aligned} \lim_{t \to \infty} P(s(t) > y) =& \lim_{t\to\infty} P(s(t) > y, r(t) > 0) \\ =& \frac{1}{\mu} \int_{y}^{\infty} [1-F(z)] \,dz. \end{aligned}\]
可见更新过程在\(t \to \infty\)时的寿命和余寿有相同的渐近分布。
注1:在应用关键更新定理时, 与更新定理的应用类似, 常常如4.10这样先关于某次更新(一般对第一次或\(t\)时刻前的最后一次)取条件而得到一个更新方程, 再利用关键更新定理.
注2:例4.10中得到的年龄与剩余寿命的极限分布是相同的,如何理解这一结论?
4.4 更新过程的推广
4.4.1 延迟更新过程
定义4.5 更新过程要求时间间隔\(X_1,X_2,\dots\)是分布函数为\(F\)的独立同分布序列. 如果放宽对\(X_1\)的要求,允许它服从别的分布\(G\), 则称由\(X_1,X_2,\dots\)确定的计数过程是延迟更新过程.
例如,设\(X_i\)表示第\(i\)个可替换零件的运行时间, 假设开始观察时第一个零件已经运行了一段时间, 则到它损坏的使用时间\(X_1\),就应认为与新零件能使用的时间\(X_2,X_3,\dots\)不同分布(除非是指数分布寿命). 但是要注意的是\(X_1,X_2,\dots\)之间的独立性仍然是必需的.
可以证明对于延迟更新过程, 节4.3中的三个更新定理依然成立, 但要注意这时\(M(t) = \sum_{n=1}^{\infty} F_n(t)\)中的\(F_n(t)\)相应用\(F_1(t) = G(t)\), \(F_n(t) = G \ast F_{n-1}(t)\)(\(n\geq 2\))来替换。 直观上这也是比较显然的, 因为我们并不认为第一次更新发生的时刻会对无穷远处的情况有很大的影响.
4.4.2 更新回报过程
定义4.6 设 \[ R(t) = \sum_{i=1}^{N(t)} R_i , \] 其中\(\{N(t), t \geq 0\}\)是一个更新过程, \(R_n\), \(n=1,2,\dots\)独立同分布且与\(\{N(t), t \geq 0\}\)独立, 则称\(R(t)\)是一个更新回报过程。
注:这一名称是由于我们可以把\(R_n\)看做第\(n\)次更新发生时带给我们的回报, \(R(t)\)看成是截止到\(t\)时刻获得的总回报。 更一般的更新回报过程, 可以允许\(R_n\)依赖于\(X_n\)(即回报的多少与等待的时间有关), 只要求随机向量列\((X_n,R_n)\)独立同分布.
命题4.9 设\(E|R_1| < \infty\), \(E|X_1| < \infty\), 则 \[ E[R(t)] = E(R_1) \cdot E[N(t)] . \] 如果\(E(R_1^2) < \infty\), \(\text{Var}[N(t)] < \infty\),则 \[ \text{Var}[R(t)] = \text{Var}(R_1) E[N(t)] + (E R_1)^2 \text{Var}[N(t)] . \]
证明 若\(E|R_1|<\infty\),则 \[\begin{aligned} E[R(t)] =& \sum_{n=0}^\infty E \left( \left. \sum_{i=1}^n Y_i \right| N(t) = n \right) P(N(t)=n) \\ =& \sum_{n=1}^\infty E \left( \sum_{i=1}^n Y_i \right) \; P(N(t)=n) \\ =& E(Y_1) \sum_{n=1}^\infty n P(N(t)=n) \\ =& E(Y_1) E[N(t)] . \end{aligned}\] 当\(\text{Var}(N(t)) < \infty\)时, \[\begin{aligned} \text{Var}[R(t)] =& E \left[ \text{Var} \left( R(t) | N(t) \right) \right] + \text{Var} \left[ E \left( R(t) | N(t) \right) \right] \\ =& E \left[ \text{Var} \left( \left. \sum_{i=1}^{N(t)} R_i \right| N(t) \right) \right] + \text{Var} \left[ E \left( \left. \sum_{i=1}^{N(t)} R_i \right| N(t) \right) \right] \\ =& E \left[ N(t) \text{Var}(R_1) \right] + \text{Var} \left[ N(t) \cdot E(R_1) \right] \\ =& \text{Var}(R_1) E[N(t)] + (E R_1)^2 \text{Var}[N(t)] . \end{aligned}\]
注:更新回报过程是复合泊松过程(3.3.2)的推广。 对复合泊松过程, \(E[N(t)] = \lambda t\), \(E(X_1) = \frac{1}{\lambda}\), \(E[R(t)] = E(Y_1) \lambda t\), 有 \[ \frac{E[R(t)]}{t} = E(Y_1) \lambda = \frac{E(Y_1)}{E(X_1)} . \] 更一般的更新回报过程可以考虑极限情形。
定理4.7 (更新回报定理) 若更新间隔\(X_1, X_2, \dots\)满足\(EX_1 < \infty\), 每次得到的回报 \(\{ R_i \}\)满足\(ER_1 < \infty\). 则 \[\begin{aligned} (1)\ & \lim_{t \to \infty} \frac{R(t)}{t} = \frac{ER_1}{EX_1} \text{ a.s.}; \\ (2)\ & \lim_{t \to \infty} \frac{E[R(t)]}{t} =\frac{ER_1}{EX_1}. \end{aligned}\]
证明: (1) 由命题4.8, \[ \lim_{t \to \infty} \frac{N(t)}{t} = \frac{1}{E(X_1)} , \text{ a.s.} \] 进一步有 \[\begin{aligned} & \lim_{t \to \infty} \frac{R(t)}{t} = \lim_{t \to \infty} \frac{R(t)}{N(t)} \lim_{t \to \infty} \frac{N(t)}{t} \\ =& E(R_1) \cdot \frac{1}{E(X_1)}, \text{ a.s.} \end{aligned}\]
(2)由命题4.9有 \[ E[R(t)] = E(R_1) E[N(t)] = E(R_1) M(t), \] 由Feller初等更新定理有 \[\begin{aligned} \lim_{t \to \infty} \frac{E[R(t)]}{t} = E(R_1) \lim_{t \to \infty} \frac{M(t)}{t} = \frac{E(R_1)}{E(X_1)} . \end{aligned}\]
注:后面所说的“长期的平均回报率”,按定理的第(2)条定义较好。
教材例题4.4.1(产品保修策略)叙述较混乱, 改为如下例题。 例题来自Ross: Introduction to Probablity Models 12th Ed P.452 例7.14。
例4.11 (产品替换策略) 考虑汽车用户甲的替换策略。 设汽车的寿命\(Z\)服从连续分布, 分布函数和分布密度分别为\(H\)和\(h\), 当现有汽车失效或者使用年限达到\(T\)时甲就废弃旧车购买新车, 购买新车的费用是\(C_1\)元, 如果汽车失效时购买新车还要有一个额外的\(C_2\)元的费用, 废弃的旧车不产生回报。 问:甲的长期的单位时间购置费用为多少? 如果汽车寿命服从0到10的均匀分布, \(C_1 = 3\), \(C_2 = \frac{1}{2}\), 如何取\(T\)使得长期单位时间购置费用最低?
解答: 将每次购置新车的时间点看作一次更新发生, 构成更新过程, 每次更新时支付的费用作为一个随机变量\(Y_i\), 这些\(Y_i\)独立同分布, 到时刻\(t\)为止购置新车花费的费用是一个更新回报过程\(\{R(t), t \geq 0 \}\)。 长期的单位时间购置费用定义为 \[ \lim_{t\to\infty} \frac{E R(t)}{t} . \] 由定理4.7上式等于 \[ \frac{E Y_1}{E X_1} , \] 其中\(X_i\)表示两次更新之间的间隔。 由题意 \[ X_1 = \begin{cases} T, & Z>T \\ Z, & Z \leq T, \end{cases} \] 其中\(Z\)表示第一辆汽车的寿命, 则 \[\begin{aligned} E(X_1) =& E\{T I[Z > T]\} + E\{Z I[Z \leq T]\} \\ =& \int_T^\infty T h(z) \,dz + \int_0^T z h(z) \,dz \\ =& T [1 - H(T)] + \int_0^T z h(z) \,dz . \end{aligned}\]
而费用 \[\begin{aligned} Y_1 =& \begin{cases} C_1, & Z > T, \\ C_1 + C_2, & Z \leq T, \end{cases} \end{aligned}\] 所以 \[\begin{aligned} E(Y_1) =& C_1 P(Z > T) + (C_1 + C_2) P(Z \leq T) \\ =& C_1 + C_2H(T) . \end{aligned}\]
于是, 长期的单位时间购置费用为 \[\begin{aligned} \mu_C = \frac{E Y_1}{E X_1} =& \frac{C_1 + C_2 H(T)}{T [1 - H(T)] + \int_0^T z h(z) \,dz} . \end{aligned}\]
若\(Z \sim \text{U}(0, 10)\), \(C_1 = 3\), \(C_2 = \frac{1}{2}\), 取\(T \leq 10\), 则\(H(T) = T/10\), \[\begin{aligned} \mu_C =& \frac{3 + \frac{T}{20}}{T(1 - \frac{T}{10}) + \frac{T^2}{20}}, \end{aligned}\] 令关于\(T\)的一阶导数等于零, 可解得\(T \approx 9.282\)。
可以用随机模拟方法验证结果。 这里只模拟一条轨道, 实际计算到是\(\frac{R(t)}{t}\)在\(t\)很大时的值(取了\(t=10^6\))。
simone <- function(Tc=5.0, end_time=1e6){
c1 = 3
c2 = 0.5
n = 0
time = 0
costs = 0
while(time < end_time){
n = n+1
# 一辆汽车实际寿命
life1 = runif(1, 0, 10)
# 使用时间
use1 = min(c(Tc, life1))
cost1 = ifelse(life1 < Tc, c1+c2, c1)
costs = costs + cost1
time = time + use1
}
costs / end_time
}
## simone(T=5.0)
set.seed(101)
tv <- seq(0.1, 9.9, by=0.1)
cv <- sapply(tv, simone, end_time=1e4)
plot(tv, cv, type="l",
xlab = "T", ylab="Mean cost")
模拟产生的平均费用关于截止时间\(T\)的曲线好像是单调减函数, 这实际是因为曲线在右端斜率过小了。 用理论值在右端放大作图:

## $minimum
## [1] 9.282025
##
## $objective
## [1] 0.6964102## [1] -4.453105e-07借助于符号计算软件wxMaxima(参见https://www.math.pku.edu.cn/teachers/lidf/docs/statcomp/html/_statcompbook/maxima.html)求导并求解最大值:
使用Julia编程可以提高速度, 前面的R程序如果令模拟时间达到\(10^6\)则计算时间太长, 无法满足绘制曲线的要求。 Julia程序的编译运行则可以使用很长的模拟时间。
# 更新过程中汽车替换例子模拟
using Random, Distributions
using Statistics, StatsBase
function simone(T=5.0;
end_time = 1e4, max_life=10.0, c1=3.0, c2=0.5)
n = 0
time = 0.0
costs = 0.0
while time < end_time
n += 1
life1 = rand()*max_life
use1 = life1 < T ? life1 : T
cost1 = life1 < T ? c1+c2 : c1
costs += cost1
time += use1
end # while
return costs / end_time
end # function simone
tv = range(0.1, 9.9, step=0.01)
cv = [simone(T; end_time=1e4) for T in tv];
using Plots
gr()
plot(tv, cv)
#Plots.savefig("renewal-carrepl-011.png")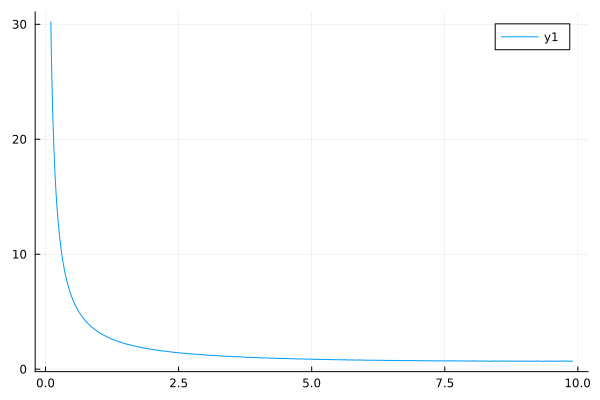
放大上图的\(T \geq 5.0\)局部来看:

将\(T \in [7,10]\)重新模拟计算, 模拟时间\(10^8\):
tv = range(7.0, 10.0, step=0.01)
cv = [simone(T; end_time=1e8) for T in tv];
plot(tv, cv)
Plots.savefig("renewal-carrepl-013.png")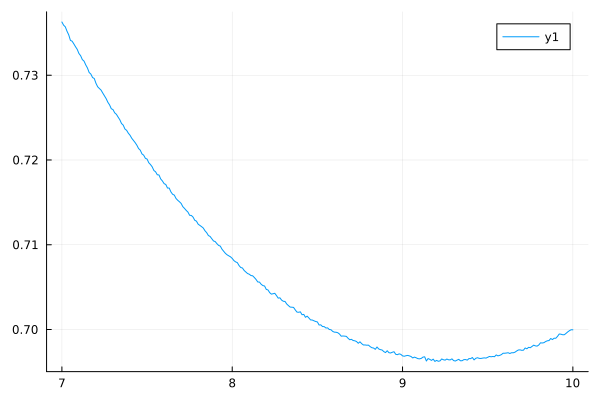
4.4.3 交替更新过程
定义4.7 在更新过程中, 我们考虑系统只有一个状态的情况, 比如机器一直是开的(即更换零件不需时间). 而实际中,零件损坏之后, 会有一个拆卸、更换的过程, 这段时间机器是“关”的. 这里我们就来考虑有”开”、“关”两种状态的更新过程, 我们将这种过程称做交替更新过程.
注1:设系统最初是开的, 持续开的时间是\(Z_1\),而后关闭, 时间为\(Y_1\), 之后再打开,时间为\(Z_2\), 又关闭, 时间\(Y_2\), ……, 交替进行, 每当系统被打开称做一次更新.
注2:我们假设随机向量列\(\{(Z_n,Y_n)\), \(n=1,2,\dots\}\)是独立同分布的, 从而\(\{Z_n\}\), \(\{Y_n\}\)都是独立同分布的, \(Z_i, Y_j\)在\(i \neq j\)时独立, 但\(Z_i, Y_i\)允许不独立.
定理4.8 设\(H\)是\(Z_n\)的分布, \(G\)是\(Y_n\)的分布, \(F\)是\(Z_n + Y_n\)的分布. 并记\(P(t) = P(t\text{时刻系统是开的})\), 设\(E(Y_n + Z_n) < \infty\),且\(F\)不是格点的, 则 \[ \lim_{t \to \infty} P(t) = \frac{E(Z_1)}{E(Z_1) + E(Y_1)} . \]
证明: 对第一次更新的时刻\(X_1 = Z_1 + Y_1\)取条件, 得 \[ P(t \text{时刻系统开着} | X_1 = x) = \begin{cases} P(Z_1 > t | X_1 = x), & t \leq x, \\ P(t-x), & t>x , \end{cases} \]
于是 \[\begin{aligned} P(t) =& E\{ I[t \text{时刻系统开着}] \} \\ =& E\{ E( I[t \text{时刻系统开着}] \;|\; X_1 ) \} \\ =& \int_0^{\infty} P(t \text{时刻系统开着} | X_1=x) \,dF(x) \\ =& \int_t^\infty P(Z_1 > t | X_1=x) \,dF(x) + \int_0^t P(t-x)\, dF(x) \end{aligned}\]
来证明\(x \geq t\)时\(\int_t^\infty P(Z_1 > t | X_1=x) \,dF(x) = \bar H(t)\)。 \[\begin{aligned} & \bar H(t) = P(Z_1 > t) = P(Z_1 > t, \ X_1 > t) \\ =& E I_{\{Z_1 > t, X_1>t \}} = E \{ E(I_{\{Z_1 > t, X_1>t \}} | X_1) \} \\ =& \int_t^\infty E(I_{\{Z_1 > t \}} | X_1 = x) \,dF(x) \\ =& \int_t^\infty P(Z_1 > t | X_1 = x) \,dF(x) . \end{aligned}\]
从而 \[\begin{align} P(t) =& \bar{H}(t) + \int_0^t P(t-x) \,dF(x) . \tag{4.14} \end{align}\]
(4.14)是更新方程, 其解为 \[ P(t) = \bar{H}(t) + \int_0^t \bar{H}(t-x) \,dM(x). \] 又\(\int_0^{\infty} \bar{H}(t) dt = EZ_1 < \infty\), 且\(\bar{H}(t)\)非负不增, 由关键更新定理得 \[ \lim_{t \to \infty} P(t) = \frac{\int_0 ^{\infty} \bar{H}(t) \,dt}{E(Y_1 + Z_1)} = \frac{EZ_1}{EZ_1+EY_1} . \]
例4.12 例题来自Ross Introduction to Probablity Models 12th Ed P.439 例7.7。
设有\(n\)个人博弈, 每次随机选择一个人胜出, 选第\(i\)个人的概率为\(p_i\)(\(i=1,2,\dots,n\)), 当连续\(k\)次都为同一个人胜出时博弈完成一局, 此局以该连续胜出者为胜方。 比如, \(k=2\)时各次结果若为\(1,2,4,3,5,2,1,3,3\)则最后第3个人胜出, 一局用时9。 问:第\(i\)个人最终胜出的概率是多少, 每局平均需要的时间是多少?
解答 先考虑简单的只有两个人的情况, 第一个人每次胜出的概率为\(p=p_1\), 进行独立重复试验直到第一个人连续\(k\)次胜出(不考虑第二个人连续\(k\)次胜出问题)。
用\(T\)表示第一个人连续\(k\)次胜出时的时间, 记\(Z\)为首次出现非第一个人胜出的时刻, 即前\(Z-1\)次都是第一个人胜出, 用\(E T = E(E(T|Z))\)求\(ET\)。 如果\(Z \geq k+1\), 则开始的\(k\)次博弈为连续的第一个人胜出, 这时\(T = k\); 对\(Z=1,2,\dots,k\), 前面的\(Z-1\)次都是第一个人胜出, 第\(Z\)次为第二个人胜出, 从第\(Z+1\)次第一个人连续\(k\)次胜出的概率变成与重新开始概率相同, 这样得 \[\begin{aligned} E(T) =& E[ E(T|Z)] \\ =& \sum_{j=1}^\infty E(T | Z=j) P(Z=j) \\ =& \sum_{j=1}^k E(T | Z=j) P(Z=j) + k P(Z \geq k+1) \\ =& \sum_{j=1}^k [j + ET] p^{j-1} (1-p) + k p^k, \end{aligned}\] 求解\(ET\)得 \[\begin{aligned} ET =& k + \frac{1-p}{p^k} \sum_{j=1}^k j p^{j-1} . \end{aligned}\] 化简得 \[\begin{aligned} ET =& \frac{k p^k + (1-p) \sum_{j=1}^k j p^{j-1}}{p^k} \\ =& \frac{k p^k + \sum_{j=1}^k j p^{j-1} - \sum_{j=1}^k j p^{j}}{p^k} \\ =& \frac{k p^k + \sum_{m=0}^{k-1} (m+1) p^m - \sum_{j=1}^k j p^{j}}{p^k} \\ =& \frac{k p^k + p^0 + \sum_{m=1}^{k-1} p^m - k p^k}{p^k} \\ =& \frac{\sum_{m=0}^{k-1} p^m}{p^k} \\ =& \frac{1 - p^k}{p^k (1-p)} . \end{aligned}\]
回到原始的问题, 设有\(n\)个人博弈, 每次有任何一个人连续\(k\)次胜出时重新开始博弈, 这样实际上每次博弈都是一个独立重复试验, 与当前在哪一局没有关系。 在这样的独立重复试验中, 对给定\(i\), 将第\(i\)人连续\(k\)次胜出作为一次更新, 这样关于第\(i\)个人构成更新过程, 用\(N_i\)表示第\(i\)人完成一局的时间, 由上面的推导可知 \[ E N_i = \frac{1 - p_i^k}{p^k (1-p_i)} . \]
由更新定理,第\(i\)个人胜出的速率(平均每次博弈胜出比例)为 \[ \lim_{t \to \infty} \frac{M(t)}{t} = \frac{1}{ E N_i} = \frac{p_i^k (1 - p_i)}{1 - p_i^k} . \] 其中\(N(t)\)是\(t\)次博弈中第\(i\)人胜出的局数。
因为每个人都可能先胜出\(k\)次博弈, 每个人先胜出的概率与其胜出的速率成正比(这里是数学直观不是严格证明), 所以长期来看第\(i\)个人胜出的概率为 \[\begin{aligned} & \frac{\text{第} i \text{个人胜出速率}}{\sum_{j=1}^n \text{第} j \text{个人胜出速率}} \\ =& \frac{\frac{p_i^k (1 - p_i)}{1 - p_i^k}}{\sum_{j=1}^n \frac{p_j^k (1 - p_j)}{1 - p_j^k}} . \end{aligned}\]
注意到每局决出胜负的时间是所有\(n\)个人先胜出\(k\)次博弈的时间的最小值, 所以将有人胜出作为一次更新, 更新的速率是\(n\)个速率之和(这需要严格证明): \[\begin{aligned} \sum_{j=1}^n \frac{p_j^k (1 - p_j)}{1 - p_j^k}, \end{aligned}\] 以\(T\)为有人先胜出\(k\)次博弈的时间, 则由更新定理 \[\begin{aligned} \sum_{j=1}^n \frac{p_j^k (1 - p_j)}{1 - p_j^k} = \frac{1}{E T}, \end{aligned}\] 即 \[ E T = \left( \sum_{j=1}^n \frac{p_j^k (1 - p_j)}{1 - p_j^k} \right)^{-1} . \]
因为上面的推导不够严格, 用随机模拟方法来验证。 取\(n=3\), \((p_1, p_2, p_3) = (1/2, 1/3, 1/6)\), \(k=2\), 每个人的胜出速率为:
## [1] 0.16666667 0.08333333 0.02380952结束一局时每个人的胜出概率为:
## [1] 0.60869565 0.30434783 0.08695652平均每局时间:
## [1] 3.652174模拟一条长度为\(N\)的轨道:
simren_one <- function(N = 10000, k = 2){
n <- 3
pv <- 1 / c(2, 3, 6)
# 每次博弈的胜出者
xv <- sample(1:n, size=N, replace=TRUE, prob = pv)
nr <- 0 # 总局数
wv <- numeric(N) # 每局的胜出人代号
tv <- numeric(N) # 每局的时间长度
# 下面循环找到每一局,条件是最后的k个为相同胜者
istart <- 1
i <- k
##print(xv)
while(i <= N){
if(all(xv[(i-k+1):i] == xv[i])){
## 找到k个连续,结束一局,开始新的一局
nr <- nr + 1
wv[nr] <- xv[i]
tv[nr] <- i - istart + 1
istart <- i+1
i <- i+k
} else {
i <- i+1
}
}
wv <- wv[1:nr]
tv <- tv[1:nr]
## 模拟估计的胜出概率与理论概率:
print(rbind(prop.table(table(wv)),
rates / sum(rates)))
## 模拟估计的每局时间长度与理论平均长度
print(c(mean(tv), 1 / sum(rates)))
invisible(list(winners=wv, lengths=tv) )
}
simren_one(N=1000000)
## 模拟估计的胜出概率与理论概率:
## 1 2 3
## [1,] 0.6092890 0.3043518 0.08635923
## [2,] 0.6086957 0.3043478 0.08695652
## 模拟估计的每局时间长度与理论平均长度:
## [1] 3.658511 3.652174可见模拟估计的值与理论值比较接近, 但是需要模拟很长时间(这里时间长度为一百万次博弈)。
使用Julia语言编程:
# 多人连胜游戏。每次某人连胜k轮时结束一局比赛。
# 输入:
# pw: 每人的获胜概率
# k: 连胜多少轮算一局结束
# N: 模拟重复的轮数
using Random, Distributions
using Statistics, StatsBase
function simone(pw::Vector; k=2, N=1000_000)
n = length(pw)
rates = pw .^ k .* (1 .- pw) ./ (1 .- pw .^ k)
# 每人理论获胜概率
probs = rates ./ sum(rates)
# 平均每局时间的理论值
mean_time = 1 / sum(rates)
# 一次性生成N轮的输赢
xv = StatsBase.sample(1:n, StatsBase.Weights(pw),
N; replace=true)
winners = Int[]
times = Int[]
# 下面循环找到每一局,条件是最后的k个为相同胜者
istart = 1
i = k
while i <= N
if all(xv[i-k+1:i-1] .== xv[i])
## 找到k个连续,结束一局,开始新的一局
push!(winners, xv[i])
push!(times, i - istart + 1)
istart = i+1
i += k
else
i += 1
end
end # while i
# 获胜者频率估计
freqs = counts(winners, 1:n)
probs_est = freqs ./ sum(freqs)
# 平均每局时间估计
mean_time_est = mean(times)
println("理论概率与模拟估计概率:")
display(round.([probs probs_est], digits=6))
println("理论平均时间与模拟估计值:")
show(round.([mean_time, mean_time_est], digits=4))
return
end
function test(N=1000)
n = 3
pw = [1/2, 1/3, 1/6]
k = 2
simone(pw, k=k, N=N)
end
Random.seed!(101)
test(1000_000)
## 理论概率与模拟估计概率:
## 3×2 Matrix{Float64}:
## 0.608696 0.608658
## 0.304348 0.303514
## 0.086957 0.087829
## 理论平均时间与模拟估计值:
## [3.6522, 3.6565]4.5 附录:一些证明
4.5.1 引理4.1证明
令\(S_n = \sum_{j=1}^n a_j\), 则\(S_n\)为非负单调增数列。 如果\(S_n\)有上界,则必有上确界, 为\(S_n\)的极限。 如果\(S_n\)无上界, 即级数等于\(+\infty\)。
设\(j_i, i=1,2,\dots\)是\(1,2,\dots\)的排列, 即\(j_i\)是\(\{1,2,\dots \}\)上的一个一一映射。 考虑级数\(\sum_{i=1}^\infty a_{j_i}\)。 分两种情况讨论。
如果\(\sum_{i=1}^\infty a_i = A < \infty\), 则\(A > 0\)(若\(A=0\)即所有\(a_i = 0\),结论显然), 对任意正整数\(n\)有 \[ \sum_{i=1}^n a_{j_i} \leq A, \] 所以级数\(\sum_{i=1}^\infty a_{j_i} \leq A < \infty\)。 \(\forall \epsilon > 0\), \(\exists N\)使得\(n \geq N\)时 \[ \sum_{i=1}^n a_i > A - \epsilon . \] \(\exists N_1 \geq N\)使得 \[ \{j_i, i=1,2,\dots, N_1 \} \supset \{1,2,\dots, N\} , \] 于是\(n \geq N_1\)时 \[ \sum_{i=1}^n a_{j_i} \geq \sum_{i=1}^{N} a_i \geq A - \epsilon, \] 进一步有 \[ \sum_{i=1}^\infty a_{j_i} \geq A - \epsilon, \] 于是 \[ A - \epsilon \leq \sum_{i=1}^\infty a_{j_i} \leq A, \] 令\(\epsilon \to 0\)即得 \[ \sum_{i=1}^\infty a_{j_i} = A = \sum_{i=1}^\infty a_{i} . \]
如果\(\sum_{i=1}^\infty a_i = +\infty\), 则\(\forall M > 0\), 存在\(N\)使得\(n \geq N\)时 \[ \sum_{i=1}^n a_i > M . \] 于是存在\(N_1 \geq N\)使得 \[ \{j_i, i=1,2,\dots, N_1 \} \supset \{1,2,\dots, N\} , \] 从而\(n \geq N_1\)时 \[ \sum_{i=1}^n a_{j_i} \geq \sum_{i=1}^{N} a_i > M, \] 于是\(\sum_{i=1}^\infty a_{j_i} = +\infty\)。
4.5.2 引理4.4证明
此引理证明较长,分为若干段。
(1)
考虑间隔时间\(X_1\)的分布函数\(F(x)\)。
简记\(X_1\)为\(X\)。
因为\(F(0) < 1\),
所以\(P(X > 0) > 0\),
而
\[\begin{aligned}
P(X>0)
=& P \left( \bigcup_{\ell=1}^\infty \{ X > \frac{1}{\ell} \} \right) \\
=& \lim_{\ell \to \infty} P(X > \frac{1}{\ell}) > 0,
\end{aligned}\]
存在\(\ell > 1\)使得\(P(X > \frac{1}{\ell})>0\),
记\(b = \frac{1}{\ell}\),则\(0 < b < 1\),且
\[\begin{align}
F(b) = P(X \leq \frac{1}{\ell}) < 1 .
\tag{4.15}
\end{align}\]
(2)
得到上述的\(0<b<1\)使得\(F(b)<1\)以后,
考虑任意固定的\(t\),
下面的讨论都假定\(t\)为某个固定值,
对此\(t\)必存在正整数\(k\)使得\(k b > t\),
这时有
\[\begin{aligned}
\{ T_k \leq t \}
\subset \{ T_k \leq kb \}
\subset \{ X_1 > b, \dots, X_k > b \}^c ,
\end{aligned}\]
(\(k\)个更新时间之和小于等于\(kb\)则不能每个间隔时间都大于\(b\)),
所以
\[\begin{aligned}
F_k(t) =&
P(T_k \leq t) \\
\leq& 1 - P(X_1 > b, \dots, X_k > b) \\
=& 1 - [ 1 - F(b) ]^k \\
=& 1 - c_1,
\end{aligned}\]
其中\(c_1 = [1 - F(b)]^k > 0\),
令\(c_2 = 1 - c_1\),
则\(0 \leq c_2 < 1\)使得
\[\begin{align}
F_k(t) \leq c_2 .
\tag{4.16}
\end{align}\]
(3)
将更新的发生分成每\(k\)个一组,
考察第\(m k\)次更新时间\(T_{mk}\)的分布\(F_{mk}(t)\),
\(m=1,2,\dots\)。
因为
\[\begin{aligned}
\{ T_{mk} \leq t \}
\subset& \{ T_{k} - T_0 \leq t, T_{2k} - T_k \leq t,
\dots, T_{mk} - T_{(m-1)k} \leq t \} ,
\end{aligned}\]
这是由于总更新时间小于等于\(t\)则更新分成\(m\)段后每一段的更新时间也小于等于\(t\)。
其中\(T_0=0\)。
由更新过程的间隔时间独立同分布性质, 可得 \[\begin{aligned} P(T_{mk} \leq t) \leq [ P(T_k \leq t) ]^m = [ F_k(t) ]^m \leq c_2^m . \end{aligned}\]
(4)
对正整数\(n\),
必存在非负整数\(m\)和\(0 \leq j \leq k-1\)使得
\[\begin{aligned}
n = m k + j,
\end{aligned}\]
实际上\(m\)是\(n\)除以\(k\)的整除商,
\(j\)是余数。
这时,
因为
\[\begin{aligned}
\{ T_{n} \leq t \} \subset \{ T_{mk} \leq t \},
\end{aligned}\]
所以
\[\begin{aligned}
F_n(t) =& P(T_n \leq t) \\
\leq& P(T_{mk} \leq t) \leq c_2^m .
\end{aligned}\]
如果\(c_2 = 0\),
则
\(F_n(t) = 0\),
定理结论成立,
下面假设\(0 < c_2 < 1\)。
利用 \[\begin{aligned} \frac{n}{k} - 1 < m \leq \frac{n}{k} \end{aligned}\] 可得 \[ c_2^m \leq c_2^{\frac{n}{k} - 1} = c_2^{-1} (c_2^{\frac{1}{k}})^n, \] 令 \[ \alpha = c_2^{\frac{1}{k}}, C = c_2^{-1} > 0 , \] 则\(0 < \alpha < 1\),使得 \[ F_n(t) \leq C \alpha^n, \] 引理得证。