K-稳定性探索 | 专访ICM2022受邀报告人李驰校友
发文时间:2021-11-02 撰稿人:徐林霄、张科伟
编者按:四年一届的国际数学家大会(International Congress of Mathematicians,ICM)是由国际数学联盟(IMU)主办的全球性数学学术会议。会议旨在促进高水平的学术交流,在开幕式上将颁发“菲尔兹奖”等世界著名的数学大奖。会议期间,将有世界各地从事国际数学前沿研究的著名数学家报告他们所在领域的重大科研成果。ICM报告人身份是极高的学术荣誉,是一个数学家的工作获得国际学术界认可和关注的重要标志。
2022年7月,第29届国际数学家大会将在俄罗斯圣彼得堡举行。今秋,2022年圣彼得堡国际数学家大会官网上公布了本届报告人名单,5位北京大学数学学科教师:鄂维南、朱小华、章志飞、董彬、刘毅受邀成为报告人,其中鄂维南院士将作一小时报告。另有8位北大校友将作45分钟报告,他们分别是:丁剑、李驰、刘钢、汪璐、王国祯、徐宙利、周鑫、朱歆文。

2014年李驰老师在加拿大Banff数学研究所访问
李驰,2000年至2007年就读于北京大学数学科学学院,获学士及硕士学位。此后赴美学习,于2012年获得普林斯顿大学博士学位。2015年至2020年任美国普渡大学助理教授、副教授,现任美国罗格斯大学副教授。他的研究方向是复微分几何、复代数几何、几何分析。2014年至2017年曾获美国国家自然科学基金资助。2017年获斯隆研究奖。
Q:首先恭喜李驰老师受邀在明年的国际数学家大会上做45分钟报告!您收到邀请时的心情是怎样的呢?
A:非常高兴能收到邀请,这当然是一件很荣幸的事情。这也算是同行对我这几年工作的一种认可吧。比较特别的一点是2002年的时候我作为志愿者参加过在北京举行的国际数学家大会,当时第一次接触到这种最高规格的数学会议;后来因为这次志愿者工作,在2006年,我又去参加了一次国际数学家大会。明年第三次参加的话,距离我第一次作为志愿者参加就有整整20年了,还是挺有缘分的。
Q:您能透露一下您明年报告的内容吗?
A:这个已经确定了,我讲的题目是Canonical Kähler Metrics and Stability of Algebraic Varieties。大概就是讲典则度量和稳定性的关系。
Q:您的工作主要集中在K-稳定性这一块,是什么原因让您选择这一方向?
A:一开始也不是说特意要研究这个,可以说是有一些偶然性,但也比较自然。我在北大跟田老师(注:田刚院士)读硕士的时候,想学习田老师最擅长的方向,于是就看了他的一些文章和专著。当时因为觉得Futaki不变量很有意思,我做过一些Hypersurface的Futaki不变量的代数的计算。后来虽然发现别人其实已经做过了,但在学习的过程中能产生一些自己的看法,我觉得还是挺有趣的。再之后我又看了一些关于Chow稳定性及其与常数量曲率Kähler度量(CSCK)的关系的文章,我也觉得挺有意思,就以这个题目写了硕士毕业论文。
去普林斯顿读博士以后,有一次碰到许晨阳,我们就聊起来,想去研究田老师关于K-稳定性两个定义等价的猜想。当时发现了一些很有意思的计算,发现Futaki不变量沿着MMP可以下降,进而证明了田老师的猜想。
做完这个内容以后其实搁置了挺长一段时间。2015年时,因为有一些新的想法,即关于normalized volume的想法,进而引出了valuative criteria这些结果。有的时候不是特意想去研究这个,但是时不时的会有一些新的看法和想法,觉得挺有意思的,然后就做了这方面的工作。

2017年李驰老师为北京国际数学研究中心短期课程授课
Q:您最近在Kähler-Einstein问题(KE)以及常数量曲率Kähler度量(CSCK)存在性方面都做出了突破性的进展,您能分享一下这些工作背后您的心路历程吗?您能取得这些突破可以归结为哪些原因呢?
A:从2015年开始到2017、2018年的时候,我主要精力放在研究normalized volume,还有一些偏代数的问题上面。后来回来做KE,是因为知道田老师跟浙江大学王枫他们在做singular的KE和Yau-Tian-Donaldson猜想。其实我以前也想过这个问题,但是没有花太多时间;后来碰到王枫,我们又聊了一下,发现这中间有一步,就像田老师跟王枫他们做的那样,中间也要到smooth resolution上去——也就是说,知道singular variety的K-稳定性,然后到smooth resolution上去先构造一个带锥奇点的KE度量来逼近,这个时候需要知道resolution上也要有一些K-稳定性的条件。因为我刚好知道valuative criteria,所以就算了一下,发现确实从底下的singular variety的K-稳定性能推出smooth的resolution上的K-稳定性,这样的话就可以用smooth variety上的Yau-Tian-Donaldson,构造ambient space是smooth的空间上的KE,当然也是有奇点的KE,就解决了这一步了。再然后结合田老师跟王枫之前的一些工作,以及我们后来又一起解决了一些比较技术性的问题,我们就做了一大类但有条件的singular variety上的KE和Yau-Tian-Donaldson。
做完这篇文章后田老师建议我们进一步去看能不能把条件给去掉。我们第一篇文章2017年就写好了;2018年下半年,我花了很长时间来想这个问题。我们当时还是想直接用某种variational approach去直接解决,但是后来一直有一些奇点的困难没有克服。到2019年2月份的时候,我去密歇根做了一个报告,开车回来的路上我突然想到可能有一个办法可以绕过去,即采用新的non-Archimedean的技术加上一些凸泛函逼近的结果,回来之后写了一下,发现确实是可以的。然后我们就一起把singular variety上的Yau-Tian-Donaldson,至少自同构群是离散的情形下做完了。后来又花了半年时间,又引进了一些新的技术,推广到了更一般的Kähler-Einstein的情况。

另外做CSCK也是因为在做KE的过程中,学了他们最近发展的一些新的non-Archimedean的技术。Boucksom在2018年ICM报告里面也提到,说他们这个non-Archimedean的框架,对CSCK来说有些困难。其中一个困难是不知道他们构造的那些destabilizing的测地线是不是可以用代数的东西来逼近。他在2018年提出的这个困难后,我当时也大概想了一下,但是也没想出来,后来我发现这个问题跟Demailly在local case的猜测有一些关系,并且研究了一些例子。
在2020年下半年,11、12月份的时候,我在普渡的办公室里面,想起一个例子后随手在白板上估计了一下,就发现有一个思路可能可以克服这种困难,后来就做出来了。想清楚以后也不是一个特别困难的问题,但是也是花了很长时间来酝酿。
Q:关于K-稳定性,您觉得还有哪些问题值得关注?
A:最近有很多人在做K-稳定性,比如许晨阳、刘雨晨、庄梓铨还有他们的合作者,还有一些外国数学工作者也在做。在座的张科伟(编者注:采访人)也在做相关的内容。里面肯定还有很多有意思的问题,包括一些例子;还有一些更一般的问题,比如说很多人关心hypersurface的K-稳定性,能否把hypersurface的degree做到最优;另外normalized volume作为K-stability theory在local singularity情形的对应, 还需要解决极小赋值有限生成的问题以及寻找更多具体的例子。这些都是很有意思的代数问题。我一直也想知道的一个问题是,光滑Fano流形上如果没有全纯向量场,它是不是可以半稳定,至少这是一个比较自然的问题。
再推广到一般的polarization对应的CSCK,我们对这种K-稳定性其实还没有一个很好的了解。里面有些问题,还是很深刻的一些代数几何量的逼近的问题,包括怎么用对更广的filtration的Futaki不变量去逼近,现在还没有看出一个很好的解决办法。这些东西值得去深入研究。

2019年李驰老师在美国亚利桑那大学访问
Q:您发表的论文中既有个人的独作,也有和田刚院士、许晨阳老师等学者的合作,您是怎么看待数学研究中的独作与合作的呢?
A:两者各有优势吧。 一方面,两个人或者是更多的人一同讨论可以优势互补、拓展思路、激发新想法,更容易有进展。但是合作也对条件有一些限制,尤其是在各种视频会议软件普及前,需要在时间上和空间上都比较方便的情况下才能进行一些深入的合作。对我来说更多的可能还是人面对面的合作比较容易,像我跟许晨阳也是面对面地交流,合作起来更容易些。另一方面,有些想法可能确实需要很长的时间去酝酿、发酵。有的时候问题可能就放在这边,偶尔就去想一想,但可能很长时间也没有太多的进展。自己一个人做问题,可以更好地掌控思考的节奏.合作也跟人的性格有关系,有些人比较喜欢跟人一起讨论,有些人就喜欢自己一个人做问题。我觉得都可以,只要能做出比较好的工作的话都是挺好的。
对于刚进入研究领域不久的学生,我建议还是多多跟人交流,如果能有合作机会当然更好。在现在这种各数学分支快速发展的背景下,很难一个人一直有好的想法并能实现。在与人合作的过程中,不管是对知识的积累,还是学术交流上,都会有很大的帮助。
Q:您的工作涉及到方程、微分几何、代数几何等多个分支,不同领域知识的碰撞是否给您的研究工作带来过灵感?
A:肯定是有的。我个人比较满意的一个想法就是之前提到的normalized volume,它就来自两个不同领域的结合。最早我是在做conical KE时接触到Martelli-Sparks-Yau关于Sasaki-Einstein度量的一个minimization的结果,是一个微分几何的结果;后来通过和许晨阳的合作,我又了解到一个双有理几何的概念,叫log discrepancy。2015年,我在考虑一个切锥的代数几何的刻画的问题时,就发现Martelli-Sparks-Yau里torus action的weight刚好就是log discrepancy的特殊例子。这个发现让我引入了关于赋值的normalized volume的概念。如果微分几何和代数几何两边的结果之一我没有了解过的话,就不可能朝这个方向想。这算是一个不同方向相互启发的例子吧。
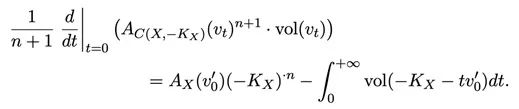
(李驰老师注:这是发表在Duke Mathematical Journal的一篇文章中得到的一个公式。该公式左边是仿射锥上normalized volume的导数,而右边量的非负条件则刻画了Fano流形X的K-semistability。)
我个人也比较喜欢找不同方向的联系。刚开始学数学的时候听说Atiyah-Singer指标定理揭示了拓扑和分析的一些联系,也对我做数学有一定的影响。

2019年李驰老师在美国普渡大学校园内与Neil Armstrong雕像合影
Q:请问您是如何学习并了解这么多方向的呢?
A:有的时候是比较偶然地发现一些联系。刚开始学习这些方向也不是为了找到联系,只是觉得它们本身也比较有意思。后来了解的多了,突然就发现它们确实有些不那么明显的联系,就十分有意思。这一点可能也和个人的数学理解和风格有关系。有些数学家喜欢把具体的数学问题做得很深入,这也是非常重要的。另一方面,问题的特点也很重要。有些问题本身就是在探寻不同数学分支的联系,比如Yau-Tian-Donaldson猜想,不可避免地就需要从不同的角度去看待问题。具体怎么在自己研究的数学的广度和深度之间找到平衡,还是要靠自己去判断。
Q:您在北大求学时,有没有哪些老师和事情给您留下了深刻的印象?
A:我在北大一共学习了七年,现在回想一下,很多时间都是在学习,时间也好像过得特别快。我从许多老师那都学到了很多数学知识,打下了比较坚实的基础。我记得我读完本科的时候挺迷茫的,不知道是否应该继续做数学研究。我那时候的班主任王正栋老师听说了我的情况,找我去谈话,鼓励我继续做数学;别的老师也给了我很多鼓励。另外我也有很多厉害的同学,包括我的室友恽之玮,都给了我很多激励。
我在同学中进入研究算是比较晚的。刚开始我还没学田老师的方向,对指标定理感兴趣,读了些相关的文献。2004年的时候我参加了特别数学讲座,这也是田老师他们最早发起的,邀请了许多知名数学家来讲座。当时请了Bismut来讲family index theorem。听完之后我跟田老师说对这些内容感兴趣,他就让我整理了一个笔记给他看,后来也得到了他的肯定。之前田老师和我说过一句引用自《功夫熊猫》的话,说做数学还是要有“inner peace”(注:内心的平静),自己要静得下心来,不要考虑太多别的东西,尽量不受外界的影响,精力要集中一些。这句话也送给大家共勉吧。