摘要
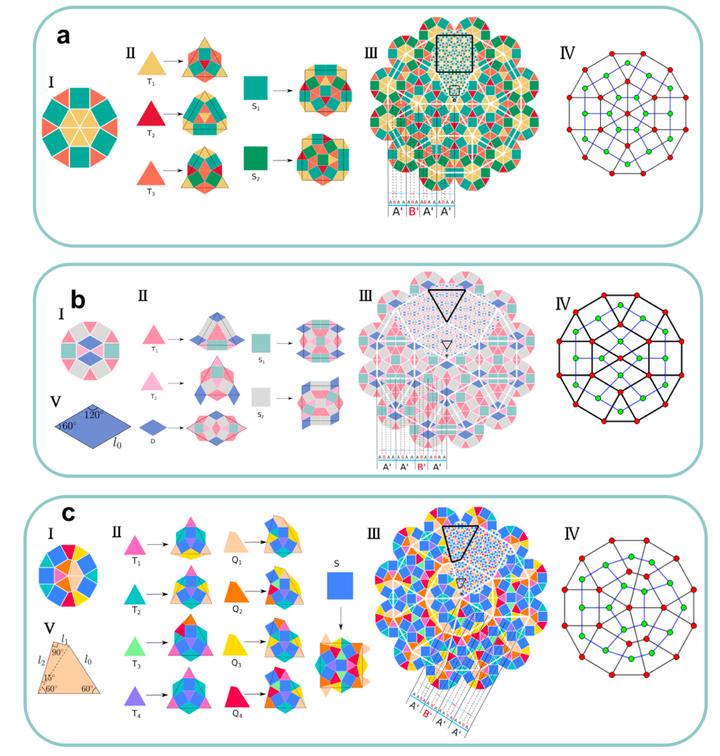
Quasicrystals are intriguing ordered structures characterized by quasiperiodic translational and noncrystallographic rotational symmetry. The tiling of different geometric units such as triangles and squares in two-dimensional space can result in a great variety of quasicrystals that could be realized by the self-assembly of liquid crystalline molecules. In this study, we introduce three self-similar dodecagonal tilings, including a novel diamond–square–triangle pattern, composed of triangular and quadrangular tiles, and examine their thermodynamic stability by using the self-consistent field theory applied to T-shaped liquid crystalline molecules. Specifically, we detail the inflation rules for the construction of these dodecagonal tilings, analyze their self-similarity, and show that these tilings can be viewed as projections of higher-dimensional periodic lattice points with projection windows. Using these dodecagonal tilings as initial configurations of the SCFT results in solutions corresponding to quasicrystals that could form from T-shaped liquid crystalline molecules. The relative stability of these aperiodic phases is analyzed to obtain design rules that could stabilize quasicrystals. Meanwhile, we provide a criterion for distinguishing three dodecagonal quasicrystals and their approximants by analyzing their diffraction peaks. These findings shed new light on the discovery of new quasicrystals in soft materials.