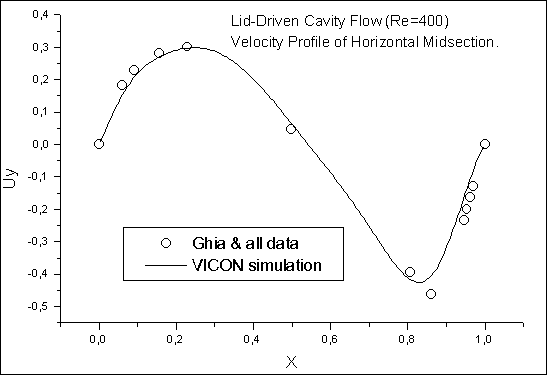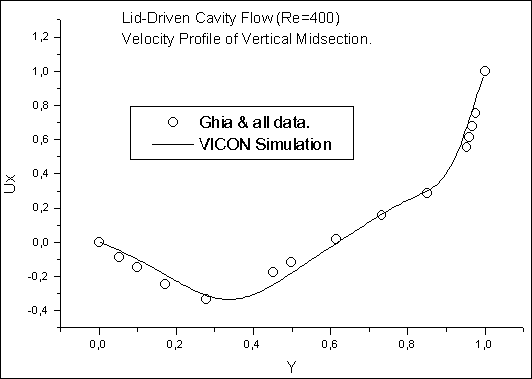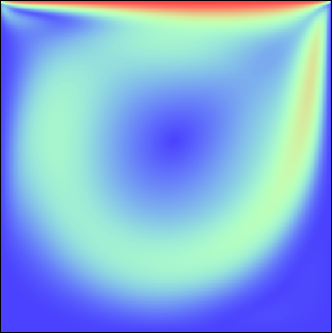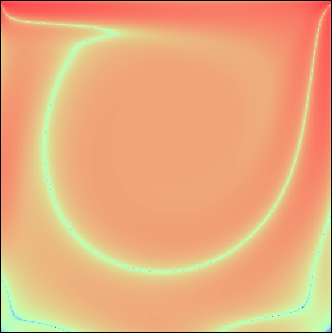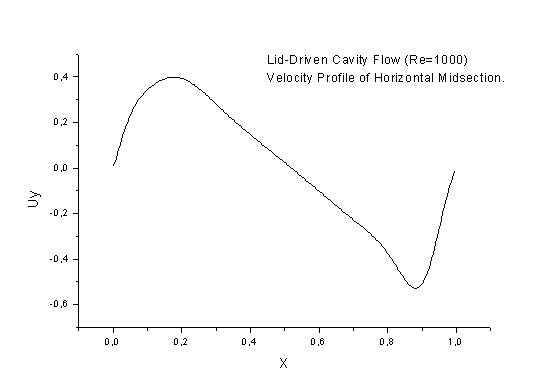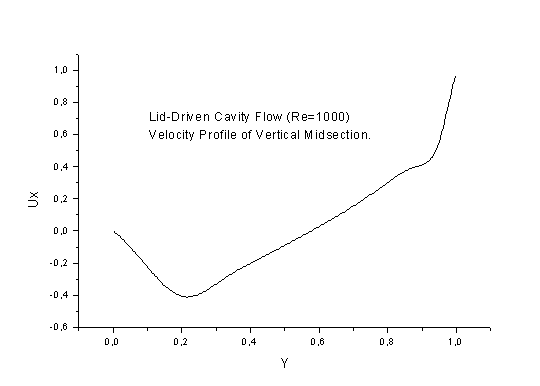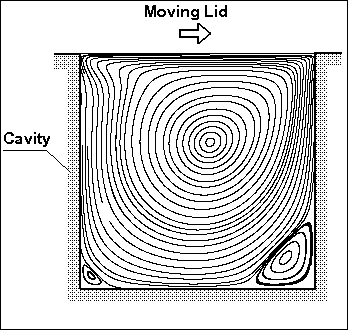

| DESCRIPTION: | The lid moves over square 2D cavity so that the flow is slightly
compressible (M=0.1). Reynolds numbers based on cavity size and lid
velocity are 400 and 1000. The grids were 161 x 161 (Re=400) and 251 x 251
(Re=1000), respectively. Calculations were carried out with Curant number
10 and took about 4000 and 8000 iterations. Streamlines, absolute value of velocity field and comparison between calculated velocity profiles (in undimensional units) and results of the work (V.Ghia, K.N.Ghia and C.T.Shin, "High-Re solutions for incompressible flow using the Navier-Stokes equations and a multi-grid method", - J.Comp.Phys., v.48, 1982, pp.387-411) are shown below. |
The governing equation: 2D incompressible Navier-Stokes equations
The computational domain: [0,1]× [0,1]
The boundary conditions: u=0,v=0 is imposed everywhere at the boundary except at the boundary {y=1}, where we impose u=1,v=0
The initial data: u=0,v=0
An Fortran code of the MAC scheme for your reference.