Probability is both a fundamental way of viewing the world, and a core mathematical discipline, alongside geometry, algebra, and analysis. In recent years, the evident power and utility of probabilistic reasoning as a distinctive method of scientific inquiry has led to an explosive growth in the importance of probability theory in scientific research. Central to statistics and commonplace in physics, genetics, and information theory for many decades, the probabilistic approach to science has more recently become indispensable in many other disciplines, including finance, geosciences, neuroscience, artificial intelligence and communication networks.
The increased influence and heightened awareness of probability carries new responsibilities and opportunities for our discipline. Although the nature of doing research has changed, there has not always been a corresponding evolution in how probability is taught in our colleges and universities. In many places, curricula today are not significantly different from those of thirty years ago. The probability community must take the lead in developing course offerings and other educational tools that accommodate widely varying audiences with diverse backgrounds.
In response to the changing role and increasing importance of probability in the scientific enterprise, we make the following five recommendations:
The purpose of the Workshop on Current and Emerging Research Opportunities in Probability was to gather assessments from the contemporary research community of outstanding and emerging open problems in the foundations and applications of probability. This perspective is well illustrated in the descriptions of research areas in the main body of this report. The challenges outlined in these descriptions clearly indicate a promising future for our field.
Much of the discussion in the workshop, however, was outside of specific research areas and was motivated by three key observations: A) Probability has a significant role to play in almost every branch of science and engineering. B) Probability is a way of thinking about the world that is distinct from the modes of thought in other areas of mathematics. C) The development and application of probability is scattered in universities and in professional organizations.
Each of these observations may seem obvious, and perhaps should be, but their implications are not always consistent with those of decisions taken in universities and elsewhere in the scientific community. The primary recommendations of this report call on decision makers at all levels to respond effectively to these observations in order to fulfill the promise of scientific advances that is so apparent in the research areas described.
A. Probability has a significant role to play in almost every branch of science and engineering.
We simply illustrate this observation with a few examples:
Just as understanding spatial relationships motivated geometry and understanding motion motivated analysis, probability was motivated by the desire to understand the uncertainty evident everywhere in our physical and social universe. To be convinced that probability is a mode of mathematical thought distinct from the others, one simply has to compare how one validates models based on probability as opposed to models given by differential equations or geometric structures. But probability is also a distinct way of thinking within mathematics. Compare the intuition of probabilistic arguments based on independence in number theory with the traditional approaches, or compare the intuitive understanding of harmonic functions that comes from the observation that a harmonic function applied to Brownian motion gives a martingale with the perspective that a harmonic function is the unique solution of the Dirichlet problem with a given set of boundary conditions. Based on its special intuition, probability generates tools and techniques that are relevant to other areas of pure mathematics. The "probabilistic method" is a central approach to problems in combinatorics and the analysis of algorithms. Probabilistic representations give new insights into a wide variety of partial differential equations from existence and smoothness of solutions to Navier-Stokes equations to properties of the spread of fluids through porous media. More examples arise in harmonic analysis, complex and Lie groups, and elsewhere.
This observation also has implications for college and university curricula. Even at the beginning undergraduate level, a course in probability may be more useful than one in calculus. The modern life of an ordinary person is steeped in probabilistic concepts. An understanding of randomness, independence, laws of large numbers, and the central limit theorem is indispensable for the correct interpretation of opinion polls and other statistical data, evaluating insurance choices, and understanding the investments that are involved in retirement plans.
C. The development and application of probability is scattered in universities and in professional organizations.
"Professional probabilists," that is, individuals who develop the mathematical foundations of probability and who discover and promote novel applications, can be found in departments of mathematics and statistics and in colleges of engineering and business as well as in many other university settings. AMS and SIAM (mathematics organizations), IMS and the Bernoulli Society (statistics organizations), IEEE and INFORMS (engineering organizations) all sponsor journals and research conferences in which probability plays a central role. However, it is all too easy for the subject that is of interest to everyone to become the responsibility of no one, and the diffuse settings in which probabilists work may lead to isolation and lack of communication. Nevertheless coherence of this scattered probability community is essential to the exchange of new ideas and methods that benefit fundamental research and inspire new applications. Innovations can be motivated by problems in one sector which modify techniques from another and then find application in a third. The mathematical objects created in probability often find application far beyond the original intent. For example the ideas of concentration of measure arose from the study of fundamental geometric and probabilistic problems but now have important applications in computer science, optimization and statistical physics.
University faculty and administrators will no doubt recognize the problems of this dispersed intellectual community as belonging to a wider collection of challenges currently forcing a revolution in academic organization. Motivated by the dramatically increased importance of interdisciplinary research and education, new academic structures are being sought and implemented on many university campuses.
1. Universities must find mechanisms that bring coherence to the currently diffuse place of probability on their campuses.
Researchers in probability reside in many different departments and academic units, and researchers who utilize probabilistic methods are found throughout the university. Instructional interest and responsibility is also dispersed. Universities must find mechanisms that unify these groups if they are to have effective and efficient instructional programs and the vital collaboration needed for successful research programs.
2. Mathematics departments should incorporate probability in the core curriculum at all levels.
As a distinct mode of mathematical thought with wide ranging applications to other areas of mathematics and throughout science, all mathematics majors at the undergraduate and graduate levels should have probability in their training. A large proportion of undergraduate mathematics majors find employment outside academia or pursue graduate degrees in fields other than mathematics. Probability plays an important role in most of these settings, so a course in probability is a valuable part of any undergraduate's training. These courses should go beyond the usual combinatorial and analytic techniques for basic probability calculations and include the use of probability-based models for the analysis of some topics outside mathematics.
3. Faculty responsible for instruction in probability need to insure that new curricula reflect recent research developments and the needs of emerging areas of application.
Research drives education. In order to be successful in the long run, the revolution in probability research must lead to changes in the teaching of probability at all levels. The explosive growth of the applications of probability presents an opportunity for mathematics departments to develop course offerings that will accommodate widely varying audiences with diverse backgrounds and needs. These courses are needed for both undergraduate and graduate majors in many fields.
4. Graduate programs must train more researchers in probability, both as a core mathematical discipline and in an interdisciplinary context.
As illustrated in this report, many emerging research problems in the sciences are highly interdisciplinary in the breadth of expertise required to identify, formulate and solve them. Probability is a significant disciplinary component. Future success requires a sustained attention to development of both the core discipline and its interconnections with the sciences and engineering.
5. Funding agencies and university administrations need to provide the resources necessary to respond to the increased demand for probabilistic methodology.
Successful scientific inquiry requires both human resource and infrastructural investments. Support needs range from traditional computing equipment, publication and conference costs to supporting graduate students, post-docs, and teaching/research faculty. Traditional departmental boundaries within university systems discourage exchanges across disciplines. Policies to reward and support exchanges among disciplinary cores across campuses should be implemented.
The remainder of this document details recent advances and emerging research opportunities in seven broad areas:
These are exciting times for probability. This list contains illustrative examples from a much larger universe of possible choices. Another committee could have produced a different list of compelling research problems in probability. While many recent breakthroughs are propelling the field to new heights, with the exception of a few historic citations we have deliberately elected not to cite specific individuals. The interested reader is invited to take advantage of web based search engines to learn more about the current status of these ground breaking discoveries and the people involved.
1.1 The Markov chain Monte Carlo (MCMC) algorithm is a general purpose method of solving the practical problem of sampling a random object from some mathematically specified probability distribution on possible objects. This problem arises in many areas of mathematical science, in particular Bayesian statistics and statistical physics. Here is an easy to state example from graph theory. A k-coloring of a graph G is an assignment of one of k colors to each vertex of G, subject to the constraint that two vertices linked by an edge must have different colors. How can we obtain a random such coloring which is uniform (each possible coloring should be equally likely)? One's first idea -- sequentially assign colors to vertices at random subject to the constraint -- doesn't work. Instead, start with an arbitrary coloring. Then simulate (Monte Carlo) the random process (Markov chain) where at each step we pick a random vertex of G, change it to a randomly-chosen color if the constraint is satisfied, and otherwise keep the coloring unchanged. Under technical conditions (in particular, it is sufficient that k be larger than twice the maximal vertex-degree of G), after suitably many steps the probabilities of each possible coloring will be almost equally likely, and one can even give a theoretical analysis of the number of steps required (the mixing time).
The underlying mathematical question of estimating the mixing time of a finite (but large) state Markov chain arises in different settings. The scheme above is the key ingredient in an algorithm for approximate counting of the number of k-colorings of a graph. Similar MCMC schemes have been devised for more important problems such as approximating the permanent of a large matrix and approximating the volume of a convex body in high dimensional space. Proofs in this area draw upon a rich variety of techniques: large deviations and coupling; spectral gap estimates, and discrete Fourier analysis; combinatorial methods involving canonical paths, flows and optimal cut sets; and geometric ideas relating isoperimetric inequalities to eigenvalues of the Laplacian.
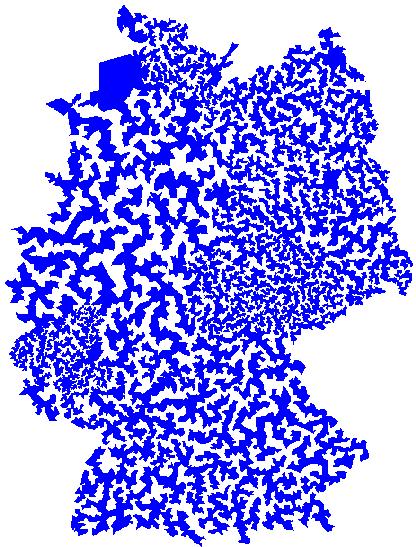
1.2. Combinatorial optimization is a classical area in the theory of algorithms, and the TSP (traveling salesman problem: find the shortest route through a set of points) is the paradigm problem in this area. In designing general purpose algorithms for such problems it is often prudent to include some randomization in choice of successive steps to avoid being trapped at non-optimal local minima. Theoretical analysis of such heuristic randomized algorithms remains a challenging problem. In a different direction, there are several hard open problems concerning the optimal TSP path on n random points in the plane. First, does the Central Limit Theorem hold, i.e. does the length of the optimal tour have a Normal distribution as n tends to infinity? Second, can one prove anything about the geometric structure of the optimal tour?

Solution of traveling salesman problem for 15,000 cities in Germany. Being a simple closed curve it has an inside (blue) and an outside (white).
The latter topic falls within the domain of probabilistic analysis of
algorithms, where one puts a probability model on the input data. Another
intriguing problem in this domain concerns the assignment problem: Given
n jobs, n machines and an n by n matrix of costs
(the cost to perform job i on machine j), find the minimum-cost
assignment of different jobs to different machines. In the deterministic setting
this is a simple special case of linear programming. Make a probability model by
assuming the costs are independent with exponential, mean 1, distribution. What
can we say about the (random) minimal cost Cn? It was
conjectured over 15 years ago, using the non-rigorous replica method of
statistical Physics, that Cn converges to 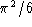 , but only recently was a
rigorous proof found. The related conjecture for the exact formula
, but only recently was a
rigorous proof found. The related conjecture for the exact formula
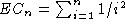
remains unproved.
2.1. Self-avoiding Random Walk, Stochastic Loewner Evolution. The self-avoiding random walk (SAW) on the two-dimensional lattice Z2 is an important although simplified model for polymers. A self-avoiding string of length n is chosen randomly (uniformly) from all self-avoiding strings of the same length. The question about the diameter of self-avoiding strings has led to many technical questions regarding non-intersection exponents. For example, b is a non-intersection exponent if the probability that two simple random walk paths on Z2 of length n, starting one unit apart, will not intersect, is of order n-b. The non-intersection exponents were defined and proved to exist in the early 90's. Their values remained unknown for about a decade, and the determination of their values was considered a challenging and difficult problem.
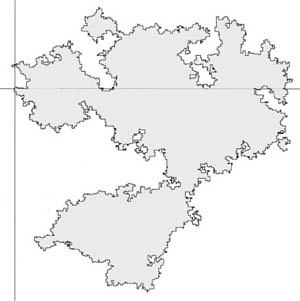
Self-avoiding random loop
The stochastic Loewner evolution (SLE) was recently introduced to successfully model the growth of a continuous path within a disc, in a random and 'conformally invariant' way. The SLE proved to be a wonderful technical tool that is allowing researchers to calculate all non-intersection exponents. As a corollary, the Hausdorff dimension of the outside boundary of the two-dimensional Brownian trace B[0,1] has been rigorously calculated. Its value 4/3 is precisely that which had been conjectured on the basis of certain heuristic principles. It has further been shown that the Hausdorff dimension of the set of cut points is 3/4. (x is called a cut point if it is the only point of intersection of B[0,t] and B[t,1] for some t.)
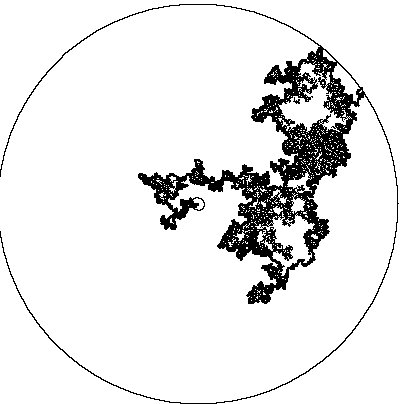
Frontier of two dimensional Brownian motion
The major open problem in the area is the conformal invariance of SAW on large scales, conjectured by physicists and confirmed by simulations. Once this conjecture is proved, the fractal dimension of the SAW paths will follow from the recently developed breakthroughs in this area.
2.2. Percolation. In the percolation model the vertices of a (homogeneous) lattice are independently declared ''open'' (with probability p) or ''closed'' (with probability 1-p). Connected components of open vertices are called clusters. For lattices in dimension 2 and higher, there exists critical value pc strictly between 0 and 1 so that with probability one, there is no infinite cluster for p < pc yet there is an infinite cluster for p > pc. A basic problem of the subject is
Question: Is there an infinite cluster for p = pc?
A negative answer is known in dimension 2 as well as in high dimensions and for lattices in hyperbolic space; but even in 3 dimensions the question is open.
A related question is to determine the probability that a given vertex is an infinite cluster for p slightly larger than pc. This probability is believed to scale like a power of p-pc, and the relevant exponent is known as a ''critical exponent'' and is believed to satisfy universality, i.e., to depend only on the ambient dimension and not on the specific lattice.

Spanning cluster (blue) in critical percolation
Spectacular progress has been obtained for critical percolation on the triangular lattice: The discovery of the SLE (stochastic Loewner evolution) and the recent proof of the existence and conformal invariance of scaling limits for cluster boundaries and convergence to the SLE model were jointly recognized with the 2001 Salem Prize. Determination of critical exponents for the triangular lattice followed. This advance makes the universality problem especially tantalizing. The only setting where universality has been established is random walks, where scaling limits of paths are Brownian motion independently of the underlying lattice.
2.3. First passage percolation. Label the edges of a two-dimensional lattice with independent positive variables (''crossing times''). The passage time Tn is the minimum over all paths from the origin to (n,0) of the total crossing time along the path. The means that the expected value E(Tn) grow linearly in n.
Question: How fast does the standard deviation of Tn grow?
For suitable constants c and C, c log(n) and Cn1/2 are lower and upper bounds. A logarithmic improvement to the upper bound was recently proved. It is conjectured that the real growth rate is n1/3; this growth rate was proved for a related ''toy model'' (oriented last passage percolation) via a connection to random matrices.
2.4. Diffusion Limited Aggregation. Some of the most exciting and challenging problems in probability come from physics. Diffusion limited aggregation (DLA) involves a growing ''cluster'' of particles on the two-dimensional integer lattice Z2. The cluster starts from a single particle. Then more particles are added to the cluster one at a time. Each new particle starts ''at infinity'' (far away from the cluster), follows the trajectory of a simple random walk on the lattice, and finally attaches to the existing cluster at the point where it hits the cluster for the first time. The model is deceptively simple. Although the physics literature on this model is abundant, there are only a few rigorous mathematical results. For example, rigorous upper bounds on the rate of growth of DLA clusters have been obtained which are better than the trivial bound cn but probably not sharp. It has recently been proved that with probability one, the cluster will contain infinitely many holes (i.e., lattice points with no particle, surrounded by the cluster) as the cluster grows. Several natural questions about DLA are still open. So far, there is no lower bound on the rate of growth of the cluster diameter, except the trivial one, cn1/2 . Nothing is known about the `fractal' dimension of DLA clusters, except for simulations, and it is not clear, even from the simulations, whether the rescaled DLA clusters converge to an asymptotic shape.

DLA cluster with 32768 sites
2.5. Disordered systems. In statistical physics, an important distinction is made between ordered systems, such as the Ising model, where the states of minimal energy (``ground states'') are apparent and disordered systems such as spin-glasses, where the interactions between various spins are random. An important example of the latter which has been the subject of a spectacular set of advances is the Sherrington-Kirkpatrick spin-glass model.
2.6. Random matrices. The theory of random matrices was initiated by the physicist Wigner to study the internal structure of complex atoms. A particularly important example, the Gaussian Unitary Ensemble of degree N, consists of the set of all N by N matrices equipped with the unique probability measure that is invariant under conjugation by unitary matrices and that makes the matrix entries become independent random variables. The eigenvalues of a random Hermitian matrix do not behave like independent random variables, so the probability of finding more than one eigenvalue in a short interval is much lower (``the eigenvalues repel''). Since 1970, evidence has accumulated that the relative spacing of zeros of the zeta function is asymptotically governed by the (explicitly known) spacing of eigenvalues under GUE. Remarkable advances on related problems have been made, but this problem on the interface of probability and number theory is still open.
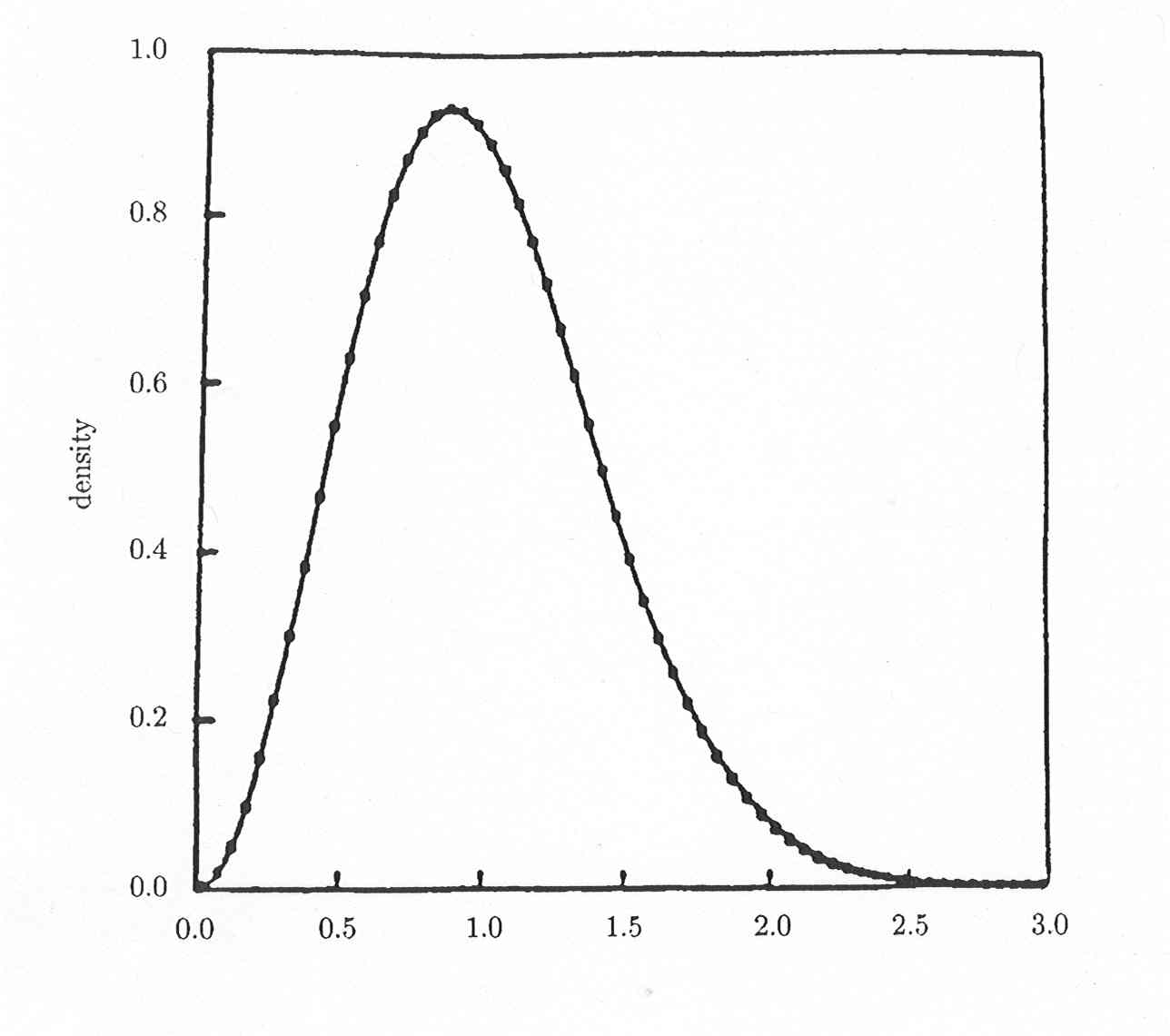
Nearest neighbor spacing among 70 million zeros beyond the 1020th zero of the zeta function compared to the Gaussian Unitary Ensemble
The analysis of dynamical and physical systems continues to be an important source of problems and progress in probability. Along with the growth in non-traditional areas of application, probability continues to be employed both in its traditional role of modeling intrinsically random physical phenomena and in the analysis of non-random equations and problems.
3.1. Stochastic partial differential equations. The initial motivation for the study of stochastic partial differential equations came from nonlinear filtering, the computation of the conditional distribution of a random `signal' given deterministically transformed and stochastically perturbed observations. Further applications include models in hydrology, oceanography and atmospheric sciences. Major outstanding questions arise in modeling at scales at which observed variabilities suggest "appropriate" stochastic refinements of physical conservation laws. For example, refinements of the numerical climate models involve energy sources and sinks at scales associated with highly variable and intermittent phenomena such as space-time rainfall and turbulent flows. Similarly prediction and understanding of river flows in a complex river basin network involves modeling considerations of large scale gravitationally driven flows in a randomly varying topography reinforced by erosion and induced by highly variable local precipitation. Such modeling problems are indeed substantially interdisciplinary.
Apart from modeling, fundamental questions include the rigorous definition of a solution, the existence and uniqueness of that solution, and the regularity and other properties of the solution. Solutions of SPDEs can frequently be viewed as Markov processes in infinite dimensional state spaces, and classical questions regarding the existence of stationary distributions and ergodic properties of the solutions arise naturally and play important roles in applications. The study of SPDEs exploits and stimulates the development of techniques in stochastic and functional analysis and the theory of partial differential equations.
Space-time simulation of Wright-Fisher SPDE
Appropriate derivation of models depends on the methods of classical applied analysis, scaling arguments starting from complex interacting stochastic systems, and techniques unique to the particular setting. Computation for SPDEs depends on the methods of numerical PDE, approximation methods for stochastic processes, and new methods based on particle simulations and resampling ideas.
Important areas for future development include better models for highly variable flows, the relationship between discretized (lattice) models and SPDEs, more robust and efficient computational methods (and in some settings the development of any kind of consistent computational scheme), better modeling in many potential areas of application, understanding the relationship between systems modeled by SPDEs and high dimensional observations of those systems, and related statistical methods.
3.2. Existence, uniqueness, and structure of steady state for randomly perturbed dynamical systems. A discrete time dynamical system is given by an evolution equation of the form xn+1 = f(xn). For many dynamical systems of interest there are infinitely many initial distributions for x0 which are preserved by the evolution. Often there is one particular invariant distribution which is distinguished by the property that for essentially any starting point x0 the proportion of times the state visits a set B converges to the invariant probability of B. Kolmogorov proposed a program for determining these distinguished probability distributions by consideration of certain random perturbations of the dynamics given by f. The steady state of this random dynamical system converges to the distinguished invariant probability distribution of the original dynamical system as the random perturbation becomes negligible. This program has been successfully carried out in certain specific cases; however, the extension to broader classes of systems remains largely open. This problem is of interest in efforts at understanding complex phenomena related to chaos and turbulence.
3.3. Homogenization and multiscale problems in random media. Problems in random media are concerned with the physical properties of highly nonhomogeneous materials. These properties are frequently determined by the solutions of partial differential equations. Probabilistic ideas and methods enter in two ways. First, the nonhomogeneities may be described in terms of stochastic models. For example, the coefficients of the partial differential equations may be random and spatially varying. Second, because of the connections between diffusion processes and partial differential equations, the PDEs may be analyzed by analyzing the corresponding diffusion process.
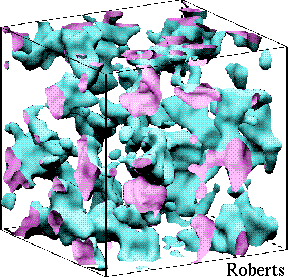
A composite material that is 13% silver (purple) and 87% tungsten (green).
In the limit of increasingly rapid oscillation, a diffusion process with spatially periodic coefficients behaves asymptotically like a Brownian motion with drift and diffusion coefficients obtained by appropriate averaging of the original coefficients. Similar results hold when the coefficients are random. These results are basically central limit theorems and give an ''homogenized'' version of the original physical model, that is, solutions of elliptic or parabolic equations with rapidly oscillating coefficients can be approximated by solutions of an homogenized equation with constant coefficients. For example, the equation for heat conduction in a composite medium can be approximated by an equation with constant coefficients. While substantial progress has been made in carrying through this program, particularly in the case of equations in divergence form, many problems are still open.
Finally, multiscale homogenizations take place in the presence of a large spatial scale parameter for the case of periodic coefficients. This means, in probabilistic terms, that different Brownian approximations show up as time progresses, with non-Gaussian intermediate phases. Extension of these results to the more general case of randomly varying coefficients remains open. Such multiscale problems arise in geosciences, for example, in the transport of contaminants in an aquifer.
Focusing and defocusing of a signal passed through a random turbulent atmospheric medium
3.4. Probabilistic Representations of PDE's. Brownian motion is a mathematical description of particles diffusing through space. Technically the model is obtained by constructing a probability measure (Wiener measure) on the space of paths that a particle could traverse. The partial differential equation description (through the heat equation) of the same phenomenon describes the probability that a particle starting at some point x arrives at another space point y in a given time t. In this way, once having established the existence of Wiener measure, one gets a probabilistic representation for solutions of the heat equation. Moreover, by averaging certain functions of the Brownian paths, one may represent solutions of elliptic equations and non-constant coefficient parabolic equations. These representations coupled with the Malliavin calculus give a very natural way of understanding, and in some cases extending, Hormander's theorem on hypoellipticity.
For example, consider the classical Dirichlet problem for a bounded domain D
contained in Rn. Specifically, let u be a solution of
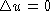 with u=f on
with u=f on 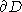 . Then u may be represented as the
average of the boundary data, f, evaluated at the point were the Brownian
path first hits the boundary of D.
. Then u may be represented as the
average of the boundary data, f, evaluated at the point were the Brownian
path first hits the boundary of D.
Although linear parabolic and elliptic differential equations in finite dimensions have been highly developed in analysis, there are still many important open problems involving partial differential equations in infinite dimensions, for example those equations related to relativistic quantum field theories. The past success in constructive quantum field theory heavily relied on probabilistic representations in the form of the Feynman-Kac formula. Nevertheless, the construction of an interacting relativistic invariant quantum field theory in four space-time dimensions is still an unsolved problem. For more in this direction the reader is referred to the construction of quantized Yang - Mills fields at the Clay mathematics institute web page.
As with infinite dimensional problems, the probabilistic representations of nonlinear PDE (in finite dimensions) is, not surprisingly, more difficult and less understood. In the remainder of this section we will describe a few examples.
3.5. Geometric PDE. Interesting classes of equations come from geometry. A harmonic map, u from D to Sk the unit sphere in k+1 dimensions , is a solution to the partial differential equation
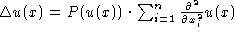 with
u=f on
with
u=f on 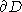
where P(u) is the orthogonal projection of Rk+1 onto the tangent plane to Sk at u. One might attempt to solve this equation in the same manner as the classical Dirichlet problem as an average of the boundary data, f; however, the average will typically not be back in the sphere. In this case, the notion of manifold-valued martingales with prescribed ending values turns out to lead to the correct generalization of average. Other geometric partial differential equations, like Hamilton's Ricci flow of a metric, do not yet have a probabilistic description. This is an important problem since it is a potential avenue towards resolving the three dimensional Poincar?problem.
3.6. Interacting Particle Systems and Super-Brownian Motion. Another probabilistic representation of a class of PDE arises from the study of interacting systems of particles diffusing through space. The simplest interaction involves particles that can either die or replicate. A rescaled limit of a large system of such particles leads to super-Brownian motion, a probabilistic object related to a family of semilinear parabolic equations of the form
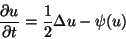
where 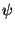 belongs to a
class of functions including
belongs to a
class of functions including 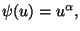 for
for 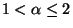 . This
also leads to a probabilistic representation of the corresponding nonlinear
elliptic equations that has been used for example to solve the problem of
classifying all solutions of the equation
. This
also leads to a probabilistic representation of the corresponding nonlinear
elliptic equations that has been used for example to solve the problem of
classifying all solutions of the equation 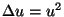 on a region in Rk. It
has recently been established that super-Brownian motion also arises as a
rescaled limit of a number of other particle systems (voter model, contact
process, Lotka-Volterra systems) as well as a number of fundamental models in
statistical physics in high dimensions suggesting a new universality class of
space-time systems.
on a region in Rk. It
has recently been established that super-Brownian motion also arises as a
rescaled limit of a number of other particle systems (voter model, contact
process, Lotka-Volterra systems) as well as a number of fundamental models in
statistical physics in high dimensions suggesting a new universality class of
space-time systems.

Measure-valued diffusion limit of colicin model
3.7. Incompressible Navier-Stokes Equations. The incompressible
Navier-Stokes equation is the law of motion governing the flow of an
incompressible viscous fluid such as water, oil, molasses, etc. These are vector
equations which are expressed in terms of the unknown velocity components u(x,t)
= (u1(t,x),u2(t,x),u3(t,x)) of the flow past a
location x at time t and an unknown scalar pressure p(x,t). The
incompressibility condition takes the form of vanishing divergence 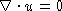 . One of the outstanding unsolved problems
in mathematics is to determine whether or not these equations have a unique
smooth solution u(x,t) for all t > 0 for any prescribed smooth initial
velocity field u(x,0)=u0(x).
. One of the outstanding unsolved problems
in mathematics is to determine whether or not these equations have a unique
smooth solution u(x,t) for all t > 0 for any prescribed smooth initial
velocity field u(x,0)=u0(x).
As in the above examples, the viscous term of Navier-Stokes also has the
Laplacian term  where
where 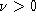 is the coefficient of
viscosity; however, the expression for acceleration of flow past a point is of
the intrinsically nonlinear form
is the coefficient of
viscosity; however, the expression for acceleration of flow past a point is of
the intrinsically nonlinear form  . While this nonlinearity may obscure a direct probabilistic
connection to the Laplacian term in physical space, by considering the
Fourier-transformed velocity, researchers have recently obtained a probabilistic
representation of u(x,t) as an expected value of a product of initial data and
forcing factors over nodes of a multi-type branching random walk in Fourier
space. This observation has led to new ways to formulate and analyze existence,
uniqueness, and regularity problems from a probabilistic point of view.
. While this nonlinearity may obscure a direct probabilistic
connection to the Laplacian term in physical space, by considering the
Fourier-transformed velocity, researchers have recently obtained a probabilistic
representation of u(x,t) as an expected value of a product of initial data and
forcing factors over nodes of a multi-type branching random walk in Fourier
space. This observation has led to new ways to formulate and analyze existence,
uniqueness, and regularity problems from a probabilistic point of view.
Vortices in three dimensional turbulence
One can open the New York Times on almost any day and read about a new crisis, or a success story surrounding some complex network. Familiar examples are
New York state power grid
Manufacturing system as queueing system (image by P.R. Kumar)
Although the application areas are distinct, these systems share many commonalities: in each case there are interacting entities; one must decide how to allocate resources (such as links, or processors, or generators); and in all of these systems there are hard constraints (e.g., communication link capacity, population bounds, or power limits).
In any of these application areas, the first critical issue is modeling: what is the best model for the particular system? The answer to this question depends upon one's goals. In particular, for accurate prediction one may require a highly complex model, similar to what is required in weather prediction. To answer other questions, a complex model may be useless.
For example, it is well-known in the academic community that optimal routing based on a natural model of the Internet may be NP-hard. This means that the complexity of an optimal routing strategy grows dramatically with complexity, and many related `network control problems' share this apparent intractability.
In recent years there has emerged new tools for constructing simple models for highly complex networks. The simplest models are based on linear, constrained ordinary differential equations, or refinements with stochastic disturbances. Frequently, it is convenient to assume Gaussian statistics, leading to a reflected diffusion model. Using a range of probabilistic tools it is possible to establish extremely tight solidarity between these naive models and more complex models. Although the simple model may not be best for prediction, in many instances they essentially solve the control problem of interest, and may also be used in performance evaluation in comparing two control solutions. Moreover, a simple model provides the added benefit that the optimization solution can be expressed in simple terms, and this may provide enormous insight to the practitioner.
The tools used to establish such solidarity are basic probabilistic limit theory; versions of the central limit theorem; large deviations bounds; and stochastic dynamic programming (based on properties of Poisson's equation).
The recent ENRON scandal surrounding power allocation and pricing in California is a warning sign that the public requires a better understanding of network behavior in a dynamic, competitive setting. There are many open problems in any one of the application areas listed above. Research will inevitably apply large deviations theory; information theory; game-theory; recent approaches to modeling complex networks; and possibly also some formulation of `machine learning'.
The application of probability to finance has revolutionized an industry. In the past 20 years the creation of multi-trillion dollar derivative security markets has facilitated the world-wide flow of capital and thereby enhanced international commerce and productivity. Without the mathematical models which provide reliable pricing of derivative securities (e.g., stock options) and guide the management of their associated risk, these markets could not exist. The underlying theme of the mathematical success has been to compute precisely the price of financial derivatives which enable companies to lay off risk by buying financial instruments that protect them from unlikely but possibly disastrous events. Equally if not more important has been the description of a recipe for the seller of the instrument to follow in order to protect himself from the risk he accepts through the sale. A complete market is one in which the theory explains how to do this in principle, and in such a market the theory often provides an explicit guide to implementation of this recipe. In other words, in complete markets a new type of insurance has been created, and this has been made possible by existing probability theory. This type of ''risk insurance'' generated the revolution mentioned above.
The theoretical needs of problems arising from mathematical finance have been a stimulus for new research in probability theory, and there has been an explosion of interest in the subject. New mathematical challenges arising from finance are how properly to measure and control risk (given that the flaws in the industry standard, Value at Risk, or VaR for short, are becoming increasingly apparent), how to model and hedge against default, how to incorporate market frictions, and more generally, how to deal with incomplete markets. In the case of incomplete markets the current theory breaks down almost completely, and considerable effort is being devoted to the development of a theory to handle these situations. In the case of VaR, methods currently used are unstable and open to manipulation, and more appropriate methods to reliably measure risk are needed. Of particular interest is how to control a portfolio in order to minimize its risk when the risk cannot be completely eliminated. This suggests a projection, in which a risky stochastic process is projected onto the space of stochastic processes whose risk can be managed. Many measures of risk are norms, but they are not associated with inner products and hence the usual projection ideas are not applicable. New ideas are needed.
Another area relevant to mathematical finance is stochastic numerical analysis. Mathematical finance was initially successful because the early models led to explicit formulas, and formulas are dear to the hearts of practitioners. But as the need develops for more sophisticated models, formulaic solutions are no longer available, and answers are computed numerically. This has led to interest in stochastic numerical analysis and its concomitant simulation problems, and one of the areas of future research is the design of efficient methods to simulate stochastic processes as well as to numerically estimate constants arising from the models.
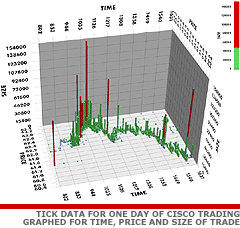
New York Stock Exchange Daily Returns (log of price ratios) Note the heavy tails and the asymmetry between up and down moves.
Financial institutions, many of which have large cash flows relative to their capitalization, are sensitive to extreme events, i.e., the nature of the tail of the distribution of a random variable. Extreme value theory, which includes a characterization of the possible distributions of the limit of a normalized maximum of a sequence of random variables, replaces the usual central limit theorem in this context. Correlation as used with jointly normal random variables is an inadequate measure of dependency when one is concerned with extreme events. Models based on correlation often underestimate the probability of joint extreme events, and large losses in the finance industry have shown this is not merely an academic fine point. Recent and ongoing research has focused on whether this problem can be treated by using copulas, a more detailed measure than correlation of the dependence between two random variables.
More generally, understanding distributions and dependencies has given new impetus to the topic self-normalized processes. These are processes normalized by an empirically observable measure of their randomness, a measure akin to volatility in financial data. This normalization permits one to deal with dependencies in data. A key example in the area of self-normalization is Student's t-statistic used to test hypotheses and construct confidence intervals on the basis of independent data. The general theory of self-normalized processes arises naturally in the context of efficient estimation in statistics. It frequently eliminates the need for independence and moment assumptions. Self-normalized processes also appear in limit problems when the variance of a process is estimated. However the study of properties for small time horizons is at an early stage. There are open problems involving the development of sharp estimates alternative to using t-statistics using dependent variables, as well as the extension of key moment inequalities used in more traditional martingale theory. (Martingales are a class of stochastic processes, often described as modeling a fair gambling game, but which also can be seen as an extension of the idea of a nested sequence of Hilbert space projections.) How to test hypotheses and construct confidence intervals for multiple, dependent processes is another open research topic.
Animals process sensory data, such as acoustical and visual signals, very rapidly and virtually flawlessly in order to localize and identify sounds and objects in the surrounding environment. What representations and methods of inference does the brain employ? Moreover, regardless of how these tasks are accomplished by living organisms, how might one construct artificial systems - computer programs and algorithms - in order to perform similar tasks, such as understanding spoken language or interpreting scenes? Solving these "perceptual inverse problems" is a major scientific challenge.
 How
do we recognize this as Abraham Lincoln?
How
do we recognize this as Abraham Lincoln?
In order to better understand the nature of the difficulties and the role of uncertainty, consider the semantic interpretation of natural scenes. Whereas so effortless for humans, it is certainly the main challenge of artificial vision, especially when searching for many different objects with unknown presentations in real, cluttered scenes with arbitrary illumination. In the figure on the left, for instance, we desire a description which mentions a street in a town, probably European, with shops and a few pedestrians, and so forth, whereas in the figure on the right the goal might "simply" be to detect the faces. The absence of a general solution (the "semantic gap") impedes scientific and technological advances in many areas, including automated medical diagnosis, industrial automation (e.g., systems for reading bank checks or detecting sleepy drivers or road signs), effective security, intelligent information retrieval and video compression (allocating more bits to faces than to foliage requires first knowing which pixels are which).


Natural scenes are notoriously ambiguous at a local level - blow up a small window and determine what you are looking at. However, they are perceived globally as largely unambiguous, due to incorporating context and likelihoods into our analysis, unconsciously weighting competing solutions which might cohere equally well with the raw data. There is then widespread agreement that stochastic modeling, analysis and computation is pivotal. As a result, probabilistic reasoning pervades courses in theoretical neuroscience, inductive learning, information extraction, computer vision and speech recognition.
How does one model the process of learning or base inference on prior knowledge? For instance, object detection must be invariant to various photometric and geometric transformations which do not change the names of things. How does one estimate the probability of making a mistake in the future based on the evidence gathered from examples, i.e., during learning? What sorts of probability distributions on image functionals have a sufficiently rich dependency structure to capture real-world patterns and correlations but at the same time are amenable to analysis and computation (for instance computing modes and expectations)? A similar dilemma is faced in neural coding: Finding tractable models of brain function which account for both "bottom-up" (data-driven) and "top-down" (hypothesis-driven) pathways and decision-making. What assumptions about the likelihoods of events make coarse-to-fine search an efficient strategy, namely first looking for everything at once and eventually generating a sequence of increasingly precise interpretations?
A natural and powerful approach to machine perception is Bayesian modeling and inference. The goal is to assign a semantic description D to the image data I. Two probability distributions are defined: P(D), over possible interpretations, reflecting our prior knowledge about the relative likelihoods of object configurations; and P(I|D), over images (say pixel grey levels) given the interpretation, which weights possible images which might result from D. Now given an image I, the assigned interpretation D*(I) might be the mode of the "posterior distribution" P(D|I). This leads naturally to constructing probability measures on complex structures, such as grammars and graphs, and to formidable challenges in simulation and optimization.
One special and vexing case is to construct realistic "clutter models" - distributions on images consistent with the special interpretation (or null hypothesis) "background" (i.e., no object(s) of interest). Realizations from such a distribution, i.e., sample pictures, ought to have a real world visual flavor. This rules out very simple distributions, such as white noise or Ising models, which lack sufficient structure. Whereas nobody anticipates a model whose typical realizations might be mistaken for real scenes, the model might at least capture the local statistics of the natural world and incorporate other observed properties, such as a degree of scale-invariance.
Biological data has been a source of challenging problems in probability for more than a hundred years. The recent explosion in the amount of available data from the genome project and other sources had led to increased opportunities for the application of probability to biological problems.
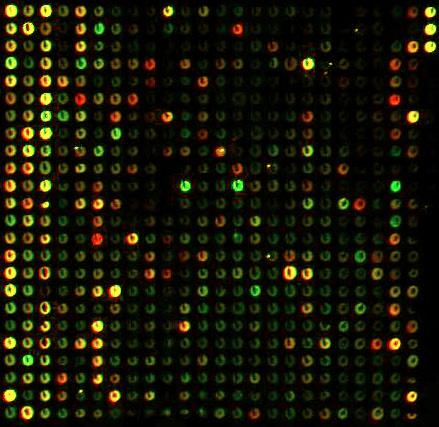
Microarray data
The number of individuals with a given gene is usually modeled as evolving in time according to the following scheme, which is called the Wright-Fisher model. The individuals in the next generation are derived from the previous by repeated binomial sampling of the genes from the parental generation. New genes may be sampled with error (corresponding to biological mutation) and some parental genes may be preferentially sampled (corresponding to Darwinian selection). This leads to a Markov chain with a state space that has the size of the population, which is typically large.
The method of diffusion approximation of Markov chains has revolutionized population genetics over the last 50 years. This technique allows one to approximate the Markov chain by a continuous Markov process that can be analyzed by solving simple ordinary differential equations. This leads to easy formulas for quantities such as the probability of and time to fixation of a particular genotype. These formulas have been important in understanding the effects of Darwinian selection and mutation in large but finite populations and has been influential in the guiding of experimental work.
Another important application of probability to the genetics of natural populations is coalescence theory. In the absence of mutation and selection, natural populations lose genetic variation by the chance effects that some individuals die childless. Coalescence theory explains this process by a simple multinomial sampling process going backwards in time. Current papers in the biological literature use deviations from the predictions of coalescent theory in the present as evidence for Darwinian selection, population subdivision, or an expanding population. Coalescent theory is also use for gene mapping and for the expected distribution of DNA markers that are used as evidence in court.
A current open problem in evolutionary theory concerns the proportion of evolutionary changes that were in fact positively selected. Many biologists believe that many if not most evolutionary changes were selectively neutral or slightly harmful, with most evolutionary advances due to extremely rare advantageous mutations. Current research in the biological literature uses diffusion approximation, coalescent theory, and other ideas in probability to attempt to answer this question.
The wealth of genetic data that is rapidly accumulating provides an important opportunity for probabilists to develop models to help understand patterns in DNA sequence data. An important new direction is the study of whole Genome evolution due to inversions, translocations between chromosomes and chromosomal fissions and fusions. These investigations are enlightened by earlier work in probability on card-shuffling problems, but also provide new interesting questions for study and have revealed surprising new connections between random walks on the permutation group and random graphs.
Stochastic modeling is currently used to extract information from large DNA data sets. The widely-used BLAST algorithm and its descendants look for approximate matches to a given sequence in a large database. The significance of matches is ascertained by theorems from extreme-value theory for probabilistic random walks in a form that was originally developed to study the maximum length of a queue.
Another example of the application of probability to the study of DNA sequences is the current use of hidden Markov models in the design of searches for genes, and for the prediction of protein structure and function.
Another important field for interaction has been mathematical ecology, which has a synergistic effect on research in stochastic spatial models. Biological systems such as the competition of viral species in a plant host have inspired models for study, and concepts from biology such as mutual invadability have guided the solution of these problems. In the other direction mathematical work has yielded insights into the impact of spatial distribution on the outcome of competition and in particular on the impact of habitat destruction on ecosystems.

Simulation of viral competition model