
专题讨论: 纽结和链环
在第三章学习了闭曲面分类定理之后, 有的同学就问: 为什么不从1维流形的分类讲起呢? 事实上, 这是因为紧致连通一维不带边流形 (也称为简单闭曲线) 只有一个同胚类, 那就是圆周.
那么是不是1维流形就没有可研究的了呢? 不是的. 让我们把简单闭曲线放到 (嵌入) E3中来看. 这时就会看到, 尽管它们相互同胚, 但 "放法" 却可以有很大的甚至是本质性的差异. 下图显示了3种最简单的放法:

事实上, 古人很早就从经验上知道了这一点: 有无数种方法在一条绳子上打结. 他们还给这些结起了各种各样好听的名字 (其中有一类就是著名的 "中国结"). 把这种打了结的绳子两端结上就是一个E3中的简单闭曲线. 因此我们就把这些闭曲线称为纽结.
定义 E3中与圆周同胚的子空间称为纽结. E3中与有限多个互不相交的圆周的并集同胚的子空间称为链环. 显然纽结就是只有一个连通分支的链环.
如果怎么样也无法把一个纽结 "挪" (或 "连续形变") 到另一个纽结所在的位置, 我们当然应该认为这两个纽结有本质的差异. 这种差异的严格数学表述为是否合痕.
定义 设K1,K2是两个链环. 如果存在一组E3上的自同胚ht, 使得h0为恒同映射, h1(K1)=K2, 并且定义在E3xI上的映射H(x,t)=ht(x)连续. 则称K1与K2合痕.
描述一个链环的最自然方法就是画它的示意图了. 不过, 不是所有的示意图都能准确反映纽结的全貌. 为了论述方便, 我们在下面的讨论中只考虑由有限条直线段构成的分段线性链环, 或与之合痕的温良链环. 前面举的几个例子都是温良纽结. 当它们温良时, 纽结或链环图是表示它们的非常有效的工具.
命题 设K是一个分段线性纽结或链环. 则存在一个方向v及与之垂直的平面F, 使得K沿v向F作的平行投影不含重数大于2的多重点, 并且每个2重点都是由K上两条线段的投影十字交叉而产生的. 在这个投影图上作记号表明相交叉的线段的上下关系后, 得到的图形称为K的一个纽结或链环图.
定理 设K1,K2是两个分段线性链环的链环图, 则它们所表示的链环合痕当且仅当从K1出发, 可以经过有限步Reidermeister变换得到K2. 这里Reidermeister变换是在纽结的局部进行的下列三种替换之一:

纽结论的最重要课题之一就是对所有纽结按合痕进行分类. 显然我们有下述结论.
命题 合痕的纽结在E3中的补空间同胚.
一个更深刻的结论是, 如果K1,K2的补空间同胚, 则存在E3上的自同胚把K1变成K2. 有趣的是这并不意味着合痕! 比如互为镜像的左右手三叶结就不合痕, 但它们的补空间显然同胚.

尽管纽结补空间是判定合痕类的一个准确度很高的工具, 但它也象纽结一样不便于理解和计算. 下面我们就来认识几个用来区分不合痕的纽结或链环的 "不变量". 第一个是反映纽结复杂程度的交叉数.
定义 与纽结K合痕的分段线性纽结的纽结图上交叉点的最少个数称为K的交叉数. 显然合痕的纽结应具有相同的交叉数.
比如平凡结的交叉数为0, 而左或右手三叶结的交叉数都是3. 事实上, 任何交叉数不超过3的纽结都与它们合痕, 而且对于每个自然数n>3, 以n为交叉数的纽结也只有有限多个 (但至少不止1个) 合痕类. 人们据此编制了庞大的纽结表, 列出交叉数不太多的纽结的所有合痕类. 这样当遇到一个一般的纽结图时, 就可以在交叉数小于该图中二重点个数的合痕类中查找并识别该纽结图的身份.
由于人们证明了下述Tait猜想, 因此对许多纽结计算交叉数也不是非常的困难.
定义 如果朝一个方向沿着纽结图走时, 总是交替地从上方和下方线段经过每个交叉点 (上, 下, 上, 下,...), 则称此图为交错纽结图.
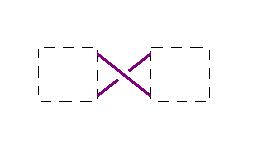
定理 如果一个交错纽结图中的每一个交叉点都不能象下图那样把纽结图分成互不相连的两部分, 那么该纽结图上交叉点的个数就是相应纽结的交叉数.
如果你认为每种不变量都要靠这种 "在所有合痕链环中取最大或最小" 的方式来构造, 那你就错了. 下面我们来看链环的一种奇妙的不变量叫做Jones多项式. 它甚至也不是借助链环补空间的拓扑构造得到的, 因为它能区分左手和右手三叶结!
设K是一个链环, 在其每个分支上取定一个沿之行走的方向, 得到的结果称为定向链环. Jones多项式是对定向链环定义的合痕不变量, 但是对于定向纽结, 反转定向后它并不改变, 因此就是一个普通纽结的合痕不变量.
定义 对于每个定向链环K, 其Jones多项式VK是一个t的函数 (当K是纽结时它是t及t-1的多项式). 这些函数满足下述三条关系:
(1) V平凡结=1.
(2) 若L+,L-,L0是三个定向链环图, 使得它们在一个局部如下图所示, 而在其它部分都完全一样, 则t-1VL+-tVL-=(t1/2-t-1/2)VL0.
(3) 若L是个定向链环, K是它的一个连通分支, 并且它在某个链环图中的投影不经过任何交叉点 (即K是个分离的圈), 则VL=-(t1/2+t-1/2)VL\K.

借助Reidermeister变换不难验证Jones多项式的合痕不变性. 注意到我们总可以通过把 "后交叉" 改为 "前交叉" 的方法解开复杂的结, 因此递归地应用上述三条性质, 就可以计算出所有定向链环的Jones多项式.
最后, 计算一下左手和右手三叶结的Jones多项式, 你会发现它们一个是t+t3-t4, 一个是t-1+t-3-t-4. 因此它们不合痕!
由于篇幅所限, 在这里我们对纽结论只能算是窥豹一斑. 其实关于纽结还有许多其它有趣的故事. 至少我听说过有化学家要合成打了结的大分子, 生物学中DNA双螺旋上的二级结构就是指它的打结情况. 而至于物理学嘛, 其实最早的纽结表就是在物理学家对大自然的一些 (可惜是错误的) 猜测的推动下编制的, 而来自量子场论的许多思想现在仍正推动着新型纽结不变量的产生. 在学完拓扑学并有了必要的知识准备以后, 有兴趣的同学可以阅读更专业的书籍进一步地去了解它.
版权所有(C): 本网页内容由包志强制作并维护, 保留所有权利.