本周作业：

尤承业书 207-211 页 12、16、17(2)、18(2)，19，60-62 页 3、4、8，72-74 页 5、7、9、10，81-84 页 13(1)，14(1)。

另外补充三道题如下。（如果你做了“选做题”中任何一道，那么上面这些尤书中的习题，你可以酌情跳过一些不做。选择权交给你自己吧。）

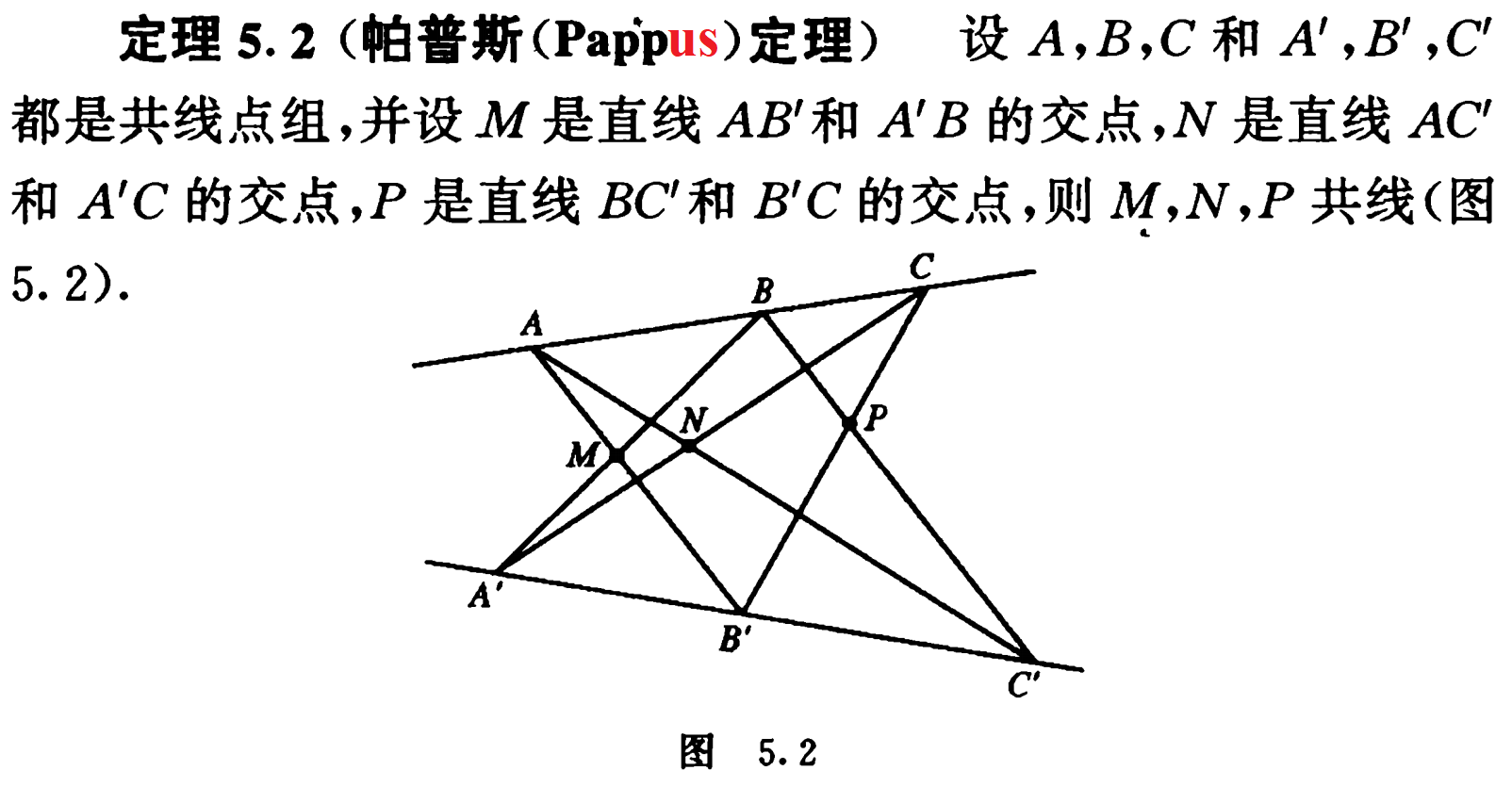
1. （选做题一）在平面上建立适当坐标系，用坐标法证Pappus定理（尤书 223 页有定理表述，对应 224 页图 5.2）。（注意课上的提醒，想想怎样才能简化计算、澄清关系。）

2. （选做题二）设 \(a\) 是一个单位四元数，也就是模长为 1 的四元数。考虑它在四元数空间上的“共轭作用” \(f_a\) 如下：任给一个四元数 \(v\)， \(f_a\) 把它映为 \(f_a(v)=av\bar{a}\) . 这里右边是三个四元数相乘， \(\bar{a}\) 是 \(a\) 的共轭（参考第 6 周习题课文档）。证明：这个作用是全体纯虚四元数（包括 0）构成的三维空间（假设 \(i,j,k\) 构成幺正基）上的一个等距变换，保定向，保原点0，从而是一个旋转。（这个旋转的转轴与这个单位四元数 \(a\) 是什么关系？）

3. （选做题三，借此总结和检验你的理解）对于空间等距变换，可以根据“是否有不动点”和“保定向/反定向”分成四类。请自选其中一类，用矩阵和特征值方法，完成这个类型的刻画与分类，并要求写清完整的讨论过程和证明。（例如，保定向且有不动点，必定是绕某个固定轴的空间旋转）。