本周作业：

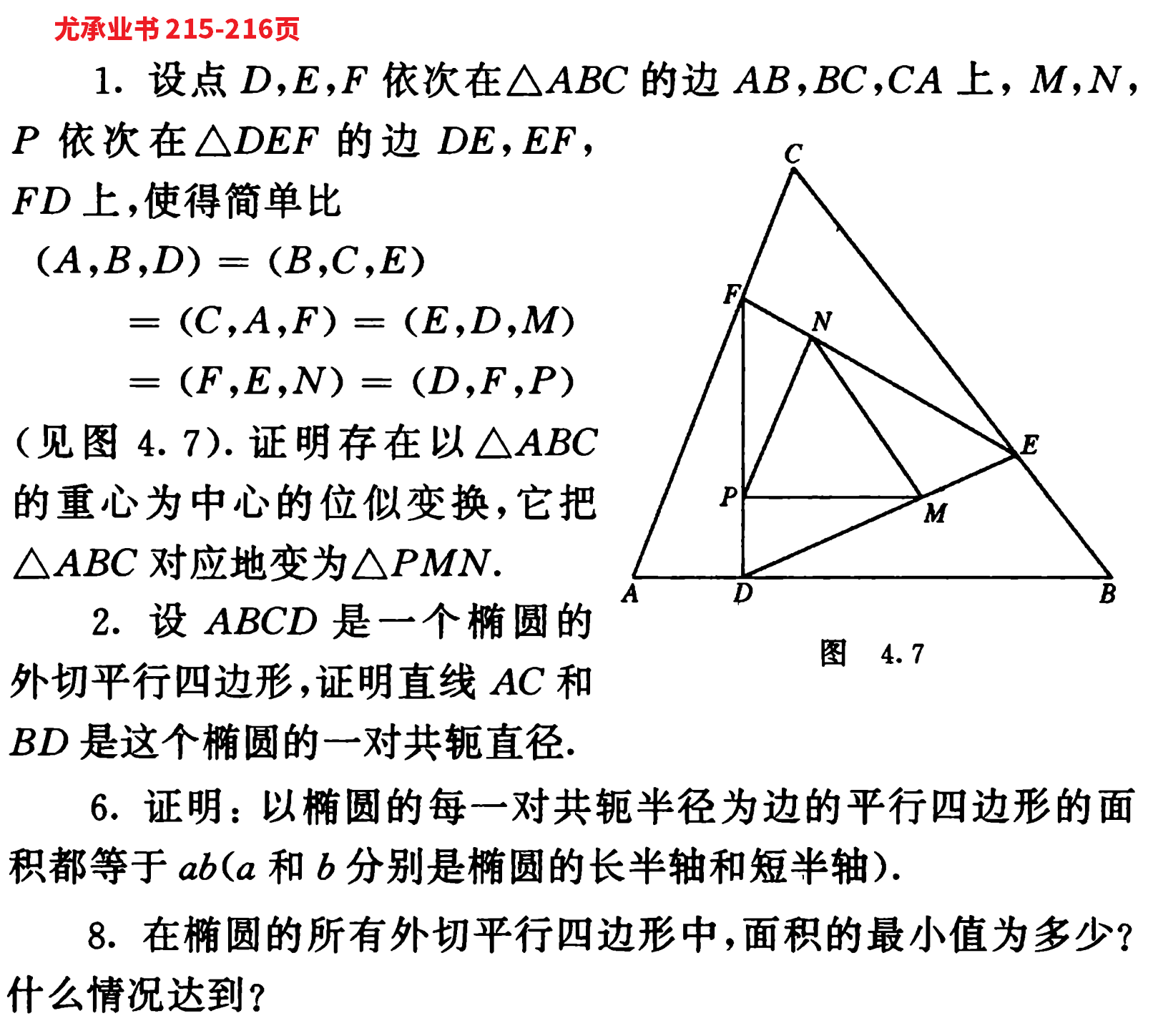
尤承业书 208-211 页 4、6、15 题（15 题第二行 \(y'\) 的公式中，系数分母有误，应该是 \(a\) ）。215-216 页 1、2、6、8。然后请看尤承业书后附录有关矩阵乘法的定义等知识，加上以下几题。

1. 在平面上一个幺正标架之下（也就是直角坐标系当中），考虑变换 \[\begin{pmatrix}x \\y \end{pmatrix}~~\mapsto~~\begin{pmatrix}x' \\y' \end{pmatrix}= \begin{pmatrix}\cos t &-\sin t \\ \sin t &\cos t\end{pmatrix}\begin{pmatrix}x \\y \end{pmatrix}.\]

1. 试验证这是一个绕原点逆时针的旋转，转角为实参数 \(t\)。
2. 记其中的二乘二矩阵为 \(A(t)\) ，试按矩阵乘法法则验证 \(A(t_1)\cdot A(t_2)=A(t_1+t_2)\).

2. 在平面上一个幺正标架下，考虑变换 \[\begin{pmatrix}x \\y \end{pmatrix}~~\mapsto~~\begin{pmatrix}x' \\y' \end{pmatrix}= \begin{pmatrix}\cosh t &\sinh t \\ \sinh t &\cosh t\end{pmatrix}\begin{pmatrix}x \\y \end{pmatrix}.\] 其中 \(\cosh t=\frac{e^t+e^{-t}}{2},\sinh t=\frac{e^t-e^{-t}}{2}\) 分别称为双曲余弦和双曲正弦函数。

1. 试证明它作用下，等轴双曲线族 \(x^2-y^2=a\) （包括 \(a=0\) 情形）中的任意一条仍然映为自身。
2. 记其中的二乘二矩阵为 \(H(t)\)，试按矩阵乘法法则验证 \(H(t_1)\cdot H(t_2)=H(t_1+t_2)\).

3. 一般情况，一个二阶方阵 \(\begin{pmatrix}a &b \\ c &d \end{pmatrix}\)，如果行列式不为0，则有逆矩阵。试求出其逆矩阵的表达式，并写出以上的矩阵 \(A(t)\) 和 \(H(t)\) 的逆矩阵是什么。

4. 对于平面上以直线 \(l\) 为不动点集（错切轴）的错切变换，我们选择它的一个不动点为基点 \(O\) ， \(e_1\) 平行于 \(l\) 方向，建立仿射标架。试写出这样一个错切变换的表达式，并证明：全体这样的错切变换只依赖于一个实参数 \(t\)，它们对应的矩阵按乘法构成一个群 \(f(t)\)，而且对于适当选择的参数 \(t\)，同样成立 \(f(t_1)\cdot f(t_2)=f(t_1+t_2)\).

5. （选做）平面到自身的相似变换（相似比 \(k\neq 1\) ）一定有不动点吗？