本周练习：

第一部分，尤书 285 页第 5, 6, 10 题。

第二部分：补充习题。

1. 证明蝴蝶定理：对于平面上任何一条非退化圆锥曲线，取其一条弦 \(EF\) 的中点 \(M\) ，过 \(M\) 作两条线，分别交 \(\Gamma\) 得弦 \(AC, BD\) 。设 \(AB\) 交 \(EF\) 于 \(L\) ， \(CD\) 交 \(EF\) 于 \(R\) ，证明 \(M\) 也是 \(LR\) 的中点。

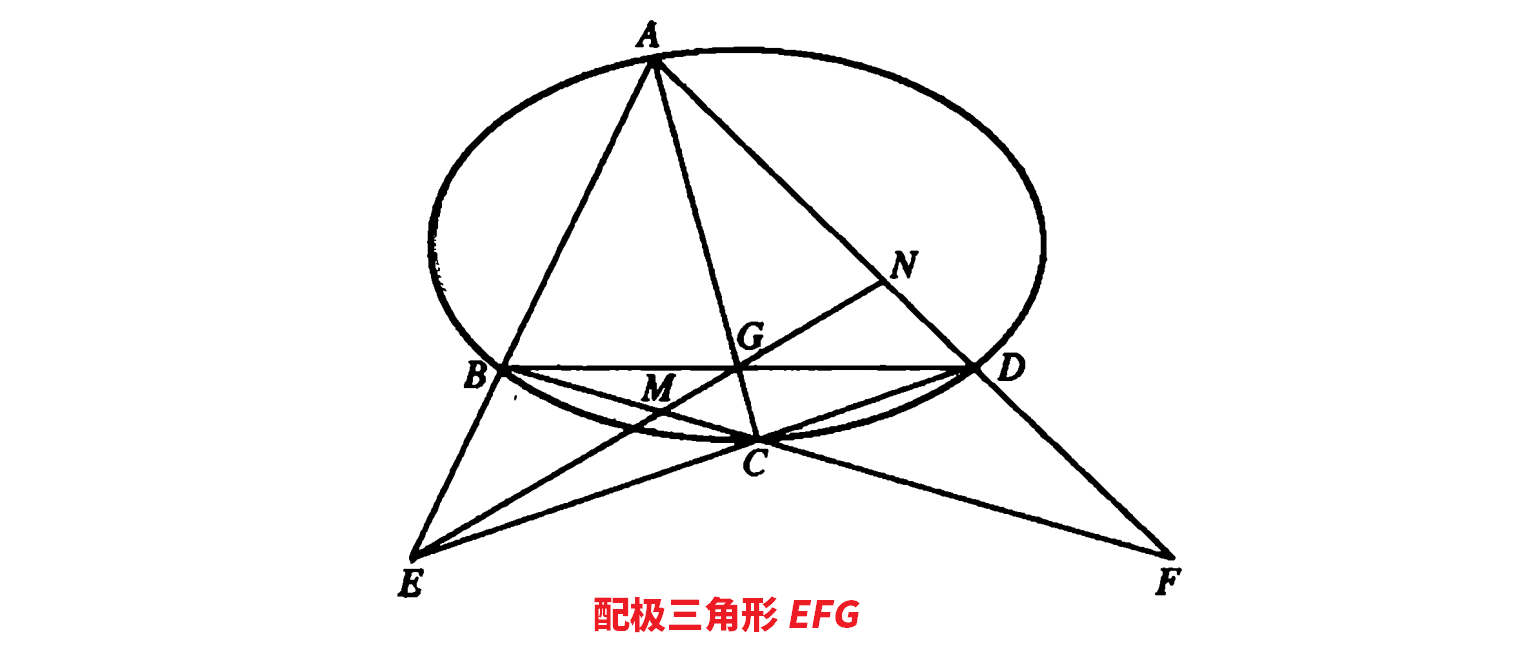
2. 读尤书 281 页例 5.10。其中的 \(E,F,G\) 三点称为“配极三角形”。请完成以下任务。

1. 证明：如果取图中的 \(EF\) 直线为无穷远直线（可以理解为用中心投影将它投到 \(l_\infty\) ），则 \(\Gamma\) 是中心型曲线（椭圆），中心恰好是 \(G\) 。
2. 固定图中 \(\Gamma\) 上三点 \(A, B, C\) 并令 \(D\) 在 \(\Gamma\) 上自由变动， \(EF\) 有没有可能与 \(\Gamma\) 相切或相交？此时“配极三角形”变成了什么形态？
3. 给定射影平面上一条非退化圆锥曲线 \(\Gamma\) ，最多可以有几个点同时关于 \(\Gamma\) 彼此两两调和共轭？证明你的结论。
4. 设一条直线与 \(\Gamma\) 交于两点，证明：只要将这条直线取为无穷远直线，则 \(\Gamma\) 还是中心型曲线（双曲线），中心恰为两个交点处的切线的交点。
5. （选做题）看似 (1) 和 (4) 中的结论有不同。如果想统一，似乎可以猜想：圆 \(\tilde{x}^2+\tilde{y}^2=1\) 的圆心到这个圆也有两条切线，而且切点连线就是无穷远直线。这个猜想靠谱吗？（提示：扩充到复数域。）

3. 读王长平老师讲义的第 5 章“射影几何”中第 7 页定义 2.3 和命题 2.3，并完成以下任务：

1. 取 \(\Sigma\) 平面上的直角坐标，并取原点 \((0,0)\) 正上方距离为 1 的点 \(O\) （作为中心直线把的中心），请显式写出定义 2.3 中的“对偶对应”的表达式。
2. 请证明命题 2.3 的结论。（借助坐标或其它论证方式均可。）
3. 如果取 \(\Sigma\) 平面上的单位圆作为圆锥曲线 \(\Gamma\) ，考虑关于它的极点和极线关系，对应记为 \(A\) 点和极线 \(A^*\) 。试在 (1) 中坐标系下，写出极点到极线的对应的表达式，并与 (1) 中“对偶对应”进行比较。
4. 请证明，对于配极对应 (3) ，命题 2.3 的类似结论也成立。（根据坐标或其它理由均可。）

4. 思考题：关于 Desargues 定理和 Pappus 定理及各自的对偶定理，有这样一个奇妙的联系：可以不借助于其它手段，也不借助一般的对偶原理，只要利用 Desargues 定理，就可以直接证明其对偶定理；利用 Pappus 定理，可直接证明其对偶定理。试找出这个证明。