本周作业：

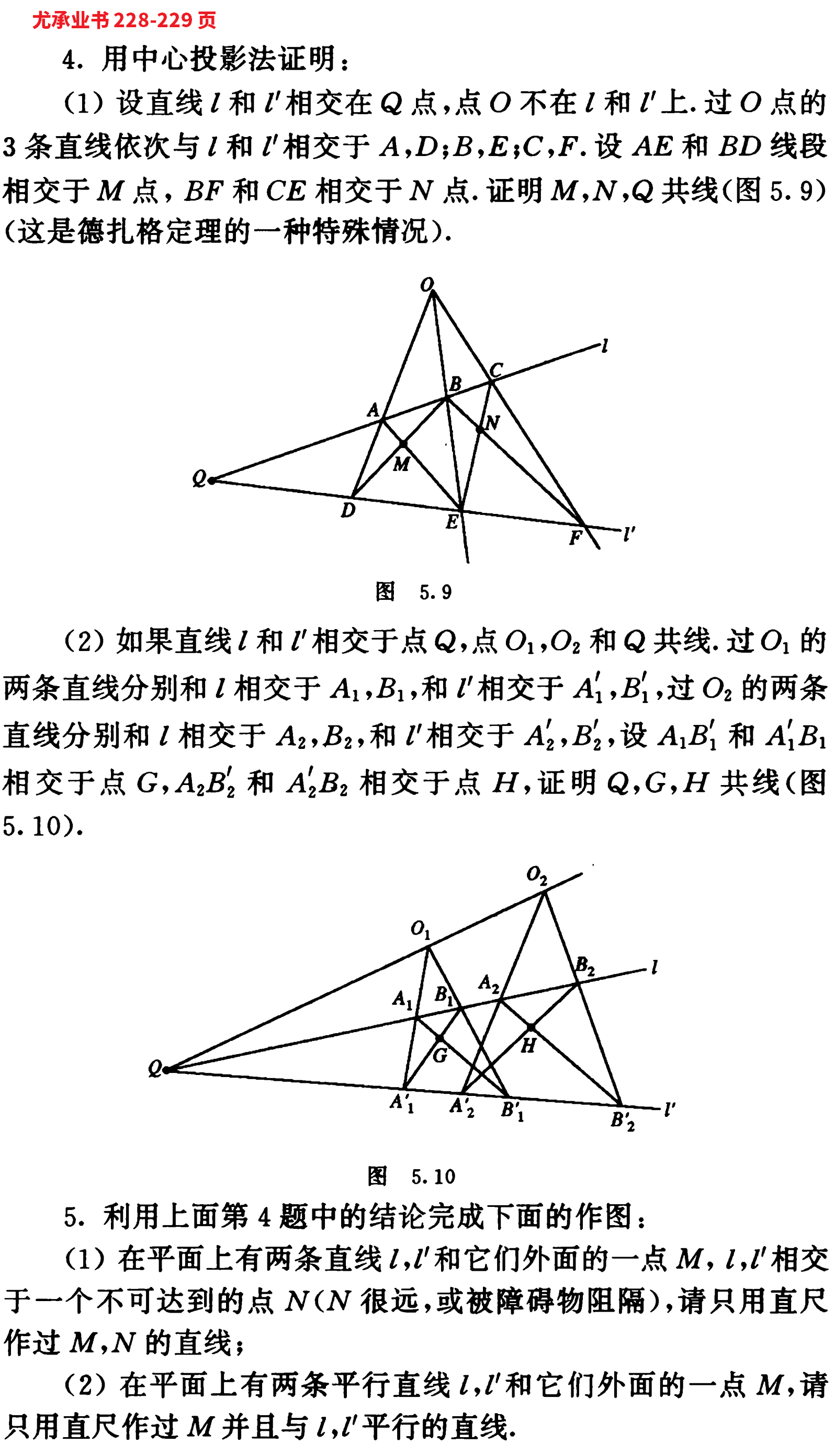
228-229 页 4，5 题。

补充题一（必做）：试写出 Desargues 定理的逆命题，并给出一个证明（可以用中心投影法，也可以考虑其它方法）。

补充题二（必做）：周五课上对于射影几何基本定理，只证明了一般位置的四点组 \(\{A,B,C,D\}\) 与一个标准单位正方形的四顶点 \(\{A_0,B_0,C_0,D_0\}\) 之间，一定存在唯一的一个射影变换。那么，对于一般情形，即两个一般位置的四点组 \(\{A,B,C,D\}\) 与 \(\{A',B',C',D'\}\) 之间，是否也成立同样的结论呢？证明你的判断。

补充题三（必做）：利用补充题五的结论 4), 5) 和射影几何基本定理，解答尤书 216 页 11、12。（12 题原题应该加“凸”的假设，即“凸四边形必有内切椭圆”。）

补充题四（选做）：试证任何一个椭圆锥面（即一个椭圆与不共面的一点 \(O\) 作为锥顶点连直线而构造出来的曲面）是一个二次曲面，而且可以经过一个适当的空间仿射变换，映为一个圆锥。（一旦证明这一点，那么周五课上所说的“中心投影把非退化二次曲线 conic section 仍然映为非退化二次曲线”，就有了充分的根据。课上当时其实只指出了，对于特殊情形的中心投影，即所连曲面为圆锥面的情形，有以上结论。）

补充题五（选做）：对于平面 \(\Sigma\) 上的一条连续、不自交的闭曲线 \(\gamma\) ，它把射影平面 \(P(\Sigma)\) 分成两部分，其中一部分包含至少一条完整的射影直线，称为 \(\gamma\) 的“外部”；另一部分不包含任何射影直线，不过可以包含有限长的线段，称为其“内部”。

1. 证明：射影变换下，闭多边形的内部依然映为内部，外部映为外部。
2. 试问：在射影变换下，一条椭圆若映为一条双曲线，那么椭圆的内部映到了什么区域？
3. 一个三角形区域的像，一定还是一个三角形区域吗？
4. 试证明： \(\Sigma\) 上的三顶点 \(\{A_i\}_{i=1}^3\) 及三角形内点 \(P\)，若在射影变换下映为另一个三角形的三顶点 \(\{A'_i\}\) 及其内点 \(P'\)，则前一个三角形的边界及任一内切椭圆，必定对应地映为后一个三角形的边界和内切椭圆。
5. 同理可证：若一个凸四边形的四顶点 \(\{A_i\}_{i=1}^4\) 映为另一个凸四边形的四顶点 \(\{A'_i\}_{i=1}^4\)，则前者的边界及任一内切椭圆，必定映为后一个四边形的边界和内切椭圆。
6. 若一个射影变换把一个正方形的四顶点映为一个凹四边形的四顶点，那么它把正方形的内部区域映到了哪里？试作图说明。

补充题六（选做）：对于平面 \(\Sigma\) 上任意给定的一个凸四边形，是否总可以通过适当选择平面外一点 \(O\) 和一个适当的投影平面 \(\Sigma'\)，经中心投影而得到后一平面上的一个正方形？