IRRATIONAL-WINDOW-FILTER PROJECTION METHOD AND APPLICATION TO QUASIPERIODIC SCHRODINGER EIGENPROBLEMS

摘要

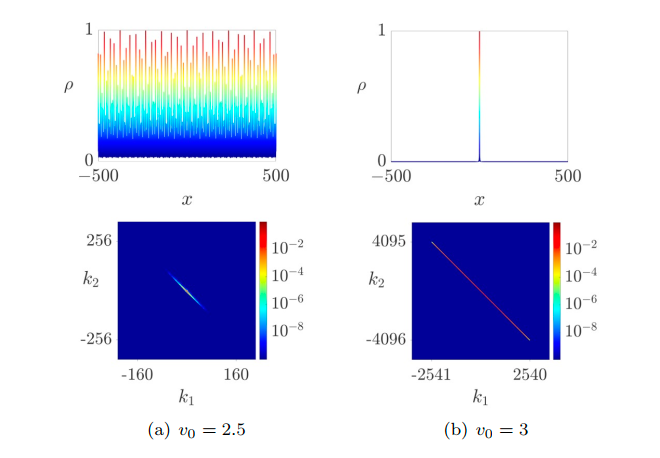
In this paper, we propose a new algorithm, the irrational-window-filter projection method (IWFPM), for quasiperiodic systems with concentrated spectral point distribution. Based on the projection method (PM), IWFPM filters out dominant spectral points by defining an irrational window and uses a corresponding index-shift transform to make the FFT available. The error analysis on the function approximation level is also given. We apply IWFPM to one-dimensional, two-dimensional (2D), and three-dimensional (3D) quasiperiodic Schro'‘textbackslashdinger eigenproblems (QSEs) to demonstrate its accuracy and efficiency. IWFPM exhibits a significant computational advantage over PM for both extended and localized quantum states. More importantly, by using IWFPM, the existence of Anderson localization in 2D and 3D QSEs is numerically verified.