许宝騄先生生平

 

程士宏

北京大学教授

    许宝騄，字闲若，出身于浙江杭州的名门世家。1910年9月1日生于北京。2岁时随家移居天津，8岁去杭州。他幼时体质虚弱，但聪明颖悟，孩提时就能拼摆“益智图”。他从小受到传统的教育。5岁至14岁在家从师读书，通读四书五经，涉猎四史及古文辞。11岁时还写过以《花生姻缘》和《神花》为题的文言小说。他临摹的小楷，古朴神似，为表兄俞平伯手写的《古槐书屋词》曾刻版印行。他还善于巧妙地利用古文诗词制作灯谜。11岁开始学习英文，两年后便能阅读英文的古典文学名著（[1]）。

    1924年，许宝騄的父亲在杭州病逝。全家迁回天津，次年又移居北京。为了考中学，北京大学吴缉熙老师给他讲授代数、几何及三角，两个月后即取得显著成绩。由此引发了他对数学的兴趣，他的数学天才也开始显露出来。1925年，许宝騄考入当时的北京名校汇文中学高中。高中学习期间，他利用暑假继续钻研数学，还坚持学习法文。两年后他的法文达到能会话和作短文的程度（[1]）。

    1928年，中学毕业的许宝騄考入燕京大学化学系学习。两年后他决定改攻数学，于1930年秋又考入清华大学数学系。这期间，他立下了要对人类知识总量有所增添的抱负。1933年他以优异的成绩从清华毕业，获得理学士学位。在清华学习期间，他不仅在数学方面学有所成，还参加了俞平伯先生组织的谷青社的活动。他会唱昆曲、会拉二胡，熟悉音律；每听一曲，不出几遍就能写出谱子，表现出良好的艺术才能（[1]）。

    许宝騄从清华毕业后即参加了赴英公费留学考试并被录取，但因体重不够未能成行。在香山休养的一年中，他注意营养，加强锻练，使身体状况大为好转。以后，到北京大学任助教。于1936年再次通过赴英庚子赔款公费留学的考试，同年赴伦敦大学学院(University College, London)学习数理统计。1938年，许宝騄获得哲学博士(Ph.D.)学位；两年后，又得到科学博士(Sc.D.)学位。当时的伦敦大学学院是公认的数理统计研究中心。现代数理统计学的奠基者费歇(R. A. Fisher)、耐曼(Neyman)和皮尔逊(E. Pearson)等都在那里工作。那里吸引着来自世界各地的许多青年人，而“最优秀的学生是中国人许宝騄”（[2]）。

    1940年，许宝騄出于爱国热诚，不畏艰险绕道好望角从海路回到了抗日烽火中的祖国，到昆明西南联大任教。当时的西南联大生活十分艰苦，许宝騄身体也日渐衰弱。但他精心教学，培养青年学生。钟开莱、王寿仁等著名学者都得到过他的指导和帮助。教学之余，他继续科学研究工作，成果十分丰富；仅1941年，就有5篇学术论文发表。在此期间，他目睹政治腐败、社会混乱、人民痛苦，认识到政治的重要意义和中国革命的必然趋势，毅然参加了中共中央直接领导的政治团体——中国民主革命同盟。

    1944年，许宝騄的导师、已受聘担任伯克利加州大学统计实验室主任的耐曼教授考虑到他的接班人问题。“照耐曼的看法，许宝騄的水平绝对可以与瓦尔特(A.Wald，著名数理统计学家)相媲美。他们是新一代的数理统计学家中的两个佼佼者”（[2]）。1945年，许宝騄应伯克利加州大学和哥伦比亚大学的联合邀请，在这两所大学各工作一个学期。他典型的中国学者的风度，对科学研究工作的高标准要求以及解决困难数学问题的能力给美国同行以极为深刻的印象。耐曼对许宝騄在哥伦比亚大学工作后去伯克利供职一事特别关心。但是，“芝加哥大学、耶鲁大学以及哥伦比亚大学都希望得到许宝騄”（[2]）。1946年秋，许宝騄和郝泰林(H.Hotelling)一起去了北卡罗来纳大学新建立的统计系。

    1947年，许宝騄谢绝美国大学方面的婉留，毅然回到祖国，在北京大学任教；1948当选为中研院院士。他认真教学、勤奋研究；还积极参加文教界的民主革命运动，迎接解放。北京解放以后，他致电美国同行，表达自己的欢悦心情。他以极大的热情投入新中国的建设事业。解放初期，一些西方国家对新中国实行封锁。为了开展对苏联的学术交流，许宝騄自学俄文，先后主持校对了《数学分析简明教程》、《概率论教程》和《微分方程教程》等俄文翻译教材。不仅如此，他还帮助北京大学数学系的其他教师学习俄语，带领他们精读俄文原版的《数学分析八讲》。当时，前苏联和波兰概率论专家邓肯(E.B.Dynkin)和费兹(Fisz)曾先后访问中国，受到许先生的亲切接待。毫无疑问，许宝騄的这些工作对解放初期数学方面的教材建设、人材培养和学术交流具有十分重要的意义。

    建国以来，许宝騄历任北京大学一级教授、概率统计教研室主任、中国科学院学部委员和第四届政协委员等重要职务。他身体状况十分差，终生未婚，把自己的身心全部贡献给祖国的教育和科学事业。50年代末他已身患肺结核、胃病和痔疮等多种疾病，行动很不方便，但仍坚持在住所主持讨论班和教研室工作。1963年他的肺部出现空洞，还坚持工作，同时领导着数理统计、马氏过程和平稳过程三个讨论班。“文化大革命”中，他受到不公正的对待，被剥夺了工作的权利。尽管这时他已瘫痪，卧床不起，但仍保持旺盛的工作精神：只要上面直接有任务下达，总是力争提前完成；只要环境相对安定，就抓紧研究工作。1970年12月18日，当他在简陋的住所溘然长逝时，人们在他的床前看到的是一叠叠的算草和一支使用多年的派克钢笔。

    许宝騄的学术成就主要是在数理统计和概率论这两个紧密相关的数学领域中。

    1938年，许宝騄发表了他关于数理统计的第一篇论文（[许3]），讨论所谓的Behrens—Fisher问题：设和是分别来自正态总体和的样本，在和未知的情形下来检验假设。记

       

许宝騄通过把形如之统计量的分布密度展成级数的方法，研究了否定域的势函数对参数和的依赖关系。据他的研究结果给出的检验方法被称为“许方法”。直到现在，“许方法”仍然被认为是解决这一检验问题最实用的方法（[3]）。

    许宝騄早期的另一重要工作是线性模型方差的二次估计问题。设是一个线性模型，其中的各分量是相互独立具有零均值和共同方差的随机变量。称的二次型是的最优二次无偏估计，如果对任何参数；的方差不依赖于未知参数；对任一符合条件和的二次型，。许宝騄的文[许4]给出了通常的的无偏估计是最优二次估计的必要充分条件。他的这一工作被看作是以后关于方差分量模型大量文献的出发点。

    在数理统计的一个重要领域¾¾多元分析中，许宝騄也作出了杰出贡献。他给出过多元分析中若干重要分布的推导（[许6]，[许9]）。其中文[许6]利用数学归纳法来推导维夏特（Wishart）分布，是这个重要分布各种推导方法中最优美的一个。他还推导了对多元分析有基本意义的一些行列式方程的根的精确分布和渐近分布（[许7]，[许11]，[许12]）。在进行这些困难的工作时，他推动了矩阵论在多元分析中的应用，也对矩阵论本身的技巧有所发展。他在北卡莱罗纳大学讲课时，曾系统讲授过计算矩阵变换雅可比（Jacobi）行列式的技巧。直到他回国4年以后，其中的一部分才由当时听课的学生第默尔（W.L.Deemer）和奥肯(I.Olkin)根据笔记加以整理并取得他的同意以后公开发表[4]。

    许宝騄在数理统计中最出色的工作之一是对一元线性假设似然比检验优良性的论证（[许13]）。他证明了似然比检验在所有功效函数仅依赖于一个非中心参数的检验类中是一致最强的。这一工作后来在两个方面继续发展。一方面他的学生把此文的方法用到多元问题中去[5]；另一方面这篇文章提供了一个获得所有相似检验的新方法。经过一系列工作，最后由雷曼(E.L.Lehmann)和谢飞(H.Scheffe)形成完全性的概念[6]。

许宝騄在概率论领域的工作主要是极限定理方面。设是个独立同分布的随机变量。令，并以记标准正态分布函数。一个从理论和应用角度都十分关心的问题是和在适当正则化以后向收敛的速度。在这方面克莱姆(Cramer)得到了的渐近展开，而Berry则给出了和之差的一致性估计。在[许18]中，许宝騄对(表的4阶矩)分别获得了克莱姆和Berry对于所得到的平行结果，还给克莱姆定理以一个初等证明。应当指出，他在那里所用的方法具有普遍意义，不仅可用来解决分布的有关问题，也可以用于解决样本高阶中心矩，样本相关系数及样本的统计量的类似问题。

    许宝騄在概率论方面的另一个有深刻影响的工作是强化了独立同分布随机变量序列强大数律的结论。设是一独立同分布均值为0方差为1的随机变量序列。文[许24]证明了

               

对任给成立。这一事实被称为：均值/有完全收敛性。人们认为，这篇文章的重要性不仅在它的结果本身，更在于“完全收敛性”的提出开辟了概率论极限理论的一个新的方向。直到今天，对完全收敛的讨论继续吸引着许多中外学者的兴趣。

    40年代前后，寻求行独立随机变量阵列行和弱极限问题的彻底解决是一个极富挑战性的问题，引起了诸如莱维(Levy),費勒(Feller)，柯尔莫哥洛夫(Kolmogorov)和格涅坚科(Gnedenko)这样一些大师级学者的关注。许宝騄参加了解决这一问题的竞争并证明了自己是一个强者（关于他参加这一竞争的经过，[7]有一段真实动人的描述）。引文[许25]原本是许宝騄1947年寄给钟开莱教授的一份手稿，在这份手稿中，他解决了上述问题。但当他得知格涅坚科已先于他解决这一问题后，立即去函钟开莱承认格涅坚科的优先权。1968年，钟开莱在把格涅坚科和柯尔莫哥洛夫《独立随机变量和的极限分布》一书翻译成英文的时候，才把许的手稿作为该书英译本的附录公开发表出来。从此文可以看出，许宝騄也独立地得到了独立随机变量和弱收敛到无穷可分分布的必要充分条件，而且方法和格涅坚科有所不同。对于无穷可分分布类中的族，许宝騄在1958年用中文发表的论文[许33]中证明了它的每一个分布函数都是绝对连续的。但是，这个结果一直未被国外所了解，以至于1963年还当成一个新成果发表出来（[8]）。

    新中国成立以后，许宝騄的学术研究工作同样取得重要进展。在矩阵论方面，在马氏过程方面，在实验设计和组合数学方面，在变叙（即次序统计量）的极限分布方面，许宝騄和他领导的讨论班都进行了卓有成效的工作。他是一位名副其实的，得到广泛承认的具有世界水平的科学家。为了纪念他，《统计学年鉴》(Annals of Statistics)1979年曾约请国际上知名的专家学者撰文介绍他的生平和他在科学研究中取得的杰出成就([9]，[10]，[11]，[7])。1981年和1983年，科学出版社和Springer-Verlag出版社曾分别出版了《许宝騄文集》和《许宝騄选集》([12],[13])。

    作为我国概率统计方面公认的学科带头人，许宝騄对学科的建设和发展作出了重要贡献。在1956年周恩来总理主持制定的全国科技发展规划中，概率统计和计算数学、微分方程一起被列为数学科学的重点发展方向。许宝騄参与组织领导了概率统计方面规划的制定和落实。在他的主持下，从北京大学及中山大学、南开大学等兄弟院校的数学系抽调了50余人，作为国内第一届概率统计专业的学生集中到北大学习。还从中国科学院数学研究所、中山大学等单位调集了一批教师，和北大的教师一起，开设出测度论、极限定理、数理统计和马氏过程等一系列专门化课程。这一有力的措施，为我国概率统计学科培养了一批教学科研骨干。同时，在他的建议和倡导下，与苏联、东欧的学术交流一度也比较活跃，对学科的发展起了有益的推动作用。

    从1956年北大在全国第一个成立概率统计教研室以后，许宝騄一直担任这个教研室的主任。他主持制订了概率统计专门化学生的培养计划和教学大纲。他还亲自讲授了一些重要的基础课和专门化课程。他的讲课精心选材，深入浅出，简明扼要，严谨生动，堪称典范。他的讲课笔记如《点集拓扑》、《多元分析》、《抽样论》和《解析函数的边界性质》等至今仍被北大的一些老教员所珍藏，仍有很好的参考价值。例如，由孙山泽同志整理的《抽样论》([许41])已于1982年由北京大学出版社出版，并获得优秀教材奖。50年代末，他的身体已经很差，不能外出去教室上课了。于是在他一室一厅寓所的室内，挂起了一块黑板，继续进行正常的教学活动。“文革”前，北大概率统计方向共培养了八届学生，他就亲自带过五届学生的毕业论文。晚年，他的主要精力用在培养青年教师和研究生上。他特别注重对他们独立工作能力的培养。一旦青年人在某个问题上有所发现，他总是十分高兴地和大家一起讨论所得结果的意义和进一步深入的可能性。他带青年人的主要形式是讨论班，经常要求和鼓励大家在讨论班上发表自己的意见。作为一个“全方位”的教研室主任，他先后领导过极限定理，多元分析，试验设计，次序统计量，过程统计，马氏过程和组合数学等多方面内容的讨论班。他所领导的讨论班往往是“校际”的，不仅有北大的同志和进修教师，而且欢迎外校外单位的同志参加。在讨论班上，他提倡学术民主、平等待人，务求达到相互交流、共同进步的目的。

许宝騄始终关心我国概率统计学科的健康发展，为了推动理论联系实际的工作，他曾建议创设统计实验室。为了促进学术交流，特别是给青年人提供发表文章的机会，
他还发起筹办过全国性的概率统计杂志。由于众所周知的原因，他的这些设想生前未能实现。今天可以告慰于许宝騄先生的是，他的建议现在都已实现了：北京大学统计实验室已于1983年建立；中国现场统计研究会主办的《数理统计与管理》已在1982年创刊；中国概率统计学会主办的《应用概率统计》也在1985年创刊。

许宝騄逝世时享年仅60。但是，他留下了举世瞩目的学术成就，留下了为我国概率统计学科的建立和发展所开创的业绩，也留下了热爱祖国、献身科学的宝贵精神财富。1980年和1990年，在他诞辰70周年和80周年的时候，北京大学分别举行了全国性的纪念许宝騄学术讨论会，表达对他的深切怀念。今年，我们纪念他诞辰90周年，要进一步学习他的奋斗精神，为创建世界一流的北京大学，为使我国的数学学科早日达到世界先进水平而不懈努力。

 

参考文献

 

说明  本文以[许n]表示本书中“许宝騄论著目录”的第n篇文章。

 

[1]  许宝騤(1980)  许宝騄事略(见本书)

[2]  瑞德(作者,1982)  耐曼¾现代统计学家,上海翻译出版公司，1985(译者：姚慕生、陈克艰、王顺义)

[3]  Dudewicz,E.J. and Mishra,S.N.(1988)  Modern Mathematical Statistics. Wiley.

[4]  Deemer,W.L. and Olkin,I.(1951)  The Jacobians of Certain Matrix Transformations Useful in Multivariate Analysis, Based on Lectures of P.L.Hsu at the University of North Carolina, 1947. Biometrika 38: 345-367.

[5]  Simaika,J.B.(1941)  On an Optimun Property of Two Important Statistical tests. Biometrika 32: 70-80.  

[6]  Lehmann,E.L. and Scheffe,H.(1950)  Completeness, Similar Regions and Unbiased Estimation. Sankhya 10: 305-340.

[7]  Chung,K.L.(1979)  Hsu’s Work in Probability. Ann. Statist. 7: 479-483.

[8]  Fisz,M. and Varadarajan,V.S.(1963)  A condition for Absolute Continuity of Infinitely Divisible Distribution Function. Z.Wahrsch.verw.Gebiete 1: 335-339.

[9]  Anderson,T.W., Chung,K.L. and Lehmann,E.L.(1979)  Pao-Lu Hsu 1909-1970. Ann. Statist. 7: 467-470.

[10]             Lehmann,E.L.(1979)  Hsu’s Work in Inference. Ann. Statist. 7: 471-473.

[11]             Anderson,T.W.(1979)  Hsu’s Work in Multivariate Analysis. Ann. Statist. 7: 474-478.

[12]            许宝騄文集  科学出版社，1981。

[13]            Pao-Lu Hsu Collected Papers. Springer-Verlag, 1983.

 

 

 

 

　

许宝騄先生年表

 

日期

年岁

说明

1910.9.1

0岁

出生于北京

1912

2

移居天津

1918

8

移居杭州

1915

5

私塾就学（至14岁，1924）

1921

11

写文言小说《花生因缘》，《神花》

1924

14

父病逝，迁回天津

1925

15

北京汇文中学念高中，与俞平伯研究移棋相间法。

1928

18

考入燕京大学化学系

1930

20

转入清华大学数学系

1933

23

清华大学毕业，考取赴英留学后在香山休养1年

1934

24

北京大学助教(至1936年)

1936

26

再次通过庚款考试，赴University College, London，学统计

1938

28

获哲学博士(Ph.D)学位

1939

29

获理学博士，赴法国Hadamard处(见《Neyman》书)

1940

30

获科学博士学位(Sc.D)，受聘为北京大学教授，回国在昆明西南联大任教

1945

35

在重庆加入民盟

1945

35

赴Berkeley，Univ. Of  California任教半年

1946

36

赴New York, Columbia University任教半年

1946

36

赴Chapel Hill,Univ. Of North Carolina任教半年，参加创建统计系

1947

37

返回北京大学任教

1948

38

任中央研究院第一批院士

1955

45

任中国科学院第一批学部委员

1956

46

北京大学成立全国第一个概率统计教研室，任主任。组织全国概率统计培训班

1959

49

北大数学力学系为许先生庆祝50大寿

1962

52

在北大概率统计教研室提出办统计杂志

1964

54

任第四届全国政协委员

1970.12.18

60

在北京家中去世

 

                                    (郑忠国)

 

 

许宝騄论著目录

 

[1]    On the limit of a sequence of point sets. Bull. Amer. Math. Soc.  41(1935)  502-504.

[2]    A note on the indices and numbers of nondegenerate critical points of biharmonic functions (with Kiang Tsai-han). Science Quarterly, Nat.  Univ. Peking,(3)  5(1935) 389-392.

[3]    Contribution to the theory of “Student's” T-test as applied to the problem of two samples.  Statist. Res. Mem. 2(1938)  1-24.

[4]   On the best unbiased quadratic estimate of the variance.

   Statist. Res. Mem. 2(1938)  91-104.

[5]    Notes on Hotelling's generalized T. Ann. Math. Statist. 9(1938) 231- 243.

[6]   On the distribution of roots of certain determinantal equations.  Ann. Eugenics.  9(1939)  250-258.

[7]   A new proof of the joint product moment distribution.

   Proc. Cambridge Philos. Soc.  35(1940)  336-338.

[8]   On n-Fold iterated limits. J. Chinese Math. Soc. 2(1940)

   40-63.

[9]   An algebraic derivation of the distribution of rectangular

   coordinates.  Proc. Edinburgh Math. Soc. (2) 6(1940)

   185-189.

[10] On generalized analysis of variance.Biometrika .31(1940)  221-237.

[11] On the limiting distribution of roots of a determinantal

    equation.  J.London Math. Soc. 16 (1941)  183-194.

[12] On the limiting distribution of the canonical correlations.

Biometrika. 32(1941)  38- 45.

[13] Analysis of variance from the power function standpoint.

    Biometrika  32(1941) 62-69.

[14] Canonical reduction of the general regression problem.

    Ann. Eugenics 11(1941) 42-46.

[15] On the problem of rank and the limiting distribution of

    Fisher's test function. Ann. Eugenics 11(1941) 39-41.

[16] The limiting distribution of a general class of statistics.

    Acad. Sinica Science Record .1(1942)  37-41.

[17] Some simple facts about the separation of degrees of

freedom in factorial experiments. Sankhya 6(1943)

253-254.

[18] The approximate distribution of the mean and variance of

    a sample of independent variables. Ann.Math.Statist

    16(1945). 1-29.

[19] On the approximate distribution of ratios. Ann. Math.

    Statist. 16(1945)    204-210.

[20] On the power functions for the E-test and the T-test. Ann.

    Math. Statist.    16(1945) 278-286.

[21] On a factorization of pseudo-orthogonal matrices. Quart.

    J. Math.  Oxford Ser. 17(1946) 162-165.

[22] Sur un theoreme de probabilite denombrables (with Kai-

    Lai Chung).C. R. Acad. Sci. Paris  223(1946),467- 469.

[23] On the asymptotic distribution of certain statistics used in

testing the independence between successive  

observations from a normal  population.  Ann. Math.

Statist. 17(1946)  350-354.

[24] Complete convergence and the law of large numbers.

(with H. Robbins) Proc. Nat. Acad. Sci. U.S.A. 33(1947)

 25-31.

[25] The limiting distributions of functions of sample means

and application  to testing hypotheses.Proc. Berkeley

Symp. Math. Statist.   Probability(1949) 359-402.

Univ. of California Press, Berkeley and Los  Angeles.

[26] 绝对动差与特征函数 .数学学报.1 (1951) 257-280.

[27]   独立机变数的化简系数. 科学记录.4(1951)

197-200.

[28]      Appendix: The Jacobians of certain matrix

transformations useful in multivariate analysis. (Based

on lectures of P.L.Hsu at The University of North

Caralina, 1947. By Walter L. Deemer and Ingram Olkin)

Biometrica 38(1951),345-367.

[29]      On symmetric, orthogonal, and skew-symmetric

     matrices.  Proc. Edinburgh Math. Soc. Ser. 2(1953)

     37-44.

[30]   在零点的邻区内彼此相等的特征函数.数学学报.4

    (1954) 21-32.

[31] 论矩阵的一种变换. 数学学报. 5 (1955) 333-346.

[31]   论矩阵偶的一种变换 .北京大学学报(自然科学版)

     1(1955) 1-16

[32]   一个厄密方阵及一个对称或斜称方阵的联合变换.

    北京大学学报(自然科学版). 3 (1957) 167-209.

[33]   L族内的分布函数的绝对连续性. 北京大学学报

    (自然科学版). 4 (1958)  145-150.

[34]   欧氏空间上纯间断的时齐马可夫过程的概率转移函

     数的可微性. 北京大学学报(自然科学版).4 (1958),

     257-270.

[35]   一个不是方案的结合方案，其s=6. 数学

     学报,14(1964)  177-178.

[37] 变序的项的极限分布(以”班成”署名发表).

     数学学报 14  694-714.

[38] 部分平衡不完全区组设计(以”班成”署名发表).数学

     进展 .7 (1964) 240--281.

[39] A general weak Limit theorem for independent

     distributions.(Appendix III in limit Theorems

     of Sums of Independent Random Variables by B.V.

     Gnedenko and A.N.Kolmogorov, translated by

     K.L.Chung, revised  edition, Addison-Wesley

     1968).

[40] 随机矩阵的重合性质 (合作者：陈家鼎，郑忠国).

    北京大学学报(自然科学版). 15 (1979) 21-47.

[41] BIB矩阵与单纯码及正交码(遗稿) . 许宝騄文集.

     科学出版社(1981). 211-225.

[42] 许宝騄文集，科学出版社 (1981).北京.

[43] 抽样论, 北京大学出版社 ( 1982). 北京

[44] Pao-Lu Hsu Collected Papers, Springer-VerLag

              (1983) .New York.

[45] Studies in Markoff chains with a finite number

      of states.应用概率统计.6(1990) 342-353.

 

 

 

许宝騄文集》前言

江泽涵   段学复

 

中国科学院院士 北京大学教授

 

    许宝騄教授是我国著名数学家、北京大学一级教授、中国科学院学部委员，曾任第四届全国政协委员。他祖籍浙江杭州，一九一零年九月一日生于北京，在“文化革命”期间曾受到林彪.“四人帮”极左路线的残酷迫害。于一九七零年十二月十八日在北京不幸病逝，终生未婚。今年是许先生诞生七十周年，我们编辑出版这部《许宝騄论文集》，表示对他的深切怀念。

    许先生最初曾研读化学（1928-1930，燕京大学化学系）。一九三零年入清华大学数学系改学数学，以后获清华大学理学学士学位。于清华毕业后，在北京大学数学系担任了两年助教。一九三六年经考试公费赴英留学，为伦敦大学研究生，同时也在剑桥大学学习。赴英后的第三年开始在伦敦大学兼任讲师。一九三八年取得哲学博士学位。一九四零 年又获科学博士学位。同年回国，受聘为北京大学教授，在昆明西南联大任教。一九四五年他应邀先后在美国加州（伯克利）大学、哥伦比亚大学和北卡罗纳大学讲学，任访问教授。一九四七年十月，他回到北京，迎接解放。从此以后，他一直在北京大学任教。

    许先生是一位爱国科学家。他热爱中国共产党，热爱社会主义祖国。解放以前，他就和党的地下工作者有接触。

一九四五年在重庆参加了地下革命组织“民主革命同盟”，反对蒋介石的反动统治。北京解放以后，他致电美国数学界的同事，表示他对于北京的解放十分高兴。同时，以巨大的热情投入新中国文教科学事业的建设工作。一九五零年，他久病初愈，就开始讲课，带研究生，主持讨论班。除此之外，还利用业余时间帮助同志们学俄文。一九五一年他再次病倒住院，组织上曾多次建议他出国疗养，但都被婉言谢绝了。他决心留在国内，带病坚持工作。这一时期，他校阅了一些俄文翻译的基础课教材。一九五六年以后，他的行动已很不方便，但是，直到“文化革命”以前，他的教学、科研活动一刻也没有停止。在他卧室的外间，挂起了一块黑板，他在那里继续给高年级学生、研究生和青年教师讲课。同时，在病床上坚持科学研究。在林彪、“四人帮”横行全国的那些日子里，许先生遭到残酷迫害；他在身患重病又备受折磨的极为困难的条件下，仍未放弃工作。约在去世前一个多月，他完成了关于实验设计和代数编码之间的联系的那篇论文。他逝世以后，人们在他的床前看到了一叠叠的算草。为了发展祖国的科学，为了培养年轻一代的数学工作者，他忘我地劳动，直至生命的最后一息。这种献身祖国、献身科学的精神，是值得我们永远学习的。

   许先生对我国概率论、数理统计两学科的发展作出了重要贡献。一九五六年周恩来总理主持制订的我国第一个科学规划中，把概率统计列为数学学科的重点方向之一。这一年，根据教育部的统一安排，一些兄弟院校的教师、学生共四十多人集中到北大，在许宝騄教授的主持下从事概率统计的学习和研究。同时，北京大学成立了由许先生任主任的全国第一个概率统计教研室。到“文化革命”以前，北大的概率统计专门化共培养了八届学生。许先生主持制订了专门化学生 的培养计划和教学大纲，指导过五届毕业论文。一些专门化课程的教材也是以他的讲稿为蓝本整理而成的。许先生领导的讨论班，不仅有北大的教师和学生，还有兄弟院校的进修教师、学生和中国科学院数学研究所的同志参加。讨论班的内容曾涉及极限定理、马氏过程、多元分析、实验设计、次序统计量、过程统计、判决函数和组合数学等各个专题。为了更好地发展我国概率统计学科，许先生曾提出过一些很好的意见。他曾经建议在北大数学系设立统计实验室。一九六三年，他又提出筹办一个概率统计的学术刊物，并表示如果经费有困难，他本人可以贡献一部分。可惜，由于种种原因，他的这些愿望没有实现。令人愤慨的是，在林彪、“四人帮”的煽动下，这些宝贵意见还被当作许先生“走资本主义道路”的材料来横加批判。这使我们今天想起来还感到十分痛心。

   许先生对待教学工作极为认真。他作风严谨，讲课条理清晰。他的《抽象积分论》、《矩阵论》和《点集拓扑》的讲稿都有鲜明的特点，对我们的教学工作至今仍有很大的参考价值。一九五六年以后，他的主要精力用在培养青年教师和高年级学生方面。他循循善诱，能使不同程度的人在自己的原有水平上都得到提高。在讨论班上，一个专题报告之后，他常把报告的内容重新整理，提出新的方法和进一步研究的方向，把青年人直接引向科研前线。他十分注意鼓励青年人在讨论班上大胆发表自己的意见，也十分注意鼓励青年人进行科研实践，告诫大家不要做那种眼高手低、最后一事无成的人。青年人取得了成果，他总是十分高兴。他不仅认真审查论文的原稿，而且在经过认真的思考以后再和作者在一起进行深入的讨论，提出中肯的意见，力求把结果向前推进。特别应该指出的是，在教学、科研的正常秩序受到冲击的情况下，他也从不随波逐流，总是在力所能及的范围内勤勤恳恳地工作，帮助青年人树立良好的学风。正因为如此，他受到他的学生们的一致的尊敬和爱戴。

   许先生有很高的学术成就。他对中国古典文学很有修养，他精通英、法、德、俄等多种语言，对概率统计学科有杰出的贡献。为了纪念他，一九七九年美国《数理统计年鉴》邀请了一些著名学者、许先生过去的同事和学生撰文介绍他的生平，高度评价了他在概率论和数理统计两方面的工作。

   许先生共有学术论文三十九篇，其中解放以后在国内发表的十三篇。由于篇幅的限制，我们只从他的全部论文中选出了十九篇，编成这部文集出版。选编的原则一是力求反映许先生在各个时期的工作，一是尽可能反映许先生在数学各个领域的工作。许先生论文集的出版，将使他的重要研究成果得以更好流传，并将激励我们在党中央的领导下树立信心，埋头苦干，为实现四个现代化，迅速提高中华民族的科学文化水平而努力奋斗。

                              

                                   一九八零年二月

 

 

许宝騄 1910-1970

T.W Anderson ，K.L.Chung，E.L.Lehmann

Stanford University and University of California，Berkeley

 

       许宝騄1909年生于北京（译者按：应为1910年9月1日出生），1933年获清华大学学士学位。1936-1940就学于伦敦University College，在那里于1938年获Ph.D，1940年获科学博士学位。他从伦敦返回中国后，任教于北京大学数学系。

       战争年代生活是十分困难的（1943年-1944年许先生给Neymann的信中曾提到过挨饿之事）。但许先生仍然坚持研究。1945年他到达美国时，刚好赶上参加第一届Berkeley概率统计会议。在UC Berkeley 教了一学期的书，接着又到Columbia教了一学期的书。刚好这一年Hotelling由Columbia转到North Carolina筹建统计系，Hotelling就把许先生带到North Carolina，并给他一个副教授的职位。之后，尽管众多的统计学家鼓动他留在美国，最后他还是回到了北京大学任教。

       北京大学的段学复教授通知我们，许宝騄先生于1970年12月18日于北大的家中去世。他死于肺结核。学校为他开了追悼会。许宝騄出身于杭州的官宦之家，并在北京长大。由于他的出身背景，他讲的是一口具有幽默感的官方普通话。从风度和气质来看，他是一个典型的中国传统知识分子。他所受的英国教育，使他偏爱上数学。他在数学研究中的风格是倾向于困难但具体的研究，而不是一般而抽象。他学术上严于律己，宽以待人。他作研究工作可以着魔。他经常感到生活中的广泛爱好与献身科学之间的矛盾。他非常喜欢与不同文化背景的人们在一起交流，同时也十分爱好传统的中国文学。他的一个特别爱好是与一部分昆曲爱好者一起欣赏古典昆曲的美好旋律。可能是由于健康的原因，他终身未婚。他于1947年夏回到中国。当时Wald等人提供他在美职位，但他最后还是回国了。他希望成为他祖国即将成立的新社会的一个成员。在他生命的最后几年里，他的身体已经很虚弱，但他仍然坚持在他的房间内进行教学。他的中国同事们在他最后告别仪式上，对他表示最深切的敬意。除了他的著作和少数几个朋友提供的一点消息外，关于许先生在解放后20多年的生活和工作，我们可以说是一无所知。许先生的学生回忆起他来，都认为他是一个对人忠诚、温和又含蓄的人。他的个人生活很严谨，但作为一个教师和科学家，对人具有很强的吸引力。他在Chapel Hill的学生Isadore Blumen写道：“许先生坚持简洁，对事物深刻的了解，不畏避困难，凡事追求高标准，这些优秀品质深深地吸引着我们，而成为他的学生。”Ralph Bradley回忆起许先生的讲课，认为他的讲课是将来的典范。Herbert Robbins评价许先生时说“他是不可被忘记的，同时又是无人能替代的”。对于他的一些学生来说，尽管许先生不是他们正式的Ph.D导师，但许先生对他们的影响是不可磨灭的。在许先生来到美国之前，如钟开莱、冷生明、王寿仁等人，来到美国之后，如Isadore Blumen、Albert Bowker、Erich Lehmann和Ingram Olkin等人。

       许先生的统计工作主要集中于单变量和多变量线性模型的统计推断以及相关联的分布理论。既有小样本的，也有渐近理论。关于他的统计和概率方面的工作，另有专题作详细介绍。

       对于下列成员的协助表示感谢，他们有的提供了许先生的有关文献，有的提供了许先生的有关信息，有的提供了合理的建议。他们是I.Blumen，R.Bradley ，陈省身，F.N.David，C.Eisenhart，J.Neyman，I.Olkin，E.S.Pearson，H.Robbins，S.Stigler，段学复。

　

注： 这是T.W.Anderson(美国科学院院士), 钟开莱(著名概率论学者)和E.L.Lehmann(美国科学院院士)的英文中译文（郑忠国译）.原文“PAO-LU HSU 1909-1970”载于The Annals of Statistics, 1979, Vol.7, No.3, 467-470

  

 

 

许宝騄在统计推断领域的工作

E.L.Lehmann

University Of California ,Berkeley

 

    许宝騄在伦敦的University College共呆了四年（1936-1940）。那段时期，E.S.Pearson已经继承了他父亲的统计系系主任的职位，而那段时期的前两年（1936-1938），Neymann正好在那儿担任统计系的Reader，许先生在英国留学期间，写了一系列关于统计推断的重要文章，这些文章都是受到Neyman-Pearson观点的影响而写成的。

    1938年，许宝騄在Neyman和Pearson主编的Statistical Research Memoirs，Vol2上发表了他的两篇文章。其中一篇[3]讨论Behrens-Fisher问题。分别记X和Y(i=1,…,m;j=1,…,n)为N(ξ,σ)和N(η,τ)的样本。许考虑统计量 u=(-)/(AS+AS)，其中S=Σ(X-)，S=Σ(Y-)。当A=A=N/[mn(N-2)]，其中N=m+n时，u变成student的t统计量。当A=1/[m(m-1)]，A=1/[n(n-1)],u就是Behrens-Fisher统计量u。

    许宝騄找到了统计量u的密度函数的一系列展开，并利用它研究统计检验中否定域u≥c的功效函数，它是参数θ=τ/σ和λ=（η-ξ）/（+）的函数。这个工作是精确的分析结果，而不是渐近意义下的近似，Scheffé（1970）称它为“数学严格的典范”。在文中，他得到了u的随机界。Hájek，Lawton等人后来推广了他的结果（见Eaton和Olshen(1972)）。许宝騄利用数字计算和分析工具得到了他的主要结论。结论认为，当=0而变化时，u和u均不能控制否定概率（m=n的情况除外）。但u对变化的敏感度较弱。

    第二篇文章[4]讨论Gauss-Markov模型中方差的最优估计问题。由Gauss-Markov定理出发，他考虑的(a)二次型和(b)无偏估计Q。此外，他还加上(c)Q的方差独立于均值这个条件（这个条件是他在文[13]中讨论方差分析检验中功效函数的先导条件）。

    许宝騄指出的通常估计在该类中具有一致最小方差的充要条件。他并且讨论了一些具体的模型。对于一样本情况， 的确具有一致最小方差这个性质。后来，C.R.Rao(1952)再次提出这个问题，并且将条件(c)改成Q为正定，而Seely(1971)进一步考虑等价的“不变性”条件。可以这么说，许宝騄的这篇文章是近年来开始大量研究的方差和方差分量的最优二次估计的开山之作。

       许宝騄接着着手于小样本推断的研究工作。研究工作主要围绕单变量及多变量的线性假设检验问题，特别是关于这些检验的功效函数的性质的研究。这个领域中的第一篇文章[5]中，许先生得到了Hotelling  检验的功效。指出在非零假设之下，分布是一个非中心的变量和一个与之相独立的中心变量的比值的分布。他同时指出检验具有局部最大功效。此外，他还指出统计量的某些新的应用。

       对统计量的研究，很自然地引向对单变量的一般线性假设问题的多变量推广。单变量的一般线性假设检验问题是由Kolodzieczyk（1935）提出的。为了推广早期文献中提出的几个例子，许宝騄在文章[10]中提出了一般多元线性假设检验问题的典型形式，并得到了协方差矩阵已知时，非零假设之下，似然比统计量的分布。对于协方差阵未知的情形，记为相关行列式方程的根。许考虑检验统计量和, 并证明了当样本量趋于无穷时，两者的渐近功效是相同的。在后来的文章[13]中，许宝騄将多元回归中的检验问题转化为典型形式，然后利用[10]中的结果得到解决。

       在这一系列小样本文章中最重要的一篇是[13]。文中许宝騄得到单变量线性假设似然比检验的第一个最优性质。事实上，这是关于多于一个参数的假设检验的第一个整体最优性质。Kolodzieczyk早已证明，对于具有两个以上约束条件的线性假设检验问题，不存在一致最大功效相似检验。记表示似然比统计量的分布所依赖的唯一的非中心参数。许宝騄指出，似然比检验在功效函数只依赖于的所有检验中具有最大功效。后来人们才认识到，这个条件等价于自然的一类变换之下功效函数的不变性，其相应的最优性质之结果等价于该检验具有一致最优不变性。

这篇文章（指[13]）所涉及的问题，后来在以下两个方面得到进一步发展。一方面，他的学生Simaika(1941)将许的理论应用到多元分析理论，主要是Hotelling 和多重相关系数理论。后来Wald(1942)，Hsu(1945)，Wolfowitz(1949)和Lehmann(1959)等人又进一步发展了他的理论。另一方面，许宝騄的这篇文章提供了得到一切相似检验的新方法。在许宝騄的建议之下，Simaika(1941)和Lehmann(1947)等将其应用到其它问题的研究中去，最后导致完全性概念的形成(Lehmann和Scheffé (1950) )。

参考文献

EATON, MORRIS  L. and OLSHEN, RICHARD A. (1972).

Random quotients and the Behrens-Fisher problem. Ann.

Math. Statist. 43 1852--1860.

HSU, P. L. (1945). On the power functions for  the -test

    and the -test. Ann. Math.  Statist. 16  278--286.

KOLODZIECZYK, S. (1935). On an important class of

    statistical hypotheses. Biometrika 21  161--190.

LEHMANN, E. L. (1947). On optimum tests of composite

 hypotheses with one constraint. Ann. Math. Statist 18

 473--494.

LEHMANN, E. L. (1959). Optimum invariant tests. Ann.

    Math. Statist. 30 881--884.

LEHMANN, E. L. and SCHEFFE, HENRY (1950).

Completeness, similar regions and unbiased estimation.

Sankhya 10 305--340.

RAO, C. RADHAKRISHNA (1952). Some theorems on 

    minimum variance estimation.  Sankhya 12 27--44.

SCHEFFE, HENRY (1970). Practical solutions of  the

Behrens-Fisher problem. J. Amer.  Statist. Assoc.

65 1501--1508.

SEELY, JUSTUS (1971).Quadratic subspaces and

    completeness.Ann. Math. Statist. 42 710-- 721.

SIMAIKA, J. B. (1941). On an optimum property of two

    important statistical tests. Biometrika  3270--80.

WALD, ABRAHAM (1942). On the power function of  the

    analysis of variance test. Ann. Math. Statist.13 434--439.

WOLFOWITZ, J. (1949). The power of the classical tests

associated with the normal distribution. Ann. Math.

Statist. 20 540--551.

 

 

许宝騄在多元分析领域的工作

                            

T.W.Anderson

（斯坦福大学）

                                                    

    从1938年到1945年，许宝騄发表了多篇处于多元分析数学理论的发展前沿的论文。可以认为，他是受到了他所接近的当时也在伦敦的大学里的R.A.Fisher的影响。1945年后他在哥伦比亚大学和北卡洛林那大学教授多元分析课程，在那里他训练在这个领域做研究的学生。作为一个训练有素的数学家，许宝騄推动了矩阵理论在统计学中的应用并且证明了有关矩阵的一些新的定理。

多元理论的一个关键要素是样本协方差阵S的分布。如果所有的p维向量都是相互独立的且来自同一个分布，则服从所谓Wishart分布且密度为

(1)           

这里A是正定的，是依赖于p阶矩阵∑的常数，n=N－1是“自由度”。对于p=2的情形，Fisher(1915)在他的著名论文中得到了a11，a22以及的分布，这标志着严格推导小样本分布理论的开始。Wishart在1928年的文章用几何方法推导了密度(1)，大致说来这个方法是Fisher方法的推广。从Wishart的文章发表后，人们给出了许多其它的证明，其中许宝騄[6]基于代数和分析给出的证明特别优美。为了推导p,n时的密度，许假定了在p－1，n－1时的密度已知。除了这个矩阵及它的密度外，还需要一个p－1维的正态向量和一个n维正态向量。经过一点代数运算，只须推导n维向量模的平方的分布即可完成证明。

    Mahalanobis, Bose和Roy(1937)通过把A写成TT'得到了A的分布，这里T是下三角矩阵(tij=0，i<j)。他们从X1, ¼, XN的分布导出了T的p(p+1)/2个元素的分布，这些元素被称为“长方形坐标”。当∑=I时T的非零元素被证明是独立的。T的对角线之外的非零元素具有标准的一元正态分布，而对角线上的第i个非负元素，服从自由度为n-i+1的分布。不同于Mahalanobis，Bose和Roy的更多几何性质的方法，许在[9]中对“长方形坐标”的分布的推导是代数和分析方法。这与他在[6]中推导Wishart分布在方法上有相同的特点。

    多元分析中另一个需要推导的基本的分布是某些行列式方程的根的分布。这些分布被许宝騄[7]，Fisher(1939)，Girshick(1939)，Mood(1951)和Roy(1939)各自独立地几乎同时发现，因而意味着这是多元理论的“自然”的发展。（Girshick和Mood的工作本来是打算作为博士论文的内容，但在了解了Fisher和许宝騄的工作后，他们转向了别的题目。关于Fisher和Roy各自独立的工作，Bose(1977)曾有有趣的评论。）对于半正定矩阵A和正定矩阵B，假定是

(2)                       

的根。若A和B独立且分别服从分布W(∑,m)和W(∑,n)，这里m≥p，n≥p，则q1,¼,qp的密度等于一个常数乘以下式

(3)         

如果的根是，则.许宝騄作变换，这里Df是以为对角线上元素的对角形矩阵。如果Wij以概率1是正的，则变换是一对一的。推导过程包括：(i)在A和B的密度中用上述表达式代入；(ii) 乘以变换的雅可比式；(iii) 对W的元素进行积分以得到的边缘密度；(iv)最后转换为q1,¼,qp的密度。这个推导过程中的困难之处是雅可比式的计算。事实上，在这篇文章中许宝騄对任意p写出了雅可比式的表达式但只对p=3的情形给出了证明。（对由偏导数组成的12阶方阵给出了显式表达和计算。）

    后来，许宝騄找到了一种容易掌握的计算雅可比式的方法并在北卡洛林那大学的课程中讲授。遗憾的是，许一直没有把讲稿成文发表。但是，当时听课的学生们把内容记录了下来。在得到已回到中国的许的同意后，Deemer和Olkin(1951)详细阐述了这些方法和结果，从而使其为人们所应用。许在[7]中也处理了m＜p的情形。的根的密度等于一个常数乘以下式

(4)         

这里，Anderson(1958)的第13章的阐述是基于许以及Deemer和Olkin的文章。上述密度中的常数因子这里未具体写出。这个常数的值是重要的（例如在计算似然比检验中的矩时），需要认真对待。

在求根的分布时关键之点是Wishart分布是中心的，假设，令

，

则A与B相互独立，B服从中心Wishart分布，而A服从非中心Wishart分布，依赖于, å 和

k-1（Y的秩是1或2时的非中心Wishart分布也被Anderson和Girshick(1944)独立地得到，且打算作为博士论文的内容）。在[11]许讨论了当B有中心Wishart分布而A有非中心Wishart分布时的根。这些随机的根的分布只通过

(5)             .

的根依赖于和å. 当时，的精确分布是十分复杂的。许讨论了当时Nt/Ns, t,s=1,¼,k和Y都不变时的渐近问题。这时 和 的元素的联合极限分布是正态分布。如果(5)的根各不相同且都是正的，则Df 或Dq与W的元素经适当正则化后有联合渐近正态分布。

    许宝騄还研究了更一般的情形：(5)有重根且有的根可以为0，设(5)的互异的非零根是，分别有重数m1, ¼,于是根0的重数为，令

(6)        

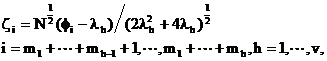
(7)        

那么，正则化后根的v+1个组按极限分布是相互独立的。对应lh>0的那个组的密度等于一个常数乘以下式

(8)        

这里x1>…>xm>0 (m=mh)，对应于零根的那个组的密度等于一个常数乘以(4)式，其中p用(5)中零根的重数代换，n用(5)中零根的重数与k-1之和代换（当k-1≥P时）。正如我们将要看到的，对零根的考虑是处理秩的问题时必不可少的。包含多重正根体现了数学上的一般性。处理这种一般性需要很高的创造才能和数学技巧。Anderson(1951)对于Df (或Dq)及同时对W作了相应的处理。

    若 和 å有如下分块：

(9)         ,

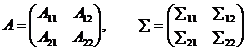其中A11和å11都是p1阶方阵，A22和å22都是p2阶方阵。样本的典型相关和总体的典型相关分别是下列方程的根

(10)       

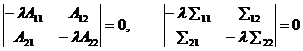
许在[12]中对于任意重数的根（包括0），找到了正则化样本典型相关的渐近分布。这篇文章是与[11]平行的。

    在[10]中，对于检验零假设：m1=…= mk,许研究了Wilks的似然比准则的统计量和Lawley的迹准则的统计量V=trAB-1。他证明了，如果上面定义的NY有极限，则NV+NlogW依概率趋向于0。实际上，这意味着当备择假设以样本量的平方根的倒数的速度接近零假设时，这两个检验的表现是相似的。[14]表明，通过化归成典则形式，上述结论对一般的线性假设的检验也成立。[15]中讨论的问题可以用上面的符号来表达。m1,¼, mk位于p维空间的一l维超平面等价于Y的秩是l或0是(5)的p-l重根。为了检验这个假设，Fisher(1938)建议使用检验统计量（Anderson(1951a)证明似然比检验是基于）。许从[11]导出，Fisher的统计量乘以N后的极限分布是自由度为(p-l)(k-1-l)的c2分布。

    比的渐近分布。在[19]和[23]中许将Cramer(1937)的渐近展开理论和Berry(1941)的定理用于比的分布上去。设，，其中所有Yi与所有Xj独立，Y1, ¼, Ym相互独立同分布，共同分布有某阶正的绝对矩，X1, ¼, Xn独立同分布，共同分布与前一分布有同样阶的正的矩。的分布可以写为

 (11)     .

     和经适当正则化后的分布函数均可展开，其误差具有Berry界。利用这两个分布的卷积，许找到了(11)的具有一定误差界的展开式。

    序列相关用于检验具有相同正态分布的随机变量X1, ¼, XN的独立性，它可以写成T=Q/S，其中，，通过一个改变尺度的正交变换：(X1, ¼, XN) ®(Y1, ¼, YN)，我们可将Q, S写成，。这样，在独立性假设下，每个Yi有分布N(0,1)，于是

(12)                   

若aij依赖于N，则依赖于N。当这些根的序列满足某些条件时，分布(12)在N 无限增大时有一个渐近展式。

作为早期工作[16]的进一步发展，许在[26]中研究了样本量无限增大时函数的极限分布，这里是独立样本的均值向量。利用均值的中心极限定理和函数f(×)的泰勒展开，许得出结论：极限分布为正态分布或正态变量平方的加权和的分布（若线性项的方差趋于0），许利用他的一般结果得到了很多检验统计量特别是多元分析中的统计量的渐近分布。

参考文献

Anderson,T.W.(1951a). Estimating linear restrictions on regression coefficients for multivariate normal distributions. Ann. Math. Statist. 22 327-351.

Anderson,T.W.(1951b). The asymptotic distribution of certain characteristic roots and vectors. Proc. Second Berkeley Symp. Math. Statist. Probability, Univ. California Press. Berkeley and Los Angeles.103-130.

Anderson, T.W. (1958). An Introduction to Multivariate Statistical Analysis. John Wiley and Sons, New York.

Anderson, T.W. and Girshick, M.A. (1944). Some extensions of the Wishart distribution. Ann. Math. Statist. 15, 345-357.

Berry, A.C. (1941). The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Amer. Math. Soc. 49 122-136

Bose, R.C. (1977). Early history of multivariate statistical analysis. J. Mult. Anal. 4 3-22.

Cramer, H. (1937). Random Variables and Probability Distributions, Chap.7 Cambridge Univ. Press.

Deemer, Walter L. And Olkin, Ingram (1951). The Jacobians of certain matrix transformations useful in multivariate analysis. Based on lectures of P.L.Hsu at the University of North Carolina, 1947, Biometrika 38 345-367.

Fisher, R.A. (1915). Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 10 507-521.

Fisher,R.A.(1938). The statistical utilization of multiple measurements, Ann. Eugen, 8 376-386.

Fisher R.A.(1939). The sampling distribution of some statistics obtained from non-linear equations ann. Eugen. 9 238-249

Girshick, M.A.(1939). On the sampling theory of roots of determinantal equations. Ann. Math. Statist. 10 203-224.

Lawley, D.N. (1938). A generalization of Fisher’s z-tes. Biometrika 30 180-187

Mahalanobis, P.C., Bose R.C. and Roy. S.N. (1937). Normalisation of statistical variates and the use of rectangular co-ordinates in the theory of sampling distributions. Sankhya 3 1-40.

Mood, A.M. (1951). On the distribution of the characteristic roots of normal second-moment matrices Ann. Math. Statist. 22 266-273.

Roy, S.N. (1939). p-statistics or some generalizations in analysis of variance appropriate to multivariate problems, Sankya 4 381-396.

Wishart, John (1928). The generalized product moment distribution in samples from a normal multivariate population. Biometrika 20 32-52

　

注： 这是美国科学院院士T.W.Anderson的英文论文的中译文（陈家鼎译）.原论文“HSU's work in multivariate analysis”载于The Annals of Statistics, 1979, Vol.7, No.3, 474-478

 

 

                          

许宝騄在概率论方面的工作

            Chung Kai-Lai

Stanford University

 

许宝騄于抗日战争中期的1940年从英国回到昆明。他开了一门很长的课程，从测度和积分开始，讲到概率论，再通向数理统计。课程的第一部分基于Caratheodory的《Vorlesungen uber Relle Funktionen》，第二部分则取材于Cramer的《Random Variables and Probability Distributions》。他是一个风度优雅而又富有激情的老师，随身带着预先写在本子上的完整的备课笔记。他喜欢在课堂上点出微妙之处。例如，在推导特征函数的反演公式的时候，他强调Lebesgue-Stieltjes积分是能在单个点上积分的。他有一本用得很旧的Cramer的书，页边上写着许多批注，用来说明该处是用一种不必要的难懂的方式写成的，但本书确实包含了概率论的所有实质性的内容。他是一位名副其实的特征函数方法的行家。他的文章[18]，[24]，[27]，[28]，[33]和[25]都显示了他对这一宝贵工具的迷恋和精通。那些年代，在昆明很难得到数学文献，那些从北京(当时叫北平)泊运来的旧图书资料也藏在山洞里以防空袭。(我们虽不住在山洞里，但当空袭或警报响起的时候，却不得不冲向防空洞并在里面待一段时间。)藏在山洞的书里有一本Kolmogorov的《Grundbegriffe der Wahrscheinlichkeitsrechnung》。在我的请求下，许从山洞里取出了这本书，他说：“这是另一种数学”。当然，他不是一个概率学家，当时这样一个称号在世界的任何地方都很难接受；由于所受的教育和个人兴趣，他更喜欢解决实质问题而不是做形式上的推广。但他绝不阻止别人追求自己的爱好和对其它的东西感兴趣。只要他被一个新课题所吸引，就坚决地投入工作并很快地作出有价值的成果。例如，当Borel关于他自己称之为“可数概率”的工作引起我的注意的时候，许也同样地有兴趣，从而导致了文[22]的出现。这就是后来经Feller的发展被称为“常返事件”方面的早期工作。文[24]和[32]也大致是在类似情况下产生的。

但是，许对概率论及其应用的主要贡献来自于使用特征函数方法的完美技巧。让我按年代顺序来描述和评论一下这些文章。

毫无疑问，文[18]是许的最重要的工作之一。此文是在A.C.Berry得到了对中心极限定理误差估计的正确的阶以后不久写成的。Berry的结果表明，如果是独立同分布的随机变量序列，均值为0，方差为1并有有限的三阶矩，则对所有的，分布

      

与标准正态分布之差不超过，而是一绝对常数。(此结果也被Esseen证明，但他的文章发表得晚些，许当时并不知道。)许推广了Berry的方法，给出当非奇异时，关于的渐近展开的Cramer定理的一个简单的证明。然而更深入而意味深长的是他用样本方差

              

取代样本均值

              

以后，也得到了相应的结果。用许自己的话来说，“关于的分布逼近有大量已知的结果。Cornish和Fisher用纯粹逻辑推理方法，得到了任何随机变量分布借助于它的半不变量来表示的逼近。把Cornish和Fisher形式的结果(无余项估计的渐近展开)转化成能给出余项估计大小的阶的渐近展开的一个数学定理，其重要性是不言自明的。我们在本文中对接近的最简单的函数做到了这一点。”解决问题的基本想法如下。以记的四阶矩并令。

         

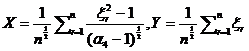
那末关系式

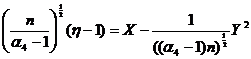
成立，许的方法的要害是通过随机向量的特征函数去逼近它的分布。由于和高度相关，即使大致考虑一下也可以看出，这是一项十分复杂的任务，绝非Berry和Esseen结果的平推。为了达到目的，许在前人所用的逼近方法的基础上又添上了一维。当他得到这个结果的时候，他正在讲着前面提到的那门课，显得兴高采烈。我记得他说过，他对该问题作过几次尝试，只有当他认识到必须正面攻克二变量逼近问题而不是逃避困难走捷径的时候，才取得突破。他的方法适用于许多统计中常用的函数，如高阶矩和学生氏统计量。其中的一些被他的学生们完成了。虽然许的论文由Bikjalis在他关于正态逼近的工作中引用过，但最近一本这方面的书却没有提到它。在写本文的过程中，我向作者提到这个明显的漏洞却得到令人遗憾的回答，他们竟没意识到许的文章！这是一个严重的失误，它说明许的方法产生的分析力量并未得到充分的发掘。

文[24]的主要结果是：对于均值为0，方差为1的独立同分布的随机变量序列和任意，我们有

       。

这个结论沿着Borel-Cantelli引理的方向有趣地加强了古典的强大数律。文章的想法大概出自Robbins，但证明的方法来自老到的许。在用了Fourier反演公式之后，此问题化为若干个含有特征函数的积分的估计——许的拿手好戏。稍后，Erdos(1949)改进了上述结果并证明加在矩上的那些条件不仅充分而且必要。(据Robbins回忆，他们原始的手稿也包含条件必要性的证明，因为太复杂而未发表。) Erdos用的是一种组合的论证方法。Baum和Katz进一步把这类结果推广到分数矩和高阶矩的情形。

文[25]形成了Genedenko-Kolmogorov书的英译本(1968)的附录III，它的故事或许值得在这里说一说。许对Feller提出的中心极限定理一般形式的充分必要条件有深刻印象，因为在那里特征函数得到巧妙的运用。1947年5月12日从Chapel Hill发出的一封信中，他告诉我他刚解决了对于所有对称稳定律的同样问题。他写道：“我相信，在弱律的一个领域内，这已经是最好的定理。这里所用的方法也适用解决更一般的弱律，即当极限是无穷可分律时的情形。但前面的困难还很大…。这个问题在我看来是如此自然，以至于常担心会和别人撞车。当你和概率方面的人们交流的时候，请传播这一消息。”此后1947年5月26日的信中，他向我宣布了最终结果。他给出了行内独立的无穷小随机变量三角阵列的行和依分布收敛到一个给定的无穷可分分布的必要充分条件。他的条件和Genedenko(1944)的不同之处是把“双尾”放在一起处理。结果的证明是直接的并用到核。那篇包含结果及其证明的完整手稿就是[25]，许在1947年夏回中国前交给了我。（我在前面提到的Genedenko-Kolmogorov书英译本的前言中误将年份写成了1946。）尽管有预感，许直到很晚才知道Genedenko(1944)的文章。在他回国后写给我的仅有的一封1950年3月19日的信中，他承认Genedenko的优先权并用强调的语气要求我为他保存好仅有的那份手稿。他清楚地显示了自己在解决这一挑战性问题时的实力，该问题是Levy，Khintchine，Kolmogorov，Marcinkiewicz(许见过他)，Feller和Gnedenko等人的一系列文章的顶点。他艰难地攀登并迅速凯旋。即使另一个奋斗者已先于他登上顶峰，又有什么关系呢？许的方法是直接而“从零开始”(start from nothing)的。这后三个词是一种更难以捉摸的中文说法的翻译，这种说法许在另外的场合也用过，意思是尽可能少地依赖以前的东西。他总是把这种非依赖性视为好的数学工作应有的品质，那是很明显的，在他所有的文章中凡是推导的中间步骤要用到前人结果的地方，都尽可能地避免掉了。Genedenko-Kolmogorov书英译本的新版(1968)出现在中国文化大革命的中期，我不知道许是否看到他这篇文章印出来了。

文[27]和[28]已由我在Mathematical Reviews第17卷(1956)第274页上做了比较详细的介绍，很容易查到，就无必要重复其内容了。只需说明一下，它们还是许的特征函数特长的产物就足够了。文[33]属于同一栏目，显然也未被索引过。此文证明了L族中每一个分布都是绝对连续的。据我所知，这是一个新结果。它于1963年被Fisz和Varadarajan再次发现(Wahrscheinlichkeitstheorie und Verw. Gebiete,Vol 1))。

许在概率论方面的工作[32]是一篇没有用到特征函数的文章。它和[33]一样，用中文写成但附有英文摘要，发表在刊物的同一期上而且未被索引过。文章处理这样一类Markov过程转移概率函数的可微性，它的状态空间是欧几里德空间而其轨道是纯跳跃的。D.G.Kendall于1955研究过这类过程，他分析过转移概率函数在处的可微性。对于Markov链，即状态空间是离散的情况，Chapman-Kolmogorov方程的导数公式

 

由Austin和我分别用分析方法和概率方法证明。(关于D.G.Kendall和Austin的结果，见Chung(1967)。)许把这些方程推广到欧几里德空间的转移概率函数，“所用的方法尤为初等，所获得的结果倒是更精确一些”。对于上面的第一个方程，他借助于post-exit过程推导出一个的积分表达式，一般化了我用的方法，但用的是纯分析的工具。分析和概率方法的内在联系隐含在他的文章中，并且很容易被看出来。

直到1972年我到达北京以后，才知道许已经去世。段学复告诉我，他在用自己的方式研究大量古典组合问题的过程中度过了最后的岁月，遗留下许多笔记。迄今为止这些笔记的内容还不为人所知。

参考文献

 

Chung, K.L. (1967). Markov Chians With Stationary

    Transition  Probabilities, 2nd ed  Springer- Verlag.

Erdos, P. (1949). On a theorem of Hsu and Robbins. Ann.

    Math.  Statist. 20 286-291.

Gnedenko, B.V. (1944). Limit theorems for sums of

    independent   random variable. Uspehi Mat. Nauk.

    10 115-165, English translation: Translation No.45,

    Amer. Math. Soc., New  York, 1951.

Gnedenko, B.V. and Kolmogorov, A.N. (1968). Limit

Distribution of Sums of Independent Random Variables,

rev. Ed. (translated by K.L.Chung, with Appendices by

J.L.Doob and P. L. Hsu). Addison-Wesley.

 

注： 这是著名概率论学者锺开萊教授的英文论文的中译文（程士宏译）. 原论文“HSU'S WORK IN PROBABILITY”载于The Annals of Statistics, 1979, Vol.7, No.3, 479-483 

 

 

许宝騄事略

 许宝骙

 

许宝騄，字闲若，祖籍浙江杭州，1910年9月1日生于北京，因小名京生。父许引之，字汲侯，自清末至民国北洋政府期间历任中级官员，至两浙盐运使。母程时嘉，江西新建人。

宝騄二岁时，随家移居天津。八岁，去杭州。宝騄幼时体质羼弱；而慧敏之秉赋已隐然可见。孩提时即能拼摆《益智图》，见者奇之。五岁，始在家延师课读，启蒙师为张　（字树之）先生；后改从吴县高德馨（字远香）先生、蕲春陈先生，至十四岁。尽读四书、五经，涉猎四史，傍及古文辞，大都能琅琅背诵。甫逾十龄，学为古文，塾师评为“简老”。曾偶发奇想，以文言撰作短篇小说，题为《花生姻缘》，老父索阅，为之开颜，其稿至今犹存，时方十一岁耳。学写小楷，临摹《玉板十三行》，颇能神似，得古朴之趣。后曾为表兄姊丈俞平伯手写其《古槐书屋词》，有刻本行世。又善就古书诗曲小说制作灯谜，颇具巧思。十一岁，始学英文、算术，塾师为杭县邵家驹（字昂士）先生，两年后能读英文古典文学名著。1924年，十四岁，父亲病逝于杭州，母亲携全家迁回天津。翌年，移居北京，时年十五。

宝騄到北京后，为求考中学，赶学数学。北京大学数学系吴缉熙老师为讲授代数及三角。从头起步，仅阅两月即成绩斐然，亦由引起兴趣，其数学天才开始崭然显露。是年暑期后，考入北京汇文中学高中一年级，肄业三年。在此期间，每年暑假中从表姊丈徐传元先生（字孟轮，毕业于美国麻省理工学院）钻研数学，得其指点，益有进步。同时，于课外从师学法文，两年，略能会话，能作短文。

始到京时，寄居于平伯家，灯下闻坐，闻长者谈及移棋相间之游戏。其法，取黑白棋子各若干，数相等，分列左右，一端黑，一端白。称之，每移必并取二子，由左而右，或由右而左，为一步。以后左右互移之，如一步左至右，则次步右至左。如一步左至右而次步仍之者，则为顺移（凡奇数完全互移，凡偶数必有一顺移）。如取黑白各三子，则移三步而毕，四子四步，五子五步，多一子则多一移。移毕则黑白各子相间排列，而两端之黑白二色互易，并较原分列时傍挪二子。宝騄性喜深究，闻此法后，勤加推衍，不久即能推移至五十子；再进则摸得四项规律；又进则竞合四律而为一。于是执简驭繁，盈天下之数尽可据以推移。此虽小道，也足见兴在数理方面之天赋。

1928年，十八岁，从汇文中学毕业后进入燕京大学，肄业一年。此时，宝騄决定专攻数学。素闻清华大学数学系最好，遂即转入，不惜仍从一年级开始。业师为熊庆来、孙光远、杨武之诸先生。同学与之游者则有王宪钧、华罗庚、孙毓棠、万家宝（即曹禺）、邵循正诸子。1933年，廿三岁，以理学士毕业。

在清华肄业期间，适平伯组织谷音社，研习昆曲，同人会唱，宝騄与焉。宝騄品娴音律，辨音极准，每听一曲，不数遍即能写出其工尺谱，试之不爽。能操二胡，时复一弄，用以自娱，又偶制图案画作书签，敷以采色，凡百数十种，莫不精美可喜。其艺术之秉赋概如此。

宝騄毕业于清华后，即赴英国庚子赔款公费留学之考试，已被录取，乃检查体格时竟以体重不能过关而遭排出。宝騄于是锐意调治身体，在香山赁屋独居，加强营卫，澄心休养。逾年，健康增进。入北京大学数学系为助教，受教于江泽涵先生，并为美国客座教授W.F.Osgood先生作助手。1936年，再试再中，遂于是年赴英国，肄业于伦敦大学，专攻数理统计。1938年，得哲学博士学位，又二年，晋科学博士。于是声誉渐起，为国际数学界所瞩目。

抗日战争期间，宝騄出于爱国热诚，于1940年离英返国，任教于昆明西南联合大学数学系。其时宝騄生活艰苦，营养不足，体力日渐削弱，而坚持工作，不稍衰馁。深夜苦读，每至蜡泪成堆，烟蒂盈器。数年之间，教学之馀，研究成果尤为丰富，仅41年一年即有论著五篇发表于国外诸刊物。与罗常培、郑天挺、袁家骅诸先生游，合伙包饭，仅餍粗粝。偶思“打牙祭”，欲烹调而苦无锅釜，乃以洗面盆盛鸡豚煮食之，谓之“吃脸盆”。又饥鼠为患，往往啮其书籍及手稿，宝騄别出心裁，剪开枕芯以饷鼠，害乃稍戢，遂喜而扬言曰：恶鼠被我感化矣。其生活之风趣又如此。在此期间，美国诸大学争相延聘，宝騄始于1945年赶美。在加州大学及哥伦比亚大学各讲学一个学期。1946年转至北卡罗兰纳州大学任教。

在国内数年期间，宝騄有见于国民党统治区政治腐败，社会混乱，人民痛苦，初步认识到政治的重要意义及中国革命的必然趋势。其时，中国民主革命同盟早于1941年秋在重庆成立。这是一个秘密政治团体，是中共中央直接领导下的一个外围组织，是在周恩来同志亲自关怀指导下组织起来的，宝騄的两兄宝驹、宝骙都参加为发起人。宝騄于赴美前夕由昆明到达重庆，与长兄宝驹一夜倾谈之后，毅然而郑重地参加了这一革命组织，并接受在美国联系海外华裔进步学者的任务，积极活动，颇有影响，曾介绍涂长望同志参加组织，即是一例。

宝騄于1947年，不顾美国大学之多方挽留，毅然返回祖国，在北京大学数学系任教授。认真教学，努力研究之余，仍在中国民主革命同盟北京地方组织的领导下积极从事文教界的民主革命运动，在白色恐怖下坚持斗争以迎接解放。

宝騄幼年时，父亲曾为作主与南方老亲某氏女订有婚约。其后父亲去世，举家北迁，宝騄稍长，乃坚决要求退婚。母亲强之不听，无可奈何，只得勉为提出解决。此可见宝騄自幼即具决断能力及抗争精神。1947年回国后，时年三十七，始又订婚。讵料不久发现身染肺疾，乃复废约。此后终身未娶。

解放后，宝騄除仍在北京大学数学系任教授兼概率论教研室主任外，并受中国科学院之聘为专门委员及数学研究所筹备处副主任。又任中国人民政治协商会议第四届全国委员会委员。二十年间，宝騄在不断与病魔斗争中不断致力于职务工作。自学俄文，亦能阅读专业论著。最后两年，双腿肌肉萎缩，瘫卧在床，犹复孜孜不息。自言身虽残废，脑尚健好，生命力还很旺盛，尽能生活工作下去。诚所谓“学而不厌，诲人不倦”。其教学成绩及研究成果，师友学生类能言之，世界学术界亦有定评，不待赘述。

文化大革命中，宝騄身蒙灾难，兢兢自克。亲属往访，辄闭门不纳；偶或遥遥一望，便挥手令去，不交一言，其精神痛苦可想见矣！

1970年10月，宝騄偶染肺炎，不数日，十八日晨七时，竟在家属毫无所闻情况下溘然长逝，得年六十。一只断去“parker”牌号的旧金笔弃置在床头小几，数页写著未竞的残稿散落在地，见之凄然掩涕，怆然神伤而已！

一九八Ｏ年四月一日于北京。

 

 

 

记许宝騄先生青少年时代事

 

俞润民

 

编者按：本文作者系许宝騄先生之外甥，应北京大学概率统计专业校友会之约写下此文。本文中提到许宝騄临摹《古槐书屋词》一事，作者提供两幅手迹，其中一幅是许宝騄大姊于1973年按许宝騄手迹的摹写本，见本书的开头部分。另外一幅是许宝騄姊姊为记念许宝騄写的后记，见本文后面。该摹写本已在香港出版。

(一)移棋相间法

清康熙二十九年，褚稼轩《坚瓠集》中载有“移棋相间法”。最初由来，始于清顺治六七年。传授来自胡君，至清末，经学大师俞樾和夫人在闲暇十之时，也做移棋之试，曾推至二十棋子，并作诗记载此事，诗云：

 

         闲将棋子试推移，黑白分明亦一奇。

         此后空留遗法在，更谁灯下运灵棋。

 

     (自注)：褚稼轩《坚瓠集》有移棋相间法，以黑白三子，三移而黑白相间，自三子至十子皆然内人复推广之，自十一子至二十子，今存其法于《春在堂随笔》。

后来俞樾先生的曾孙俞平伯先生及其内弟许宝騄先生(时年仅十几岁，正在中学读书)，根据《春在堂随笔》记载，又设法查找《坚瓠集》，知道了最初之法，他们就研究推增至五十子。以后并非不能再推加，因过于繁琐而止。过约一年后，许宝騄先生以研究所得移棋相间“合四为一”，的新律相告，俞平伯先生有一段文字记此事，文曰：

 

已已新正二日之夜，忽以电话觅谈，适余外出，越曰访之，乃以合四为一之新律相告，其法简而整，其言明且清，虽其根柢不出四律，而去其繁冗，正其谬误，使人一览豁然贯通，于应用上方便至多，……依新律，则口耳授受一分钟可毕，真庶乎儿童不乱矣。

 

清初以来的“移棋相间法”，本是一种有数学性质的游戏，许宝騄先生在中学时代与俞平伯先生一起，先是推至五十棋子，以后又总结出四条规律，本来还想成一公式，因许宝騄先生赴英国留学，科学研究任务繁重，对少年时代的游戏也就无暇再问了。

 

(二)书写俞平伯先生《古槐书屋词》

许宝騄先生出身浙江杭州名门，自幼通读经史子书，临池王羲之十三行书法，俞平伯先生是他的姊丈，在清华大学任教，著有《古槐书屋词》，当时许宝騄先生正在清华大学读书，在功课之余，经常到俞家来，这时俞平伯先生就请他代为抄写《古槐书屋词》，后有印本流传，印数不多，四十年后，家中只存有一本，为恐其遗失，他的长姊许宝驯(即俞平伯夫人)按其弟许宝騄的手迹临摹，字体极为近似，并得以流传至今，其姊并为此作一跋，回忆当年在清华大学南院，她的七弟许宝騄在灯下制做书签的往事，因这时许宝騄先生已谢世，故跋语最后云：“当年朝夕相聚，思之怅然欲涕，儿嬉情事，如尘如烟，偶记纤琐，不尽所怀也。” 以上两事均我幼年所知，至今记忆犹新。

 

                                （1998年10月7日于北京）

 

 

 

许宝騄先生的青少年时代事

 

——— 俞润民先生访问记

郑忠国 杨瑛

 

一九九八年九月二十六日，笔者在北京市建外永安南里俞润民先生的寓所就许宝騄先生的青少年时代的学习和生活进行了访问，现将有关情况记述如下，仅供参考，许先生的学术成就已有不少记载，这里不再赘述。

   许、俞两家乃故家故亲。俞先生的高祖俞樾(1821-1907)是清朝大学者，浙江德清人，道光进士，官翰林院编修，著有《春在堂全书》二百五十卷。俞樾的二女儿嫁到许家，成了许宝騄先生的祖母(祖父许佑申)，许先生的父亲是许引之。许先生在家排行第七，系俞润民先生的七舅。许先生的大姐又嫁给俞平伯先生，即俞润民先生的母亲，许俞两家是亲上加亲，按现代优生学的观点来看，是不符合优生学原理的，值得庆幸的是在两家后代中并没有发生不幸，其后代皆学有所成。

许家在清朝时，是杭州的望族，许家住在杭州的“横河桥”。当时皇帝给许家赐匾“七子登科”，意为许家府上出现过七位有才学的人。

宝騄先生幼年十分聪颖，中学时代在北京汇文中学读书。汇文中学是北京有名的中学。中学毕业之后，许先生考入燕京大学，到二年级时转入清华大学。在考上大学时，许先生还有典故，许先生品学兼优，在上高中时，就对一些高深学问有所研究。当时考大学是各校单独命题考试招生，而不像现在这样，全国统一命题考试招生。许先生当时报考两所大学：燕京大学和清华大学。按许先生当时的水平和成绩，考入清华大学是没有问题的。许先生文笔快捷，思想敏锐，当时，有不少认识他的人问他题目怎样做，他帮助别人做题，因而清华大学没有录取，而被燕京大学录取了。入学不久，由于出众的才能，第二年就转入清华大学继续深造，当时俞润民的父亲俞平伯是清华大学教授，俞先生正在上小学，许先生常到俞先生家吃饭。许先生除了数学特别出色之外，他的兴趣、爱好十分广泛。他爱好文学、昆曲、二胡、桥牌等。说起桥牌，当时西方的桥牌刚刚传入清华，所以很多人对打桥牌这种娱乐形式很感兴趣，许当时钻研桥牌方面的书籍，他精通桥牌，牌艺出众，他在西南联大任教时，参加清华的校队，参加桥牌比赛。许先生还常和朱自清、浦江清、俞平伯在俞家打桥牌。许先生怕别人说笨话，喜欢聪明人，对于“笨话”许先生非常敏感。俞先生清楚的记得他曾说过一句话：“七舅，你学的是算术”，许先生听后很生气，就说“不是算术，而是数学”。

许先生在清华读书，成绩十分优秀，当时清华数学系教授是熊庆来，杨武之等，他们对于许先生的才华十分看重，当时拔尖的青年人物是许宝騄、华罗庚。当时可用庚子赔款去英国留学。在清华大学每年有一名额，这当然是非华、许莫属。他们两个先后被送到英国留学。许先生是1936年去的英国。到英国之后，许常和俞家有书信来往。在到英国之前，许先生在1935年到香山疗养过。当时住在香山脚下的一所房子里。润民先生和熊庆来先生的儿子曾骑自行车到香山看望许先生。当时，他患有肺结核，经过一段时间的疗养之后，才去的英国。

许宝騄先生终生未婚。关于他的个人婚姻事宜，有各种说法，润民先生的说法可以认为是可靠的。根据润民先生回忆，事情是这样的，润民先生有一姑父，郭则澐，是清朝翰林，曾在北洋政府徐世昌处任秘书长。郭有一女儿，与许先生年龄相仿。按中国旧的传统来说，许郭辈份不合，许先生比这位郭女士长一辈。郭则澐认为虽然辈份不合，但郭先生与许宝騄先生的父亲在北洋政府时期是同事，作为儿女之事也是合适的。所以郭先生还是赞同这桩婚事。据推算，1936年许先生留英以前，两人已有恋爱关系而往来，后来之所以没有成，是郭先生的儿子(郭女士的弟弟)所致，旧社会由男的当家，郭的儿子反对这桩婚姻，欲将他的姐姐嫁给国民党的一个官吏。后来，郭女士嫁给了一个铁路局长。这样，许先生的婚事就告吹了。这件事情发生在抗战时期(40-45)，许郭之间相处的时间不长，外面传说，许先生因肺结核未能成婚，这不符合事实，只是对外的一种托辞。另据润民先生回忆，许先生在美国时，曾有一女士有意于他，这一次不是父母之命，是自由恋爱。据润民先生回忆，许先生给俞平伯先生的信中提到他采取的策略是“以退为进”，现在已搞不清楚以退为进的具体含义。但这四个字是很合乎许先生的性格和他的用语特征的。从现在恋爱方式来看，应是双方主动。这也许是许先生终身独身的原因之一。

许先生不仅学问做的好，业余兴趣也很广泛。“移棋相间法”和“书写俞平伯先生《古槐书屋词》”可见其兴趣之一斑。(见本书俞润民先生文)

本文的大部分读者应是许先生的学生，或是敬仰许先生的学者，本文未谈及许先生的学术成就。关于学术成就，大家可以从他的学术著作与其它介绍其生平的文章中了解到。作为一个统计学大师，他的生活环境，家庭背景，对于他的学术是有很大影响的。从他的生活经历可以看出，许先生的学术成就具有源远流长的文化背景。俞平伯先生的文章中提到的移棋相间法(见本书附录)可追溯到清朝初期，许先生最后完善地解决了这个游戏问题，给出了一个一般的公式。

本文的另外一个目的是让我们了解许宝騄先生的为人，经历，而不仅仅是一个抽象的统计学家。

 

编者注：本文作者郑忠国是北京大学教授，杨瑛是北京大学副教授

 

 

回忆西南联大时代的老师许宝騄先生

 

徐利治

大连理工大学教授

 

（一）

 国际一流的对多元统计作出了卓越贡献的许宝騄先生离别人世将近30年了。今年2000年正好是许先生诞生90周年，相信海内外的弟子们都将以崇敬缅怀的心情来纪念我国这位世界级的统计数学大家和导师。

 40年代我求学于昆明西南联大（抗日战争年代由北大、清华、南开三校联合而成的大学）时期，由于钟开莱先生的热诚介绍，我有幸接触到许宝騄先生，并能不时从他那里得到教诲和指导，至今印象清新，仍历历在目。1948-49年许先生任教于北大，有一段时间长住一所德国医院疗养身体。那时我在清华做助教，曾多次进城去拜望许先生。他往往神态显得十分爽健，也很健谈，例如，可以从恩格斯的《自然辩证法》谈到国家大事和世界发展趋势等等。

 记得有一次许先生忽然告诉我，他很想读读《自然辩证法》。谈话中他很赞赏前苏联的数学成就，尤其是对Kolmogorov学派十分推崇。在1948年辽沈战役后，许先生已确信“国民党败局已定”，并对当年北大、清华的学生爱国民主运动十分同情，还提到了一二九运动时期他所熟悉的个别先进人物的名字…。

 以上所诉，都是50年前的事了。我的印象是，许先生作为体弱多病的杰出数学家，当年能深切关心国家大事、能接受先进思想且有明辨是非的爱国主义正义感，这在旧社会老一辈的知识界人物中确是难能可贵的！

(二)

1951年秋我从英国返回国内后，每次从清华去北大时总要抽时间去拜访许先生。1952年冬我调到长春吉林大学工作后，就不能走访许先生了。但只要每次到北京出差或开会时，也总要去看望许先生并且往往能长谈一二小时。

在与许先生多次接触交谈中，我感到在数学学术思想方面得到他的教益和启发是很多的。

我们知道，许先生是一位英国派硬分析工夫极深的数学家，理所当然地他对英国分析数学家Hardy与Littlewood是很称道的。但是有一次他却对我说，如果把Hardy的贡献与德国数学大家Hilbert的成就作比较，那么他认为：“每一个数学系毕业生可以不知道Hardy的贡献成果，但却不可以不知道Hilbert所贡献的数学知识。”这些话给我的印象极深而且在实际上对我产生了影响。

50年代初，王湘浩先生和我担任吉林大学数学系正、副主任期间，曾一致鼓励我们的同事江泽坚先生（也曾是许先生的学生）为本科四年级开设了“Hilbert空间理论”课。又为了相互配合我也曾为三年级学生讲授“Banach空间引论”课。就这样，通过教、学、研互相促进的办法，我们曾努力为本科生毕业前传授了Hilbert所贡献的重要知识，而这正是体现了许先生所说过的观点主张。（事实上，我们在西南联大时期，谁也没有学过这些课程。就我来说，我在清华大学任助教时，还不知道Hilbert空间与Banach空间的基本概念。）

50年代，在王湘浩、江泽坚二位鼓励下，我曾为吉大高年级生开设了一门课程，叫作“数学分析方法”（后来出版的书名为《数学分析的方法及例题选讲》）。这门课没有规定大纲，可以自由选材，故在讲课中能有一些灵活性与趣味性。但对选材是否恰当实不敢自信。于是趁赴京开会机会我曾把全部讲稿（书稿）带到许先生那里，当初只是想请他浏览指点一下。而使我特别感激的是，他竟十分乐意花时间将全部书稿仔细审阅一遍，还帮助作了修订和润色，以致使书稿增色不少，从而能在出版后得到数学专业师生们的广泛采用。

记得在讨论书稿的选材问题时，许先生很是赞赏“Abel方法”（分步求和法及其变种）被置于首要一章的地位。他认为经典分析学中的Cauchy-Weierstrass惯用取优函数法或取绝对值法来判别无穷级数与无穷积分的敛散性状时，实际上是排除了大量可判别的例子，而Abel方法恰恰是突破了原有判别法的局限性，使得具有“奇异振荡性质”的级数与积分的敛散性，也纳入可判别范围。但很可惜的是现代一般高等数学教材中，常常忽略了Abel方法的应有地位。许先生还特别指出“Abel方法”与“不等式”是分析学领域中的两套重要工具，例如英国的Hardy-Littlewood学派的许多漂亮工作，包括Hardy的名著《发散级数》等，也都是这些工具灵活运作的结果。所以他很是赞同并出了些主意要求在我的书稿中突出上述分析工具应用上的灵活性与广泛性。

50年代至80年代上述拙著已由高教出版社再版重印数次，累计发行达5万余册，也算是一本畅销书了（1983年的修订版还获得国家优秀教材奖）。这一切都应感谢许先生当年的指点和帮助。

（三）

在海内外我曾遇见过有些分析数学家，特别是一些搞应用分析数学的专家，在言谈中大多是不十分敬重抽象代数的。可是许先生却认为要搞代数研究，就应该研究抽象代数。

记得1944年左右，我在西南联大求学时曾一度喜欢代数学，有一次我去看许先生想问问他的意见。他立即告诉我说，数学是离不开抽象的，最基本最深刻的东西都是要经过抽象才能揭示或显示出来的。许多看来很难很复杂的东西一经抽象就显得简单而易于掌握了。所以要搞代数研究，就必须研究抽象代数。他说，他自己不搞抽象代数但他知道抽象代数主要是由德国数学家发展起来的。

同时他还说到，有些数学家一辈子搞的数学题材很具体很特殊，但也能有贡献。例如英国有位叫Muir的学者，数十年致力于行列式计算，他出版过一本巨著，算出了各种特殊类型行列式的数值。这其中并没有什么一般理论，但对于要用到特殊行列式数值的学者们，Muir的著作还是很有用的。他还认为在数学家群体中也不能缺少像Muir这样的人物。

由上可知，许先生的数学价值观念中，除了十分敬重抽象代数之外，也还充分肯定比较特殊的具体的数学分支的作用与价值。这很可能是他长期从事统计数学理论与方法应用研究经验中形成的价值观念（我个人也是很赞同这种价值观念的）。

（四）

许先生出生于书香门第，自幼受过很好的文学熏陶，所以他善于运用形象思维的语言来解释现代数学基本概念产生的必然性。

例如，有一次在闲谈中他对我谈到拓扑学中“拓扑变换（或同胚变换）”的概念时，他说，当我们看到杨柳的摇曳或是小河流水的流动时，如果要把它们描述成是质点（或分子）集团的变换，那就只能而且必须抽象出“拓扑变换”（即双向连续的一到一映射）的概念。这也说明作为描述空间形体最一般变换的几何学——拓扑学的产生是十分自然的、必然的。

他的谈话还启发我联想到，如果当我们仰观天空看到亿多形状怪异、厚薄不匀的云彩时，设想采用Jordan量度法去度量它的体积，可以想见那显然是不可能得到精确结果的。而要想从理论上能精确无误地量出其体积，那就必须采用容许“可数无限可加性”（所谓σ-可加性）的Lebesgue测度法。这样看来，人们为了发展无限精度的测量各种点集容积的技艺，Lebesgue测度论的出现也是很自然的事情。

江泽坚告诉我，他听过许先生有关概率统计学的报告。他说许先生讲演的特点是，许能慢条斯理地用不多的言词，阐明事情的要点、关键和概貌。表面看讲话时间不长，但内容信息量还是很多的。我猜想，这也与许先生的古文修养有关，因为中国的古文（或文言文）就体现着意义表述方面的简明、概括和浓缩化的特点。

许先生在西南联大讲过“微分几何”课，我曾听过他两堂课。看来他讲这门课只是一种“任务”，而本人并不感兴趣。上第一堂课时他就坦率地向学生们声明说微分几何只是微分学的一种应用而已，方法技术比较单调乏味。我想这些话肯定会挫伤当时学生们的学习积极性，看来是不符合“教学心理学”原则的。但是他却用不多的语言成功地概述了古典微分几何学的基本思想方法。只要懂得这些思想方法自学微分几何就不难。这也就是为什么当年我只听了两堂课而不再继续听下去的道理。现在回想起来也有些后悔，因为许先生的讲课艺术确实是有很多可学之处的。

（五）

有时候许先生也和我谈到数学史。他认为笛卡尔引进变量概念将形与数对应联系起来而发明解析几何学实是人类数学史上最伟大的事件。从而相对说来，后来牛顿和莱布尼茨发明微积分学就要容易一些。我认为许先生的说法是很有道理的，但猜想分析学家们也未必都会同意这种观点，因为考虑到微积分包含有极限观点。

还有一件鲜为人知的事情是，许先生至少并不欣赏Cantor的无穷集合理论和超穷数论。许先生并没有直接对我说过他不喜欢Cantor集合论，而有关情况都是由王湘浩先生30年前告诉我的。

40年代王湘浩在西南联大讲过“集合论”课程，而我是选修课学生之一。王和江泽坚后来和我又在吉林大学共事二十多年，所以我从他们那里也闻知一些有关许先生在昆明时期的故事。

一个有趣的故事是江泽坚告诉我的。许先生当年在西南联大简陋的教室讲课，往往无法听到上下课的摇铃声，而他又没有手表，于是每次上课时他就将装有一只闹钟的布袋放在讲台上。当上课的学生们第一次忽然听到讲台上布袋里铃声大作，而许先生又笑着说了一声“下课了”时，大家真是惊喜交加。

回到正题，再谈一点许先生的“无限观”以及有关王湘浩先生和他的意见分歧。今日看来，他们的两种观点都不错，只是要看你选取哪一种“无限模式”的问题。归根到底，人们关于无限与无穷集合观点上的基本分歧都表现在对“自然数无限性”的看法上。

大家知道，自古以来“潜无限论者”把自然数序列理解为永远延伸着的序列：1,2,3,…,n,…。在这个序列中，自然数不断被创造，但是永远创造不完的。因此它是一个开放的不能完成的进程，从而不能成为一个整体性的集合（所谓“序集”）。

持此种“潜无限”思想观点的著名数学家有Gauss，Kronecker ，Poincaré，Brouwer，Weyl等。近、现代的数学直觉主义派，即坚持以潜无限观点为基础。

另一方面，“实无限论者”把自然数序列理解为“从延伸到穷竭”的过程，因而形成一个完成了的无穷集合{1,2,3,…,n,…}。Cantor的超穷集合论就是从这里开始的。

赞成“实无限”思想观点的著名人物有Dedekind，Weierstrass，Hilbert，Russell，Gödel等。近、现代的数学公理主义派是认可Cantor的基本贡献的。事实上，现代数学诸分支的理论表述形式大都采用了实无限观点和Cantor所创始的集合论语言。

王湘浩先生和我都是赞赏Cantor集合论的。但据王所说，许先生曾把Cantor的一套实无限思想评议为“唯心论的东西”。王先生当然不同意这种说法，而且还带有一点激情地评议说，“不相信Cantor集合论真理那倒真可能是唯心论了。”

自从60年代A.Robinson创始“非标准分析”以来，人们已经在超实数域*R上作成许多事情。特别，利用*R中的超自然数集*N的部分内容可以构筑自然数序列的“双相无限模型”。这种模型包含着“潜无限”作为其片段，而且还包含有“实无限”作为飞跃段。因此，从“数学模型论”观点来看，只要抓住不同侧面特征来表述自然数的各种无限性，就可以分别有“潜无限模式”、“实无限模式”和“双相无限模式”。这些模式都是彼此独立的但都具有逻辑合理性与形式客观性。这就表明在各种可能的无限观之间并不存在谁对谁错的问题。进而可知，曾于20世纪上半叶彼此争论了数十年的直觉主义派与公理主义派，也并不存在谁对谁错的问题。应该说，各自的理论都没有错，但各自坚持自己认可的“无限模式”而否定同样客观地存在的另外模式，则就造成争论之源了。

同样的分析可以得知，关于王湘浩先生与许先生对待集合论的意见分歧，也不存在对或错的问题。本质上他们的分歧反映了公理主义派与直觉主义派的基本分歧，但他们本人未必意识到这一事实。很遗憾，曾是我大学时代老师的许、王两位先生已先我而逝了。要是他们能活到今天，能同他们一起讨论客观存在的三种无限模式，进而共同认识数学真理不拘一格，那将是多么高兴而愉快的事！

熟知，已为现代计算数学界普遍欢迎的自觉主义派的一条重要原则是“存在即构造”。显然，凡是联系实际应用的统计数学理论也必定是要强调上述原则的。这样说来，许先生之自觉和不自觉地采用自觉主义派的观点立场，也就十分容易理解了。

(六)

关于许先生的个人生活历史我知道的很少。我只知道他在抗日战争年代单身耽在昆明的那段时期的生活是十分艰苦俭朴的。他住一间宿舍，既是卧室又是书房，除了书桌、床铺和一块大黑板外，别无其它大型家具。

他的黑板上有时写些数学之类的题材。有一次我看到黑板上写着一对数论上的Möbius反演公式，那是钟开莱先生的笔迹。我没有问许先生但立即联想到那一定是我的另一位老师华罗庚先生传去的信息。那是1944年左右华先生曾出差去重庆一次为当时的国防部长俞大维解决了一个关于日军军用密码的破密问题。华先生发现密码的转换工具即数论中的Möbius公式（这对我们当时选修数论课程真是一种意外的鼓舞）。华先生回到昆明后信息很快传遍数学系，所以许先生和钟先生讨论Möbius公式想必是出自好奇心的驱动，显然也表明许先生对新鲜事物的关注。

在昆明时期，许先生的衣着也很简朴。他喜欢穿一件风雨衣出外散步。在校园附近漫步时学生们常能看到他的儒雅风度。

据我所知，那时期他的大弟子钟开莱先生（我曾向他学习了概率论）和他的交往较多。钟和许一样也是一位才智出众的人物。他俩出生于历史名城杭州市，都对中国古典文学有深深的爱好和素养，他俩都能写出典雅的中文文章和英文文章，这似乎是一般数学研究工作者所难以企及的。我想，他俩之具有高水准的东西方复合型文化的教养与素质，都是事业成功的重要因素，也是两人间师生友谊经久不衰的原因之一。

熟知40年代前英国著名经济学家Keynes的学说曾盛极一时。Keynes还是一位数学家，出版过论述“概率概念”的专著。在昆明时许、钟二先生还讨论过Keynes著作的翻译问题。看来他俩对Keynes的概率论基本思想都是比较赞赏的。

钟对许先生在统计数学领域的贡献是非常崇敬的。80年代中期，在旅美华裔统计学家郑清水的协助下，曾由德国Springer出版社委托钟主编出版了英文版的《许宝騄选集》。无疑，这是对世界统计数学文库的重要贡献。后来又在钟开莱、郑清水、徐利治联名倡议下，创立了“许宝騄概率统计数学奖”，并且发布了一次奖。但终于由于基金匮乏和人力不济等原因，未能使这项具有深远意义的数学奖顺利地继续运作下去。

1994年春我曾去Stanford大学钟先生家作客三天，谈起了多年前我访问Pittsburgh大学遇见印度著名数学家C. R. Rao的情形。钟说，“Rao是世界一流的统计数学家，而许先生是和他处于同等地位的。”事实上，Rao是印度民族的光荣，而许宝騄是中华民族的骄傲。

许先生一生淡泊明志，为人谦和，热心提携后进。晚年虽在体弱多病条件下，仍不遗余力地为提升我国统计数学事业作出了令人难忘的贡献。无疑，许先生的贡献、成就、学术思想和事业精神将会被后辈们永远纪念和怀念。

 

（2000年3月25日于北京）

  注：作者许利治(1920--)是大连理工大学教授。

 

 

 

 

回忆许宝騄老师

 

――中科院系统所张里千教授访问记

郑忠国 周劬 张松岭

 

   一九九九年四月三日上午，我们叩开了中关园张里千教授的家门，在接下来的两个多小时里，张教授回忆了他所知道的许宝騄先生：

    许先生当然是一位值得纪念的数学家。许先生天资聪颖。先是在燕京大学化学系求学，后转至清华数学系，当时清华的教授有杨武之、熊庆来等。杨武之就是杨振宁的父亲，他是一位家教很严的父亲，有时甚至杖责儿子，听说一度因此而使父子关系紧张。不过，后来杨振宁成为诺贝尔奖得主也许与其家教甚严有关，杨武之教授自认学术声望不算高，但对优秀的学生总是赞许有加，曾作诗书赠先生，首句即为：“许公宝騄，颇有天才”。

    当时清华可算中国数学的一个学术中心，学校当时请了两个著名的外国教授，其中之一便是维纳，清华面向全国办数学培训班，培养了一批教员。当时，杨武之公开承认自己的数学成就、解题能力不及他的学生，但他认为解不出难题的教授也可以培养出杰出的学生，因为老师知道哪些题难，哪些题重要，可以布置给学生去想。许先生等数学家也许正得益于在清华的这些训练，据华罗庚先生后来回忆，当时他们一个班有约40人，这门课老师出了几道难题，他（华罗庚）就上图书馆查题鉴、查参考书，向助教请教，每天晚上开夜车，匆匆忙忙完成才发现当天就要交作业了，每次都以为只有他一人按期交作业并得全分，但发下来的，才发现每次都是四个人，另外三人就是陈省身、许宝騄、柯召，我想，他们的数学底子也许正是通过这一段的竞争，打得比较牢固。

    后来，许先生去英国念书，他的老师就是费歇(Fisher)，费歇也承认许的解题能力强于他。许在30年代做的论文，被一些人士认为他可能是继Fisher之后执掌统计大旗的人，但是许先生身体很差，学术工作不能不受到一些影响。所以，后来成就就稍逊于皮尔逊(Pearson)和耐曼(Neyman)，但仍是世界一流的统计学家。后来，美国发展统计时，就邀请过许先生去美国，从以上不难看到，数学要学好，就要做难题，搞科研才有基础。许先生，华先生都信奉“拳不离手，曲不离口”，他们俩在西南联大时都抢着开课，哪门课自己想补一补就要求开哪门课。

    我敬重许先生，尤其是他提拔后进的作风，可以这么说，是许宝騄造就了钟开莱，若没有许宝騄的提拔，钟开莱恐怕就难以成名。钟开莱在中学时成绩很好，以双百、第一的成绩考进了西南联大，在大学期间成绩也很好，师从华罗庚研究数论。但钟与华都较自负，两人关系不很融洽，华罗庚出的论文题钟觉得不满意，钟就自己找题做。据说他们在讨论数学问题时，都曾拍案而起，互相反问“你有什么了不起？”学位答辩时，结果是全票通过。之后，询问导师的意见，决定他是否留校，华罗庚立即回答“不留”，但许宝騄马上说：“你不留我留”。一般来说，如果一个教授决定不留某一学生，别的教授不便再留，但许先生实在爱惜钟的才华，又知华、钟二人关系不好，结果钟开莱改从许先生。当时，如果不能留校就可能去中学教书，中学教书课比较重，那样钟开莱可能就出不来（成果）了。所以，钟开莱很敬重许先生，《许宝騄全选集》(英文)就是他筹资出版的，还在“Annals of Statistics”上带头写了纪念许先生的文章。

    许先生身体一直不好。在清华时，体重还不到40公斤，他有肺病和胃病，肺病需要加强营养，但因为同时有胃病，营养得不到吸收。许先生体育成绩大概不及格。许先生在北卡罗莱纳大学开创了统计系之后，肺病复发了，他于47年底回北大数学系任教，次年初曾开设《矩阵论》。许先生回国可能也为了结婚，后来同女朋友散步时受了凉，肺病又犯了。50年前后，他主动与女友提出分手说“我不耽误你了”。由于种种原因，许先生终身未婚。

    我是47年考入北大数学系的，决定报考北大也是慕许宝騄的名。当时的说法是北大文科强、清华理工好，但在南京的张素诚老师写信劝我报考北大，说清华虽有陈省身，华罗庚这样的教授，但他们长期不在国内，现在北大已有了不少好教授，并且许宝騄，很快就要回北大任教了。于是我进了北大数学系，那时系主任是江泽涵先生，他比许先生高一辈，不过，他却十分尊重许先生。高年级的学生也很尊敬许先生，我们低年级的学生看在眼里，知道许先生声望很高，更觉得应该尊敬他。在大一下学期，我就很想听许先生的《矩阵论》，但因为大一课程太紧，而且当时兼任学生自治会理事，挤不出时间而没能去。

    我在大四选了许先生的《实变函数》课，这个时候，许先生身体恢复得很好，比起其他的数学家来，许先生有一个更突出的特点是：善整理笔记。他的授课笔记可以说是国内最拔尖的，也属世界一流。在讲述一个命题时，他把这个命题的种种重要条件整理到一起，转着圈子论证一遍，给我们留下了很深的印象。许先生的很多授课笔记，如《矩阵论》《实变函数》《弱极限理论》《抽样论》《点集拓扑》都堪称典范。他讲课也很高明，但还不能说是最好的。许先生讲课内容很透彻，没有什么漏洞，因此启发性略显不足。相比之下，华罗庚的讲课相对粗糙，却更具启发性。

    我毕业时是第一次100％全国统一分配，我想申请做北大研究生，后几经周折，去了科学院数学所（筹建中）。大四做论文时，很想受许先生的指导，因为进校就是慕许名而来。但因为江泽涵教授的拓扑方向仅我一人选课，自然由他来指导我了。许先生指导汪掬方。解放后许先生的第一个研究生，应是赵仲哲，他是1948年入校读研究生，我不算是许先生解放后的第一个学生。

    去了数学所后，我与许先生就只有业余的师生关系了。当时数学所是王寿仁搞概率论，我搞数理统计，许是科学院的学部委员，因此我仍受许先生的指导。许先生身体不太好，我们便隔一段时间去看望他，他社会关系不少，于是我们也告知他一些社会上的事情。他身体较好时，就在家里开讨论班，这对我们初学（统计）者受益很大。近代数学比较抽象，没有人带就会感觉吃力，不好学。在54、55年我做的论文，一些错误自己往往看不出来，但经许先生一指点，往往恍然大悟。其中有两篇论文，起初以为自己做对了，在许先生家做报告，讲着讲着卡住了，发现有问题，当时没有解决。回来后我开夜车，举反例发现结论错了，再过一段时间就把全部解求出来了。这时，许先生用矩阵方法也得到了同样的结果。当时，我提出与许先生联名发表，但他在署名权上很谦让，多次拒绝了我的提议，只建议在论文末尾注明作者借此机会指出，许宝騄教授通过矩阵方程的求解，得到与文中同样的结果。（《科学记录》新辑第4卷，第1期，1960年，第14页），以后这一成果被引用时，都被称为“Chang-Graph”，而不是“Hsu-Chang-Graph”，这也是许先生建议的结果。当时，刚做论文时，英文提要是许先生帮忙改的，许先生说：“刚开始写文章，我要帮着改一改，以后我就不改了”。

    56年开始，许先生在北大面向全国开讨论班，发展国内统计事业，我在第一年开设了《初等概率论》，第二年开设了《数理统计》，当时王寿仁，赵仲哲，郑曾同也开设了相关课程，许宝騄先生当时的思想顾虑是身体，但让他休养，他又觉得闲不住。

文革时，张景昭老师去世后，我们就估计许先生恐怕不行了。尽管相对于他的声望，他所受冲击算小的，但他身体很差经受不住。我们虽然担心许先生，但也不敢去探望许先生，心里感觉对不起许老师。

 

(编者注：本文作者郑忠国(1938--)是北京大学教授，周劬和张岭松北大学生

          

 

 

学精德馨  泽被后人

――回忆许先生及其主持的三次讨论班

 

成    平

中国科学院研究员

 

五六十年代，我曾有幸参加了许先生主持的三个概率统计方面的讨论班，我之所以能在数理统计的科研道路上取得一些成绩，全赖以那时候打下的扎实基础，而且先生的为学为师之道，使我受益匪浅。

记得第一个讨论班是弱极限理论讨论班。那是54年，我刚大学毕业，很荣幸随同王寿仁、张里千教授一同到许先生家里参加了这个由他主讲的讨论班，当时参加的还有江泽培、赵仲哲先生等人。我当时是最年轻的一个，受到了许先生特别的照顾，先生指定我坐在他家唯一一把最好的转椅上，而且只许我坐，可见他对年轻人的爱护。讨论班休息时，许先生热情的用糕点招待大家，正是因为许先生的这种关怀、爱护，讨论班成了一个很和睦的集体。当时我们数学所的三位同志，除了听许先生主讲外，回到所里，我和张里千教授还要当场抽签重讲一次，所以弱极限理论给我留下了极深的印象。确实，那些知识在我以后的科研中多次用到。许先生讲课从来不看讲稿，而是一面讲一面写黑板，条理非常清楚。当时的笔记我保留至今，80年代初，我特别整理油印了几十份。许先生对讲稿是精益求精的，除了54－55年讲过一次，后来又讲过一次，比前一次更精炼了。可惜当时弱极限理论由于柯尔莫柯洛夫和格涅坚科出版了一本同样内容的书，许先生的讲稿未能出版，但我至今仍记得有一个提法是所有弱极限理论书上没有的，就是“冒牌无穷可分律”，无穷可分律特征函数（记为I.D.），一种表达形式是：

ψ为（－∞，∞）上的测度，记为（a, ψ）。许先生提出允许ψ是符号测度又会如何？仍保持唯一  ，若（a1, ψ1）＝（a2, ψ2），则a1＝a2，ψ1＝ψ2，而且可能是特征函数，但当ψ不是测度，上述f(u)就不是I.D.，称为冒牌I.D.，这由上述唯一性所确定，例如

所对应的分布是p(X=-1)=，P（X=n）=证明上述f(u)是特征函数，但同时：

若取，,可见f(u)是冒牌I.D.，但是I.D.，可见两个非I.D.之积可以是I.D.，并指出凡二点分布是不可分的，它也是冒牌I.D.。

听完两次许先生讲的弱极限理论之后，我也曾对它很感兴趣，试图做一点工作，用许先生“特征函数展开式与矩的关系”一文，得到了I.D.，α>0阶矩有限的必要与充分条件，但当时自己判断水平不行，也未发表，可惜也未请教许先生，到80年代初。从Petrov书上的习题里才知道1969年国际上才发表此结果。

第二个讨论班是Doob随机过程讨论班。那时根据国家十二年远景规划，国家把中山大学郑曾同、梁之舜教授及一些教师调到北大，共同培养由北大、南开、中山大学调集的同学，同时许先生也招了几位研究生，有殷涌泉、梁文棋，邓伟才等，复旦郑绍濂这时刚好在数学所进修，张尧庭毕业也在北大参加了工作，队伍比较大，这时许先生开始了Doob讨论班，上面参加了弱极限讨论班的成员除了江泽培外都参加了，江先生是因为出国留学没有参加，讨论班形式也有所变化，不全是由许先生讲，赵先生、郑绍濂等人都讲过，许先生讲的是supplement的补充，指出附录主要讲可测转变论和表示论，还布署哪些章节讲，哪些章节不讲，许先生着重讲了表示论的改造及可测转换，给了这个supplement以评价，指出哪些精彩哪些可以改进，使听讲人收益很大。讨论班仍然是在许先生家里进行的，只是没有多长时间就停了下来，那时因为接待波兰专家Fisz来我国讲学，许先生就介绍Fisz在杂志上发表的几篇文章，后来Fisz来时在数学所讲了“不变理论”，介绍苏联学者的工作，这个理论当时刚起步，后来发展成为经验过程的一个很重要的工具，可惜由于反右运动，没有人坚持下来，播下的种子没有发芽。许先生因身体不好也未参与此项活动。

第三个讨论班是次序统计讨论班。62年，我从波兰留学回来，不久许先生主持了次序统计讨论班，参加者除张尧庭、孙山泽几位教师外，主要成员就是当时北大概率统计专业的63年毕业学生，这个讨论班也是由许先生在自己家里讲的，我也参加了，可惜我当时感兴趣的是判决函数，只是听，没有深入做工作，为此许先生让我在讨论班介绍了判决函数，但讨论班是出了成果的，由吴传义解决了极值统计极限分布的三个分类问题（当时苏联也有学者同时解决了），后来以“班成”名义发表的“多个次序量的联合极限分布”（收集在许先生文集里）就是当时的成果，程士宏教授是作者之一，至今仍从事次序统计研究工作，也是从那时打下根底开始的，当时，许先生有一个计划，就是把这班同学中强的留在北京，讨论班继续下去，我与张尧庭商量，经许先生、段先生同意，把程士宏、吴传义分配到我所工作，但最后只有吴传义来了，程士宏留在北大。讨论班由于当时的运动未能如意举行，但这班同学不少成为概率统计界的骨干。一件事如果能坚持数年，必然能出人才、出成果。特别有许先生这样高水平的世界级专家指导，定有出色人才和成果出现，可惜后来由于“四清运动”，“文化大革命”一搞十年多，一切科研停止了。许先生在文革的摧残下离开了人世，这是我国概率统计界的最大损失。

先生虽然离我们去了，但先生那和蔼可亲、博大精深的为学为师之道永远是我们学习的榜样。

 

（1999年3月）

   编者注：本文作者成平(1932--)是中国科学院系统科学研究所研究员。

 

                                                             

 

 

 

 

深深的怀念

――我所知道的许宝騄先生

 

张尧庭

上海大学教授

 

   今年是许宝騄先生诞生80周年、逝世20周年。他一生感人的事迹甚多，印象最深的两点是：对科学事业的执着追求；对学生的真切关心。在他的身上，很好体现了中国传统文化中宝贵的精神财富。我有幸在他身边学习、工作了10年左右，亲眼目睹了不少事情，以前在某些场合也作过介绍，不少人要我写下来发表，自己总还想多收集一些，作个完整的介绍。然而我自己已将近60岁了，记忆力日益衰退，如再不写，将来可能连零碎的片断也没有了。我写这篇长文是想使他的品格能感染后代的人，这也许是对他最好的纪念。

1.虚弱的身体、顽强的意志

我是1955年认识许先生的，第一次见到他是他来给我们班上“概率论”的课。记得第一堂课还没开始，教室里坐满了人，其中相当一部份还是从外校赶来的，有的年龄也不小了，只听说许先生课讲得非常好，概率论的课还是第一次开，所以听众很多。上课铃响后，许先生进来了，手里提一个小的草包，里面放着自备的黑板擦、一个小暖瓶和一只杯子。我心想，大教授上课还带自己的黑板擦，和别的教师就是不一样。讲课开始了，声音不大，但很清楚，一堂课下来，说真的，当时并没有感到他讲课的特别之处。每次擦黑板时，看他额上沁出颗颗汗珠，这时才体会到他的身体的差，为什么他要自己带特制的轻巧的黑板擦。讲了三次课后，他因身体不行，就不再上了，这样课由赵仲哲先生一直讲到完。自那以后，许先生再也没有在教室中上过课，我们这一班同学是听他在教室中上课的最后一班学生。

许先生身高1米76，但体重只有70斤，每天主食只吃2两或3两，靠一磅半牛奶维持所需的营养。当时的学生，体育锻炼都应通过劳卫制，否则不予毕业，他笑着对我说：“我也要通过劳卫制，因为我有痨病（肺结核）、胃病和痔疮。”从我认识他起，他大部份的时间是在床上过的，念书和写作时，面前放一硬纸板，背靠着软的靠垫，在床上工作。吃饭和参加讨论班时，下来坐在沙发上，尽管这样，他每天都工作六个小时以上。文革后期，工宣队交给他一个任务，校对几十万字的一本俄文书，那时他已瘫痪了，他问工人师傅，这需要多久完成？师傅告诉他，最好在一个月内完成，他回答说：“我只要十天。”实际上他只用了九天多一点时间就完成了。在那种条件下，他这样顽强地工作，平时也就可想而知了。

许先生在生活上很少提什么要求，1957年他肺结核发展时，组织上安排他去国外或国内一些地方去疗养，他都婉言拒绝了，就在离北京大学很近的黑山扈疗养院住了几个月，他希望能经常了解校内的情况。1963年，X光检查发现他肺上有空洞，并且他带的菌具有抗药性时，组织上安排他去疗养，他又拒绝了。他对我说：“我知道时间不多了，我再带你们去闯一个新方向，好让你们知道新方向该怎么闯。”从那时起，他一个人领导了三个讨论班：数理统计、马氏过程、平稳过程，他给三个讨论班分别取了笔名：班成、班果、班绩，希望这三个讨论班能有成绩，能有成果。可惜这三个讨论班进行不久，北京大学就开始社会主义教育运动，中央派来了工作组，讨论班就只能中途停止了。讨论班是停了，然而他的这种坚韧不拔的顽强意志给我留下了深刻的印象。

早在40年代，还是在昆明西南联大执教期间，当时杂志和书都是很缺的，我在许先生的书架上就见到他那时候手抄的梯其玛希写的函数论一书，那时他致力于相互独立随机变量之和的极限律型的研究，得到了一系列的结果，由于消息闭塞，大部分的结果由柯莫廓洛夫和格涅坚科都已发表了，他并不知道，然而方法是不同的。这一材料在他生前没有刊印过，在他去世后的第一年，由钟开莱先生翻成英文的、柯氏和格涅坚科合著的书《相互独立随机变量之和的极限分布》中作为附录出版了。此外，他还写了一些统计方面很有价值的论文。耐曼传中这样写道：“许宝騄在某处一个地窖里从事科学研究。他的工作居然能够印出来，简直是一个奇迹。”他对科学研究怀有极大的热情，文化大革命中期，他已满头白发，瘫在床上，然而他仍然在研究组合数学中的问题，有一位工人师傅说：“许宝騄整天在床上画0，1，不知道是干什么”，因为他在文革开始前，领导了一个组合数学的讨论班，想把矩阵方法系统地用于组合数学，组合设计的结合阵和设计阵都是0，1阵，可见在文革中，他也没有停止研究。他的最后一篇手稿，是在临终前交给段学复先生的，就是BIB设计与编码的关系。他哥哥许宝骙先生回忆说：“当我知道宝騄去世的消息后，赶到北大时，只见他床头边放着未完成的手稿，和一支铔去了Parker标记的金笔。”他的一生和研究工作是分不开的，他的生命就是研究学问，科学研究就是他的生命。

60年代初，他对我谈起他自己的希望，他说：“30年代末期，我在英国留学，当时有三个中国人在那里学统计，日本也有三个人在那里学，可是我们三个中国人（许、唐培经、徐钟济）比日本人强多了。那时日本已侵略中国，我们想，在统计、概率方面，我们将来回国之后一定把它搞好，超过日本人，当时很有信心。”我感到他的这个想法一直是指导他的行动的准则。快解放时，他急于回国，其中就有想回来后好好干一番科学事业的愿望。即使到了文革时期，他已病在床上，还对探望他的亲友说：“我身体不行了，不能动了，但我的头脑还是很清楚的，我还可以用脑子为祖国服务。”可见他念念不忘的还是想尽自己的力量，振兴国家的科学事业。

2.认真治学、勤奋工作

许宝騄先生治学是严谨的、认真的。他比一般的人要认真很多。有几件事我印象是特别深。我跟他念测度论时，我整理的读书笔记他拿去逐字逐句地改，不仅对标点符号有严格的要求，就是简化字，报纸上没有公布的，他也要给我改正。做的习题，不仅批改对与不对，还要指出这个题解的方法好或不好，对不好的，批示给出另外更好的方法。他要求我们谈一个材料，必须非常认真。我刚跟他念费勒的《概率论及其应用》第一卷时，在读了第十三章后，他就问我有没有发现问题，是否注意到循环事件的定义有问题？当时我是快大学毕业的学生了，数学已学了很多年，还从来没有想过书上的定义会有问题，我认为定义就是定义，谁愿意怎么规定就可以定义，只要不自相矛盾就行了，特别象费勒这样的大专家，他写的书，定义还会有问题，似乎是难以想象的。许先生就告诉我，书上的定义为什么不妥，应该如何修改。隔了一年，费勒的书出英文的修订版了，新书拿过时，我翻到第十三章，循环事件的定义真的改了，而且和许先生说的是一样的。这一件事大大地教育了我，我以后念书时对新的概念特别注意它的定义是否合适。

许先生的认真还给我很深的印象是关于做练习。我认识他不久，有一次去他家里，他正与赵仲哲先生在讨论那汤松《实变函数论》书上的习题。我当时刚念完实变这门课，知道这本书的习题不好做，偶而做一到二个，还留下相当的部分没有做，想不到像许这样有名的教授还在做这本书的习题。后来接触多了，知道他看书有一个习惯，就是每一个练习都是认真做的。他对我说：“如果这个题很容易做，那不费什么，很快就可以做了；如果这个题不容易做，那正说明你应该做这个题目。”三年困难时期，他整理了一次留存的材料，曾给我看一个练习本，上面全是他在40年代做的代数的练习题，我后来带的学生的毕业论文，用有限域上的矩阵来构造PBIB设计，其中一个有效的计数方法，就是从这练习本上一个解题方法中获得的，可惜的是这份材料在文革中连我整理的有关线性代数的笔记一起丢失了。我目前保存的两本他读过的书（T.W.Anderson的多元统计分析和U.Grenander和M.Rosenblatt的平稳时间序列的统计分析）上还留有他做的习题的手迹和批注。正因为他做过了大量的练习和问题，他在阅读论文时有一种习惯，看此文研讨的问题和结论，自己去思考如何导出这些结论，不少场合，他用的方法和论文作者的是迥然不同。他对我们读书也是这样要求，看清楚了一条定理的条件和结论后，应自己去设法证明，写出来与书上的进行比较，看哪些是书上的好，什么地方是自己的好，弄清原因，然后再整理，这样才能真正吸收书上的内容。这样做当然很费功夫，没有勤奋好学的毅力，是很难坚持的。

许先生讲课条理非常清晰，把问题处理得干净、漂亮，十分简洁。从我跟他学习开始听了他多次的讲课，还没听到一次有一条定理的证明在一堂课内没有讲完的。我们举行的讨论班，大家报告了很多次，有的证明很长，但是，他只需几次课进行总结，就把我们所述内容都包括了，并且处理的方法既统一又简短，这是与他认真治学，追求问题的彻底密切相关。在讨论班上，我们都有体会，一个人在上面报告，大家听着都觉得很明白，忽然许先生说他听不懂。这时并不是许先生真的不理解所说的内容；而是讲的人在讲法或黑板的写法上有了弊病，使人会产生混淆，或者有错误。在这种时候，大家都会认真去思考刚才讲的人是否有什么毛病，指出毛病的所在，得到许先生的赞同，然后才能继续下去。相当多数的场合是大家看不出来，经许先生一点，恍然大悟。所以在讨论班上，报告人最怕的是许先生说他听不懂，这往往意味着有问题，许所以能发现大家一般不能发现的问题，也就与他平时认真仔细的处理每一个步骤的习惯有关。

他治学严谨、一丝不苟的态度还表现在他运用别人的工作上。他曾对我说过，他一生中只引用了一个关于曲面积分的定理，是自己没有证明过的。任何其他的工具，只要是他用来解决问题的，他必须自己把它弄明白。我跟随他10年左右，他读过的书几乎都被他找出各种大大小小的错。我刚跟他念书时，他对我说：“你念一本书，就要故意和作者作对，尽量去挑书上的毛病，不要认为写书的人是大专家，不会有错，很难找到一本一点错也没有的书。”这实际上是教我怎样认真念书的一个方法。几十年来的实践使我认识到这是非常重要的起点。古人云：尽信书不如无书。在科学研究的道路上，必须有一种认真、踏实的批判精神，才可能有创新的见解和独到的方法。当然，他并不是只强调批判的一面，他是很强调继承的。他的研究工作都是阅读了这一专题的大量文献，比较消化之后，在这个基础上再往前推进一步。他一再强调，研究是消化整理的自然的后继。换句话说，没有消化整理，谈不上什么研究。他说：“一个好的讨论班，好象是一个酒缸，时间越长，酒就越香，一个人在这种讨论班里去耽一阵子，他就会散发出酒的香味来。”这是生动的比喻，充分强调了继承传统的必要性和它的优点。回想在北大学习、教书的时期，凡是在许先生主持的讨论班耽过的人，那一个没有受到感染？可惜的是讨论班时起时落，到文革时就完全冲垮了。现在再要维持一个高质量的讨论班，是多么的不易啊？！

他在世时，一再告戒我们，必需认真下功夫钻研学问，切不可买空卖空。对于我们教学的态度，他也十分认真。我记得在1962年，他把我教测度论课的这一班学生的笔记全部收了，化了几天的时间，都看了一遍。他对我说：“看来，你能传热了。”这是自1955年以来，从跟他学习的第一天起，第一次听到一句带有表扬的话，以前经常听到的是批评。当时的心情是很激动的。然而，他告诉我：“要做一个好的教师，很不容易，必需自己有相当的根底，才能讲好。应该做到以十当一，自己会十，但讲出来的是一，而现在有些教师是以一当十，这怎么教得好呢？”他又说：“一个教师在台上讲课，就象一个举重运动员，应该是举重若轻，很重的东西，一下就举起来了，让人看了，感到非常舒服，而不应该是举轻若重，一个很轻的份量，举也举不起，两腿颤抖，让人感到难受。”他在讨论班上，也是这样强调的，要求报告的人把所看过的材料消化好了，然后再讲。要把论文中非常难懂的部分弄明白，搞清作者的想法和思路，总结归纳出作者使用的概念和工具，把问题处理得很自然，这样才是真心念懂了。用他常用的话来表示，就是“化神奇为腐朽”，把难以想象巧妙的思想变成十分浅显明白的道理。在这一方面可以说，他每一次讲课都是示范性的，所以他的课具有很强的吸引力，我到后来才能真心体会到他的功夫。这样的功夫是化了多少心血和劳动才能得到呢？真令人感到折服。

他很欣赏华罗庚先生对学生常说的念书方法，读一本书要经过变厚再变薄的几个阶段。第一个阶段要变厚，就是要补充书上未详细给的、甚至未给的证明；找出书上的错误给以更正；自己想到的内容，给以补充……等等，这样念完了一本书，这本书就变厚了。第二个阶段是由厚再变薄。这就是要把书中的关系、推理的关键步骤和基本方法提炼出来，掌握了这些，全书的内容都了然如指。这第二阶段是不容易的，这实际上是要从感性的认识上升为理性的认识。没有这第二阶段，就不易进入研究的领域。许先生自己在这一方面是做得相当好的，他死后由北京大学出版社出版的《抽样论》，就是一个很好的例子。这是1960年讨论班念科克伦的《抽样技术》一书，最后许先生作了一个总结，这个总结用很少的篇幅，概括和证明了科克伦全书的内容。

在培养教育学生上，他也是非常认真，从不吝惜自己的时间和精力。且不说前面我提到过的批改作业、听学生讲读过的论文等一般老师还可以理解的事，他的认真还在于有些是一般教师难以想象的事。1959年他招收了潘捷建（潘已于1978年5月去世）为研究生，潘是青年社会主义建设积极分子，由组织推荐的，但是潘的基础较差，尤其是外语。潘在研究生毕业时，他的毕业论文被译成英文在日本刊印出版了。为了让潘能阅读外文资料，许先生亲身教潘的专业英语，每周留出一定的时间，两个面对面逐字逐句的讲授，这样，潘在两年不到的时间内英语阅读能力就很快得到提高。他对参加讨论班的每个成员都相当关心，如果有一个成员在几次讨论中均未发言、或在讨论班上反应迟钝，他都要我去了解情况，是什么原因？有什么困难。他逝世后，1980年在纪念许诞生70周年的大会上，许宝骙先生，他的胞兄，回忆道：“60年代的一个暑假，宝騄回家住几天和家人相聚，他说：我自己现在好像是老牛拉破车，走的是上坡路，很吃力，但是我还是要尽自己的力量拉着向前走。”这是多么感人的肺腑之言。

他自己一生发表的论文，篇数并不算多，总数不超过40。他对自己的工作要求很严，一个问题在他的手中没有彻底解决好，他往往不肯放手。他对科研工作的评价有他自己的标准，给我印象最深的是下面两段话：

“一篇文章的价值不是在它表发的时候得到了承认，而是在后来不断被人引用的时候才得到证实。”

“我不希望自己的文章登在有名的杂志上因而出了名；我希望一本杂志因为刊登了我的文章而出名。”

这对自己的研究工作是以什么样的标准来要求的，不是可以看得很清楚了吗？一些别人认为不错的工作，在他看来是不算什么的，他就从不发表。例如，正态变量二次型遵从x2分布的充要条件，在正态变量的协差阵Σ正定时，早已解决了，然而当Σ是半正定阵时，这一条件在1962年的讨论班上，许先生是由一条定理作为推论导出的，而到1966年在国外的杂志上才刊印这一结果作为论文发表。他平时看文章、看书时随手解决的问题，都批注在书上，可惜的是这些材料都未能保存下来。我印象中他逝世后，他的杂志和书籍是想留给当时北京大学数学力学系的系图书馆，由于他患有抗药性的肺结核，图书馆怕结核菌会传染，而拒收这些资料，后来全部作为旧书卖掉了，那时正在文革期间，谁都无法保留，现在回想起来，这是很可惜的。

他很想办一个概率统计的杂志，目的是可以让一大批年青的人有发表作品的地方，让世界上其他国家的同行了解到我们中国的工作。他愿意拿出他的积蓄来创办一个杂志。后来由于文化大革命，这事也就成了泡影。文革以后，在改革开放政策的鼓舞下，终于办成了这样的杂志，而且现在还不止一个；目前国际性的学术交流活动也有一定的规模，这些成绩的取得，与许先生生前的努力是分不开的。1983年冬天，我访问威斯康星大学统计系时，系里年龄最大的教授盖兰，他要求系主任一定安排出一段时间让我能与他个别谈谈。他告诉我他是P.L.许的学生，那时许在伯克莱大学执教，他很高兴留他作为助教，许对他的帮助和信任使他终身难忘。许宝騄先生在美国的几所有名的大学，都教过一些学生，伯克莱、哥伦比亚和北卡罗莱纳等大学都有他的影响。斯坦福大学的统计系走廊中，悬挂着许的画象。他的教学和科研，给世界上的统计界人士留下了一份宝贵的遗产。一些听过他讲课的美国著名学者，都一致赞许他的讲课是“无与伦比的”，有的说：“我在后来再也没有听到象他那样讲得清晰的课了，听他的课真是一种享受。”许在40年代教学的影响，在美国是明显的，这与他辛勤的工作是分不开的。

3.敏锐的眼光、求实的精神

和他接触过的人都会感到他的看法往往和一般的人不同，这与他具有广博的学识与深邃的洞察力有关。他在分析问题时，很强调要有一种“内视(insight)”的能力。他说：“数学中的抽象能力是重要的，一些问题经过抽象之后，不仅问题简明了，而且它的实质也更清楚了。”所以他在教学和科研中常常用实例来教育我们，应如何进行抽象的训练。这就是要求我们经常分析和比较，能把表面上看起来似乎是不相干的内容，经抽象后看出来实质上是一样的。在这一点上，他的两项工作可以给我们作为范例。第一项工作是他在1938年发表的工作2，他注意到线性模型中期望值μ的估计是观察值y的线性函数，方差σ2的估计是y的二次型，而实际上二次型也可以看成是某一向量的线性函数，这样就可以用处理μ的线性估计的办法来处理σ2的估计，从而获得了σ2二次估计具有极小方差的充分条件。如果用n×1的向量y表示观察值，利用矩阵迹的运算规则，就有

y′Ay=trAyy′

而trAB′实际上是矩阵A与B对应的元素相乘后全部相加，它是把矩阵看成向量时的欧氏空间的内积，因此y′Ay就是A与yy′的内积，它是向量yy′的线性函数。这一方法在70年代末期被发展为处理方差分量估计的一种重要手段。另一项工作是在60年代初期实验设计讨论班上他报告的内容。当时张里千用组合数学的方法证明了三角方案的唯一性和不唯一性的特款的全部解，从而彻底地解决了有关三角方案唯一性的问题。许对这一类问题产生了兴趣，经他的研究，发现结合矩阵的特征根的重数必定是整数这一条件十分重要，许多结合方案类都在重数v=2的这一类之内，如格子方案，三角方案等，而这一类方案的存在与唯一性问题都与结合阵中是否含有一个特殊的四阶的子阵有关，这一发现，使得这一类v=2的存在与唯一性问题得到了彻底的解决。

    许先生经常告诫我们，要进行比较，不同的处理方法的优缺点是什么，有些为什么要这样做而不那样做，只有经过认真的比较，才会真正体会前人工作的精妙之处，他还常常用自己亲身的体会来教育我们。记得在1962年关于正态变量二次型的讨论班上，他要我们报告冯·诺依曼关于时间序列循环相关系数精确分布的论文。他说在40年代，他也考虑了这个问题，但是解决不了，因为一个特定矩阵的特征值很难求，而诺依曼却把特征值和特征向量放在一起来求，这样问题反而解决了，所以从这里他学到了新的东西。他的确是经常剖析自己，那些不行，那些应该学习，几十年来，他一直能站在科研的前线，带领一些人去赶上世界的学术潮流，这与他敏锐的眼光是分不开的。他的研究工作有一明显的特点，就是在方法上往往是与别人很不相同，富有新意。他用的方法比较自然、易懂，而且推理清晰、简单。我体会这与他对数学研究工作的要求有关。他自己是什么主义的数学家，从未正面谈论过，然而从他的研究工作和对自己的要求来看，我认为他是倾向于直觉主义的。例如他不用超限归纳法，他只用可数的对角线的选择公理，他追求构造性的证明，他要求证明能演算化。为了说明他的这种看法是行的，他在1963－1964年间，专门给我们讲了点集拓扑的课。点集拓扑一般都认为是难以用算式来表示和证明的，他却都是用演算来证的，可惜的是由于社教运动就中断了，未能留下一个完整的材料，我相信他是已经完全处理好了，应有象《抽象论》这样的一本小册子。可后来在整理他遗留的手稿和其他材料时，没有发现这一部分的材料。我根据自己听课的笔记，整理后发表在1980年武汉大学学报纪念许宝騄先生的专刊上。为什么要证明能够演算化，他认为这是避免出错的最好的途径。因为演算对不对，人人都可以检查，如果证明是靠说明来完成的，不同的说法要弄清楚是否一样还并不容易，说明时容易隐藏着错误而看不出来。当然，从现在的眼光来看，证明能演算化，这与使用计算机来搞数学的研究有密切的联系，实际上也是数学研究中的一个重要的方向。

许宝騄先生的演算技巧很高明，他能把非常复杂而难以处理的计算弄得清晰易懂，这与他追求构造性、初等方法的证明有关。在这一方面的工作可以用他在1939年的关于协方差矩阵特征根的联合分布的工作来说明4。一个矩阵的特征根一定是这一矩阵的系数的连续函数，然而要把这个函数形式用普通的运算表示出来是不行的。但在多元统计分析中，这是一项基础性的工作，因为一系列统计问题都归结协方差阵的特征根的分布，如何导出特征根的联合分布就成为当时的一些名家关注的中心课题。就在1939年前后，有四个人同时得到了多元正态分布样本协方差矩阵特征根的联合分布，费歇，劳埃(Roy)，莫特(Mood)和许用不同的方法均导出了精确分布，以许的方法最为清晰、易懂，实际上是大量的矩阵微分的演算，目前各种教材中采用的讲法，大都是在此基础上演变而成的。这一方法后来在40年代中期，许在北卡罗莱纳讲多元统计分析时，系统地讲授了这一方法，用它导出了一些相当复杂的雅可比行列式的表达式，这一内容由奥肯(Olkin)等人整理发表，成为这一方面的一份教材5。

他的敏感的眼光是他长期在科研前线从事辛勤劳动的结果，他的研究工作始终是与那时的重大课题相联系的。30年代末期，正是纳曼――皮尔逊理论的开创时期，当时的中心课题是要解决假设检验中零假设不成立时拒绝的概率，即求出功效函数的表达式。这就涉及到统计量的非中心分布以及一类极值问题。许在这一方面一开始就有出色的工作：求出了T2的非中心分布6，第一次证明了F检验的优良性7。这两项工作是为纳曼的理论奠定了两块基石，很快就引起重视。30年代末期、40年代初也正是多元统计分析形成自己系统的时期，许引入了矩阵的技巧，解决了许多难以理清的问题，例如有重根时，重数不同的最一般情形下协方差阵特征根的极限分布，很一般的样本均值函数的极限分布，……等等，这是他的工作最多、最出色的时期。解放以前，在西南联大时，他埋头于独立和的极限律型的研究，这也是当时的中心课题。解放以后，经过第一次全国科学规划，大大调动了他的积极性，他看准了极限定理、不变原理等重要的工作，马氏链的分析方法，但因为一些政治运动和其他原因，只能半途停顿了。1958年大跃进以后，他认识到数理统计在实际工作中很能起作用，决心带一批人闯一下，先后在实验设计、次序统计量的极限分布，二次型与二次型之比的精确分布，过程统计等多方面带领青年人搞讨论班。他在60年代初期，就注意到了指数分布的假设检验问题，后来就成可靠性统计分析的重要基础。他认为不了解世界上这一方向的动态，就很难找到有意义的重要方向。他曾经生动地用儒林外史中的语言来描述这种能力。儒林外史中说到有一个瞎子，不用看文章，只要把文章在他面前用火一烧，他就能从气味闻出是好文章还是臭文章。在科学研究中，要有这种嗅觉，要训练这种能力。

他对于发表文章要求是严的，他自己为我们树立了一个榜样。他认为一篇文章不在于它的长短（顺便说一句，他的论文最长的有五十页，最短的只有一页多一点，是举一个反例。），而在于是否真正有内容。他不希望我们稍有一些结果就满足于此，而急于发表，应力求把问题做到底，敢于去碰难处，要知难而进。对写文章的要求是不要罗嗦，而要把关键之处交待得明明白白，他很不欣赏那种在关键之处一带而过，写“显然”两字的那种文风。他告诉我们：“良工示人以朴。”要把自己的想法、技巧都告诉别人，以便交流。用他的标准来看一些发表过的论文，就会感到有很大的不同，我深感自己能力很差，自己写的东西是水平不高的，并没有做到“底”就发表了，真是愧对老师。

许宝騄先生对于自己的工作从无溢美之词，往往是把自己的工作和后来的人改进的工作相提，并说明自己的不足和别人改进的原因。在学术上实事求是，不涉及个人的好恶，对学术负责。我记得在1964年他发表《一个不是L3方案的M3结合方案，其S=6》一文后，他说自己是做了一项“家庭妇女的工作”，表示这项工作只要有耐心，按部就班地去做，一定会有结果，不需要动很多脑筋。当他得知张里千解决了三角方案唯一性的问题时，他立即推荐张的论文在《科学记录》上发表。在他生命的最后阶段，他也没有放弃过研究，他全力注意于组合设计的问题，一心想在这一方面，系统地引入矩阵的方法，给出漂亮的处理，遗憾的是，他没有完成这项工作就离开我们了。

许宝騄先生把数学家分成三流，他说：“第一流的数学家，是有天才的，他们能开闯新的领域，如柯尔莫廓洛夫，冯·诺依曼，维纳这一类人，这些人是可望而不可及的。第二流数学家是靠刻苦学习而成的，认真消化整理前人的东西，在这个基础上有所创造发现，象欣钦这样的数学家就是这一类的，他写的《公用事业理论的数学方法》、《信息论基础》等就是消化整理的结果。这种工作对后人影响较大，年青人可以在这个基础上较快地进入科学的前沿，中国缺少一批做这一类工作的人。第三流的数学家只在某一、二个问题上有一点贡献，不能象第二流的那样有系统的工作。剩下的就是不入流的数学家了。”他认为自己没有才能，是刻苦学习得到的，他也没有经验去培养有天才的人，他只能传授如何认真学习，努力钻研，埋头苦干的经验。他衷心希望他的学生超过他，一次他在讨论班上说：“自古以来，只有做状元的老师是光荣的，做状元的学生是没有什么的。”他对新的一代寄于殷切的希望。

许宝騄先生已经去世20年了，他的言行已化为无形的力量，鼓舞着一代又一代的新人，为中国的科学事业去努力奋斗。

 

<参考文献>

 

[1]    许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   550－566。

[2] 许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   55－68。

[3] 许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   484－489。

[5]   许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   82－90。

[6]   许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   567－589。

[7]   许宝騄。许宝騄选集（英文版）.Springer出版社，1983；

   69－81。

[26] 许宝騄。许宝騄选集（英文版）.Springer出版社，1983；150－157。

                               (写于1990年)

 

 

往事杂忆

陈希孺

中国科学院院士, 中国科技大学研究生院教授

                              

我在大学学习期间孤陋寡闻，对当时数学界名人知之甚少，在这 “甚少” 的当中，有许宝騄教授，这纯出于一个偶然的机缘。

1955年上半年一天，我去李国平教授家拜访，他是首批聘任的中科院学部委员，刚从北京参加学部成立大会归来，谈话中提及华罗庚先生，李先生说：“华先生名声很大，我过去一直不知他深浅，这次趁开会的机会，我准备了几个问题向他请教，他当场就给了仔细的回答，确是名不虚传”，李先生又说，华先生讲“许宝騄矩阵比我好”，华先生大名无人不知，他如此推崇许先生，给了我极深刻的印象。自然，当时我对许先生的为人，经历和工作毫无了解，仅由李国平先生介绍，知道他是知名统计学家，北京大学教授。

1956年9月，我自武大数学系毕业，分配到中科院数学所工作，根据当时的需要，当年来所的青年人，绝大多数编入概统组，我是其中之一。不久传来消息，许先生要请我们吃饭，也有组内老同志参加，当时很高兴，可以见到这位仰慕已久的大学者。可临期未见许先生出席，听成平同志谈，组内每有新人来，许先生常出资请客，但因他健康欠佳，很少亲自出席云云，当时颇感到有些失望。

    直到几个月后我才有机会见到许先生，当时是准备波兰的Fisz教授来访。许先生在他家里为我们青年人讲弱极限理论，大体上是依据柯尔莫哥洛夫等著的独立和极限分布一书。我们每隔几天去许先生家一次，在他住所的客厅中挂了一块小黑板，每讲半小时左右，许先生进内间休息一段时间，一上午讲3节，许先生讲课看似节奏不快，但一个多小时下来，讲的东西不少，条理清楚扼要，不多几次，就把弱极限的基本理论讲完。我过去在大学未学过概统方面的课程，完全是从零开始，由于许先生讲授得法，得以入门，虽经过四十多年，至今仍记得比较清楚。

    自那以后，我经历了去波兰一年，下放一年及各种运动，业务几近荒疏，也无缘再接受许先生的教晦，直到1962年才有机会再见到许先生。记得是在他家里开了一个小会，北京概统界的许多同志都参加了，当时看许先生，虽然仍显清瘦，但感觉他的身体状况比56年见到时还好一些，那次小会好像是一般性地议论怎么发展国内的概率统计学科的问题。许先生在会上也作了发言，只记得他讲到要注意发挥京外力量的作用，其他已记不起来了，这是我最后一次见到许先生。

    1969年，我随学校下迁到安徽，许先生去世的消息，我是在1971年冬才听到，离他去世已有1年多，那时我已读过许先生的一些论文，了解到他在1945年以前已取得了领先国际的杰出成就，可惜后来由于众所周知的原因，他的作用未能充分发挥，心里觉得很惋惜，我对许先生生平较仔细的了解，还是在1980年纪念他70诞辰的会上，听到他亲属及其他同志的介绍，那以后几年从概统界前辈和学长如王寿仁，张里千，殷涌泉和张尧庭等先生处，听到他们讲述的不少和许先生接触的亲身经历，他们对许先生的人品和学问都交口称赞，给了我很深的印象。

    我在50年代，就已了解到许先生是有很大国际声望的统计学者。到80年代，我有机会去美国访问，更有了亲身的感受。1986年秋，我应伯克利加州大学统计系Le Cam教授的邀请去该系访问，在与Le Cam教授的交谈中，他回忆了许先生在该系工作时的情况。他讲到，许先生当时是J.Neyman最器重的人，Neyman曾作了很多努力要把许先生留下来长期工作，可惜未能成功。他感叹地说：“要是他能留下来就好了”。1987年春我去纽约哥伦比亚大学统计系访问，在Robbins教授的办公室与他交谈，墙上挂着好几位统计学家的照片，许先生的也在其列。Robbins指着这张照片，带点自豪的口吻对我说：“他是我的同事”（一说应是老师，未详），1988年春在康乃尔大学访问时，L.D.Brown教授也曾谈及许先生，他称许先生是“美国统计界早期的著名人物”。

    回想起来，我虽然受到许先生的亲身教晦不多，但在学术道路上，我受到他不少的启迪，我感受比较大的是他工作的深度，诸如他关于t统计量的工作，关于方差分析F检验优良性的工作，关于样本方差分布的Berry-Esseen界限的工作等，都是在简单模型下，经过精细分析，作出极有深度的结果，我在自己的工作中曾有意模仿这种风格，我自己有一篇自认还比较可以的工作――线性回归模型方差估计的Berry-Esseen界限，可以明显看出这种影响。可惜由于我愚钝的资质，所获成绩极为有限。

    许先生离开我们已有30年了，我自己也开始步入老年，读他的遗篇，想见其为人。在当时有很多困难，使我未能在他生前执弟子礼，更多地向他请教学问，终觉是一件憾事。

 

（写于1999年春）

                                                  

 

 

忆 恩 师

－－写在许宝騄先生诞生九十周年－－

胡迪鹤

武汉大学教授

（一）听鹂馆庆五十大寿

1959年的一个中秋季节，1958年的大跃进已过，1960年的新高潮未来，正值许先生五十大寿。教研室同仁们议论，先生一向深居简出，何不借此机会，请先生出门走走。一则有利于先生的心身健康，二则聊表我等的敬意。遂议定不惊动领导，用《红楼梦》中“凑份子”的方式为先生祝寿。每人多则十元，少则二元，凑得百多元款项，在颐和园中的听鹂馆，预订酒席两桌，为先生祝寿。

中秋时节的北京，特别是颐和园，正是海棠结子，绵桂飘香的宜人季节。下午四时许，许先生与几位教授乘小车来到颐和园。当年的颐和园，绝无当今红男绿女摩肩接踵之拥挤。更兼当日并非周日，园内十分清幽。由于建国十周年庆典在即，园内繁花似锦，建筑油漆一新，长廊壁画，也由工艺美术师重新描绘。先生入园以后，兴致颇高，漫步长廊，点评壁画。廊上壁画，大多“三国”、“水浒”、“西厢”、“红楼”之故事。

五时左右，进听鹂馆入席。上首一席，除寿星许先生以外，有中科院数学所华罗庚先生、王寿仁先生；还有北大数学系江泽涵、段学复、程民德、廖山涛、江泽培等诸先生。下首一席，坐我等小字辈人物。记得师兄张尧庭、卢崇飞等亦入此席。

寿宴之间，并无繁文褥礼，套话官腔。纯系至亲好友，家庭便宴。气氛甚为宽松和谐，典雅温馨。北大数学系主任段学复先生致简短祝词之后，即随意交谈吃喝。

记得华先生曾当场赋诗一首，可惜未曾实录，年深月久，也就忘却了。王先生常常妙语连珠，给宴会气氛增色不少。他发布一条“独家新闻”：“许先生多才多艺，对昆曲颇有研究，年青时还粉墨登场过呢！请许先生唱一支。”许先生笑而不语。廖先生话语不多，只给许先生敬酒一次而已。宴至半酣，突起高潮，某公提议，请张师兄献舞一支为贺。张兄亦不固辞，慨然应诺，翩翩起舞。张兄舞姿，博得个满堂彩，许先生亦兴致大增。寿宴至落暮方散。

我跟许先生学习十余年，记得这是唯一一次陪许先生离北大燕园外出。因此印象至深。

（二）落实12年科研远景规划

1956年，我国制定了第一个科学研究规划――12年远景规划。规划中确定数学研究的三个重点方向：计算数学；微分方程；概率统计。为了落实这一规划，在许先生的领导下，对概率统计的发展采取了下列积极措施。

（1）集中力量，培养人才

1956年秋，国家把中科院数学所的王寿仁、张里千先生，中山大学的郑曾同、梁之舜先生请到北大，再从北大选择30多名学生、中山大学与南开大学各抽调10名学生到北大集中培养（这时江泽培、胡国定、王梓坤诸先生尚在苏联留学未归）。同时，全国各重点综合大学也选派部分进修教师来北大。许先生亲自主持“极限理论”讨论班。后来陆续给这一第一批学生授课的内容，不少来自此讨论班的内容。这是我国第一批培养的为数很可观的概率论与数理统计人才。作者系当年学生之一。

（2）延聘外籍专家来华讲学

从1957年到1958年，先后来北大讲学的概率论与数理统计的专家有：波兰的菲茨教授，他讲授统计分析；波兰的乌尔巴尼克教授，他讲授广义随机过程；苏联的邓肯教授，他讲马氏过程。许先生亲自与这些专家共同制定讲学计划，帮助青年人消化整理专家们的讲学内容。

（3）引进教材，更新教学内容

五十年代，我国采用的概率论教材，多为苏联数学家格涅坚科所写的“概率论教程”（丁寿田译）。此书作为教材并不十分理想。许先生建议在无力自编好教材的情况下，可先翻译一些外国（包括西方国家）的教材或教学参考书，以应急需。当时W.Feller所著的“An introduction to probability theory and its applications”出版不久。许先生建议我与另一教师试译。1958年动笔，1959年脱稿。译稿送请许先生审订。许先生逐字逐句审阅。其中有三点给我印象极深，至今难忘。一、原言语中有好几处的“Now”，在译文中都翻成“现在”。许先生很严肃的批评我：学外语不查字典怎么行？两种不同的语  言，其辞汇之间不可能存在数学中的一一对应。你只知道“Now”可以当“现在”用，就不知道“Now”在叙述句中可以当“于是”、“然后”用。这样硬译怎么行！二、我在译文中用到转接词“然而”，在“然而”之前用了句号。许先生看到此处，批曰：“不看上文，就知此处句号用错了。转接词“然而”之前，只能用逗号。”三、对我翻译得较好的章节，又充分予以肯定。译稿批文上还有“此译稿第九章――随机变量译得不错，既是意译，又不失原意。”许先生对一位毛头小子的试笔之作，尚如此认真，其学风之严谨可想而知。

许先生倡导的上述三项措施，在建国后概率论与数理统计发展的初期，起了十分关键的作用。

（三）从理论联系实际到马氏过程讨论班

1958年“大跃进”的风暴，很快就刮进了北大燕园。其影响之一，便是“停课闹革命”，低年级的大学生编大学教材，高年级的大学生与部分教师搞“理论联系实际”。记得我与函数论的几位教师和几位四年级的学生分在一组，组成一个“理论联系实际”小组。积极向有关的应用研究机构与一些企、事业单位了解有何数学问题。奔跑了一两个月，终于选定了北京市电话局西单分局作我们组的联系实际的基地。在此呆了一个多月，其间与电话局的工程师们也讨论过几次。发现他们关心的一个技术问题是：在不增加设备的情况下，如何提高“通话率”。许先生由于身体不好，已多年不轻易外出了，但他仍很关心我们“理论联系实际”的“具体成果”。我只得实言相告：我们这几个青年教师和同学，既无深厚的理论功底，又无实际工作经验，才只两三个月的功夫，并无多少成果。许先生沉思片刻说：“我建议你们学点理论吧，欣钦写过一本专著，题名《公用事业理论的数学方法》，张里千等翻译的，读读或许有帮助。”欣钦是苏联著名数学家，该书还获得过斯大林奖，确实是一本好书。

入秋以后，由于台海局势紧张，“理论联系实际”的活动变成了“全民大炼钢铁”。1958年，许先生倒还清静，既不必花很多时间指导青年人，又不用参加政治学习，可以安心在他的“佟府8丙号”（坐落在北大西校门内的一室一厅的小平房）潜心研究。许先生到是真正的“大跃进”了。

1959年春，北大校园恢复了昔日最高学府的常态。各项教学科研活动正常开展起来了。这时许先生领导我们搞了一个“马氏过程讨论班”。与其说是讨论班，还不如说是许先生给我们系统讲授马氏过程的一些最新结果，并把我们引导到研究的前沿，因为讨论班几乎是许先生一人主讲。讨论班上讲授的内容，正是我们在“大跃进”时，许先生在家中研究和整理的材料。内容有两部分：一为可数状态的时齐的马氏过程的分析理论；二为马氏过程在一些实际问题中的应用，主要是在排队论中的应用。这第二部分内容，是根据我们1958年夏从电话局带回的实际问题而准备的。

许先生有极为深厚的矩阵论的功底。在这个讨论班上，许先生的矩阵论的技巧，得到了淋沥尽至的发挥，因为可数状态的时齐的马氏过程的分析理论，如果抛开概率背景，完全可以从一个带有连续参数的可数无穷阶的非负实值矩阵出发来进行研究。正是这个讨论班，用一两年的功夫，把我（一个刚从大学毕业的大学生）带到了纯间断马氏过程理论研究的前沿。后来，我为北大数学系56级与其后的年级的概率论专门化的学生讲授的两个课程：“马氏过程”和“排队论”，其主要内容，均采自此讨论班的内容及欣钦的专著《公用事业理论的数学方法》。

在此讨论班上，许先生经常批评我们把他看成“神”而不是看成“人”。意思是说，我们不与他争辩，不与他讨论，不提自己的看法，只是作为听众来参加讨论班。他常常提醒我们：任何人的知识和经验都是有片面性的，讨论班就是要讨论。后来我主持讨论班时，看到一些年青人也和我当年一样，我才领会到当年许先生对我的批评的意义。

（四）办刊物，几度筹划几度空

自1960年秋开始，进入“三年困难时期”。全国人民的生活异常艰苦，知识分子也不例外，然而我们的学术活动却很活跃，原因之一就是，这段时间政治气氛比较宽松，各种会议和政治学习比较少。北大概率论与数理统计教研室除江泽培先生领导一个平稳过程讨论班以外，许先生亲自领导两个讨论班：极限理论与马氏过程讨论班；数理统计讨论班。在1956年和1959年两个准备阶段的基础上，通过1960年以后的三年努力，北大概率论与数理统计教研室的一批青年人已先后逐步成长起来，获得了一批科研成果。当时全国性的数学刊物极少，除了《中国科学》、《数学学报》、《数学进展》等刊物以外，几乎就没有什么全国性的数学方面的学术刊物，而年青人的作品要挤进这些刊物亦非易事。在这种背景下，许先生几次跟我们谈起要办概率统计方面的学术刊物。他认为这有几大好处：一可发现人材；二可培养人材；三可促进国内外学术交流。这确是一件大好事。但是，要办刊物，第一要钱，第二要人，第三要稿源，而最重要的是争取领导的支持。钱，许先生准备从他的积蓄及每月的工资中抽取一部分来资助；人，包括编委会及编辑部人选，许先生亦有初步考虑；稿源估计亦无大问题，因为当时国内数学刊物极少，而向国外投稿又几乎不可能，随着年青人逐步成长，稿源会不断充实的。关键是争取领导的支持，因为在当时的环境下，创办一份刊物，实在是太不容易了。要争取领导的支持，特别是有关的出版部门的领导的支持，非得一位干员向领导陈明利弊得失不可。可惜当时竟难以找出这样一位合适的人选，所以办刊物之事，结局是：几度筹划几度空，好事终难成。

（五）最后一面

1969年一个深秋的下午，北大南校门内的马路两旁的洋槐在西风中瑟瑟颤抖，落叶成阵，行人稀少。就在16斋与17斋转角处的水泥地上，坐着一位枯瘦的老人。我近前一看，竟是许先生。他坐一方小棉垫上，身旁放着一个空心草编的小篮子，小篮子里放着一个玻璃瓶。我知道这玻璃瓶是先生常年用来当作“密闭的小痰盂”的，那棉垫是因为先生太瘦，铺在沙发上防亘的，现在铺在水泥地上，不仅可以防亘，也可以防凉。

我问先生何往，答曰：“去接受教育！”后来我才知道，他是去参加一个小型“批判会”，实则是“陪批”的。一位从北大佟府走到北大南校门都力不能支的病弱老人，一位终身独居，为国家的科教事业而呕心沥血的爱国者，一位享誉国内外的学术泰斗，仍难逃此劫难，实为我们国家的不幸，民族的不幸。在林彪和“四人帮”的淫威下，我又能说什么呢？只有心在流泪而已。与先生告别时，我就有一种不祥的预感。果不期然，这次分别，竟成了我与先生之永诀。

1969年的初冬，林彪和“四人帮”派往清华和北大的那一对“金童玉女”，秉承他们主子的旨意，把清华和北大的大批教师和干部，赶往江西鄱阳湖畔的鲤鱼洲劳动锻炼。我等自然是被赶者之一。鲤鱼洲是一个由抚河与鄱阳湖环绕的半岛，人烟稀少，几乎与世隔绝。我们白天劳动，晚上学习文件，“斗私批修”。

1971年春天，由北大校本部来鲤鱼洲的一位教师告诉我：“许宝騄先生1970年冬天已经去世。去世时，身边无一亲朋好友。”听后良久，我才说出一个“哦”字。一种透骨的悲凉，堵在我的心头，半天说不出话来。一代宗师，竟这样走完他的人生之旅。先生虽然早年患过肺结核和胃病，但这些均非不治之症，更何况50年代末已治癒。若不是那场“史无前例”的运动，先生何至英年早逝，六十而亡。写到此处，我不知这篇短文是对先生九十华诞的纪念抑或是迟到的悼文，或许是兼而有之罢。

 

 

 

            回忆许宝騄先生对我的教导

                       陈家鼎

                北京大学教授

 

许宝騄先生离开我们已三十年了。每当想起这位伟大学者当年对我的教导，心情激动不已。我于1959年7月从北大数学力学系毕业后留校工作，被分配到概率统计教研室当助教。9月起我参加了许先生主持的概率论讨论班，学习独立和的极限定理和马氏过程理论。许先生对每个青年的成长十分关心。对每人的特点和缺点有细微的观察并及时坦率指出。记得刚到教研室不久，我单独找许先生汇报自己研究过Kummer关于级数收敛性的判别法，Kummer的判别法是一类相当广的判别法，达朗贝尔判别法，拉阿伯判别法，伯尔特昂判别法等均是其特殊情形，我的研究结果是可数个Kummer型判别法仍不足以判断任一无穷级数的收敛与否，我企图证明א1个Kummer型判别法就够用了。许先生仔细听了我的汇报后明确指出:“你在分析上有基础，但这种研究没有意义，你的缺点是喜欢抽象。一定要研究具体问题。”这次谈话给我很深的印象，研究问题首先要注意问题的意义，一定要研究有意义的具体问题，不能为抽象而抽象。

1961年我向许先生请教柯尔莫果洛夫(Kolmogorov)定理的推广问题。大家知道，对于因子空间是数直线的情形，柯氏在1933年首先建立并证明了概论中的一条基本定理：从一族相容的有限维分布族出发，可构造出无穷维乘积空间上的相关概率测度以给定的各有限维分布为边缘分布。这就是所谓柯氏定理。一些人猜想，对因子空间不加任何限制时结论仍真，但在1948，年E.S.Andersen和B.Tessen举出反例说明对因子空间不加任何限制的情形下柯氏定理不保持成立。1953年，Marczewski证明了：只要因子空间上的任何有限测度是“紧测度”，则柯氏定理仍可推广到这种无穷维乘积空间上。著名概率论专家邓肯（E.B.Dynkin）在他的“马尔可夫过程理论基础”（原文是俄文（1959），中译本是1962年出版的）中给出了柯氏定理的另一推广（对因子空间加的条件相当宽），即该书第一章定理1.2（见中译本21页）但未给出证明。我问许先生，如何证明这个定理？许先生对我说“这个问题我们向Dynkin提出过（Dynkin于1958年到北京讲学），他很坚持他的结果，但未给出证明，你可以研究。”许先生还对我说，要好好研究Anderson等人的反例，研究柯尔莫果洛夫定理不能无限制推广的原因。在许先生的指导下我学习了有关知识，两年后在他的帮助下我举出了反例，说明Dynkin的“定理1.2”是不成立的并给出了比较宽的条件推广柯氏定理。许先生对我的论文稿进行了逐字逐句的修改，论文后来发表在“数学进展”上。 

许先生教导我要“具体”，不要“从抽象到抽象”。他自己又言传身教，告诉我们如何抓住事情的实质进行科学的抽象。在讨论班上，他总是在听完别人报告文献之后不久，以他特有的方式，单刀直入，严密而简练的把文献上的内容从新的角度加以整理，概括和推广。我记得在1962年讨论班上学习苏联学者谢列金随机过程的连续性的论文，在我报告完这篇论文之后，许先生就用非常简练的文字把该文进行了化简，条件大为简化；又如在1964年的马氏过程讨论班（除北大的教员外还有中国科大的王寿仁，殷涌泉先生及严加安，李国英，王柱同志等参加）上我们学习Hunt关于Mantin边界的论文，在听完报告人的报告之后不久，许先生把文章内容从新角度（用他的话说“编一个主题”系统的加以改述，指出Hunt的主要结果是什么，令人钦佩的地方在哪里，并提出多项值得研究的问题，给我们很深的印象；又如在1964年，他主持的讨论班上，郑忠国同志首先就遍历情形论证了以同一矩阵为转移阵的两个相互独立的马氏链具有重合性质，但推导比较复杂。许先生在听完郑的报告之后不久，通过引入必离集的概念及对无穷维矩阵的运算，不仅化简了郑的证明，而且给出了在很宽条件下的推广。这一切使参加讨论班的同志体会到，什么叫做抓住问题的实质，怎样去推广现有的结果。

和许先生接触过的人都会感觉到，许先生是绝顶聪明的人，但他并不恃聪明而不努力工作。相反地，尽管有多种严重疾病，多年因病卧床，但他在床上异常勤奋，努力工作。无论是阅读文献，研究问题或是批改青年教员和学生的写作，他都抓得很紧。记得在1962年，我教58级概率班学生的“测度论”课并兼班主任，在学生们的要求下，经许先生同意，我带全班学生到许先生的住处，请许先生和同学们谈学习方法。同学们向许先生提了很多问题，特别是问学好数学的方法是什么，怎样才能掌握一个定理。大家期待着这位伟大的学者会介绍很巧妙的学习方法，一旦掌握就事半功倍。可是许先生却平静地对大家说：“学习是没有方法的。有人问齐白石，您是怎样学好画画的？齐白石的回答很干脆：你跟我一样天天画，画五十年就成了。”由此可见，许先生非常重视学习上勤奋努力，持之以恒。他并不是不要人注意学习方法（他在这次座谈会还是介绍了许多具体的方法，例如当时有学生问：一个定理有几个证明，要不要都掌握？许先生回答说搞清楚一个证明就可以了），而是向学生强调，最重要的是勤奋努力。          

 许先生对分析和代数有很深的功夫，对数学精益求精，追求最高的学术水准。1963年冬天他对我说“要把一些工具掌握得纯熟。要脚踏实地，不要做梁上君子。现在数学界有的人是梁上君子，没有根。要注意学习别人的长处，要时常想到自己的绝技是别人的末技，但有时要想到，别人的绝技是自己的末技。” 

1963年至1966年文化革命前我是教研室秘书，和许先生在工作上有较多的接触，深深体会到许先生的忘我精神与杰出的才智。他对课程设置，教学大纲，毕业班论文指导工作等等很关心，每当我向他请示时，他都给予明确的回答。他不仅带病坚持科研工作，而且十分关心青年的学术成长。江泽培教授于1963年初被上级抽调到二机部从事国防建设的重要工作，那时许先生对我说“江公调走对我们有很大影响，使工作母机受影响。”我说“现在就只靠许先生来全面指导了.”许先生说：“我躺在床上怎么指导？”话虽这样说，他却默默地了解各个科研组的具体情况。1963年秋，他给教研室全体青年教师系统地讲“点集拓扑”（讲课的手稿存留至今），后来同时主持三个教员讨论班（数理统计，马氏过程，平稳过程与过程统计）。在每个讨论班上，他不只是听大家的报告，而且亲自作系统的报告，提出新见解和要研究的问题，使大家收获很大。他对每个青年教师的发展都十分关心，对教研室工作要注意的问题时常提醒我。一次他对我说“毕业论文的题目要针对每个人的情况选好不容易。孙山泽能力很强，我出的题目对他估计不足，他很快就做出来了。”又有一次对我说：“甘章泉从苏留学回来，要注意发挥他的作用。历来有两种倾向，一种是把出国留学回来的人看成是通天的，什么都行；一种是把出国留学回来的不当一回事，认为没什么。这两种倾向都是不对的。”北大当时正在极左路线下不断大搞政治运动，时常把业务工作放在一边，对知识分子不重视，根本谈不上发挥归国留学生的作用。四人帮跨台后，我回忆起许先生的深刻教导，心情很激动。甘章泉同志在留苏期间师从著名概率专家斯果洛霍德（A.V.Skorohod），是我国最早学习并掌握随机微分方程的学者，来北大后碰上社教运动及后来的文化革命，未能发挥他的专长，使我们深深遗憾。

 

（2000年5月）

 

 

 

 

回忆许宝騄先生

郑忠国

北京大学教授

 

    我从小喜欢数学，也喜欢听人讲数学家的故事，从小学，中学到大学，听到老师同学说的最多的是华罗庚先生的故事，至于许宝騄先生，一直到进入大学，才听到一些关于许先生的事，直到最近，由于工作需要，查阅了许先生的一些记录，发现在40－50年代，当时数学界评论，说国内学术水平最高的两位数学家一位是华罗庚，另一位是许宝騄。这时我才体会到，这两位著名的数学家在风格上各有他们的特点。

    我第一次听到许先生的名字是来自我的大一同学，杨振复。他是原清华教授杨武之先生的幼子，许先生派人送来一个纸条，称杨振复为小五弟，我当时以为许宝騄是一位女士，后经杨振复介绍，知道许先生是一位很知名的教授，对许先生的第一印象仅此而已。

    第二次听到许先生的名字是在57－58年，当时北大数学系经常召开全系大会，有一次，在大饭厅召开全系大会，会议内容大约是与反右，大跃进等政治运动有关。具体内容已经记不起来，大会快结束的时候，程民德先生突然转变口气，谈到大家很关心许宝騄先生的健康问题。提到许先生病情严重，但经过治疗，现已处于康复阶段，为了保证他身体的康复，希望大家不要去看他，对大家的关心，表示感谢。

    第三次印象是在1958年大跃进时期，学校举办教育革命展览。当时的大学生受到狂热性的影响，从我个人的角度，觉得放卫星，大跃进才是鼓舞人心的，一到展览会上，到数学系那一部分，在一面墙上，订上几篇论文的抽印本，而第一篇论文却是许宝騄先生的论文抽印本。当时，同去的同学评论，别的系都是献礼和成果，我们数学系展示的与这很不相称。现在看起来，当时的确幼稚，也不懂数学是什么，而许先生，当时虽然有病，仍然坚持搞科研，他不是随风倒，也不怕出“洋相”，尽管当时自己的思想受大跃进的影响，但许先生的人品风格也给我很深的影响。

    大四的时候，我被分配到概率统计专业。我记得有一次在平房教室上课（地点在现理科主楼东北角位置）时，突然在我位置的后面，坐了一位老者，他穿着一件对襟深色中式短衫，看上去像一个老农，听着胡迪鹤先生讲分析概率论。上完课以后，我们都回宿舍，突然老先生又返回教室，说丢了一个东西，同学们就帮助他找，先生说要找一个瓶子，后来，同学顾怀谨帮助他找到了瓶子，先生就正式警告顾怀谨，回宿舍以后一定要用肥皂洗手，因为这个瓶子是他吐痰用的瓶子，而他本人患有肺结核病，每当我们在宿舍中谈起许先生的时候，立刻被他的那种可亲的形象所感染。当时在分配毕业论文小组时，同学们都希望被分配到许先生领导的那个组。

    大学毕业的时候，我作为江泽培先生的研究生继续深造。在研究生一年级的时候，江先生被调离北大，那时教研室无人指导，决定将我改成助教，由许先生亲自找我谈话，当时，我表示愿意将研究生改成助教，许先生对此大加赞场和鼓励，他认为，做助教一样能够在科研上成长，参加教学工作、或许更加有助于科研工作。后来，学校和系里考虑到，如果条件允许，还应让我继续完成我的学业，改聘科学院王寿仁先生作为我的指导教师，在接受王寿仁老师的指导的同时，许先生实际上也把我当成他的学生。在64年左右，让我参加他领导的马氏过程讨论班，念Hunt的位势理论，我记得当时参加讨论班的有王寿仁先生，殷涌泉先生，还有严加安，李国英同学，我系教员有陈家鼎，甘章泉，胡迪鹤等。当时，王寿仁先生为首称许先生为老师，可以说几代同堂，当时讨论班设在许先生的家里，后来，王先生回忆起来，许先生从五十年代起，为了开展学术活动，特地在家里开辟一间屋子，作为开展学术活动之用（他家一共两间屋子，其中一间作为教室）。王先生还说，许先生家里的黑板还是数学所的财产，我记不起来，许先生的这一块黑板是否为我们概率教研室所继承，如果是的话，它一直从29楼被用到一院，它是数学系几个教研室所用的黑板中最好的一块，一直到85年建系以后，我们还是用的这一块黑板，后来概率统计系搬家到老化学楼新地址，化学楼的教室走廊里留下不少玻璃黑板，当时，由我作主，将这块黑板送给林源渠（现在为数学系教员）的教研室，我之所以要提及许先生的房子与黑板，是要讲讲许先生的精神。50－60年代，他为健康与其它条件所困，但他所追求的是事业，除了事业，他是一无所求，他虽然学术上有名望，但从来不追求它，也从来不与别人计较名利地位问题。对于事业，他可以贡献一切，他可以把自己的两间平房中的一间腾出来做讨论班的场所。我虽然不是许先生名下的研究生，但江先生离校以后，许先生作为教研室主任，好象对我也负有责任似的，他让我在他的讨论班上报告我的毕业论文，并亲自加以评论。记得我在论文中，证明了一条引理，利用了归纳法，他就评论说，做科研的关键一是要判定一个结论，二是要找到证明方法，一旦明确了用归纳法，下面的工作就十分简单了。

    许先生除了精于理论研究，对于统计应用也是十分重视的。我记得当时有一位国家科委副主任，得知日本工业发展速度很快，得益于田口玄一的正交设计法，特地将田口玄一那一本书给许先生。许先生组织概率统计教研室的教员进行学习，并且由卢崇飞写出讲义进行推广。

    60年代初，许先生虽然身体不好，但学术上还是非常活跃的，他组织了几乎概率统计所有方向的讨论班。65年以后，一直到文化大革命，业务上处于停顿阶段，我就没有机会再见到许先生。下面是唯一的一次。有一天我从18楼教师宿舍到大饭厅吃中午饭时, 看见许先生坐在16楼到17楼之间的台阶上。那可能是他从18楼回家时，由于体力不支，而坐在台阶上。据说许先生在文革中曾经出来过两次（从家里走到办公地区）在文革后期他只能瘫在床上了，这与他仅有的出来两次有关。

    许先生学术上非常活跃，他的思想并不像他的身体那样干瘦，记得他曾在教研室的联欢会上，让大家用6个“种”字造一句句子，用连着的5个“that”造一句英语句子，这件事，在当时研究生中传为美谈。

    许先生在国际上是声望很高的统计学家，我最近在许先生的个人档案内看到他自己写的记录45.8－47.8系在北京大学留职停薪2年，47年按时返校。当时，赴美路费是Neyman从44年开始设法筹措的。在Berkeley任教期间，加州大学主要教员有两位，一位是Neyman，另一位就是许宝騄，Neyman看到许宝騄在履历表上填上“统计学讲师”时，大为不满（可能是由于薪水关系）并向斯泼罗尔提出抗议（许先生此时，已经是北大教授），并亲自散发了“关于许宝騄博士的声明”。在这两年中，许先生先后在哥大，北卡任教，而且各学校争相聘他任教，许先生两年期满后坚持回国。98年我在访问许先生的亲戚俞润民先生时，谈到许先生当时为什么坚持回国时，俞先生说：“当时许先生作为北京人来说，一个很自然的想法是‘不回国干什么？’。这里边还是有爱国的因素在起作用。

    80年我访美时，江泽培先生让我在美找一篇统计应用的博士毕业论文，我特地去找了Neyman教授。Neyman教授说“我的所有的学生写的论文都是有用的”，在谈到许先生时，Neyman说“P.L.Hsu是我的最好的学生”。后来我在Neyman的传记中看到许宝騄的事迹时，才体会到这句话的价值。

许先生在华人统计学家中，也具有很高的声望。90年代，美国的统计学家林丕二，访问北大，听说许先生在北大时住两间平房，一定要我带领他去看一看许先生住过的平房，并说不去那看一看，访问北大就没有意义，我领他去佟府8丙（北大校内平房），由于当时房主不在家，没有能进入房间，只在门口录相留念。我想，许先生的一生，可以作为我们后人的榜样。

                                                         （写于1999年春）  

 

 

 

 

对许先生的回忆

 

程士宏

北京大学教授

 

    (1)  1957年，我考入北京大学。到了北京以后不久，见到在科学院力学所工作的表哥李毓昌。他问我学什么专业。我说数学力学系的数学专业。他立即反应道：“北大数学最有名的教授是许宝騄。”这是我第一次听到许先生的名字。大学五年级(当时数学专业是六年制)的时候开始分专门化，我被分到了概率统计专门化。以后又分了研究方向，我又被分到了数理统计方向，有幸成为许先生名副其实的学生。许先生带学生的形式是讨论班，而因为许先生的身体不好，讨论班只能在许先生的家里进行。他当时住在北大佟府的一个套间，有点像现在的一室一厅。厅里挂着一块黑板，摆着各式各样的凳子和椅子，充当讨论班的教室。许先生非常瘦弱，坐在沙发上还要垫一个软垫子，几乎不能外出。但是，他精神不错，反映灵敏，语言幽默。我们看到许先生在这样的身体条件下还坚持工作，坚持带学生，都非常感动。在许先生忘我工作精神的感召下，大家学习都非常努力。张尧庭先生是我们的副导师。听他说，许先生对我们57级的学生也比较满意。我们快毕业的时候，许先生还和全体讨论班同学一起在南北阁附近合影留念。毕业以后，我还听过许先生讲点集拓扑，参加过他主持的平稳过程讨论班；可惜一年之后，就被派往农村参加两年“四清”，接着又是文化大革命，无法继续聆听许先生的教诲了。

    (2)  当时讨论班的内容是念斯米尔诺夫的小册子《变叙的项的极限分布》(注：变叙即次序统计量)。先由我们念这本书，然后同学们分别在讨论班上报告。在讨论的过程中，许先生经常有画龙点睛之笔。例如，有一次一位同学证明一个定理的过程中要用到Lebesgue-Stieltjes积分的分部积分公式，对该公式的最一般的形式及其证明却怎么也弄不清楚。许先生当即用Fubini定理给出了公式的一般形式及其证明，使大家豁然开朗。但是，讨论班最精彩的部分是在大家报告完了之后许先生所作的一个总结。设是i.i.d.的共同分布函数为的随机变量，是它们的次序统计量，则有

             ，

其中是参数为贝塔分布函数。许先生在总结中所使用的方法基于如下的事实：如果是i.i.d.按标准指数分布的随机变量，那末遵从参数为的伽玛分布，遵从参数为的贝塔分布。利用这些特殊分布之间的关系，推导关于次序统计量中项和固定名次边项极限分布的基本定理变得十分简单、直观。大家知道，斯米尔诺夫关于次序统计量极限分布的基本定理是用纯分析的方法得到的。许先生的方法则可以称之为概率方法。他的方法的突出优点是容易推广到多维，我和马逢时同志的毕业论文就是在此基础上完成的。我从许先生的讨论班上不仅学到了很多知识，更重要的是学会了如何读书，如何在学习、消化前人工作的基础上做学问。

    (3)  1982年，我作为国家公派的访问学者前往许先生曾经工作过的北卡罗来那大学(Chapel Hill)的随机过程中心进修。当时，著名的概率统计学家Hoeffding教授已经退休，但仍旧保留着办公室，每天照常上班。有一次，他主动向我说起他是许先生当年的同事，他们一块开过《测度和积分》的课，而讲义是许先生写的。今年，北卡统计系教授Merron来访，又提到许当时的讲义已拍成照片予以保留，可见那里的同行们在时隔50年之后对许先生还是很怀念的。

当时，主持北卡随机过程中心的教授之一是地位很高的Kallianpur。有一次，他请我们这些访问学者去他家聚会，向我讲起这样一件事。1950年前后，当他还是一个博士生的时候，就十分仰慕许先生。他曾经写了一封信给许，表示要到中国来跟随许先生学习。因为当时刚刚解放，情况还不十分稳定，许先生便回信婉言谢绝了他。我告诉他，许先生已经去世，他感到十分遗憾，但仍有访问中国的愿望。从北卡回来以后，我向江澤培先生汇报了这件事，江先生便邀请他访问了北大。

                                                      ( 2000年6月 )

 

附录

 

移棋相间法序

俞平伯

 

编者按：俞平伯著移棋相间法，序中谈及许宝騄先生研究移棋法之事。文中“闲若”系许宝騄先生的字；序中许子、闲若、闲均指许先生。

 

序一

忆乙丑（1925，民14）岁灯下侍家大人，谈及幼年曾学移棋相间法於曾祖母姚太夫人，时许君闲若亦在座，许固近戚，且故人也，共怂恿试之，良验。迢迢数十载，家大人亦不能悉忆，移至七八子而止，而予等已苦其繁，各出片纸录而怀之，视同瑰宝。闲寻返津。此後书札往返，互相推衍，而闲喜深思，所得视予尤多，已至五十子矣？然自此以上，闲亦不复为之，非不能更进一筹，乃数既无穷，多则愈繁，实不胜其为也，因此意绪阑珊。闲虽就学来京，而其成绩品则阁置於于书案抽斗中。又一年余，逮丙寅腊尽，颇多暇日，纵论往事，兴会复多，爰出旧记重加紬绎，终日栗六，钩稽谈论，如罹脑疾，最先假设律宜依倍数而立，如四八同法是也，惟又不尽然，十二为六之倍数，又决不可通融也，况素数无穷，其律亦将无穷也，即幸而有之，其浩瀚繁琐，亦与无律相差无几耳。嗣重新思索，始得今律，虽未必尽 善，而已得执简驭繁之要，盈天下之数，悉入此四律之内而无或遗，此闲若之功为多，予则聊尽赞助整理之事而已。荏苒又二年，顷复值岁莫，拟加编次，俾久其传，试检春在堂集则当日曾祖母口授吾父之成法秩然在焉，集中明言出坚瓠集，案头无此，托清华大学朱佩弦君代检之，则最初之法亦具焉；於是二百八十年来渊源授受之迹，较然昌明矣。（坚瓠集序於清康熙二十九年庚午，而褚君言三十馀年前学於胡君，则可考之最初传授，约在顺治十六七年左右）。此虽小道亦有可观，今之视昔宁无寸进，後之览者又复云何？然缀此短书，略存鸿印，异日重开，譬诸再寻断梦，重理故书，乐固在我，不必求知於人，虽不足备艺囿之珍闻，亦吾家之故实也，写录既竟，欣然命笔。戊辰（1928）祀竈日，於北平东城老君堂七十九号。

 

序二

前序既竟，携示许子，属为本篇，然许子治科学者也，无意为文，姑阁置之。己巳新正二日之夜忽以电话觅谈，适余外出，越日访之，乃以合四为一之新律相告，其法简而整，其言明且清，虽其根柢不出四律，而去其繁冗，正其谬误，使人一览豁然贯通，於应用上方便至多。坚瓠集诀曰：「就是儿童也不乱」，实凑均之游词耳。若依新律，则口耳授受一分钟可毕，真庶乎儿童不乱矣。於是昔之视为奇巧者，今且一文不值矣。遂述其梗概，庶後之来者无所惑焉。己巳人日又记。

 

序三

前二序成於十七十八年，收入杂拌二集中，则二十二年癸酉也。其本编迄未付刊，所以者何？小道无足观览，况乎解之者众，未曾识面如惕闇君，友人中如陈盛可君，皆善为之。仓卒宣布，惧为辽东之豕，一也。闲当时曾有从数理上研究之之意，犹望他日得一较完善之记载，二也。仆於数目字为十足之门外汉，不胜述者之任，三也。积是三因，弃置勿陈者又八载，而其间人事之变，殆非陵谷海桑所可喻也。闲丙子渡海，庚辰返国，南天羁滞，雁足稀至，知其於泰西畴人之术已深造有得，而视昔日之儿嬉如泥孩竹马，常不复措意乎。仆索居槐市，局迹榆庭，胜赏难逢，佳游不再，良如水东花隐所云，半涂梦觉之人难为遣也。偶检箧，旧记犹存，於时烽尘未靖，惧其久而放失，则他年或遂无书，以期吾友为之，又不可骤得也。遂稍加整治，俾广流传，存其真面，所谓小不足悔者非耶？文字疵病，仆自当之，斯於读者为尤歉也。辛巳中元节记。
                               

  (1900.1.8—1990.10.15）

附录

 

关于许宝騄先生的美国之行

 

(编者注: 此文是从传记“J.Neyman”一书的中译本《耐曼》中摘录下来的几段组成。标题是我们加的。郑忠国同志在各段后加了注，以便读者了解当时的背景。该书是著名传记作家C.Reid所著，姚慕生等译，上海翻译出版公司出版(1987)。耐曼(Neyman)是著名统计学大师，在其一生中，与许宝騄相遇两次。1936-1938年，在英国大学学院时，耐曼是许的老师。他后来称许是他最好的学生。1945-1947年，许先生去美国时，他们又相遇了。从下文可以看出，耐曼对许先生十分器重。围绕许先生在美的两年，可以说出现了一场激烈的人才争夺战。从《耐曼》一书引述的几段，可见许先生在学术界的地位。)

 

    这一时期，大西洋两岸书信频繁。大学学院的生活一如往常：讲课，听课，考试，通过毕业论文。

那时耐曼最优秀的学生是中国人许宝騄（Hsu Pao Lu）即 P·L·许。（耐曼用一个波兰短语向我称赞了许，这个短语他译成英文就成了“请坐！”，他微微欠身用手致意地表示了一下。) 然而一个加拿大学生，昆虫学家杰弗里·比尔（Geoffrey Beall）无意中使他获得了一个非常有用的科学结论。比尔在处理与杀虫药剂的现场试验有关的问题时试图利用泊松分布但没有成功，他来请教耐曼。耐曼问了他一些问题，他解释了飞蛾怎样按不同的大小片块产卵，由此孵化出幼虫，然后爬出去寻找食物。耐曼从比尔的这些描述中受到启发，得到了“传染分布”这一新的思想，他与“聚类”的数学模型有联系，以后他还要反复的用到它。

耐曼正在清理一九三七年写的许多研究论文；次年有九篇论文发表，这是他最多产的一年。论文“拟合良度的‘修匀’检验”是其中的一篇，在这篇论文中他首次提出了一种技巧，这种技巧最终影响了很大一部分有关渐近理论的工作。这篇论文以纪念卡尔·皮尔逊为题，“是他，最早提出了拟合良度的问题，并最先去求解。”

（郑忠国注：《耐曼》第P224页上  这一段是Neyman对1936-1938在伦敦University College这一时期的回忆。此处提到“P·L·许是Neyman最好的学生。”这句话，钱敏平和我在访问Berkeley时，曾分别从不同场合听到Neyman说过这句话。这句话是Neyman对许先生的最权威的评价，足以看出许先生在世界统计界的地位。)

 

对于耐曼个人来说，此时离开伯克利并非上策。耐曼夫人动了一次大手术刚刚出院，统计学的教学“一蹶不振”，陶罗兹·波恩斯坦的接替者还没有找到（好几次,耐曼问伊万思，让还未获得哲学博士学位的人教高级课程是否“合法”）。英国又一次遭受着可怕的轰炸。希特勒亮出了讹诈已久的“秘密武器”——无人火箭，后来的事实表明，他们的战斗力并不像当时人们设想的那麽大。耐曼感到他已受到召唤，必须投身行动。伊万思支持他，敦促斯泼罗尔同意。

找一个适当的接班人的问题依然存在，耐曼始终认为，在战争时期坚持教育质量是非常重要的，美国显然已没有多余的老资格统计学家，但是在中国——

上一年，他收到过许宝騄一篇论文的抽印本。许宝騄于一九三九年获得理学博士学位后离开剑桥，在巴黎阿达玛那儿待了一年，然后回到他的故土，在北京大学担任统计学教授。照耐曼的看法，许宝騄的水平绝对可以与瓦尔特相媲美，他们是新一代数理统计学家中的两个佼佼者。

一九四四年夏，耐曼一直在为许宝騄的旅费问题伤脑筋。中国的形势一片混乱，天下三分，其一在日本人的统治下，其二由共产主义者领导，第三部分属于民族主义者。许宝騄在某处一个地窖里从事科学研究。他的工作居然能够印出来，简直是个奇迹。他渴望到美国来。

耐曼第一脚踏上赴英的旅程，就给许宝騄发了一份电报，邀请他到伯克利来讲六个月课，并在来年担任一个收入有保证的职务。在许宝騄到达之前，耐曼的老朋友鲍耶将每星期从帕洛阿尔托来两天替耐曼上课，他在斯坦福大学有个并不合适的职位，仅是个副教授。

（郑忠国注：第283 页  这一段提到美国人才紧缺，Neyman培养的学生，一个个地被军方调走。在考虑接班人时，想到了他的学生许宝騄。）

学校预算委员会同意了最后的那个建议并表示相信让耐曼教授出任研究所所长会使他要求发展统计学的愿望以及要求与他的地位相称的自主权这一愿望得到满足。耐曼在给斯泼罗尔与伊万思的信中提出的其他要求，包括薪金问题，预算委员会认为可以做出安排使耐曼与校方都满意。

做出这些决定的时候，耐曼正驱车奔驰在回来的途中。他在南方稍事停留去看望了在查佩尔希尔的郝泰林，又去看了许宝騄。他仍想劝许到伯克利或哥伦比亚去，可是他发现这位中国学者郁郁寡欢，他失恋了，一心想返回中国去。

（郑忠国注：第311页   此处讲Neyman访问Chapel Hill的一段插曲，他仍然抱着希望许宝騄返回Berkeley。但他发现许先生此时希望返回中国。）

大选将在三月三十一日举行，但耐曼马上就要到华盛顿去做一段时间的准备工作。在一封匆忙写给伊万思的信中，他对在他离开期间统计学的教学与实验室的领导工作做了安排。他对许宝騄在他与郝泰林的哥伦比亚大学学期结束后到伯克利来供职一事特别关心。在一份单行空白打印的四页长的信中他又一次称赞了许，“在这个问题上我们已取得了一致的意见。”他已经得到了郝泰林的消息，郝泰林说他正打算秋天离开哥伦比亚到北卡罗来那大学去。（在那里他最终将领导一个独立的数理统计系，这是他长期以来一直倡导的。）郝泰林说，芝加哥大学、耶鲁大学以及哥伦比亚大学都希望得到许宝騄。

“我担心如果我们贻误时机，”耐曼警告伊万思说：“我们将得不到一位优秀的人才。”

当他飞抵奥马哈时，他变得烦躁起来。

“天气不错，我的座位也很好，可是我并不愉快。”他在飞机上给夫人写信道。

他的信东拉西扯，从实验用的甲虫，关于他“曾与欧里奇匆匆谈了十分钟”，一直到打听奥斯卡·朗的讲话在社会上可能引起的骚乱。朗现在正充当“中间人”的角色——他甚至想象西红柿和臭鸡蛋正在朝这位波兰新任驻美国大使身上扔去。他心中的第六个问题是讨论会的与会者在休息室喝咖啡的事情是否已经落实。

在华盛顿，他情绪沮丧地写信给勒曼道：

“讨论会似乎前景不妙。朗刚才打电话给我说他病了，不知为什麽我总是担心许宝騄博士会不来参加。我自己的论文是匆匆准备的。天知道会发生什麽意外。”

“不管怎样，我们必须尽量把事情办好。”

到达首都后不几天，他收到了爱佛琳·费克斯小姐写来安慰他的信，耐曼夫人将他的信交给她看过了。一切都进展顺利，就是许宝騄宣布他在哥伦比亚学期结束后将随郝泰林去北卡罗来那大学这件事使大家感到遗憾。

远在大陆另一侧的耐曼陷入了忧郁之中：

   “唉！又是功亏一篑！”

   （郑忠国注：第294-295页，这一段描写Neyman在失去许宝騄时的心情。当时美国名大学争相邀请许先生去任教，Neyman当然希望许回到Berkeley。但最后，许先生决定在哥伦比亚大学的教学工作结束后跟着Hotelling到北卡去筹建统计系。Neyman哀叹，功亏一篑！）

一九四五年秋，耐曼盼望能回到教学和研究上来而不是陷身于事务之中。他热切的重新提出了在密西西比河以西建立宏大的美国统计中心的任务。关于数学系内统计学的发展计划以及为了便于统计实验室与其他系合作的方案，这长长的公文送到了伊万思及其他系负责人的手里。

他建议在一九四五年下半学年开设的十门统计学课程将由爱德华·巴朗金（从普林斯顿来到这里的新成员），马克·尤代，爱佛琳·费克斯，约翰·苟兰特（又一位新来者），欧里奇·勒曼，伊丽莎白·司各特以及耐曼与许宝騄执教。这些人除了后面两位以外，都还不曾获得博士学位。

耐曼因有许宝騄这样才华出众的数理统计学家在伯克利而感到高兴。因此，当他看到许宝騄在一张表中仅仅被称为统计学讲师后，便对这个“令人不快的错误”向斯泼罗尔提出了抗议。

他说：“有人也许会说在一张表格中怎麽称呼关系不大，但是既然写上了头衔就有其目的，否则写它做什麽。对许宝騄来说，在这样的失误中所受到的损害比美国人更多。作为一个中国学者，两所美国的重要大学邀请他来当访问教授，这是一种很高的荣誉。事实上，要是那张表能真实的反映他的工作，那就好了，那样一份东西留在他家中，子孙后代看了也会感到自豪的。”

（郑忠国注：第291至292员上 （1946）这一段讲述许宝騄到达Berkeley后Neyman的心情，许宝騄当时是Neyman的得力助手。里面也提到一件令人不痛快的事情。）

 

 

 

 

附录

中央研究院首批院士名单

编者按：本文摘自1997年5月16日的《南方周末》，其内容来自《中国院士》一书(张建伟等著)。

 

1928年，在中央研究院的早期“组织法”中，就有设会员（Member）的规定，因条件不成熟而未实行。本应由院士承担的工作之一——指导联络奖励学术研究——却赫然在目。因此，没有院士，却有一个“评议会”，由选自全国科学学术机关的“评议员”组成。

这一次，好象是因为翻译问题，阻滞了中国院士尽早诞生的时间。

又是Academy（阿卡德米），这个推动西方诞生了院士和院士制的古希腊英雄，使中国的翻译家不知用一个什么样的词来匹配，才能表达出它应有的深邃和高雅。而如果直译为阿卡德米，难以表达科学家中精英分子的“身价”，也许，正是因为这个原因，中国的院士制只好先放一放了。

这一放就放了20年。

1946年，中国的科学家们觉得，无论是否能准确地翻译Academy，中国院士也必须诞生了。

为了Academy，科学家们还是煞费心思。起初拟为“会员”，觉得太俗。而后称为“学侣”，“院侣”，没有科学味倒有了宗教味。又说译为“院员”吧，更不好听，好像是扫大街的清洁工。几经周折，傅斯年（一说是萨本栋）倡议称“院士”。真是一个好词，听着看着，都有了深邃和高雅的感觉。交给评议员们去表决，一致通过。

1948年3月，中国院士终于诞生了。

通过对全国科学家的层层选拔，拟定出了一个450人的名单，再由评议会审定其中的150人为院士候选人。最后，评议会进行了选举，结果，81人当选为第一届中国院士。

这批院士，体现了20世纪中国上半叶的科学水平，属于中国现代科学家的第一代和第二代。

让我们记住他们的名字——

数理组（含数学、物理、化学、天文、地学、技术科学）28人：

姜立夫

许宝騄

陈省身

华罗庚

苏步青

吴大猷

吴有训

李书华

叶企孙

赵忠尧

严济慈

饶毓泰

吴  宪

吴学周

庄长恭

曾昭抡

朱家骅

李四光

翁文灏

黄汲清

杨钟健

谢家荣

竺可桢

周  仁

侯德榜

茅以升

凌鸿勋

萨本栋

 

 

生物组（含生物学、农学、医学、药学、人类学、心理学）25人：

王家楫

伍献文

贝时璋

秉  志

陈  桢

童第周

胡先骕

殷宏章

张景钺

钱崇澍

戴芳澜

罗宗洛

李宗恩

袁眙瑾

张孝骞

陈克恢

吴定良

汪敬熙

林可胜

汤佩松

冯德培

蔡  翘

李先闻

俞大绂

邓叔群

 

 

 

 

 

人文组（社会科学）28人：

吴敬恒

金岳霖

汤用彤

冯友兰

余嘉锡

胡  适

张元济

杨树达

柳诒徵

陈  垣

陈寅恪

傅斯年

顾颉刚

李方桂

赵元任

李  济

梁思永

郭沫若

董作宾

梁思成

王世杰

王宠惠

周鲠生

钱端升

肖公权

马寅初

陈  达

陶孟和

 

 

 

正是这批中国现代科学的开路人，拉开了即将上演的中国院士史的序幕。