32 R相关与回归

本章所用例子数据下载：

32.1 相关分析

考虑连续型随机变量之间的关系。相关系数定义为 \[\rho(X, Y) = \frac{E\left[ (X - EX)(Y-EY) \right]} {\sqrt{\text{Var}(X)\text{Var}(Y)}} \] 又称Pearson相关系数。

\(-1 \leq \rho \leq 1\)。\(\rho\)接近于\(+1\)表示\(X\)和\(Y\)有正向的相关； \(\rho\)接近于\(-1\)表示\(X\)和\(Y\)有负向的相关。

相关系数代表的是线性相关性， 对于\(X\)和\(Y\)的其它相关可能反映不出来， 比如\(X \sim \text{N}(0,1)\)，\(Y = X^2\)， 有\(\rho(X, Y) = 0\)。

给定样本\((X_i, Y_i), i=1,2,\dots,n\)，样本相关系数为 \[r = \frac{\sum_{i=1}^n (X_i - \bar X) (Y_i - \bar Y)} {\sqrt{\sum_{i=1}^n (X_i - \bar X)^2 \sum_{i=1}^n (Y_i - \bar Y)^2}} \]

用散点图和散点图矩阵直观地查看变量间的相关。

例如，线性相关的模拟数据的散点图:

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
y <- 20 + 0.5*x + rnorm(nsamp,0,0.5)
plot(x, y)
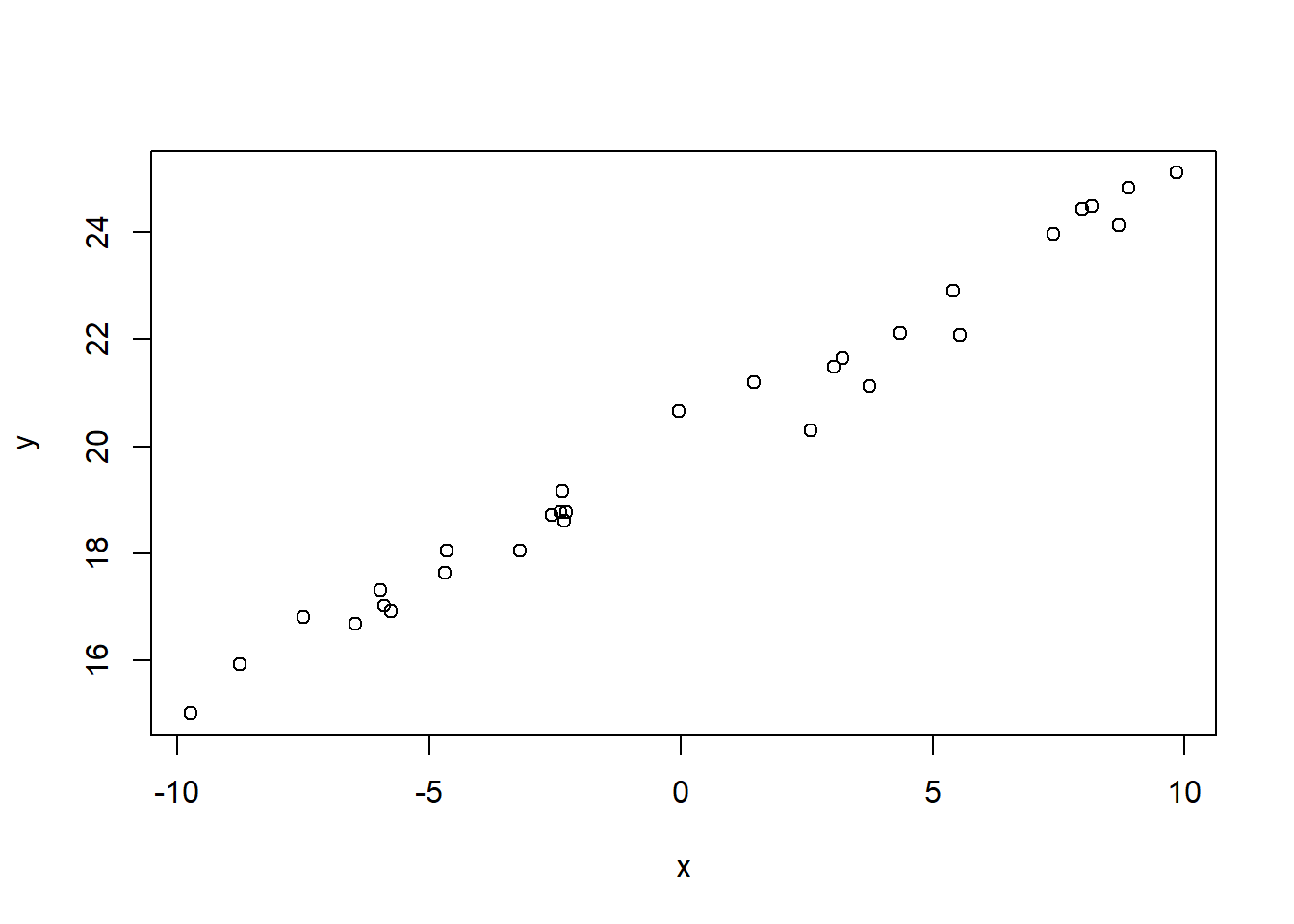
线性相关数据

图32.1: 线性相关数据

二次曲线相关的模拟数据散点图:

set.seed(1)
y2 <- 0.5*x^2 + rnorm(nsamp,0,2)
plot(x, y2)
二次曲线相关数据

图32.2: 二次曲线相关数据

指数关系的例子:

set.seed(1)
y3 <- exp(0.2*(x+10)) + rnorm(nsamp,0,2)
plot(x, y3)
指数关系相关数据

图32.3: 指数关系相关数据

对数关系的例子:

set.seed(1)
y4 <- log(10*(x+12)) + rnorm(nsamp,0,0.1)
plot(x, y4)
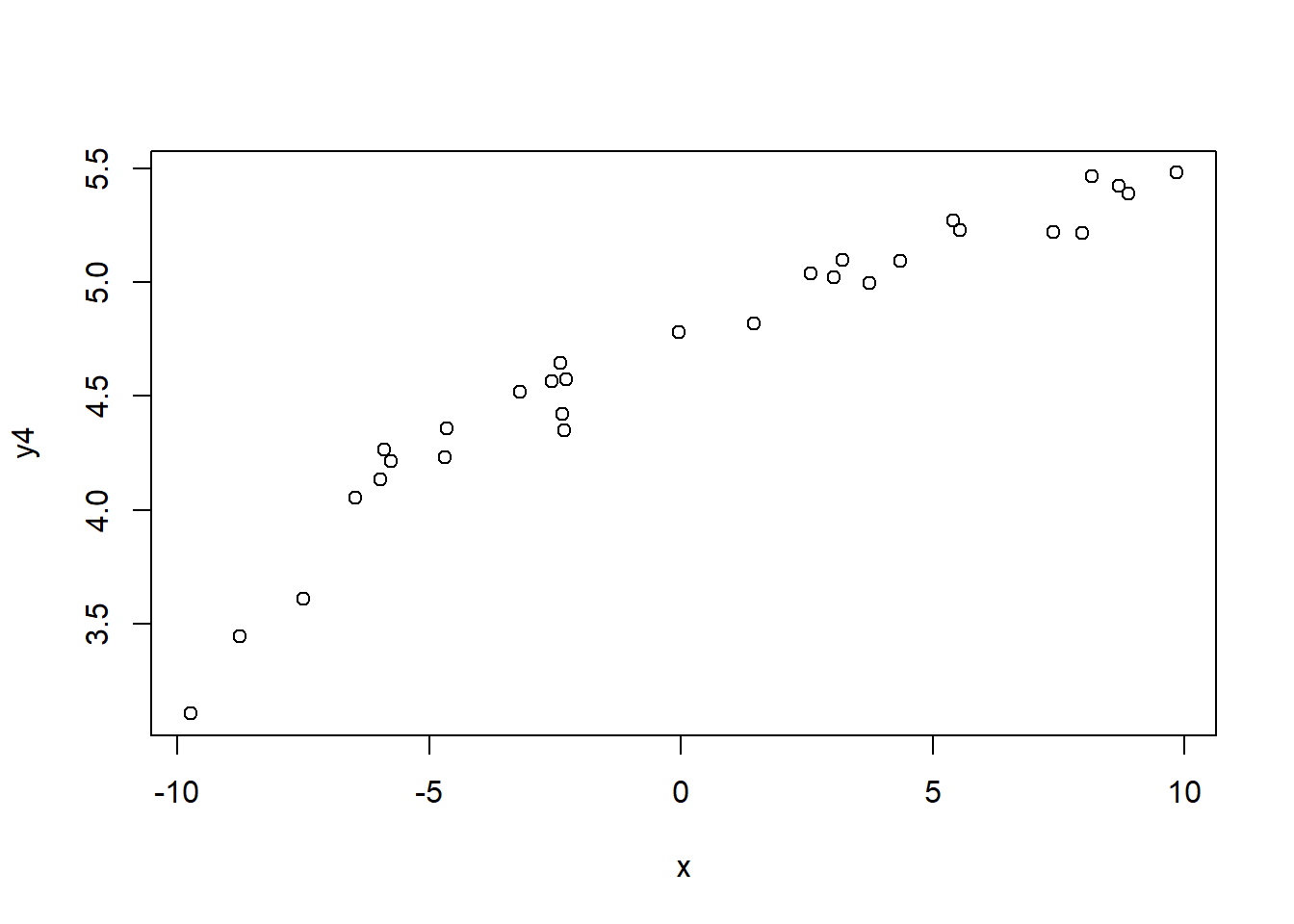
对数关系相关数据

图32.4: 对数关系相关数据

32.1.1 相关系数的性质

  • 取值\(-1 \leq r \leq 1\)。
  • \(r>0\)表示正线性相关； \(r<0\)表示负线性相关。
  • 当\(r=1\)时\((x_i, y_i), i=1,\dots,n\)这\(n\)个点完全在一条正斜率的直线上， 属于确定性关系。
  • 当\(r=-1\)时\((x_i, y_i), i=1,\dots,n\)这\(n\)个点完全在一条负斜率的直线上， 属于确定性关系。
  • 计算相关系数时与\(x, y\)的次序或记号无关。
  • 如果对变量\(x\)或者\(y\)分别乘以倍数，再分别加上不同的平移量， 相关系数不变。 即：\(a + bx\)与\(c + dy\)的相关系数， 等于\(x, y\)的相关系数。 这样，相关系数不受单位、量纲的影响。 相关系数是无量纲的。
  • 如果\(x\)和\(y\)之间是非线性相关， 相关系数不一定能准确反映其关系， 只能作为一定程度的近似。

设变量\(X\)和\(Y\)的样本存放于R向量x和y中， 用cor(x,y)计算样本相关系数。

set.seed(1)
x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40 - (x-7)^2 + rnorm(30)
yy <- 40 - (xx-7)^2
plot(x, y, pch=16)
lines(xx, yy)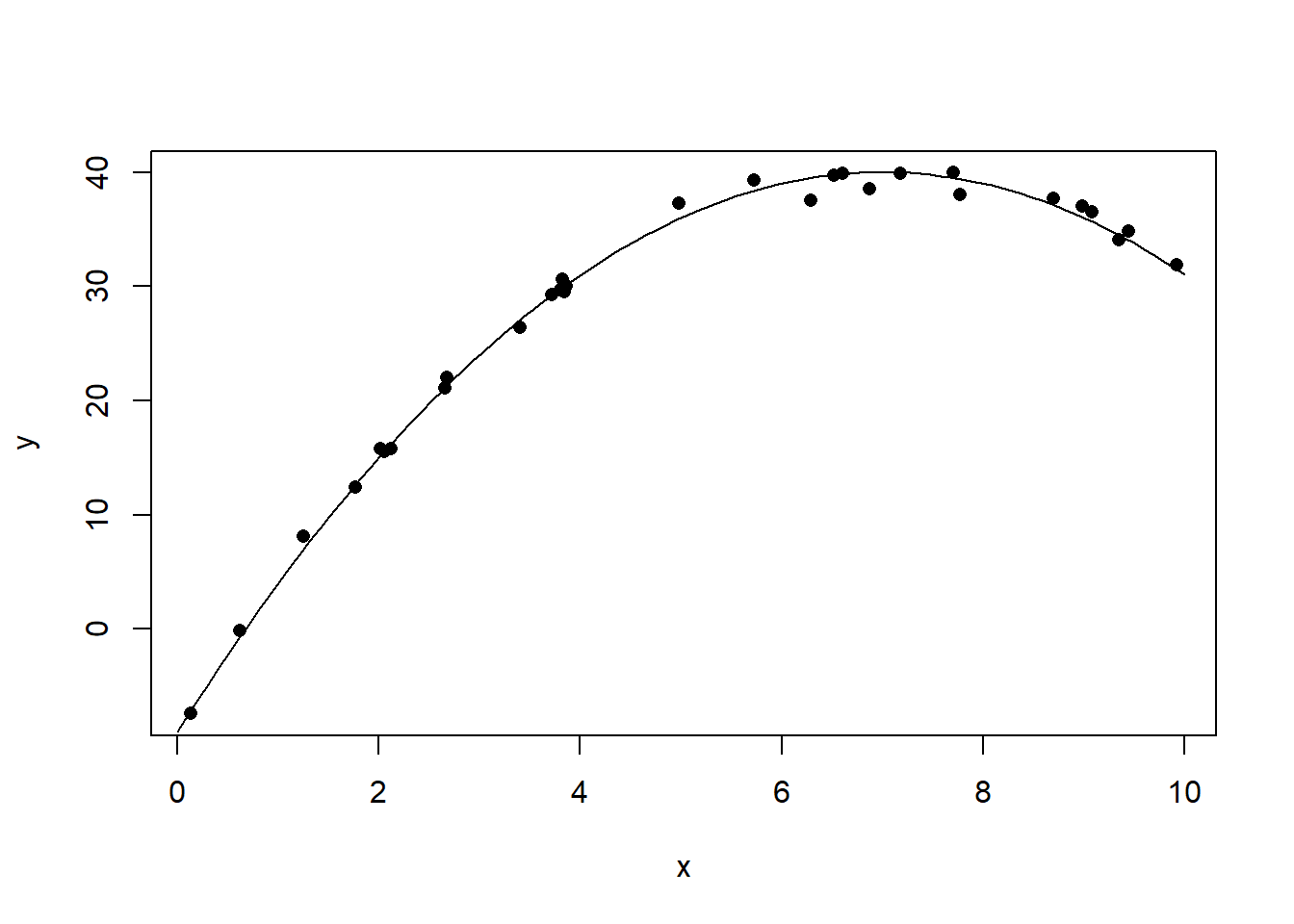
曲线相关数据的相关系数例1

图32.5: 曲线相关数据的相关系数例1 

cor(x, y)
## [1] 0.8244374
x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40 - (x-5)^2 + rnorm(30)
yy <- 40 - (xx-5)^2
plot(x, y, pch=16)
lines(xx, yy)
曲线相关数据的相关系数例2

图32.6: 曲线相关数据的相关系数例2 

cor(x, y)
## [1] -0.042684
x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40*exp(-x/2) + rnorm(30)
yy <- 40*exp(-xx/2)
plot(x, y, pch=16)
lines(xx, yy)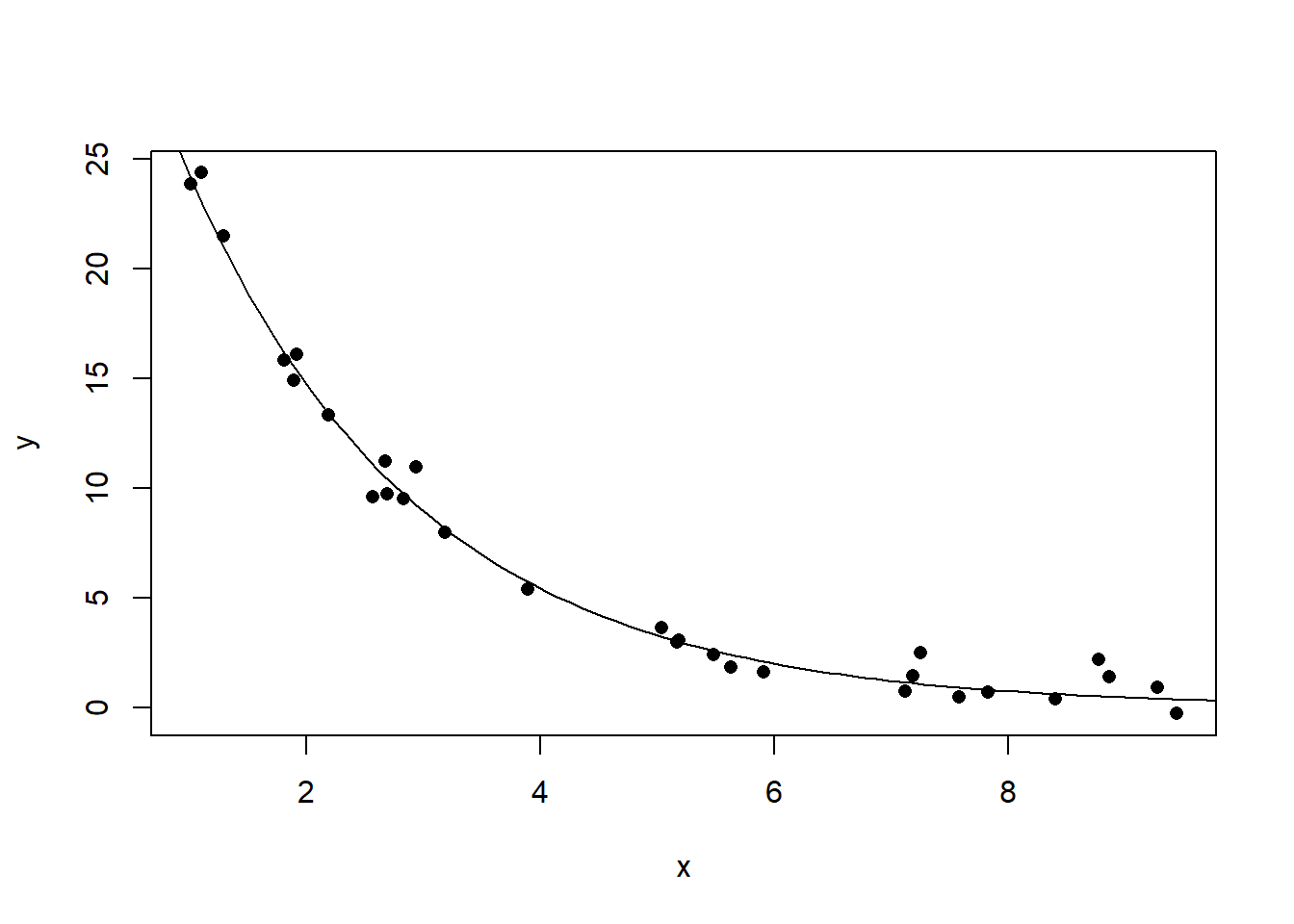
曲线相关数据的相关系数例3

图32.7: 曲线相关数据的相关系数例3 

cor(x, y)
## [1] -0.8841117

32.1.2 相关与因果

相关系数是从数据中得到的\(x\)和\(y\)两个变量关系的一种描述， 不能直接引申为因果关系。

例如，增加身高，不一定增长体重。

实际中有许多错误理解相关与因果性的例子。 例如：研究发现喝咖啡的人群比不喝咖啡的人群心脏病发病率高。 于是断言喝咖啡导致心脏病危险增加。 进一步研究更多的因素发现， 喝咖啡放糖很多的人心脏病发病率才增高了。

32.1.3 相关系数大小

  • 相关系数绝对值在0.8以上认为高度相关。
  • 在0.5到0.8之间认为中度相关。
  • 在0.3到0.5之间认为低度相关。
  • 在0.3以下认为不相关或相关性很弱以至于没有实际价值。
  • 当然，在特别重要的问题中， 只要经过检验显著不等于零的相关都认为是有意义的。

32.1.4 相关系数的检验

相关系数\(r\)是总体相关系数\(\rho\)的估计。 \[H_0: \rho=0 \longleftrightarrow H_a: \rho\neq 0\] 检验统计量 \[t = \frac{r \sqrt{n-2}}{\sqrt{1 - r^2}}\] 当总体\((X, Y)\)服从二元正态分布且\(H_0: \rho=0\)成立时， \(t\)服从\(t(n-2)\)分布。 设\(t\)统计量值为\(t_0\)，p值为 \[P(|t(n-2)| > |t_0|)\]

在R中用cor.test(x,y)计算检验。

例如：

cor.test(d.class$height, d.class$weight)
## 
##  Pearson's product-moment correlation
## 
## data:  d.class$height and d.class$weight
## t = 7.5549, df = 17, p-value = 7.887e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7044314 0.9523101
## sample estimates:
##       cor 
## 0.8777852

得身高与体重的相关系数为0.88，检验的p值为7.887e-07， 95%置信区间为\([0.70, 0.95]\)。

可以用ggstatsplot包将相关系数检验进行图示：

library(ggstatsplot)
## You can cite this package as:
##      Patil, I. (2021). Visualizations with statistical details: The 'ggstatsplot' approach.
##      Journal of Open Source Software, 6(61), 3167, doi:10.21105/joss.03167
ggscatterstats(
  data  = d.class,
  x     = height,
  y     = weight,
  xlab  = "身高",
  ylab  = "体重",
  title = "体重与身高的相关性"
)
## Registered S3 method overwritten by 'ggside':
##   method from   
##   +.gg   ggplot2
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.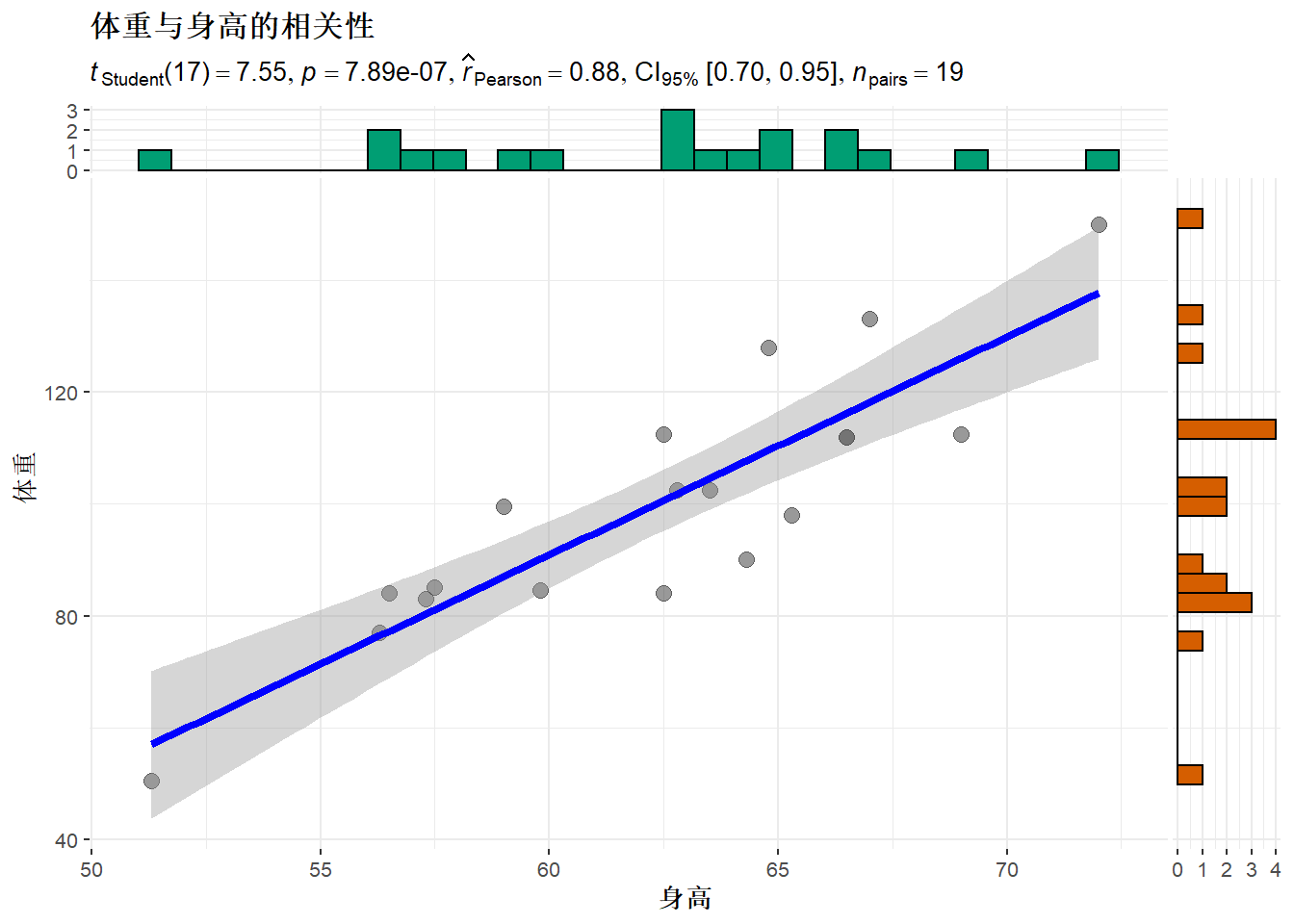

再例如:

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
y <- 0.5*x^2 + rnorm(nsamp,0,2)
cor.test(x, y)
## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = 0.93076, df = 28, p-value = 0.3599
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.1994815  0.5021658
## sample estimates:
##       cor 
## 0.1732378

得x与y的样本相关系数为0.17, p值为0.36，不显著。

32.1.4.1 相关系数检验的功效和样本量

pwr包的pwr.r.test()可以计算相关系数检验的功效和样本量。 用相关系数绝对值作为效应大小， 常用值为：

  • 小：\(0.1\);
  • 中: \(0.3\);
  • 大: \(0.5\)。

比如，样本量为30， 检验“大”的效应， 计算其功效：

library(pwr)
## Warning: package 'pwr' was built under R version 4.2.2
cohen.ES(test = "r", size = "large")
## 
##      Conventional effect size from Cohen (1982) 
## 
##            test = r
##            size = large
##     effect.size = 0.5
pwr.r.test(
  r = 0.5,
  n = 30,
  alternative = "two.sided"
)
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 30
##               r = 0.5
##       sig.level = 0.05
##           power = 0.8250298
##     alternative = two.sided

功效为\(83\%\)。

检验“小”的效应， 功效为\(80\%\)， 需要的样本量：

cohen.ES(test = "r", size = "small")
## 
##      Conventional effect size from Cohen (1982) 
## 
##            test = r
##            size = small
##     effect.size = 0.1
pwr.r.test(
  r = 0.1,
  power = 0.80,
  alternative = "two.sided"
)
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 781.7516
##               r = 0.1
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided

需要的样本量为\(782\)。

32.1.5 相关阵

如果x是一个仅包含数值型列的数据框， 则cor(x)计算样本相关系数矩阵； var(x)计算样本协方差阵。

corrgram::corrgram()可以绘制相关系数矩阵的图形， 用颜色和阴影浓度代表相关系数正负和绝对值大小， 用饼图中阴影部分大小代表相关系数绝对值大小。 如：

library(corrgram)
corrgram(
  baseball[,c("Assists","Atbat","Errors","Hits","Homer","logSal",
           "Putouts","RBI","Runs","Walks","Years")], 
  order=TRUE, main="Baseball data PC2/PC1 order",
  lower.panel=panel.shade, upper.panel=panel.pie)
相关阵图形

图32.8: 相关阵图形

其中选项order=TRUE重排各列的次序使得较接近的列排列在相邻位置。

ggcorrplot包也提供了类似的功能：

library(ggcorrplot)
baseball |>
  select(all_of(c(
  "Assists","Atbat","Errors","Hits","Homer","logSal",
  "Putouts","RBI","Runs","Walks","Years"))) |>
  cor(use="pairwise.complete.obs") |>
  ggcorrplot(hc.order=TRUE)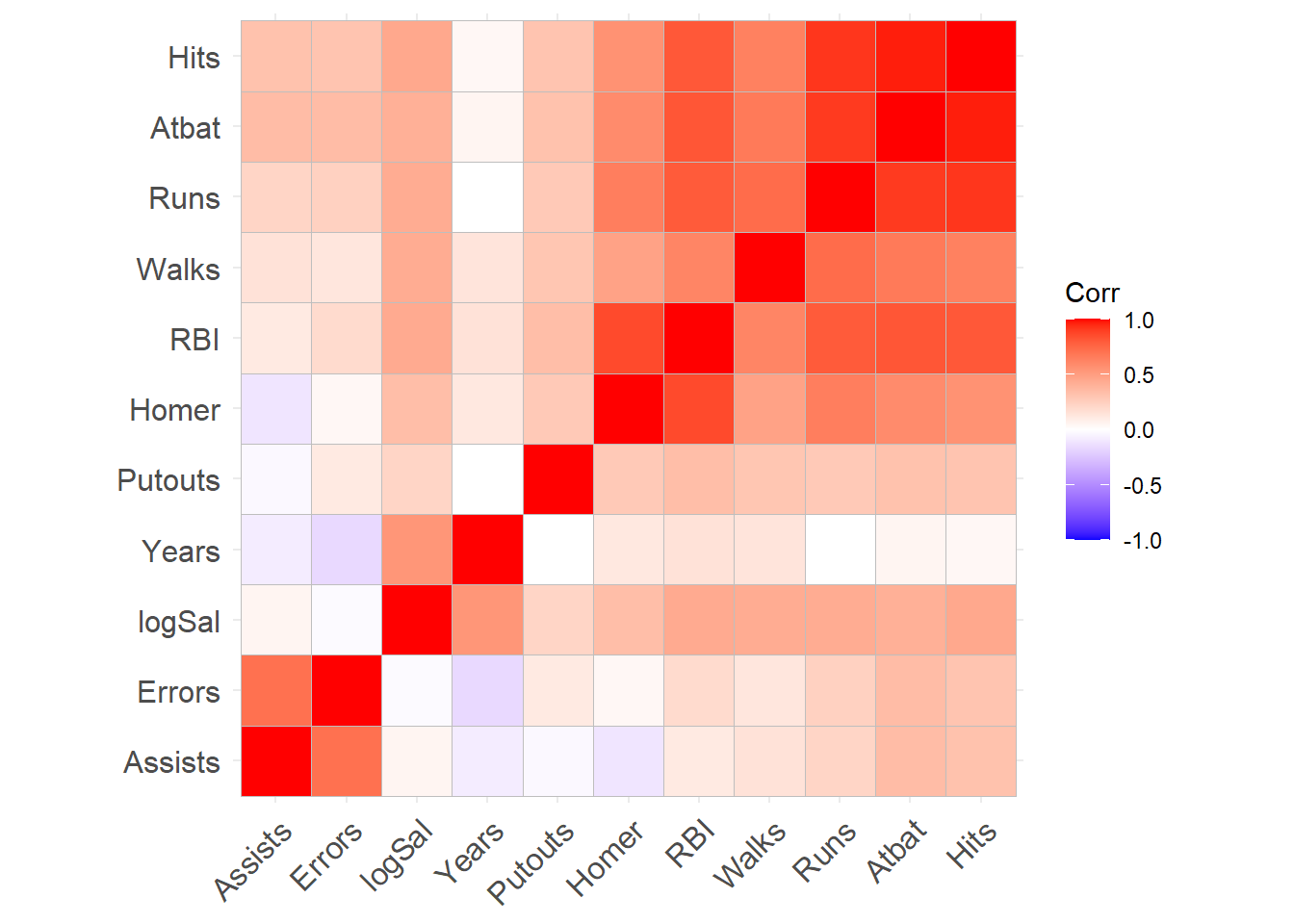
相关阵图形（ggcorrplot）

图32.9: 相关阵图形（ggcorrplot）

ggstatsplot包也提供了这样的功能， 并且进行检验：

library(ggstatsplot)
ggcorrmat(
  data     = baseball[,c("Assists","Atbat","Errors","Hits","Homer","logSal",
             "Putouts","RBI","Runs","Walks","Years")]
)
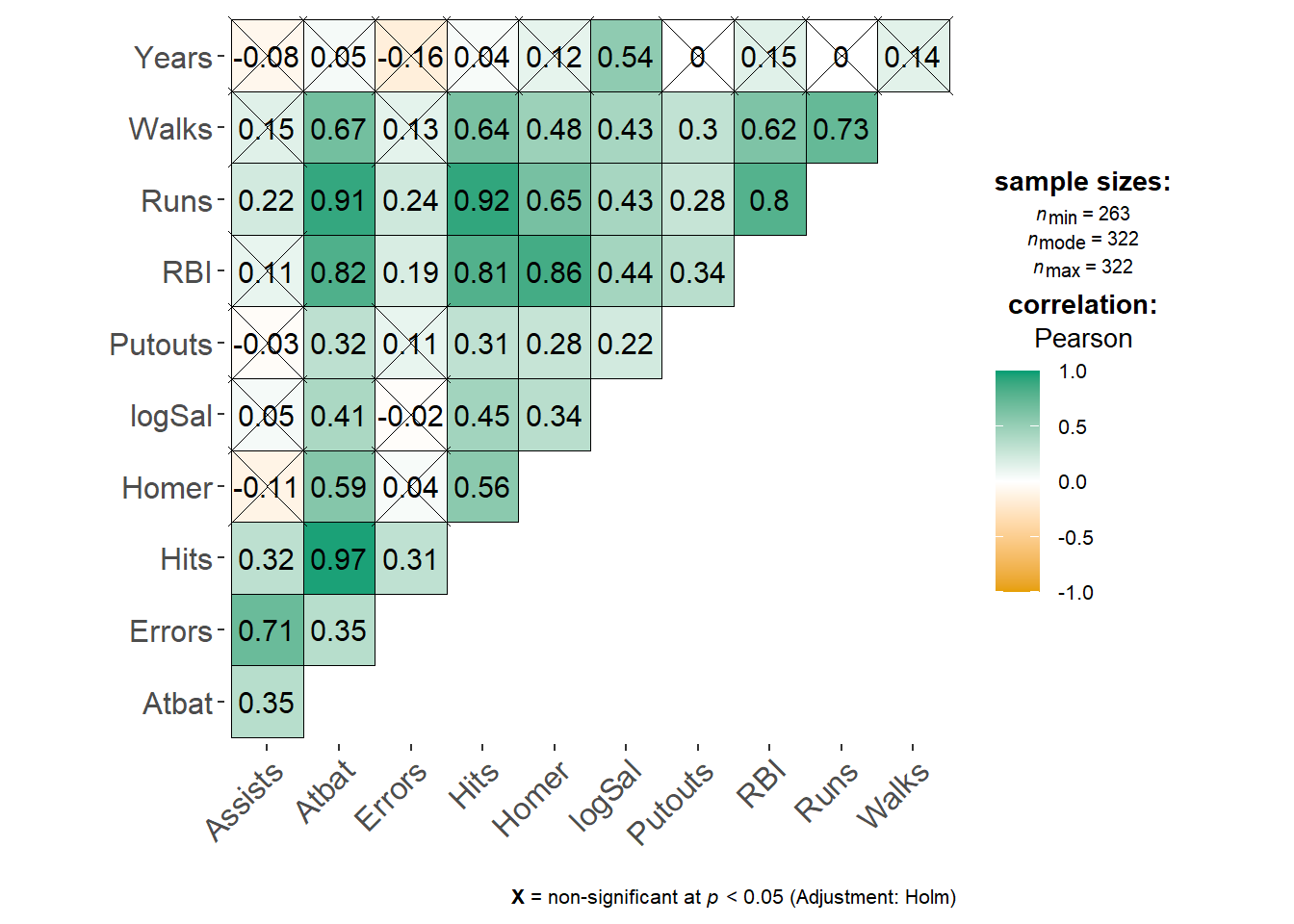
相关阵图形（ggstatsplot）

图32.10: 相关阵图形（ggstatsplot）

32.1.6 Spearman秩相关系数

Spearman秩相关系数也成为Spearman rho系数， 是两个变量的秩统计量的相关系数。 计算如：

cor.test(d.class$height, d.class$weight,
  method="spearman")
## Warning in cor.test.default(d.class$height, d.class$weight, method =
## "spearman"): Cannot compute exact p-value with ties
## 
##  Spearman's rank correlation rho
## 
## data:  d.class$height and d.class$weight
## S = 164.43, p-value = 2.983e-06
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.8557611

秩相关系数值为\(0.8558\)。

32.1.7 Kendall tau系数

当变量\((X, Y)\)正相关性很强时， 任意两个观测的\(X\)值的大小顺序应该与\(Y\)值的大小顺序相同； 如果独立， 一对观测的\(X\)值比较和\(Y\)值比较顺序相同与顺序相反的数目应该基本相同。 Kandall tau系数也是取值于\([-1, 1]\)区间， 用这样的思想表示两个变量的相关性和正负。

如：

cor.test(d.class$height, d.class$weight,
  method="kendall")
## Warning in cor.test.default(d.class$height, d.class$weight, method = "kendall"):
## Cannot compute exact p-value with ties
## 
##  Kendall's rank correlation tau
## 
## data:  d.class$height and d.class$weight
## z = 4.2136, p-value = 2.513e-05
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
## 0.7142984

Kendall tau系数的值为\(0.7143\)。

32.2 一元回归分析

32.2.1 模型

考虑两个变量\(Y\)与\(X\)的关系，希望用\(X\)值的变化解释\(Y\)值的变化。 \(X\)称为自变量(independent variable)，\(Y\)称为因变量(response variable)。

假设模型 \[\begin{aligned} Y = a + b X + \varepsilon, \quad \varepsilon \sim \text{N}(0,\sigma^2) \end{aligned} \]

在回归分析理论中通常假定\(X\)是非随机的， 因变量\(Y\)的随机性来自误差项\(\varepsilon\)。 实际应用中\(X\)常常也是随机的。

设观测值为\((X_i, Y_i), i=1,2,\dots,n\)，假设观测值满足上模型。 即 \[\begin{aligned} Y_i = a + b X_i + \varepsilon_i, \quad \varepsilon_i \text{ iid }\sim \text{N}(0,\sigma^2) . \end{aligned} \]

32.2.2 最小二乘法

直观上看，要找最优的直线\(y=a+bx\)使得直线与观测到的点最接近。 例如：

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
y <- 20 + 0.5*x + rnorm(nsamp,0,0.5)
plot(x, y)
abline(lm(y ~ x), col="red", lwd=2)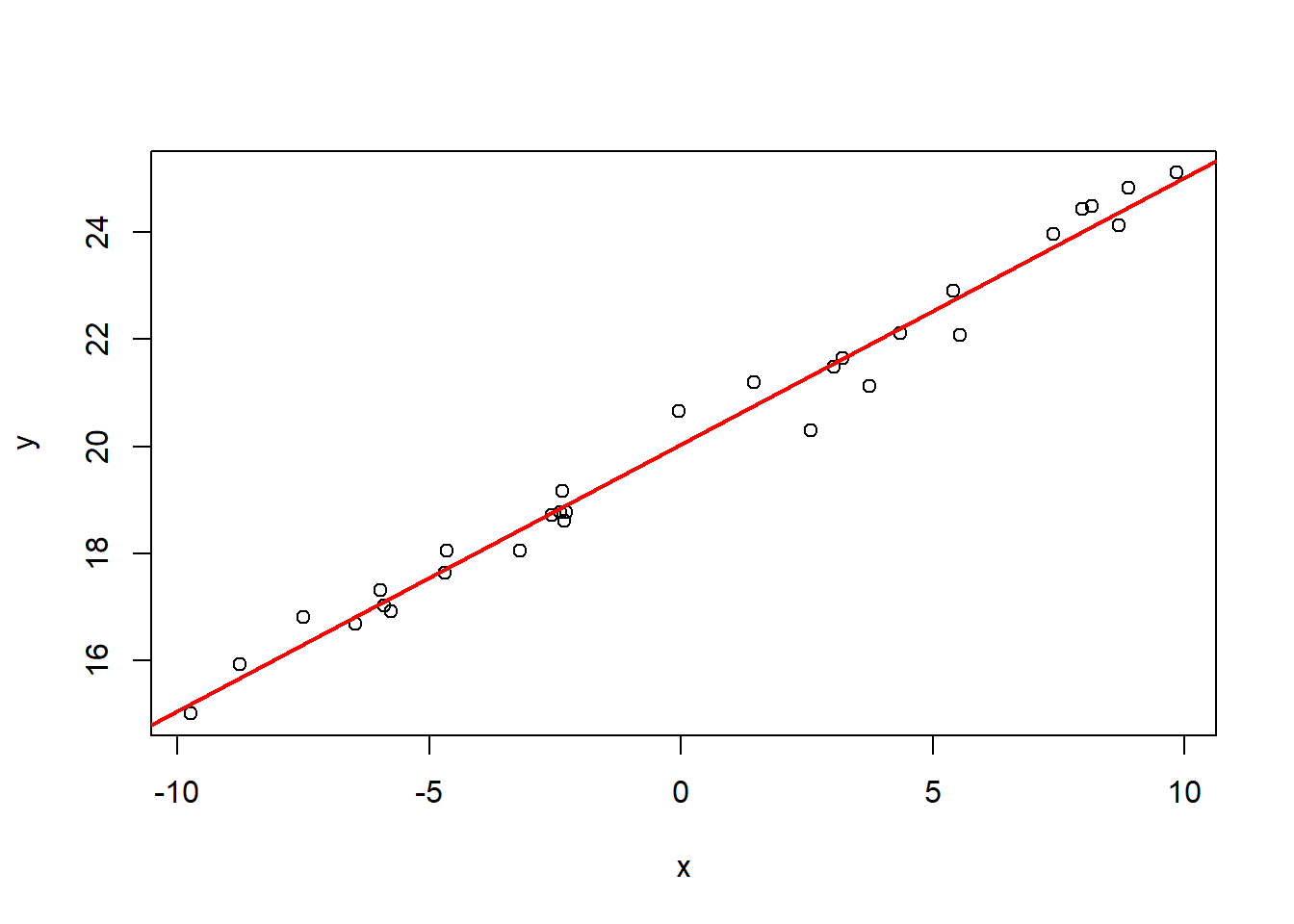
一元线性回归最小二乘估计

图32.11: 一元线性回归最小二乘估计

\(a,b\)的解用最小二乘法得到:

\[\min_{a,b} \sum_{i=1}^n \left( y_i - a - b x_i \right)^2\]

最小二乘解表达式为

\[\begin{aligned} \hat b =& \frac{\sum_i (x_i - \bar x)(y_i - \bar y)} {\sum_i (x_i - \bar x)^2} = r_{xy} \frac{S_y}{S_x} \\ \hat a =& \bar y - \hat b \bar x \end{aligned}\] 其中\(r_{xy}\)为\(X\)与\(Y\)的样本相关系数， \(S_x\)与\(S_y\)分别为\(X\)和\(Y\)的样本标准差。

随机误差方差\(\sigma^2\)的估计取为

\[ \hat\sigma^2 = \frac{1}{n-2}\sum_i (y_i - \hat a - \hat b x_i)^2 \]

标准误差: 为衡量\(\hat a\)和\(\hat b\)的估计精度， 计算\(\text{SE}(\hat a)\)和\(\text{SE}(\hat b)\)。

估计结果:

  • 系数估计\(\hat a\), \(\hat b\)以及相应的标准误差估计\(\text{SE}(\hat a)\)和\(\text{SE}(\hat b)\);
  • 拟合值(预测值) \[\hat y_i = \hat a + \hat b x_i, \quad i=1,2,\dots,n\]
  • 残差 \[e_i = y_i - \hat y_i, \quad i=1,2,\dots,n\]
  • \(\text{SSE}=\sum_i e_i^2\) 称为残差平方和，残差平方和小则拟合优。

32.2.3 回归有效性

32.2.3.1 拟合优度指标

按照最小二乘估计公式，只要\(x_1, x_2, \dots, x_n\)不全相等， 不论\(x, y\)之间有没有相关关系， 都能计算出参数估计值。 得到的回归直线与观测数据的散点之间的接近程度代表了回归结果的优劣。

残差平方和为 \[ \text{SSE}=\sum_{i=1}^n (y_i - \hat a - \hat b x_i)^2 . \] 残差平方和越小， 说明回归直线与观测数据点吻合得越好。 均方误差为 \[ \text{MSE}= \frac{1}{n} \sum_{i=1}^n (y_i - \hat a - \hat b x_i)^2 . \]

\(y\)是因变量， 因变量的数据的离差平方和 \[ \text{SST}=\sum_{i=1}^n (y_i - \bar y)^2 \] 代表了因变量的未知变动大小， 需要对这样的变动用自变量进行解释， 称SST为总平方和。

可以证明如下平方和分解公式： \[ \text{SST} = \text{SSR} + \text{SSE} . \] 其中SSR称为回归平方和。

令\(\hat y_i = \hat\beta_0 + \hat\beta_1 x_i\)称为第\(i\)个拟合值， 回归平方和为 \[ \text{SSR}=\sum_{i=1}^n (\hat y_i - \bar y)^2 = \hat b^2 \sum_{i=1}^n (x_i - \bar x)^2 . \]

在总平方和中， 回归平方和是能够用回归斜率与自变量的变动解释的部分， 残差平方和是自变量不能解释的变动。 分解中，回归平方和越大，误差平方和越小， 拟合越好。 令 \[ R^2 = \frac{\text{SSR}}{\text{SST}} = 1 - \frac{\text{SSE}}{\text{SST}} . \] 称为回归的复相关系数，或判定系数。

\(0 \leq R^2 \leq 1\)。判定系数越大，回归拟合越好。 \(R^2=1\)时，观测点完全落在一条直线上面。 一元回归中\(R^2\)是\(x\)和\(y\)的样本相关系数的平方。 在多元回归时只能用复相关系数。

估计误差项方差\(\sigma^2\)为 \[ \hat\sigma^2 = \frac{1}{n-2}\sum_{i=1}^n (y_i - \hat a - \hat b x_i)^2 = \frac{1}{n-2} \text{SSE} . \]

\(\hat\sigma\)是\(\sigma\)的估计， R的回归结果中显示为“residual standard error”（残差标准误差）。 \(\hat\sigma\)是残差\(e_i = y_i - \hat y_i\)的标准差的一个粗略估计。

32.2.3.2 线性关系显著性检验

当\(b=0\)时，模型退化为\(Y = a + \varepsilon\)，\(X\)不出现在模型中， 说明\(Y\)与\(X\)不相关。检验 \[ H_0: b=0 \longleftrightarrow H_\text{a}: b \neq 0 \]

取统计量 \[F = \frac{\text{SSR}}{\text{SSE}/(n-2)}\] 检验p值为\(P(F(1, n-2) > c)\)(设\(c\)为\(F\)统计量的值)。 取检验水平\(\alpha\), p值小于等于\(\alpha\)时拒绝\(H_0\)， 认为\(y\)与\(x\)有显著的线性相关关系， 否则认为\(y\)与\(x\)没有显著的线性相关关系。

也可以使用t统计量 \[t = \frac{\hat b}{\text{SE}(\hat b)}\] 其中 \[ \text{SE}(\hat b) = \hat\sigma / \sqrt{\sum_{i=1}^n (x_i - \bar x)^2} \] 设t统计量的值为\(c\)， 检验p值为\(P(|t(n-2)| > |c|)\)。

32.2.4 R程序

设数据保存在数据框d中，变量名为y和x，用R的lm()函数计算回归，如:

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
y <- 20 + 0.5*x + rnorm(nsamp,0,0.5)
d <- data.frame(x=x, y=y)
lm1 <- lm(y ~ x, data=d); lm1
## 
## Call:
## lm(formula = y ~ x, data = d)
## 
## Coefficients:
## (Intercept)            x  
##     20.0388       0.4988

结果只有回归系数。需要用summary()显示较详细的结果。如

summary(lm1)
## 
## Call:
## lm(formula = y ~ x, data = d)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.03030 -0.16436 -0.05741  0.29511  0.64046 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 20.03883    0.07226   277.3   <2e-16 ***
## x            0.49876    0.01244    40.1   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3956 on 28 degrees of freedom
## Multiple R-squared:  0.9829, Adjusted R-squared:  0.9823 
## F-statistic:  1608 on 1 and 28 DF,  p-value: < 2.2e-16

结果中\(H_0: b=0\)的检验结果p值为\(<2e-16\)。 这个结果可以从输出最后一行的F统计量检验结果看到， 也可以从稀疏估计中自变量x所在行的t检验结果看到。

又如对d.class数据集，建立体重对身高的回归方程:

lm2 <- lm(weight ~ height, data=d.class)
summary(lm2)
## 
## Call:
## lm(formula = weight ~ height, data = d.class)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -17.6807  -6.0642   0.5115   9.2846  18.3698 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -143.0269    32.2746  -4.432 0.000366 ***
## height         3.8990     0.5161   7.555 7.89e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.23 on 17 degrees of freedom
## Multiple R-squared:  0.7705, Adjusted R-squared:  0.757 
## F-statistic: 57.08 on 1 and 17 DF,  p-value: 7.887e-07

身高对体重的影响是显著的(p值7.89e-7)。

32.2.5 回归诊断

除了系数的显著性检验以外， 对误差项是否符合回归模型假定中的独立性、方差齐性、正态性等， 可以利用回归残差进行一系列的回归诊断。 还可以计算一些异常值、强影响点的诊断。

对\(n\)组观测值，回归模型为 \[ y_i = a + b x_i + \varepsilon_i . \] 拟合值为 \[ \hat y_i = \hat a + \hat b x_i . \] 残差（residual）为 \[ e_i = y_i - \hat y_i . \]

残差相当于模型中的随机误差， 但仅在模型假定成立时才是随机误差的合理估计。 所以残差能够反映违反模型假定的情况。

\(e_i\)有量纲，不好比较大小。 定义标准化残差（内部学生化残差）： \[ r_i = \frac{e_i}{S_e\sqrt{1 - \frac{1}{n} - \frac{(x_i - \bar x)^2}{\sum_{k=1}^n (x_k - \bar x)^2}}} . \] 样本量较大时标准化残差近似服从标准正态分布， 于是取值于\([-2,2]\)范围外的点是可疑的离群点。

R中用residuals()从回归结果计算残差， 用rstandard()从回归结果计算标准化残差。

R中plot(lmres)(lmres为回归结果变量)可以做简单回归诊断。

plot(lm2)

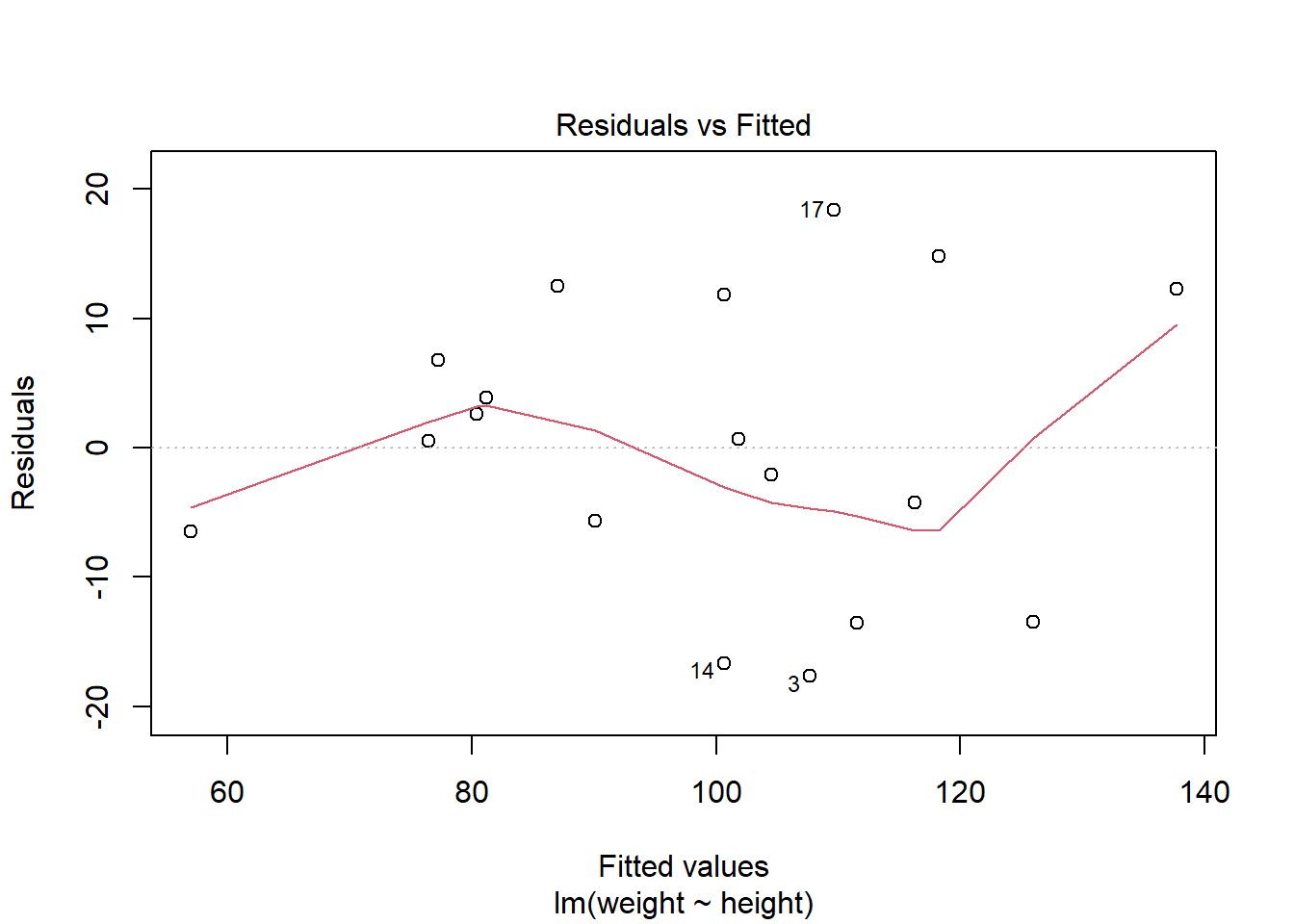
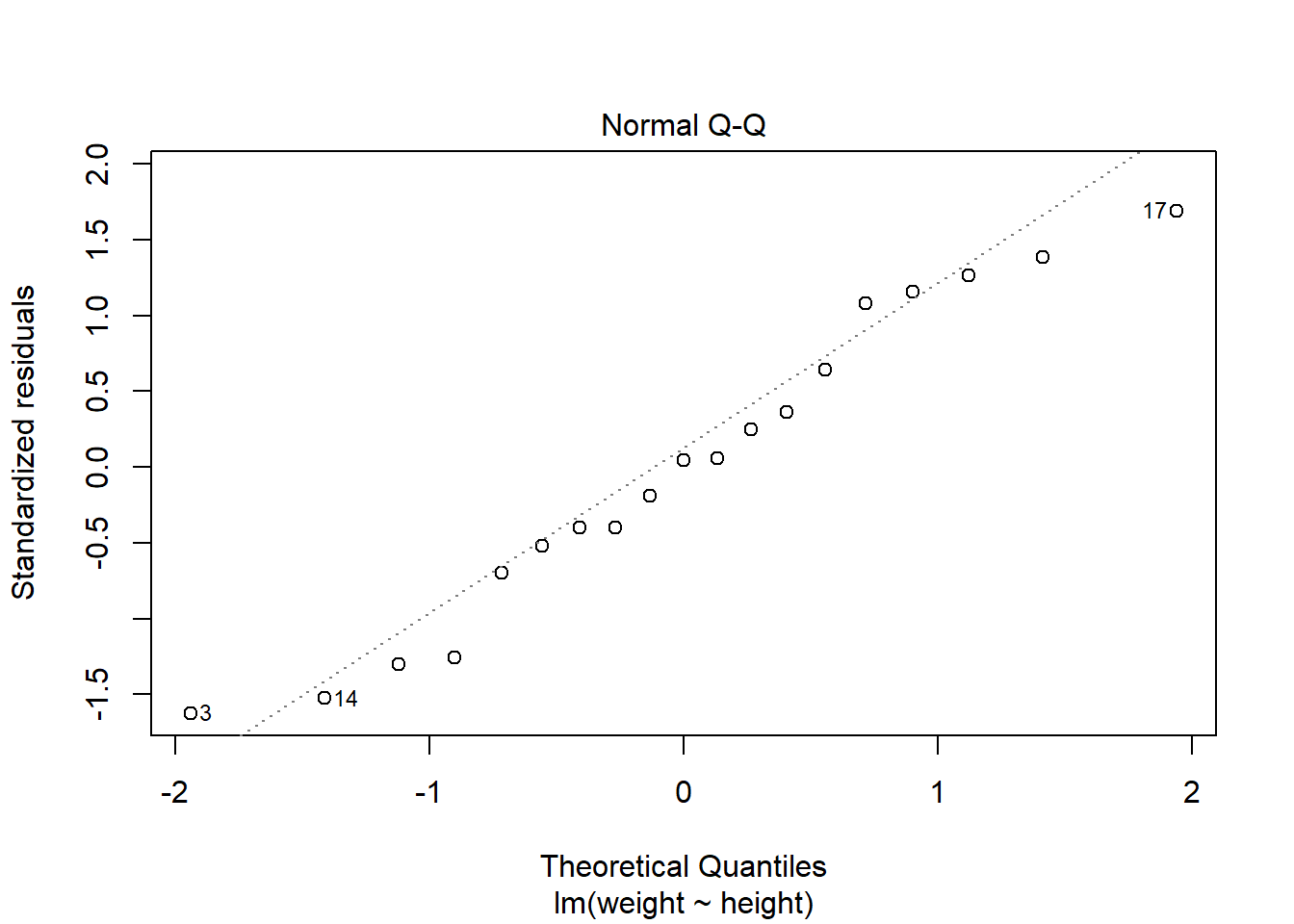
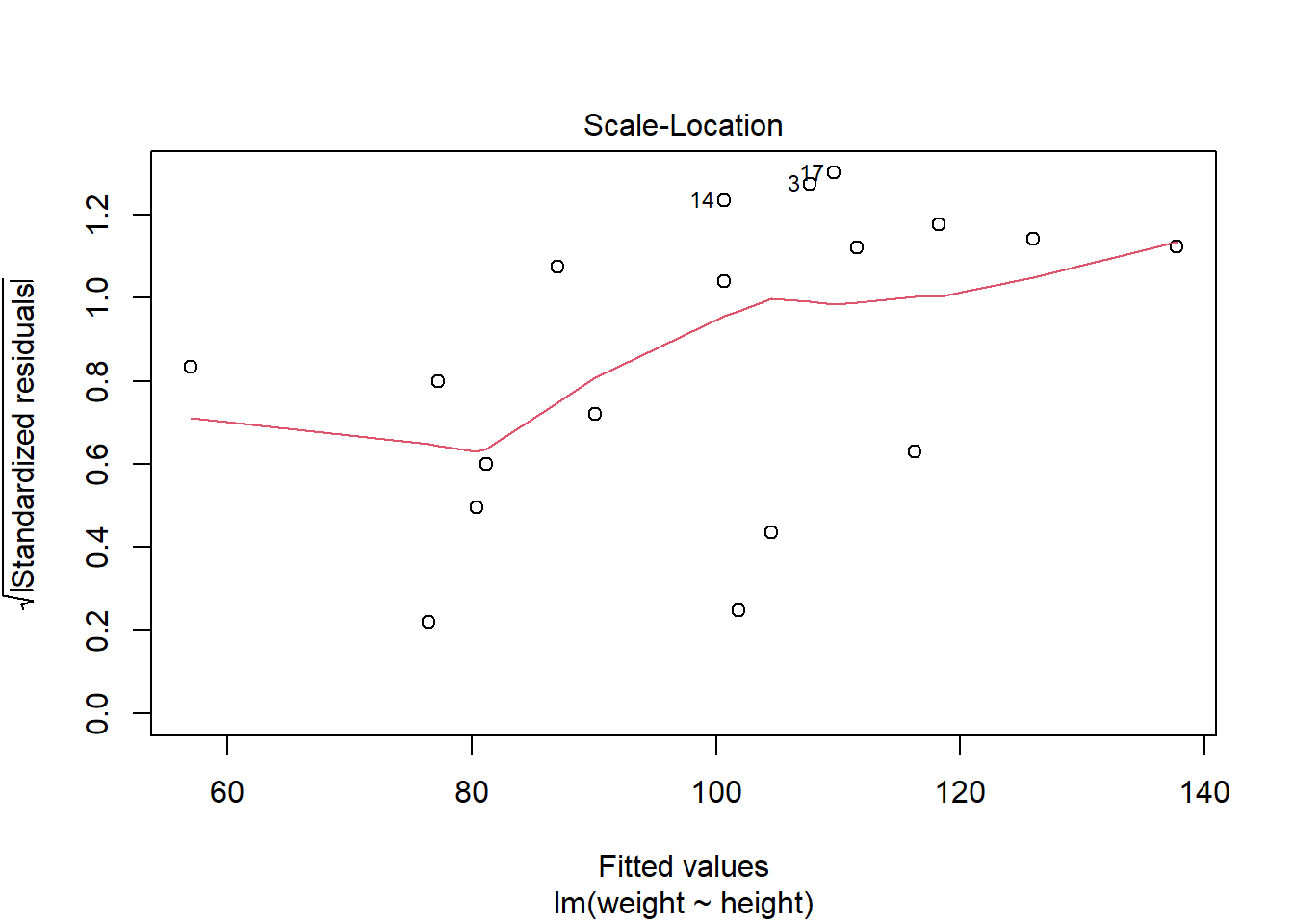
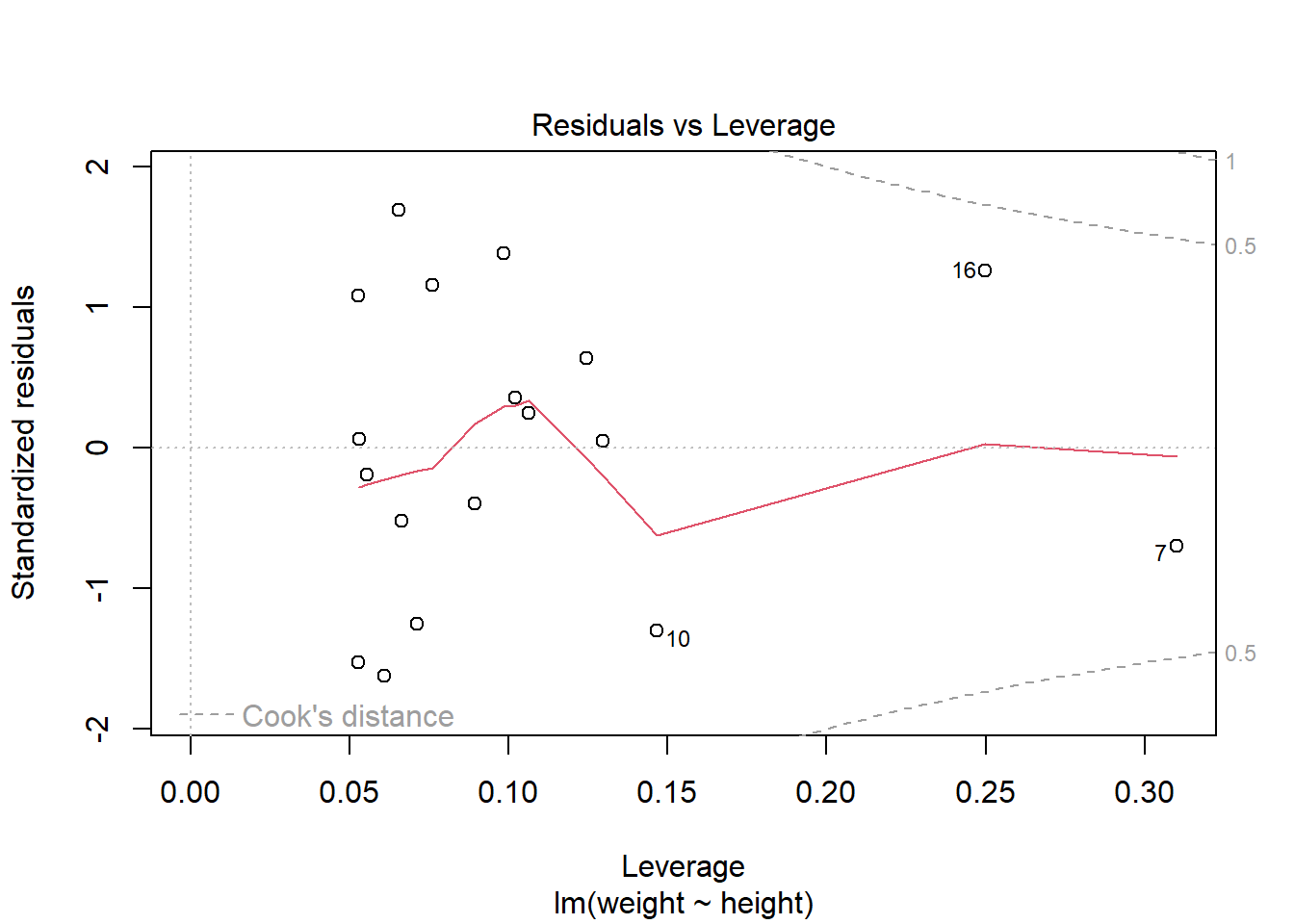
第一幅图是残差对预测值散点图， 散点应该随机在0线上下波动，不应该有曲线模式、分散程度增大模式、 特别突出的离群点等情况。

第二幅图是残差的正态QQ图， 散点接近于直线时可以认为模型误差项的正态分布假定是合理的。

第三幅图是误差大小(标准化残差绝对值的平方根)对拟合值的图形， 可以判断方差齐性假设(方差\(\sigma^2\)不变)。

第四个幅是残差对杠杆量图，并叠加了Cook距离等值线。 杠杆量代表了回归自变量对结果的影响大小， 超过\(4/n\)的值是需要重视的。 Cook距离考察删去第\(i\)个观测对回归结果的影响， 如果有超出两条虚线范围之外的点， 就可能是强影响点。

显示残差与标准化残差：

knitr::kable(cbind("残差"=residuals(lm2), 
    "标准化残差"=rstandard(lm2)),
    digits=2)
残差 标准化残差
6.73 0.64
-13.58 -1.26
-17.68 -1.63
0.51 0.05
-5.64 -0.52
-4.26 -0.40
-6.49 -0.70
11.84 1.08
0.67 0.06
-13.51 -1.30
-2.06 -0.19
14.79 1.39
2.61 0.25
-16.66 -1.52
12.48 1.16
12.30 1.26
18.37 1.69
3.83 0.36
-4.26 -0.40

可以用\(e_i\)或\(r_i\)作为纵坐标， \(x_i\)或者\(\hat y_i\)作为横坐标， 作残差图。

下面给出残差图的几种常见的缺陷：

非线性:

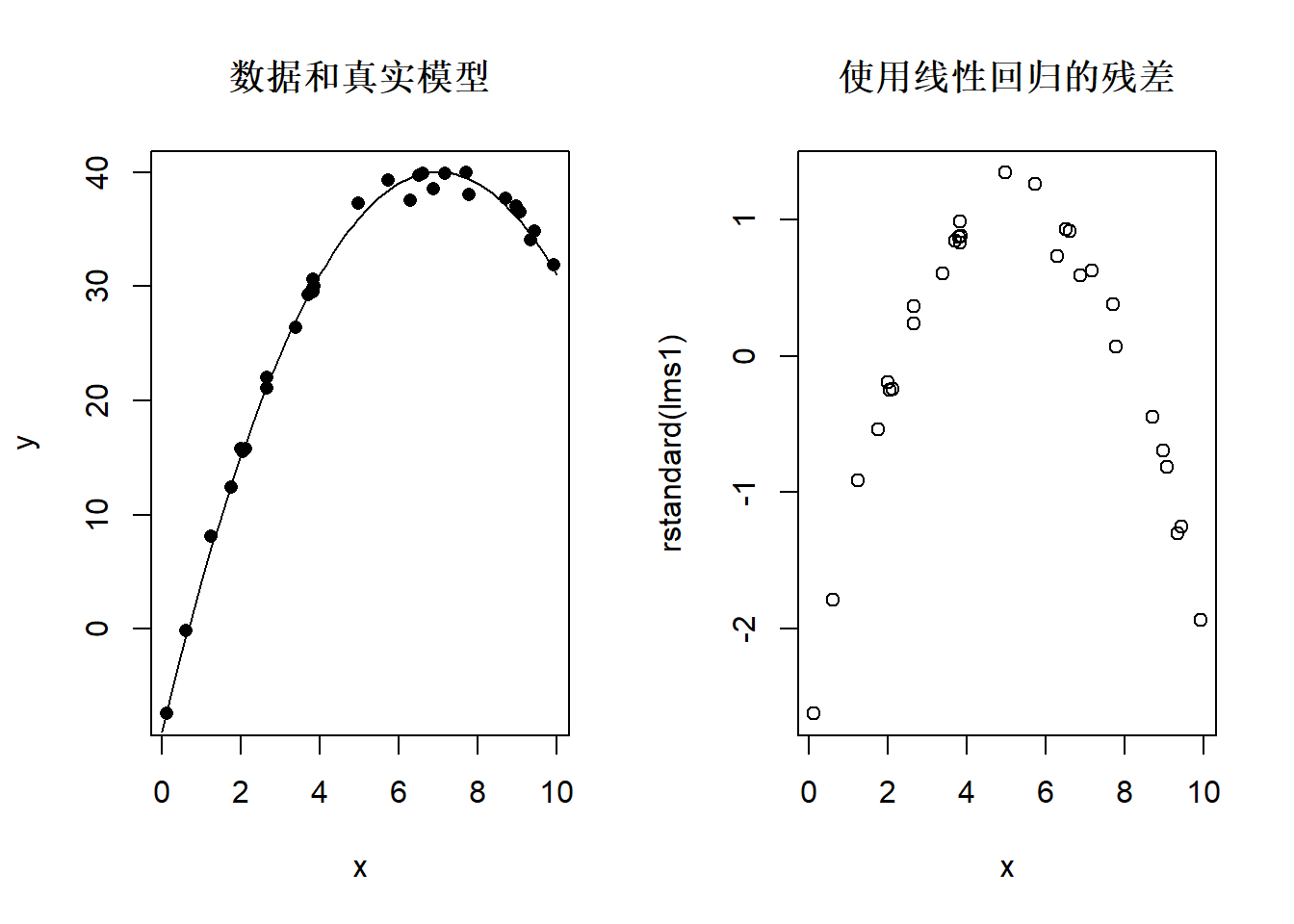
残差中非线性模式

图32.12: 残差中非线性模式

异方差:

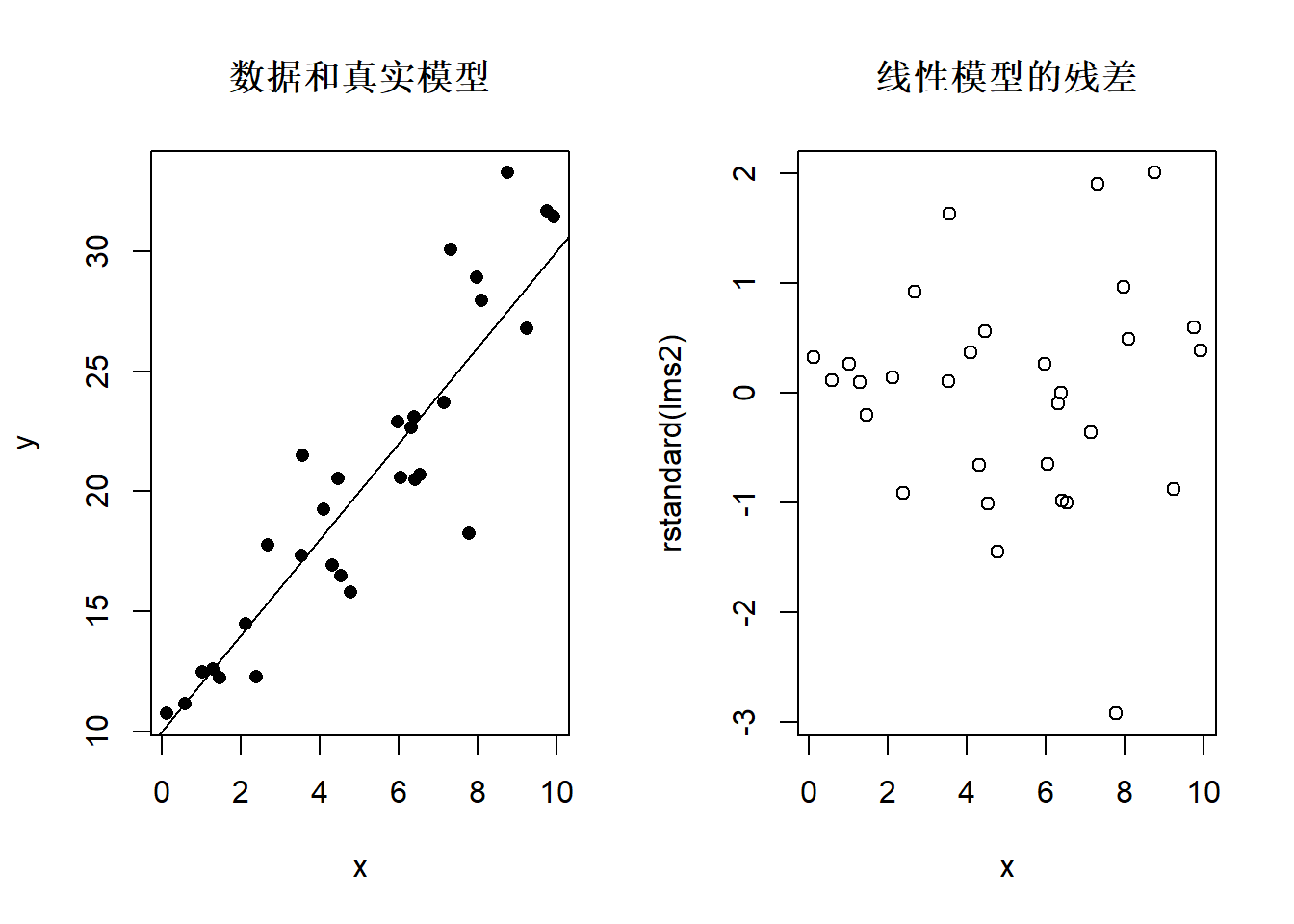
异方差情况下的残差图

图32.13: 异方差情况下的残差图

car::ncvTest()检验方差齐性。零假设是方差齐性成立。 如

car::ncvTest(lms2)
## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 4.182918, Df = 1, p = 0.040833

当数据随时间变化时，还需要考虑前后是否有序列自相关。 自相关残差图形例子：

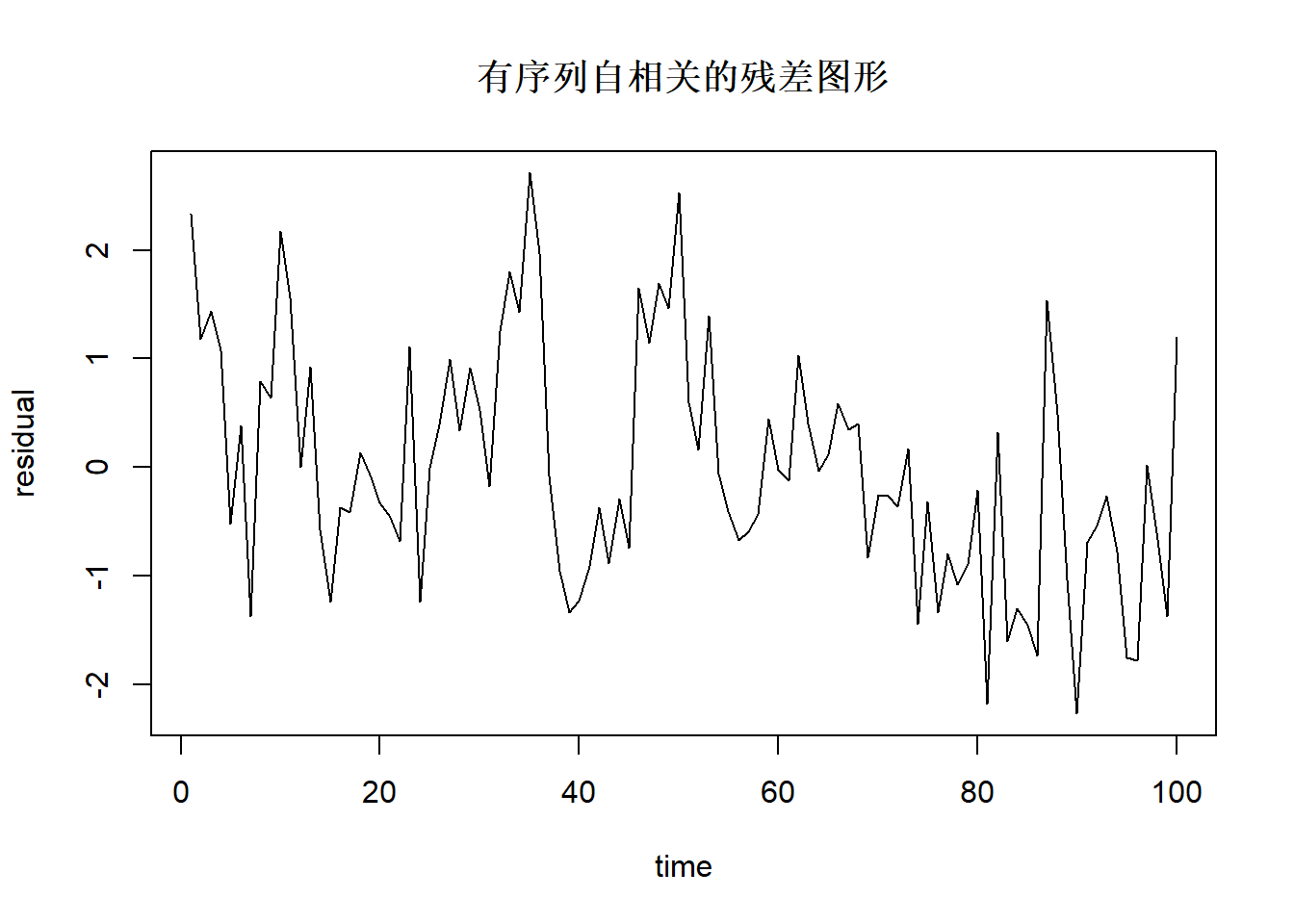
图中横坐标是观测序号。

用Durbin-Watson检验（DW检验）可以检验残差中是否有序列自相关， 零假设是没有序列自相关。 R中用car::durbinWatsonTest()检验。 序列自相关检验仅当数据中数据是沿时间等间隔记录时有意义。 如

car::durbinWatsonTest(lms3)
##  lag Autocorrelation D-W Statistic p-value
##    1       0.4736699     0.9937971       0
##  Alternative hypothesis: rho != 0

也可以对回归残差绘制ACF图， 如果除了横坐标0之外都落在两条水平界限内则认为没有序列自相关， 如果有明显超出界限的就认为有序列自相关。 如

forecast::Acf(residuals(lms3), lag.max = 10, main="")
## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo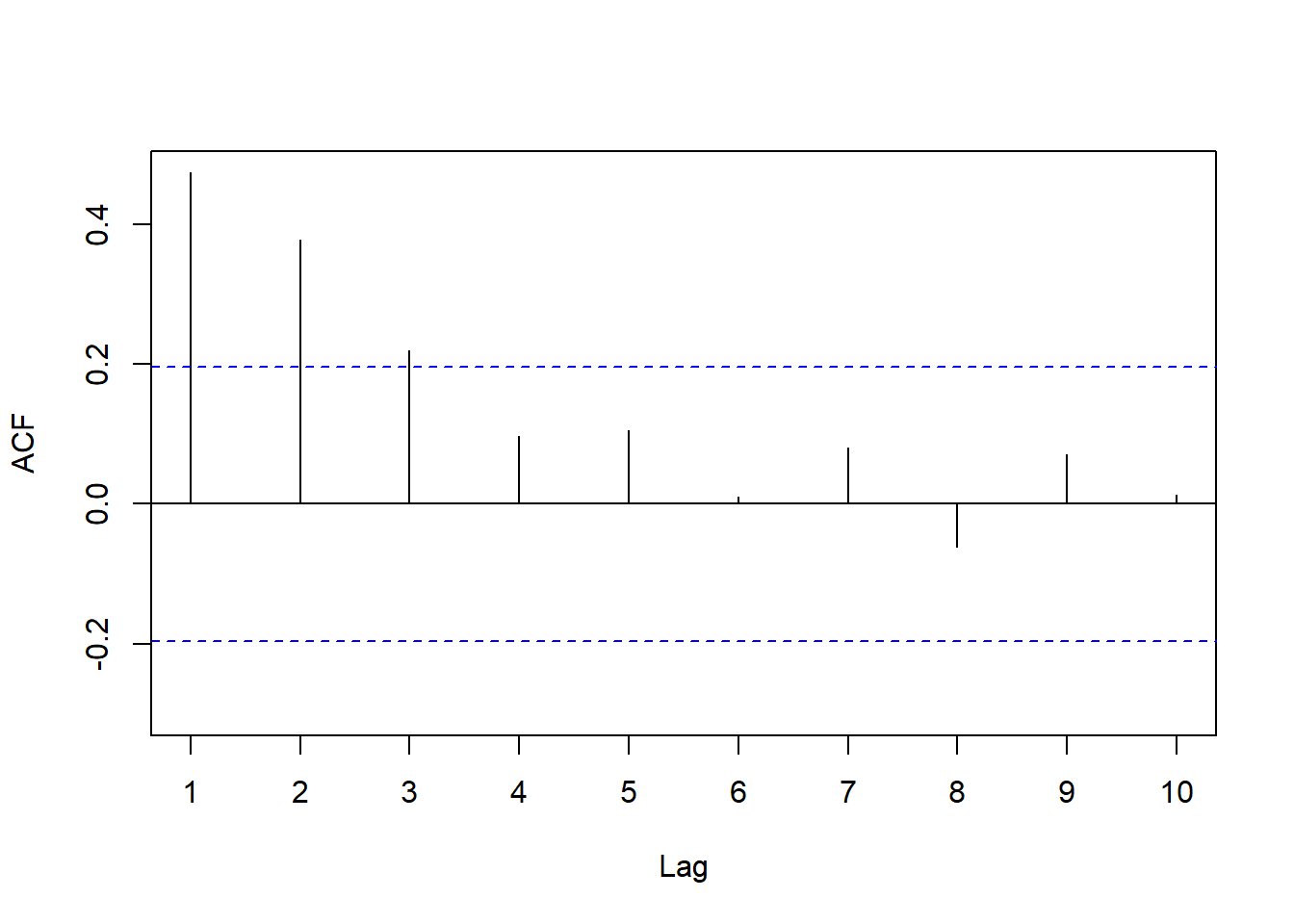

32.2.6 预测区间

设\(X\)取\(x_0\)，\(Y\)的预测值为\(\hat y_0 = \hat a + \hat b x_0\)。 置信水平为\(1-\alpha\)的预测区间为 \[\hat y_0 \pm \lambda \hat\sigma \sqrt{1 + \frac{1}{n} + \frac{(\bar x - x_0)^2}{\sum_i (x_i - \bar x)^2}} . \] 其含义是\(P(y_0 \in \text{预测区间}) = 1 - \alpha\)。 \(\lambda\)是标准正态分布双侧\(\alpha\)分位数qnorm(1 - alpha/2)。

用predict(lmres)得到\(\hat y_i, i=1,\dots,n\)的值， lmres表示回归结果变量。

用predict(lmres, interval="prediction") 同时得到预测的置信区间， 需要的话加入level=选项设定置信度。

回归的置信区间有两种， 上述的区间是“预测区间”(CLI)， 使得\(P(y_0 \in \text{预测区间}) = 1 - \alpha\); 另一种区间称为均值的置信区间(CLM)， 使得\(P(Ey_0 \in \text{均值置信区间}) = 1 - \alpha\)。

32.2.7 控制

如果需要把\(Y\)的值控制在\([y_l, y_u]\)范围内，问如何控制\(X\)的范围， 可以求解\(x_0\)的范围使上面的置信区间包含在\([y_l, y_u]\)内。

近似地可以解不等式 \[\begin{aligned} \hat a + \hat b x_0 - z_{1-\frac{\alpha}{2}} \hat \sigma \geq & y_l \\ \hat a + \hat b x_0 + z_{1-\frac{\alpha}{2}} \hat \sigma \leq & y_u \end{aligned}\] 其中\(z_{1-\frac{\alpha}{2}}\)为标准正态分布双侧\(\alpha\)分位数 （用qnorm(1-alpha/2)计算）。