《概率论》期末考试试题
1. 一本书共有1,000,000个印刷符号, 排版时每个符号被排错的概率为0.0001, 校对时每个排版错误被改正的概率为0.9, 求在校对后错误不多于15个的概率.
解:

注:可以认为每个字符最终被排错的概率为0.00001,而无须分两步考虑。
完毕
2. 某赌庄有资产100,000元. 另有一赌徒拥有无穷大的赌资, 试图使该赌庄破产. 他每次压注1000元, 每次赢钱的概率为0.49而输钱的概率为0.51. 问该赌徒能使赌庄破产的概率为多大?
解:可以先假设赌徒的赌本为M![]()
设 赌庄先输光的概率为p
赌徒先输光的概率为q 则p+q=1
该模型可以等价于在Z上的带吸收壁的随机游动:
X(0)=100![]()
增加1![]() 的概率为0.51 (赌庄赢钱) 减少1
的概率为0.51 (赌庄赢钱) 减少1![]() 的概率为0.49 (赌庄输钱)
的概率为0.49 (赌庄输钱)
吸收壁为: (100+M)![]() (赌徒输光) 0
(赌徒输光) 0![]() (赌庄输光)
(赌庄输光)
则  (参考《概率论引论》 P216 问题2)
(参考《概率论引论》 P216 问题2)
令M![]() 即可得本题所求的概率:赌庄破产的概率为
即可得本题所求的概率:赌庄破产的概率为![]()
完毕
3. 考虑[0,∞]上的Poisson过程, 参数为λ. T是与该Poisson过程独立的随机变量,服从参数为μ的指数分布.
以![]() 表示[0,T]中Poisson过程的增量, 求
表示[0,T]中Poisson过程的增量, 求![]() 的概率分布.
的概率分布.
解:

完毕
4. 设ξ1ξ2……ξn是独立同分布随机变量, 且三阶中心矩等于零, 四阶矩存在,求![]() 和
和![]() 的相关系数.
的相关系数.
解:
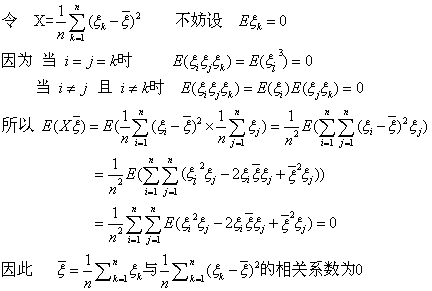
完毕
5. 设X是连续型随机变量,密度函数fX(x)= (1/2)exp(-|x|), -∞< x < ∞.
a. 证明特征函数φX(t) = 1/(1+t2).
b. 利用上述结果和逆转公式来证明![]()
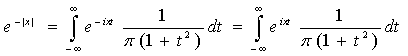
证明:
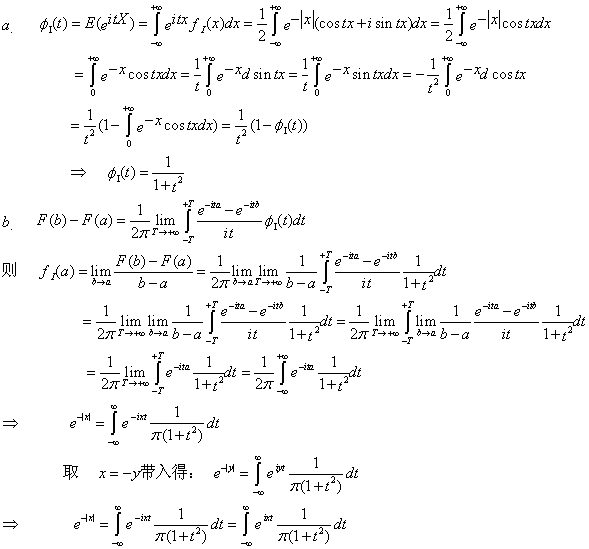
证毕
6. ![]() 设随机变量序列ξn依概率收敛于非零常数a, 而且ξn≠0. 证明1/ξn依概率收敛于1/a.
设随机变量序列ξn依概率收敛于非零常数a, 而且ξn≠0. 证明1/ξn依概率收敛于1/a.
证明:
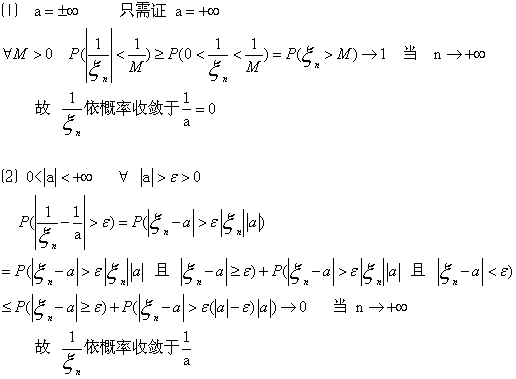
证毕
7. 假设X与Y是连续型随机变量.记Var[Y|X=x]为给定X=x的条件下Y的方差. 如果E[Y|X=x]=μ与X无关, 证明EY=μ而且VarY=![]() .
.
证明:
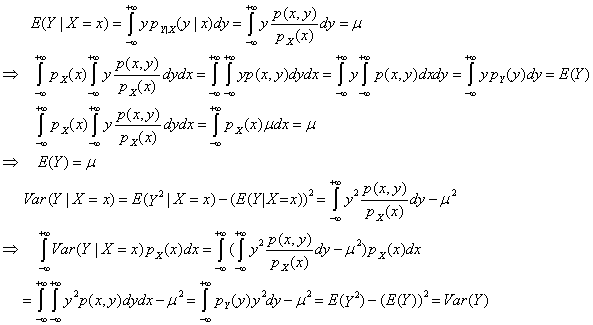
证毕
8. 设{ξn}为独立随机变量序列, 且ξn服从( -n, n)上的均匀分布, 证明对{ξn}中心极限定理成立.
证明:
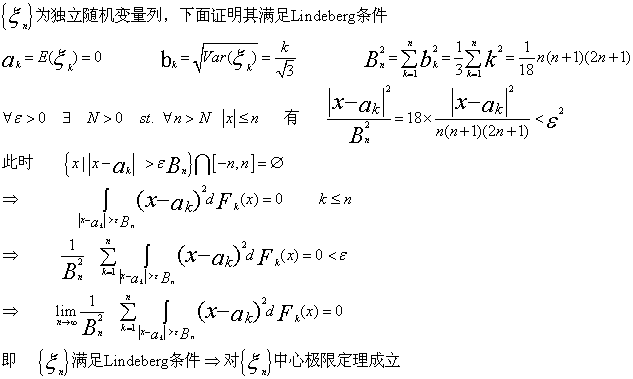 证毕
证毕
9. 设X,Y和Z的数学期望均为0, 方差均为1. 设X与Y的相关系数为ρ1, Y与Z的相关系数为ρ2, X与Z的相关系数为ρ3. 证明
![]()
![]()
![]() .
.
证明:
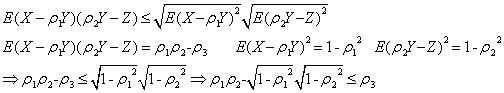
证毕
10. 用概率方法证明如下Weierstrass定理:对区间[0,1]上任何连续函数f(x), 必存在多项式序列{bn(x)}, 使在区间[0,1]上一致地有bn(x) → f(x).
证明:
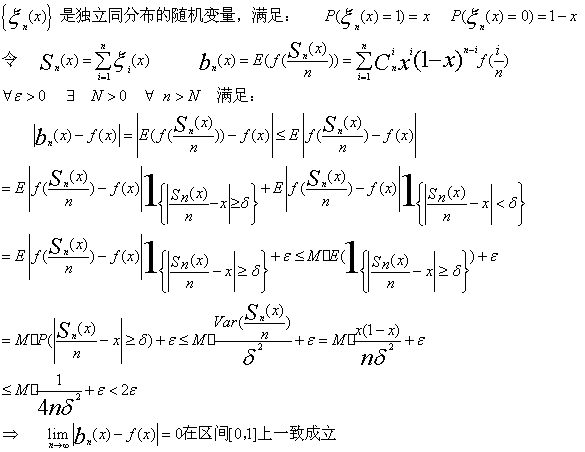
证毕
附: 常用正态分布函数值: Φ(1.28)= 0.9, Φ(2)= 0.977, Φ(2.33)= 0.99, Φ(2.58)= 0.995
Φ(1.64)= 0.95, Φ(1.96)= 0.975,