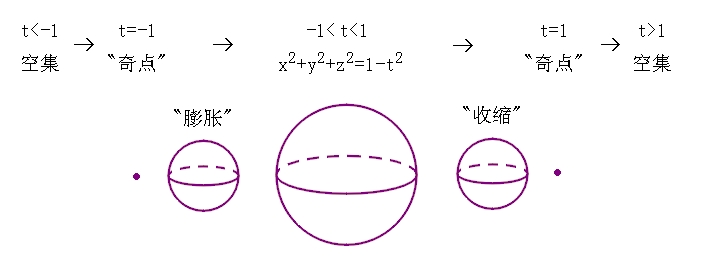
专题讨论: 三维球面
我们已经学过, 对闭曲面可以进行完整的分类, 其同胚类由可定向性及欧拉示性数所决定. 相比之下, 如何区分三维流形则是一个要复杂深奥得多的问题. (举个简单的例子: 闭三维流形的欧拉示性数永远是0!) 那些内容就是再讲一学期也讲不完.
虽然如此, 我们仍可以试图理解一个让许多初学者感到困惑的问题: 如何去 "想象一个弯曲的三维空间"? 下面, 我们就来 "想象" 一下最简单的三维流形的例子S3, 用一系列不同的方式从侧面认识它, 从而达到了解熟悉的目的.
定义 E4中的子集{(x,y,z,t)|x2+y2+z2+t2=1}称为三维单位球面, 记作S3.
想象E4的最通俗做法是把它看成 "时空", 并把最后一维坐标t看成时间参数. S3上对应于每个时刻t的 "截面" 是E3中的 (可能退化的) 二维球面{(x,y,z)|x2+y2+z2=1-t2}. 如下图所示.
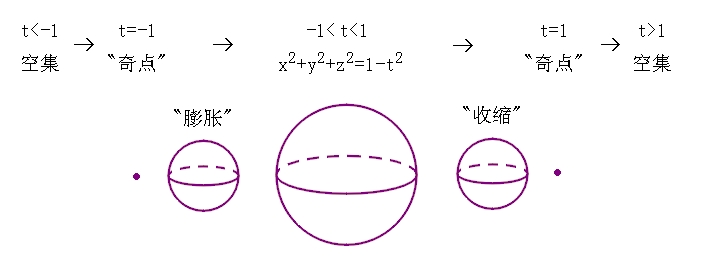
另一种办法是想象一下进入这样的世界会看到什么. 当然, 我们不会考虑相对论和量子力学等复杂的物理问题, 并且我们需要假定在S3中光线是按Fermat法则 (不是数论里的Fermat大定理呦:) ) 沿局部最短路径传播的. 注意S3是E4的子集, 而这里所说的S3中弧线的长度也是指它作为E4中的弧线的长度. 因此局部最短路径就是S3中半径为1的大园上的弧, 正如S2上两点之间的最短连线在穿过它们的大园上一样.
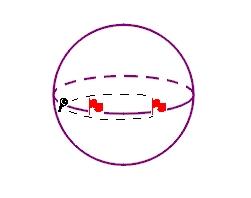
在这样的假设下, 在观察者附近非常小的范围内所看到的还不至于与在E3中看到的物体有太大的区别 (这也正是 "流形" 这个概念所要反映的特征). 但是随着观察范围逐渐扩大, 看见的景象就会变化. 一个物体向远离观测者的方向运动, 距离 (最短路径的长度) 达到并超过π/2时, 观测者眼中看到的它的尺寸会达到一个最小值然后变大! 最后, 在S3中也可以象在S2中或在地球表面上那样作环球旅行, 旅行一圈回来所走过的路径总长是2π. 你甚至可以让 "视线" 去作环球旅行, 只要能够看清物体的距离 (能见度) 达到2π的话. 不过包老师可不喜欢那种感觉, 因为无论向哪个方向看都会看见一个黑乎乎的背景填满整个视野, 而这个背景恰恰是自己的后脑勺 (颠倒的影像).
这些直观的描述虽然有趣, 但是对于研究S3的拓扑性质来说都太过复杂. 比较起来下述观察就简洁多了.
命题1 S3是E3的一点紧化. 通俗地说, 就是S3等于E3加上无穷远点.
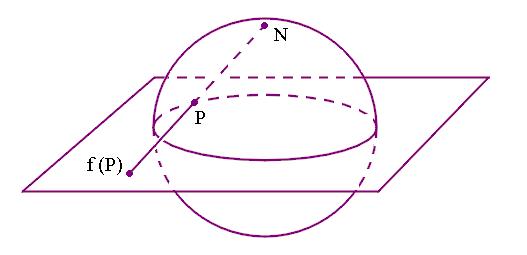
事实上, 球极投影h(x,y,z,t)=(1-t)-1(x,y,z)就是S3\{N}到E3的同胚, 这里N=(0,0,0,1). 注意二维球面到平面球极投影如下图所示. 而上面写的式子正是该映射的三维推广.
命题2 S3中t>0的部分M+及t<0的部分M-均同胚于E3中的开实心球, 而t=0的部分M0同胚于球面S2. 注意M+和M-并上M0之后都是S3中的闭子集.
借助于球极投影h, 也可以在E3中描述上述分解. 事实上h(M0)就是单位球面S2, h(M+\{N})是E3中在S2以外的部分 (同胚于实心球去掉一点), 而h(M-)是E3中S2所界定的实心球. 更一般地, 可以证明下述结论.
命题3 任取球面S2上的一个自同胚f, 用f将两个三维闭实心球沿表面 (都是球面) 粘合, 得到的空间一定同胚于S3.
我们也可以用两个复坐标(z1,z2)来表示三维球面.
命题4 S3={(z1,z2)| |z1|2+|z2|2=1}.
命题5 S3中|z1|>|z2|的部分T+及 |z1|<|z2|的部分T-均同胚于E3中去掉表面的实心环, 而|z1|=|z2|的部分T0同胚于环面. 注意T+及T-并上T0后都是E3中的闭子集.
我们还是借助球极投影h到E3中来看清T+,T-及T0的形状. 将球极投影逆映射的公式带入T0的定义可知h(T0)={(x,y,z)|(x2+y2+z2-3)2=8(1-z2)}, 这正是xz平面上的圆周C={(x,0,z)|(x-21/2)2+z2=1}绕z轴旋转所得的旋转环面. h(T+)是该环面在E3中界定的实心环T, 而h(T-\{N})则对应于其余的部分. T的形状如下图所示. 其中红线所标出的正是圆周C所在的位置.
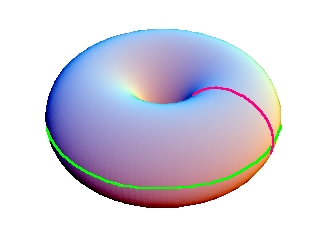
我们还可以进一步把T-也同胚到T的位置. 取g为T-到T+的同胚, g(z1,z2)=(z2,z1). 则h与g的复合f就是T-到T的同胚. 需要注意的是原来在T-的表面有一条曲线通过h与上图中的红线所对应 (其实就是h-1(C)), 但是现在它被f对应到了上图中T表面的绿线.
也可以用粘合的语言来叙述上述事实.
命题6 取两个实心环T的拷贝, 用一个它们两者的表面 (都是环面) 之间的同胚将两者粘合, 并确保其中一个的红色纬圆粘合到另一个的绿色经圆 (参见上图), 则得到的一定是S3.
这种把复杂流形表示成一些简单的 "小块" 沿表面粘合的办法, 是除了写坐标表达式以外, 想象复杂三维流形的另一种基本途径. 需要注意的是, 在一般情况下粘合方式的选取会极大地影响最后得到的空间的同胚类.
例 将两个实心环T的拷贝, 用T表面的恒同映射粘合起来, 这相当于要求其中一个的红色纬圆要粘合到另一个的红色纬圆. 注意到每个实心环同胚于D2×S1, 上述粘法等价于将两个圆盘D2先沿边界粘合然后再与S1作乘积, 其结果与S2×S1同胚!
通过复坐标, 我们还可以定义S3上的Hopf流: Ht(z1,z2)=(e2πitz1,e2πitz2). 当时间t变化时, S3上的每个点(z1,z2)都在沿着S3作匀速运动, 并保持相互之间的距离不变. 不仅如此, 没有一个点是静止的 (比较一下, 当你旋转一个篮球时球面上就总有两点是静止的, 它们之间的连线就是转轴). 在学了同伦的概念以后, 我们还可以对Hopf流作更进一步的讨论.
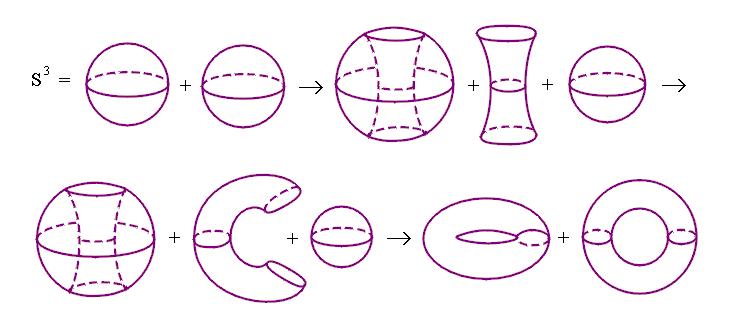
最后, 我们也可以不用复坐标而用贴空间的语言直接来论证两个实心环沿表面粘合可以得到S3.
版权所有(C): 本网页内容由包志强制作并维护, 保留所有权利.